HTML
-
Processes mediated by Flavor Changing Neutral Currents (FCNCs) are very rare in the Standard Model (SM) due to the Glashow-Iliopoulos-Maiani (GIM) mechanism [1]. However, because of the extended flavor structures existing in many New Physics (NP) models, the two-body FCNC decays t
$ \to $ qX (q = u/c and X = g/γZ/H) can be greatly enhanced: for example, in the Minimal Supersymmetric Standard Model (MSSM) with branching ratio Br(t$ \to $ cH) ~ 10-5 [2], in R-parity violating Supersymmetry (SUSY) with branching ratio Br(t$ \to $ cH) ~ 10-6 [3], in 2-Higgs-Doublet Models (2HDMs) with branching ratio Br(t$ \to $ cH) ~ 10-5-10-3 [4], in the little Higgs model with T-parity and the warped extra dimensions both with branching ratio Br(t$ \to $ cH) ~ 10-5 [5, 6] and so on. Thus any experimental signatures of such FCNC processes will serve as a clear signal for NP Beyond the SM (BSM) [7]. Up to now, top-Higgs FCNC interactions have been studied widely via anomalous top decays or anomalous production processes of single top quark [8-16].Currently, the ATLAS and CMS collaborations have carried out searches [17-21] for tqH interactions with 7, 8 and 13 TeV data from the LHC. For example, using 13 TeV data, the ATLAS and the CMS experiments have studied the tqH FCNC processes in top quark pair events with H
$ \to $ γγ for ATLAS and$H \to b\bar b$ for CMS. The resulting observed (expected) limits for Br(t$ \to $ qH) at 95% Confidence Level (CL) have been found to be [19, 20]:$ \begin{eqnarray}Br(t\to Hu)\le \left\{\begin{array}{ll}2.4\ (1.7)\times {10}^{-3}&{\rm{ATLAS}}\\ 4.7\ (4.3)\times {10}^{-3}&{\rm{CMS}}\end{array}\right.\\ Br(t\to Hc)\le \left\{\begin{array}{ll}2.2\ (1.6)\times {10}^{-3}&{\rm{ATLAS}}\\ 4.7\ (4.4)\times {10}^{-3}&{\rm{CMS}}\end{array}\right.\end{eqnarray} $
(1) Very recently, a search for production of top pairs in which one top quark decays via t
$ \to $ qH is reported by the ATLAS Collaboration [21], with the subsequent Higgs boson decay to final states with at least one electron or muon. The upper limits on the branching fractions Br(t$ \to $ Hc) < 0.16% and Br(t$ \to $ Hu) < 0.19% at 95% CL are obtained (with expected limits of 0.15% in both cases). Apart from direct collider measurements, the upper limits of Br(t$ \to $ qH) < 5 × 10-3 and Br(t$ \to $ qH) < 0.21% can be obtained by bounding the tqH vertex from the observed${D^0} - {{\bar D}^0}$ mixing [22] and$Z\to c\bar{c}$ [23], respectively.The upcoming project of the HL-LHC is expected to reach 3 ab-1. Preliminary sensitivity studies for the HL-LHC suggest the upper bound on Br(t
$ \to $ qH) to become about 1.5 × 10-4 at 95% CL by the ATLAS Collaboration [24]. Further, many phenomenological studies within model-independent methods have been performed from different channels [25-33]. In this work, we study the prospects of probing the anomalous tHq couplings by considering the processes of tH associated production and$t\bar{t}$ production at the HL-LHC. We analyze two kinds of final states through leptonic top quark decays and H$ \to $ WW*, one with Same Sign 2-Lepton (SS2L) and the other with 3-Lepton (3L) topology, where the Higgs boson decays into a semi-leptonic (H$ \to $ WW*$ \to $ $\ell$ +νjj) or fully leptonic ($H\to W{W}^{\ast }\to {\ell }^{+}\nu {\ell }^{-}\bar{\nu }$ ) mode. The advantage of these channels is that their final states including the SS2L or 3L topologies can be used to significantly suppress QCD backgrounds [34], which have not been fully studied in previous literature.The organization of this paper is as follows. In Sec. Ⅱ, we discuss two kinds of final states for the processes of tH associated production with the decay chain t
$ \to $ W+b$ \to $ $\ell$ +νb and H$ \to $ WW* as well as$t\bar{t}$ production with the decay chain t$ \to $ $\ell$ +ν$\ell$ b and$\bar{t}\to H(\to W{W}^{\ast })\bar{q}$ . Then we discuss the HL-LHC sensitivity to the anomalous tHq couplings. We summarize in Sec. Ⅲ.
-
The general Lagrangian for FCNC top interactions with the Higgs boson can be written as
$ \begin{eqnarray} {\mathcal L} ={\kappa }_{tuH}\bar{t}Hu+{\kappa }_{tcH}\bar{t}Hc+{\rm{h}}.{\rm{c}}.,\end{eqnarray} $
(2) where the FCNC coupling parameters, κtuH and κtcH, are real and symmetric since we do not consider here the CP violating effects.
We perform systematic Monte Carlo (MC) simulations and study the sensitivity to the anomalous tHq couplings through the associated tH and
$t\bar{t}\to tH\bar{q}$ processes at HL-LHC. We first extract the relevant Feynman rules via the FeynRules package [35] and generate the events with MadGraph5-aMC@NLO [36]. The signal and backgrounds samples are simulated at parton level with the NN23LO1 Parton Distribution Function (PDF) set [37] and then passed through PYTHIA6.4 [38] and DELPHES 3 [39] for parton shower and detector simulations, with the MLM matching scheme [40] adopted. Finally, event analysis is performed by using MadAnalysis5 [41]. -
For the final states including the SS2L topology, the signals are generated through the following processes,
$ \begin{eqnarray}pp\to t(\to {W}^{+}b\to {\ell }^{+}\nu b)H(\to W{W}^{\ast }\to {\ell }^{+}\nu jj),\end{eqnarray} $
(3) $ \begin{eqnarray}pp\to t(\to {W}^{+}b\to {\ell }^{+}\nu b)\bar{t}(\to Hq\to W{W}^{\ast }q\to {\ell }^{+}\nu jjq),\ \end{eqnarray} $
(4) where
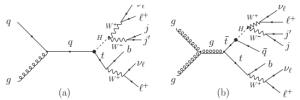
$\ell$ =e, µ. The representative Feynman diagrams are shown in Fig. 1.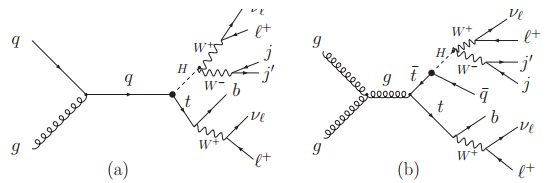
Figure 1. Representative Feynman diagrams for the associated tH process (left) and the FCNC decay of the top pair production process (right). Here q = u, c.
For this channel, the typical signal is exactly two same-sign leptons plus at least three jets, with at least one jet identified as b-jet, and missing transverse energy. The main backgrounds are
$t\bar{t}V$ (V = W, Z), W+W+jj and W+Zjj. The$t\bar{t}$ process, which has large cross section, may also contribute to background if a same-sign lepton pair comes from a B-hadron semi-leptonic decay in the b-jet. We do not consider other backgrounds from$t\bar{t}H$ ,$t\bar{t}t\bar{t}$ , tri-boson events and tHj. They are neglected because the cross sections are all negligible after applying the selection cuts.The cross sections of dominant backgrounds at Leading Order (LO) are adjusted to Next-to-LO (NLO) by means of K-factors, which are 1.04 for W+W+jj jets [42], 1.24 for
$t\bar{t}W$ [43] and 1.39 for [44]. The dominant background is normalized to the NNLO QCD cross section of 953.6 pb [45]. For the tH production cross section, the K-factor is taken as 1.5 at the 14 TeV LHC [12].The decay chain H
$ \to $ WW*$ \to $ $\ell$ νjj may result in soft leptons and light jets, especially when they are coming from an off-shell W boson. To analyze the signal sensitivity, we thus employ the following basic cuts to select the events:Basic cuts: pT(
$\ell$ ) > 10 GeV, pT(j, b) > 15 GeV, |η$\ell$ , j, b| < 2.5, where$\ell$ = e, µ.In order to choose appropriate kinematic cuts, we plot in Fig. 2 examples of kinematic distributions for the signal and backgrounds. Based on these distributions, we impose a further set of cuts.
1) Cut-1: Exactly two same-sign leptons (N(
$\ell$ +) = 2) with pT($\ell$ 1) > 20 GeV and pT($\ell$ 2) > 10 GeV ($\ell$ 1 and$\ell$ 2 denote the higher and lower pT lepton, respectively) plus exactly one b-tagged jet (N(b) = 1). To remove contamination from hadron decay chains including$\ell$ +$\ell$ - and Z boson, we choose the invariant mass larger than 12 GeV and |M$\ell$ $\ell$ -mZ| > 10 GeV.2) Cut-2: At least two jets in the events are required to be successfully reconstructed, i.e., N(j)≥2. Among those reconstructed jets, there is at least one pair of jets which could come from a W boson either on-shell or off-shell. Thus the invariant mass of the W boson is required to be Mjj < 90 GeV.
3) Cut-3: The invariant mass of M
$\ell$ 2jj is required to be smaller than 120 GeV.4) Cut-4: Since the first lepton,
$\ell$ 1, is assumed to originate from the leptonically decaying top quark, the invariant mass of the b-jet and the leading lepton should be Mb$\ell$ 1<140 GeV.5) Cut-5: The scalar sum of transverse momenta, HT, is to be smaller than 250 GeV.
The effects of the cuts on the signal and background processes are illustrated in Table 1 for the SS2L channel, where the anomalous coupling parameters are taken as κtuH = 0.1 or κtcH = 0.1, while fixing the other to zero. From Table 1 we can see that, after all these cuts, the
$t\bar{t}$ backgrounds for the SS2L channel with fake leptons from heavy-flavor jets or charge mis-identifications can be significant.cuts signal backgrounds ug cg $t\bar{t}\to tHq$ $t\bar{t}V$ WWjj WZjj $t\bar{t}$ basic cuts 3.12 0.34 3.77 6.73 6.42 20.9 61004 Cut 1 0.48 0.056 0.69 0.85 0.21 0.25 6.52 Cut 2 0.225 0.027 0.34 0.27 0.04 0.046 2.54 Cut 3 0.18 0.022 0.28 0.092 0.016 0.011 1.7 Cut 4 0.15 0.019 0.24 0.058 0.009 0.0063 1.36 Cut 5 0.14 0.017 0.21 0.048 0.007 0.005 1.16 Table 1. The cut flow of the cross sections (in fb) for the signal and SM backgrounds for the SS2L channel. The coupling parameters are taken as κtuH = 0.1 or κtcH = 0.1, while fixing the other to zero.
Obviously, the non-prompt backgrounds may also be significant, where non-prompt leptons are from heavy-flavor decays, mis-identified hadrons, muons from light-meson decays or electrons from un-identified conversions of photons into jets. Recently, the CMS collaboration searched for SS2L signatures [46] and found that the overall non-prompt backgrounds are about 1.5 times the
$t\bar{t}W$ background after all cuts. These non-prompt backgrounds are not properly modeled in our MC simulations. Therefore, for simplicity, we add a non-prompt background that is 1.5 times$t\bar{t}W$ [46] after selection cuts to the overall background. Accounting for the theoretical and experimental systematic uncertainties on the background predictions would certainly improve the reliability of the results, yet they can only be neglected in our simulation. -
Next, we consider the final states including 3L via the following processes:
$ \begin{eqnarray}pp\to t(\to {W}^{+}b\to {\ell }^{+}\nu b)h(\to W{W}^{\ast }\to {\ell }^{+}\nu {\ell }^{-}\bar{\nu }),\end{eqnarray} $
(5) $ \begin{eqnarray}pp\to t(\to {W}^{+}b\to {\ell }^{+}\nu b)\bar{t}(\to Hq\to W{W}^{\ast }q\to {\ell }^{+}\nu {\ell }^{-}\bar{\nu }q),\end{eqnarray} $
(6) where
$\ell$ = e, µ.The dominant SM backgrounds are
$t\bar{t}V$ (V = W, Z),$t\bar{t}H$ , WZ+ jets and$t\bar{t}$ . The multi-jet backgrounds (where jets can fake electrons) are not included since they are negligible in multi-lepton analyses [47].The pre-selection cuts are taken as follows: there must exist exactly three isolated leptons (
$\ell$ = e, µ) and exactly one b-tagged jet with pT($\ell$ 1) > 20 GeV, pT($\ell$ 2, 3) > 10 GeV, pT(j, b) > 20 GeV,${\rlap{/}{E}}_{{\rm{T}}}\gt 100$ GeV and |η$\ell$ , j, b| < 2.5. These cuts can strongly reduce the$t\bar{t}$ background and its di-boson components.In Fig. 3, we show the invariant mass distribution of M
$\ell$ 2$\ell$ 3 and Mb$\ell$ 1 from the signal and backgrounds at the 14 TeV LHC. To remove contamination from hadron decay chains including$\ell$ +$\ell$ - pairs and resonant Z bosons, we choose the invariant mass M$\ell$ 2$\ell$ 3 cuts$ \begin{eqnarray*}12{\rm{GeV}}\lt M({\ell }_{2}{\ell }_{3})\lt 55\ {\rm{GeV}}.\end{eqnarray*} $
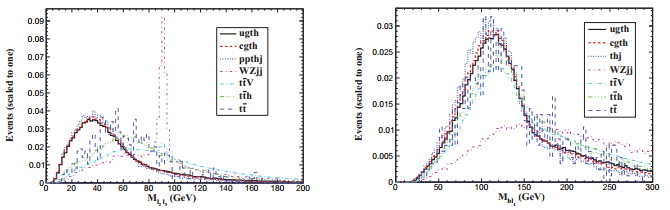
Figure 3. (color online) Normalized invariant mass distributions of M
$\ell$ 2$\ell$ 3 (left) and Mb$\ell$ 1 (right).Similarly, the invariant mass of the b-jet and the leading lepton, Mb
$\ell$ 1, should be smaller than 140 GeV. The effects of the cuts on the signal and background processes are illustrated in Table 2 for the 3L channel. One can see that significant backgrounds also come from the top pair production process with fake leptons or charge mis-identifications.cuts signals backgrounds ug cg $t\bar{t}\to tHq$ $t\bar{t}$ $t\bar{t}V$ WZjj $t\bar{t}h$ basic cuts 1.39 0.17 2.05 21843 1.85 46.2 0.025 after cuts 0.14 0.018 0.106 0.23 0.024 0.021 1.7 × 10-5 Table 2. The cut flow of the cross sections (in fb) for the signal and background processes for the 3L channel.
Using the Poisson formula [48],
$ \begin{eqnarray*}SS=\sqrt{2{ {\mathcal L} }_{{\rm{int}}}[(S+B){\rm{ln}}(1+S/B)-S]}\end{eqnarray*} $
we estimate the Signal Significance (SS) with fixed coupling parameters κtqH and a given integrated luminosity
${ {\mathcal L} }_{{\rm{int}}}$ . In Figs. 4 and 5, we plot the contours of SS = 3 and SS = 5, respectively, for two channels in the plane of${ {\mathcal L} }_{{\rm{int}}}-{\kappa }_{tqH}$ . It is clear that, for an integrated luminosity of 3000 fb-1, the FCNC couplings κtuH (κtcH) can be probed to 0.045 (0.052) and 0.035 (0.049) at 3σ statistical sensitivity for the SS2L and 3L channels, respectively. After neglecting the masses of light quarks, the branching ratio of t$ \to $ qH is approximately given by [13, 49]$ \begin{eqnarray}\begin{array}{ll}Br(t\to qH)&=\displaystyle \frac{{\kappa }_{tqH}^{2}}{\sqrt{2}{m}_{t}^{2}{G}_{{\rm{F}}}}\displaystyle \frac{{(1-{x}_{h}^{2})}^{2}}{{(1-{x}_{W}^{2})}^{2}(1+2{x}_{W}^{2})}{\lambda }_{{\rm{QCD}}}\\ &\simeq 0.58{\kappa }_{tqH}^{2},\end{array}\end{eqnarray} $
(7) 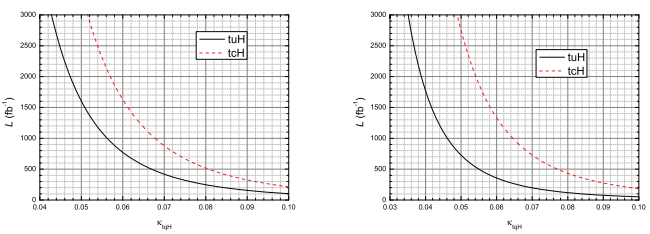
Figure 4. (color online) The 3σ contour plots for the signal in the
${ {\mathcal L} }_{{\rm{int}}}-{\kappa }_{tqH}$ plane for the SS2L (left) and 3L (right) channels at the 14 TeV LHC.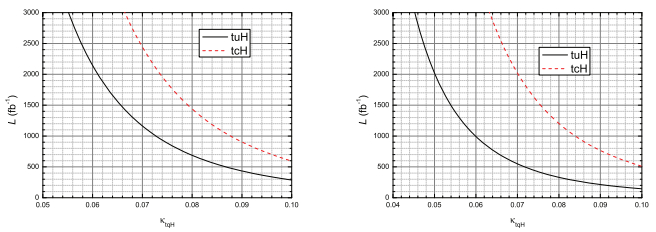
Figure 5. (color online) The 5σ contour plots for the signal in the
${ {\mathcal L} }_{{\rm{int}}}-{\kappa }_{tqH}$ plane for the SS2L (left) and 3L (right) channels at the 14 TeV LHC.in terms of the Fermi constant GF and with xi = mi/mt (i = W, h). In our numerical calculation, the relevant SM input parameters are taken as [50]:
$ \begin{eqnarray}{m}_{H}=125\ {\rm{GeV}},\,\,\,{m}_{t}=173.1\ {\rm{GeV}},\,\,\,{m}_{W}=80.379\ {\rm{GeV}},\end{eqnarray} $
(8) $ \begin{eqnarray}\begin{array}{l} {m}_{Z}=91.1876\ {\rm{GeV}},\;\;\;{\alpha }_{s}({m}_{Z})=0.1185,\\ {G}_{{\rm{F}}}=1.166370\times {10}^{-5}{{\rm{GeV}}}^{-2}.\end{array}\end{eqnarray} $
(9) Using Eq. (7), the limits can be translated in terms of constraints on the branching fractions of rare top decays. The 3σ CL upper limits on Br(t
$ \to $ qH) are Br(t$ \to $ uH) = 1.17 × 10-3 and Br(t$ \to $ cH) = 1.56 × 10-3 for the SS2L channel, and Br(t$ \to $ uH) = 7.1 × 10-4 and Br(t$ \to $ cH) = 1.39 × 10-3 for the 3L channel. The projected limits from different channels are summarized in Table 3. We can see from the table that our results are comparable with the sensitivity limits at the HL-LHC of Br(t$ \to $ uH) < 0.036% via the H$ \to $ γγ channel [29], Br(t$ \to $ uH) < 0.05% via the multi-lepton channel and Br(t$ \to $ uH) < 0.02% via the di-photon channel [51].channels data set limits tH $ \to $ $\ell$ νbτ+τ-LHC, 100 fb-1 @ 13 TeV, 95% CL Br (t $ \to $ uH) < 0.15 % [13]tH $ \to $ $\ell$ νb$\ell$ +$\ell$ -XLHC, 100 fb-1 @ 13 TeV, 95% CL Br (t $ \to $ uH) < 0.22 % [13]$t\bar{t}\to Wb+Hc\to jjb+\tau \tau c$ LHC, 100 fb-1 @ 13 TeV, 95% CL Br (t $ \to $ cH) < 0.25 % [14]$tH\to jjbb\bar{b}$ LHC, 100 fb-1 @ 13 TeV, 95% CL Br (t $ \to $ uH) < 0.36 % [13]Wt $ \to $ WHq$ \to $ $\ell$ νbγγqLHC, 3000 fb-1 @ 14 TeV, 3σ Br (t $ \to $ qH) < 0.24 % [28]tH $ \to $ $\ell$ νbγγqLHC, 3000 fb-1 @ 14 TeV, 3σ Br (t $ \to $ uH) < 0.036 % [29]$t\bar{t}\to WbqH\to \ell \nu b\gamma \gamma q$ LHC, 3000 fb-1 @ 14 TeV, 3σ Br (t $ \to $ uH) < 0.23 % [30]${e}^{-}p\to {\nu }_{e}\bar{t}\to {\nu }_{e}H(\to b\bar{b})\bar{q}$ LHeC, 200 fb-1 @ 150 GeV ⊕ 7 TeV, 95% CL Br (t $ \to $ qH) < 0.013 % [31]$t\bar{t}\to tqH\to \ell \nu bb\bar{b}q$ ILC, 3000 fb-1 @ 500 GeV, 95% CL Br (t $ \to $ qH) < 0.112 % [32]$t\bar{t}\to tqH\to \ell \nu bb\bar{b}q$ ILC (unpolarized), 500 fb-1 @ 500 GeV, 3σ Br (t $ \to $ qH) < 0.119 % [33]$t\bar{t}\to tqH\to \ell \nu bb\bar{b}q$ ILC (polarized), 500 fb-1 @ 500 GeV, 3σ Br (t $ \to $ qH) < 0.088 % [33]$t\bar{t}\to Wb+Hq\to \ell \nu b+\gamma \gamma q$ LHC, 3000 fb-1 @ 14 TeV, 95% CL Br (t $ \to $ qH) < 0.02 % [51]$t\bar{t}\to Wb+hq\to \ell \nu b+\ell \ell qX$ LHC, 3000 fb-1 @ 14 TeV, 95% CL Br (t $ \to $ qH) < 0.05 % [51]This work for tde SS2L channel LHC, 3000 fb-1 @ 14 TeV, 3σ Br (t $ \to $ uH) < 0.117 %,Br (t $ \to $ cH) < 0.156 %This work for tde 3L channel LHC, 3000 fb-1 @ 14 TeV, 3σ Br (t $ \to $ uH) < 0.071 %,Br (t $ \to $ cH) < 0.139 %Table 3. The projected limits on Br(t
$ \to $ qH) from different channels. The last two lines of the table are the results of this work.
2.1. 2.1. Analysis of the SS2L channel
2.2. Analysis of the 3L channel
-
The discovery of the 125 GeV Higgs boson opens the door to probe NP processes that involve Higgs boson associated production or decay. In this paper, we have investigated the signal of tH associated production via FCNC tqH couplings and
$t\bar{t}$ production with$\bar{t}\to H\bar{q}$ at the 14 TeV LHC. We focused on the final states including SS2L and 3L signals from the decay modes t$ \to $ b$\ell$ +ν$\ell$ , H$ \to $ WW*$ \to $ $\ell$ +νjj or$H\to W{W}^{\ast }\to {\ell }^{+}\nu {\ell }^{-}\bar{\nu }$ . We have then shown that, at 3σ level, the branching ratios Br(t$ \to $ uH) and Br(t$ \to $ cH) are, respectively, about Br(t$ \to $ uH) ≤ 1.17 × 10-3 and Br(t$ \to $ cH) ≤ 1.56 × 10-3 for the SS2L channel, and Br(t$ \to $ uH) ≤ 7.1 × 10-4 and Br(t$ \to $ cH) ≤ 1.39 × 10-3 for the 3L channel at the future HL-LHC.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: