-
The pion-nucleon interaction is an interesting topic and has attracted considerable attention of the nuclear physics community in the past decades. There are two very close excited states of the nucleon in the
$ S_{11} $ channel,$ N(1535) $ and$ N(1650) $ , which are difficult to describe within the framework of the constituent quark model [1]. However, in the unitary coupled-channel approximation of the Bethe-Salpeter equation, most of the excited states of the nucleon are treated as resonance states of the pseudoscalar meson and the baryon in the$ SU(3) $ flavor space, as are these two particles. In Ref. [1], it is pointed out that the hidden strange channels of$ K\Lambda $ and$ K \Sigma $ might play an important role in the dynamical generation of the$ N(1535) $ particle.The
$ N(1535) $ particle, generated dynamically in the unitary coupled-channel approximation with a three-body$ N\pi\pi $ final state, was considered in [2]. However, the inclusion of$ N\pi\pi $ as a final state in the calculation is complex, especially as there are six arbitrary constants in the real part of the three-body$ N\pi\pi $ loop function, and thus it must be treated as a free function consistent with experimental data. This approach was studied again by including the$ \rho N $ and$ \pi \Delta $ channels in a non-relativistic approximation, besides the pseudoscalar meson-baryon octet channels [3]. In fact, the elastic scattering process$ \rho N\rightarrow \rho N $ gives the main contribution to the dynamical generation of the$ N(1650) $ resonance, as was shown in Ref. [4]. In the processes$ \rho N \rightarrow \pi N $ and$ \rho N \rightarrow \pi \Delta $ , the Kroll-Ruderman term supplies a constant potential and plays a dominant role, while the$ \pi $ -exchange potential is trivial and proportional to the square of the three-momentum of the final state in the center-of-mass frame. Moreover, the structure of$ N(1535) $ and$ N(1650) $ particles was also studied in the unitary coupled-channel approximation in [5, 6], where a loop function of the intermediate pseudoscalar meson and the baryon in the on-shell approximation is taken into account when the Bethe-Salpeter equation is solved.In Ref. [7], the
$ N(1535) $ and$ N(1650) $ resonance states were studied in the unitary coupled-channel approximation with the Lagrangian of the pseudoscalar meson and the baryon octet up to the next-to-leading-order. By fitting the$ S_{11} $ partial wave amplitude with the experimental data up to the energy$ \sqrt{s} = 1.56 $ GeV, the resonance state corresponding to the$ N(1535) $ particle is generated dynamically. In addition, it is amazing that the$ N(1650) $ resonance state can be produced at the same time at higher energies.The properties of the
$ N(1535) $ particle have also been studied by solving the relativistic Lippmann-Schwinger equation, where the corresponding Hamiltonian is divided into two parts, a non-interacting part and an interacting part, and the couplings and the bare mass of the nucleon are determined by fitting the experimental data. This method is called the Hamiltonian effective field theory by the authors [8]. Recently, the different partial wave phase shifts were analyzed by calculating the K-matrix of the pion-nucleon interaction [9]. It is interesting that the internal wave functions of the$ \Delta(1232) $ ,$ N(1535) $ and$ N(1650) $ resonance states were investigated, and it was announced that the$ \pi N $ ,$ \eta N $ ,$ K \Lambda $ and$ K \Sigma $ components are negligible in these resonance states [10]. It is apparent that the conclusion made in Ref. [10] is inconsistent with the previous results due to the chiral unitary models.In this work, the interaction of the pseudoscalar meson and the baryon octet is studied in the unitary coupled-channel approximation, and the contribution of the
$ s- $ and$ u- $ channel potentials in the S-wave approximation is taken into account besides the Weinberg-Tomozawa contact term. Furthermore, a revised loop function of the Bethe-Salpeter equation is used in the calculation [11], where the relativistic correction is included.By adjusting the subtraction constants for different intermediate particles of the loop function in the sector of isospin
$ I = 1/2 $ and strangeness$ S = 0 $ , a pole at$ 1518-{\rm i}46 $ MeV in the complex energy plane is detected, which might correspond to the$ N(1535) $ particle of the PDG review [12].This article is organized as follows. In Section 2, the potential of the interaction between the pseudoscalar meson and the baryon octet is constructed, where the Weinberg-Tomozawa contact term, and the
$ s- $ channel and$ u- $ channel interactions are all taken into account in the S-wave approximation. In Section 3, the fundamental formula for solving the Bethe-Salpeter equation in the unitary coupled-channel approximation is presented. The cases of isospin$ I = 1/2 $ and$ I = 3/2 $ are discussed in Section 4 and Section 5, respectively. Finally, the summary is given in Section 6. -
The effective Lagrangian of the pseudoscalar meson and baryon octet interaction can be written as
$ {L} = \langle \bar{B}({\rm i}\gamma_\mu D^\mu - M) B \rangle+\frac{D/F}{2} \langle \bar{B} \gamma_\mu \gamma_5 [u^\mu, B]_{\pm} \rangle. $

(1) In the above equation, the symbol
$ \langle...\rangle $ denotes the trace of matrices in the$ SU(3) $ flavor space, and$ D^\mu B = $ $ \partial^\mu B + \displaystyle\frac{1}{2} \left[ [u^\dagger, \partial^\mu u], B \right] $ with$ u^2 = U = \exp \left( {\rm i}\displaystyle\frac{\Phi}{f_0} \right) $ and$u^\mu = $ $ {\rm i}u^\dagger \partial^\mu u - {\rm i} u \partial^\mu u^\dagger $ , where D=0.80, F=0.46 and$ f_0 $ =92.40 MeV is the meson decay constant in the chiral limit.The matrices of the pseudoscalar meson and the baryon octet are given as follows
$ \begin{align} \Phi = {}&\sqrt{2} \begin{pmatrix} \displaystyle\frac{1}{\sqrt{2}}\pi^{0}+\displaystyle\frac{1}{\sqrt{6}}\eta & \pi^{+} & K^{+}\\ \pi^{-} & -\displaystyle\frac{1}{\sqrt{2}}\pi^{0}+\displaystyle\frac{1}{\sqrt{6}}\eta & K^{0}\\ K^{-} & \bar{K}^{0} & -\displaystyle\frac{2}{\sqrt{6}}\eta \end{pmatrix} \end{align} $

(2) and
$ \begin{align} B = {}& \begin{pmatrix} \displaystyle\frac{1}{\sqrt{2}}\Sigma^{0}+\displaystyle\frac{1}{\sqrt{6}}\Lambda & \Sigma^{+} & p\\ \Sigma^{-} & -\displaystyle\frac{1}{\sqrt{2}}\Sigma^{0}+\displaystyle\frac{1}{\sqrt{6}}\Lambda & n\\ \Xi^{-} & \Xi^{0} & -\displaystyle\frac{2}{\sqrt{6}}\Lambda \end{pmatrix}. \end{align} $

(3) The first term in the Lagrangian in Eq. (1) represents the contact interaction of the pseudoscalar meson and the baryon octet, which is usually called the Weinberg-Tomozawa term, while the other terms which are relevant to the coefficients
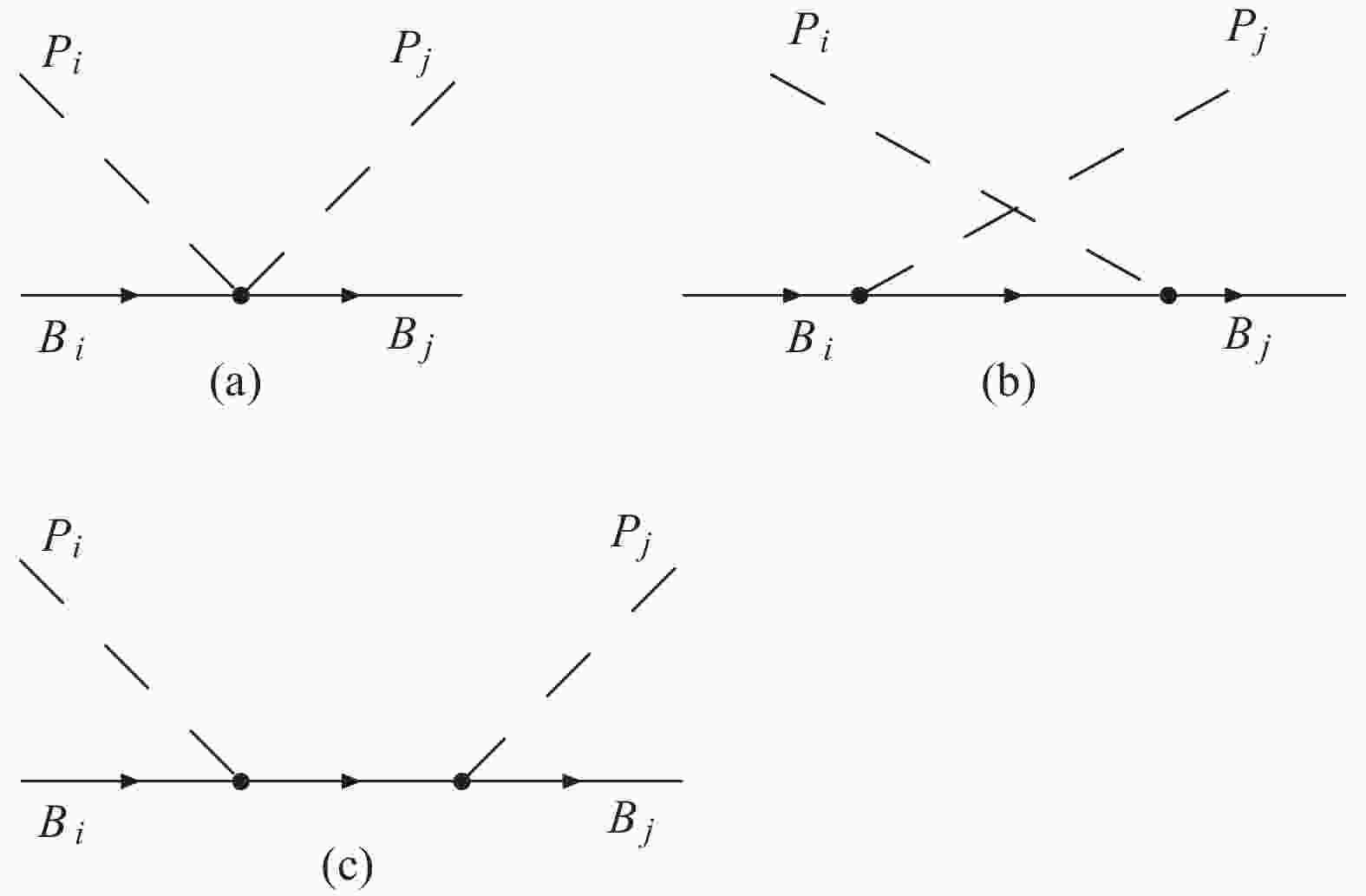
$ D $ and$ F $ give a contribution to the$ s- $ and$ u- $ channel interactions, as shown in Fig. 1.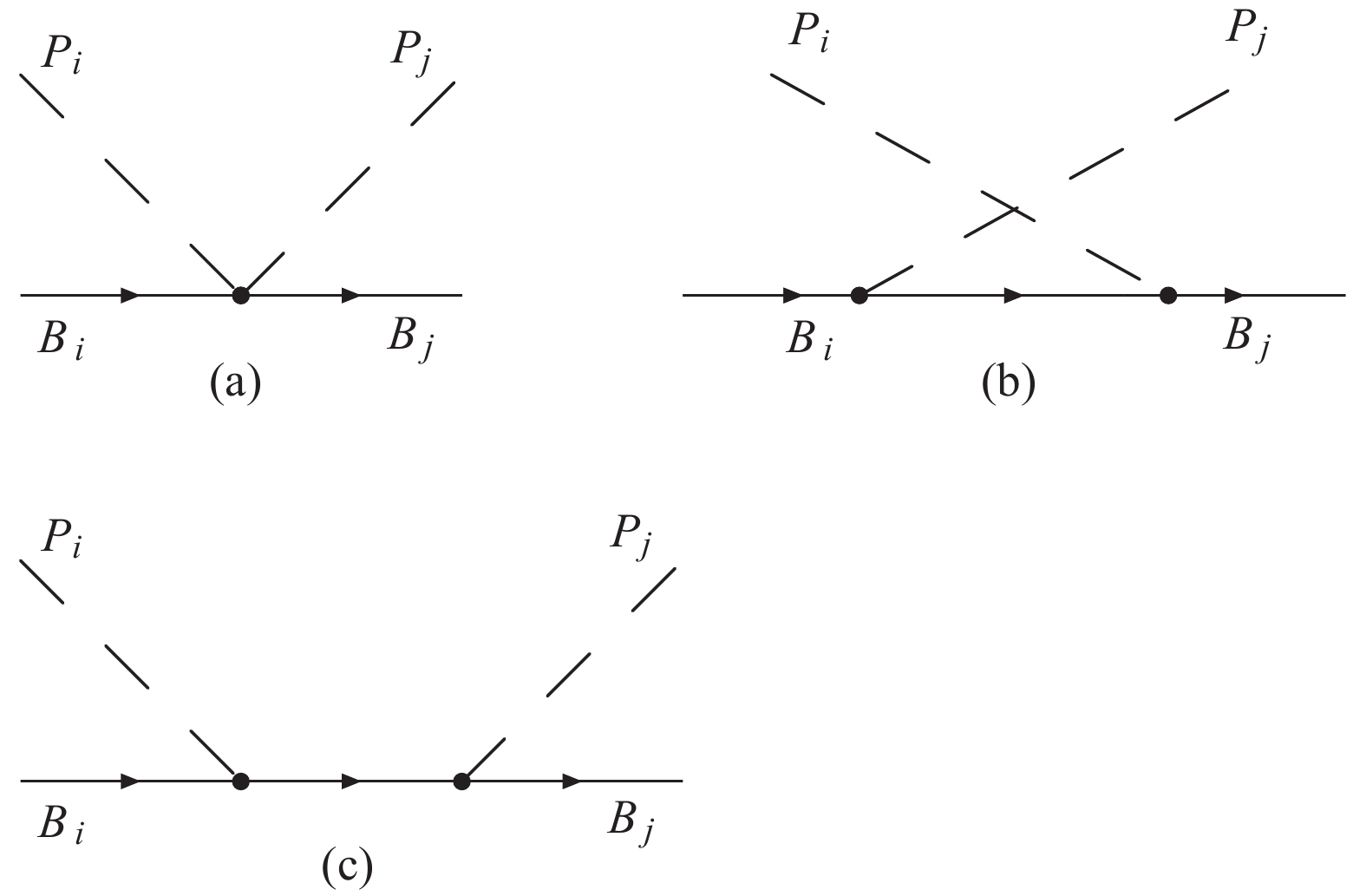
Figure 1. Feynman diagrams of the pseudoscalar meson-baryon octet interaction.
${\rm (a)}$ contact term,${\rm (b)}$ $u-$ channel and${\rm (c)}$ $s-$ channel.According to the Feynmann rules, the Weinberg-Tomozawa contact potential of the pseudoscalar meson and baryon octet interaction can be written as
$ V^{{\rm con}}_{ij} = -C_{ij}\frac{1}{4f_i f_j}\bar{U}(p_j, \lambda_j)\gamma_\mu U(p_i, \lambda_i)(k_i^\mu+k_j^\mu), $

(4) where
$ p_i, p_j(k_i, k_j) $ are the momenta of the initial and final baryons (mesons), and$ \lambda_i, \lambda_j $ denote the spin orientations of the initial and final baryons. For low energies, the three-momenta of the incoming and outgoing mesons can be neglected, and thus the potential in Eq. (4) is simplified as$ V^{{\rm con}}_{ij} = -C_{ij}\frac{1}{4f_i f_j}\bar{U}(p_j, \lambda_j)\gamma_0 U(p_i, \lambda_i)(k_i^0+k_j^0). $

(5) As
$ U(p_i, \lambda_i) $ and$ \bar{U}(p_j, \lambda_j) $ are the wave functions of the initial and final baryons, the matrix$ \gamma_0 $ in Eq. (5) can be replaced by the unit matrix$ I $ in the low energy region, i.e.,$ \gamma_0 \rightarrow I $ . Finally, the Weinberg-Tomozawa contact potential of the pseudoscalar meson and baryon octet interaction takes the form$ \begin{align} V^{{\rm con}}_{ij} = {}&-C_{ij}\frac{1}{4f_i f_j}(2\sqrt{s}-M_{i}-M_{j}) \left(\frac{M_{i}+E}{2M_{i}}\right)^{\frac{1}{2}} \left(\frac{M_{j}+E^{\prime}}{2M_{j}}\right)^{\frac{1}{2}}, \end{align} $

(6) where
$ \sqrt{s} $ is the total energy of the system,$ M_{i} $ and$ M_{j} $ denote the initial and final baryon masses, while$ E $ and$ E^\prime $ stand for the initial and final baryon energies in the center-of-mass frame. The coefficients$ C_{ij} $ for the sector of strangeness zero and charge zero are listed in Table 1. Moreover, we assume that the values of the decay constants are only relevant for the pseudoscalar meson with$ f_{\eta}\!\! = \!\!1.3f_{\pi} $ ,$ f_K\!\! =\!\! 1.22 f_{\pi} $ and$ f_{\pi}\!\! =\!\! 92.4 $ MeV, as given in Ref. [2, 7].$C_{ij}$ 

$K^+ \Sigma^-$ 

$K^0 \Sigma^0$ 

$K^0 \Lambda$ 

$\pi^- p$ 

$\pi^0 n$ 

$\eta n$ 

$K^+ \Sigma^-$ 

1 $-\sqrt{2}$ 

$0$ 

$0$ 

$-\frac{1}{\sqrt{2}}$ 

$-\sqrt{\frac{3}{2}}$ 

$K^0 \Sigma^0$ 

0 0 $-\frac{1}{\sqrt{2}}$ 

$-\frac{1}{2}$ 

$\frac{\sqrt{3}}{2}$ 

$K^0 \Lambda$ 

0 $-\sqrt{\frac{3}{2}}$ 

$\frac{\sqrt{3}}{2}$ 

$-\frac{3}{2}$ 

$\pi^- p$ 

1 $-\sqrt{2}$ 

0 $\pi^0 n$ 

0 0 $\eta n$ 

0 Table 1. The coefficients
$C_{ij}$ in the pseudoscalar meson and baryon octet interaction with strangeness$S=0$ and charge$Q=0$ ,$C_{ji}=C_{ij}$ .The second term in Eq. (1) represents the antibaryon-baryon-meson vertices, and can be rewritten as
$ L = A_{lmn}\bar{N}_l \gamma_\mu \gamma_5 \partial^\mu M_m N_n, $

(7) with
$ N = \{\Sigma^+, \Sigma^-, \Sigma^0, p, \Xi^-, n, \Xi^0, \Lambda \} $ and$M = \{\pi^+, \pi^-, \pi^0, K^+, $ $ K^-, K^0, \bar{K}^0, \eta \} $ .The coefficient
$ A_{lmn} $ in Eq. (7) takes the form$ A_{lmn} = -\frac{1}{2f_0} \left[(D+F)C_{lmn}+(D-F)C_{lnm} \right] $

(8) where
$ C_{lmn} = \frac{1}{2} \sum\limits_{i, j, k = 1}^8 X^\dagger_{il} X_{jm} X_{kn} \langle \lambda_i \lambda_j \lambda_k \rangle, $

(9) with
$ \lambda $ the matrix of the SU(3) generator and$ \begin{aligned} X = \frac{1}{\sqrt{2}} \left( \begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ i & -i & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \sqrt{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i & -i & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & i & -i & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \sqrt{2} \\ \end{array}\right). \end{aligned} $

(10) Thus, the
$ s- $ and$ u- $ channel interaction of the pseudoscalar meson and the baryon octet can be constructed according to the vertices in Eq. (7).If the three-momenta of the incoming and outgoing particles are neglected in the calculation, the
$ s-$ channel potential of the pseudoscalar meson and baryon octet interaction can be written approximately as$ V^s_{ij} \approx A A^\prime \frac{\left(\sqrt{s}-E \right) \left(\sqrt{s}-E^\prime \right)}{\sqrt{s}+M}, $

(11) where
$ M $ denotes the mass of the intermediate baryon,$ A $ and$ A^\prime $ represent the coefficients given in Eq. (8).Similarly, the
$ u- $ channel potential can be obtained as$ \begin{aligned} V^u_{ij} &\approx& A A^\prime \frac{(\sqrt{s}-E)(E+E^\prime-\sqrt{s}-M)(\sqrt{s}-E^\prime)}{u-M^2}, \end{aligned} $

(12) with the Mandelstam variable
$ u = (p_i-k_j)^2 $ .In the calculation of Eqs. (11) and (12), a physical baryon mass is adopted so as to obtain the
$ s $ -channel and$ u $ -channel interaction potentials. The mass renormalization of baryons has to be accomplished before the tree-level diagrams in the interaction of the pseudoscalar meson and the baryon octet are studied. In the chiral unitary model, the loop function of the intermediate pseudoscalar meson and baryon is considered in the on-shell approximation when the Bethe-Salpeter equation is solved, which will be discussed in Sect. 3, so that the whole interaction chain is taken into account without a cutoff. Therefore, we can examine whether a resonance state can be generated dynamically or not.The Weinberg-Tomozawa term and the
$ s-$ channel potential of the pseudoscalar meson and baryon octet interaction are only related to the Mandelstam variable$ s $ , therefore, they only give a contribution to the S-wave amplitude in the scattering process of the pseudoscalar meson and the baryon octet.As is well known, a function can be expanded with the Legendre polynomials, i.e.,
$ f(x) = \sum\limits_{n = 0}^{+\infty} c_n P_n(x), $

(13) with
$ P_n(x) $ the$ n $ th Legendre polynomial and the coefficients$ c_n = \frac{2n+1}{2} \int_{-1}^{1} f(x) P_n(x) {\rm d}x. $

(14) In the S-wave approximation, only the coefficient
$ c_0 $ is necessary.The denominator
$ u-M^2 $ in Eq. (12) can be written as$ \begin{split} u-M^2 = &M_i^2+m_j^2-M^2-2(p_i^0 k_j^0- \vec{p}_i \cdot \vec{k}_j) \\ = &(M_i^2+m_j^2-M^2-2p_i^0 k_j^0)\\ &\times \left(1- \frac{2|\vec{p}_i| |\vec{k}_j| \cos \theta }{M_i^2+m_j^2-M^2-2p_i^0 k_j^0} \right), \end{split} $

(15) where
$ \theta $ is the angle between the three-momenta of incoming and outgoing mesons, and$ \vec{p}_i(\vec{k}_j) $ and$ M_i(m_j) $ are the three-momentum in the center-of-mass frame and the mass of the initial baryon (final meson). Taking$ \alpha = \displaystyle\frac{2 |\vec{p}_i| \vec{k}_j| }{M_i^2+m_j^2-M^2-2E (\sqrt{s}-E^\prime)} $ and$ x = \cos \theta $ , we obtain$ \frac{1}{2}\; \int^1_{-1} \frac{1}{1-\alpha x} {\rm d}x = -\frac{1}{2}\; \frac{1}{\alpha}\ln \left(\frac{1-\alpha}{1+\alpha} \right). $

(16) Thus, the
$ u-$ channel potential of the pseudoscalar meson and baryon octet interaction in the S-wave approximation can be easily calculated as$\begin{split} V^u_{ij}(S) =& A A^\prime \frac{(\sqrt{s}-E)(E+E^\prime-\sqrt{s}-M)(\sqrt{s}-E^\prime)} {M_i^2+m_j^2-M^2-2E (\sqrt{s}-E^\prime)}\\&\times \frac{-1}{2\alpha} \ln \left(\frac{1-\alpha}{1+\alpha} \right).\end{split} $

(17) Therefore, the S-wave potential of the pseudoscalar meson and baryon octet interaction can be written as
$ V_{ij} = V_{ij}^{{\rm con}}+V_{ij}^s+V_{ij}^u(S). $

(18) -
The Bethe-Salpeter equation can be expanded as
$ \begin{split} T = V+VGT = V+VGV+VGVGV+.... \end{split} $

(19) When the Bethe-Salpeter equation in Eq. (19) is solved, only the on-shell part of the potential
$ V_{ij} $ in Eq. (5) gives a contribution to the amplitude of the pseudoscalar meson and baryon octet interaction, and the off-shell part of the potential can be reabsorbed by a suitable renormalization of the decay constants of mesons$ f_i $ and$ f_j $ . A more detailed discussion can be found in Refs. [13, 14]. Therefore, if the potential in Eq. (5) is adopted, the second term$ VGV $ in Eq. (19) can be written as$ V_{jl}G_{l} V_{li} \sim \bar{U}(p_j, \lambda_j) G_{l} U(p_i, \lambda_i)(k_i^0+k_j^0)^2. $

(20) If the relativistic kinetic correction of the loop function of the pseudoscalar meson and baryon octet interaction is taken into account, the loop function
$ G_{l} $ can be written as$ G_{l} = {\rm i}\int\frac{{\rm d}^{d}q}{(2\pi)^{4}}\frac{\rlap{/}\!\!q+M_{l}} {q^{2}-M_{l}^{2}+{\rm i}\epsilon}\frac{1}{(P-q)^{2}-m_{l}^{2}+{\rm i}\epsilon}, $

(21) with
$ P $ the total momentum of the system,$ m_{l} $ the meson mass, and$ M_{l} $ the baryon mass.The loop function in Eq. (21) can be calculated in the dimensional regularization (See Appendix 1 of Ref. [11] for details), and thus the loop function takes the form
$ \begin{split} G_{l} = &\frac{\gamma_{\mu} P^{\mu}}{32P^{2}\pi^{2}}\left[(a_{l}+1)(m_{l}^{2}-M_{l}^{2})+\left(m_{l}^{2}\ln\frac{m_{l}^{2}}{\mu^{2}}-M_{l}^{2}\ln\frac{M_{l}^{2}}{\mu^{2}}\right)\right]\\& +\left(\frac{\gamma_{\mu} P^{\mu}[P^{2}+M_{l}^{2}-m_{l}^{2}]}{4P^{2}M_{l}}+\frac{1}{2}\right)G_{l}^{\prime}, \end{split} $

(22) where
$ a_l $ is the subtraction constant,$ \mu $ is the regularization scale, and$ G_{l}^{\prime} $ is the loop function in Ref. [15],$ \begin{split} G^\prime_{l}(s) = & \frac{2 M_l}{16 \pi^2} \left\{ a_l(\mu) + \ln \frac{m_l^2}{\mu^2} + \frac{M_l^2-m_l^2 + s}{2s} \ln \frac{M_l^2}{m_l^2} \right.\\ & + \frac{\bar{q}_l}{\sqrt{s}} \left[ \ln(s-(M_l^2-m_l^2)+2\bar{q}_l\sqrt{s})+ \ln(s+(M_l^2-m_l^2)\right.\\ & +2\bar{q}_l\sqrt{s}) - \ln(-s+(M_l^2-m_l^2)+2\bar{q}_l\sqrt{s})\\&\left. -\ln(-s-(M_l^2-m_l^2)+2\bar{q}_l\sqrt{s}) \right] \Bigg\}, \end{split} $

(23) with
$ \bar{q}_l $ the three-momentum of the meson or the baryon in the center-of-mass frame.Since the total three-momentum
$ \vec{P} = 0 $ in the center-of-mass frame, only the$ \gamma_{0} P^{0} $ part remains in Eq. (22). Similarly, the matrix$ \gamma_{0} $ can be replaced by the unit matrix$ I $ since$ U(p_i, \lambda_i) $ and$ \bar{U}(p_j, \lambda_j) $ are the wave functions of the initial and final baryons. Thus, the loop function of the intermediate pseudoscalar meson and baryon octet becomes$ \begin{split} G_{l} = &\frac{\sqrt{s}}{32\pi^{2}s}\left[(a_l+1)(m_{l}^{2}-M_{l}^{2})+\left(m_{l}^{2}ln\frac{m_{l}^{2}}{\mu^{2}}-M_{l}^{2}ln\frac{M_{l}^{2}}{\mu^{2}}\right)\right]\\& +\left(\frac{s+M_{l}^{2}-m_{l}^{2}}{4M_{l}\sqrt{s}}+\frac{1}{2}\right)G_{l}^{\prime}. \end{split} $

(24) When the
$ s- $ channel and$ u- $ channel interactions are considered, the loop function in Eq. (24) is still suitable. However, the off-shell part of the potential is reabsorbed by the renormalization, so that the decay constants of mesons and the masses of intermediate baryons all take physical values when the Bethe-Salpeter equation is solved.In our calculations, we make a transition
$ \begin{split} \tilde{V} = &V\; \sqrt{M_i M_j}, \\ \tilde{G}_l = &G_l/M_l, \end{split} $

(25) so that the scattering amplitude
$ \tilde{T} = [1-\tilde{V}\tilde{G}]^{-1}\tilde{V} $

(26) becomes dimensionless.
-
In the sector of isospin
$ I = \frac{1}{2} $ and strangeness$ S = 0 $ , the wave function in the isospin space can be written as$ | \pi N; \frac{1}{2}, -\frac{1}{2} \rangle = -\sqrt{\frac{2}{3}} |\pi^- p \rangle + \sqrt{\frac{1}{3}} | \pi^0 n \rangle, $

(27) $ | \eta N; \frac{1}{2}, -\frac{1}{2} \rangle = |\eta n \rangle, $

(28) $ |K \Lambda; \frac{1}{2}, -\frac{1}{2} \rangle = |K^0 \Lambda \rangle, $

(29) and
$ |K \Sigma; \frac{1}{2}, -\frac{1}{2} \rangle = -\sqrt{\frac{1}{3}} |K^0 \Sigma^0 \rangle + \sqrt{\frac{2}{3}} |K^+ \Sigma^- \rangle. $

(30) Thus, the coefficients
$ C_{ij} $ in the Weinberg-Tomozawa contact potential of the pseudoscalar meson and baryon octet interaction can be obtained in the isospin space, which are summarized in Table 2.$C_{ij}$ 

$\pi N$ 

$\eta N$ 

$K \Lambda$ 

$K \Sigma$ 

$\pi N$ 

2 0 $\frac{3}{2}$ 

$-\frac{1}{2}$ 

$\eta N$ 

0 $-\frac{3}{2}$ 

$-\frac{3}{2}$ 

$K \Lambda$ 

0 0 $K \Sigma$ 

2 Table 2. The coefficients
$C_{ij}$ in the pseudoscalar meson and baryon octet interaction with isospin$I=\frac{1}{2}$ and strangeness$S=0$ ,$C_{ji}=C_{ij}$ .The
$ s- $ channel,$ u- $ channel and Weinberg-Tomozawa contact potentials in the S-wave approximation are depicted in Fig. 2. From Fig. 2, it is seen that the$ \pi N $ $ s-$ channel potential is repulsive and the other$ s- $ channel potentials are weaker than the$ \pi N $ potential, while all$ u- $ channel potentials in the S-wave approximation are attractive. Although the curves for$ \eta N $ and$ K\Sigma $ are not smooth when$ \sqrt{s}<1300 $ MeV, this occurs far away from the energy region we are interested in, and we assume that there is no effect on the pole position of the amplitude. As the Weinberg-Tomozawa term is dominant, the correction from the$ s- $ channel potential and the S-wave$ u- $ channel potential is not important.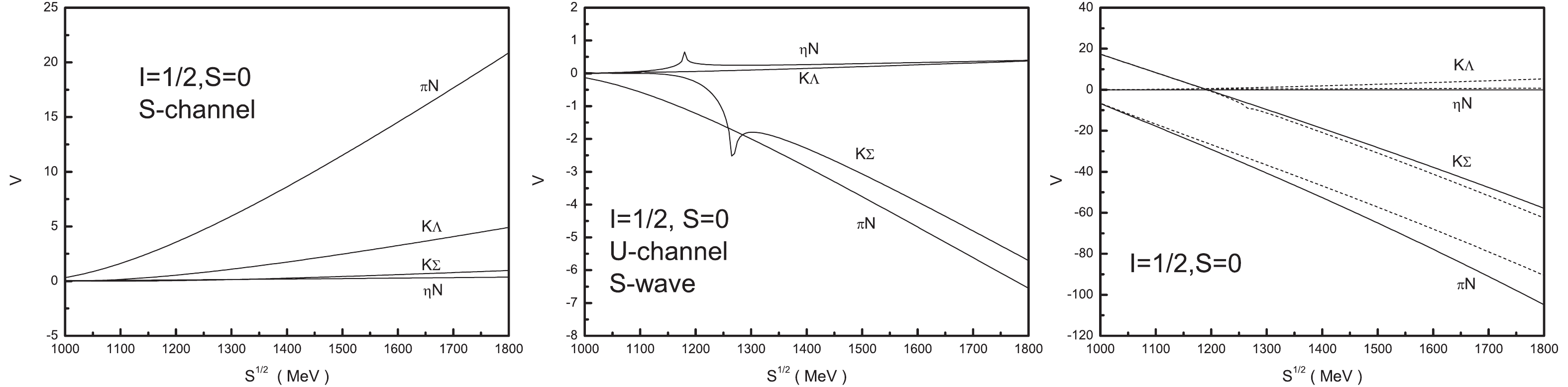
Figure 2. Potentials of the pseudoscalar meson and baryon octet interaction as functions of the total energy of the system
$\sqrt{s}$ in the sector of isospin$I=1/2$ and strangeness$S=0$ . (left):$s-$ channel. (middle):$u-$ channel in the S-wave approximation. (right): The solid lines denote the Weinberg-Tomozawa contact interaction, while the dashed lines stand for the total S-wave potential from Eq. (18).The total potential for the different pseudoscalar meson and baryon systems with isospin
$ I = 1/2 $ and strangeness$ S = 0 $ are depicted in the right side of Fig. 2, which shows that the$ \pi N $ and$ K \Sigma $ potentials are attractive, while the$ \eta N $ and$ K \Lambda $ interactions are weak.Although the
$ s- $ channel and$ u- $ channel potentials are weaker than the Weinberg-Tomozawa contact interaction in the sector of isospin$ I = 1/2 $ and strangeness$ S = 0 $ , the subtraction constants must be readjusted in the calculation when the contribution of the$ s- $ and$ u- $ channel potentials are taken into account.According to the PDG data, the
$ N(1535) $ particle is assumed to lie in the region of Re (pole position) = 1490~1530 MeV, and −2Im (pole position) = 90~250 MeV in the complex energy plane of$ \sqrt{s} $ [12]. When the Bethe-Salpeter equation is solved in the unitary coupled-channel approximation, we set the regularization scale to$ \mu = 630 $ MeV, just as is done in most works using this method[3, 4, 11, 14]. Moreover, all subtraction constants change from$ -3.2 $ to$ -0.5 $ with a step of$ 0.3 $ , and we hope a resonance state can be generated dynamically in a reasonable energy region. In the previous works, the subtraction constant was usually chosen to be$ -2 $ , which is thought to be a natural value. We changed the subtraction constants in the neighborhood of$ -2 $ in order to find the influence of different values on the mass and decay width of the resonance state.Altogether, we found 39 sets of subtraction constants suitable for producing a pole in the energy region constrained by the PDG data, listed in Table 3. The pole positions and the couplings to
$ \pi N $ ,$ \eta N $ ,$ K \Lambda $ and$ K \Sigma $ are also listed. A resonance state with a mass of about$ 1520 $ MeV and a decay width of about$ 90 $ MeV is generated using 12 sets of subtraction constants, while both the mass and the decay width increase slightly when the other 27 sets are used in the calculation. The 39 sets of subtraction constants are depicted in Fig. 3. It is found that the subtraction constant$ a_{\pi N} $ changes from$ -3.2 $ to$ -0.5 $ in successive steps . Since the$ \pi N $ threshold is far lower than the energy region where the$ N(1535) $ particle might be generated dynamically, it is understandable that the pole position is not sensitive to the value of the subtraction constant$ a_{\pi N} $ . The changes of the other three subtraction constants$ a_{\eta N} $ ,$ a_{K \Lambda} $ and$ a_{K \Sigma} $ are not so large. Especially, the subtraction constant$ a_{K \Lambda} = -3.2 $ in 38 sets of parameters, while for the eighth set it takes the value of$ -2.9 $ . The$ K \Lambda $ threshold is close to the energy region we are interested in, and as the subtraction constant$ a_{K \Lambda} $ is stable, it plays an important role in the generation of the$ N(1535) $ particle.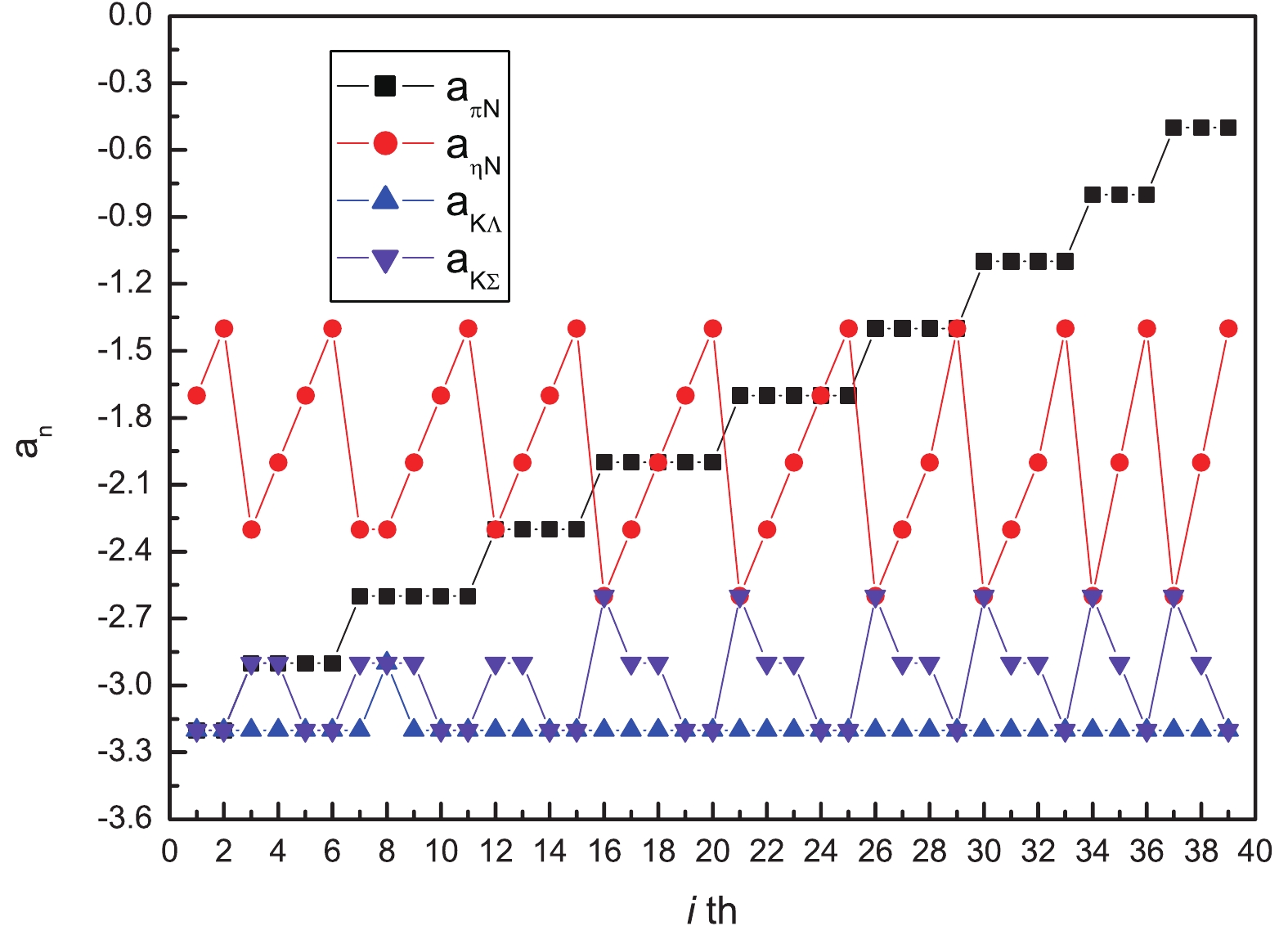
Figure 3. (color online) The subtraction constants
$a_{\pi N}$ ,$a_{\eta N}$ ,$a_{K \Lambda}$ ,$a_{K \Sigma}$ with the regularization scale$\mu=630$ MeV in the loop function in Eq. (24).A pole is generated dynamically at
$ 1518-{\rm i}46 $ MeV in the complex energy plane of$ \sqrt{s} $ when the Bethe-Salpeter equation is solved in the unitary coupled-channel approximation with the 19th set of parameters, i.e.$ a_{\pi N} = -2.0 $ ,$ a_{\eta N} = -1.7 $ ,$ a_{K \Lambda} = -3.2 $ and$ a_{K \Sigma} = -3.2 $ . The amplitude squared$ |T|^2 $ as a function of the total energy$ \sqrt{s} $ for different channels with isospin$ I = 1/2 $ and strangeness$ S = 0 $ is depicted in Fig. 4. The real part of the pole position is higher than the$ \eta N $ threshold, and is lower than the$ K \Lambda $ threshold, so we assume that it might be a resonance state corresponding to the N(1535) particle of the PDG review.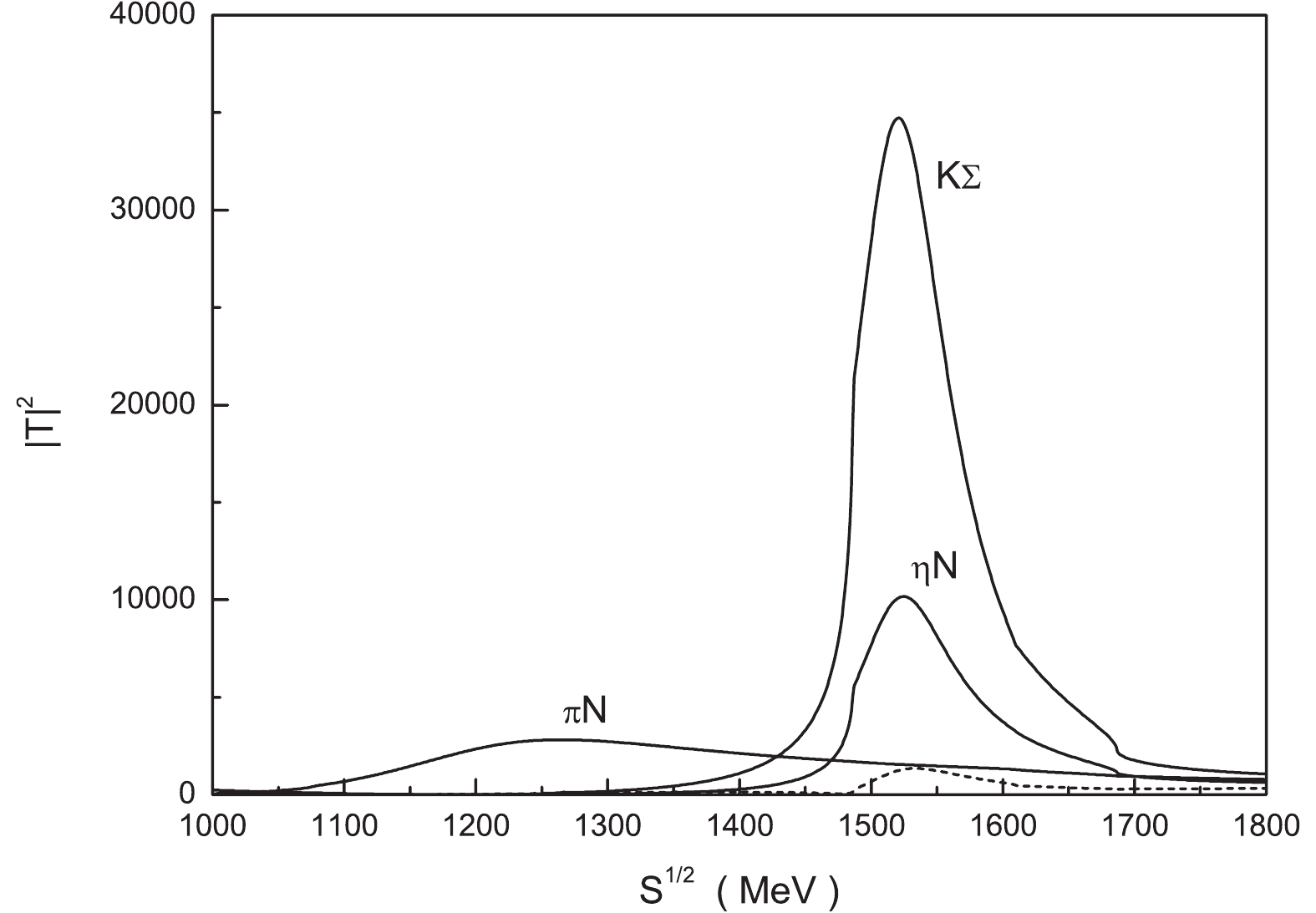
Figure 4. The amplitude squared
$|T|^2$ as a function of the total energy$\sqrt{s}$ for different channels with isospin$I=1/2$ and strangeness$S=0$ . The$\pi N$ ,$\eta N$ and$K\Sigma$ channels are labeled in the figure, while the$K \Lambda$ channel is drawn with the dashed line.The couplings of the N(1535) resonance state to different channels are listed in Table 3. If different sets of subtraction constants are used, the changes of couplings are not significant, as shown in Table 3.
In Ref. [7], the
$ N(1535) $ particle couples more strongly to the$ K^{+} \Lambda $ channel, which is different from the results listed in Table 3. The different values of the coupling constants might be relevant to the next-to-leading-order chiral Lagrangian used in Ref. [7], while it is not included in this work.$n$ 

$a_{\pi N}$ 

$a_{\eta N}$ 

$a_{K \Lambda}$ 

$a_{K \Sigma}$ 

$ \rm{Pole~position(MeV)}$ 

$g_{\pi N}$ 

$|g_{\pi N}|$ 

$g_{\eta N}$ 

$|g_{\eta N}|$ 

$g_{K \Lambda}$ 

$|g_{K \Lambda}|$ 

$g_{K \Sigma}$ 

$|g_{K \Sigma}|$ 

1 −3.2 −1.7 −3.2 −3.2 1518-46i −3+ 1i 4 −65+ 25i 70 41+ 0i 41 94-27i 98 2 −3.2 −1.4 −3.2 −3.2 1530-58i −4+ 1i 4 −66+ 28i 72 40+ 3i 40 95-27i 99 3 −2.9 −2.3 −3.2 −2.9 1520-41i −3+ 5i 7 −62+ 21i 66 47+ 0i 47 96-24i 99 4 −2.9 −2.0 −3.2 −2.9 1532-51i −4+ 5i 7 −64+ 22i 68 45+ 3i 45 97-24i 100 5 −2.9 −1.7 −3.2 −3.2 1518-46i −3+ 2i 4 −65+ 25i 70 42+ 0i 42 94-27i 98 6 −2.9 −1.4 −3.2 −3.2 1530-58i −4+ 1i 4 −66+ 28i 72 40+ 4i 40 95-27i 99 7 −2.6 −2.3 −3.2 −2.9 1520-41i −2+ 6i 7 −62+ 21i 66 47+ 1i 47 96-24i 99 8 −2.6 −2.3 −2.9 −2.9 1527-41i −2+ 4i 5 −60+ 19i 64 48+ 1i 48 95-21i 98 9 −2.6 −2.0 −3.2 −2.9 1532-51i −3+ 6i 7 −64+ 22i 68 45+ 4i 45 97-24i 100 10 −2.6 −1.7 −3.2 −3.2 1518-46i −3+ 2i 4 −65+ 25i 70 42+ 0i 42 94-27i 98 Table 3. The subtraction constants
$a_{\pi N}$ ,$a_{\eta N}$ ,$a_{K \Lambda}$ ,$a_{K \Sigma}$ , the pole positions in the complex energy plane of$\sqrt{s}$ and the couplings of the resonance states to different channels. The regularization scale is fixed to$\mu=630$ MeV in the loop function in Eq. (24).Table 3-continued from previous page $n$ 

$a_{\pi N}$ 

$a_{\eta N}$ 

$a_{K \Lambda}$ 

$a_{K \Sigma}$ 

$\rm{Pole~position(MeV)}$ 

$g_{\pi N}$ 

$|g_{\pi N}|$ 

$g_{\eta N}$ 

$|g_{\eta N}|$ 

$g_{K \Lambda}$ 

$|g_{K \Lambda}|$ 

$g_{K \Sigma}$ 

$|g_{K \Sigma}|$ 

11 −2.6 −1.4 −3.2 −3.2 1530-59i −4+ 2i 5 −67+ 28i 73 40+ 4i 40 95-27i 99 12 −2.3 −2.3 −3.2 −2.9 1520-41i −2+ 7i 8 −62+ 21i 66 47+ 1i 47 96-25i 99 13 −2.3 −2.0 −3.2 −2.9 1532-51i −2+ 6i 8 −64+ 23i 68 45+ 4i 46 97-24i 100 14 −2.3 −1.7 −3.2 −3.2 1518-46i −2+ 3i 4 −65+ 25i 70 42+ 1i 42 94-27i 98 15 −2.3 −1.4 −3.2 −3.2 1530-59i −3+ 2i 5 −67+ 28i 73 40+ 4i 40 95-27i 99 16 −2.0 −2.6 −3.2 −2.6 1535-47i 0+ 11i 12 −62+ 18i 65 51+ 5i 52 97-22i 100 17 −2.0 −2.3 −3.2 −2.9 1520-41i 0+ 7i 8 −62+ 21i 66 48+ 1i 48 95-25i 99 18 −2.0 −2.0 −3.2 −2.9 1531-51i −1+ 7i 8 -64+ 23i 68 46+ 4i 46 96-24i 100 19 −2.0 −1.7 −3.2 −3.2 1518-46i −2+ 3i 5 −65+ 25i 70 42+ 1i 42 94-27i 98 20 −2.0 −1.4 −3.2 −3.2 1530-59i −3+ 3i 5 −67+ 28i 73 40+ 4i 40 95-27i 99 21 −1.7 −2.6 −3.2 −2.6 1534-47i −1-12i 12 −62+ 18i 65 52+ 5i 52 97-22i 100 22 −1.7 −2.3 −3.2 −2.9 1519-41i −1 -8i 8 −62+ 21i 66 48+ 1i 48 95-25i 99 23 −1.7 −2.0 −3.2 −2.9 1531-51i 0+ 7i 8 −64+ 23i 69 46+ 4i 46 96-24i 99 24 −1.7 −1.7 −3.2 −3.2 1518-46i −1+ 3i 5 −65+ 25i 70 42+ 1i 42 94-27i 98 25 −1.7 −1.4 −3.2 −3.2 1530-59i −2+ 3i 5 −67+ 28i 73 40+ 5i 41 95-27i 99 26 −1.4 −2.6 −3.2 −2.6 1534-47i −3-11i 11 −62+ 19i 65 53+ 4i 53 97-22i 99 27 −1.4 −2.3 −3.2 −2.9 1519-41i −2 -8i 8 −62+ 21i 66 49+ 1i 49 95-25i 98 28 −1.4 −2.0 −3.2 −2.9 1531-51i −1 -8i 8 −64+ 23i 69 47+ 4i 47 96-25i 99 29 −1.4 −1.4 −3.2 −3.2 1530-59i −2+ 4i 5 −67+ 28i 73 41+ 5i 41 95-28i 99 30 −1.1 −2.6 −3.2 −2.6 1534-46i −4-10i 11 −62+ 19i 65 53+ 4i 53 96-22i 99 31 −1.1 −2.3 −3.2 −2.9 1519-41i −3 -7i 8 −62+ 21i 66 49+ 0i 49 95-25i 98 32 −1.1 −2.0 −3.2 −2.9 1531-51i −2 -7i 7 −64+ 23i 69 47+ 4i 47 96-25i 99 33 −1.1 −1.4 −3.2 −3.2 1530-59i −1+ 4i 5 −67+ 28i 73 41+ 5i 41 95-28i 99 34 −0.8 −2.6 −3.2 −2.6 1533-46i −5 -9i 10 −62+ 19i 65 53+ 3i 53 96-22i 98 35 −0.8 −2.0 −3.2 −2.9 1531-51i −2 -7i 7 −64+ 23i 69 47+ 3i 48 95-24i 99 36 −0.8 −1.4 −3.2 −3.2 1530-59i 0+ 3i 4 −67+ 28i 73 41+ 5i 41 95-28i 99 37 −0.5 −2.6 −3.2 −2.6 1533-46i −6 -8i 10 −62+ 19i 65 54+ 3i 54 95-21i 98 38 −0.5 −2.0 −3.2 −2.9 1531-51i −3 -6i 7 −64+ 23i 69 48+ 3i 48 95-24i 98 39 −0.5 −1.4 −3.2 −3.2 1530-59i 0 -4i 4 −67+ 28i 73 41+ 4i 42 94-28i 99 -
The wave functions with isospin
$ I = 3/2 $ and strangeness$ S = 0 $ can be written as$ | \pi N; \frac{3}{2}, -\frac{1}{2} \rangle = \sqrt{\frac{2}{3}} |\pi^0 n \rangle + \sqrt{\frac{1}{3}} | \pi^- p \rangle, $

(31) and
$ |K \Sigma; \frac{3}{2}, -\frac{1}{2} \rangle = \sqrt{\frac{2}{3}} |K^0 \Sigma^0 \rangle + \sqrt{\frac{1}{3}} |K^+ \Sigma^- \rangle. $

(32) From Eqs. (31) and (32), the coefficients
$ C_{ij} $ in the isospin space can be calculated and are listed in Table 4. Since the coefficients are all negative, the Weinberg-Tomozawa contact interaction between the pseudoscalar meson and the baryon octet is repulsive for isospin$ I = 3/2 $ and strangeness$ S = 0 $ . Even when the correction from the$ s- $ channel and$ u- $ channel interaction is taken into account, the total potential is still repulsive, as shown in Fig. 5. Thus, no resonance state can be generated in the S-wave approximation.$C_{ij}$ 

$\pi N$ 

$K \Sigma$ 

$\pi N$ 

$-1$ 

$-1$ 

$K \Sigma$ 

$-1$ 

Table 4. The coefficients
$C_{ij}$ in the pseudoscalar meson and baryon octet interaction with isospin$I=\frac{3}{2}$ and strangeness$S=0$ ,$C_{ji}=C_{ij}$ .
Figure 5. The potential of the pseudoscalar meson and baryon octet interaction as a function of the total energy of the system
$\sqrt{s}$ in the sector of isospin$I=3/2$ and strangeness$S=0$ . The solid lines denote the contact interaction, while the dashed lines stand for the total S-wave potential from Eq. (18). -
In this work, the interaction of the pseudoscalar meson and the baryon octet was studied within a nonlinear realized Lagrangian. The
$ s- $ ,$ u- $ channel potentials and the Weinberg-Tomozawa contact interaction are obtained when the three-momenta of the particles in the initial and final states are neglected in the S-wave approximation.In the sector of isospin
$ I = 1/2 $ and strangeness$ S = 0 $ , a resonance state is generated dynamically by solving the Bethe-Salpeter equation, which might be regarded as the$ N(1535) $ particle listed in the PDG review. We find that hidden strange channels, such as$ \eta N $ ,$ K \Lambda $ and$ K \Sigma $ , play an important role in the generation of this resonance state when the Bethe-Salpeter equation is solved in the unitary coupled-channel approximation. The coupling constants of this resonance state to different channels were calculated, and it was found that it couples strongly to the hidden strange channels.Bao-Xi Sun would like to thank Han-Qing Zheng and Yu-Fei Wang for useful discussions.
Pseudoscalar meson and baryon octet interaction with strangeness zero in the unitary coupled-channel approximation
- Received Date: 2019-01-21
- Available Online: 2019-06-01
Abstract: The interaction of the pseudoscalar meson and the baryon octet is investigated by solving the Bethe-Salpeter equation in the unitary coupled-channel approximation. In addition to the Weinberg-Tomozawa term, the contribution of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























 DownLoad:
DownLoad: