Top quark pair production at complete NLO accuracy with NNLO+NNLL′ corrections in QCD

Top quark pair production is one of the most important processes at the Large Hadron Collider (LHC). It allows one to precisely study the properties of the top quark, which are related to many important questions in particle physics, such as the hierarchy problem, the stability of the electroweak (EW) vacuum, and the origin of fermion masses. Further, top quark pair production is a major background in searches for many rare processes in the Standard Model (SM) and in new physics models beyond the SM.

Currently, the most precise fixed-order calculation in quantum chromodynamics (QCD) for top quark pair production reaches the next-to-next-to-leading order (NNLO) [1-9]. The high precision of the NNLO result is sufficient for the total cross section and generic phase-space regions of differential distributions. However, in certain extreme kinematic regions, it is desirable to include even high-order corrections, for instance through resummation. In particular, top quarks produced at the LHC may have energies that are considerably larger than their rest mass $ m_t $, because of the large collider energy. Such boosted top quarks require dedicated studies beyond the fixed-order calculations because the NNLO results in this regime are sensitive to the choice of factorization and renormalization scales [7]. This scale dependence can be significantly reduced by resumming two kinds of large logarithms to all orders in the strong coupling [10]. The first are threshold logarithms, which are important when the partonic center-of-mass energy is close to the $ t\bar{t} $ invariant mass $ M_{t\bar{t}} $, and the second are the small-mass logarithms of the form $ \ln^n(m_t^2/M_{t\bar{t}}^2) $, which are enhanced in the boosted region $ M_{t\bar{t}} \gg m_t $.

Besides QCD corrections, at high energies, EW corrections also become important [11-28]. In [26], the complete next-to-leading order (NLO) corrections of QCD and EW origin were combined with the NNLO QCD results using the multiplicative approach (denoted as QCD×EW in this paper). Their results show that at high transverse momentum, the EW effects can significantly reduce the differential cross section, and they should be considered for the accurate modeling of the spectrum.

In this study, we combined four calculations for the differential cross sections in $ t\bar{t} $ production:

1. The NNLO QCD calculation of [1-9];

2. the soft gluon resummation of [29] at next-to-next-to-leading logarithmic (NNLL) accuracy;

3. the boosted soft gluon resummation of [30-32] at NNLL′ accuracy; and

4. the complete-NLO predictions of QCD and EW origin [26,28,33].

In this work, all the currently-available perturbative contributions to these observables are combined. Therefore, the results presented here are the state-of-the-art theoretical predictions from the perturbation theory within the SM. To the best of our knowledge, this is the first study to perform such a complicated combination of radiative corrections.

In this section, we briefly introduce the four sets of corrections used in the combination and then discuss the matching procedure employed to combine them. The matching procedure is necessary to remove the overlap of various calculations.

To illustrate the idea, we discuss the matching procedure for the particular case of theinvariant-mass distribution; the combination procedure for other distributions follows exactly the same pattern. We start with the factorization formula

where $ M_{t\bar{t}} $ is the invariant mass of the $ t\bar{t} $ pair; $ \tau \equiv M_{t\bar{t}}^2/s $ and $ z \equiv M_{t\bar{t}}^2/\hat{s} $, with $ \sqrt{s} $ and $ \sqrt{\hat{s}} $ being the hadronic and partonic center-of-mass energies, respectively; $ \beta_t = \sqrt{1-4m_t^2/M_{t\bar{t}}^2} $; $ {\cal{L}}_{ij}(x,\mu_f) $ is the parton luminosity function, where $ \mu_f $ is the factorization scale; $ C_{ij} $ is the partonic hard-scattering kernel where $ \Theta $ is used to collectively denote additional kinematic variables. The sum in the above formula runs over the initial-state partons $ i,j = q,\bar{q},g $, and the prefactor is introduced by convention.

It is convenient to perform a Mellin transform of Eq. (1) with respect to $ \tau $. After the transform, the differential cross section becomes

where $ N $ is the Mellin moment, and the fucntions with a tilde are the Mellin transform of the corresponding functions in Eq. (1). In the following, we deal with the perturbative contributions to the hard-scattering kernel $ \widetilde{c}_{ij} $ within the SM.

In the fixed-order perturbation theory, $ \widetilde{c}_{ij} $ can be expanded as a double series in the strong coupling constant $ \alpha_s $ and the fine-structure constant $ \alpha $. The NNLO QCD result contains the $ \alpha_s^2 $, $ \alpha_s^3 $, and $ \alpha_s^4 $ terms in the expansion; while the complete-NLO result includes the $ \alpha_s^2 $, $ \alpha_s\alpha $, $ \alpha^2 $ terms at the leading order (LO), and the $ \alpha_s^3 $, $ \alpha_s^2\alpha $, $ \alpha_s\alpha^2 $, $ \alpha^3 $ terms at NLO. Such a fixed-order expansion is formally correct in the generic phase-space regions. However, in certain kinematic limits, the fixed-order expansion breaks down due to the appearance of large logarithms at each order in the perturbation theory. In such cases, especially for pure QCD, the resummation of these logarithms is necessary to avoid bad convergence and/or the large scale dependence of the fixed-order results.

One of the limits in which potentially large logarithms arise is the threshold limit $ z \to 1 $ in the momentum space that corresponds to the $ N \to \infty $ limit in the Mellin space. In this limit, the Mellin-space hard-scattering kernel $ \widetilde{c}_{ij} $ develops large logarithms of the form $ \alpha_s^nL^k $, where $ L \sim \ln N $. The all-order resummation of these logarithms was studied in [29,34,35]. In [29], the resummation was carried out at the NNLL accuracy with the soft scale chosen in the momentum space. The NNLL threshold resummation was re-evaluated in [10,31] with the soft scale chosen in the Mellin space, to match the settings used in the boosted-soft resummation. By ignoring the technical subtleties such as matrix-formed renormalization group (RG) evolution, the resummed hard-scattering kernel in the Mellin space can be schematically written as

for $ ij = q\bar{q},\bar{q}q,gg $. All other partonic channels are power-suppressed in the $ N \to \infty $ limit. The coefficient function $ h_{ij}(\alpha_s) $ comes from the fixed-order calculation of the hard and soft functions [29], while the exponent $ g_{ij}(\alpha_s,\alpha_sL) $ comes from the RG evolution. At NNLL accuracy, $ h_{ij}(\alpha_s) $ needs to be evaluated up to NLO, namely, order $ \alpha_s^1 $. For the exponent $ g_{ij} $, $ \alpha_sL \sim 1 $ or $ L \sim 1/\alpha_s $, and the orders $ \alpha_s^{-1} $, $ \alpha_s^0 $ and $ \alpha_s^1 $are maintained. By doing this, all terms of the form $ \alpha_s^nL^m $ resummed into the exponent, with $ n-1 \leqslant m \leqslant n+1 $. Upon expansion, this generates the terms $ \alpha_s^nL^k $ in the fixed-order perturbation theory up to $ k = 2n $. The various elements required for achieving this level of logarithmic accuracy are given in [29,36,37]. In this work, this result is denoted as NNLL_m, where the subscript "m" means "massive", to indicate that full dependence on the top quark mass is retained.

In the threshold resummation framework discussed above, additional large logarithms of the form $ \alpha_s^n\ln^l(m_t^2/M_{t\bar{t}}^2) $ ($ l \leqslant 2n $) might arise in the boosted limit $ M_{t\bar{t}} \gg m_t $ or $ \beta_t \to 1 $. In this limit both the top and anti-top quarks are highly boosted in the $ t\bar{t} $ rest frame. In [30], a framework was developed to simultaneously resum the two kinds of logarithms $ \ln N $ and $ \ln(m_t^2/M_{t\bar{t}}^2) $. The form of the resummed result is very similar to Eq. (3), with much more complicated functions $ h_{ij} $ and $ g_{ij} $. In addition, $ {\cal{O}}(m_t^2/M_{t\bar{t}}^2) $ power corrections are neglected in this boosted-soft resummation. With the elements evaluated in [30,38-40], the boosted-soft resummation was carried out at the NNLL′ accuracy in [31], where the prime indicates that the coefficient function $ h_{ij} $ has to be evaluated to one order higher, namely, to NNLO or order $ \alpha_s^2 $. The net effect of computing the $ h_{ij} $ functions to one higher order is that the resummation captures the effect of one additional logarithm at each order in $ \alpha_s $. In the following, we will denote this result as ${\rm{NNLL}}'_{\rm{b}} $, where "b" implies "boosted."

Table 1 lists the contributions included (and not included) in the four types of corrections used in the final combination. One immediately sees that there are overlaps among them, particularly among the three QCD-based calculations. These need to be carefully removed to avoid double-counting or triple-counting of certain sets of corrections. This matching was done in [10,31] for the three purely QCD contributions. We first combine the NNLL′_b and the NNLL_m results to obtain an NNLL$ '_{{{\rm{b}}+{\rm{m}}}} $ result. For this, we need to remove the overlap between the NNLL′_b and NNLL_m results to all orders in $ \alpha_s $. This can be done by exploiting the fact that the boosted-soft resummation formula is the small-mass limit of the soft-gluon resummation formula at any given order in $ \alpha_s $. Therefore,

	Included	Not included
NNLO QCD	$ \alpha_s^n (n = 2, 3, 4) $	$ \alpha_s^n (n> 4) $; $ \alpha_s^n\alpha^m (m> 0) $
NNLLm	$ \alpha_s^n\ln^kN $ ($ n \geqslant 2 $)	$ \alpha_s^n {\cal{O}}(1/N) $ ($ n>2 $); $ \alpha_s^n\alpha^m (m>0) $
NNLL′b	$ \alpha_s^n\ln^kN\ln^l(m_t^2/M_{t\bar{t}}^2) $ ($ n \geqslant 2 $)	$ \alpha_s^n {\cal{O}}(1/N,m_t^2/M_{t\bar{t}}^2) $ ($ n> 2 $); $ \alpha_s^n\alpha^m $ $ (m> 0) $
Complete NLO	$ \alpha_s^n\alpha^m $ ($ n+m = 2,3 $)	$ \alpha_s^n\alpha^m $ ($ n + m> 3 $)

Table 1.  Contributions included in the four types of corrections in the combination. See the text for detailed explanation.

where the terms in the parenthesis account for the contributions suppressed by $ \alpha_s^nm_t^2/M_{t\bar{t}}^2 $ for $ n > 2 $.

Subsequently, the matching with the NNLO QCD calculation proceeds by subtracting the NNLO expansion of the resummed formula

where the terms in the parentheses account for contributions which are suppressed by $ \alpha_s^n/N $ for $ n = 3,4 $.

Finally, the complete-NLO contributions can be incorporated by first combining them with the NNLO QCD contributions in the multiplicative approach,^① arriving at the QCD×EW result, and then matching them against the resummation results as in Eq. (5). This gives us the final matching formula:

In this section, we present the numerical results based on the matching formula Eq. (6) and compare them with the predictions of previous studies. For all the results, we take the top quark mass as $ m_t $=172.5 GeV. The results for other top quark masses can be obtained from the authors upon request. For purely QCD-based predictions, we used the NNPDF3.1 NNLO PDF sets with $ \alpha_s(m_Z) = 0.118 $ [41]. When EW corrections are included, we used the NNPDF3.1 NNLO LUXQED PDF sets [42] with the same $ \alpha_s(m_Z) $. There are a few unphysical scales in the fixed-order and resummed calculations. Their default choices in the results shown below are

For the meanings of these scales, refer to [10,31]. The variations in the unphysical scales around the default values listed above are used to estimate the impact of the higher order corrections that are not included in the calculations. The scales are varied individually up and down by a factor of 2, and the resulting variations in the cross section are added in the quadrature to give the combined uncertainty [10,31]. For the settings on the EW parameters, refer to [26]. The NLO EW calculation was performed by using the latest public version of MADGRAPH5_AMC@NLO [33].

Fig. 1 shows the predictions for the distributions differential with respect to

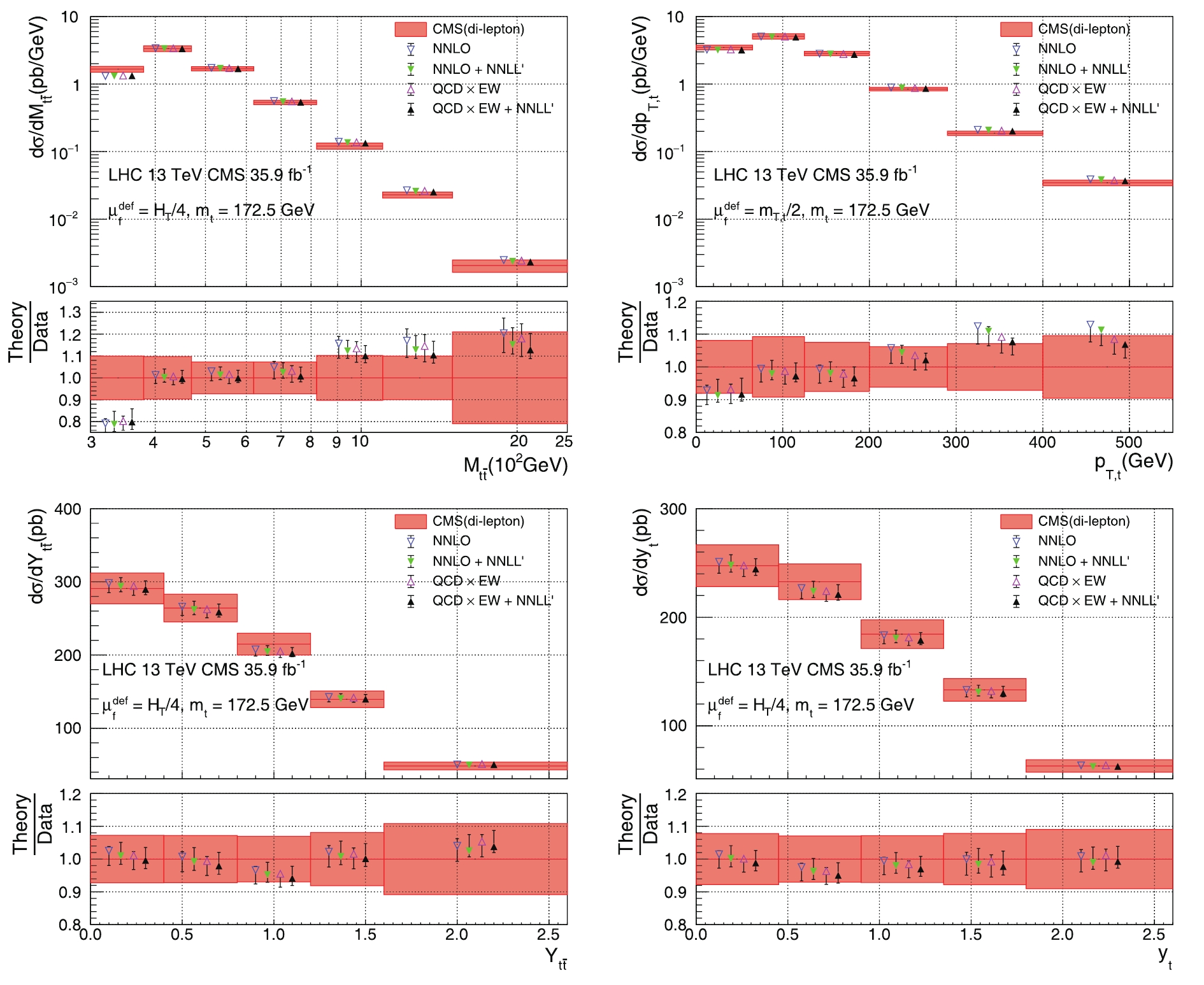
Figure 1.  (color online) Theoretical predictions compared with CMS data in the di-lepton channel [43].

$ i) $ the $ t\bar{t} $ invariant mass $ M_{t\bar{t}} $,

$ ii) $ the transverse momentum $ p_{T,t} $ of the top quark,

$ iii) $ the rapidity $ Y_{t\bar{t}} $ of the $ t\bar{t} $ pair,

$ iv) $ and the rapidity $ y_{t} $ of the top quark.

The four kinds of vertical bars correspond to the four kinds of theoretical predictions discussed in the last section: NNLO QCD, NNLO+NNLL′, QCD×EW, and QCD×EW+NNLL′. The bands in red correspond to the CMS measurement in the di-lepton channel at the 13 TeV LHC using 35.9 fb⁻¹ of data [43].

From the plots, one can conclude that the predictions are generically stable against the inclusion of various sets of corrections. This indicates that the convergence of the perturbative series and the estimate of the residual theoretical uncertainty affecting the predictions are well under-control. The effects of including QCD resummation and EW corrections are more evident in the large $ M_{t\bar{t}} $ region and in the high $ p_{T,t} $ tail (see inset in the first and second panel in Fig. 1). In these cases, QCD resummation and EW corrections both tend to reduce the differential cross sections, which appear to be more compatible with the experimental data than when the corrections are not included. In addition, the resummation effects enlarge the scale uncertainty in the first $ M_{t\bar{t}} $ bin near the $ 2m_t $ threshold, where a small discrepancy is present between the theoretical predictions and the experimental measurement, thus slightly reducing the discrepancy. A recent study [44] showed that a Coulomb resummation can significantly enhance the differential cross section in this region and can partly resolve the discrepancy.^② In principle, Coulomb resummation can be combined with the results of this work to provide a good description of the $ M_{t\bar{t}} $ spectrum in the whole phase space. For the rapidity distributions, we can see that all the theoretical predictions almost completely lie within the uncertainty bands associated with the experimental measurements, indicating excellent agreement for this observable. While the effect of the resummation on the uncertainty bands for these observables is minimal, we can see that the effect of the higher order terms captured by the resummation slightly soften the rapidity spectrum compared with the corresponding fixed order predictions.

In this paper, we described a combination of four calculations for the differential cross sections in $ t\bar{t} $ production: the NNLO QCD calculations, NNLL QCD threshold resummation, NNLL′ QCD resummation for boosted top quarks, and complete-NLO predictions of QCD and EW origin. To the best of our knowledge, this is the first work to present such a complicated combination. The result represents the state-of-the-art prediction in the perturbation theory for $ t\bar{t} $ differential distributions within the SM, which includes all sets of corrections available at the moment. Numerical results are presented for the invariant-mass distribution, transverse-momentum distribution, and rapidity distributions. We compared our predictions with the CMS measurements in the di-lepton channel at the 13 TeV LHC with an integrated luminosity of 35.9 fb⁻¹, and we found good agreement overall.