-
In the last few decades, numerous possible candidates for exotic Hadrons have been experimentally established. Specifically, in 2015, the LHCb Collaboration announced the observation of two pentaquark states, one narrow
$ P_c(4450) $ , and one broad$ P_c(4380) $ , in the$ J/\psi p $ -invariant mass distribution in the$ \Lambda_b^0\to J/\psi K^- p $ decay [1]. In 2019, the LHCb Collaboration updated knowledge of the pentaquarks, with multiple collected data samples of the same decay [2]. A new narrow pentaquark candidate,$ P_c(4312) $ , was observed, whereas the old$ P_c(4450) $ peak was found to be resolved into two narrower structures,$ P_c(4440) $ and$ P_c(4457) $ , owing to the larger statistics. In a coupled-channel approach, it is argued that the existence of a narrow$ P_c(4380) $ is required by heavy quark spin symmetry [3]. After their discovery, numerous discussions in association with their properties were triggered, and various interpretations have been proposed for their internal structure. Because their masses are close to the$ \Sigma_c\bar{D}^{(*)} $ thresholds, many studies assigned them as$ \Sigma_c\bar{D}^{(*)} $ molecular states [3-17]. Alternative explanations include hadro-charmonium states [18], compact diquark–diquark–antiquark states [11, 19-21], etc. A data-driven analysis of$ P_c(4312) $ found it to be a virtual state [22]. In contrast, several recent works found that the spin parity assignments for$ P_c $ (4440) and$ P_c $ (4457) are sensitive to the details of the one-pion exchange potential [3, 15, 23, 24]. The fits of the measured$ J/\psi p $ -invariant mass distributions indeed point to different quantum numbers for$ P_c(4440) $ and$ P_c(4457) $ [3]. Notably, a hidden charm pentaquark was predicted [25, 26] before it was observed by the LHCb. Moreover, other possible pentaquarks in a strange and bottom sector were suggested [27-30]; however, they have not yet been observed experimentally. For more details, refer to the comprehensive reviews in [31-39].However, since its discovery, it has been noted that the narrow peaks of the pentaquarks could be caused by triangle singularities [40, 41], and it was recently suggested to distinguish them in isospin breaking decays [39, 42]. Furthermore, their decay and production properties are extensively studied in various scenarios [43-50]. To discriminate their nature, the production of pentaquarks has been proposed in photo-induced [51-55] and pion-induced reactions [56-59], because a triangle singularity cannot be present in the two-body final states of the production process. Thus, if they are observed in the
$ J/\psi p $ or open charm production [52], they should be genuine states other than kinematic effects. Subsequently, an experimental study of pentaquarks through photoproduction was proposed at the JLab [60]. The GlueX Collaboration searched for the pentaquark states through the near-threshold$ J/\psi $ exclusive photoproduction off proton [61]. No evidence for pentaquark photoproduction was determined, and model-dependent upper limits on their branching fraction$ {\cal{B}}(P_c\to J/\psi p) $ were set. The photoproduction rate was investigated in model-dependent calculations [47, 62], where the coupling of the$ P_c $ radiative decay was evaluated by the vector meson dominance (VMD) model. Although the extracted branching ratio,$ {\cal{B}}(P_c\to J/\psi p) $ , is dependent on the details of the VMD, e.g., off-shell form factor, the photoproduction rate tends to not be high compared to the non-resonant contribution. Double polarization observables were proposed to be useful in the search of pentaquark photoproduction [45]. However, the LHCb results indicate a model-independent lower limit of$ {\cal{B}}(P_c\to J/\psi p) $ [62]; thus, it is expected to observe pentaquark eletro and photoproduction after enough events are accumulated, if$ P_c $ is a real resonant state. Moreover, it is expected that the distributions of$ J/\psi $ from a pentaquark and Pomeron are different in large angles of the differential cross-sections [47, 51], which could be helpful for identifying a pentaquark in cross-sections.After the update of the JLab accelerator to 12 GeV, the search for pentaquark electroproduction at JLab12 will continue. Recently, an electron-ion collider at China (EicC) was proposed, where Hadron physics is a main concern [63]. Its designed center of mass (c.m.) energy of
$ 15-20 $ GeV covers charmonium electroproduction. In this study, we investigate the electroproduction of pentaquark states in these machines. The main concern here is on the final state distributions, from which a kinematic cut would isolate a feeble pentaquark signal from a large non-resonant background. This paper is organized as follows. In Sec. 2, we will briefly describe the analytic formalism in our computation, following which the results and discussions will be introduced in Sec. 3. Finally, we will present a short summary. -
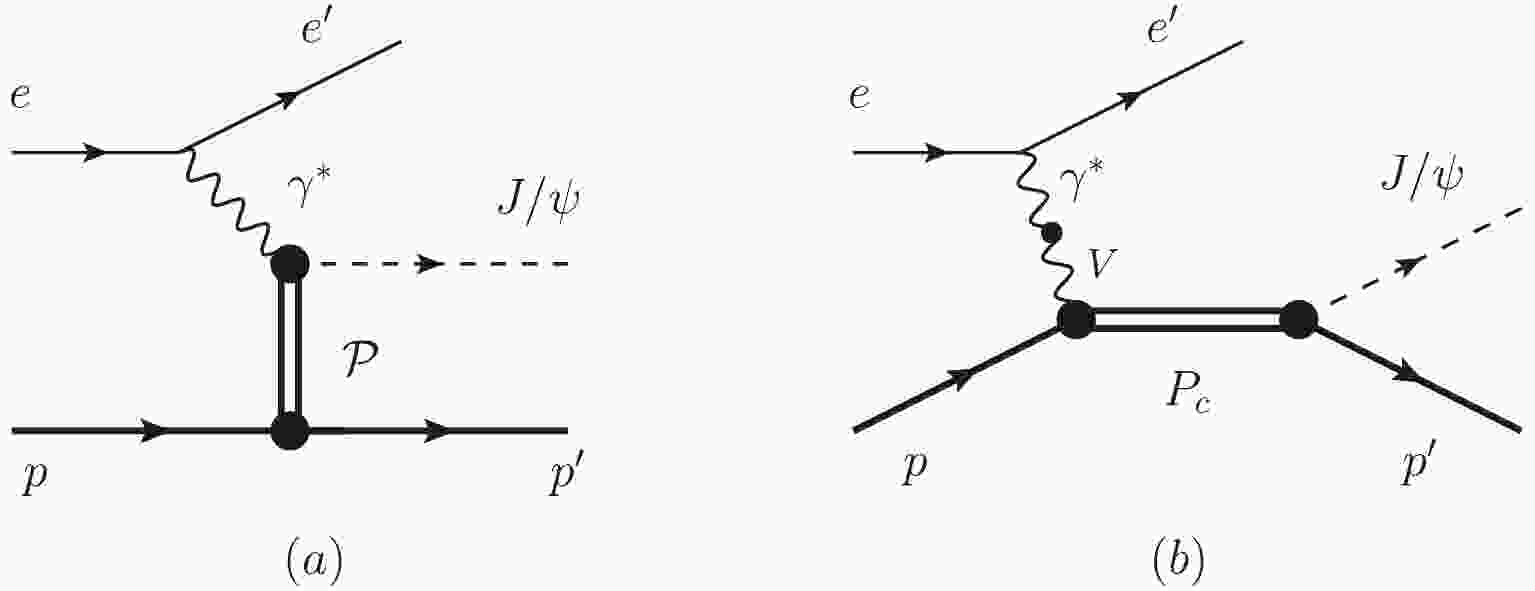
As shown in Fig. 1,
$ pJ/\psi $ in the final states of$ e p \to e p J/\psi $ can be produced from a pentaquark decay (b) and non-resonant$ t $ -channel (a). Here,$ u $ -channel contribution is from a$ P_c $ or$ p $ exchange, but both of them are negligible because of the highly off-shell intermediate$ P_c $ state and the significantly small coupling between$ J/\psi p $ , respectively. Several phenomenological models were constructed to parameterize the$ t $ -channel diagram with a gluon or Pomeron exchange. A detailed comparison of these models can be found in Ref. [64] for the$ \Upsilon $ photoproduction. Here, we employ the soft dipole Pomeron model, which can describe vector meson photoproduction from low to high energies [65]. We use a covariant orbital–spin (L–S) scheme to construct the Langrangians of the$ P_c $ couplings [66], which has been used widely for normal$ N^* $ and$ \Delta^* $ resonances [67-69]. -
The Pomeron exchange model [70-72] accounts for the dominant contribution in the leptoproduction process. The Pomeron mediates the long-range interaction between the nucleon and confined (anti-)quarks within a quarkonium. This is an effective and useful model to parameterize the diffractive process for the production of neutral vector mesons in a high-energy region. By including a double Regge pole with an intercept equal to one, the soft dipole Pomeron model does not violate the unitarity bounds and can describe nearly all the available cross-section data of the photo and electroproduction of vector mesons, from light to heavy and near the threshold to a high-energy region in a consistent manner [65].
We start from the photoproduction of vector meson
$ V $ off proton in the soft dipole Pomeron model with the formula of the$ t $ -dependent cross-section [65],$ \begin{array}{l} \dfrac{{\rm d}\sigma}{{\rm d}t} = 4\pi\,|{\cal{M}}^{\cal{P}}_{\gamma p\to Vp}|^2, \end{array} $

(1) where the amplitudes are defined as
$ \begin{array}{l} {\cal{M}}^{\cal{P}}_{\gamma p\to Vp} = {\cal{P}}(z,t,M_V^2,Q^2) + {\cal{F}}(z,t,M_V^2,Q^2), \end{array} $

(2) $ \begin{array}{l} {\cal{P}}(z,t,M_V^2,Q^2) = {\rm i} g_0 (-{\rm i}z)^{\alpha_P(t)-1} + {\rm i} g_1 {\rm{ln}}(-{\rm i}z) (-{\rm i}z)^{\alpha_P(t)-1}, \end{array} $

(3) $ \begin{array}{l} {\cal{F}}(z,t,M_V^2,Q^2) = {\rm i} g_f (-{\rm i}z)^{\alpha_f(t)-1}. \end{array} $

(4) The
$ {\cal{P}} $ and$ {\cal{F}} $ terms indicate the dipole Pomeron and Reggeon.$ Q^2 = -q^2 $ and$ M_V $ represent the photon virtuality and mass of a vector meson, respectively. Variable$ z \sim \cos \theta $ , where$ \theta $ is the scattering angle of the final states in the c.m. system of$ \gamma^* p $ . The nonlinear Pomeron trajectory is$ \alpha_{\mathbb{P}}(t) = 1+\gamma(\sqrt{4 m_{\pi}^{2}}-\sqrt{4 m_{\pi}^{2}-t}) $ with$ m_{\pi} $ as the pion mass, and the Reggeon trajectory is$ \alpha_f(t) = \alpha_{f}(0)+\alpha^{\prime}_{f}(0)t $ with$ \alpha_{f}(0) = 0.8 $ and$ \alpha^{\prime}_{f}(0) = 0.85\;\text{GeV}^{-2} $ . The parameters,$ \gamma = 0.05\;\text{GeV}^{-1} $ ,$ g_0 = -0.03 $ ,$ g_1 = 0.01 $ , and$ g_f = 0.08 $ , can be obtained by fitting the vector meson photoproduction; more details regarding this can be found in Ref. [65]. The advantage of this model is that it includes exclusive photoproduction of all the vector mesons for both real and virtual photons, as shown in the above amplitudes. This is convenient for our calculation of electroproduction. The results for the$ J/\psi $ photoproduction are shown in Fig. 2.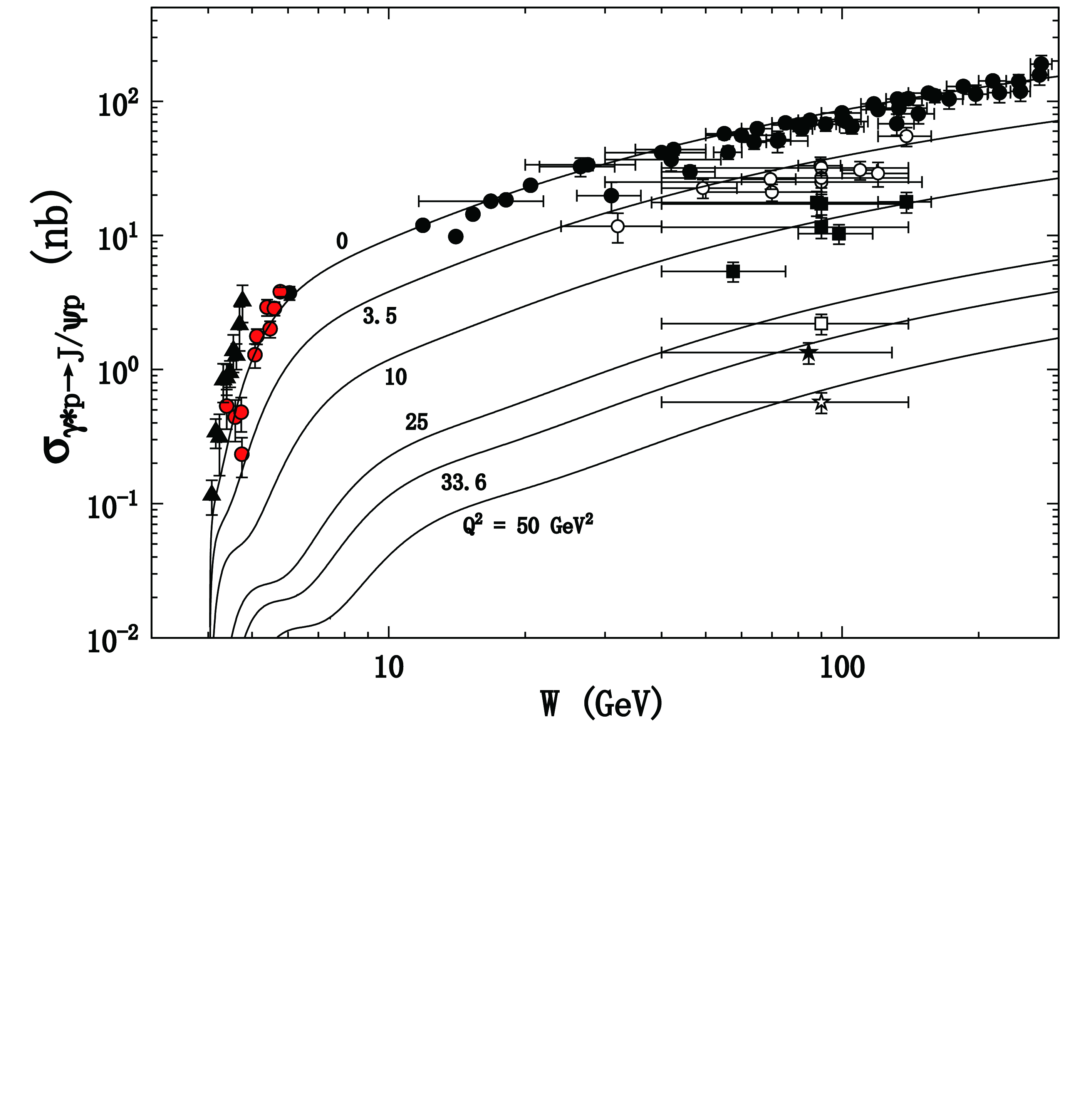
Figure 2. (color online) Photoproduction cross-section in terms of the invariant mass of the
$ J/\psi $ proton system. The near-threshold data with error bars are the experimental measurements from GlueX [61] (solid triangle) and SLAC [73] (red circle), whereas the other data are from H1 [74-76] and ZEUS [77, 78]. The line is the fit from the dipole Pomeron.The electroproduction amplitude for the Pomeron exchange is evaluated as
$ \begin{array}{l} {\cal{M}}_{ep\to eVp} = M_{R_1}^{\mu}\dfrac{-g_{\mu\nu}}{q^2}{\cal{M}}_{R_2}^{\nu}, \end{array} $

(5) where
$ R_1 $ is a sub-reaction,$ e\to e\gamma $ ,$M_{R_1}^{\mu} = {\rm i} e \bar{u}(k') \gamma^\mu u(k)$ , and$ R_2 $ is a sub-reaction,$ \gamma p\to Vp $ . By neglecting the polarization correlations between the two sub-reactions, we obtain the amplitude square,$ \begin{split} |{\cal{M}}_{ep\to eVp}|^2 = \frac{1}{3(q^2)^2} \sum_{\lambda_1,\lambda_2}|M_{R_1}^{\mu}\epsilon_{\mu}^{*\lambda_1}|^2 |{\cal{M}}_{R_2}^{\nu}\epsilon_{\nu}^{\lambda_2}|^2, \end{split} $

(6) where
$ \epsilon $ is the polarization vector of an intermediate photon with spin of$ z $ -direction$ \lambda_{1,2} $ . The amplitude for sub-reaction,$ R_2 $ , can be determined from differential cross-section${\rm d}\sigma/{\rm d}t$ by the dipole Pomeron model mentioned in Eq. (1) with the relation,$ |{\cal{M}}^{\cal{P}}_{\gamma p\to Vp}|^2 = \sum_{\lambda_2}|{\cal{M}}_{R_2}^{\nu}\epsilon_{\nu}^{\lambda_2}|^2 $ . An alternative approach to investigate the electroproduction of a vector meson is using a microscopic description of the Pomeron exchange [79, 80]. -
Here, we only consider
$ P_c $ with quantum number$ \frac{3}{2}^- $ in line with GlueX [61], where the branching fractions are determined using the JPAC model [53]. A similar conclusion could be obtained for the alternative assignment of$ J^P $ . The effective Lagrangian for the coupling of$ P_c $ and$ J/\psi p $ is written as [47, 67]$ \begin{array}{l} {\cal L}^{3/2^-}_{V BR} = g \overline{B} {{\tau }} \cdot {{{V^\mu}} } R_{\mu} + h.c., \end{array} $

(7) where
$ R $ and$ B $ denote$ P_c $ resonance and a nucleon, respectively. The coupling constant,$ g $ , can be determined from the corresponding decay widths. Here, we use the total decay widths of$ P_c $ as the measured values by the LHCb and the upper limits of branching fractions,$ {\cal{B}}(P_c\to J/\psi p) $ , determined by GlueX [61]. The propagator of$ P_c $ can be written as$ \begin{split} G^{3/2}_{R}(p_R) = \frac{ -{\rm i} ({\not\!\! p }_R + M_R) G_{\mu\nu}(p_R)}{p_R^2-M^2_{R}+{\rm i}M_{R}\Gamma_{R}}, \end{split} $

(8) where
$ p_R $ is the momentum of the propagator, and$ M_R $ the mass, and$ \Gamma_{R} $ the decay width of$ P_c $ . The term,$ G_{\mu\nu}(p_R) $ , is defined as$ \begin{split} G_{\mu \nu}(p_R) = & - g_{\mu \nu} + \frac{1}{3} \gamma_\mu \gamma_\nu + \frac{1}{3 M_R}( \gamma_\mu p_{R\nu} - \gamma_\nu p_{R\mu}) \\&+ \frac{2}{3 p_R^2} p_{R\mu} p_{R\nu}. \end{split} $

(9) We assume that the pentaquark resonances couples to a photon via a vector meson pole using the VMD model. Therefore, the
$ \gamma p\to P_c $ vertex can be considered as$ \gamma p\to V p\to P_c $ , as shown in Fig. 1(b). The coupling of the vector meson and photon is expressed as$ \begin{split} {\cal{L}}_{V\gamma} = \sum\limits_V \frac{e M_V^2}{f_V} V_\mu A^\mu, \end{split} $

(10) where
$ M_V $ is the mass of the vector meson, and$ V^{\mu} $ and$ A^\mu $ are the vector meson and photon field, respectively. Then, the coupling constant of the vector meson to photon,$ e/f_V $ , can be extracted from the partial decay width,$ \Gamma_{V\to e^+e^-} $ , from the formula,$ \begin{split} \frac{e}{f_V} = \left[\frac{3 \Gamma_{V\to e^+e^-}}{2 \alpha_{em} |{ p}_e|}\right]^{\frac{1}{2}}, \end{split} $

(11) where the masses of the electrons and positrons have been neglected, and
${ p}_e$ is the three-vector momentum of an electron in the vector meson rest frame.For an off-shell vector meson in the VMD, we choose the form factor,
$ \begin{split} {\cal{F}}(q^2) = \frac{\Lambda^4}{\Lambda^4+(q^2-M_V^2)^2}, \end{split} $

(12) where
$ \Lambda $ is the cut-off parameter. The choice of the vector meson and cut-off parameter will not change the distribution of the final state, which is the main concern. Thus, we choose the vector meson to be$ J/\psi $ and cutoff to be$ \Lambda = 0.5 $ GeV. -
We explore the electroproduction of the pentaquarks observed by the LHCb Collaboration as listed in Table 1, together with the contributions from the Pomeron exchange in the JLab12 and EicC energy configurations. JLab12 is a fixed-target experiment with 12-GeV electrons and rest protons, whereas the EicC is a colliding experiment with
$ 3.5 $ -GeV electrons and$ 20 $ -GeV protons. The pentaquark and Pomeron contributions were added incoherently. The interference terms may have large contributions to the total cross-section, but distribute smoothly in the phase space. Furthermore, it is too premature to consider the interference at present, because we do not know the relative phase between the different contributions. Notably, these terms can be neglected for searching a pentaquark because we focus on a pentaquark-dominant phase space area, from which we obtain the main conclusion of this study. In our calculation, we choose the laboratory frame with an electron moving in the opposite$ z $ direction. The cross-sections were evaluated by the VEGAS program [81], which numerically integrates the kinematic events generated by RAMBO [82] with the dynamics described by the formula above. We also obtain the final state distributions simultaneously.$ M $ /MeV

$ \Gamma $ /MeV

$ J^P $ 

$ P_c $ (4312)

$ 4311.9\pm0.7^{+6.8}_{-0.6} $ 

$ 9.8\pm2.7^{+3.7}_{-4.5} $ 

$ \frac{3}{2}^- $ 

$ P_c $ (4440)

$ 4440.3\pm1.3^{+4.1}_{-4.7} $ 

$ 20.6\pm4.9^{+8.7}_{-10.1} $ 

$ \frac{3}{2}^- $ 

$ P_c $ (4457)

$ 4457.3\pm0.6^{+4.1}_{-1.7} $ 

$ 6.4\pm2.0^{+5.7}_{-1.9} $ 

$ \frac{3}{2}^- $ 

The total production cross-sections for both JLab12 and EicC are summarized in Table 2. We can observe that the cross-sections of the non-resonant background are a few orders of magnitude larger than those of the pentaquarks. For the cross-sections of the pentaquarks, the model-dependent branching fractions determined by GlueX and the cut-off parameter in the form factor appear as the overall factor, which suggests the cross-sections rather than the final state distributions are considerably model-dependent. Thus, the distributions are our main concern here.
Background Pentaquarks JLab12 1.4 0.0016 EicC 111 0.013 Table 2. Electroproduction cross-sections (in units of pb) of the pentaquarks and non-resonant backgound in JLab12 and EicC.
The three-momentum and polar angle distributions of the final proton from either the Pomeron exchange process or pentaquark production are shown separately in Fig. 3 for JLab12 and in Fig. 4 for EicC. The left panels are for the final proton from the Pomeron contribution, whereas the right ones are for the proton from the pentaquark decay. For a better comparison, we use the same range in the axes of the two panels for each figure. Because of the completely different energy configurations, the final proton moves in the electron and proton forward angles in JLab12 and EicC, respectively. Notably, the polar angle distributions of the final proton are significantly different for the Pomeron exchange and pentaquark production. This is because the
$ t $ -dependent cross-section in Eq. (1) is suppressed at large$ t $ for the Pomeron exchange, whereas the shape from the pentaquarks is completely flat across the full$ t $ range. This fact has been already noted in several papers [47, 51, 62], that is, the final particles from different contributions have different behaviours at large angles.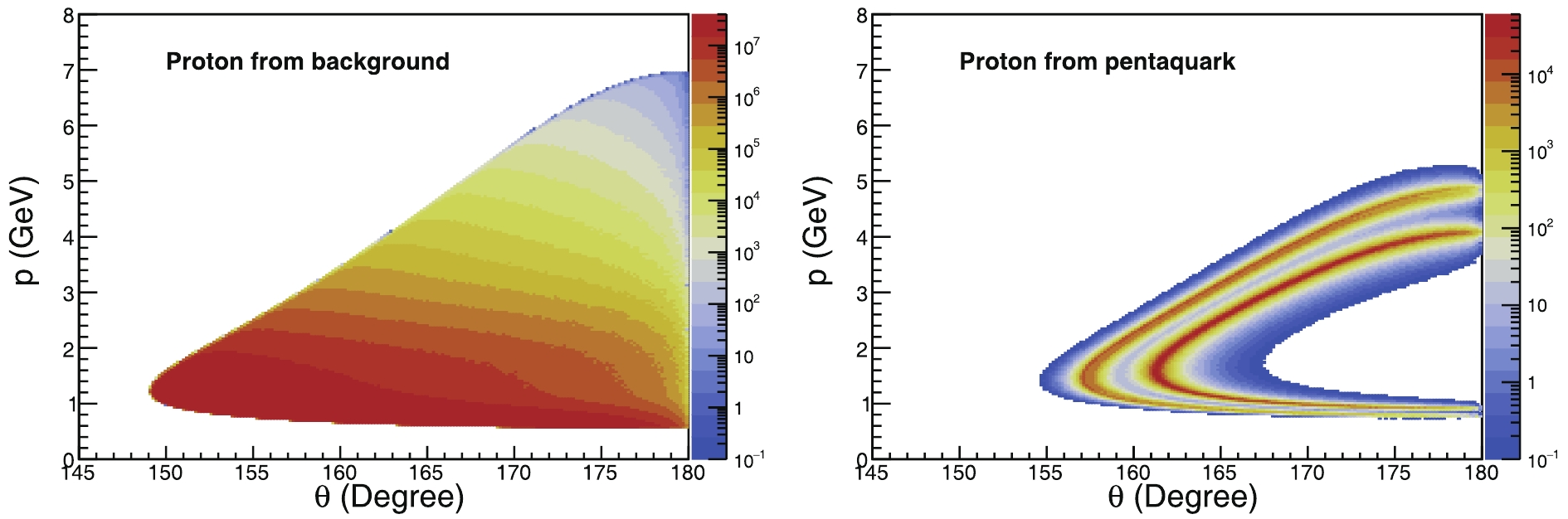
Figure 3. (color online) Distribution of the momentum versus scattering angles of the final proton in the laboratory frame in the JLab energy configuration, with a 12-GeV electron beam projectile on the rest protons. We set the electron beam moving in the opposite
$ z $ direction. The left panel is the final proton from the Pomeron exchange, whereas the right is from the pentaquark. The colors represent the differential cross-section.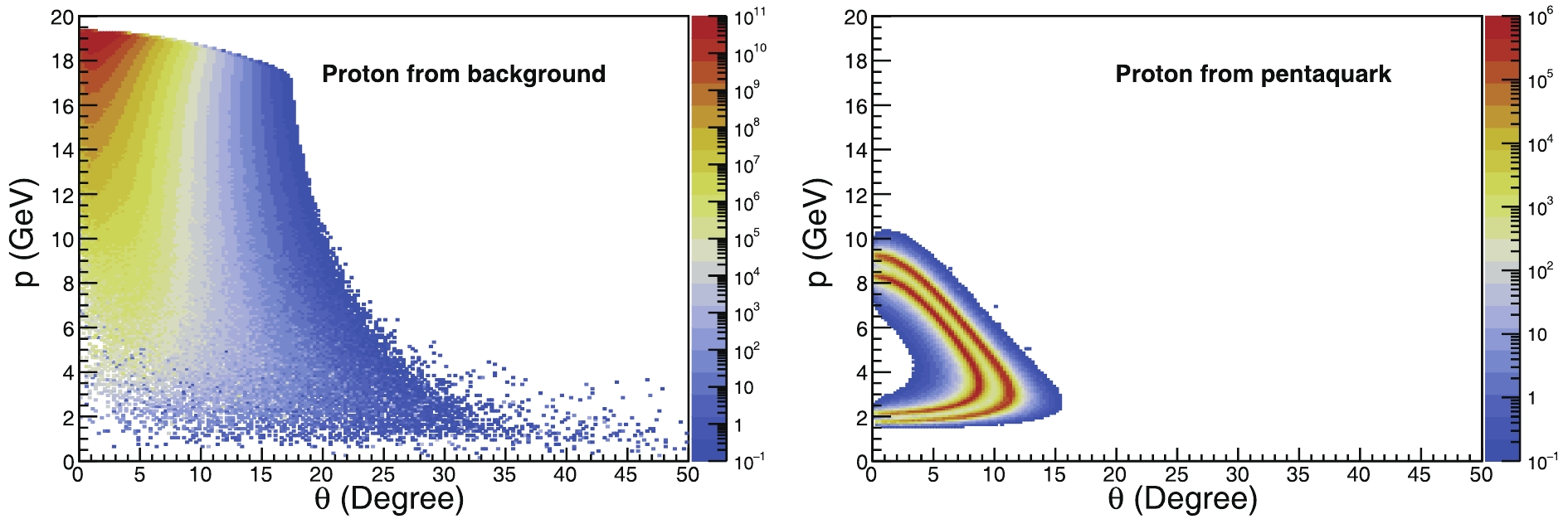
Figure 4. (color online) Same as Fig. 3, but in the EicC energy configuration, which is 20-GeV protons colliding with 3.5-GeV electrons. For a better comparison, we selected the same range in the axes of the two panels.
In both the energy configurations of JLab12 and EicC, the distributions of the protons decaying from the pentaquarks are quite similar in shape but different in range. The three pentaquarks are characteristized by noticeable resonant bands. Among them,
$ P_c $ (4457) and$ P_c $ (4440) overlap with each other because of the closeness of their masses; thus, a good energy resolution is needed to distinguish them. This is a challenge for future detector design.In particular, for each energy configuration, the protons from the non-resonant background and pentaquarks present significant differences in the phase space, as shown in Fig. 3 and Fig. 4. Consequently, we can take advantage of this feature to enhance the
$ P_c $ peaks relative to that of the Pomeron exchange. This originates from the main conclusion of this study in Fig. 5, which shows the differential cross-section of the electroproduction process in the energy configurations of JLab12 and EicC. The dashed and solid curves in Fig. 5 show the results with and without the cut on the three-momentum and angle of the final proton, respectively. Note that a simple cut$ p > 3\;\text{GeV} $ can remove more Pomeron contribution than a pentaquark in JLab12. In comparison, for EicC, a cut$ p <10$ GeV and$ \theta>5^{\circ} $ also works well to depress the background. Quantitatively, in the case of$ P_c(4312) $ in JLab12, the signal to background ratio increases from 0.3 to 19 with the kinematic cut. Therefore, the kinematic cut can make the$ P_c $ peaks more prominent and present a huge potential in experimental analysis, although the total number of events would decrease after the cuts are used. Thus, more complex cuts would further improve the situation.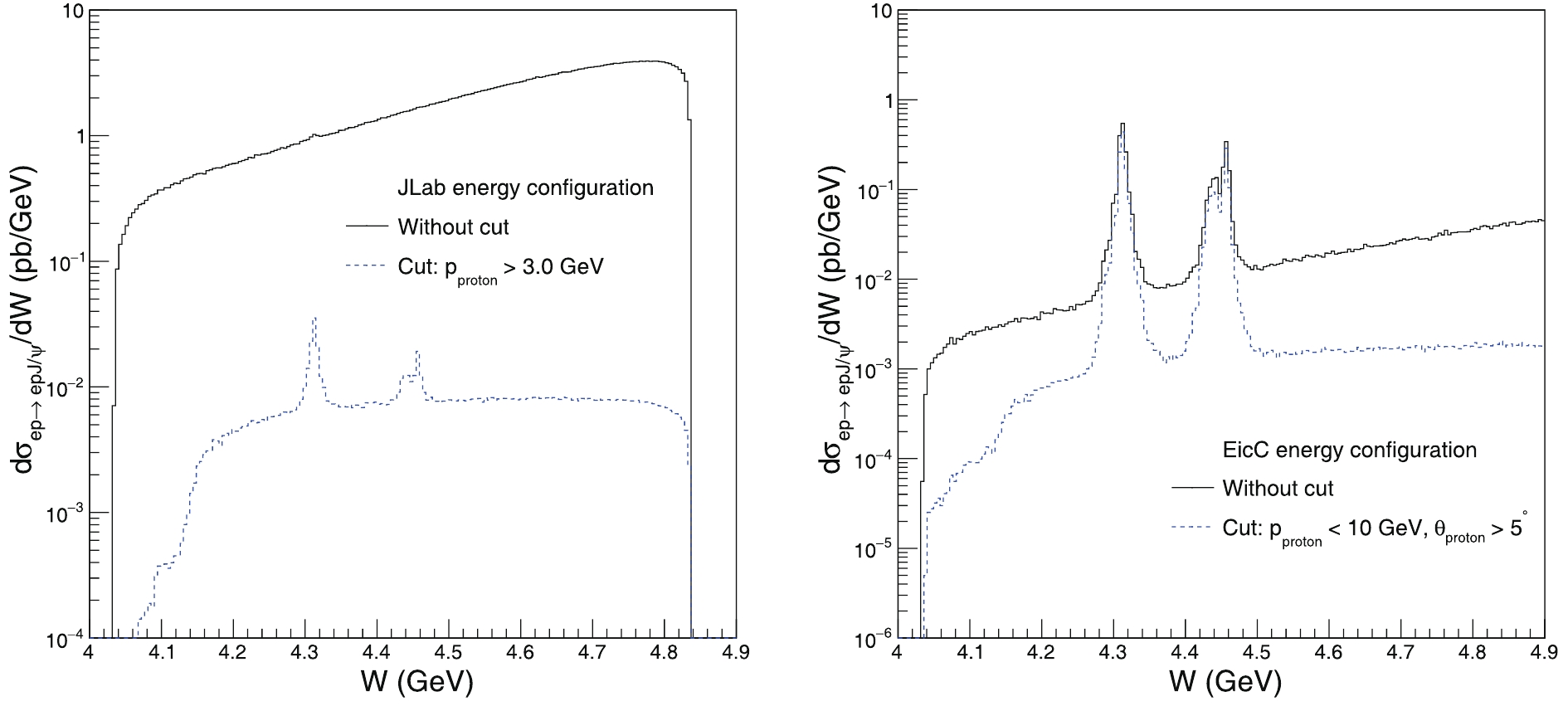
Figure 5. (color online) Differential cross-section of the electroproduction process in terms of the invariant mass of the
$ J/\psi $ proton system in JLab (left) and EicC (right). The solid and dashed lines are for the one without and with the cut, respectively. The peaks correspond to the three pentaquarks.Finally, we would like to emphasize the great potential of both EicC and JLab12 to search for a pentaquark. EicC has a higher signal to background ratio, whereas JLab12 has a much higher luminosity. The center of mass energy of EicC is approximately 16.7 GeV, wich is much larger than the 4.8 GeV of JLab12. As listed in Table 2, the larger center of mass energy would make the total cross-section 8 and 80 times larger for the pentaquark signal and non-resonant background, respectively. However, EicC has 15 times larger phase space in the invariant mass,
$ W $ , for the background than JLab. Therefore, the pentaquark signal could be presented more prominently in the differential cross-section in EicC in Fig. 5. Conversely, the differential cross-section is less reduced in EicC than that in JLab12 after the kinematic cut is employed, which shows that the colliding mode could be more useful to study a pentaquark than the fixed-target mode. -
The GlueX Collaboration at the JLab has searched for pentaquark photoproduction and obtained negative results at the present precision [61]. One possibility is that the pentaquark signal has a smaller total cross-section compared to that of the non-resonant contribution. The production rates have been already investigated in many efforts [47, 62], and the signal of a pentaquark in hidden charm photoproduction would be considerably small in cross-sections.
In this study, we calculated the
$ ep\to e^{\prime}p^{\prime}J/\psi $ process with both a non-resonant$ t $ -channel contribution and a hidden charm pentaquark in the$ s $ -channel. After the non-resonant contribution was normalized using the soft dipole Pomeron model and photoproduction data, the distributions of the final particles from both the sources were investigated. In view of the different shapes of the final proton in the phase space, owing to the different underlying mechanisms, we proposed that the three-momentum and angle cuts on the proton could largely suppress the non-resonant contribution, whereas the signal to background ratio would be significantly increased. For both the energy configurations of JLab12 and EicC, we found promising strategies even with simple cuts, which will be beneficial for future experimental analysis of electroproduction in these machines. In addition, it is promising to search for pentaquarks in a higher energy collider, e.g., US EIC. A similar cut like the one used for EicC would also be helpful. Our criterion is also enlightening for the electroproduction of$ P_b $ , bottom analog of$ P_c $ states [64].Here, we focus on the method to supress the background rather than the total production cross-section of the pentaquarks, because the total cross-section of the pentaqurks is greatly model-dependent, owing to the unknown coupling constant and cut-off parameter appearing as the overall factors. Finally, we noted that our framework could be used in a full simulation, the selection criterion of final particles, and the optimization of the detector design in the future.
Z. Yang gratefully acknowledges the hospitality at ITP where part of this work was performed. We are grateful to F. K. Guo, Q. Wang, Q. Zhao, and B. S. Zou for their insightful discussions and comments.
Identifying hidden charm pentaquark signal from non-resonant background in electron–proton scattering
- Received Date: 2020-03-18
- Available Online: 2020-08-01
Abstract: In this study, we analyze the electroproduction of the LHCb pentaquark states with the assumption that they are resonant states. Our main concern is to investigate the final state distribution in the phase space to extract a feeble pentaquark signal from a large non-resonant background. The results indicate that the signal to background ratio will increase significantly with a proper kinematic cut, which will be beneficial for future experimental analysis.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: