Isospin dependence of the nuclear binding energy

Study of the symmetry energy is of great interest at the current research frontiers of both nuclear physics and astrophysics [1-5]. The symmetry energy characterizes the isospin dependence of the binding energy in atomic nuclei and infinite nuclear matter, thus playing a key role in understanding the structure of exotic nuclei, reaction dynamics in heavy ion collisions, properties of neutron stars and supernova, and so on [6-14]. Much effort has been devoted to constrain the symmetry energy coefficients, both experimentally and theoretically.

It is well known that the $I^2$ term [where $I = (N-Z)/A$] is the leading term of the symmetry energy. While the $I^2$ symmetry energy coefficient extracted from nuclear reaction data and the properties of neutron stars has a large uncertainty (especially for high density regions) [15-18], that from nuclear binding energies has a high level of accuracy. Recent developments regarding the description and prediction of binding energies can be found in Refs. [19-26]. In Ref. [27], Jiang et al. define the "experimental" symmetry energy as

where the terms $a_{\rm v}$, $a_{\rm s}$, $a_{\rm{Coul}}$, and $a_{\rm{pair}}$ correspond to the volume, surface, Coulomb, and pairing energies, and the adopted values (in units of MeV) are $a_{\rm v} = -15.6223$, $a_{\rm s} = 18.0571$, $a_{\rm{Coul}} = 0.7194$, and $a_{\rm{pair}} = -5.4423$, respectively [28]; $\delta_{np}$ is the same as in Ref. [28], and $E_{\rm W}$ is the Wigner energy. Using the local mass relation, i.e., the double difference of $e_{\rm s}$ for the neighboring four nuclei, the calculated coefficient of the $I^2$ volume term is equal to $32.10 \pm 0.31$ MeV, and the coefficient of the $I^2$ surface term is $-58.91\pm1.08$ MeV.

The possible next leading $I^4$ term of the symmetry energy may have effects on the incompressibility of infinite nuclear matter, the proton fraction in $\beta$-equilibrium neutron-star matter [29], the transition density and pressure at the inner edge separating the liquid core from the solid crust of neutron stars [30, 31], and the critical density for the direct Urca process, which leads to faster cooling of neutron stars [32]. Various theoretical approaches have been applied to evaluate the coefficient of the $I^4$ term. However, even for atomic nuclei or nuclear matter at normal saturation density, these approaches result in very different values, ranging from $-3$ to $20$ MeV [32-37]. Using the double difference of the "experimental" symmetry energy, Ref. [38] reported two different values for the $I^4$ coefficient: $3.3$ and $8.5$ MeV.

The Wigner energy is also important for characterizing the isospin dependence of nuclear binding energies. However, in Refs. [27, 38], the Wigner energy coefficient was considered to be a fixed value, rather than a free parameter. It is therefore the purpose of this paper to revisit the $I^2$ symmetry energy, Wigner energy, and possible $I^4$ symmetry energy terms, which are treated on the same footing, in binding energy formulae, along the line of Refs. [27, 38]. We remove the contributions of the volume, surface, Coulomb, and pairing energies from the experimental binding energy, and the residual result, denoted as $e_{\rm{sW}}$, is assumed to be our "experimental" symmetry-Wigner energy. We show that the double difference of $e_{\rm{sW}}$ is appropriate for simultaneously evaluating the $I^2$ symmetry energy and Wigner energy coefficients. The $I^4$ symmetry energy term is strongly correlated with the Wigner energy term.

We begin with the definition of the symmetry energy in the Bethe-Weizsäcker binding energy formula:

Here, we investigate the $I^2$ volume, $I^2$ surface, and $I^4$ volume terms, where $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, and $c^{({\rm V})}_{4}$ are the coefficients, respectively. Higher order terms, such as the $I^2$ curvature, $I^4$ surface, and $I^6$ volume terms are not discussed in this work. We use the definition of the Wigner energy given in Refs. [39-44]

where $\delta_{N,Z}$ is equal to 1 if $N = Z$ and 0 otherwise, and $\pi_{N,Z}$ is equal to 1 for odd-odd nuclei and vanishes for other $(N,Z)$ parities. We call the first term of Eq. (3) the ${ W}$ term and the second term the ${d}$ term, where $a_{W}$ and $a_{d}$ are the respective coefficients.

The equation for the double difference of a physical quantity $q$ considering the neighboring four nuclei is

which is akin to the second partial derivative of $q$:

A popular application of the double difference in nuclear physics is the empirical proton-neutron interaction between the last $i$ proton(s) and $j$ neutron(s), i.e., $\delta V_{i{p}j{n}}$ [41, 45-51], which is defined by the double difference of the binding energy, $D_{i{p}j{n}}(B)$. Using Eqs. (2) and (4), one can obtain the double difference of the symmetry energy term:

The $I^2$ volume term contributes the $A^{-1}$ leading term of $D_{i{p}j{n}}(E_{\rm{sym}})$. Similarly, using Eqs. (3) and (4), the double differences $D_{1{p}2{n}}$, $D_{2{p}1{n}}$, and $D_{2{p}2{n}}$ of the Wigner energy term are

By adopting the values $a_{\rm W} = 42.7$ MeV and $a_d = 28.7$ MeV, estimated in Ref. [44], we present the calculated $D_{1{p}2{n}}(E_{\rm W})$, $D_{2{p}1{n}}(E_{\rm W})$, and $D_{2{p}2{ n}}(E_{\rm W})$ in Fig. 1. For nuclei far away from the $N = Z$ line, $D_{i{p}j{ n}}(E_{\rm W})$ is positive and very close to 0. This can be seen from Eqs. (7)-(9), where $D_{i{p}j{n}}(E_{\rm W})$ is approximately proportional to $A^{-3}$. From Fig. 1, it is also clear that the absolute values of $D_{i{p}j{n}}(E_{\rm W})$ for nuclei with $N \sim Z$ are exceptionally large. These "anomalies" follow several compact trajectories, which can be explained by Eqs. (7)-(9). We exemplify this with the case of $D_{2{p}2{n}}(E_{\rm W})$ in Fig. 1(c). Using Eq. (9) and assuming $A$ is large, we obtain $D_{2{ p}2{n}}(E_{\rm W}) \approx -171/A$ MeV for even-even nuclei with $N = Z$, $-113/A$ MeV for odd-odd nuclei with $N = Z$, $-85/A$ MeV for nuclei with $|N-Z| = 1$, and $-29/A$ MeV for odd-odd nuclei with $|N-Z| = 2$. In Fig. 1(c), one sees that the "anomalies" follow these four relations.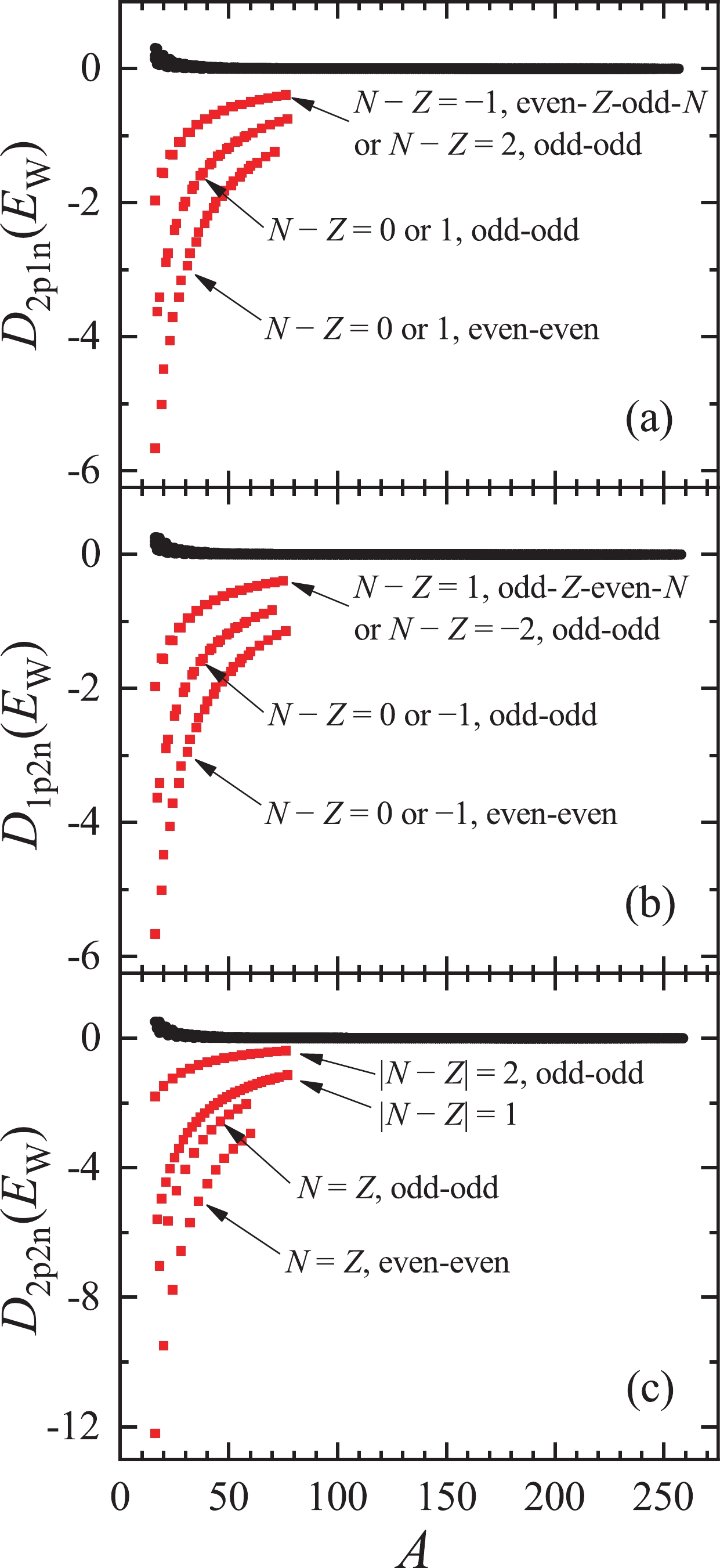

Figure 1.  (color online) Double differences of the Wigner energy, $D_{1{ p}2{ n}}(E_{\rm W})$, $D_{2{p}1{n}}(E_{\rm W})$, and $D_{2{p}2{ n}}(E_{\rm W})$, for nuclei with $A \geq 16$ in units of MeV [see Eqs. (7)-(9)]. The double difference of the Wigner energy is significantly enhanced for nuclei with $N \sim Z$ (see the squares in red) and becomes small and positive for the others (see the dots in black).

We simultaneously evaluate the $I^2$ symmetry energy and the Wigner energy coefficients, $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, $a_W$, and $a_d$, using the double difference formulae. The detailed procedure is as follows. First, we derive the "experimental" symmetry-Wigner energy as

where the experimental binding energy is taken from the AME2016 data table [52]. Our "experimental" symmetry-Wigner energy characterizes the isospin dependent part of the nuclear binding energy. Second, we calculate the double difference of the "experimental" symmetry-Wigner energy, i.e., $D_{i{p}j{n}}(e_{\rm{sW}})$. The double differences of the volume, surface, Coulomb, and pairing energy terms are close to zero [28, 50, 51], and we assume that

for nuclei with $A \geqslant 16$. We evaluate the coefficients $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, $a_W$, and $a_d$ via least squares fitting. In Table 1, the results of $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, $a_W$, and $a_d$ are clearly stable for different $(i,j)$, with small uncertainties. The values of $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, and $a_W$ are reasonably close to those given in Ref. [27] ($c^{({\rm V})}_{2} = 32.10$ MeV and $c^{({\rm S})}_{2} = -58.91$ MeV) and in Ref. [44] ($a_W = 42.7$ MeV). The value of $a_d$ is smaller than that given in Ref. [44] ($a_d = 28.7$ MeV). This is because the latter was extracted using the lowest $T = 0$ state energies, instead of the binding energy, in the odd-odd $N = Z$ nuclei.

	$D_{1p2n}$	$D_{2p1n}$	$D_{2p2n}$	average
$c^{({\rm V})}_{2}$	$31.23\pm0.96$	$31.23\pm0.95$	$31.19\pm0.71$	$31.22\pm0.51$
$-c^{({\rm S})}_{2}$	$50.38\pm3.17$	$50.63\pm3.12$	$50.48\pm2.35$	$50.50\pm1.68$
$a_W$	$39.11\pm1.48$	$38.81\pm1.45$	$38.63\pm1.25$	$38.85\pm0.81$
$a_d$	$18.59\pm2.68$	$17.33\pm2.63$	$20.35\pm3.23$	$18.76\pm1.65$

Table 1.  $I^2$ symmetry energy and Wigner energy coefficients, $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, $a_W$, and $a_d$, obtained by the double difference approach (in units of MeV). The uncertainties represent the 95% confidence interval for the coefficients.

The shell correction on the empirical proton-neutron interaction (i.e., the double difference of binding energies) was discussed in Refs. [50, 51], where it was shown that the proton-neutron interaction is stronger if the valence protons and neutrons fill in similar single particle orbits. This effect may also have an impact on the symmetry energy and the Wigner energy. We use the same shell correction term,

where $a_{\rm{sh}}$ and $b_{\rm{sh}}$ are parameters, for which we adopt the same values given in Table 1 of Ref. [51]; $N_{p}$ ($N_{n}$) is the valence proton (neutron) number with respect to the nearest closed shell; $\delta_{p}$ ($\delta_{n}$) is equal to $+1$ if the valence protons (neutrons) are particle-like and $-1$ if they are hole-like; and $\Omega_Z$ ($\Omega_N$) is half of the occupation number for the valence proton (neutron) shell. We remove $\Delta_{\rm{sh}}$ from $e_{\rm{sW}}$ and re-evaluate the $I^2$ symmetry energy and the Wigner energy coefficients, $c^{({\rm V})}_{2}$, $c^{({\rm S})}_{2}$, $a_W$, and $a_d$. Compared with the coefficients in Table 1, the value of $c^{({\rm V})}_{2}$ remains substantially unchanged, but the values of $-c^{({\rm S})}_{2}$, $a_W$, and $a_d$ are reduced to $43.03$, $30.28$, and $10.23$ MeV, respectively. The single particle orbit filling has a notable effect on the isospin dependence of nuclear binding energies.

One might ask whether the parametrization of the $I^4$ symmetry energy coefficient $c^{({\rm V})}_{4}$ using the double difference of $e_{\rm{sW}}$ is accurate. Unfortunately, this is not the case. In Eq. (6), one sees that the $I^4$ symmetry term contributes a high-order $A^{-3}$ term in $D_{i{ p}j{n}}(E_{\rm{sym}})$, which is much smaller than the leading terms contributed by the $I^2$ symmetry term. Furthermore, such a small term is strongly affected by the high-order $A^{-3}$ term in $D_{i{ p}j{n}}(E_{\rm W})$. This can be manifested by assuming

and evaluating $c^{({\rm V})}_{4}$ via the $\chi^2$ fitting for nuclei with $N-Z>2$. Here, we make use of three different forms of the Wigner term: $E_{\rm W}$ defined in Eq. (3) and $E_{\rm W}^{(1)}$ and $E_{\rm W}^{(2)}$ used in Ref. [28], i.e.,

where $a_{\rm W1} = 29.2$ MeV, $a_{\rm W2} = 10$ MeV, and $W_2 = 42$ MeV. Table 2 presents the results for $c^{({\rm V})}_{4}$. The value of $c^{({\rm V})}_{4}$ statistically deviates from zero and is strongly correlated with the forms of the Wigner energy. This explains why the $c^{({\rm V})}_{4}$ values obtained by the double difference approach are not self consistent in Ref. [38].

$c^{({\rm V})}_{4}$	$D_{1p2n}$	$D_{2p1n}$	$D_{2p2n}$
$E_{\rm W}$	$-0.99\pm0.02$	$-0.98\pm0.02$	$-0.97\pm0.02$
$E_{\rm W}^{(1)}$	$-6.27\pm0.32$	$-7.03\pm0.34$	$-5.86\pm0.25$
$E_{\rm W}^{(2)}$	$1.76\pm0.06$	$1.89\pm0.06$	$1.72\pm0.06$

Table 2.  $I^4$ coefficient $c^{({\rm V})}_{4}$ (in units of MeV) obtained by fitting the double difference of the Wigner energy terms $D_{i{ p}j{ n}}(E_{\rm W})$, $D_{i{ p}j{n}}(E_{\rm W}^{(1)})$, and $D_{i{p}j{n}}(E_{\rm W}^{(2)})$ with that of the $I^4$ symmetry energy term.

In a triple difference formula, the contributions of the $I^2$ symmetry energy and the Wigner energy to the binding energy are severely canceled out, and the $I^4$ term is expected to play a role if it is important. The triple difference of a physical quantity $q$ for neighboring nuclei is defined by

Using Eq. (2), the triple difference of the symmetry energy term is

Both the $I^2$ and $I^4$ symmetry energy terms contribute terms approximately proportional to $A^{-3}$ in $T_{i{p}j{ n}kt}(E_{\rm{sym}})$. Similar to Eqs. (1) and (10), we remove the contributions of the volume, surface, Coulomb, pairing, $I^2$ symmetry, and Wigner energies from the experimental binding energy:

The residual $e_{ I4}$ is assumed to be the "experimental" $I^4$ symmetry energy. Then, we calculate the triple differences $T_{i{p}j{ n}kt}(e_{I4})$ and $T_{i{ p}j{ n}kt}(I^4A)$ for nuclei with $A \geq 16$ and $N-Z >2$. If the $I^4$ symmetry energy is important, one would obtain $T_{i{ p}j{ n}kt}(e_{I4}) \approx c^{({\rm V})}_{4} T_{i{ p}j{n}kt}(I^4A)$.

Figure 2 presents the results of $T_{i{ p}j{n}kt}(e_{I4})$ versus $T_{i{ p}j{n}kt}(I^4A)$ for $(i,j,k) = (1,2,1)$ and $(1,2,2)$. $T_{i{p}j{n}kt}(e_{I4})$ does not exhibit a statistical correlation with $T_{i{p}j{n}kt}(I^4A)$. We calculate the Pearson correlation coefficients, and the absolute values are smaller than 0.1. The average of the $T_{i{p}j{n}kt}(e_{I4})$ values is very close to zero, and the root mean square deviation is approximately $0.3$ MeV. This fluctuation reflects nonsmooth changes in the binding energy for neighboring nuclei caused by microscopic effects such as the shell evolution, nuclear phase transition, and quantum chaos [53-55].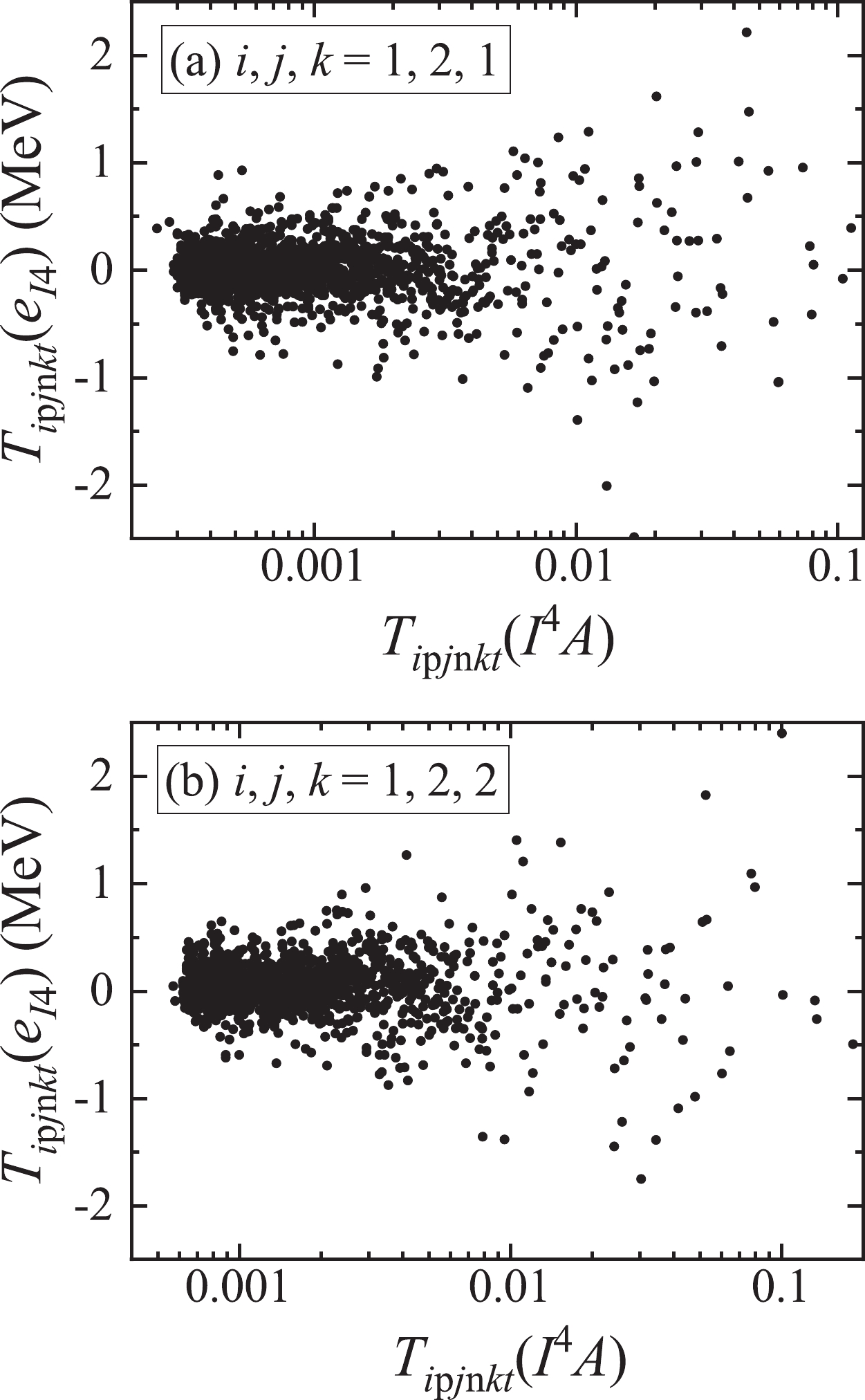

Figure 2.  Relationship between the triple difference of the "experimental" $I^4$ symmetry energy data, $T_{i{p}j{n}kt}(e_{I4})$, and that of the $I^4$ term, $T_{i{p}j{n}kt}(I^4A)$, for $(i,j,k) = (1,2,1)$ and $(1,2,2).$

We investigate the contributions of the $I^2$ symmetry energy, Wigner energy, and possible $I^4$ symmetry energy terms to the "experimental" symmetry-Wigner energy $e_{\rm{sW}}$. For a given isobar chain with $A = 4n$ ($n$ is an integer), the $I^2$ symmetry term in Eq. (2) and the Wigner term in Eq. (3) are reduced to

We fit $e_{\rm{sW}}$ data using various combinations of $E_{\rm s2}$, $E_{W}$, and $E_{\rm s4}$, as well as a constant $C$: $C+E_{\rm s2}$, $C + E_{\rm s2} + E_{\rm W}$, $C + E_{\rm s2} + E_{\rm s4}$, and $C + E_{\rm s2} + E_{\rm W} + E_{\rm s4}$. Figures 3(a)-3(d) present the difference between the $e_{\rm{sW}}$ values and the fitting results, denoted as $\Delta e_{\rm{sW}}$, for isobar chains with $A = 40$, 52, 64, and 100, respectively. Table 3 presents the results of the coefficients.

Figure 3.  (color online) Fitting the "experimental" symmetry-Wigner energy, $e_{\rm{sW}}$, with $C+E_{\rm s2}$, $C + E_{\rm s2} + E_{\rm W}$, $C + E_{\rm s2} + E_{\rm s4}$, and $C + E_{\rm s2} + E_{\rm W} + E_{\rm s4}$ (where $C$, $E_{\rm s2}$, $E_{\rm W}$, and $E_{\rm s4}$ are the constant, $I^2$ symmetry energy, Wigner energy, and $I^4$ symmetry energy terms, respectively), for isobar chains with $A =$40, 52, 64, and 100. $\Delta e_{\rm{sW}}$ denotes the difference between the $e_{\rm{sW}}$ value and the fitting result.

coefficients	$C + E_{\rm s2}$	$C + E_{\rm s2} + E_{\rm W}$	$C + E_{\rm s2} + E_{\rm s4}$	$C + E_{\rm s2} + E_{\rm W} + E_{\rm s4}$
$A = 40$
$C$	$5.08\pm1.76$	$2.22\pm1.06$	$4.08\pm1.64$	$2.04\pm1.31$
$a_{2}$	$20.00\pm1.11$	$15.78\pm1.36$	$23.20\pm3.10$	$14.46\pm4.78$
$a_{\rm W}$	−	$55.21\pm17.14$	−	$63.00\pm32.78$
$c^{\rm (V)}_{4}$	−	−	$-37.87\pm35.38$	$8.51\pm29.40$
$A = 52$
$C$	$2.59\pm1.71$	$0.24\pm1.37$	$1.72\pm1.55$	$0.10\pm1.80$
$a_{2}$	$20.59\pm0.97$	$16.95\pm1.77$	$23.29\pm2.66$	$15.94\pm6.73$
$a_{\rm W}$	−	$54.40\pm25.51$	−	$61.65\pm54.20$
$c^{\rm (V)}_{4}$	−	−	$-40.29\pm38.17$	$7.92\pm50.08$
$A = 64$
$C$	$3.54\pm1.21$	$1.87\pm0.91$	$2.69\pm0.70$	$2.15\pm0.93$
$a_{2}$	$22.20\pm0.62$	$19.96\pm1.02$	$24.32\pm1.04$	$21.99\pm3.17$
$a_{\rm W}$	−	$38.67\pm17.04$	−	$22.27\pm28.98$
$c^{\rm (V)}_{4}$	−	−	$-36.35\pm17.12$	$-18.47\pm27.56$
$A = 100$
$C$	$-0.31\pm3.44$	$-8.35\pm0.53$	$-3.49\pm2.56$	$-8.65\pm0.5$
$a_{2}$	$23.74\pm1.08$	$17.54\pm0.34$	$28.45\pm2.28$	$16.42\pm0.98$
$a_{\rm W}$	−	$173.55\pm9.58$	−	$188.49\pm14.78$
$c^{\rm (V)}_{4}$	−	−	$-76.66\pm35.67$	$9.45\pm7.94$

Table 3.  The coefficients $a_{2}$, $c^{\rm (V)}_{4}$, and $a_{\rm W}$, as well as the constant $C$, obtained by fitting the "experimental" symmetry-Wigner energy, $e_{\rm{sW}}$, for isobar chains with $A =$40, 52, 64, and 100, respectively (in units of MeV).

In Figs. 3(a)-3(d), one sees that neither $C+E_{\rm s2}$ nor $C+E_{\rm s2}+E_{\rm s4}$ reproduces the data correctly, especially for the $N = Z$ nuclei. This discrepancy is explained by the Wigner energy [39]. The formula $C + E_{\rm s2} + E_{\rm W}$ is good enough to reproduce the macroscopic isospin dependence of the $e_{\rm{sW}}$ data, and the $I^2$ symmetry energy coefficient, $a_2$, obtained by fitting is equal to 15.78, 16.95, 19.96, and 17.54 MeV for $A = 40$, 52, 64, and 100, which is reasonably close to $c^{\rm (V)}_2 + c^{\rm (S)}_2 A^{-1/3} =$ 14.87, 16.32, 17.37, and 19.41 MeV, respectively. The Wigner energy coefficient, $a_{\rm W}$, obtained by fitting for $A = 40$, 52, and 64 is close to 42.7 MeV, as given by Ref. [44], but that for $A = 100$ is extraordinarily large. A possible reason for this anomaly is that the Coulomb energy for heavy nuclei is overestimated by $0.7194 \times Z^{2}A^{-1/3}(1-Z^{-2/3})$ MeV in Eq. (1). The formula $C + E_{\rm s2} + E_{\rm W} + E_{\rm s4}$ predicts almost the same energies as $C + E_{\rm s2} + E_{\rm W}$ does, but the uncertainties of the coefficients $a_{\rm W}$ and $c^{\rm (V)}_{4}$ in the former are very large. This indicates that the $I^4$ symmetry energy term is strongly correlated with the Wigner energy term, while considering the $I^4$ term in the binding energy formula does not substantially improve the results.

For nuclei not very far away from the stability line in the $sd$ shell and the $pf$ shell, the binding energies calculated by the nuclear shell model with the USDA [56] and GXPF1 [57] effective interactions are quite similar to the experimental data. Refs. [58-60] show that the symmetry energy and the Wigner energy can be explained in terms of the monopole interaction in the framework of the shell model. The monopole interaction is derived from the shell-model effective two-body interaction, and in the single particle space of one major shell, it is written as [61-63]

where ${\hat{A}_{m\tau}^{JT}(j_1 j_2) }^{\dagger} = ( \hat{a}_{j_1}^{\dagger} \times \hat{a}_{j_2}^{\dagger} )_{m\tau}^{JT}$ is the creation operator of a nucleon pair, and $V_{JT}(j_1 j_2 j_3 j_4)$ is the two-body matrix element.

The monopole interaction $\hat{V}_m$ also can be written by

where

$\hat{V}_m$ exhausts the contribution of the monopole force, which is composed of number and isospin operators, and thus provides the average energy of configurations at a fixed number of particles and isospin for each orbit. From Eq. (23), it can be seen that the isospin-isospin dot product term of the monopole interaction, $\hat{T}_{j_1} \cdot \hat{T}_{j_2}$, may explain the isospin dependence of binding energies. In a simplified single-$j$ shell case, the total energy of a system with the monopole interaction can be written analytically as

Here, the isospin linear term is the Wigner energy, and the isospin quadratic term is the $I^2$ symmetry energy.

For multi-$j$ shell cases, we extract the $I^2$ symmetry energy coefficients using shell-model calculations with the effective interaction and the monopole interaction. Specifically, using the NushellX code [64], we calculate the ground-state energies for 73 nuclei in the $sd$ shell ($^{17\sim24}{\rm{O}}$, $^{18\sim25}{\rm{F}}$, $^{20\sim28}{\rm{Ne}}$, $^{22\sim29}{\rm{Na}}$, $^{24\sim30}{\rm{Mg}}$, $^{26\sim31}{\rm{Al}}$, $^{28\sim34}{\rm{Si}}$, $^{30\sim35}{\rm{P}}$, $^{32\sim36}{\rm{S}}$, $^{34\sim37}{\rm{Cl}}$, $^{36\sim38}{\rm{Ar}}$, and $^{38\sim39}{\rm{K}}$), for which we use the effective USDA interaction, and the ground-state energies for 41 nuclei in the $pf$ shell ($^{41\sim48}{\rm{Ca}}$, $^{42\sim49}{\rm{Sc}}$, $^{44\sim50}{\rm{Ti}}$, $^{46\sim51}{\rm{V}}$, $^{48\sim52}{\rm{Cr}}$, $^{50\sim53}{\rm{Mn}}$, $^{52\sim54}{\rm{Fe}}$), for which we use the effective GXPF1 interaction. Using the double difference $D_{1p2n}$ and the binding energies from our shell-model calculations, we obtain the symmetry energy coefficients. In Table 4, one sees that $c^{({\rm V})}_{2}$ and $c^{({\rm S})}_{2}$ obtained with the monopole interaction are similar to those obtained by the effective interactions and the experimental binding energy data. Theoretically, an isospin quartic term of the monopole interaction, such as $(\hat{T}_{j_1} \otimes \hat{T}_{j_2}) \cdot (\hat{T}_{j_3} \otimes \hat{T}_{j_4})$, is considered to be responsible for the $I^4$ symmetry energy, but even state-of-the-art shell-model calculations have not essentially dealt with effective four-body interactions.

	Expt.	effective	monopole
$c^{({\rm V})}_{2}$	34.53	35.09	37.61
$-c^{({\rm S})}_{2}$	63.59	65.79	69.22

Table 4.  The $I^2$ symmetry energy coefficients, $c^{({\rm V})}_{2}$ and $c^{({\rm S})}_{2}$, extracted using the double difference $D_{1p2n}$ for nuclei in the $sd$ shell and the $pf$ shell (in the unit of MeV). "Expt." represents the result extracted from experimental binding energy data; "Effective" represents the result extracted from binding energies calculated using the shell model with the USDA and GXPF1 interactions; "Monopole" represents the result extracted from binding energies calculated using the shell model with the monopole interaction.

In summary, we revisit the symmetry and Wigner energy terms in the binding energy formula, along the line of Refs. [27, 38]. Using the double difference (denoted by $D_{i{ p}j{ n}}$) for the "experimental" symmetry-Wigner energies of four neighboring nuclei, we simultaneously evaluate the $I^{2}$ symmetry energy and the Wigner energy coefficients. The results are stable for different sets of $(i,j)$ with small fluctuations, and the optimal values are $c^{({\rm V})}_{2} = 31.22 \pm 0.51$ MeV, $c^{({\rm S})}_{2} = 50.50 \pm 1.86$ MeV, $a_{\rm W} =$$38.85 \pm 0.81$ MeV, and $a_d = 18.76 \pm 1.65$ MeV.

We find that the double difference approach is not appropriate for extraction of the $I^{4}$ symmetry energy coefficient. We calculate the triple differences for the "experimental" $I^{4}$ symmetry energies and for the $I^{4}$ symmetry energy terms of eight neighboring nuclei. The Pearson correlation coefficient between them is close to zero. We show that the macroscopic isospin dependence of our "experimental" symmetry-Wigner energy is well explained by the $I^{2}$ symmetry energy and the Wigner energy, and further considering the $I^{4}$ term does not substantially improve the calculation result; no contribution of the $I^{4}$ symmetry energy is found in the binding energy of atomic nuclei. It is worth noting that the binding energy data are still not very far away from the stability line. For neutron-rich regions or high-density nuclear matter, the contribution of the $I^{4}$ symmetry energy may become non-negligible.