-
Although the discovery of Higgs boson [1, 2] demonstrated the viability of the Standard Model (SM), there is convincing evidence of physics beyond SM, such as the origin of dark matter (DM) and tiny neutrino masses. Recent Plank data indicate that dark matter accounts for approximately 85% of the total matter content in the universe [3]. Among various candidates of particle DM, the weakly interacting massive particles (WIMPs) are the most popular recipes [4, 5], owing to the fact that thermally produced WIMPs with weak-scale cross section can naturally facilitate the observed DM relic density.
The Inert Doublet Model (IDM) [6-8] is one of the simplest extensions of the SM that provides a candidate for DM. This model introduces an inert Higgs doublet, which is odd under the unbroken
$ Z_2 $ symmetry. There are four additional scalars similar to the usual two Higgs doublet models [9], i.e., neutral CP-even (H), neutral CP-odd (A), and charged scalars ($ H^\pm $ ). The imposed unbroken$ Z_2 $ symmetry not only inhibits Yukawa interactions of inert scalars with SM fermions but also protects the lightest inert scalar to be stable. In this study, we consider the neutral CP-even scalar H as a DM candidate. If we further introduce$ Z_2 $ -odd right-hand neutrinos, the tiny neutrino masses can also be realized by the Scotogenic mechanism [10-14]. The phenomenology of the IDM has been extensively studied in Refs. [15-45].It is evident that the current positive validations of DM all originate from cosmological observations, which are based on the gravitational effects of DM. Therefore, the nature of DM remains an open question. To verify its nature, searches have been performed along three directions: direct detection, indirect detection, and collider signature directions. Despite the non-observation of direct detection signal, which has already put stringent constraints on the parameter space of IDM [34, 46], it remains appealing to extract positive indirect detection or collider signatures. For instance, low mass DM in IDM can explain the Galactic center excess reported by Fermi-LAT [47]. Meanwhile, a large parameter space of high mass DM in IDM is detectable at the Cherenkov Telescope Array [48, 49]. Regarding collider searches, the promising signatures available are the dilepton [50, 51], trilepton [52], and teralepton channels [22, 53] at LHC. The vector boson fusion (VBF) channel
$ pp\to HHjj $ is also considered in Refs. [54, 55]. Other promising collider signatures can be found in Refs. [56-62].The same-sign pair production of charged Higgs bosons via vector boson fusion (VBF) in two Higgs doublet model was recently proposed by Ref. [63] to explore the nature of the Higgs potential, where two typical decay modes
$ H^\pm\to \tau \nu $ and$ H^\pm \to tb $ are considered. The decay modes$ H^\pm \to W^\pm A $ with$ A\to b\bar{b} $ or$ A\to \tau^+\tau^- $ were also studied in Ref. [64]. In this study, we consider the decay mode$ H^\pm \to W^\pm H $ with H as the DM candidate, which triggers the same-sign dilepton signature$ pp\to $ $ H^\pm H^\pm jj \to (W^\pm H)(W^\pm H)jj\to l^\pm l^\pm jj+{\not\!\!{E}}_T $ . Notably, the well studied opposite-sign dilepton signature in IDM is only promising with compressed mass spectrum$ \Delta m = m_A-m_H\in [40, 80] $ GeV [50]. A distinct nature of the same-sign dilepton signature is that its production cross section is enhanced with an increase in mass splitting$ \Delta m $ [63]. Meanwhile, the SM background of the same-sign dilepton signature [65-68] is significantly smaller than the opposite-sign dilepton. Therefore, we expect the same-sign dilepton signature to be promising for a large$ \Delta m $ , which complements the opposite-sign dilepton signature.This paper is organized as follows. In Sec. II, we briefly review the inert doublet model. Focusing on the low mass region
$ m_H<100 $ GeV, a viable parameter space is explored by considering certain constraints. A detailed study of the same-sign dilepton signature is presented in Sec. III. Finally, a conclusion is provided in Sec. IV. -
In this study, we consider the IDM proposed in Ref. [6, 8]. In addition to the SM Higgs doublet
$ H_1 $ , an inert Higgs doublet$ H_2 $ is further introduced. The inert doublet$ H_2 $ is odd under an imposed$ Z_2 $ symmetry; hence,$ H_2 $ does not directly couple to SM fermions but solely to gauge bosons. The$ Z_2 $ symmetry also ensures the stability of the DM candidate. Provided the$ Z_2 $ symmetry is not broken spontaneously, then$ H_2 $ will not develop a vacuum expectation value (VEV). The Higgs doublets can be denoted as$ H_1 = \left( \begin{array}{c} G^+\\ \dfrac{1}{\sqrt{2}}(v+h+{\rm i} G^0) \end{array}\right),\quad H_2 = \left( \begin{array}{c} H^+\\ \dfrac{1}{\sqrt{2}}(H+ {\rm i} A) \end{array}\right), $

(1) where
$ G^\pm,G^0 $ , v, and h represent the would-be Goldstone bosons, VEV of$ H_1 $ , and SM Higgs boson, respectively. The Higgs potential under the exact$ Z_2 $ symmetry is given by$ \begin{aligned}[b] V =& \mu_1^2 H_1^\dagger H_1+\mu_2^2 H_2^\dagger H_2+\lambda_1 (H_1^\dagger H_1)^2 + \lambda_2 (H_2^\dagger H_2)^2 \\&+\lambda_3 (H_1^\dagger H_1) (H_2^\dagger H_2)+ \lambda_4 (H_1^\dagger H_2)(H_2^\dagger H_1) \\&+\frac{\lambda_5}{2} \left[ (H_1^\dagger H_2)^2 +{\rm{h.c.}} \right]. \end{aligned} $

(2) Here, all the free parameters are considered real. Owing to the unbroken
$ Z_2 $ symmetry, the term$ \mu_{12}^2(H_1^\dagger H_2 + H_2^\dagger H_1) $ is forbidden. Therefore,$ H_1 $ and$ H_2 $ do not mix. After the electroweak symmetry breaking, masses of scalars are given by$ m_h^2 = -2\mu_1^2 = 2\lambda_1 v^2, $

(3) $ m_H^2 = \mu_2^2 + \frac{1}{2}(\lambda_3+\lambda_4+\lambda_5)v^2, $

(4) $ m_A^2 = \mu_2^2 + \frac{1}{2}(\lambda_3+\lambda_4-\lambda_5)v^2, $

(5) $ m_{H^\pm}^2 = \mu_2^2 +\frac{1}{2}\lambda_3 v^2. $

(6) H is considered the DM candidate in the following studies, which corresponds to
$ \lambda_5<0 $ . For A being DM candidate, one can simply make the replacement$ \lambda_5\leftrightarrow -\lambda_5 $ . The parameters$ \mu_1 $ and$ \lambda_1 $ can be fixed by the SM Higgs mass$ m_h $ and VEV v. Then, we are left with five free parameters, i.e.,$ \{\mu_2,\lambda_2,\lambda_3,\lambda_4,\lambda_5\} $ . A more convenient set of parameters are$ \{m_H,m_A,m_{H^\pm},\lambda_2,\lambda_L\} $ , where$ \lambda_L = (\lambda_3+\lambda_4+\lambda_5)/2 $ describes the Higgs-DM interaction$ hHH $ .Extensively discussed in previous studies, the above parameter set is constrained by various theoretical and experimental bounds. Benchmark points (BPs), which satisfy all constraints, have been provided in Ref. [60]. Here, we briefly discuss the relevant constraints to the low mass region we adopted. More details can be found in Refs. [34, 60].
● Perturbativity: The model is perturbative when the quartic couplings satisfy
$ |\lambda_1,\lambda_2,\lambda_3,\lambda_4,\lambda_5|\leq 4\pi. $

(7) ● Vacuum stability: The stability of the Higgs potential at tree level is guaranteed by the boundary from the conditions
$ \begin{aligned}[b] & \lambda_1>0,\;\;\;\;\lambda_2>0,\;\;\;\;\lambda_3+2\sqrt{\lambda_1\lambda_2}>0, \;\;\;\; \\ & \lambda_3+\lambda_4-|\lambda_5| +2\sqrt{\lambda_1\lambda_2}>0. \end{aligned} $

(8) ● Global minimum: To ensure the locality of the inert minimum, the following must be satisfied [69]:
$ \frac{\mu_1^2}{\sqrt{\lambda_1}}\leqslant \frac{\mu_2^2}{\sqrt{\lambda_2}}. $

(9) Using Eqs. (3) and (4), the above condition can be translated to
$ \lambda_L\leqslant \frac{\sqrt{2\lambda_2}m_h v+2m_H^2}{2v^2}. $

(10) ● Unitarity: The unitarity of the S-matrix, which originates from scattering processes among scalars and gauge bosons, requires that the corresponding absolute eigenvalues of the scattering matrix should be less than
$ 8\pi $ [70]. By requiring the unitarity conditions to be valid up to approximately 10 TeV, the mass splittings are determined to be in the region [53, 71]$ m_A-m_H\lesssim 300\; {{\rm{GeV}}},\; m_{H^\pm}-m_H\lesssim 300\; {{\rm{GeV}}}. $

(11) ● Electroweak precision tests: The inert Higgs doublet will contribute to the oblique S and T parameters. Analytic expressions can be found in Ref. [34]. Regarding the experimental limits, we adopt the global fit result in Ref. [72]
$ S = 0.06\pm 0.09,\;\;\;\; T = 0.01\pm 0.07, $

(12) with correlation coefficient + 0.91.
● Gauge boson widths: The measurement of decay widths of gauge bosons
$ W^\pm $ and Z indicate that masses of inert scalars should satisfy the following conditions$ m_{A,H}+m_{H^\pm}>m_W,\;\;\;\; m_A+m_H>m_Z,\;\;\;\; 2m_{H^\pm}>m_Z. $

(13) Thus, decays of
$ W^\pm,\;Z $ to inert scalars are not kinetically open.● Collider searches: Searches for supersymmetric particles at LEP via dijet or dilepton signals have excluded the following mass region [17]
$ m_A\leqslant 100\; {{\rm{GeV}}},\;\;\;\; m_H\leqslant 80\; {{\rm{GeV}}},\;\;\;\; m_A-m_H\geqslant 8\; {{\rm{GeV}}}, $

(14) when the above conditions are satisfied simultaneously. Meanwhile, chargino searches have set a lower limit on the charged scalar [73]
$ m_{H^\pm}\geqslant 70 \; {{\rm{GeV}}}. $

(15) Since the
$ Z_2 $ symmetry is unbroken in IDM, the inert scalars do not directly couple to SM fermions. Hence, single production channels, such as$ pp\to A, H, H^\pm tb $ , are absent at the LHC. In this way, the searches for usual 2HDM at LHC are not applicable for the IDM [9, 74, 75]. The promising signatures at LHC are the dilepton and trilepton signals via associated production$ pp \to AH\to ZHH\to l^+l^- + {\not\!\!{E}}_T, $

(16) $ pp \to H^\pm A \to W^\pm H+ZH\to l^\pm l^+l^-+ {\not\!\!{E}}_T. $

(17) The reinterpretation of SUSY electroweakino searches for the dilepton and trilepton signals in the IDM indicates that existing LHC electroweakino searches are not sensitive to the IDM [55]. The recent recasting of mono-Z and mono-W signals in Ref. [42] also indicates that the parameter space of IDM is safe at the current LHC. Basically, the parameter space of IDM is still allowed at the current LHC, provided the above LEP limits are satisfied [41].
● SM Higgs data: Because the inert scalars do not mix with SM Higgs, the SM Higgs couplings to fermions and gauge bosons are the same as in the SM at tree-level. Meanwhile, loop corrections to these couplings are beyond the conventional precision of Higgs coupling measurements at LHC. The Higgs invisible decay channel receives an additional contribution when DM is sufficiently light, i.e.,
$ m_H<m_h/2 $ . The current experimental limit on the branching ratio of Higgs invisible decay is [76]$ {\rm{BR}}(h\to {\rm{invisible}})<0.24. $

(18) The charged scalar
$ H^\pm $ will also impact the Higgs to$ \gamma\gamma $ and$ Z\gamma $ channels via one loop contribution [23]. The experimental signal strength of diphoton$ \gamma\gamma $ is [77]$ \mu_{\gamma\gamma} = 1.14^{+0.38}_{-0.36}. $

(19) The observed upper limit of the signal strength
$ h\to Z\gamma $ is 3.6 times the SM prediction [78]. Because the deviations in the branching ratio of$ h\to Z\gamma $ is always smaller than the deviations in$ h\to \gamma\gamma $ [23], the$ h\to Z\gamma $ limit is always satisfied when the$ h\to \gamma\gamma $ limit is considered.● Relic density: The DM relic density observed by the Planck experiment is [3]
$ \Omega h^2 = 0.1200\pm 0.0012. $

(20) In this study, the theoretical DM relic density of H is required to be within the
$ 3\sigma $ range of the observed value. MicrOmegas [79] is adopted to calculate the relic density.● Direct detection: In this study, we consider the direct detection limit on the spin-independent cross section based on the XENON1T experiment [80], which is currently the most stringent one.
Focusing on the low mass region, we randomly scan the parameter space in the following regions
$ \begin{aligned}[b]& m_H\in[50,80]\; {{\rm{GeV}}}, \;\;\;\; \lambda_L\in[-0.04,0.04],\;\;\;\; \lambda_2\in[0,1]\\ & m_A-m_H\in[0,300]\; {{\rm{GeV}}},\;\;\;\; m_{H^\pm}-m_H\in[0,300]\; {{\rm{GeV}}}. \end{aligned} $

(21) This parameter space was primarily selected based on previous results in Ref. [34]. Basically, the limits on Higgs invisible decay exclude the region
$ m_H\lesssim 53 $ GeV with correct relic density. However, for$ m_H\gtrsim 76 $ GeV, the correct relic density requires$ |\lambda_L|>0.04 $ , which is already excluded by the LUX experiment [81].Scanned results are presented in Fig. 1. The relic density requirement within the
$ 3\sigma $ range, together with the direct detection limit from XENON1T, strictly constrain the parameter space. From Figs. 1(a) and (b), it is clear that the allowed samples of our scan fall into three separated regions. One is the Higgs resonance region at approximately$ m_H\lesssim m_h/2 $ . Another region is the vector boson annihilation region at$ m_H\sim71.5 $ GeV, where the dominant annihilation channel is$ HH\to VV (V = Z,W) $ . The mass region$ 63\; {{\rm{GeV}}}\lesssim m_H\lesssim 71 $ GeV with$ m_A>100 $ GeV is then excluded by XENON1T. The third region is the narrow coannihilation region$ m_A-m_H\sim 8 $ GeV. Since degenerate$ m_A $ and$ m_H $ will trigger the elimination of the same-sign charged Higgs pair at LHC [63], we will not consider such coannihilation region in the following. In Fig. 1(c), results in the$ (m_A,m_{H^\pm}) $ plane are also presented. All the survived points satisfy$ m_A\lesssim m_{H^\pm} $ , primarily owing to constraints from S and T parameters in Eq. (12). The mass gap between$ 80\; \lesssim $ $ m_A<100 $ GeV corresponds to the excluded region of LEP in Eq. (14). Because the same-sign dilepton signature is sensitive to the mass splitting$ \Delta m = m_A-m_H $ , corresponding results are also depicted in Fig. 1(d).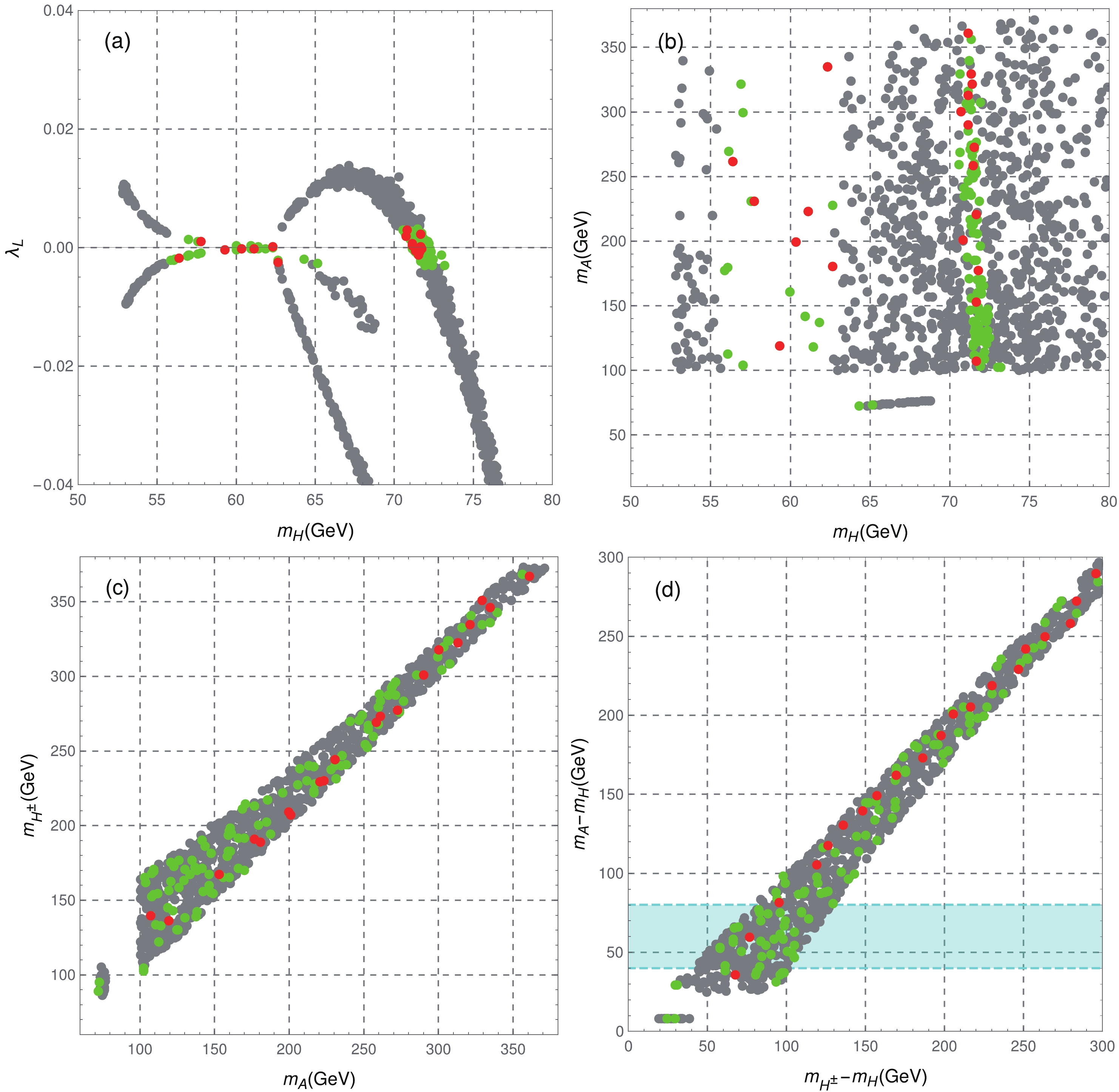
Figure 1. (color online) Scanned results of the low mass region. Distribution of samples in the
$(m_H,\lambda_L)$ plane (panel a),$(m_A,m_H)$ plane (panel b),$(m_{H^\pm},m_A)$ plane (panel c), and$(m_{H^\pm}-m_H,m_A-m_H)$ plane (panel d). The gray points satisfy the constraints discussed from Eqs. (7) to (20); however, they are excluded by the XENON1T result [80]. The green and red points are allowed by all constraints. The red points, which have been listed in Table 1, are the BPs selected to follow the same-sign dilepton signature. The light blue band in panel d corresponds to the promising region of the opposite-sign dilepton signature [50].Based on the above scanned results, we have selected 20 BPs (red BPs in Fig. 1) for the following study. Detailed information on these BPs can be found in Table 1. In contrast to Ref. [60], we have selected more BPs with
$ \Delta m >150 $ GeV. For BP1 to BP10, they could also be probed at the 380 GeV CLIC with the 1 ab$ ^{-1} $ data, whereas the other ten BPs are at approximately 1.5 TeV CLIC with 2.5 ab$ ^{-1} $ data [61].No. $ m_H $ /GeV

$ m_A $ /GeV

$ m_{H^\pm} $ /GeV

$ \lambda_2 $ 

$ \lambda_L $ 

$ \Omega h^2 $ 

$ \sigma $ @14TeV/fb

$ \sigma $ @27TeV/fb

BP1 71.69 107.5 139.6 0.4097 0.002203 0.1210 0.054 0.160 BP2 59.30 119.1 136.3 0.09806 −0.0004655 0.1213 0.154 0.451 BP3 71.67 152.9 167.0 0.1750 0.0001029 0.1233 0.214 0.657 BP4 71.76 177.0 190.9 0.3855 −0.0002066 0.1180 0.285 0.914 BP5 62.64 180.5 189.1 0.7473 −0.002478 0.1177 0.355 1.139 BP6 70.82 201.1 206.8 0.8602 0.002879 0.1233 0.373 1.232 BP7 60.37 199.7 208.8 0.6200 −0.0002771 0.1210 0.409 1.351 BP8 71.63 220.8 229.1 0.5264 −0.0007215 0.1193 0.399 1.362 BP9 61.12 223.2 230.3 0.4692 −0.0002002 0.1227 0.454 1.553 BP10 57.76 230.7 244.3 0.9192 0.0009435 0.1185 0.454 1.578 BP11 71.44 258.6 269.0 0.6848 −0.0007471 0.1214 0.446 1.616 BP12 71.55 272.6 277.1 0.00294 −0.001236 0.1205 0.483 1.765 BP13 56.40 261.4 273.1 0.5082 −0.001733 0.1191 0.495 1.799 BP14 71.17 290.1 301.2 0.5216 0.0006213 0.1200 0.467 1.788 BP15 70.72 299.9 317.8 0.7495 0.001944 0.1235 0.451 1.755 BP16 71.12 312.9 322.7 0.04812 0.0002456 0.1221 0.482 1.892 BP17 71.39 321.4 334.9 0.7437 −0.0001886 0.1172 0.468 1.883 BP18 71.31 329.1 350.8 0.1182 −0.0005298 0.1204 0.441 1.813 BP19 62.32 334.6 346.0 0.2196 0.0001064 0.1180 0.498 2.037 BP20 71.14 360.8 366.8 0.1079 0.0005207 0.1192 0.495 2.087 Table 1. BPs for the same-sign dilepton signature. Here,
$ \sigma $ denotes the cross section of$ pp\to H^\pm H^\pm jj $ with preselection cuts in Eq. (22). -
Before discussing the same-sign dilepton signature, we first consider the branching ratio of the charged scalar
$ H^\pm $ . There are two possible decay modes of$ H^\pm $ in the IDM. One is$ H^\pm\to W^\pm H $ , and the other is$ H^\pm \to W^\pm A $ . For the special scenario$ m_H\sim m_A<m_{H^\pm} $ ,$ {\rm{BR}}(H^\pm\to $ $ W^\pm H)\approx {\rm{BR}}(H^\pm\to W^\pm A)\approx 0.5 $ is obtained. However, the precise measurements of S and T parameters require$ m_H<m_A\lesssim m_{H^\pm} $ , which triggers a phase space suppression of the$ H^\pm \to W^\pm A $ mode. In Fig. 2, we illustrate the branching ratio of$ H^\pm $ . For$ m_{H^\pm}-m_A = 30 (15) $ GeV,$ {\rm{BR}}(H^\pm\to W^\pm A)<0.01 $ is obtained, i.e.,$ {\rm{BR}}(H^\pm\to $ $ W^\pm H)>0.99 $ , when$ m_{H^\pm} > 135 (100) $ GeV. In other words,$ H^\pm\to W^\pm H $ is always the dominant decay mode (approximate to one) for the BPs in Table 1.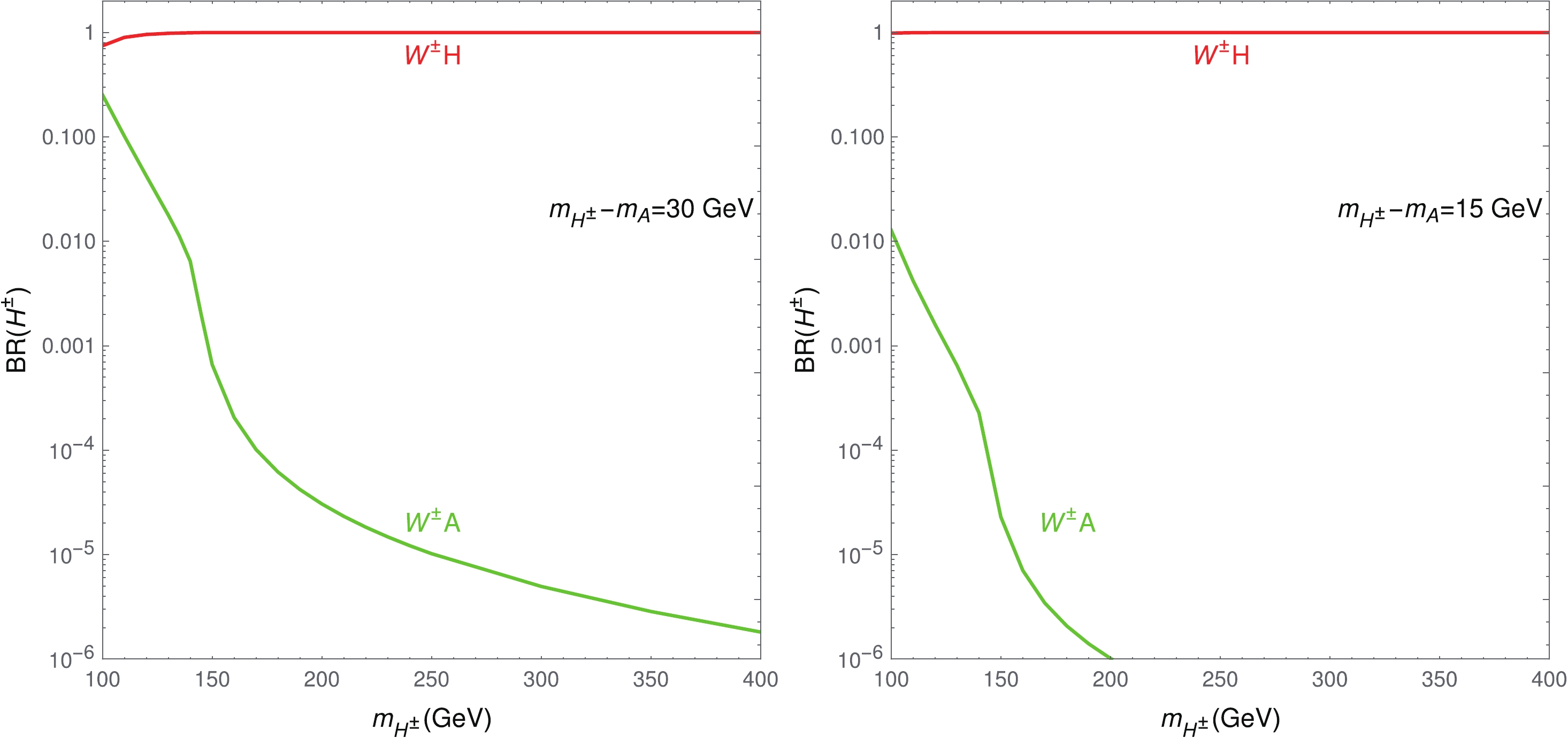
Figure 2. (color online) Branching ratio of the charged scalar
$H^\pm$ for$m_{H^\pm}-m_A=30 $ GeV (left panel) and$m_{H^\pm}-m_A=15 $ GeV (right panel), where$m_H$ is fixed to be 62 GeV in both cases. The package 2HDMC [82] is used to calculate these branching ratios.An important validation of the process
$ pp\to H^\pm H^\pm jj $ is that its cross section is approximately proportional to the square of the mass splitting$ \Delta m $ [64]. The dependence of the cross sections$ \sigma(pp\to H^\pm H^\pm jj) $ at different mass splittings$ \Delta m $ is depicted in Fig. 3. During the calculation, Madgraph5_aMC@NLO [83] is employed with the preselection cuts for VBF processes at parton level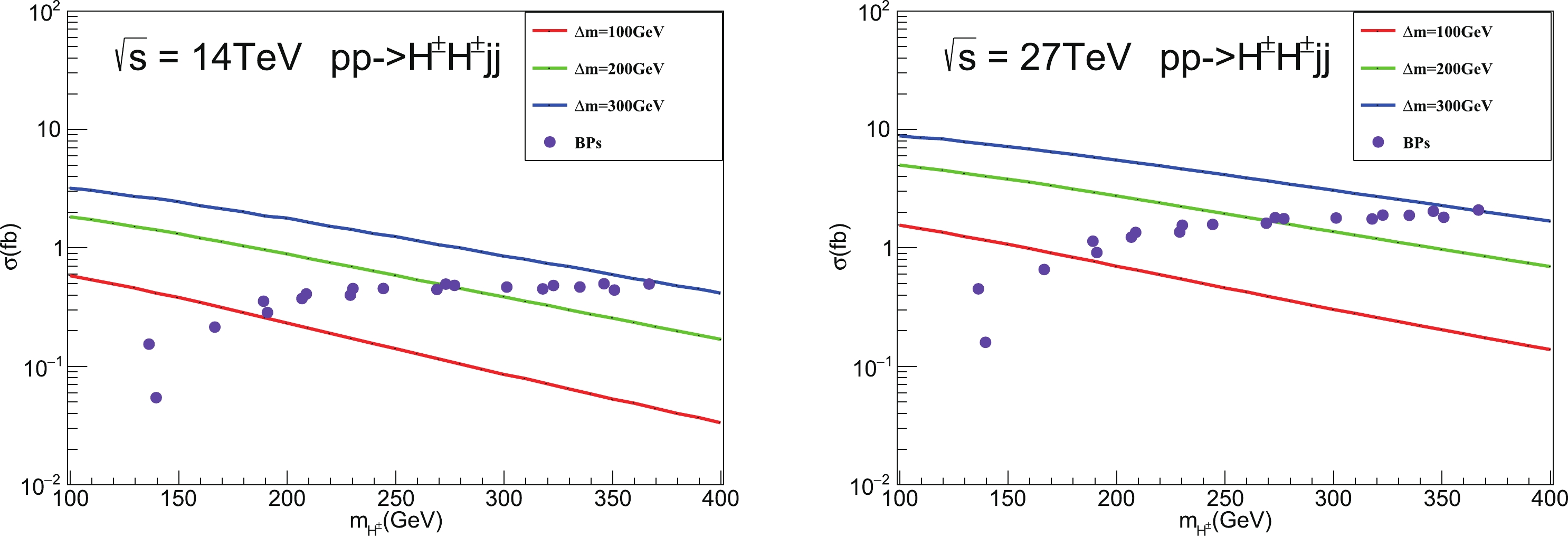
Figure 3. (color online) Production cross section of process
$pp\to H^\pm H^\pm jj$ at$\sqrt{s}=14$ TeV HL-LHC (left panel) and$\sqrt{s}=27$ TeV HE-LHC (right panel) as a function of$m_{H^{\pm}}$ with$\Delta{m}=$ 100, 200, 300 GeV, respectively. Here, we also fix$m_H=62$ GeV. Furthermore, the cross sections of the BPs listed in Table 1 are depicted here. Note that the preselection cuts in Eq. (22) are already applied.$ \eta_{j_1}\times \eta_{j_2} <0,\; |\Delta \eta_{jj}|>2.5. $

(22) From Fig. 3, it can be observed that following the enlargement of
$ \Delta m $ from$ \Delta m = 100 $ GeV to$ \Delta m = 300 $ GeV, the production cross section is enlarged approximately ten times for the same value of$ m_{H^\pm} $ . In the actual model,$ m_A\lesssim m_{H^\pm} $ should be satisfied. Hence, the results of BPs in Table 1 are further illustrated. It is obvious that at the 14 TeV HL-LHC, the cross section usually increases as$ m_{H^\pm} $ becomes larger when$ m_{H^\pm}\lesssim 250 $ GeV. While for$ m_{H^\pm}\gtrsim 250 $ GeV, the cross section does not change significanltly as$ m_{H^\pm} $ increases. At the 27 TeV HE-LHC, the cross section always tends to increase when$ m_{H^\pm} $ increases, which is approximately three to four times larger than what it was at the 14 TeV HL-LHC.Next, we discuss the same-sign dilepton signature and its corresponding backgrounds at hadron colliders. The full process of such signature is
$ \begin{aligned}[b] pp &\to W^{\pm *}W^{\pm *}j j \to H^\pm H^\pm jj \to (W^\pm H) (W^\pm H)jj\\& \to (l^\pm \nu)H (l^\pm \nu)H jj \to l^\pm l^\pm {\not\!\!{E}}_Tjj, \end{aligned}$

(23) in the IDM, where j represents the forward and energetic jet from the initial parton, and the leptons contain electrons and muons (
$ l = e,\mu $ ). In the following, we select BP10, BP15, and BP20 in Table 1 to demonstrate the distribution of certain variables and corresponding cut flow at colliders.The main SM backgrounds originate from
$ W^\pm W^\pm jj $ ,$ WZjj $ ,$ ZZjj $ ,$ VVVjj $ , and$ t\bar{t}V $ . Both the strong and electroweak productions of the$ VVjj $ process are considered. According to the experimental result of the ATLAS collaboration [66], there should be additional contributions from$ V\gamma $ , electron charge misreconstruction, and non-prompt leptons, which are sub-dominant; hence, they are not considered in this study. After generating the parton level events for all BPs and corresponding SM backgrounds using Madgraph5_aMC@NLO [83], Pythia8 [84] is used for parton showering and hadronization. Finally, the detector simulation is performed with Delphes3 [85]. In this work, all signals and backgrounds are simulated at the leading order.After the above simulation, several cuts are applied to highlight the signal, which are simply categorized into four parts, i.e, cuts-1 to cuts-4. First, cuts-1 aims to select the same-sign dilepton signature, where we require exactly two leptons carrying the same charge in the final states,
$ N(l^\pm) = 2,\;\;\;\; P_T^{l^\pm}>20\; {\rm{GeV}},\;\;\;\; |\eta_{l^\pm}|<2.5 $

(24) Then, in cuts-2, for the forward jet pair, events with at least two jets and with b-jet veto can pass the selection
$ N(j) \geqslant 2,\;\;\; P_T^j>30\; {\rm{GeV}},\;\;\;|\eta_j|<5,\;\;\;N(b) = 0. $

(25) Here, the b-jet veto criteria is to suppress the
$ t\bar{t}V $ background. As presented in Table 2, at this level of cuts, the SM background is approximately three orders of magnitudes larger than the signal. Therefore, additional cuts are expected to further eliminate the background.Cross section/fb BP10 BP15 BP20 $W^{\pm} W^{\pm}jj$ 

$WZjj$ 

Others Preselection $1.88\times10^{-2}$ 

$1.89\times10^{-2}$ 

$2.04\times10^{-2}$ 

$1.35\times10^{1}$ 

$5.50\times10^{1}$ 

$3.05\times10^{0}$ 

$N(l^\pm) = 2,\;\;P_T^{l^\pm}>20~{\rm{GeV}}$ 

$|\eta_{l^\pm}|<2.5$ 

$1.01\times10^{-2}$ 

$1.08\times10^{-2}$ 

$1.19\times10^{-2}$ 

$5.29\times10^{0}$ 

$6.43\times10^{0}$ 

$3.66\times10^{-1}$ 

$N(j) \geq 2,\;\; P_T^j>30$ GeV,

$|\eta_j|<5,\;\;N(b)=0$ 

$8.62\times10^{-3}$ 

$9.13\times10^{-3}$ 

$1.02\times10^{-2}$ 

$4.60\times10^{0}$ 

$5.43\times10^{0}$ 

$2.05\times10^{-1}$ 

$\Delta P_T>0,\;\;\overline{\Delta {\eta}}_{jl} > 3,$ max

$(z_{l}^{*})< 0.3$ 

$1.56\times10^{-3}$ 

$2.48\times10^{-3}$ 

$3.06\times10^{-3}$ 

$1.34\times10^{-1}$ 

$2.834\times10^{-2}$ 

$1.12\times10^{-3}$ 

${\not\!\!{E} }_T > 100gt; 100gt; 100$ GeV,

$M_{T2}>100$ GeV

$3.71\times10^{-4}$ 

$8.41\times10^{-4}$ 

$1.33\times10^{-3}$ 

$7.31\times10^{-4}$ 

$1.10\times10^{-4}$ 

$8.87\times10^{-5}$ 

Significance 0.67 1.52 2.39 — — — Table 2. Cut flow table for BP10, BP15, BP20 signals and various background processes at
$\sqrt{s}=14$ TeV. The$ZZjj$ ,$VVVjj$ and$t\bar{t}V$ backgrounds are classified as others because their contributions to the total backgrounds are below 10% after applying all cuts. The significance$ S/\sqrt{B} $ is calculated by assuming an integrated luminosity${\cal{L}} = 3\;{\rm{ab}}^{-1}$ .To determine proper cut criteria, the normalized distribution of certain parameters is presented in Fig. 4. Specifically, the up-left panel illustrates the
$ P_T^l $ variable. The distributions of$ P_T^l $ are not optimally separated for signals and backgrounds. Instead, we consider the$ \Delta P_T $ parameter defined as$ \Delta P_T = (P_{T}^{l_{1}}+P_{T}^{l_{2}}) - (P_{T}^{j_{1}}+P_{T}^{j_{2}}) $ , which is depicted in the up-right panel. For the BP signals, the distributions of$ \Delta P_T $ tend to be larger than those of the backgrounds. Based on this feature, we require$ \Delta P_T>0 $ . In other words, the scalar sum of the transverse momentum of two leptons is larger than the scalar sum of the transverse momentum of leading and sub-leading jets. In the middle-left panel, we depict the distribution of the$ \overline{\Delta \eta}_{jl} $ variable, where$ \overline{\Delta \eta}_{jl} $ is defined as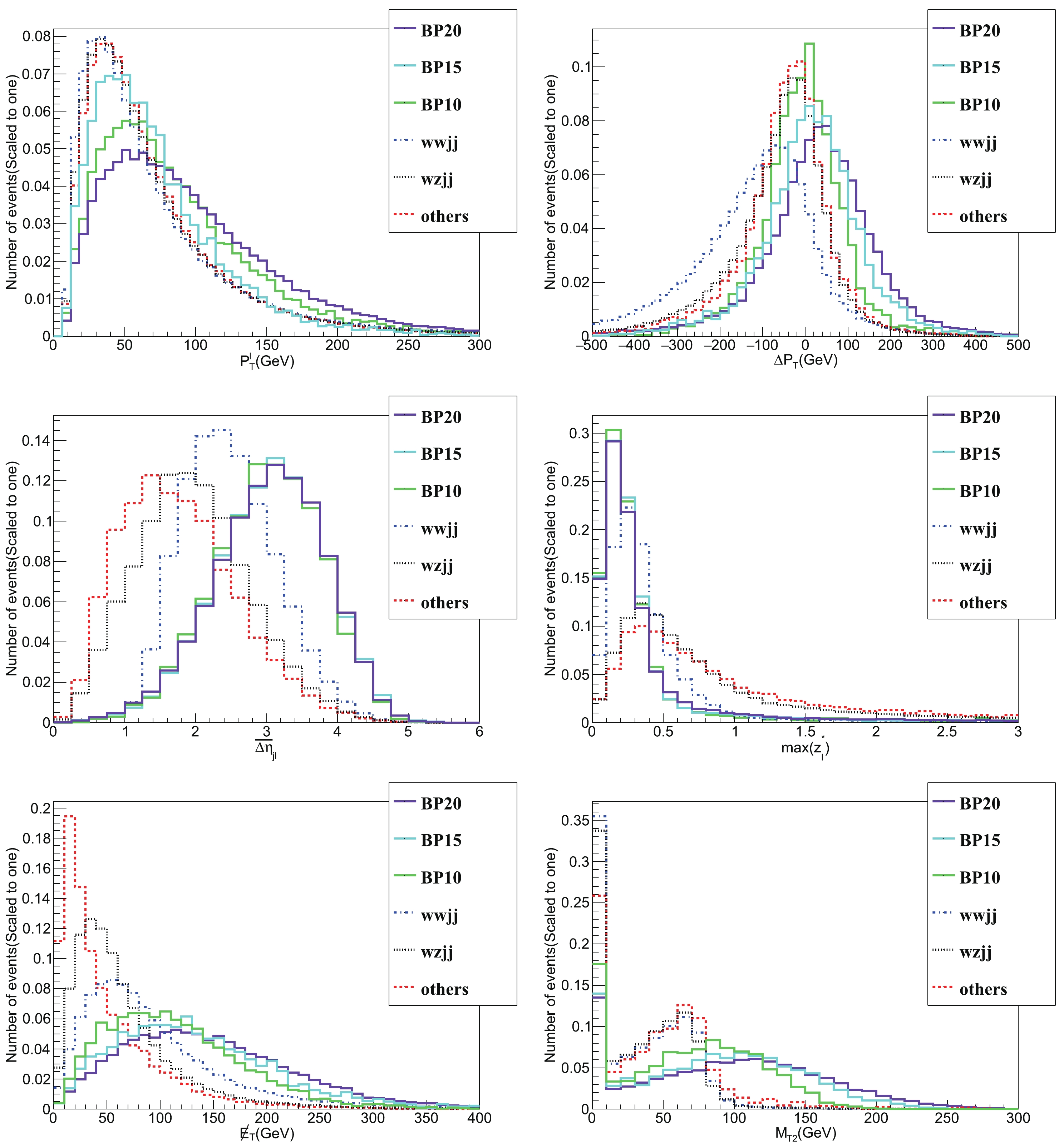
Figure 4. (color online) Normalized distribution of
$P_T^l$ (up-left panel),$\Delta P_T$ (up-right panel),$\overline{\Delta \eta}_{jl}$ (middle-left panel), max$(z_{l}^{*})$ (middle-right panel),${\not\!\!{E}}_T$ (down-left panel), and$M_{T2}$ (down-right panel) variables for BP10, BP15, BP20 (solid line) and corresponding SM backgrounds (dashed line) at$\sqrt{s} = 14$ TeV. The$P_T^l$ ,$\Delta P_T$ ,$\overline{\Delta \eta}_{jl}$ , max$(z_{l}^{*})$ , and${\not\!\!{E}}_T$ variables are obtained after the cuts in Eqs. (22), (24), (25) are applied, whereas the$M_{T2}$ variable is obtained after the cuts in Eqs. (22), (24), and (25), and when${\not\!\!{E}}_T > 100$ GeV is applied.$ \overline{\Delta \eta}_{jl} = \sqrt{ \sum\limits_{m = 1}^{2} \sum\limits_{n = 1}^{2}\frac{(\eta_{jm} - \eta_{ln})^{2}}{4}}. $

(26) Here,
$ \eta_{jm} $ represents the pseudorapidity of leading and sub-leading jets with$ m = 1, 2 $ and$ \eta_{ln} $ is the pseudorapidity of leading and sub-leading leptons with$ n = 1, 2 $ . The$ \overline{\Delta \eta}_{jl} $ variable characterizes the averaged pseudorapidity separation between jets and leptons, where$ \overline{\Delta \eta}_{jl} $ variable larger than three can sufficiently separate the signals and backgrounds. Another distinguishable variable used by the experimental groups is the Zeppenfeld variable$ z_{l}^{*} $ , which is defined as [86]:$ z_{l}^{*} = \; \left|\eta_{l} - \frac{\eta_{j1} + \eta_{j2}}{2}\right| / |\eta_{j1} - \eta_{j2}|. $

(27) The max
$ (z_l^*) $ variable is used by the CMS collaboration to define the$ W^\pm W^\pm jj $ and$ WZjj $ signal regions [67]. Because both$ W^\pm W^\pm jj $ and$ WZ jj $ are the backgrounds in this study, we adopt a more stringent cut max$ (z_l^*)<0.3 $ , i.e., the largest$ z_{l}^{*} $ variable less than 0.3. In summary, we adopted the following as cuts-3$ \Delta P_T>0 , \;\;\;\; \overline{\Delta \eta}_{jl} > 3, \;\;\;\; {\rm{max}}(z_{l}^{*})< 0.3. $

(28) The results for both the signal and background at the level of cuts-3 are presented in the fourth row of Table 2. At this level, the cross section of the
$ ZZjj $ ,$ VVVjj $ , and$ t\bar{t}V $ backgrounds are smaller than the signal. The dominant ones are$ W^\pm W^\pm jj $ and$ WZ jj $ . From Fig. 4, it is also clear that for the$ W^{\pm} W^{\pm} jj $ background process,$ \Delta P_T $ ,$ \overline{\Delta \eta}_{jl} $ , and$ z_{l}^{*} $ variables are not so distinguishable from signal to background. This is because the main part of$ W^\pm W^\pm jj $ generated from the electroweak production process has a similar topological structure to signal.To suppress the
$ W^\pm W^\pm jj $ background efficiently, more advanced cuts should be applied. Despite the additional two forward jets in the same-sign dilepton signature, the decay chain of the charged scalar$ H^\pm \to W^\pm H\to l^\pm \nu H $ is actually the same as the decay chain of chargino$ \tilde{\chi}_1^\pm \to W^\pm \tilde{\chi}_1^0\to l^\pm \nu \tilde{\chi}_1^0 $ , which indicates that we can apply similar cuts for the opposite-sign dilepton signature as in Ref. [87]. Here, we take the variables$ {\not\!\!{E}}_T $ and$ M_{T2} $ . The$ M_{T2} $ variable is defined as [88, 89],$ M_{T2} = \underset{{{q}}_{T,1} + {{q}}_{T,2} = \; {\not{{E}}}_T}{\rm{min}} \left\{{\rm{max}}\left[M_{T} ({{P}}_{T}^{l_{1}},{{q}}_{T,1}),M_{T}({{P}}_{T}^{l_{2}},{{q}}_{T,2})\right]\right\}, $

(29) where
$ {{P}}_{T}^{l_{1}} $ and$ {{P}}_{T}^{l_{2}} $ are the transverse momentum vectors of the two leptons,$ {{q}}_{T,1} $ and$ {{q}}_{T,2} $ represent all possible combinations of two transverse momentum vectors that satisfy${{q}}_{T,1} + {{q}}_{T,2} = {\not\!\!{{E}}}_T$ . The$ M_{T2} $ variable is calculated by applying the algorithms proposed in Ref. [90].The distributions of
${\not\!\!{E}}_T$ and$ M_{T2} $ are also illustrated in Fig. 4. For the signal process, both neutrinos$ \nu $ and dark matter H contribute to the missing transverse energy$ {\not\!\!{E}}_T $ , which usually leads to a larger$ {\not\!\!{E}}_T $ than the backgrounds. It can also be observed that the$ M_{T2} $ variable functions as the most efficient cut. This phenomenon exists because, theoretically, this variable can not exceed the mass of the W boson at$ m_W = 80.4 $ GeV for the background process, whereas the theoretical upper limit for the signal process is$ m_{H^{\pm}} $ . Therefore, when exceeding$ 80 $ GeV, the$ M_{T2} $ variable decreases severely and nearly disappears when$ M_{T_2}>100 $ GeV for all background processes. But for the signals, a large part of it still existed, especially for BP20 owing to the largest$ M_{H^{\pm}} $ it possessed. In summary, the missing transverse energy$ {\not\!\!{E}}_T $ is required to be greater than$ 100 $ GeV and the$ M_{T2} $ variable is greater than$ 100 $ GeV for cuts-4:$ {\not\!\!{E}}_T > 100 \; {\rm{GeV}}, \;\;\;\; M_{T2} > 100\; {\rm{GeV}}. $

(30) Results obtained after applying cuts-4 are presented in the fifth row of Table 2. After applying all the cuts, the contributions of the
$ W^{\pm} W^{\pm} jj $ process to the total backgrounds is greater than 80%, the contributions of the$ WZjj $ process to the total backgrounds is greater than 10%, and the part named as others originates from the sum of the$ t \bar{t} V $ ,$ VVVjj $ , and$ ZZjj $ processes, which provides less than 10% of the contributions to the total backgrounds. For the signal process after the full cuts are applied, BP20 exhibits the largest cross section because it possesses both the largest$ \Delta m $ and$ m_{H^{\pm}} $ , where the former facilitates a large cross section in the simulation, whereas the latter triggers the highest efficiency when passing the cut flow. The total cross section of backgrounds is$ 9.30\times10^{-4} $ fb, which is larger than that of BP10 and BP15, but is smaller than that of BP20. Although an optimal signal-to-background ratio is achieved, the cross sections for the signals after all cuts are relatively too small to probe. For instance, assuming an integrated luminosity of$ {\cal{L}} = 3\; {\rm{ab}}^{-1} $ , we expect approximately 1.1 events for BP10, 2.5 events for BP15 and 4.0 events for BP20, with 2.8 events for total the backgrounds, of which the corresponding significance$S/\!\!\sqrt{B}$ is 0.67, 1.52 and 2.39, respectively. Hence, the same-sign dilepton signature is not substantially promising at the HL-LHC.Before concluding the discussion on the 14 TeV simulation, let us briefly summarize the search strategy. The main backgrounds originate from the
$ W^{\pm} W^{\pm} jj $ and$ WZjj $ processes with production cross sections greater than 10 fb after preselection cuts. Owing to the similar distributions of certain variables (such as$ P_T^{l^\pm},z_l^* $ ) from the dominant background to the signal, we can solely select the simplest cuts in cuts-1 and cuts-2. Then, we have to apply the cuts extremely in cuts-3 and cuts-4, even if this will trigger a faint signal and low significance. The above analysis can be improved by considering more sophisticated selection criteria, such as employing a boosted decision tree, which is beyond the scope of this work. Instead, we further consider the same-sign dilepton signature at the 27 TeV HE-LHC.The normalized distribution of
$ P_T^l $ ,$ \Delta P_T $ ,$ \overline{ \Delta \eta}_{jl} $ , max$ (z_{l}^{*}) $ ,$ {\not\!\!{E}}_T $ , and$ M_{T2} $ variables at 27 TeV are depicted in Fig. 5, which are similar to the results of 14 TeV. Hence, we adopt the same criteria as in 14 TeV for cuts-1 to cuts-3. Meanwhile, considering the fact that the final states of neutrinos$ \nu $ and dark matter H are more energetic at 27 TeV than at 14 TeV, we slightly tighten cuts-4 as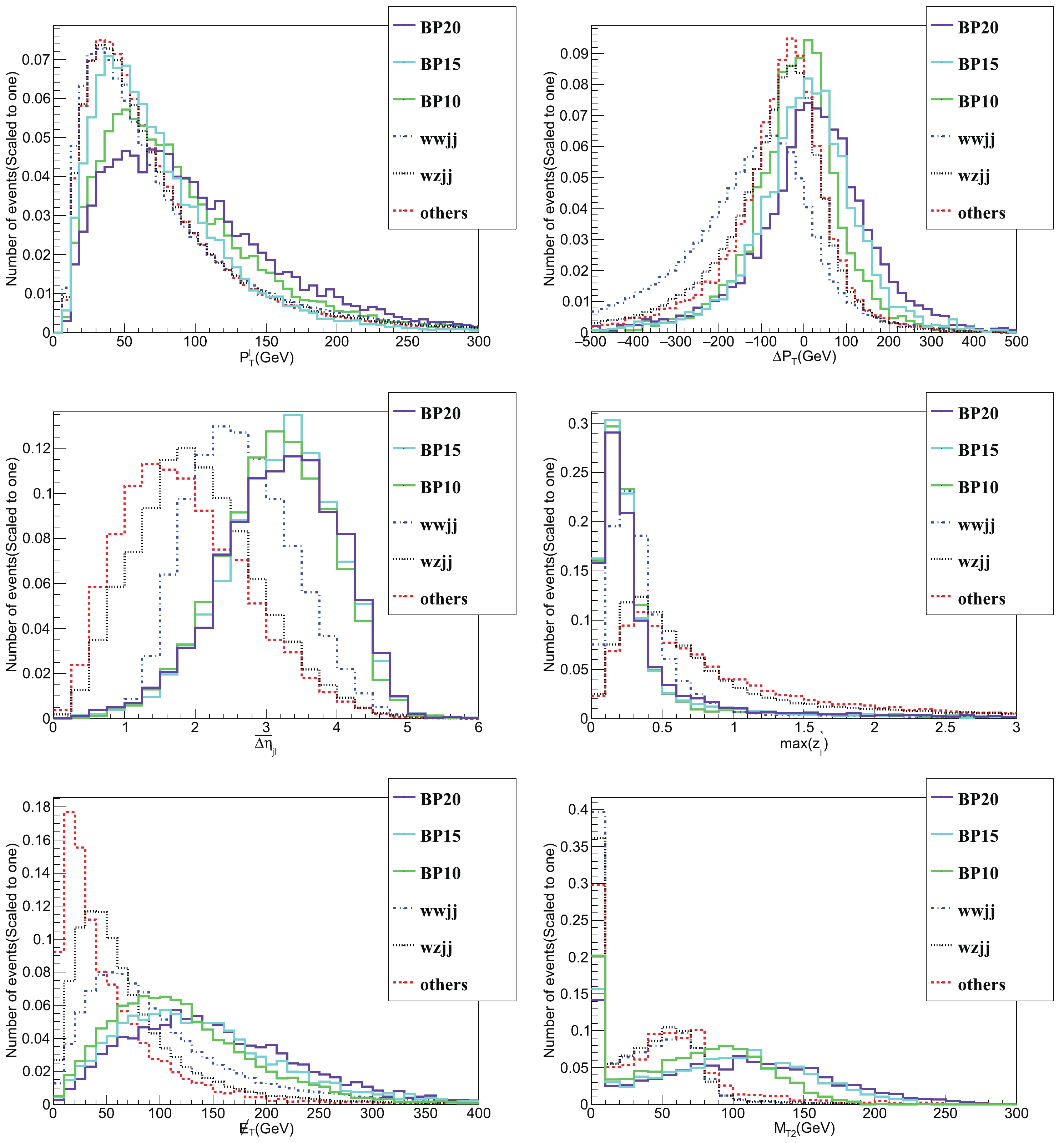
Figure 5. (color online) Same caption as in Fig. 4, but at
$\sqrt{s}=27$ TeV.$ {\not\!\!{E}}_T>110\; {\rm{GeV}}, \;\;\;\; M_{T2}>125\; {\rm{GeV}}. $

(31) The cross sections for both signals and backgrounds with the cut flows are presented in Table 3. After applying the full cuts at
$ \sqrt{s} = 27 $ TeV, only two processes make substantial contributions to the total backgrounds. The main part of the total backgrounds originates from the$ W^{\pm} W^{\pm} jj $ process, with the contribution to the total backgrounds greater than 85%. The rest of the total backgrounds originates from the$ WZjj $ process. The part named as others, which originates from the sum of the$ ZZjj $ ,$ VVVjj $ , and$ t\bar{t}V $ processes, has negligible contributions to the total backgrounds owing to the more stringent cuts we have used. With a larger production cross section and higher luminosity of$ {\cal{L}} = 15\; {\rm{ab}}^{-1} $ , we infer that the dilepton signature is promising for some BPs at the 27 TeV HE-LHC. Quantitatively, we expect approximately 8, 31, and 56 events for BP10, BP15 and BP20, respectively, with 48 events for the total backgrounds, of which the corresponding significance$S/\!\!\sqrt{B}$ is 1.21, 4.54, and 8.08, respectively.Cross section/fb BP10 BP15 BP20 $W^{\pm} W^{\pm}jj$ 

$WZjj$ 

Others Preselection $6.57\times10^{-2}$ 

$7.40\times10^{-2}$ 

$8.59\times10^{-2}$ 

$4.61\times10^{1}$ 

$1.95\times10^{2}$ 

$1.38\times10^{1}$ 

$N(l^\pm) = 2,\;\;P_T^{l^\pm}>20~{\rm{GeV}}$ ,

$|\eta_{l^\pm}|<2.5$ 

$3.19\times10^{-2}$ 

$3.77\times10^{-2}$ 

$4.54\times10^{-2}$ 

$1.47\times10^{1}$ 

$1.95\times10^{1}$ 

$1.32\times10^{0}$ 

$N(j) \geq 2,\;\; P_T^j>30$ GeV,

$|\eta_j|<5,\;\;N(b)=0$ 

$2.49\times10^{-2}$ 

$3.06\times10^{-2}$ 

$3.74\times10^{-2}$ 

$1.13\times10^{1}$ 

$1.58\times10^{1}$ 

$8.67\times10^{-1}$ 

$\Delta P_T>0,\;\;\overline{\Delta {\eta}}_{jl} > 3$ , max

$(z_{l}^{*})< 0.3$ 

$6.13\times10^{-3}$ 

$9.74\times10^{-3}$ 

$1.23\times10^{-2}$ 

$4.94\times10^{-1}$ 

$1.21\times10^{-1}$ 

$4.33\times10^{-3}$ 

${\not\!\!{E} }_T > 110$ GeV,

$M_{T2}>125$ GeV

$5.58\times10^{-4}$ 

$2.09\times10^{-3}$ 

$3.72\times10^{-3}$ 

$2.79\times10^{-3}$ 

$3.90\times10^{-4}$ 

0 Significance 1.21 4.54 8.08 — — — Table 3. Cut flow table for BP10, BP15, BP20 signals and various background processes at
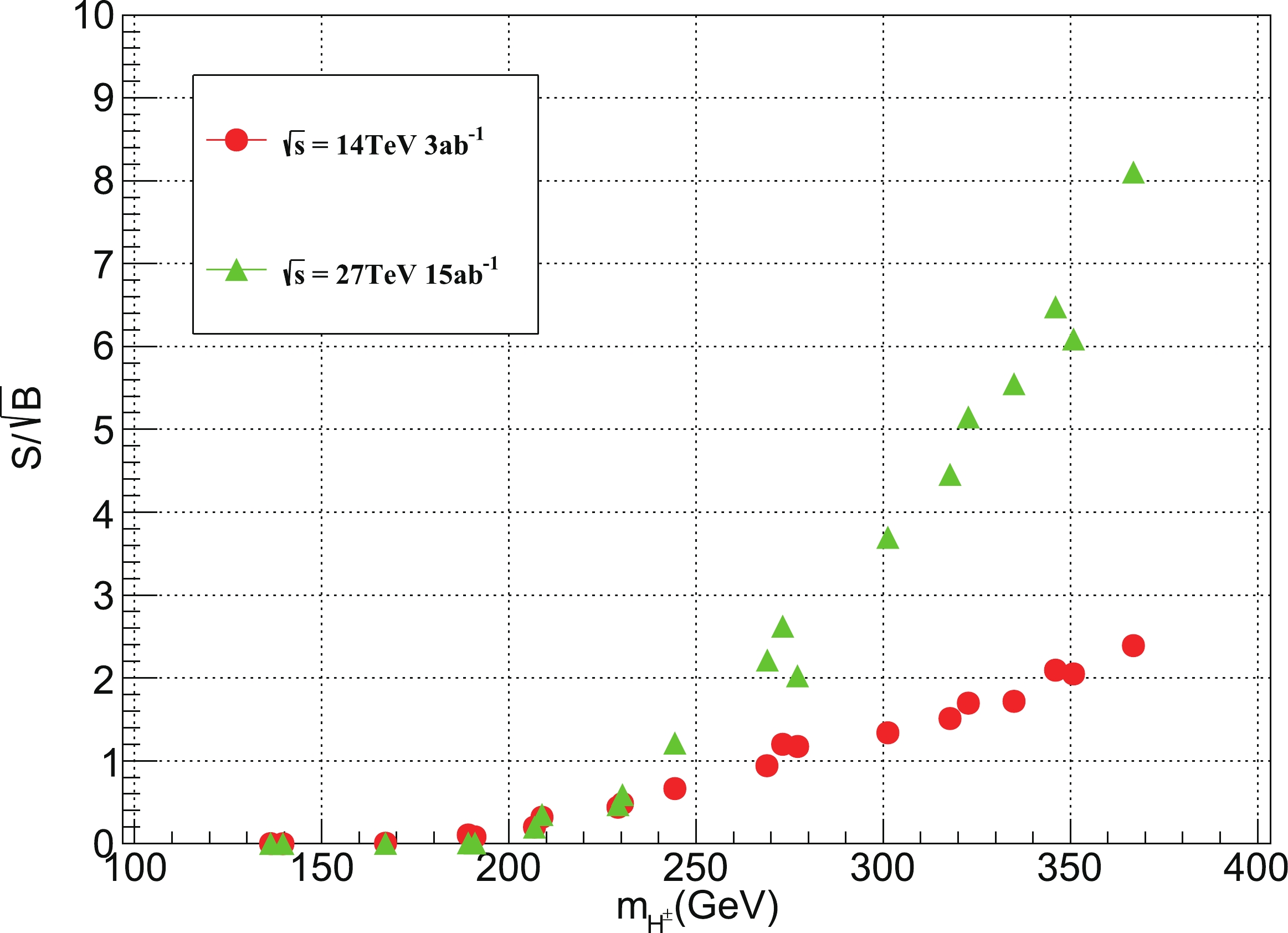
$\sqrt{s}=27$ TeV. The$ZZjj$ ,$VVVjj$ , and$t\bar{t}V$ backgrounds are classified as others because their contributions to the total backgrounds are negligible after applying all cuts. The significance$S/\!\!\sqrt{B}$ is calculated by assuming an integrated luminosity${\cal{L}} = 15\;{\rm{ab}}^{-1}$ .Finally, based on the cuts adopted in the above discussion, we extend our analysis to all the 20 BPs listed in Table 1. The significance results obtained for the BPs at 14 TeV HL-LHC and 27 TeV HE-LHC are presented in Fig. 6. It can be observed that following the increase in
$ m_{H^{\pm}} $ , the significance increased at a larger$ m_{H^{\pm}} $ , thereby leading to a higher cut efficiency. At$ \sqrt{s} = 14 $ TeV, which is limited by the faint signal, even for BP20 with the largest$ m_{H^{\pm}} $ , the significance can only slightly exceed 2. At$ \sqrt{s} = 27 $ TeV, which has a larger cross section and higher luminosity, we determine that BP16–BP20 can have a significance larger than 5. In other words, the promising region of the same-sign dilepton signature at$ \sqrt{s} = 27 $ TeV is$ 250\; {\rm{GeV}}\lesssim m_{H^\pm}-m_H\lesssim 300 $ GeV, with a DM mass$ m_H\sim 60 $ or 71 GeV. -
The IDM is a 2HDM imposed with an exact
$ Z_{2} $ symmetry, which leads to a DM candidate. This model facilitates rich phenomenology, which has been extensively studied. In this study, we perform a detailed analysis on the same-sign dilepton signature$pp\to W^{\pm *}W^{\pm *}jj \to $ $ H^\pm H^\pm jj\to (l^\pm \nu)H (l^\pm \nu)H jj \to l^\pm l^\pm {\not\!\!{E}}_Tjj$ in the IDM, where H is the DM candidate. According to our simulation, this signature is promising for large mass splitting$ \Delta m = m_A-m_H $ , which complements the well-studied opposite-sign dilepton signature.First, we performed a random scan over the low mass region of IDM with various constraints considered. By requiring the relic density within the
$ 3\sigma $ range of the Planck observation value$ \Omega h^2 = 0.1200\pm 0.0012 $ , we determined three viable parameter spaces. The first region is the Higgs resonance region around$ m_H\lesssim m_h/2 $ . Another region is the vector boson annihilation region around$ m_H\sim71.5 $ GeV. Finally, the third region is the coannihilation region with$ m_A-m_H\sim 8 $ GeV and$ m_H\sim 65 $ GeV. Because the coannihilation region provides a vanishing cross section of the same-sign dilepton signature, we selected 20 BPs from the Higgs resonance and vector boson annihilation regions, which are presented in Table 1.Subsequently, we simulated the same-sign dilepton signature for the BPs and SM backgrounds both at
$ \sqrt{s} = 14 $ TeV HL-LHC and$ \sqrt{s} = 27 $ TeV HE-LHC. Owing to the similar decay of the topological structure to the signal, the dominant background originated from$ W^{\pm} W^{\pm} jj $ . The most efficient cut that suppressed the background was the$ M_{T2} $ variable. According to our simulation, at$ \sqrt{s} = 14 $ TeV, with luminosity$ {\cal{L}} = 3\; {\rm{ab}}^{-1} $ , a maximum of four signal events survived after applying the full cuts. Limited by the number of signal events, the BPs could only achieve a significance slightly greater than 2. At$ \sqrt{s} = 27 $ TeV with a luminosity$ {\cal{L}} = 15\; {\rm{ab}}^{-1} $ , we can probe BPs with a large mass$ \Delta m $ . For example, BP16–BP20 can have a significance larger greater than 5.In summary, the same-sign dilepton signature is not promising at
$ \sqrt{s} = 14 $ TeV HL-LHC; however, it is promising at$ \sqrt{s} = 27 $ TeV, with the viable region of$ 250\; {\rm{GeV}}\lesssim $ $ m_{H^\pm}-m_H\lesssim 300 $ GeV and DM mass$ m_H\sim 60 $ or 71 GeV.
Same-Sign Dilepton Signature in the Inert Doublet Model
- Received Date: 2021-01-20
- Available Online: 2021-07-15
Abstract: In this study, we perform a detailed analysis on the same-sign dilepton signature in the inert doublet model. Focusing on the low dark matter mass region, we randomly scan the corresponding parameter space. Viable samples allowed by various constraints are obtained, and among them are twenty benchmark points that are selected for further study on collider signature. At hadron colliders, the same-sign dilepton signature is produced via






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: