-
Recently, a narrow structure near
$ 6.9\,\mathrm{GeV} $ in the di-$ J/\psi $ invariant mass spectrum was reported by the$ {\mathsf{ LHCb}}$ experiment, with a global significance above$ 5\sigma $ [1]. This relatively unexpected discovery of the$ X(6900) $ resonance has spurred a plethora of intensive theoretical investigations to unravel its nature (for an incomplete list of references, refer to [2-25]).$ X(6900) $ has been interpreted as the P-wave fully-charmed tetraquark [2, 8, 16], the radially excited S-wave tetraquark [4, 6, 10, 12, 14, 16, 22, 23, 25], or even the ground state S-wave tetraquark [15]. Alternatively, the$ X(6900) $ is also suggested to be a$ \chi_{c0}\chi_{c0} $ or$ P_c P_c $ molecular state [9, 24],$ 0^{++} $ hybrid [20], the resonance formed in charmonium-charmonium scattering [3, 5], or the kinematic cusp originating from final-state interactions [11, 13, 17, 19]. There have even been attempts to connect$ X(6900) $ with some beyond the Standard Model scenarios [18, 21].Unlike dozens of
$ XYZ $ states intertwined with the excited charmonia spectra discovered in the past two decades, which necessarily contain light quark in their leading Fock component (for a recent review of$ XYZ $ , refer to [26-29]),$ X(6900) $ is an entirely different exotic state, as its leading Fock component merely involves four heavy quarks. Therefore, it is natural to envisage that, without polluting the brown muck degrees of freedom, the$ X(6900) $ particle, among other members in the$ T_{4c} $ family, should be significantly cleaner and more amenable to study than its$ XYZ $ cousins. In particular, the asymptotic freedom of QCD may facilitate the handling of some dynamical features of the$ T_{4c} $ family within perturbative QCD, owing to$ m_c\gg \Lambda_{\rm QCD} $ .Theoretical explorations of the compact fully-heavy tetraquarks date back to the 1970s [30-32]. Since then, the mass spectra and decay pattern of the fully-charmed tetraquarks (hereafter
$ T_{4c} $ ) have been extensively investigated in various phenomenological models, such as quark potential models [2, 3, 5-7, 10, 12, 14, 15, 23, 25] and QCD sum rules [4, 8, 20, 22, 33]. The studies on$ T_{4c} $ production are relatively rare [7, 34-40], most of which significantly rest upon some phenomenological ansatz, such as the quark hadron duality and color evaporation model.It is intuitively appealing that, to produce the
$ T_{4c} $ state, one has to first create four heavy quarks simultaneously at relatively short spatial distances, subsequently followed by the nonperturbative hadronization process. The first stage necessarily involves the hard momentum transfer, which can thus be accessed by perturbative QCD. This is essentially the same physical consideration underlying the celebrated nonrelativistic QCD (NRQCD) factorization approach to address the ordinary quarkonium production. Recently, by drawing a close analogy with quarkonium production, several groups have proposed the adoption of the NRQCD factorization approach to study the$ T_{4c} $ production of hadron colliders [16, 41, 42], as well as$ e^+e^- $ colliders [43].To date, only the productions of the
$ 0^{++} $ and$ 2^{++} $ S-wave$ T_{4c} $ have been investigated in the aforementioned studies, mainly motivated by the C-even objective of$ X(6900) $ by the${\mathsf{ LHCb}} $ experiment. Nevertheless, there is a remaining$ 1^{+-} $ member in the S-wave$ T_{4c} $ family, which has only received little attention to date. This C-odd tetraquark can decay into$ J/\psi+\eta_c $ exclusively. It is interesting to speculate on where to look for this C-odd tetraquark. In this work, our objective is to fill this gap by presenting a dedicated NRQCD analysis for the inclusive$ 1^{+-} $ $ T_{4c} $ production at the B factory. In particular, the production proceeds through$ e^+e^-\to T_{4c}(1^{+-})+gg $ , where charge conjugation invariance enforces the fully-charmed tetraquark to bear a negative C parity. This study is especially of experimental interest, because analogous inclusive and exclusive quarkonium production processes have already been extensively measured by$ {{\mathsf{Belle}}} $ experiments in the past two decades, exemplified by$ e^+e^-\to J/\psi+X $ [44] and$ e^+e^-\to J/\psi+\eta_c $ [45-47]. Moreover, because the$ e^+e^- $ collision experiment has a significantly cleaner background than LHC, the B factory might be an ideal place to look for the cousins of the$ X(6900) $ particle.The rest of this paper is organized as follows. In Section II, we specify the NRQCD factorization formula for the inclusive production of the
$ 1^{+-} $ $ T_{4c} $ associated with light hadrons. In Section III, we present the results for the short-distance coefficient (SDC) in the factorization formula. In Section IV, we provide an approximate estimate of the value of the NRQCD long-distance matrix elements (LDMEs) based on the quark potential model. Subsequently, we perform phenomenological analysis on the production rate at the B factory and assess its observation prospect in the${{\mathsf{Belle}} \;{\mathsf{2}}}$ experiment. Finally, in Section V, we summarize the study. -
Our primary goal is to predict the energy spectrum of the
$ 1^{+-} $ tetraquark at the$ e^+e^- $ collider. According to the NRQCD factorization, we can express the differential cross section for the$ T_{4c} $ inclusive production as the sum of the product of SDCs$ \mathrm{d} F_n $ and the LDMEs$ \langle {\cal O}_n^{T_{4c}}\rangle $ :$ \mathrm{d}\sigma(e^+e^-\to T_{4c}(E)+X) = \sum\limits_{n} \dfrac{\mathrm{d} F_{n}(E)}{m_c^8}(2M_{T_{4c}})\langle 0|\mathcal{O}_{n}^{T_{4c}}| 0\rangle, $

(1) where X represents any unobserved hadronic state. The sum on the right hand side indicates the velocity expansion of the NRQCD factorization.
In this study, we concentrate on the S-wave
$ 1^{+-} $ tetraquark. In the context of the diquark picture, it is feasible to ensure that the diquark and antidiquark pair is in the$ {\bar {\bf{3}}}\otimes{\bf{3}} $ color state; consequently, Fermi statistics enforces the diquark/antidiquark to carry spin$ 1 $ . Bearing zero orbital angular momentum, the diquark and anti-diquark then form a total spin-$ 1 $ tetraquark①. The lowest-order NRQCD production operator would not involve any derivative. Within the diquark-antidiquark basis, the color-singlet production operator can be uniquely defined as$ \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{T_{4 c}} = \sum\limits_{m_j,X} \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{i\dagger} |T_{4 c}(m_j)+X\rangle \langle T_{4 c} (m_j) +X\vert \mathcal{O}^i_{{\bar {\bf{3}}}\otimes{\bf{3}}}, $

(2) where the magnetic quantum number is represented by
$ m_j $ . Here, the quadrilinear color-singlet NRQCD operator$ \mathcal{O}_{{\bf{3}}\otimes{\bar {\bf{3}}}}^{i} $ can be considered the interpolating current bearing the same quantum number of the$ 1^{+-} $ tetraquark, whose explicit form is expressed as$ \mathcal{O}^{i}_{{\bar {\bf{3}}}\otimes{\bf{3}}} = {\mathrm{i}\over \sqrt{2}}\epsilon^{ijk}{\mathcal C}^{ab;cd}_{{\bar {\bf{3}}}\otimes{\bf{3}}} \, \left(\psi_a^\dagger\sigma^j \mathrm{i} \sigma^2\psi_b^{*}\right)\left(\chi_c^T \mathrm{i} \sigma^2\sigma^k\chi_d\right). $

(3) Here
$ \psi $ and$ \chi^\dagger $ are Pauli spinor fields that annihilate the heavy quark and antiquark, respectively.$ \sigma^i $ denotes Pauli matrix. The Latin letters$ i,j,k = 1,2,3 $ signify the Cartesian indices, whereas$ a,b,c,d = 1,2,3 $ denote the color indices. The color projection tensor in (3) is given by$ \mathcal{C}^{ab;cd}_{{\bar {\bf{3}}}\otimes{\bf{3}}}\equiv \left(\!\!\sqrt{1\over 2}\,\right)^2 \epsilon^{abe}\epsilon^{cdf}\frac{\delta^{ef}}{\sqrt{3}} = \frac{1}{2\sqrt{3}}(\delta^{ac}\delta^{bd}-\delta^{ad}\delta^{bc}). $

(4) It can be readily verified that the NRQCD current in (3) has the prescribed properties of the
$ 1^{+-} $ state under P, C transformations. -
The SDCs in (1) can be determined by the standard perturbative matching procedure. Because these coefficients are insensitive to the long-distance nonperturbative dynamics, it is possible to replace the physical tetraquark state by a “fictitious” tetraquark comprising four free charm quarks, calculate both sides of (1) using perturbative QCD and perturbative NRQCD, and then solve for SDCs.
We first use the standard trick to deduce the unpolarized production rate of
$ T_{4c}+gg $ in$ e^+e^- $ annihilation from the corresponding decay rate of a virtual photon:$\begin{aligned}[b]& \mathrm{d}\sigma\left[e^+e^-\rightarrow T_{4c}(P)+g(k_1)g(k_2)\right]\\ =&\dfrac{4 \pi\alpha}{s^{3/2}}{\mathrm{d}\Gamma\left[\gamma^*\rightarrow T_{4c}(P)+g(k_1)g(k_2)\right]}, \end{aligned}$

(5) where
$ \sqrt{s} $ denotes the center-of-mass energy of the$ e^+e^- $ pair, and$ P,k_1,k_2 $ denote the momenta of the tetraquark and two accompanying gluons. For convenience, we introduce the following dimensionless ratios:$ z = {2 P^0 \over \sqrt{s}},\quad x_1 = {2 k_1^0\over \sqrt{s}},\quad x_2 = {2 k_2^0\over \sqrt{s}};\quad r = {16m_c^2\over s}. $

(6) The first three variables represent the energy fractions of
$ T_{4c} $ , together with two accompanying gluons, respectively, which are subject to the constraint$ x_1+x_2+ $ $ z = 2 $ via energy conservation.At the lowest order in
$ \alpha_s $ , there are in total$ 392 $ Feynman diagrams for$ \gamma^* \to c c \bar{c}\bar{c} + gg $ in the perturbative QCD side, one of which has been depicted in Fig. 1. Among all the diagrams,$ 48 $ diagrams, in which two final-state gluons are emitted from a three-gluon vertex, vanish because the$ cc\bar{c}\bar{c} $ is in color octet. It can be observed that all topologies of these diagrams start with$ {\cal O}(\alpha_s^4) $ , because the C conservation demands that at least two gluons are emitted in the final state, and two charm quark lines must be connected by the hard gluon exchange to ensure that four charm quarks move in the same direction, such that there is a substantial probability of hadronization into a$ T_{4c} $ state.
Figure 1. One of the 392 Feynman diagrams for
$e^+e^-\to T_{4c}(1^{+-})+ $ $ gg$ at$ {\cal O}(\alpha_s^4) $ .Since we are interested in the lowest order velocity expansion, we can simply assign each charm quark with momentum
$ P/4 $ , i.e. equally partitioning the momentum of the fictitious tetraquark state. This is justified by the fact that the NRQCD current in (3) contains no derivative. To expedite the projection of the$ cc\bar{c}\bar{c} $ state onto the fictitious tetraquark with the prescribed color/spin/orbital quantum number, we adopt a shortcut in the QCD-side calculation by making the following substitution in the quark amplitude:$ \bar u^a_i\bar u^b_j v^c_k v^d_l\to (\textsf{C}\Pi_\mu)^{ij}(\Pi_\nu \textsf{C} )^{lk}\mathcal{C}^{ab;cd}_{\bar{{\bf{3}}}\otimes{\bf{3}}} J^{\mu\nu}_{1}(\varepsilon), $

(7) where
$ \textsf{C} = \mathrm{i}\gamma^0\gamma^2 $ is the charge conjugate matrix,$ \Pi_\mu $ is the standard spin-triplet projector of bi-fermions [41], and the role of the projection tensor$ J_{1}^{\mu \nu}(\varepsilon) = -\mathrm{i}\epsilon^{\mu \nu \rho \sigma}\epsilon_\rho^* P_\sigma/{\sqrt{2 P^{2}}} $ is to combine the two spin-$ 1 $ diquark-antidiquark pair into a S-wave spin-$ 1 $ fictitious tetraquark state with a polarization vector$ \varepsilon^\rho $ . We simply take$ P^2 = M^2_{T_{4c}}\approx 16m_c^2 $ .For the NRQCD-side calculation, a fictitious tetraquark state can also be prepared by setting all four charm quarks at rest. The involved NRQCD matrix elements can be readily computed at the lowest order in the perturbation theory:
$ \left\langle\mathcal{T}_{{\bar {\bf{3}}}\otimes{\bf{3}}}(m_j) \left|\mathcal{O}^i_{{\bar {\bf{3}}}\otimes{\bf{3}}}\right|0 \right\rangle = 4\varepsilon^{i*}(m_j), \tag{8a}$

$ \langle 0|\mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{{\cal T}_{4c}}| 0\rangle \approx \sum\limits_{m_j} \langle 0| \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{i\dagger} |{\cal T}_{4 c}(m_j)\rangle \langle {\cal T}_{4 c} (m_j) \vert \mathcal{O}^i_{{\bar {\bf{3}}}\otimes{\bf{3}}}\vert 0\rangle = 48,\tag{8b} $

where
$ \varepsilon_{i}^{(m_j)} $ denotes the polarization tensor of the$ 1^{+-} $ state with a magnetic number$ m_j $ . In the second line, we infer the inclusive production NRQCD matrix element from the vacuum-to-“tetraquark” matrix element (8a) by invoking vacuum saturation approximation (VSA).To deduce the SDC affiliated with the differential production rate of
$ T_{4c} $ in (1), we need to integrate further, over the phase space integration of the gluons recoiling against$ T_{4c} $ ②. We use the following formula for the three-body phase space integration:$ \int \!\! {\rm d}\Phi_3 = \dfrac{s}{2(4\pi)^{3}}\int_{2\sqrt{r}}^{1+r}\mathrm{d} z\int_{x_1^-}^{x_1^+}\mathrm{d} x_1, $

(9) where the integration boundaries of
$ x_1 $ are$ x_1^{\pm} = \dfrac{1}{2}(2-z)\pm\dfrac{1}{2}\sqrt{z^2-4r}. $

(10) After some straightforward algebra, we obtain the intended SDC
$ \mathrm{d} F_{{\bar {\bf{3}}}\otimes{\bf{3}}} $ for the differential$ T_{4c} $ energy distribution in (1). Unfortunately, the full analytical expression is too lengthy to be presented in text. As a compromise, we decide to present its limit near the upper endpoint:$ \begin{aligned}[b] { \mathrm{d} F_{{\bar {\bf{3}}}\otimes{\bf{3}}}\over \mathrm{d} z}\bigg |_{z\to 1+r} = & \dfrac{2^2\pi^3\alpha^2\alpha_s^4}{ 3^8s^2 (3-r)^2 (2-r)^2 (3+r) (6+r)} \Big(550800+482112 \ln 2-803628 r-183168 r \ln 2+275616 r\ln r \\ &+27 \left(17856-16992 r-844 r^2+4764 r^3-779 r^4-336 r^5+70 r^6+r^7\right) \ln(2-r) \\ &+16 \left(-30132+11448 r-3897 r^2+8403 r^3-2489 r^4-475 r^5+166 r^6\right) \ln(3-r) \\ &+235854 r^2 +62352 r^2 \ln 2+85140 r^2 \ln r+62742 r^3-134448 r^3 \ln 2-263076 r^3\ln r \\ &-50316 r^4 +39824 r^4 \ln 2+60857 r^4 \ln r+2706 r^5+7600 r^5 \ln 2+16672 r^5 \ln r \\ &+1842 r^6-2656 r^6 \ln 2-4546 r^6 \ln r-27 r^7 \ln r\Big). \end{aligned} $ 
(11) We can also obtain the integrated production rate for
$ e^+e^-\to T_{4c}+X $ by integrating (1) over z. To obtain the closed form, we interchange the order of integration over$ x_1 $ and z in (9). The resulting SDC for the integrated cross section is also too lengthy to be presented here. However, it is enlightening to present a compact asymptotic expression in the high energy limit$ \sqrt{s}\gg 4m_c $ :$ \begin{aligned}[b] F_{{\bar {\bf{3}}}\otimes{\bf{3}}}\big |_{r\to 0} =& \dfrac{\pi^3\alpha^2\alpha_s^4 }{2^23^8s^2}\Bigg[48(288\ln 3-167) \ln\left({s\over 16 m_c^2}\right) - 417996\mathrm{Li}_2\left(\dfrac{1}{3}\right)-3744\text{Li}_2\left(\frac{3}{8}\right) \\ &+43005 \pi^2-386712+98082\ln^2 3+34128\ln^2 2+486032\ln 2+55296\ln 2\ln 3 \\ &-218456\ln 3+11232\ln 2\ln 5-3744\ln 3\ln 5+167920\coth^{-1}2\Bigg]. \end{aligned} $ 
(12) It is interesting to observe that at a very high energy, the cross section asymptotically decreases as
$ \ln s/s^2 $ . -
In this section, we proceed to assess the observation prospect of the
$ 1^{+-} $ tetraquark for the${{\mathsf{Belle}}\; {\mathsf{2}}} $ experiment. With the explicit knowledge of the desired SDC at hand, we still need a key ingredient, e.g., the nonperturbative NRQCD matrix element, to make a concrete phenomenological prediction of the$ T_{4c} $ production at the B factory. The ideal tool for conducting a model-independent prediction for the LDME would be the lattice NRQCD simulation, which, unfortunately, is presently unavailable. Therefore we must adopt phenomenological models to infer the value of the LDME.An influential approach is to deduce the
$ T_{4} $ mass spectra in the context of the Cornell potential model, by invoking the hyperspherical expansion method to numerically solve the four-body Schrödinger equation [14]. Within this approach, after some straightforward yet tedious algebra, the nonperturbative vacuum-to-$ 1^{+-} $ tetraquark NRQCD matrix element turns out to be$ \left\langle T_{{\bar {\bf{3}}}\otimes{\bf{3}}} (m_j)\left|\mathcal{O}^i_{{\bar {\bf{3}}}\otimes{\bf{3}}}\right|0\right\rangle \approx \sqrt{\frac{105}{2}}\frac{\varepsilon^{i*}(m_j)}{\pi^2} R^{[4]}(0),$

(13) where
$ R^{[4]}(0) $ signifies the four-body radial wave function of the$ 1^{+-} $ tetraquark at the origin.Upon applying VSA, the desired vacuum matrix element of the NRQCD production operator can be deduced as introduced in (2):
$ \langle 0 | \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{T_{4 c}} |0\rangle \approx \sum\limits_{m_j}\left|\left\langle T_{4c}(m_j) \left|\mathcal{O}_{{\bar{\bf 3}\otimes{\bf{3}}}}^i\right|0\right\rangle\right|^2 = \frac{315}{2\pi^4}\left|R^{[4]}(0)\right|^2. $

(14) To assess the theoretical uncertainty inherent in the NRQCD LDME, we also consider the simplified diquark model for an independent estimate. The results read
$ \left\langle T_{{\bar {\bf{3}}}\otimes{\bf{3}}} (m_j)\left|\mathcal{O}^i_{{\bar {\bf{3}}}\otimes{\bf{3}}}\right|0\right\rangle \approx \frac{\varepsilon^{i*}(m_j)}{2\pi^{3/2}} R_{D}^{2}(0) R_{T}(0),\tag{15a}$

$ \langle 0 | \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{T_{4 c}} |0\rangle \!\!\approx\! \!\sum\limits_{m_j}\!\left|\left\langle \!T_{4c}(m_j)\! \left|\!\mathcal{O}_{{\bar{\bf 3}\otimes{\bf{3}}}}^i\right|\!0\!\right\rangle\right|^2 \!\!\!=\! \frac{3}{4\pi^3}\!\!\!\left|{R_D(0)}\right|^4\!\left|{R_T(0)}\right|^2. \tag{15b} $

where
$ R_D(0) $ and$ R_T(0) $ denote the radial wave functions at the origin for the diquark/anti-diquark and the entire diquark-antidiquark cluster, respectively.In the phenomenological analysis, we take
$\sqrt{s} = $ $ 10.58 ~\mathrm{GeV}$ ,$m_c = 1.5 ~ {\rm{GeV}}$ ,$\alpha\left(10.58 ~ {\rm{GeV}}\right) = 1/130.9$ [48],$ \alpha_s(2m_c) = 0.2355 $ [49]. For the nonperturbative input parameters, we take the four-body radial wave function at the origin$R^{[4]}(0) = 3.15 ~ \mathrm{GeV}^{9/2}$ [14] and the diquark wave function at the origin$ R_{D}(0) = 0.523\;\mathrm{GeV}^{3/2} $ [50], as well as the radial wave function at the origin for the diquark-antidiquark cluster$ R_T(0) = 2.902 \;\mathrm{GeV}^{3/2} $ [51]③. Accordingly, the values of the NRQCD LDME in two phenomenological models can be inferred as$\langle 0 | \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{T_{4 c}} |0\rangle\approx 16\;\mathrm{GeV}^9, \quad\;\;\;{\rm{four}}\;-{\rm{body}}\;{\rm{solution}},\!\! \tag{16a}$

$\langle 0 | \mathcal{O}_{{\bar {\bf{3}}}\otimes{\bf{3}}}^{T_{4 c}} |0\rangle\approx 0.015\;\mathrm{GeV}^9,\qquad{\rm{diquark}}\;{\rm{model}}. \tag{16b}$

It is interesting to note that the LDME derived from the compact tetraquark model is approximately three orders of magnitude greater than the one from the diquark model.
In Fig. 2, we plot the
$ 1^{+-} $ tetraquark energy spectrum at B factory energy, taking the value of LDME from the compact tetraquark model (16a). We observe that the$ 1^{+-} $ tetraquark events favor to populate near the maximum allowed energy.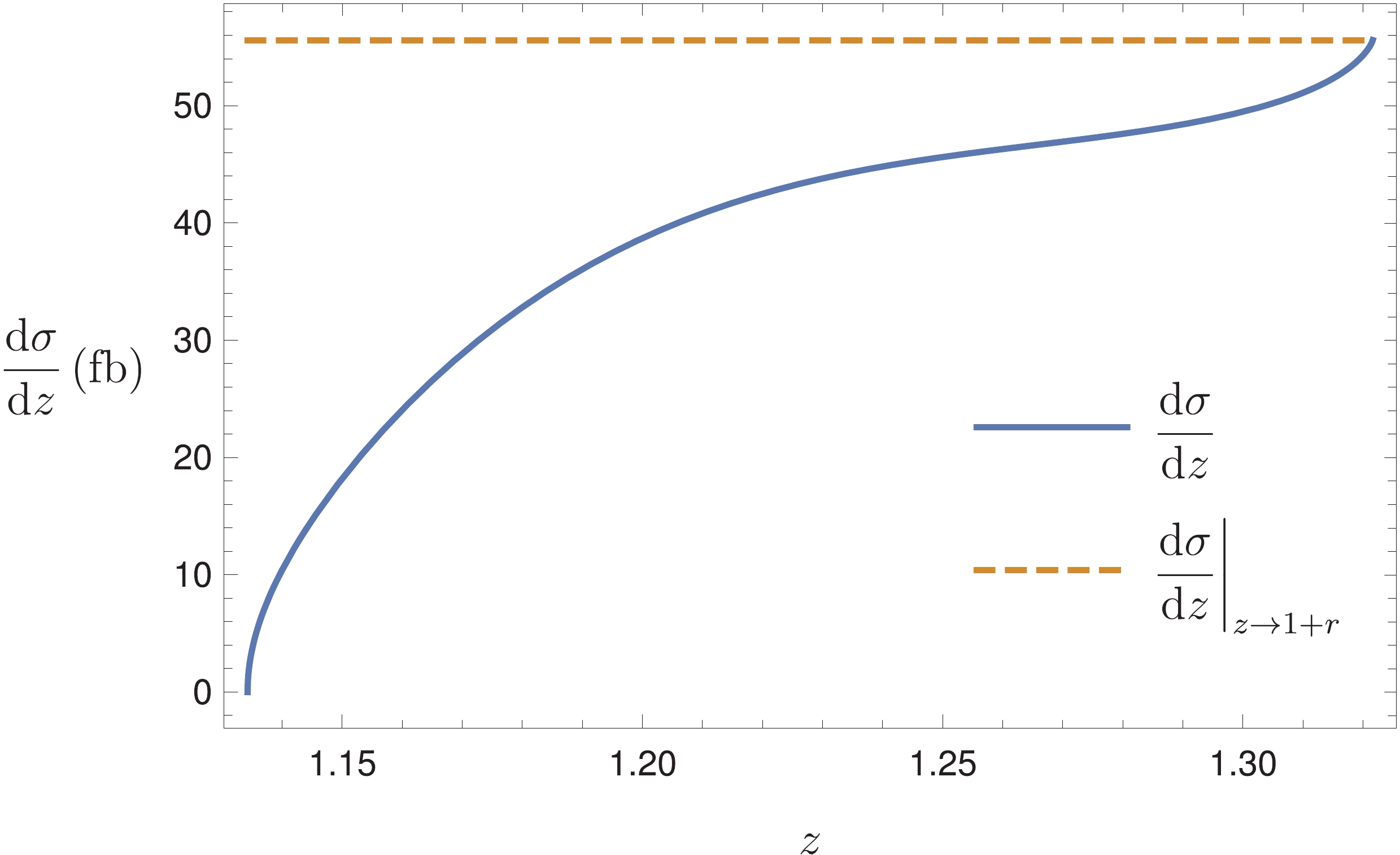
Figure 2. (color online) Energy distribution of
$ T_{4c} $ in the inclusive production from$ e^+e^- $ annihilation at$ \sqrt{s} = 10.58\,\mathrm{GeV} $ . The LDME is taken from (16a), which is estimated from the four-body potential model. The asymptotic value is given by (11).At
$ \sqrt{s} = 10.58\,\mathrm{GeV} $ , the integrated cross section is$ \sigma(e^+e^-\to T_{4c}(1^{+-})+X) \approx 7.3\,\mathrm{fb}, \quad{\rm{four}}\;-{\rm{body}}\;{\rm{solution}}, \tag{17a}$

$\sigma(e^+e^-\to T_{4c}(1^{+-})+X) \approx 0.0069\,\mathrm{fb},\quad{\rm{diquark}}\;{\rm{model}}\tag{17b}.$

Taking the projected integrated luminosity of
${{\mathsf{Belle}} \;{\mathsf{2}}}$ to be$ 50\,\mathrm{ab}^{-1} $ , we estimate that there would be$ 3.6\times 10^5 $ events in the compact tetraquark model.In Fig. 3, we also illustrate the integrated cross section as a function of
$ \sqrt{s} $ . One readily observes that, provided$ \sqrt{s}\geqslant 40 $ GeV, the asymptotic expression in (12) converges to the full result relatively well.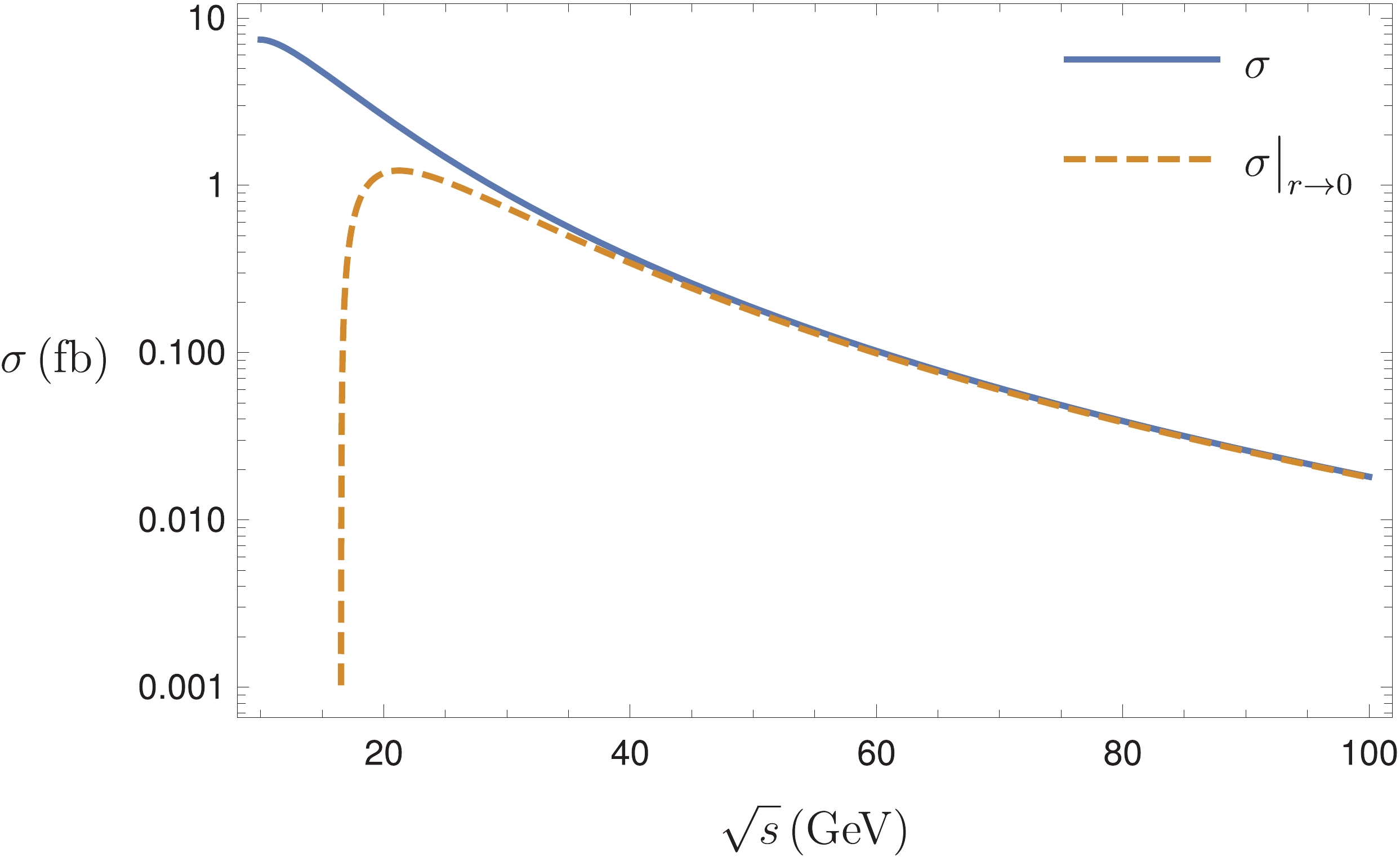
Figure 3. (color online) Integrated cross section as a function of center-of-mass energy. The LDME is estimated from the four-body potential model (16a). The asymptotic curve is taken from (12).
We stress that the numerical prediction (17a) may not need be considered too seriously, as it is extremely sensitive to the nonperturbative input of the NRQCD LDME, which is poorly known presently. Based on the alarming discrepancy of the predicted NRQCD LDME, we hope that future experimental endeavor to search for the fully-heavy tetraquark may provide crucial clues for discriminating these two different models.
-
The recent discovery of the
$ X(6900) $ particle during the${\mathsf{ LHCb}}$ experiment has paved a new path toward studying exotic hadrons, as it is likely that the first genuine tetraquark comprises four charm quarks. It might be naturally interpreted as a$ 0^{++} $ or$ 2^{++} $ S-wave tetraquark. In this work, we study the inclusive production of the close cousin of$ X(6900) $ , a would-be fully-charmed S-wave tetraquark state with quantum number$ 1^{+-} $ , in$ e^+e^- $ annihilation. In particular, we investigate the inclusive production rate of this C-odd$ T_{4c} $ in association with light hadrons of the${{\mathsf{Belle}} \;{\mathsf{2}}}$ experiment, at the lowest order in the NRQCD factorization approach. We adopt a four-body Schrödinger wave function and a naive diquark-antidiquark cluster model to assess the encountered long-distance NRQCD matrix element and consequently predict the production rate. We infer that the prediction made with the four-body solution is approximately three orders of magnitude times larger than the diquark model.Obviously, future experimental search for fully-charmed tetraquarks at B factory will provide crucial guidance to our exploratory study, especially in helping to identify the model that is more favorable.
-
We thank Jiaxing Zhao for providing the four-body wave functions of fully-heavy tetraquarks.
Inclusive production of fully-charmed 1+− tetraquark at B factory
- Received Date: 2021-04-09
- Available Online: 2021-09-15
Abstract: Inspired by the recent discovery of the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: