-
A muon anomalous magnetic moment (muon
$ g-2 $ ) is experimentally and theoretically analyzed with high precision, and it is a promising observation, to test/verify novel physics beyond the standard model (SM). Recently, the E989 Run 1 experiment at Fermilab (FNAL) [1] provided new data for muon$ g-2 $ , where the previous measurement at the E821 experiment at Brookhaven National Lab (BNL) two decades ago [2] indicates a deviation from the SM prediction by$ \sim 3 \sigma $ . Combining the BNL results, the deviation from the SM prediction [3, 4] is given by$ \begin{align} \Delta a_\mu = (25.1\pm5.9)\times 10^{-10}, \end{align} $

(1) where the deviation reaches
$ 4.2\sigma $ with a positive value from the SM prediction. Moreover, a further update of Fermilab E989 and an upcoming J-PARC E34 [5] experiment will provide better results with higher precision. To explain the deviation theoretically, several mechanisms have been proposed over time, such as, gauge contributions [6-8], Yukawa contributions at one-loop level [9], and Barr-Zee contributions [10] at two-loop level. In particular, if muon$ g-2 $ is related to other phenomenologies such as neutrino mass generations, dark matter, and various flavor physics, the new Yukawa interactions become important, where muon$ g-2 $ would be explained at a one-loop level via such interactions [9, 11-42] (also refer to recent approaches after new FNAL results [43-78]). In such a case, it is required to simultaneously satisfy several constraints of lepton flavor violations (LFVs), such as$ \ell_i\to \ell_j\gamma $ ,$ \ell_i\to\ell_j\ell_k\bar\ell_\ell $ ($ i,j,k,\ell = (e,\mu,\tau) $ ), including lepton flavor conserving (violating) Z boson decays$ Z\to\ell\bar\ell' $ ,$ Z\to\nu\bar\nu' $ [79]. In particular, the$ \ell_\mu\to \ell_e\gamma $ process presents the most stringent constraint, where the current upper bound on the branching ratio is$ 4.2\times10^{-13} $ [80], and its future bound will reach the sensitivity at$ 6\times10^{-14} $ [81]. In addition, Z boson decays will be tested in future experiments such as CEPC [82]. Previously, we analyzed models introducing multi-charged fields (scalars and vector-like leptons) with general$ U(1)_Y $ hypercharges, to obtain a positive muon$ g-2 $ , and explored the parameter region satisfying several experimental constraints [38]. Another interesting study includes a new$ U(1)' $ that explains the same case [83].Another interesting hint for new physics includes experimental anomalies of semileptonic B-meson decays, deviations in the measurements of the angular observable
$ P'_5 $ in the decay of the B meson ($ B \to K^* \mu^+ \mu^- $ ) [84-88], the ratio of branching fractions,$R_K = {\rm BR}(B^+ \to K^+ \mu^+\mu^-)/ $ $ {\rm BR}(B^+ \to K^+ e^+e^-)$ [89-91], and$R_{K^*} = {\rm BR} (B \to K^* \mu^+ \mu^-)/ $ $ {\rm BR} (B \to K^* e^+ e^-)$ [92]. Various global fits to corresponding Wilson coefficients are also carried out [93-96], thus indicating that the negative contribution to the Wilson coefficient associated with the$ (\bar s_R \gamma^\mu b_L)( \bar \mu \gamma_\mu \mu) $ operator is preferred in explaining the anomalies. We can explain the anomalies by introducing a$ U(1)_{\mu - \tau} $ gauge symmetry when we include a few extra field contents such as vector-like quarks [97-104].Hence, it is worthwhile to consider a model with multi-charged particles– vector-like quarks, vector-like leptons, and charged scalar fields– under a local
$ U(1)_{\mu - \tau} $ framework, where we can combine the ideas in the model discussed in [38] and [97, 102]. The advantages of this approach are as follows: (1) we can constrain the flavor structure of Yukawa couplings associated with extra fermions, to suppress the constraints from lepton flavor violations (LFVs), (2) we have more contributions to muon$ g-2 $ from one loop diagrams with$ Z' $ and vector-like leptons, (3) collider signature is controlled by the$ U(1)_{\mu - \tau} $ charge assignment to provide predictions. Subsequently, we investigate if both muon$ g-2 $ and B-anomalies can be explained simultaneously by analyzing the correlation among the parameters considering experimental constraints, and then discuss collider physics to demonstrate possible signatures of this scenario.In this paper, we discuss the model introducing multi-charged fields (scalars and fermions) under a local
$ U(1)_{\mu - \tau} $ framework, as an extension of the model in [38] and [97, 102]. We investigate contributions to muon$ g-2 $ from one-loop diagrams, including the new particles such as vector-like lepton, charged scalar, and$ Z' $ boson. Extra vector-like quarks are introduced and Wilson coefficient is calculated to explain B-anomalies. Constraints from meson anti-meson mixing are discussed in addition to LFV and Z decays. Then, we explore the parameter region accommodating both muon$ g-2 $ and B-anomalies. We search for the parameters satisfying all the constraints, and from the allowed model parameters, we consider the benchmark points (BP's) for the collider study.Because the multi-charged fields can be produced at the Large Hadron Collider (LHC), the signature of the exotic charged particles are also explored. We particularly focus on the LHC signatures of an exotic lepton doublet. Here, the exotic leptons decay
$ via $ the charged scalar, which in turn produces different collider signatures w.r.t the standard scenario, where exotic leptons (singly charged) decay into SM particles directly ($ W\nu $ ,$ Z\ell $ , and$ H\ell $ ) [105]. We will demonstrate that a small mass difference between the charged scalar and the exotic lepton is naturally favored by the sizable muon ($ g-2 $ ). Hence, the collider signature of this particular model will contain very soft muons. We particularly focus on the signature of the two oppositely charged muon and tau pairs at LHC.The remainder of this paper is organized as follows. In Sec. II, we present the setup of the model and formulate the Wilson coefficient for B-decay, meson anti-meson mixing, LFV's, muon
$ g-2 $ , and Z boson decays. In Sec. III, we perform numerical analysis to identify the allowed region of parameter space. In Sec. IV, we discuss possible extension of the model by introducing the$ U(1)_{\mu - \tau} $ gauge symmetry and discuss the collider physics signature. We conclude in Sec. V. -
We consider a model with gauge symmetry
$ G_{\rm SM} \times U(1)_{\mu - \tau} $ where$ G_{\rm SM} $ is the SM gauge symmetry and$ U(1)_{\mu - \tau} $ is an extra gauge symmetry. In our setup of the model, we introduce isospin doublet fermions$L'_a\equiv $ $ [\psi^{-}_a,\psi^{–}_a]^T (a = 1-3)$ ,$ Q'_a\equiv[q'^{-1/3}_a,q'^{-4/3}_a]^T\equiv [u'_a,d'_a]^T $ and a singly-charged boson$ s^{+} $ , as presented in Table 1①; here x and y for$ U(1)_{\mu - \tau} $ refer to any real number, and the SM quarks are not charged under$ U(1)_{\mu -\tau} $ . For vector-like fermions, we introduce three generations to match with the SM. We also introduce three right-handed neutrinos with the$ U(1)_{\mu - \tau} $ charge. In this paper we do not discuss neutrino mass. Neutrino masses under$ U(1)_{\mu - \tau} $ can be found e.g. in Refs. [106, 107]. Here, we also introduce a scalar field φ with non-zero VEV to break$ U(1)_{\mu -\tau} $ spontaneously. The Lagrangian involving the interaction of new particles and SM, including the potential, is given by,$L_{L_\mu}$ 

$L_{L_\tau}$ 

$e_{R_\mu}$ 

$e_{R_\tau}$ 

$\nu_{R_\mu}$ 

$\nu_{R_\tau}$ 

$L'_{}$ 

$Q'_{}$ 

H $s^{+}$ 

φ $SU(3)$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{3}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

$SU(2)_L$ 

${\bf{2}}$ 

${\bf{2}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

${\bf{2}}$ 

${\bf{2}}$ 

${\bf{2}}$ 

${\bf{1}}$ 

${\bf{1}}$ 

$U(1)_Y$ 

$-\dfrac12$ 

$-\dfrac12$ 

$-1$ 

$-1$ 

$0$ 

$0$ 

$-\dfrac{3}2$ 

$-\dfrac{5}6$ 

$\dfrac12$ 

$+1$ 

$0$ 

$U(1)_{\mu -\tau}$ 

$1$ 

$-1$ 

$1$ 

$-1$ 

$1$ 

$-1$ 

$1+x$ 

x 0 $-x$ 

y Table 1. Charge assignments of fields under
$ SU(2)_L\times U(1)_Y \times U(1)_{\mu - \tau} $ for the extended model. We introduce three generations of vector-like fermions$ L' $ and$ Q' $ .$\begin{aligned}[b]-\mathcal{L}^n_{Y} =& f_{2a} \bar L_{L_2} L'_{R_a} s^+ + g_{ia} \bar Q_{L_i} Q'_{R_a} s^+ +h_{ij} \bar L^c_{L_i}\cdot L_{L_j} s^+ \\&+ k_{ij} \overline{\nu^c_{R_i}} e_{R_j} s^+ + M_{Q'_a} \bar Q'_{L_a} Q'_{R_a} + M_{\psi_a} \bar L'_{L_a} L'_{R_a} + {\rm h.c.}\\ =& f_{2a}[\bar \nu_{2} P_R\psi^-_a s^+ + \bar\ell_2 P_R\psi^{--}_a s^+] +g_{ia}[\bar u_{i} P_R u'_a s^- \\&+ \bar d_i P_R d'_a s^+] + h_{ij}[\bar \nu^c_{i} P_L \ell_j s^+ - \bar \ell^c_i P_L \nu_j s^+] \\ & + k_{ij} \overline{\nu^c_{R_i}} e_{L_j} s^+ + M_{Q'_a} \bar Q'_{L_a} Q'_{R_a} + M_{\psi_a} \bar L'_{L_a} L'_{R_a}+ {\rm h.c.} , \end{aligned}$

(2) $ \begin{aligned}[b] {\cal {V}} =& \mu_H^2|H|^2 + \mu_S^2 |s^+|^2 +\lambda_H|H|^4 +\lambda_s|s^+|^4 \\& +\lambda_{Hs}|H|^2|s^+|^2 + \mu^2_\varphi |\varphi|^2 + \lambda_{\varphi} |\varphi|^4 \\ & + \lambda_{H \varphi} |H|^2 |\varphi|^2 + \lambda_{S \varphi} |s^+|^2 |\varphi|^2, \end{aligned} $

(3) where
$ (i,j,a) = 1-3 $ represent generation indices, ($ \cdot\equiv i\sigma_2 $ ), with$ \sigma_2 $ being the second Pauli matrix, and$ L'_{L[R]_a}(Q'_{L[R]_a}) \equiv P_{L[R]} L'_a(Q'_a) $ . The SM Yukawa term$ y_{\ell_{ii}}\bar L_{L_i}e_{R_i}H $ provides masses for charged leptons$ (m_{\ell_i}\equiv y_{\ell_{ii}}v/\sqrt2 $ ) by developing a nonzero vacuum expectation value (VEV) of H, which is denoted by$ \langle H\rangle\equiv v/\sqrt2 $ . The exotic fermion mass eigenvalues are, respectively,$ M_{Q{'}}, M_{\psi} $ for Q', L'. We expect that the interaction term involving$ h_{ij} $ plays a role in the$ s^+ $ decay into SM fields appropriately. However, because this term negatively contributes to the muon$ g-2 $ , we assume the scale of$ h_{ij} $ is not significantly large. This implies that we do not discuss the LFVs and muon$ g-2 $ of this term. In addition, note that non-zero components of$ h_{ij} $ and$ k_{ij} $ are changed by our choice of parameter x; hence, the decay pattern of$ s^+ $ depends on x. More concretely, the structure of the third and fourth terms in Eq. (2) depends on the value of x, such that$ h_{ij} \bar L^c_{L_i}\cdot L_{L_j} s^+ = h_{\{12, 13 \}} \bar L^c_{L_{\{e,e\} } } \cdot L_{L_{\{\mu,\tau\}}} s^+ \quad \text{for}~~ x = \{1, -1 \}, $

(4) $ \begin{aligned}[b] & k_{ij} \overline{\nu^c_{R_i}} e_{R_j} s^+ = k_{ \{ 12(21), 13(31), 22, 33 \}} \overline{ \nu^c_{R_{\{ e(\mu), e(\tau), \mu, \tau \}}} } \; e_{R_{\{ \mu(e), \tau(e), \mu, \tau \} }} s^+ \\& \text{for}~~ x = \{1, -1, 2, -2 \}, \end{aligned} $

(5) where we cannot have the Yukawa interaction for
$ x \neq 0 $ . Therefore, the decay pattern of$ s^+ $ is determined by the choice of x, where we consider that our right-handed neutrinos are assumed to be light, such that$ s^+ $ can decay into states containing them. For$ x = -2 $ , the constraint from the collider experiment is weaker because$ s^\pm $ only decays into the third generation of leptons, while we have stronger constraints for$ x = \pm 1 $ or$ 2 $ , because it decays into electrons and/or muons. Hence, we chose$ x = -2 $ in our numerical analysis. In addition, we do not have an extra term in any choice of y, where$ x\neq0 $ and$ y\neq0 $ .In a scalar sector, we assume coupling
$ \lambda_{H \varphi} $ is small, such that mixing between φ and H is negligible for simplicity. Under the assumption, the VEV of φ is simply given by$ v_\varphi \simeq \sqrt{-\mu_\varphi^2/\lambda_\varphi} $ . After φ develops a VEV, we have massive$ Z' $ boson, whose mass is given by$ m_{Z'} = y g' v_\varphi, $

(6) where
$ g' $ denotes the gauge coupling associated with$ U(1)_{\mu - \tau} $ . The mass eigenvalue of$ s^+ $ is given by$ \begin{align} m_S = \mu_S^2+ \frac{\lambda_{Hs}}{2} v^2+ \frac{\lambda_{S \varphi }}{2} v_\varphi^2. \end{align} $

(7) In our numerical analysis, we take
$ m_S $ as a free parameter. -
The parameter space of our model get constrained from the neutral meson mixings, where the VLQs appear in the loop. The relevant expressions, as presented in [108], are
$ \Delta M_Q\approx \frac{ m_Q f_Q^2}{3(4\pi)^2} \sum_{a,b = 1}^3{{\rm Re}[g_{ka} g_{ai}^* g_{jb} g_{b \ell }^*]} F_{\rm {box}}(M_{Q'_a},M_{Q'_b},m_s), $

(8) $ F_{\rm {box}}(m_1,m_2,m_3) = \int [{\rm d}x]^3 \frac{z}{x m_1^2+y m_2^2+z m^2_3}, $

(9) where
$\int [{\rm d}x]^3 \equiv \int_0^1 {\rm d}x {\rm d}y {\rm d}z \delta(1-x-y-z)$ ,$ B_s-\bar B_s $ mixing corresponds to$ (i,j,k,\ell) = (2,3,3,2) $ ,$ B_d-\bar B_d $ mixing corresponds to$ (i,j,k,\ell) = (1,3,3,1) $ , while$ K-\bar K $ and$ D-\bar D $ correspond to$ (i,j,k,\ell) = (1,2,2,1) $ . The neutral meson mixing formulas should be lower than the experimental bounds, as given in [108, 109]:$ \Delta m_K \lesssim 3.48\times10^{-15} \ [{\rm {GeV}}], $

(10) $ 3.29\times10^{-13} \ [{\rm {GeV}}]\lesssim\Delta m_{B_d} +\Delta m_{B_d}^{\rm SM} \lesssim 3.37\times10^{-13} \ [{\rm {GeV}}], $

(11) $ 1.16\times10^{-11} \ [{\rm {GeV}}] \lesssim\Delta m_{B_s} + \Delta m_{B_s}^{\rm SM} \lesssim 1.17\times10^{-11} \ [{\rm {GeV}}], $

(12) $ \Delta m_D \lesssim 6.25\times10^{-15} \ [{\rm {GeV}}], $

(13) where we have taken the 3σ interval, and
$ m_{M} $ and$ f_M $ are the meson mass and the meson decay constant, respectively. The following values of the parameters are used in our analysis:$ f_K \approx 0.156 $ GeV,$ f_{B_d(B_s)} \approx 0.191(0.274) $ GeV [110, 111],$ f_{D} \approx 0.212 $ GeV,$ m_K \approx 0.498 $ GeV,$m_{B_d(B_s)} \approx $ $ 5.280(5.367)$ GeV, and$ m_{D} \approx 1.865 $ GeV. The SM contributions are given by [112]:$ 2.96\times10^{-13} \ [{\rm {GeV}}]\lesssim\Delta m_{B_d}^{\rm SM} \lesssim 5.13\times10^{-13} \ [{\rm {GeV}}], $

(14) $1.06\times10^{-11} \ [{\rm {GeV}}] \lesssim\Delta m_{B_s}^{\rm SM} \lesssim 1.44\times10^{-11} \ [{\rm {GeV}}]. $

(15) Subtracting the SM contributions from the experimental results, the following bounds can be obtained:
$ -1.85\times10^{-13} \ [{\rm {GeV}}]\lesssim\Delta m_{B_d} \lesssim 4.05\times10^{-14} \ [{\rm {GeV}}], $

(16) $ -2.77\times10^{-12} \ [{\rm {GeV}}] \lesssim\Delta m_{B_s} \lesssim 1.07\times10^{-12} \ [{\rm {GeV}}]. $

(17) -
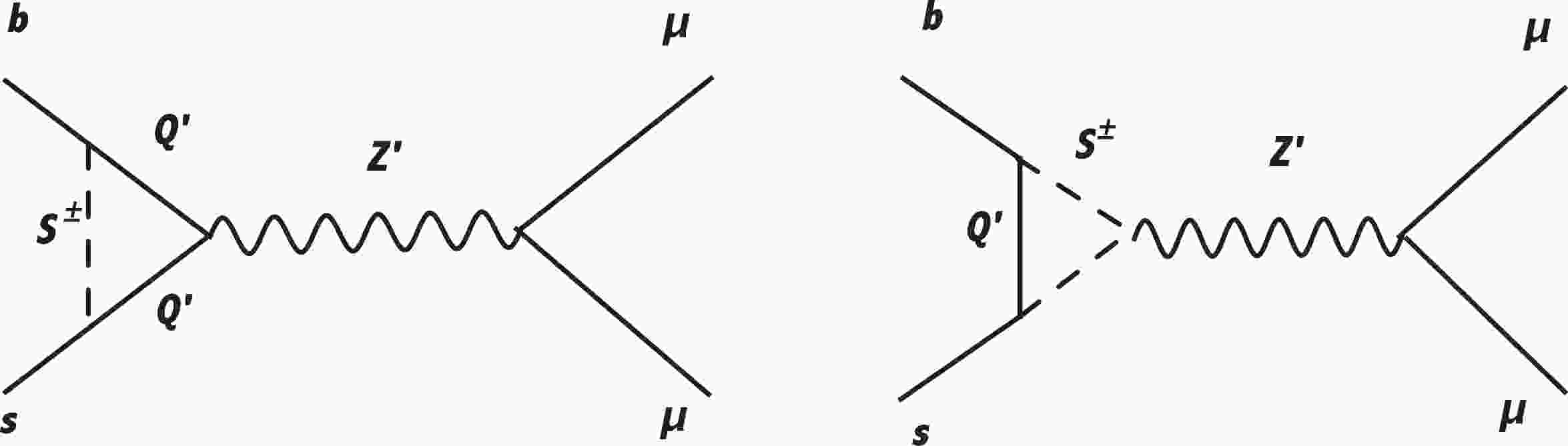
In our model, we apply the same mechanism in [97, 102] to generate
$ \Delta C_9^\mu $ using$ Z' $ interaction; other mechanisms with$ U(1)_{\mu -\tau} $ can be found in [103, 104]. We obtain the contribution to$ \Delta C_9^{\mu} $ from diagrams in Fig. 1. Subsequently, we obtain the contribution to$ \Delta C_9^{\mu, Z'} $ as in [97, 102]$\begin{aligned}[b] \Delta C_9^{\mu, Z'} \simeq& \frac{x g'^2}{(4\pi)^2 m_{Z'}^2 C_{\rm SM}} \sum_{a = 1}^{3} g_{3a} g^*_{a2} \\&\times\int[dx]^2 \ln \left(\frac{\Delta[M_{Q'_a},m_S]}{\Delta[m_S,M_{Q'_a}]} + \frac{M^2_{Q'_a}}{x m_S^2 + y M^2_{Q'_a}} \right), \\ C_{\rm SM} \equiv &\frac{V_{tb} V^*_{ts} G_{\rm F} \alpha_{\rm em}}{\sqrt2 \pi}, \\ \Delta[m_1,m_2] =& x m_1^2 + y m_{2}^2,\end{aligned} $

(18) where
$\displaystyle\int [{\rm d}x]^2 \equiv \displaystyle\int_0^1 {\rm d}x {\rm d}y \delta(1-x-y)$ and quark masses are ignored. We can obtain$ \Delta C_9^{\mu, Z'} \sim -1 $ satisfying all the experimental constraints as shown in [97, 102] with$ M_{Q'_{a}} = \mathcal{O}(1) $ TeV,$ m_S = \mathcal{O}(100) $ GeV and$ m_{Z'} = \mathcal{O}(100) $ GeV, where$ Z' $ contribution to muon$ g-2 $ is negligible in this region.Here, we simplify the above formula by carrying out an integration
$ \Delta C_9^{\mu, Z'} \simeq \sum_{a} \frac{g_{3a} g^*_{a2} x g'^2}{ 2 (4\pi)^2 m_{Z'}^2 C_{\rm SM}} . $

(19) In addition, we also obtain an Effective Lagrangian to induce
$ b\to s\ell\bar\ell $ decay$ via $ box diagram, such that$ \begin{aligned}[b] {\cal {L}}^{\rm [box]} =& - \sum_{a,b} \frac{g_{2a}g^*_{a3} f_{2b} f^*_{b2}}{4(4\pi)^2} (\bar s\gamma_\mu P_L b)\\&\times(\bar\ell_2 \gamma^\mu \ell_2 - \bar\ell_2 \gamma^\mu \gamma_5\ell_2) F_{\rm {box}}(M_{Q'_a} , M_{\psi_b} ,m_s), \end{aligned} $

(20) which corresponds to
$ {\cal O}_9 = -{\cal O}_{10} $ [93].$ \begin{align} \Delta C_9^{\mu {\rm [box]}} = - \Delta C_{10 }^{\mu {\rm [box]}}\approx \sum_{a,b} \frac{g_{2a} g^*_{a3} f_{2 b} f^*_{b 2}}{4 (4\pi)^2 C_{SM}}F_{\rm {box}}(M_{Q'_a} , M_{\psi_b} ,m_s), \end{align} $

(21) where
$C_{\rm SM}\equiv \dfrac{V_{tb} V^*_{ts} G_{\rm F} \alpha_{em}}{\sqrt{2} \pi}$ . In total, we obtain the new physics contribution to the Wilson coefficient,$ \Delta C_9^{\ell} $ , as$ \Delta C_9^{\mu} = \Delta C_9^{\mu, Z'} + \Delta C_9^{\mu {\rm [box]}}. $

(22) Furthermore, we should consider the diagrams replacing
$ Z' $ by Z in Fig. 1, which induce flavor universal contributions to$ C_9 $ and$ C_{10} $ $ via $ the Z boson exchange. Calculating the diagrams, we obtain$ \begin{aligned}[b]\Delta C_9 (Z) \simeq & \sum_{a} \frac{g_{3a} g^*_{a2} g_2^2}{ 4 (4\pi)^2 m_{Z}^2 c_W^2 C_{\rm SM}}\\&\times \left( -\frac12 +\frac43 s_W^2 \right) \left( - \frac12 + 2 s^2_W \right), \end{aligned} $

(23) $ \begin{aligned} \Delta C_{10} (Z) \simeq \sum_{a} \frac{g_{3a} g^*_{a2} g_2^2}{ 8 (4\pi)^2 m_{Z}^2 c_W^2 C_{\rm SM}} \left( -\frac12 +\frac43 s_W^2 \right), \end{aligned} $

(24) where
$ c_W = \cos \theta_W $ , with$ \theta_W $ being the Weinberg angle. Because structures of$ C_{9,10}(Z) $ are similar to$ \Delta C_9^{\mu, Z'} $ , we obtain the relationship$ \begin{align} & \frac{\Delta C_9 (Z)}{\Delta C_9^{\mu, Z'}} \simeq \frac{g_2^2}{m_Z^2 c_W^2} \frac{m_{Z'}^2}{x g'^2} \frac12 \left( -\frac12 +\frac43 s_W^2 \right) \left( - \frac12 + 2 s^2_W \right), \end{align} $

(25) $ \begin{align} & \frac{\Delta C_{10} (Z)}{\Delta C_9^{\mu, Z'}} \simeq \frac{g_2^2}{m_Z^2 c_W^2} \frac{m_{Z'}^2}{x g'^2} \frac14 \left( -\frac12 +\frac43 s_W^2 \right). \end{align} $

(26) Then, the
$ b\to s \mu \bar \mu $ anomalies can be explained by$ \Delta C_9^{\mu, Z'} = -0.97 $ as the best fit value,$ [-1.12,-0.81] $ at 1σ, and$ [-1.27,-0.65] $ at the 2σ interval [96]. The flavor universal$ \Delta C_9 (Z) $ is significantly smaller than$ \Delta C_9^{\mu, Z'} $ , owing to the suppression factor$ (-1/2 + 2 s_W^2) $ . For$ \Delta C_{10}(Z) $ , we consider constraint from the$ B_s \to \mu^+ \mu^- $ measurement. Recent LHCb measurement of the branching ratio is given by [113, 114]$ {\rm BR}(B_s^0 \to \mu^+ \mu^-)^{\rm exp} = (3.09^{+0.46 + 0.15}_{-0.43-0.11}) \times 10^{-9}, $

(27) where the first uncertainty is statistical and the second one is systematic. We can estimate the branching ratio in the model, such that [115]
$ {\rm BR}(B_s^0 \to \mu^+ \mu^-)^{\rm th} = |1-0.24 \Delta C_{10}^{\mu \mu}|^2 {\rm BR}(B_s^0 \to \mu^+ \mu^-)^{\rm SM}, $

(28) where
${\rm BR}(B_s^0 \to \mu^+ \mu^-)^{\rm SM} = (3.65 \pm 0.23) \times 10^{-9}$ is the theoretical predication in the SM [116]. In the numerical analysis, we impose that the branching ratio in our model is within the$ 1\sigma $ region in Eq. (27). In addition, note that$ x<0 $ is preferred because we realize a positive$ C_{10} $ to fit the data. -
In our model, we do not have lepton flavor violations from Yukawa coupling
$ f_{ia} $ because only components associated with muon,$ f_{2a} $ , are non-zero. Hence, we only focus on the contribution to muon$ g-2 $ from the Yukawa interactions.The muon anomalous magnetic moment (
$ \Delta a_\mu $ ): We can estimate the scalar loop contribution to the muon anomalous magnetic moment via (muon$ g-2 $ ), which is given by$ \begin{align} \Delta a^{S}_\mu \approx -m_\mu (a_L+a_R)_{22}. \end{align} $

(29) The amplitude
$ a_{L/R} $ can be expressed as,$ \begin{aligned}[b] (a_{L})_{22} \approx & (a_{R})_{22} \approx - m_{\mu} \sum_{a = 1-3} \frac{f_{2a} f^*_{a2}}{(4\pi)^2} \\&\times {\left[ F(M_{\psi^{--}_a} , m_{S}) + 2 F(m_{S},M_{\psi^{--}_a})\right]}, \end{aligned} $

(30) where
$M_{\psi^{--}}\equiv M_{\psi}$ .It is worthwhile considering
$ \Delta a_\mu $ $ via $ $ Z' $ , although it would not be required because we already have the contribution$ via $ $ f_{2a} $ , and the preferred mass range is lighter than that for the B anomalies. The$ Z' $ boson loop contribution is obtained as [117]$ \begin{align} \Delta a^{Z'}_\mu = \frac{g'^2m_\mu^2}{4\pi^2}\int_0^1 {\rm d} x \frac{x^2(1-x)}{x^2 m^2_\mu +(1-x) m_{Z'}^2}. \end{align} $

(31) In summary, muon
$ g-2 $ is given by$ \Delta a_\mu = \Delta a^{S}_\mu + \Delta a^{Z'}_\mu. $

(32) The measured value exhibit a
$ 3.3\sigma $ deviation from the SM prediction, given by$ \Delta a_\mu = (26.1\pm8)\times10^{-10} $ [3], which is also a positive value. Note here that the charged scalar contribution using$ h_{23} $ is negligible, as we consider$ h_{23} $ to be small, as discussed below Eq. (3). -
Here, we consider the Z boson decay into two leptons using the Yukawa terms involving
$ f_{2a} $ at one-loop level [25]. Because some components of$ f_{2a} $ are expected to be large, to obtain a sizable$ \Delta a_\mu $ value, the experimental bounds on Z boson decays could be an issue at the one-loop level. Note that Z boson decays are modified only when the second generation of leptons are involved due to the$ U(1)_{\mu -\tau} $ symmetry. This is why we consider the flavor conserving processes of Z boson only.First, the relevant Lagrangian is given by③
$\begin{aligned}[b] {\cal {L}}\sim & \frac{g_2}{c_w} \left[\bar\ell\gamma^\mu \left(-\frac12 P_L+s_W^2\right)\ell +\frac12\bar\nu\gamma^\mu P_L\nu \right] Z_\mu\\ &+ \frac{g_2}{c_w} \left[ \left(-\frac12 P_L+ s_W^2\right)\bar\psi^+\gamma^\mu \psi^- \right.\\&\left.+ \left(-\frac12 P_L+ 2 s_W^2\right)\bar\psi^{++}\gamma^\mu \psi^{--} \right] Z_\mu \\ & + {\rm i}\frac{g_2 s_W^2}{c_W}(s^+\partial^\mu s^- - s^-\partial^\mu s^+)Z_\mu, \end{aligned} $

(33) where
$ s(c)_W\equiv\sin(\cos)\theta_W\sim0.23 $ represents the sine (cosine) of the Weinberg angle. The decay rate of the SM at tree level is then given by$ \begin{align} &{\rm \Gamma}(Z\to\ell^-_i\ell^+_j)_{\rm SM} \approx \frac{m_Z}{12\pi} \frac{g_2^2}{c_W^2} \left(s_W^4-\frac{s_W^2}2 + \frac18 \right)\delta_{ij}, \end{align} $

(34) $ \begin{align} &{\rm \Gamma}(Z\to\nu_i\bar\nu_j)_{\rm SM} \approx \frac{m_Z}{96\pi} \frac{g_2^2}{c_W^2} \delta_{ij}. \end{align} $

(35) Combining all the diagrams in Fig. 2, the ultraviolet divergence cancels out and only the finite part remains [25] and is given by,
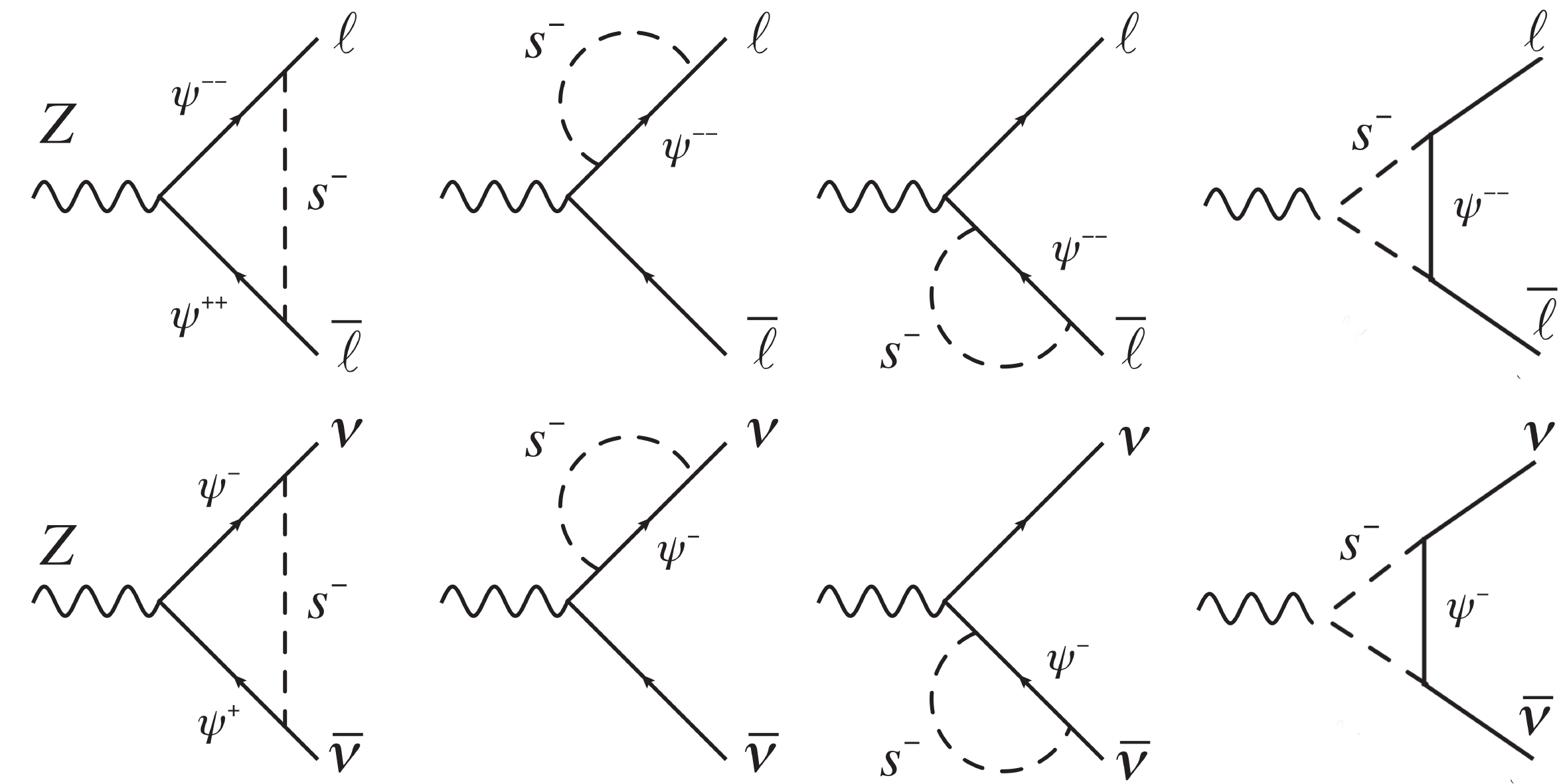
Figure 2. Feynman diagrams for
$ Z\to \ell_i\bar\ell_j $ (up) and$ Z \to \nu_i \bar \nu_j $ (down).$ \begin{aligned}[b] \Delta{\rm \Gamma}(Z\to\mu^- \mu^+) \approx &\frac{m_Z}{12\pi} \frac{g_2^2}{c_W^2} \left[ \frac{|B_{22}^{\ell}|^2}{2} - {\rm Re}[A_{22} (B^{\ell})^*_{22}] \right.\\&\left. -\left( -\frac{s_W^2}2 + \frac18\right) \right] , \end{aligned} $

(36) $ \begin{align} &\Delta{\rm \Gamma}(Z\to\nu_\mu \bar\nu_\mu) \approx \frac{m_Z}{24\pi} \frac{g_2^2}{c_W^2} \left[ {|B_{22}^{\nu}|^2} -\frac{1}{4}\right] , \end{align} $

(37) where,
$ \begin{aligned}[b] &A_{22}\approx s^2_W, \quad B^{\ell}_{22}\approx \frac{1}{2} - \sum_{a} \frac{f_{2a} f^\dagger_{a2}}{(4\pi)^2} G^{\ell}(M_{\psi_a},m_S), \\& B^{\nu}_{22}\approx \frac{1}{2} + \sum_{a} \frac{f_{2a} f^\dagger_{a2}}{(4\pi)^2} G^{\nu}(M_{\psi_a},m_S), \end{aligned} $

(38) $ \begin{aligned}[b] G^{\ell}(M_{\psi_a},m_S)\approx & - s^2_W\left(-\frac12 +s_w^2\right) H_1(M_{\psi_a},m_S)\\& -\left(-\frac12 +s_w^2\right)^2 H_2(m_{\psi_a},m_S) \\ & +\left(-\frac12 +2 s_w^2\right) H_3(M_{\psi_a},m_S),\end{aligned}$

(39) $ \begin{aligned}[b] G^{\nu}(M_{\psi_a},m_S)\approx & -s^2_W\left(-\frac12 +s_w^2\right) H_1(M_{\psi_a},m_S) \\&- \frac12 H_2(M_{\psi_a},m_S) +\left(-\frac12 + s_w^2\right) H_3(M_{\psi_a},m_S), \end{aligned} $

(40) $ H_1(m_1,m_2) = \frac{m_1^4-m_2^4+4 m_1^2 m_2^2\ln\left[\dfrac{m_2}{m_1}\right]}{2(m_1^2-m_2^2)^2}, $

(41) $ \begin{aligned}[b] &H_2(m_1,m_2) \\=& \frac{m_2^4 - 4m_1^2 m_2^2 +3m_1^4 - 4 m_2^2(m_2^2-2m_1^2)\ln[m_2]-4m_1^4\ln[m_1]}{4(m_1^2-m_2^2)^2}, \end{aligned} $

(42) $ \begin{align} &H_3(m_1,m_2) = m_1^2\left( \frac{m_1^2-m_2^2 + 2 m_2^2\ln\left[\dfrac{m_2}{m_1}\right]}{(m_1^2-m_2^2)^2}\right). \end{align} $

(43) Notice here that the upper indices of B and G;
$ \ell,\nu $ , respectively, represent pairs of the muon and muon-neutrino final states. We consider ψ as$\psi^{--}$ inside the argument of$ G^\ell $ , while ψ as$ \psi^{-} $ inside the argument for$ G^\nu $ . The current bounds on the lepton-flavor-(conserving) changing Z boson decay branching ratios at 95 % CL are given by [79]:$ \Delta {\rm BR}(Z\to {\rm Invisible})\approx \sum_{i,j = 1-3}\Delta {\rm BR}(Z\to\nu_i\bar\nu_j)< \pm5.5\times10^{-4} , $

(44) $ \begin{align} & \Delta {\rm BR}(Z\to \mu^\pm\mu^\mp) < \pm6.6\times10^{-5} \; , \end{align} $

(45) where
$ \Delta {\rm BR}(Z\to f_i\bar f_j) $ ($ i = j $ ) is defined by$ \begin{align} \Delta {\rm BR}(Z\to f_i \bar f_j)\approx \frac{{\rm \Gamma}(Z\to f_i \bar f_j)- {\rm \Gamma}(Z\to f_i \bar f_j)_{\rm SM}} {\Gamma_{Z}^{\rm tot}}, \end{align} $

(46) where the total Z decay width
$ \Gamma_{Z}^{\rm tot} = 2.4952 \pm 0.0023 $ GeV [79]. We consider all these constraints in the numerical analysis in the next section. -
Here, we discuss the experimental constraints for the gauge interaction associated with
$ Z' $ . The gauge coupling and$ Z' $ mass are restricted by the neutrino trident process$ \nu N \to \nu N \mu^+ \mu^- $ , where N is a nucleon [6, 118]. The approximated bound is given by$ m_{Z'}/g' \gtrsim 550 \ {\rm {GeV}} $ for$ m_{Z'} > 1 $ GeV, and we apply the bound in our numerical analysis below.The gauge interaction is also constrained by the LHC experiment searching for the signal of
$ pp \to \mu^+ \mu^- Z' $ $ (\to \mu^+ \mu^-) $ , as given in [119]. The experimental results put the constraint on a new gauge coupling, in the mass range$ 5 \lesssim m_{Z'} \lesssim 70 $ GeV. We will compare parameter region, explaining B anomalies with the constraint. -
Finally, we discuss the decay of charged scalar that provides implication to collider physics when we introduce
$ U(1)_{\mu -\tau} $ symmetry. As discussed below, Eq. (2) charged scalar decays into only the third generation of leptons when we chose$ x = -2 $ . We then chose$ x = -2 $ to relax the collider constraint from the charged scalar signature. The decay width of$ s^+ $ for$ x = -2 $ is given by$ \Gamma_{s^\pm \to \tau_R^\pm \nu_{R_\tau}} \simeq \frac{k_{33}^2}{16 \pi} m_{S}, $

(47) where we ignored the lepton mass in the final state assuming light right-handed neutrino. In addition, we assume right-handed neutrinos are long-lived and it will be just missing energy at collider experiments. Furthermore, note that the lightest particle among
$ Q' $ ,$ L' $ , and$ s^+ $ would be stable when there is no interaction associated with$ h_{ij} $ or$ k_{ij} $ in other choices of x value. -
In this section, we perform a numerical analysis to search for parameter sets that accommodate all the phenomena discussed above. Here, we scan our relevant free parameters
$ \{g_{ia}, f_{2a}, g', m_{Z'}, M_{\psi_a}, M_{Q_a}, m_S\} $ globally in the following range:$ \begin{aligned}[b] & g_{ia} \in [10^{-5}, 1], \quad f_{2a} \in [10^{-2}, 1], \quad g' \in [10^{-3}, 1], \\& m_{Z'} \in [10, 1000] \ {\rm {GeV}}, \quad M_{\psi_1} \in [100,500] \ {\rm {GeV}}, \\& M_{\psi_2} \in [M_{\psi_1}, 750] \ {\rm {GeV}}, \quad M_{\psi_3} \in [M_{\psi_2}, 1000] \ {\rm {GeV}}, \\& M_{Q'_1} \in [1000, 5000] \ {\rm {GeV}}, \quad M_{Q'_2} \in [M_{Q'_1}, 5000] \ {\rm {GeV}}, \\& M_{Q'_3} \in [M_{Q'_2}, 5000] \ {\rm {GeV}}, \quad m_{S} \in [M_{\psi_1}-20, M_{\psi_1} -10] \ {\rm {GeV}}, \end{aligned} $

(48) where we also chose
$ x = -2 $ for the$ U(1)_{\mu - \tau} $ charge assignment. Here, we chose$ M_{\psi_1} $ and$ m_S $ values to be nearly degenerated to avoid constraints from the heavy-charged lepton search at collider experiments. We find that$ b\to s\mu\bar\mu $ and the neutral meson mixing mainly depends on following Yukawa coupling combinations:$ \begin{aligned}[b]& C_9^{\mu}\sim g_{21}g^*_{13} |f_{21}|^2,\quad \Delta m_K \sim g_{21}g^*_{11},\\& \Delta m_{B_s} \sim g_{31}g^*_{12},\quad\Delta m_{B_d} \sim g_{31}g^*_{11}, \\& \Delta m_{D} \sim g_{11}g^*_{12}. \end{aligned} $

(49) Because we would like to increase
$ C_9^{\mu} $ to as large as possible, while all the meson mixings should be within the experimental ranges, the following hierarchy is preferred$ \begin{align} g_{11}<<g_{21}\lesssim g_{31}. \end{align} $

(50) Then, we estimate
$ C_9^\mu $ and muon$ g-2 $ imposing experimental constraints. In Fig. 3 we present the allowed parameter space in terms of$ m_{Z'} $ and$ g' $ to explain the$ b\to s\mu\bar\mu $ anomalies$ via $ $ \Delta C_9^{Z'} $ within the$ 1\sigma $ region of global fit. We also present the parameter region excluded by the LHC measurement searching for$ pp \to \mu \bar \mu Z'(\to \mu \bar \mu) $ process [119]. We determine that the parameter region of$ m_{Z'} \lesssim 50 $ GeV is excluded by the LHC constraints while heavier$ Z' $ region can accommodate the B anomalies. For the allowed region, the upper limit of$ g' $ for fixed$ m_{Z'} $ is determined by the constraint from the neutrino trident while the lower limit is given by constraint from${\rm BR}(B^0_s \to \mu^+ \mu^-)$ . Consequently, we determine the narrow range of parameter space where the region close to the neutrino trident limit$ m_{Z'}/g'>550 $ is allowed. Note that the maximum$ |C_9^{\mu [{\rm {box}}]}| $ is 0.115 at most, which is out of the 3σ range of experimental results due to the stringent constraint emerging from$ \Delta m_{B_s} $ , because they ($ \Delta C_9^{\mu [{\rm {box}}]} $ and$ \Delta m_{B_s} $ ) are proportional to the same combination$ g_{31}^{}g_{21}^{} $ . If one extends$ g_{ai} $ to be complex, then one can evade the constraint of$ \Delta m_{B_s} $ and keep large value of$ |\Delta C^\mu_9| $ . However, in this case, another experimental bound of CP asymmetry$ A_{CP} $ arises and it gives more stringent constraint [120]. Therefore, we need the contribution from$ Z' $ interaction to explain B anomalies.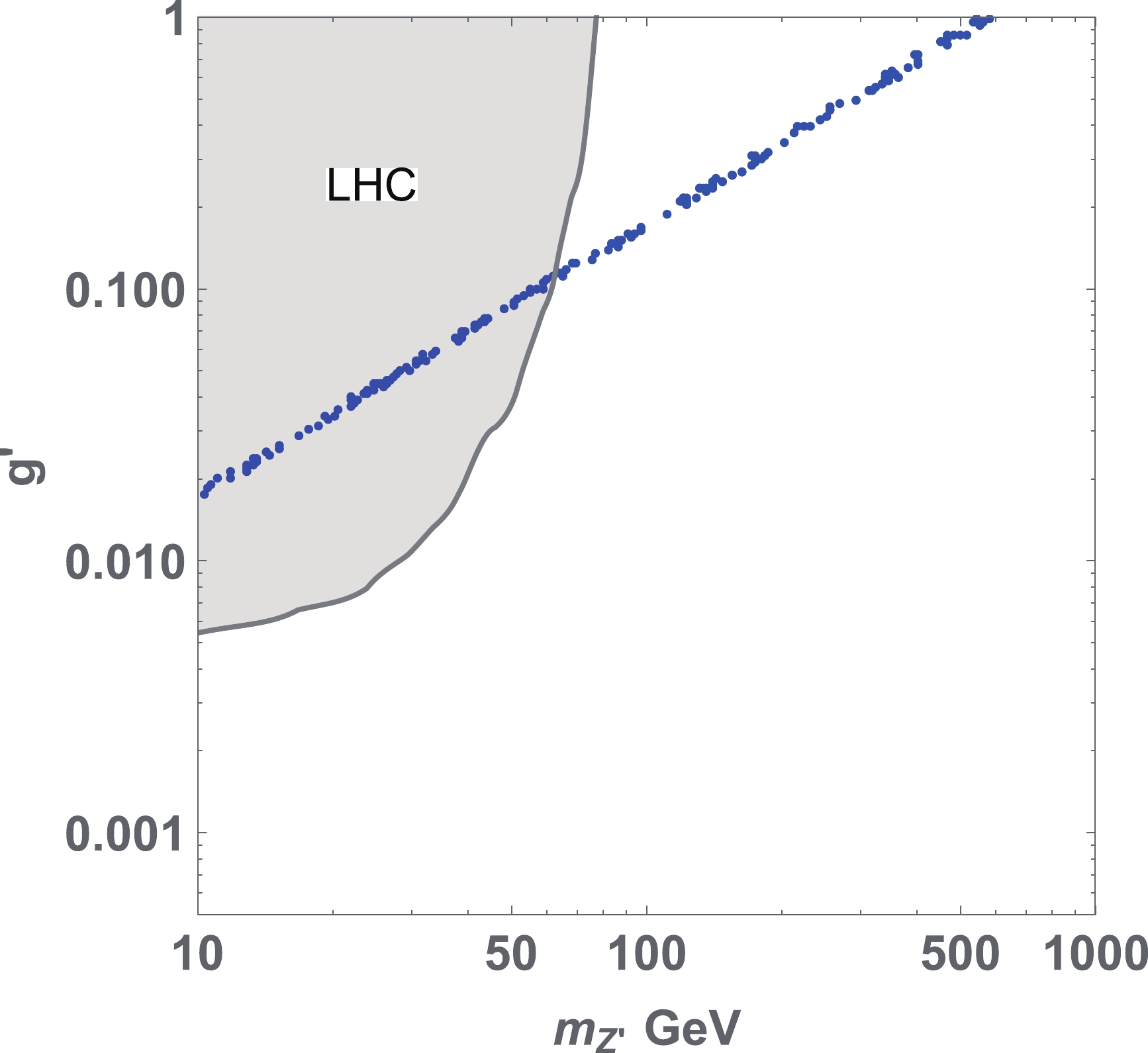
Figure 3. (color online) Allowed points in the parameter space of
$ m_{Z'} $ and$ g' $ that can explain the anomaly of$ b\to s\mu\bar\mu $ , providing$ \Delta C_9 $ within 1σ interval of global fit. We also present the region excluded by the$ pp \to \mu^+ \mu^- Z' (\to \mu^+ \mu^-) $ search at the LHC experiment.Next, we show muon
$ g-2 $ for allowed parameter sets satisfying all experimental constraints and explaining the B anomalies. In the left(center) plot of Fig. 4, we present the contribution to muon$ g-2 $ from the scalar ($ Z' $ ) loop as a function of$ M_{\psi_1}(m_{Z'}) $ , and the total muon$ g-2 $ is shown in the right plot of the figure. We find that the contribution from the$ Z' $ loop can be larger than$ 2 \times 10^{-10} $ for$ m_{Z'} \lesssim 600 $ GeV. Note here that the upper bound up to$ 600 $ GeV comes from$ m_{Z'}/g'>550 $ GeV while that above$ 600 $ GeV comes from our choice of$ g' < 1 $ . The contribution from the scalar loop can be larger than$ 10^{-10} $ for$ m_{\psi_1} \lesssim 260 $ GeV. In particular, it can be close to$ 10^{-9} $ for$ m_{\psi_1} \sim 100 $ GeV region. It is thus possible to explain muon$ g-2 $ within the$ 2 \sigma $ level when we add both$ Z' $ and scalar contributions for light$ m_{\psi_1} $ region. We also note that the upper bound on$ f_{21} $ is$ \sim 0.6 $ , which restricts the maximum value of$ \Delta a_\mu^{S} $ . Here, this upper bound of$ f_{21} $ originates from the constraints of Z boson decays.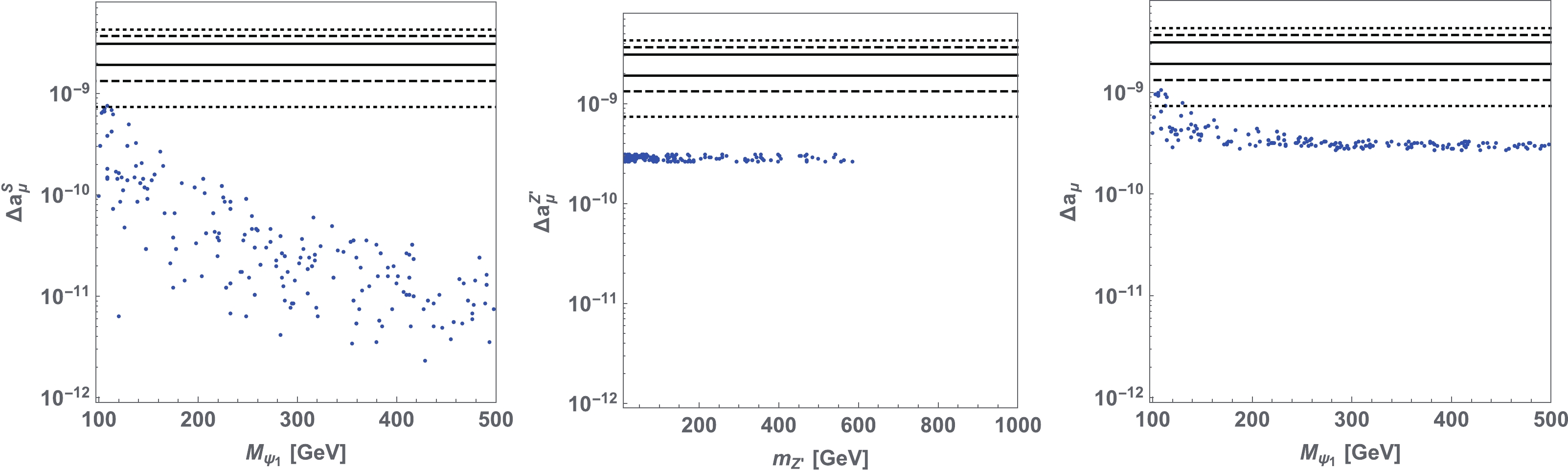
Figure 4. (color online) Left : Contribution to muon
$ g-2 $ from scalar loop diagrams. Center : Contribution to muon$ g-2 $ from the$ Z' $ loop diagram. Right: Sum of scalar and$ Z' $ contributions. The regions between solid, dashed, and dotted lines indicate the 1 σ, 2 σ, and 3 σ regions of deviation between the observed value and SM prediction respectively. -
As discussed in the previous subsections, to get sizable muon
$ g-2 $ that satisfies the flavor constraints together, the mass scale (M) of the exotic lepton doublet is required to be light; to obtain$ \Delta a_\mu^S \gtrsim \mathcal{O}(10^{-10}) $ we need$ M \lesssim 300 $ GeV. Here, we are interested in the production and decay modes of the doubly charged vector like lepton (VLL) given by,$\begin{array}{*{20}{l}} p p \rightarrow \psi^{++}\psi^{--}, \psi^{++} \rightarrow (\mu ^+ s^+)\rightarrow \mu ^+(\nu_l l^+), \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \psi^{--} \rightarrow (\mu ^- s^-)\rightarrow \mu ^-(\bar \nu_l l^-). \end{array}$

Hence, the final state is 1 oppositely charged muon pair + 1 oppositely charged lepton (l) + MET. Because we choose
$ f_{21} = 0.5 $ ,$ \psi^{\pm \pm} $ will decay mostly in to muon and a charged scalar. Now the coupling of the charged scalar with the SM lepton and neutrino is defined by$ k_{33} $ , as discussed in Sec. II.F, and we consider it to be of the order 0.01 where$ s^+ $ decays into$ \tau^+ \bar \nu_{R_\tau} $ with 100 % branching ratio.Vector-like leptons and quarks are constrained from the collider physics experiments. The ATLAS Collaboration performed a search for heavy lepton resonances decaying into a Z boson and a lepton in a multi lepton final state at a center-of-mass energy of 8 TeV [121], constraining the singlet VLL model and excluding its mass range of 114 – 176 GeV. For the doublet VLL model, the L3 Collaboration at LEP placed a lower bound of
$ \sim $ 100 GeV on additional heavy leptons [122]. It has been demonstrated in [105] and [123] that the VLL's in the mass range 120 – 740 GeV are excluded with 95% CL in different multilepton signals. In these analyses, the vectorlike leptons were singly charged and hence it only decays to a SM boson (H, W, Z) and SM leptons. However, in our case, VLLs decay in to a charged scalar and muon specifically, followed by the decay of the off-shell or on-shell charged scalar into a neutrino and another τ lepton. Here, we assume that$ M_{\psi} \sim m_{S} $ and the produced muon is less energetic, which would be missed at detectors by the kinematical cut. Hence, the characteristic of our signal is significantly different from [105] and [123]. Similarly, for vectorlike quarks, the current limit is 1–1.3 TeV [124], but in our model, it decays$ via $ the charged scalar, thereby resulting in different final states not searched so far at LHC.LEP experiment excludes the charged Higgs masses below 80 GeV [125]. At the LHC, searches for the charged Higgs have been performed through various decay channels,
$ H^{\pm}\rightarrow cs $ [126],$ tb $ [127] and$ \nu \tau^{\pm} $ [128], and most of these searches exclude$ m_H^{\pm} < m_t $ . Other searches such as that of [128] give upper limit on the cross section$ \times $ BR as a function of the charged scalar mass. Notice that the$ s^\pm $ only pair produced via the$ Z/\gamma $ propagator in the$ s- $ channel and the cross section is below the current limit.In this analysis, we made our selections differently from [105] and [123]. As a negligible mass difference between the charged Higgs and the VLL naturally implied from the muon (
$ g-2 $ ), the muon will have a very small$ pT(\sim 10 $ ) GeV, but the other two leptons will have a much higher$ pT $ . Other two leptons are τ in our case because we chose the$ U(1)_{\mu -\tau} $ charge, such as charged scalar couples only τ and τ-neutrino. This scenario is still allowed for the VLL mass$ \leq 300 $ GeV. There are scenarios [129, 130] when the doubly charged VLLs decay to a$ W^{\pm} $ and lepton($ l^{\pm} $ ), giving a final state of two oppositely charged lepton pair ($ l^{\pm} $ ) + MET. In this study we have focused on a more exotic scenario, as proposed by the$ U(1)_{\mu - \tau} $ extended model, where the charged exotic leptons decays to tau lepton and a neutrino$ via $ the charged scalar. Hence, in this study, we select our signal to be 1 oppositely charged muon pair with very small pT + 1 oppositely charged tau pair with a moderate pT + MET, and we keep the mass difference between the charged Higgs and the VLL$ \sim $ 10 GeV. The same final state has also been studied for a more general model of vector-like leptons in [131]. One of the advantages of VLL with small mass is that the cross section is large, which can negate the effect of the suppression due to more than one tau tagging. Moreover, in the VLL signatures studied so far by CMS and ATLAS, the assumption was that VLL decays to a W or Z, which is unlikely in our case. Consequently, the$ W/Z $ veto can increase the signal efficiency.We express the model Lagrangian of Eq. (2) in FeynRules (v2.3.13) [132, 133]. We generate the model file for MadGraph5_aMC@NLO (v2.2.1) [134] using FeynRules. Then, we calculate the production cross section using the NNPDF23LO1 parton distributions [135] with the factorization and renormalization scales at the central
$ m_T^2 $ scale after the$ k_T $ -clustering of the event. We have computed the signal cross section of$ p p \to \psi^{++} \psi^{–} $ , where$ p = q, \bar q, \gamma $ . The cross sections are normalized to the 5-flavor scheme. The inclusion of the photon PDF increases the signal cross section significantly, as the coupling is proportional to the charge of the fermion. We plot the the production cross section in Fig. 5 for 13 TeV, as well as 27 TeV. Production cross section$ pp \to s^+ s^- $ is much smaller than that of$ \psi^{++} \psi^{--} $ and mass region$ M(m_S) < 150 $ GeV is still allowed by current experimental constraint [128]. After showering events in PYTHIA [136], events were passed through DELPHES 3 [137] for the detector simulation. In DELPHES, we choose the isolation cut for leptons to be$\Delta R_\max} = 0.5$ , to ensure no hadronic activity inside this isolation cone. While generating the events, we kept the min$ pT $ for muons to be 6 GeV, and also follow other trigger requirements for the soft muons following [138]. The tau tagging efficiency is considered to be 0.6, and the misidentification efficiency is 0.01.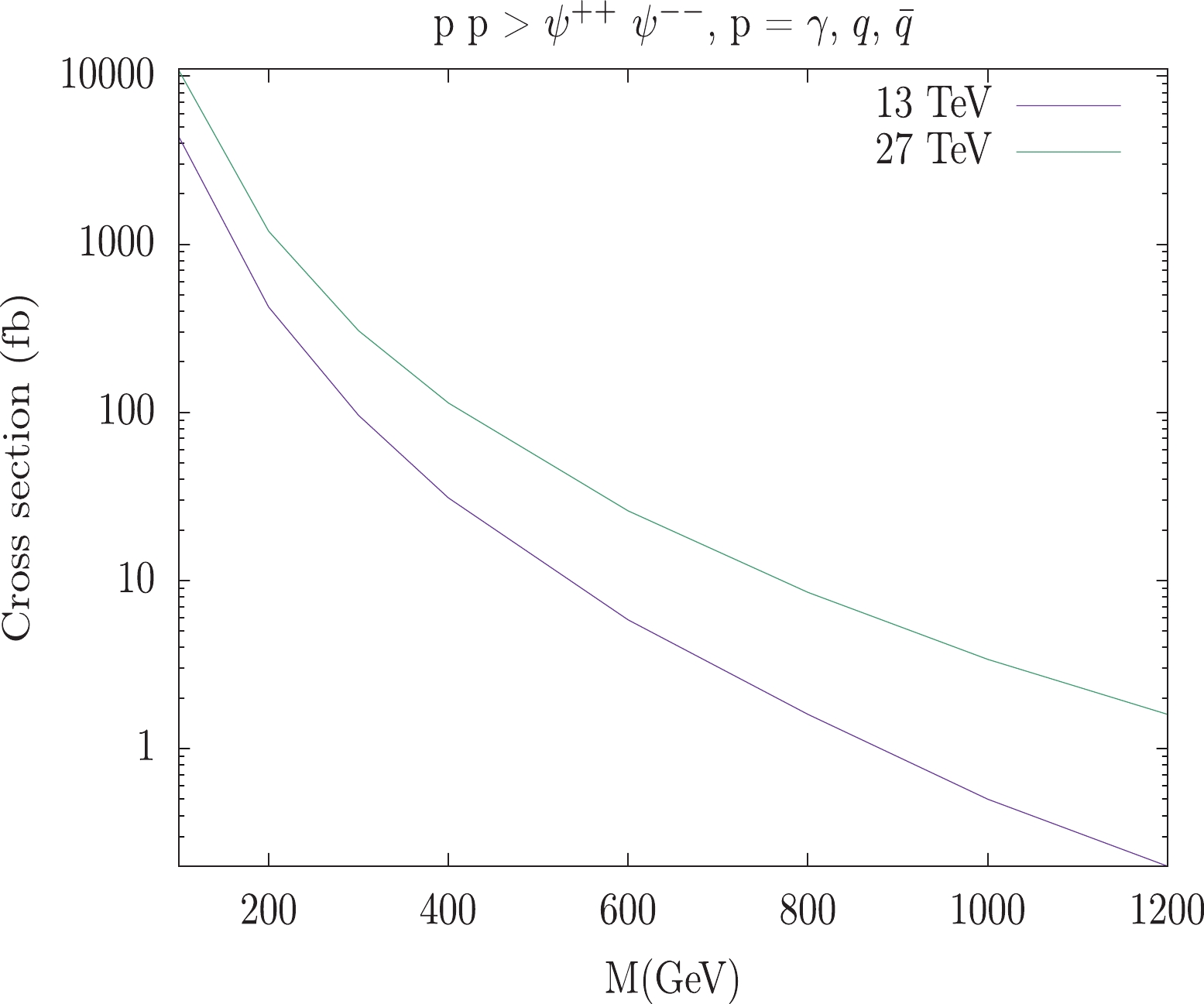
Figure 5. (color online) The cross section for the pair production process
$p p \to \psi^{++} \psi^{--}$ as a function of the VLL mass at 13 TeV and 27 TeV.The
$ pT $ distribution of the leading and subleading tau and muon is presented in Fig. 6 for BP1. In Fig. 7 (left), we present the transverse missing energy and$ H_T(l) = \sum_{i} p_T(l)_i $ distribution and (right) the ratio${\rm MET}/m_{\rm eff}$ ($m_{\rm eff} = E_T+ H_T(l)+ H_T(j)$ ), which is effective to reduce the QCD-jet backgrounds. Based on these distributions we select a set of simple cuts on different kinematic variables.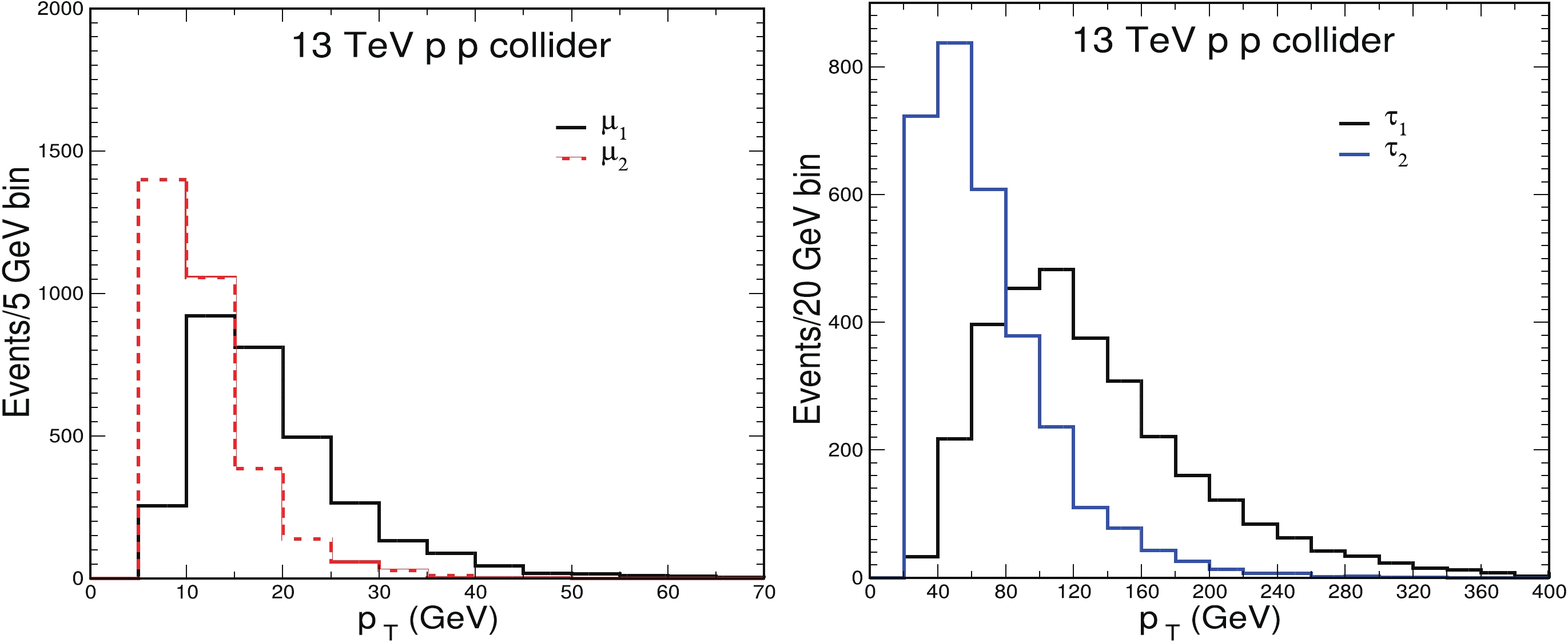
Figure 6. (color online) The transverse momentum distribution of the leading(1) and the subleading(2) muon (left) and tau pairs (right) in unweighted events of
$p p\to \Psi^{++} \Psi^{--}$ at 13 TeV p-p collision for BP1.
Figure 7. (color online) The transverse missing energy (MET) and sum of all lepton
$ pT $ distribution are presented in the left. In the right, the distribution is for the ratio of the MET and$m_{\rm eff}$ . Events are unweighted and generated by$p p \to \Psi^{++} \Psi^{--}$ at 13 TeV p-p collision for BP1.Selection 1:
● Opposite sign same flavor pair of mu and tau (
$ \mu^+\mu^- $ ) + ($ \tau^+ \tau^- $ ),●
$ p_T(\mu_1)> $ 6 GeV,$ p_T(\mu_2)> $ 6 GeV,$ p_T(\tau_1)> $ 60 GeV,$ p_T(\tau_2)> $ 40 GeV,●
$ |\eta (\mu,\tau)|< 2.5 $ ,$ \Delta R(l,l) > 0.3 $ ,Selection2:
● b-jet veto,
$\rm MET > 100$ GeV,$ H_T>150 $ GeV,●
${\rm MET}/m_{\rm eff} > 0.5$ ,Selection3:
● Z veto with
$ M_Z\pm 10 $ GeV.We present the signal cross section after the selections in Table 2 for three BP's. It can be observed that for this multilepton channel, the cross section is well above 1 fb after the selections. The signal does not suffer much from the Z-veto, which is a big advantage for our signal as the Z veto is effective for reducing the backgrounds from Z decays. The b -jet veto and the requirement of the higher ratio of MET and
$m_{\rm eff}$ will also be effective to reduce the background for these types of signal. For the discussion on the background of this particular channel, refer to [131]. In general, the multilepton channel possesses less background compared to the other processes. After Selection 3, the number of events at 150 fb$ ^{-1} $ is always more than 150 if background is very small, which makes this channel a good candidate look for new physics at 13 TeV LHC run.BP1 BP2 BP3 $ k_{33}=0.01 $ 

$ g_{31}\approx-0.368 $ ,

$ M_{Q{'}} =1083 $ 

$ g_{31}\approx 0.32 $ ,

$ M_{Q{'}} =1200 $ 

$ g_{31}\approx-0.1080 $ ,

$ M_{Q{'}} =1201 $ 

$ g_{21} \approx 0.166 $ ,

$ m_s \approx 272 $ 

$ g_{21} \approx 0.2060 $ ,

$ m_s \approx 230 $ 

$ g_{21} \approx -0.6240 $ ,

$ m_s \approx 304 $ 

$ g_{11} \approx -0.0468 $ ,

$ M \approx 284 $ 

$ g_{11} \approx -0.0014 $ ,

$ M \approx 250 $ 

$ g_{11} \approx 0.0071 $ ,

$ M \approx 320 $ 

Selection 1 3.44 (9.58) fb 2.87 (11.06) fb 2.67 (9.62)fb Selection 2 1.76 (7.31)fb 1.22 (4.88)fb 1.49 (4.36)fb Selection 3 1.63 (5.82)fb 1.06 (3.28)fb 1.38 (4.96)fb Table 2. Signal cross section (fb) after the selections at three different benchmark points at 13 TeV and 27 TeV (italic). Masses are in GeV.
-
We analyzed muon (
$g-2 $ ), LFVs, Z decays,$ \Delta C_9^\mu $ for B-anomalies, and M–$ \bar M $ mixing in a framework of multi-charged particles, which includes exotic scalars, leptons, and quarks under the local$ U(1)_{\mu - \tau} $ . Owing to the gauge symmetry, we can suppress the LFV process, which could appear from the Yukawa interactions among the exotic lepton, charged scalar, and SM lepton. Accordingly, we found that the sizable Yukawa couplings are naturally allowed to explain muon$ g-2 $ . First, we formulated phenomenological observables mentioned above in our model and performed numerical analyses to search for allowed parameter sets.Via numerical calculations, we determined that our
$ \Delta C_9^\mu $ can accommodate B-anomalies where the$ Z' $ boson contribution is dominant. However, the contribution from the box diagram in$ \Delta C_9^{\mu [{\rm {box}}]} $ can only reach$ \sim -0.1 $ when we impose constraints from the$ Z\to\nu_i\bar\nu_j $ invisible decay,$ Z\to\mu\bar\mu $ decay, and$ B_s $ –$ \bar B_s $ mixing. This is owing to the stringent constraints from$ B_s $ –$ \bar B_s $ mixing and$ Z\to\mu\bar\mu $ , which restrict the relevant Yukawa coupling constants. We demonstrated that the muon$ g-2 $ in our model is a sum of the contributions from the scalar boson loop and$ Z' $ loop diagrams. It was inferred that we can explain muon$ g-2 $ within the$ 2 \sigma $ level when we include both of these contributions. Finally, we studied the collider physics focusing on the production of doubly charged leptons, using some benchmark points allowed by the numerical analysis. We verified that the channel with pairs of oppositely charged muon and tau has some unique features that distinguish our model signatures from other vector-like lepton signatures at LHC. The exotic vector-like quarks and the$ Z' $ will also provide interesting collider phenomenology; however, we reserve it for a future study. -
This research was supported by the Korean Local Governments - Gyeongsangbuk-do Province and Pohang City (H.O.). H. O. is sincerely grateful to the KIAS member, and log cabin at POSTECH for providing a comfortable space to come up with this project. N.K. acknowledges the support from the Dr. D. S. Kothari Postdoctoral scheme (201819-PH/18-19/0013). N. K. also acknowledges "(9/27-28 @APCTP HQ) APCTP Mini-Workshop - Recent topics on dark matter, neutrino, and their related phenomenologies" where the problem was proposed and also thanks the hospitality of APCTP, Korea.
A multi-charged particle model with local U(1)μ-τ to explain muon g–2, flavor physics, and possible collider signature
- Received Date: 2021-08-16
- Available Online: 2022-04-15
Abstract: We consider a model with multi-charged particles, including vector-like fermions, and a charged scalar under a local






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: