Measuring CP violation in rare W decays at the LHC

The standard model (SM) of particle physics has been proven to be extremely successful in describing all known fundamental particles and interactions. However, there are still several questions that remain unanswered. For example, one of the main mysteries in this field is the origin of tiny neutrino masses. Within the framework of the SM, neutrinos are predicted to be massless. However, the discovery of neutrino oscillations has firmly indicated that neutrinos are massive particles and lepton flavors are mixed [1]. Another important mystery is how to explain the observed matter-antimatter asymmetry of the Universe. It is argued that baryon asymmetry in the Universe can be characterized by the baryon-to-photon density ratio $\eta=n_B/n_\gamma$. From a careful analysis of recent Planck measurements of the cosmic microwave background, the value of η has been determined to a good degree of accuracy, $\eta \simeq (6.12 \pm 0.03) \times 10^{-10}$ [2], which is too large compared with the SM expectation. Going beyond the SM, the simplest way to accommodate neutrino masses is to introduce n right-handed Majorana neutrino fields $N_{\rm R}$, which can couple to left-handed neutrino fields through Yukawa interactions to form Dirac mass terms, $\overline{\nu_{\rm L}}M_{\rm D}N_{\rm R}$. As SM gauge singlets, the introduced right-handed neutrino fields $N_{\rm R}$ are also allowed to couple to their charge conjugate fields to constitute the Majorana mass terms $\overline{N^c_{\rm R}}M_{\rm R}N_{\rm R}$. This is known as the famous type-I seesaw mechanism, and tiny neutrino masses can be given by $M_\nu \approx -M_{\rm D} M^{-1}_{\rm R} M^{\rm T}_{\rm D}$ [3, 4]. In this canonical seesaw mechanism, the smallness of the left-handed neutrinos can be attributed to the heaviness of the right-handed Majorana neutrinos. As for the origin of baryon asymmetry in the Universe, one popular explanation is the leptogenesis mechanism [5]. In this case, the CP-violating and out-of-equilibrium decays of heavy Majorana neutrinos thermally produced in the early Universe may first generate lepton number asymmetry, and the latter may be subsequently converted into baryon number asymmetry through sphaleron processes [6, 7]. While initial calculations suggested that the Majorana neutrino mass scale required for leptogenesis is significantly larger than the electroweak scale, it was soon realized that the mass of Majorana neutrinos can be below the TeV scale, which is light enough to be produced at colliders [8].

The key point behind the seesaw mechanism and the associated leptogenesis mechanism is the existence of heavy Majorana neutrinos, which causes lepton number violation by two units ($\Delta L =2$) simultaneously, and the possibility of lepton-number-violating processes, such as neutrinoless double-beta decay ($0\nu\beta\beta$) [9, 10]. The underlying process with $\Delta L =2$ can be generically expressed as a W decay via Majorana neutrino exchange, which can be identified by the signature of a same-sign dilepton in the final state. This rare W decay, specifically, $W^- \rightarrow \ell_{1}^{-} N \rightarrow \ell_{1}^{-}\ell_{2}^{-}(q\bar{q}^\prime)^{+}$, has been well studied in literature (see, e.g., Refs. [11, 12]). For example, in the mass range $M_N < M_W$, the $\Delta L =2$ same-sign dilepton production signal has been explored in rare meson decays [13–17], tau lepton decays [18–20], and even top quark decays [21–24]. For heavy Majorana neutrinos with masses above $M_W$, the same signal has been extensively investigated at various collider experiments, such as electron-positron colliders [25–28], electron-proton colliders [29–34], and proton-proton colliders [35–40]. The difference between the rates of $W^- \rightarrow \ell_{1}^{-}\ell_{2}^{-}(q\bar{q}^\prime)^{+}$ and its CP-conjugate process $W^+ \rightarrow \ell_{1}^{+}\ell_{2}^{+}(\bar{q}q^\prime)^{-}$ may induce nonzero CP asymmetry, which arises from the significant interference of different Majorana neutrinos. The generated CP violation effects can serve as a smoking gun for new physics beyond the SM. A great deal of work has been conducted to measure CP violation effects in the decays of mesons [41–44] and tau leptons [45, 46]. Recently, according to Ref. [47], CP violation was explored in rare W decays at the LHC; however, the CP violation effect produced in this case was influenced by the initial parton distribution functions in protons. To avoid this, in a recent study [48], we investigated the possibility of measuring CP violation in $t\bar{t}$ pair production and rare decays at the LHC. Because the $W^-$ and $W^+$ bosons originate from the decays of the $\bar{t}$ and t quarks, respectively, they have the same quantity. In contrast to previous studies, in this paper, we explore the prospects of measuring CP violation in $W^+W^-$ pair production and rare decays at the LHC, where the $W^-$ and $W^+$ bosons are produced directly from $pp$ collisions. In principle, the number n of introduced right-handed Majorana neutrinos in the seesaw mechanism is a free parameter. Because two neutrino mass-squared differences between light neutrinos have been observed, $n \geq 2$ is required. Nonzero direct CP asymmetry also requires the existence of at least two different Majorana neutrinos. For illustration, we consider two heavy Majorana neutrinos, and the general case with more Majorana neutrinos can be analyzed in a similar manner.

This paper is organized as follows. A theoretical framework for heavy Majorana neutrinos is briefly introduced in Sec. II. Rare W decays via Majorana neutrinos are discussed in Sec. III. In Sec. IV, we explore the experimental prospects of measuring CP violation at the LHC. Finally, we conclude with Sec. V.

Throughout this paper, we only consider a minimal extension of the SM by introducing two right-handed Majorana neutrinos. In the notation of Ref. [38], the flavor eigenstates $\nu_{\ell}$ (with $\ell= e, \mu, \tau$) of three active neutrinos can be expressed by the mass eigenstates of light and heavy Majorana neutrinos.

Therefore, the weak charged-current interaction Lagrangian can now be written in terms of the mass eigenstates as follows:

Here, $V_{\ell m}$ is the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix [49, 50] responsible for neutrino oscillations. Note that $R_{\ell m^\prime}$ describes light-heavy neutrino mixing and can be generally parameterized as

It is worth noting that heavy Majorana neutrinos in the conventional type-I seesaw mechanism are typically too heavy (e.g., of the order of the GUT-scale) and their mixings with light neutrinos are severely suppressed. However, there are also several low-scale seesaw scenarios in which the heavy Majorana neutrino masses are significantly lower and the strength of light-heavy neutrino mixings are sufficiently large (see, e.g., Refs. [51, 52]). The CP-phase $\phi_{\ell m^\prime}$ is related to leptogenesis [53]. In this paper, we adopt a model-independent phenomenological approach by taking the heavy neutrino masses $m_{N}$ and light-heavy neutrino mixings $R_{\ell m^\prime}$ as free parameters.

Constraints on the free parameters $m_{N}$ and $R_{\ell m^\prime}$ can be derived from experimental observations, and a detailed summary can be found in Ref. [11]. In our calculations, to be conservative, we take

for $15 < {m}_{N}^{} < 70\; {{\rm{GeV}}}$, which are consistent with $0\nu\beta\beta$-decay searches [54], a global fit to lepton flavor and electro-weak precision data [55], a reanalysis of Large Electron Positron (LEP) collider data [56], and direct searches by Large Hadron Collider (LHC) experiments [57].

Rare W decays can be induced by heavy Majorana neutrinos. Here, we consider both the rare lepton-number-violating decays of the $W^-$ and $W^+$ bosons via two intermediate on-shell Majorana neutrinos $N_{i}$ (with $i=1, 2$) (depicted in Fig. 1).

Figure 1.  Feynman diagrams for rare $W^-$ decay via heavy Majorana neutrino exchange.

where $\alpha, \beta = e, \mu, \tau$. Note that $p_1$, $p_2$, etc., denote the four-momentum of the corresponding particles. The squared matrix elements averaged (summed) over the initial (final) particles for the process in Eq. (5) can be obtained as follows:

where $p_w = p_4 + p_5$. $D_W\left(p^2\right) = 1/(p^2 -m_W^2 + {\rm i}m_W\Gamma_W)$, where $m_W$and $\Gamma_W$ are the mass and total decay width of the W boson, respectively. Note that $V_{qq^\prime}$ is the Cabibbo-Kobayashi-Maskawa (CKM) matrix element [58, 59], which is set as diagonal with unit entries for simplicity. Moreover, $R_{\alpha i }$ (with $\alpha = e, \mu, \tau$ and $i = 1, 2$) is the light-heavy neutrino mixing matrix element defined in Eq. (3), and the complex phase $\Delta\phi=\phi_{\alpha 2} - \phi_{\alpha 1} + \phi_{\beta 2} - \phi_{\beta 1}$ originating from the significant interference between $N_1$ and $N_2$ can serve as a new source of CP violation. The explicit expressions of ${\cal T}_i$ ($i = 1, 2$) and ${\cal T}_{12}$ are shown in Appendix A.

Furthermore, the corresponding differential decay width can then be expressed as

where ${\rm d}{\cal L}ips_4$ is the Lorentz invariant phase space of the four final particles. The decay modes of heavy Majorana neutrino have been well studied in Ref. [38]. Because the decay width of a heavy Majorana neutrino is significantly smaller than its mass in the mass range of interest, the narrow-width approximation (NWA) [60] can be applied. Therefore, the total decay width for the process in Eq. (5) can be factorized as follows:

where $\Gamma_{0}$ is a function of Majorana neutrino mass, and the “effective mixing parameter” $S_{ \alpha\beta}$ is defined as

The oscillations and lifetime of Majorana neutrinos are naturally interweaved, with the possibility of production in high energy collisions. The time-evolution of the initial Majorana will be characterized by a typical oscillating behavior with frequency $\Delta M = M_{N_2}-M_{N_1}$. The interesting region occurs when $\Delta M$ is of the order of the lifetime $\tau = 1/ \Gamma_{N_i}$ [61]. This region would contain valuable information about the origin of neutrino masses. In our numerical calculations, we employ the following approximations:

The normalized branching ratio of $W^- \to \ell_{\alpha}^- \ell_{\beta}^- (q \bar{q}^\prime)^+$ and $W^+ \to \ell_{\alpha}^+ \ell_{\beta}^+ (\bar{q}q^\prime)^{-}$ as a function of $m_{N_{1}}$ are shown in Fig. 2. To illustrate, the CP phase difference is set to $\Delta\phi=0, +\pi/2, -\pi/2, \pi$. It is found that the normalized branching ratio decreases slowly as the Majorana neutrino mass increases for $15 < m_{N_{1}} < 70\; {{\rm{GeV}}}$. When the Majorana neutrino mass is similar to the W boson mass, the normalized branching ratio falls off sharply. The difference between the rates of $W^- \rightarrow \ell_{1}^{-}\ell_{2}^{-}(q\bar{q}^\prime)^{+}$ and $W^+ \rightarrow \ell_{1}^{+}\ell_{2}^{+}(\bar{q}q^\prime)^{-}$ may induce the CP asymmetry, which can be defined as

Figure 2.  (color online) Normalized branching ratio of (a) $W^- \to \ell_{\alpha}^- \ell_{\beta}^- (q \bar{q}^\prime)^+$ and (b) $W^+ \to \ell_{\alpha}^+ \ell_{\beta}^+ (\bar{q}q^\prime)^{-}$ versus the Majorana neutrino mass $m_{N_{1}}$ for $\Delta\phi=0, +\pi/2, -\pi/2, \pi$.

As shown in Eq. (6), this CP asymmetry arises from the interference of contributions from two different heavy Majorana neutrinos. Therefore, to generate such CP asymmetry, the following two necessary conditions must be satisfied: (i) the existence of at least two heavy Majorana neutrinos and (ii) a non-zero CP phase difference $\Delta\phi$. The numerical results of ${\cal A}_{CP}$ versus the Majorana neutrino mass $m_{N_{1}}$ for various values of $\Delta\phi$ are shown in Fig. 3(a). Taking $m_{N_{1}} = 20\; {{\rm{GeV}}}$ as an example, the value of ${\cal A}_{CP}$ as a function of $\Delta\phi$ is also displayed in Fig. 3(b). It is clear that, for fixed $\Delta\phi$, ${\cal A}_{CP}$ is independent of the Majorana neutrino mass in the mass range $15 < {m}_{N}^{} < 70\; {{\rm{GeV}}}$. Furthermore, CP asymmetry vanishes for $\Delta\phi=0, \pi$, and ${\cal A}_{CP} \to -{\cal A}_{CP}$ for $\Delta\phi \to -\Delta\phi$. When $\Delta\phi\approx\pm3\pi/5$, the maximal value of $|{\cal A}_{CP}|_{\rm max}\approx0.22$ can be reached.

Figure 3.  (color online) (a) Value of ${\cal A}_{CP}$ as a function of $m_{N_{1}}$ for $\Delta\phi=0, +\pi/2, -\pi/2, \pi$. (b) Value of ${\cal A}_{CP}$ as a function of $\Delta\phi$ for $m_{N_{1}} = 20\; {{\rm{GeV}}}$.

With unprecedented high energy and high luminosity, the LHC offers a great opportunity to probe new physics beyond the SM. In this paper, we explore the prospects of measuring CP violation in rare W decays at the LHC and consider the following process:

where the $W^\pm W^\mp$ pairs are produced directly from $pp$ collisions. In the following numerical calculations, we restrict our study to the same-sign dimuon production channel and employ CTEQ6L1 [62] for the parton distribution functions in protons. In Fig. 4, the total cross sections for the process in Eq. (12) are shown as a function of $m_{N_{1}}$ for $\Delta\phi=0, +\pi/2, -\pi/2, \pi$ at 14 TeV and 100 TeV LHC. With an integrated luminosity of $\cal{L}$=300 ${\rm fb}^{-1}$, there are only a few events produced for $m_{N_{1}} < 70\; {{\rm{GeV}}}$ at 14 TeV LHC, whereas more than ten events can be produced at 100 TeV LHC.

Figure 4.  (color online) Total cross sections for (a) $pp \to W^+W^- \to \mu^+ \mu^+ 4j$ and (b) $pp \to W^+W^- \to \mu^- \mu^- 4j$ at 14 TeV LHC and (c) $pp \to W^+W^- \to \mu^+ \mu^+ 4j$ and (d) $pp \to W^+W^- \to \mu^- \mu^- 4j$ at 100 TeV LHC versus Majorana neutrino mass $m_{N_{1}}$ with $\Delta\phi=0, +\pi/2, -\pi/2, \pi$.

Analogously, the difference between $\sigma(pp \to \mu^+ \mu^+ 4j)$ and $\sigma(pp \to \mu^- \mu^- 4j)$ can also lead to non-zero CP asymmetry, which can be expressed as

In this case, the underlying CP violation effect is similarly caused by the rate difference between rare $W^-$ decay and its CP-conjugate process. Therefore, the CP asymmetry defined in Eq. (13) is equivalent to that given in Eq. (11). In Fig. 5, we display the value of $\overline{{\cal A}_{CP}}$ with respect to $m_{N_{1}}$ and $\Delta\phi$. As expected, the CP asymmetry in Fig. 5 behaves almost the same as that in Fig. 3.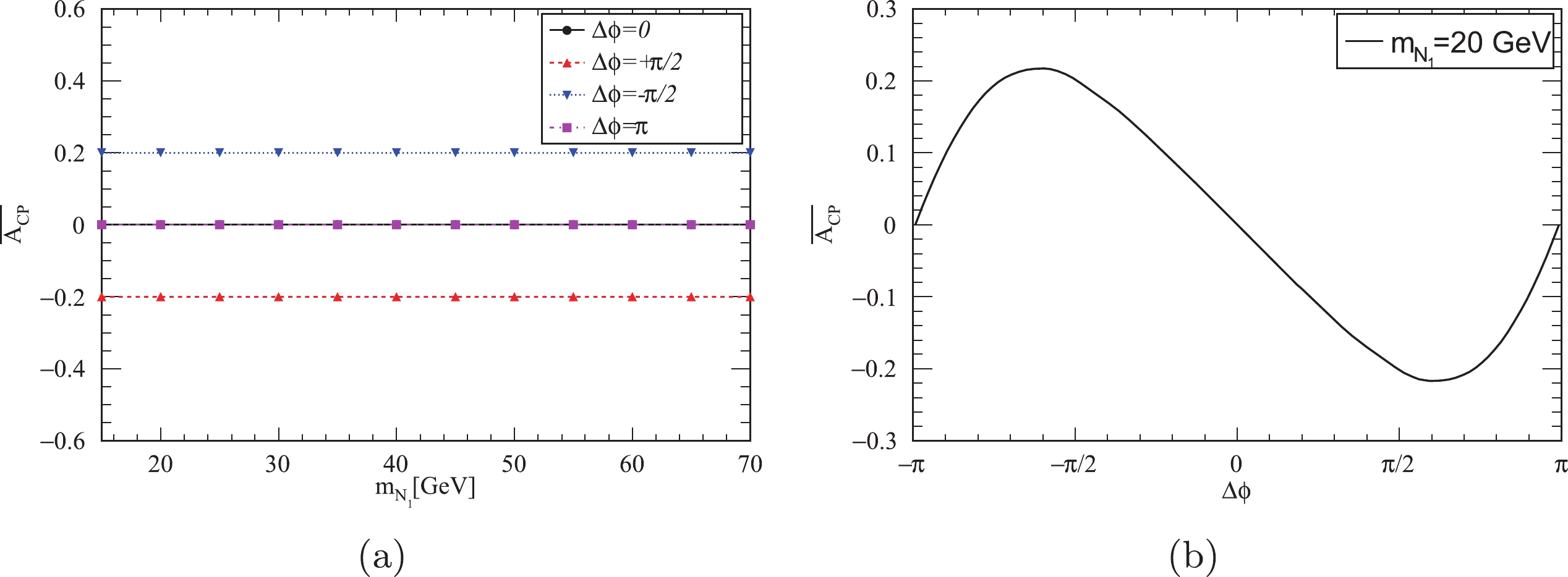

Figure 5.  (color online) (a) Value of $\overline{{\cal A}_{CP}}$ as a function of $m_{N_{1}}$ for $\Delta\phi=0, +\pi/2, -\pi/2, \pi$. (b) Value of $\overline{{\cal A}_{CP}}$ as a function of $\Delta\phi$ for $m_{N_{1}} = 20\; {{\rm{GeV}}}$.

In order to simulate detector response, the lepton and jet energies are smeared according to the assumption of Gaussian resolution parametrization

where $\delta(E)/E$ represents the energy resolution, and $\oplus$ denotes a sum in quadrature. In our calculations, we take $a=5\ $% and $b=0.55\ $% for leptons and $a=100\ $% and $b=5\ $% for jets [63, 64]. The isolated leptons and jets are identified by angular separation, which can be defined as

where $\Delta\phi_{ij}$ ($\Delta \eta_{ij}$) is the azimuthal angle (rapidity) difference of the corresponding particles.

Because jets from rare $W^\pm$ decay $W^\pm \to \ell_{}^\pm \ell_{}^\pm jj$ are significantly softer than those from the hadronic decay $W^\mp \to j j$, the former two jets can be merged into one large jet using the anti-$k_t$ clustering algorithm with a distance parameter of 0.4 [65]. Therefore, we only require three jets ($n_j=3$) in the final state of our signal process. To quantify the signal observability, we impose the following basic acceptance cuts on leptons and jets (referred to as cut-I):

Our signal process in Eq. (12) consists of two same-sign dileptons and three jets. To purify the signal, the missing transverse energy is required to satisfy (referred to as cut-II)

For our signal process, the main backgrounds in the SM originate from $pp \to W^{\pm}W^{\pm}W^{\mp}W^{\mp}$, $pp \to W^{\pm}W^{\pm}W^{\mp}j$, and $pp \to W^{\pm}W^{\pm}W^{\mp}Z$. Specifically, the SM backgrounds are simulated by $\textsf{MadGraph5_aMC@NLO}$ [66]. The parton shower is performed with $\textsf{Pythia-8.2}$ [67], and jet-clustering is achieved with the anti-$k_t$ algorithm using the same distance parameter as in the signal process.

Comparing our signal process with the backgrounds, we fully reconstruct the two Ws. One W boson, which decays hadronically, can be reconstructed from the two jets ($j_1,j_2$). The invariant mass of these two jets is closest to $m_W$. After reconstructing one W boson, the remaining ingredients are grouped to reconstruct the other W boson. We adopt the following cut (referred to as cut-III):

where $j_3$ refers to the left jet, and $\ell \ell$ are the two same-sign dileptons.

After implementing all the above cuts, we obtain the total cross sections for the signal and background processes at 14 and 100 TeV. To illustrate, we use $m_{N_{1}}=20\; {{\rm{GeV}}}$ and $\Delta\phi=\pi/2$. At 14 TeV, the signal cross section after all cuts is only $1.93\times 10^{-3} \; \mathrm{fb}^{}$, which is too small to be detected experimentally. We list the total cross sections for the signal and background processes at 100 TeV LHC in Table 1. The statistical significance $S/\sqrt{B}$ with an integrated luminosity of $\cal{L}$=300 and 3000 $\mathrm{fb}^{-1}$ is also given, where S and B denote the signal and background event numbers, respectively, after all cuts. It is shown that the signal cross section after all cuts remains $1.16\times 10^{-2} \; \mathrm{fb}^{}$ at 100 TeV LHC, and the corresponding statistical significance can reach 3.60 (11.38) with $\cal{L}$=300 $\mathrm{fb}^{-1}$ ($\cal{L}$=3000 $\mathrm{fb}^{-1}$), which offers us a great opportunity to explore CP violation effects in rare W decays at the LHC. Moreover, in Fig. 6, we display the statistical significance $S/\sqrt{B}$ as a function of $m_{N_1}$ at 100 TeV LHC by taking $\Delta \phi=\pi/2$. As shown in Fig. 6, a $3\sigma$ discovery can be made for $m_{N_1} <$ 30 GeV with $\cal{L}$=300 $\mathrm{fb}^{-1}$. With $\cal{L}$=3000 $\mathrm{fb}^{-1}$, the mass region can reach $m_{N_1} \simeq$ 55 GeV. After adopting all the kinematic cuts, we display $\overline{{\cal A}_{CP}}$ versus $m_{N_{1}}$ and $\Delta\phi$ at 100 TeV LHC in Fig. 7. It can be found that CP asymmetry is almost unchanged after all the selection cuts.

	100 TeV
	$\sigma_S$/$\mathrm{fb}$	$\sigma_{pp\to W^\pm W^\pm W^\mp W^\mp}$/$\mathrm{fb}$	$\sigma_{pp\to W^\pm W^\pm W^\mp j}$/$\mathrm{fb}$	$\sigma_{pp\to W^\pm W^\pm W^\mp Z}$/$\mathrm{fb}$
Cut-I	$2.00\times 10^{-2}$	$2.9\times 10^{-2}$	$5.56$	$1.53\times 10^{-2}$
Cut-II	$1.72\times 10^{-2}$	$5.45\times 10^{-4}$	$1.59\times 10^{-1}$	$2.88\times 10^{-4}$
Cut-III	$1.16\times 10^{-2}$	$1.21\times 10^{-5}$	$3.10\times 10^{-3}$	$3.02\times 10^{-6}$
$S/\sqrt{B}$ with $\cal{L}$=300 $\mathrm{fb}^{-1}$	3.60
$S/\sqrt{B}$ with $\cal{L}$=3000 $\mathrm{fb}^{-1}$	11.38

Table 1.  Cross sections for the signal and background processes at 100 TeV LHC after all cuts. Also shown is the statistical significance $S/\sqrt{B}$ with an integrated luminosity of $\cal{L}$=300 $\mathrm{fb}^{-1}$ and $\cal{L}$=3000 $\mathrm{fb}^{-1}$. To illustrate, we use $m_{N_{1}}=20\; {{\rm{GeV}}}$ and $\Delta\phi=\pi/2$.

Figure 6.  (color online) Statistical significance $S/\sqrt{B}$ as a function of $m_{N_1}$ with an integrated luminosity of $\cal{L}$=300 $\mathrm{fb}^{-1}$ and $\cal{L}$=3000 $\mathrm{fb}^{-1}$ at 14 TeV LHC, where the CP phase difference is set to $\Delta \phi=\pi/2$.

Figure 7.  (color online) (a) Value of $\overline{{\cal A}_{CP}}$ after all cuts as a function of $m_{N_{1}}$ for $\Delta\phi=0, +\pi/2, -\pi/2, \pi$. (b) Value of $\overline{{\cal A}_{CP}}$ after all cuts as a function of $\Delta\phi$ for $m_{N_{1}} = 20\; {{\rm{GeV}}}$.

The simplest way to extend the SM is to introduce heavy Majorana neutrinos and allow for lepton number violation. The introduced heavy Majorana neutrinos can simultaneously explain tiny neutrino masses via the seesaw mechanism and baryon asymmetry of the Universe via leptogenesis. In this paper, we explore the prospects of measuring CP violation in rare W decays at the LHC, where CP asymmetry between $W^- \to \ell_{\alpha}^- \ell_{\beta}^- (q \bar{q}^\prime)^+$ and $W^+ \to \ell_{\alpha}^+ \ell_{\beta}^+ (\bar{q}q^\prime)^{-}$ arises from the significant interference of contributions from two different Majorana neutrinos. We find that CP asymmetry for fixed $\Delta\phi$ is independent of the Majorana neutrino mass in the mass range of interest $15 < {m}_{\rm{N}}^{} < 70\; {{\rm{GeV}}}$. Taking $m_{N_{1}}=20\; {{\rm{GeV}}}$ and $\Delta\phi=\pi/2$ as an example, we investigate the possibility of measuring such CP violation at 14 TeV and 100 TeV LHC. Although the signal cross section at 14 LHC is too small to be detected experimentally, the high energy, 100 TeV LHC offers us a great opportunity to explore CP violation effects. The measurement of such CP violation would provide important information on underlying new physics.

P. C. Lu, Z. G. Si, Z. Wang, and X. H. Yang thank the members of the Institute of Theoretical Physics of Shandong University for helpful discussions.

The functions ${\cal T}_i$ ($i = 1, 2$) and ${\cal T}_{12}$ in Eq. 6 can be expressed as

respectively, where $p_N=p_2-p_1$, and $p_N^\prime=p_1-p_3$. $D_{N_i}\left(p^2\right) (i=1,2)$ is the Breit-Wigner propagator and can be defined as

where $m_{N_i}$ and $\Gamma_{N_i}$ are the mass and total decay width of the two Majorana neutrinos $N_1$ and $N_2$.

The explicit expressions of ${\cal F}$, ${\cal I}$, and ${\cal J}$ introduced in Eq. (A1) and Eq. (A2) can be given by

where $\epsilon_{p_1 p_2 p_3 p_5}=\epsilon_{\mu \nu \rho \sigma}p_1^\mu p_2^\nu p_3^\rho p_5^\sigma$.