Mono-γ production of a dark vector at future e⁺e⁻ colliders

The gravitational effects of dark matter (DM) have been unambiguously observed in astrophysical and cosmological measurements [1–3]. Moreover, DM is an excellent candidate for explaining several fundamental theoretical questions in the standard model (SM). There are also abnormalities, for instance, the muon $ g-2 $ [4], that can be accounted for by DM. However, it is known that the particles observed to date cannot be DM. Extending the particle content of the SM by adding new states that interact weakly with SM particles is the most profound approach to studying the physical properties of the dark sector. It is highly desirable to adopt effective field theory (EFT) involving DM, known as DMEFT [5–7], to study the physics of the dark sector in a model-independent manner. In general, DM can come into play at both tree and loop levels [8, 9], and a variety of theoretical DM models have been proposed [10]. Numerous experimental searches for DM in direct [11], indirect [12], and collider signatures [13] have been conducted, but, so far, no clear evidence has been reported.

In general, DM can be a scalar [14–21], fermion (Dirac or Majorana) [17–26], or vector state [18–20, 27–31]. In this study, we focus on a vector model of DM, whose kinematical Lagrangian is given as

where $ X_\mu $ is a massive vector field with mass $ m_{X} $, and $ X_{\mu\nu} $ is its field strength. The dark photon (DP) model [32], in which a dark vector state interacts with SM particles through a kinematical mixing term $ \epsilon\, X^{\mu\nu} F_{\mu\nu} $ [32, 33], is a representation of this class. The photon component of DM can induce decay into charged particles and can be described by the following effective operator:

where ψ is a charged fermion in the SM. If the above kinematical mixing is the only building block of the DM model, the mixing parameter $ \epsilon $ must be very small (with a typical value $ \epsilon \sim 10^{-10} $) such that the theory is consistent with experimental measurements [34–38]. However, these strong constraint can be removed if additional new states are involved, for instance, axion-like particles [39].

On the other hand, DM can also couple to SM fermions at $ D5 $ via a magnetic dipole interaction (Pauli operator) [40–42].

where $ \varLambda_2 $ is the energy scale parameter. The above dipole interaction can appear at the one-loop level in a UV completed model [40, 41]. Hence, the energy scale $ \varLambda_2 $ is of the same order as the mass of the heavy particles running in the loop, which is the scale of new physics (NP), i.e., $\varLambda_2 \sim M_{\rm NP}$. In contrast with the photon-like operator (2), whose contribution to the cross section of the mono-γ process decreases by $ 1/s $ at high energy, the Pauli operator (3) can initiate the mono-γ signal at a constant rate. Therefore, in dimensional analysis, the significance of the Pauli operator is considerably larger than that of the photon-like operator at high energy colliders, as long as the EFT description is valid. To date, lower bounds on the energy scale $ \varLambda_2 $ have not been reported. It has been shown that future muon colliders with the center of mass energy (CoM) $ \sqrt{s} = 3~{{\rm{TeV}}}, 10~{{\rm{TeV}}} $ are expected to be useful for studying this [40].

In this paper, we study the following triple gauge boson couplings:

where $ F_{\mu\nu} $, $ Z_{\mu\nu} $, and $ W_{\mu\nu}^{\pm} $ are the field strengths of the photon, neutral, and charged weak bosons, respectively, $ \widetilde{X}_{\mu\nu} $ is the dual field strength of DM, and $ \varLambda_{3,4,5,6} $ are the energy scale parameters of the corresponding interactions. Henceforth, we refer to these operators as DM triple gauge boson couplings (DMTGCs). Owing to the restriction on Bose statistics, the above operators cannot exist in DMEFT, where the DM field is included before the breaking of $S U_{W}(2)\times U_{Y}(1)$ gauge symmetry by the SM Higgs doublet [20]. A similar situation occurs in the neutral sector of triple gauge boson interactions within the SM content [43–45], i.e., the couplings of $ \gamma\gamma Z $, $ \gamma ZZ $, and $ ZZZ $ [46, 47]. Therefore, signals of such interactions indicate that either there are enhancement effects in some higher dimensional operators containing these vertices, or the NP scale is not far from the EW scale, such that the DM field can be effectively included after EW symmetry breaking [48]. A recently reported anomaly in the W boson mass measurement may be an indication of NP near the EW scale [49]. However, when DM couples to an SM current, which is broken by the chiral anomaly, Wess-Zumino type interactions between X and SM gauge bosons can appear when heavy fermions are introduced to cancel the anomaly [50]. Furthermore, if X couples to purely right-handed currents [51], the triple interaction $ XWW $ disappears, and only the coupling $ XZ\gamma $ is allowed. Experimental constraints on the charged sector of DMTGCs are expected to be stronger and can be further complicated if kinematical mixing between DM and the photon is not neglected. Considering this, we will study this part elsewhere.

In this paper, we focus on the neutral sector of DMTGCs. We study the mono-γ production of X at future $ e^+e^- $ colliders, and our analysis includes photon-like and Pauli operators as well as DMTGCs. We do not consider any real DM model of the vector field X or cosmological and astrophysical constraints on its parameters. The vector field X can be a real DM candidate, for instance, in dark parity symmetry (DPS) under which dark particles are odd, but all SM particles are even [20]. However, DMTGCs are not allowed if we assume DPS is conserved exactly at all energy scales. The vector X may also be a mediator between real DM and SM particles [14, 52] and can be invisible at colliders by assuming that it dominantly couples to a completely dark sector (or decays into neutrinos), even through its interaction with SM particles is non-zero. In this case, the mono-γ event configuration is still valid.

The paper is organized as follows. In Sec. II, we study the invisibility of the vector X by assuming that NP operators are the only available couplings below the scale under consideration, i.e., $ \varLambda_i $ (or $M_{\rm NP}$). This condition can provide constraints on the scale parameters if the vector X is required to be invisible at the detector. In Sec. III, we study the properties of mono-γ events at $ e^+e^- $ colliders, including their differential cross sections (Sec. III.A), and beam polarization effects (Sec. III.B). In Sec. IV, we study the constraints on the scale parameters using the BaBar experiment (Sec. IV.A), DELPHI experiment (Sec. IV.B), and the anomalous magnetic dipole moments of an electron (Sec. IV.C). Experimental significances at the future colliders CECP and ILC are studied in Sec. V, and conclusions are given in Sec. VI.

In general, the final state configuration used to probe DM at colliders depends on its invisibility or decay width $ \varGamma_{X} $. If DM decays with a relatively high rate, it can be visible at the detector. The typical decay length of X in the mono-γ process at a CoM energy $ \sqrt{s} $ is given as

When $ m_X > 2 m_{\ell} $ ($ \ell = e, \mu, \tau $), DM can decay into a charged lepton pair via photon-like and Pauli operators. The corresponding decay widths are given as

where $ r_{\ell} = m_{\ell}/m_{X} $. The rates of these two channels are roughly of the same order if $ e\epsilon \sim m_{X}/\varLambda_{2} $ because the DMTGC operators and the anomalous decay $ Z\to X\gamma $ can occur when $ m_{X} < m_{Z} $, and the corresponding decay width is given as

where $ r_{X} = m_{X}/m_{Z} $. The L3 [53] and DELPHI [54] collaborations at the LEP experiment have searched for single photons at the Z resonance and obtained an upper limit on the branching ratio, $ {\cal{B}}_{Z\to X\gamma} < 10^{-6} $. This bound can exclude parameter space on the $ \varLambda_{3(4)}-m_X $ plane. We discuss this in detail in Sec. V.

However, DMTGC operators can initiate three-body decays at the elementary particle level, $ X \to Z^{\ast} \gamma \to f\bar{f}\gamma $, where the fermion f is a lepton, neutrino, or quark. Such processes are suppressed by $ m_{X}^{4}/m_{Z}^{4} $; hence, they are significantly smaller unless $ m_{X} $ is very close to $ m_{Z} $. In the case of $ f=q $, the two-body hadronic decay channels $ X \to h\gamma $ can offer a non-trivial contribution. We study these hadronic decay channels in a separate paper. For now, let us focus on the on-shell two-body decay $ X\to Z \gamma $, which occurs if $ m_{X} > m_{Z} $. The corresponding decay width is given as

where $ r_{Z} = m_{Z}/m_{X} $. The width is suppressed by a factor of $ m_{X}^{4}/\varLambda_{3,4}^{4} $.

The X decays inside the detector must give constraints on the energy scale parameters and the mass of the vector field X, and lower limits on $ L_{X} $ depend on the real configuration of the detector. However, when we study experimental significance in Sec. V, we do not use limits on $ L_{X} $ to obtain constraints on the parameters. We show two reference points, $ L_{X} =1m, 0.1m $ [42, 55], with the assumption ${\rm Br} (X\to\ell^+\ell^-) = 1$, such that readers can gain intuitive insight into the validation of mono-γ event configuration for the real DM models under consideration.

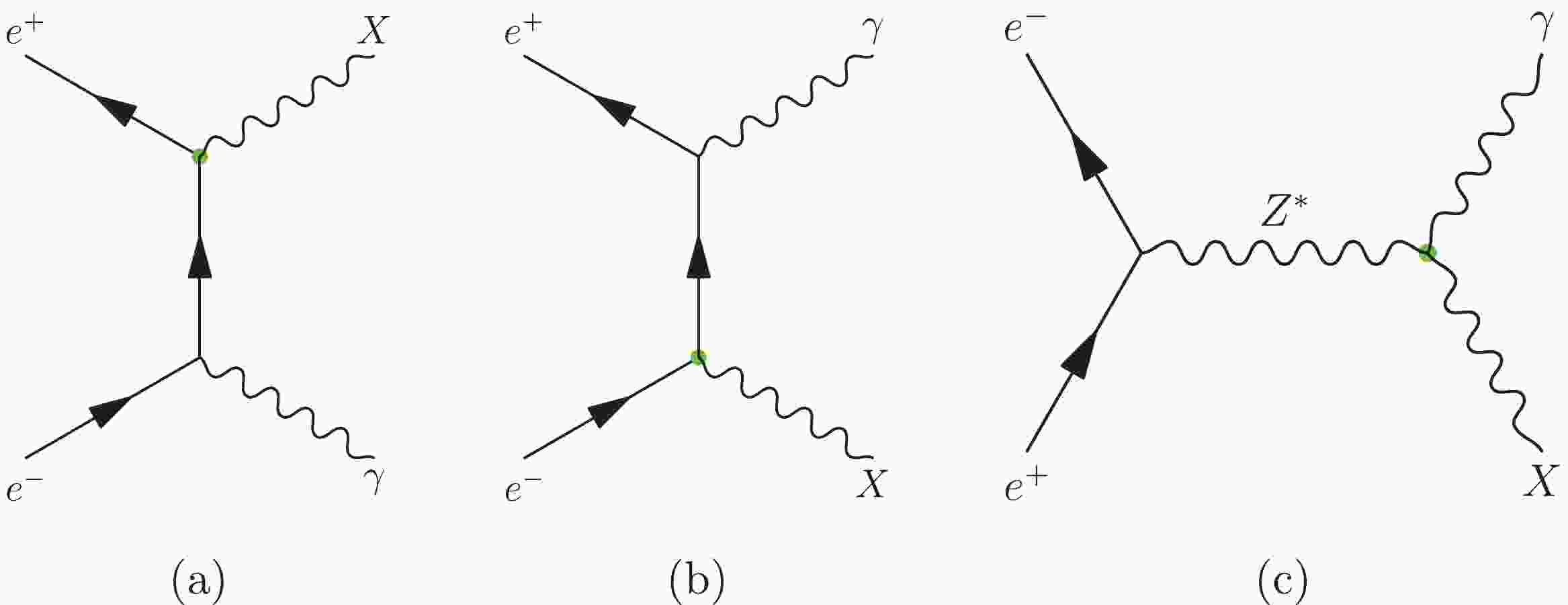
In this section, we investigate mono-γ signals at $ e^+e^- $ colliders, i.e., the process $ e^+e^- \to \gamma X $. Representative Feynman diagrams are shown in Fig. 1(a)–(c). In cases of photon-like and Pauli operators, a photon is generated via initial state radiation, whereas for the DMTGC operator, a photon can be produced via s-channel exchange of a (virtual) Z-boson. The invisible X results in missing transverse energy at the detector. The dominant irreducible SM background is the production of a single photon in association with a neutrino pair, i.e., $ e^+e^- \to \gamma \nu\bar{\nu} $. However, in contrast with the pair production of fermionic DM (or the production of a single fermionic DM with a neutrino), where the invariant mass of the missing momentum has a continuous distribution, it is peaked at $ m_{X} $ in our case because there is only one invisible particle. This can significantly reduce the background, and the efficiency depends on the precision of the momentum measurement of γ, the beam energy spectrum, etc. We consider such effects in Sec. V, where the experimental significances of the signals are studied. Furthermore, one of the advantages of $ e^+e^- $ colliders is that beam particles can be polarized. Therefore, before analyzing experimental sensitivities, let us discuss the production properties of the signals, including the differential cross section given in Sec. III.A, and the beam polarization effects given in Sec. III.B.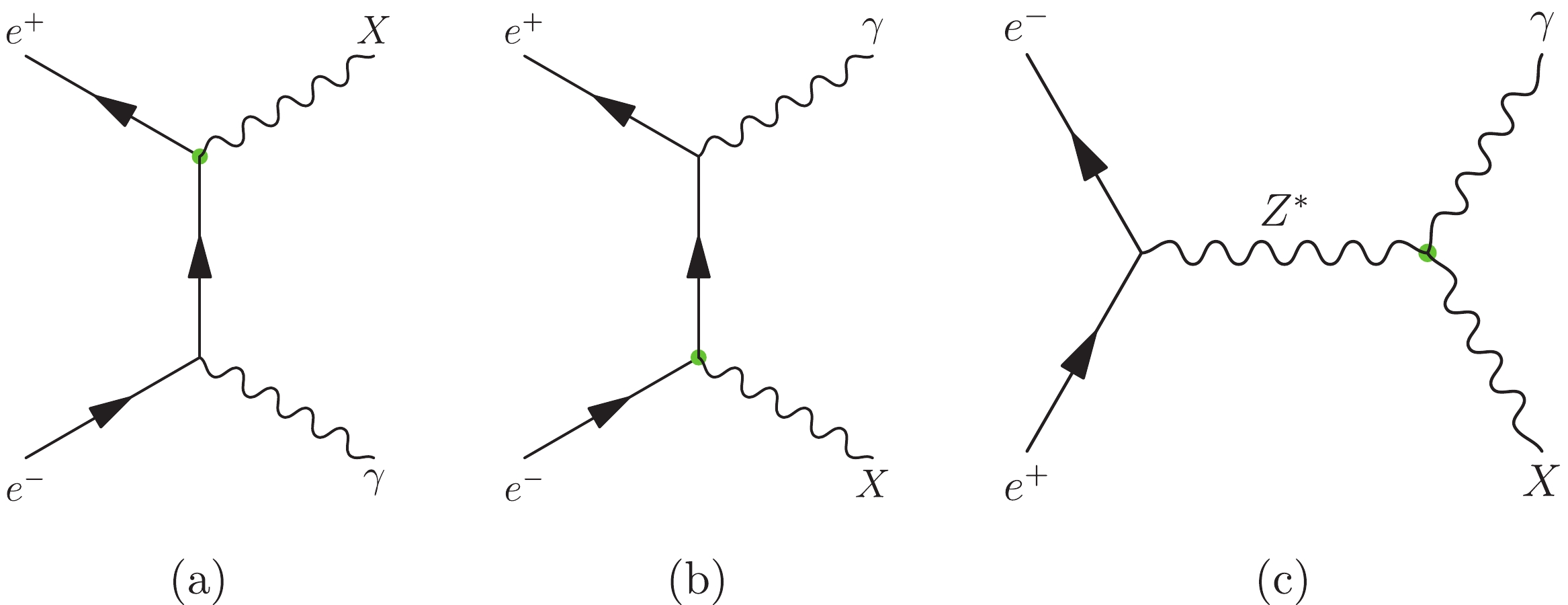

Figure 1.  (color online) Feynman diagrams of mono-γ production at $ e^+e^- $ colliders. Fig. 1(a) and Fig. 1(b) show the initial state radiation of a photon, which can be induced by the operators (2) and (3). In constrast, the DMTGC operators, (6) and (7), can generate a photon via the exchange of a (virtual) Z-boson in the s-channel, as shown in Fig. 1(c).

In this section, we study the total and differential cross sections of the signals. In the massless limit of the beam particles, the polarized differential cross sections are given as

where $ z_X = m_X/\sqrt{s} $, $ z_Z = m_Z/\sqrt{s} $, $ y_Z = \varGamma_Z/m_{Z} $, $ \theta_\gamma $ is the polar angle of the photon in the laboratory frame, where the z-axis is defined along the flying direction of the incoming electron, and $ \sigma_{i,\, \lambda_{e^{-}} \lambda_{e^{+}} } $ are the cross sections with helicities $ \lambda_{e^{-}}, \lambda_{e^{+}} = \pm 1 $ of the electron and positron, respectively. Owing to spin conservation, the photon-like and DMTGC operators can give non-zero contributions only when $ \lambda_{e^{-}} = - \lambda_{e^{+}} $, whereas for the Pauli operator, only helicity combinations with $ \lambda_{e^{-}} = \lambda_{e^{+}} $ survive. In addition, because of parity violation of the electroweak neutral current in the SM, $ \sigma_{+-} $ and $ \sigma_{-+} $ differ depending on the product between the vector and axial-vector couplings, i.e., $ g_{V}g_{A} $ of the electron (see (15)).

We can also see that there are singularities at $ \theta_\gamma=0,\pi $ for the photon-like operator, similar to the well-known property of the background. Such singularities disappear in channels induced by the Pauli and DMTGC operators. To avoid kinematical space, we implement our operators in FeynRules [56] and use MadGraph5 [57] to estimate cross sections with the following kinematical cuts:

Figure 2(a) shows the polar angle distributions of the signal and background with the above kinematical cuts at a typical center of mass energy $ \sqrt{s}= 500~{{\rm{GeV}}} $, and for the signal we have set $ m_{X}=0 $, $ e\epsilon=0.1 $, and $ \varLambda_i=1~{{\rm{TeV}}} $ for reference. The signal of the photon-like operator is similar to the background. However, the Pauli operator possesses a constant polar angle distribution, as shown by (14), in the case of $ z_{X}=0 $. For the DMTGC operators, the two operators have the same distribution, as shown by (15). However, signal events are dominated in the central region of the detector. This is completely different from the background and results in a higher kinematical selection efficiency. Furthermore, this property is purely because of the transverse part contribution of a spin-1 particle exchanged in the s-channel and hence is independent of the DM mass $ m_{X} $ (see (15)). The above polar angle distributions can be used to distinguish NP operators, and we discuss the details in Sec. V.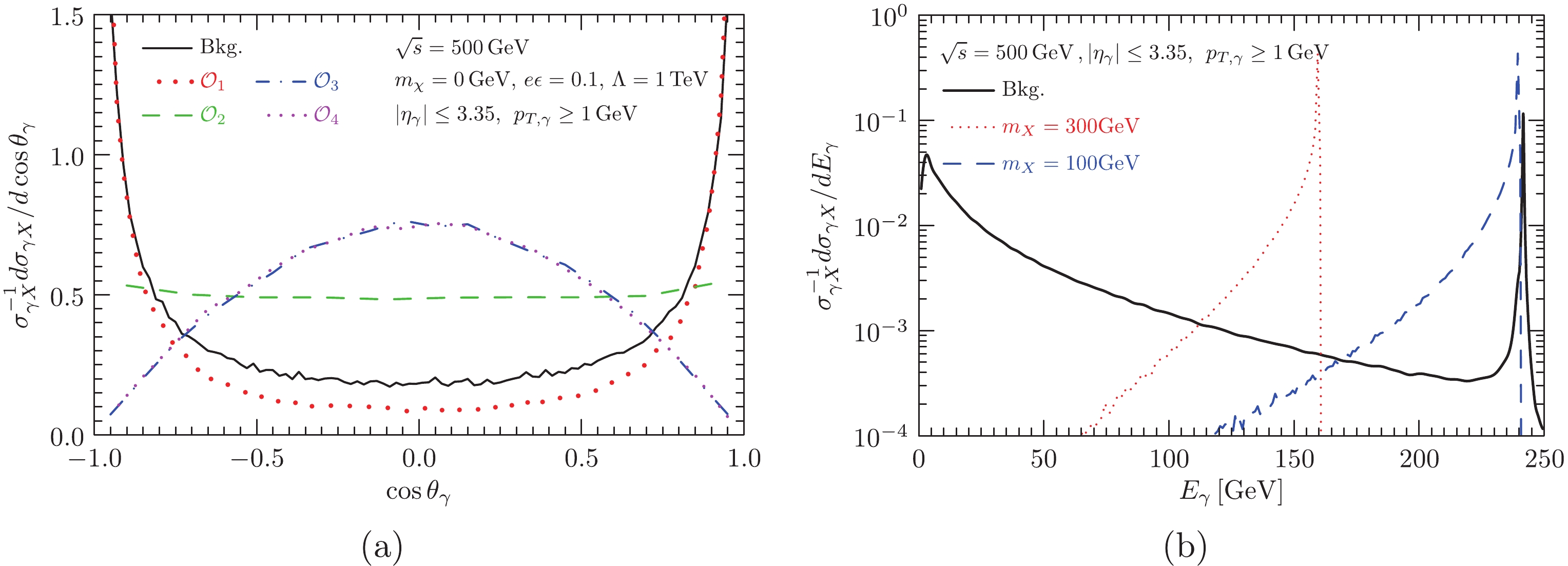

Figure 2.  (color online) Fig. 2(a): Normalized distributions of the polar angle of the photon in the CoM frame with $ \sqrt{s} = 500~{{\rm{GeV}}} $ and $ m_{\chi}=0~{{\rm{GeV}}} $. Fig. 2(b): Normalized distributions of the energy of the photon in the CoM frame with $ \sqrt{s} = 500~{{\rm{GeV}}} $. Because $ E_\gamma $ is determined under purely kinematical conditions, the distributions of $ E_\gamma $ for the signals are illustrated using DMTGC operators with $ m_{\chi}=100~{{\rm{GeV}}} $ and $ m_{\chi}=300~{{\rm{GeV}}} $. In addition, we insert the kinematical cuts $ \big|\eta_\gamma \big| < 3.35 $ and $ p_{T,\gamma} > 1~{{\rm{GeV}}} $ into both plots.

Neglecting the practical limitations on experimental measurements, the energy of the radiated photon has a fixed value for the signal. For the CoM energy $ \sqrt{s} $, this is given as

This is determined under purely kinematical conditions, where the photon has the same energy $ E_\gamma $ for all operators. However, photons of the background have a continuous energy spectrum dominated at a soft region, as shown in Fig. 2(b). The peak at $ (1 - m_{Z}^{2} /s)\sqrt{s}/2 \approx 241.7~{{\rm{GeV}}} $ is due to the resonant channel $ e^+e^- \to Z(\nu\bar{\nu})\gamma $. This can introduce a problem for probing signals when $ m_{X} $ is near $ m_{Z} $. The situation gets worse if $ \sqrt{s} \gg m_{Z}, m_{X} $, in which case $ E_\gamma \sim \sqrt{s}/2 $ for both signals and background. In any case, since the energy of the signal always peaks at $ E_\gamma $, background events can be suppressed by a factor of $ 10^{-1} $ to $ 10^{-4} $, depending on the mass of the DM. Nevertheless, due to initial state radiation (ISR) and emission of beamstrahlung photons [58], beam energies are characterized by continuous spectra. The energy of the photon is hence smeared. In Fig. 2(b), distributions of $ E_\gamma $ for $ {\cal{O}}_3 $ are shown for $ m_X=100~{{\rm{GeV}}} $ and $ 300~{{\rm{GeV}}} $. The ISR effect is taken into account by using the plugin MGISR [59, 60] in MadGraph. We can clearly see the smearing effect. It turns out that selection efficiency of the signal is reduced.

Figure 3(a) and 3(b) show the CoM energy and mass dependence of the total cross section, respectively. We can see that, although the cross section of the photon-like operator is dominant at low energy, and the one of the Pauli operator maintains a constant value across the entire range of $ \sqrt{s} $, contributions from the DMTGC operators increase rapidly with increasing CoM energy. Conversely, the cross section of the background decreases slightly between $ \sqrt{s}=200~{{\rm{GeV}}} $ to $ \sqrt{s}=400~{{\rm{GeV}}} $. This behavior is closely related to the resonance channel $ e^+e^- \to Z(\nu\bar{\nu})\gamma $. The cross section reaches an approximately constant value in the high energy region. For the DMTGC operators, the $ m_{X} $ dependence shows normal kinematical suppression in the large mass region. However, for both the photon-like and Pauli operators, the distributions exhibit enhancement as $ m_X \to \sqrt{s} $. This is due to a soft singularity (in the massless limit of the incoming electrons), as shown in (13) and (14) (the factor $ 1-z_{X}^{2} $ can be found in the denominator in both cases).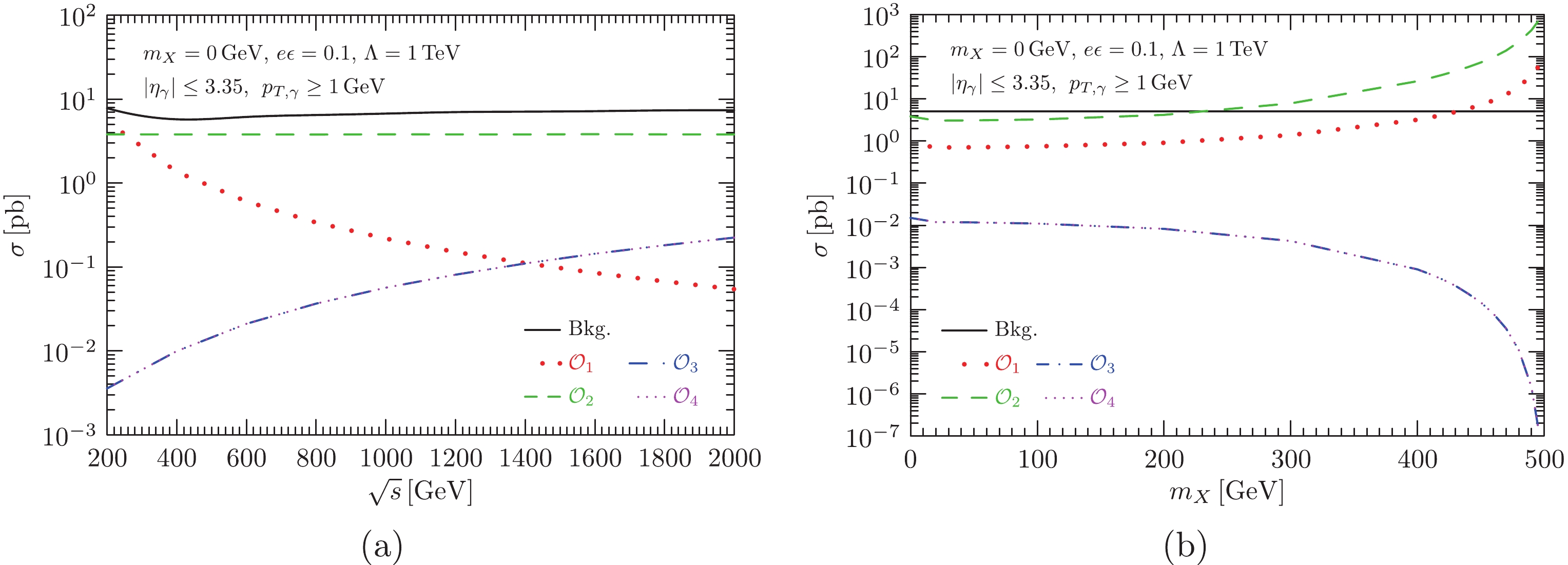

Figure 3.  (color online) Fig. 3(a): Cross sections of mono-photon production with respect to center of mass energy $ \sqrt{s} $ for $ m_{\chi}=0~{{\rm{GeV}}} $, $ e\epsilon=0.1 $, and $ \varLambda_i=1~{{\rm{TeV}}} $ Fig. 3(b): Mass dependence of the total cross section at $ \sqrt{s}=500~{{\rm{GeV}}} $ for $ e\epsilon=0.1 $ and $ \varLambda_i=1~{{\rm{TeV}}} $. In addition, we insert the kinematical cuts $ \big|\eta_\gamma \big| < 3.35 $ and $ p_{T,\gamma} > 1~{{\rm{GeV}}} $ into both plots.

One of the biggest advantages of $ e^+e^- $ colliders is that the beam particles can be polarized. Because the background contributes mainly through the chiral couplings of the SM, particularly the $ e\nu W $ coupling in the high energy region, polarized beams help to reduce the background. The cross section with electron beam polarization $ P_{e^-} $ and positron beam polarization $ P_{e^+} $ is given by

where $ \sigma_{\lambda_{e^{-}} \lambda_{e^{+}} } $ are cross sections with 100% polarization. For signals, these are given in Eqs. (13)–(15). Figure 4 shows the polarized cross sections with typical polarizations of $ P_{e^-}=\pm80 $% and $ P_{e^+}=\pm30 $%. For the background, the cross sections are shown without contributions from the resonance channel ($ e^+e^- \to Z(\nu\bar{\nu})\gamma $), which is less affected by beam polarization and is not essential when $ E_\gamma $ is not close to $ E_\gamma^{Z} $. The remaining contributions originate from the left-handed charged currents in the SM, where the dominant background is $ \sigma_{-+} $. Hence, $ \sigma_{\rm Bkg}(-80{\text%}, +30{\text%}) $ is the largest, as shown in the bottom-left panel. The other polarized channels are roughly suppressed by a factor of $ 0.06 $ to $ 0.54 $. For the Pauli operator, chirality is flipped in the neutral current, and $ \sigma_{\pm\pm} $ are the only non-zero contributions. Hence, the largest polarized channels are $ \sigma_{2}(\pm80{\text%}, \pm30{\text%}) $, and the others are suppressed by a factor of approximately $ 0.61 $. In contrast, for both the photon-like and DMTGC operators, the non-vanishing $ 100\ $% polarized cross sections are $ \sigma_{\pm\mp} $. This property results in the largest contributions $ \sigma_{1,3,4}(\pm80{\text%}, \mp30{\text%}) $. Contributions from the other polarization configurations are reduced by a factor of approximately $ 0.61 $.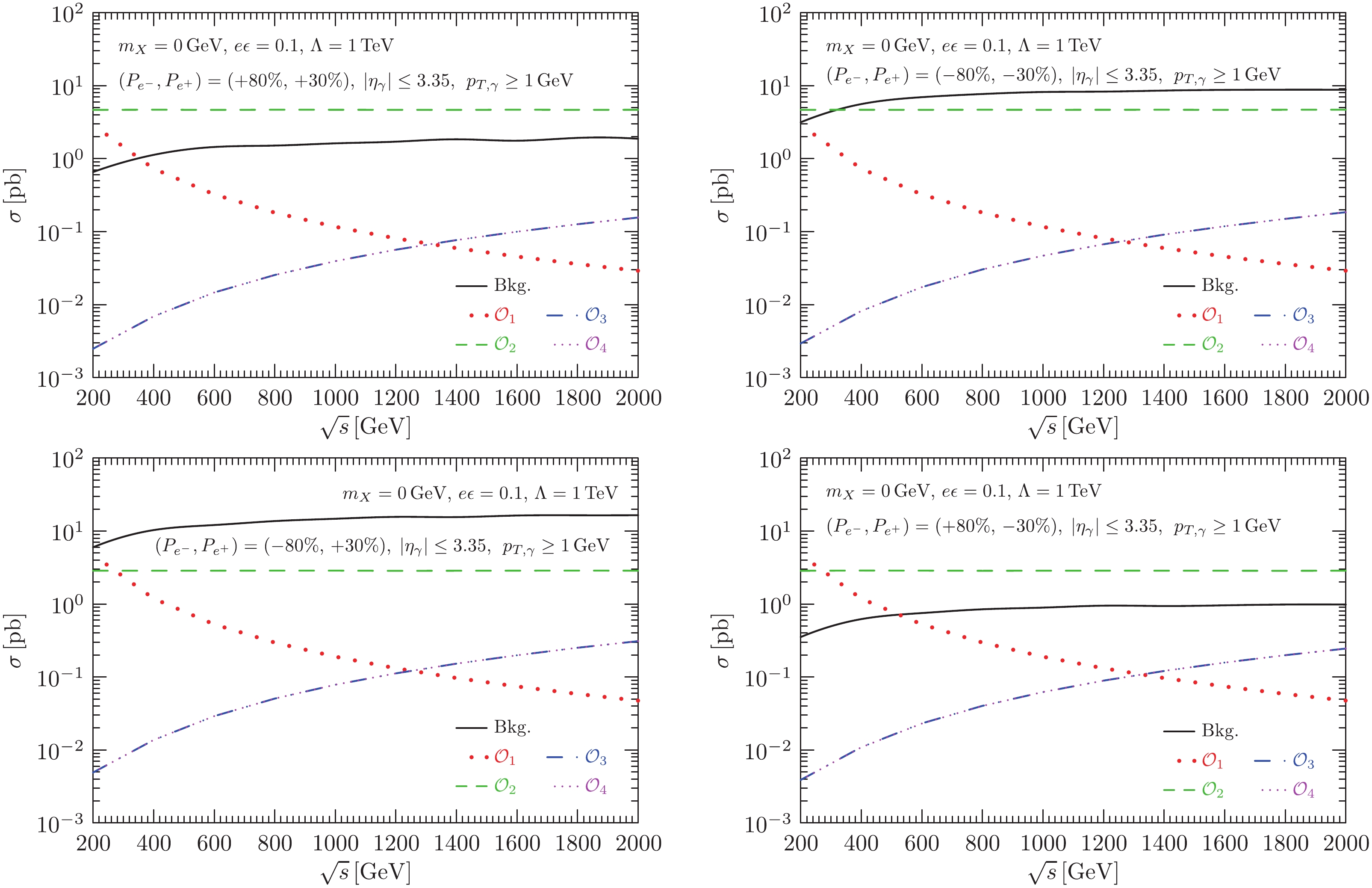

Figure 4.  (color online) Energy dependence of cross sections with the beam polarizations $ (P_{e^-},\, P_{e^+})=(+80{\text{%}}, -30{\text{%}}) $ (top-left panel), $ (-80{\text{%}}, -30{\text{%}}) $ (top-right panel), $ (-80{\text{%}}, +30{\text{%}}) $ (bottom-left panel), and $ (+80{\text{%}}, -30{\text{%}}) $ (bottom-right panel). Signals are shown with $ m_{X}=0~{{\rm{GeV}}} $, $ e\epsilon=0.1 $, and $ \varLambda_i=1~{{\rm{TeV}}} $.

In this section, we study the constraints on various NP operators using searches at the BaBar [61] and DELPHI [62] experiments, as well as measurements of the anomalous magnetic dipole moment of an electron [63, 64]. There are also astrophysical and cosmological constraints [50], for example, the bounds on the photon-like operator are particularly strong [39]; however, we do not consider these limits here.

The BaBar experiment with a CoM energy of $ 10.58~{{\rm{GeV}}} $ at the PEP-II B-factory has searched for dark photons using mono-γ events with a total luminosity of $ 53\;{{\rm{fb}}}^{-1} $ [61]. A search for dark photons in the resonance channel [65] $ e^+e^- \to \gamma X,\, X \to \ell^+\ell^- $ ($ \ell = e,\mu $) was also conducted by the BaBar Collaboration. However, exclusion limits on this channel depend on the branching ratio of the decay $ X \to \ell^+\ell^- $. Here, we re-interpret the mono-γ results for the Pauli and DMTGC operators. A single photon is required to have a polar angle in the following ranges:

in the CoM frame. Here, $ m_X=5.5~{{\rm{GeV}}} $ is the critical value for defining the low ($ m_X < 5.5~{{\rm{GeV}}} $) and high mass ($ m_X>5.5~{{\rm{GeV}}} $) regions. In addition, the photon is further selected by the cuts $ E_\gamma > 3~{{\rm{GeV}}} $ and $ E_\gamma > 1.5~{{\rm{GeV}}} $ in the low and high mass regions, respectively. The cuts $ E_\gamma > 3(1.5)~{{\rm{GeV}}} $ are helpful to reduce background, but are useless for signals because the polar angle requirements reject events with $ E_{\gamma} \lesssim 3.86~{{\rm{GeV}}} $ in the low mass region and $ E_{\gamma} \lesssim 2.27~{{\rm{GeV}}} $ in the high mass region (with $ m_X < 8~{{\rm{GeV}}} $, which corresponds to the maximum searched for in the experiment). Hence, we ignore the effects of the cuts on $ E_\gamma $. However, as shown in Fig. 2(a), the polar angle distributions of the operators are completely different; therefore, the efficiencies of the geometric cuts can be very different. The BaBar Collaboration used a boosted-decision-tree (BDT) based on the characteristics of $ E_\gamma $ and $ \cos\theta_\gamma $ to select signals. Here, we consider only the effects of the geometric cuts, which are accounted for by implementing the cuts at generator level. The corresponding acceptance efficiencies are estimated at the selected representative points $ (\epsilon=\epsilon_{\rm BarBar}, m_{X}=m_{X}^{\rm BarBar}) $ on the 90% C.L. exclusion line of BaBar. Assuming that the trigger and reconstruction efficiencies of the photon are the same for all operators, for a given mass $ m_{X} = m_{X}^{\rm BarBar} $, the 90% C.L. lower limits on the energy scales $ \varLambda_{i} $ are given as

where $ \kappa = 2, 4 $ for $ i=2, 3(4) $, respectively. The cross sections are calculated after the geometric cuts. Our results are shown in Sec. V.

Constraints on the emission of an invisible graviton from the low-scale extra-dimension and supersymmetric models were studied by the DELPHI experiment at the LEP [62] and have been re-interpreted as limits on DM, for instance, in Ref. [66]. DELPHI data were obtained with different CoM energies [67] ranging from 180.8 GeV to 209.2 GeV. Single-photon events were selected using three different triggers: the High density Projection Chamber (HPC), Forward ElectroMagnetic Calorimeter (FEMC), and Small angle TIle Calorimeter (STIC). Here, we focus on the HPC, which covers a wider range of $ E_\gamma $,

compared to the FEMC and STIC. However, the HPC module has a relatively low trigger efficiency and worse energy resolution. The trigger efficiency strongly depends on the photon energy and is approximately 52% at $ E_\gamma = 6~{{\rm{GeV}}} $, above 77% when $ E_\gamma > 30~{{\rm{GeV}}} $, and reaches a maximum of 84% when $ E_\gamma \simeq E_{\rm Beam} $. Because the energies of the photons generated with the parameters considered in this paper are all mostly larger than $ 20~{{\rm{GeV}}} $, we will use a constant trigger efficiency $ \epsilon^{\rm Trig} = 80 $% in our analysis. Furthermore, the energy of mono-γ (given by Eq. (17)) can be significantly smeared by the energy resolution, particularly for hard photons (or equivalently, smaller $ m_X $). It turns out that the selection efficiencies of the signals decrease in the low $ m_X $ region. In the following analysis, we require $ \left| E_{\gamma} - E_\gamma(m_X) \right| < 1~{{\rm{GeV}}} $, and the energy dependence of the efficiency due to energy resolution is considered using a systematic uncertainty of $ \pm8 $% [67]. The experimental significances are estimated by calculating the following $ \chi^2 $ function:

where $N_{\rm Bkg/Sig/Bkg+Sig}\big(\sqrt{s_{i}}, \overline{\theta}_j \big) = {\cal{L}}_{i} \cdot \epsilon^{\rm Trig} \cdot \sigma_{\rm Bkg/Sig/Bkg+Sig} \big( \sqrt{s_{i}}, \overline{\theta}_j \big)$ are the number of events of the background, the signal, and the summation of the background and signal, respectively. The polar angle distribution is also binned to enhance the significance, and $ \overline{\theta}_j $ represents $ c_{j-1} <|\cos\theta_{\gamma, j}| < c_j $, where $ c_{j} $ is the boundary values of the bin. The results are discussed in Sec. V.

A discrepancy between the theoretical prediction and experimental measurements of the magnetic dipole moment of the muon was reported long ago (refer to Refs. [68, 69] for recent reviews). A combination of recent measurements by the FNAL Muon $ g-2 $ experiment [70] and the old BNL result [71] has pushed this discrepancy to a level of $ 4.2\sigma $. The implications of this anomaly have been widely studied. In this paper, we focus on the anomalous magnetic dipole moment of the electron. An improved measurement of the fine structure constant using a matter-wave interferometer of cesium-133 atoms [72] showed a $ 2.4\sigma $ tension with the SM prediction [73],

Importantly, its sign differs from that of $ \Delta a_{\mu} $. Even though it is still suggestive, such a discrepancy challenges theoretical models that attempt to explain both $ \Delta a_{e} $ and $ \Delta a_{\mu} $ simultaneously. However, the most recent atomic physics measurement of $ \alpha_{\rm em} $ using Rubidium-87 atoms implied [63, 64]

which differs from the Berkeley-2018 result by more than $ 4\sigma $. More interestingly, the deviation is positive and has the same sign as $ \Delta a_{\mu} $. Even though the experimental uncertainties are at the same level, it is clear that further improved measurements are necessary to clarify the discrepancies reported in these two experiments, and consistent experimental results can be expected in forthcoming years. In the following analysis, we ignore this sign problem and use the result given by Eq. (25) to study the constraints on the mixing parameter $ \epsilon $. The contribution of the photon-like operator to $ \Delta a_{e} $ is given as [27, 52]

where $ r_e = m_e/m_X $, and the function $ F_{X}(r_e) $ is expressed as

which is always positive. For the TGC operator, its contribution to the electron g-2 vanishes because chirality is conserved in the triangle diagram. The contribution of the Pauli operator to the electron g-2 at the 1-loop level is non-zero but divergent owing to the derivatives of the field X. A UV complete model is necessary to obtain a reasonable estimation of the contribution, but this is not of interest in this study.

In practical measurements, the energy of the photon can be smeared by, for instance, the ISR of the beams and the bremsstrahlung emission of the photons [74]. To avoid overestimation of the experimental sensitivities and also select most of the signal events, the above detector activity should be considered. Take the ILC as an example [74]; it was shown that nearly 70% of the beam particles have energy lying in the window $ \big| E_{\rm Beam} - 250~{{\rm{GeV}}} \big| \le 1~{{\rm{GeV}}} $ (also see our simulation results in Fig. 2(b)). In the following calculations of experimental sensitivity, we estimate both signal and background events by assuming that the beam energy has a fixed value of $ \sqrt{s}/2 $, and the cross section of the signal is multiplied by an efficiency factor, $ \epsilon_{\rm ISR} = 70{\text%} $, no matter which collider is under consideration. Furthermore, the background is estimated by collecting all cross sections, as long as the energy of the photon lies in the window $\big| E^{\rm Bkg}_\gamma - E^{\rm Sig}_\gamma \big| < 1~{{\rm{GeV}}}$. The above simple approximation does not capture all the signal (and also background) information but is considerably conservative. However, as shown in Fig. 2(a), the polar angle of the photon is highly sensitive to the signal and hence useful to enhance the experimental sensitivities. Considering this, the distribution of the variable $ \cos\theta_{\gamma} $ is divided into ten bins, and the experimental significance is estimated by calculating the following $ \chi^2 $ function:

where $ N^{\rm Sig}_i $ and $ N^{\rm Bkg}_i $ are signal and background events in the i-th bin, and $ \epsilon_{\rm Syst} $ denotes the systematic uncertainty, which can reduce the sensitivity significantly, as shown in Ref. [75]. We also assume that $ \epsilon_{\rm Syst} = 1\ $% in the following calculations. The radiative Bhabha process can also contribute to the background. However, this contribution can be significantly reduced by using only one reconstructed BeamCal cluster, as reported in Ref. [74]. Therefore, we neglect the background originating from the radiative Bhabha process.

The CEPC experiment is designed to be a Higgs factory [76]; however, it is also relevant for probing particles and dynamics in the dark sector [77]. Three different running modes at the CEPC have been proposed [76]. In this study, we focus on the mode with $ \sqrt{s} = 240~{{\rm{GeV}}} $, in which a total luminosity of $ 5.6{\rm{ab}}^{-1} $ will be accumulated at two interaction points after seven years of operation. There are also other $ e^+e^- $ colliders, for instance, the ILC, FCC-ee, and CLIC, operating at similar CoM energies. Here, we choose the CEPC as a representative collider to probe the operators considered in this paper. In our simulations, the following kinematical cuts are used to estimate the signal significance defined in (28):

Figure 5(a), Fig. 5(b), and Fig. 5(c) show our results for the operators $ {\cal{O}}_{1} $, $ {\cal{O}}_{2} $, and $ {\cal{O}}_{3(4)} $, respectively.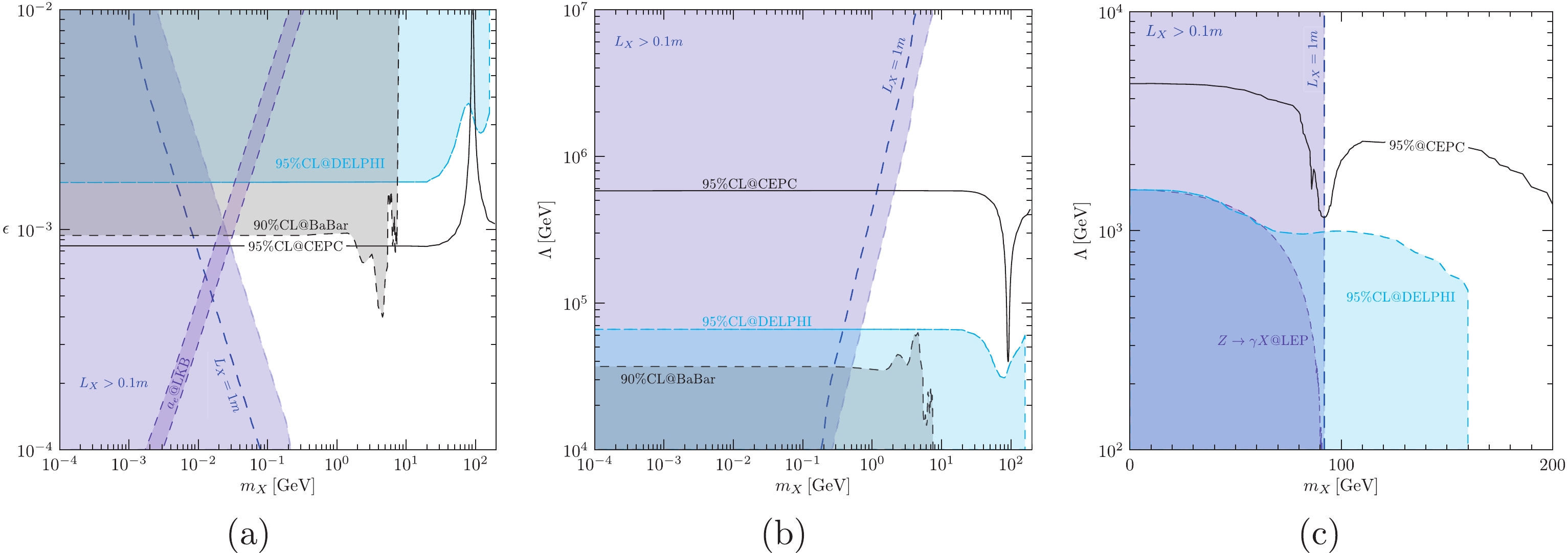

Figure 5.  (color online) Expected sensitivities at the 95% CL for the operators $ {\cal{O}}_1 $ (Fig. 5(a)), $ {\cal{O}}_2 $(Fig. 5(b)), and $ {\cal{O}}_{3(4)} $ (Fig. 5(c)) at the CEPC with a total luminosity of $ 5.6\;{\rm{ab}}^{-1} $. The shaded regions represent constraints from other experiments and are explained in the text.

The shaded region in blue represents $ L_{X} > 0.1m $ with the assumption ${\rm Br}(X\to\ell^+\ell^-) = 1$. For reference, we also show the contour with $ L_{X} = 1m $ using a dashed-blue line. We can see that the decay widths do not change rapidly with respect to the energy scale and mass of X. We present these results such that readers can gain intuitive insight into the validation of mono-γ event configuration for the real DM models under consideration. However, as previously mentioned, this condition can be removed if the particle X decays into dark particles. The gray region in Fig. 5(a) is obtained using data extracted from Ref. [61] and represents the 90% CL excluded region from the BaBar experiment. The gray region in Fig. 5(b) is obtained by reinterpreting the same data for the operator $ {\cal{O}}_2 $ using the method explained in Sec. IV.A. For the operator $ {\cal{O}}_{3(4)} $, owing to suppression of $ s/m_{Z}^2 $, the constraint from the BaBar experiment is rather weak, and the excluded region is outside the plot range in Fig. 5(c). The purple region represents the $ 1\sigma $ bound of $ a_{e} $. We can see that parameter space remains, which can account for $ a_{e} $, but is not constrained by existing experiments (if we do not consider astrophysical and cosmological constraints).

Based on the method explained in Sec. IV.B for the DELPHI experiment, the expected exclusion regions at the 95% CL are shown in cyan. We can see that for the operator $ {\cal{O}}_1 $, the constraint in the low mass region is slightly weaker than the BaBar limit. The reasons are as follows: 1) the cross section for the operator $ {\cal{O}}_1 $ decreases with respect to CoM energy; 2) the total luminosity of DELPHI is approximately a factor of three larger than that of BaBar. Conversely, for the operator $ {\cal{O}}_2 $, the DELPHI constraint is stronger because, on the one hand, the cross section of the signal does not depend on s, and on the other hand, more background events are removed by the central cut on $ \cos\theta_\gamma $ (see (22)). We can see that in the small region of $ m_{X} $, the constraint on the Pauli operator already reaches approximately $ 60~{{\rm{TeV}}} $ and is approximately $ 2~{{\rm{TeV}}} $ for the DMTGC operators.

The black-solid lines show the expected 95% CL experimental sensitivities at the CEPC with an integrated luminosity of $ 5.6{\rm{ab}}^{-1} $. The CoM energy of the CEPC is not much higher than that of DELPHI, but the luminosity is approximately 40 times larger; hence, the expected sensitivity is enhanced. For low mass scenarios, the mixing parameter can be probed at a level of $ 7\times10^{-4} $. The operator $ {\cal{O}}_2 $ with an energy scale $ \varLambda_2 \sim 600~{{\rm{TeV}}} $ can be searched for at the CEPC. Compared to the sensitivities at future muon colliders [40], the CEPC can already probe most of the parameter space. For the operators $ {\cal{O}}_{3(4)} $, the 95% sensitivity to $ \varLambda_{3(4)} $ can reach $ 1~{{\rm{TeV}}} $ across the entire mass region (within the plot range) and approximately $ 5~{{\rm{TeV}}} $ in the low mass region.

The ILC collider was originally proposed to be run at a CoM energy $ \sqrt{s}=500~{{\rm{GeV}}} $ [78], and recently scenarios with $ \sqrt{s}=250~{{\rm{GeV}}} $ and $ \sqrt{s}=1~{{\rm{TeV}}} $ [79] were also considered. Here, we focus on the mode with $ \sqrt{s}= $ 500 GeV, at which data will be collected with a total luminosity of $ 4{\rm{ab}}^{-1} $. In addition, the H20 running scenario [80], in which both electron and position beams are polarized, aimed to optimize the physics performance of the experiment. In this paper, we consider three polarization configurations, which are listed in Table 1. The experimental significances are estimated by applying the following kinematical cuts [74]:

$ (P_{e^{-}}, P_{e^{+}}) $	(0, 0)	(+80%, 0)	(+80%, −30%)
${\cal{L} }_{\rm Int.} [{\rm{ab} }^{-1} ]$	$ 4 $	$ 1.6 $	$ 1.6 $

Table 1.  Polarization configurations and the corresponding luminosities studied in this paper.

Figure 6(a), Fig. 6(b), and Fig. 6(c) show the 95% CL sensitivities for the operators $ {\cal{O}}_1 $, $ {\cal{O}}_2 $, and $ {\cal{O}}_{3(4)} $, respectively. The shaded regions are the same as those shown in Fig. 5(a)–(c). For the operator $ {\cal{O}}_1 $, even though the total luminosity of the ILC is smaller and the cross section of the signal is reduced, the experimental sensitivity is enhanced by roughly a factor of two for $ \big(P_{e^-}, P_{e^+}\big) = (0{\text%}, 0{\text%}) $. This is due to the following reasons: 1) in the low energy region, the background also decreases with respect to s, as shown in Fig. 3(a); 2) the stronger transverse momentum cut removes more background. However, because the background tends to be constant at high s, such enhancement is not expected at colliders with higher CoM energies. In contrast, as expected, the polarization configuration $ \big(P_{e^-}, P_{e^+}\big) = (+80{\text{%}}, -30{\text{%}}) $ gives a better sensitivity. However, the enhancement is not so promising because the projected total luminosity is $1.6~{\rm{ab}}^{-1}$, which is smaller than that of the unpolarized scenario by a factor of more than two. For the same reason, polarized beams cannot provide sizable optimization for the operators $ {\cal{O}}_2 $ and $ {\cal{O}}_{3(4)} $, as shown in Fig. 6(b) and Fig. 6(c), respectively. Sensitivity to the operator $ {\cal{O}}_2 $ is significantly enhanced at the ILC500 and reaches a level of $ \sim10^3~{{\rm{TeV}}} $, which is significantly higher than the expectation at future muon colliders [42]. This is due to the distinctive polar angle distribution between the signal and background, as shown in Fig. 2(a), and hence the background is strongly suppressed by the stronger cut $ p_{T,\gamma} > 6~{{\rm{GeV}}} $. Similar enhancement occurs for the operator $ {\cal{O}}_{3(4)} $ but is reduced because the cross section depends on $ \varLambda^{-4}_{3(4)} $. However, probing the power in the high mass region is significantly enhanced. The sensitivity at the 95% CL can reach a level of $ 7~{{\rm{TeV}}} $, which is approximately five times larger than the exclusion limit given by $ Z\to\gamma X $ at the LEP and $ e^{+}e^{-} \to \gamma X $ by DELPHI in the low mass region.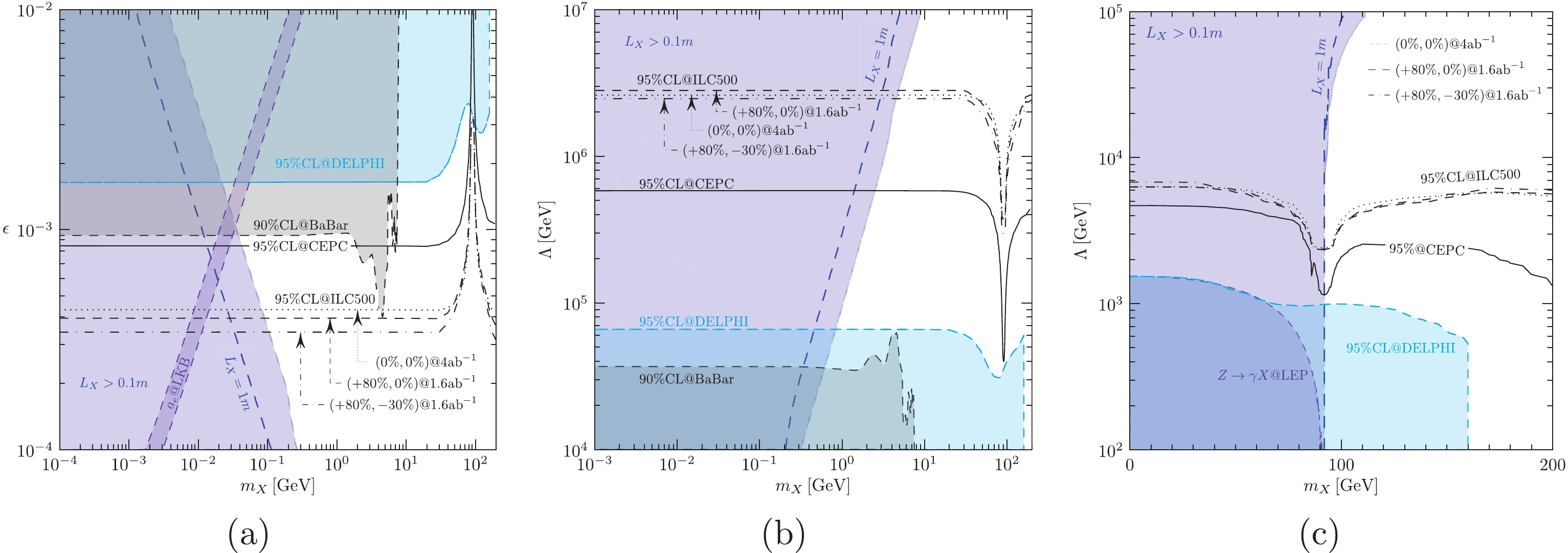

Figure 6.  (color online) Expected sensitivities at the 95% CL for the operators $ {\cal{O}}_1 $ (Fig. 6(a)), $ {\cal{O}}_2 $(Fig. 6(b)) and $ {\cal{O}}_{3(4)} $ (Fig. 6(c)) at the ILC500. The shaded regions are the same as those shown in Fig. 5. The black-dotted, -dashed, -dash dotted lines show the cases for $ \big(P_{e^-}, P_{e^+}\big) = (0{\text{%}}, 0{\text{%}}), (+80{\text{%}}, 0{\text{%}}) $, and $ (+80{\text{%}}, -30{\text{%}}) $, respectively. The 95% CL line for the CEPC is also indicated by a black-solid line for reference.

In summary, we study mono-γ production induced by photon-like, Pauli, and DMTGC operators at future $ e^+e^- $ colliders. We show that, although the energy of the photon is purely determined by kinematics, the polar angle distribution of the photon is very distinctive for the various operators and the background. Particularly, for the DMTGCs, X and γ are generated via an s-channel virtual Z-boson; hence, photons are dominantly produced in the central region, as shown in Fig. 2(a). Furthermore, the behaviors of the total cross sections in the high energy region are also different. Although the contribution of the photon-like operator decreases by $ 1/s $, and that of the Pauli operator does not depend on s, the cross sections for the DMTGCs increase rapidly with respect to s. Hence, at high energy colliders, DMTGC operators are more promising than Pauli operators.

Previous $ e^+e^- $ experiments have searched for dark particles via the mono-γ channel. Focusing on the BaBar [61] and DELPHI [62] experiments, we re-interpret the results as constraints on the parameters considered in this study. In the small mass region of $ m_{X} $, the constraint from the DELPHI experiment on the Pauli operator already reaches approximately $ 60~{{\rm{TeV}}} $ and is approximately $ 2~{{\rm{TeV}}} $ for the DMTGC operators. We also consider the anomalous magnetic dipole moment of an electron [63, 64]. We show that parameter space remains, which can account for $ a_{e} $ but is not constrained by existing experiments (except for astrophysical and cosmological constraints). We further study the expected experimental significance at the CEPC and ILC. Our results indicate that very high energy colliders, for instance Muon colliders at $ 3, 10~{{\rm{TeV}}} $, cannot give a significantly more profound limit on the Pauli operators. This is because the cross section for the Pauli operator does not depend on s. The 95% lower limit on $ \varLambda_2 $ can reach $ 600~{{\rm{TeV}}} $ at the CEPC and can be enhanced to $ \sim 10^3~{{\rm{TeV}}} $ at the ILC500. However, because the production rates induced by the DMTGC operators increase rapidly with increasing s, it is more interesting to search for the signals of the DMTGC at high energy colliders. The expected lower limit of $ \varLambda_{3(4)} $ at the 95% CL is approximately $ 5~{{\rm{TeV}}} $ at the CEPC and approximately $ 7~{{\rm{TeV}}} $ at the ILC500. Possible enhancement via beam polarization is also studied. However, because of its smaller integrated luminosity, the bounds on the scale parameters can only be enhanced slightly.