-
The Relativistic Heavy Ion Collider (RHIC) at the Brookhaven National Laboratory (BNL) and the Large Hadron Collider (LHC) at CERN have been used to create a near perfect fluid known as quark-gluon plasma (QGP) [1, 2]. QGP expands rapidly and collectively such that the collision geometry and initial state fluctuations are transformed into long-range multi-particle correlations at the final state [3, 4]. For example, the momentum anisotropy of final state hadrons is sensitive to spatial eccentricity at the initial state. A question to consider is whether the final state observables are also affected by the initial state nuclear structure, such as the nuclear size, nuclear shape deformation, neutron skin, and α clusters inside nucleus. Furthermore, will the nuclear structure signal survive the violent collision, especially since the colliding nuclei are highly relativistic and the initial state might be dominated by color glass condensates?
Relativistic heavy ion collisions, especially isobar collisions, have been employed to study nuclear shape deformation [5–10], neutron skin thickness [11–13], the nucleon-nucleon correlation [14], and the α clustering structure inside the nucleus [12, 15–21]. Both the RHIC and LHC are planning to collect data for
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions, which is a medium-sized system [17, 22] that can serve as a control group for the peripheral collisions of large nuclei and high multiplicity$ p+p $ and$p+{\rm Pb}$ events in small systems. There have been many theoretical studies on$ ^{16}\text{O}+{}^{16}\text{O} $ collisions [23, 24].$ ^{16}\text{O}+{}^{16}\text{O} $ collisions provide a unique opportunity to study the α clustering structure in the oxygen nucleus because$ ^{16}\text{O} $ at the ground state is suggested to be a tetrahedral structure composed of four α clusters [25–29]. The concept of the α cluster was proposed by Gamow in the 1930s [30], who noticed that light nuclei are more stable if their nucleons can form several αs. Increasing evidence indicates that the mean field cannot break the α cluster structure in light nuclei, such as$ ^{12}\text{C} $ and$ ^{16}\text{O} $ [31–34]. The experimental evidence for clustering originates from fragmentation studies [35]. Nuclear lattice effective field theory (NLEFT) also suggests that nucleons in oxygen cluster together like α particles.α clusters inside a nucleus bring a significantly different nuclear shape deformation from the Woods-Saxon (WS) distribution [36, 37]. Wojciech proposed the study of α clusters in light nuclei using relativistic heavy ion collisions [38, 39]. Others have proposed the study of collision systems between light nuclei (
$ ^{12}\text{C} $ ) with α clustering structures and heavy nuclei without them, such as Pb and Au [40–43]. Many studies have focused on observables such as collective flows with particle multiplicity and the eccentricity coefficient as functions of the number of wounded nucleons.Relativistic hydrodynamic simulations of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions have shown signals of α-clustering in the oxygen nucleus [18]. In this study, the Trento Monte Carlo model is used to generate the initial conditions of$ ^{16}\text{O}+{}^{16}\text{O} $ collisions for iEBE-VISHNU hydrodynamic simulations. The nucleon distributions in$ ^{16}\text{O} $ are provided by ab initio calculations using NLEFT [44, 45]. This ab initio calculation suggests the existence of α-clusters in the oxygen nucleus. It has been observed that α-clustering suppresses$ v_3\{2\}/v_2\{2\} $ and enhances$v_4\{2\}/ v_2\{2\}$ , whereas sub-nucleon fluctuations always have the opposite effect.Moreover, using a multi phase transport model (AMPT) to simulate
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions, it was discovered that the forward-backward (FB) multiplicity correlation is smaller for the four-α tetrahedron structure than the WS distribution. The FB correlation has thus been proposed as a probe for α-clustering inside the oxygen nucleus [15].In this study, we attempt to search for more signals of α-clusters in the oxygen nucleus using relativistic hydrodynamic simulations of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions [46]. We calculate the multiplicity, transverse momentum spectra, and anisotropy of charged particles using relativistic hydrodynamic simulations with different nucleon distributions of$ ^{16}\text{O} $ . We use the Trento Monte Carlo model to generate the initial entropy density distributions in the transverse plane for$ ^{16}\text{O}+{}^{16}\text{O} $ collisions with the WS distribution, deformed WS distribution, and four-α tetrahedral structure for the oxygen nucleus. The cross-section of nucleon-nucleon collisions at$ \sqrt{s_{NN}} = 7 $ TeV (LHC) is set to$ \sigma_{NN} = 7.1 \text{ fm}^2 $ . The initial entropy density profile from Trento is fed into CLVisc model (a 3+1D hydrodynamic model) to simulate the expansion of QGP [47] and its transformation into hadrons. The remainder of this paper is organized as follows. In Section II, we introduce three different distributions of nucleons inside the oxygen nucleus and the relativistic hydrodynamic model CLVisc. Section III compares the charged particle multiplicities and their$ p_T $ spectra and$ p_T $ -differential$ v_n $ using three different oxygen structures. Signals of α-clustering in the oxygen nucleus are collectively presented in the summary. -
The WS distribution is a good approximation to describe the coordinates of nucleons inside a double magic nucleus, e.g.,
$^{208}{\rm Pb}$ , whose shape is approximately a perfect sphere, i.e.,$ \rho(r) = \frac{\rho_0}{1+\exp{\left[ \dfrac{r-R}{a} \right]}}, $

(1) where r is the radial distance to the center of the nucleus,
$ \rho_0 $ is the nuclear density determined using$A = 2\pi\int{\rho(r,\theta)r^2\sin{\theta}{\rm d}r {\rm d}\theta}$ , a is the surface diffuseness parameter, and R is the effective radius of the nucleus.For most nuclei whose number of protons or neutrons is not a magic number, the nuclear shape is deformed. The deformed WS distribution is usually employed to describe the nucleons inside non-spherical nuclei,
$ \rho(r,\theta) = \frac{\rho_0}{1+\exp{\left[ \dfrac{r-R\left(1+\beta_2Y_{20}(\theta)+\beta_4Y_{40}(\theta)\right)}{a} \right]}}, $

(2) where θ is the polar angle with respect to the symmetry axis of the nucleus, and
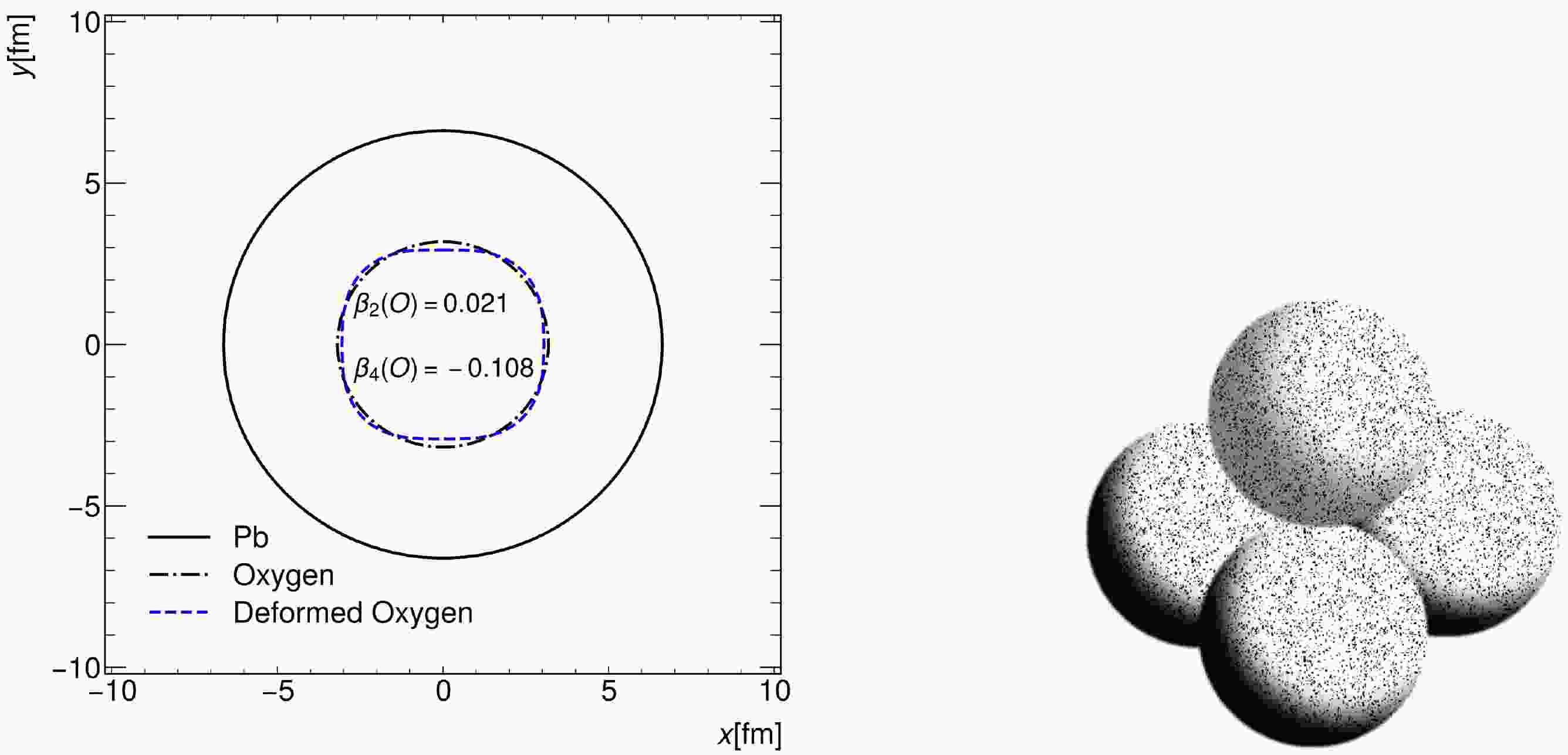
$ Y_{20}(\theta) =\dfrac{1}{4}\sqrt{\dfrac{5}{\pi}}(3\cos^2{\theta}-1) $ and$Y_{40}(\theta) = \dfrac{3}{16\pi}(35\cos^4{\theta}-30\cos^2{\theta}+3)$ are spherical harmonic functions. The quadrupole deformation parameter$ \beta_2 $ and hexadecapole parameter$ \beta_4 $ control the magnitude of deformation from the spherical shape. As shown in the left window of Fig. 1, the shape change is caused by deformation on the transverse plane, and unlike the spherical Pb nucleus, the O nucleus is more like a square.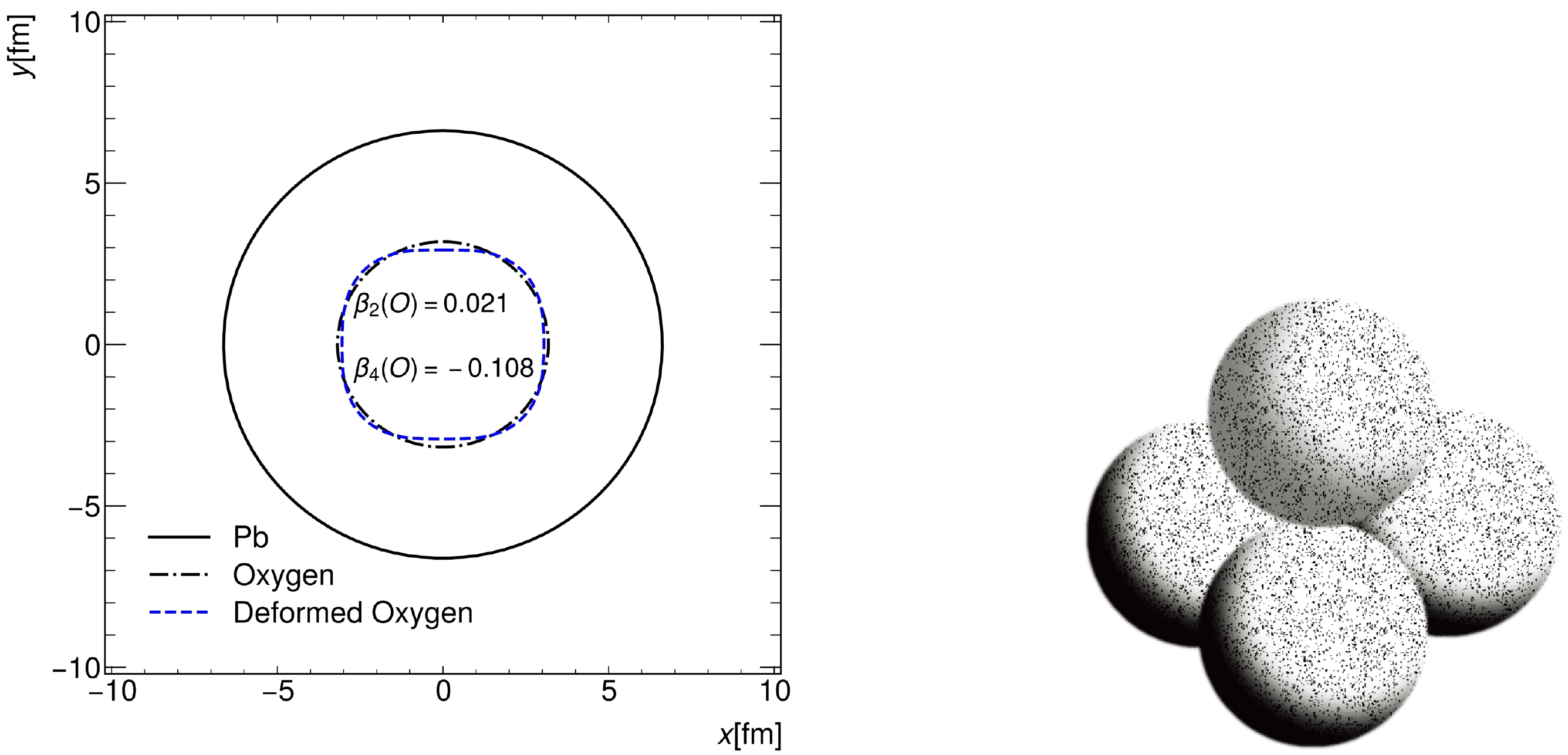
Figure 1. (color online) Left: Shape of Pb and oxygen. The Woods-Saxon and deformed Woods-Saxon distributions have been used for oxygen. Right: Four-α tetrahedral structure of oxygen, with four nucleons in each α sampled from the Woods-Saxon distribution.
In this study, we use the WS and deformed WS distributions to sample the coordinates of 16 nucleons inside each oxygen nucleus. For the deformed WS distribution, the values of the parameters for oxygen are
$ A = 16 $ ,$ R = 3.18\text{ fm} $ ,$ a = 0.662 $ fm,$ \beta_2 = 0.021 $ , and$ \beta_4 = -0.108 $ [48]. For the WS distribution, we set$ \beta_2 = \beta_4 = 0 $ and fix other parameters as in the deformed WS distribution. The resulting nuclear shapes from these two groups of parameters are shown on the left of Fig. 1, along with the${}^{208}\rm Pb$ nucleus as a reference. For deformed nuclei, different orientations correspond to different collision geometries. To generate realistic collisions of deformed nuclei, we rotate the entire oxygen nucleus randomly after all nucleons inside the oxygen are sampled from the deformed WS distribution. -
The four-α tetrahedron structure of
$ ^{16}{\rm O} $ is provided by the extended quantum molecular dynamics (EQMD) model [16, 37] with the effective Pauli potential. In this configuration, four αs are located at the vertices of a regular tetrahedron with a side length of$ 3.42 $ fm, as shown on the right of Fig. 1. The side length is fixed to produce a similar RMS-radius (2.699 fm) [16] as the experimental data (2.6991 fm) [49]. For each α cluster, the coordinates of two protons and two neutrons are sampled from a three-parameter distribution function,$ \begin{equation} \rho(r) = \rho_0\left(1+w\frac{r^2}{R^2}\right)\left[1+\exp\left(\frac{r-R}{a}\right)\right]^{-1} ,\end{equation} $

(3) where
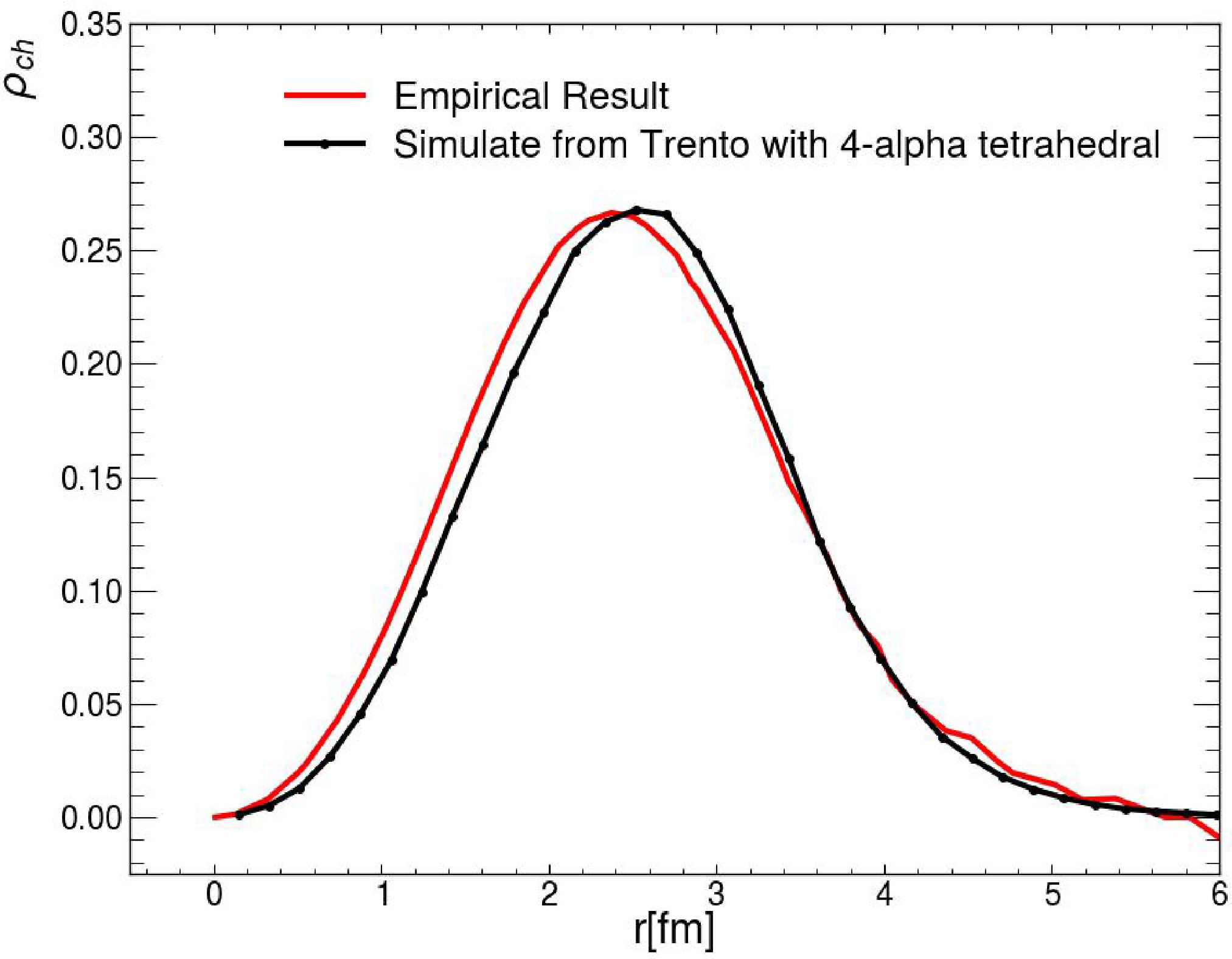
$ \rho_0 $ is the nuclear density at the center of the alpha,$ w=0.517 $ ,$ R=0.964\text{ fm} $ , and$ a=0.322\text{ fm} $ . Note that we apply three successive Eulerian rotations to each sampled oxygen nucleus before the collision, and the minimum distance between two nucleons inside the same oxygen is larger than$ dr = \sqrt{0.5} $ fm to avoid overlapping. This configuration has also been used in AMPT [16] simulations to search for signatures of α clustering in$ ^{16}{\rm O} $ . Using the same initial state nuclear configuration in relativistic hydrodynamic simulations helps to further investigate the effect of dynamical evolution on the signature of α clustering.We verify that the simulated radial distribution of charge density agrees well with the empirical result [45], as shown in Fig. 2.
-
The initial entropy density in the transverse plane is locally proportional to the reduced thickness function
$ T_R $ ,$\frac{{{\rm d}S}}{{{\rm d}y}}{\bigg|_{\tau = {\tau _0}}} \propto {T_R}\left( {p;{T_A},{T_B}} \right), $

(4) where
$ \begin{equation} T_R\left(p;T_A,T_B\right)= \begin{cases} \max(T_A,T_B), & p \to +\infty,\\ T_A+T_B, & p = +1,\\ \sqrt{T_AT_B}, & p = 0,\\ 2T_AT_B/\left(T_A+T_B\right), & p = -1,\\ \min(T_A,T_B), & p \to -\infty. \end{cases} \end{equation} $

(5) where
$ T_A $ and$ T_B $ indicate the participant nucleon thickness functions of the two colliding nuclei. In this study, we employ the default option,$ p=0 $ , because of its excellent agreement with the IP-Glasma results and experimental data. Using this configuration, relativistic hydrodynamic simulations can describe not only the centrality dependence of charged multiplicity, but also the$ v_3 $ to$ v_2 $ ratio in Pb+Pb collisions [50].For the longitudinal direction, we use an envelope function that extends along the space-time rapidity,
$ \begin{equation} H\left(\eta_{s}\right)=\exp \left[-\frac{\left(|\eta_{s}|-\eta_{w}\right)^{2}}{2 \sigma_{\eta}^{2}} \theta\left(|\eta_{s}|-\eta_{w}\right)\right], \end{equation} $

(6) where
$ \sigma_{\eta}= 2.0 $ and$ \eta_{w}= 1.7 $ are used for$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV.The CLVisc model is a (3+1)D viscous hydrodynamic model that is parallelized on GPU using OpenCL. This model simulates the hydrodynamic evolution of hot and dense QCD matter (QGP) and hadron resonance gas (HRG) before kinetic freeze-out by solving the following equations together with the Israel-Stewart equations for
$ \pi^{\mu\nu} $ :$ \begin{equation} \nabla_\mu T^{\mu\nu} = 0, {\ \rm with\ } T^{\mu\nu}= (e+P) u^\mu u^\nu - Pg^{\mu\nu}+\pi^{\mu\nu}, \end{equation} $

(7) where in the energy-momentum tensor
$ T^{\mu\nu} $ , e is the energy density, P is the pressure as a function of energy density given by the equation of state (EoS),$ u^\mu $ is the fluid four-velocity obeying$ u^\mu u_\mu=1 $ , and$ \pi^{\mu\nu} $ is the shear stress tensor [51].We assume that hydrodynamic evolution starts at
$ \tau_0=0.6 $ fm. In this study, we use the partial chemical equilibrium EoS with a chemical freeze-out temperature of 165 MeV and a smooth crossover between QGP at high temperatures and the HRG EoS at low temperatures [52], as inspired by the lattice QCD study in [52] (s95p-pce).The momentum distribution of hadron freeze-out from the hyper-surface follows the Cooper-Frye formula,
$ \begin{equation} \frac{{\rm d}N_i}{{\rm d}y p_T {\rm d} p_T {\rm d} \phi}=\frac{g_i}{(2\pi)^3}\int{p^\mu {\rm d}\Sigma_\mu f(p\cdot u)}(1+\delta f), \end{equation} $

(8) where
$ g_i = 2 s_i + 1 $ is the spin degeneracy of particle species i with spin$ s_i $ ,$ p^{\mu} $ is the four-momenta of these particles in the lab frame,$ \Sigma_{\mu} $ is their freeze-out hyper-surface,$ f(p\cdot u) $ is their Fermi-Dirac/Bose-Einstein distribution function,$ \begin{equation} f(p\cdot u) =\frac{1}{\exp \left[\left(p \cdot u-\mu_{i}\right) / T_{\mathrm{frz}}\right] \pm 1} , \end{equation} $

(9) $ \delta f $ is responsible for the non-equilibrium correction and is given by considering the contribution of the shear stress tensor$ \pi^{\mu\nu} $ ,$ \begin{equation} \delta f =\left(1 \mp f_{\mathrm{eq}}\right) \frac{p_{\mu} p_{\nu} \pi^{\mu \nu}}{2 T_{\mathrm{frz}}^{2}(\varepsilon+P)}. \end{equation} $

(10) We choose the freeze-out temperature
$ T_{\mathrm{frz}}=137~\rm MeV $ for light hadrons.The anisotropic collective flow
$ v_n $ is calculated from the Fourier expansion of the particle momentum spectrum in the transverse plane of the collisions [53–55],$ \begin{equation} \frac{{\rm d}^{3} N}{p_{\mathrm{T}} {\rm d} p_{\mathrm{T}} {\rm d} y {\rm d} \phi}=\frac{{\rm d}^{2} N}{2 \pi p_{\mathrm{T}} {\rm d} p_{\mathrm{T}} {\rm d} y}\left[1+\sum\limits_{n=1}^{\infty} 2 v_{n} \cos \left(n\left(\phi-\Psi_{\mathrm{EP}}\right)\right)\right], \end{equation} $

(11) where
$ \Psi_{\mathrm{EP}} $ denotes the azimuth angle of the event plane.In this study, we simulate event-by-event
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV for three centralities, with 1000 events in each centrality. -
To calibrate the scale factor of the initial entropy density from the Trento model, we use the empirical formula
$ \begin{equation} \text{Total }~ N_{\rm ch} / <N_{\rm part}/2>=As^p\log s +B \end{equation} $

(12) for the 0–5% most central collisions [56]. This expresses the total number of charged hadrons,
$\text{Total } N_{\rm ch}$ , produced in the most central heavy-ion collisions as a function of the squared collision energy$ s([\text{GeV}]^2) $ , which is the square of the collision energy of a pair of nucleons in their center of mass frame. The data for the most central collisions at the AGS (0–5% Au-Au) [57, 58], SPS (0–5% Pb-Pb) [59, 60], RHIC (0–5% and 0–6% Au-Au) [61–63], and LHC (0–5% Pb-Pb) [64] are used for calibration. The parameters$ A = 0.632 $ ,$ B = 0.244 $ , and$ p = $ 0.137 are used, and the value of the scale factor for$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV is 205.Shown in the left window of Fig. 3 is the charged multiplicity as a function of pseudo-rapidity from CLVisc relativistic hydrodynamic simulations of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV, with nucleons in oxygen sampled from the WS distribution (blue-dashed line), deformed WS distribution (red-solid line), and four-α tetrahedron distribution (black-solid line with dots). The multiplicity as a function of pseudo-rapidity is shown to overlap for the WS and deformed WS distributions in$ 0-5\% $ ,$20\%-30\%$ , and$40\%-60\%$ collisions. The small deformation parameters$ \beta_2 $ and$ \beta_4 $ shown in the initial condition do not seem to make any difference in the distribution of charged particle multiplicity as a function of centrality. This is also confirmed by the probability distribution of initial total entropy shown in the right window of Fig. 3, which is calculated from 1 million events.
Figure 3. (color online) Left: Charged particle multiplicity as a function of pseudo-rapidity from CLVisc relativistic hydrodynamic simulations of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV, with nucleons in oxygen sampled from the Woods-Saxon distribution (blue-dashed line), deformed Woods-Saxon distribution (red-solid line), and four-α tetrahedron distribution (black-solid line with dots). Right: Probability density distribution of total entropy calculated from Trento for these three different initial configurations of the oxygen nucleus.Using the same number of nucleons in oxygen and the same initial scaling factor, Trento produces more entropy using the four-α tetrahedron distribution than using WS and deformed WS for oxygen in
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions. It was studied in [65] that increasing the Gaussian smearing width of hot spots in the initial condition of heavy ion collisions leads to a higher total entropy at the initial state and more particles at the final state. The present study shows that different distributions of nucleons inside nuclei also bring different values of the total entropy and the final state charged multiplicity of the colliding system. As shown in the left window of Fig. 3, the charged multiplicity in the most central collisions using the four-α structure is$ \sim 10\% $ higher than that using the WS and deformed WS distributions.Note that the enhancement of charged multiplicity is not sufficient to tell whether α clusters exist in oxygen. It was verified that the oxygen structure calculated from the harmonic oscillator potential also increases the charged multiplicity in the most central
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions by 15% compared with the WS distribution [24]. However, using the harmonic oscillator potential to calculate the nucleon distribution inside the oxygen nucleus gives a different nucleon density profile. The enhancement of charged multiplicity can be used together with other observations to search for α clusters inside the oxygen nucleus.Figure 3 shows that the charged particle multiplicity as a function of centrality is sensitive to the nucleon distribution inside the oxygen nucleus. The ratios of charged particle multiplicity between different centralities are distinct for different nuclear structures, as shown in Table 1. The ratio of charged particle multiplicity between
$ 0-5\% $ and$20\%-30\%$ for the four-α equilateral structure is approximately 2.29, which is smaller than that for the WS and deformed WS distributions by$ 6\% $ percent. The ratio of charged multiplicity between$ 0-5\% $ and$40\%-60\%$ for the four-α equilateral structure is 5.38, which is approximately$ 9\% $ smaller than that for the WS and deformed WS distributions. The experimental measurements of these two ratios can easily reveal whether the α-cluster structure plays a role in final state observables in heavy ion collisions. Usually, the total multiplicity in$ 0-5\% $ collisions is used to determine the overall scaling factor. Owing to the lack of experimental data, the current calculation is merely a prediction for$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at the LHC. There might be uncertainties in the scaling factor, but the ratio between different centrality bins seems to be a sensitive probe for the nuclear structure.Cent1/Cent2 WS Deformed WS Four-α (0–5%)/(20%–30%) 2.44 2.44 2.29 (0–5%)/(40%–60%) 5.99 5.91 5.38 Table 1. Ratio of charged multiplicity at middle pseudo-rapidity between different centralities.
Figure 4 shows the
$ p_T $ spectrum of charged hadrons given by event-by-event hydrodynamic simulations of$ ^{16}\text{O}+{}^{16}\text{O} $ collisions for three different initial conditions, with nucleons in oxygen sampled from the WS distribution (black-dashed line), deformed WS distribution (red-solid line), and four-α tetrahedron distribution (black-solid line with dots). No significant differences are observed between the$ p_T $ spectra with the WS and deformed WS distributions. This is consistent with the small differences between the shapes of oxygen and deformed oxygen, as demonstrated in Fig. 2. The quadrupole deformation of deformed oxygen can be neglected because the$ \beta_2 $ parameter is too small to make a difference. Using the four-α tetrahedral structure, the$ p_T $ spectrum is slightly enhanced at$ p_T>1 $ GeV. This is also in agreement with the higher charged multiplicity using oxygen with α-clusters than WS and deformed WS distributions.
Figure 4. (color online) Transverse momentum spectra of charged hadrons given by event-by-event hydrodynamic simulations of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV, with nucleons in oxygen sampled from the Woods-Saxon distribution (black-dashed line), deformed Woods-Saxon distribution (red-solid line), and four-α equilateral distribution (black-solid line with dots).The centrality dependence of the
$ p_T $ differential$ v_n $ shown in Fig. 5 indicates that another difference may be used to look for α clusters inside the oxygen nucleus. Comparisons among the WS, deformed WS, and four-α tetrahedron distributions show that the α cluster structure decreases the$ p_T $ differential$ v_2 $ in$ 0-5\% $ and$20\%-30\%$ collisions and the$ p_T $ differential$ v_3 $ in$20\%-30\%$ collisions, but slightly increases$ v_4 $ in$20\%-30\%$ collisions compared with the other two initial nuclear structures without α clusters. A previous study shows that the eccentricity in$ ^{16}\text{O}+{}^{16}\text{O} $ collisions is only weakly dependent on the α clustering structure [66]. The ordering of the$ p_T $ differential$ v_n $ seems to be a better signal than the absolute values of$ v_n $ at different centralities.$ v_3(p_T) $ in$ ^{16}\text{O}+{}^{16}\text{O} $ collisions deceases as the centrality increases from central (0–5%) to peripheral (40%–60%) collisions. This feature is universal for the three different oxygen nuclear configurations and thus cannot be used to detect the α cluster in the oxygen nucleus.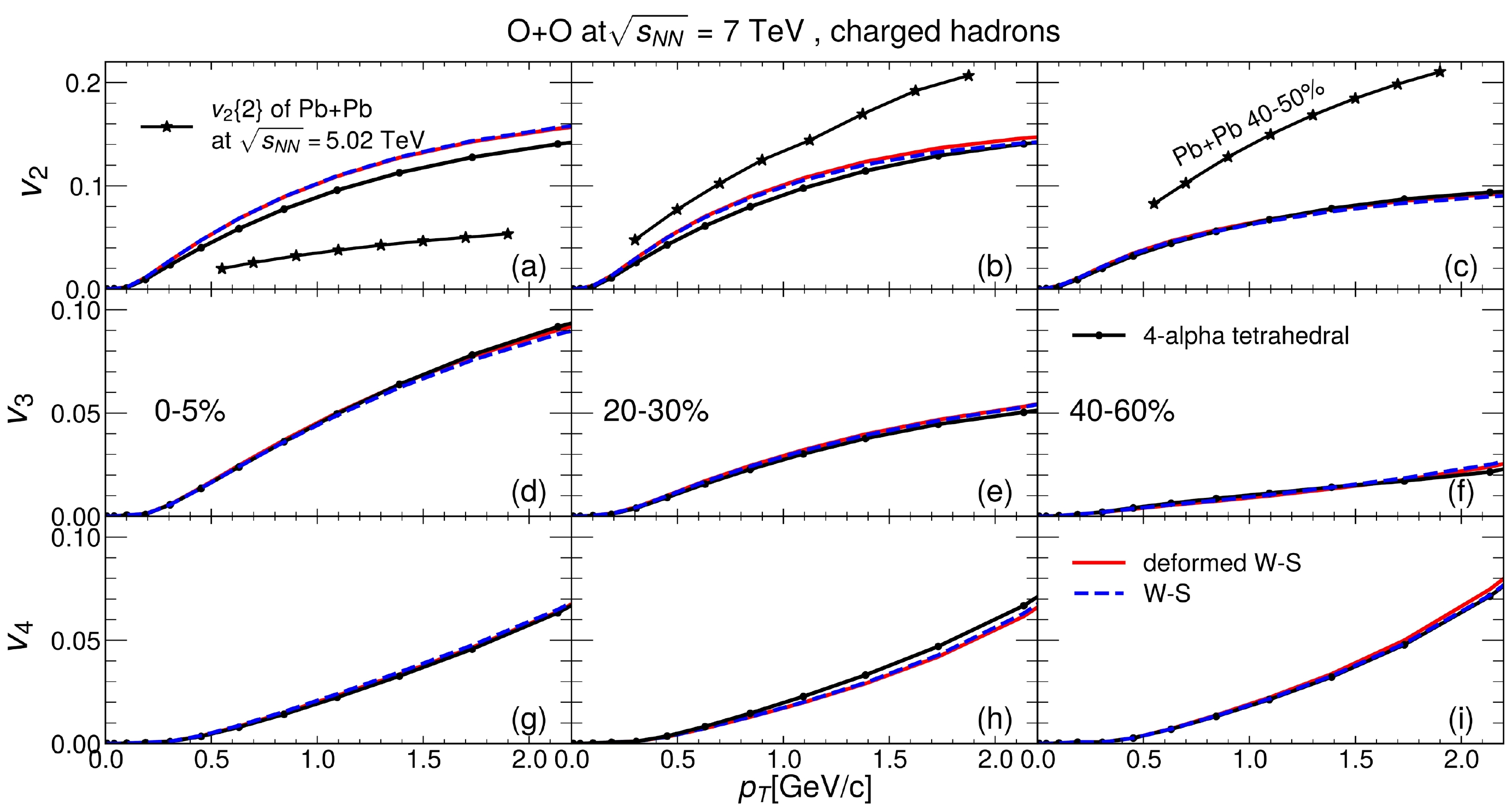
Figure 5. (color online) Anisotropic flow of charged hadrons in the CLVisc simulation of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions at$ \sqrt{s_{NN}}=7 $ TeV with and without the α-cluster structure using the event-plane method.It was observed in Ref. [67] that two-nucleon correlations in oxygen have only a moderate effect, and no significant differences should be expected in a comparison between
$ ^{16}\text{O}+{}^{16}\text{O} $ and Pb+Pb collisions. In another study [22], a system size scan was conducted for the D meson$ v_2\{2\}(p_T) $ using initial conditions + hydrodynamics + the heavy flavor Langevin model. It is argued that the D meson$ v_2\{2\}(p_T) $ is independent of system size because of the competing effects between a larger geometric eccentricity, which will increase$ v_2 $ , and a smaller system size, which will suppress$ v_2 $ , for$ ^{16}\text{O}+{}^{16}\text{O} $ collisions compared with the case of Pb+Pb collisions. A realistic hydrodynamic simulation in the present study shows a considerably larger$ p_T $ differential$ v_2 $ for$ ^{16}\text{O}+{}^{16}\text{O} $ than Pb+Pb collisions in the$ 0-5\% $ centrality because of the dominant large initial eccentricity. The effect of system size can be observed from the centrality dependence of$ v_2(p_T) $ , which decreases with decreasing centrality in$ ^{16}\text{O}+{}^{16}\text{O} $ collisions but increases in Pb+Pb collisions. Our results are supported by the study in [68], which also observes a large$ v_2(p_T) $ at$ 0-5\% ~ {}^{16}\text{O}+{}^{16}\text{O} $ collisions using the AMPT. If this is verified by experimental data in the near future, it may also suggest a considerably larger D meson$ v_2\{2\}(p_T) $ in$ ^{16}\text{O}+{}^{16}\text{O} $ collisions than Pb+Pb collisions if low$ p_T $ D mesons approach local equilibrium [69].Because of larger event-by-event fluctuations in smaller collision systems, as shown in Fig. 6, the initial state eccentricity in
$0-5\% ~ {}^{16}\text{O}+{}^{16}\text{O}$ collisions is considerably larger than that in Pb+Pb collisions. In previous studies [70], the ratio$ v_n/\varepsilon_n $ is typically compared between large and small collision systems, where$ \varepsilon_n $ is the n-th order geometric eccentricity, to eliminate the effect of initial state fluctuations as well as the differences between nuclear structures. This makes sense for the study of the properties of QGP. However, to study the effect of nuclear structure and initial state fluctuations, it is better to compare the$ p_T $ differential$ v_n $ between large and small systems directly. Indeed,$ v_n $ has a strong dependence on the size of the colliding nuclei, as shown in Fig. 5.
Figure 6. (color online) Initial entropy density distributions of
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions and Pb+Pb collisions at a centrality of 0–5%. The entropy density distribution in the transverse plane of a single colliding event for (a) O-O collisions with the Woods-Saxon distribution, (b) O-O collisions with the deformed Woods-Saxon distribution, (c) O-O collisions with the four-α tetrahedral distribution, and (d) Pb-Pb collisions. Sub-figures (e), (f), (g), and (h) are the corresponding averaging entropy density distributions with each event rotated to their participant plane. -
We study
$ ^{16}\text{O}+{}^{16}\text{O} $ collisions using relativistic hydrodynamics with initial conditions given by the Trento Monte Carlo model for three different nucleon distributions inside the oxygen nucleus, i.e., the WS distribution, deformed WS distribution, and four-α tetrahedral structure. We observe that the four-α structure in the oxygen nucleus generates more entropy at the initial state of collisions than the WS and deformed WS distributions. As a result, more charged hadrons are produced at the$ 0-5\% $ most central collisions using the four-α structure than with the other two configurations. The ratios between$ 0-5\% $ and$20\%-30\%$ and between$ 0-5\% $ and$40\%-60\%$ using the four-α structure are smaller than those for the WS and deformed WS distributions by$6\% - 9\%$ . The$ p_T $ differential elliptic flow$ v_2(p_T) $ in$ 0-5\% $ collisions using the four-α structure is also smaller than that for the WS and deformed WS distributions; however,$ v_4(p_T) $ in$20\%-30\%$ collisions is larger than that for the WS and deformed WS distributions. These observations thus provide multiple signals of the α-cluster structure inside the oxygen nucleus. -
LG Pang and C Ding also acknowledge the support provided by Huawei Technologies Co., Ltd.
Signals of α clusters in 16O+16O collisions at the LHC from relativistic hydrodynamic simulations
- Received Date: 2022-08-17
- Available Online: 2023-02-15
Abstract: In relativistic heavy ion collisions, the fluctuations of initial entropy density convert to the correlations of final state hadrons in momentum space through the collective expansion of strongly interacting QCD matter. Using a (3+1)D viscous hydrodynamic program, CLVisc, we consider whether the nuclear structure, which provides initial state fluctuations as well as correlations, can affect the final state of heavy ion collisions, and whether one can find signals of α cluster structures in oxygen using final state observables in





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: