-
The optical model potential (OMP) is a mathematical tool to describe the physical interaction between two composite nuclei. This potential is an effective interaction that only considers the relative coordinates between the two nuclei and freezes the internal degree of freedom inside them [1, 2]. Thus, the elastic scattering (relative coordinates between the projectile and target) and the absorption (internal degree of freedom inside the projectile and target) can be accounted for by the model directly and indirectly, respectively. The uncertainties of the OMP play an important role in nuclear reactions. In principle, the OMP can be obtained from the many-body calculations, such as in the no core shell model in the multiple scattering theory [3] or self-consistent Green’s function theory [4]. However, the numerical calculations of these methods are very difficult, in particular for nucleus-nucleus systems. Therefore, in most cases, the OMPs are deduced from directly fitting the experimental data of the elastic scattering.
Directly fitting from experimental data of a single elastic scattering can bring systematic uncertainties. A simple solution to this is to use the global OMPs, such as CH89 [5], KD02 [6], Madland [7], and Menet [8], which are the nucleon global OMPs, and An [9], Bojowald [10], Daehnick [11], and Han [12], which are deuteron global OMPs. Furthermore, the global OMPs are widely used to study the new phenomena far from the valley of stability for new experiments performed at FRIB [13–15] and HIRFL [16–22]. Theoretically, global phenomenological OMPs are commonly used for nucleon-nucleus systems. These potentials can provide a convenient average description of the overall trend of the interaction as a function of mass and energy and are the only option when the experimental data and a microscopic approach are not available for nuclides. As a result, many sets of global OMPs are widely applied to the relevant reaction models [23–29].
Typically, the OMP has the volume, surface, and spin-orbit coupling terms with the Woods-Saxon form [5, 6]. The global OMPs with different parameter sets can well reproduce the elastic scattering angular distributions within the fitting uncertainties [5–12]. The influence of different global OMPs on the transfer reaction has been discussed in Refs. [30, 31]. Here, we performed a systematic study on the effects of different global OMPs on the same transfer reacion. In addition, Stanley [32] noted that the spin-orbit coupling term typically has little impact on the elastic scattering differential cross sections. In contrast, the analyzing power (
$ A_y $ ) is extremely spin-sensitive [6, 33]. There has not been a thorough discussion of how the spin-orbit coupling term affects the cross section of the transfer process. In addition, ignoring the spin-orbit interaction can make the theoretical calculations much simpler, and in most cases, this term is dropped in calculations [34–36]. Therefore, the influence of the spin-orbit interaction on the (differential) cross section of the transfer reaction is investigated in this study.In this study, to analyze the effects of different global OMPs on the transfer reaction, we consider
$ (d,p) $ transfer reactions on the target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ at different energy levels. Hence, we introduce the$\xi_{\rm s.o.}^{2}$ function (see more details in Sec. II.C) to describe the influence of different global OMPs on the transfer (differential) cross sections. In addition, the effects of the spin-orbit coupling term of different OMPs on the transfer cross sections are also investigated.The paper is organized as follows. Sec. II is dedicated to the theoretical framework of transfer reactions. In Sec. III, we report the scope of application of several representative global OMPs for nucleon and deuteron. In Sec. IV, the effects of different deuteron and nucleon global OMPs and the influences of the spin-orbit interaction on (differential) cross sections of
$ (d,p) $ transfer reactions are systematically investigated. In Sec. V, we summarize the main results of this work. -
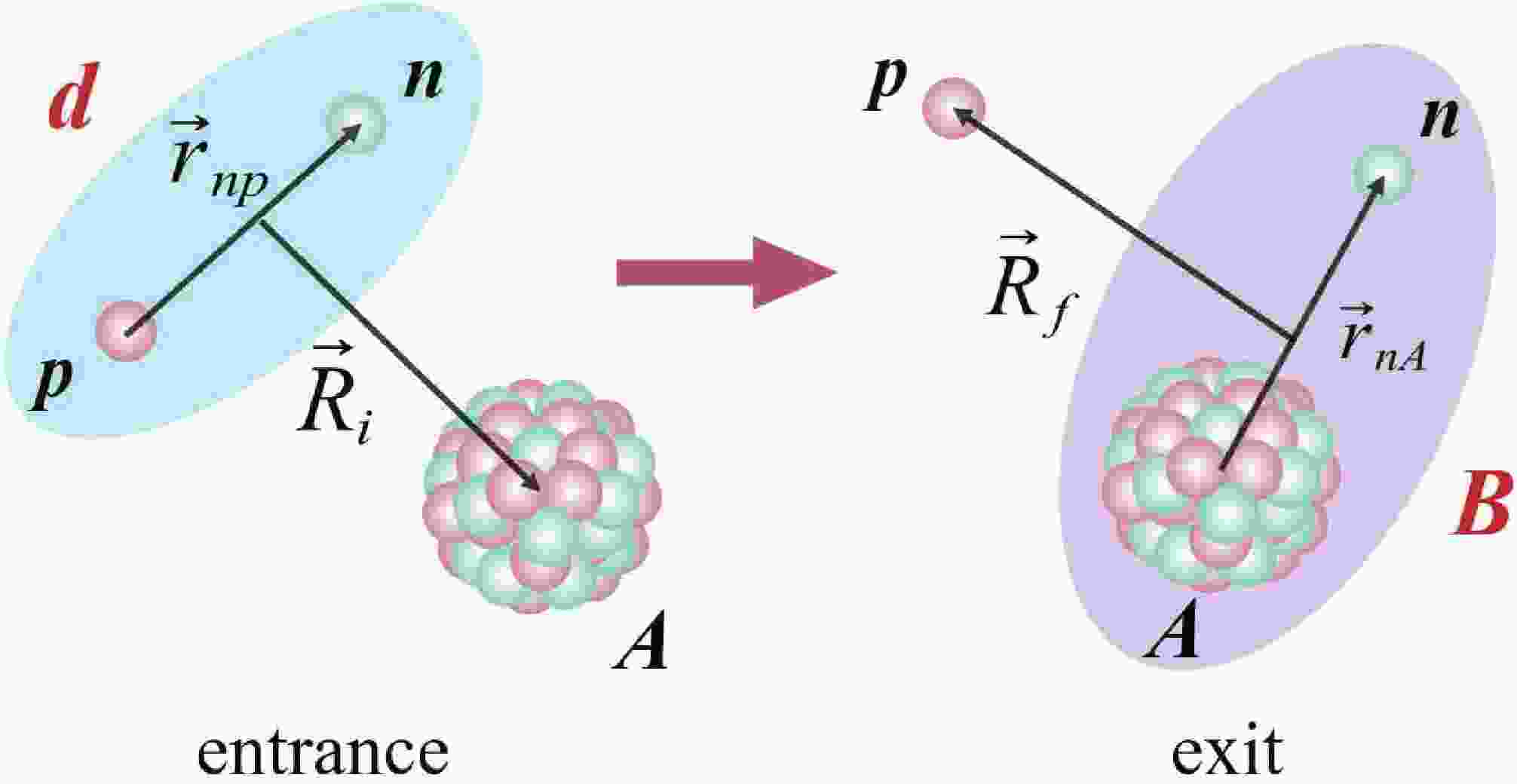
Transfer reactions have been widely used to extract information on the valence orbitals of the nuclei [37]. Consider a transfer process
$ {A(d,\; p)}B $ ,$d+A\to p+B$

(1) where projectile d transfers a neutron onto the target nuclei A, forming a bound state
$ B = A + n $ . The relevant coordinates are displayed in Fig. 1.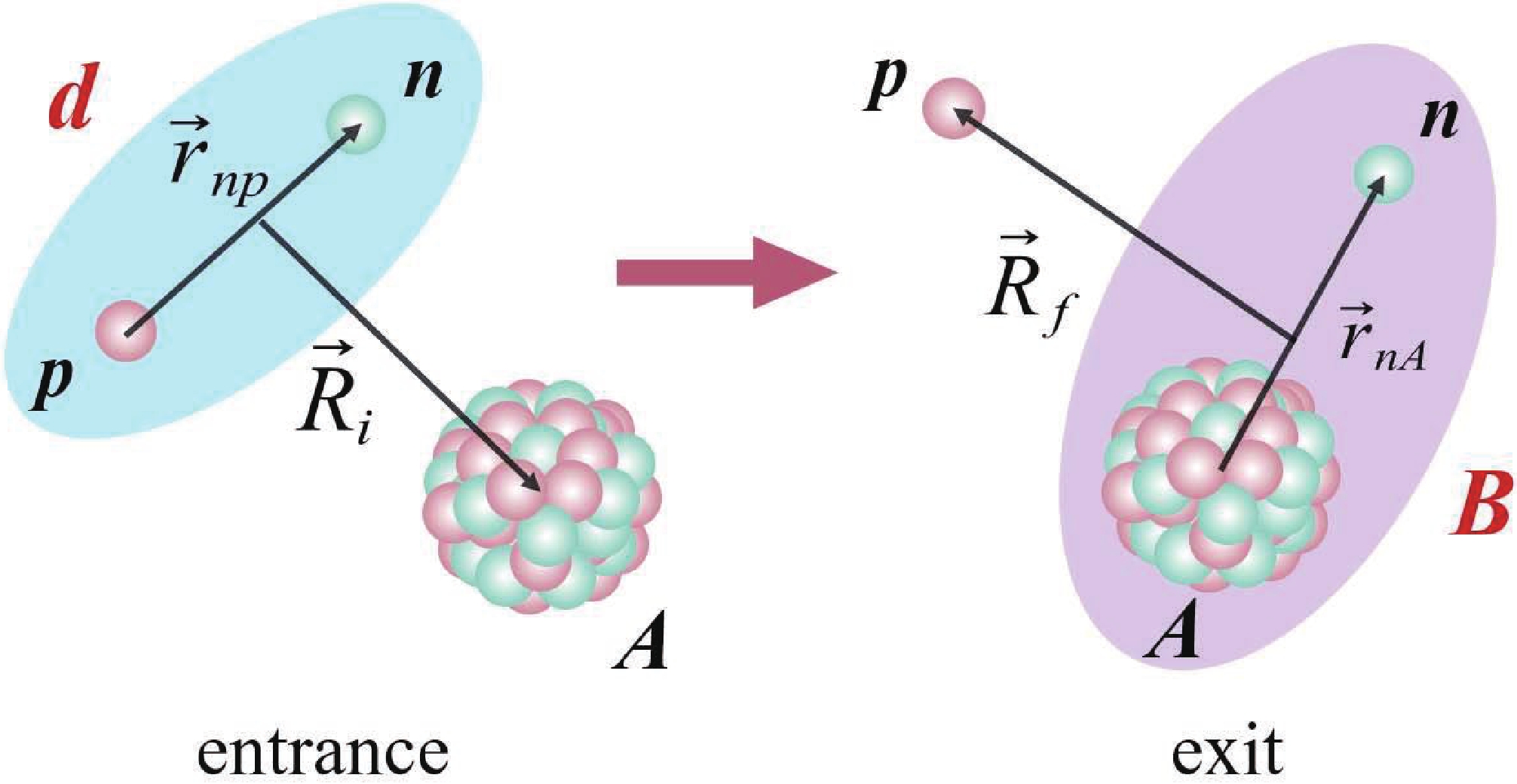
Figure 1. (color online) Coordinates in the entrance and exit partitions for the transfer reaction
$ {A(d, p)}B $ , where$ d = b + p $ and$ B = n + A $ .Transfer cross section is a valid meeting point between theory and experiments, used to describe the reaction rates of nuclear reactions [38]. For
$ (d,p) $ transfer reactions, the differential cross sections for the outgoing protons in the transfer process can be expressed as$ \begin{aligned}[b]\frac{{\rm d} \sigma}{{\rm d} \Omega}=&\frac{m_\alpha m_\beta}{(2 \pi \hbar^2)^2} \frac{k_\beta}{k_\alpha}\frac{1}{(2 J_{d}+1)(2 J_{A}+1)}\\ &\times \sum\limits_{M_{d} M_{A} M_{p} M_{B}} |T^{M_{d} M_{A} M_{p} M_{B}}|^2 \, , \end{aligned}$

(2) where
$ m_\alpha $ and$ m_\beta $ are the reduced mass of the entrance and exit channels, respectively.$ {k_\alpha} $ is the wave number between projectile d and the target nuclei A, and$ {k_\beta} $ is the wave number between the ejected proton p and residual nuclei B. In addition,$ J_{d} $ ,$ J_{A} $ ,$ J_{p} $ and$ J_{B} $ are the spins of the deuterons, target nuclei, outgoing protons, and residual nuclei B, respectively. Furthermore,$ M_d $ ,$ M_A $ ,$ M_p $ and$ M_B $ are the z-axis components of the spins$ J_{d} $ ,$ J_{A} $ ,$ J_{p} $ and$ J_{B} $ , respectively. Finally, T is the T-matrix, which is discussed next.T-matrix can be expanded in either the post or prior form, and the results of the post form equal those of the prior form [39]. For simplicity, we only consider the post form, which can be written as
$ T_{\text {post}}^{M_{d} M_{A} M_{p} M_{B}}=\langle\Phi_{n A}^{M_A}\chi_{p B}^{(-) M_B M_p}|{\cal{V}}| \Psi^{(+)M_A M_d}\rangle, $

(3) with
$ {\cal{V}}=V_{n p}+U_{p A}-U_{p B} $ , where$ V_{np} $ stands for the potential binding bound state of the deuteron in the entrance channels. U stands for the optical potential, which generates the corresponding scattering wave function$ {\rm{\chi}}^{(+)} $ . Here,$ U_{pA} $ stands for the optical potential between the proton and target nuclei A.$ U_{pB} $ denotes the optical potential between the proton and residual nuclei B. Moreover,$ {\rm{\Phi}}_{nA} $ is the bound state wave function between the transferred neutron and target nuclei A, and$ {\rm{\Psi}}^{(+)} $ represent the scattering wave functions in the entrance channels.DWBA (Distorted Wave Born Approximation) [43, 44] method is the most widely used and simple tool to analyze the
$ (d,\; p) $ transfer reaction. However, the DWBA method does not treat the three body problem exactly. This can be done with the CDCC (Continuum Discretized Coupled Channel) [40] and ADWA (Adiabatic Wave Approximation) [41, 42] method, which treats the breakup effect of the deuteron effectively by simply replacing the deuteron-target potential with the proton- and neutron-target potential evaluated at the half incident energies. For the purpose of current study, we consider using the DWBA is sufficient. The DWBA theory, which has been widely used to extract spectroscopic factors from the experimental data [45–48], involves replacing the exact solution$ \Psi^{(+)} $ of a three body problem by a scattering state multiplying a corresponding bound state, i.e.,$\Psi^{(+)} \approx \phi_{d} \chi_{d A}^{(+)}$ . Then, the post form of the T-matrix for the transfer process can be expressed as$ T_{\rm post}^{\text{DWBA}(M_{{ {d}}} M_{{ {A}}} M_{{ {p}}} M_{{ {B}}})}= \langle\Phi_{n A}^{M_A} \chi_{p B}^{(-) M_B M_p}|{\cal{V}}|\phi_{d}^{M_d} \chi_{d A}^{(+) M_A M_d}\rangle. $

(4) -
In most cases, we assume the optical potential is local and characterized by its real and imaginary parts, which can be written as
$ U(r)=V(r)+{\rm i} W(r). $

(5) Generally, we assume the optical potential consists of the volume terms, surface terms, and spin-orbit coupling terms with the Woods-Saxon form. For example, the general form of the optical potential is as follows:
$ \begin{aligned}[b] U(r)=&-V_{r} f_{{\rm{ws}}}(r, r_{v}, a_{v})-{\rm i} W_{{\rm{v}}} f_{{\rm{ws}}}(r, r_{{\rm{w}}}, a_{{\rm{w}}})\\ & +4{\rm i} W_{{\rm{s}}} a_{{\rm{w}}} \frac{{\rm{d}}}{{\rm{d}} r} f_{{\rm{ws}}}(r, r_{{\rm{w}}}, a_{{\rm{w}}})+V_{\rm C}(r) \\ & +2(V_{{\rm{so}}}+{\rm i} W_{{\rm{so}}}) \frac{1}{r} \frac{{\rm{d}}}{{\rm{d}} r} f_{{\rm{ws}}}(r, r_{{\rm{so}}}, a_{{\rm{so}}}) l \cdot \sigma \end{aligned} ,$

(6) with the Woods-Saxon form factor
$ f_{{\rm{ws}}} $ can be expressed as$ f_{{\rm{ws}}}(r, r_0, a) = \frac{1}{1+\exp[(r-R_0)/a]}, $

(7) where
$ R_0=r_{0}(A_{P}^{1/3}+A_{T}^{1/3}) $ is the radius of the nuclear potential.$ A_P $ and$ A_T $ are the mass numbers of the projectile and target nuclei, respectively. The parameter$ r_{0} $ is the single particle radius and a denotes the diffuseness.$ V_{r} $ and$ W_{v} $ are the depth factors of the real and imaginary parts of the volume term, respectively.$ W_{s} $ is the depth factor of the imaginary part of the surface term.$V_{\rm so}$ and$W_{\rm so}$ are the depth factors of the real and imaginary parts of the spin-orbit coupling potential, respectively.$V_{\rm C}$ is the Coulomb potential, which can be written as follows:$ V_{\rm C}(r)= \left\{ {\begin{array}{*{20}{l}} {\dfrac{Z_{P} Z_{T} e^{2}}{r},}&{r \geq R_{\rm C}}\\ {\dfrac{Z_{P} Z_{T} e^{2}}{2 R_{\rm C}}\left(3-\dfrac{r^{2}}{R_{\rm C}^{2}}\right),}&{r < R_{\rm C}} \end{array}} \right. ,$

(8) where
$ Z_{P} $ and$ Z_{T} $ are the charge numbers of deuteron and the target nuclei, respectively.$R_{\rm C}$ is a free parameter that describes the Coulomb radius. -
The global OMPs parameters are determined based on the standard criterion of the minimum deviation between the results of the optical model calculations and experimental data [49, 50]. For instance, many optimization procedures obtain its parameters via minimizing the
$ \chi^{2}/N $ value [6, 26, 51], and its definition can be written as follows [52].$ \chi^{2}/N = \sum\limits_{i=1}^P \left(\frac{\sigma_i^{\rm{th}}-\sigma_i^{\exp}}{\Delta \sigma_i}\right)^2 ,$

(9) where
$ N = P - F $ is the number of degrees of freedom, with P the number of the experimental data points and F the number of freely varying parameters.$ \sigma_{i}^{\exp} $ and$\sigma_{i}^{\rm th}$ are the ith experimental and theoretical cross sections, respectively.$ \Delta \sigma_i $ is the uncertainty of the experimental cross sections.In Refs. [5–12], there are many sets of the global OMPs, and most of them are usually obtained from the experimental data fitting of specific energies and target nuclei. The global optical potential can describe the corresponding elastic scattering effectively. However, the variations between these global OMPs for the same three body observable, such as the transfer cross section, have not been studied yet.
In addition, disregarding the spin-orbit interaction can greatly simplify the theoretical computations, and this factor is neglected in most cases. Meanwhile, the spin-orbit coupling potential is usually spin-dependent. Elastic scattering observables, such as differential cross sections, are not sensitive to the spin-orbit coupling term [32], whereas the analyzing powers (
$ A_y $ ) is quite sensitive to the spin-orbit coupling potential [6]. Therefore, the effects of the spin-orbit coupling term on the three body observables, such as the transfer cross sections, still need to be studied.In this paper, we investigate the sensitivity of the spin-orbital potentials in the
$ (d,p) $ transfer reactions. For this analysis, similar to the analysis of$ \chi^{2}/N $ , herein we define the$\xi^{^{2}}_{\rm s.o.}$ function to describe the difference between different theoretical values. In detail, the value of$\xi^{^{2}}_{\rm s.o.}$ represents the deviation of the calculated (differential) cross section and scattering wave function with and without the spin-orbit coupling potential, which can be expressed as$ \xi^{^{2}}_{\rm s.o.}=\frac{1}{M} \sum\limits_{i=1}^{M} \left(\frac{C^{\rm s.o.}_{i} - C_{i}}{ \Delta C_{i}}\right)^{2} , $

(10) where
$C^{\rm s.o.}_{i}$ and$ C_{i} $ are the (differential) cross sections when the spin-orbit coupling potential is taken into account and neglected, respectively. We take 10% of$ C_{i} $ to be$ \Delta C_{i} $ . M is the number of differential cross section points to be considered. When the value of$\xi^{^{2}}_{\rm s.o.}$ approaches$ 0 $ , it can be demonstrated that the spin-orbit coupling term has little effect on the (differential) cross section. On the contrary, if the value of$\xi^{^{2}}_{\rm s.o.}$ is much larger than$ 0 $ , it can be shown that the spin-orbit coupling term has considerable influences on the (differential) cross section. -
To study the effects of different global OMPs on the (differential) cross section of the transfer reaction, we investigate the
$ (d,p) $ transfer reactions on the target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ and$ ^{208}{\rm{Pb}} $ with different global OMPs at different energies. For this analysis, we list some representative global OMPs for nucleons and deuterons, which is explained in detail in the following.For the global OMPs of neucleons, VARNER et al. [5] developed the CH89 parametrization of the nucleon-nucleus optical model potential appropriate to the target-nucleus mass range from
$ ^{40}{\rm{Ca}} $ to$ ^{209}{\rm{Bi}} $ and the proton laboratory energy range from 16 to 65 MeV. Koning and Delaroche [6] presented the optical model potentials for the incident neutrons and protons with energies from 1 keV up to 200 MeV, and for nuclei with masses ranging from$ ^{24}{\rm{Mg}} $ to$ ^{209}{\rm{Bi}} $ . Madland [7] addressed an energy range of 50 MeV to 400 MeV and a target mass range from$ ^{12}{\rm{C}} $ to$ ^{208}{\rm{Pb}} $ . Menet et al. [8] proposed a set of global optical potential parameters for protons, which are available for nuclei ranging from nuclei$ ^{12}{\rm{C}} $ to$ ^{208}{\rm{Pb}} $ with the incoming proton energy from 30 MeV to 60 MeV.For the global OMPs of deuterons, An et al. [9] proposed a set of global optical potential parameters for deuterons that are available for nuclear model calculations up to 183 MeV and for the target nuclei ranging from
$ ^{12}{\rm{C}} $ to$ ^{238}{\rm{U}}$ . Bojowald et al. [10] derived a set of global optical potential parameters that are suitable for nuclei with masses ranging from$ ^{12}{\rm{C}} $ to$ ^{208}{\rm{Pb}} $ and the incoming energies from 52 MeV to 85 MeV. Daehnick et al. [11] developed a set of global optical potentials for deuterons that covers the energy range from 11.8 MeV to 90 MeV and includes many targets ranging in mass from$ ^{27}{\rm{Al}} $ to$ ^{238}{\rm{Th}} $ . Han et al. [12] presented a set of global phenomenological optical model potential parameters for deuterons on nuclei with masses ranging from$ ^{12}{\rm{C}} $ to$ ^{209}{\rm{Bi}} $ and the incident energies from 0 MeV up to 200 MeV.In summary, these nucleon and deuteron global OMPs above and their scope of application are shown in Tables 1 and 2. All transfer (differential) cross sections are calculated using the code FRESCO [53].
Table 1. Scope of application of the nucleon global OMPs (the first column lists four sets of nucleon global OMPs, the second column denotes the applicable scope of the target nuclei, and the third column represents the applicable energy ranges for protons).
-
In this section, we report the results of the effects of deuteron and nucleon global OMPs on (differential) cross sections of the
$ (d,p) $ transfer reactions on target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ and$ ^{208}{\rm{Pb}} $ at different energies. To begin with, we analyse the changes in the angular distributions for the elastic scattering caused by different choices of the deuteron and nucleon global OMPs. Then, we study the influences of different deuteron global OMPs on the differential cross sections of the$ (d,p) $ transfer reactions on different target nuclei. In addition, we investigate the effects of the spin-orbit coupling term of deuteron global OMPs on the transfer cross-section angular distributions and scattering wave functions in the entrance channels. Moreover, the$\xi^{2}_{\rm s.o.}$ function is applied to represent the influences of the spin-orbit coupling potential on the (differential) cross sections and scattering wave functions. Furthermore, we discuss the effects of different deuteron and nucleon global OMPs on the cross sections of the$ (d,p) $ transfer reaction on different target nuclei at different energies. Finally, the influences of the spin-orbit coupling term of deuteron and nucleon global OMPs on the transfer cross sections are systematically studied. -
In this section, we analyze the changes in the angular distributions for the elastic scattering of deuterons and different target nuclei caused by different choices of the deuteron global OMPs. We calculate the angular distributions for the elastic scattering of deuterons and different target nuclei
$ ^{40}{\rm{Ca}} $ ,$ ^{90}{\rm{Zr}} $ ,$ ^{118}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ . We use deuteron potentials listed in Table 2 as the potential I - IV in the calculations of the elastic scattering angular distribution, and the theoretical results are shown in Fig. 2. Figure 2(a)–(d) represent the results of the target nuclei$ ^{40}{\rm{Ca}} $ ,$ ^{90}{\rm{Zr}} $ ,$ ^{118}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ , respectively. The incident deuteron energy is$ 56.0 $ MeV. The black solid line, red dashed line, blue dash-dotted line, and green densely dash-dot-dotted line represent the computational results of potentials I - IV, respectively. The yellow solid circles represent the experimental data cited from Ref. [54].
Figure 2. (color online) Angular distributions of the elastic scattering of deuteron and different target nuclei with subfigures (a)–(d) representing the results of the target nuclei
$ ^{40}{\rm{Ca}}$ ,$ ^{90}{\rm{Zr}}$ ,$ ^{118}{\rm{Sn}}$ , and$ ^{208}{\rm{Pb}}$ , respectively. The incident deuteron energy is 56.0 MeV. The black solid line, red dashed line, blue dash-dotted line, and green densely dash-dot-dotted line represent the computational results of potentials I - IV, respectively. The yellow solid circles represent the experimental data cited from Ref. [54].As we can see in Fig. 2, the theoretical results of the angular distributions of the elastic scattering, produced by different deuteron potential sets, are in good agreement with the experimental data except for potential II. Specifically, the computational results corresponding to potentials I - IV can effectively reproduce the experimental data at small angles. However, the elastic angular distributions corresponding to potential II are smaller than those in the experimental data at large angles.
We also report the changes in the angular distributions for the elastic scattering of protons and different target nuclei caused by different choices of the nucleon global OMPs. We calculate the angular distributions for the elastic scattering of protons and different target nuclei
$ ^{40}{\rm{Ca}} $ ,$ ^{90}{\rm{Zr}} $ ,$ ^{118}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ . We use deuteron potentials listed in Table 1 as the potentials I - IV in the calculations of the elastic scattering angular distributions, and the theoretical results are shown in Fig. 3. Figure 3(a)–(d) represent the results when the proton energies are 51.9, 57.5, 55.0, and 55.0 MeV for the target nuclei$ ^{40}{\rm{Ca}} $ ,$ ^{90}{\rm{Zr}} $ ,$ ^{118}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ , respectively. The yellow solid circles represent the experimental data cited from Refs. [55, 56].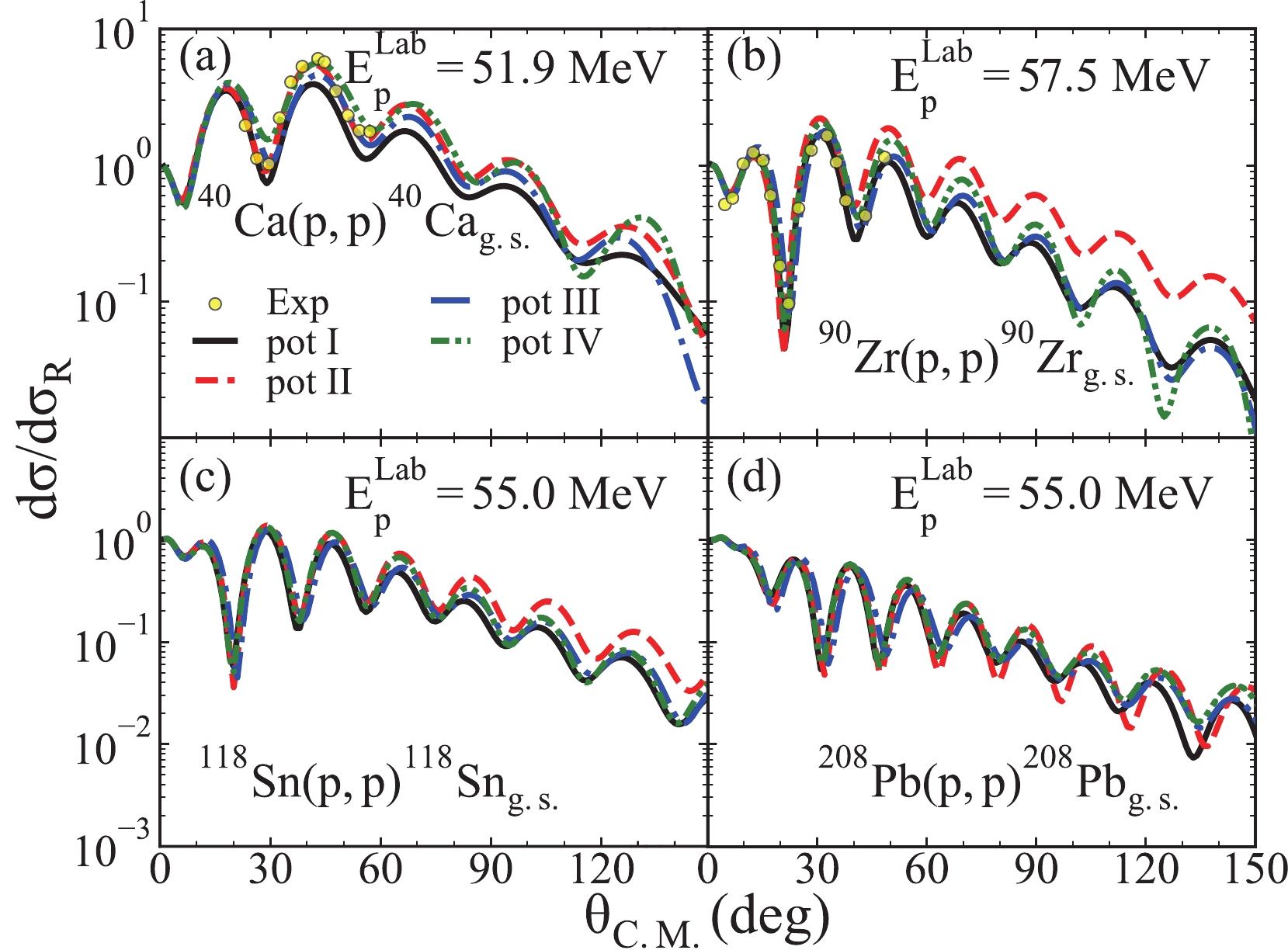
Figure 3. (color online) Similar to Fig. 2 but for protons and different target nuclei. The proton energies are 51.9, 57.5, 55.0, and 55.0 MeV for the target nuclei
$ ^{40}{\rm{Ca}}$ ,$ ^{90}{\rm{Zr}}$ ,$ ^{118}{\rm{Sn}}$ , and$ ^{208}{\rm{Pb}}$ , respectively. The experimental data are cited from Refs. [55, 56].As shown in Fig. 3, the theoretical results of the elastic angular distributions, produced by different sets of nucleon global OMPs, are in good agreement with the experimental data for all energies and target nuclei. Specifically, in Fig. 3 (a) and (b), the elastic angular distributions produced by different potentials can effectively reproduce the experimental data, and the results of different potentials are similar to one another at small angles. In Fig. 3(c) and (d), the theoretical results of different sets of nucleon global OMP are similar to one another. These results show that the global OMPs with different parameter sets can effectively reproduce the elastic scattering angular distributions.
-
In this part, we will report the effects of different deuteron global OMPs on the cross-section angular distributions of the
$ (d,p) $ transfer reactions on the target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ and$ ^{208}{\rm{Pb}} $ . As listed in Table 3, we use the potential sets I - IV in the calculations of differential cross sections. According to Refs. [57–60], the binding potential between the transferred neutron and target nuclei has the typical Woods-Saxon form with the standard parameters (radius$ r_0 = 1.25 $ fm and diffuseness$ a = 0.65 $ fm) and the depth adjusted to reproduce the experimental binding energies. For that calculation, we assume the$ ^{13}{\rm{C}}_{\rm{g.s.}} $ is the$ ^{12}{\rm{C}} $ core plus a neutron staying in the$ 1p_{1/2} $ orbit with the binding energy of 4.946 MeV. The inner potential of the deuteron is taken as a Gaussian potential with$ a = 1.484 $ fm, and the depth$ V = 72.14 $ MeV. For the purpose of systematic research and comparison with the experimental data, it is common to use systematic potentials in situations where the energy of the deuteron and proton falls beyond the scope of the corresponding global OMPs.Table 3. Summary of the potential parameters used in calculations. The first column denotes the potential sets used in the computations. The second column lists the four sets of global OMPs for deuteron d and target nuclei A. The third column represents the optical potential between proton p and residual nuclei B. The fourth column denotes the optical potential between proton p and target nuclei A.
Firstly, we analyze the cross-section angular distributions of the transfer reaction
$ ^{12}{\rm{C}}({d,\; p})^{13}\rm C_{g.s.} $ produced by different sets of the global OMPs. For this analysis, we compute the differential cross sections at 4.5, 11.8, 15.0, and 19.6 MeV, and we find the same effects for all energies. For simplicity, we only display the results when the deuteron energy is 11.8 MeV in Fig. 4. The black solid line, red dashed line, blue dash-dotted line, and green densely dash-dot-dotted line represent the computational results of the potential sets I - IV, respectively. The pink shaded area represents the difference in the angular distributions between different sets of the global OMPs. The yellow solid circles represent the experimental data cited from Ref. [61], and the spectroscopic factors are cited from Ref. [62].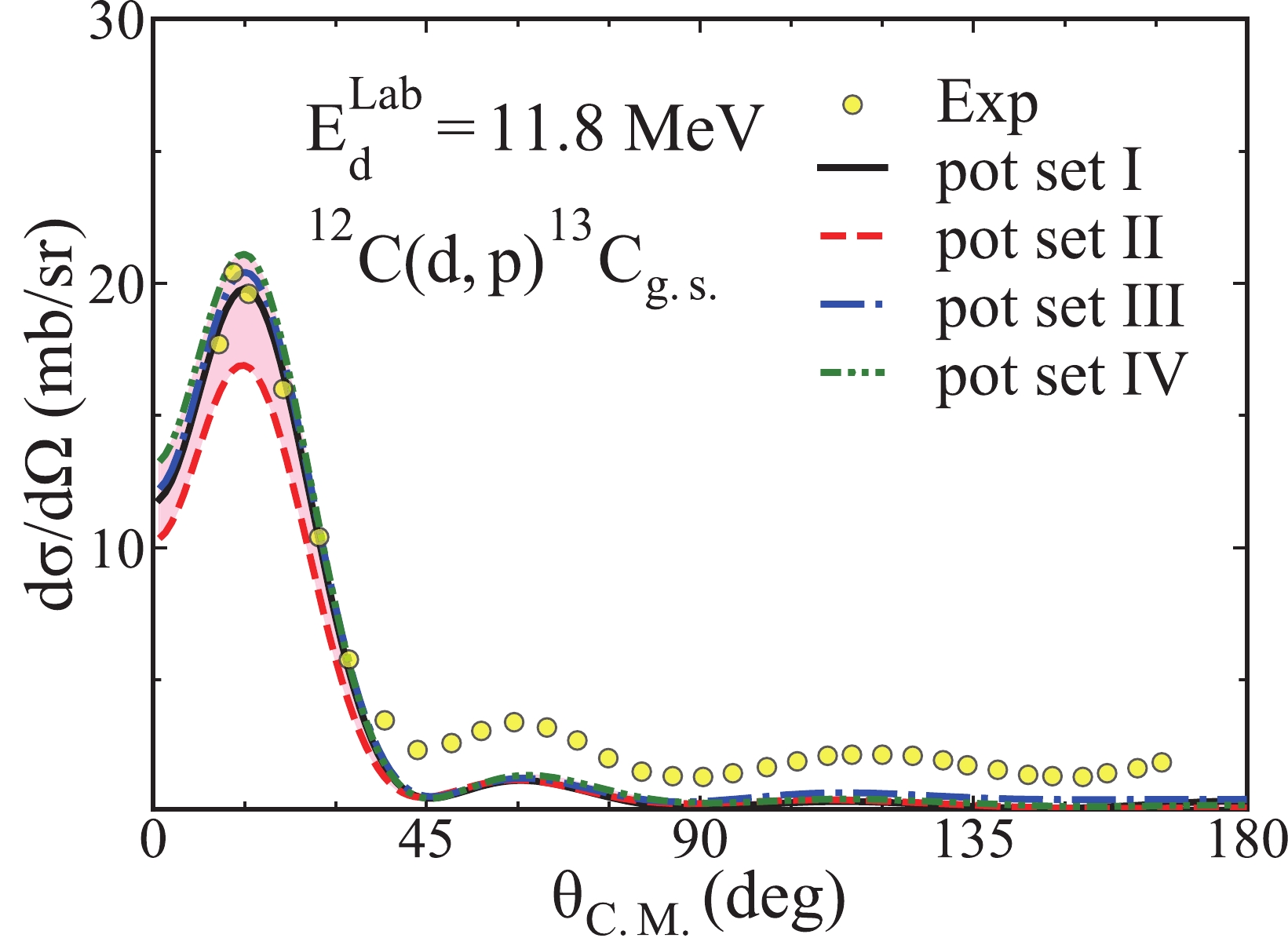
Figure 4. (color online) Cross-section angular distributions of
$^{12}{\rm{C}}({d,\; p})^{13}\rm C_{g.s.}$ calculated based on different sets of global OMPs when the deuteron energy is 11.8 MeV. The black solid line, the red dashed line, the blue dashdotted line and the green densely dashdotdotted line represent the computational results of potential sets I - IV, respectively. The pink shaded area represents the difference in angular distributions between different sets of global OMPs. The yellow solid circles represent the experimental data cited from Ref. [61], and the spectroscopic factors are cited from Ref. [62].As we can see in Fig. 4, the differential cross sections of the
$ (d,p) $ transfer reactions on the target nuclei$ ^{12}{\rm{C}} $ , using different potential sets, are in good agreement with the experimental data in the area smaller than 40 degrees, except for the results obtained using the potential set II. It shows that the cross-section angular distribution produced by the potential set II is smaller than that of the experimental data and results of other sets of global OMPs. However, in the area larger than 40 degrees, the calculation results of the potential sets I - IV do not correspond well with the experimental data. One can note that there are considerable deviations between the cross-section angular distributions produced by different sets of the global potentials, especially in the small-angle area. Meanwhile, at small angles, the theoretical results of the potential sets I, III, and IV are similar to one another. Specifically, in the area less than 40 degrees, the potential set IV produces the largest differential cross sections, whereas the potential set II produces the smallest differential cross sections.We also study the effects of different sets of the deuteron global OMPs on the cross-section angular distributions of the transfer reaction
$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ . For this analysis, we use the potential sets I - IV in the calculations of the differential cross sections. Additionally, we assume the$ ^{49}{\rm{Ca}}_{\rm{g.s.}} $ is the$ ^{48}{\rm{Ca}} $ core plus a neutron staying in the$ 2p_{3/2} $ orbit with a binding energy of 5.146 MeV. We compute the differential cross sections at 11.9, 15.0, 19.3, and 25.0 MeV, and we find the same conclusion for all energies. For simplicity, we only display the results when the deuteron energy is 19.3 MeV in Fig. 5.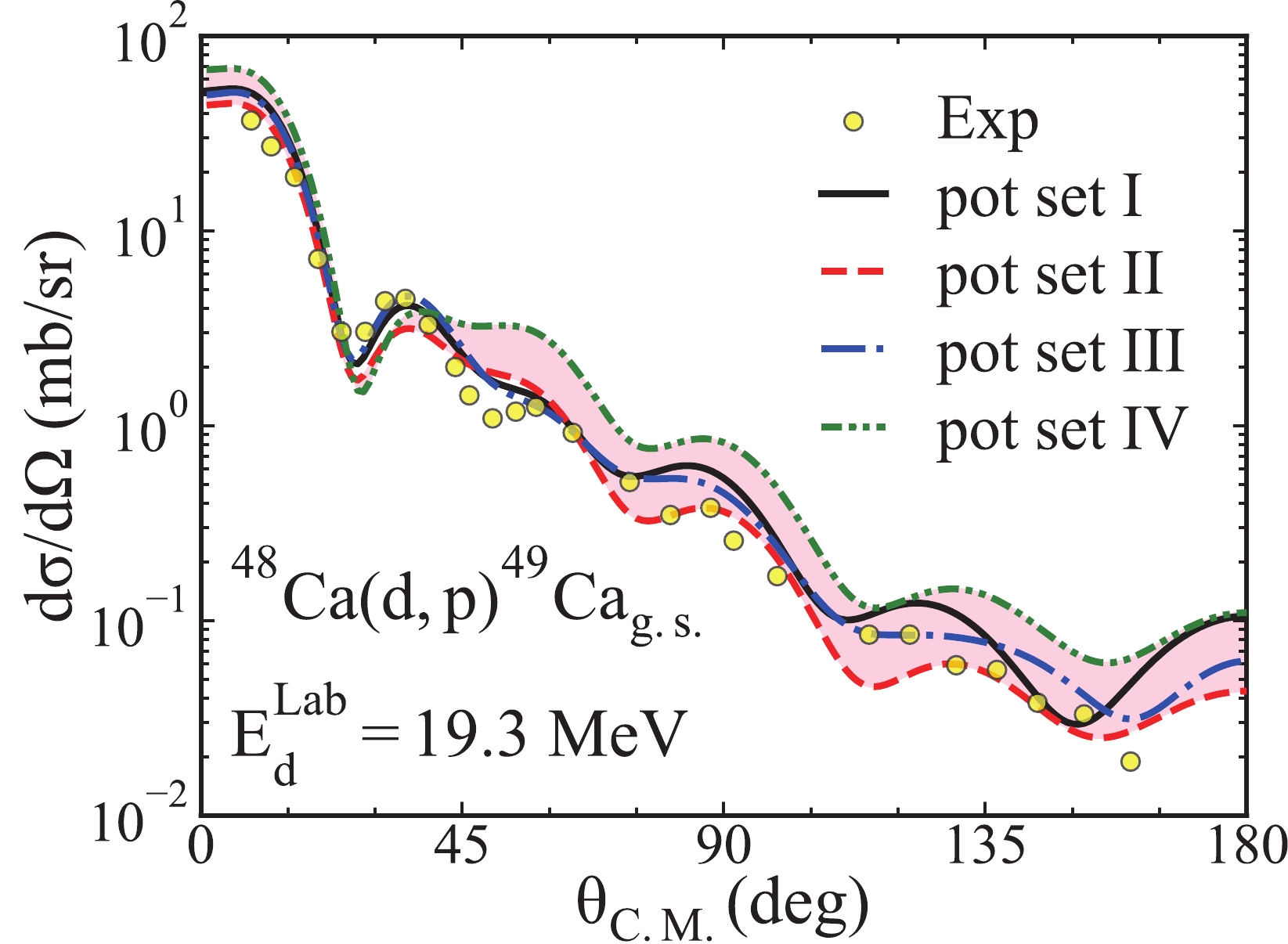
Figure 5. (color online) Similar to Fig. 4 but for the transfer reaction
$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ and the incoming deuteron energies. The experimental data and the spectroscopic factors are cited from Ref. [58].As shown in Fig. 5, the theoretical results of the potential sets I - III can effectively reproduce the experimental data in an area smaller than 160 degrees. Although the computational results of the potential set IV are in good agreement with the experimental data in the small-angle area, the differential cross sections are larger than those in the experimental data in the area larger than 40 degrees. One can note that the theoretical results of different sets of potentials are similar to one another in the small-angle area. But there are considerable deviations between the cross-section angular distributions produced by different potential sets in the area above approximately 40 degrees. In detail, the transfer cross-section angular distribution calculated based on the potential set II is the smallest among those from the four sets of the potential results. On the contrary, the potential set IV produces the largest differential cross sections in the area larger than 40 degrees.
Moreover, the cross-section angular distributions of the
$ (d,p) $ transfer reaction on the medium-mass nuclei$ ^{124}{\rm{Sn}} $ are reanalyzed in the same way. For this analysis, we use the potential sets I - IV in the calculation of different cross sections. Additionally, we assume the$ ^{125}{\rm{Sn}}_{\rm{g.s.}} $ is the$ ^{124}{\rm{Sn}} $ core plus a neutron staying in the$ 1h_{11/2} $ orbit with a binding energy of 5.733 MeV. We compute the differential cross sections at 22.0, 26.8, 33.5, and 40.2 MeV, and we find the same effects for all energies. Thus, for simplicity, we only display the results when the deuteron energy is 22.0 MeV in Fig. 6.
Figure 6. (color online) Similar to Fig. 4 but for the transfer reaction
$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ and the incoming deuteron energies. The experimental data and the spectroscopic factors are cited from Ref. [63].As we can see from Fig. 6, the theoretical results of the potential sets I - IV can effectively reproduce the experimental data for areas between 20 and 45 degrees. To be specific, the computational results of the potential set I are the most similar to the experimental data for areas between 20 and 45 degrees. However, there are considerable deviations between the theoretical results and the experimental data in the area smaller than 20 degrees. In addition, the theoretical results show that the cross-section angular distributions computed by the potential sets I - IV differ significantly from each other, especially in areas larger than 40 and smaller than 20 degrees. Specifically, the potential set III produces the largest differential cross sections in an area smaller than 10 degrees but generates the smallest transfer cross section in an area greater than 45 degrees. The potential set IV produces the largest differential cross section in the area greater than 40 degrees.
Furthermore, we investigate the effects of different deuteron global OMPs on the cross-section angular distributions of the
$ (d,p) $ transfer reaction on the heavy target$ ^{208}{\rm{Pb}} $ . For this calcualtion, we use the potential sets I - IV in the calculation of the differential cross sections. We assume that$^{209}{\rm{Pb}}_{\rm g.s.}$ is the$ ^{208}{\rm{Pb}} $ core plus a neutron staying in the$ 2g_{9/2} $ orbit with the binding energy of 3.937 MeV. We calculate the differential cross sections at 22.0, 30.5, 40.6, and 50.7 MeV, and we find the same conclusion for all energies. For simplicity, we only show the results when the deuteron energy is 22.0 MeV in Fig. 7.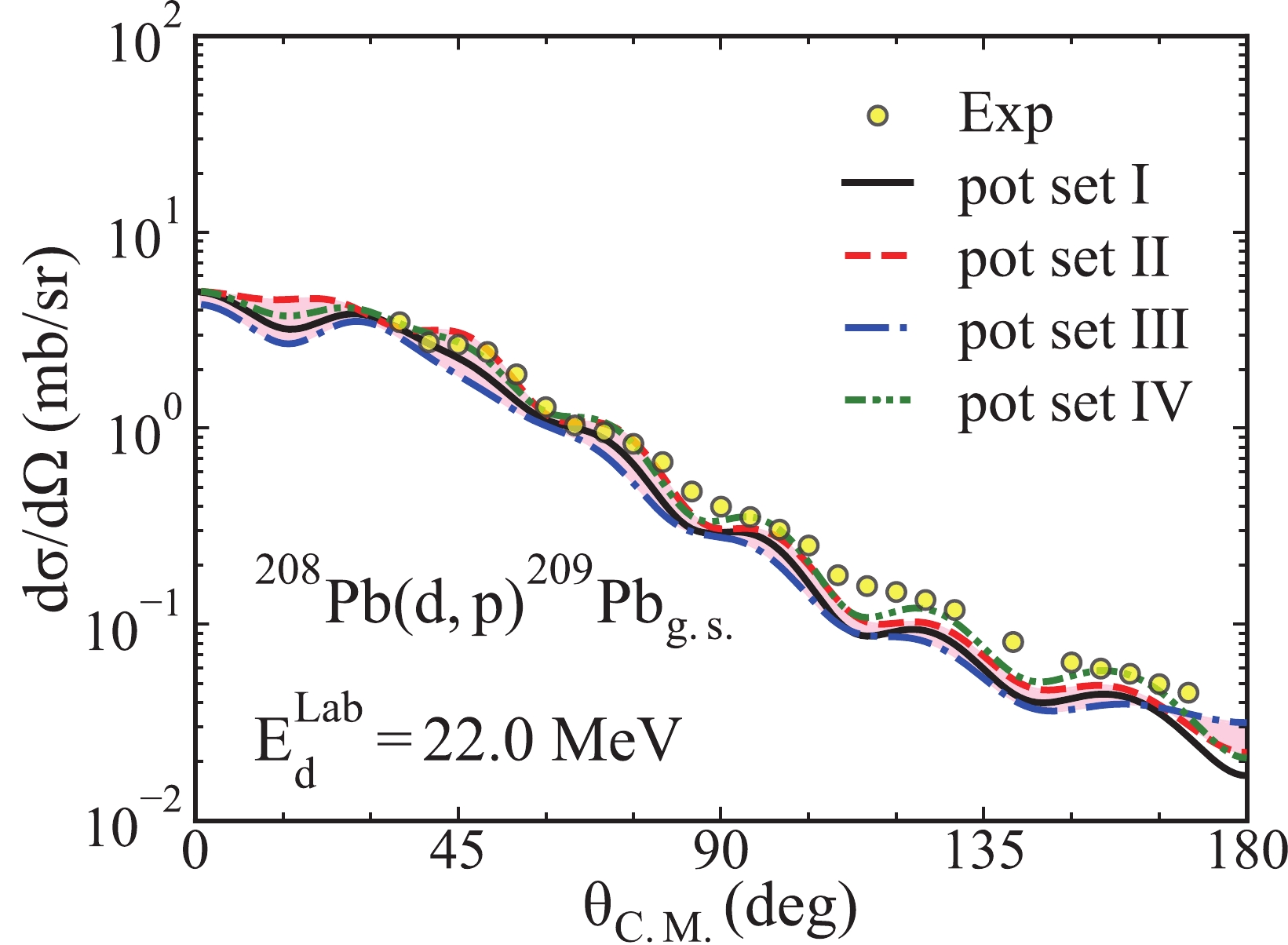
Figure 7. (color online) Similar to Fig. 4 but for the transfer reaction
$^{208}{\rm{Pb}}({d,\; p})^{209}\rm Pb_{g.s.}$ and the incoming deuteron energies. The experimental data and the spectroscopic factors are cited from Ref. [64].We can observe from Fig. 7 that the transfer cross-section angular distributions produced by different sets of the deuteron global OMPs show good agreement with the experimental data. The computational result of the potential set IV can best reproduce the experimental data in an area larger than 40 degrees. Additionally, the cross-section angular distributions produced by different sets of the global OMPs are rather similar to one another. Specifically, the potential set II produces the largest differential cross section in the area smaller than 60 degrees. Furthermore, in the area greater than 60 degrees, the potential set IV results in the largest cross-section angular distribution. Moreover, the potential set III computes the smallest differential cross sections except for the area greater than 165 degrees.
-
In this section, we investigate the sensitivity of spin in the
$ (d,p) $ transfer reactions on the target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ and$ ^{208}{\rm{Pb}} $ . Herein, the effects of the spin-orbit coupling term of the deuteron global OMPs on the differential cross section have been systematically analyzed. For this analysis, the$\xi^{^{2}}_{\rm s.o.}$ function is applied to describe the difference between different theoretical values.For that purpose, we first consider the
$ (d,p) $ transfer reaction on the target nuclei$ ^{12}{\rm{C}} $ with different sets of deuteron global OMPs. Specifically, we use the potential sets I - IV and the same binding potentials from the previous discussion in the calculations of differential cross sections. Additionally, we compute the differential cross sections at 4.5, 11.8, 15.0, and 19.6 MeV and find the same effects for all energies. For simplicity, we only present results when the deuteron energy is 11.8 MeV in Fig. 8. In detail, Fig. 8 (a)–(d) represent the computational results of the potential sets I - IV, respectively. The black solid line and red dashed line represent the angular distributions when the spin-orbit coupling term of the deuteron global OMPs is accounted for and neglected, respectively. The yellow solid circles represent the experimental data cited from Ref. [61], and the spectroscopic factors are cited from Ref. [62].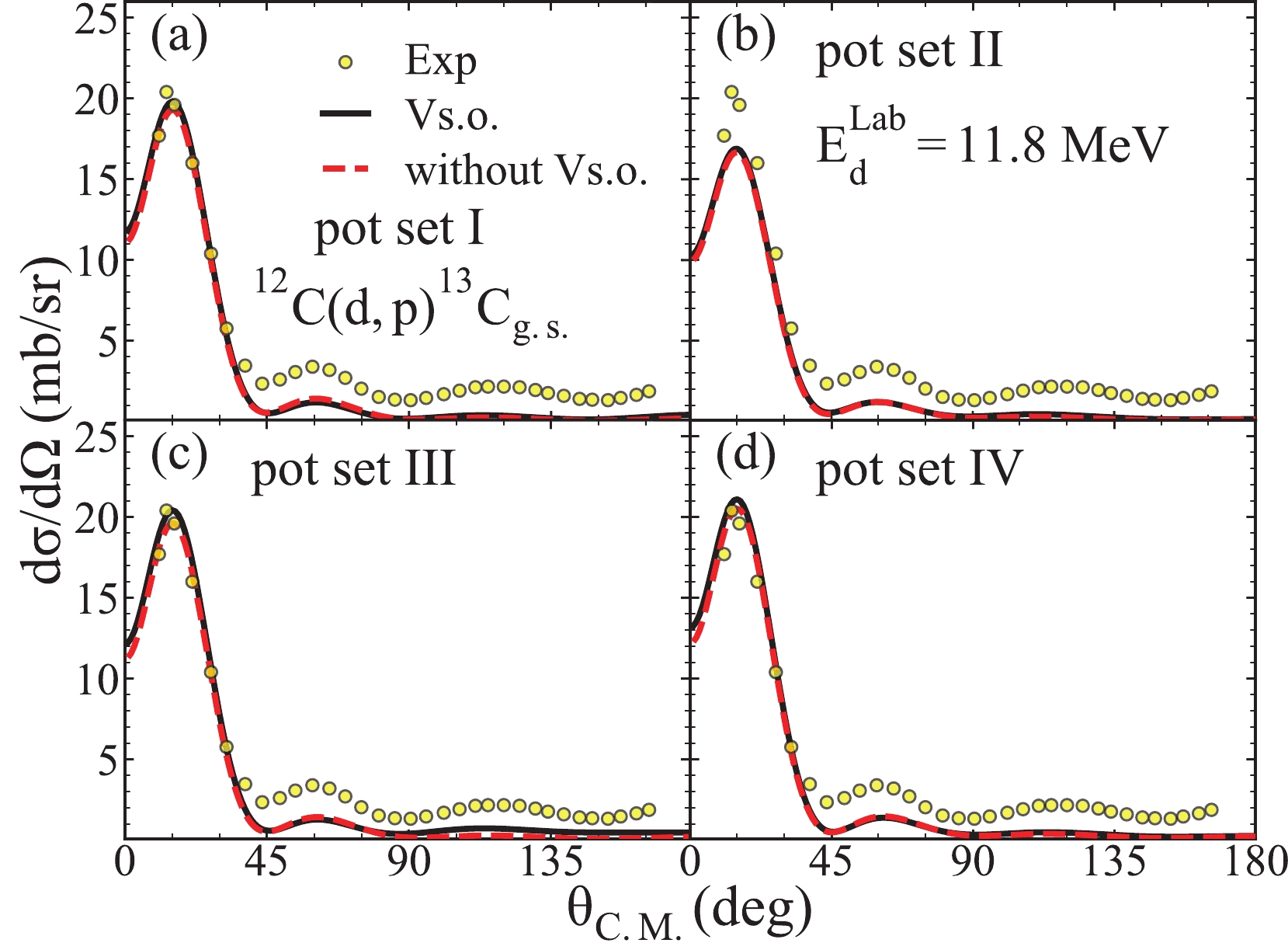
Figure 8. (color online) For
${ {E_d^{\rm Lab}}}=11.8$ MeV, the cross-section angular distributions of the transfer reaction$^{12}{\rm{C}}({d,\; p})^{13}\rm C_{g.s.}$ calculated based on different potential sets. (a)–(d) represent the computational results of the potential sets I - IV, respectively. The black solid line and the red dashed line represent the angular distributions when the spin-orbit coupling term of the deuteron global OMPs is accounted for and neglected, respectively. The yellow solid circles represent the experimental data cited from Ref. [61], and the spectroscopic factors are cited from Ref. [62].As shown in Fig. 8, both the differential cross sections can effectively reproduce the experimental data in the small-angle area when the spin-orbit coupling term of the deuteron global OMPs is accounted for and neglected. In the area less than 40 degrees, both the theoretical results of the potential sets I, III, and IV with and without spin show good agreement with the experimental data. However, the differential cross sections calculated based on the potential set II are smaller than those in the experimental data with and without the spin-orbit coupling term at small angles. One can observe that the spin-orbit coupling term of the deuteron global OMPs has little impact on the cross-section angular distributions. From Fig. 8(b), the spin-orbit coupling potential has little and relatively big influence on the transfer angular distributions at small and big angles, respectively. We discuss this phenomenon specifically in the following part.
We study the effects of the spin-orbit potential on the scattering wave functions in the entrance and exit channels, and we obtain the same conclusion for the two situations above. For simplicity, we only show the effects of the spin-orbit coupling term of the Bojowald [10] global OMPs on angular distribution and scattering wave functions, with the deuteron energy
${ {E_d^{\rm Lab}}} = 11.8$ MeV. The results are shown in Fig. 9. In this figure, the x-axis denotes different partial waves, and the$\xi^2_{\rm s.o.}$ represents the influence of the spin-orbit interaction on the partial waves. The bars with blue left slash, green mesh, and red right slash represent the situations when the value of angular momentum number equals$ l + s_d $ , l, and$ l - s_d $ , respectively. The subplot inside the main plot represents the angular distribution of the transfer reaction$^{12}{\rm{C}}({d,\; p})^{13}\rm C_{g.s.}$ computed by the potential set II. The black solid line and red dashed line represent the angular distributions when the spin-orbit coupling term of deuteron global OMPs is accounted for and neglected, respectively.
Figure 9. (color online) The effects of the spin-orbit coupling term of the deuteron global OMPs on the scattering waves in the entrance channels for the deuteron energy of 11.8 MeV. The x-axis denotes different partial waves, and
$\xi^2_{\rm s.o.}$ represents the influence of the spin-orbit interaction on the partial waves. The bars with blue left slash, green mesh, and red right slash represent the situations when the value of angular momentum number equals$ l + s_d$ , l, and$ l - s_d$ , respectively. The subplot inside the main plot represents the angular distribution of the transfer reaction$^{12}{\rm{C}}({d,\; p})^{13}\rm C_{g.s.}$ computed by the potential set II. The black solid line and red dashed line represent the angular distribution when the spin-orbit coupling term of deuteron global OMPs is accounted for and neglected, respectively.As we can see from Fig 9, the spin-orbit coupling term of the Bojowald [10] global OMPs has different influences on different partial waves. Generally, the
$\xi^{2}_{\rm s.o.}$ value decreases as the orbital angular momentum number increases, especially for the situation$ J=l $ , suggesting that the spin-orbit coupling potential has more significant influences on the low partial waves than high partial waves. In addition, the effects are more significant when the spin and orbit angular momentum is in the same or opposite direction ($ J=l+s_d $ ,$ J=l-s_d $ ) than that in the other situation ($ J=l $ ). Then, as shown in the subplot, the low partial waves of the scattering waves pass the influences caused by the spin-orbit coupling potential to the cross-section angular distributions, especially in the big angles.We also analyze the effects of the spin-orbit coupling term of the deuteron global OMPs on the differential cross sections of
$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ . Specifically, we use different potential sets and the same binding potentials from the previous discussion in the calculations of differential cross sections. We compute the differential cross sections at 11.9, 15.0, 19.3, and 25.0 MeV and find the same effects for all energies. For simplicity, we only show the results when deuteron energy is 19.3 MeV in Fig. 10.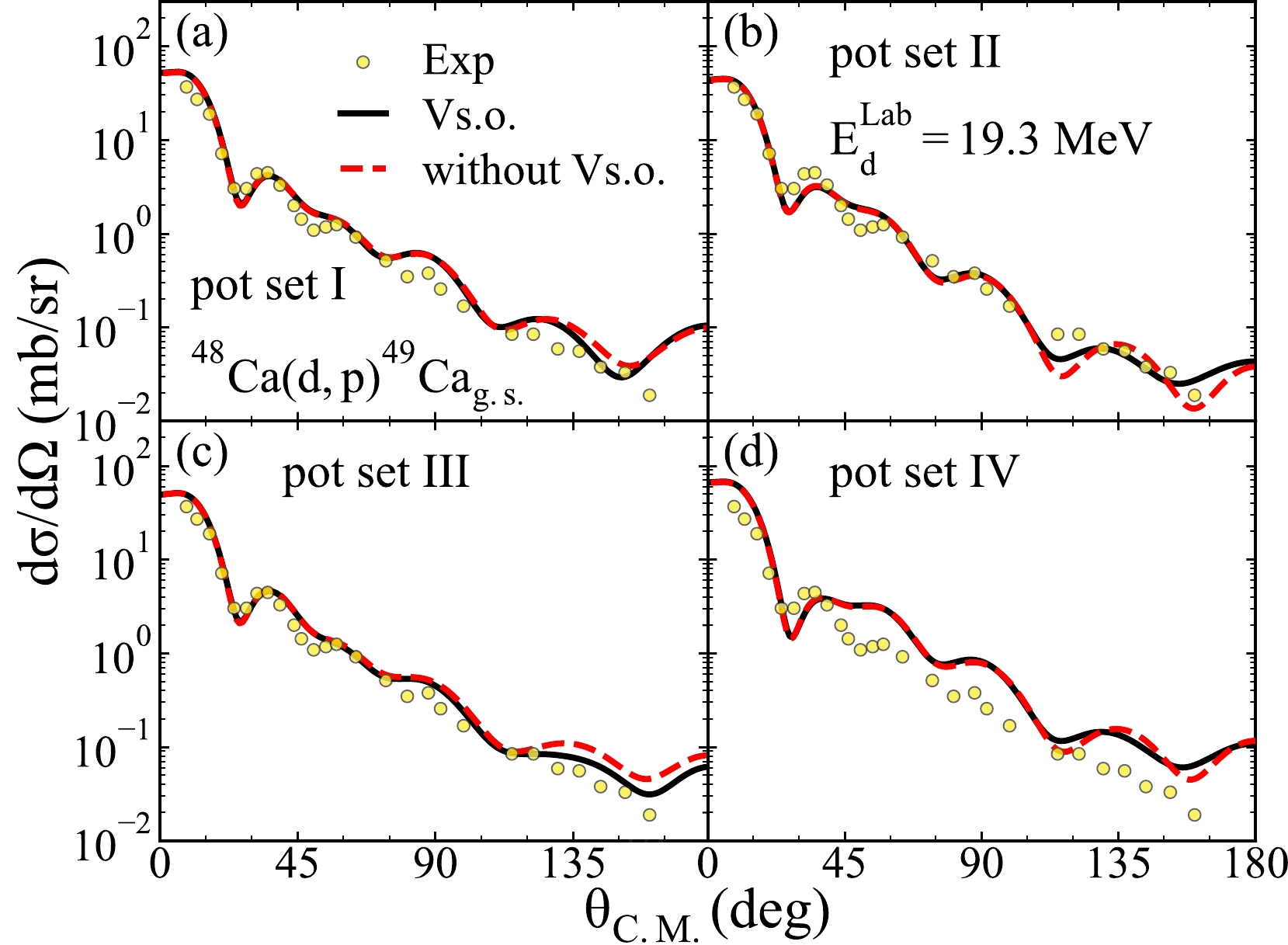
Figure 10. (color online)Similar to Fig. 8 but for the transfer reaction
$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ and the incoming deuteron energies. The experimental data and the spectroscopic factors are cited from Ref. [58].It can be noted that in Fig. 10, both computational results of the potential sets I - III when the spin-orbit coupling term is accounted for and nelglected are in good agreement with the experimental data. For the computation results of the potential set IV, the differential cross sections can reproduce the experimental data in the small-angle area, but the results are larger than the experimental data in the area greater than 40 degrees. Additionally, from the theoretical results, the spin-orbit coupling term of the deuteron global OMPs mainly affects the cross-section angular distributions in the large-angle area. Furthermore, the spin-orbit coupling terms of the deuteron global OMPs have little effect on the angular distributions in the small angles.
In the same way, the effects of the spin-orbit coupling term of the deuteron global OMPs on the differential cross sections of
$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ are analyzed. In detail, we use different potential sets and the same binding potentials from the previous discussion in the calculations of differential cross sections. Moreover, we compute the differential cross sections at 22.0, 26.8, 33.5, and 40.2 MeV and obtain the same conclusion for all energies. For simplicity, we only display the results when the deuteron energy is 22.0 MeV in Fig. 11.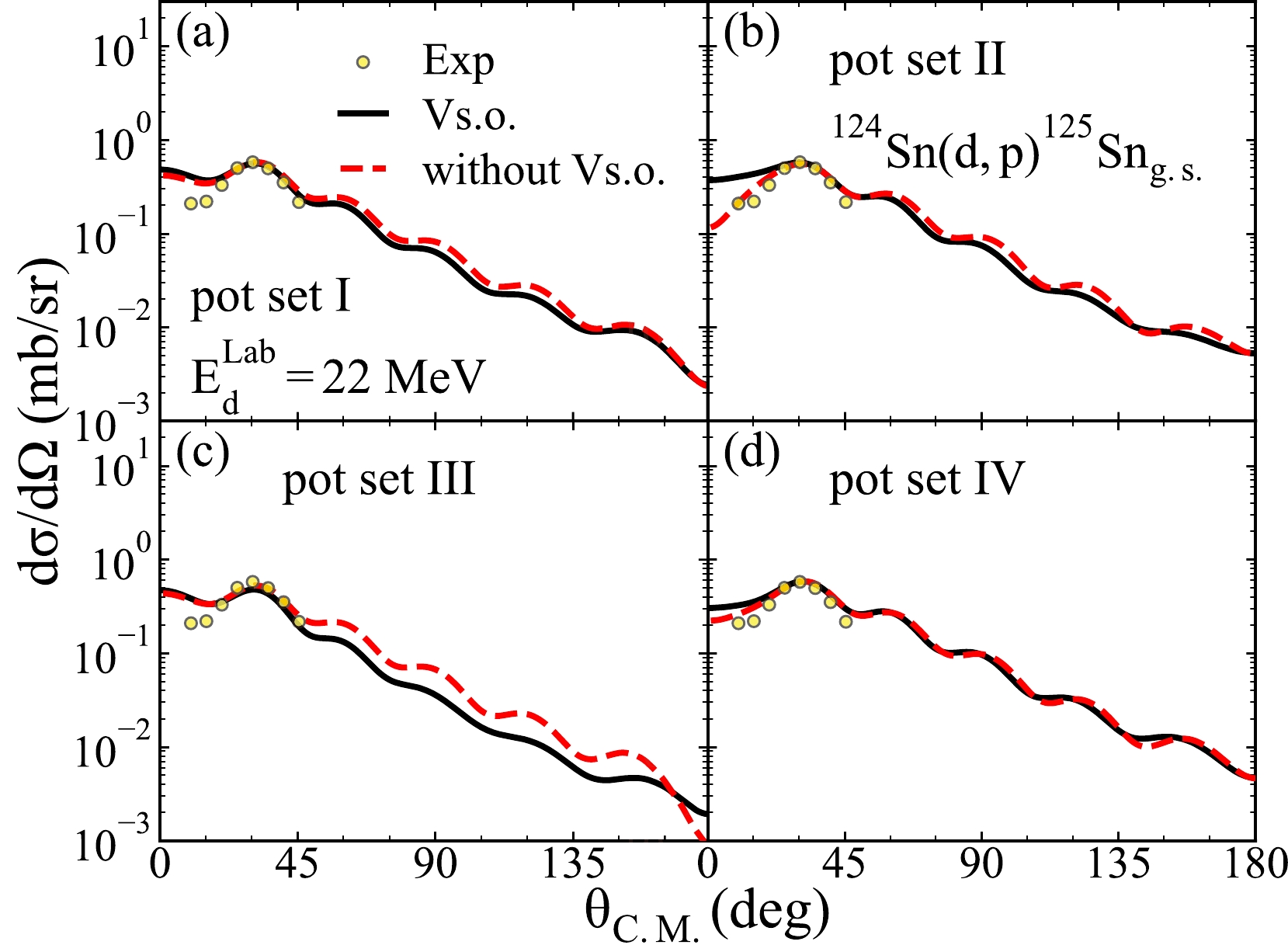
Figure 11. (color online) Similar to Fig. 8 but for the transfer reaction
$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ and the incoming deuteron energies. The experimental data and the spectroscopic factors are cited from Ref. [63].It can be shown in Fig. 11 that both the computational results of the potential set I and III with and without the spin-orbit coupling term can equally and effectively reproduce the experimental data in the area between 20 and 45 degrees. However, the results calculated based on the potential sets II and IV with spin show better agreement with the experimental data compared to when the spin-orbit coupling term is neglected. In addition, the spin-orbit coupling term of different deuteron global OMPs has dramatically different effects on the cross-section angular distributions. To be specific, the small-angle and big-angle area of the angular distribution calculated based on the potential sets II and III are more affected by the spin-orbit coupling term than other sets of the deuteron optical potentials. Meanwhile, both the small and big angles of the cross-section angular distribution computed by the potential set IV are slightly influenced by the spin-orbit coupling potential.
Finally, the influences of the spin-orbit coupling term of the deuteron global OMPs on the transfer differential cross sections of
$^{208}{\rm{Pb}}({d,\; p})^{209}\rm Pb_{g.s.}$ are studied. To be specific, we use different potential sets and the same binding potentials from the previous discussion in the calculation of differential cross sections. We calculate the differential cross sections at 22.0, 30.5, 40.6, and 50.7 MeV and find the same conclusion for all energies. For simplicity, we only display the results when the deuteron energy is 22.0 MeV in Fig. 12.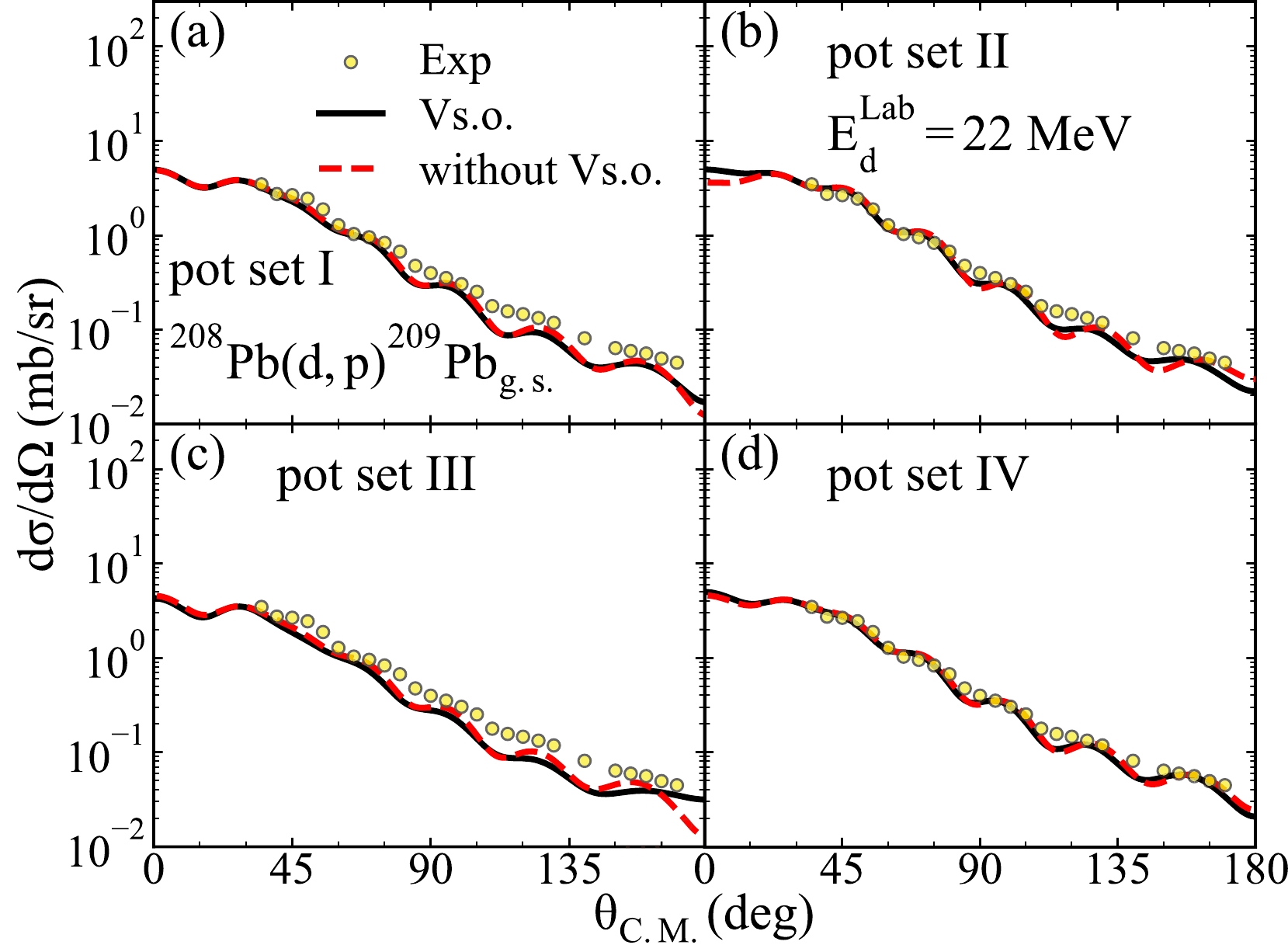
Figure 12. (color online) Similar to Fig. 8 but for the transfer reaction
$^{208}{\rm{Pb}}({d,\; p})^{208}\rm Pb_{g.s.}$ and the incoming deuteron energy is 22.0 MeV. The experimental data and the spectroscopic factors are cited from Ref. [64].As displayed in Fig. 12, both the computational results of different potential sets with and without the spin-orbit coupling term are in good agreement with the experimental data. Additionaly, the relatively slight influences of the spin-orbit coupling term of the deuteron global OMPs on the cross-section angular distributions mainly exist at large angles. In detail, as shown in Fig. 12 (b) and (c), the angular distributions were calculated based on the potential sets II and IV are only slightly affected by the spin-orbit coupling term at large and small angles.
-
In this section, the effects of different combinations of the deuteron and nucleon global OMPs on the transfer cross sections of the target nuclei
$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ ,$ ^{208}{\rm{Pb}} $ are systematically studied for different energies. In addition, the influences of the spin-orbit coupling term of the deuteron and nucleon global OMPs on the transfer cross sections are also analyzed. -
In this part, we study the effects of different deuteron and nucleon OMPs on the cross sections of the
$ (d,p) $ transfer reactions on the target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ . Additionally, the influences of the spin-orbit coupling term of deuteron global OMPs on transfer cross sections at different incident deuteron energies are investigated as well.For that purpose, we first consider the transfer reactions on the target nuclei
$ ^{12}{\rm{C}} $ with different deuteron and nucleon global OMPs at different deuteron energies. We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potentials. The same binding potentials from the previous discussion are used in the computation. Then, the transfer cross sections produced by different combinations of the deuteron and nucleon global OMPs and the binding potentials are shown in Fig. 13. In this figure, the x-axis represents different sets of the nucleon global OMPs, including global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8]. The y-axis denotes the value of the transfer cross sections. In addition, the values of the$\xi^2_{\rm s.o.}$ function is shown in the colorbar, which describes the effects of the spin-orbit coupling term of the deuteron global OMPs on the transfer cross sections. The circles, diamonds, squares, and left triangles represent the computational results calculated based on the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12], respectively. Fig. 13 (a)–(d) represent the results corresponding to different deuteron energies, including${{E_{d}^{\rm Lab}}}=$ 4.5,$ 11.8 $ ,$ 15.0 $ , and$ 19.6 $ MeV, respectively.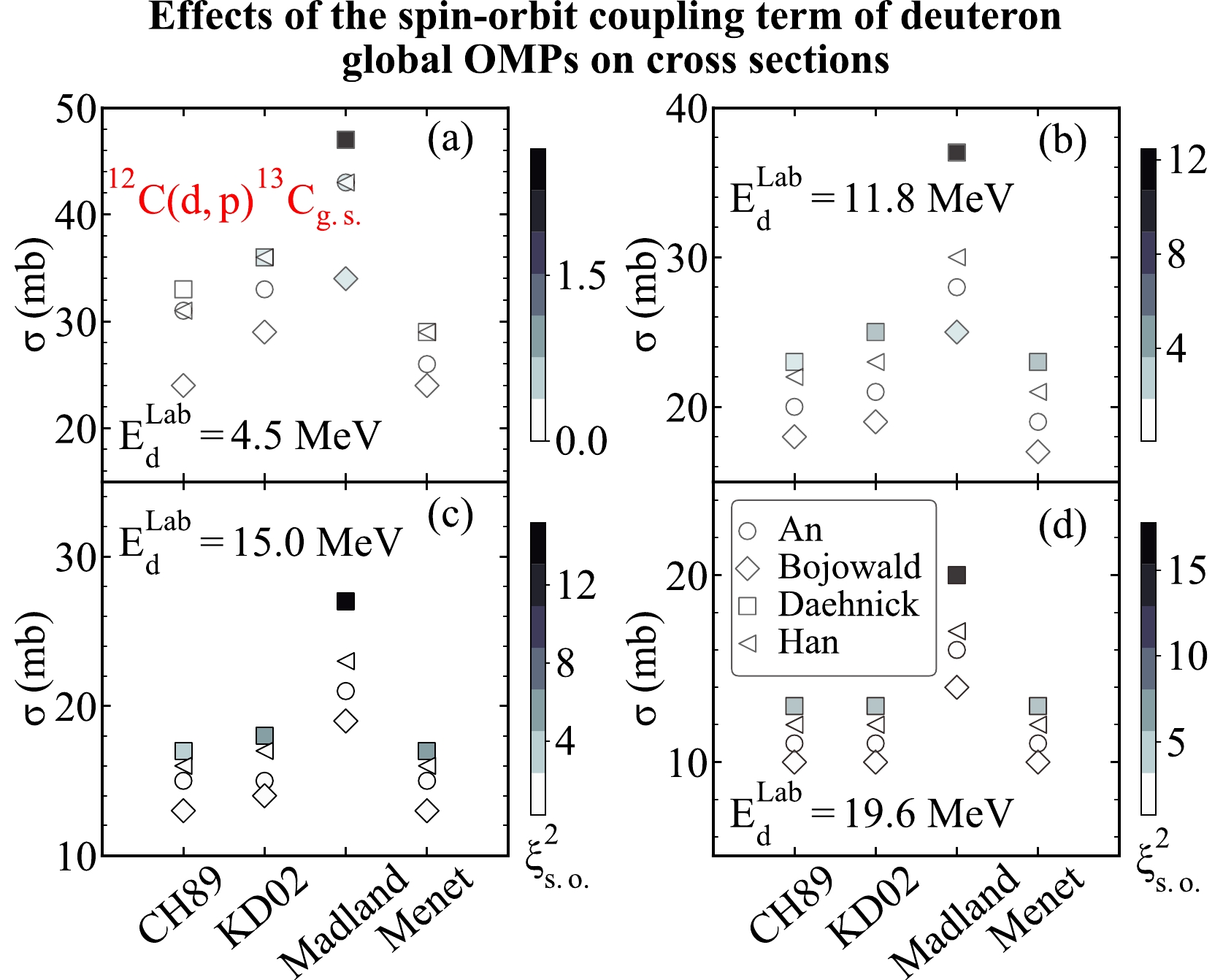
Figure 13. (color online) The effects of different combinations of the deuteron and nucleon global OMPs on the transfer cross sections at different incoming deuteron energies and the influence of spin-orbit coupling term of the deuteron global OMPs on the transfer cross sections for the transfer reaction
$^{12}{\rm{C}}({d,~ p})$ ${}^{13}\rm C_{g.s.} $ . The x-axis represents different sets of nucleon global OMPs, including the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8]. The y-axis denotes the value of the transfer cross sections. In addition, the values of the$\xi^2_{\rm s.o.}$ function is shown in the colorbar, which describes the effects of the spin-orbit coupling term of the deuteron global OMPs on the transfer cross sections. The circles, diamonds, squares, and left triangles represent the computational results calculated based on the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12], respectively. (a)–(d) represent the results corresponding to different deuteron energies, including${{E_{d}^{\rm Lab}}}=4.5 $ , 11.8, 15.0, and 19.6 MeV, respectively.As we can observe from Fig. 13, different combinations of the deuteron and nucleon global OMPs produce dramatically different transfer cross sections. The largest transfer cross section calculated based on the global OMPs from Daehnick [11] and Madland [7] is nearly two times the smallest cross section computed by the global OMPS from Bojowald [10] and CH89 [5]. However, it also shows a pattern that the global OMPs from Madland [7] and Daehnick [11] always produce the largest transfer cross sections among the nucleon and deuteron global OMPs. On the contrary, the global OMPs from Bojowald [10] usually produce the smallest cross section among all deuteron global OMPs. This pattern remains the same as the deuteron energy increases. In addition, the theoretical results calculated based on the global OMPs from Daehnick [11] always get the largest
$\xi^2_{\rm s.o.}$ value, suggesting that its spin-orbit coupling term has the most significant effect on the transfer cross section. The$\xi^2_{\rm s.o.}$ value increases as the deuteron energy goes up, demonstrating that the effects of the spin-orbit coupling term of the deuteron global OMPs on the transfer cross sections enhance as the deuteron energy increases.Then, in the same way, we also study the effects of different deuteron and nucleon global OMPs on the transfer cross section of
$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ at different energies. We consider the$ (d,p) $ transfer reactions on the target nuclei$ ^{48}{\rm{Ca}} $ . We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potential. The same binding potentials from previous discussion are used in the computation. We compute the transfer cross sections at 11.9, 15.0, 19.3, and 25.0 MeV. The theoretical results are shown in Fig. 14.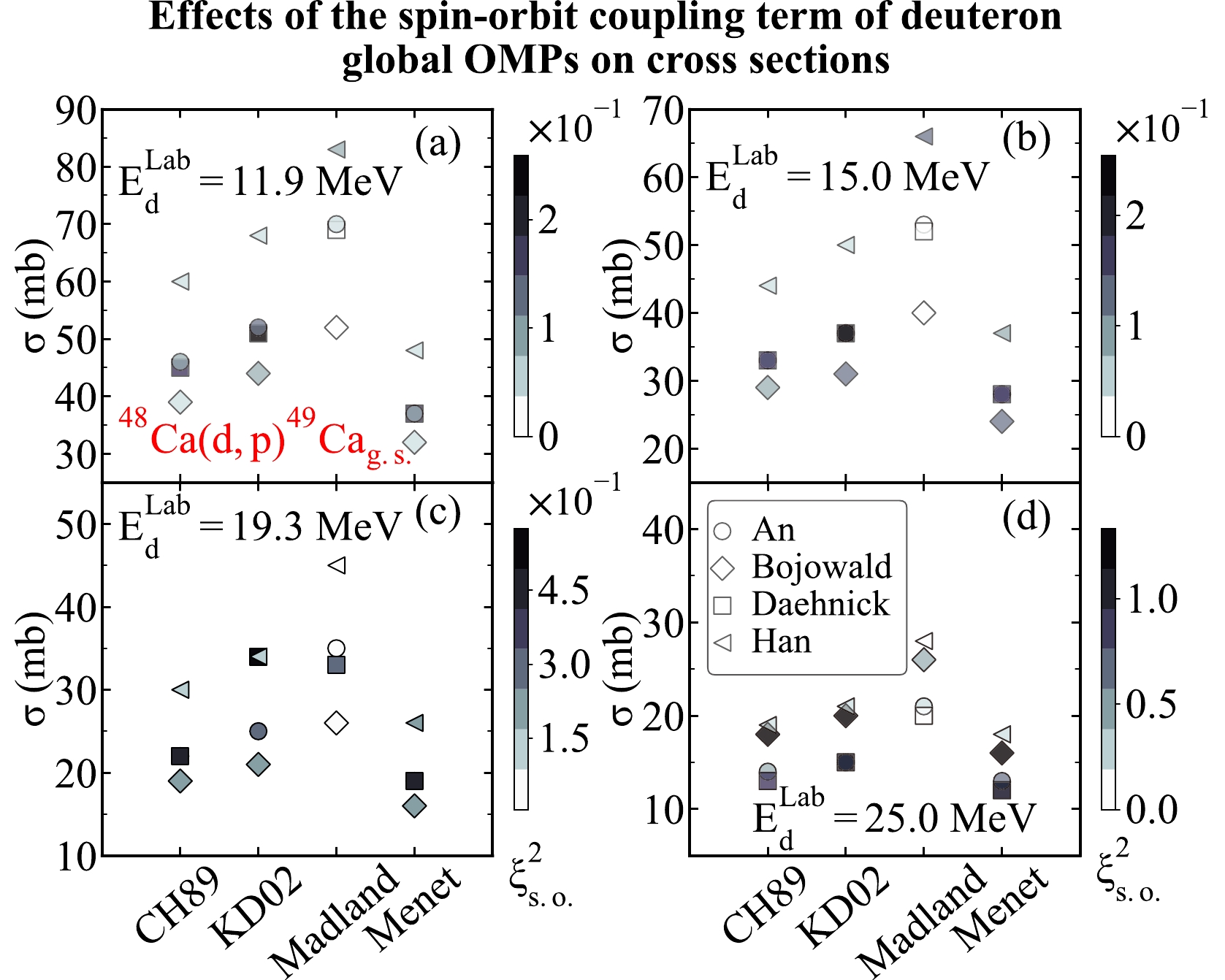
Figure 14. (color online) Similar to Fig. 13 but for the transfer reaction
$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ and the incoming deuteron energies. (a)–(d) represent the results corresponding to different deuteron energies, including${{E_{d}^{\rm Lab}}}= $ 11.9, 15.0, 19.3, and 25.0 MeV, respectively.As shown in Fig. 14, the cross sections were calculated based on different combinations of the deuteron and nucleon global OMPs are very different. In detail, the combination of the global OMPs from Han [12] and Madland [7] usually computes the largest transfer cross sections at different energies. The global OMPs from Bojowald [10] tend to produce the smallest cross sections among the deuteron global OMPs. As for the proton optical potentials, the global OMPs from Madland [7] and Menet [8] usually produce the largest and smallest transfer cross sections, respectively. Additionally, it can be noted that the theoretical results computed by the global OMPs from Daehnick [11] always generate the biggest
$\xi^2_{\rm s.o.}$ value, suggesting that its spin-orbit coupling term produces the most significant influences on transfer cross sections.$\xi^2_{\rm s.o.}$ value increases as energy increases, which shows that the influences of the spin-orbit coupling term of the deuteron global OMPs on the cross section were strengthen as the incident deuteron energy increases.Furthermore, we also investigate the effects of different deuteron and nucleon global OMPs on the transfer cross section of
$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ at different energies. For that purpose, we consider the$ (d,p) $ transfer reactions on the medium-mass target nuclei$ ^{124}{\rm{Sn}} $ . We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potentials. The same binding potentials from the previous discussion are used in the computation. We calculate the transfer cross sections at 22.0, 26.8, 33.5, and 40.2 MeV. We present the theoretical results in Fig. 15.
Figure 15. (color online) Similar to Fig. 13 but for the transfer reaction
$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ and the incoming deuteron energies. (a)–(d) represent the results corresponding to different deuteron energies, including${{E_{d}^{\rm Lab}}}= $ 22.0, 26.8, 33.5 and 40.2 MeV, respectively.As displayed in Fig. 15, one can observe that the transfer cross sections of different combinations of the deuteron and nucleon global OMPs are rather different. Specifically, as for deuteron global OMPs, the global OMPs from Han [12] result in the largest transfer cross sections. On the contrary, the global OMPs from Daehnick [11] tend to yield the smallest cross section. As for proton potentials, the global OMPs from Madland [7] and KD02 [6] always produce larger cross sections than other nucleon global OMPs. In addition, the
$\xi^2_{\rm s.o.}$ value corresponding to the the global OMPs from Daehnick [11] is the largest. In other words, the influences of the spin-orbit coupling term of the global OMPs from Daehnick [11] have the most significant influence on the transfer cross sections.$\xi^2_{\rm s.o.}$ value of the deuteron global OMPs increases as the deuteron energies increase, suggesting that the effects of the spin-orbit coupling term of the deuteron global OMPs on the transfer cross sections strengthen as the incident deuteron energies increase.Finally, we study the effects of different combinations of the deuteron and nucleon global OMPs on the transfer cross section of
$^{208}{\rm{Pb}}({d,\; p})^{209}\rm Pb_{g.s.}$ at different energies. For that purpose, we consider the$ (d,p) $ transfer reactions on the heavy target nuclei$ ^{209}{\rm{Pb}} $ . We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] global OMPs as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potentials. The same binding potentials from the previous discussion are used in the computation. We compute the transfer cross sections at 22.0, 30.5, 40.6, and 50.7 MeV. We display the theoretical results in Fig. 16.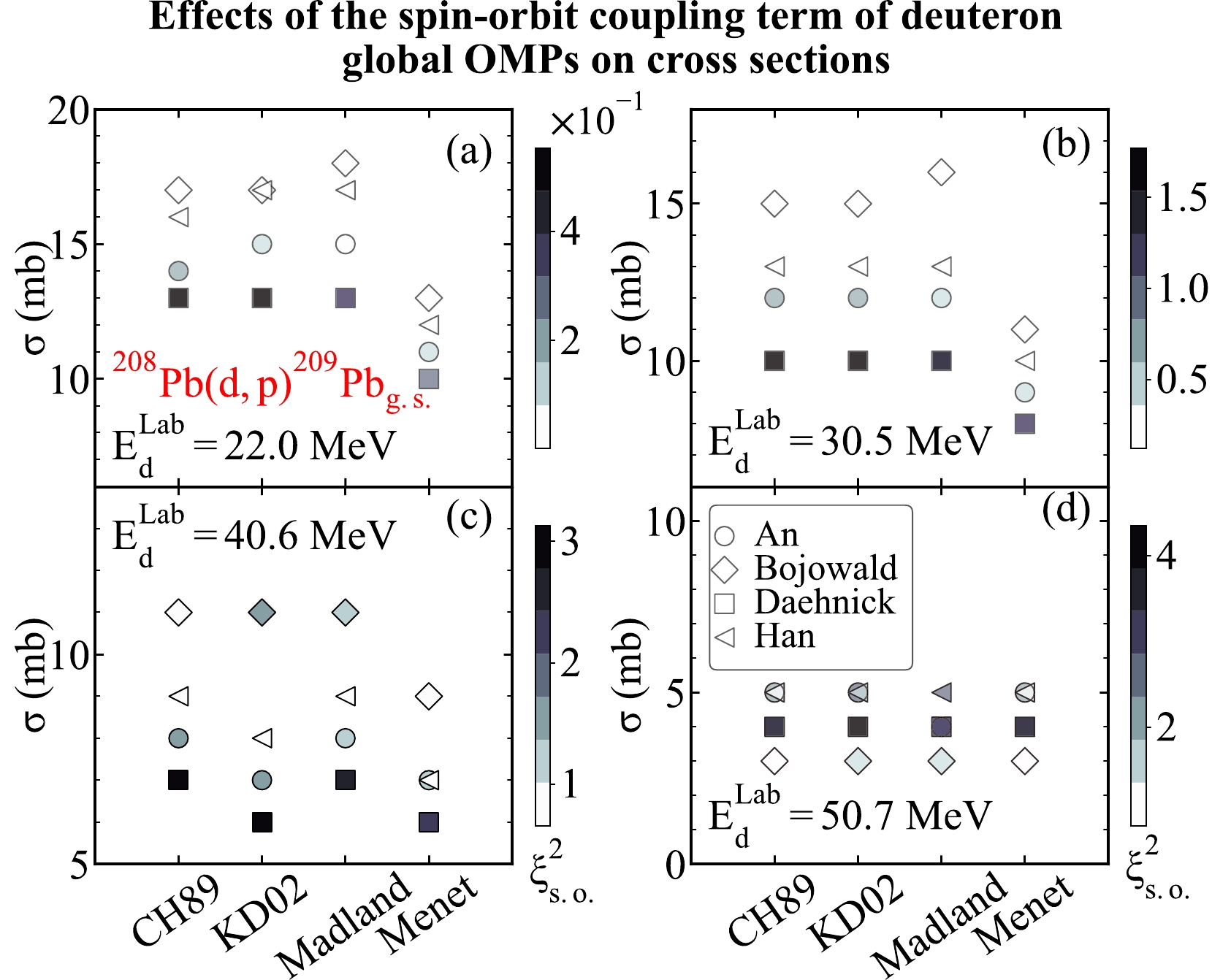
Figure 16. (color online) Similar to Fig. 13 but for the transfer reaction
$^{208}{\rm{Pb}}({d,\; p})^{209}\rm Pb_{g.s.}$ and the incoming deuteron energies. (a)–(d) represent the results corresponding to different deuteron energies, including${{E_{d}^{\rm Lab}}}= $ 22.0, 30.5, 40.6 and 50.7 MeV, respectively.As we can see from Fig. 16, the transfer cross sections vary with the different combinations of deuteron and nucleon global OMPs and energies. In detail, different deuteron and nucleon global OMPs yield rather different transfer cross sections. The transfer cross sections decrease as the deuteron energy increases. It can also be seen that the global OMPs from Madland [7] and Menet [8] result in the largest and the smallest transfer cross sections (smaller than 50.7 MeV). In addition, the
$\xi^2_{\rm s.o.}$ value corresponding to the global OMPs from Daehnick [11] is the largest, suggesting that the influences of the spin-orbit coupling term of the global OMPs from Daehnick [11] on the transfer cross sections are the greatest. Additionally, the$\xi^2_{\rm s.o.}$ value of the deuteron global OMPs increase as deuteron energies increase, demonstrating that the effects of the spin-orbit coupling term of the deuteron global OMPs on the transfer cross sections also strengthen as the incident deuteron energies increase. -
Since the effects of different combinations of the deuteron and nucleon OMPs on the transfer cross sections have been studied in Sec. IV.D.1, for simplicity, we only discuss the influences of the spin-orbit coupling term of the nucleon global OMPs on the cross sections at different proton energies in this section.
For that purpose, we first consider the transfer reactions on the target nuclei
$ ^{12}{\rm{C}} $ with different deuteron and nucleon global OMPs at different proton energies and compute the$\xi^2_{\rm s.o.}$ values of different proton global OMPs. We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] global OMPs as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potentials. The same binding potentials from the previous discussion are used in the computation. The transfer cross sections produced by different combinations of the deuteron and nucleon global OMPs, binding potentials, and the effects of the spin-orbit coupling term of the nucleon global OMPs on the transfer cross sections are shown in Fig. 17. In this figure, the x-axis represents different sets of nucleon global OMPs, including CH89 [5], KD02 [6], Madland [7], and Menet [8] global OMPs. The y-axis denotes the value of transfer cross sections. In addition, the value of the$\xi^2_{\rm s.o.}$ function is shown in the colorbar, which describes the effects of the spin-orbit coupling term of the nucleon global OMPs on the transfer cross sections. The circles, diamonds, squares, and left triangles represent the theoretical results of the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12], respectively. Fig. 17 (a)–(d) represent the results corresponding to different proton energies, including$ {{E_{p}}}=7.1 $ ,$ 13.8 $ ,$ 16.8 $ , and$ 21.0 $ MeV, respectively.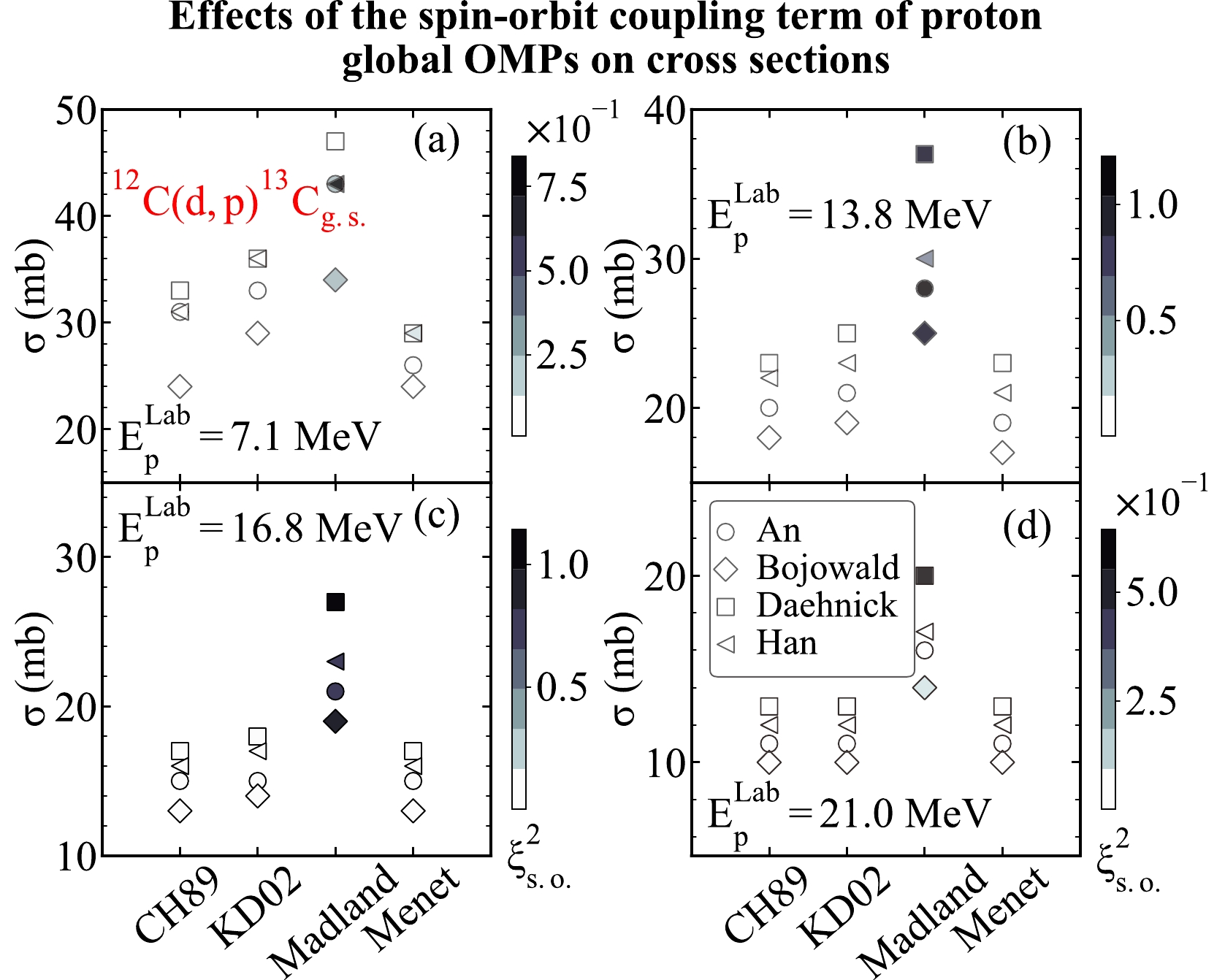
Figure 17. (color online) Similar to Fig. 13 but for the
$\xi^2_{\rm s.o.}$ function describing the influence of spin-orbit coupling potential of nucleon global OMPs on the cross sections of the transfer reaction$^{12}{\rm{C}}({d,\; p})^{13}\rm C_{g.s.}$ and different outgoing proton energies. (a)–(d) represent the results corresponding to${{E_{p}}}= $ 7.1, 13.8, 16.8, and 21.0 MeV, respectively.As presented in Fig. 17, the effects of the spin-orbit coupling term of different nucleon global OMPs on the transfer cross sections are rather different from one another. Specifically, the maximum value of
$\xi^2_{\rm s.o.}$ can always be obtained by the global OMPs from Madland [7], illustrating that the spin-orbit coupling term of the global OMPs from Madland [7] has the most significant influences on the transfer cross sections. Moreover, the effects of the spin-orbit coupling term of the nucleon global OMPs on the transfer cross sections vary with the proton energy. In detail, the influence of the spin-orbit term of different nucleon global OMPs on the transfer cross sections reaches its maximum at 16.8 MeV. From the theoretical results, the$\xi^2_{\rm s.o.}$ value increases first and then decreases as the proton energies increase, suggesting that the influence of the spin-orbit term of different nucleon global OMPs on the transfer cross sections strengthens first and then weakens as the proton energy increases.In the same way, we investigate the effects of the spin-orbit coupling term of the nucleon global OMPs on the cross sections at different proton energies. For this analysis, we consider the
$ (d,p) $ transfer reactions on the target nuclei$ ^{48}{\rm{Ca}} $ and compute the$\xi^2_{\rm s.o.}$ values of different proton global OMPs. We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potential. The same binding potentials from the previous discussion are used in the computation. We compute the transfer cross sections when the proton energies are at 14.6, 17.7, 21.9, and 27.5 MeV. The theoretical results are shown in Fig. 18.As displayed in Fig. 18, the effects of the spin-orbit coupling term of different nucleon global OMPs on the transfer cross sections are dramatically different from one another. Specifically, the global OMPs from Madland [7] always produce the maximum value of
$\xi^2_{\rm s.o.}$ , illustrating that its spin-orbit coupling term has the most significant influences on the transfer cross sections of$^{48}{\rm{Ca}}({d,\; p})^{49}\rm Ca_{g.s.}$ . Moreover, the effects of the spin-orbit coupling term of the nucleon global OMPs on the transfer cross sections also vary with energies. In detail, the influence of the spin-orbit term of different nucleon global OMPs on the transfer cross sections reach its peak at 17.7 MeV, and then the effects start to wane with the energy reaching 21.9 and 27.5 MeV. From the theoretical results, the$\xi^2_{\rm s.o.}$ value increases first and then decreases as the proton energies increase, suggesting that the influence of the spin-orbit term of different nucleon global OMPs on the transfer cross sections strengthens first and then weakens with the proton energy rising.Furthermore, we investigate the effects of the spin-orbit coupling term of the nucleon global OMPs on the cross sections of
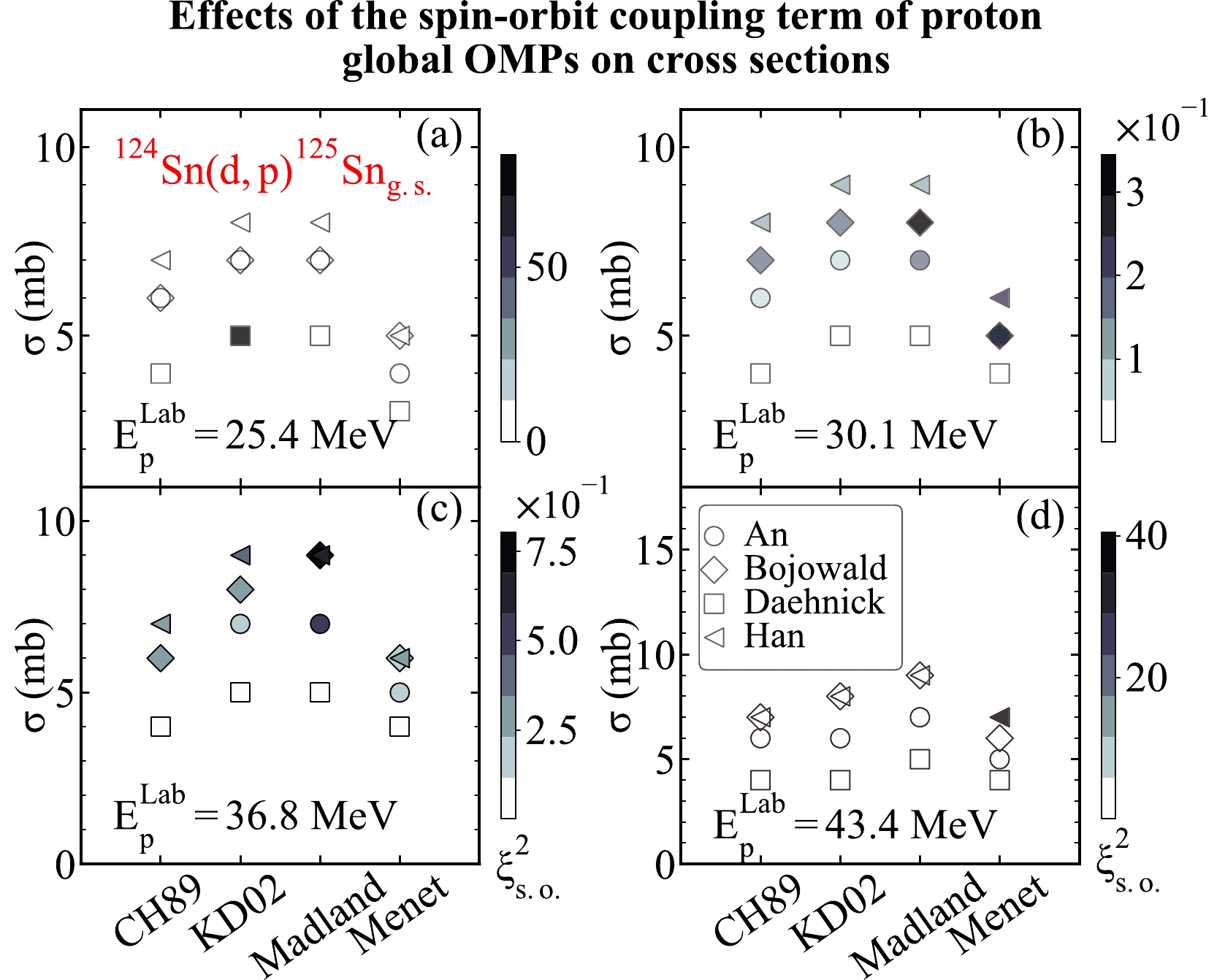
$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ at different proton energies. For that purpose, we consider the$ (d,p) $ transfer reactions on the medium-mass target nuclei$ ^{124}{\rm{Sn}} $ and compute the$\xi^2_{\rm s.o.}$ values of different proton global OMPs. We take the global OMPs from An et al . [9], Bojowald et al. [10], Daehnick [11], and Han [12] as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potentials. The same binding potentials from the previous discussion are used in the computation. We calculate the transfer cross sections when the proton energies are at 25.4, 30.1, 36.8, and 43.4 MeV. We present the theoretical results in Fig. 19.As shown in Fig. 19, the spin-orbit coupling term of different nucleon global OMPs has different effects on the transfer cross sections. To be specific, the global OMPs from KD02 [6] have a rather large influence on the transfer cross section produced by the global OMPs from KD02 [6] and Daehnick [11] at 25.4 MeV. Similarly, the global OMPs from Menet [8] have a considerable influence on the transfer cross section produced by the global OMPs from Menet [8] and Han [12] at 52.2 MeV. In other situations, the global OMPs from Madland [7] tends to produce the maximum value of
$\xi^2_{\rm s.o.}$ , illustrating that its spin-orbit coupling term has significant influences on transfer cross sections of$^{124}{\rm{Sn}}({d,\; p})^{125}\rm Sn_{g.s.}$ . Moreover, the effects of the spin-orbit coupling term of the nucleon global OMPs on the transfer cross sections also vary with energy. In detail, the influences of the spin-orbit term of most nucleon global OMPs on the transfer cross sections reach their peaks at 30.1 MeV, and then, the effects start to wane when the energy reaches 36.8 MeV. From the theoretical results, the$\xi^2_{\rm s.o.}$ value increases first and then decreases as the proton energies increase, suggesting that the influence of the spin-orbit term of different nucleon global OMPs on transfer cross sections strengthens first and then weakens as the proton energy increases.Finally, we study the effects of the spin-orbit coupling term of the nucleon global OMPs on the cross sections of
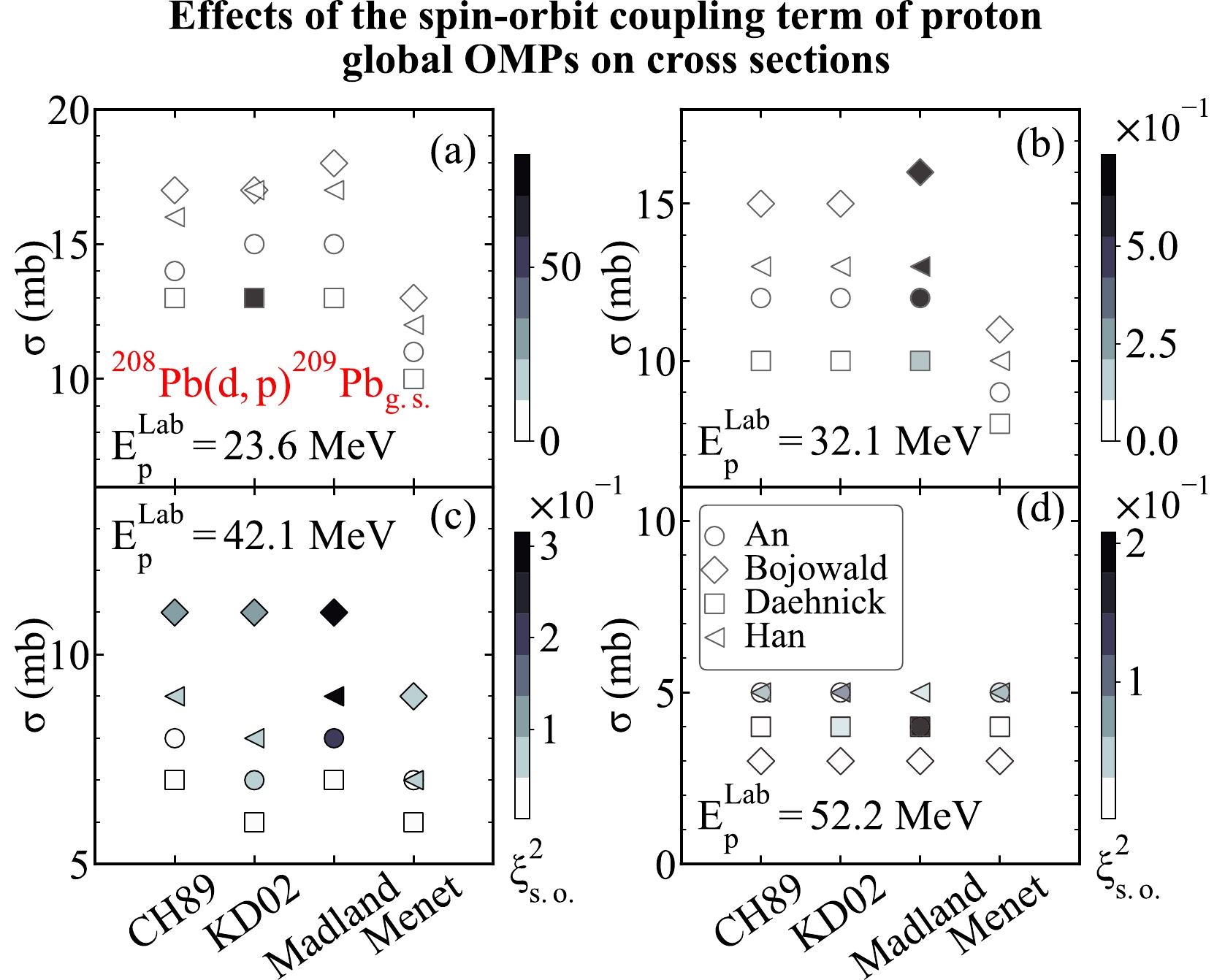
$^{208}{\rm{Pb}}({d,\; p})^{209}\rm Pb_{g.s.}$ at different proton energies. For that purpose, we consider the the$ (d,p) $ transfer reactions on the heavy target nuclei$ ^{209}{\rm{Pb}} $ . We take the global OMPs from An [9], Bojowald [10], Daehnick [11], and Han [12] as the deuteron optical potentials. We take the global OMPs from CH89 [5], KD02 [6], Madland [7], and Menet [8] as the proton optical potentials. The same binding potentials from the previous discussion are used in the computation. We compute the transfer cross sections when the proton energies are at 23.6, 32.1 42.1, and 52.2 MeV. We display the theoretical results in Fig. 20.As shown in Fig. 20, the spin-orbit coupling term of different nucleon global OMPs also has different effects on the transfer cross sections of
$^{208}{\rm{Pb}}({d,\; p})^{209}\rm Pb_{g.s.}$ . To be specific, the global OMPs from KD02 [6] have a huge influence on the transfer cross section produced by the global OMPs from KD02 [6] and Daehnick [11] at 23.6 MeV. In other situations, the value of$ \xi^2_{\rm s.o.} $ corresponding to global OMPs from Madland [7] tends to be large, illustrating that its spin-orbit coupling term has significant influences on the transfer cross sections. In addition, the effects of the spin-orbit coupling term of the global OMPs from Madland [7] on the transfer cross sections vary with the proton energy. In detail, the effect of the$\xi^2_{\rm s.o.}$ value corresponding to the global OMPs from Madland [7] on the transfer cross sections reaches its maximum at 32.1 MeV and begins to decrease as the energy increases. From the theoretical results, the$\xi^2_{\rm s.o.}$ values corresponding to the global OMPs from CH89 [5] and KD02 [6] behave irregularly with the proton energy. -
In this study, the effects of different global OMPs on transfer (differential) cross sections were systematically investigated. First, we analyzed the effects of different deuteron global OMPs on the cross-section angular distributions of
$ (d,p) $ transfer reactions on target nuclei$ ^{12}{\rm{C}} $ ,$ ^{48}{\rm{Ca}} $ ,$ ^{124}{\rm{Sn}} $ , and$ ^{208}{\rm{Pb}} $ , respectively, at different energies. It showed that nearly all computational results of different deuteron OMPs could effectively reproduce the experimental data. The changes in the differential cross sections of transfer reactions caused by different choices of the deuteron global OMPs varied with the mass of target nuclei and deuteron energies.In addition, we discussed the influences of the spin-orbit coupling term of deuteron global OMPs on transfer differential cross sections. Generally, the theoretical results showed that both the results, when considering and neglecting the spin-orbit coupling term of deuteron global OMPs, are in good agreement with the experimental data. The spin-orbit coupling term of deuteron global OMPs slightly affected the transfer cross-section angular distribution of light nuclei
$ ^{12}{\rm{C}} $ and$ ^{48}{\rm{Ca}} $ in the large-angle area. However, for medium-mass nuclei$ ^{124}{\rm{Sn}} $ and heavy nuclei$ ^{208}{\rm{Pb}} $ , the small effects of the spin-orbit coupling term on differential cross sections become irregular.Furthermore, effects of different combinations of deuteron and nucleon global OMPs on transfer cross sections were systematically discussed. The transfer cross sections of different combinations of deuteron and nucleon global OMPs varied dramatically with energy and mass of target nuclei. The global OMPs from Madland [7] tended to produce the largest transfer cross sections.
Finally, the influences of the spin-orbit coupling term of the deuteron and nucleon global OMPs, respectively, on transfer cross sections were also systematically analyzed. The theoretical results illustrate that the effects of the spin-orbit coupling term of deuteron global OMPs on transfer cross sections strengthen with increasing deuteron energies. Meanwhile, the effects of the spin-orbit coupling term of nucleon global OMPs on transfer cross sections become irregular with the proton energies.
Our studies suggest that the spin-orbit interaction is not negligible in differential cross sections, but the overall effect is small.
Systematic study of global optical model potentials in (d, p) transfer reactions
- Received Date: 2022-11-30
- Available Online: 2023-04-15
Abstract: In the T-matrix form of the transfer reaction, the optical model potentials (OMPs) are used to compute the scattering wave function and transition operator. For most cases, the elastic scattering cross sections, normally used to generate the OMPs, are not directly given in the same experiment. Then, the global OMPs, which fit the experimental data over a broad mass and energy range, are widely used in the theoretical calculations. Different sets of global OMPs with different parameter sets can reproduce the scattering cross section equally well within the uncertainty. Here, we apply different global OMPs to calculate the (differential) cross sections of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: