-
Spontaneous radioactivity of nuclei has always been a popular topic in the field of nuclear physics [1]. To date, more than 2000 nuclei have been discovered, most of which are unstable [2], and they become stable by spontaneous emission of radiation and/or particles. In the regions of heavy and superheavy nuclei, cluster radioactivity is one of the main decay modes. In this radioactive process, an unstable parent nucleus emits a cluster particle, which is heavier than an α particle but lighter than the lightest fission fragment. This was first predicted by S
$\rm\check{a}$ ndulescu, Poenaru, and Greiner in 1980 [3]. A few years later, Rose and Jones observed the release of$ ^{14}{\rm{C}} $ emitted from$ ^{223}{\rm{Ra}} $ in experiments, which verified the realistic existence of this radioactivity [4]. Since then, cluster radioactivity has evolved as a popular subject, and a great deal of works have been devoted to researching and exploring it [5−8, 9]. To date, many types of clusters, such as$ ^{14}{\rm{C}} $ ,$ ^{20}{\rm{O}} $ ,$ ^{23}{\rm{F}} $ ,$ ^{24,25,26}{\rm{Ne}} $ ,$ ^{28,30}{\rm{Mg}} $ , and$ ^{32,34}{\rm{Si}} $ , have been discovered and confirmed to emit from parent nuclei ranging from$ ^{221}{\rm{Fr}} $ to$ ^{242}{\rm{Cm}} $ in experiments [10−14]. At the same time, during the launch, parent nuclei were found to decay into the doubly magic daughter nucleus$ ^{208}{\rm{Pb}} $ or its adjacent daughter nuclei, which garnered the interest of many people because this can provide vital information on the nuclear structure, such as the ground state lifetime, nuclear spin and parity, shell effects, and nuclear deformation [15, 16].Theoretically, there are two ways of explaining the cluster radioactivity process: the spontaneous fission process with super asymmetric mass and the α-like process [17−20]. In the former, the cluster is considered to be formed continuously with the shape evolution of the parent nucleus as it penetrates the nuclear barrier [9, 21]. In the latter, as a traditional α-decay approach, the cluster is assumed to be preformed in the parent nuclei with a certain probability before penetrating the potential barrier [22−24]. Based on the above theories, extensive theoretical models have been put forward to address this type radioactivity, such as the Coulomb and proximity potential model (CPPM) [25], preformed cluster model (PCM) [26, 27], generalized liquid drop model (GLDM) [9], effective liquid drop model (ELDM) [28], modified unified fission model (MUFM) [29], density-dependent cluster model (DDCM) [30], and so on [31−36]. The calculated results using these models are essentially consistent with the experimental data. There are also many valid and useful empirical or semi-empirical formulas used to calculate cluster radioactivity half-lives, such as the universal decay law (UDL) proposed by Qi et al. [37], an extension of the Viola-Seaborg formula from α decay to cluster radioactivity proposed by Ren et al. [38], a unified formula for the half-lives of α decay and cluster radioactivity proposed by Ni et al. [39], a new Geiger-Nuttall law for α decay and cluster radioactivity half-lives proposed by Ren et al. [40], and so on [41−47].
In 2005, Tavares et al. first proposed a phenomenological one-parameter model (OPM) to evaluate the α decay half-lives of bismuth isotopes on account of Wentzel-Kramers-Brillouin (WKB) theory and considering the overlapping effect [48]. Since then, the OPM has been successfully applied to evaluate the α decay half-lives of platinum and neptunium isotopes, and the calculated results can reproduce the experimental data well [49, 50]. Recently, Zou et al. successfully extended this model to the aspect of proton radioactivity [51]. Meanwhile, based on the OPM, considering the screened electrostatic barrier, Xu et al. successfully calculated the α decay half-lives of uranium isotopes [52]. Because cluster radioactivity shares the same mechanism of the tunneling effect with proton radioactivity and α decay, whether the OPM considering the screened electrostatic barrier can be extended to study cluster radioactivity is an interesting question. To this end, considering the screened electrostatic effect of the Coulomb potential and using the OPM, we systematically study the cluster radioactivity half-lives of 22 nuclei ranging from
$ ^{221}{\rm{Fr}} $ to$ ^{242}{\rm{Cm}} $ . The calculated results indicate that this model can effectively reproduce the experimental data.This article is organized as follows. In Sec. II, the theoretical framework for calculating the cluster radioactivity half-life is briefly described. The calculations and discussion are presented in Sec. III. Finally, a brief summary is given in Sec. IV.
-
The cluster radioactivity half-life is defined as [53]
$ \begin{eqnarray} {T}_{1/2} = \frac{{\rm{ln2}}}{\lambda}=\frac{{\rm{ln2}}}{\nu{S}_{c}{P}}, \end{eqnarray} $

(1) where λ is the decay constant. It consists of three parts. One of its components, ν, is the assault frequency, which represents the number of assaults on the barrier per unit time. It can be calculated via [54, 55]
$ \begin{eqnarray} \nu=\frac{\pi\hbar}{2\mu{a}^{2}}, \end{eqnarray} $

(2) where
$ \hbar $ is the reduced Planck constant.$ a=R_{p}-R_{c} $ represents the inner turning point of the potential barrier, where$ R_{p} $ and$ R_{c} $ are the radius of the parent nucleus and emitted cluster, respectively. Detailed information about$ R_{p} $ and$ R_{c} $ is presented in the next paragraph.$\mu=\dfrac{m_{d}m_{c}}{m_{d}+m_{c}}$ denotes the reduced mass between the daughter nucleus and emitted cluster, where$ m_{d} $ and$ m_{c} $ are the atomic mass of the daughter nucleus and emitted cluster, respectively. In this study,$ m_{c} $ is taken from AME2020 [56], and$ m_{d} $ can be obtained using$ \begin{eqnarray} m_{d}=A_{d}+\frac{\Delta{M}_{d}}{F}-\left(Z_{d}m_{e}-\frac{10^{-6}kZ_{d}^{\beta}}{F}\right), \end{eqnarray} $

(3) where
$ m_{e} $ =0.548579911$ \times{10^{-3}}u $ is the electron rest mass, with u being the atomic mass,$ F=931.494 $ MeV$ u^{-1} $ is the mass-energy conversion factor,$ A_{d} $ ,$ Z_{d} $ , and$ \Delta{M}_{d} $ are the mass number, proton number, and mass excess of the daughter nucleus, respectively, and the quantity$ kZ^{\beta} $ represents the total binding energy of the Z electron in the atom, where$ k=8.7 $ eV, β=2.517 for$ Z\ge60 $ , whereas$ k=13.6 $ eV β=2.408 for$ Z<60 $ [57].The other two components,
$ {S}_{c} $ , which represents the spectroscopic factor (the probability of finding the cluster at the nuclear surface), and$ {P} $ , which represents the penetrability factor (the probability of the cluster penetrating the external barrier) [58], can be calculated using$ \begin{eqnarray} S_{c}=\exp^{-G_{\rm ov}}, \;\;G_{\rm ov}=\frac{2}{\hbar}\int_{a}^{b} \sqrt{{2\mu}\left[{V(r)-Q_{c}}\right]}{\rm d}r, \end{eqnarray} $

(4) $ \begin{eqnarray} P=\exp^{-G_{\rm se}}, \;\;G_{\rm se}=\frac{2}{\hbar}\int_{b}^{c} \sqrt{{2\mu}\left[{V(r)-Q_{c}}\right]}{\rm d}r. \end{eqnarray} $

(5) Here,
$G_{\rm ov}$ is the G-factor of the overlapping region, where the cluster particle drives away from the parent nucleus until the outer surfaces of the nucleus touch each other,$G_{\rm se}$ is the G-factor of the separate region,$ b=R_{d}+ R_{c} $ , and c represents the separating point and outer turning point of the potential barrier, where$ R_{d} $ is the radius of the daughter nucleus.$ R_{p} $ and$ R_{d} $ are calculated using the droplet model of the atomic nucleus, which can be expressed as [48, 59]$ \begin{eqnarray} R_{i}=\frac{Z_{i}}{A_{i}}R_{pi}+\left(1-\frac{Z_{i}}{A_{i}}\right) R_{ni}, &\;\;i=p,\;d, \end{eqnarray} $

(6) where
$ R_{pi} $ and$ R_{ni} $ are given by$ \begin{eqnarray} R_{ji}=r_{ji}\left[1+\frac{5}{2}\left(\frac{w}{r_{ji}}\right)^{2} \right],&\;~j=p,\;n,&i=p,\;d. \end{eqnarray} $

(7) Here,
$ w = 1 $ fm is the diffuseness of the nuclear surface, and$ r_{ji} $ represents the equivalent sharp radius of the proton$ (j = p) $ or neutron$ (j = n) $ density distribution of the parent nucleus$ (i = p) $ or daughter nucleus$ (i = d) $ , respectively. According to the finite-range droplet model theory of nuclei proposed by M$ \ddot{o} $ ller et al. [59], the equivalent sharp radius can be expressed as$ \begin{eqnarray} r_{pi}=r_{0}\left(1+\bar{\epsilon_{i}}\right)\left[1-\frac{2}{3}\left(1-\frac{Z_{i}}{A_{i}}\right)\left(1-\frac{2Z_{i}}{A_{i}}-\bar{\delta_{i}}\right)\right]A_{i}^{1/3}, \end{eqnarray} $

(8) $ \begin{eqnarray} r_{ni}=r_{0}\left(1+\bar{\epsilon_{i}}\right)\left[1+\frac{2}{3}\frac{Z_{i}}{A_{i}}\left(1-\frac{2Z_{i}}{A_{i}}-\bar{\delta_{i}}\right)\right]A_{i}^{1/3}, \end{eqnarray} $

(9) where
$ r_{0}=1.16 $ fm,$ i = p $ (parent nucleus) or d (daughter nucleus), and$ \bar{\epsilon_{i}} $ and$ \bar{\delta_{i}} $ can be given by$ \begin{eqnarray} \bar{\epsilon_{i}}=\frac{1}{4 {\rm e}^{0.831A_{i}^{1/3}}}-\dfrac{0.191}{A_{i}^{1/3}}+\frac{0.0031Z_{i}^{2}}{A_{i}^{4/3}}, \end{eqnarray} $

(10) $ \begin{eqnarray} \bar{\delta_{i}}=\left(1-\frac{2Z_{i}}{A_{i}}+0.004781\frac{Z_{i}}{A_{i}^{2/3}}\right)\mathbf{/}\left(1+\frac{2.52114}{A_{i}^{1/3}}\right). \end{eqnarray} $

(11) The above radius parameterization does not apply to lighter nuclei with
$ Z<8 $ and$ A<16 $ [59, 60]. For unity, the radius of all emitted clusters is parameterized as follows [51]:$ \begin{eqnarray} R_{c}=1.28A_{c}^{1/3}-0.76+0.8A_{c}^{-1/3}, \end{eqnarray} $

(12) where
$ A_{c} $ is the mass number of the emitted cluster.$ Q_{c} $ represents the cluster radioactivity released energy. It can be obtained using$ \begin{eqnarray} Q_{c}=\Delta{M}_{p}-(\Delta{M}_{d}+\Delta{M}_{c})+10^{-6}k(Z_{p}^{\beta}-Z_{d}^{\beta}), \end{eqnarray} $

(13) where
$ \Delta{M}_{p} $ and$ \Delta{M}_{c} $ are the mass excess of the parent nucleus and emitted cluster, respectively. They are extracted from the evaluated nuclear properties table NUBASE2020 [61]. The term$ k(Z_{p}^{\beta}-Z_{d}^{\beta}) $ represents the screened effect of the atomic electrons, where$ k=8.7 $ eV, β = 2.517 for$ Z\ge60 $ , whereas$ k=13.6 $ eV, β = 2.408 for$ Z<60 $ [57].$ V(r) $ , roughly shown in Fig. 1, is the total interaction potential between the daughter nucleus and emitted cluster. At the two points a and c, the condition$ V(a)=V(c)=Q_{c} $ is satisfied. In general, the total interaction potential$ V(r) $ consists of the nuclear potential$ V_{N}(r) $ , Coulomb potential$ V_{C}(r) $ , and centrifugal potential$ V_{\ell}(r) $ and can be expressed as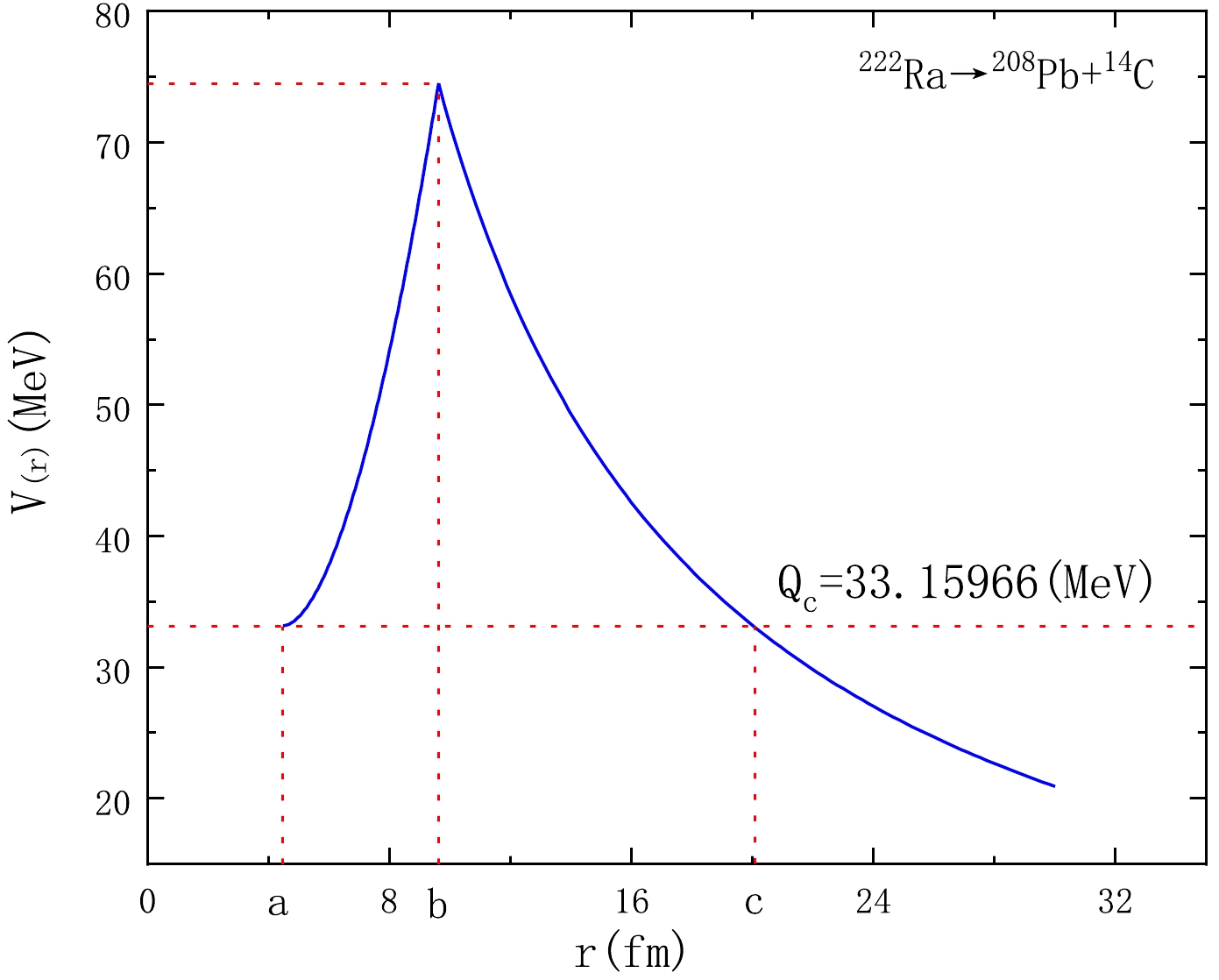
Figure 1. (color online) Schematic diagram of the interaction potential
$V(r)$ between the cluster and daughter nucleus. a, b, and c are the three turning points of the potential energy. The barrier of a to b is the overlapping region, and barrier of b to c is the separation region.$ \begin{eqnarray} V(r)=V_{N}(r)+V_{C}(r)+V_{\ell}(r). \end{eqnarray} $

(14) In this study, for the centrifugal potential
$ V_{\ell}(r) $ , we adopt the Langer modified centrifugal potential [62] because$ {\ell}({\ell+1})\to({\ell+\dfrac{1}{2}})^{2} $ is a necessary correction for one-dimensional problems. It can be expressed as$ \begin{eqnarray} V_{\ell}(r)=\frac{\left(\ell+1/2\right)^{2}\hbar^{2}}{2\mu{r}^{2}}, \end{eqnarray} $

(15) where
$ \ell $ is the angular momentum carried by the emitted cluster, which can be obtained via$ \begin{eqnarray} \ell=\left\{\begin{array}{llll} \Delta_{j}, & {\rm{for}}\;\;{\rm{ even}}~~ \Delta_{j} ~~{\rm{and}}~~ \pi_{p} = \pi_{d},\\ \Delta_{j}+1, & {\rm{for}}\;\;{\rm{ even}}~~ \Delta_{j} ~~{\rm{and}}~~ \pi_{p} \neq \pi_{d},\\ \Delta_{j}, & {\rm{for }}\;\;{\rm{odd}} ~~ \Delta_{j} ~~{\rm{and}}~~ \pi_{p} \neq \pi_{d},\\ \Delta_{j}+1, &{\rm{for }}\;\;{\rm{odd}} ~~ \Delta_{j} ~~{\rm{and}}~~ \pi_{p} = \pi_{d}, \end{array}\right. \end{eqnarray} $

(16) where
$ \Delta_{j} $ =$ \lvert {j_{p}-j_{d}-j_{c}} \rvert $ ,$ j_{p} $ ,$ \pi_{p} $ ,$ j_{d} $ ,$ \pi_{d} $ , and$ j_{c} $ ,$ \pi_{c} $ represents the spin and parity values of the parent, daughter, and cluster nuclei, respectively. They are taken from NUBASE2020 [61].The Coulomb potential
$ V_{C}(r) $ is usually defined as$ \begin{eqnarray} V_{C}(r)=\frac{Z_{c}Z_{d}e^{2}}{r}, \end{eqnarray} $

(17) where
$ e^{2}=1.4399652 $ MeV$ \cdot $ fm is the square of the electronic elementary charge. Because the cluster radioactivity process involves the superposition of the involved charges, the inhomogeneous charge distribution of the nucleus, and the movement of the emitted cluster, which generates a magnetic field, the electrostatic potential of the emitted cluster-daughter nucleus behaves as a Coulomb potential at short distances and drops exponentially at large distances, that is, the screened electrostatic effect. This behaviour of electrostatic potential can be described as the Hulthen type potential$ V_{H}(r) $ , which is defined as [63−65]$ \begin{eqnarray} V_{H}(r)=\frac{tZ_{c}Z_{d}e^{2}}{e^{tr}-1}, \end{eqnarray} $

(18) where t is the screening parameter.
In the overlapping region, μ and
$ V(r) $ cannot be calculated as a oversimplified two-body system because the cluster is still in the parent nucleus. To deal with this problem accurately, according to Refs. [48, 66, 67], μ and$ V(r) $ are rewritten in the following forms:$ \begin{eqnarray} \mu(r)=\left( \frac{m_{d}m_{c}}{m_{d}+m_{c}}\right) \left( \frac{r-a}{b-a}\right)^{p},p\ge{0}, \end{eqnarray} $

(19) $ \begin{eqnarray} &V(r)=Q_{c}+\left( V(b)-Q_{c}\right) \left( \frac{r-a}{b-a}\right)^{q},q\ge{1}, \end{eqnarray} $

(20) with
$ \begin{eqnarray} V(b)=\frac{tZ_{c}Z_{d}e^{2}}{e^{tb}-1}+\frac{\left(\ell+1/2\right)^{2}\hbar^{2}}{2\mu{b}^{2}}. \end{eqnarray} $

(21) Using Eqs. (4), (19), (20), and (21),
$ G_{\rm ov} $ can be expressed as$ \begin{aligned}[b] G_{\rm ov}=&\sqrt{\frac{931.494}{9\times10^{46}}}\frac{2\sqrt{2}(b-a)g}{\hbar}\\&\times \sqrt{\mu\left[\frac{tZ_{c}Z_{d}e^{2}}{e^{tb}-1}+\frac{9\times10^{46}}{931.494}\frac{\hbar^{2}(\ell+1/2)^{2}}{2\mu{b}^{2}}-Q_{c}\right]}\\ =&0.4374702(b-a)g\\&\times \sqrt{\mu\left[\frac{tZ_{c}Z_{d}e^{2}}{e^{tb}-1}+\frac{20.9008(\ell+1/2)^{2}}{\mu{b}^{2}}-Q_{c}\right]}, \end{aligned} $

(22) where
$ g=(1+\dfrac{p+q}{2})^{-1} $ is related to the strength of the spectroscopic factor with$ 0\le{g}\le{\dfrac{2}{3}} $ . In the separated region, the cluster is separated from the parent nucleus and the entire system is regarded as a simple two-body system. Using$ \mu=\dfrac{m_{d}m_{c}}{m_{d}+m_{c}} $ and Eqs. (5), (14), (15), and (18),$ G_{\rm se} $ can be obtained as$ \begin{aligned}[b] G_{\rm se}&=\sqrt{\frac{931.494}{9\times10^{46}}}\frac{2\sqrt{2}e^{2}{Z_{c}}{Z_{d}}}{\hbar}\sqrt{\dfrac{\mu}{Q_{c}}}\times{F}\\ &=0.62994397{Z_{c}}{Z_{d}}\sqrt{\dfrac{\mu}{Q_{c}}}\times{F}, \end{aligned} $

(23) where
$ \begin{aligned}[b] F=&\frac{x^{1/2}}{2y}\times\ln\left[\dfrac{\sqrt{x(x+2y-1)}+x+y}{(x/y)\left(1+\sqrt{1+x/y^{2}}\right)^{-1}+y}\right]\\ &+\arccos\sqrt{\frac{1}{2}\left(1-\frac{1-1/y}{\sqrt{1+x/y^2}}\right)}\\ &-\sqrt{\dfrac{1}{2y}(1+x/2y-1/2y)}, \end{aligned} $

(24) with
$ \begin{eqnarray} x=\frac{9\times10^{46}}{931.494}\frac{\hbar^{2}(\ell+1/2)^{2}}{2\mu{b}^{2}Q_{C}}=\frac{20.9008(\ell+1/2)^{2}}{\mu{b}^{2}Q_{C}}, \end{eqnarray} $

(25) $ \begin{eqnarray} y=\dfrac{\ln(tZ_{c}Z_{d}e^{2}/Q_{c}+1)}{2tb}. \end{eqnarray} $

(26) Based on the above, the cluster radioactivity half-life can be expressed as
$ \begin{eqnarray} \begin{aligned} T_{1/2}&=\frac{931.494}{9\times10^{46}}\times\frac{2\ln{2}}{\pi\hbar}\mu{a}^{2}S_{c}^{-1}P^{-1}\\ &=6.93868752\times10^{-24}\mu{a}^{2}S_{c}^{-1}P^{-1}. \end{aligned} \end{eqnarray} $

(27) -
In 2009, based on α-like R-matrix theory, Qi et al. proposed the UDL [37, 68]. It can be expressed as
$ \begin{eqnarray} {\rm{lg}}{T_{1/2}}= a Z_{c}Z_{d}\sqrt{\frac{\mathcal{A}}{Q_{c}}}+b\sqrt{\mathcal{A}Z_{c}Z_{d}(A_{c}^{1/3}+A_{d}^{1/3})}+c, \end{eqnarray} $

(28) where
$ \mathcal{A}=A_{c}A_{d}/(A_{c}+A_{d}) $ is the reduced mass of the emitted cluster-daughter nucleus system measured in units of nucleon mass with$ Z_{d} $ ,$ A_{d} $ and$ Z_{c} $ ,$ A_{c} $ as the proton and mass numbers of the daughter and cluster nuclei, respectively,$ Q_{c} $ represents the cluster radioactivity released energy, and$ a=0.4314 $ ,$ b=-0.3921 $ , and$ c=-32.7044 $ are the adjustable parameters. -
In 2008, based on the Geiger-Nuttall law, Santhosh et al. proposed a semi-empirical model to calculate the half-lives of α decay and cluster radioactivity [69]. It can be expressed as
$ \begin{eqnarray} {\rm{log}}_{10}{T_{1/2}}= a Z_{c}Z_{d}Q_{c}^{-1/2}+b\eta_{A}+c, \end{eqnarray} $

(29) where
$ \eta_{A}=\dfrac{A_{d}-A_{c}}{A} $ is the mass asymmetry,$ Q_{c} $ represents the α decay energy and cluster radioactivity released energy, and$ a=0.727356 $ ,$ b=40.3887 $ , and$ c=-85.1625 $ are the adjustable parameters. -
In 2008, Ni et al. proposed a unified formula for the half-lifes of α decay and cluster radioactivity using the WKB approximation [39]. It can be expressed as
$ \begin{eqnarray} {\rm{lg}}{T_{1/2}}= a \sqrt{\mathcal{A}}Z_{c}Z_{d}Q_{c}^{-1/2}+b\sqrt{\mathcal{A}}(Z_{c}Z_{d})^{1/2}+c, \end{eqnarray} $

(30) where
$ \mathcal{A}=A_{c}A_{d}/(A_{c}+A_{d}) $ is the reduced mass, as in the UDL,$ Q_{c} $ represents the α decay energy and cluster radioactivity released energy, and$ a=0.38617 $ ,$ b=-1.08676 $ ,$ c_{e-e}=-21.37195 $ , and$ c_{o-e,o-e}=-20.11223 $ are the adjustable parameters. -
Based on WKB theory, considering the screened electrostatic effect of the Coulomb potential, we propose a phenomenological model by modifying the OPM to calculate the cluster radioactivity half-lives of 22 nuclei, which contains two adjustable parameters, t and g. The standard deviation between the experimental and calculated data is taken as the objective function. Using the experimental data of the 22 nuclei in the genetic algorithm, we obtain the optimal adjustable parameters
$ g=0.416617 $ and$ t=9.176915 \times10^{-3} $ . In this study, the standard deviation σ is defined as$ \begin{eqnarray} \sigma = \sqrt{\sum{({\rm{lg}}{T_{1/2}^{{\rm{cal}}}}-{\rm{lg}}{T_{1/2}^{{\rm{exp}}}})^2}/n}\ , \end{eqnarray} $

(31) where
$ {\rm{log}}_{10}{T_{1/2}^{{\rm{exp}}}} $ and$ {\rm{log}}_{10}{T_{1/2}^{{\rm{cal}}}} $ are the logarithmic forms of the experimental and calculated cluster radioactivity half-lives, respectively, and n is the number of nuclei involved in different decay cases. We calculate the standard deviation σ between the experimental data and data calculated using our model, the OPM, UDL, Santhosh's semi-empirical formula, and Ni's formula, denoted as$ \sigma_{\rm Cal} $ ,$ \sigma_{\rm OPM} $ ,$ \sigma_{\rm UDL} $ ,$ \sigma_{\rm San} $ , and$\sigma_{\rm Ni}$ , respectively. The results are shown in Table 1. From the table, we can clearly see that the standard deviation σ of our result is 0.660, which is better than those of the OPM, UDL, and Santhosh's semi-empirical formula results (0.904, 1.237, and 2.470, respectively) but worse than that of the Ni's formula result (0.456). In particular, the σ value for the 22 nuclei within the modified OPM decreased by$\dfrac{0.904-0.660}{0.904}=26.99$ % relative to that within the OPM. This indicates that the calculated half-lives given by our modified OPM can better reproduce the experimental data.Cases Model $\sigma_{\rm Cal}$ 

$\sigma_{\rm OPM}$ 

$\sigma_{\rm UDL}$ 

$\sigma_{\rm San}$ 

$\sigma_{\rm Ni}$ 

22 nuclei 0.660 0.904 1.237 2.470 0.456 Table 1. Standard deviation σ between the experimental half-lives and those calculated using different formulas and/or models for cluster radioactivity.
Furthermore, using the optimal parameter values of t and g and our modified OPM, we systematically calculate the cluster radioactivity half-lives of 22 nuclei. For comparision, the UDL, Santhosh's semi-empirical formula, and Ni's formula are also used. Detailed results are given in Table 2. In this table, the first to third columns contain the decay processes of the cluster, the angular momentum l taken away by the emitted cluster, and the cluster radioactivity released energy
$ Q_{c} $ , respectively. The fourth and fifth columns show the spectroscopic factor$ S_{c} $ and penetrability factor P in logarithmic form, respectively. The sixth to tenth columns contain the experimental data of the cluster radioactivity half-lifes and those calculated ones using our model, the UDL, Santhosh's semi-empirical formula, and Ni's formula in logarithmic form, denoted as$ {\rm{log}}_{10}{T_{1/2}^{{\rm{exp}}}} $ ,$ {\rm{log}}_{10}{T_{1/2}^{{\rm{cal}}}} $ ,$ {\rm{log}}_{10}{T_{1/2}^{{\rm{UDL}}}} $ ,$ {\rm{log}}_{10}{T_{1/2}^{{\rm{San}}}} $ , and$ {\rm{log}}_{10}{T_{1/2}^{{\rm{Ni}}}} $ , respectively. As shown, the calculated half-lives using our model are in good agreement with experimental data as well as the calculated results obtained using Ni's formula. To intuitively compare these results, we plot the differences between the experimental cluster radioactivity half-lives and those calculated ones using our model, the UDL, Santhosh's semi-empirical formula, and Ni's formula in logarithmic form in Fig. 2. From this figure, we can clearly see that the differences between the experimental data and the calculated results from our model and Ni's formula are within or near$ \pm1 $ overall. For the UDL, there are three nuclei beyond the scale of$ \pm2 $ , whereas this is up to seven nuclei for Santhosh's semi-empirical formula. In the case of$ ^{231}{\rm{Pa}}\to^{208}{\rm{Pb}} +^{23}{\rm{F}} $ and$ ^{242}{\rm{Cm}}\to^{208}{\rm{Pb}}+^{34}{\rm{Si}} $ , the discrepancies can even reach 4.44 and 5.59, respectively. Furthermore, from the overall trend, the results in our model and Ni's formula are more converging on the neighboring zero line area, whereas the distribution of the results of Santhosh's semi-empirical formula is slightly scattered. Based on the above, we find that the cluster radioactivity half-life calculated ones using our model can effectively reproduce the experimental data.Cluster decay $\ell$ 

$Q_{c}$ 

$S_{c}$ 

P ${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,exp}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,cal}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,UDL}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,San}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,Ni}}}$ 

$^{221}$ Fr

$\to^{207}$ Tl

$+^{14}$ C

$3$ 

$ 31.4002 $ 

$ -9.0144 $ 

$ -26.1482 $ 

$ 14.56 $ 

$ 14.45 $ 

$ 12.47 $ 

$ 13.19 $ 

$ 14.41 $ 

$^{221}$ Ra

$\to^{207}$ Pb

$+^{14}$ C

$3$ 

$ 32.5072 $ 

$ -8.9798 $ 

$ -25.1296 $ 

$ 13.39 $ 

$ 13.40 $ 

$ 11.23 $ 

$ 12.87 $ 

$ 13.27 $ 

$^{222}$ Ra

$\to^{208}$ Pb

$+^{14}$ C

$0$ 

$ 33.1597 $ 

$ -8.8685 $ 

$ -23.9449 $ 

$ 11.22 $ 

$ 12.11 $ 

$ 9.85 $ 

$ 12.28 $ 

$ 10.82 $ 

$^{223}$ Ra

$\to^{209}$ Pb

$+^{14}$ C

$4$ 

$ 31.9390 $ 

$ -9.0515 $ 

$ -26.0547 $ 

$ 15.05 $ 

$ 14.40 $ 

$ 12.33 $ 

$ 13.48 $ 

$ 14.35 $ 

$^{224}$ Ra

$\to^{210}$ Pb

$+^{14}$ C

$0$ 

$ 30.6454 $ 

$ -9.1609 $ 

$ -27.9956 $ 

$ 15.87 $ 

$ 16.45 $ 

$ 15.13 $ 

$ 14.82 $ 

$ 15.64 $ 

$^{226}$ Ra

$\to^{212}$ Pb

$+^{14}$ C

$0$ 

$ 28.3077 $ 

$ -9.4243 $ 

$ -32.3293 $ 

$ 21.20 $ 

$ 21.05 $ 

$ 20.66 $ 

$ 17.48 $ 

$ 20.68 $ 

$^{223}$ Ac

$\to^{209}$ Bi

$+^{14}$ C

$2$ 

$ 33.1768 $ 

$ -8.9726 $ 

$ -24.6986 $ 

$ 12.60 $ 

$ 12.97 $ 

$ 10.84 $ 

$ 13.04 $ 

$ 12.98 $ 

$^{228}$ Th

$\to^{208}$ Pb

$+^{20}$ O

$0$ 

$ 44.8739 $ 

$ -13.0015 $ 

$ -29.5698 $ 

$ 20.73 $ 

$ 21.95 $ 

$ 21.66 $ 

$ 19.37 $ 

$ 21.27 $ 

$^{231}$ Pa

$\to^{208}$ Pb

$+^{23}$ F

$1$ 

$ 52.0539 $ 

$ -14.8949 $ 

$ -30.1885 $ 

$ 26.02 $ 

$ 24.49 $ 

$ 24.57 $ 

$ 21.58 $ 

$ 25.30 $ 

$^{230}$ Th

$\to^{206}$ Hg

$+^{24}$ Ne

$0$ 

$ 57.9453 $ 

$ -15.7237 $ 

$ -29.8159 $ 

$ 24.63 $ 

$ 24.95 $ 

$ 25.05 $ 

$ 23.24 $ 

$ 24.28 $ 

$^{231}$ Pa

$\to^{207}$ Tl

$+^{24}$ Ne

$1$ 

$ 60.5984 $ 

$ -15.4928 $ 

$ -27.5145 $ 

$ 22.89 $ 

$ 22.42 $ 

$ 21.95 $ 

$ 22.52 $ 

$ 22.80 $ 

$^{232}$ U

$\to^{208}$ Pb

$+^{24}$ Ne

$0$ 

$ 62.5013 $ 

$ -15.3769 $ 

$ -26.2290 $ 

$ 20.39 $ 

$ 21.02 $ 

$ 20.27 $ 

$ 22.31 $ 

$ 20.07 $ 

$^{233}$ U

$\to^{209}$ Pb

$+^{24}$ Ne

$2$ 

$ 60.6771 $ 

$ -15.6747 $ 

$ -28.3978 $ 

$ 24.84 $ 

$ 23.49 $ 

$ 23.30 $ 

$ 23.47 $ 

$ 24.11 $ 

$^{234}$ U

$\to^{210}$ Pb

$+^{24}$ Ne

$0$ 

$ 59.0168 $ 

$ -15.9235 $ 

$ -30.4173 $ 

$ 25.93 $ 

$ 25.76 $ 

$ 26.17 $ 

$ 24.58 $ 

$ 25.50 $ 

$^{233}$ U

$\to^{208}$ Pb

$+^{25}$ Ne

$2$ 

$ 60.8954 $ 

$ -16.0720 $ 

$ -28.4021 $ 

$ 24.84 $ 

$ 23.90 $ 

$ 23.66 $ 

$ 22.99 $ 

$ 24.57 $ 

$^{234}$ U

$\to^{208}$ Pb

$+^{26}$ Ne

$0$ 

$ 59.6043 $ 

$ -16.7010 $ 

$ -30.2412 $ 

$ 25.93 $ 

$ 26.38 $ 

$ 26.65 $ 

$ 23.51 $ 

$ 26.20 $ 

$^{234}$ U

$\to^{206}$ Hg

$+^{28}$ Mg

$0$ 

$ 74.3372 $ 

$ -18.1723 $ 

$ -27.9477 $ 

$ 25.53 $ 

$ 25.56 $ 

$ 25.40 $ 

$ 26.55 $ 

$ 24.93 $ 

$^{236}$ Pu

$\to^{208}$ Pb

$+^{28}$ Mg

$0$ 

$ 79.9042 $ 

$ -17.6878 $ 

$ -24.2891 $ 

$ 21.52 $ 

$ 21.43 $ 

$ 20.29 $ 

$ 25.71 $ 

$ 20.45 $ 

$^{238}$ Pu

$\to^{210}$ Pb

$+^{28}$ Mg

$0$ 

$ 76.1457 $ 

$ -18.3360 $ 

$ -28.0659 $ 

$ 25.70 $ 

$ 25.86 $ 

$ 25.89 $ 

$ 27.74 $ 

$ 25.63 $ 

$^{238}$ Pu

$\to^{208}$ Pb

$+^{30}$ Mg

$0$ 

$ 77.0272 $ 

$ -19.0051 $ 

$ -27.4707 $ 

$ 25.70 $ 

$ 25.94 $ 

$ 25.68 $ 

$ 26.59 $ 

$ 25.77 $ 

$^{238}$ Pu

$\to^{206}$ Hg

$+^{32}$ Si

$0$ 

$ 91.4554 $ 

$ -20.3917 $ 

$ -25.8916 $ 

$ 25.28 $ 

$ 25.75 $ 

$ 25.09 $ 

$ 29.55 $ 

$ 25.24 $ 

$^{242}$ Cm

$\to^{208}$ Pb

$+^{34}$ Si

$0$ 

$ 96.8219 $ 

$ -20.7044 $ 

$ -23.2721 $ 

$ 23.15 $ 

$ 23.46 $ 

$ 21.96 $ 

$ 28.74 $ 

$ 23.13 $ 

Table 2. Comparison of the discrepancy in logarithmic form between the experimental cluster radioactivity half-lives and those calculated ones using our model, the UDL, Santhosh's semi-empirical formula, and Ni's formula. The cluster released energy and half-lives are in units of
$({\rm MeV})$ and$(\rm s)$ , respectively. The experimental cluster radioactivity half-lives are taken from Refs. [30, 70, 71].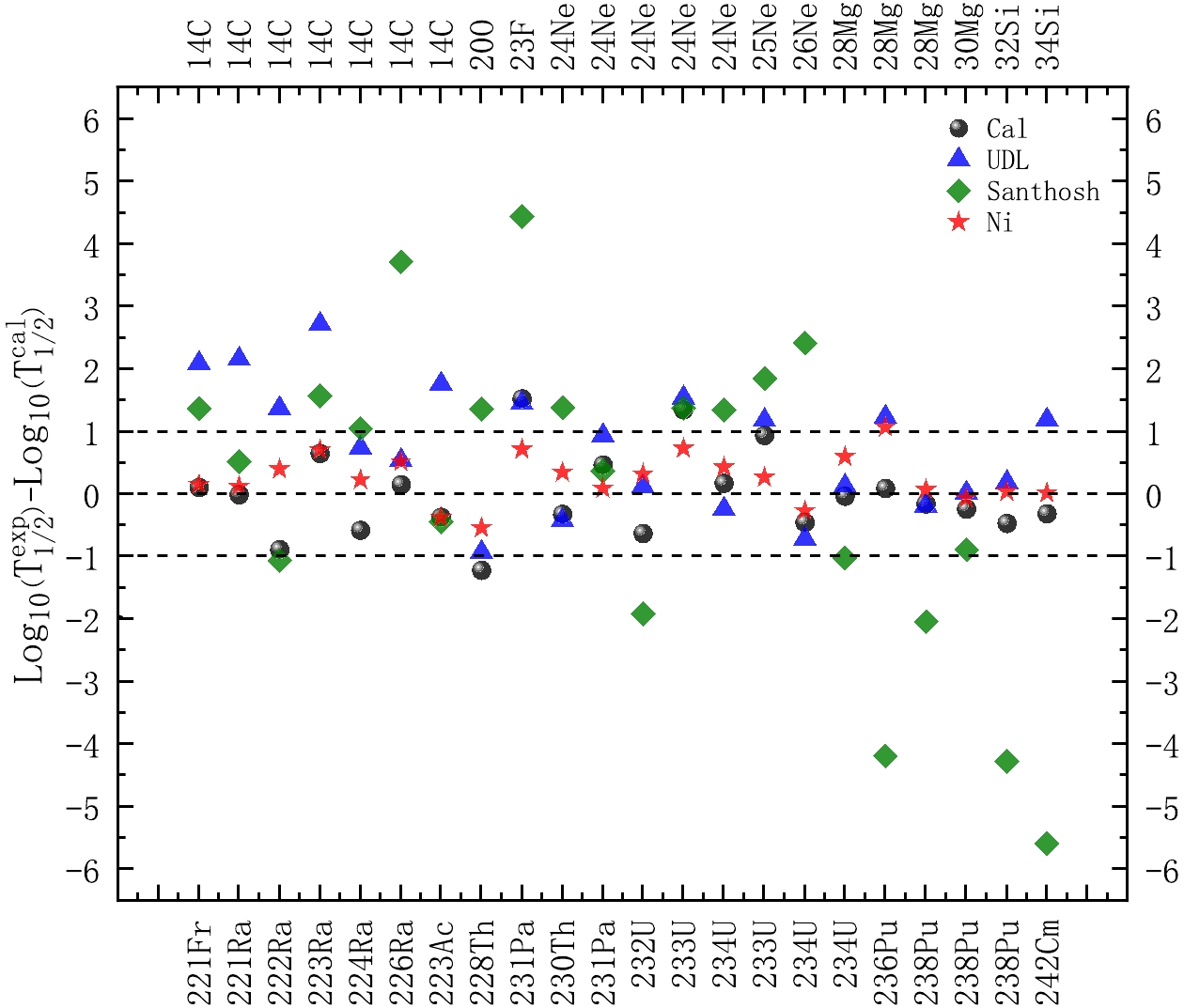
Figure 2. (color online) Comparison of the discrepancy between the experimental cluster radioactivity half-lives and those calculated ones using our model, the UDL, Santhosh's semi-empirical formula, and Ni's formula in logarithmic form.
In addition, we show the relationship between the 22 cluster radioactivity nuclei and the corresponding preformation probability calculated using our model in logarithmic form in Fig. 3. In this figure, the preformation probability value is found to decrease as the size of the cluster increases. For different cluster radioactivity nuclei, most of the preformation probabilities of emitting clusters with the same number of protons are consistent. The structure of this curve matches well with the other preformation probability values from Ref. [72]. Nevertheless, the results of their calculations vary greatly, which may have a model dependent reason. The nucleon pairing effect also has an important impact on the radioactivity of nuclei. To understand this in depth, we plot the relationship of the cluster radioactivity half-lifes and penetration probability in logarithmic form with the neutron number of the corresponding daughter nuclei in Figs. 4 and 5, respectively. From Fig. 4, it is clear that for different emitted clusters,
$ {\rm{log}}_{10}{T}_{1/2} $ first linearly decreases with an increase in the neutron number of daughter nuclei, reaches the minimum value, where it drops to the magic number of the neutron$ (N_{d}=126) $ , and finally linearly increases. The tendency is exactly opposite for$ {\rm{log}}_{10}{P} $ depicted in Fig. 5. However, they both have a turning trend when the daughter nucleus reaches the double magic number nucleus$ ^{208}{\rm{Pb}} $ , at which point they obtain the minimum and maximum values. Consequently, this indicates that neutron shell closure plays a more important role than proton shell closure in the cluster radioactivity process [73].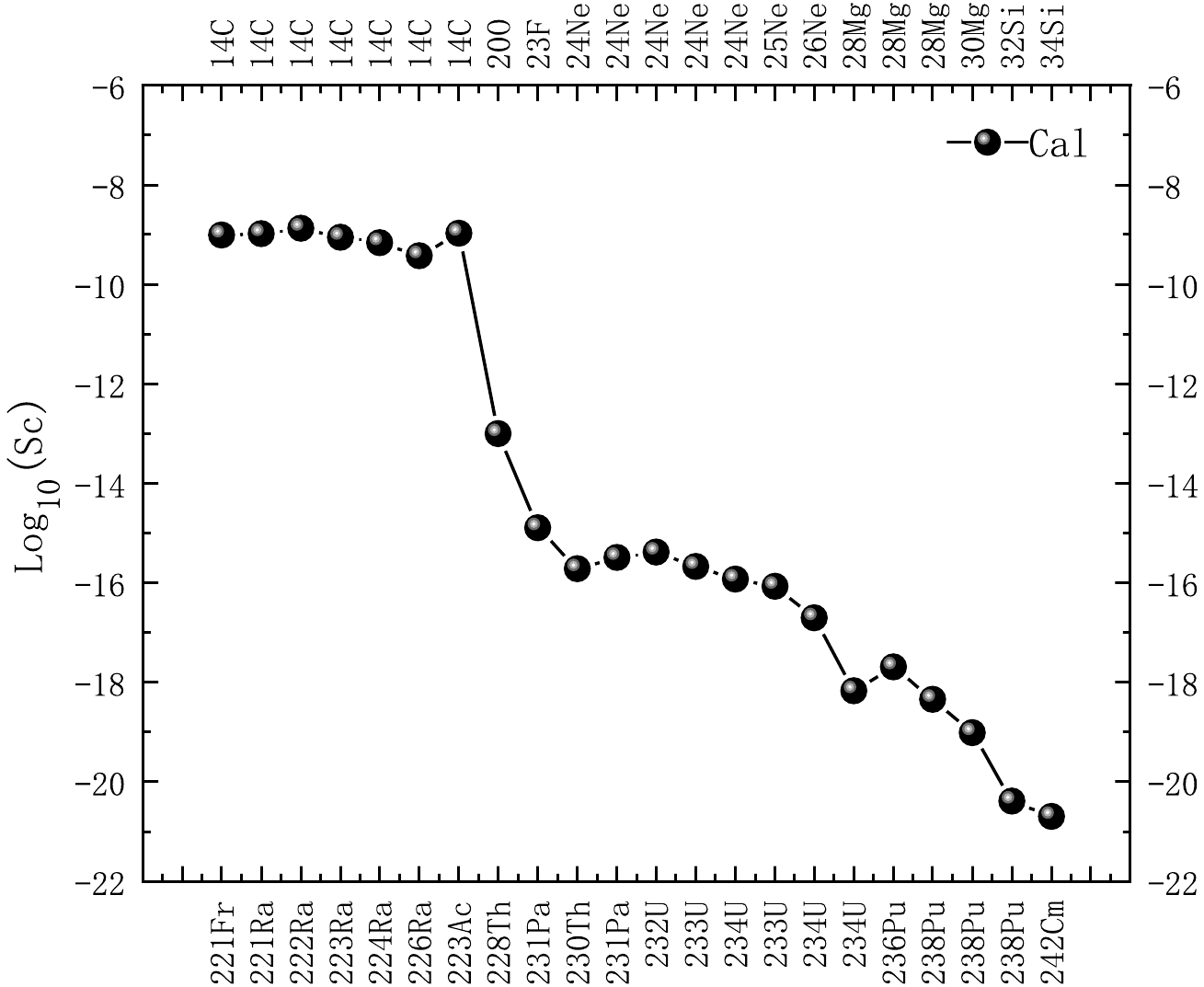
Figure 3. Relationship between the preformation probability calculated using our model in logarithmic form and the corresponding 22 cluster radioactivity nuclei.
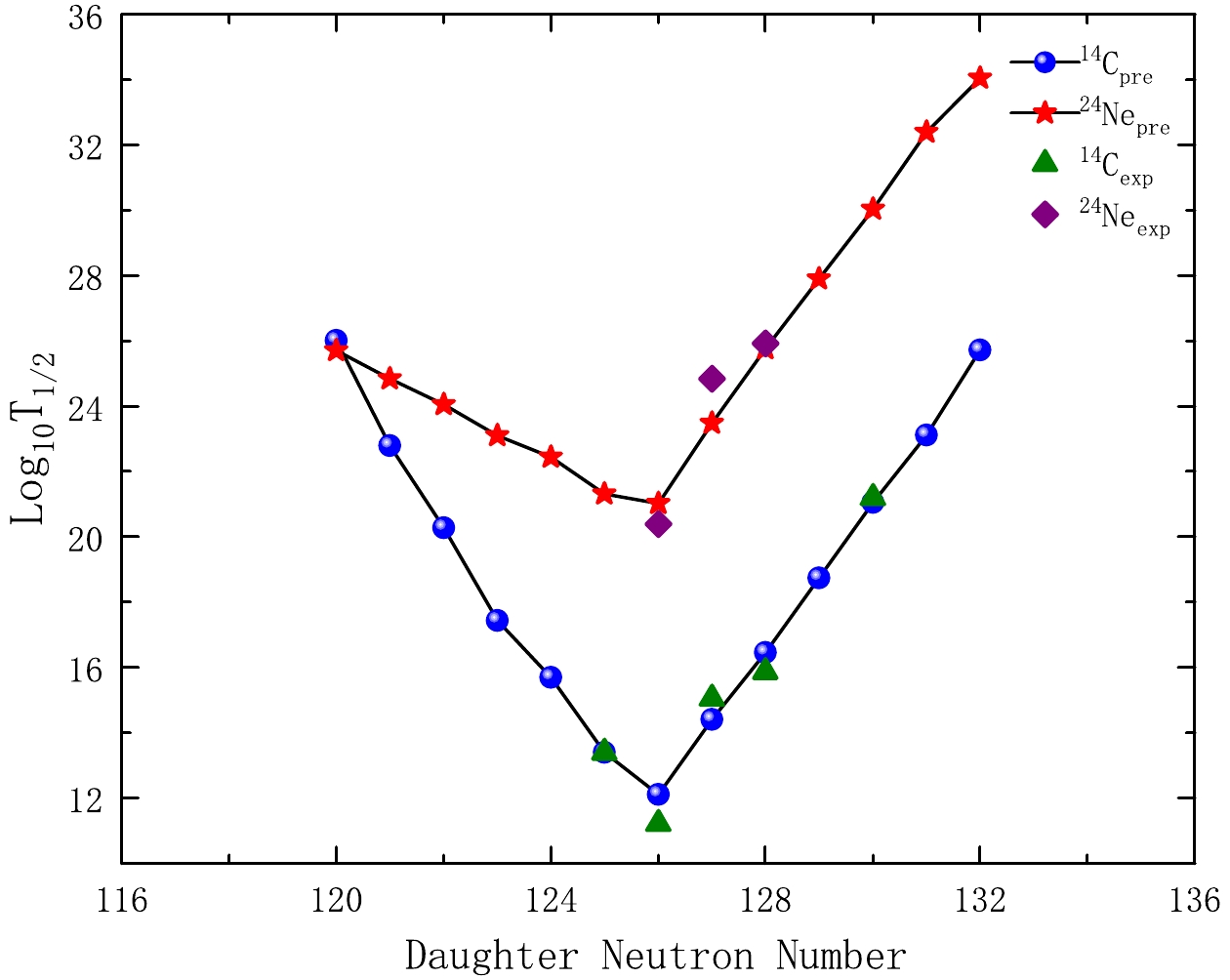
Figure 4. (color online) Plot of the calculated
${\rm{log}}_{10}{{T}}_{1/2}$ values from our model versus the neutron number of the daughter for the emission of the cluster$ ^{14}{\rm{C}}$ from$ {\rm{Ra}} $ isotopes and the emission of the cluster$ ^{24}{\rm{Ne}}$ from$ {\rm{U}} $ isotopes.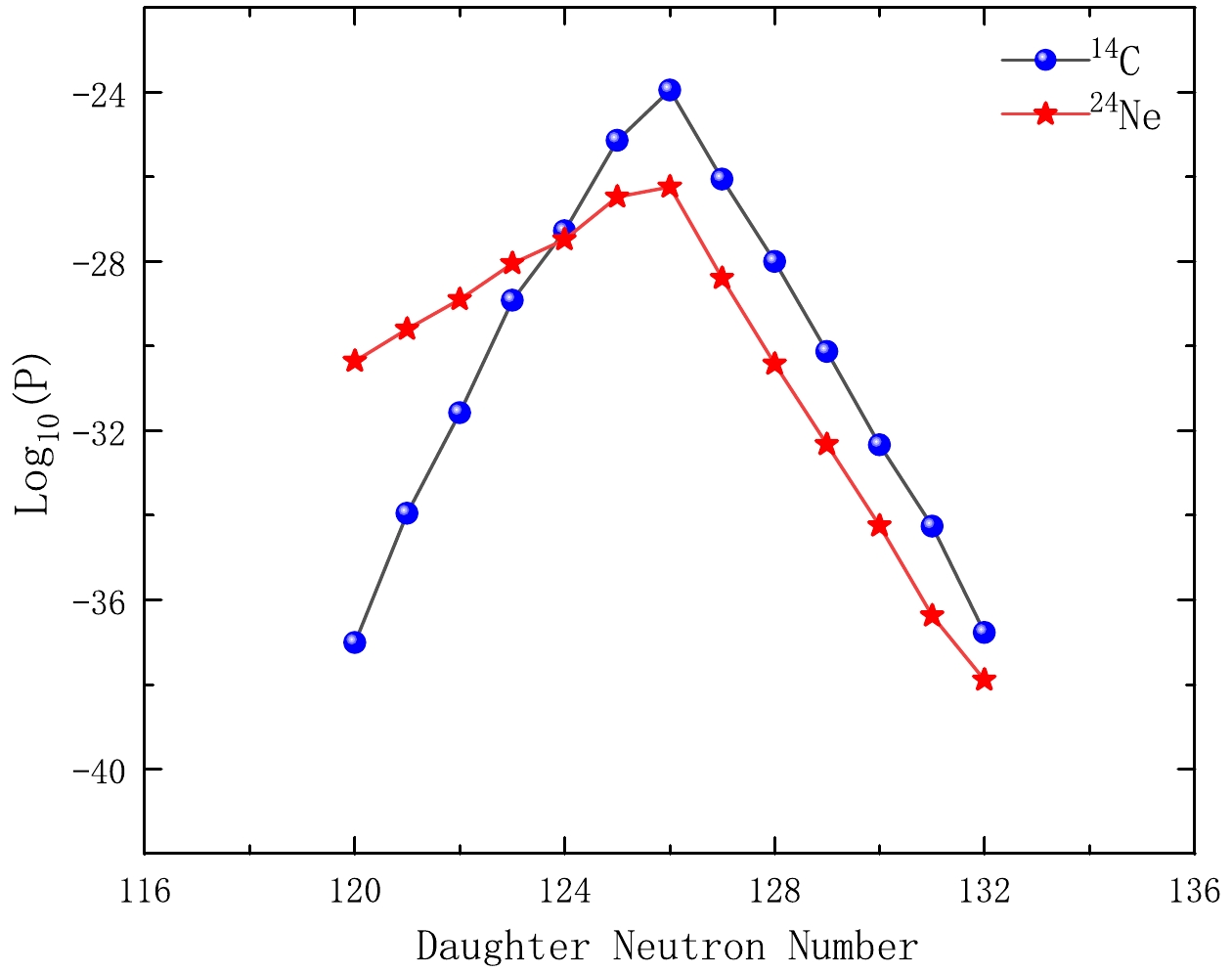
Figure 5. (color online) Plot of the calculated
${\rm{log}}_{10}{{P}}$ values from our model versus the neutron number of the daughter for the emission of the cluster$ ^{14}{\rm{C}}$ from$ {\rm{Ra}} $ isotopes and the emission of the cluster$ ^{24}{\rm{Ne}}$ from$ {\rm{U}} $ isotopes.Encouraged by the good agreement between the experimental cluster radioactivity half-lives and those calculated using our model, we extend this model to predict the half-lives of other possible cluster radioactive candidates. The detailed predictions are shown in Table 3. In this table, the heading of each column is exactly the same as in Table 2. From Table 3, it is clear that the predicted results from our model are essentially consistent with those obtained using the UDL and Ni's formula. This shows that our model is reliable for calculating cluster radioactivity. Meanwhile, these predicted values will be helpful in the search for new cluster emitters in future experiments.
Cluster decay $\ell$ 

$Q_{c}$ 

$S_{c}$ 

P ${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,exp}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,cal}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,UDL}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,San}}}$ 

${\rm{log}}_{10}{{T}}_{1/2}^{{\rm{\,Ni}}}$ 

$^{219}$ Rn

$\to^{205}$ Hg

$+^{14}$ C

$ 3 $ 

$ 28.2045 $ 

$ -9.3106 $ 

$ -31.1945 $ 

$ - $ 

$ 19.79 $ 

$ 18.82 $ 

$ 15.80 $ 

$ 20.05 $ 

$^{220}$ Rn

$\to^{206}$ Hg

$+^{14}$ C

$ 0 $ 

$ 28.6452 $ 

$ -9.2286 $ 

$ -30.1550 $ 

$ - $ 

$ 18.67 $ 

$ 17.68 $ 

$ 15.32 $ 

$ 17.82 $ 

$^{216}$ Ra

$\to^{202}$ Pb

$+^{14}$ C

$ 0 $ 

$ 26.3232 $ 

$ -9.7120 $ 

$ -37.0122 $ 

$ - $ 

$ 26.01 $ 

$ 26.44 $ 

$ 19.74 $ 

$ 25.40 $ 

$^{217}$ Ra

$\to^{203}$ Pb

$+^{14}$ C

$ 3 $ 

$ 27.7672 $ 

$ -9.5651 $ 

$ -33.9485 $ 

$ - $ 

$ 22.80 $ 

$ 22.46 $ 

$ 17.93 $ 

$ 23.14 $ 

$^{218}$ Ra

$\to^{204}$ Pb

$+^{14}$ C

$ 0 $ 

$ 28.8470 $ 

$ -9.4112 $ 

$ -31.5791 $ 

$ - $ 

$ 20.28 $ 

$ 19.66 $ 

$ 16.67 $ 

$ 19.42 $ 

$^{219}$ Ra

$\to^{205}$ Pb

$+^{14}$ C

$ 1 $ 

$ 30.2554 $ 

$ -9.2436 $ 

$ -28.9125 $ 

$ - $ 

$ 17.44 $ 

$ 16.24 $ 

$ 15.12 $ 

$ 17.67 $ 

$^{220}$ Ra

$\to^{206}$ Pb

$+^{14}$ C

$ 0 $ 

$ 31.1487 $ 

$ -9.1266 $ 

$ -27.2797 $ 

$ - $ 

$ 15.70 $ 

$ 14.18 $ 

$ 14.21 $ 

$ 14.61 $ 

$^{225}$ Ra

$\to^{211}$ Pb

$+^{14}$ C

$ 4 $ 

$ 29.5772 $ 

$ -9.3203 $ 

$ -30.1227 $ 

$ - $ 

$ 18.74 $ 

$ 17.57 $ 

$ 16.00 $ 

$ 19.13 $ 

$^{227}$ Ra

$\to^{213}$ Pb

$+^{14}$ C

$ 4 $ 

$ 27.4727 $ 

$ -9.5527 $ 

$ -34.2551 $ 

$ - $ 

$ 23.11 $ 

$ 22.80 $ 

$ 18.52 $ 

$ 23.90 $ 

$^{228}$ Ra

$\to^{214}$ Pb

$+^{14}$ C

$ 0 $ 

$ 26.2145 $ 

$ -9.6532 $ 

$ -36.7678 $ 

$ - $ 

$ 25.72 $ 

$ 26.24 $ 

$ 20.16 $ 

$ 25.76 $ 

$^{226}$ Th

$\to^{212}$ Po

$+^{14}$ C

$ 0 $ 

$ 30.6625 $ 

$ -9.3402 $ 

$ -29.5282 $ 

$ >16.76 $ 

$ 18.17 $ 

$ 17.28 $ 

$ 16.42 $ 

$ 17.59 $ 

$^{221}$ Fr

$\to^{206}$ Hg

$+^{15}$ N

$ 3 $ 

$ 34.2477 $ 

$ -10.3874 $ 

$ -31.9446 $ 

$ - $ 

$ 21.64 $ 

$ 21.27 $ 

$ 19.35 $ 

$ 21.90 $ 

$^{223}$ Ac

$\to^{208}$ Pb

$+^{15}$ N

$ 3 $ 

$ 39.6028 $ 

$ -9.9588 $ 

$ -25.2032 $ 

$ >14.76 $ 

$ 14.47 $ 

$ 12.69 $ 

$ 16.14 $ 

$ 14.25 $ 

$^{223}$ Ra

$\to^{205}$ Hg

$+^{18}$ O

$ 1 $ 

$ 40.4495 $ 

$ -12.4298 $ 

$ -33.7972 $ 

$ - $ 

$ 25.58 $ 

$ 26.13 $ 

$ 21.90 $ 

$ 26.13 $ 

$^{225}$ Ra

$\to^{205}$ Hg

$+^{20}$ O

$ 1 $ 

$ 40.6339 $ 

$ -13.3417 $ 

$ -34.5083 $ 

$ - $ 

$ 27.22 $ 

$ 27.93 $ 

$ 21.07 $ 

$ 28.03 $ 

$^{226}$ Ra

$\to^{206}$ Hg

$+^{20}$ O

$ 0 $ 

$ 40.9665 $ 

$ -13.2818 $ 

$ -33.8685 $ 

$ - $ 

$ 26.52 $ 

$ 27.13 $ 

$ 20.81 $ 

$ 26.11 $ 

$^{227}$ Ac

$\to^{207}$ Tl

$+^{20}$ O

$ 1 $ 

$ 43.2390 $ 

$ -13.0992 $ 

$ -31.1446 $ 

$ - $ 

$ 23.62 $ 

$ 23.63 $ 

$ 19.79 $ 

$ 24.26 $ 

$^{226}$ Th

$\to^{208}$ Pb

$+^{18}$ O

$ 0 $ 

$ 45.8800 $ 

$ -11.9610 $ 

$ -27.3505 $ 

$ - $ 

$ 18.67 $ 

$ 17.86 $ 

$ 19.24 $ 

$ 17.56 $ 

$^{227}$ Th

$\to^{209}$ Pb

$+^{18}$ O

$ 4 $ 

$ 44.3529 $ 

$ -12.1921 $ 

$ -29.6290 $ 

$ >15.30 $ 

$ 21.18 $ 

$ 20.70 $ 

$ 20.47 $ 

$ 21.43 $ 

$^{229}$ Th

$\to^{209}$ Pb

$+^{20}$ O

$ 2 $ 

$ 43.5582 $ 

$ -13.1959 $ 

$ -31.5903 $ 

$ - $ 

$ 24.17 $ 

$ 24.31 $ 

$ 20.47 $ 

$ 24.96 $ 

$^{227}$ Pa

$\to^{209}$ Bi

$+^{18}$ O

$ 2 $ 

$ 46.0248 $ 

$ -12.0873 $ 

$ -28.0729 $ 

$ - $ 

$ 19.52 $ 

$ 18.88 $ 

$ 20.01 $ 

$ 19.75 $ 

$^{229}$ Ac

$\to^{206}$ Hg

$+^{23}$ F

$ 2 $ 

$ 48.5111 $ 

$ -15.1129 $ 

$ -33.3699 $ 

$ - $ 

$ 27.89 $ 

$ 28.58 $ 

$ 22.30 $ 

$ 28.83 $ 

$^{228}$ Th

$\to^{206}$ Hg

$+^{22}$ Ne

$ 0 $ 

$ 55.9268 $ 

$ -15.1472 $ 

$ -31.9105 $ 

$ - $ 

$ 26.45 $ 

$ 27.14 $ 

$ 25.24 $ 

$ 25.76 $ 

$^{229}$ Th

$\to^{205}$ Hg

$+^{24}$ Ne

$ 3 $ 

$ 58.0103 $ 

$ -15.7425 $ 

$ -29.8573 $ 

$ - $ 

$ 25.01 $ 

$ 25.00 $ 

$ 23.16 $ 

$ 25.42 $ 

$^{231}$ Th

$\to^{207}$ Hg

$+^{24}$ Ne

$ 2 $ 

$ 56.4396 $ 

$ -15.9642 $ 

$ -31.8145 $ 

$ - $ 

$ 27.19 $ 

$ 27.77 $ 

$ 24.29 $ 

$ 28.04 $ 

$^{231}$ Th

$\to^{206}$ Hg

$+^{25}$ Ne

$ 2 $ 

$ 56.9830 $ 

$ -16.3195 $ 

$ -31.3968 $ 

$ - $ 

$ 27.14 $ 

$ 27.56 $ 

$ 23.57 $ 

$ 27.99 $ 

$^{232}$ Th

$\to^{208}$ Hg

$+^{24}$ Ne

$ 0 $ 

$ 54.8535 $ 

$ -16.1971 $ 

$ -33.9632 $ 

$ >29.20 $ 

$ 29.58 $ 

$ 30.76 $ 

$ 25.44 $ 

$ 29.53 $ 

$^{232}$ Th

$\to^{206}$ Hg

$+^{26}$ Ne

$ 0 $ 

$ 56.0969 $ 

$ -16.8859 $ 

$ -32.8647 $ 

$ >29.20 $ 

$ 29.18 $ 

$ 30.01 $ 

$ 23.86 $ 

$ 29.12 $ 

$^{229}$ Pa

$\to^{207}$ Tl

$+^{22}$ Ne

$ 2 $ 

$ 59.1442 $ 

$ -14.8614 $ 

$ -28.8286 $ 

$ - $ 

$ 23.09 $ 

$ 22.99 $ 

$ 24.07 $ 

$ 23.34 $ 

$^{230}$ U

$\to^{208}$ Pb

$+^{22}$ Ne

$ 0 $ 

$ 61.5800 $ 

$ -14.6702 $ 

$ -26.8616 $ 

$ >18.20 $ 

$ 20.93 $ 

$ 20.42 $ 

$ 23.50 $ 

$ 19.81 $ 

$^{226}$ U

$\to^{202}$ Pb

$+^{24}$ Ne

$ 0 $ 

$ 59.4134 $ 

$ -15.9530 $ 

$ -30.3525 $ 

$ - $ 

$ 25.71 $ 

$ 26.01 $ 

$ 24.03 $ 

$ 24.77 $ 

$^{227}$ U

$\to^{203}$ Pb

$+^{24}$ Ne

$ 1 $ 

$ 59.9744 $ 

$ -15.8542 $ 

$ -29.5899 $ 

$ - $ 

$ 24.85 $ 

$ 24.94 $ 

$ 23.70 $ 

$ 25.15 $ 

$^{228}$ U

$\to^{204}$ Pb

$+^{24}$ Ne

$ 0 $ 

$ 60.4732 $ 

$ -15.7588 $ 

$ -28.8952 $ 

$ - $ 

$ 24.06 $ 

$ 24.00 $ 

$ 23.42 $ 

$ 23.12 $ 

$^{229}$ U

$\to^{205}$ Pb

$+^{24}$ Ne

$ 1 $ 

$ 61.1246 $ 

$ -15.6438 $ 

$ -28.0475 $ 

$ - $ 

$ 23.10 $ 

$ 22.80 $ 

$ 23.05 $ 

$ 23.38 $ 

$^{230}$ U

$\to^{206}$ Pb

$+^{24}$ Ne

$ 0 $ 

$ 61.5439 $ 

$ -15.5599 $ 

$ -27.4727 $ 

$ >18.20 $ 

$ 22.45 $ 

$ 22.02 $ 

$ 22.82 $ 

$ 21.49 $ 

$^{231}$ U

$\to^{207}$ Pb

$+^{24}$ Ne

$ 3 $ 

$ 62.4014 $ 

$ -15.4240 $ 

$ -26.4674 $ 

$ - $ 

$ 21.31 $ 

$ 20.50 $ 

$ 22.34 $ 

$ 21.47 $ 

$^{235}$ U

$\to^{211}$ Pb

$+^{24}$ Ne

$ 1 $ 

$ 57.5552 $ 

$ -16.1488 $ 

$ -32.3277 $ 

$ >27.65 $ 

$ 27.90 $ 

$ 28.80 $ 

$ 25.59 $ 

$ 29.19 $ 

$^{236}$ U

$\to^{212}$ Pb

$+^{24}$ Ne

$ 0 $ 

$ 56.1369 $ 

$ -16.3590 $ 

$ -34.2490 $ 

$ - $ 

$ 30.04 $ 

$ 31.45 $ 

$ 26.62 $ 

$ 30.37 $ 

$^{237}$ U

$\to^{213}$ Pb

$+^{24}$ Ne

$ 4 $ 

$ 54.7375 $ 

$ -16.5943 $ 

$ -36.3721 $ 

$ - $ 

$ 32.40 $ 

$ 34.17 $ 

$ 27.66 $ 

$ 34.14 $ 

$^{238}$ U

$\to^{214}$ Pb

$+^{24}$ Ne

$ 0 $ 

$ 53.6341 $ 

$ -16.7265 $ 

$ -37.8870 $ 

$ - $ 

$ 34.05 $ 

$ 36.38 $ 

$ 28.52 $ 

$ 34.92 $ 

$^{235}$ U

$\to^{210}$ Pb

$+^{25}$ Ne

$ 3 $ 

$ 57.8750 $ 

$ -16.5626 $ 

$ -32.2852 $ 

$ >27.65 $ 

$ 28.28 $ 

$ 29.04 $ 

$ 25.03 $ 

$ 29.54 $ 

Continued on next page Table 3. Predicted half-lives for possible cluster radioactive nuclei.
-
In summary, based on WKB theory, considering the screened electrostatic effect of the Coulomb potential, we systematically calculate the cluster radioactivity half-lives of 22 nuclei using a phenomenological model. The calculated results obtained using our model are in satisfactory agreement with the experimental data. Moreover, we extend this model to predict the cluster radioactivity half-lives of 66 possible cluster radioactive candidates. The predictions have good consistency with those of several other models and/or formulas. Finally, the low values of the cluster radioactivity half-lives at daughter neutron number
$ (N_{d}=126) $ confirm the important role of neutron magicity. It also shows that neutron shell closure is more influential than proton shell closure in the cluster radioactivity process. This study may be useful for future experimental research on cluster radioactivity.
Systematic calculations of cluster radioactivity half-lives with a screened electrostatic barrier
- Received Date: 2023-04-24
- Available Online: 2023-09-15
Abstract: In this study, based on Wentzel-Kramers-Brillouin theory, we systematically investigate the cluster radioactivity half-lives of 22 nuclei ranging from





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: