-
After more than one hundred years since its inception, Einstein gravity remains the most promising theory of relativistic gravity. However, there are several reasons to consider alternative theories of gravity, for instance, the need for a renormalizable quantum theory of gravity, the interpretation of the expanding universe, and galaxy rotation curves. Among the many extended theories of gravity, conformal gravity has attracted considerable interest, partly because of its on-shell equivalence to Einstein gravity and its power counting renormalizability [1], and partly because its spherically symmetric solution contains a linear term in the radial coordinate, which may play a role in explaining galaxy rotation curves as an alternative for dark matter [2, 3]. As a physically viable model of relativistic gravitation, it is natural to look into more detailed behaviors of conformal gravity, and the study of its black hole solutions and the corresponding thermodynamic properties [4–6] is of great importance in this regard.
There are several formalisms for studying black hole thermodynamics. The traditional formalism focuses on the initial establishment of the basic laws of black hole thermodynamics and the calculation of thermodynamic quantities [7–11]. A relatively modern formalism known as the extended phase space (EPS) formalism emerged approximately fifteen years ago [12], which takes the negative cosmological constant (hence it is only applicable to AdS black holes) as one of the thermodynamic quantities (proportional to the pressure) and thus extends the space of macro states. This formalism has attracted considerable interest because it reveals various critical behaviors and the possible existence of different types of phase transitions in black hole physics [13–36]. There is a plethora of literature pertaining to this topic, and it would be impossible to present a full list. Thus, we only cite those that have had a significant impact on our line of thinking and research. In particular, the critical phenomena of charged spherically symmetric AdS black holes in conformal gravity, whose strange behavior is a significant motivator of this study, is analyzed in [37]. Further development of the EPS formalism includes the exploration of black hole microstructures [38–40], and the inclusion of the central charge and its conjugate variable in the list of thermodynamic variables [41–43], which is inspired by the AdS/CFT correspondence.
Although studies based on the EPS formalism prove to be very fruitful, several issues are inevitable in this formalism, as first pointed out in [44]. To name a few, the requirement of a variable cosmological constant leads to a theory-changing problem, which we call the ensemble of theories problem, the interpretation of the total energy as enthalpy instead of internal energy seems to contradict the thermodynamic understanding of total energy, and some thermodynamic behaviors in various black hole solutions of different gravity models are so bizarre that there are no precedent examples of macroscopic systems with similar behaviors. The charged spherically symmetric AdS black hole solution in conformal gravity is among the example cases exhibiting strange behaviors in the EPS formalism [37], including the intersecting isotherms of different temperatures, the discontinuous change in Gibbs free energy in thermodynamic processes, the branched or multivalued thermal equations of state (EOSs), and the appearance of a maximal specific thermodynamic volume (or radius of the event horizon) at a fixed temperature.
Above all, the lack of complete Euler homogeneity in both the traditional and EPS formalisms of black hole thermodynamics is considered the most severe problem constituting a barrier in understanding the zeroth law of black hole thermodynamics. To solve the problem of Euler homogeneity, we proposed a novel formalism for black hole thermodynamics known as the restricted phase space (RPS) formalism by fixing the cosmological constant but including the effective number of microscopic degrees of freedom and its conjugate chemical potential in the list of thermodynamic variables. The application of the RPS formalism to the cases of RN-AdS [44] and Kerr-AdS [45] black holes in Einstein gravity indicated that this new formalism is free of all the issues mentioned above. Subsequent studies revealed that the RPS formalism also works for non-AdS black holes [46, 47] and is applicable to a large class of higher curvature gravity models known as black hole scan models [48]. According to the behaviors of charged spherically symmetric AdS black holes in different black hole scan models, these models can be subdivided into two universality classes: the Einstein-Hilbert-Born-Infield class and Chern-Simons class. Most recently, we found that the high temperature limit of
$ (D+2) $ -dimensional Tangherlini-AdS black holes can be precisely matched to the low temperature limit of the quantum phonon gases that appear in nonmetallic crystals residing in D-dimensional flat space [49]. Moreover, this AdS/phonon gas correspondence does not appear to be limited to Tangherlini-AdS black holes because the high temperature limit of the heat capacities of charged AdS black holes in black hole scan models also behaves similarly to that of the low temperature Debye heat capacities of D-dimensional quantum phonon gases [48]. More applications of the RPS formalism can be found in [50–53].The aim of this study is two-fold. First, we present the applicability of the RPS formalism to the case of four dimensional conformal gravity and resolve the bizarreness that appeared in the EPS formalism for the thermodynamic behaviors of charged AdS black holes in this model. Second, we wish to take conformal gravity as yet another example case for the AdS/phonon gas correspondence. These two aims are perfectly accomplished, as described in the following sections.
-
The model considered in this study is best described by its classical action,
$ S=\alpha\int {\rm{d}}^4x \sqrt{-g}\left(\frac{1}{2}C^{\mu\nu\rho\sigma} C_{\mu\nu\rho\sigma} +\frac{1}{3} F^{\mu\nu}F_{\mu\nu}\right), $

(1) where the unusual sign in front of the Maxwell term is inspired by critical gravity [4] and is necessary for Einstein gravity to emerge in the infrared limit [1].
The static charged AdS black hole solution for this model is found in [5], with the metric
$ {\rm{d}} s^2=-f(r){\rm{d}}t^2+\frac{{\rm{d}}r^2}{f(r)}+r^2{\rm{d}} \Omega_{2,\epsilon}^2, $

(2) $ f(r)=-\frac{1}{3}\Lambda r^2+c_1 r+c_0+\frac{d}{r}, $

(3) and the Maxwell field
$ A=-\frac{Q}{r}{\rm{d}}t. $

(4) The parameter
$ \epsilon $ can take three discrete values,$ -1 $ , 0, 1, which correspond, respectively, to the hyperbolic, planar, and spherical geometries of the two-dimensional "internal space" characterized by the line element$ {\rm{d}}\Omega_{2,\epsilon}^2 $ . The solutions with$ \epsilon=0,-1 $ are known as topological black holes, which exist only in AdS backgrounds. The other parameters$ Q, c_0, c_1, d, \Lambda $ are all integration constants that must obey an additional constraint$ 3c_1d+\epsilon^2+Q^2=c_0^2. $

(5) The above solution describes a charged AdS black hole, provided
$ \Lambda<0 $ and the equation$ f(r_0)=0 $

(6) has a nonvanishing real positive root
$ r_0 $ , which corresponds to the radius of the event horizon. Note that the function$ f(r) $ does not contain the term$ Q^2/r^2 $ as in the usual RN-AdS black hole solution. The parameter Q (related to the electric charge) only affects the geometry of the spacetime implicitly through constraint condition (5). Because Q appears only in squared form in Eq. (5), the spacetime geometry does not discriminate between positive and negative values of Q. Therefore, in this study, we exclusively consider the choice$ Q\geq0 $ . The opposite choice is permitted but makes no difference regarding the geometry and thermodynamic behaviors.In the absence of the parameter
$ c_1 $ (which represents a massive spin-2 hair [5, 6]), metric (2) looks similar to that of the standard Schwarzschild-(A)dS black hole, provided d takes a negative value. Let us stress that unlike in most other gravity models, the cosmological constant Λ arises purely as an integration constant; therefore, this model was once considered very appropriate for pursuing thermodynamic analysis following the EPS approach because a variable cosmological constant in this model does not cause the ensemble of theories problem, which appears in other theories of gravity. -
Before getting to the RPS formalism for the thermodynamics of the above black hole solution, let us first briefly review the EPS description and point out some of its pathologies.
To begin with, we present the relevant thermodynamic quantities in the EPS formalism. First, the total energy E of the black hole spacetime, as calculated using the Noether charge associated with the timelike Killing vector [6], reads as
$ E =\frac{\alpha\omega_2}{24\pi}\left[ \frac{(c_0-\epsilon)(\Lambda r_0^2-3c_0)}{3 r_0} +\frac{(2\Lambda r_0^2-c_0+\epsilon)d}{r_0^2}\right], $

(7) which is regarded as the enthalpy, where
$ r_0 > 0 $ represents the radius of the event horizon of the black hole and is a real root of$ f(r) $ , and$ \omega_2 $ is the volume of the internal$ 2d $ space designated by the line element$ {\rm{d}}\Omega_{2,\epsilon}^2 $ . The pressure P and its conjugate, the thermodynamic volume V, are respectively given as$ P=-\frac{\Lambda}{8\pi},\qquad V=-\,{\frac {\alpha\omega_2d}{3 }}. $

Next comes the black hole temperature and entropy, which are given by [5]
$ T =-\,{\frac {\Lambda\,r_0^{3}+3c_{0}r_{0}+6d}{12\pi{r_{0}}^{2}}}, \quad S=\,{\frac {\alpha\omega_2\left(\epsilon r_0-c_{0}r_{0}-3d \right) }{6r_{0}}}. $

(8) The electric charge (defined as the conserved charge associated with the
$ U(1) $ gauge symmetry of the electromagnetic field) and conjugate potential are respectively given as$ Q_{{e}}=\,{\frac {\alpha\omega_2Q}{12\pi }},\qquad \Phi=-{\frac {Q}{r_{0}}}. $

(9) The parameter
$ c_1 $ is a massive spin-2 hair, which is also taken as one of the thermodynamic variables. This variable is denoted as$ \Xi=c_1 $ , and its conjugate Ψ is given by$ \Psi=\,{\frac {\alpha\omega_2\left( c_{0}-\epsilon \right) }{24\pi }}. $

In the above expressions for thermodynamic quantities, the parameter
$ c_0 $ is considered to be implicitly determined using relation (5), and thus it cannot be taken as a simple constant while considering thermodynamic behaviors. Conversely, the coupling constant α is always kept as a real constant in the EPS formalism.We can check that the energy E obeys the following relations:
$ \begin{align} {{\rm{d}} E}&=T{{\rm{d}} S}+\Phi\,{{\rm{d}} Q}_{{e}}+ \Psi\,{\rm{d}} \Xi + V\,{\rm{d}} P,\\ E&=2PV+\Psi\,\Xi. \end{align} $

These relations are interpreted as the first law and Smarr relation, respectively, in the EPS formalism.
As mentioned in the introduction, the behavior of EPS thermodynamics, as outlined above, appears to be very strange, and the problems may be attributed either to the gravity model itself or the EPS formalism. We find that with new insights from the RPS formalism, the problems can be perfectly avoided; therefore, it is clear that the problems arise from the EPS formalism.
-
The entire logic of the RPS formalism reads as follows: First, we must introduce a new pair of thermodynamic variables, that is, the effective number N of the microscopic degrees of freedom (or dubbed black hole molecules) of the black hole and its conjugate, the chemical potential μ. These two objects are universally defined as
$ N=\frac{L^D}{G},\qquad \mu=\frac{GT I_{\rm E}}{L^D}, $

(10) where L is an arbitrarily chosen constant length scale, G is the Newton constant, and
$I_{\rm E}$ is the on-shell Euclidean action, which corresponds to the black hole solution. The arbitrariness of L may be attributed to the fact that we do not know what a black hole molecule is; however, this does not prevent us from describing the macroscopic properties of the black hole, just like in studies on the thermodynamics of ordinary matter systems, in which the precise nature of individual molecules does not matter, and the total number of molecules can be taken as an arbitrary number as long as the entire system remains macroscopic, which means that L should be sufficiently large in our case.In the present case,
$ D=2 $ and [5]$ I_E=\frac{\alpha\omega_2\left[2(c_0-\epsilon)\epsilon r_0+(3\epsilon-\Lambda r_0^2)d\right]} {24\pi r_0^2 T}. $

(11) Since the Newton constant does not explicitly appear in action (1), we must relate the coupling constant α to G in some way. Because G has the dimension
$ [L]^2 $ , whereas α has the dimension$ [L]^0 $ , this relationship cannot be$ \alpha=1/16\pi G $ but rather must be modified by a factor of the dimension$ [L]^2 $ . Therefore, we assume that$ \alpha=\frac{L^2}{16\pi G}, $

(12) owing to the arbitrariness of L. This assumption is not an absolutely necessary step. What actually matters is that the number of black hole molecules N should be proportional to the overall factor in the action to ensure that N is the thermodynamic conjugate of the chemical potential μ (which in turn is defined in terms of the Euclidean action
$I_{\rm E}$ ). Assumption (12) is introduced simply to illustrate that the overall factor$ 1/16\pi G $ in Einstein gravity and the factor α in conformal gravity play similar roles in the RPS formalism.Before checking the thermodynamic relations in the RPS formalism, there is something else to be fixed in solutions (2) and (3). To guarantee the existence of a reasonable weak field limit with an attractive Newtonian potential, we must require that
$ 1/|c_1|\gg r_0, \quad 1/\sqrt{-\Lambda}\gg r_0, \quad d<0. $

(13) Moreover, in the extremal case with
$ c_1=d=0 $ , the solution must fall back to that of the vacuum AdS background. Therefore, for each choice of$ \epsilon=-1,0,1 $ ,$ c_0 $ must always be equal to$ \epsilon $ .Let us remark that in previous studies,
$ c_0 $ was considered an implicit function in$ c_1, d $ , and Q. The present choice$ c_0=\epsilon $ is more physically motivated, which makes a big difference. In fact, if$ c_0 $ and$ \epsilon $ were kept independent besides constraint (5), the first law to be introduced below in the RPS formalism would not hold.In the following, we work exclusively with the choice
$ c_0=\epsilon=1 $ , which corresponds to the spherically symmetric case with$ \omega_2=4\pi $ . Inserting$ c_0=\epsilon=1 $ ,$ \omega_2=4\pi $ and Eq. (12) into Eqs. (7)−(11), we get$ E =\frac{\Lambda L^2 d }{48\pi G}, $

(14) $ S =-{\frac {L^2 d }{8 G r_{0}}}, \quad T=-\frac {r_0(\Lambda\,r_0^{2}-3)+6(d+r_{0})}{12\pi{r_{0}}^{2}}, $

(15) $ Q_{{e}} =\,{\frac {L^2 Q}{48\pi G }},\quad\,\,\, \qquad \Phi=-{\frac {Q}{r_{0}}}, $

(16) $ N =\frac{L^2}{G}={16\pi\alpha},\quad\,\,\, \mu= -\frac{(\Lambda r_0^2-3)d}{96\pi r_0^2}. $

(17) It is now more transparent that to ensure non-negativity of the entropy and total energy, d and Λ must both be negative. This is why the solution is considered an AdS black hole solution from the very beginning.
In the above equations,
$ d, Q, G $ , and$ r_0 $ are considered implicit functions in the thermodynamic variables. However, these objects are not all independent owing to constraint condition (5) and the equation for the event horizon (6). The joint system of Eqs. (5) and (6) has two different sets of solutions for d and$ c_1 $ , among which only one ensures the negativity of d,$ d = \frac{r_0}{6}\left[\Lambda r_0^2-3 - \sqrt{(\Lambda r_0^2-3)^2+12Q^2}\right], $

(18) $ c_1 =\frac{1}{6r_0} \left[\Lambda r_0^2-3 + \sqrt{(\Lambda r_0^2-3)^2+12Q^2}\right]. $

(19) The other solution with reversed signs in front of the square roots corresponds to strictly non-negative values of d, which results in a non-positive entropy and is therefore henceforth dropped.
Note that in the RPS formalism, we do not introduce the
$ (\Xi,\Psi) $ variables. The reason behind this choice is the symmetry principle. Let us quote C.N. Yang's celebrated dictum: "Symmetry dictates dynamics." Here, we would like to extend this statement a step further: Symmetry dictates thermodynamics, which means that different thermodynamic systems with the same underlying symmetries should be described by the same set of thermodynamic variables, although their detailed thermodynamic behaviors may differ. The black hole solution under study bears the same spherical symmetry and$ U(1) $ gauge symmetry as the well-known RN black hole solution in Einstein gravity; thus, the space of macro states for these two black hole systems must be spanned by the same set of macroscopic variables. This may help to understand why we exclude the variables$ (\Xi, \Psi) $ from the list of allowed thermodynamic quantities in the RPS formalism. Let us stress that it is the underlying symmetries, rather than the number of integration constants, that determine the dimension of the space of macro states. One may wonder why conformal symmetry is not considered here. The reason is clear: any concrete choice of metric in conformal gravity automatically breaks the conformal symmetry. Therefore, no charges associated with conformal symmetry can enter the thermodynamic description for black holes in conformal gravity.Using the results presented in Eqs. (14)−(17), we can check by straightforward calculations that the first law
$ {\rm{d}} E= T{\rm{d}} S+\Phi{\rm{d}} Q_e +\mu{\rm{d}} N $

(20) and Euler relation
$ E=TS+\Phi Q_e+\mu N $

(21) simultaneously hold, which ensures that E is a first order homogeneous function in
$ (S, Q_e, N) $ and$ T, \Phi, \mu $ are zeroth order homogeneous functions in$ (S, Q_e, N) $ . The last two equations constitute the fundamental relations for the RPS formalism of black hole thermodynamics. As a direct consequence, the Gibbs-Duhem relation$ {\rm{d}} \mu =-s{\rm{d}} T-q {\rm{d}}\Phi $

(22) also holds, where
$ s=\frac{S}{N}=-\frac{d}{8r_0}, \quad q=\frac{Q_e}{N}=\frac{Q}{48\pi}, $

where both are zeroth order homogeneous functions in
$ (S, Q_e, N) $ . The Gibbs-Duhem relation indicates that the intensive variables$ \mu, T, \Phi $ are not independent of each other, whereas each is independent of the size of the black hole. -
The explicit values of the various thermodynamic quantities collected in the last section allow for a detailed analysis of the thermodynamic behavior of the black hole solution under consideration. To proceed, we must first re-express the parameters
$ r_0, G, Q $ in terms of the extensive variables$ N, S, Q_e $ or, better yet, in terms of N and$ s,q $ . The latter set of variables has the advantage that the EOSs re-expressed in these variables are independent of N, which is a characteristic property of standard extensive thermodynamic systems, known as the law of corresponding states.To rewrite
$ r_0, G, Q $ as functions of$ (N,s,q) $ , we must solve the first equations in Eqs. (15)−(17) as a system of algebraic equations for$ r_0, G, Q $ , which yields$ Q=48\pi q,\quad G=\frac{L^2}{N},\quad r_0=\ell s^{-1/2}(8s^2-s-96\pi^2q^2)^{1/2}, $

(23) where
$\ell\equiv\left(\dfrac{3}{\Lambda}\right)^{1/2} > 0$ . The condition for$ r_0 $ to be real and positive reads as$ 8s^2-s-96\pi^2q^2>0. $

(24) Since
$ q^2\geq0 $ and$ s>0 $ (a macro state of zero entropy cannot be understood as a black hole), we can deduce that$ s>1/8 $ using the above inequality. In other words, there are no black hole states with$ s\leq 1/8 $ .There is another, negative-valued, unphysical, solution for
$ r_0 $ , which is omitted.Inserting Eq. (23) into Eq. (14) and the remaining equations in Eqs. (15)−(17), we have
$ {\cal{E}} = s^{1/2} (8s^2-s-96\pi^2q^2)^{1/2}, $

(25) $ \tau = \frac{12s^2-s-48\pi^2q^2}{s^{1/2}(8s^2-s-96\pi^2q^2)^{1/2}}, $

(26) $ \phi = -\frac{96\pi^2 q s^{1/2}}{(8s^2-s-96\pi^2q^2)^{1/2}}, $

(27) $ m = -\frac{4s^{1/2}(s^2-12\pi^2q^2)}{(8s^2-s-96\pi^2q^2)^{1/2}}, $

(28) where, for convenience, we introduce the new variables
$ {\cal{E}}=\frac{2\pi\ell}{N} E,\quad \tau= 2\pi\ell T,\quad \phi= 2\pi\ell \Phi,\quad m= 2\pi\ell \mu, $

(29) each with the dimension
$ [L]^0 $ . The first order homogeneity of E and the zeroth order homogeneity of$ T,\Phi, \mu $ are transparent in the above expressions. Note that condition (24) automatically ensures the non-negativity of T; therefore, there is no further constraints over the parameters s and q.Besides the above thermodynamic quantities, we also need the explicit expression for the Helmholtz free energy
$ F=E-TS $ , which, in terms of the rescaled variable$ f\equiv 2\pi\ell F/N $ , is given as follows:$ f={\cal{E}}-\tau s =- \frac{4s^{1/2}(s^2+12\pi^2q^2)}{(8s^2-s-96\pi^2q^2)^{1/2}}. $

(30) The first thing to note from the above results is the absence of the Hawking-Page (HP) transition in the present case. The HP transition is a phase transition from an AdS black hole to a pure thermal gas, which occurs at the zero of the Gibbs free energy (or equivalently of the chemical potential) for neutral AdS black holes [54]. Such a transition is known to exist in most AdS black hole solutions in four and higher spacetime dimensions. However, in the present case, the chemical potential is strictly negative in the neutral limit, as can be inferred from Eq. (28). This seems to indicate that the AdS black hole solution in conformal gravity belongs to a novel universality class that differs from the classes of AdS black holes in both Einstein-Hilbert and Born-Infield like theories and Chern-Simons like theories.
The concrete thermodynamic behaviors of the black hole can be graphically illustrated by plotting the EOS (26)−(28).
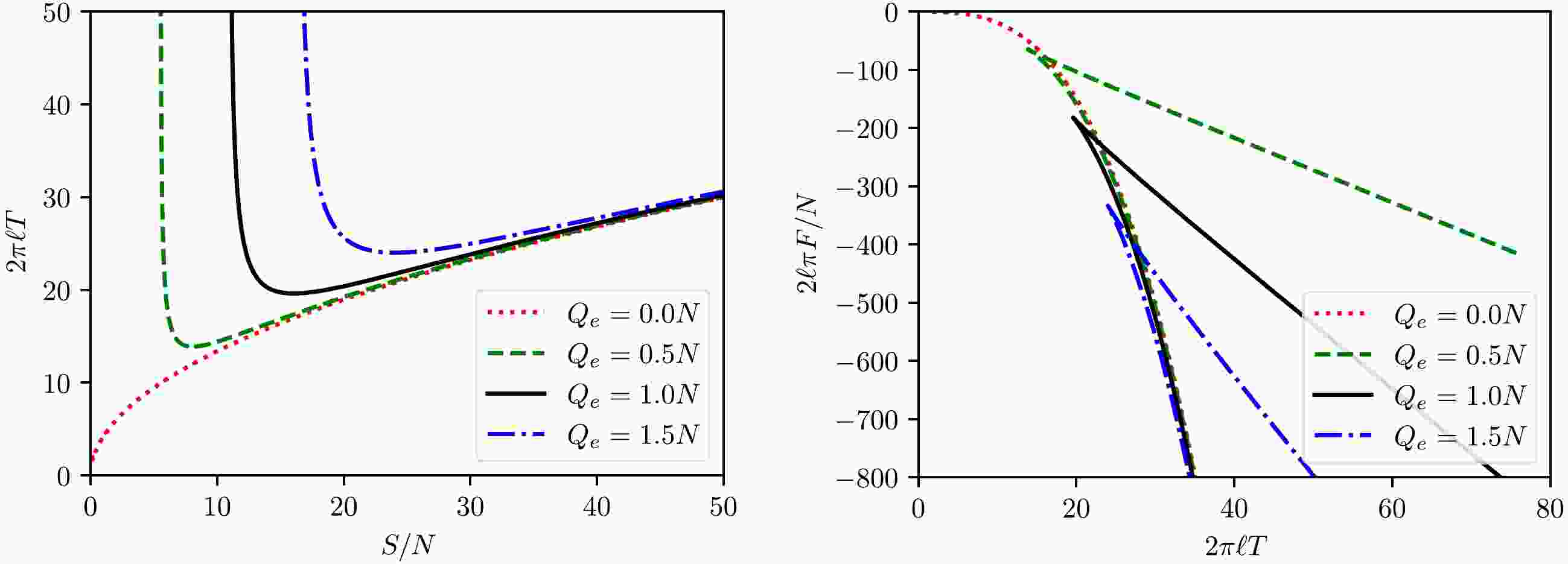
First let us look at the isocharge
$ T-S $ and$ F-T $ curves presented in Fig. 1. Each isocharge$ T-S $ curve contains a single minimum, which divides the black hole states of the same temperature and charge into two branches, that is, unstable small black holes and stable large black holes. Correspondingly, the$ F-T $ curves are also branched, with the lower branch corresponding to the stable large black hole states. Above the minimal temperature, the transition from the unstable small black hole state to the large stable black hole state should take place under small perturbations. There is no equilibrium condition for such transitions.From the curves depicted in Fig. 1, the description of the behavior of the isocharge
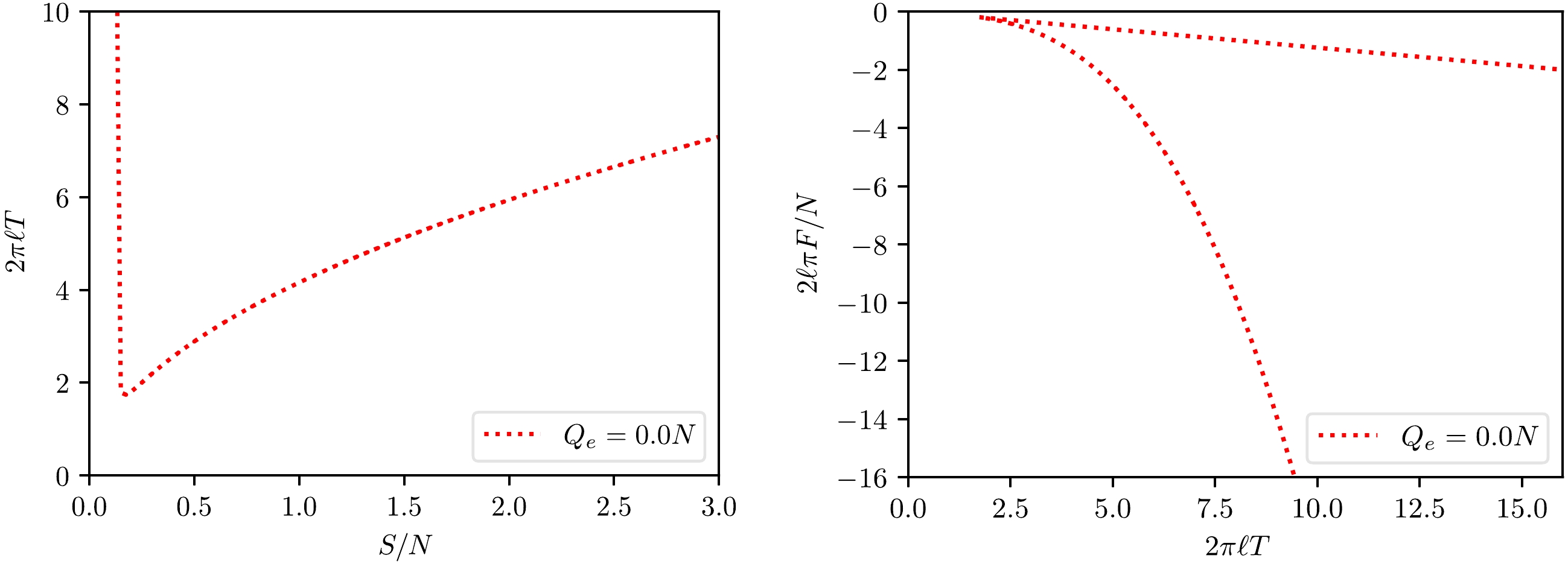
$ T-S $ and$ F-T $ curves presented in the last paragraph does not appear to work in the case with$ Q=0 $ . This is not true. Figure 2 presents the zoomed-in plots for the isocharge$ T-S $ and$ F-T $ curves near the origin. It is shown that the above branched behavior persists at$ Q=0 $ .The above isocharge
$ T-S $ behavior is in sharp contrast to the case of charged AdS black holes in Einstein-Hilbert, Born-Infield, or Chern-Simons like theories of gravity. In the case of Einstein-Hilbert and Born-Infield like theories, the isocharge$ T-S $ processes always contain an equilibrium phase transition, which is of the first order above the critical temperature and becomes second order at the critical point, whereas in the case of Chern-Simons like theories, the isocharge$ T-S $ curves are monotonic and there is only one stable black hole state at each fixed temperature and electric charge. The present model gives a third universality class that interpolates the Einstein-Hilbert-Born-Infield and Chern-Simons classes.The branched behavior of the isocharge processes can also be revealed from the behavior of the isocharge heat capacity
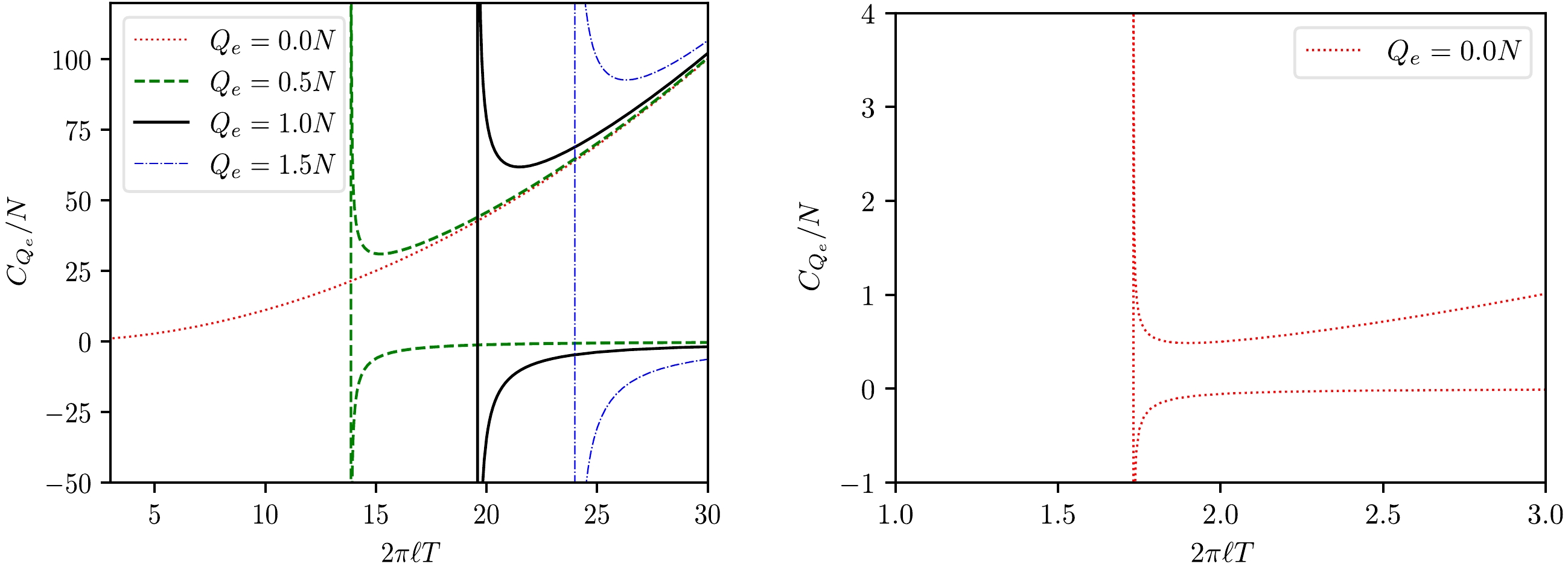
$ C_{Q_e} $ . In the present case, the isocharge specific heat capacity$ c_q\equiv C_{Q_e}/N $ can be calculated explicitly using EOS (26),$ \begin{aligned}[b] c_q &= T \left(\frac{\partial s}{\partial T}_q\right) =\frac{\tau}{\left(\dfrac{\partial\tau}{\partial s}\right)_q}\\ &=-\frac{s \left[s (8 s-1)-96 \pi ^2 q^2\right] \left[s (12 s-1)-48 \pi ^2 q^2\right]}{8 \left(288 \pi ^4 q^4+144 \pi ^2 q^2 s^2-6 s^4+s^3\right)}. \end{aligned}$

(31) Based on this result, the isocharge heat capacity versus temperature curves are plotted in Fig. 3, wherein the right figure is the zoomed-in plot of the curve with
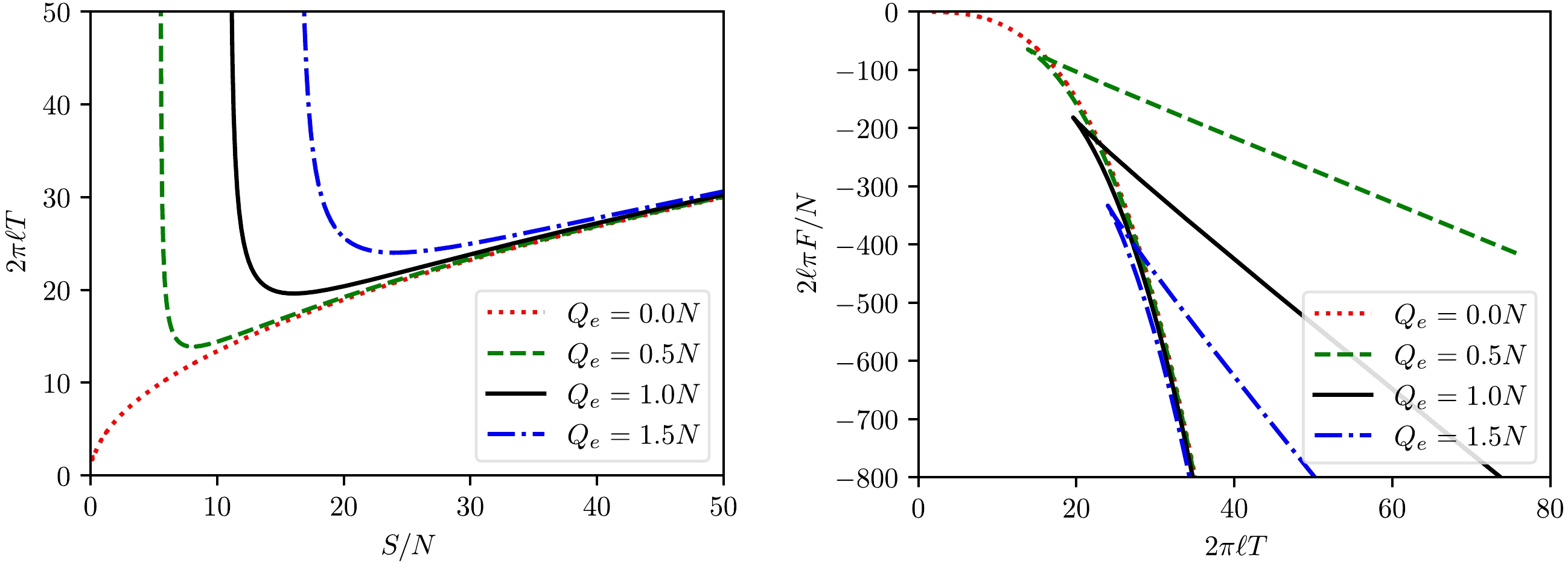
$ Q_e=0 $ . The branched behavior is transparent, and only the large black hole branch has positive heat capacity, which indicates its stability.The branched behavior also appears in isovoltage
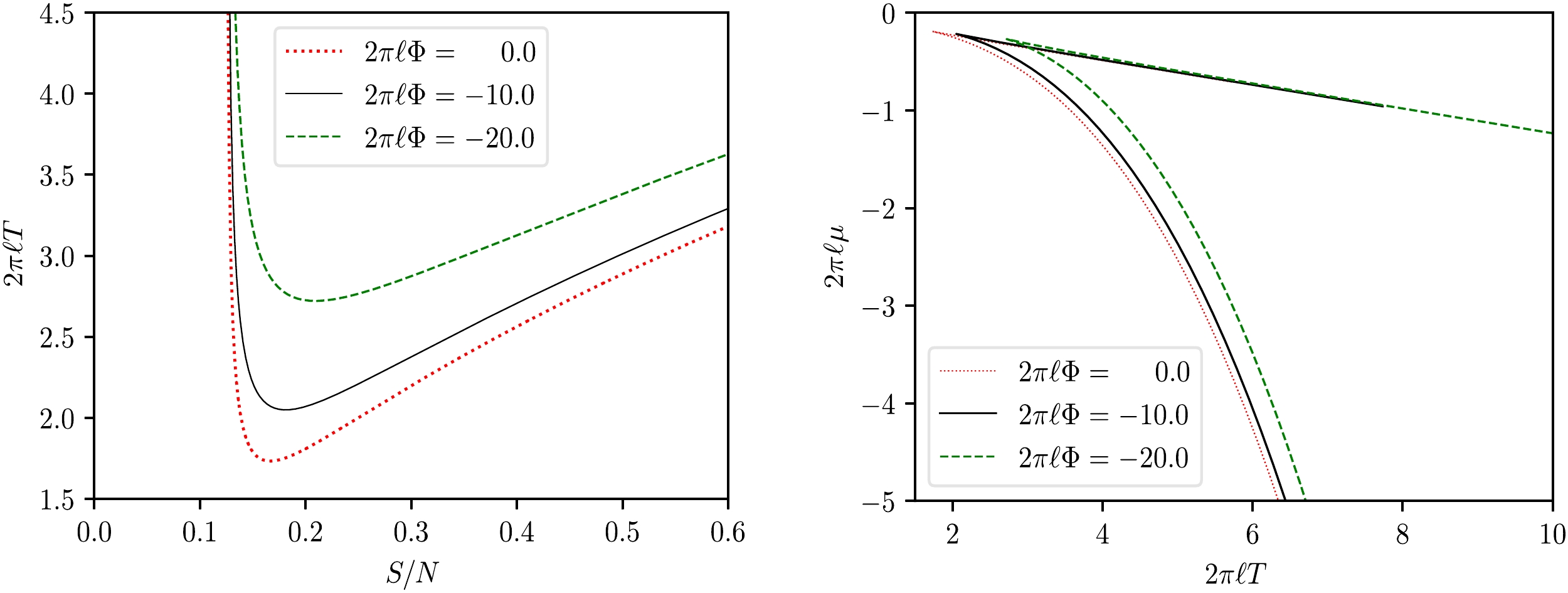
$ T-S $ processes, as depicted in Fig. 4 along with the isovoltage$ \mu-T $ curves. The isovoltage$ T-S $ curves are qualitatively similar to those of charged AdS black holes in the Einstein-Hilbert-Born-Infield class of theories. However, in the isovoltage processes, μ is strictly negative for any choice of T, which is consistent with the earlier statement on the absence of the HP transition.Besides the
$ T-S $ processes, one may also be interested in$ \Phi-Q_e $ processes. There are two possible types of$ \Phi-Q_e $ processes: adiabatic and isothermal. The corresponding$ \Phi-Q_e $ curves are depicted in Fig. 5. In the adiabatic processes, the electric potential decreases monotonically as the charge increases, and there is an upper bound for$ Q_e $ at each fixed S, as shown by Eq. (24). The isothermal$ \Phi-Q_e $ processes appear to be more involved. Besides the existence of an upper bound for$ Q_e $ at each fixed T, at each fixed T, the black hole may experience a cyclic charging-discharging process, which makes the black hole a potential battery. This type of charge-potential process has not previously been found within the RPS formalism for the thermodynamics of charged AdS black holes.Let us now examine the isothermal
$ \mu-\Phi $ curves presented in Fig. 6. As expected, the isothermal$ \mu-\Phi $ curves also possess a branched behavior at each fixed T, with the lower branch being the stable large black hole branch.As a final remark, let us consider the special case
$ c_{1}=Q=0 $ . The metric function$ f(r) $ now becomes$ f(r)=1+\dfrac{d}{r}-\dfrac{1}{3}\Lambda r^{2}. $

With negative d, the corresponding metric takes the same form as that of the four-dimensional Schwarzschild-AdS black hole solution in Einstein gravity. However, this similarity does not imply that the thermodynamic behaviors should also degenerate to those of the four-dimensional Schwarzschild-AdS black hole solution in Einstein gravity because only part of the thermodynamic quantities (for example, the temperature T and electric potential Φ) of the black hole is determined solely by the solution, while the other part of the thermodynamic quantities, including the energy E, entropy S, charge
$ Q_e $ , and chemical potential μ, is determined by the action of the underlying gravity model. Thus, the same metric as the solution of different gravity models does not necessarily have the same thermodynamic behavior. This final statement is justified by the absence of the HP transition in the case of conformal gravity, as illustrated in Fig. 4, and the presence of the HP transition in the case of the neutral limit of RN-AdS black holes in Einstein gravity [44]. -
Our recent study [49] on the Tangherlini-AdS black hole solution in Einstein gravity revealed a remarkable connection between the high temperature limit of AdS black holes and the low temperature limit of phonon gases in nonmetallic crystals. It is natural to test whether this AdS/phonon gas correspondence still holds in the case of charged spherically symmetric AdS black holes in conformal gravity.
Note that the AdS/phonon gas correspondence revealed in [49] holds only in the stable large black hole branch. Therefore, we also consider the high temperature limit of the stable large black hole branch. Using the results presented in Eqs. (25)−(30), we can easily get
$ \lim\limits_{s\to\infty} \frac{{\cal{E}}}{\tau^3} = \frac{1}{27},\quad \lim\limits_{s\to\infty} \frac{f}{\tau^3} = -\frac{1}{54}, $

(32) $ \lim\limits_{s\to\infty} \frac{s}{\tau^2} = \frac{1}{18},\quad \lim\limits_{s\to\infty} \frac{c_q}{\tau^2} = \frac{1}{9}. $

(33) In the stable large black hole branch,
$ s\to\infty $ implies$ T\to\infty $ . Therefore, the above limits can be easily translated into the following high temperature limits for the thermodynamic quantities:$ \lim\limits_{T\to\infty} E = \frac{1}{27}(2\pi\ell)^2 N T^3,\quad \lim\limits_{T\to\infty} F = -\frac{1}{54}(2\pi\ell)^2 N T^3, $

(34) $ \lim\limits_{T\to\infty} S = \frac{1}{18} (2\pi\ell)^2 N T^2,\quad \lim\limits_{T\to\infty} C_{Q_e} = \frac{1}{9}(2\pi\ell)^2 N T^2. $

(35) The high temperature limit means that the physical temperature is high above some constant characteristic temperature. In the present case, the characteristic temperature can be chosen as
$ T_{\rm bh} = \frac{3\sqrt{2}}{2\pi\ell}. $

(36) With this choice, the above high temperature behaviors can be rewritten as
$ E \approx \frac{2}{3}NT\left(\frac{T}{T_{\rm bh}}\right)^2,\quad\,\,\, F\approx -\frac{1}{3}NT\left(\frac{T}{T_{\rm bh}}\right)^2, $

(37) $ S \approx N\left(\frac{T}{T_{\rm bh}}\right)^2,\quad\quad C_{Q_e}\approx 2NT\left(\frac{T}{T_{\rm bh}}\right)^2 $

(38) under the condition
$ T\gg T_{\rm bh} $ . These behaviors coincide precisely with what we obtained for Tangherlini-AdS black holes in the generic spacetime dimensions$ D+2\geq 4 $ , and even the numerical coefficients are the same if we set$ D=2 $ . As mentioned in [49], such high temperature asymptotic behaviors also coincide with the low temperature behaviors of quantum phonon gases in nonmetallic crystals. Moreover, we examine the cases of four dimensional Kerr-AdS and Kerr-Newman-AdS black holes and find that the high temperature asymptotic behaviors of the above thermodynamic quantities are exactly the same. For different choices of AdS black holes, the high temperature asymptotic behaviors differ the most based on the choice of different characteristic temperatures. -
The thermodynamics of charged spherically symmetric AdS black holes in four dimensional conformal gravity theory is reconsidered using the RPS formalism. The strange thermodynamic behaviors found previously within the EPS formalism completely disappear, including the strange multivalued and intersecting isotherms, and the zeroth order phase transitions with discontinuities in the Gibbs free energies. Instead, the complete Euler homogeneity, which is known to be absent in the EPS formalism, is restored in the RPS formalism. Therefore, the results of the RPS formalism look simpler and are physically more reasonable.
A detailed study on the thermodynamic processes seems to indicate that the RPS thermodynamics of charged spherically symmetric AdS black holes in conformal gravity theory may belong to a brand new universality class as opposed to the classes of charged spherically symmetric AdS black holes in Einstein-Hilbert/Born-Infield like and Chern-Simons like theories of gravity.
Let us recall that the major difference between the latter two universality classes lies in the following: In the case of Einstein-Hilbert/Born-Infield like theories, isocharge
$ T-S $ processes contain a first order supercritical phase transition, which becomes second order at the critical point, whereas in the case of Chern-Simons like theories, isocharge$ T-S $ processes contain no phase transitions at all. The common property of these two classes of theories is that in both cases, each of the isovoltage$ T-S $ curves contains a single minimum, indicating the existence of non-equilibrium and noncritical phase transition from the small unstable black hole branch to the large stable black hole branch. Moreover, in the high temperature limit, the thermodynamic behaviors of the black holes can be precisely matched to those of the low temperature limit of the quantum phonon gases residing in D dimensional flat space, where D is equal to the dimension of the bifurcation horizon of the black holes. Another common feature of the above two universality classes is the existence of the HP transition in the neutral limit.The results presented in this paper indicate that the thermodynamic behavior of the present model is different from those of the above two universality classes. Here, we can list three distinguished features of the present case. First, each of the isocharge
$ T-S $ curves contains a single minimum, just like the isovoltage$ T-S $ curves, indicating the existence of non-equilibrium and noncritical phase transitions even in isocharge processes. Second, the adiabatic and isothermal$ \Phi-Q $ behaviors are also distinct. Finally, the present model does not allow for the HP transition in the neutral limit. There are also several features that are common to the present model and the other two universal classes, for example, the isovoltage$ T-S $ curves are all similar, and, more importantly, the high temperature limit of the present case agrees precisely with those of the other two classes of theories, even up to constant numerical coefficients. With further evidence from studies on Kerr-AdS and Kerr-Newman-AdS black holes in Einstein gravity (details not presented here), it appears that the recently reported AdS/phonon gas correspondence [49] is universal, irrespective of the spacetime dimensions, the gravity models, the symmetry of the event horizons, and the amount of charges carried by the black hole solutions.Over the course of our series of studies on the RPS formalism for black hole thermodynamics, we have repeatedly encountered the question of what is meant by a variable gravitational coupling constant. The answer is two-fold. On the one hand, in a full theory of gravitation in which the quantum features of gravity are considered, the gravitational coupling constant can indeed be variable along the renormalization group orbit. In such a setting, it is natural to consider the effect of a variable gravitational coupling constant on the macroscopic behavior of black holes as macroscopic objects. On the other hand, a variable gravitational coupling constant is necessary to make the thermodynamic description of black holes extensive, that is, to ensure Euler homogeneity holds [46]. Without Euler homogeneity, the thermodynamic properties would become scale dependent. In particular, the intensive properties of black holes would become dependent on the size or mass of the black hole, which contradicts the meaning of the word "intensive." This has long been a problem in black hole thermodynamics, which is also the underlying reason behind us proposing the RPS formalism.
Despite the necessity of considering the gravitational coupling constant as a variable to make the thermodynamic description extensive, there is still a possibility of keeping it fixed, such as in our observational universe. In such a scenario, the
$ \mu{\rm{d}} N $ term in the first law may be removed, just like in the thermodynamic description of a closed thermodynamic system consisting of ordinary matter. Even in such cases, the Euler relation (21) must still contain the$ \mu N $ term, albeit as a constant term. The only consequence of fixing the coupling constant is considering black holes as closed thermodynamic systems. In other words, in a universe with a fixed gravitational coupling constant, all black holes as thermodynamic systems must be closed.
Restricted phase space thermodynamics of charged AdS black holes in conformal gravity
- Received Date: 2023-05-10
- Available Online: 2023-09-15
Abstract: The thermodynamics of charged spherically symmetric AdS black holes in conformal gravity is revisited using the recently proposed restricted phase space (RPS) formalism. This formalism avoids all the bizarreness arising in the extended phase space formalism for this model. It is found that the charged AdS black holes in this model may belong to a new universality class that is different from all previously studied cases under the RPS formalism. Besides the distinguished isocharge






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: