Abstract
HTML
Reference
Related
PDF
-
To explain the observed cosmological matter-antimatter asymmetry, baryon number B violation is one of three basic ingredients for an initially symmetric universe [1]. The baryon number is necessarily violated in the Grand Unified Theories (GUTs) [2, 3], which can unify the strong, weak, and electromagnetic interactions into a single underlying force at a scale of
MGUT≃2×1016GeV . A general prediction of the GUTs is proton decay. However, no experimental evidence of proton decay, B-violating neutron decay, or neutron-antineutron oscillation has been found [4]. Fortunately, a new generation of underground experiments, JUNO [5, 6], Hyper-Kamiokande [7], and DUNE [8], with large target masses and different detection technologies will continue to search for proton decay and test the GUTs.Among the many possible proton decay modes [4],
p→e+π0 andp→ˉνK+ are the two dominant modes predicted by most of the GUTs. The former is expected to be the leading mode in many GUTs, particularly in non-supersymmetric GUTs, which typically predict the lifetime of the proton to be approximately1035 years [9]. In comparison, the decay modep→ˉνK+ is favored by a number of supersymmetric GUTs. For these two decay modes, the best measured upper limits of proton partial lifetime areτ/B(p→e+π0)>2.4×1034 years [10] andτ/B(p→ˉνK+)>5.9×1033 years [11] at the 90% C.L. from the Super-Kamiokande (Super-K) experiment, which uses a water Cherenkov detector.Compared to water Cherenkov detectors, liquid scintillator (LS) detectors have a distinct advantage in detecting the proton decay mode
p→ˉνK+ [5, 12–14]. In this study, we investigate the sensitivity of the future LS detector, JUNO. Here, the decay gives rise to a three-fold coincidence feature in time, which is usually composed of a prompt signal by the energy deposit ofK+ , a short-delayed signal (τ=12.38 ns) by the energy deposit of the decay daughters ofK+ , and a long-delayed signal (τ=2.2 μs) by the energy deposit of the final Michel electron. Using the time-correlated triple coincidence, the JUNO detector can effectively identifyp→ˉνK+ and reject atmospheric neutrino backgrounds [14].Preliminary studies have given a rough estimate of the sensitivity of JUNO to the proton decay mode
p→ˉνK+ [5]. In this study, the JUNO potential based on a detailed detector performance analysis is investigated using Monte Carlo (MC) simulation. Sec. II briefly introduces the JUNO detector and its expected performance. In Sec. Ⅲ, MC simulation ofp→ˉνK+ and the atmospheric ν backgrounds is described. In Sec. IV, the multi-pulse fitting method and other selection criteria to discriminatep→ˉνK+ from the backgrounds are investigated. We present the expected sensitivity of JUNO top→ˉνK+ in Sec. V. Finally, a conclusion is given in Sec. VI. -
JUNO is a multi-purpose neutrino observatory under construction in South China. As a low background observatory, it has a vertical overburden of 700 m of rock (1800 m.w.e) to shield the detector from cosmic muons. Its central detector (CD) is a 12 cm thick acrylic sphere with a diameter of 35.4 m, containing a 20 kton LS. The CD is immersed in a cylindrical water pool and supported by a stainless steel lattice structure. Moreover, the CD is equipped with 17612 20-inch PMTs (LPMTs) and 25600 3-inch PMTs (SPMTs), which are uniformly distributed outside the acrylic sphere. 5000 LPMTs are dynode (DYN) PMTs produced by Hamamatsu Photonics K.K., whereas the remaining LPMTs are Micro Channel Plate (MCP) PMTs manufactured by North Night Vision Technology Co., Ltd. (NNVT) [15]. Their transit time spread (TTS) values are 1.1 ns and 5.0 ns, respectively, in σ according to the result of the PMT mass test [16]. The total photocathode coverage of the LPMT is around 75%. The SPMTs, which contribute another 2.5% of photocathode coverage, are also deployed to serve as an additional independent calorimeter. The TTS (σ) of the SPMTs has been measured to be approximately 1.5 ns [17]. For each MeV energy deposition in the LS when detecting low energy events, around
1.3×103 photonelectrons (PE) are expected to be received by the LPMTs.A VETO system, including a Top Tracker (TT) detector and water Cherenkov PMT system, is designed to prevent the influence of cosmic muons. A TT detector is a plastic scintillator detector complex that partly covers the water pool and CD, which helps reject the cosmic muons passing it. The water Cherenkov PMT system is assembled on the outer surface of the stainless steel lattice structure and measures the Cherenkov light produced by the cosmic muons passing the water pool. The rejection ratio of cosmic muons is estimated to be more than 99%.
-
To understand the behavior of
p→ˉνK+ and discriminate it from the backgrounds in the JUNO detector, an MC simulation is performed in two steps: generator production and detector simulation. The generator ofp→ˉνK+ and its backgrounds is produced with GENIE (version 3.0.2) [18], in which the primary processes ofp→ˉνK+ and the atmospheric ν interactions in the LS are simulated. The detector simulation, which is a simulation of the final states ofp→ˉνK+ and the atmospheric ν interaction in the JUNO detector, is processed in SNiPER [19], which is a Geant4 [20] based simulation software developed by the JUNO collaboration. All related optical processes, including the quenching effect, are considered. The profiles of the LS, including the fluorescence times can be found in Ref. [21]. In total, 10 kp→ˉνK+ (PD) events and 160 k atmospheric ν events are simulated with vertex positions uniformly distributed over the entire LS volume.This study does not yet use full event reconstruction of energy, position, and hit time information. Instead, they are smeared according to the expectation from the detector MC simulation and used as the inputs for further analysis. The visible energy (
Evis ) is the energy deposition reconstructed from the number of PE received by the LPMTs. For a conservative consideration, it is smeared by 3%/√Evis(MeV) when the energy deposition is smaller than 60 MeV and by a resolution of 1% when greater [22]. The position of the event is described by the center of energy deposition position, which is the averaged position weighted by the energy deposition each time. It is smeared by a Gaussian distribution with a resolution of 30 cm. In this study, the detected times of photon hits on the cathode of the SPMT are collected to form a hit time spectrum for each event, after the correction of photon time-of-flight (TOF) relative to the reconstructed deposition center. The TTS of the SPMTs is set randomly according to the measurement results introduced in Sec. II. The reason for not using the LPMTs is introduced in Sec. III.A. -
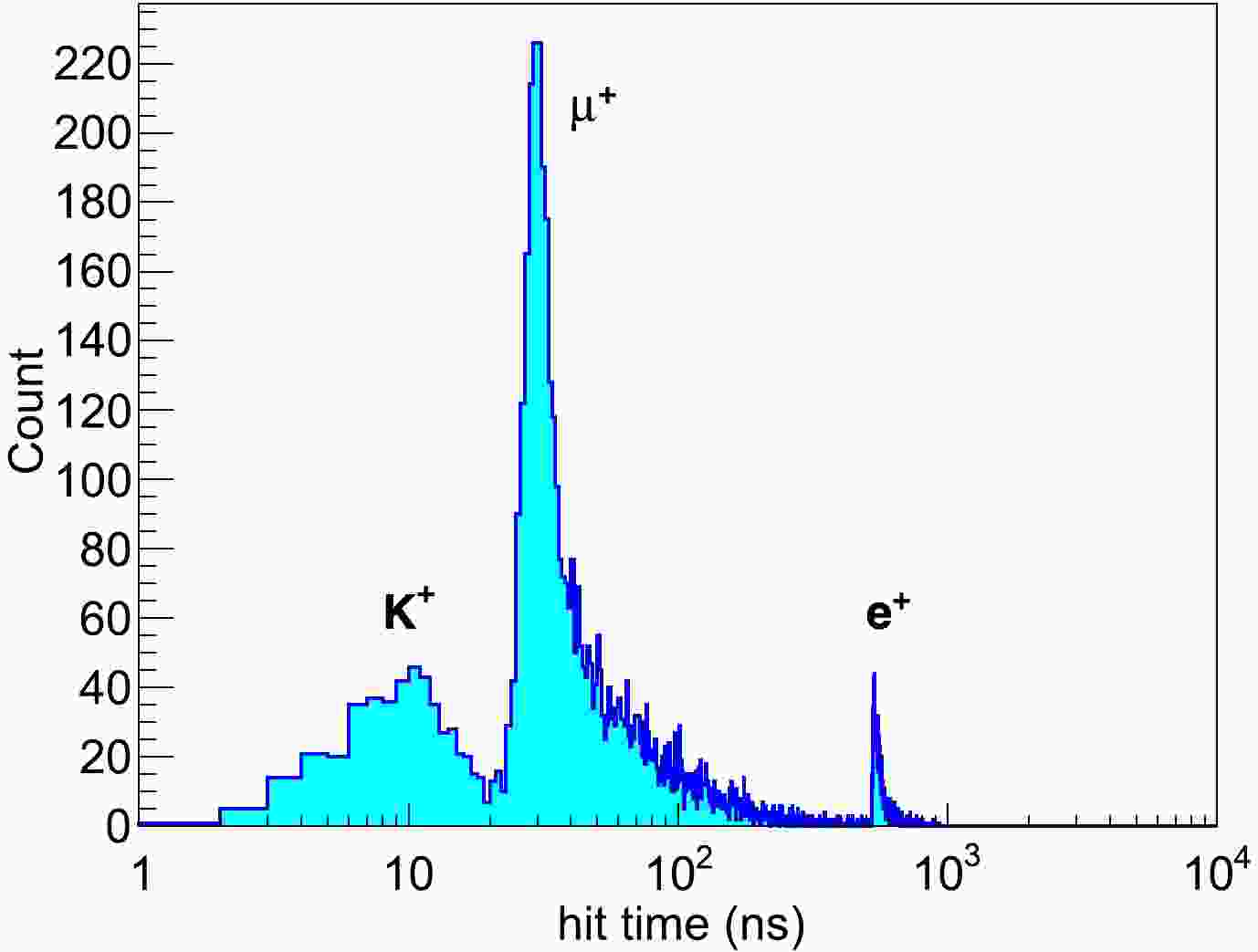
Based on the JUNO LS components, the initial proton of
p→ˉνK+ may originate from free protons (in hydrogen) or bound protons (in carbon). In free proton decay, the final statesˉν andK+ have fixed kinetic energies of 339 MeV and 105 MeV, respectively. According to a toy MC simulation with the corresponding monochromaticK+ in the JUNO detector, it is found that 92.4% ofK+ will deposit all of their kinetic energy within 1.2 ns, which means a signal can be immediately found in the hit time spectrum. Then, theseK+ will stay at rest until decaying into their daughter particles after an average of 12.38 ns.K+ has six main decay channels. The most dominant channels areK+→μ+νμ andK+→π+π0 , with branching ratios of 63.56% and 20.67%, respectively [4]. In the first channel, the producedμ+ has a kinetic energy of 152 MeV and decays into a Michel electron with a lifetime of approximately 2.2μs . The producedπ0 andπ+ in the second channel will decay into two gammas, aμ+ and aνμ , respectively, and consequently produce a Michel electron. All daughter particles will deposit their kinetic energies immediately and give a second signal. After the TOF correction, the hit time spectrum ofK+ and the decay particles will form an overlapping double-pulse pattern. Given the relatively long lifetime of the muon, a later third pulse from the Michel electron, as a delayed feature ofp→ˉνK+ , will be found on the hit time spectrum. This triple coincidence, as introduced in Sec. I, is one of the most important features for distinguishing ap→ˉνK+ event from the backgrounds. This triple coincidence is illustrated in Fig. 1.
Figure 1. (color online) Illustration of the hit time spectrum of a typical
p→ˉνK+ event, containing the signals ofK+ , the decay daughter ofK+ (μ+ in this event), and the Michel electron.As introduced in Sec. II, both the LPMTs and SPMTs are used in JUNO. However, as shown in Fig. 2, they have different performances in hit time spectrum collection. When an LPMT is triggered by a hit, the waveform will be digitized and recorded by the electronics. Then, hit time reconstruction (from the waveform to the hit time of each PE) will be performed to obtain the hit time spectrum. For low energy events such as inverse β decay (IBD), hit time reconstruction is possible because only a few photons can be received by most LPMTs. However, a typical
p→ˉνK+ event usually has an energy deposition of more than 200 MeV. In this case, many PEs would be received by the LPMTs in a few tens of ns (as shown in Fig. 2(a)), and hit time reconstruction would be difficult. As shown in Fig. 2(b), the overlapping of the first two pulses of the triple coincidence time feature would be smeared if hit time reconstruction is not performed. Thus, the LPMTs are not used to collect the hit time spectrum in this study. In comparison, considering that the receiving area of the SPMTs is around 1/40 times that of the LPMTs, most SPMTs will work in single hit mode in which the SPMTs are usually hit by a maximum of one PE. Advantageously, the triple coincidence time feature ofp→ˉνK+ can be well preserved. Thus, only the SPMTs in single hit mode are used in this study to collect the hit time spectrum.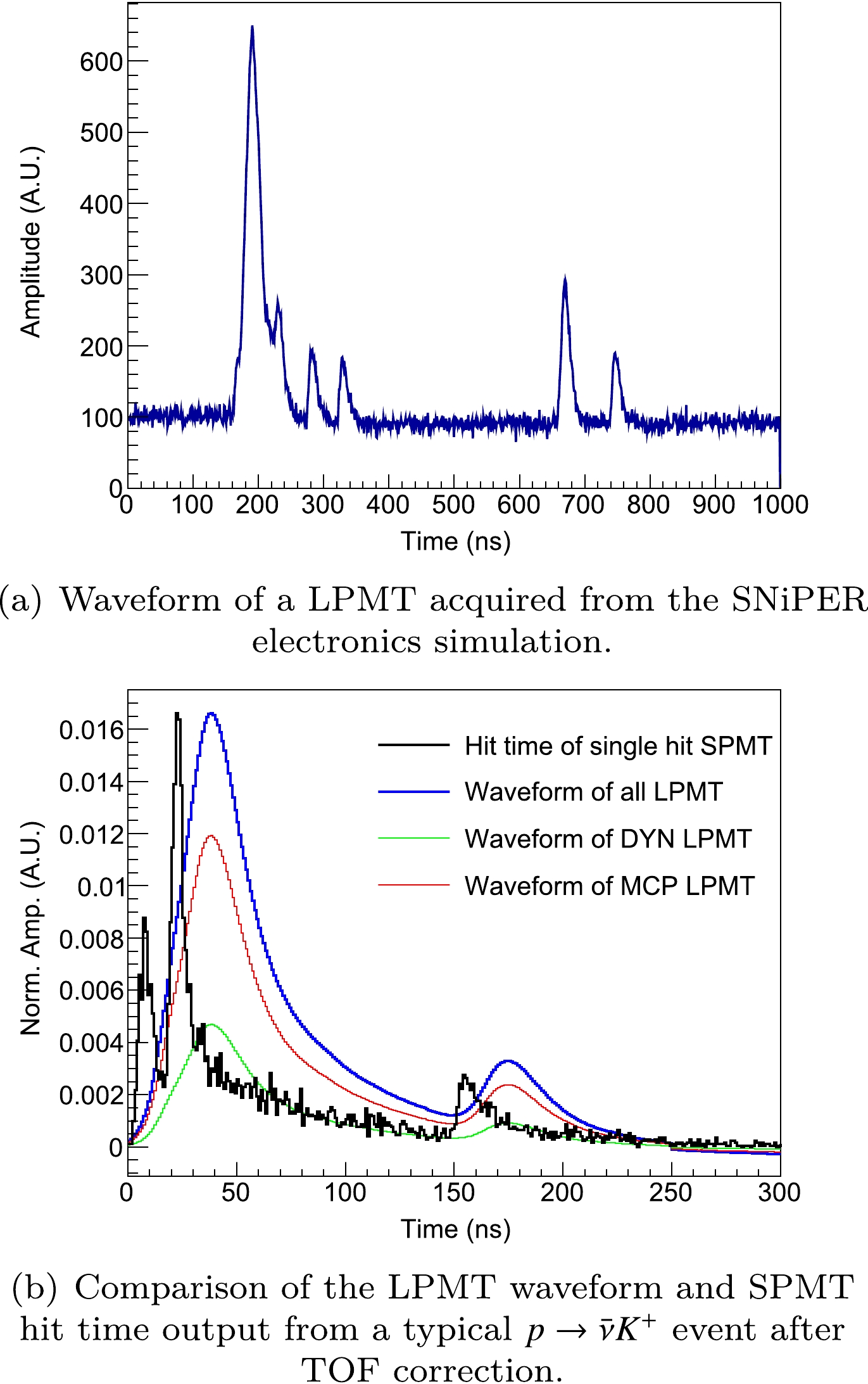
Figure 2. (color online) Simulated PMT output of a typical
p→ˉνK+ event. The total visible energy of this event is 275 MeV, andK+ decay occurs 13.7 ns after this. Photon hit time reconstruction is not easy to achieve when using LPMTs to detect a hundreds-of-MeV event. Therefore, an SPMT is used for hit time spectrum collection. More details can be found in the text.The protons bound in carbon nuclei are influenced by nuclear effects [11], including the nuclear binding energy, Fermi motion, and nucleon-nucleon correlation. The kinetic energies of the produced
K+ are smeared around 105 MeV, which is relative to that in the free proton case. In addition, theK+ kinetic energy is also changed by final state interactions (FSIs). Before theK+ escapes from the residual nucleus, it may interact with spectator nucleons and knock one of them out of the remaining nucleus. It can also exchange its charge with a neutron and turn intoK0 viaK++n→K0+p . Furthermore, the de-excitation of the residual nucleus will produce γ, neutrons, or protons, etc. Obviously, FSIs and de-excitation processes will change the reaction products, which are crucial to a later analysis.The GENIE generator (version 3.0.2) [18] is used to model these nuclear effects. Some corrections are made to the default GENIE. First, the nuclear shell structure is considered, which is not included in the default nuclear model of GENIE. A spectral function model, which provides a two-dimensional distribution of momentum k and the removal energy
ER for protons in12C , is applied to describe the initial proton states [23]. Then, the initial proton energy is determined byEp=mp−ER , wheremp is the mass of a free proton. In this case, approximately 2.2% of the protons from12C cannot decay intoˉν andK+ because the corresponding proton invariant mass is smaller than theK+ mass [24].Second, we turn on the hadron-nucleon model in GENIE. The default GENIE uses the hadron-atom model to evaluate the FSIs, which takes less time but does not include the
K++n→K0+p interaction. Meanwhile, we modify the target nucleon energy and binding energy withmp−ER (ormn−ER ) andEB=ER−k2/(2M11B) [25], respectively. In addition, the fraction ofK+ -nucleon charge exchange and elastic scattering interactions is corrected in terms of the numbers of spectator protons and neutrons in the remaining nucleus. With all these modifications, we finally obtain a distribution of theK+ kinetic energies, as shown in Fig. 3. The charge exchange probability is approximately 1.7% forp→ˉνK+ in12 C according to the results of the modified GENIE.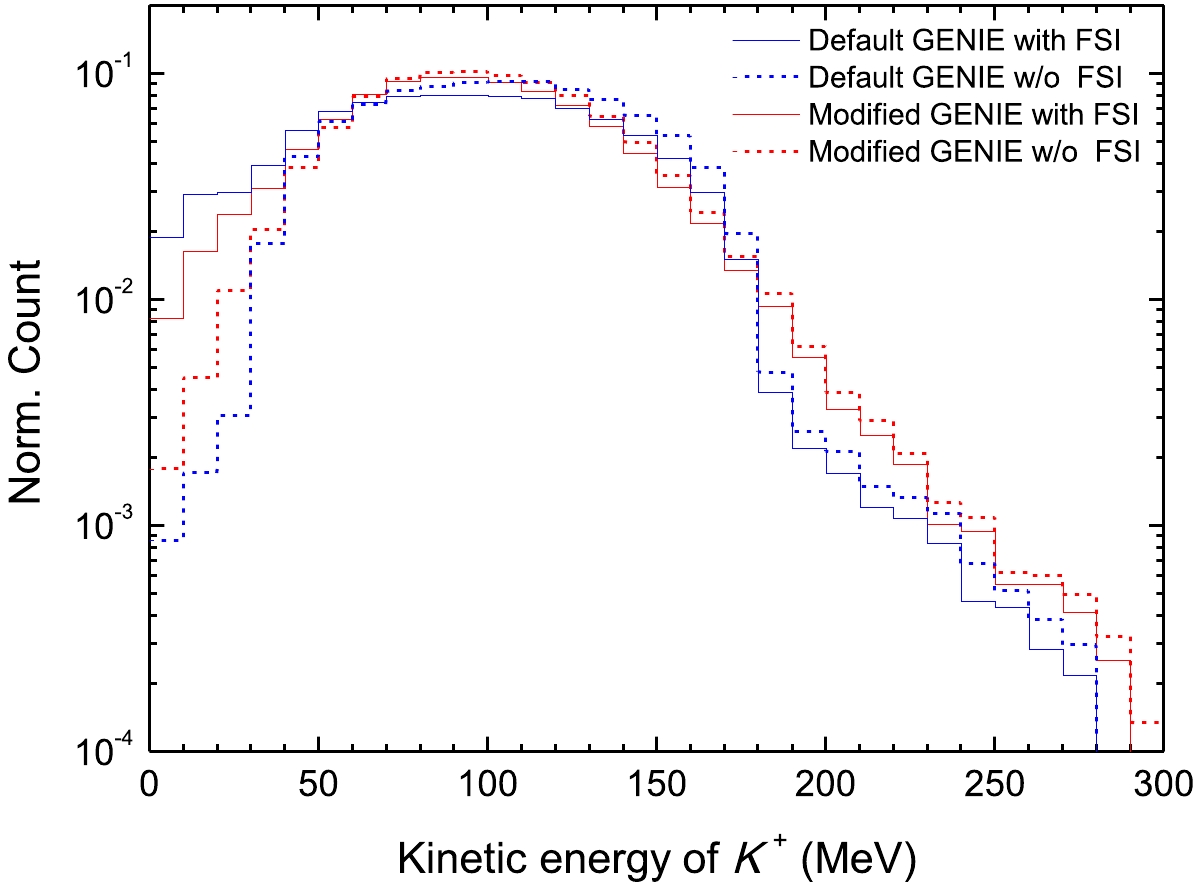
Figure 3. (color online)
K+ kinetic energy distributions forp→ˉνK+ in 12C with (solid line) and without (dashed line) the FSIs from the default (blue) and modified (red) GENIE.Third, all residual nuclei in the default GENIE are generated in the ground state; thus, no de-excitation processes are considered. The TALYS (version 1.95) software [26] is then applied to estimate the de-excitation processes due to the excitation energy
Ex .Ex of the residual nucleus can be calculated throughEx=Minv−MR , whereMinv andMR are the corresponding invariant and static masses, respectively. Forp→ˉνK+ in12C ,11B∗ ,10B∗ , and10Be∗ account for 90.9%, 5.1%, and 3.1% of the residual nuclei, respectively. Among these residual nuclei,10B∗ and10Be∗ originate from the final state interactions betweenK+ and one of the nucleons in11B∗ . The de-excitation modes and corresponding branching ratios of the residual nuclei11B∗ ,10B∗ , and10Be∗ have been reported in Ref. [24].According to the results, many de-excitation processes can produce neutrons. In the case of
s1/2 proton decay, the dominant de-excitation modes of the11B∗ states, includingn+10B ,n+p+9Be ,n+d+8Be ,n+α+6Li , and2n+p+8Be , will contribute to a branching ratio of 45.8% [24]. Approximately 56.5% of highly excited11B∗ states can directly emit one or more neutrons from their exclusive de-excitation modes. In addition, non-exclusive de-excitation processes and the de-excitation modes ofd+9Be andd+α+5He can also produce neutrons [24]. Most of these neutrons give a 2.2 MeV γ from neutron capture in the JUNO LS, which influences the setting of the criteria (introduced in Section. IV.B). -
The dominant backgrounds of
p→ˉνK+ are caused by atmospheric ν and cosmic muons because the deposited energy ofp→ˉνK+ events are usually larger than 100 MeV. Cosmic muons originate from the interaction between cosmic rays and the atmosphere. The produced cosmic muons usually have a very high energy and produce obvious Cherenkov light when passing through the water pool outside the JUNO CD. With the VETO system, JUNO is expected to discriminate more than 99% of cosmic muons. The muons not detected by the VETO system usually clip the corner of the water pool with a very low energy deposited and few Cherenkov photons produced and therefore escape from the watch of the VETO system. Thus, most VETO survived cosmic muons leave no signal in the CD and will not be background forp→ˉνK+ observations. For the muons that are VETO survived, producing entering and leaving signals in the CD, the energy deposition processes are mainly caused by the energetic primary muon. Consequently, with the visible energy, VETO, and volume selection, as well as the expected triple coincidence feature selection, this type of background is considered negligible. Therefore, the main background discussed in this paper arises from atmospheric ν events.The expected number of observed atmospheric ν events is calculated with the help of the atmospheric ν fluxes at the JUNO site [27], the neutrino cross sections from GENIE [18], and the best-fit values of the oscillation parameters in the case of the normal hierarchy [4]. The JUNO LS detector will observe 36 k events over ten years. We use GENIE in its default configuration to generate 160 k atmospheric ν events, which corresponds to 44.5 years of JUNO data collection or 890 kton-years exposure mass. Each atmospheric ν event has a weight value, which indicates the possibility of this event occurring for JUNO's 200 kton-years exposure considering neutrino oscillation. Then, these atmospheric ν events are simulated in SNiPER as our sample database.
Atmospheric ν events can be classified into the following four categories [28]: charged current quasi-elastic scattering (CCQE), neutral current elastic scattering (NCES), pion production, and kaon production. The categories and their ratios are shown in Table 1. The most dominant backgrounds in the energy range of
p→ˉνK+ (sub-GeV) are formed by elastic scattering, including CCQE and NCES events. The final states of the elastic scattering events usually deposit all of their energy immediately, eventually followed by a delayed signal. Consequently, requiring a triple coincidence feature effectively suppresses these two categories of backgrounds.Type Ratio (%) Ratio with Evis in [100 MeV, 600 MeV] (%)
Interaction Signal characteristics NCES 20.2 15.8 ν+n→ν+n, 
ν+p→ν+p 
Single pulse CCQE 45.2 64.2 ¯νl+p→n+l+, 
νl+n→p+l− 
Single pulse Pion Production 33.5 19.8 νl+p→l−+p+π+, 
ν+p→ν+n+π+ 
Approximate single pulse (Second pulse too low) Kaon Production 1.1 0.2 νl+n→l−+Λ+K+, 
νl+p→l−+p+K+ 
Double pulse Table 1. Categories of atmospheric ν backgrounds. The data are summarized based on the results of GENIE and SNiPER.
Other significant backgrounds are CC and NC pion production, which are caused by single pion resonant interactions and coherent pion interactions, respectively. The produced pions decay into muons with an average time of 26 ns. These muons, together with those produced in CC pion production, consequently produce Michel electrons. It can be found that pion-production events may feature a triple coincidence in time, similar to the search for
p→ˉνK+ . However, the muon contributing to the second pulse of the triple coincidence has a kinetic energy of 4 MeV, which is too small compared to the total energy deposition.Atmospheric ν interactions with pion production have a greater possibility of producing the accompanying nucleons. Some of the created energetic neutrons have a small probability to propagate freely for more than 10 ns in the LS. In this case, the neutron interaction can cause a sufficiently large second pulse. Therefore, pion production events with an energetic neutron, for example,
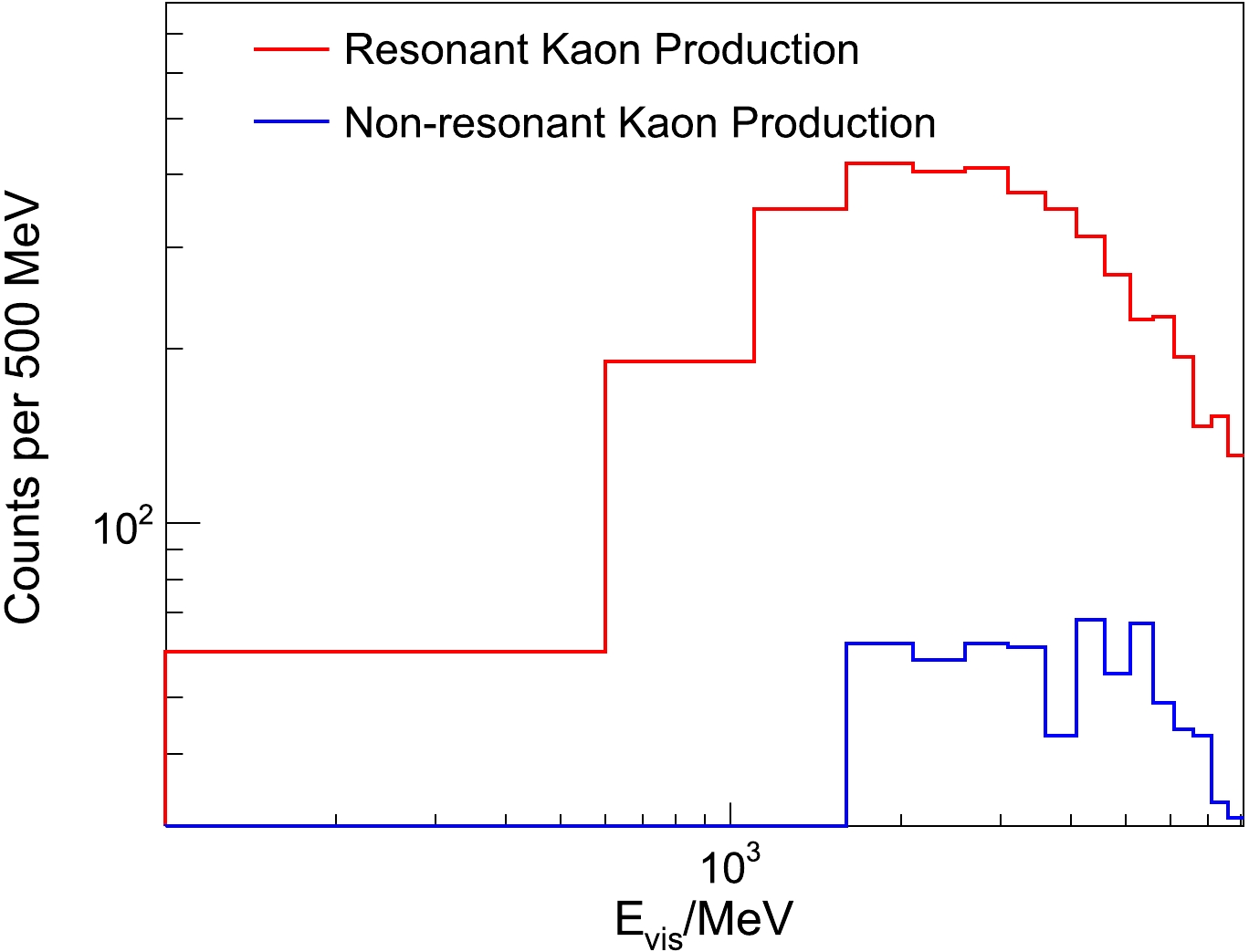
v+p→v+n+π+ , can mimic the signature ofp→ˉνK+ . In fact, theˉνμ CC quasi-elastic scatteringˉνμ+p→n+μ+ can also contribute to this type of background. It should be noted that this type of event was not observed by KamLAND [14]. However, because of its larger target mass and proton exposure compared to KamLAND, it is possible for JUNO to observe these backgrounds. Because the energetic neutron usually breaks up the nucleus and produces many neutrons, a large amount of neutron capture can be used to suppress this type of background.Another possible source of background is resonant and non-resonant kaon production (with or without Λ). The visible energy distribution of the kaon is shown in Fig. 4. The Nuwro generator [29] is applied to help estimate the non-resonant kaon production because this type of event is not included in GENIE owing to strangeness number conservation. Based on the results of the simulation, this type of background has a negligible contribution in the relevant energy range (smaller than 600 MeV), which is similar to the LENA [13] and KamLAND [14] conclusions.
Figure 4. (color online) Visible energy distribution of kaon production from atmospheric ν backgrounds. According to the plot, the resonant kaon production has a negligible contribution and the non-resonant background can be eliminated, with an upper
Evis cut at 600 MeV. -
To quantify the performance of background discrimination, we design a series of selection criteria to evaluate the detection efficiency of
p→ˉνK+ and the corresponding background rate based on the simulation data sample. According to the physics mechanisms introduced in the previous section, the key part of the selections is based on the triple coincidence signature in the hit time spectrum. Many beneficial studies searching for proton decay with an LS detector have been discussed by the LENA group and performed by the KamLAND collaboration [13, 14]. However, the situation in JUNO is more challenging because of the considerably larger detector mass compared to KamLAND. Owing to the relative masses, in ten years, the detected number of atmospheric ν would be approximately 20 times that of the KamLAND experiment. Therefore, more stringent selection criteria must be defined to suppress background to a level that is at least as low as that of KamLAND. Besides the common cuts on energy, position, and temporal features, additional criteria must be explored. For the JUNO detector, a possible additional way to distinguishp→ˉνK+ is using delayed signals, including the Michel electron and neutron capture gammas. -
Basic event selection uses only the most apparent features of the decay signature. The first variable considered is the visible energy of the event. The visible energy of
p→ˉνK+ originates from the energy deposition ofK+ and its decay daughters. The average energy deposition ofK+ is 105 MeV, whereas that of the decay daughters is 152 MeV and 354 MeV in the two dominantK+ decay channels. Therefore, as illustrated in Fig. 5, the visible energy ofp→ˉνK+ is mostly concentrated in the range200MeV≤Evis≤600MeV , which is comparable to that of the atmospheric ν backgrounds. Nearly half of the atmospheric ν events in the simulated event sample can be rejected with theEvis cut, whereas thep→ˉνK+ survival rate is more than 94.6%. The left and right peaks mainly correspond to theK+→μ+νμ andK+→π+π0 decay channels, respectively.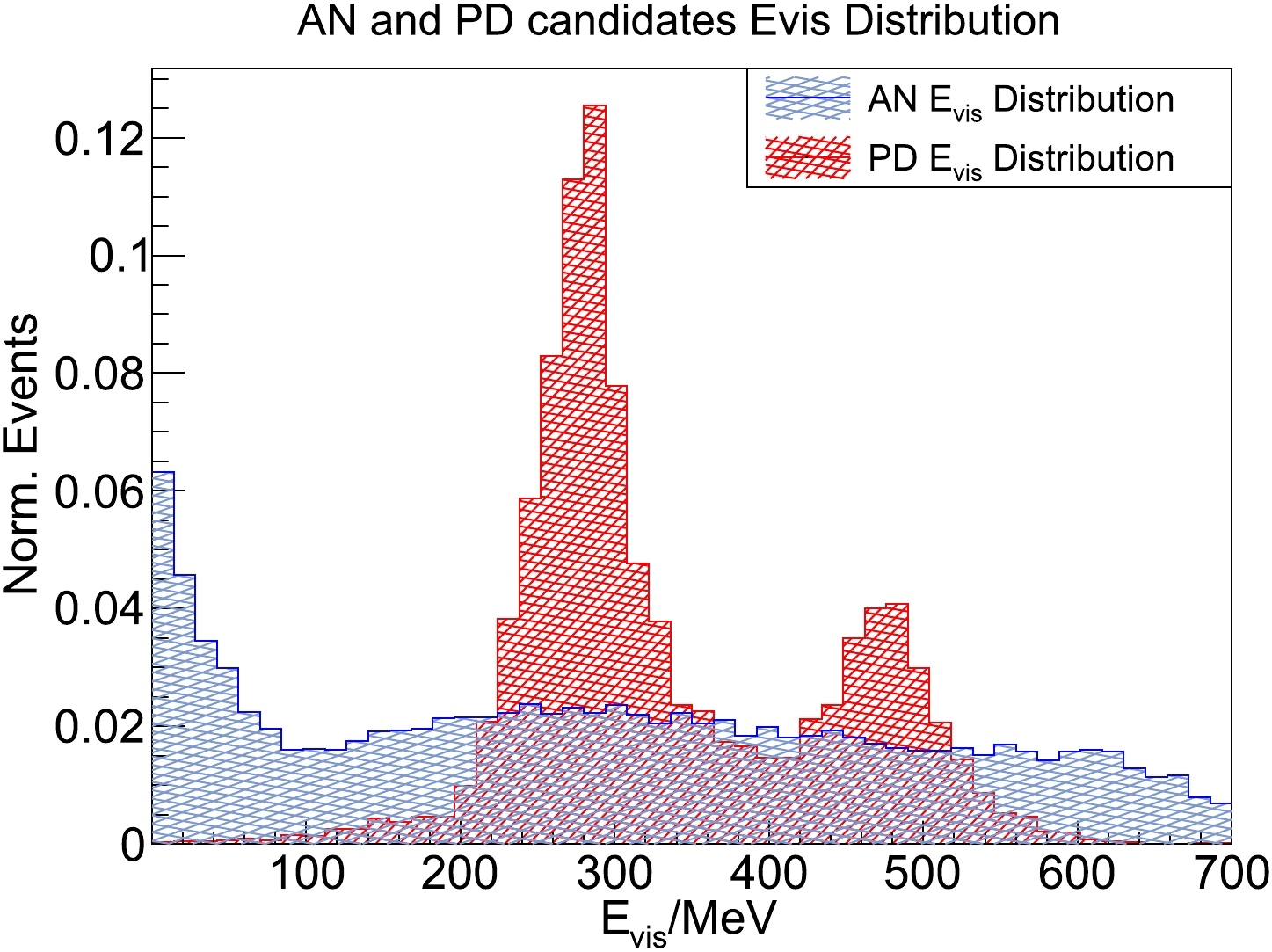
Figure 5. (color online) Visible energy distributions of
p→ˉνK+ (PD) and atmospheric ν (AN) events.In the second step, if the CD is triggered, the VETO detector must be quiet in two consecutive trigger windows of 1000 ns, which are before and after the prompt signals. In this way, most muons can be removed, and the remaining muons usually pass through the CD near its surface. The remaining muons usually have smaller visible energies and shorter track lengths. Thus, the track of the remaining muons should be closer to the boundary of the CD. Consequently, they can be further removed by a volume cut. The volume within
RV≤17.5 m is defined as the fiducial volume of the JUNO detector inp→ˉνK+ searches; therefore, the fiducial volume cut efficiency is 96.6% and will be counted into the selection efficiency.As shown in Table 2, after the basic cuts
Criteria Survival rate of p→ˉνK+ (%)
Survival count (fraction) of atmospheric ν Sample 1 Sample 2 Sample 3 Sample 1 Sample 2 Sample 3 Basic selection Evis 
94.6 51299 (32.1%) RV 
93.7 47849 (29.9%) Delayed signal selection NM 
74.4 4.4 20739 (13.0%) 1143 (0.7%) ΔLM 
67.0 4.4 13796 (8.6%) 994 (0.6%) Nn 
48.4 17.9 – 5403 (3.4%) 6857 (4.3%) – ΔLn 
– 16.6 – – 4472 (2.8%) – Time character selection Rχ 
45.9 9.0 3.8 4326 (2.7%) 581 (0.4%) 716 (0.4%) ΔT 
28.3 7.7 2.4 121 (0.07%) 18 (0.01%) 30 (0.02%) E1,E2 
27.4 7.3 2.2 1 (0.0006%) 0 0 Total 36.9 1 Table 2. Detection efficiencies of
p→ˉνK+ and the number of atmospheric ν backgrounds after each selection criterion. The total number of atmospheric ν backgrounds simulated is 160 k, which corresponds to an exposure of 890 kton-years.(Cut-1): visible energy
200MeV≤Evis≤600MeV ,(Cut-2-1): VETO system is not triggered in 1000 ns windows before and after the prompt signals,
(Cut-2-2): volume cut is set as
RV≤17.5 m,the survival rate of
p→ˉνK+ in the simulated signal sample is 93.7%, whereas that of the atmospheric ν events is 29.9% from the total atmospheric ν events. Further selection methods are required to reduce the atmospheric ν background. -
Owing to its good energy and time resolution, JUNO can measure the delayed signals of
p→ˉνK+ and atmospheric ν events, including the Michel electron and neutron capture. Approximately 95% ofp→ˉνK+ is followed by a Michel electron, whereas only 50% of the background events exhibit a delayed signal after the basic selections. On the other hand,p→ˉνK+ on average has a smaller number of captured neutrons per event than the atmospheric ν events. Criteria can be set to further reduce the remaining background after the basic selection based on the differences between the characteristics of the delayed signals.The Michel electron is the product of muon decay with a kinetic energy of up to 52.8 MeV, and the muon lifetime is 2.2 μs. For Michel electron signals, we can obtain the visible energy
EM , the correlated time differenceΔTM to the prompt signal, and the correlated distanceΔLM to the deposition center of the prompt signal from the MC simulation. Based on the physical properties ofp→ˉνK+ and background events, it is assumed that JUNO can fully identify a Michel electron with10MeV<EM<54 MeV and150ns<ΔTM<10000 ns. In this case, the efficiency of distinguishing Michel electrons is 89.2%. The lower limit ofEM is set to avoid the influence of low energy backgrounds, such as natural radioactivity. Fig. 6 shows the distributions ofNM andΔLM of identified Michel electrons forp→ˉνK+ and atmospheric ν events. Approximately 5.58% of thep→ˉνK+ events exhibitNM=2 Michel electrons, which corresponds to theK+ decay channelK+→π+π+π− . For theNM=2 case,ΔLM is taken to be the average value of two correlated distances. It is clear that proton decay has a smallerΔLM on average than the backgrounds. We can consequently useΔLM to reduce the atmospheric ν backgrounds by applying the criteria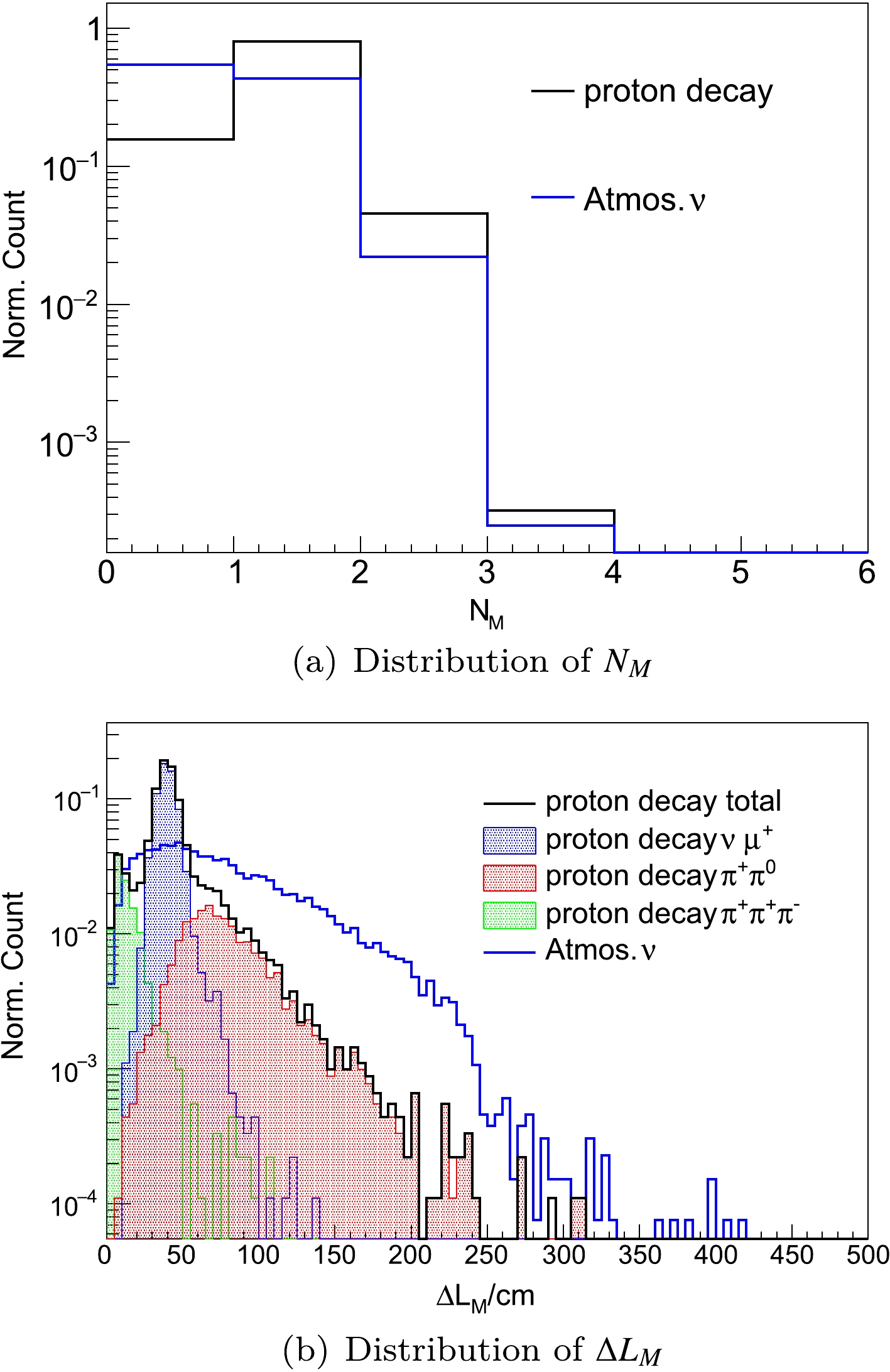
Figure 6. (color online)
NM andΔLM distributions of identified Michel electrons forp→ˉνK+ and atmospheric ν events with the basic selection and the selection of the time and energy properties of Michel electrons. Unit area normalization is used.(Cut-3): tagged Michel electron number
1≤NM≤2 ,(Cut-4): correlated distance
ΔLM≤80 cmin the remaining proton decay candidates after the basic selection. It can be found that 71.4% of
p→ˉνK+ and 9.2% of atmospheric ν events survive in the simulated event samples.Similar to the Michel electron, neutron capture is another potential selection criterion. Here, we assume that the delayed neutron capture signal can be fully identified by requiring the visible energy to lie within
1.9MeV≤En≤2.5 MeV and the correlated time difference to be 1μs≤ΔTn≤2.5 ms. In this way, 89.5% of the neutrons produced by atmospheric ν events can be distinguished. Fig. 7 shows the identified neutron distributions ofp→ˉνK+ signals and backgrounds after the basic selections. The proton decay events have a smallerNn on average than the atmospheric ν events. Therefore, we use the selection cutNn≤3 to suppress the background. As shown in Fig. 7, the distanceΔLn , which is defined similar toΔLM , can also be a powerful tool to reduce the backgrounds. Thus, a cut ofΔLn≤70 cm is required. Note that the criteria onNn andΔLn can reduce an important class of backgrounds, namely, events with a high energy neutron in the final state of the primary atmospheric ν interaction. Such a high energy neutron has a small probability of not losing its energy within 10 ns until it interacts with the LS to give a second pulse. If the final states includeμ± orπ+ , this background event will mimic the three fold coincidence ofp→ˉνK+ . Because a high energy neutron usually produces more neutrons and largerΔLn , we choose the cuts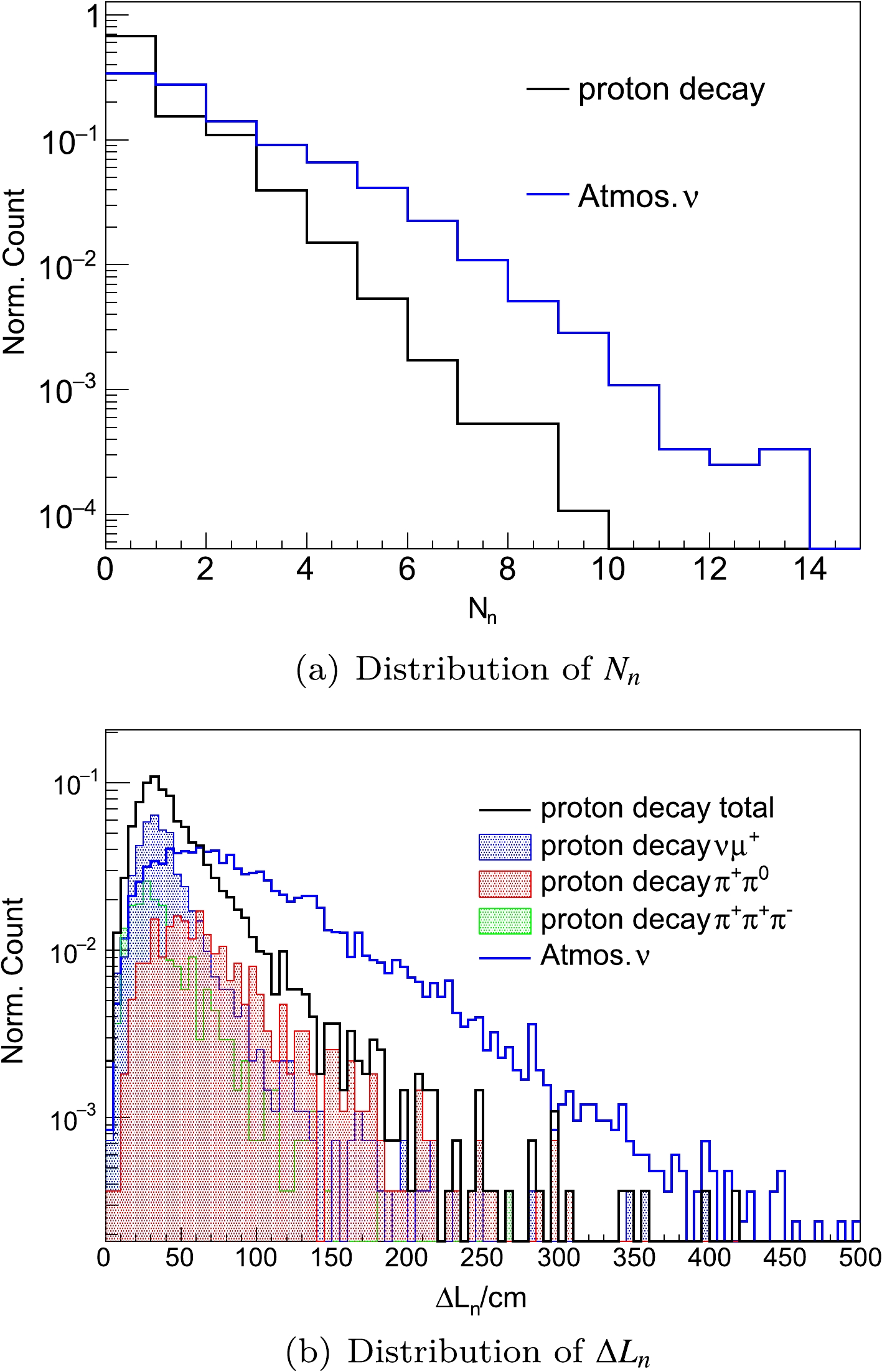
Figure 7. (color online)
Nn andΔLn distributions of identified neutron capture forp→ˉνK+ and atmospheric ν events with the basic selection. Unit area normalization is used.(Cut-5): tagged neutron number
Nn≤3 forNM=1 ,(Cut-6):
ΔLn≤70 cm ifNM=1 and1≤Nn≤3 ,to suppress this type of background.
Based on the above discussions on delayed signals, we naturally classify the MC events into the following three samples:
Sample 1:
NM=1,ΔLM≤80cm,Nn=0 ;Sample 2:
NM=1,ΔLM≤80cm, 1≤Nn≤3,ΔLn≤ 70cm ;Sample 3:
NM=2,ΔLM≤80cm .The survival rate of
p→ˉνK+ and the atmospheric ν events in the simulation can be found in Table 2. Approximately 6.8% of the total atmospheric ν events would survive, requiring further selection methods to reduce the background. -
As introduced in Sec. III.A, a
p→ˉνK+ event usually has a triple coincidence signature on its hit time spectrum. The first two pulses of the triple coincidence overlap each other in terms of the decay time ofK+ , which is a distinctive feature ofp→ˉνK+ compared to the atmospheric ν backgrounds. This means thatp→ˉνK+ can be distinguished from the backgrounds according to the characteristics of the overlapping double pulses. Therefore, the hit time spectrum is studied further using the multi-pulse fitting method [14] to reconstruct the time difference and energy ofK+ and its decay daughters.For each event, its hit time spectrum can be fitted with double-pulse
ϕD(t) and single-pulseϕS(t) templates of the hit time t,ϕD(t;ϵK,ϵi,a,ΔT)=ϵKϕK(t)+ϵiϕi[a(t−ΔT)],
(1) ϕS(t;ϵS)=ϵSϕAN(at),
(2) where
ϕK(t) is the TOF-corrected template ofK+ ,ϕi(t) is that of a decay daughter ofK+ , andi=μ and π refer to the two dominant decay channelsK+→μ+νμ forEvis≤400MeV andK+→π+π0 otherwise, respectively. These templates are produced by the MC simulations in which the particles are processed by SNiPER with their corresponding kinetic energies.ϕAN(t) is the template of the backgrounds, generated as the average spectrum of all the atmospheric ν events with energy depositions from 200 to 600 MeV. Owing to the influence of reflection, the hit time spectrum is widened when the energy deposition center is close to the boundary. To deal with this effect, the templates are separately produced in the inner (< 15 m) and outer volumes (> 15 m) and applied to the fitting of events in the corresponding volumes.In Eqs. (1) and (2),
ΔT is the correlated time difference of the delayed component, a is a scaling factor to account for shape deformation of the second pulse caused by the electromagnetic showers, andϵK ,ϵi , andϵS are the corresponding energy factors. They are free parameters in the fitting. For illustration, we use Eq. (1) to fit two typical events, as shown in Fig. 8.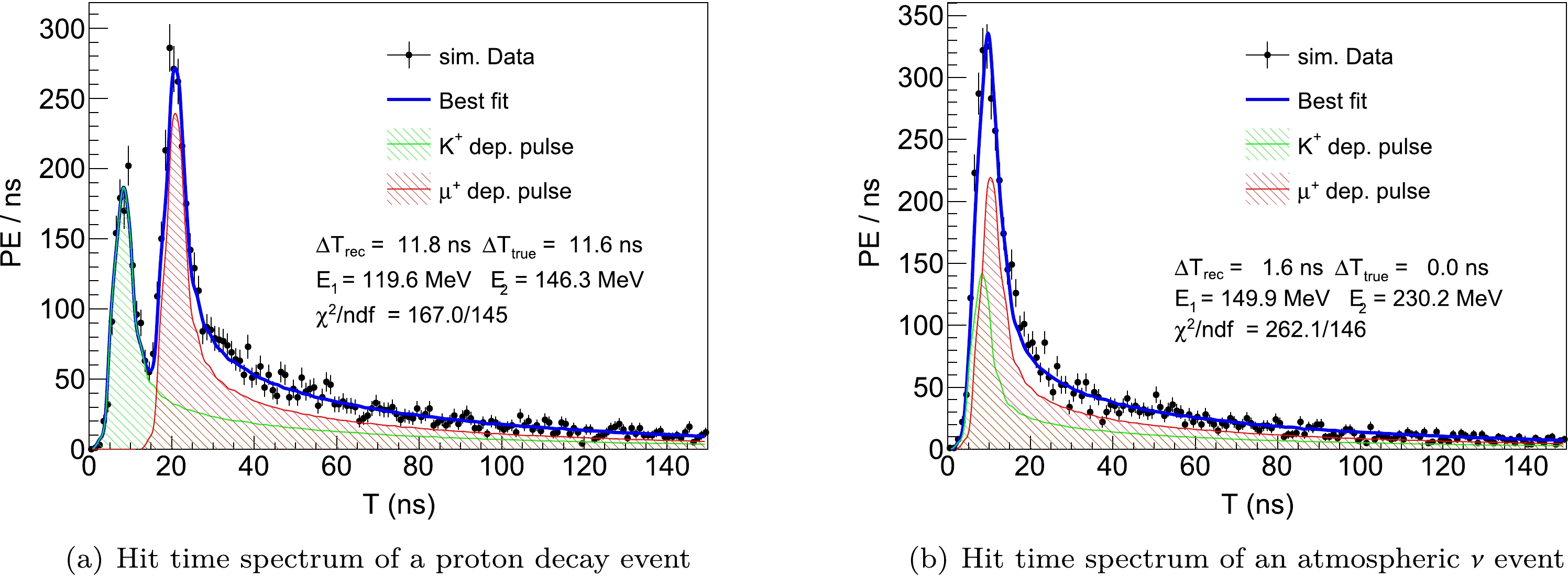
Figure 8. (color online) Illustration of multi-pulse fitting to the hit time spectra of a proton decay event (left) and an atmospheric ν event (right). The x axis is the hit time after TOF correction. The black dots indicate the observed spectrum from the simulation. The blue line is the fitting result. The green and red filled histograms are the fitted result of the two components in the hit time spectrum, contributed by the
K+ andK+ decay daughters.After fitting the hit time spectra with the templates of Eqs. (1) and (2), we calculate
χ2 of the double and single pulse fittings usingχ2D=∑[ϕ(t)−ϕD(t)]2σ2[ϕ(t)],
(3) χ2S=∑[ϕ(t)−ϕS(t)]2σ2[ϕ(t)],
(4) where
σ2[ϕ(t)] is the sample variance of the observed spectrumϕ(t) at the t-th bin. Theχ2 ratioRχ≡χ2S/χ2D is taken as a further selection criterion. From the double-pulse fitting using Eq. (1), the energiesE1 andE2 of the overlapping double pulses from the depositions of the postulatedK+ and its decay daughters are calculated fromϵK ,ϵi , and a introduced in Eq. (1),E1=ϵKTKϵKTK+ϵiTi/aEfit
(5) E2=ϵiTi/aϵKTK+ϵiTi/aEfit,
(6) where
TK=105 MeV is the initial kinetic energy ofK+ from the free proton decay.Tμ=152 MeV andTπ=354MeV are the initial kinetic energies of the muon and pion from theK+ decay at rest. The fitted total energy is defined asEfit=Evis−∑EM−∑En , which is the visible energy minus the energies of Michel electrons and neutron capture.The way to select
p→ˉνK+ from the atmospheric ν backgrounds according to the parameters acquired above is introduced next. In Fig. 9, we plot theRχ distributions for proton decay and the atmospheric ν events after applying the selections from Cut-1 to Cut-6. We find thatRχ is a tool to reject the background. In fact,Rχ can be regarded as an indicator that the fitted event tends to be a double pulse overlapping event or a single pulse event. The larger theRχ , the stronger it tends to be an event with two pulses overlapping in the hit time spectrum. A cut ofRχ>1 can be applied to roughly perform the selection. IfRχ>1 , this fitted event may be preliminarily identified as a proton decay candidate. Otherwise, it would be rejected as a background candidate. However, a general cut ofRχ is not justified to the three samples defined at the end of Sec. IV.B. Compared to Sample 1, which is composed of the commonp→ˉνK+ and atmospheric ν events, Sample 2 is additionally composed of background events with energetic neutrons, as introduced in Sec. III.B. The second pulse caused by an energetic neutron gives these atmospheric ν events a fake double pulse overlapping shape in the hit time spectrum. A stricter requirement onRχ is consequently necessary to reduce the background.K+ produced in thep→ˉνK+ events in Sample 3 decays viaK+→π+π+π− owing to the cut on the number of Michel electronsNM=2 . As a result,p→ˉνK+ should be easier to distinguish from the backgrounds withNM=2 . Therefore it is reasonable to set a less stringent cut onRχ to maintain a high detection efficiency. Consequently,Rχ will be set separately for the three samples. To sufficiently reject atmospheric ν backgrounds, we require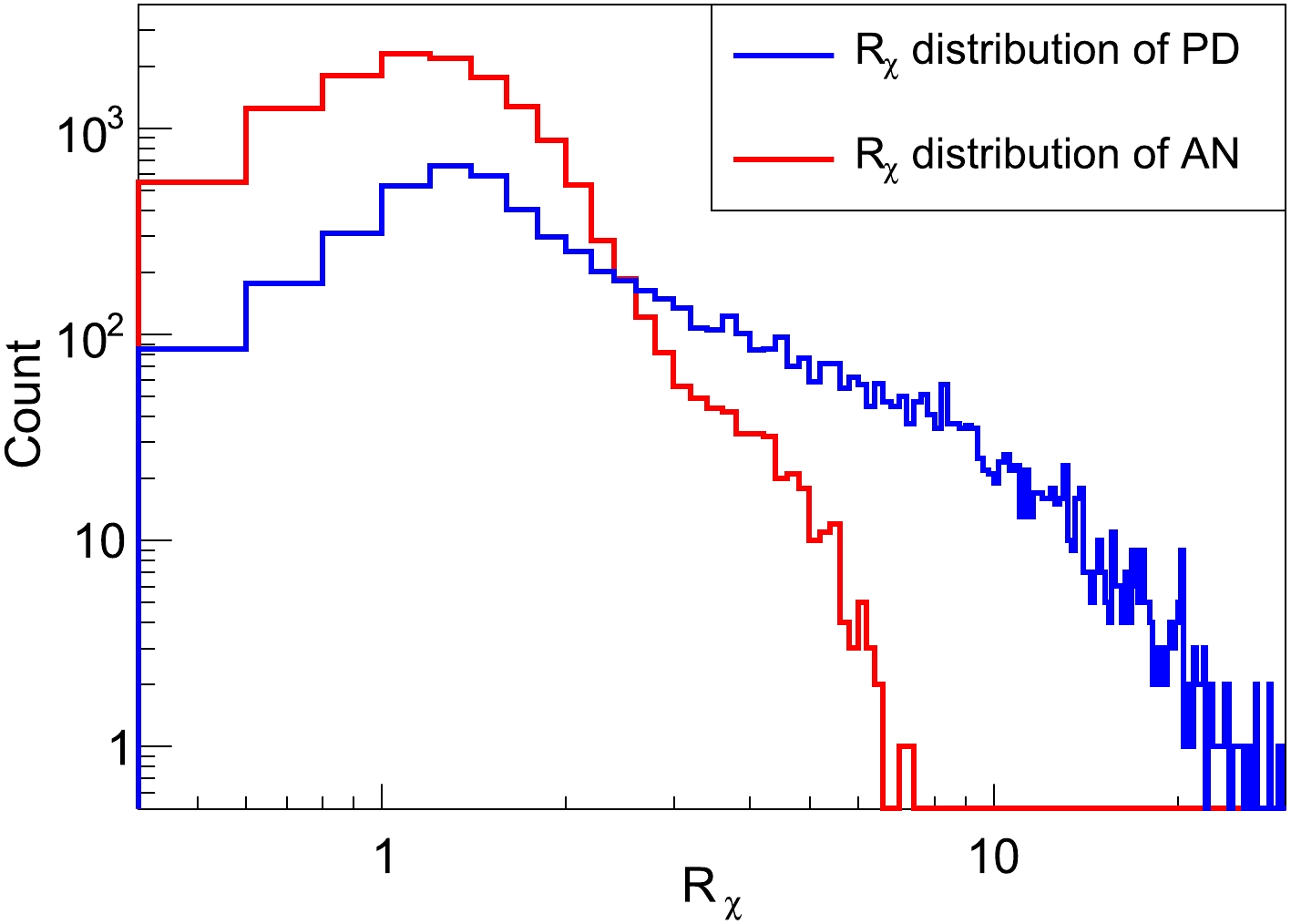
Figure 9. (color online) Distributions of the
χ2 ratioRχ≡ χ2S/χ2D fromp→ˉνK+ (PD) and atmospheric ν (AN) events after the basic and delayed signal selections.(Cut-7-1):
Rχ>1.1 for Sample 1,(Cut-7-2):
Rχ>2.0 for Sample 2,(Cut-7-3):
Rχ>1.0 for Sample 3.The distributions of fitted
ΔT are shown in Fig. 10(a), where a rough cut ofRχ>1 is applied top→ˉνK+ and the backgrounds. From the figure, we find thatΔT for the remaining backgrounds, which are mis-identified asp→ˉνK+ candidates, are mostly distributed at smallΔT because atmospheric ν events are usually a single pulse. Meanwhile, whenK+ decays in a few nanoseconds, the fitting has low efficiency because both components are too close to be distinguished from each other (as shown in Fig. 10(b)). Consequently,ΔT is required as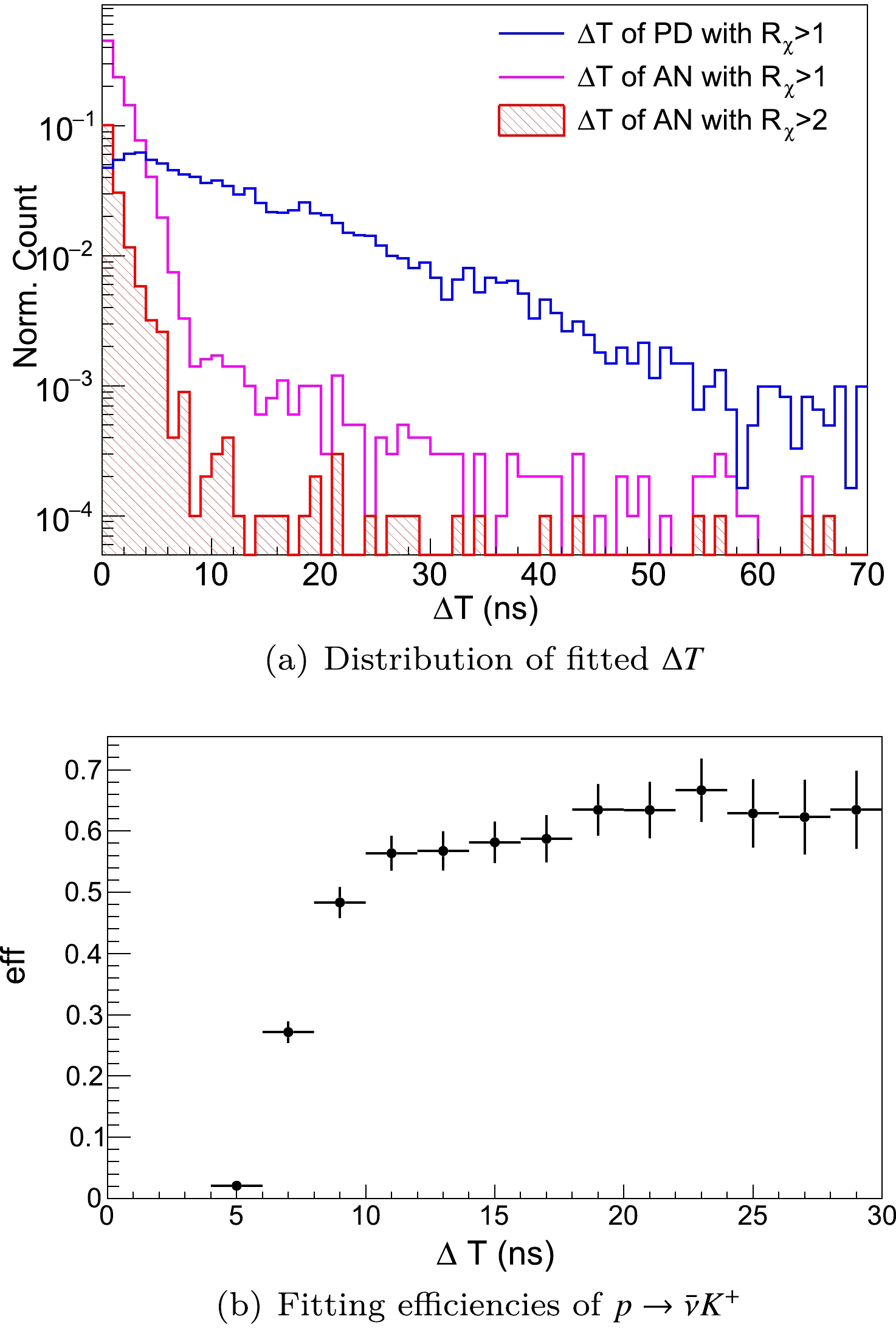
Figure 10. (color online)
ΔT distribution and fitting efficiencies. (a) Distribution of fittedΔT (Eq. (1)) ofp→ˉνK+ (PD, in blue) and atmospheric ν (AN, red filled and pink) events with differentRχ cuts after the basic and delayed signal selections. (b) Fitting efficiencies forp→ˉνK+ with different trueΔT (K+ decay time). The efficiencies are low whenK+ decays within several ns because both pulse components are too close.(Cut-8): correlated time difference should be
ΔT≥7 ns.Regarding the kinematics of
K+ and its decay daughters, the sub-energyE1 should be distributed from 0 to more than 200 MeV, with an average of 105 MeV, whereasE2 should be fixed around 152 MeV or 354 MeV depending on the decay mode. As shown in Fig. 11, we plot the correlated sub-energy deposition distributions ofp→ˉνK+ and the background events. Two obvious groups can be observed in the left panel, corresponding to the two dominant decay channels ofK+ . Only a small group of atmospheric ν events remains in the bottom right corner of the right panel of Fig. 11, which originates from the mis-identification of a tiny second peak. It is clear that a box selection onE1 andE2 can efficiently reject the atmospheric ν backgrounds. Therefore, the selections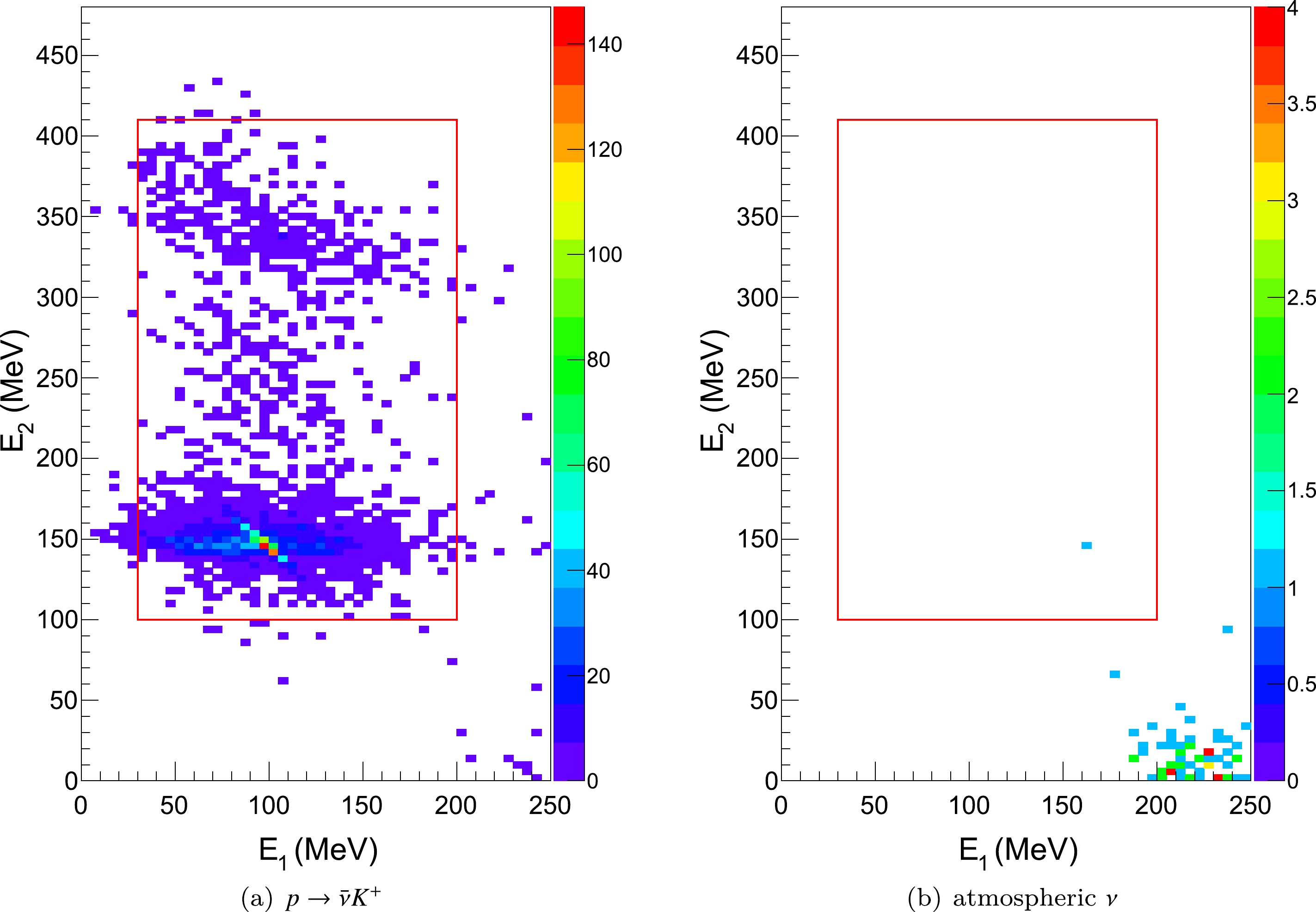
Figure 11. (color online) Correlated
E1 andE2 distributions (in colored scale) forp→ˉνK+ (a) and atmospheric ν (b) events with the basic selection, delayed signal selection,Rχ cut, andΔT cut. The events outside the red boxes are rejected as background. More details can be found in the text.(Cut-9-1):
30MeV≤E1≤200 MeV,(Cut-9-2):
100MeV≤E2≤410 MeV,are required. The lower boundary of
E1 is set to avoid the influence of the coincidence with low energy events, such as reactor antineutrinos or radioactive backgrounds.The detection efficiencies under each selection criterion are listed in Table 2, where the number of remaining backgrounds are also shown, from which the elimination power of each criterion can be found. After applying these criteria, the total efficiency for
p→ˉνK+ is estimated to be 36.9%, and only one event in Sample 1 remains from the simulated 160 k atmospheric ν events (corresponding to an exposure of 890 kton-years or an exposure time of 44.5 years at the JUNO site). Because the volume cut in the basic selections provides a selection efficiency of 96.6% to the total efficiency, it will not be counted in the exposure mass calculation. The three samples contribute 27.4%, 7.3%, and 2.2% of the detection efficiencies, respectively. Considering the statistical error and weighting value, which accounts for the oscillation probability, the background level corresponds to 0.2 events, which is scaled to 10 years of data collection by JUNO. -
The detection efficiency uncertainties of
p→ˉνK+ are estimated and shown in Table 3. The statistical uncertainty is estimated to be 1.6% in the MC simulation. So far, we have been using the ideal setting for position reconstruction (30 cm for the energy deposition center position uncertainty without bias). Considering the performance of the vertex reconstruction algorithm, it is assumed that the residual bias of the position reconstruction ofp→ˉνK+ is 10 cm. In this case, the efficiency uncertainty caused by a volume cut of 17.5 m is 1.7%.Source Uncertainty (%) Statistic 1.6 Position reconstruction 1.7 Nuclear model 6.8 Energy deposition model 11.1 Total 13.2 Table 3. Detection efficiency uncertainties for
p→ˉνK+ .Another important systematic uncertainty on the detection efficiency arises from the inaccuracy of the nuclear model, which influences the ratio of the accompanying particles of
p→ˉνK+ . To estimate this uncertainty, anotherp→ˉνK+ sample base is simulated with the FSI and de-excitation processes of the residual nucleus disabled. After applying all criteria, the difference in the detection efficiency is found to be 6.8%, which is the estimated uncertainty from the nuclear model.The dominant uncertainty originates from the energy deposition model. Owing to the lack of studies on sub-GeV particle behavior, especially the quenching effect of hundreds of MeV
K+ in LAB based LS, the deposition simulation in the LS detector might be inaccurate. Therefore, the simulated waveform of the hit time spectrum may differ from the real one. According to the study of KamLAND [14], this type of uncertainty is estimated as 11.1%. We conservatively use this value considering the similar detection method. Therefore, the uncertainty of the proton lifetime is estimated as 13.2%, considering all the sources introduced above.The uncertainties of the background level in ten years is composed of two parts. The first is the systematic uncertainty contributed by the uncertainty of the atmospheric neutrino flux (20%) and atmospheric neutrino interaction cross-section (10%) [5]. Another uncertainty originates from the number
Nn of neutron capture, which can be affected by the secondary interactions of the hadronic daughter particles of atmospheric neutrino events in the LS. This is estimated as 10% assuming the same uncertainty as Super-K [30]. The statistic uncertainty is estimated following the1/√N rule. Considering that only one event survives in the selection, it is calculated as±0.2 in ten years. With 160 k events in the current MC simulation, this is difficult to improve because it will consume vast computing resources. We hope to update this value with a larger MC simulation data volume when it permits. Consequently, the background is estimated as0.2±0.05(syst)±0.2(stat) .The sensitivity for
p→ˉνK+ is expressed asτ/B(p→ˉνK+)=NpTϵn90,
(7) where
Np=6.75×1033 is the total number of protons (including1.45×1033 free protons and5.3×1033 bound protons) in the JUNO CD, T is the running time, which is assumed to be 10 years to achieve an exposure mass of 200 kton-years,ϵ=36.9% is the total signal efficiency, andn90 is the upper limit of the 90% confidence level of the detected signals. This depends on the number of observed events and the background level. According to the Feldman-Cousins method [31],n90 is estimated as 2.61 given an expected background of 0.2 in 10 years. Thus, the JUNO sensitivity forp→ˉνK+ at the 90% C.L. with 200 kton-years would beτ/B(p→ˉνK+)>9.6×1033years.
(8) Compared to the representative LS detector, the detection efficiency on
p→ˉνK+ of JUNO is relatively lower than that of LENA [13]. This is reasonable considering that the study is based on an overall detector simulation of JUNO. Based on the background level of 0.02 events per year, we plot the JUNO sensitivity as a function of running time, as shown in Fig. 12. After six years of running (120 kton-years), JUNO will overtake the current best limit of the Super-K experiment.
Figure 12. (color online) JUNO sensitivity for
p→ˉνK+ as a function of running time.Moreover, the proton lifetime measured by JUNO will reach
1034 years for the first time after 10.5 years of data collection. In the case of no event observation after ten years, the 90% C.L. limit on the proton lifetime would reach1.1×1034 years. In the case of one event observation (16.4% probability), the corresponding limit would be6.0×1033 years. -
A simulation study is conducted to estimate the performance of the JUNO detector in searching for proton decay via
p→ˉνK+ . It is found that the expected detection efficiency ofp→ˉνK+ is 36.9% ± 4.9%, whereas the background is estimated to be0.2±0.05(syst)±0.2(stat) after ten years of exposure. Assuming no proton decay events are observed, the sensitivity of JUNO forp→ˉνK+ is estimated to be9.6×1033 years at the 90% C.L. based on a total exposure of 200 kton-years (or a live fiducial exposure of 193 kton-years). This is higher than the current best limit of5.9×1033 years from the excellent effort of the Super-K experiment with a live fiducial exposure of 260 kton-years [11].It shows that an LS detector such as JUNO will be competitive with the planned Hyper-Kamiokande [7] and DUNE [8] experiments. Using different target nuclei
12C from the LS and the newly developed analysis method considering delayed signals (Michel electrons and neutron capture), JUNO will provide a complementary search to test the GUTs from the perspective ofp→ˉνK+ . Besides thep→ˉνK+ mode, JUNO will have some sensitivity to the other nucleon decay modes listed in Ref. [4], particularly the decay modes that also exhibit the three fold coincidence feature in time, such asn→μ−K+ ,p→e+K∗(892)0 ,n→νK∗(892)0 , andp→νK∗(892)+ . These will be analyzed in the future.
JUNO sensitivity on proton decay p → νK+ searches
- Received Date: 2023-01-10
- Available Online: 2023-11-15
Abstract: The Jiangmen Underground Neutrino Observatory (JUNO) is a large liquid scintillator detector designed to explore many topics in fundamental physics. In this study, the potential of searching for proton decay in the
DownLoad: