-
The study of nucleon resonances (
$ N^\ast $ 's) and Δ resonances ($ \Delta^\ast $ 's) has always attracted significant interest from the hadron physics community because a thorough understanding of the structure and properties of N and Δ resonances is essential to understand clearly the nonperturbative behavior of quantum chromodynamics (QCD), the fundamental theory of strong interactions. It is well known that the experimental and theoretical studies of$ \pi N $ scattering and π photoproduction reactions provide most of the knowledge about the$ N^\ast $ 's and$ \Delta^\ast $ 's. Nevertheless, quark models [1−3] predicted larger numbers of$ N^\ast $ 's and$ \Delta^\ast $ 's than those experimentally observed. The possible reason might be that some of the unobserved$ N^\ast $ 's or$ \Delta^\ast $ 's couple weakly to the$ \pi N $ channel and thus escape from the observation. Further, there are many one-star and two-star$ N^\ast $ 's and$ \Delta^\ast $ 's whose parameters, especially the decay branching ratios to various final states, are not known in the most recent Particle Data Group (PDG) review [4]. These situations force us to investigate the$ N^\ast $ 's and$ \Delta^\ast $ 's in reaction channels other than π hadro- and photoproductions. In the past few years, substantial experimental and theoretical efforts have been devoted to the study of$ \eta N $ ,$ \eta' N $ ,$ KY $ ,$ \omega N $ ,$ K^\ast Y $ , and$ KY^\ast (Y=\Lambda, \Sigma) $ photoproduction reactions, and valuable results have been obtained [5−21]. In the present study, we concentrate on the photoproduction reaction of the$ f_1(1285) $ meson off the proton target.$ f_1(1285) $ is an axial-vector meson with quantum numbers$ I^G J^{PC}=0^+ 1^{++} $ , mass$ M=1281.9\pm 0.5 $ MeV, and width$ \Gamma=22.7\pm 1.1 $ MeV [4]. As the$ f_1(1285) p $ threshold is above$ 2.2 $ GeV, this reaction is more suitable than π production reactions to investigate the$ N^\ast $ 's with a higher mass in the less-explored energy region. Furthermore, the$ f_1(1285) p $ photoproduction reaction acts as an “isospin filter,” isolating the nucleon resonances with isospin$ I=1/2 $ and eliminating the interference of the Δ resonances with isospin$ I=3/2 $ .Experimentally, the differential cross-section data for
$ \gamma p \to f_1(1285) p $ with$ f_1(1285) \to \eta \pi^+\pi^- $ in the energy range from the$ f_1(1285) p $ threshold up to the center-of-mass energy$ W\approx 2.8 $ GeV were released in$ 2016 $ by the CLAS Collaboration at the Thomas Jefferson National Accelerator Facility (JLab) [22]. Compared with the simultaneously released cross-section data for$ \gamma p \to \eta'(958)p $ with$ \eta'(958)\to \eta\pi^{+}\pi^{-} $ , the$ f_1(1285) $ cross sections are much flatter in$ \cos\theta $ angular dependence, indicating less important t- and u-channel contributions and possible s-channel nucleon resonance contributions.Several theoretical studies have been committed to the investigation of the
$ \gamma p \to f_1(1285) p $ photoproduction reaction. Before the publication of the CLAS data, predictions of the differential cross sections for$ \gamma p \to f_1(1285) p $ from various theoretical models were available in Refs. [23−25]. Nevertheless, none of them seemed to be able to even qualitatively describe the CLAS data reported in 2016 [22]. Since the CLAS differential cross-section data for$ \gamma p \to f_1(1285) p $ became available, two theoretical studies analyzed them, both in the framework of the so-called interpolated Regge model [26, 27]. However, the conclusions drawn from these two analyses are quite different. In Ref. [26], all the contributions from the resonance-pole diagrams,$ NN\gamma $ vector coupling ($ \propto {\bar N}\gamma_\mu A^\mu N $ ) in the s-channel N-pole diagram and u-channel N-exchange diagram, and contact term were omitted. Only the contributions from the t-channel ρ- and ω-exchange diagrams together with those from the$ NN\gamma $ tensor coupling ($ \propto {\bar N}\sigma^{\mu\nu}\partial_\nu A_\mu N $ ) in the s-channel N-pole diagram and u-channel N-exchange diagram were considered in the calculation. It was concluded that the CLAS differential cross-section data can be reproduced without considering any nucleon resonances. In Ref. [27], besides the t-channel ρ- and ω-exchange diagrams, s-channel N-pole diagram, u-channel N-exchange diagram, and contact term contributions, the$ N(2300){1/2}^+ $ -pole diagram was further considered in constructing the reaction amplitudes. It was reported that the contribution from the$ N(2300){1/2}^+ $ -pole diagram plays an important role in reproducing the CLAS differential cross-section data.As both Refs. [26] and [27] used the interpolated Regge model and analyzed the same set of data, it is not clear whether the differences in their conclusions about the
$ \gamma p \to f_1(1285) p $ reaction mechanisms and the extracted resonance contents are due to the fact that the contributions from the contact term and$ NN\gamma $ vector coupling ($ \propto {\bar N}\gamma_\mu A^\mu N $ ) were omitted in Ref. [26]. Furthermore, one is curious whether the$ N(2300){1/2}^+ $ resonance is the only one that is needed to describe the CLAS differential cross-section data for$ \gamma p \to f_1(1285) p $ in an interpolated Regge model, as in Ref. [27]. Besides, one wants to make clear whether the traditional Feynman model and/or Regge model are capable of describing the available cross-section data from the CLAS Collaboration for the$ \gamma p \to f_1(1285) p $ reaction.To eliminate the above-mentioned confusions, in the present study, we present an independent and comprehensive analysis of the CLAS data [22] on differential cross sections for
$ f_1(1285)p $ photoproduction in an effective Lagrangian approach. We build three different reaction models, that is, the Feynman, Regge, and interpolated Regge models, where the reaction amplitudes of t-channel ρ and ω exchanges are constructed in Feynman, Regge, and interpolated Regge types, respectively. In each of these three models, the t-channel ρ- and ω-exchange diagrams, s-channel N-pole diagram, u-channel N-exchange diagram, and generalized interaction current are considered as background ingredients. Moreover, the s-channel pole diagrams of a minimum number of nucleon resonances are considered to obtain a satisfactory description of the available data. The gauge invariance of the photoproduction amplitude is guaranteed by introducing an auxiliary current, which ensures that the full reaction amplitude satisfies the generalized Ward-Takahashi identity and thus is fully gauge invariant, independent of any specific type of form factors introduced in hadronic vertices [28−31].The present paper is organized as follows. In Sec. II, we introduce the framework of our theoretical model. In Sec. III, we present our theoretical results and a discussion of them. Finally, a brief summary and conclusions are given in Sec. IV.
-
The full photoproduction amplitudes for
$\gamma N \to f_1(1285) N$ can be expressed as$ \begin{array}{*{20}{l}} M^{\nu\mu} = M^{\nu\mu}_s + M^{\nu\mu}_t + M^{\nu\mu}_u + M^{\nu\mu}_{\rm int}, \end{array} $

(1) with ν and μ being Lorentz indices of the
$ f_1(1285) $ meson and photon, respectively. The first three terms,$ M^{\nu\mu}_s $ ,$ M^{\nu\mu}_t $ , and$ M^{\nu\mu}_u $ , stand for the s-, t-, and u-channel amplitudes, respectively, with s, t, and u being the Mandelstam variables of the internally exchanged particles. They arise from the photon attaching to the external particles in the underlying$ NNf_{1} $ interaction vertex. The last term,$ M^{\nu\mu}_{\rm int} $ , stands for the interaction current that arises from the photon attaching to the internal structure of the$ NNf_{1} $ interaction vertex. All four terms in Eq. (1) are diagrammatically presented in Fig. 1.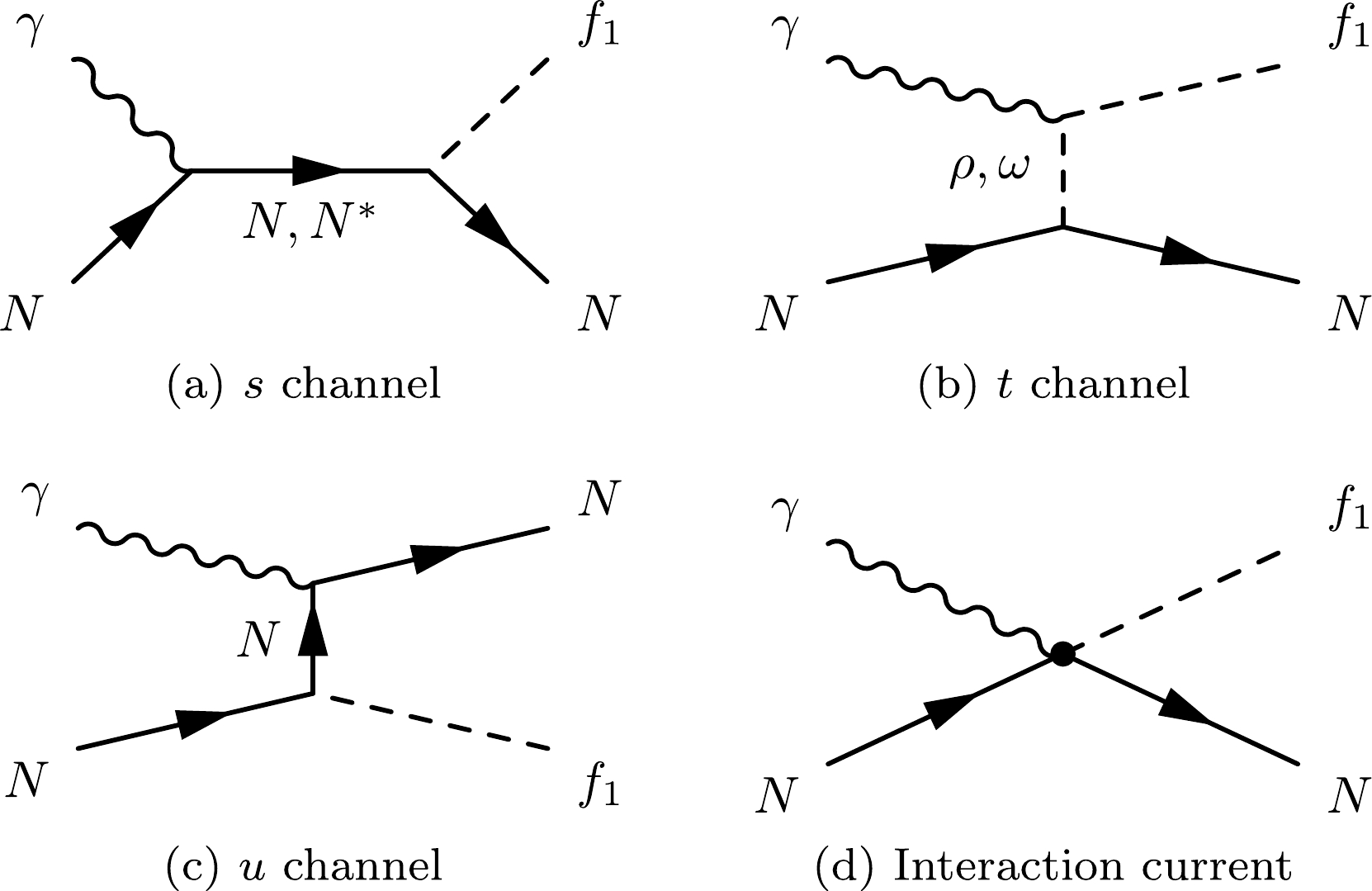
Figure 1. Generic structure of the amplitude for
$\gamma N\to $ $ f_1(1285) N$ . Time proceeds from left to right. The symbols$ f_1 $ denote$ f_1(1285) $ .As shown in Fig. 1, in the present study, contributions from the following interaction diagrams are considered in constructing the s-, t-, and u-channel reaction amplitudes: (i) s-channel N- and
$ N^\ast $ -pole diagrams, (ii) t-channel ρ- and ω-exchange diagrams, and (iii) u-channel N-exchange diagram. Note that the u-channel interaction is expected to contribute significantly at high energy backward angles. However, the available cross section data for$ \gamma p\to f_1(1285) p $ are sparse in this energy and angle regime. In this situation, we simply ignore the u-channel resonance exchanges in the present study, as the additional parameters introduced with these interactions cannot be well determined by the available data. The expressions for all the s-, t-, and u-channel amplitudes can be obtained straightforwardly by evaluating the corresponding Feynman diagrams, except that in Regge and interpolated Regge models, appropriate substitutions are made for the propagators of intermediate ρ and ω mesons in the t-channel Feynman amplitudes (cf. Sec. II.D). The interaction current$ M^{\nu\mu}_{\rm int} $ in Eq. (1) cannot be calculated directly, and we follow Refs. [28−31] to model this term by a generalized contact current,$ \begin{array}{*{20}{l}} M^{\nu\mu}_{\rm int} = \Gamma^\nu_{NNf_{1}}(q) \, C^\mu. \end{array} $

(2) Here,
$ \Gamma^\nu_{NNf_{1}}(q) $ is the vertex function of the$ NNf_{1} $ coupling given by the Lagrangian of Eq. (12),$ \Gamma^\nu_{NNf_{1}}(q) = {\rm i} g_{NNf_1} \left(1 + \frac{\kappa_{f_1}}{2m_{N}} \not {q} \right) \gamma^\nu \gamma^5, $

(3) with q being the four-momentum of the outgoing
$ f_{1} $ meson;$ C^\mu $ is an auxiliary current, which is nonsingular and is introduced to ensure that the full photoproduction amplitudes of Eq. (1) satisfy the generalized Ward-Takahashi identity and thus are fully gauge invariant. Following Refs. [29, 30], we choose$ C^\mu $ for$ \gamma p \to f_1(1285) p $ as$ C^\mu = - Q_{N_{u}}\frac{f_{u}-\hat{F}}{u-p'^{2}}(2p'-k)^{\mu}- Q_{N_{s}}\frac{f_{s}-\hat{F}}{s-p^2}(2p+k)^{\mu}, $

(4) with
$ \begin{array}{*{20}{l}} \hat{F} = 1 - \hat{h} \left(1 - f_u\right) \left(1 - f_s\right). \end{array} $

(5) Here, p,
$ p' $ , and k are the four-momenta for the incoming N, outgoing N, and incoming photon, respectively;$ Q_{N_u} $ and$ Q_{N_s} $ are electric charges of the u-channel N and s-channel N, respectively;$ f_u $ and$ f_s $ are the phenomenological form factors attached to the amplitudes of the u-channel N-exchange diagram and s-channel N-pole diagram, respectively;$ \hat{h} $ is an arbitrary function that goes to unity in the high-energy limit to prevent the “violation of scaling behavior” [32]. In the present study, we choose$ \hat{h}=1 $ for the sake of simplicity. -
The effective interaction Lagrangians used in the present study for constructing the production amplitudes are given below. For further convenience, we define the operators
$ \begin{array}{*{20}{l}} \Gamma^{(+)}=\gamma_5 \qquad \text{and} \qquad \Gamma^{(-)}=1, \end{array} $

(6) and the field-strength tensors
$ f_1^{\mu\nu} = \partial^\mu f_1^\nu - \partial^\nu f_1^\mu, $

(7) $ F^{\mu\nu} = \partial^\mu A^\nu - \partial^\nu A^\mu, $

(8) with
$ f_1^\nu $ and$ A^\mu $ denoting the$ f_1 $ vector-meson field and electromagnetic field, respectively.The electromagnetic interaction Lagrangians for the s-channel N-pole diagram, u-channel N-exchange diagram, and t-channel ρ- and ω-exchange diagrams read
$ {\cal L}_{NN\gamma} = -e \bar{N} \left[ \left( \hat{e} \gamma^\mu - \frac{ \hat{\kappa}_N} {2M_N}\sigma^{\mu \nu}\partial_\nu\right) A_\mu\right] N, $

(9) $ {\cal L}_{Vf_1\gamma } = {\rm i} g_{Vf_1\gamma} \varepsilon_{ \mu \nu \alpha \beta} \left(\partial ^{\mu } A^{\alpha }\right) \left(\partial^2 V^\nu\right) f_1^\beta, $

(10) where e is the elementary charge unit;
$ \hat{e} $ stands for the charge operator;$ \hat{\kappa}_N = \kappa_p\left(1+\tau_3\right)/2 + \kappa_n\left(1-\tau_3\right)/2 $ , with the anomalous magnetic moments$ \kappa_p=1.793 $ and$ \kappa_n = -1.913 $ ;$ M_N $ stands for the masse of N;$ \varepsilon_{ \mu \nu \alpha \beta} $ is the totally antisymmetric Levi-Civita tensor with$ \varepsilon_{0123}=1 $ ; and V represents the vector meson ρ or ω. The coupling constant$ g_{\rho f_{1}\gamma} $ can be determined by the decay width of$ f_1\to\rho\gamma $ ,$ \Gamma _{f_1 \to \rho \gamma } = \frac{ g_{\rho f_1 \gamma }^2 m_{\rho }^{2} }{96\pi m_{f_1}^5} \left(m_{f_1}^2 + m_{\rho }^2 \right) \left(m_{f_1}^2 - m_{\rho }^2 \right)^3. $

(11) With the value
$ \Gamma _{f_1 \to \rho \gamma } \simeq 0.45 $ MeV from the CLAS experiment [22], one obtains$ g_{\rho f_1\gamma} = 0.94 $ GeV$ ^{-2} $ . The coupling constant$ g_{\omega f_1\gamma } $ can be estimated within a quark model assuming that$ f_1 $ consists of two-flavor$ u,d $ quarks, which results in$ g_{\omega f_1\gamma } \approx g_{\rho f_1\gamma}/3 $ [23].The hadronic interaction Lagrangians for the s-channel N-pole diagram, u-channel N-exchange diagram, and t-channel ρ- and ω-exchange diagrams read
$ {\cal L}_{NNf_1} = g_{NNf_1} \bar{N} \left( f_1^\mu - {\rm i}\frac{\kappa_{f_1}}{2m_N} \gamma^\nu \partial_\nu f_1^\mu \right) \gamma_\mu \gamma^5 N, $

(12) $ {\cal L}_{NNV} = -g_{NNV} \bar{N} \left[ \gamma_\mu V^\mu - \frac{\kappa_V}{2m_{N}} \sigma_{\mu\nu}\partial^\nu V^\mu \right] N. $

(13) The value of coupling constant
$ g_{NNf_1}= 2.5 $ is obtained according to the relation between the reduced elements F and D from a study of the axial vector currents in Ref. [33]. The coupling$ \kappa _{f_1} $ is treated as a parameter to be fixed by fitting the CLAS experimental data [22]. For nucleon and vector meson couplings, the empirical values$ g_{NN\rho }=3.25 $ ,$ g_{ NN\omega}=11.76 $ ,$ \kappa_{\rho}=6.1 $ , and$ \kappa_{\omega} = 0 $ from Refs. [30, 34] are quoted.The Lagrangians for resonance-nucleon-photon transition read
$ {\cal L}_{RN\gamma}^{1/2\pm} = e\frac{g_{RN\gamma}^{(1)}}{2M_N}\bar{R} \Gamma^{(\mp)}\sigma_{\mu\nu} \left(\partial^\nu A^\mu \right) N + {\rm{H}}{\rm{. c}}{\rm{.}}, $

(14) $ \begin{aligned}[b] {\cal L}_{RN\gamma}^{3/2\pm} =& -\, {\rm i}e\frac{g_{RN\gamma}^{(1)}}{2M_N}\bar{R}_\mu \gamma_\nu \Gamma^{(\pm)}F^{\mu\nu}N \\ &+\, e\frac{g_{RN\gamma}^{(2)}}{\left(2M_N\right)^2}\bar{R}_\mu \Gamma^{(\pm)}F^{\mu \nu}\partial_\nu N + {\rm{H}}{\rm{. c}}{\rm{.}}, \end{aligned} $

(15) $ \begin{aligned}[b] {\cal L}_{RN\gamma}^{5/2\pm} = & e\frac{g_{RN\gamma}^{(1)}}{\left(2M_N\right)^2}\bar{R}_{\mu \alpha}\gamma_\nu \Gamma^{(\mp)}\left(\partial^{\alpha} F^{\mu \nu}\right)N \\ & \pm\, {\rm i}e\frac{g_{RN\gamma}^{(2)}}{\left(2M_N\right)^3}\bar{R}_{\mu \alpha} \Gamma^{(\mp)}\left(\partial^\alpha F^{\mu \nu}\right)\partial_\nu N + {\rm{H}}{\rm{. c}}{\rm{.}}, \end{aligned} $

(16) $ \begin{aligned}[b] {\cal L}_{RN\gamma}^{7/2\pm} =& {\rm i}e\frac{g_{RN\gamma}^{(1)}}{\left(2M_N\right)^3}\bar{R}_{\mu \alpha \beta}\gamma_\nu \Gamma^{(\pm)}\left(\partial^{\alpha}\partial^{\beta} F^{\mu \nu}\right)N \\ &-\, e\frac{g_{RN\gamma}^{(2)}}{\left(2M_N\right)^4}\bar{R}_{\mu \alpha \beta} \Gamma^{(\pm)} \left(\partial^\alpha \partial^\beta F^{\mu \nu}\right) \partial_\nu N + {\rm{H}}{\rm{. c}}{\rm{.}}, \end{aligned} $

(17) where R designates the nucleon resonance, and the superscripts of
$ {\cal L}_{RN\gamma} $ denote the spin and parity of the resonance R. The coupling constants$ g_{RN\gamma}^{(i)} (i=1,2) $ are treated as fit parameters.The effective Lagrangians for hadronic vertices including nucleon resonances read
$ \begin{aligned}[b] {\cal L}_{RN f_1}^{1/2\pm} =& - \frac{g_{RN f_1}}{2M_N}\bar{R}\Gamma^{(\pm)} \left[ \left(\frac{\gamma_\mu\partial^2}{M_R\mp M_N} \pm {\rm i}\partial_\mu \right) f_1^\mu\right] N + {\rm{H}}{\rm{. c}}{\rm{.}}, \end{aligned} $

(18) $ {\cal L}_{RN f_1}^{3/2\pm} = {\rm i} \frac{g_{RN f_1}}{2M_N}\bar{R}_\mu \gamma_\nu \Gamma^{(\mp)}f_1^{\mu \nu} N + {\rm{H}}{\rm{. c}}{\rm{.}}, $

(19) $ {\cal L}_{RN f_1}^{5/2\pm} = - \frac{g_{RN f_1}}{\left(2M_N\right)^2}\bar{R}_{\mu \alpha}\gamma_\nu \Gamma^{(\pm)}\left(\partial^{\alpha} f_1^{\mu \nu}\right) N + {\rm{H}}{\rm{. c}}{\rm{.}}, $

(20) $ \begin{aligned}[b] {\cal L}_{RN f_1}^{7/2\pm} =& - {\rm i} \frac{g_{RN f_1}}{\left(2M_N\right)^3}\bar{R}_{\mu \alpha \beta}\gamma_\nu \Gamma^{(\mp)} \left(\partial^{\alpha}\partial^{\beta} f_1^{\mu \nu}\right) N + {\rm{H}}{\rm{. c}}{\rm{.}} \end{aligned} $

(21) The couplings
$ g_{RN f_1} $ are fit parameters. Actually, in a single-channel calculation as the one performed in the present study, only the products of the electromagnetic coupling constants and hadronic coupling constants are relevant to the reaction amplitudes. In practice, we fit these products directly instead of fitting the hadronic and electromagnetic couplings separately. -
In the present study, contributions from s-channel pole diagrams of a minimal number of nucleon resonances with various spin and parity are included to describe the data. For spin-
$ 1/2 $ resonance, the propagator reads$ S_{1/2}(p) = \frac{\rm i}{\not {p} - M_R + {\rm i} \Gamma/2}, $

(22) where
$ M_R $ , Γ, and p are the mass, width, and four-momentum of resonance R, respectively.Following Refs. [35−37], the prescriptions of the propagators for resonances with spin-
$ 3/2 $ , -$ 5/2 $ , and -$ 7/2 $ read$ S_{3/2}(p) = \frac{\rm i}{\not {p} - M_R + {\rm i} \Gamma/2} \left( \tilde{g}_{\mu \nu} + \frac{1}{3} \tilde{\gamma}_\mu \tilde{\gamma}_\nu \right), $

(23) $ \begin{aligned}[b] S_{5/2}(p) =& \frac{\rm i}{\not {p} - M_R + {\rm i} \Gamma/2} \,\bigg[ \, \frac{1}{2} \big(\tilde{g}_{\mu \alpha} \tilde{g}_{\nu \beta} + \tilde{g}_{\mu \beta} \tilde{g}_{\nu \alpha} \big) \\ & -\, \frac{1}{5}\tilde{g}_{\mu \nu}\tilde{g}_{\alpha \beta} + \frac{1}{10} \big(\tilde{g}_{\mu \alpha}\tilde{\gamma}_{\nu} \tilde{\gamma}_{\beta} + \tilde{g}_{\mu \beta}\tilde{\gamma}_{\nu} \tilde{\gamma}_{\alpha} \\ & +\, \tilde{g}_{\nu \alpha}\tilde{\gamma}_{\mu} \tilde{\gamma}_{\beta} +\tilde{g}_{\nu \beta}\tilde{\gamma}_{\mu} \tilde{\gamma}_{\alpha} \big) \bigg], \end{aligned} $

(24) $ \begin{aligned}[b] S_{7/2}(p) =& \frac{\rm i}{\not {p} - M_R + {\rm i} \Gamma/2} \, \frac{1}{36}\sum_{P_{\mu} P_{\nu}} \bigg( \tilde{g}_{\mu_1 \nu_1}\tilde{g}_{\mu_2 \nu_2}\tilde{g}_{\mu_3 \nu_3} \\ & -\, \frac{3}{7}\tilde{g}_{\mu_1 \mu_2}\tilde{g}_{\nu_1 \nu_2}\tilde{g}_{\mu_3 \nu_3} + \frac{3}{7}\tilde{\gamma}_{\mu_1} \tilde{\gamma}_{\nu_1} \tilde{g}_{\mu_2 \nu_2}\tilde{g}_{\mu_3 \nu_3} \\ & -\, \frac{3}{35}\tilde{\gamma}_{\mu_1} \tilde{\gamma}_{\nu_1} \tilde{g}_{\mu_2 \mu_3}\tilde{g}_{\nu_2 \nu_3} \bigg), \end{aligned} $

(25) where
$ \tilde{g}_{\mu \nu} = -\, g_{\mu \nu} + \frac{p_{\mu} p_{\nu}}{M_R^2}, $

(26) $ \tilde{\gamma}_{\mu} = \gamma^{\nu} \tilde{g}_{\nu \mu} = -\gamma_{\mu} + \frac{p_{\mu}\not{p}}{M_R^2}. $

(27) -
Each hadronic vertex obtained from the Lagrangians given in Sec. II.A is accompanied by a phenomenological form factor to parametrize the structure of the hadrons and normalize the behavior of the production amplitude. Following Refs. [38, 39], for intermediate baryon exchange, we take the form factor as
$ f_B(p^2) = \left[\frac{\Lambda_B^4}{\Lambda_B^4 + \left(p^2-M_B^2\right)^2}\right]^2, $

(28) where p denotes four-momentum of the intermediate baryon, and
$ M_B $ is the mass for the exchanged baryon B. For intermediate meson exchange, we take form factor as$ f_M(q^2) = \frac{\Lambda_M^2-M_M^2}{\Lambda_M^2-q^2}, $

(29) where q represents the four-momentum of the intermediate meson, and
$ M_M $ is the mass of the exchanged meson M. The cutoffs$ \Lambda_{B(M)} $ for each exchanged baryon (meson) in Eqs. (28) and (29) are treated as fit parameters. -
The t-channel reaction amplitudes are usually constructed in three different types, that is, the Feynman, Regge, and interpolated Regge types [40]. In the present study, we implement these three possibilities to explore how the reaction mechanisms of
$ \gamma p \to f_1(1285) p $ and the extracted resonance contents and parameters depend on the choices of different types of t-channel interactions. In addition, we determine what we can learn from the available cross-section data for$ \gamma p \to f_1(1285) p $ . -
In the Feynman model, the reaction amplitudes from t-channel ρ and ω exchanges are constructed directly by evaluating the Feynman diagram in Fig. 1(b). The electromagnetic and hadronic vertices can be obtained directly using the Lagrangians given in Sec. II.A. The amplitudes for ρ and ω exchanges read
$ \begin{aligned}[b] {\cal M}_V^{\nu\mu} = & - {\rm i} \, g_{NNV} \, g_{Vf_1\gamma} \, \epsilon^{\alpha\beta\mu\nu} \, k_\alpha \, t \,\frac{-g_{\beta\eta} + q_\beta q_\eta / m_V^2}{t-m_V^2} \\ & \times \left[\gamma^\eta - {\rm i}\frac{\kappa_V}{2M_N} \sigma^{\eta\delta} q_\delta \right], \end{aligned} $

(30) where V represents ρ or ω, and q denotes the four-momentum of the exchanged vector meson.
-
In the high energy region, the differential cross sections are dominated at forward angles, where the effects of high-spin meson exchanges are important. An economic way to describe the t- and s-dependence of the cross sections in forward direction is Regge phenomenology [41−43]. The standard Reggeization of the t-channel Feynman amplitudes of ρ and ω exchanges corresponds to the following replacements of the propagators:
$ \begin{aligned}[b] \frac{1}{t-m^2_V} \quad\Longrightarrow\quad {\cal P}^V_{\rm R} = & \; \left(\frac{s}{s_0}\right)^{\alpha_V(t)-1} \frac{\pi \alpha'_V}{\sin[\pi\alpha_V(t)]} \\ & \times \frac{1}{\Gamma[\alpha_V(t)]}. \end{aligned} $

(31) Here,
$ s_0 $ is a mass scale, which is conventionally taken as$ s_0=1 $ GeV$ ^2 $ , and$ \alpha'_V $ is the slope of the Regge trajectory$ \alpha_V(t) $ . For$ V=\rho $ and ω, the trajectories are parametrized as [44]$ \alpha_{\rho}(t) = 0.55 + 0.8\; {\rm GeV}^{-2} t, $

(32) $ \alpha_{\omega}(t) = 0.44 + 0.9\; {\rm GeV}^{-2}t . $

(33) Note that, in Eq. (31), the degenerate trajectories are employed for ρ and ω exchanges, and thus, the corresponding signature factors reduce to
$ 1 $ . Such a choice is preferred by data, which has been tested by our numerical calculation. -
It is believed that the Regge model works properly in the large-s and small-
$ |t| $ region, whereas the Feynman model works properly in the low-energy region. In literature, the so-called interpolated Regge model is widely used [40, 45−47]. In this model, an interpolating form factor is introduced to parametrize the smooth transition from Feynman amplitudes to Regge amplitudes. Instead of the replacement given in Eq. (31), in the interpolated Regge model, one has the following replacement of the propagators of t-channel ρ and ω exchanges in Feynman amplitudes:$ \frac{1}{t-m^2_V} \quad\Longrightarrow\quad {\cal P}^V_{\rm IR} = {\cal P}^V_{\rm R} F + \frac{1}{t-m^2_V} \left(1-F\right), $

(34) where
$ F = F_s F_t $ with$ F_s = \frac{1}{1+{\rm e}^{-\left(s-s_R\right)/s_0}}, $

(35) $ F_t = \frac{1}{1+{\rm e}^{-\left(t+t_R\right)/t_0}}. $

(36) Here,
$ s_R $ ,$ s_0 $ ,$ t_R $ , and$ t_0 $ are parameters to be fixed by fitting the data. The parameters$ s_R $ and$ t_R $ denote where the amplitudes transit from the Feynman type to Regge type, and$ s_0 $ and$ t_0 $ indicate how fast this transit occurs.It can be observed that, by making the replacement of Eq. (34), the t-channel amplitude is a combination of the Regge and Feynman amplitudes, with a weight factor F for the former and
$ (1-F) $ for the latter. In the low-energy$ (s\ll s_R) $ region, the factor F tends towards$ 0 $ , ensuring that one has an almost pure Feynman amplitude. In the high-energy$ (s\gg s_R) $ and small-$|t| \; (|t|\ll t_R)$ region, the factor$ (1-F) $ tends towards$ 0 $ , ensuring that one has an almost pure Regge amplitude. In the intermediate energy region, the amplitude is constructed as a mixture of Feynman and Regge amplitudes, which transits smoothly to a Feynman amplitude in the low-energy region and to a Regge amplitude in the high-energy region. -
In the present study, we perform a comprehensive investigation of the
$ \gamma p \to f_1(1285) p $ reaction within an effective Lagrangian approach. The contributions from the s-channel N-pole diagram, u-channel N-exchange diagram, t-channel ρ- and ω-exchange diagrams, and interaction current are considered as background ingredients in constructing the reaction amplitudes. We build three reaction models, that is, the Feynman, Regge, and interpolated Regge models, where the t-channel reaction amplitudes of ρ and ω exchanges are built in the Feynman, Regge, and interpolated Regge types, respectively (cf. Sec. II.D). In each model, we consider pole diagrams in the s channel of as few as possible nucleon resonances in order to achieve satisfactory descriptions of the available differential cross-section data.In the most recent PDG review [4], there are nine nucleon resonances with spin
$ J=1/2 \sim 7/2 $ in the energy region considered in the present study, namely, the$ N(1990){7/2}^+ $ ,$ N(2000){5/2}^+ $ ,$ N(2040){3/2}^+ $ ,$ N(2060){5/2}^- $ ,$ N(2100){1/2}^+ $ ,$ N(2120){3/2}^- $ ,$ N(2190){7/2}^- $ ,$ N(2300){1/2}^+ $ , and$ N(2570){5/2}^- $ resonances. As it is not clear how many and what nucleon resonances are really needed in the$ \gamma p \to f_1(1285) p $ reaction, we follow the strategy employed in Refs. [7, 12−14, 17−20] to choose nucleon resonances, that is, we strive to describe the available data by introducing as few as possible nucleon resonances in our theoretical models. In practice, we make numerous trials of various numbers and different combinations of these nine nucleon resonances in our calculations. First, we attempt to reproduce the data without considering any nucleon resonance. If that fails, we introduce one nucleon resonance to the model by testing the above-mentioned nine nucleon resonances one by one. If the data still cannot be well reproduced, various combinations of two nucleon resonances will be further considered in the model. In principle, more nucleon resonances should be further introduced in the calculations unless the data can be satisfactorily described. Nevertheless, for the$ \gamma p \to f_1(1285)p $ reaction, so far, we only have differential cross-section data with relatively large error bars at five energy points. Adding more than two nucleon resonances to the model will bring in too many parameters (masses, widths, cutoffs, coupling constants, etc.) to the model, which are difficult to be well determined by the available (very limited) data. Therefore, in each model, we stop introducing more than two nucleon resonances if the data cannot be satisfactorily described.In the following, we show and discuss the results from each model separately.
-
In the Feynman model, it is expected that the near threshold structures exhibited in the angular distributions of
$ \gamma p \to f_1(1285)p $ are dominated by contributions from nucleon resonances, and the cross-section peaks in the high-energy region at forward angles are governed by contributions from t-channel ρ and ω exchanges. However, after numerous tests, we found that in the cases when no nucleon resonance or any one or any two of the above-mentioned nine nucleon resonances are introduced in the calculations, the available differential cross-section data for$ \gamma p \to f_1(1285)p $ from CLAS Collaboration [22] cannot be well reproduced in the Feynman model.In Fig. 2, we show the results of differential cross sections of
$ \gamma p \to f_1(1285)p $ as a function of cosine of scattering angle θ in the center-of-mass frame obtained in the Feynman model with the$ N(2000){5/2}^+ $ and$ N(2060){5/2}^- $ contributions being considered. The fit with these two nucleon resonances being considered is the best one as the corresponding$ \chi^2/N $ ($ \chi^2 $ per data point) is the smallest among all the fits with no nucleon resonance, one nucleon resonance, or two nucleon resonances being considered. In Fig. 2, the black solid lines represent the results from the full calculation. The blue dash-double-dotted, green dashed, and red dash-dotted lines represent the individual contributions from the t-channel ρ- and ω-exchange diagrams, s-channel$ N(2060){5/2}^- $ -pole diagram, and s-channel$ N(2000){5/2}^+ $ -pole diagram, respectively. The scattered symbols denote the CLAS data from Ref. [22]. The numbers in parentheses denote the centroid value of the photon laboratory incident energy (left number) and the corresponding total center-of-mass energy of the system (right number), in MeV. As can be observed from Fig. 2, the differential cross-section data in the low-energy region can be well described, whreas the data in the high-energy region near the forward angles are excessively underestimated. Therefore, this set of results is not considered as acceptable. The model parameters corresponding to this set of theoretical results are listed in Table 1. One sees that the fitted mass and width of$ N(2000){5/2}^+ $ are a little bit far away from the corresponding values advocated in the PDG review [4]. If we manually restrict these parameters in the fitting procedure in a range, as advocated in the PDG review [4], the agreement of the fitted differential cross sections with the corresponding data will be even worse than that shown in Fig. 2.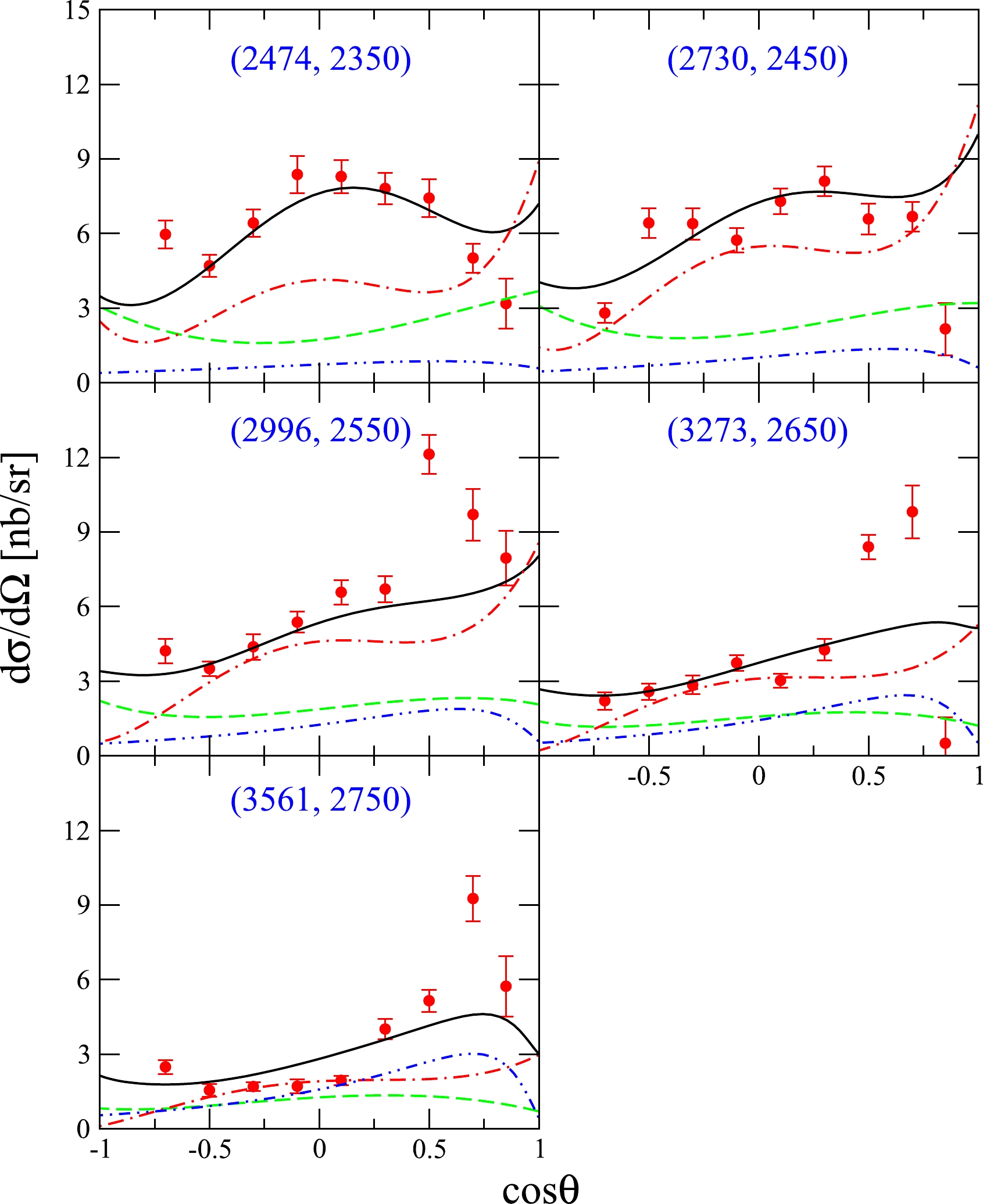
Figure 2. (color online) Differential cross sections of
$\gamma p \to $ $ f_1(1285)p$ as a function of the cosine of scattering angle θ in the center-of-mass frame obtained in the Feynman model considering the contributions from the$ N(2000){5/2}^+ $ and$ N(2060){5/2}^- $ resonances. The black solid lines represent the results from the full calculation. The blue dash-double-dotted, green dashed, and red dash-dotted lines represent the individual contributions from the t-channel ρ- and ω-exchange diagrams, s-channel$ N(2060){5/2}^- $ -pole diagram, and s-channel$ N(2000){5/2}^+ $ -pole diagram, respectively. The scattered symbols denote the CLAS data in Ref. [22]. The numbers in parentheses denote the centroid value of the photon laboratory incident energy (left number) and the corresponding total center-of-mass energy of the system (right number), in MeV.$ \kappa_{f_1} $ 

$ -5.96\pm 5.0 $ 

$ \Lambda_{N} $ /MeV

$ 578\pm8 $ 

$ \Lambda_{\rho} $ /MeV

$ 769\pm1 $ 

$ \Lambda_{\omega} $ /MeV

$ 834\pm3 $ 

$ N(2000){5/2}^+ $ 

$ N(2060){5/2}^- $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ M_R $ /MeV

$ 2250\pm3 $ 

$ 2030\pm7 $ 

[ $ \sim2000 $ ]

[ $ 2030\sim2200 $ ]

$ \Gamma_R $ /MeV

$ 126\pm30 $ 

$ 450\pm52 $ 

[ $ \sim300 $ ]

[ $ \sim400 $ ]

$ \Lambda_R $ /MeV

$ 1396\pm 28 $ 

$ 1399\pm 59 $ 

$ g_{RN\gamma}^{(1)} g_{RNf_1} $ 

$ 0.013\pm0.002 $ 

$ -18.5\pm0.8 $ 

$ g_{RN\gamma}^{(2)} g_{RNf_1} $ 

$ 16.8\pm0.7 $ 

$ -61.0\pm2.0 $ 

Table 1. Fitted values of parameters in the Feynman model with the
$ N(2000){5/2}^+ $ and$ N(2060){5/2}^- $ resonances being considered. The asterisks below the resonance names denote the overall status of these resonances evaluated by the PDG review [4]. The numbers in brackets below resonance mass$ M_R $ and width$ \Gamma_R $ represent the range of the corresponding quantities given by the PDG review [4].The differential cross-section data of
$ \gamma p \to f_1(1285)p $ in the high-energy region near the forward angles cannot be well reproduced in the Feynman model. The possible reason is that the Feynman type amplitudes of t-channel ρ and ω exchanges do not result in proper angular dependence of the high-energy differential cross sections as demonstrated by the data. As so far we only have differential cross-section data at five energy points, introducing more nucleon resonances to this model to improve the quality of the theoretical description of the data does not make too much sense. We thus conclude that the available differential cross-section data of$ \gamma p \to f_1(1285)p $ cannot be well reproduced in the Feynman model. -
As indicated in Sec. II.D.2, the Regge type amplitudes of t-channel ρ and ω exchanges have rather different angular dependence than the Feynman type amplitudes. Thus, although the Feynman model fails, the Regge model may still have the opportunity to describe the available differential cross-section data for
$ \gamma p \to f_1(1285)p $ .We conducted numerous tests and found that if no contribution from the s-channel
$ N^\ast $ -pole diagram is considered in the Regge model, the resulted$ \chi^2/N $ will be greater than$ 10 $ , indicating significantly poor fitting quality of the obtained results. This means that in the Regge model when no nucleon resonance is considered, the shapes of angular distributions in the low- and high-energy regions cannot be simultaneously described by non-resonant contributions, which are mainly t-channel ρ and ω exchanges only. We then tried to add one of those nine nucleon resonances as mentioned in Sec. II.A to this model. We tested them one by one, and it was found that by adding any one of those nine nucleon resonances in the Regge model, the available differential cross-section data of$ \gamma p \to f_1(1285)p $ can always be satisfactorily described with similar fitting qualities,$ 4.0 < \chi^2/N < 6.5 $ , as listed in Table 2.$ N^\ast $ 

$ N(1990){7/2}^+ $ 

$ N(2000){5/2}^+ $ 

$ N(2040){3/2}^+ $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \chi^2/N $ 

$ 6.5 $ 

$ 4.0 $ 

$ 4.1 $ 

$ N^\ast $ 

$ N(2060){5/2}^- $ 

$ N(2100){1/2}^+ $ 

$ N(2120){3/2}^- $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \chi^2/N $ 

$ 5.1 $ 

$ 6.5 $ 

$ 4.9 $ 

$ N^\ast $ 

$ N(2190){7/2}^- $ 

$ N(2300){1/2}^+ $ 

$ N(2570){5/2}^- $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \chi^2/N $ 

$ 6.2 $ 

$ 4.7 $ 

$ 4.6 $ 

Table 2.
$ \chi^2/N $ for differential cross sections fitted by including one nucleon resonance in the Regge model. The asterisks below resonance names denote the overall status of these resonances rated by the PDG review [4].In Fig. 3, we show the theoretical results, compared with the corresponding data, for differential cross sections of
$ \gamma p \to f_1(1285)p $ as a function of the cosine of scattering angle θ in the center-of-mass frame obtained in the Regge model with the contribution from the s-channel$ N(2000)5/2^+ $ -pole diagram being considered. The notations in this figure are the same as those in Fig. 2. The fitted values of model parameters corresponding to this set of results are listed in the second column of Table 3. It can be observed that the fitted resonance mass and width are consistent with the values advocated in the most recent PDG review [4]. Note that the resonance electromagnetic and hadronic couplings are not shown separately because in a single-channel calculation as that performed in the present study, the reaction amplitudes depend only on their products. In the PDG review [4], no electromagnetic decay amplitudes or$ f_1(1285)p $ hadronic branching ratio for the two-star resonance$ N(2000){5/2}^+ $ are advocated. If we use the helicity amplitudes$ A_{1/2}= $ 0.031 GeV$ ^{-1/2} $ and$ A_{3/2}=-0.043 $ GeV$ ^{-1/2} $ from a BnGa partial wave analysis [48] to fix the electromagnetic couplings, we obtain$ g_{RN\gamma}^{(1)}=-3.9 $ ,$ g_{RN\gamma}^{(2)}=3.6 $ . A refit of the hadronic coupling results in$ g_{RNf_1}=19.8 $ , while the cross-section results change very little.
Figure 3. (color online) Differential cross sections of
$\gamma p \to $ $ f_1(1285)p$ as a function of the cosine of scattering angle θ in the center-of-mass frame obtained in the Regge model with the contribution from the s-channel$ N(2000)5/2^+ $ -pole diagram being considered. Notations are the same as those in Fig. 2.Regge interpolated Regge $ \kappa_{f_1} $ 

$ 14.4\pm 7.0 $ 

$ 14.6\pm 5.0 $ 

$ \Lambda_{N} $ /MeV

$ 500\pm 103 $ 

$ 500\pm 124 $ 

$ \Lambda_{\rho} $ /MeV

$ 1083\pm 17 $ 

$ 1079\pm 5 $ 

$ \Lambda_{\omega} $ /MeV

$ 745\pm 83 $ 

$ 749\pm 51 $ 

$ N(2000){5/2}^+ $ 

$ N(2000){5/2}^+ $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ \ast $ 

$ M_R $ /MeV

$ 2042 \pm 33 $ 

$ 2042 \pm 11 $ 

[ $ \sim 2000 $ ]

[ $ \sim 2000 $ ]

$ \Gamma_R $ /MeV

$ 450 \pm 57 $ 

$ 450 \pm 72 $ 

[ $ \sim 300 $ ]

[ $ \sim 300 $ ]

$ \Lambda_R $ /MeV

$ 1167 \pm 17 $ 

$ 1172 \pm 3 $ 

$ g_{RN\gamma}^{(1)} g_{RNf_1} $ 

$ -64.7 \pm 0.5 $ 

$ -62.8 \pm 0.5 $ 

$ g_{RN\gamma}^{(2)} g_{RNf_1} $ 

$ 27.9\pm 1.5 $ 

$ 28.6 \pm 1.5 $ 

Table 3. Fitted values of parameters in the Regge model (second column) and interpolated Regge model (third column) with the
$ N(2000){5/2}^+ $ resonance being considered. The asterisks below resonance names denote the overall status of these resonances evaluated by the PDG review [4]. The numbers in brackets below resonance mass$ M_R $ and width$ \Gamma_R $ represent the range of the corresponding quantities given by the PDG review [4].It can be observed from Fig. 3 that the angular distribution data for
$ \gamma p \to f_1(1285)p $ in the entire energy region considered are quite well described in the Regge model with the$ N(2000)5/2^+ $ resonance being considered. In the high-energy region, the peaks at forward angles are dominated by the t-channel ρ and ω Regge exchanges. In the low-energy region, the resonance contribution also provides significant contributions to the observed cross sections. Note that, compared with the contributions from the t-channel ρ- and ω-exchange diagrams in the Feynman model (cf. Fig. 2), the contributions from the t-channel ρ- and ω-trajectory exchanges in the Regge model provide much steeper uplifts of the angular distributions at forward angles, which is the main reason why the Regge model succeeds in reproducing the data, while the Feynman model fails. Considering that a meson trajectory exchange is an economic treatment of the exchanges of all mesons lying on the trajectory, such a fact may indicate that, for the$ \gamma p \to f_1(1285)p $ reaction, contributions from the t-channel exchanges of high-spin mesons are important.$ \chi^2/N $ is$ 4.0 $ for this set of solution. For the other eight sets of solutions, each with one of the other eight nucleon resonances being considered, the resulting$ \chi^2/N $ are between$ 4.0 $ and$ 6.5 $ . They all reproduce the available differential cross-section data for$ \gamma p \to f_1(1285)p $ satisfactorily. The reaction mechanisms in those sets of solutions are shown to be quite similar — the t-channel ρ and ω exchanges dominate the high-energy peaks at forward angles, and the s-channel resonance contribution provides considerable contributions in the low-energy region. Nevertheless, the available differential cross-section data are not sufficient to distinguish those different sets of solutions in the Regge model.The predicted total cross sections with dominant individual contributions for
$ \gamma p \to f_1(1285)p $ in the Regge model with the$ N(2000){5/2}^+ $ resonance being considered are shown in Fig. 4. As can be observed, in the high-energy region, it is the t-channel interaction that dominates the cross sections, while in the low-energy region, the$ N(2000){5/2}^+ $ resonance also contributes significantly. This observation is consistent with the behavior of the differential cross sections as shown in Fig. 3. The results for models with other nucleon resonances are very close to those with the$ N(2000){5/2}^+ $ resonance.
Figure 4. (color online) Predicted total cross sections with dominant individual contributions for
$ \gamma p \to f_1(1285)p $ in the Regge model with the contribution from s-channel$ N(2000){5/2}^+ $ -pole diagram being considered. The notations are the same as those in Fig. 3.In Fig. 5 we show the predictions of target nucleon asymmetries at two selected energies in the Regge model with each of the
$ N(2100){1/2}^+ $ ,$ N(2300){1/2}^+ $ ,$ N(2040){3/2}^+ $ ,$ N(2120){3/2}^- $ ,$ N(2000){5/2}^+ $ ,$ N(2060){5/2}^- $ ,$ N(1990){7/2}^+ $ ,$ N(2190){7/2}^- $ , and$ N(2570){5/2}^- $ resonances. It can be observed that the signs and magnitudes of the target nucleon asymmetries predicted in the Regge model with various nucleon resonances are different. Future data on this quantity are expected to be used to distinguish the Regge models with various nucleon resonances.
Figure 5. (color online) Predicted target nucleon asymmetries as functions of
$ \cos\theta $ for$ \gamma p \to f_1(1285)p $ at two selected energies. The numbers in parentheses denote the photon laboratory incident energy (left number) and the total center-of-mass energy of the system (right number), in MeV. The black solid, blue dotted, green dashed, red long-dashed, cyan dot-dashed, brown dot-long-dashed, magenta dash-double-dotted, violet dot-double-dashed, and orange solid curves represent the results for the Regge model considering the contribution from s-channel$ N(2100)1/2^+ $ ,$ N(2300)1/2^+ $ ,$ N(2040)3/2^+ $ ,$ N(2120)3/2^- $ ,$ N(2000)5/2^+ $ ,$ N(2060)5/2^- $ ,$ N(1990)7/2^+ $ ,$ N(2190)7/2^- $ , and$ N(2570){5/2}^- $ , respectively. -
As mentioned in the introduction section, two studies [26, 27] have already been devoted to the investigation of
$ \gamma p \to f_1(1285)p $ photoproduction reaction in the interpolated Regge model. Although these two theoretical studies used the same reaction model, their results and conclusions are quite different. In Ref. [26], it was claimed that the available differential cross-section data for$ \gamma p \to f_1(1285)p $ can be reproduced without considering any nucleon resonances. However, in Ref. [27], it was argued that the$ N(2300){1/2}^+ $ resonance plays an important role in describing the available differential cross-section data for$ \gamma p \to f_1(1285)p $ . In the present study, we also perform a comprehensive investigation of$ \gamma p \to f_1(1285)p $ in the interpolated Regge model, paying special attention to whether the available data for$ \gamma p \to f_1(1285)p $ can be reproduced in the interpolated Regge model without or with the contributions from any nucleon resonances.As the interpolated Regge model contains four additional parameters, compared with those in the Regge model [cf. Eqs. (35) and (36) in Sec. II.D.3], naively, one may expect that the interpolated Regge model can describe the data better than the Regge model. However, this is not the truth.
First, we varied the parameters in non-resonant contributions by use of MINUIT to fit the data in the interpolated Regge model without considering any nucleon resonances. After numerous trials, it was found that the fitting quality of the results is poor, as
$ \chi^2/N $ is$ 7.9 $ . The fitted results are illustrated in Fig. 6, from which one can clearly observe that the available differential cross-section data for$ \gamma p \to f_1(1285)p $ cannot be reasonably described in the interpolated Regge model when no s-channel$ N^\ast $ -pole diagrams are considered. Such a conclusion contradicts Ref. [26] but is in agreement with Ref. [27]. Note that, in Ref. [26], the contributions from the$ NN\gamma $ vector coupling [$ \propto {\bar N}\gamma_\mu A^\mu N $ , cf. Eq. (9)] in the s-channel N-pole diagram and u-channel N-exchange diagram, as well as the contact term [cf. Eqs. (1) and (2)], were totally omitted, which requires further justification.
Figure 6. (color online) Differential cross sections of
$ \gamma p \to f_1(1285)p $ as a function of the cosine of scattering angle θ in the center-of-mass frame obtained in the interpolated Regge model with no resonance being considered. The notations are the same as those in Fig. 2.We then tried to add one of those nine nucleon resonances as mentioned in Sec. III.A to the interpolated Regge model to reproduce the data. Surprisingly, for each set of results, the obtained
$ \chi^2/N $ is very close to that of the solution in the Regge model with the same resonance content. Actually, the corresponding values of$ \chi^2/N $ in these two models only differ in the second digits (see Table 2 for$ \chi^2/N $ in the Regge model). Moreover, the fitted values of the model parameters in the interpolated Regge model are also very close to those in the Regge model when the same nucleon resonance is considered. As an example, the fitted values of the model parameters with the$ N(2000){5/2}^+ $ resonance considered in the interpolated Regge model are listed in the third column of Table 3. As can be observed, they are very close to those listed in the second column of this table for the Regge model.This unusual phenomenon is not difficult to be understood from the fitted values of those four auxiliary parameters introduced in the interpolated Regge model, as listed in Table 4. The parameter
$ s_R $ indicates the approximate energy point at which the Feynman amplitude transits to the Regge amplitude, and the parameter$ s_0 $ demonstrates how fast this transition occurs. As can be observed from Table 4, for the$ \gamma p \to f_1(1285)p $ reaction, the t-channel amplitudes transit from Feynman type to Regge type around$ s_R=0.8 $ GeV$ ^2 $ , and the transition occurs very fast as$ s_0 $ is a very small number,$ 0.26 $ GeV$ ^2 $ . This means that above the$ f_1(1285)p $ threshold, that is,$ s\sim 4.95 $ GeV$ ^2 $ , the t-channel amplitudes are almost purely in the Regge type. In other words, the so-called interpolated Regge model is in substance the Regge model for the$ \gamma p \to f_1(1285)p $ reaction. In Ref. [27], the values of these two parameters also indicate that the interpolated Regge model claimed by the authors is essentially the Regge model.$ s_0 $ 

$ s_R $ 

$ t_0 $ 

$ t_R $ 

$ 0.26\pm 0.35 $ 

$ 0.80 \pm 2.30 $ 

$ 0.05\pm 0.70 $ 

$ 10.20\pm 6.25 $ 

Table 4. Fitted values of auxiliary parameters introduced in the interpolated Regge model. See Sec. II.D.3 for the definitions of these parameters. All numbers are in GeV
$ ^2 $ .If we manually force the parameter
$ s_R $ to be greater than the$ f_1(1285)p $ threshold value,$ \sim 4.95 $ GeV$ ^2 $ , and$ s_0 $ to be not excessively small in the fitting procedure so that the reaction amplitudes indeed have the spirits of the interpolated Regge model, that is, they transit smoothly from the Feynman type in the low-energy region to the Regge type in the high-energy region, the resulting$ \chi^2/N $ will be greater than$ 10.0 $ , and consequently, the fitting quality will be too inferior to be accepted. We thus conclude that the available angular distribution data for$ \gamma p \to f_1(1285)p $ cannot be reproduced in the interpolated Regge model. -
The CLAS differential cross-section data for the
$ \gamma p \to f_1(1285) p $ reaction [22] have so far been analyzed in Refs. [26, 27]. Although both these theoretical studies used the interpolated Regge model, their conclusions are quite different. In Ref. [26], it was claimed that the available data for$ \gamma p \to f_1(1285) p $ can be reproduced in the interpolated Regge model without considering any nucleon resonances. However, in Ref. [27], it was argued that the$ N(2300)1/2^+ $ resonance is needed in the interpolated Regge model to describe the data.In the present study, we performed a comprehensive investigation of the
$ \gamma p \to f_1(1285) p $ reaction in an effective Lagrangian approach. We considered the contributions from the s-channel N-pole diagram, u-channel N-exchange diagram, t-channel ρ- and ω-exchange diagrams, and generalized interaction current in constructing the non-resonant reaction amplitudes. We built three reaction models, that is, the Feynman, Regge, and interpolated Regge models, where the t-channel amplitudes were constructed in the Feynman, Regge, and interpolated Regge types, respectively. In each model, we introduced as few as possible nucleon resonances to reproduce the data. All nine nucleon resonances listed in the most recent PDG review [4] with spin$ J=1/2 \sim 7/2 $ in the energy region considered in the present study, namely the$ N(1990){7/2}^+ $ ,$ N(2000){5/2}^+ $ ,$ N(2040){3/2}^+ $ ,$ N(2060){5/2}^- $ ,$ N(2100){1/2}^+ $ ,$ N(2120){3/2}^- $ ,$ N(2190){7/2}^- $ ,$ N(2300){1/2}^+ $ , and$ N(2570){5/2}^- $ resonances, are allowed in practice. The purpose of the present study was to find concise and clear answers of the following questions: i) Can the available differential cross-section data for$ \gamma p \to f_1(1285) p $ be reproduced in the Feynman, Regge, and interpolated Regge models? ii) If yes, how many nucleon resonances are at least needed and what are the resonance contents and associated parameters in these three models?Our results showed that the available angular distribution data for
$ \gamma p \to f_1(1285) p $ from the CLAS Collaboration [22] cannot be well reproduced in either the Feynman or interpolated Regge models. In the Regge model, when no nucleon resonance is considered, the data cannot be satisfactorily described either. However, when any one of the$ N(1990){7/2}^+ $ ,$ N(2000){5/2}^+ $ ,$ N(2040){3/2}^+ $ ,$ N(2060){5/2}^- $ ,$ N(2100){1/2}^+ $ ,$ N(2120){3/2}^- $ ,$ N(2190){7/2}^- $ ,$ N(2300){1/2}^+ $ , and$ N(2570){5/2}^- $ resonances is taken into account in the Regge model, the experimental data can be well described. The resulted resonance masses and widths are consistent with those advocated in the PDG review [4]. In each set of results in the Regge model, it was found that in the high-energy region, the peaks of differential cross sections at forward angles are dominated by t-channel ρ and ω exchanges, and in the low-energy region, the resonance contribution also provides significant contributions.The fact that the available differential cross-section data for
$ \gamma p \to f_1(1285) p $ can only be reproduced in the Regge model but not in the Feynman model or interpolated Regge model reveals that the angular and energy dependence of the$ f_1(1285) $ photoproduction amplitudes is rather unusual. This indicates that the$ f_1(1285) $ meson might have an unconventional$ q{\bar q} $ content, which deserves further investigations.
Analysis of data for γp → f1(1285)p photoproduction
- Received Date: 2023-07-03
- Available Online: 2024-02-15
Abstract: The photoproduction of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






























 DownLoad:
DownLoad: