-
In recent years, nuclear processes involving weakly bound (WB) projectiles, such as 6Li and 7Li nuclei, have been extensively investigated [1–5]. The primary reason for this interest is the opportunity to investigate how distinct reaction mechanisms affect each other when the binding energy of the projectile is relatively low. The 6,7Li WB projectiles are characterized by a high clusterization probability that emerges at a relatively low excitation energy (Ex), 6Li→α + d at Ex ~ 1.474 MeV and 7Li→α + t at Ex ~ 2.468 MeV, making them good candidates for this.
The scattering processes between heavy nuclei at energies approaching the Coulomb barrier (VB) are characterized by a peculiar behavior of the optical potential (OP), which is referred to as the threshold anomaly (TA) [6]. The term TA was introduced to define the manner in which the real and imaginary potentials vary with energy around VB. For systems with tightly bound projectiles, the TA can be identified as a bell-shaped peak in the real potential and a significant reduction in the strength of the imaginary potential as the energy reduces below VB. However, for systems induced by WB projectiles, this is considerably different. As the WB projectiles are characterized by their weak nature and high dissociation probability that is not suppressed below and close to VB, the coupling to the continuum creates a dynamic polarization potential (DPP) that causes the typical TA to disappear [7]. Owing to the high breakup probability that is present strongly below and close to VB, the imaginary potential is expected to increase instead of falling to zero to account for the non-vanishing breakup cross sections below VB. These characteristics have been proposed to explain why the usual TA does not exist in systems including the WB 6,7Li projectiles. The absence of TA at energies around VB was observed in many systems induced by the WB 6,7Li projectiles, and this was introduced as a new anomaly called the breakup threshold anomaly (BTA) [8]. Although the BTA is well presented in various systems induced by 7Li projectiles, among them 7Li + 27Al [9], 28Si [10], 138Ba [11], and other systems such as 7Li + 59Co [12], 80Se [13], 134Ba [7], and 208Pb [14], revealed the occurrence of the usual TA. These controversial results related to the occurrence of the BTA in systems induced by 7Li make it an active research area [15, 16].
In addition to the available experimental measurements for the 7Li + 144Sm system [17−21], many theoretical studies have focused on investigating this system [22−26]. In Ref. [17], the 6,7Li + 144Sm elastic scattering angular distributions (ADs) were measured experimentally at energies around VB for the two systems. The ADs were investigated using the optical model (OM) with a nuclear potential of the usual Woods-Saxon (WS) shape. None of the weakly bound systems studied (6,7Li + 144Sm) exhibited the TA, which is well presented in systems with tightly bound projectiles such as (12C, 16O + 144Sm). In addition to the various studies that determined a systematic global potential for 7Li [22−24], the 7Li + 144Sm system was investigated microscopically using the continuum discretized coupled channel (CDCC) method [25, 27−30]. In Ref. [25], the ADs for 7Li projectiles scattered by 59Co, 144Sm, and 208Pb targets at energies around VB were investigated using the CDCC method to determine the significance of the Coulomb-nuclear interference. The differences and similarities between the results for the 6Li and 7Li were also explored. The analysis showed that the 6Li total breakup cross sections are greater than those for 7Li.
The current study complements our ongoing research plan that investigates the peculiarities and interaction mechanisms of different nuclear systems induced by the WB projectiles [31−42]. In the current study, we examine the ADs and reaction cross sections (σR) for the 7Li + 144Sm system within various interaction potentials and calculation approaches. Finally, information on the absence of the typical TA is presented. In Section II, the potentials that were implemented in the theoretical calculations are discussed. The obtained results are presented in Section III, along with their discussion. The findings and interpretations of this work are discussed in Section IV.
-
The elastic scattering 7Li + 144Sm ADs at energies between 21.6 and 52 MeV [17, 18] are investigated within various potentials and approaches, starting with the fundamental phenomenological OM and the semi-microscopic São Paulo potential (SPP). The cluster folding model (CFM) was used to account for the 7Li→α + t cluster structure. The CFM computations with and without the inclusion of a surface DPP were performed to reproduce the considered data. Finally, the CDCC computations were carried out by considering the coupling to resonant states only, as well as that to resonant and non-resonant continuum. As a result, we believe that the analyses using different potentials could aid in clarifying the various characterizations of the 7Li + 144Sm system and in determining the optimal potentials that accurately reproduce the data.
-
The applicability of the OM model is predicated on the existence of a smooth-varying average potential and the premise that the influence of the various reaction channels can be reflected by an imaginary potential. As a result, the OM is applied primarily to the data that varied smoothly with the energy. If one of these premises does not hold and the behavior of cross sections deviates from being reasonably smooth, the OM will be a non-useful concept. The considered 7Li + 144Sm elastic scattering ADs are analyzed within the OM, which has the following central potential:
$\begin{aligned}[b] U(r) =& {V_C}(r) - {V_0}{\left[ {1 + \exp \left( {\frac{{r - {R_V}}}{{{a_V}}}} \right)} \right]^{ - 1}}\\& - {\rm i} {W_0}{\left[ {1 + \exp \left( {\frac{{r - {R_W}}}{{{a_W}}}} \right)} \right]^{ - 1}} , \end{aligned} $

(1) Here,
$ {V_C}(r) $ is the Coulomb potential, characterized by the radius$ {R_C} = {r_C}{\text{ }}A_t^{1/3},{\text{ }}{r_C} = 1.3{\text{ fm}} $ . The real and imaginary parts of the nuclear potential appear as the second and third terms in Eq. (1), have the standard volume WS shape, and are identified by the parameters: V0 and W0 (potential depth), rV and rW (reduced radius parameter), aV and aW (diffuseness), respectively. -
The 7Li + 144Sm interaction potential was constructed microscopically to address the various ambiguities inherited from the OM potentials. The SPP is conceptually comparable to the conventional double folding potential since it is derived by folding the densities of the projectile and target nuclei with an effective interaction potential
$ v_{NN}^{{\text{SPP2}}} $ [43–47], and it is expressed as:$ {V_F}(R) = \iint \rho_{P} (\overrightarrow{r_{P}}) \rho_{T} (\overrightarrow{r_{T}}) v_{NN}^{\rm SPP2} (\overrightarrow{R} - \overrightarrow{r_{P}} + \overrightarrow{r_{T}}) {\rm d} \overrightarrow{r_{P}} {\rm d} \overrightarrow{r_{T}}. $

(2) The density distribution
$\rho_{P}(r_{P})$ of 7Li was taken from Ref. [48] and has the following form:$ \rho (r) = (\xi + \gamma {r^2})\exp {\text{ }}( - \beta {r^2}){\text{f}}{{\text{m}}^{-3}} $

(3) where
$ \xi $ =0.1387,$ \gamma $ =0.0232, and$ \beta $ =0.3341. The density distribution$\rho_{T}(r_{T})$ of 144Sm nucleus was calculated within the Dirac-Hartree-Bogoliubov model [49] using the REGINA code. The new version SPP2 [47] was employed, and the effective interaction$ v_{NN}^{{\text{SPP2}}} $ , which is energy- dependent, is expressed as$ v_{NN}^{{\text{SPP2}}}(\overrightarrow r ) = - {U_0}{\text{ }}{{\rm e}^{ - {{(r/a)}^2}}}{\text{ }}{{{\rm e}}^{ - {\text{4}}{{\text{V}}^{\text{2}}}{\text{/}}{C^{\text{2}}}}} $

(4) where
$ {U_0} $ = 735.813 MeV, a = 0.5 fm, V is the relative velocity between the colliding nuclei, and C is the speed of light. -
The CFM was implemented to describe the 7Li + 144Sm elastic scattering ADs by considering the 7Li→α + t cluster nature that emerges at a low excitation energy ~ 2.468 MeV. The real (
$ {V^{CF}} $ ) and imaginary ($ {W^{CF}} $ ) cluster folding potentials (CFPs) for the 7Li + 144Sm system were prepared as follows:$\begin{aligned}[b] {V}^{CF}(R)=&{\displaystyle \int }\left[{V}_{\text{ }\alpha -{\text{ }}^{144}\text{ Sm}}\left(R-\frac{\text{3}}{\text{7}}r\right)+{V}_{t-^{144}\text{ Sm}}\left(R+\frac{\text{4}}{\text{7}}r\right)\right]\\&\times\text{ }{\left|{\text{χ}}_{\alpha -t}(r)\right|}^{2} {\rm d} r\text{,} \end{aligned}$

(5) $ \begin{aligned}[b]{W}^{CF}(R)=&{\displaystyle \int }\left[{W}_{\text{ }\alpha -{\text{ }}^{144}\text{ Sm}}\left(R-\frac{\text{3}}{\text{7}}r\right)+{W}_{t-^{144}\text{ Sm}}\left(R+\frac{\text{4}}{\text{7}}r\right)\right]\\&\times\text{ }{\left|{\text{χ}}_{\alpha -t}(r)\right|}^{2} {\rm d}\text{ }r\text{,}\end{aligned} $

(6) where
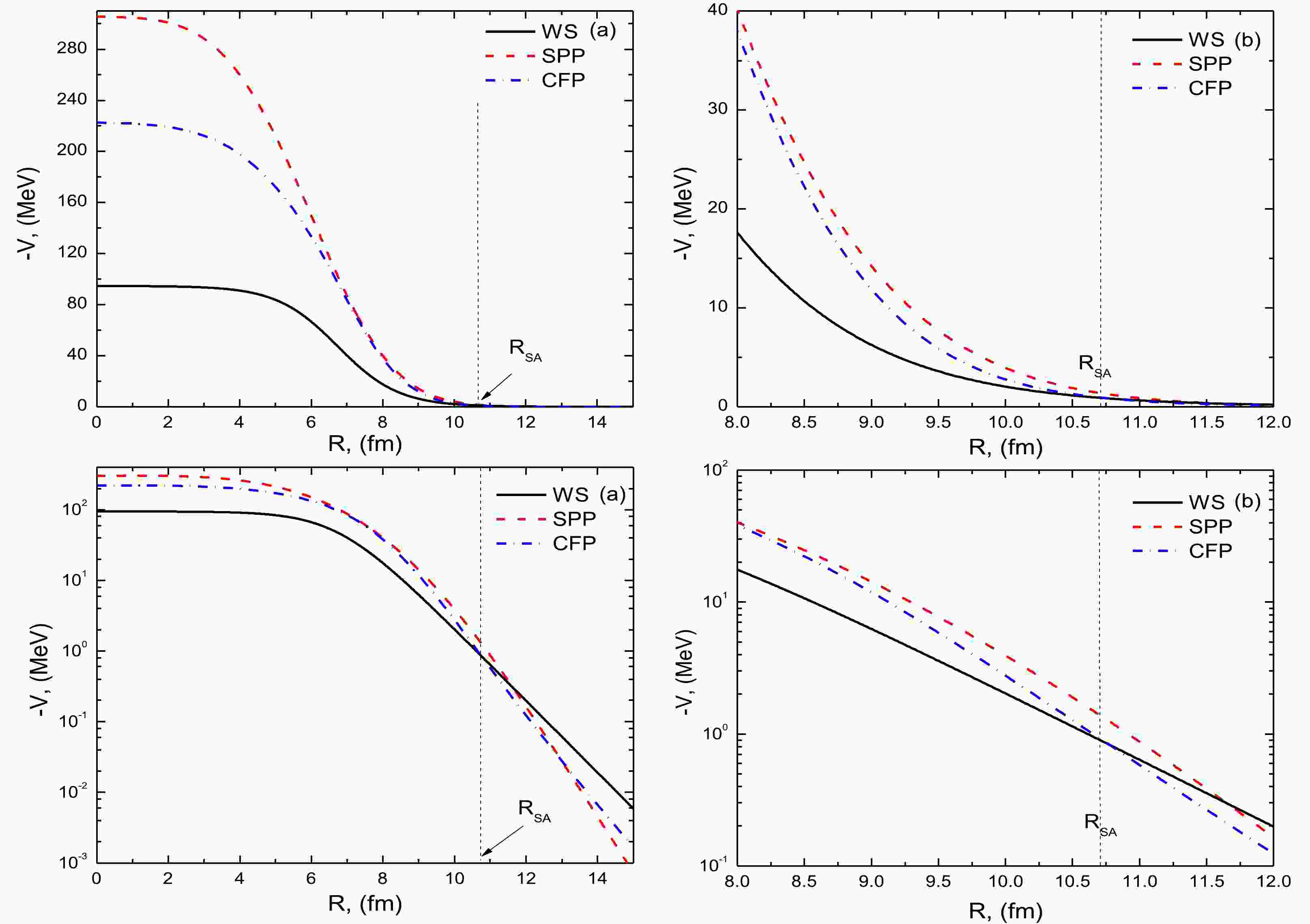
$ {V_{{\text{ }}\alpha - {{\text{ }}^{144}}{\text{ Sm}}}} $ ,$ {W_{{\text{ }}\alpha - {{\text{ }}^{144}}{\text{ Sm}}}} $ ,$ {V_{t{ - ^{144}}{\text{ Sm}}}} $ , and$ {W_{t{ - ^{144}}{\text{ Sm}}}} $ are the real and imaginary potentials for the t + 144Sm and α + 144Sm channels at appropriate energies Et ≈ 3/7ELi and Eα ≈ 4/7ELi [50,51]. The intercluster wave function$ {{{\chi }}_{\alpha - t}}(r) $ represents a 2P3/2 state in a real WS potential, and it is characterized by the parameters RV = 1.83 fm, aV = 0.65 fm, and the depth (V0) was varied till the binding energy for the cluster was reproduced. As the maximum considered energy was 52 MeV, the suitable t + 144Sm and α + 144Sm potentials for constructing the 7Li + 144Sm CFPs were Ut + 144Sm at Elab=3/7 × 52 = 22.29 MeV and Uα+144Sm at Elab = 4/7 × 52 = 29.71 MeV, (U = V + W). The potentials U t + 144Sm at Elab = 22.29 MeV “taken from the global potential for tritons” [50] and Uα + 144Sm at Elab = 50 MeV [51] were adopted to generate the CFPs for the 7Li + 144Sm. The three potentials used − WS, SPP, and CFP − to study the 7Li + 144Sm system at E = 52 MeV close to the strong absorption radius (RSA) are shown in Fig. 1. Despite the observed differences between the considered potentials in the low radial region, all fairly reproduced the data. This is consistent with the fact that most of the available heavy ion scattering data is sensitive only to the tail of the nucleus-nucleus potential, in the vicinity of the strong absorption radius (RSA), which is typically ~$ 1.5{\text{ }}(A_P^{1/3} + A_T^{1/3}) $ . The employed OM and SPP are energy-dependent, while the employed CFP is energy-independent. -
The 7Li + 144Sm elastic scattering ADs were reanalyzed phenomenologically at energies between 21.6 and 52 MeV [17, 18] using OMP with a Coulomb and nuclear part, as shown in Eq. (1). The OM calculations were performed using the geometrical parameters rV , rW, aV, and aW fixed to 1.286, 1.739, 0.853, and 0.809 fm, respectively, in accordance with Cook’s study [22]. This allowed us to explore how the potential depths evolve with energy. The OM computations employed two varying parameters, V0 and W0, which were adjusted to describe the experimental data. The FRESCO code [52] upgraded with the χ2 minimization SFRESCO code was implemented to describe the data and obtain the optimal potential parameters by minimizing the χ2 value, which gives the deviation between the experimental data and the calculations.
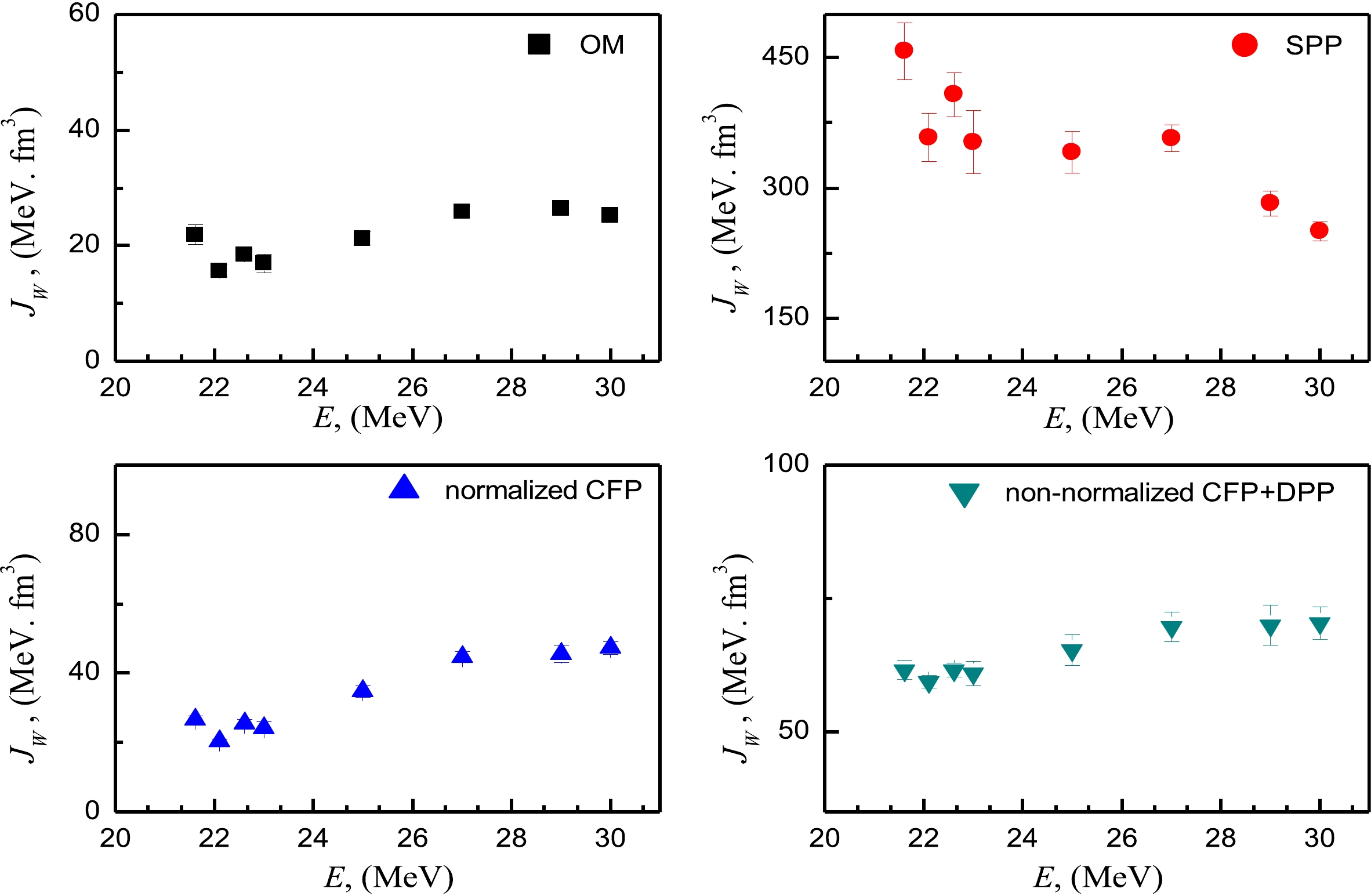
The experimental 7Li + 144Sm ADs at all the considered energies below and above the barrier are fairly reproduced utilizing the OM approach as depicted in Fig. 2, and the extracted optimal parameters are listed in Table I. To examine the applicability of the dispersion relation on the real (JV) and imaginary (JW) volume integrals, these quantities were calculated, and their values are displayed in Table 1. The JV and JW values do not follow the typical dispersion relation, where the imaginary potential depth does not drop to zero as the energy decreases below the barrier. The OM analysis revealed that the TA, which is well presented in systems with tightly bound projectiles [53, 54], is not present in the 7Li + 144Sm system under consideration.
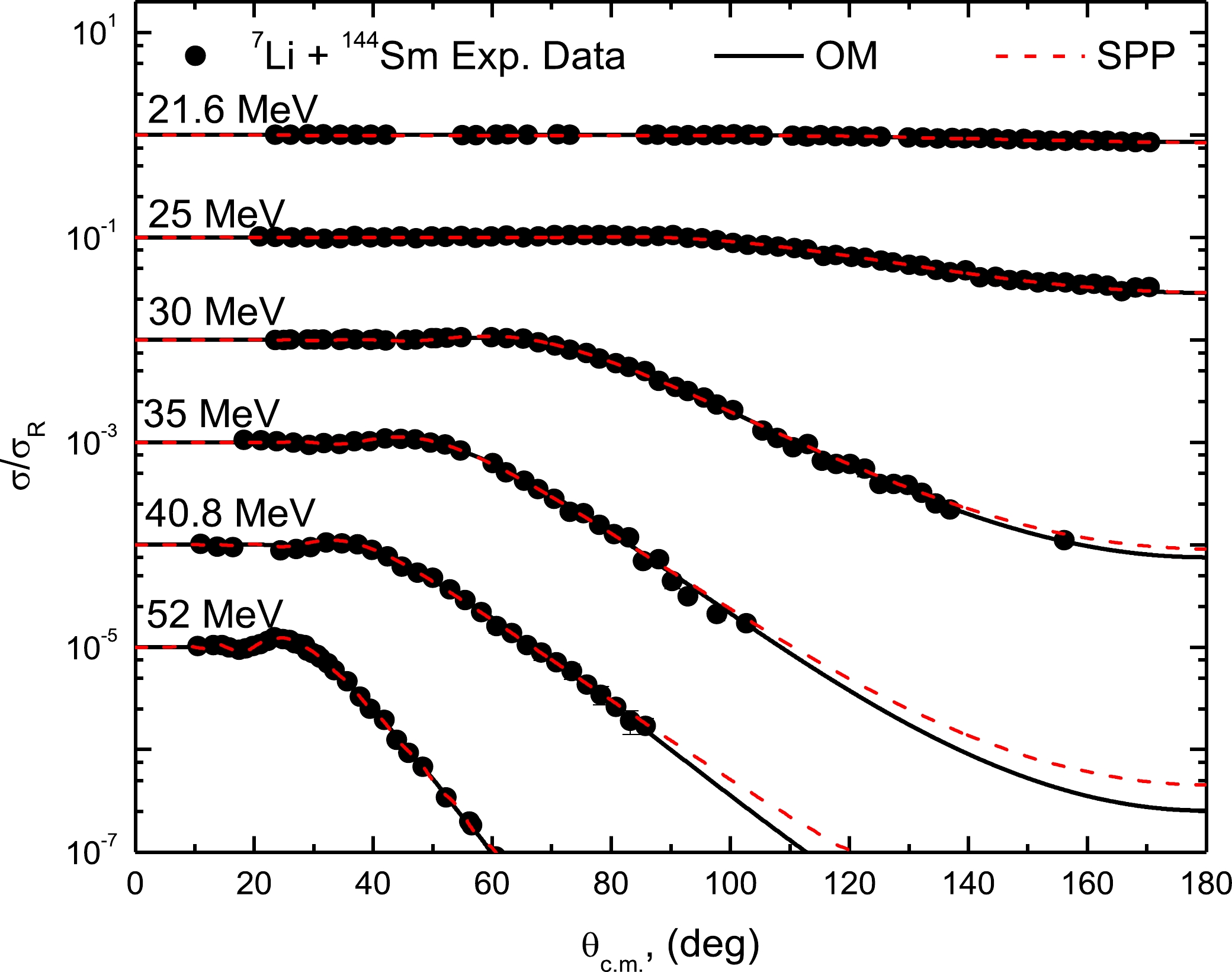
Figure 2. (color online) 144Sm(7Li,7Li)144Sm experimental ADs versus theoretical calculations within WS potential (solid curves) and SPP (dashed curves) at Elab = 21.6, 25, 30, 35, 40.8, and 52 MeV. Data is displaced by 0.1.
The extracted V0 and W0 values from the present OMP analysis are far from those reported in Ref. [17] owing to the different geometrical parameters considered. Hence, we compared the behavior of the obtained OM-WS potential from this work with that potential in Ref. [17]. It was found that the two potential families at the sensitive radius (~ 10.7 fm) have a minimum uncertainty and are nearly independent of the geometrical shape.
E/MeV Pot. V0 (MeV)/NRSPP W0 (MeV)/NISPP χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ /mb

JV /(MeV·fm3) JW /(MeV·fm3) 21.6 WS 163.15±17.28 6.48±0.49 1.22 39.9±3.6 240.45±25.47 21.98±1.66 SPP 1.881±0.125 1.120±0.080 1.61 252.7±18.2 769.08±51.11 457.93±32.71 22.1 WS 165.51±10.26 4.63±0.31 1.43 40.9±3.2 243.93±15.12 15.70±1.05 SPP 1.421±0.096 0.877±0.068 1.82 209.9±16.4 580.41±39.21 358.21±27.77 22.6 WS 161.5±7.26 5.42±0.28 0.87 65.2±3.9 238.02±10.67 18.38±0.95 SPP 1.301±0.070 0.999±0.063 1.13 256.6±16.1 531.15±28.58 407.85±25.72 23 WS 167.82±10.87 5.01±0.47 0.59 79.7±8.3 247.34±16.02 16.99±1.59 SPP 1.318±0.089 0.865±0.089 0.63 245.4±24.4 537.89±36.32 353.02±36.32 25 WS 133.77±4.14 6.28±0.34 1.24 251.7±11.0 197.15±6.10 21.29±1.15 SPP 1.089±0.029 0.839±0.059 1.16 402.7±19.8 443.60±11.81 341.77±24.03 27 WS 111.96±2.39 7.65±0.26 1.91 501.1±9.6 165.01±3.52 25.95±0.88 SPP 1.026±0.015 0.879±0.038 1.40 646.4±13.5 417.18±6.10 357.41±15.45 29 WS 103.71±1.46 7.82±0.30 2.6 723.7±10.7 152.85±2.15 26.52±1.02 SPP 1.015±0.016 0.696±0.036 1.78 814.1±14.2 411.94±6.49 282.47±14.61 30 WS 103.34±1.63 7.43±0.22 0.82 813.7±9.0 152.30±2.40 25.20±0.75 SPP 0.967±0.014 0.617±0.028 1.44 882.9±12.0 392.10±5.68 250.18±11.35 32 WS 101.08±2.37 8.63±0.43 1.3 1037±13.0 148.97±3.49 29.27±1.46 SPP 1.028±0.025 0.728±0.051 1.75 1117±21.0 416.06±10.12 294.64±20.64 35 WS 82.82±1.91 8.96±0.36 2.4 1266±14.0 122.06±2.81 30.39±1.22 SPP 0.899±0.020 0.675±0.035 3.1 1314±16.0 362.85±8.07 272.44±14.13 40.8 WS 38.15±4.77 15.61±0.98 0.93 1791±29.0 56.23±7.03 52.94±3.32 SPP 0.859±0.040 1.268±0.108 0.94 1862±38.0 344.85±16.06 509.05±43.36 52 WS 94.59±3.76 8.93±0.94 0.18 2063±42.0 139.41±5.54 30.29±3.19 SPP 0.863±0.122 0.373±0.123 0.14 1925±85.0 342.90±48.47 148.20±48.87 Table 1. Optimal parameters extracted from the analysis of the 7Li + 144Sm system within both WS and SPP. The JV, JW and reaction cross sections (σR) values are given.
-
It is always desirable to derive the interaction potential within microscopic approaches, such as the SPP, for minimizing the various parameter ambiguities that may arise during the phenomenological OM analysis. Therefore, the new SPP2 [47] version was implemented to investigate the 7Li + 144Sm ADs. The real portion of SPP was computed using Eq. (2), and the imaginary portion was determined by multiplying the real portion by a factor. The shape of the central potential is as follows:
$ U(R) = {V_C}(R) - {N_{\rm RSPP}}{\text{ }}{V^{\rm SPP}}(R) - {\rm i} {N_{\rm ISPP}}{\text{ }}{V^{\rm SPP}}(R). $

(7) The second and third terms denote the real and imaginary SPP, with their corresponding normalization factors, NRSPP and NISPP, respectively. Consequently, two changeable parameters (NRSPP and NISPP) were used to fit the data. The small number of fitting parameters and the non-biased search (NRSPP and NISPP were permitted to freely vary between 0.1 and 2.0), and they result in an obvious energy dependence on the potentials. The computations within the SPP, as shown in Fig. 2, reasonably agree with the experimental 7Li + 144Sm ADs using the NRSPP and NISPP values displayed in Table 1. With an average value of 0.69 ± 0.09, the extracted NRSPP values in the energy range of 21.6–52 MeV (close to and above the barrier VB) are close. The NRSPP values moderately change as the energy falls below the barrier VB, whereas the NISPP values demonstrate an increasing trend. This observed behavior deviates strongly from the typical TA, in which the imaginary potential vanishes as the energy falls below the barrier. In other words, the analysis performed within the SPP confirms the existence of the BTA, which agrees with the findings of Ref. [17]. The analysis reveals the necessity of decreasing the real SPP strength by ~ 31% in order to fairly fit the 7Li + 144Sm ADs. This decrease is primarily owing to the 7Li breakup effects.
-
Motivated by the appreciable clusterization probability of 7Li into t + α cluters, we investigate the considered 7Li + 144Sm ADs using CFPs defined in Eqs. (5) and (6). The form of the central potential is as follows:
$ U(R) = {V_C}(R) - {N_{\rm RCF}}{\text{ }}{V^{CF}}(R) - {\rm i} {\text{ }}{N_{\rm ICF}}{\text{ }}{W^{CF}}(R). $

(8) The second and third terms denote the real and imaginary CFP, with their corresponding normalization factors, NRCF and NICF, respectively. Consequently, two changeable parameters (NRCF and NICF) were used to fit the data. The obvious advantage of the analysis performed within the CFP is that both the real and imaginary potentials are prepared semi-microscopically. Second, the limited number of fitting parameters (NRCF and NICF) can indicate a clear energy dependence on the real and imaginary potential strengths, which provides a better understanding of the presence or absence of the BTA in the studied system. Some systems induced by the WB 7Li projectile [9–11, 17] showed the presence of BTA at energies around VB, where the imaginary potential strength increaed instead of dropping to zero. Other systems induced by the 7Li projectiles [12–14] showed the absence of the BTA.
The theoretical analysis within the CFP successfully reproduced the 7Li + 144Sm ADs at all considered energies and throughout the whole angular range, as depicted in Fig. 3. The extracted NRCF values in the energy range of 25–52 MeV (above the barrier VB) are quite consistent, with an average value of 0.62 ± 0.20. Furthermore, by reducing the energy below VB, the extracted NRCF exhibits an increasing trend, as listed in Table 2. The non-vanishing trend observed for the imaginary CFP part when the energy decreases below the barrier indicates the presence of the BTA. In addition, the analysis revealed that the strength of the real CFP must be decreased by ~ 38% to adequately describe the 7Li + 144Sm ADs in the energy range 25–52 MeV (above VB).
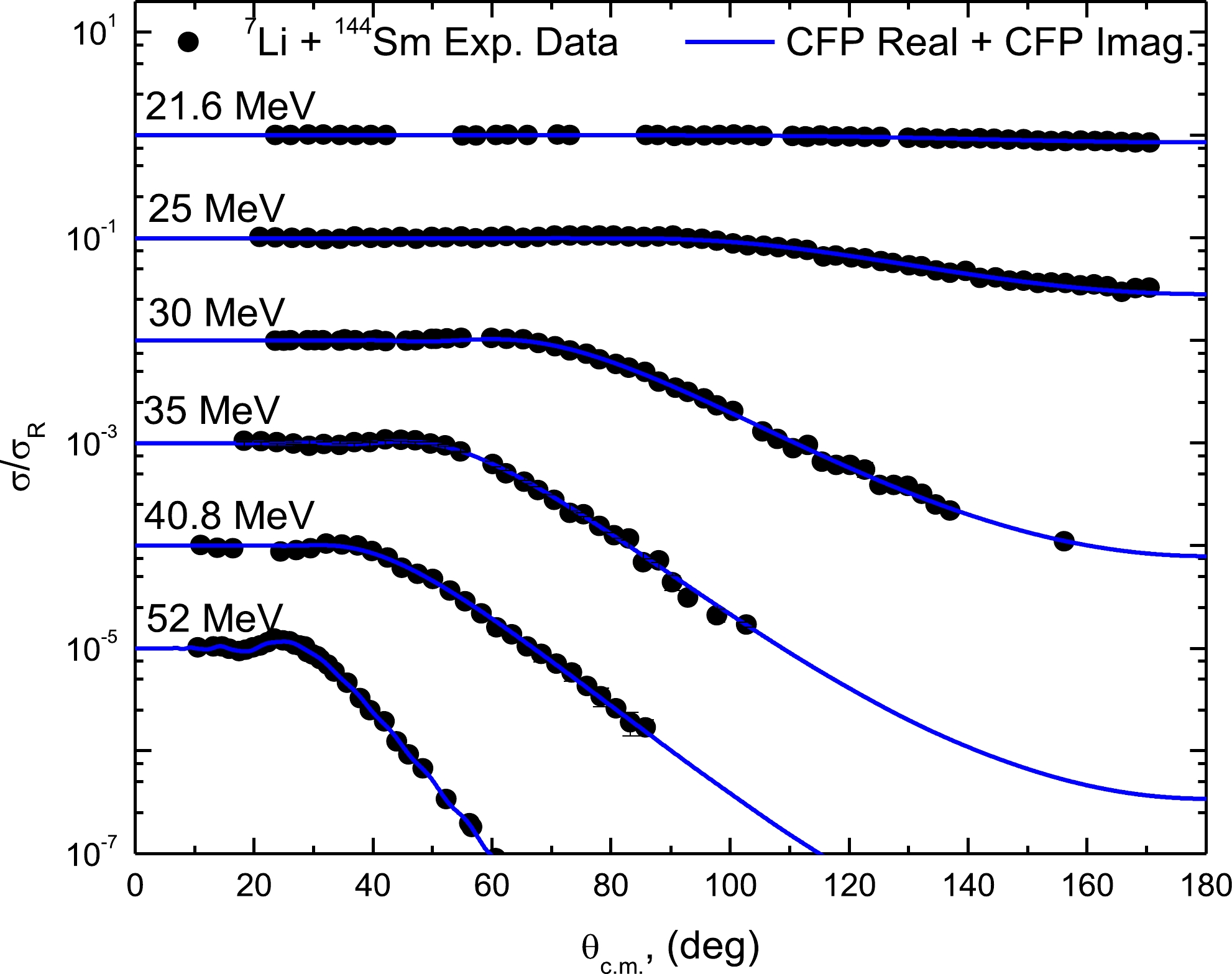
Figure 3. (color online) 144Sm(7Li,7Li)144Sm experimental ADs versus the calculations within CFP at Elab = 21.6, 25, 30, 35, 40.8, and 52 MeV. Data is displaced by 0.1.
E/MeV NRCF NICF χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ /mb

JV /(MeV·fm3) JW/(MeV·fm3) 21.6 1.663±0.066 0.308±0.013 1.08 47.87±2.2 826.11±32.79 26.66±1.13 22.1 1.479±0.015 0.236±0.007 1.6 48.98±1.3 734.70±7.45 20.43±0.61 22.6 1.358±0.036 0.297±0.012 0.99 76.84±3.3 674.59±17.88 25.71±1.04 23 1.338±0.048 0.281±0.019 0.63 92.09±6.1 664.66±23.84 24.32±1.64 25 0.945±0.021 0.403±0.020 1.08 272.7±9.7 469.43±10.43 34.88±1.73 27 0.754±0.014 0.517±0.017 2.72 527.2±9.5 374.55±6.95 44.75±1.47 29 0.669±0.016 0.528±0.029 3.7 742.8±16.4 332.33±7.95 45.70±2.51 30 0.649±0.014 0.547±0.021 1.24 850.4±12.7 322.39±6.95 47.35±1.82 32 0.626±0.022 0.634±0.038 1.42 1073±22.0 310.97±10.93 54.88±3.29 35 0.468±0.016 0.720±0.032 2.8 1319±19.0 232.48±7.95 62.33±2.77 40.8 0.251±0.015 0.950±0.005 2.1 1880±4.0 124.18±7.42 82.24±0.43 52 0.581±0.038 0.563±0.122 0.1 2024±81.0 288.61±18.88 48.73±10.56 Table 2. Optimal NRCF and NICF values extracted from the calculations within CFP.
-
The considerable coupling impact on the breakup channel is the main source for the evident reduction in the strength of the SPP and CFP. This impact can be modelled by including an additional DPP to simulate the effects that result from coupling to all the other states (continuum) or by carrying out the microscopic CDCC computations. Both methods were considered to reproduce the 7Li + 144Sm ADs. In the present work, we have suggested a simple approach to simulate the DPP. The following form (Eq. 9) was employed to calculate the DPP based on the previously generated CFPs.
$ {U_{\rm DPP}}(R) = {N_{\rm RDPP}}\frac{\rm d}{{{\rm d}R}}{V^{\rm CFP}}(R) + {\rm i} {N_{\rm IDPP}}\frac{\rm d}{{{\rm d}R}}{W^{\rm CFP}}(R). $

(9) As previously demonstrated, the 7Li + 144Sm ADs in the energy range of 25–52 MeV were reasonably described within the CFPs when the real and imaginary CFP strengths were decreased by ~ 38% and 39%, respectively. We describe the considered ADs using non-normalized CFPs such that “both NRCF and NICF are fixed to unity” by incorporating an additional DPP. As a simple approach, the DPP was taken as a factor multiplied by the derivative of the real and imaginary CFPs. Thus, two parameters, NRDPP and NIDPP, which denote the normalization factors for the DPP, were employed to fit the data. The same methodology was followed in our previous works [5, 55, 56]. As shown in Fig. 4, the experimental 7Li + 144Sm ADs agree well with the (non-normalized CFPs + DPP) calculations, and the optimally obtained NRDPP and NIDPP values are listed in Table 3. The nature of the implemented DPP changed from an attractive one (for the data above the VB) to a repulsive one (for the data below the VB), as shown from the extracted values listed in Table 3. Consequently, the nature of the DPP highly depends on the interaction energy.
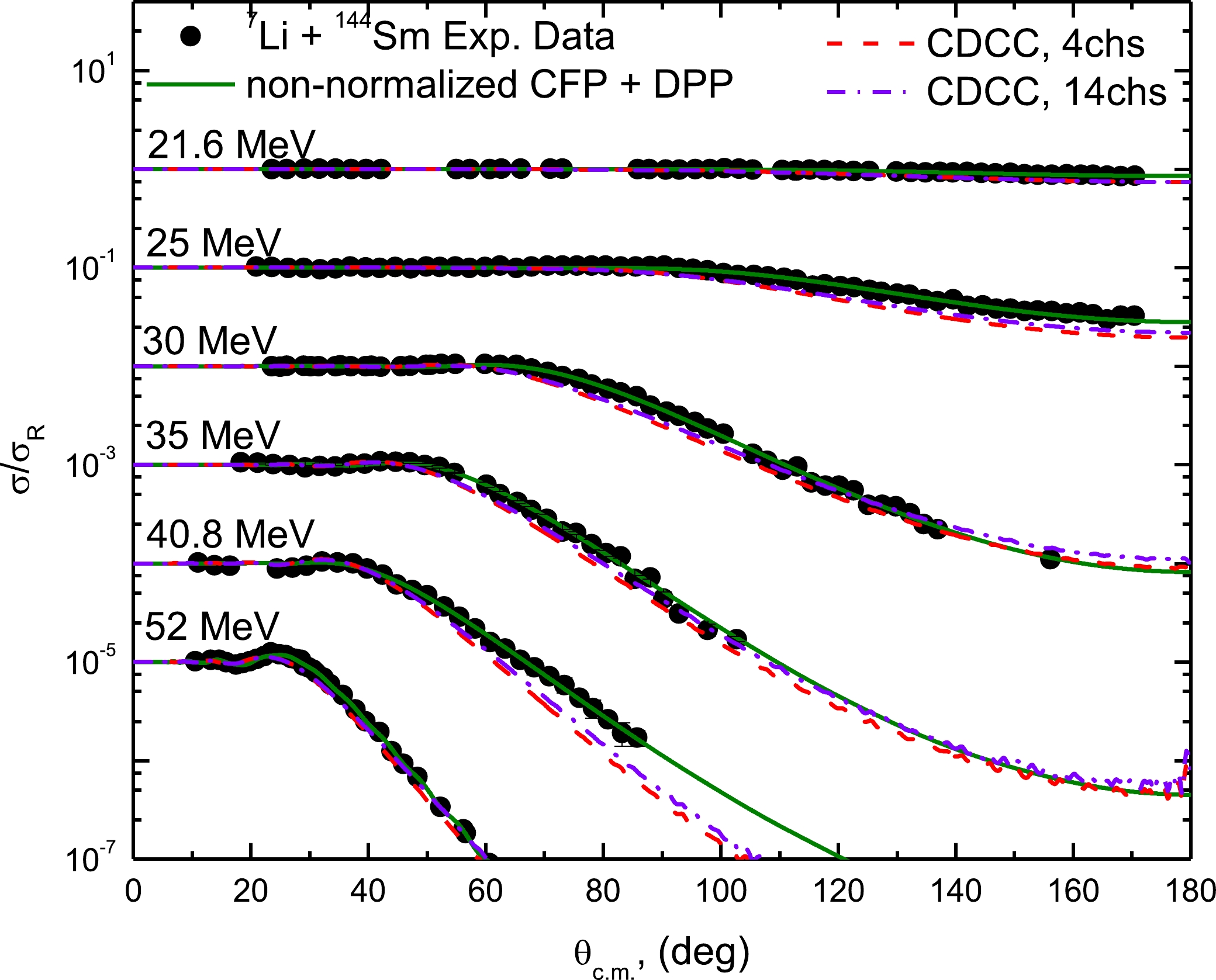
Figure 4. (color online) 144Sm(7Li,7Li)144Sm experimental ADs at Elab = 21.6, 25, 30, 35, 40.8, and 52 MeV versus the (non-normalized CFPs + DPP) calculations (curves), 4-channels CDCC computations (dashed curves), and 14-channels CDCC computations (dashed dot curves).
E/MeV NRDPP NIDPPP χ2/N $ {\mathit{\sigma }}_{\mathit{R}} $ /mb

JV /(MeV·fm3) JW /(MeV·fm3) 21.6 −0.473±0.070 0.778±0.023 1.09 47.17±3.6 594.19±87.94 61.67±1.82 22.1 −0.319±0.044 0.846±0.017 1.64 49.35±3.4 562.47±77.58 59.49±1.20 22.6 −0.240±0.029 0.778±0.016 1.02 77.14±3.9 546.19±66.00 61.67±1.27 23 −0.231±0.045 0.798±0.029 0.64 91.93±8.6 544.34±106.04 61.03±2.22 25 0.027±0.020 0.661±0.029 1.85 272.1±13.6 491.19±127.35 65.41±2.87 27 0.155±0.011 0.526±0.021 2.72 528.4±11.2 464.82±32.99 69.73±2.78 29 0.204±0.008 0.517±0.028 3.6 743.9±14.7 454.73±17.83 70.02±3.79 30 0.214±0.008 0.504±0.022 1.24 848.8±12.2 452.67±16.92 70.44±3.07 32 0.230±0.013 0.406±0.041 1.4 1072±22.0 449.37±25.40 73.57±7.43 35 0.317±0.009 0.337±0.034 2.8 1311±19.0 431.45±12.25 75.78±7.65 40.8 0.513±0.017 −0.234±0.073 0.89 1856±34.0 391.08±12.96 94.05±29.34 52 0.250±0.020 0.521±0.121 0.09 2005±83.0 445.25±35.62 69.89±16.23 Table 3. Optimal NRDPP and NIDPP values extracted from the (non-normalized CFPs + DPP) calculations. JV, JW, and σR values are displayed.
Then, we employed the microscopic CDCC approach [57–59] to investigate the considered 7Li + 144Sm ADs. The inclusion of couplings to the continuum states, which makes it possible to analyze the impacts of projectile breakup, is an obvious advantage of the CDCC approach. The CDCC computations were carried out using the FRESCO code, considering the coupling to resonant (7/2– and 5/2–) states of widths 0.2 and 2.0 MeV, the bound non-resonant (1/2–) state, and the non-resonant continuum (discretized into 10 bins). These computations were referred to as the "14-channels CDCC". In addition, the CDCC computations, named "4-channels CDCC", were performed by ignoring the coupling to the non-resonant continuum; these computations are illustrated in Fig. 4. Our test computations revealed that the coupling to resonant states has the most important contributions, while the contributions from other continuum states are minimal. By using Eqs. (5) and (6), the diagonal and coupling potentials were determined. The continuum above the α + t breakup threshold energy was divided into momentum bins of width Δk = 0.25 fm-1, k is extended from 0.0 to 0.75 fm-1. The implemented model space for truncation and discretization of 7Li was taken from Ref. [60].
It is important to clarify that the calculations performed within the CFP approach could be considered a particular case of the CDCC calculations with only a single channel. Within the CFP approach, we reproduced the 7Li + 144Sm ADs using normalized real and imaginary CFP parts, as illustrated in Table 2. However, in the CDCC calculations (4 and 14 channels), the calculations are free of any adjusting parameters; therefore, we could study the effects arising from the couplings to resonant and non-resonant continuums on the elastic scattering channel. Therefore, it is not surprising that the CFP calculations (1-channel CDCC) using normalized CFPs work very well (Fig. 3), whereas the more physical CDCC calculations (4 and 14 channels, Fig. 4) failed to reproduce the data.
Additionally, the elastic scattering ADs for the 7Li + 144Sm system were analyzed using an effective potential Ueff extracted from the CDCC computations. The Ueff was taken as the sum of the cluster folding potential (UCF) and the dynamic polarization potential (UTELP). The latter arises from the coupling to the continuum states and is generated from the CDCC computations utilizing the so-called trivially equivalent local potential (TELP) approach [61]. The implemented Ueff in the theoretical calculations is expressed in Eq. (10). The generated UCF, UTELP, and Ueff for the 7Li + 144Sm system at Elab = 40.8 and 52 MeV in the radial region 8–12 fm, near the RSA, are shown in Fig. 5.
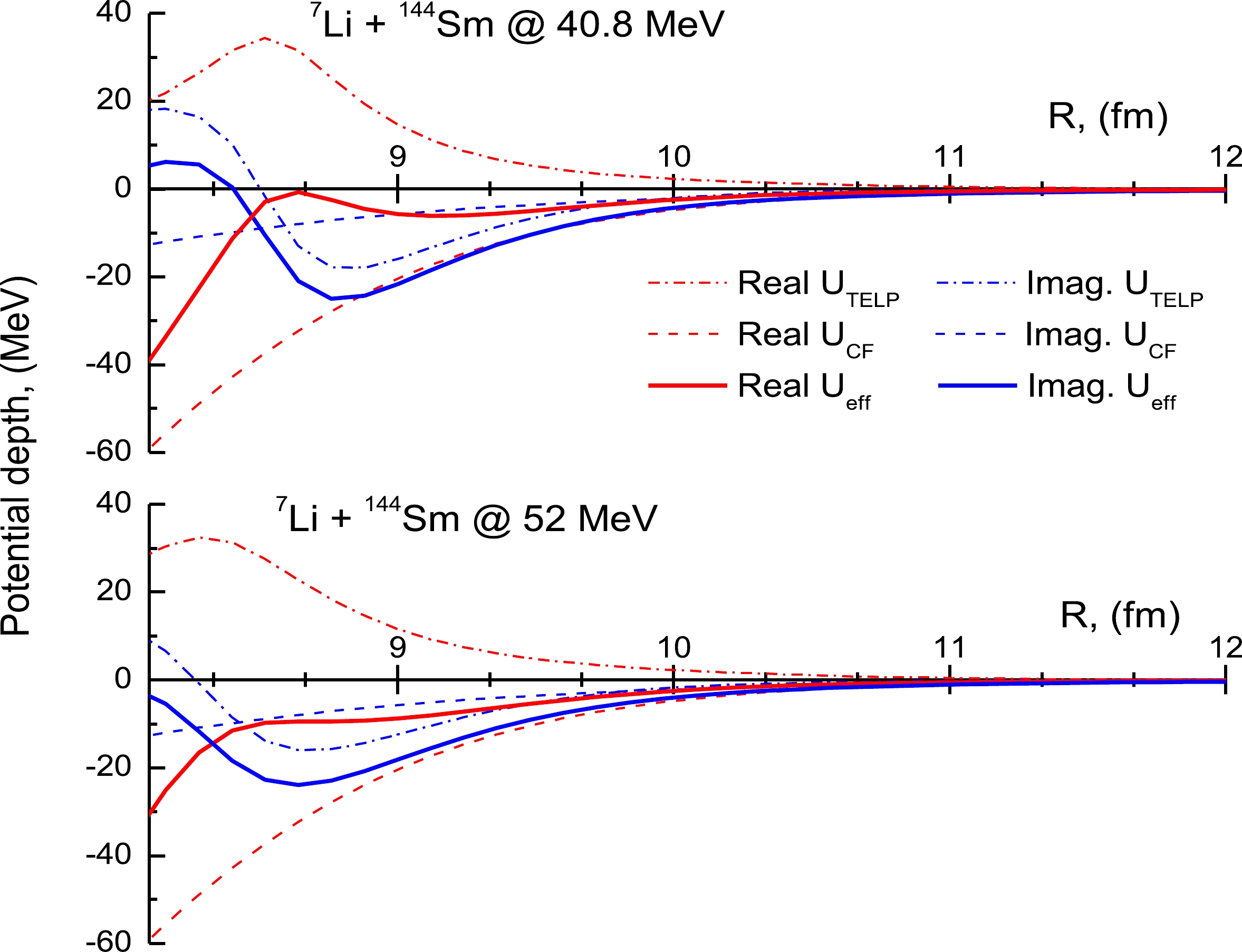
Figure 5. (color online) UCF, UTELP, and Ueff potentials generated from the CDCC computations for the 7Li + 144Sm system at E = 40.8 and 52 MeV.
$ {U_{\rm eff}}(r) = {U_{\rm CF}}(r) + {U_{\rm TELP}}(r), U = V + {\rm i} W. $

(10) The considered ADs are reproduced utilizing normalized Ueff, which is characterized by two normalization factors, NReff and NIeff, for the real and imaginary parts of the Ueff, respectively. The 7Li + 144Sm elastic ADs and the calculations within the normalized Ueff agreed well, as shown in Fig. 6 using the NReff and NIeff values listed in Table 4.

Figure 6. (color online) 144Sm(7Li,7Li)144Sm experimental ADs versus the calculations within the normalized Ueff at Elab = 21.6, 25, 30, 35, 40.8, and 52 MeV.
E/MeV NReff NIeff χ2/N 21.6 1.711±0.047 0.292±0.008 2.3 22.1 1.664±0.008 0.208±0.007 2.4 22.6 1.803±0.009 0.253±0.006 2.2 23 1.953±0.006 0.204±0.016 0.8 25 1.634±0.009 0.277±0.017 1.6 27 1.483±0.018 0.438±0.011 2.7 29 1.449±0.018 0.568±0.011 4.9 30 1.495±0.012 0.486±0.011 2.1 32 1.586±0.017 0.489±0.017 1.4 35 1.308±0.021 0.489±0.013 2.5 40.8 1.029±0.034 0.794±0.053 0.9 52 0.658±0.001 0.189±0.006 7.1 Table 4. Optimal NReff and NIeff values extracted from the theoretical computations within the normalized Ueff.
The energy dependence on the JV and JW values extracted from the various implemented potentials showed a nearly consistent pattern despite the different numerical values, as shown in Figs. 7 and 8. The studied dependence could be useful for identifying the presence or absence of the usual TA, which is identified as a bell-shaped peak in the real potential and a dramatic reduction in the strength of the imaginary potential as the energy reduces below the barrier. As shown in Fig. 8, there was no dramatic reduction in the JW values as the energy decreased below the barrier; the JW values demonstrated an increasing trend rather than dropping to zero as it approached the barrier, especially for those extracted from the calculations within SPP. This analysis demonstrates the absence of the typical TA, and that the BTA is well presented in the 7Li + 144Sm system.
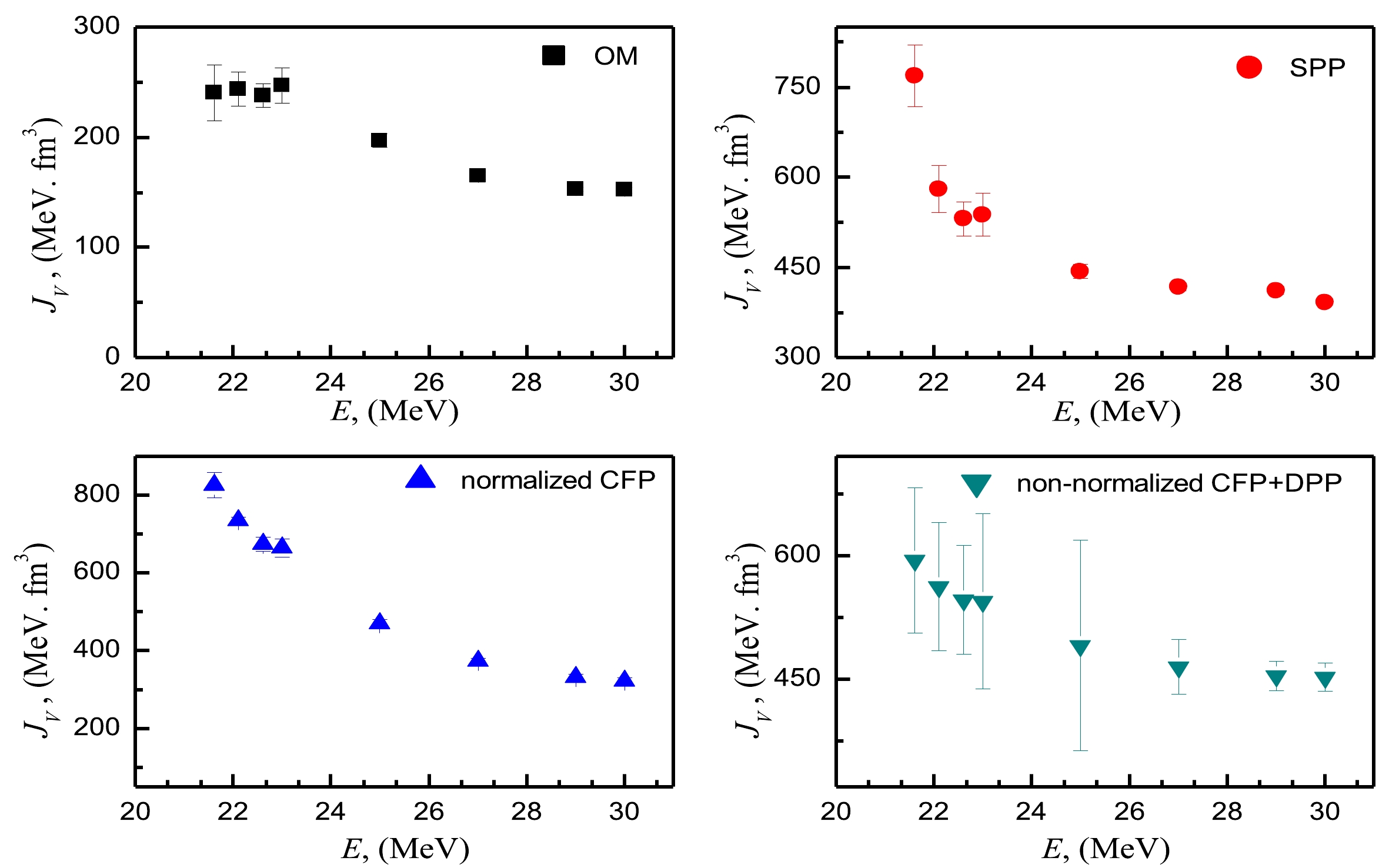
Figure 7. (color online) Energy dependence on the JV values extracted from the various applied potentials.
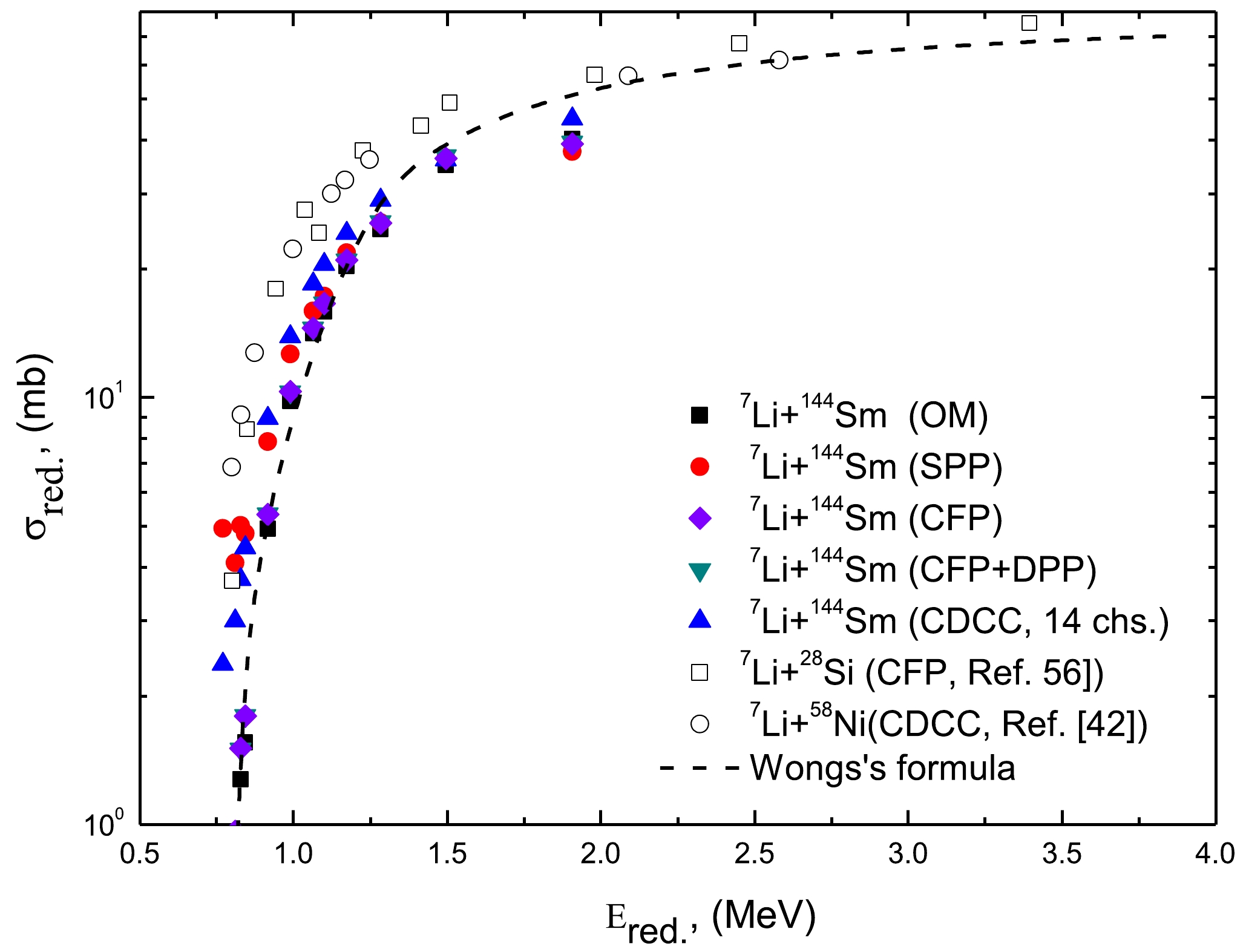
Within the framework of the various employed approaches, we investigated the energy dependence on the extracted σR values, as shown in Fig. 9. A commonly utilized reduction approach [62–64] was employed to clarify the comparison of the total reaction cross sections for the system under consideration. The reduced cross section is scaled as
${\sigma _{\rm red}} = \dfrac{{{\sigma _R}}}{{\left( {A_P^{1/3} + A_T^{1/3}} \right)}}$ and the reduced energy is scaled as${E_{\rm red}} = {E_{\rm c.m.}}\dfrac{{A_P^{1/3} + A_T^{1/3}}}{{{Z_P}{Z_T}}}$ . The symbols P and T denote the projectile and target, respectively; σR denotes the total reaction cross section; Z denotes the charge; and A denotes the masses of the involved nuclei. Figure 9 illustrates the reduced energy dependence on the extracted reduced reaction cross sections for the 7Li + 144Sm system as well as for the 7Li + 28Si [56] and 7Li + 58Ni [42] systems. The black dashed curve in the figure represents the energy dependency based on the Wong formula [64], which has the following form:$ {\sigma _{\rm red}} = \frac{{{\varepsilon _0}r_0^2}}{{2{E_{\rm red}}}}\ln \left[ {1 + \exp \left( {\frac{{2\pi \left( {{E_{\rm red}} - {V_{\rm red}}} \right)}}{{{\varepsilon _0}}}} \right)} \right], $

(11) where
$ {\varepsilon _0} = \hbar {\omega _0}\dfrac{{A_P^{1/3} + A_T^{1/3}}}{{{Z_P}{Z_T}}} $ ,${V_{\rm red}} = {V_0}\dfrac{{A_P^{1/3} + A_T^{1/3}}}{{{Z_P}{Z_T}}}$ , and${E_{\rm red}} = {E_{\rm c.m.}}\dfrac{{A_P^{1/3} + A_T^{1/3}}}{{{Z_P}{Z_T}}}$ . The parameters of the Wong model were used with the fitting parameters$ {\varepsilon _0} $ = 0.178, r0 = 0.13 fm, and${V_{\rm red}}$ = 0.83 MeV. However, the reliability of these fit parameters may be limited owing to the scarcity of data. It is clearly shown that the extracted σR values exhibit an increasing trend as the energy increased, and they are nearly consistent except for the extracted σR values from the CDCC computations, which showed a remarked increase, especially at the low energies studied, mainly owing to the breakup effects of 7Li.To observe the effect of channel coupling on the 7Li + 144Sm AD at Elab = 40.8 MeV, we compared the 1 channel (1 Ch) CDCC calculation to those of the 4 and 14 channels, as shown in Fig. 10. As expected, the more channels were coupled, the better fitting the achieved. Further, one of the unsettled issues observed in nuclear reactions induced by the weakly bound clusterized nuclei such as 7Li projectiles is the origin of the incomplete fusion and large α particle production. A few years ago, the most accepted explanation for the aforementioned behavior was the breakup into α + t structure followed by the capture of triton (t). In recent studies [65, 66], this issue was investigated through pioneering experimental measurements for the 7Li + 93Nb and 7Li + 209Bi systems, respectively, allowing, for the first time, a significant population of the region to be accessible only to the direct triton stripping process and not to breakup followed by the capture of triton. The main conclusion drawn from these studies was the dominance of the direct cluster-stripping mechanism in the large alpha production. To further study this effect on the considered 7Li + 144Sm AD at Elab = 40.8 MeV, we studied the breakup effect and the combined effects of breakup and triton transfer on the elastic scattering channel, as depicted in Fig. 10.
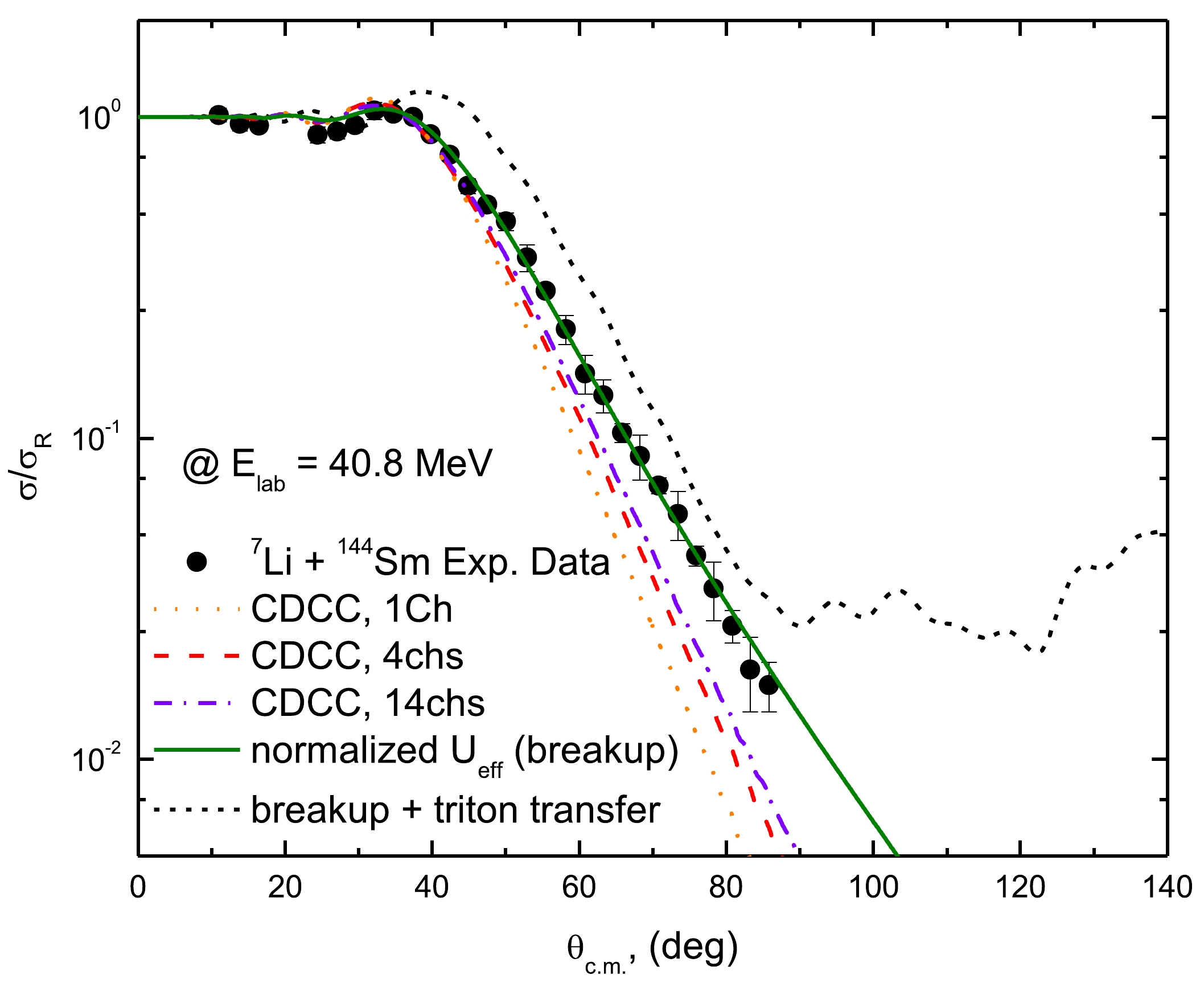
Figure 10. (color online) 144Sm(7Li,7Li)144Sm experimental AD at Elab = 40.8 MeV versus the 1-channel (dotted curve), 4-channels (dashed curve), and 14-channels (dashed dotted curve) CDCC computations. The figure also demonstrates the effect of breakup (solid curve) in comparison with the combined effects of breakup and triton transfer (short dashed curve).
The triton was assumed to be transferred as a single entity from the 7Li ground state to a t + 144Sm state f 147Eu. The potential for the entrance channel (7Li + 144Sm) is the normalized Ueff at Elab = 40.8 MeV (with normalizations, NReff = 1.029 and NReff = 0.794), which considers the 7Li breakup effect. For the exit channel (t + 147Eu), the SPP was employed with the standard form (NRSPP = 1.0 and NISPP = 0.78). The bound state potential for the configurations 7Li→ α + t and 147Eu→ 144Sm + t were taken in the standard WS form with RV = 1.25, aV = 0.65 fm and the depth was adjusted to reproduce the binding energies for the considered clusters, 2.467 and 10.529 MeV, respectively. The spectroscopic amplitudes for the
$ \left\langle {{{}^{\text{7}}{\text{Li}}}} \mathrel{\left | {\vphantom {{{}^{\text{7}}{\text{Li}}} {\alpha + t}}} \right. } {{\alpha + t}} \right\rangle $ and$ \left\langle {{{}^{{\text{147}}}{\text{Eu}}}} \mathrel{\left | {\vphantom {{{}^{{\text{147}}}{\text{Eu}}} {^{144}{\text{Sm}} + t}}} \right. } {{^{144}{\text{Sm}} + t}} \right\rangle $ overlaps were taken as unity. The calculation, considering the combined effects of breakup and triton transfer, demonstrated a substantial increase in the cross-section values, indicating that there is a significant impact from the triton transfer mechanism. -
The study provides a thorough analysis of the existing 7Li + 144Sm ADs at energies comparable to the barrier energy VB, utilizing various potentials and approaches starting from the simplest WS volume-shaped phenomenological potential of two changeable parameters (V0 and W0) and fixed geometrical parameters. As a result, either the presence or absence of TA may be indicated by the energy dependence on both the V0 and W0 values. The analysis highlighted the presence of the BTA behavior; the imaginary potential depth exhibits a non-vanishing trend as the energy reduces below the VB, which agrees with the findings of Refs. [9−11, 17] and contradicts those of Refs. [12-14].
The analysis within the SPP revealed the following features. The imaginary SPP strength showed a remarked increase as the energy reduced below VB. Therefore, the analysis using the SPP approach confirmed the presence of the BTA. In addition, the analysis revealed the need to reduce the real SPP strength by ~ 31% in order to fairly reproduce the 7Li + 144Sm ADs.
The considered data were reanalyzed later within the CFM by considering the 7Li → t + α cluster nature. The CFM analysis revealed the need to reduce the real CFP strength by ~ 38% to adequately reproduce the 7Li + 144Sm ADs, while confirming the presence of the BTA phenomenon. The real CFP strength showed an increasing trend as the energy decreased below the barrier. This rise in the real CFP strength was accompanied by a non-vanishing trend in the imaginary CFP strength.
Generally, the analyses conducted within the SPP and CFP revealed the necessity of reducing the real potential strength to accurately reproduce the data under consideration. This observed behavior originates from the strong coupling to the 7Li breakup continuum states, which generates a repulsive DPP. Two different strategies were followed for modeling the coupling effects: by introducing an additional DPP and by carrying out the full microscopic CDCC method. The CDCC computations revealed that the coupling to the resonant states has the most significant contribution. The analyses also showed that both the 7Li breakup and the triton transfer mechanism have significant impacts on the elastic channel data.
Dynamics of 7Li breakup and its influence on elastic scattering: a study of 7Li + 144Sm system
- Received Date: 2023-09-07
- Available Online: 2024-02-15
Abstract: The angular distributions of 7Li + 144Sm elastic scattering over the energy range of 21.6–52 MeV are reanalyzed utilizing various interaction potentials. The analysis aims to study the consistency of the implemented potentials in representing the considered data and investigate the cluster nature of the weakly bound 7Li projectile. This will aid in the better understanding the impacts of 7Li breakup on the elastic scattering channel. Strong coupling to the breakup channel has a substantial impact on the elastic data and reproduces a repulsive dynamical polarization potential, which drastically diminishes the real potential strength. This reported impact was simulated by introducing a semi-microscopic repulsive DPP and by implementing the method of continuum discretized coupled channels. The analysis was also extended to understand the impact of triton transfer on the elastic scattering data.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: