-
Dynamical chiral symmetry breaking is an important feature of quantum chromodynamics (QCD). With the rapid development of heavy ion experiments and observation in astronomy, restoration of chiral symmetry and deconfinement phase transitions are expected to occur in ultra-relativistic heavy-ion collisions or in the interior of neutron stars [1−4]. Many famous research institutions, such as FAIR GSI, NICA JINR, and J-PARK, have conducted experiments to study the properties of high-density matter, which may help clarify the phase structure of quark matter.
As a gauge theory at short distances, perturbative QCD is a remarkably successful and rich theory of strong interactions. However, many physical phenomena at long distances must be addressed using non-perturbative methods; in particular, when handling problems related to low-energy physics, the non-perturbation model is highly useful. In many effective models, pions play a crucial role because they occupy a special place in nuclear and particle physics. In the standard picture, pions are described as (pseudo-) Nambu-Goldstone bosons, which arise as a consequence of the dynamical breakdown of chiral symmetry [5, 6]. In the chiral limit, where the masses of the two lightest quarks are turned off, the pion mass is zero. When chiral symmetry is broken spontaneously, the quark condensate represents the leading order parameter. Nambu-Goldstone bosons can interact if they carry momentum. Weinberg's low energy theorems state that pion-pion scattering lengths are related to pion mass via
$ a_0\sim7M_\pi^2/(32\pi f_\pi^2) $ and$ a_2\sim-M_\pi^2/(16\pi f_\pi^2) $ . In the chiral limit, the pion-pion S-wave scattering lengths vanish, and these quantities can be used as sensitive probes of chiral symmetry breaking.Pion-pion scattering, as one of the most fundamental hadronic processes of QCD at the mesonic level, provides a direct link between the theoretical formalisms of chiral symmetry and experiments. Most calculations to date have been performed in the infinite volume limit [7−13]. Studies on the chiral phase transition are focused on the influence of temperature, baryon density, and other external parameters such as the magnetic field [14−17]. However, the quark-gluon plasma (QGP) system produced by heavy-ion collision experiments always has a finite size. The volume of homogeneity before freeze out for Au-Au and Pb-Pb collisions is approximately
$50 -250$ fm3. It is estimated that the volume of the smallest QGP system may be as low as (2 fm)3 [18], motivated by the estimated plasma size potentially formed in high-energy nucleus-nucleus collisions at the RHIC [1]. Studies show that chiral behavior depends on the volume size of quark matter and chiral symmetry breaking is closely related to finite volume effects in QCD [19−22]. Furthermore, the effect of finite size on the dissociation and diffusion of chiral partners, the phase structure of the NJL model in D = 3 Euclidean dimensions, and the viscosity, bulk viscosity, electrical conductivity has been investigated [23−25].Because pion mesons play an important role in low-energy physics, it is worth clarifying their behaviors via extrapolation to high temperatures and small volume sizes.
The chiral phase transition of a finite system depends on the choice of boundary conditions [26, 27]. For quark fields, the time direction is constrained by an anti-period requirement, but the choice of boundary conditions in the spatial direction is significant. Typical boundary conditions are the anti-period boundary condition (APBC) and period boundary condition (PBC), which are used to weaken the impact from the physical boundary.
In this study, the proper time regularization scheme is adopted [28]. The benefit of using proper time regularization is that we can perform the sum over the thermal Matsubara frequencies analytically. Unlike most previous studies that used a cutoff scheme, we first use proper time regularization to study the pion-pion scattering length at a finite volume size. We expect to extract the signals of chiral phase transition from pion-pion interactions in a hot medium while considering the finite volume effect.
The paper is organized as follows. In Section II, the volume and temperature dependences of the effective quark mass are deduced using the Nambu–Jona-Lasinio (NJL) model under proper time regularization. In Section III, the equations for the meson mass and pion decay constant at finite volume are obtained. We also provide numerical results and analyze them in detail. The scattering length formula and its corresponding numerical results are presented in Section IV, followed by a short conclusion in Section V.
-
We use a two-flavor NJL Lagrangian model, which is motivated by the symmetries of QCD, to describe the coupling between quarks and the chiral condensate in the scalar-pseudoscalar sector. It reads as [29, 30]
$ \begin{aligned}[b] \mathcal{L}_{NJL} =&\bar \psi ({\rm i}\gamma_\mu \partial^\mu- m_q)\psi \\ &+G[(\bar \psi \psi)^2+(\bar \psi {\rm i}\gamma_5\tau \psi)^2], \end{aligned} $

(1) where
$ m_q $ is the current quark mass of flavor q, and G is the four quark effective coupling. In the limit of exact isospin symmetry,$ m_u=m_d=m $ . The pion mass can be exploited through the effective interaction for the exchange of a pion in the random-phase approximation.The second term of the four quark interaction in Eq. (1) is responsible for exciting the pion as an isovector pseudoscalar. In the mean field approximation, the effective quark mass is
$ \begin{array}{*{20}{l}} M=m+\sigma \end{array} $

(2) with
$ \begin{array}{*{20}{l}} \sigma=-2G\langle { \bar \psi \psi} \rangle \end{array} $

(3) and the two-quark condensate is defined as
$ \langle { \bar \psi \psi} \rangle=-\int \frac{{\rm d}^4p}{(2\pi)^4}{\rm Tr} [S(p)], $

(4) where
$ S(p) $ is the dressed quark propagator, and the trace is taken in the color, flavor, and Dirac spaces.The integration of Eq. (4) is ultraviolet divergent. For simplicity, a cutoff is typically applied on the momentum integration, which is valid when the cutoff is larger than the relevant momenta. We use proper time regularization [16, 31−35] for two reasons. First, we work with a PBC or APBC; however, the cutoff on the momentum breaks the symmetry in the spatial direction. Second, a translation of the quark momentum is required to obtain the equation of meson mass, which requires the cutoff to tend to infinity. The proper time method can overcome these difficulties by introducing a new integration. Under this type of regularization scheme, the trace term in Eq. (4) is replaced by an integral with a suitable choice of the cutoff function. Here, in the quark gap equation, the key equation is the replacement
$ \frac{1}{A^n } \rightarrow \frac{1}{(n-1) !}\int_{\tau_{\rm UV}}^ {\tau_{\rm IR}} {\rm d}\tau \tau^{n-1} {\rm e}^{-\tau A }. $

(5) Here,
$\tau_{\rm UV}$ is introduced to regularize the ultra-violet divergence, and an infrared cutoff$\tau_{\rm IR}$ is adopted, which also appears in Refs. [35, 36].Using a Wick rotation, the two quark condensate at infinite volume and zero temperature can be written as
$ \begin{aligned}[b] \langle { \bar \psi \psi} \rangle=&-N_cN_f\int\frac{{\rm d}^4p}{(2\pi)^4}\frac{4M}{p^2+M^2} \\ =&-24M\int^\infty_{-\infty} \frac{{\rm d}^4p}{(2\pi)^4}\int^ {\tau_{\rm IR}}_{\tau_{\rm UV}} {\rm d}\tau {\rm e}^{-\tau(p^2+M^2)} \\ =&-\frac{3M}{2\pi^2}\int^ {\tau_{\rm IR}} _{\tau_{\rm UV}} {\rm d}\tau\frac{ {\rm e}^{-\tau M^2}}{\tau^2}, \end{aligned} $

(6) where the color number is
$ N_c=3 $ and the flavor number is$ N_f=2 $ . At non-zero temperature, the quark four-momentum is replaced by$ p_k=(\vec{ p}, \omega_k) $ , with$ \omega_k=(2k+1)\pi T $ ,$ k \in \mathbb{Z} $ . The integration on the fourth momentum in Eq. (6) is replaced by a sum of all the fermion Matsubara frequencies$ \omega_k $ . The two-quark condensate is given by$ \begin{aligned}[b] \langle { \bar \psi \psi} \rangle=&-24M \int^ {\tau_{\rm IR}} _{\tau_{\rm UV}} {\rm d}\tau {\rm e}^{-\tau M^2} \\ & \times \bigg[T\sum\limits^\infty_{k=-\infty}\int^\infty_{0} \frac{{\rm d}p}{2\pi^2} \vec{p}^2 {\rm e}^{-\tau( \vec{p} ^2+\omega_k^2)}\bigg] \\ =&-\frac{3MT}{\pi^{3/2}}\int^ {\tau_{\rm IR}} _{\tau_{\rm UV}} {\rm d} \tau\frac{ {\rm e}^{-\tau M^2}}{\tau^{3/2}}\theta_2(0,{\rm e}^{-4\pi^2\tau T^2}), \end{aligned} $

(7) where the Jacobi function is defined as
$ \theta_2(0,q)= 2\sqrt[4]{q}\sum\nolimits_{n=0}^\infty q^{n(n+1)}. $ Then, the quark mass is$ M=m+\frac{6GMT}{\pi^{3/2}}\int^ {\tau_{\rm IR}} _{\tau_{\rm UV}} {\rm d}\tau\frac{ {\rm e}^{-\tau M^2}}{\tau^{3/2}}\theta_2(0,{\rm e}^{-4\pi^2\tau T^2}). $

(8) For a specific boundary condition of finite volume, the quark momentum is discretized and the integral over all spatial momenta is replaced by a sum over discrete momentum modes. Considering a cubic box with volume size L, the discrete momenta that depend on the boundary conditions are
$ \vec{p}_{\rm PBC}^2=\frac{4\pi^2}{L^2}\sum\nolimits_{i=1}^{3}n_i^2, \qquad n_i=0,\pm 1,\pm 2\cdots, $

(9) $ \vec{ p}_{\rm APBC}^2=\frac{4\pi^2}{L^2}\sum\nolimits_{i=1}^{3}\left(n_i+\frac{1}{2}\right)^2,\quad n_i= \pm 1,\pm 2\cdots $

(10) for the PBC and APBC, respectively. The integration measure is replaced by the sum of discrete momentum by replacing
$ \int {\rm d} p \left(\cdots\right)\rightarrow \frac{2\pi}{L}\sum\limits_{ n_i }\left( \cdots\right). $

(11) Then, the quark mass is constrained by
$ \begin{aligned}[b] M=&m+48GM\int^ {\tau_{\rm IR}} _{\tau_{\rm UV}} {\rm d}\tau {\rm e}^{-\tau M^2}\\ & \times \bigg[T \sum\limits^\infty_{k=-\infty}{\rm e}^{-\tau \omega_k^2}\prod \limits_{i=1}^3 \sum\limits_{n_i } {\rm e}^{-\tau p_i^2}\bigg] \\ =& m+48GMT\int^ {\tau_{\rm IR}}_{\tau_{\rm UV}} {\rm d}\tau {\rm e}^{-\tau M^2}\\ &\times \theta_2(0,{\rm e}^{-4\pi^2\tau T^2}) \left[\frac{f(\theta)}{L}\right]^3, \end{aligned} $

(12) with
$ \begin{array}{*{20}{l}} { f(\theta) }=\left\{ \begin{array}{l} { \theta_2(0,{\rm e}^{-4\tau \pi^2/L^2}) \qquad \qquad \text{for APBC,}} \\ {\theta_3(0,{\rm e}^{-4\tau \pi^2/L^2}) \qquad \qquad \text{for PBC.}} \\ \end{array} \right. \end{array} $

(13) Here,
$ \theta_3(0,q)=1+2\sum\nolimits_{n=1}^\infty q^{n^2} $ , and$ \theta_2 $ is defined as before. Although the momentum integrals are given by two different functions, these two functions approach the same limit as L increases to a very large value. Thus, the quark mass does not depend on the boundary condition in the infinite volume limit. -
The pion, which is associated with exact
$S U_L(2)\times S U_R(2)$ symmetry, occupies a special place in nuclear and particle physics. It is the most relevant degree of freedom in the low energy regime of the strong interaction and is both a (pseudo-)Nambu-Goldstone boson and quark-antiquark bound-state. The pion mass and decay constant are measures of the strength of chiral symmetry breaking [5, 13].In the Lagrangian of Eq. (4), the four quark interaction term
$ (\bar \psi \psi)^2 $ is associated with the scalar σ meson, whereas the term$ (\bar \psi i\gamma_5\tau \psi)^2 $ is associated with the π meson. By comparing with the amplitude of$ qq $ scattering for the exchange of a pion, the meson mass is deduced from the proper polarization insertion of the four quark interaction. In the random phase approximation, the polarization insertion is related to the quark propagator via$ \begin{aligned}[b]& \Pi_{ps}(k^2)\delta_{\alpha\beta} =\\& -{\rm i}\int\frac{{\rm d}^4p}{(2\pi)^4}{\rm Tr}[{\rm i}\gamma_5T_\alpha {\rm i} S(p+k/2) {\rm i}\gamma_5T_\beta {\rm i} S(p-k/2)].\end{aligned} $

(14) Here,
$ T_i $ acts on the external quarks, p is the quark momentum, and k is the meson momentum. The trace is taken in Dirac, flavor, and color space. Then, the meson mass is the solution of$ \begin{array}{*{20}{l}} 1-2G\Pi_{ps}(k^2=m^2)=0, \end{array} $

(15) and the effective coupling strength between the pion meson and quarks
$ g_{\pi qq} $ is defined as$ g_{\pi q q}^{2}=({\partial \Pi_{ps}}/{\partial k^2})^{-1}\big|_{k^2=m^2}. $

(16) Performing the trace in Eq. (14), the proper polarization is
$ \begin{aligned}[b] \Pi_{ps}(k^2) =&-4{\rm i}N_cN_f\int\frac{{\rm d}^4p} {(2\pi)^4} \\ &\times \frac{M^2+p^2-k^2/4}{[(p+k/2)^2-M^2][(p-k/2)^2-M^2]}.\; \; \end{aligned} $

(17) After applying appropriate shifts of the quark momentum, we obtain
$ \begin{aligned}[b] \dfrac{1}{i}\Pi_{ps}(k^2) =& 4N_cN_f\int\frac{{\rm d}^4p} {(2\pi)^4} \frac{1}{p^2-M^2} \\ &-2N_cN_f k^2I(k) \end{aligned} $

(18) with
$ I(k)=\int\frac{{\rm d}^4p}{(2\pi)^4}\frac{1}{[(p+k)^2-M^2](p^2-M^2)}. $

(19) Comparing Eq. (4) with Eq. (18), we have
$ 2G\Pi_{ps}=1-\frac{m}{M}+4 {\rm i} GN_cN_fm_{\pi}^2 I(m_{\pi}^2). $

(20) By inserting it into Eq. (15), the mass of the pion meson is deduced with
$ m_\pi^2=-\frac{m}{M}\frac{1}{4{\rm i} GN_cN_f I(m_{\pi}^2)}. $

(21) The meson mass is proportional to the current quark mass and depends on the effective quark mass. In the chiral limit with
$ m=0 $ , the meson mass is$ m_\pi^2=0 $ .Now, the main task is to integrate
$ I(k) $ . After Wick rotation, the calculation on$ I(k) $ is available by introducing the Feynman parameters, which gives$ \begin{aligned}[b] I(k)=&\int_0^1 {\rm d}z \int\frac{{\rm d}^4p}{(2\pi)^4}\\ & \times \frac{1}{ \{[p - k (1 - z)]^2 - M^2 + k^2 (1 - z) z\}^2}. \end{aligned} $

(22) In the proper time scheme, we have
$ \begin{aligned}[b] I(m_\pi^2)=&\int_0^1 {\rm d}z \int_{\tau_{\rm UV}}^{\tau_{\rm IR}} {\rm d}\tau \int\frac{{\rm d}^4p}{(2\pi)^4} \\ &\times { \tau {\rm e}^{-\tau[ p ^2 + M^2 -m_\pi^2 (1 - z) z]}}. \end{aligned} $

(23) At nonzero temperature and finite volume size, the discretization in the temporal and spatial directions gives
$ \begin{aligned}[b] I(m_\pi^2)=&T\int_0^1 {\rm d} z \int_{\tau_{\rm UV}}^{\tau_{\rm IR}}{\rm d}\tau {\rm e}^{-\tau [M^2 -m_\pi^2 (1 - z) z]}\\ &\times \tau \theta_2(0,{\rm e}^{-4\pi^2\tau T^2}) \left[\frac{f(\theta)}{L}\right]^3, \end{aligned} $

(24) where
$ f(\theta) $ is defined as in Eq. (13).The pion decay constant is an important quantity in low energy phenomena and can be extracted from measurements of the decay
$ \pi^-\to\mu^-+\nu_\mu $ . From vacuum to one pion and axial vector current matrix element$ \left<0 \left| J^i_{5\mu}\right|\pi^j\right> $ , the decay constant is given by$ \begin{aligned}[b] {\rm i} k_\mu f_\pi\delta^{ij}=&-N_cg_{\pi qq } \int\dfrac{{\rm d}^4p}{(2\pi)^4}{\rm tr}[\gamma_\mu\gamma_5 \\ & \times S\left(p+\frac{1}{2}k \right)\gamma_5S \left(p-\frac{1}{2}\right)k]. \end{aligned} $

(25) Using the relation
${\rm tr}\, \tau ^i\tau^j=2\delta^{ij}$ and performing the traces over spin labels yields$ {\rm i} k_\mu f_\mu=N_c g_{\pi qq}4 Mk_\mu I(k^2). $

(26) The effective coupling
$ g_{\pi qq} $ is obtained by substituting Eq. (18) into Eq. (16). Then, the square of the decay constant is$ \begin{array}{*{20}{l}} f_\pi^2=-4{\rm i} N_cN_fM^2\dfrac{I^2(m_\pi)}{I(0)+I(m_\pi)-m_\pi^2K(m_\pi)}. \end{array} $

(27) The equation for the pion decay constant, independent of the regularization scheme, is related to the quark mass. We can obtain the relation
$ \begin{array}{*{20}{l}} f_\pi^2g_{\pi qq}^2=4M^2\dfrac{I^2(m_\pi)}{[I(0)+I(m_\pi)-m_\pi^2K(m_\pi)]^2}. \end{array} $

(28) The function K is defined as
$ K(k)=\int\frac{{\rm d}^4p}{(2\pi)^4}\frac{1}{[(p+k)^2-M^2](p^2-M^2)^2}, $

(29) and it can be calculated through
$ I(k) $ using$ \begin{array}{*{20}{l}} K(k)=\dfrac{1}{k^2-4M^2}\left[12M^2 \dfrac{{\rm d}I}{{\rm d}k^2}(0)-I(k)+I(0)\right]. \; \; \end{array} $

(30) However, to calculate the function
$ K(k) $ and the function$ L(k) $ directly from Eq. (29), we can use the following Feynman parameter formula:$ \begin{aligned}[b] \dfrac{1}{A^nB^m}=&\dfrac{(n+m-1)!}{(n-1)!(m-1)!} \\ &\times \int_0^1 {\rm d} x\dfrac{x^{n-1}(1-x)^{m-1}}{[Ax+B(1-x)]^{n+m}}. \end{aligned} $

(31) For an approximation, taking the function
$ I(k) $ as a smooth function of$ k^2 $ , we have$ K(k)=0 $ . Then, the decay constant is simplified to [30]$ f_\pi^2=-4 {\rm i}N_cN_fM^2I(0). $

(32) Because the meson mass is small, the combination of Eq. (21) for the pion mass with Eq. (32) for the decay constant gives
$ m_\pi^2f_\pi^2=mM(N_fG)^{-1}. $

(33) Comparing it with Eq. (2) and Eq. (3) for a small m, we have
$ m_\pi^2f_\pi^2=-m\left<\bar\psi\psi \right>, $

(34) which is the lowest order approximation to the current algebra result and is known as the Gell-Mann–Oakes–Renner (GOR) relation [37].
The parameters we use in this study are
$ m=4.8 $ MeV,$ G=3.19*10^{-6} $ MeV$ ^{-2} $ ,$ \tau_{\rm UV}=1/1080^{2} $ MeV$ ^{-2} $ , and$ \tau_{\rm IR}= 1/190^{2} $ MeV$ ^{-2} $ . In this parameter set, the effective quark mass is 202.3 MeV and the pion meson mass is 135.1 MeV. The quark mass scaled to the mass at zero temperature is only slightly dependent on different sets of parameters [35], and we do not set the coupling G as dependent on the volume size L and other properties. The corresponding decay constant$ f_\pi =93.0 $ MeV, and from Weinberg's formula, the scalar pion-pion scattering lengths in units of$ m_\pi^{-1} $ are$ a_0=0.147 $ and$ a_2=-0.042 $ .Figures 1 and 2 show the pion mass and decay constant as functions of temperature with different cubic volume sizes, respectively. The pion mass increases and the decay constant decreases as temperature increases. Data with volume size L larger than 5 fm are close to the infinite volume limit.
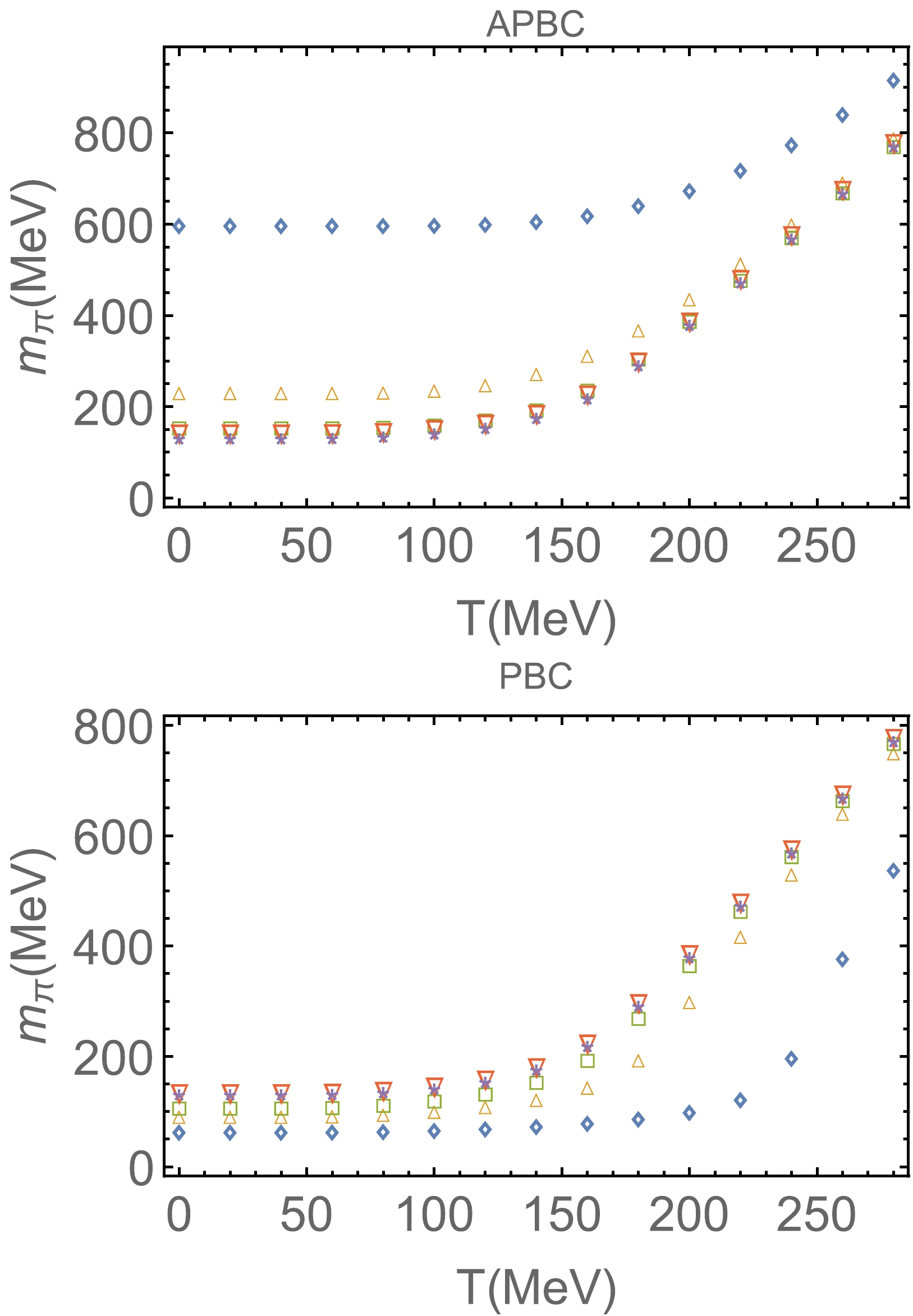
Figure 1. (color online) Pion meson mass as a function of temperature with different boundary conditions and volume sizes. The plot markers
$ \Diamond, \Delta,\square, \nabla $ , and$ \star $ denote the volume size$ L=1 $ , 1.5, 2, 3, and 5 fm, respectively.
Figure 2. (color online) Decay constant as a function of temperature with different boundary conditions and volume sizes. The plot markers
$ \Diamond, \Delta,\square, \nabla $ , and$ \star $ denote the volume size$ L=1 $ , 1.5, 2, 3, and 5 fm, respectively.The GOR relation only holds well at low temperature and in the infinite volume limit. On the right hand side of the GOR relation in Eq. (34), the current quark mass originates from the Higgs mechanism, which does not depend on the size effect and is a constant parameter in the NJL model. The chiral symmetry is almost restored at high temperature and finite size; hence, the quark condensate is close to zero. Then, the right hand side of the GOR equation is almost temperature and volume size independent. However, on the left hand side of the equation, the pion mass multiplied by the decay constant still depends on T, which results in the GOR no longer holding.
Furthermore, with a different choice of boundary conditions, the influences of volume size on the mass and decay constant are different. This will also reflect on the scattering length.
When the temperature increases, the effective quark mass decreases and the pion mass increases. Because
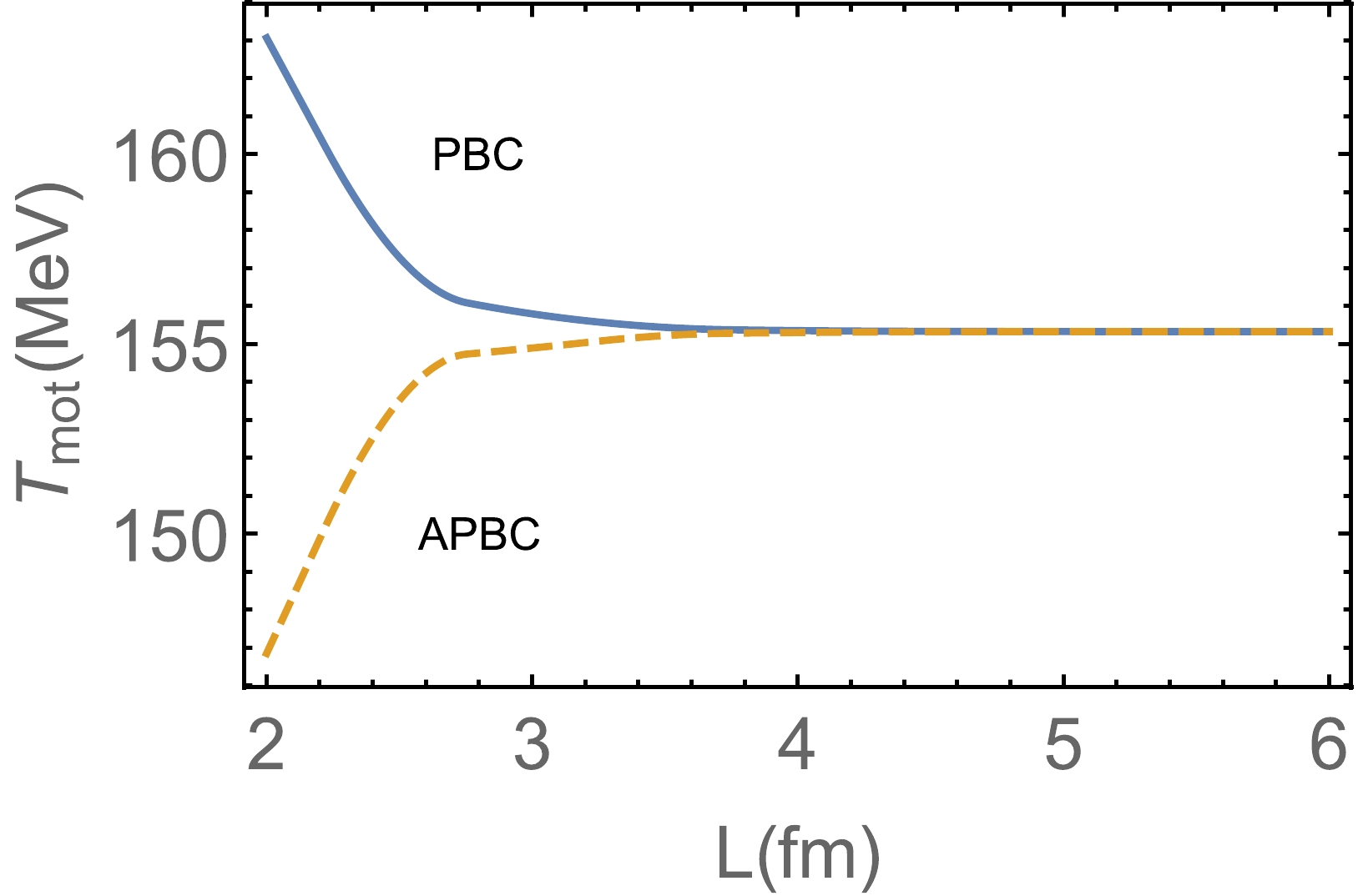
$ m_q(T) $ =$ 2M(T) $ , which means that the pion can dissociate into a constituent quark and an antiquark, it defines the Mott temperature$T_{\rm Mott}$ of the pion meson. As shown in Fig. 3, the Mott temperature is approximately 155 MeV in the infinite volume limit. In Fig. 3, we present the Mott temperature as a function of volume size for the PBC and APBC. The Mott temperature decreases (increases) with decreasing volume size for the APBC (ABC), which may suggest that when the effect of volume size cannot be neglected, the APBC is favored at relatively low temperatures to obtain QGP. -
From Weinberg's low energy theorems [38], the pion scattering lengths are related to the pion mass and decay constant, which also represents a symmetry breaking effect. The scattering of a pion by pions involves only the lightest pseudoscalar modes. It provides a direct link between the theoretical formalism of chiral symmetry and experiment.
Three isospin channels are available for the pion-pion scattering process. The invariant scattering amplitude
$ \left(\Pi^a\Pi^b\to\Pi^c\Pi^d \right) $ can be written as$ \begin{aligned}[b] T_{ab,cd}(k,p\to k',p')=&A(s,t,u)\delta_{ab}\delta_{cd} \\ & +B(s,t,u)\delta_{ac}\delta_{bd}+C(s,t,u)\delta_{ad}\delta_{bc}, \end{aligned} $

(35) with incoming momenta
$ (k,p,k',p') $ and isospin indices$ (a,b,c, d) $ . The Mandelstam variables s, t, and u are defined as$ s=(k+p)^2 $ ,$ t=(k-k')^2 $ , and$ u=(k-p')^2 $ . Six diagrams (box and σ-propagation) contribute to pion-pion scattering at tree level, which can be found in Refs. [7−10]. We present them in Fig. 4.The scattering lengths at the kinematic threshold are
$ \begin{array}{*{20}{l}} a_i=\dfrac{1}{32\pi}A_i(s=4m_\pi^2,t=0,u=0), \end{array} $

(36) with the three isospin amplitudes
$ \begin{array}{*{20}{l}} A_0=3A+B+C,\quad A_1=B-C,\quad A_2=B+C.\; \; \; \end{array} $

(37) Here, A, B, and C can be calculated from
$ T_a $ ,$ T_b $ ,$ T_c $ ,$ T_d $ ,$ T_e $ , and$ T_f $ , which correspond to the amplitudes of the six scattering diagrams. From these diagrams, we have$ T_a=T_b $ and$ T_e=T_f $ . Then, A, B, and C in Eqs. (35) and (37) are given by$ \begin{array}{*{20}{l}} A=2T_a-T_c+T_d,\quad B=C=T_c+T_d. \end{array} $

(38) Because
$ B=C $ , we have$ A_1=0 $ . Therefore,$ a_1 $ cannot be calculated in this study. The nonzero amplitudes are$ \begin{array}{*{20}{l}} A_0=6T_a-T_c+3T_d+2T_e \end{array} $

(39) and
$ \begin{array}{*{20}{l}} A_2=2(T_c+T_e). \end{array} $

(40) Note that in most studies, a superscript is used to indicate the different isospins. Because we only consider the s-wave scattering length and to avoid confusion with power exponents, we use a subscript to distinguish the different isospin scattering lengths, as in Ref. [9].
The six
$ T_i $ values corresponding to the scattering diagrams are$ T_a = \dfrac{4N}{i}g_{\pi q q}^4[k^2K(k)-I(0)-I(k)], $

(41) $ T_c = \dfrac{8N}{i}g_{\pi q q}^4 [2k^2K(k)-I(0)-\dfrac{1}{2}k^4L(k)], $

(42) $ T_ d= \dfrac{8N}{i}g_{\pi q q}^4\dfrac{I^2(k)}{(1-k^2/M^2)I(2k)+k^2/(4M^2)I(k)}, $

(43) $ T_e =\dfrac{8N}{i}g_{\pi q q}^4\dfrac{[I(0)-k^2K(k)]^2}{I(0)+k^2/(4M^2)I(k)}, $

(44) with
$ T_b=T_a $ and$ T_f = T_e $ . Here,$ L(k) $ is given by$ L(k) =\int\frac{{\rm d}^4p}{(2\pi)^4}\frac{1}{[(p+k)^2-M^2]^2(p^2-M^2)^2}. $

(45) From Eq. (28),
$ g_{\pi qq}^4 $ is given as$ g_{\pi qq}^{-4} =-N_c^2N_f^2[I(0)+I(k)-m_\pi^2K(k)]^2. $

(46) Here,
$ k^2=m_\pi^2 $ . After performing the calculations of$ I(k) $ ,$ L(k) $ , and$ K(k) $ , the scattering lengths in Eq. (36) can be obtained.The numerical results are presented in Figs. 5 and 6 for the PBC and APBC, respectively. The scattering lengths are calculated as a function of temperature at several volume sizes. At volumes larger than 5 fm, the curve is close to the infinite volume limit. The results is similar to the results with cutoff regularization, that is,
$ a_0 $ and$ a_2 $ vary slowly at first and then exhibit steep singularity near the Mott temperature [8, 10]. The difference results of the two regularizations appear beyond the Mott temperature. In the cutoff regularization, there are no results beyond the Mott temperature because the chiral phase transition is of the first order. In proper time regularization, the chiral phase transition is a crossover. Therefore, the effective quark mass and scattering lengths can have continuous values beyond the Mott temperature or pseudo critical temperature of the chiral phase transition.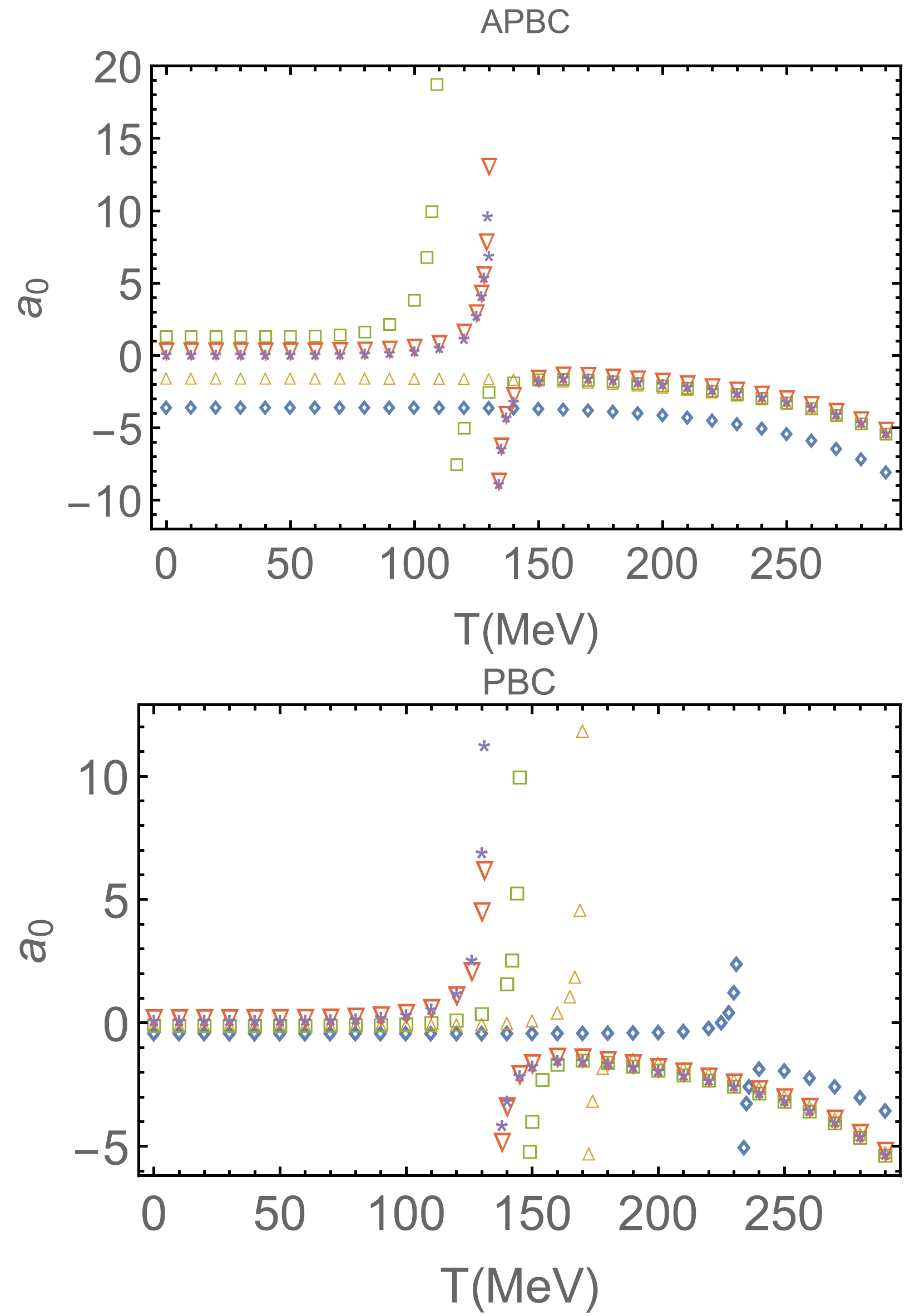
Figure 5. (color online) Scattering lengths
$ a_0 $ for the (anti-) period boundary condition. The plot markers$ \Diamond, \Delta,\square, \nabla $ , and$ \star $ denote the volume size$ L=1,~ 1.5,~ 2,~ 3 $ , and 5 fm, respectively.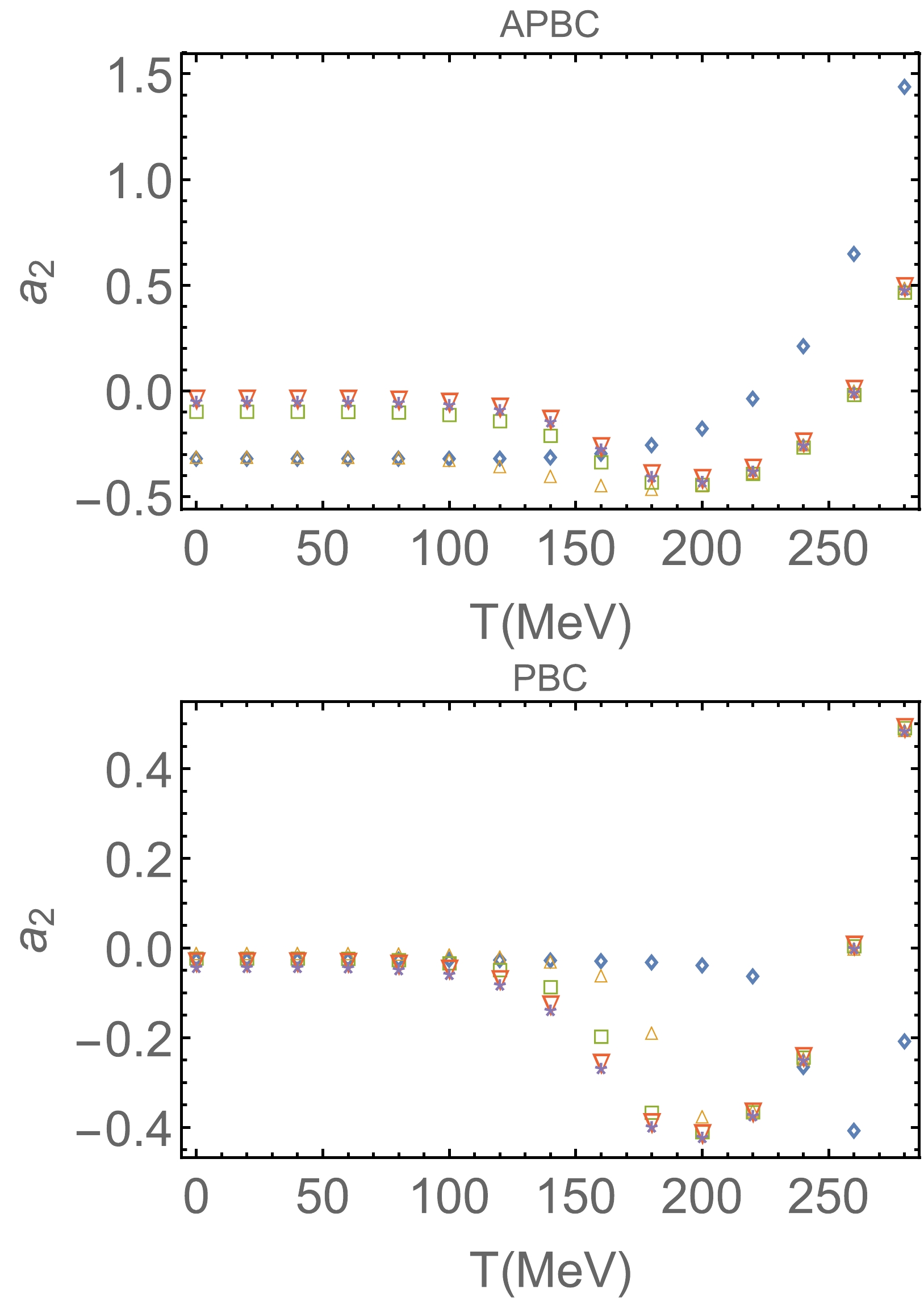
Figure 6. (color online) Scattering lengths
$ a_2 $ for the (anti-) period boundary condition. The plot markers$ \Diamond, \Delta,\square, \nabla $ , and$ \star $ denote the volume size 1, 1.5, 2, 3, and 5 fm, respectively.The scattering lengths reveal different behaviors as the volume size decreases for the two types of boundary conditions. This can be expected from the behaviors of the quark mass, meson mass, and decay constant with varying volume size. Direct analysis of Weinberg's formula
$ a_0\sim7M_\pi^2/(32\pi f_\pi^2) $ with the results of$ M_\pi $ and$ f_\pi $ , shown in Figs. 1 and 2, reveals that the scattering length$ a_0 $ at temperatures lower than the pseudo critical temperature increases as the volume size decreases for the APBC but decreases as the volume size decreases for the PBC. The same analysis can be used for$ a_2 $ with$ a_2\sim-M_\pi^2/ (16\pi f_\pi^2) $ . However, as shown in Fig. 5,$ a_0 $ increases and then decreases as volume size decreases at low temperature.The scattering length
$ a_0 $ exhibits a jump when the volume size is not sufficiently small. We define this jump as the pseudo critical temperature ($ T_c $ ), which is lower than the Mott temperature. For the PBC, the jump position in the$ a_0 $ curve increases as volume size decreases and the jump always exists. For the APBC,$ T_c $ in the$ a_0 $ curve decreases as volume size decreases. When the volume size in sufficiently small, the jump disappears. When the volume size is sufficiently large and the temperature is less than$ T_c $ , the scattering length$ a_0 $ is larger than zero and increases with temperature; when the temperature is larger than$ T_c $ , the scattering length$ a_0 $ is less than zero and first increases and then decreases as temperature increases.The scattering length
$ a_0 $ can be negative at small volume sizes, which can be used to examine the existence of a phase transition. Unlike the PBC, for the APBC,$ a_0 $ is a continuous function of temperature at$ L=1 $ fm, which may be because chiral symmetry is partly restored at small finite volume [27]. Because the volume of the smallest QGP system can be as low as (2 fm)$ ^3 $ [18], a continuous scattering length$ a_0 $ can serve as a criterion for testing volume effects and different boundary conditions.The scattering length
$ a_2 $ is always a connected function of temperature and is also different from the cut off results. At very small volume sizes, the scattering length$ a_2 $ monotonically increases. As the volume size gradually increases,$ a_2 $ first decreases with temperature and then increases. A minimum exists but does not occur at$ T_c $ .For the cut off regularization scheme,
$ a_0 $ increases within a narrow area near the Mott temperature, and no data exist beyond the Mott temperature for$ a_0 $ and$ a_2 $ [8, 10]. -
In this study, we investigate the temperature and volume size dependence of the pion decay constant and pion-pion scatterings for different boundary conditions. We show the chiral phase transition of quark matter at finite temperature and in finite spatial volume. Under proper regularization, the phase transition indicated from the effective quark mass is a crossover, which differs from the results of cutoff regularization, where the phase transition is of the first order, and the pi-pi scattering length
$ a_0 $ with temperature beyond the Mott temperature varies between the two regularization schemes.The calculated pi-pi scattering lengths
$ a_0 $ and$ a_2 $ in finite spatial volume exhibit different behaviors for different boundary conditions. Although we cannot determine which boundary condition is the best, the results deserve further attention.Pion-pion scattering, as one of the most fundamental hadronic processes of QCD at the mesonic level, may serve as a tool to verify different boundary conditions and regularization schemes, and we hope the results obtained here will be verified using other theoretical methods.
-
The authors thank the Chinese Institute of High Energy Physics and Prof. Huang Mei for authorizing the download of the doctoral dissertation.
Temperature and volume dependence of pion-pion scattering lengths
- Received Date: 2023-10-13
- Available Online: 2024-02-15
Abstract: The s-wave pion-pion scattering lengths






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: