-
Evidence of the accelerated expansion of the Universe comes from studies of Supernova Type Ia (SNeIa), the Cosmic Microwave Background (CMB), and Baryon Acoustic Oscillations (BAO) [1−3]. Dark energy (DE) is a peculiar type of energy density proposed to explain this elusive phenomenon in the framework of General Relativity (GR). It is associated with significant negative pressure. According to the most current CMBR data, our cosmos comprises 76% DE. The Universe's expansion is slowed by a massive amount of ordinary matter, but exotic energy sources can dramatically alter the Universe's behavior. A reconstruction technique targeted at building DE models has been supported by several cosmologists [4]. However, other researchers have examined the relationship between the magnitude and redshift of Type Ia supernovae [5]. The fundamental ideas of DE depend on Einstein's theory of gravity. The equation of state
$ (\omega) $ , which coincides with the cosmological constant on the right side of Einstein's field equation, causes the Universe to accelerate late in time. A possible replacement for DE is the mathematical concept of the cosmological constant, which explains the impact of vacuum energy on the curvature of space-time. Nevertheless, it encounters difficulties such as coincidence and fine-tuning problems [6]. The Equation of State (EoS) parameter is defined as$ \omega= {p}/{\rho} $ . Several researchers have proposed that when the EoS parameter approaches$ \omega=-1 $ , the Universe enters an expanded stage. The EoS parameter$ \omega $ characterises different cosmic eras: We can denote a stiff fluid with$ \omega=1 $ , the matter-dominated epoch with$ \omega=0 $ , the radiation-dominated stage with$ \omega= {1}/{3} $ , the quintessence stage with$ -1<\omega\leq - {1}/{3} $ , the phantom model with$ \omega<-1 $ , and the$ \Lambda $ CDM model with$ \omega=-1 $ [7].Several alternative theories that do not employ the cosmological constant have been proposed to determine the acceleration period of the Universe. Based on modifications to Einstein's GR, such alternate theories of gravity are commonly referred to as modified gravity theories. Modified gravity is an appealing hypothesis because it offers significant solutions to many basic questions about DE and the late time speeding Universe. Innovative approaches in agreement with recent observational data can be obtained from DE models based on modified gravity. Models such as
$ f(R) $ gravity [8],$ f(G) $ , also known as Gauss-Bonnet gravity [9], were discovered as a result of modifications in the geometry of space-time. Other models that have been discovered include Lovelock gravity [10], scalar-tensor theories [11], and braneworld models [12]. The non-metricity-derived$ f(Q) $ gravity may offer a plausible alternate method to create different types of modified gravities [13, 14]. Although the modified theories are identical at the equation level, the multiple types of aforementioned modified gravity result from concepts of curvature, torsion, and non-metricity. This is because, in contrast to the standard Levi-Civita Ricci scalar$ \overset{\circ}R $ in GR, the torsion scalar T and non-metricity scalar Q have a total divergence term, which results in equations such as$ \overset{\circ}R=-T+B $ and$ \overset{\circ}R=Q+C $ . This demonstrates that there is an insufficient complete derivative between the arbitrary functions$ f(\overset{\circ}R) $ ,$ f(T) $ , and$ f(Q) $ . With teleparallel gravities, the boundary B can be incorporated within the Lagrangian to generate$ f(T, B) $ hypotheses that intrinsically have interesting phenomenology [15]. Nevertheless, in the non-metricity paradigm, the significance of C is absent from the Lagrangian of symmetric teleparallel gravity. The$ f(Q, C) $ hypothesis thus established continues to be of interest to cosmologists [16, 17].In addition to the deficiencies of the standard cosmological model, many unanswered questions from observations remain. For instance, the
$ \Lambda $ CDM model was modified in certain studies by incorporating a dynamic DE model with$ H_{2.34} $ data. In [18, 19], multiple hypotheses that enable the development of DE theories based on BAO, CMB, and SN data are evaluated, and dynamic DE models are matched using$ H_{2.34} $ data. A lower value than predicted by the$ \Lambda $ CDM model is observed for the Hubble parameter's observed value with a redshift of$ z=2.34 $ in BOSS data [20]. Developing a model of the Universe that includes novel empirical forms of DE-dark matter (DM) interaction is the primary objective of this paper. Our research focuses on cosmological expansion in an instance in which both DE and MD interact. Various hypotheses have explained the interplay between DM and DE, revealing new characteristics for each component. According to a theoretical framework in particle physics, any two matter components may interact with one another. This is known as the DM and DE interaction. Numerous potential results of this specific descriptive theory have generated interest within the cosmological field. Similar to the interaction model in which DE decays to DM, the interacting models of DM and DE provide a compatible and well-researched overview of the dark sector of our Universe. They are driven by a workable solution to the problem of coincidence and cosmological constant [21−23]. To alleviate or circumvent the paradox of the coincidence challenge, certain investigations make reasonable presumptions regarding a DM-DE correlation. This links the energy densities of DE and DM, making them both dynamic and comparative while decreasing their correlation [24]. Several studies that emphasize the relationship among DE and DM interaction have been published [25−28]. In recent years, interacting models have been explored in the framework of cosmic stress resolution [29, 30]. Although a single, comprehensive guideline for selecting interaction functions does not exist, the literature presents a range of linear and non-linear functions from which novel functions may be selected. Non-linear interaction functions are typically laborious to detail when discussing the behavior of an interacting model; therefore, non-linear models of interaction are not frequently found in the literature [31, 32]. However, non-linear interaction models continue to be intriguing when investigating the nature of the Universe to determine if any new insights may be obtained. The dynamical systems approach in modified gravity, specifically focusing on the interaction between DE and DM in$ f(Q) $ gravity, is analysed by [33]. Motivated by the interacting circumstances, we investigate an interacting model using a model-independent approach.Determining if this type of odd model can adequately account for the broader development of the cosmos is the motivation for selecting such a dynamical system. A system of non-linear differential equations underlies the cosmological models. Discovering precise solutions for non-linear systems is often impossible [34]. By applying the dynamical system to the investigation of non-linear systems, we can gain a deeper understanding of the system's stability feature. In most cases, the dimensionless time variable is provided together with normalized variables to express the system as an independent system [35]. According to [36], these variables behave well and have a strong association with physically measurable values. By pinpointing the critical point and stability of the system, we can qualitatively examine the beginning and possible conclusion of the Universe. It is possible that the Universe began at an unstable critical point and moved towards a stable one, similar to every heteroclinic solution, which begins at an unstable critical point and ends up at a stable fixed point. This type of technique is not new in cosmology or GR. Nearly all significant GR and cosmological models have been examined within the context of dynamical systems analysis [37].
Motivated by these findings, our analysis will focus on the dynamical system method of
$ f(Q, C) $ gravity. The remainder of this article is structured as follows: We present an illustration of the field equations in$ f(Q, C) $ gravity in Sec. II. In Sec. III, we outline the dynamical system within$ f(Q, C) $ gravity and illustrate the equilibrium points along with phase diagrams. Conclusions are given in Sec. IV. -
The Levi-Civita connection
$ (\overset{\circ}{\Gamma^{\eta}}_{\mu\nu}) $ is widely acknowledged as the sole affine connection that satisfies both the metric compatibility and torsion-free conditions. With this restriction removed, we attempt to construct the symmetric teleparallel gravity by presuming an affine connection$ \Gamma^{\eta}_{\mu\nu} $ that is torsion- and curvature-free. The lower exponent symmetry of the affine connection, which is the result of the torsion-free condition, is referred to as "symmetric". The non-metricity tensor suggests that the metric provided by this affine connection is incompatible with$ \begin{aligned} Q_{\alpha\mu\nu}=\nabla_{\alpha}g_{\mu\nu}=\partial_{\alpha}g_{\mu\nu}-\Gamma^{\beta}_{\alpha\mu}g_{\beta\nu} \Gamma^{\beta}_{\alpha\nu}g_{\beta\mu}\neq 0, \end{aligned} $

(1) where
$ \Gamma^{\alpha}_{\mu\nu}=\overset{\circ}{\Gamma^{\alpha}}_{\mu\nu}+L^{\alpha}_{\mu\nu} $ . This implies that$ \begin{aligned} L^{\alpha}_{\mu\nu}=\frac{1}{2}(Q^{\alpha}_{\mu\nu}-Q_{\mu\;\;\nu}^{\;\;\alpha}-Q_{\nu\;\;\mu}^{\;\;\alpha}). \end{aligned} $

(2) We can generate two different types of non-metricity vectors as
$ \begin{aligned} Q_{\mu}=g^{\nu\alpha}Q_{\mu\nu\alpha}=Q_{\mu\;\;\nu}^{\;\;\nu}, \quad \tilde{Q}_{\mu}=g^{\nu\alpha}Q_{\nu\mu\alpha}=Q_{\nu\mu}^{\;\;\;\;\nu}. \end{aligned} $

(3) The superpotential tensor
$ P^{\alpha}_{\mu\nu} $ is computed as follows:$ \begin{aligned} P^{\alpha}_{\mu\nu}=\frac{1}{4}\bigg[-2L^{\alpha}_{\mu\nu}+Q^{\alpha}g_{\mu\nu}-\tilde{Q}^{\alpha}g_{\mu\nu} -\delta^{\alpha}_{\mu} Q_{\nu}\bigg]. \end{aligned} $

(4) This yields the non-metricity scalar Q as
$ \begin{aligned} Q=Q_{\eta\beta\gamma}P^{\eta\beta\gamma}. \end{aligned} $

(5) With the torsion- and curvature-free restrictions, the following connections are easily derived:
$ \begin{aligned} \overset{\circ}R_{\mu\nu}+\overset{\circ}\nabla_{\eta}L^{\eta}_{\mu\nu}-\overset{\circ}\nabla_{\nu}\tilde{L}_{\mu} +\tilde{L}_{\eta}LL^{\eta}_{\mu\nu}-L_{\eta\beta\nu}L^{\beta\eta}_{\mu}=0, \end{aligned} $

(6) $ \begin{aligned} \overset{\circ}R+\overset{\circ}\nabla_{\eta}(L^{\eta}-\tilde{L}^{\eta})-Q=0. \end{aligned} $

(7) Applying the connections mentioned earlier, the boundary term
$ (C) $ is defined as$ \begin{aligned} C=\overset{\circ}R-Q=-\overset{\circ}\nabla_{\eta}(Q^{\eta}-\tilde{Q}^{\eta}), \end{aligned} $

(8) where
$ Q^{\eta}-\tilde{Q}^{\eta}=L^{\eta}-\tilde{L}^{\eta} $ .In the
$ f(Q, C) $ theory, the gravitational action is given by$ \begin{aligned} S=\; \int \bigg(\frac{1}{2k}f(Q, C)+\mathcal{L}_{m}\bigg)\sqrt{-g}{\rm d}^{4}x. \end{aligned} $

(9) The function that consists of the non-metricity scalar Q and the boundary term C is described by
$ f(Q, C) $ , whereas$ \mathcal{L}_{m} $ symbolizes the matter Lagrangian.With changing the action of equation (ref9) concerning the metric, the field equation can be constructed as follows:
$ \begin{aligned}[b] \kappa T_{\mu\nu}=\;&-\frac{f}{2}g_{\mu\nu}+\frac{2}{\sqrt{-g}}\partial_{\alpha}\bigg(\sqrt{-g}f_{Q}P^{\alpha}_{\mu\nu}\bigg) \\&+\bigg(P_{\mu\eta\beta}Q_{\nu}^{\eta\beta}-2P_{\eta\beta\nu}Q^{\eta\beta}_{\mu}\bigg)f_{Q}\\ &+\bigg(\frac{C}{2}g_{\mu\nu}-\overset{\circ}\nabla_{\mu}\overset{\circ}{\nabla_{\nu}}+g_{\mu\nu}\overset{\circ}{\nabla^{\eta}}\overset{\circ}\nabla_{\eta}-2P^{\alpha}_{\mu\nu}\partial_{\alpha}\bigg)f_{C}. \end{aligned} $

(10) The covariant form is
$ \begin{aligned}[b] \kappa T_{\mu\nu}=\;&-\frac{f}{2}g_{\mu\nu}+2P^{\alpha}_{\mu\nu}\nabla_{\alpha}(f_{Q}-f_{C})+\bigg(\overset\circ G_{\mu\nu}+\frac{Q}{2}g_{\mu\nu}\bigg)f_{Q}\\ &+\bigg(\frac{C}{2}g_{\mu\nu}-\overset{\circ}\nabla_{\mu}\overset{\circ}\nabla_{\nu}+g_{\mu\nu}\overset{\circ}{\nabla^{\eta}}\overset{\circ}\nabla_{\eta}\bigg)f_{C}. \end{aligned} $

(11) The specifications for the effective energy momentum tensor are as follows:
$ \begin{aligned}[b] T_{\mu\nu}^{eff}=\;&T_{\mu\nu}+\frac{1}{k}\bigg(\frac{f}{2}g_{\mu\nu}-2P^{\alpha}_{\mu\nu}\nabla_{\alpha}(f_{Q}-f_{C}) -\frac{Qf_{Q}}{2}g_{\mu\nu}\\&-\bigg[\frac{C}{2}g_{\mu\nu}-\overset{\circ}\nabla_{\mu}\overset{\circ}\nabla_{\nu}+g_{\mu\nu}\overset{\circ}{\nabla^{\eta}}\overset{\circ}\nabla_{\eta}\bigg]f_{C}\bigg). \end{aligned} $

(12) We may create an equation that is comparable to GR by utilising the equation above:
$ \begin{aligned} \overset{\circ}G_{\mu\nu}=\frac{k}{f_{Q}}T_{\mu\nu}^{\rm eff}. \end{aligned} $

(13) For an ideal fluid, we interpret the energy-momentum tensor as
$ \begin{aligned} T_{\mu\nu}=pg_{\mu\nu}+(\rho+p)u_{\mu}u_{\nu}. \end{aligned} $

(14) The four-velocity of the fluid is represented by
$ u^{\mu} $ , the pressure is denoted by p, and the energy density is denoted by$ \rho $ . The Friedmann–Robertson–Walker (FRW) model of the Universe, represented by the line element, is assumed to be spatially flat, homogeneous, and isotropic.$ \begin{aligned} {\rm d}s^{2}=-{\rm d}t^{2}+a^{2}(t)({\rm d}x^{2}+{\rm d}y^{2}+{\rm d}z^{2}), \end{aligned} $

(15) where
$ a(t) $ is the scale factor. We compute the required values as follows using the diminishing affine connection$ \Gamma^{\eta}_{\mu\nu}=0 $ :$ \begin{aligned} \overset{\circ}R=6(2H^{2}+\dot{H}), \quad Q=-6H^{2}, \quad C=6(3H^{2}+\dot{H}). \end{aligned} $

(16) The following formulas for equation (16) are used to generate the field equations:
$ \begin{aligned} \kappa\rho=\frac{f}{2}+6H^{2}f_{Q}-(9H^{2}+3\dot{H})f_{C}+3H\dot{f}_{C}, \end{aligned} $

(17) $ \begin{aligned} \kappa p=-\frac{f}{2}-(6H^{2}+2\dot{H})f_{Q}-2H\dot{f}_{Q}+(9H^{2}+3\dot{H})f_{C}-\ddot{f}_{C}, \end{aligned} $

(18) where the derivative with respect to time
$ ''t'' $ is represented by the over dot, and$ f_{Q}=\dfrac{\partial f}{\partial Q} $ ,$ f_{C}=\dfrac{\partial f}{\partial C} $ . We take the mapping in the$ f(Q, C) $ gravity to be$ f(Q, C)\rightarrow Q+F(Q,C) $ . Therefore, by applying the aforementioned mapping, the equations (17) and (18) may be reduced as$ \begin{aligned} 3H^{2}=\kappa(\rho+\rho_{de}), \end{aligned} $

(19) $ \begin{aligned} 2\dot{H}+3H^{2}=\kappa(p+p_{de}). \end{aligned} $

(20) Subsequently, the following is the evaluation of the energy density and pressure for DE:
$ \begin{aligned} \kappa \rho_{de}=-\frac{F}{2}-6H^{2}F_{Q}+(9H^{2}+3\dot{H})F_{C}-3H\dot{F}_{C}, \end{aligned} $

(21) $ \begin{aligned} \kappa p_{de}=\;&\frac{F}{2}+(6H^{2}+2\dot{H})F_{Q}+2H\dot{F}_{Q}\\&-(9H^{2}+3\dot{H})F_{C}+\ddot{F}_{C}. \end{aligned} $

(22) The EoS parameter can be expressed in the DE stage as
$ \begin{aligned} \omega_{de}=\frac{\kappa p_{de}}{\kappa \rho_{de}}=-1+\frac{2\dot{H}F_{Q}+2H\dot{F}_{Q}+\ddot{F}_{C}-3H\dot{F}_{C}} {(9H^{2}+3\dot{H})F_{C}-\frac{F}{2}-6H^{2}F_{Q}-3H\dot{F}_{C}}. \end{aligned} $

(23) -
In this section, we briefly outline the fundamentals of dynamical systems analysis, focusing on relevant components that we have utilized in our research. Functions and their derivatives are related in differential equations. The first description of the dynamical system was by Newton in the mid-17th century. Newton employed it to simplify the two-body system, "the motion of the sun and earth" in gravity theory. Long-standing and appearing to be unsolvable was the "three body problem" or the movement of the sun, earth, and moon. The breakthrough was made in the late 1800 s by Poincar
$ \acute{e} $ , who discovered a geometrical approach to evaluating a system qualitatively instead of quantitatively. This resulted in the subject of dynamical systems analysis. An differential equation with only one independent variable is called an ordinary differential equation (ODE). We discuss on the ODE because it will be used later. Let us examine an ODE that appears as$ \dot{u}=h(u) $ , where$ \dot{u}= {{\rm d}u}/{{\rm d}t} $ ,$u=(u_{1},u_{2},u_{3},\cdots,u_{m})$ $ \in $ $ \mathbb{R}^{m} $ , and$ u:\mathbb{R}^{m}\rightarrow \mathbb{R}^{m} $ . An equation system that is not explicitly dependent on time is called an autonomous system [38]. We will also focus on autonomous systems during the discussion. By adding a new variable called time "t", we can treat a non-autonomous system as autonomous, such that$ u_{m+1}=t $ and$ \dot{u}_{m+1}=1 $ . Consequently, the system will gain an additional dimension. The curves in a space with m dimensions such as$u_{1},u_{2},u_{3},\cdots,u_{m}$ represent the solutions [39]. The region known as the phase space is associated with the curves known as phase paths. An essential step in determining the qualitative behavior of a dynamical system is assessing the system's equilibrium points. Equilibrium points are those at which the solutions do not change. Equilibrium points are evaluated by solving the equation$ h(u)=0 $ . The equilibrium points fall into three categories: stable, unstable, and saddle [40]. The stability of an equilibrium point can be determined by introducing perturbations to the system at a distance from the equilibrium point [41]. Equilibrium points are stable when the system returns to that point and unstable when the system never does. When all of the characteristic values have negative values, an equilibrium point is a stable point or attractor [42]. Every single characteristic value being positive indicates that the equilibrium point is unstable or repulsive. If a mixture of both positive and negative eigenvalues exists, the equilibrium point is saddle [43]. Beyond these two categories, equilibrium points can also be classified as hyperbolic or non-hyperbolic. The equilibrium point is defined as the hyperbolic equilibrium point if any of the Jacobian matrix's eigenvalues vanish; otherwise, it is non-hyperbolic [44].We are currently experiencing an accelerated expansion of the Universe dominated by DE. If one travels back in time, the Universe was denser than it is now, when matter predominated. In the evolving cosmos, the swift consumption of radiation takes precedence over matter, making radiation the primary concern in the Universe's dominance. Before the radiation-dominated epoch, evidence shows the occurrence of accelerated expansion known as inflation, linking the initiation of the Big Bang with the radiation epoch following inflation. Consequently, the Universe has undergone two periods of accelerated expansion: one during its early stages driven by inflation, and another during its later phases fueled by DE. Therefore, any decent cosmological model must incorporate at least some aspects of the standard cosmological model, depicted as "Inflation
$ \rightarrow $ Radiation$ \rightarrow $ Matter$ \rightarrow $ Accelerating Expansion" [45]. For the cosmological model derived from the above relation, inflation points should be categorized as unstable, and matter and radiation points as stable within the Universe, and the accelerated phase should serve as an attractor.We proceed to construct a cosmological model with only matter and radiation, operating under the assumption of non-interaction between these elements. Subsequently, the energy density and pressure of matter can be expressed as follows:
$ \begin{aligned} \rho=\rho_{m}+\rho_{r}, \quad p=\frac{\rho_{r}}{3}, \end{aligned} $

(24) where
$ \rho_{m} $ and$ \rho_{r} $ represents matter and radiation energy densities, respectively. During the phase dominated by matter, the pressure$ p_{m} $ equals zero, resulting in the disappearance of$ \omega_{m} $ , whereas$ \omega_{r}= {1}/{3} $ during the radiation phase. We now examine the phase space of equilibrium points by utilizing a dynamical system analysis for our model. Derivation of the dynamical system requires the introduction of supplementary variables derived from Eq. (17). With the assistance of these variables, exact solutions to the field equations can be obtained, and their stability properties can be analyzed. The following group of dimensionless variables are used:$ \begin{aligned} x=-\frac{F}{6H^{2}}, \quad y=\frac{F_{C}\dot{H}}{H^{2}}, \quad z=-\frac{\dot{F}_{C}}{H}, \quad r=F_{C}, \quad m=\frac{\kappa \rho_{r}}{3H^{2}}. \end{aligned} $

(25) We also designate the mentioned variables as Expansion Normalized (EN) variables. From equation (19) we obtain
$ \begin{aligned} \Omega_{m}+\Omega_{r}+\Omega_{de}=1. \end{aligned} $

(26) where
$ \Omega_{m}=\dfrac{\kappa \rho_{m}}{3H^{2}} $ ,$ \Omega_{r}=\dfrac{\kappa \rho_{r}}{3H^{2}} $ , and$ \Omega_{de}=\dfrac{\kappa \rho_{de}}{3H^{2}} $ . The density parameter can be formulated using the variables mentioned earlier in the following manner:$ \begin{aligned} \Omega_{m}=1-x+2F_{Q}-3r-y-z-m, \quad \Omega_{r}=m, \end{aligned} $

(27) $ \begin{aligned} \Omega_{de}=x-2F_{Q}+3r+y+z. \end{aligned} $

(28) The conservation equations are outlined as follows:
$ \begin{aligned} \dot{\rho}_{m}+3H\rho_{m}=0, \quad \dot{\rho}_{r}+4H\rho_{r}=0, \quad \dot{\rho}_{de}+3H(\rho_{de}+p_{de})=0. \end{aligned} $

(29) Additionally, we obtain the subsequent equations for two cosmological parameters: the deceleration and EoS parameters, which are fundamental to characterizing the Universe's expansion history. These parameters can be computed utilizing Eq. (25) as
$ \begin{aligned} q-1-\frac{\dot{H}}{H^{2}}=-1-\frac{y}{r}, \end{aligned} $

(30) $ \begin{aligned} \omega_{de}=\frac{\kappa p_{de}}{\kappa\rho_{de}}=-\frac{(m+3)r+2y}{3r(3r+y-2F_{Q}+z+x)}. \end{aligned} $

(31) The formula for
$ \omega_{\rm tot} $ can be derived from the connection between the deceleration parameter and EoS parameter$ (\omega) $ as$ \begin{aligned} \omega_{\rm tot} =\frac{2 q-1}{3}=-1-\frac{2}{3}\frac{\dot{H}}{H^{2}}=-1-\frac{2y}{3r}. \end{aligned} $

(32) The system of ODEs can be formulated based on the variables outlined in Eq. (25) as follows:
$ \begin{aligned} \frac{{\rm d}x}{{\rm d}N}=-6y-\lambda r-\frac{2xy}{r}-\frac{2yF_{Q}}{r}, \end{aligned} $

(33) $ \begin{aligned} \frac{{\rm d}y}{{\rm d}N}=-\frac{y}{r}(z+2y)+\lambda r, \end{aligned} $

(34) $ \begin{aligned} \frac{{\rm d}z}{{\rm d}N}=\;&m+3-3x+6F_{Q}+\frac{2y}{r}-9r-3y\\&+\frac{2yF_{Q}}{r}+\frac{2\dot{F}_{Q}}{H}-\frac{zy}{r}, \end{aligned} $

(35) $ \begin{aligned} \frac{{\rm d}r}{{\rm d}N}=-z, \end{aligned} $

(36) $ \begin{aligned} \frac{{\rm d}m}{{\rm d}N}=-\frac{2m}{r}(2r+y), \end{aligned} $

(37) where
$N={\rm log} a$ . In Eqs. (33) and (34), an extra parameter is present, which is defined by$ \lambda=\frac{\ddot{H}}{H^{3}} $ . To construct dynamical system in$ f(Q, C) $ gravity, only two possible approaches of$ \lambda $ are available, i.e.,$ \lambda=\frac{\ddot{H}}{H^{3}}=constant $ or a dimensionless variable term. If$ \lambda $ is treated as a dimensionless variable, the differentiation of$ \lambda $ with respect to N yields$\frac{{\rm d}\lambda}{{\rm d}N}=\frac{\dddot H}{H^{3}}-\frac{3\lambda y}{r}$ , which involves the third order derivative of H. This makes determining the solution of the dynamical system more difficult, as it requires fourth-order differential equations of H; it is impossible to obtain this term from field equations. Thus,$ \lambda=constant $ is the only possible option for determining the solution. Thus, we assume$ \lambda=\frac{\ddot{H}}{H^{3}}=constant $ to avoid higher-order derivatives of the Hubble parameter H and reduce the complexity of solving the dynamical system [46−48]. This assumption fully determines the cosmic expansion history, including the Hubble parameter$ H(t) $ , scale factor$ a(t) $ and the time derivative of the Hubble parameter$ \dot{H}(t) $ independent of the underlying gravitational theory, whether it is$ f(Q, C) $ gravity or another model. If$ \lambda = 0 $ , it yields the precise de Sitter scalar factor$a(t) = {\rm e}^{\Lambda t}$ , where$ \Lambda $ remains constant or, form a quasi de Sitter scalar$a(t)= {\rm e}^{H_{0}t+H_{1}t^{2}}$ , where$ H_{0} $ and$ H_{1} $ are constants. When$\lambda= {9}/{2}$ , it yields a scalar factor dominated by matter,$ a(t)\sim 9 t^{\frac{2}{3}} $ . To explore stability analysis, it's essential to define a specific form of$ f(Q, C) $ . Thus, we have explored two variations of$ f(Q, C) $ that correspond to two different models. -
To formulate a physically reasonable model that aligns with the ongoing Universe's accelerated expansion, we select the form of
$ F(Q,C) $ in the following manner:$ \begin{aligned} F(Q,C)=\alpha Q+\beta C {\rm log}C. \end{aligned} $

(38) where
$ \alpha $ and$ \beta $ are model parameters. The form$ F(Q,C) $ $ = $ $\alpha Q+\beta C {\rm log}C$ is motivated by its potential to model scenarios in which the contribution of the non-metricity scalar Q is linearly related to the gravitational dynamics, whereas the term involving$\beta C {\rm log}C$ can introduce non-linear corrections that may account for complex interactions in the early Universe or during phases of accelerated expansion. The logarithmic term is particularly interesting because it can modify the evolution of the Hubble parameter, resulting in rich cosmological dynamics. The logarithmic model has exhibited noteworthy findings within the context of teleparallel gravity [49−51]. Many researchers have employed the logarithmic form to conduct dynamical system analyses in different gravitational theories. Note that when$ \beta=0 $ , it corresponds to the function$ F(Q,C)=\alpha Q $ , which reflects the scenario of GR theory. Utilizing the form provided in Eq. (38), we redefine the variable “$z$ ” as$ \begin{aligned} z=-\frac{\dot{F}_{C}}{H}=-\frac{\beta(6y+\lambda r)}{3r+y}. \end{aligned} $

(39) This implies that it is contingent on the variables y and r. Therefore, Eqs. (33)−(37) can be reformulated using Eq. (39) in the following manner:
$ \begin{aligned} \frac{{\rm d}x}{{\rm d}N}=-\bigg(\frac{6yr+\lambda r^{2}+2xy+2\alpha y}{r}\bigg), \end{aligned} $

(40) $ \begin{aligned} \frac{{\rm d}y}{{\rm d}N}=\frac{\beta y(6y+\lambda r)}{r(3r+y)}+\lambda r-\frac{2y^{2}}{r}, \end{aligned} $

(41) $ \begin{aligned} \frac{{\rm d}r}{{\rm d}N}=\frac{\beta(6y+\lambda r)}{3r+y}, \end{aligned} $

(42) $ \begin{aligned} \frac{{\rm d}m}{{\rm d}N}=-\frac{2m}{r}(2r+y). \end{aligned} $

(43) The density parameter can be formulated using the Eq. (38) in the following manner:
$ \begin{aligned} \Omega_{m}=1-x+2\alpha-3r-y-z-m, \quad \Omega_{r}=m, \end{aligned} $

(44) and
$ \begin{aligned} \Omega_{de}=x-2\alpha+3r+y+z. \end{aligned} $

(45) Our first objective is to ascertain the equilibrium points of the system delineated by Eqs. (40)−(43). We ascertain the equilibrium points by solving the equations
${{\rm d}x}/{{\rm d}N}={{\rm d}y}/{{\rm d}N}={{\rm d}r}/{{\rm d}N}={{\rm d}m}/{{\rm d}N}=0$ . We calculate the eigenvalues from the Jacobian matrix at each equilibrium point to analyze the stability criteria of our model. The table shows the equilibrium points along with their corresponding cosmological parameters as outlined in Table 1. The stability conditions and characteristic values are depicted in Table 2. The behaviors of the scale factor are given in Table 3.Points x y r m q $\omega_{\rm tot}$ 

$ \omega_{de} $ 

Exists for A $ -3a_{1}-\alpha $ 

$ -2a_{1} $ 

$ a_{1} $ 

$ m_{1} $ 

1 ${1}/{3}$ 

${1}/{3}$ 

$ a_{1}\neq 0 $ ,

$ m_{1}\neq 0 $ 

B $ \frac{11a_{2}}{6}+\alpha $ 

$ -\frac{3a_{2}}{2} $ 

$ a_{2} $ 

0 $ \frac{1}{2} $ 

0 0 $ a_{2}\neq 0 $ 

C $ a_{3} $ 

0 $ a_{4} $ 

0 –1 –1 –1 $ a_{3}\neq 0 $ ,

$ a_{4}\neq 0 $ 

D $ -3a_{5}-\alpha $ 

$ a_{6} $ 

$ a_{5} $ 

0 –1 –1 –1 $ a_{5}\neq 0 $ ,

$ a_{6}\neq 0 $ 

Table 1. Critical points & physical parameters for the system of Eqs. (40)−(43).
Points $ \gamma_{1} $ 

$ \gamma_{2} $ 

$ \gamma_{3} $ 

$ \gamma_{4} $ 

Criteria A 4 8 0 0 unstable B 3 6 0 –1 unstable saddle C 0 0 0 –4 stable D $ -\frac{2a_{6}}{a_{5}} $ 

$ -\frac{4a_{6}}{a_{5}} $ 

0 $ -\frac{2(2a_{5}+a_{6})}{a_{5}} $ 

stable Table 2. Characteristic values and their stability criteria.
Points Accelerating equation Scale factor Phase A $ \dot{H}=-2H^{2} $ 

$a(t)=a_{0}(2t+b_{2})^{{1}/{2} }$ 

radiation dominated B $ \dot{H}=-\frac{3}{2}H^{2} $ 

$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3} }$ 

matter dominated C $ \dot{H}=0 $ 

$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ 

de-Sitter D $ \dot{H}=0 $ 

$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ 

de-Sitter Table 3. Physical behavior of the scale factor at each equilibrium point.
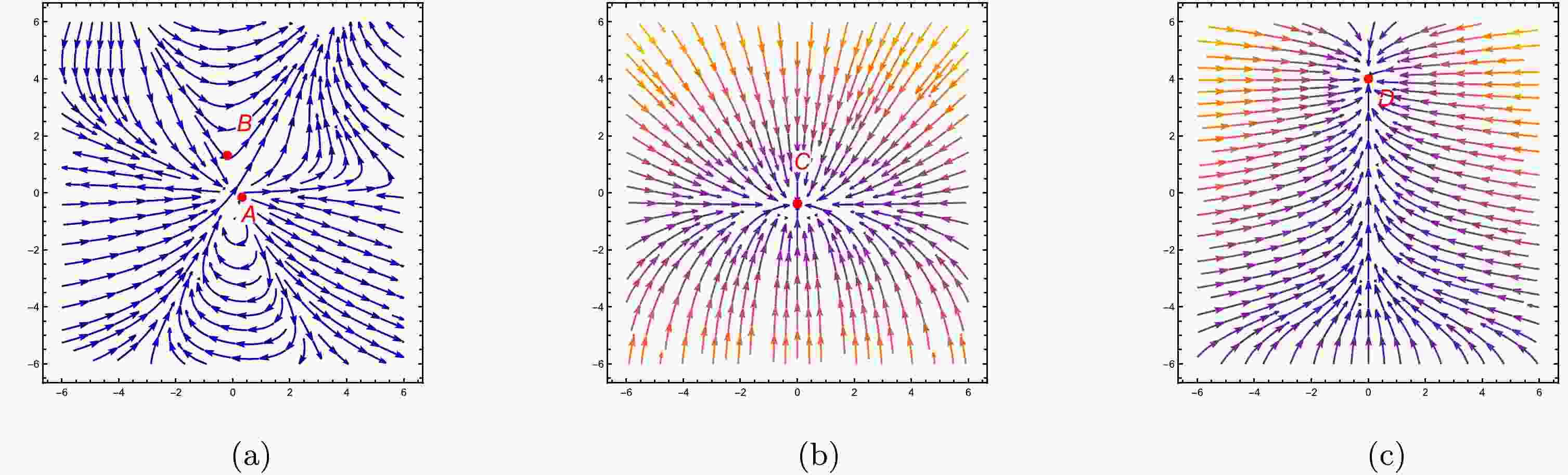
$ \bullet $ Point A: Eqs. (40)−(43) yield four critical points, as elaborated in Table 1. Table 2 indicates that for critical point A, the characteristic values are$ \gamma_{1}=4 $ ,$ \gamma_{2}=8 $ ,$ \gamma_{3}=0 $ , and$ \gamma_{4}=0 $ . As all four characteristic values, namely$ \gamma_{1} $ ,$ \gamma_{2} $ ,$ \gamma_{3} $ , and$ \gamma_{4} $ are positive, critical point A exhibits an unstable node. Upon inspection of Fig. 1(a), we observe that all trajectories originating from point A indeed verify its unstable nature. At point A, the density parameters are$ \Omega_{m}=0 $ ,$ \Omega_{r}=1 $ , and$ \Omega_{de}=0 $ , which signify the Universe's radiation-dominated phase. Furthermore, at critical point A, the deceleration and EoS parameters take on the values$ q=1 $ and$\omega _{de}=\omega_{\rm tot}= {1}/{3}$ , respectively, illustrating the decelerating phase of the Universe. The scale factor for point A is expressed as$ a(t)=a_{0}(2t+b_{2})^{\frac{1}{2}} $ , which signifies the Universe's radiation-dominated stage, where$ b_{2} $ is the integration constant.$ \bullet $ Point B: Table 2 indicates that for critical point B, the characteristic values are$ \gamma_{1}=3 $ ,$ \gamma_{2}=6 $ ,$ \gamma_{3}=0 $ , and$ \gamma_{4}=-1 $ . As two characteristic values,$ \gamma_{1} $ and$ \gamma_{2} $ , are negative, whereas the other one,$ \gamma_{3} $ , is positive, critical point B exhibits unstable saddle behavior. Figure 1(a) depicts trajectories converging towards point B as well as diverging from it, confirming the saddle behavior of point B. The density parameters at this point are$ \Omega_{m}=1 $ ,$ \Omega_{r}=0 $ , and$ \Omega_{de}=0 $ , signifying the matter-dominated phase of the Universe. Furthermore, at critical point B, the deceleration and EoS parameters take on the values$q= {1}/{2}$ and$\omega _{de}=\omega_{\rm tot}=0$ , respectively, illustrating the decelerating phase of the Universe. The scale factor for point B is expressed as$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage, where$ b_{2} $ is the integration constant.$ \bullet $ Point C: Table 2 indicates that for critical point C, the characteristic values are$ \gamma_{1}=0 $ ,$ \gamma_{2}=0 $ ,$ \gamma_{3}=0 $ , and$ \gamma_{4}=-4 $ . With three zero eigenvalues and one negative eigenvalue, this critical point possesses a non-hyperbolic nature. Linear stability theory cannot offer insights into the stability of critical points that possess zero eigenvalues. Additionally, if we examine the central manifold theorem, we notice that the nonlinear part at zero does not vanish after separating from the linear and nonlinear parts of the given equations. Thus, it cannot elucidate the stability of this critical point. In such scenarios, relying on the phase diagram is the only option to analyze the stability behavior at this point. In Fig. 1(b), all paths lead towards point C, suggesting the stable nature of critical point C. Point C is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrates the exponential growth typical of the Universe's dominance by DE, where$ b_{3} $ is the integration constant. Additionally, according to Table 1, critical point C is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$\omega_{de}=\omega_{\rm tot}= -1$ , which signify the accelerating phase of the Universe.$ \bullet $ Point D: Table 2 indicates that for critical point D, the characteristic values are$ \gamma_{1}=-\frac{2a_{6}}{a_{5}} $ ,$ \gamma_{2}=-\frac{4a_{6}}{a_{5}} $ ,$ \gamma_{3}=0 $ , and$ \gamma_{4}=-\frac{2(2a_{5}+a_{6})}{a_{5}} $ . These characteristics values exist only for$ a_{5}\neq 0 $ . As all characteristic values are negative, point D demonstrates stable behavior. In Fig. 1(c), all paths lead towards point D, verifying its stable nature. Point D is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrates the exponential growth typical of the Universe's dominance by DE, where$ b_{3} $ is the integration constant. Additionally, according to Table 1, critical point D is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$\omega_{de}=\omega_{\rm tot}=-1$ , which signify the accelerating phase of the Universe. -
To formulate a physically reasonable model that aligns with the ongoing Universe's accelerated expansion, we select the form of
$ F(Q,C) $ in the following manner:$ \begin{aligned} F(Q,C)=\alpha Q+\frac{\beta}{C}. \end{aligned} $

(46) where
$ \alpha $ and$ \beta $ are model parameters. The form$ F(Q,C) $ $ = $ $ \alpha Q+\frac{\beta}{C} $ is motivated by the desire to include a term that depends on the inverse of C, where the curvature term C plays a dominant role at small scales or during late-time cosmic evolution. The inverse term$ \frac{\beta}{C} $ can lead to corrections that might be important in addressing problems such as the late-time acceleration of the Universe without invoking DE. Many researchers have employed this type of form to conduct dynamical system analyses in different gravitational theories. Note that when$ \beta=0 $ , it corresponds to the function$ F(Q,C)=\alpha Q $ , which reflects the scenario of GR theory. Dagwal investigates the Universe's accelerated expansion in$ f(T) $ gravity within this model [52]. The cosmological acceleration is examined by using the above model in [53]. Utilizing the form provided in equation (46), we redefine the variable$ "z" $ as$ \begin{aligned} z=-\frac{\dot{F}_{C}}{H}=\frac{2r(6y+\lambda r)}{3r+y}. \end{aligned} $

(47) This implies that it is expressed with the variables y and r. Therefore, Eqs. (33)−(37) can be reformulated using Eq. (47) in the following manner:
$ \begin{aligned} \frac{{\rm d}x}{{\rm d}N}=-\bigg(\frac{6yr+\lambda r^{2}+2xy+2\alpha y}{r}\bigg), \end{aligned} $

(48) $ \begin{aligned} \frac{{\rm d}y}{{\rm d}N}=-\frac{2r(6y+\lambda r)}{3r+y}+\lambda r-\frac{2y^{2}}{r}, \end{aligned} $

(49) $ \begin{aligned} \frac{{\rm d}r}{{\rm d}N}=-\frac{2r(6y+\lambda r)}{3r+y}, \end{aligned} $

(50) $ \begin{aligned} \frac{{\rm d}m}{{\rm d}N}=-\frac{2m}{r}(2r+y). \end{aligned} $

(51) The density parameter can be formulated using the Eq. (46) in the following manner:
$ \begin{aligned} \Omega_{m}=1-x+2\alpha-3r-y-\frac{2r(6y+\lambda r)}{3r+y}-m, \quad \Omega_{r}=m, \end{aligned} $

(52) $ \begin{aligned} \Omega_{de}=x-2\alpha+3r+y+\frac{2r(6y+\lambda r)}{3r+y}. \end{aligned} $

(53) Our first objective is to ascertain the equilibrium points of the system delineated using Eqs. (48)−(51). We ascertain the equilibrium points by solving the equations
${{\rm d}x}/{{\rm d}N}={{\rm d}y}/{{\rm d}N}={{\rm d}r}/{{\rm d}N}={{\rm d}m}/{{\rm d}N}=0$ . We calculate the eigenvalues from the Jacobian matrix at each equilibrium point to analyze the stability criteria of our model. The table exhibits the equilibrium points along with their corresponding cosmological parameters as outlined in Table 4. The stability conditions and characteristic values are depicted in Table 5. The behavior of the scale factor are given in Table 6.Points x y r m q $\omega_{\rm tot}$ 

$ \omega_{de} $ 

Exists for $ A_{1} $ 

$ -3a_{7}-\alpha $ 

$ -2a_{7} $ 

$ a_{7} $ 

$ m_{2} $ 

1 ${1}/{3}$ 

${1}/{3}$ 

$ a_{7}\neq 0 $ ,

$ m_{2}\neq 0 $ 

$ B_{1} $ 

$ -\frac{3a_{8}}{2}-\alpha $ 

$ -\frac{3a_{8}}{2} $ 

$ a_{8} $ 

0 ${1}/{2}$ 

0 0 $ a_{8}\neq 0 $ 

$ C_{1} $ 

$ a_{9} $ 

0 $ a_{10} $ 

0 −1 −1 −1 $ a_{9}\neq 0 $ ,

$ a_{10}\neq 0 $ 

$ D_{1}^{+} $ 

$ -3a_{11}-\sqrt{\frac{\lambda}{2}}a_{11}-\alpha $ 

$ \sqrt{\frac{\lambda}{2}}a_{11} $ 

$ a_{11} $ 

0 −1 −1 −1 $ a_{11}\neq 0 $ ,

$ \lambda \geq0 $ 

$ D_{1}^{-} $ 

$ -3a_{12}+\sqrt{\frac{\lambda}{2}}a_{12}-\alpha $ 

$ \sqrt{\frac{\lambda}{2}}a_{12} $ 

$ a_{12} $ 

0 −1 −1 −1 $ a_{12}\neq 0 $ ,

$ \lambda \geq0 $ 

Table 4. Critical points & physical parameters for the system of Eqs. (48)−(51).
Points $ \xi_{1} $ 

$ \xi_{2} $ 

$ \xi_{3} $ 

$ \xi_{4} $ 

Criteria $ A_{1} $ 

4 −16 −8 0 unstable saddle $ B_{1} $ 

3 36 8 0 unstable $ C_{1} $ 

0 0 0 −4 stable $ D_{1}^{+} $ 

$ -\sqrt{2\lambda} $ 

$-\frac{24\sqrt{{\lambda}/{2} } }{3+\sqrt{{\lambda}/{2} } }$ 

$-\frac{4(3\lambda+\sqrt{{\lambda}/{2} })}{(3+\sqrt{{\lambda}/{2} })^{2} }$ 

$ -4-\sqrt{2\lambda} $ 

stable $ D_{1}^{-} $ 

$ -\sqrt{2\lambda} $ 

$-\frac{24\sqrt{{\lambda}/{2} } }{3+\sqrt{{\lambda}/{2} } }$ 

$-\frac{4(3\lambda+\sqrt{{\lambda}/{2} })}{(3+\sqrt{{\lambda}/{2} })^{2} }$ 

$ -4-\sqrt{2\lambda} $ 

stable Table 5. Characteristic values and their stability criteria.
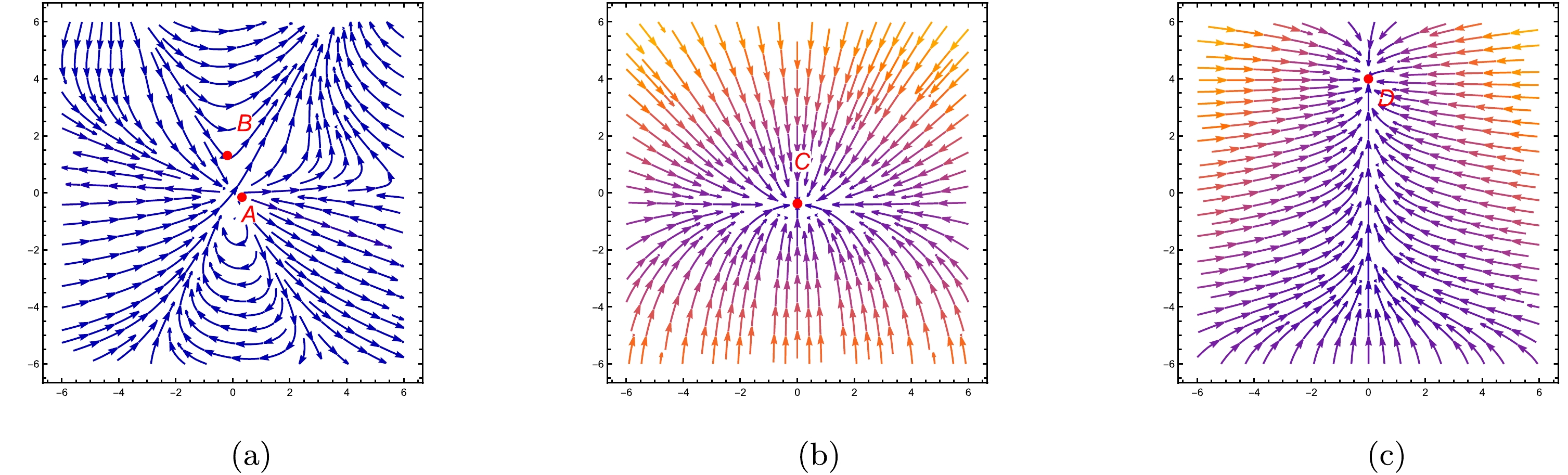
$ \bullet $ ${{\bf{Point}}\;{A_1}}$ : Eqs. (48)−(51) yield five critical points, as elaborated in Table 4. Table 5 indicates that for critical point$ A_{1} $ , the characteristic values are$ \xi_{1}=4 $ ,$ \xi_{2}=-16 $ ,$ \xi_{3}=-8 $ , and$ \xi_{4}=0 $ . As two characteristic values,$ \xi_{2} $ and$ \xi_{3} $ , are negative whereas the other one,$ \xi_{1} $ , is positive, critical point$ A_{1} $ exhibits unstable saddle behavior. Figure 2(a) depicts trajectories converging towards point$ A_{1} $ as well as diverging from it, confirming the saddle behavior of point$ A_{1} $ . At point$ A_{1} $ , the density parameters are$ \Omega_{m}=0 $ ,$ \Omega_{r}=1 $ , and$ \Omega_{de}=0 $ , which signify the Universe's radiation-dominated phase. Furthermore, at critical point$ A_{1} $ , the deceleration and EoS parameters take on the values$ q=1 $ and$ \omega _{de}=\omega_{tot}= {1}/{3} $ , respectively, illustrating the decelerating phase of the Universe. The scale factor for point$ A_{1} $ is expressed as$ a(t)=a_{0}(2t+b_{2})^{\frac{1}{2}} $ , which signifies the Universe's radiation-dominated stage. Here,$ b_{2} $ is integration constant.$ \bullet $ ${{\bf{Point}}\;{B_1}}$ : Table 5 indicates that for critical point$ B_{1} $ , the characteristic values are$ \xi_{1}=3 $ ,$ \xi_{2}=36 $ ,$ \xi_{3}=8 $ , and$ \xi_{4}=0 $ . As all four characteristic values, namely$ \xi_{1} $ ,$ \xi_{2} $ ,$ \xi_{3} $ , and$ \xi_{4} $ are positive, critical point$ B_{1} $ exhibits an unstable node. Upon inspection of Fig. 2(a), we observe that all trajectories originating from point$ B_{1} $ indeed verify its unstable nature. The density parameters at this point are$ \Omega_{m}=1 $ ,$ \Omega_{r}=0 $ , and$ \Omega_{de}=0 $ , signifying the matter-dominated phase of the Universe. Furthermore, at critical point$ B_{1} $ , the deceleration and EoS parameters take on the values$ q= {1}/{2} $ and$ \omega _{de}=\omega_{tot}=0 $ , respectively, illustrating the decelerating phase of the Universe. The scale factor for point$ B_{1} $ is expressed as$ a(t)=a_{0}(\frac{3t}{2}+b_{2})^{\frac{2}{3}} $ , which signifies the Universe's matter-dominated stage. Here,$ b_{2} $ is integration constant.$ \bullet $ ${{\bf{Point}}\;{C_1}}$ : Table 5 indicates that for critical point$ C_{1} $ , the characteristic values are$ \xi_{1}=0 $ ,$ \xi_{2}=0 $ ,$ \xi_{3}=0 $ , and$ \xi_{4}=-4 $ . With three zero eigenvalues and one negative eigenvalue, this critical point is non-hyperbolic. Linear stability theory cannot offer insights into the stability of critical points that possess zero eigenvalues. Additionally, if we examine the central manifold theorem, we notice that the nonlinear part at zero does not vanish after separating from the linear and nonlinear parts of the given equations. Thus, it cannot elucidate the stability of this critical point. In such scenarios, relying on the phase diagram is the only option to analyze the stability behavior at this point. In Fig. 4(a), all paths lead towards point$ C_{1} $ , suggesting the stable nature of critical point$ C_{1} $ . Point$ C_{1} $ is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrates the exponential growth typical of the Universe's dominance by DE. Here,$ b_{3} $ is integration constant. Additionally, according to Table 4, critical point C is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$\omega_{de}=\omega_{\rm tot}=-1$ , which signify the accelerating phase of the Universe.$ \bullet $ ${{\bf{Points}}\;{D_{1}^{+}\;{\rm{and}} \;D_{1}^{-}}}$ : Table 5 shows that the characteristic values for critical points$ D_{1}^{+} $ and$ D_{1}^{-} $ are identical. The characteristic values for the points ($ D_{1}^{+} $ &$ D_{1}^{-} $ ) are$ \xi_{1}=-\sqrt{2\lambda} $ ,$\xi_{2}=-\frac{24\sqrt{{\lambda}/{2}}}{3+\sqrt{{\lambda}/{2}}}$ ,$\xi_{3}=-\frac{4(3\lambda+\sqrt{{\lambda}/{2}})}{(3+\sqrt{{\lambda}/{2}})^{2}}$ , and$ \xi_{4}= -4 -\sqrt{2\lambda} $ . These characteristics values are exists only for$ \lambda> 0 $ . As all characteristic values are negative, points ($ D_{1}^{+} $ and$ D_{1}^{-} $ ) demonstrate stable behavior. In Fig. 4(b), all paths lead towards point ($ D_{1}^{+} $ and$ D_{1}^{-} $ ), verifying its stable nature. Points$ D_{1}^{+} $ and$ D_{1}^{-} $ are characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ U, which signify the DE-dominated phase of the Universe. The scale factor for these two points, denoted by$a(t)= a_{0}(\sqrt{\frac{\lambda}{2}}t+ b_{4 })^{\sqrt{{2}/{\lambda}}}$ , illustrates the different stages of the Universe's evolution depend on the value of$ \lambda $ . If we take$ \lambda=0 $ , then we obtain$ \dot{H}=0 $ , which implies that$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrating the de-Sitter phase of the Universe. Again, if we take$ \lambda= {9}/{2} $ , then$ \dot{H}=- {3}/{2}H^{2} $ , which implies that$a(t)=a_{0}({3t}/{2}+ b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage. Here,$ b_{2}, b_{3} $ , and$ a_{0} $ are constants. Additionally, according to Table 4, critical points$ D_{1}^{+} $ and$ D_{1}^{-} $ are characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$\omega_{de}=\omega_{\rm tot}=-1$ , which signify the accelerating phase of the Universe. -
In this section, we develop the autonomous dynamical system within the context of
$ f(Q, C) $ gravity theory, emphasising the interaction between DE and DM. The energy density of each fluid component j (where j represents radiation$ (r) $ , baryons$ (b) $ , cold DM$ (c) $ , and DE$ (d) $ , respectively) for the concordance model is independently conserved, accordidng to the equation$\dot{\rho_{j}}+3H\rho_{j}(1+\omega_{j}) =0$ . In interacting models, the total energy density of the dark sector remains conserved, whereas the densities of DM and DE evolve according to the following equations [54]:$ \begin{aligned} \dot{\rho_{m}}+3H\rho_{m}=-\mathcal{Q}, \end{aligned} $

(54) $ \begin{aligned} \dot{\rho_{r}}+3H\rho_{r}=0, \end{aligned} $

(55) $ \begin{aligned} \dot{\rho_{de}}+3H(\rho_{de}+p_{de})=\mathcal{Q}. \end{aligned} $

(56) In this case, the transfer of energy between DE and DM is represented by the interaction coefficient
$ \mathcal{Q} $ . This is necessary to address the coincidence problem and is consistent with the principles of the second law of thermodynamics. Currently,$ \mathcal{Q} $ is not defined explicitly; the only assumption is that$ \mathcal{Q} $ maintains a consistent sign throughout the Universe's evolution. Because the exact nature of the two dark components (DM and DE) is unknown, we cannot determine the specific form of their interaction based solely on initial assumptions or phenomenological considerations. Moreover, an assumption exists that the interaction term might result in a significant problem to be addressed in researching the physical aspects of DE. Additionally, interaction between the dark components appears intuitively from the perspective of field theory. We will assume that the interaction constitutes only a minor adjustment to the Universe's evolution history. If$ \mathcal{Q}>0 $ , the Universe remains in the matter-dominated regime. If$ \mathcal{Q}<0 $ , the Universe transitions from the matter-dominated period to the phase of galaxy and large-scale structure formation. Analogous to interactions in particle physics, we would anticipate that the kernel depends on the energy densities involved,$ \rho_{m} $ and$ \rho_{de} $ , as well as on the Hubble parameter,${1}/{H}$ . The first-order Taylor expansion of the interaction terms is expressed as follows:$ \mathcal{Q}=\zeta H(\chi_{1}\rho_{m}+\chi_{2}\rho_{de}) $ , where$ \chi_{1} $ and$ \chi_{2} $ are arbitrary constants. Owing to the insufficient information available, it is preferable to utilize a single parameter instead of two. Here, we can select between$ \chi_{1}=0 $ ,$ \chi_{2}=0 $ , and$ \chi_{1}=\chi_{2} $ . That brings us to$({\rm{i}})$ $ \mathcal{Q}=\zeta H \rho_{m} $ ,$({\rm{ii}})$ $ \mathcal{Q}=\zeta H \rho_{de} $ , and$({\rm{iii}})$ $ \mathcal{Q}=\zeta H (\rho_{m}+\rho_{de}) $ [55]. To perform the dynamical system, we adopt$ \mathcal{Q}=\zeta H \rho_{m} $ , where the parameter$ \zeta $ is a dimensionless, positive, and small constant [56]. Based on Friedmann's Eq. (17), the dimensionless variable can be described as follows:$ \begin{aligned} x=-\frac{F}{6H^{2}}, \quad y=\frac{F_{C}\dot{H}}{H^{2}}, \quad z=-\frac{\dot{F}_{C}}{H},\\ r=F_{C}, \quad m=\frac{\kappa \rho_{r}}{3H^{2}}, \quad n=\frac{\kappa \rho_{m}}{3H^{2}}. \end{aligned} $

(57) With the use of Eq. (39) and the variables mentioned before (57), the set of ordinary differential equations is obtained in terms of z as follows:
$ \begin{aligned} \frac{{\rm d}x}{{\rm d}N}=-\bigg(\frac{6yr+\lambda r^{2}+2xy+2\alpha y}{r}\bigg), \end{aligned} $

(58) $ \begin{aligned} \frac{{\rm d}y}{{\rm d}N}=\frac{\beta y(6y+\lambda r)}{r(3r+y)}+\lambda r-\frac{2y^{2}}{r}, \end{aligned} $

(59) $ \begin{aligned} \frac{{\rm d}r}{{\rm d}N}=\frac{\beta(6y+\lambda r)}{3r+y}, \end{aligned} $

(60) $ \begin{aligned} \frac{{\rm d}m}{{\rm d}N}=-\frac{2m}{r}(2r+y), \end{aligned} $

(61) $ \begin{aligned} \frac{{\rm d}n}{{\rm d}N}=-\frac{n}{r}\bigg[(\zeta+3)r+2y\bigg]. \end{aligned} $

(62) With the aid of Eq. (38), the density parameter can be expressed from the field Eq. (17) as follows:
$ \begin{aligned} \Omega_{r}=m, \quad \Omega_{m}=n, \quad \Omega_{de}=1-x+2\alpha-3r-y-z-m-n. \end{aligned} $

(63) We observe that the above equations exist for
$ r\neq 0 $ . Now, we compute the equilibrium points of the system, which are defined by Eqs. (58)−(62). Solving${{\rm d}x}/{{\rm d}N}= {{\rm d}y}/{{\rm d}N}={{\rm d}r}/{{\rm d}N}={{\rm d}m}/{{\rm d}N}={{\rm d}n}/{{\rm d}N}=0$ yields the equilibrium points. To examine the stability requirements of our model, we compute the eigenvalues from the Jacobian matrix at every equilibrium point. As presented in Table 7, the Table displays the equilibrium points and the associated cosmological parameters. Table 8 shows the characteristic values and stability conditions. We obtain five equilibrium points for the above system of equations.The behavior of the scale factor are given in Table 9.Points x y r m n q ${\omega_{\rm tot}}$ 

$ \omega_{de} $ 

Exists for $ A^{\star} $ 

$ 3\epsilon-\alpha $ 

$ -2\epsilon $ 

$ \epsilon $ 

$ m_{3} $ 

0 1 ${1}/{3}$ 

${1}/{3}$ 

$ \epsilon,m_{3}\neq 0 $ 

$ B^{\star} $ 

$ -\frac{15\epsilon_{1}}{8}-\alpha $ 

$ -\frac{(\zeta+3)\epsilon_{1}}{2} $ 

$ \epsilon_{1} $ 

$ m_{4} $ 

0 1 ${1}/{3}$ 

${1}/{3}$ 

$ m_{4},\epsilon_{1} \neq 0 $ 

$ C_{+}^{\star} $ 

$ -3\epsilon_{2}-\sqrt{\frac{\lambda}{2}}\epsilon_{2}-\alpha $ 

$ \sqrt{\frac{\lambda}{2}}\epsilon_{2} $ 

$ \epsilon_{2} $ 

0 0 –1 –1 –1 $ \epsilon_{2}\neq 0 $ ,

$ \lambda\geq 0 $ 

$ C_{-}^{\star} $ 

$ 3\epsilon_{3}-\sqrt{\frac{\lambda}{2}}\epsilon_{3}-\alpha $ 

$ -\sqrt{\frac{\lambda}{2}}\epsilon_{3} $ 

$ \epsilon_{3} $ 

0 $ n_{1} $ 

${1}/{2}$ 

0 0 $ \epsilon_{3}, n_{1}\neq 0 $ ,

$ \lambda \geq0 $ 

$ D^{\star} $ 

$ -3\epsilon_{4}-\alpha $ 

0 $ \epsilon_{4} $ 

0 0 –1 –1 –1 $ \epsilon_{4}\neq 0 $ .

Table 7. Critical points & physical parameters for the system of equations (58)−(62).
Points $ \nu_{1} $ 

$ \nu_{2} $ 

$ \nu_{3} $ 

$ \nu_{4} $ 

$ \nu_{4} $ 

Criteria $ A^{\star} $ 

4 8 0 0 1 unstable $ B^{\star} $ 

$ \zeta+3 $ 

$ 2(\zeta+3) $ 

0 $ \frac{-2(\zeta+3)}{\epsilon_{1}} $ 

0 unstable at $ \zeta=1 $ ,

$ \epsilon_{1}=-\frac{4}{7} $ 

$ C_{+}^{\star} $ 

$ -\sqrt{2\lambda} $ 

$ -2\sqrt{2\lambda} $ 

$-\frac{(18+\lambda)\sqrt{{\lambda}/{2} } }{(3+\sqrt{{\lambda}/{2} })^{2} }$ 

$ -4-\sqrt{2\lambda} $ 

$ -(\zeta+3)-\sqrt{2\lambda} $ 

stable at $ \lambda\geq0 $ 

$ C_{-}^{\star} $ 

$ \sqrt{2\lambda} $ 

$ -2\sqrt{2\lambda} $ 

0 $ -2(2-\sqrt{2\lambda}) $ 

$ -(\zeta+3)-\sqrt{2\lambda} $ 

saddle at $ \lambda=\frac{9}{2} $ ,

$ \zeta=1 $ 

$ D^{\star} $ 

0 0 0 –4 –3 stable Table 8. Characteristic values and their stability criteria.
Points Accelerating equation Scale factor Phase $ A_{1} $ 

$ \dot{H}=-2H^{2} $ 

$ a(t)=a_{0}(2t+b_{2})^{\frac{1}{2}} $ 

radiation dominated $ B_{1} $ 

$ \dot{H}=-\frac{3}{2}H^{2} $ 

$ a(t)=a_{0}(\frac{3t}{2}+b_{2})^{\frac{2}{3}} $ 

matter dominated $ C_{1} $ 

$ \dot{H}=0 $ 

$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ 

de-Sitter $ D_{1}^{+} $ 

$ \dot{H}=\sqrt{\frac{\lambda}{2}}H^{2} $ 

$a(t)=a_{0}(-\sqrt{\frac{\lambda}{2} }t+b_{4})^{\sqrt{{2}/{\lambda} } }$ 

de-Sitter $ D_{1}^{-} $ 

$ \dot{H}=-\sqrt{\frac{\lambda}{2}}H^{2} $ 

$a(t)=a_{0}(\sqrt{\frac{\lambda}{2} }t+b_{4 })^{\sqrt{{2}/{\lambda} } }$ 

de-Sitter Table 6. Physical behavior of the scale factor at each equilibrium point.
Points Accelerating equation Scale factor Phase $ A^{\star} $ 

$ \dot{H}=-2H^{2} $ 

$a(t)=a_{0}(2t+b_{2})^{{1}/{2} }$ 

radiation dominated $ B^{\star} $ 

$ \dot{H}=-2H^{2} $ 

$a(t)=a_{0}(2t+b_{2})^{{1}/{2} }$ 

radiation dominated $ C_{+}^{\star} $ 

$ \dot{H}=\sqrt{\frac{\lambda}{2}}H^{2} $ 

$a(t)=a_{0}(-\sqrt{\frac{\lambda}{2} }t+b_{4})^{\sqrt{{2}/{\lambda} } }$ 

de-Sitter $ C_{-}^{\star} $ 

$ \dot{H}=-\frac{3}{2}H^{2} $ 

$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3} }$ 

matter dominated $ D^{\star} $ 

$ \dot{H}=0 $ 

$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ 

de-Sitter Table 9. Physical behavior of the scale factor at each equilibrium point.
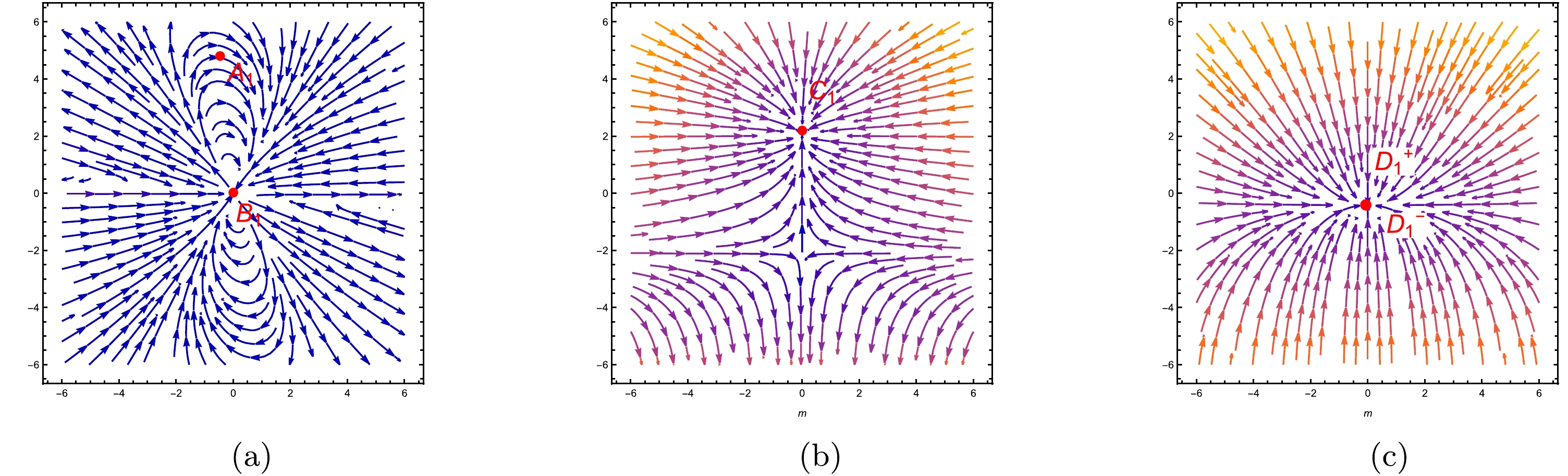
$ \blacktriangleright $ ${{\bf{Point}}\;{A^{\star}}}$ : Table 8 indicates that for critical point$ A^{\star} $ , the characteristic values are$ \nu_{1}=4 $ ,$ \nu_{2}=8 $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=0 $ , and$ \nu_{5}=1 $ . Because three characteristic values, specifically$ \nu_{1} $ ,$ \nu_{2} $ , and$ \nu_{5} $ are positive, whereas two eigenvalues$ \nu_{3} $ and$ \nu_{4} $ vanish, the critical point$ A^{\star} $ demonstrates an unstable node. Upon inspection of Fig. 3, we observe that all trajectories originating from point A indeed verify its unstable nature. At point$ A^{\star} $ , the density parameters are$ \Omega_{m}=0 $ ,$ \Omega_{r}=1 $ , and$ \Omega_{de}=0 $ , which signify the Universe's radiation-dominated phase. Furthermore, at critical point$ A^{\star} $ , the deceleration and EoS parameters take on the values$ q=1 $ and$ \omega _{de}=\omega_{\rm tot}= {1}/{3} $ , respectively, illustrating the decelerating phase of the Universe. The scale factor for point$ A^{\star} $ is expressed as$a(t)=a_{0}(2t+b_{2})^{{1}/{2}}$ , which signifies the Universe's radiation-dominated stage. Here,$ b_{2} $ is integration constant.$ \blacktriangleright $ ${{\bf{Point}}\;{B^{\star}}}$ : Table 8 indicates that for critical point$ B^{\star} $ , the characteristic values are$ \nu_{1}=\zeta+3 $ ,$ \nu_{2}=2(\zeta+3) $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=-\frac{2(\zeta+3)}{\epsilon_{1}} $ , and$ \nu_{5}=0 $ . For$ \zeta=1 $ and$ \epsilon_{1}=-{4}/{7} $ , the eigenvalues become$ \nu_{1}=4 $ ,$ \nu_{2}=8 $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=14 $ , and$ \nu_{5}=0 $ . Because three characteristic values, specifically$ \nu_{1} $ ,$ \nu_{2} $ , and$ \nu_{4} $ are positive, whereas two eigenvalues$ \nu_{3} $ and$ \nu_{5} $ vanish, the critical point$ B^{\star} $ demonstrates an unstable node. Looking at Fig. 3, we observe that every trajectory that starts at point$ B^{\star} $ does confirm that it is unstable. At point$ B^{\star} $ , the density parameters are$ \Omega_{m}=0 $ ,$ \Omega_{r}=1 $ , and$ \Omega_{de}=0 $ , indicating that the Universe is in its radiation-dominated phase. Furthermore, at critical point$ B^{\star} $ , the deceleration and EoS parameters acquire the values$ q=1 $ and$\omega _{de}=\omega_{\rm tot}= {1}/{3}$ , respectively, illustrating the decelerating phase of the Universe. The scale factor for point$ B^{\star} $ is expressed as$a(t)=a_{0}(2t+b_{2})^{{1}/{2}}$ , which signifies the Universe's radiation-dominated stage. Here,$ b_{2} $ is integration constant.$ \blacktriangleright $ ${{\bf{Point}}\;{C_{+}^{\star}}}$ : From Table 8, the characteristic values for the point$ C_{+}^{\star} $ are$ \nu_{1}=-\sqrt{2\lambda} $ ,$ \nu_{2}=-2\sqrt{2\lambda} $ ,$\nu_{3}=-\frac{(18+\lambda)\sqrt{{\lambda}/{2}}}{(3+\sqrt{{\lambda}/{2}})^{2}}$ ,$ \nu_{4}=-4-\sqrt{2\lambda} $ , and$ \nu_{4}=-(\zeta+3)-\sqrt{2\lambda} $ . These characteristic values exists only for$ \lambda\geq 0 $ . As all characteristic values are negative, point$ C_{+}^{\star} $ demonstrates stable behavior. In Fig. 3, all paths lead towards point$ C_{+}^{\star} $ , verifying its stable nature. Point$ C_{+}^{\star} $ is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)= a_{0}(\sqrt{\frac{\lambda}{2}}t+b_{4 })^{\sqrt{{2}/{\lambda}}}$ , illustrates that the different stages of the Universe's evolution depend on the value of$ \lambda $ . If we take$ \lambda=0 $ , then we obtain$ \dot{H}=0 $ , which implies that$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrating the de-Sitter phase of the Universe. Again, it we take$ \lambda=\frac{9}{2} $ , then$ \dot{H}=-\frac{3}{2}H^{2} $ , which implies that$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage. Here,$ b_{2}, b_{3} $ , and$ a_{0} $ are constants. Additionally, according to Table 4, the critical point$ C_{+}^{\star} $ is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$ \omega_{de}=\omega_{\rm tot}=-1 $ , which signify the accelerating phase of the Universe.$ \blacktriangleright $ ${{\bf{Point}}\;{C_{-}^{\star}}}$ : From Table 8, the characteristic values for the point$ C_{-}^{\star} $ are$ \nu_{1}=\sqrt{2\lambda} $ ,$ \nu_{2}=-2\sqrt{2\lambda} $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=-2(2-\sqrt{2\lambda}) $ , and$ \nu_{5}=-(\zeta+3)-\sqrt{2\lambda} $ . For$ \zeta=1 $ and$\lambda={9}/{2}$ , the eigenvalues become$ \nu_{1}=3 $ ,$ \nu_{2}=-6 $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=-1 $ . and$ \nu_{5}=-7 $ . As three characteristic values,$ \nu_{2} $ ,$ \nu_{4} $ , and$ \nu_{5} $ , are negative, whereas the other one,$ \nu_{1} $ is positive, the critical point$ C_{-}^{\star} $ exhibits unstable saddle behavior. The saddle behaviour of point$ C_{-}^{\star} $ is confirmed by the trajectories that both diverge from and converge towards it, as shown in Fig. 3. The density parameters at$ C_{-}^{\star} $ are$ \Omega_{m}=1 $ ,$ \Omega_{r}=0 $ , and$ \Omega_{de}=0 $ , demonstrating the matter-dominated phase of the Universe. Additionally, at critical point$ C_{-}^{\star} $ , the deceleration and EoS parameters are$ q=1 $ and$\omega _{de}=\omega_{\rm tot}= {1}/{3}$ , respectively, indicating the Universe is in a decelerating phase. The scale factor for point$ C_{-}^{\star} $ is expressed as$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage. Here,$ b_{2} $ is integration constant.$ \blacktriangleright $ ${{\bf{Point}}\;D^{\star} }$ : Table 8 indicates that for critical point$ D^{\star} $ , the characteristic values are$ \nu_{1}=0 $ ,$ \nu_{2}=0 $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=-4 $ , and$ \nu_{5}=-3 $ . With three zero eigenvalues and two negative eigenvalues, this critical point possesses a non-hyperbolic nature. Linear stability theory cannot offer insights into the stability of critical points that possess zero eigenvalues. Additionally, if we examine the central manifold theorem, we observe that the nonlinear part at zero does not vanish after separating from the linear and nonlinear parts of the given equations. Thus, it cannot elucidate the stability of this critical point. In such scenarios, relying on the phase diagram is the only option to analyze the stability behavior at this point. In Fig. 3, all paths lead towards point$ D^{\star} $ , suggesting the stable nature of critical point$ D^{\star} $ . Point$ D^{\star} $ is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrates the exponential growth typical of the Universe's dominance by DE. Here,$ b_{3} $ is integration constant. Additionally, according to Table 7, critical point$ D^{\star} $ is characterized by a deceleration parameter of$ q=-1 $ and Equation of State (EoS) parameters$\omega_{de}=\omega_{\rm tot}=-1$ , which signify the accelerating phase of the Universe.$ \bullet $ ${{\bf{Model\;2:}}\;F(Q,C)\;=\;\alpha Q+\frac{\beta}{C}}.$ Utilizing the aforementioned model, the set of ODEs in terms of z is derived by applying Eq. (47) and the previously mentioned variables (57):
$ \begin{aligned} \frac{{\rm d}x}{{\rm d}N}=-\bigg(\frac{6yr+\lambda r^{2}+2xy+2\alpha y}{r}\bigg), \end{aligned} $

(64) $ \begin{aligned} \frac{{\rm d}y}{{\rm d}N}=-\frac{2y(6y+\lambda r)}{(3r+y)}+\lambda r-\frac{2y^{2}}{r}, \end{aligned} $

(65) $ \begin{aligned} \frac{{\rm d}r}{{\rm d}N}=-\frac{2r(6y+\lambda r)}{3r+y}, \end{aligned} $

(66) $ \begin{aligned} \frac{{\rm d}m}{{\rm d}N}=-\frac{2m}{r}(2r+y), \end{aligned} $

(67) $ \begin{aligned} \frac{{\rm d}n}{{\rm d}N}=-\frac{n}{r}\bigg[(\zeta+3)r+2y\bigg]. \end{aligned} $

(68) Using the aforementioned model and the field Eq. (17), the density parameter may be determined as follows:
$ \begin{aligned} \Omega_{r}=m, \quad \Omega_{m}=n, \quad \Omega_{de}=1-x+2\alpha-3r-y-z-m-n. \end{aligned} $

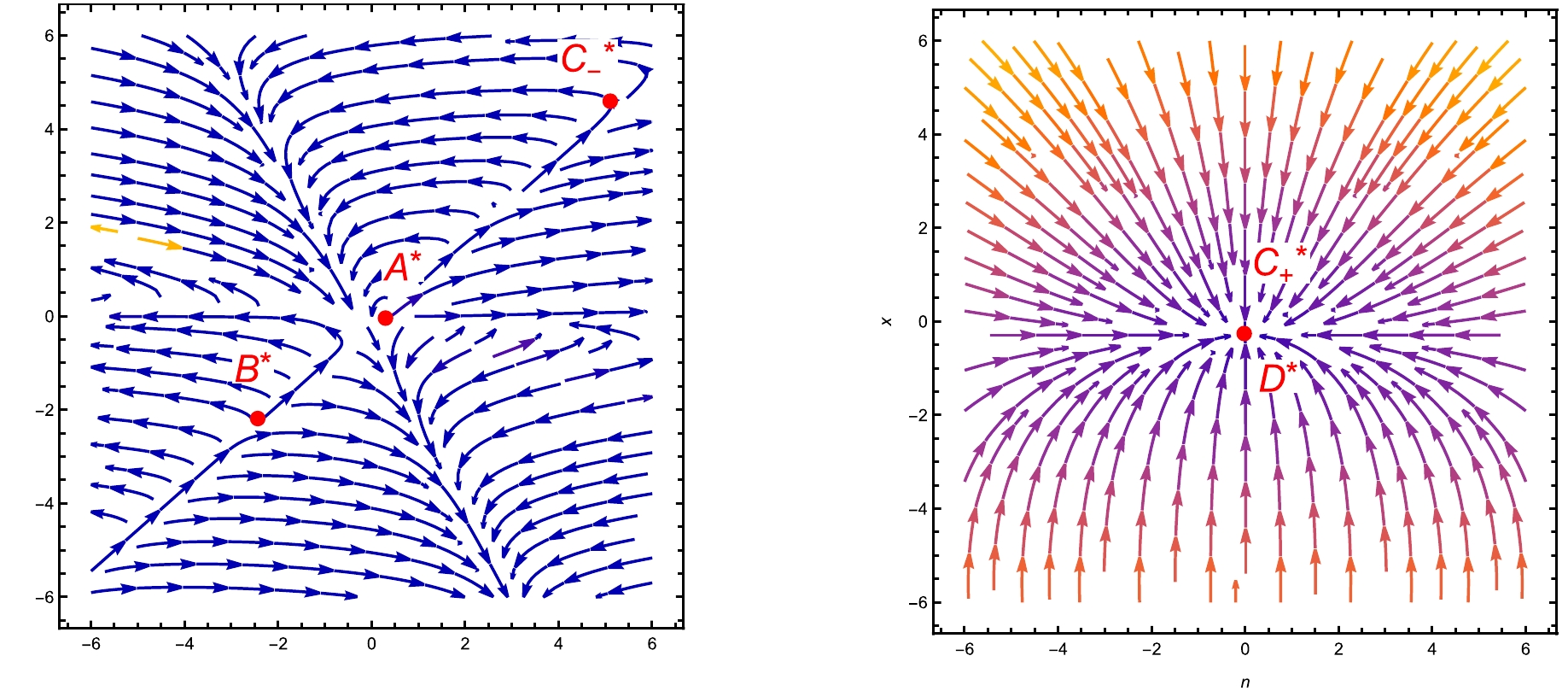
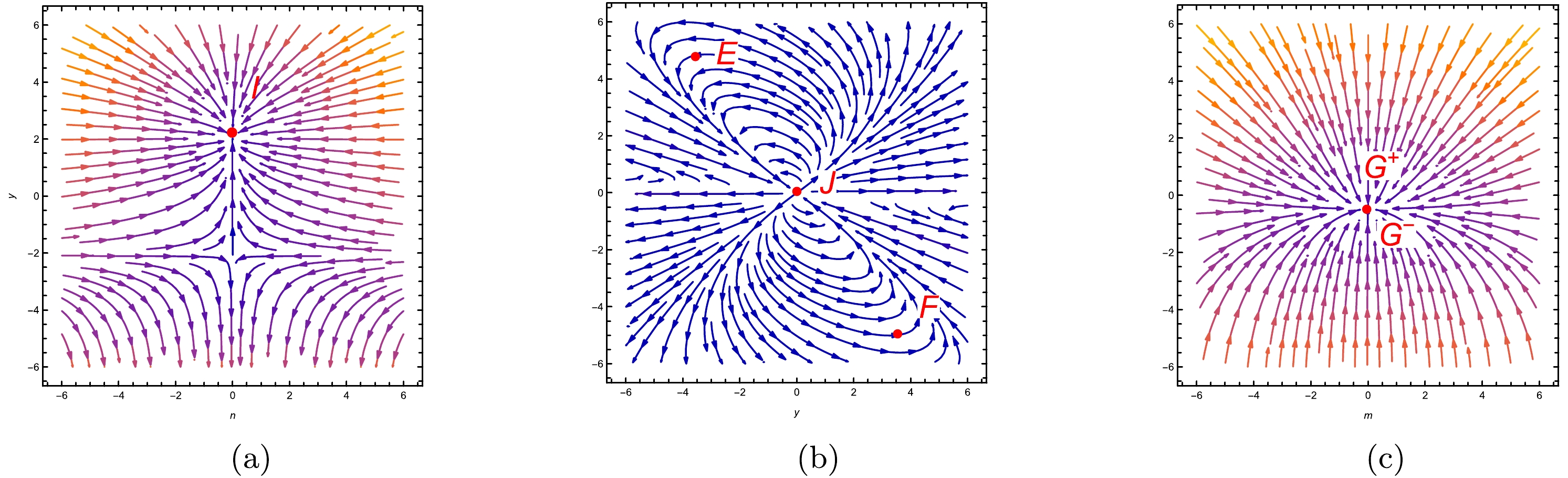
(69) $ \blacktriangleright $ ${{\bf{Point}}\;{E}}$ : From Table 11, the characteristic values for the point E are$ \nu_{1}=4 $ ,$ \nu_{2}=-16 $ ,$ \nu_{3}=-8 $ ,$ \nu_{4}=0 $ , and$ \nu_{5}=0 $ . As two characteristic values,$ \nu_{2} $ and$ \nu_{3} $ , are negative, whereas the other one,$ \nu_{1} $ is positive, the critical point E exhibits unstable saddle behavior. The saddle behaviour of point E is confirmed by the trajectories that both diverge from and converge towards it, as shown in Fig. 4(a). The density parameters at E are$ \Omega_{m}=0 $ ,$ \Omega_{r}=1 $ , and$ \Omega_{de}=0 $ , demonstrating the radiation-dominated phase of the Universe. Additionally, at critical point E, the deceleration and EoS parameters are$ q=1 $ and$\omega _{de}=\omega_{\rm tot}=\frac{1}{3}$ , respectively, indicating the Universe is in a decelerating phase. The scale factor for point E is expressed as$ a(t)=a_{0}(2t+b_{2})^{\frac{1}{2}} $ , which signifies the Universe's radiation-dominated stage. Here,$ b_{2} $ is integration constant.Points $ \nu_{1} $ 

$ \nu_{2} $ 

$ \nu_{3} $ 

$ \nu_{4} $ 

$ \nu_{4} $ 

Criteria E 4 -16 -8 0 0 saddle F 4 -24 -12 0 0 saddle $ G^{+} $ 

$ -\sqrt{2\lambda} $ 

$ -2\sqrt{2\lambda} $ 

$-\frac{2\lambda(6+\sqrt{2\lambda})}{(3+\sqrt{{\lambda}/{2} })^{2} }$ 

$ -4-\sqrt{2\lambda} $ 

$ -(\zeta+3)-\sqrt{2\lambda} $ 

stable at $ \lambda\geq0 $ 

$ G^{-} $ 

$ -\sqrt{2\lambda} $ 

$ -2\sqrt{2\lambda} $ 

$-\frac{2\lambda(6+\sqrt{2\lambda})}{(3-\sqrt{{\lambda}/{2} })^{2} }$ 

$ -2(2-\sqrt{2\lambda}) $ 

$ -(\zeta+3)-\sqrt{2\lambda} $ 

stable at $ \lambda\geq0 $ 

I 0 0 0 –4 –4 stable J 3 36 8 0 1 unstable Table 11. Characteristic values and their stability criteria.
$ \blacktriangleright $ ${{\bf{Point}}\;{F}}$ : From Table 11, the characteristic values for point F are$ \nu_{1}=4 $ ,$ \nu_{2}=-24 $ ,$ \nu_{3}=-12 $ ,$ \nu_{4}=0 $ , and$ \nu_{5}=0 $ . As two characteristic values,$ \nu_{2} $ and$ \nu_{3} $ , are negative, whereas the other one,$ \nu_{1} $ is positive, critical point F exhibits unstable saddle behavior. The saddle behaviour of point F is confirmed by the trajectories that both diverge from and converge towards it, as shown in Fig. 4(b). The density parameters at F are$ \Omega_{m}=0 $ ,$ \Omega_{r}=1 $ , and$ \Omega_{de}=0 $ , demonstrating the radiation-dominated phase of the Universe. Additionally, at critical point E, the deceleration and EoS parameters are$ q=1 $ and$ \omega _{de}=\omega_{\rm tot}={1}/{3} $ , respectively, indicating the Universe is in a decelerating phase. The scale factor for point F is expressed as$ a(t)=a_{0}(2t+b_{2})^{\frac{1}{2}} $ , which signifies the Universe's radiation-dominated stage. Here,$ b_{2} $ is integration constant.$ \blacktriangleright $ ${{\bf{Point}}\;{G^{+}}}$ : From Table 11, the characteristic values for the point$ G^{+} $ are$ \nu_{1}=-\sqrt{2\lambda} $ ,$ \nu_{2}=-2\sqrt{2\lambda} $ ,$\nu_{3}= -\frac{2\lambda(6+\sqrt{2\lambda})}{(3+\sqrt{{\lambda}/{2}})^{2}}$ ,$ \nu_{4}=-4-\sqrt{2\lambda} $ , and$ \nu_{4}=-(\zeta+3)-\sqrt{2\lambda} $ . These characteristic values exists only for$ \lambda\geq 0 $ . As all characteristic values are negative, point$ G^{+} $ demonstrates stable behavior. In Fig. 4(c), all paths lead towards point$ G^{+} $ , verifying its stable nature. Point$ G^{+} $ is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)= a_{0}\cdot $ $(\sqrt{{\lambda}t/{2}}+b_{4 })^{\sqrt{{2}/{\lambda}}}$ , shows that the different stages of the Universe's evolution depend on the value of$ \lambda $ . If we take$ \lambda=0 $ , then we obtain$ \dot{H}=0 $ , which implies that$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrating the de-Sitter phase of the Universe. Again, it we take$ \lambda= {9}/{2} $ , then$ \dot{H}=-{3}/{2}H^{2} $ , which implies that$a(t)= a_{0}({3t}/{2}+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage. Here,$ b_{2}, b_{3} $ , and$ a_{0} $ are constants. Additionally, according to Table 12, the critical point$ G^{+} $ is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$ \omega_{de}=\omega_{\rm tot}=-1 $ , which signify the accelerating phase of the Universe.Points Accelerating equation Scale factor Phase E $ \dot{H}=-2H^{2} $ 

$a(t)=a_{0}(2t+b_{2})^{{1}/{2} }$ 

radiation dominated F $ \dot{H}=-2H^{2} $ 

$a(t)=a_{0}(2t+b_{2})^{{1}/{2} }$ 

radiation dominated $ G^{+} $ 

$ \dot{H}=\sqrt{\frac{\lambda}{2}}H^{2} $ 

$a(t)=a_{0}(-\sqrt{\frac{\lambda}{2} }t+b_{4})^{\sqrt{{2}/{\lambda} } }$ 

de-Sitter $ G^{-} $ 

$ \dot{H}=-\sqrt{\frac{\lambda}{2}}H^{2} $ 

$a(t)=a_{0}(-\sqrt{\frac{\lambda}{2} }t+b_{4})^{\sqrt{{2}/{\lambda} } }$ 

de-Sitter I $ \dot{H}=0 $ 

$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ 

de-Sitter J $ \dot{H}=-\frac{3}{2}H^{2} $ 

$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3} }$ 

matter dominated Table 12. Physical behavior of the scale factor at each equilibrium point.
$ \blacktriangleright $ ${{\bf{Point}}\;{G^{-}}}$ : From Table 11, the characteristic values for the point$ G^{-} $ are$ \nu_{1}=-\sqrt{2\lambda} $ ,$ \nu_{2}=-2\sqrt{2\lambda} $ ,$\nu_{3}= -\frac{2\lambda(6+\sqrt{2\lambda})}{(3-\sqrt{{\lambda}/{2}})^{2}}$ ,$ \nu_{4}=-4-2\sqrt{2\lambda} $ and$ \nu_{4}=-(\zeta+3)-\sqrt{2\lambda} $ . These characteristic values exists only for$ \lambda\geq 0 $ . As all characteristic values are negative, point$ G^{-} $ exhibits stable behavior. In Fig. 4(b), all paths lead towards point$ G^{-} $ , verifying its stable nature. Point$ G^{-} $ is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)= a_{0} (\sqrt{\frac{\lambda}{2}}t+ b_{4 })^{\sqrt{{2}/{\lambda}}}$ , shows that the different stages of the Universe's evolution depend on the value of$ \lambda $ . If we take$ \lambda=0 $ , then we obtain$ \dot{H}=0 $ , which implies that$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrating the de-Sitter phase of the Universe. Again, it we take$ \lambda= {9}/{2} $ , then$ \dot{H}=-{3}/{2}H^{2} $ , which implies that$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage. Here,$ b_{2} $ and$ b_{3} $ are constants, and$ a_{0} $ is the scale factor at$ t=0 $ . Additionally, according to Table 12, the critical point$ G^{-} $ is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$\omega_{de}= \omega_{\rm tot}=-1$ , which signify the accelerating phase of the Universe.$ \blacktriangleright $ ${{\bf{Point}}\;{I}}$ : Table 11 indicates that for critical point I, the characteristic values are$ \nu_{1}=0 $ ,$ \nu_{2}=0 $ ,$ \nu_{3}=0 $ ,$ \nu_{4}=-4 $ and$ \nu_{5}=-4 $ . With three zero eigenvalues and two negative eigenvalues, this critical point is non-hyperbolic. Linear stability theory cannot offer insights into the stability of critical points that possess zero eigenvalues. Additionally, if we examine the central manifold theorem, we observe that the nonlinear part at zero does not vanish after separating from the linear and nonlinear parts of the given equations. Thus, it cannot elucidate the stability of this critical point. In such scenarios, relying on the phase diagram is the only option to analyze the stability behavior at this point. In Fig. 4(c), all paths lead towards point I, suggesting the stable nature of critical point I. Point I is characterised by the density parameters$ \Omega_{m}=\Omega_{r}=0 $ and$ \Omega_{de}=1 $ , which signify the DE-dominated phase of the Universe. The scale factor for this point, denoted by$a(t)=a_{0}{\rm{e}}^{b_{3}t}$ , illustrates the exponential growth typical of the Universe's dominance by DE. Here,$ b_{3} $ is integration constant. Additionally, according to Table 10, critical point I is characterized by a deceleration parameter of$ q=-1 $ and EoS parameters$\omega_{de}=\omega_{\rm tot}=-1$ , which signify the accelerating phase of the Universe.Points x y r m n q $\omega_{\rm tot}$ 

$ \omega_{de} $ 

Exists for E $ -3a_{1}^{\star}-\alpha $ 

$ -2a_{1}^{\star} $ 

$ a_{1}^{\star} $ 

$ m_{1}^{\star} $ 

0 1 ${1}/{3}$ 

${1}/{3}$ 

$ a_{1}^{\star}, m_{1}^{\star}\neq 0 $ 

F $ -3a_{2}^{\star}-\alpha $ 

$ -\frac{(\zeta+3)a_{2}^{\star}}{2} $ 

$ a_{2}^{\star} $ 

$ m_{2}^{\star} $ 

0 1 ${1}/{3}$ 

${1}/{3}$ 

$ m_{2}^{\star}, a_{2}^{\star} \neq 0 $ 

$ G^{+} $ 

$ -3a_{3}^{\star}-\sqrt{\frac{\lambda}{2}}a_{3}^{\star}-\alpha $ 

$ \sqrt{\frac{\lambda}{2}}a_{3}^{\star} $ 

$ a_{3}^{\star} $ 

0 0 –1 –1 –1 $ a_{3}^{\star}\neq 0 $ ,

$ \lambda\geq 0 $ 

$ G^{-} $ 

$ -3a_{4}^{\star}+\sqrt{\frac{\lambda}{2}}a_{4}^{\star}-\alpha $ 

$ -\sqrt{\frac{\lambda}{2}}a_{4}^{\star} $ 

$ a_{4}^{\star} $ 

0 0 –1 –1 –1 $ a_{4}^{\star}\neq 0 $ ,

$ \lambda \geq0 $ 

I $ a_{5}^{\star} $ 

0 $ a_{6}^{\star} $ 

0 0 –1 –1 –1 $ a_{5}^{\star}, a_{6}^{\star}\neq 0 $ .

J $ -\frac{3a_{7}^{\star}}{2}-\alpha $ 

$ -\frac{3a_{7}^{\star}}{2} $ 

$ a_{7}^{\star} $ 

0 $ n_{1}^{\star} $ 

$ \frac{1}{2} $ 

0 0 $ a_{7}^{\star}, n_{1}^{\star}\neq 0 $ 

Table 10. Critical points & physical parameters for the system of Eqs. (64)−(68).
$ \blacktriangleright $ ${{\bf{Point}}\;{J}}$ : Table 11 indicates that for critical point J, the characteristic values are$ \nu_{1}=3 $ ,$ \nu_{2}=36 $ ,$ \nu_{3}=8 $ ,$ \nu_{4}=0 $ , and$ \nu_{5}=1 $ . Because three characteristic values, specifically$ \nu_{1} $ ,$ \nu_{2} $ , and$ \nu_{5} $ are positive, whereas one eigenvalue$ \nu_{4} $ vanishes, the critical point J is an unstable node. Upon inspection of Fig. 4(c), we observe that all trajectories originating from point J indeed verify its unstable nature. The density parameters at J are$ \Omega_{m}=1 $ ,$ \Omega_{r}=0 $ , and$ \Omega_{de}=0 $ , demonstrating the matter-dominated phase of the Universe. Additionally, at critical point J, the deceleration and EoS parameters are$ q= {1}/{2} $ and$\omega _{de}=\omega_{\rm tot}=0$ , respectively, indicating the Universe is in a decelerating phase. The scale factor for point J is expressed as$a(t)=a_{0}(\frac{3t}{2}+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated stage. Here,$ b_{2} $ is integration constant.In Table 8, one critical point
$ C_{-}^{\star} $ , as well as the critical point J in 11, has a zero eigenvalue, indicating that these points are non-hyperbolic. Coley [57] has demonstrated that for non-hyperbolic critical points, the dimension of the set of characteristic values is equal to the number of vanishing characteristic values, which is 1. Therefore, the set of characteristic values is typically hyperbolic, making the critical point stable, although it is not necessarily a global attractor. Our computation yields a single disappearing characteristic value and a single-dimensional set of characteristic value. In simpler terms, the number of characteristic values that vanish from a collection of distinct values determines its dimension. Thus, the latest data show the accelerated stage of the Universe and are compatible for the equilibrium points ($ C_{-}^{\star} $ and J). -
Our study explores
$ f(Q, C) $ gravity theory through the analysis of dynamical systems. We identify four critical points for model 3.1. Table 1 shows the critical points along with their respective cosmic parameters that have been examined. The characteristic values are as follows:$ A=(-3a_{1}-\alpha,-2a_{1},a_{1},m_{1}) $ ,$ B=(\frac{11a_{2}}{6}+\alpha,-\frac{3a_{2}}{2},a_{2},0) $ ,$C= (a_{3},0,a_{4},0)$ , and$ D=(-\alpha-3a_{5}, a_{6}, a_{5}, 0) $ . The critical point$ (A) $ exhibits instability. Moreover, with$ q=1 $ and$ \omega_{de}=\omega_{\rm tot}= {1}/{3} $ , it indicates that the Universe is experiencing a decelerated stage. The scale factor at this point is$a(t)=a_{0}(2t+b_{1})^{{1}/{2}}$ , which signifies the Universe's radiation-dominated phase. The critical point$ (B) $ is an unstable saddle point. Moreover, with$ q= {1}/{2} $ and$\omega_{de}=\omega_{\rm tot}=0$ , it indicates that the Universe is experiencing a decelerated stage. The scale factor at this point is$a(t)=a_{0}(\frac{3}{2}t+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated phase. Critical points C and F are stable. With$ q=-1 $ and$\omega_{de}=\omega_{\rm tot}=-1$ , the Universe is in an accelerated stage. The scale factor for these points is$a(t)=a_{0}{\rm{e}}^{a_{2}t}$ , signifying the Universe's DE-dominated phase. Again, we identify five critical points for model 3.2, the characteristic values are as follows:$ A_{1}=(-3a_{7}-\alpha,-2a_{7},a_{7},m_{2}) $ ,$B_{1}= (-\frac{3a_{8}}{2}-\alpha,-\frac{3a_{8}}{2},a_{8},0)$ ,$ C_{1}=(a_{9},0,a_{10},0) $ ,$D_{1}^{+}=(-3a_{11}- \sqrt{\frac{\lambda}{2}}a_{11}- \alpha,\sqrt{\frac{\lambda}{2}}a_{11},a_{11},0)$ , and$D_{1}^{-}=(-3a_{12}+\sqrt{\frac{\lambda}{2}}a_{12}-\alpha, -\sqrt{\frac{\lambda}{2}}a_{12},a_{12},0)$ . The critical point$ (A_{1}) $ is an unstable saddle point. Moreover, with$ q=1 $ and$\omega_{de}=\omega_{\rm tot}= {1}/{3}$ , it indicates that the Universe is experiencing a decelerated stage. The scale factor at this point is$a(t)=a_{0}(2t+b_{1})^{{1}/{2}}$ , which signifies the Universe's radiation-dominated phase. The critical point$ (B_{1}) $ exhibits instability. Moreover, with$q= {1}/{2}$ and$\omega_{de}=\omega_{\rm tot}=0$ , it indicates that the Universe is experiencing a decelerated stage. The scale factor at this point is$a(t)=a_{0}(\frac{3}{2}t+b_{2})^{{2}/{3}}$ , which signifies the Universe's matter-dominated phase. Critical points$ C_{1} $ ,$ D_{1}^{+} $ and$ D_{1}^{-} $ are stable. With$ q=-1 $ and$\omega_{de}=\omega_{\rm tot}=-1$ , the Universe is in an accelerated stage. The scale factor for these points is$a(t)=a_{0}{\rm{e}}^{a_{2}t}$ , signifying the Universe's DE-dominated phase. The phase portraits for both models are shown in Figs. 1 and 2. The details regarding the critical points and characteristic values of models 3.1 and 3.2 are presented in Tables [1−6]. Therefore, we have successfully demonstrated the accelerated stage of the Universe and the stability of our model.We again execute the dynamical system by presuming the interaction term
$ \mathcal{Q}=\zeta H \rho_{m} $ for our models. For model 3.1, where$ F(Q,C) $ $ = $ $\alpha Q+\beta C {\rm log}C$ , five critical points are identified; among these two critical points,$ C_{+}^{\star} $ and$ D^{\star} $ are stable,$ A^{\star} $ and$ B^{\star} $ are unstable, and$ C_{-}^{\star} $ is saddle. For model 3.2, where$ F(Q,C) $ $ = $ $ \alpha Q+\frac{\beta}{C} $ , six critical points are identified; among these three critical points,$ G^{+} $ ,$ G^{-} $ , and I are stable, E and F are saddle, and J is unstable. The stable critical points manifest during the de-Sitter stage, whereas the unstable and saddle behaviors occur during the radiation and matter-dominated stages of the Universe. The characterization of the critical points is determined by analyzing the eigenvalue signatures, which is further validated through the phase portrait. The trajectories clearly show movement towards both unstable critical points and stable attractors. Saddle points are indicated by trajectories diverging from and converging towards these points. At the stable critical points, both the values of the deceleration and EoS parameters are −1, indicating an accelerating stage consistent with the$ \Lambda $ CDM model.
Phase space analysis of interacting and non-interacting models in f(Q, C) gravity
- Received Date: 2024-07-17
- Available Online: 2025-01-15
Abstract: Using a dynamical system method, we study a Friedmann-Robertson-Walker (FRW) cosmological model within the context of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: