Quark stars in f(R, T) gravity: mass-to-radius profiles and observational data

The studies of alternative theories of gravity have recently gained significant attention, motivated by the desire to address various unresolved issues in cosmology and astrophysics [1−4]. Among these theories, $ f(R,T) $ gravity, proposed by Harko et al. [5], introduced coupling between the matter content and the geometry of spacetime [6−8]. This theory extends the well-known $ f(R) $ gravity [9] by including a dependence on the trace of the energy-momentum tensor T [10]. Such modifications can lead to interesting phenomenological consequences, especially in the context of compact astrophysical objects like neutron stars and QSs [11−15].

$ f(R,T) $ gravity, where the gravitational action depends on the Ricci scalar R and the trace of T, results in modified Einstein field equations, impacting the structure and dynamics of stellar objects significantly [16, 17]. Numerous studies have explored the cosmological and astrophysical applications of $ f(R,T) $ gravity, highlighting its potential to explain dark energy, dark matter, and other phenomena beyond the standard model of cosmology [18−21]. In particular, several researchers have investigated the impact of $ f(R,T) $ gravity on cosmological models, providing insights into the accelerated expansion of the universe without invoking dark energy [22−24]. Additionally, $ f(R,T) $ gravity has been applied to the study of gravitational lensing, suggesting that it can account for the observed anomalies in lensing phenomena [25, 26]. The theory has also been used to address the hierarchy problem and late-time cosmic acceleration, further emphasizing its versatility and potential [27].

QSs, which are hypothetical compact objects composed entirely of deconfined quark matter, provide an excellent testbed for studying the effects of modified gravity theories [28]. In particular, interacting quark matter (IQM) [14] equations of state (EoS) incorporating perturbative QCD corrections and color superconductivity have been considered to describe the internal composition of QSs [29]. Such models can predict the existence of extremely dense and massive compact stars, potentially observable through gravitational wave events and pulsar timing measurements [30−32].

The Tolman-Oppenheimer-Volkoff (TOV) equations [33, 34], which describe the equilibrium structure of spherically symmetric stars, are modified in $ f(R,T) $ gravity due to the additional matter-geometry coupling terms. Previous studies have shown that these modifications can lead to significant deviations from the predictions of General Relativity (GR), particularly in the context of neutron stars, black holes, and wormholes [35−38]. The resulting mass-radius relations, stability criteria, and other properties of compact stars in $ f(R,T) $ gravity have been the subject of extensive research [39, 40].

The study primarly investigates the structural properties of QSs within the framework of $ f(R,T) $ gravity. We derive the modified Einstein field equations and the corresponding TOV equations for a spherically symmetric, static spacetime. Using these equations, we explore the mass-radius relation, stability criteria, and energy conditions for QSs described by an IQM EoS. We compare our results with recent observational data to assess the viability of $ f(R,T) $ gravity in describing compact stars.

The remainder of the paper is organized as follows: In Sec. II, we review the $ f(R,T) $ gravity theory and derive the modified field equations. Sec. III discusses the structural equations for QSs in this theoretical framework. In Sec. IV, we introduce the equations of state for quark matter and boundary conditions. The numerical results and their implications are presented in Sec. V. Section VI provides an analysis of the stability criteria, adiabatic index, energy conditions, sound speed and causality, and polytropic index. Finally, we summarize our findings and discuss future research directions in Sec. VII.

Here, we review the $ f(R,T) $ gravity theory proposed by Harko et al [5], and the action integral is given by

where the action of the gravitational field depends on a generic function of curvature scalar $ R = g^{\mu\nu}R_{\mu\nu} $ and the trace T of the energy-momentum tensor. Here, $ {\cal{L}}_m $ stands for the matter Lagrangian density and is related to the stress-energy tensor of the matter fields in the usual way as

Assuming $ {\cal{L}}_m $ depends on the metric components $ g_{\mu\nu} $and not on its derivatives, which implies that [5]

and varying action (1), we obtain the modified Einstein field equations in $ f(R,T) $ gravity as follows:

where $ f_R (R,T) = \partial f(R,T)/\partial R $, $ f_T (R,T) = \partial f(R,T)/\partial T $, $ \Box \equiv \partial_{\mu}(\sqrt{-g} g^{\mu\nu} \partial_{\nu})/\sqrt{-g} $, $ R_{\mu\nu} $ is the Ricci tensor, $ \nabla_\mu $ denotes the covariant derivative with respect to the metric $ g_{\mu\nu} $, and we have defined $ \Theta_{\mu\nu} = g^{\alpha\beta}\delta T_{\alpha\beta}/\delta g^{\mu\nu} $. Now, taking covariant derivatives with respect to the field Eq. (4), and we have

which is significant in discussing the energy properties of the model. Furthermore, we also assume that the matter content described by a standard perfect fluid with stress-energy tensor $ T_{\mu\nu} $ can be written as

where ρ and P are the energy density and pressure for the isotropic fluid sphere, and $ u^{\mu} $ is the four-velocity of the fluid with $ u^{\mu}u_{\mu} = 1 $. Additionally, we assume the matter Lagrangian $ {\cal{L}}_m = -P $, which allows us to rewrite $ \Theta_{\mu\nu} $ as

Herein, we opt for the simplest linear functional form $ f(R,T) = R+ 2\beta T $, which was considered in Ref. [5]. This choice has been widely employed in numerous cosmological solutions of $ f(R,T) $ gravity. Based on this assumption, the field Eq. (4) and the conservation equation Eq. (5) is reduce to

where $ G_{\mu\nu} $ is the Einstein tensor and β is an arbitrary constant. One may also verify that when $ \beta = 0 $, the standard Einstein field equation is recovered. Moreover, Eq. (9) clearly demonstrates that $ f(R,T) $ gravity leads to non-conservation of the energy-momentum tensor. Therefore, $ f(R,T) $ theory can be treated as a curvature-matter coupling theory, and an exchange of energy and momentum between both produces an extra force [41].

In this theoretical framework, we consider a static and spherically symmetric spacetime described by the following metric

where the metric functions $ \Phi(r) $ and $ \Lambda(r) $ depend on the radial coordinate, r. Then, using Eqs. (10) and (6) together with the modified field equation (8), we obtain the following $ (tt) $ and $ (rr) $ components of field equations in the $ f(R,T) $ theory [42] as follows:

Under this assumption, the conservation equation (9) can be rewritten as follows [43, 44]:

where prime represents the derivative of r. To recast Eqs. (11)−(13) into a more familiar form, we introduce a mass parameter, $ m(r) $, defined by ${\rm e}^{-2\Lambda} = 1-\dfrac{2 m(r)}{ r}$. Since $ m(r) $ is the mass within a sphere of radius r. After some straightforward calculations, two autonomous equations are obtained, which are expressed as [45, 46]

Naturally, by setting $ \beta \to 0 $, we restore the usual TOV equation. Notably, in $ f(R,T) $ gravity, the coupling constant β has some constraints from NS mass measurements [47]. In this context, authors in [48] have studied the radial perturbations and stability of compact stars by calculating the oscillation mode frequency square. For a complete description of the stellar configuration, Eqs. (14) and (15) must be supplemented by an EoS. In this study, we aim to demonstrate the possible existence of QSs entirely composed of interacting quark matter, including perturbative QCD corrections and color superconductivity (see [49] and the references therein).

QSs hypothetically exist as compact objects made of strange quark matter (SQM), and they can potentially exist in different unusual forms of matter, such as quarkyonic matter [50, 51], color superconductivity [52, 53], ∆-isobar configurations, and hyperons [54−56], among others. In Ref. [49], we found an interacting quark matter (IQM) EoS with a superconducting effect and quantum chromodynamics (pQCD) corrections. Thus, this study will explore the possible existence of QSs composed entirely of IQM within the framework of $ f(R,T) $ gravity. According to the definition provided in Refs. [49, 57], the energy density and pressure (i.e., the EoS) are expressed as

where the effective bag constant is represented by $ B_{\rm{eff}} $, which represents the nonperturbative contribution from the QCD vacuum, and the constant coefficient λ is expressed as

where $ m_s $ is the mass of the strange quark and ∆ is the gap parameter. The pQCD corrections are represented by the $ (1-a_4) $ term up to $ O(\alpha_s^2) $. Importantly, the quartic coefficient $ a_4 $ can vary from the value $ a_4 = 1 $ [58] when no strong interactions are considered. Moreover, the value of λ is positive as long as $ \Delta^2/m_s^2 > \xi_{2b}/\xi_{2a} $, and we restrict ourselves to consider only positive λ values. The coefficients in λ for various color-superconducting phases are defined as:

Taking a step towards more realistic situation, Zhang and Mann [49] proposed a dimensional rescaling as follows:

and

Now, utilizing these rescalings in (19) and (20), we can redefine the equation of state (16) in a dimensionless form as follows:

Note that for $ \bar{\lambda} \to 0 $, the above expression becomes a noninteracting quark matter, $ \bar{p} = \dfrac{1}{3}(\bar{\rho}-1) $. Moreover, $ \bar{\lambda}\gg 0 $ i.e., a sufficiently large value of $ \bar{\lambda} $ gives,

Equivalently, $ p = {\rho}-2B_{\rm{eff}} $ after reverting the scaling using Eq. (19). This study only considers the positive values of λ, as $ \lambda<0 $ does not yield a finite form. For instance, the above EoS (19) and a significantly broader range of $ \lambda>0 $ leads to heavier QSs that are consistent with the 2$ M_{\odot} $ constraint (see, e.g., [49, 57, 59] for a review of recent works). In Figs. 1 and 2, we plot the energy density and isotropic pressure for the given IQM EoS (21). The utilized parameter sets are provided in Table 1 and 1, respectively. The figures show a monotonic decrease in both energy density and pressure towards the surface of the star.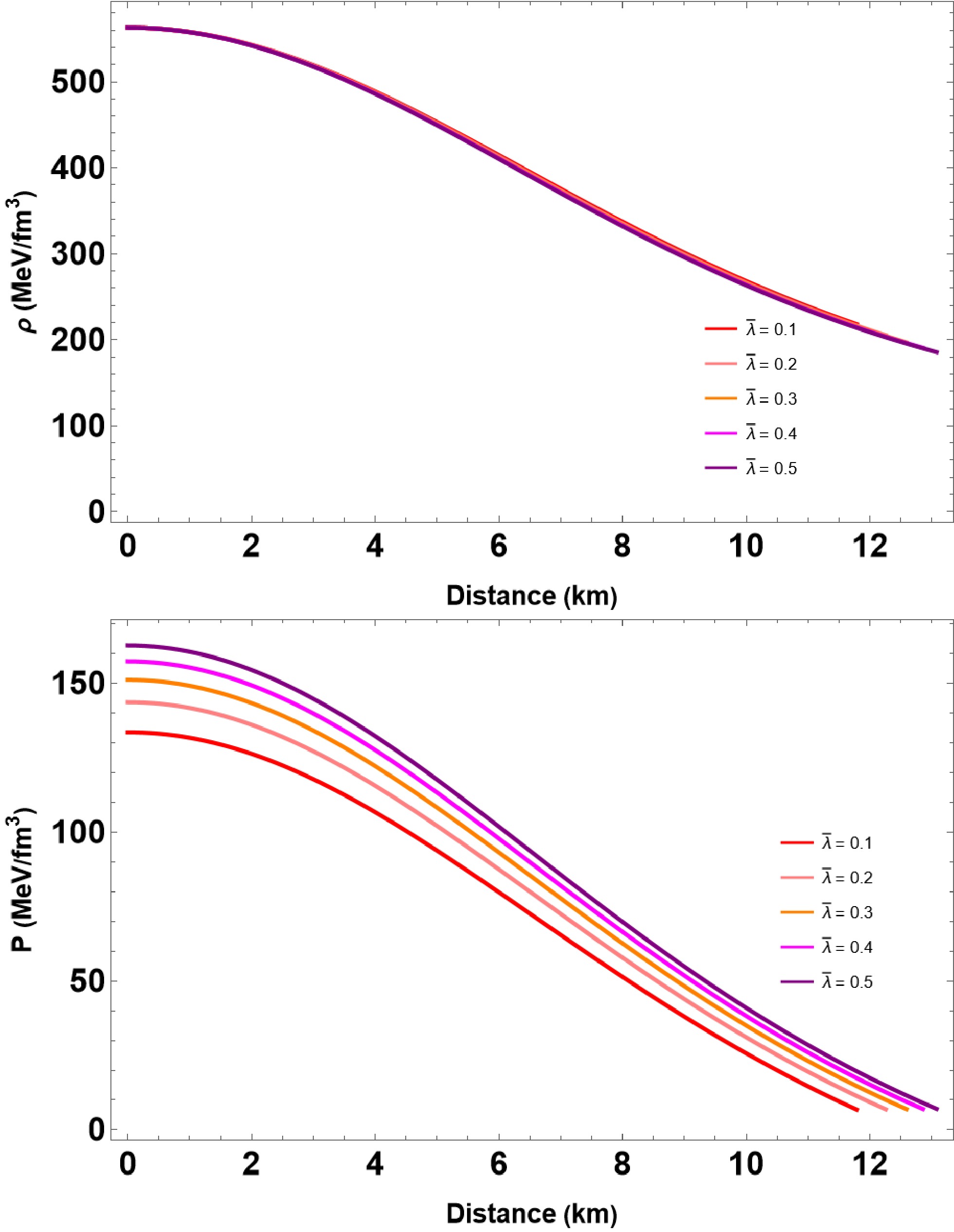

Figure 1.  (color online) We plot the energy density and isotropic pressure for solving the TOV equations (14) and (15) with the given EoS (21). For computation, we vary $\bar{\lambda} \in [0.1, $$ 0.5]$ and set the other parameters as $ B_{\rm{eff}} = 60 $ MeV/fm³ and $ \beta = 0.1 $, respectively.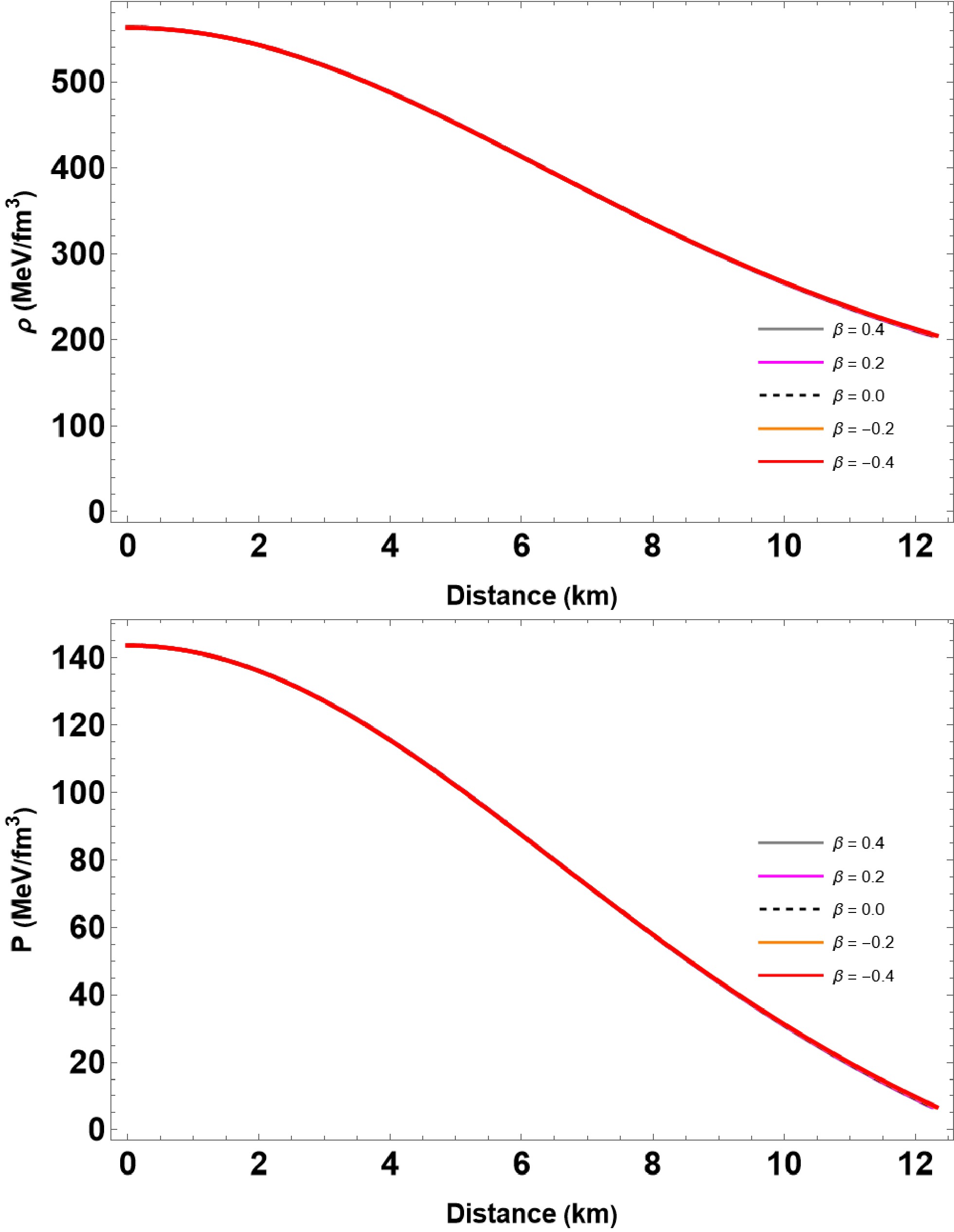

Figure 2.  (color online) We plot the energy density and isotropic pressure for solving the TOV equations (14) and (15) with the given EoS (21). For computation, we vary $\beta \in [-0.2, $$ 0.2]$ and set the other parameters as $ B_{\rm{eff}} = 60 $ MeV/fm³ and $ \bar{\lambda} = 0.2 $, respectively.

$ \bar{\lambda} $	M/$ M_{\odot} $	R/km	$ \rho_c $/(MeV/fm3)	$ M/R $
0.1	2.28	12.08	900	0.280
0.2	2.41	12.60	844	0.284
0.3	2.51	13.00	788	0.286
0.4	2.60	13.36	731	0.288
0.5	2.67	13.70	675	0.289

Table 1.  We present the structural properties of QSs in $ f(R,T) $ gravity. We set a fixed value for $ B_{\rm{eff}} = 60 $ MeV/fm³ and $ \beta = 0.1 $ and different values of $ \bar{\lambda} $.

Notably, the absolutely stable condition is an important condition that must be satisfied for strange QSs [60−63]. This condition states that the energy per baryon of SQM must be less than 930 MeV, while the energy per baryon of up-down quark matter (udQM) should exceed 930 MeV. We have carefully examined this stability criterion for the parameter sets used in our model. The energy per baryon, $ E/A $, is given by $ E/A = E_{\text{total}}/n_B $, where $ E_{\text{total}} $ represents the total energy [64] and $ n_B $ is the density of the baryon number.

In the case of SQM, the total energy [52, 65] can be expressed as

where $ g = 2 $, $ \Delta = 0.2 \; \text{MeV} $, and $ m_s = 150 \; \text{MeV} $. Meanwhile, g represents the coupling constant of the strong interaction and ∆ refers to the gap parameter in the context of color superconductivity in quark matter. Using this, we calculate the energy per baryon for SQM as $ E/A_{\text{SQM}} = $ 400 MeV, which is well below the 930 MeV threshold, thus satisfying the absolutely stable condition.

For udQM, with $ m_s = 0 $, we obtain:

yielding an energy per baryon of $ E/A_{\text{udQM}} = 401.33 \, \text{MeV} $. This result indicates that the udQM energy per baryon is slightly higher than that of SQM but still within the expected range, further supporting the stability of QSs.

Hence, the parameter sets utilized in this research confirm that the SQM meets the absolutely stable condition, affirming the reliability of our model in representing QSs.

In the following, we explore the characteristics of QSs in the framework of $ f(R,T) $ gravity by solving the modified TOV equations (14) and (15) for the given EoS (21). The mass and radius of QSs are obtained by numerically integrating the TOV equations with the initial boundary conditions at the center of the star $ (r = 0) $ as $ m(0) = 0 $ and $ \rho(0) = \rho_c $, where $ \rho_c $ is the central energy density. The total mass of the QS is defined as $ M = m(R) $, where R represents the radius of the star. In this analysis, we concentrate two variable parameters: the EoS parameter $ \bar{\lambda} $ and the coupling constant β. Here, the stellar mass is measured in solar masses, $ M_{\odot} $, the radius of the stars in $ {\rm{km}} $, and the bag constant in $ \text{MeV/fm}^3 $, respectively.

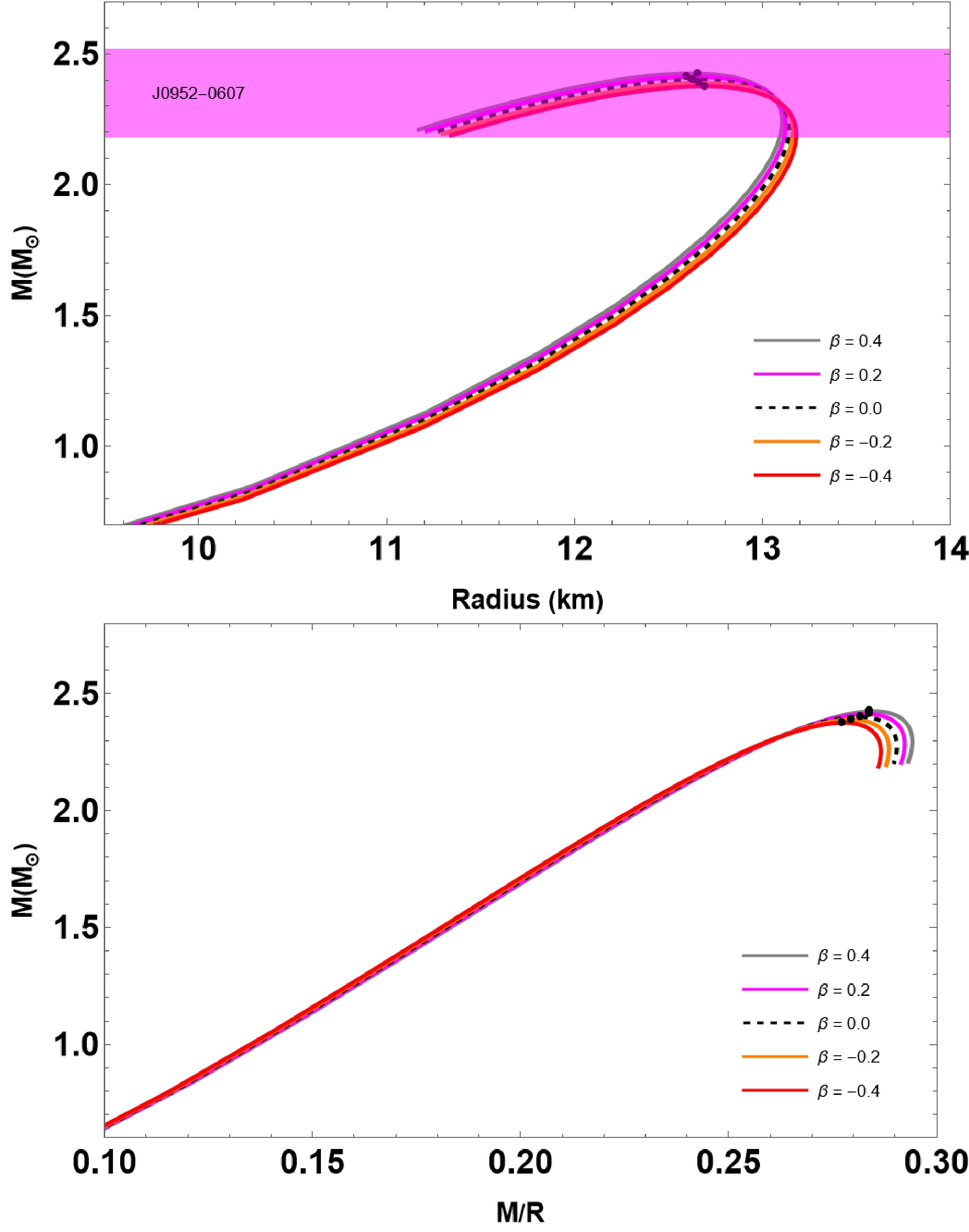
In Fig. 3, we illustrate the mass-radius $ (M-R) $ and mass-compactness $ (M-M/R) $ curves from solving the TOV equations and considering the most probable parameters: $ B_{\rm{eff}} = 60 $ MeV/fm³, $ \beta = 0.1 $ and varying the parameter $ \bar{\lambda} \in [0.1, 0.5] $. The resulting $ M-R $ curves show that the maximum mass and their radii increase with increasing values of $ \bar{\lambda} $, comfortably exceeding the 2$ M_\odot $ limit. The maximum mass reached 2.67 $ M_\odot $ at $ \bar{\lambda} = 0.5 $ in our study of nonrotating QSs. The colored bands represent observational data from the pulsars PSR J0952-0607 with a mass of $ M = 2.35 \pm 0.17 M_{\odot} $ (Magenta) [66] and from the analyses of the gravitational wave signal from the GW190814 event with a mass of $ 2.59^{+0.08}_{-0.09} M_{\odot} $ (Lightgray) [67]. The range of allowable parameters is further constrained by the contours of HESS J1731-347 [68] and the GW170817 event [69], described by the shaded regions in Fig. 3. All the parameters used for the studies are provided in Table 1 with the maximum gravitational mass being $ 2.28 M_{\odot} \leq M_G \leq 2.67 M_{\odot} $, and the radius of the star ranging from $ 12.08 $ km–$ 13.70 $ km. We also demonstrate the effect $ \bar{\lambda} $ on the properties of maximum compactness in the lower panel of Fig. 3. Notice that the maximum compactness increases with increasing values of $ \bar{\lambda} $, often ranging between 0.280 and 0.289, as can be observed in Table 1. The table also indicates that the Buchdahl limit remains intact i.e., $ M/R < 4/9 $.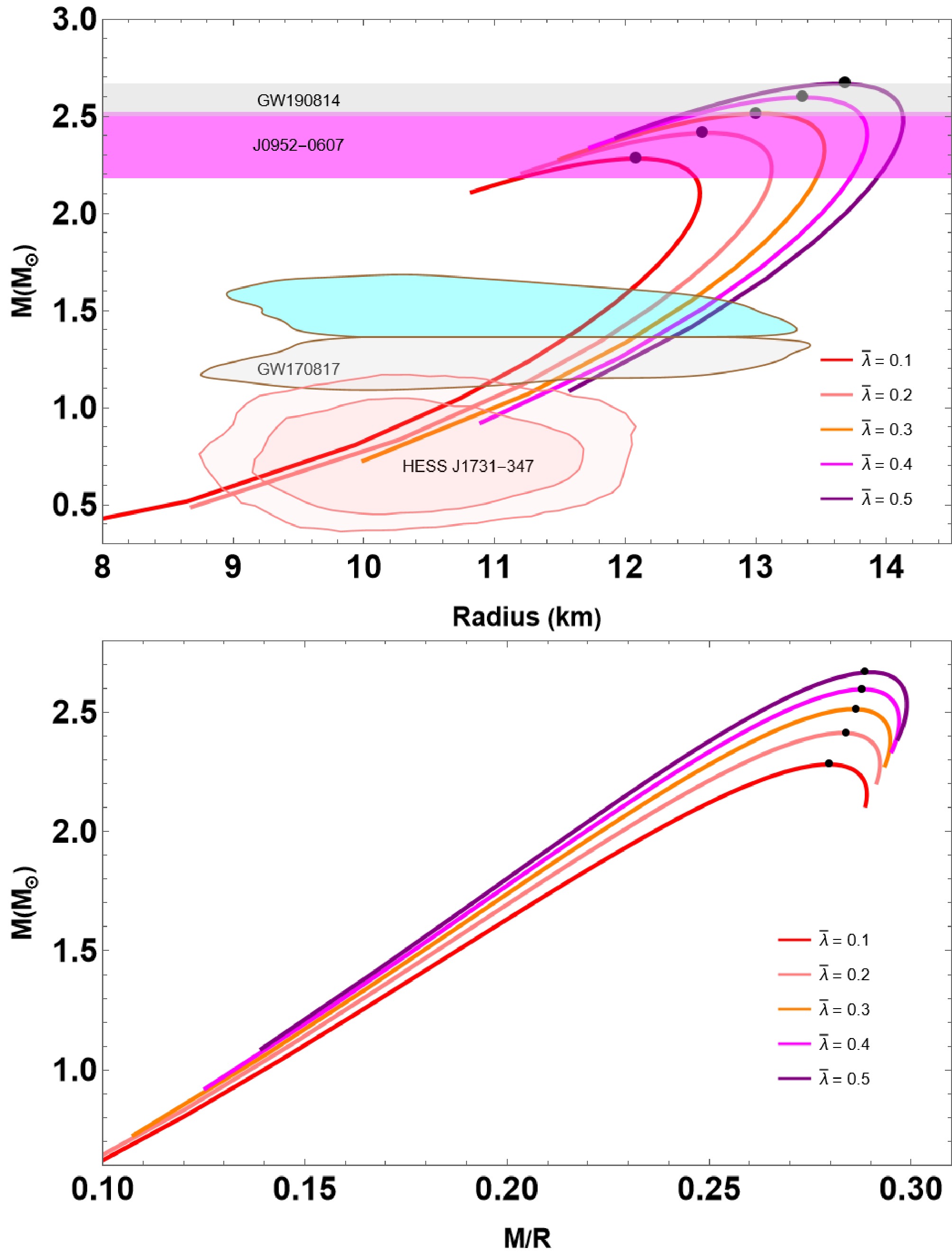

Figure 3.  (color online) The mass-radius $ (M-R) $ and mass-compactness $ (M-M/R) $ curves of QSs for the IQM EoS (21). The model parameters used are listed in Table 1. Additionally, the $ M-R $ diagrams are compared with more recent observational data PSR J0952-0607 (Magenta) [66] and the gravitational wave signal from the GW190814 event (light gray) [67]. The range of allowable parameters is further constrained by the contours of HESS J1731-347 [68] and the GW170817 event [69].

In Fig. 4, we demonstrate the $ (M-R) $ and $ (M-M/R) $ curves by varying the coupling constant $ \beta \in [-0.2, 0.2] $. The other model parameters used in the numerical calculations are: $ \bar{\lambda} = 0.2 $ and $ B = 60 $ MeV/fm³, respectively. Fig. 4 shows that the maximum mass value increases with increasing values of β, and this value reaches 2.42 $ M_{\odot} $ at $ \beta = 0.2 $. Concurrently, we recorded that the maximum mass is 2.40 $ M_{\odot} $ in GR ($ \beta = 0 $). Our findings imply that the $ M-R $ profiles around the maximum mass do not significantly differ from the standard GR in the β variation. However, the obtained GR result is consistent with a QS governed by the IQM EoS (21), as reported in Ref. [49]. Here, we continue our analysis by comparing the $ M-R $ diagrams with more recent observational data PSR J0952-0607 (Magenta) [66]. As shown in Fig. 4, we find that our model is consistent with the observational data. Finally, we show how β affects the maximum compactness characteristics in the lower panel of Fig. 4. As expected, increasing or decreasing the values of β does not result in a significant deviation between GR and $ f(R,T) $ gravity for maximum compactness, and its value is in the range of $ 0.277< M/R < 0.281 $. The results are listed in Table 2.

Figure 4.  (color online) The mass-radius $ (M-R) $ and mass-compactness $ (M-M/R) $ curves of QSs for the IQM EoS (21). The model parameters used are shown in Table 2. Additionally, the $ M-R $ diagrams are compared with more recent observational data PSR J0952-0607 (Magenta) [66].

β	M/$ M_{\odot} $	R/km	$ \rho_c $/(MeV/fm3)	$ M/R $
−0.2	2.37	12.70	844	0.277
−0.1	2.39	12.60	844	0.279
0.0	2.40	12.63	844	0.281
0.1	2.41	12.60	844	0.279
0.2	2.42	12.65	788	0.277

Table 2.  We present the structural properties of QSs in $ f(R,T) $ gravity. We set a fixed value for $ B_{\rm{eff}} = 60 $ MeV/fm³ and $ \bar{\lambda} = 0.2 $ and different values of β.

Besides the mass-radius relationships, our main concern is the stability of the configuration. Below, we provide an in-depth discussion of the methods used to determine the stability of these stars.

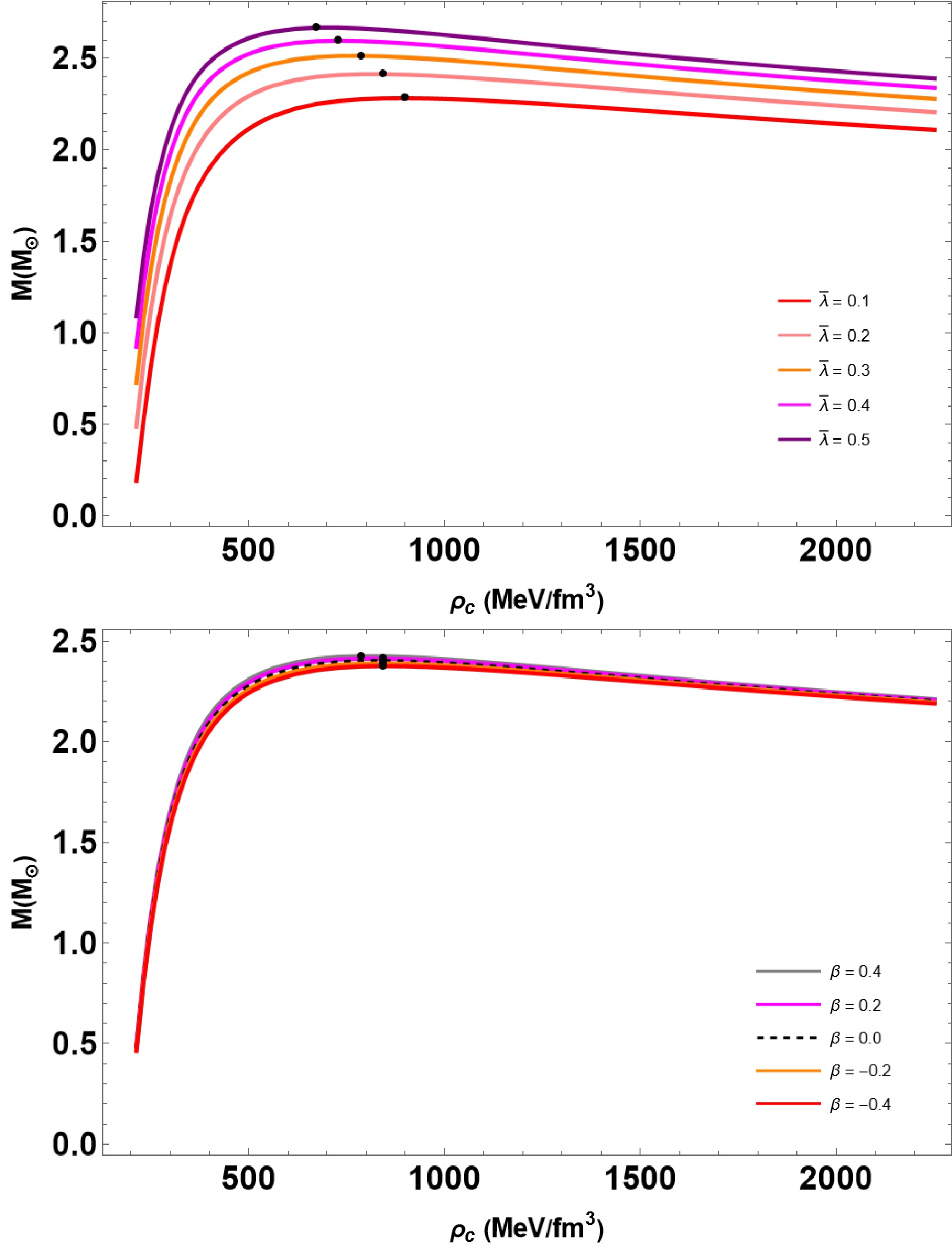
The static stability criterion [70, 71] is a widely applied condition for discussing the stability analysis of an equilibrium configuration. However, this is a necessary but insufficient condition for confirming the stability of a spherical body. Interestingly, this condition is extensively applied, irrespective of any modified gravity theories (see Refs. [72−74] and therein). This condition is expressed by the following inequalities:

We analyze the inequalities by plotting $ M-\rho_c $ curves, where M is the mass QS and $ \rho_c $ is the central density. In Fig. 5, we present our results using the same parameter sets as in Figs. 1 and 2, respectively. In the figures, the turning points (indicated by the black circle) are represented by the region separating a stable configuration from an unstable one, and the stable region is indicated by the inequality ${\rm d}M/{\rm d}\rho_c > 0$.

Figure 5.  (color online) $ M-\rho_c $ curve profiles. The same parameter set used in Figs. 1 and 2 is considered. The pink points represent the boundary separating the stable configuration region indicated by ${\rm d}M/{\rm d}\rho_c > 0$ from the unstable one.

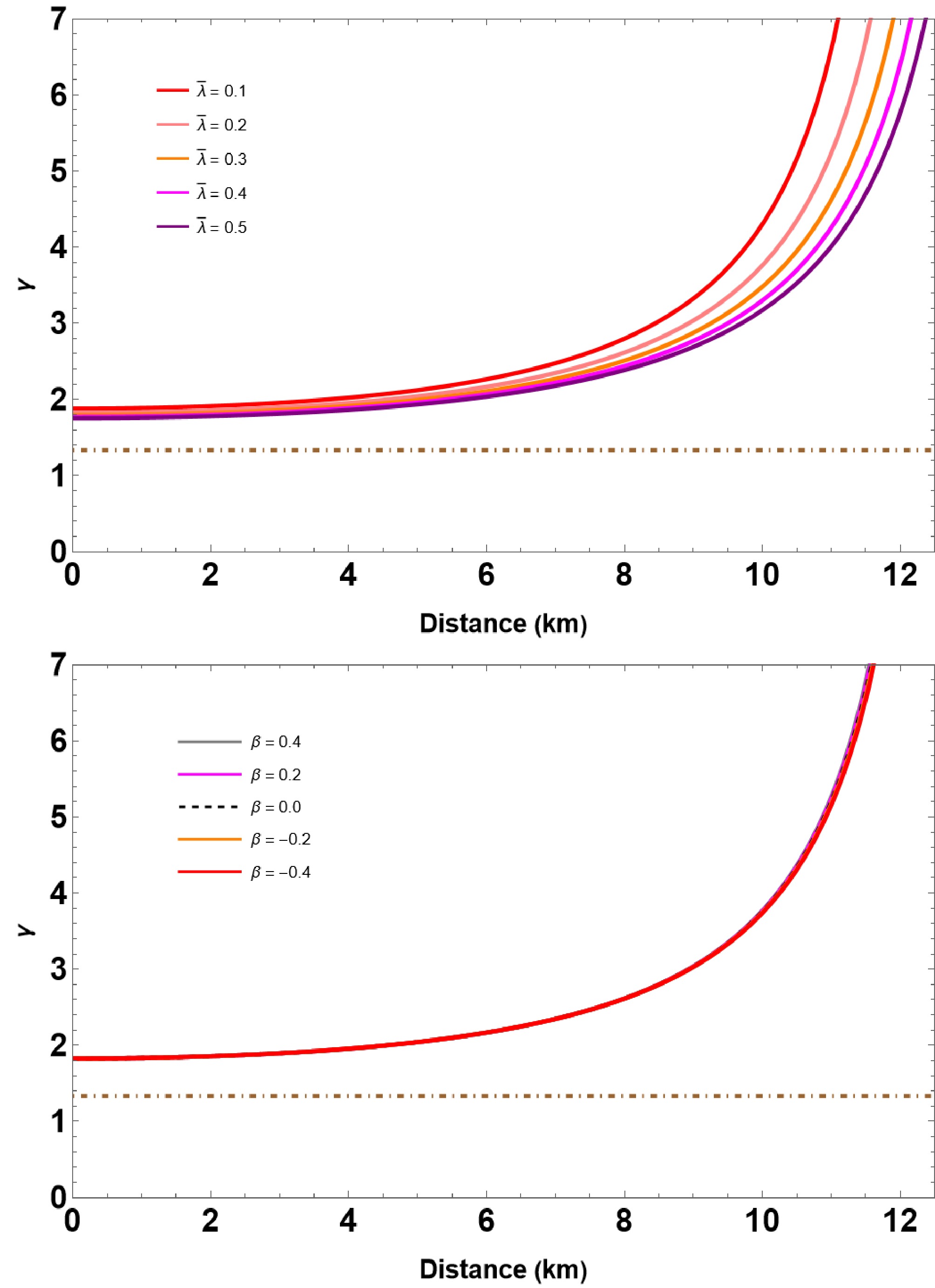
We also calculate the adiabatic index γ to check the viability of our QS model using the conventional method established by Chandrasekhar in 1964 [75]. The condition for γ explicitly reads

The Eq. (27) is related to the sound speed (in units of the speed of light), and the subscript S indicates the derivation at constant entropy. In the case of an isotropic fluid sphere, the value of γ is associated with the dynamical instability of relativistic objects and has a restricted value. This value is known as the critical adiabatic index and is denoted as $ \gamma_{cr} $. Ref. [76] demonstrated that a star would be dynamically stable if $ \left<\gamma \right> >\gamma_{cr} $, where $ \left<\gamma\right> $ stands for the averaged adiabatic index. However, in the GR context, this critical value can be expressed as $\gamma_{cr} = \dfrac{4}{3}+\dfrac{19}{42} C$, where $ C = 2 M/R $ is the compactness parameter [76]. In such a scenario, the critical value of $ \gamma_{cr} $ exceeds 4/3. Generally, the adiabatic index ranges from 2 to 4 for most of the NSs EoS (see Ref. [77] for more). The dependence of the adiabatic index as a function of the radial distance is shown in Fig. 6 for several representative values of $ \bar{\lambda} $ and β. Notably, for the QSs composed of IQM, the averaged adiabatic index is much larger than the critical value.

Figure 6.  (color online) The adiabatic index γ is plotted as a function of radial coordinate r for the selected EoS (21). We consider the same parameter set as in Figs. 1 and 2. We also indicate the value of $ \gamma_{cr} = 4/3 $ using the brown dotted-dash line.

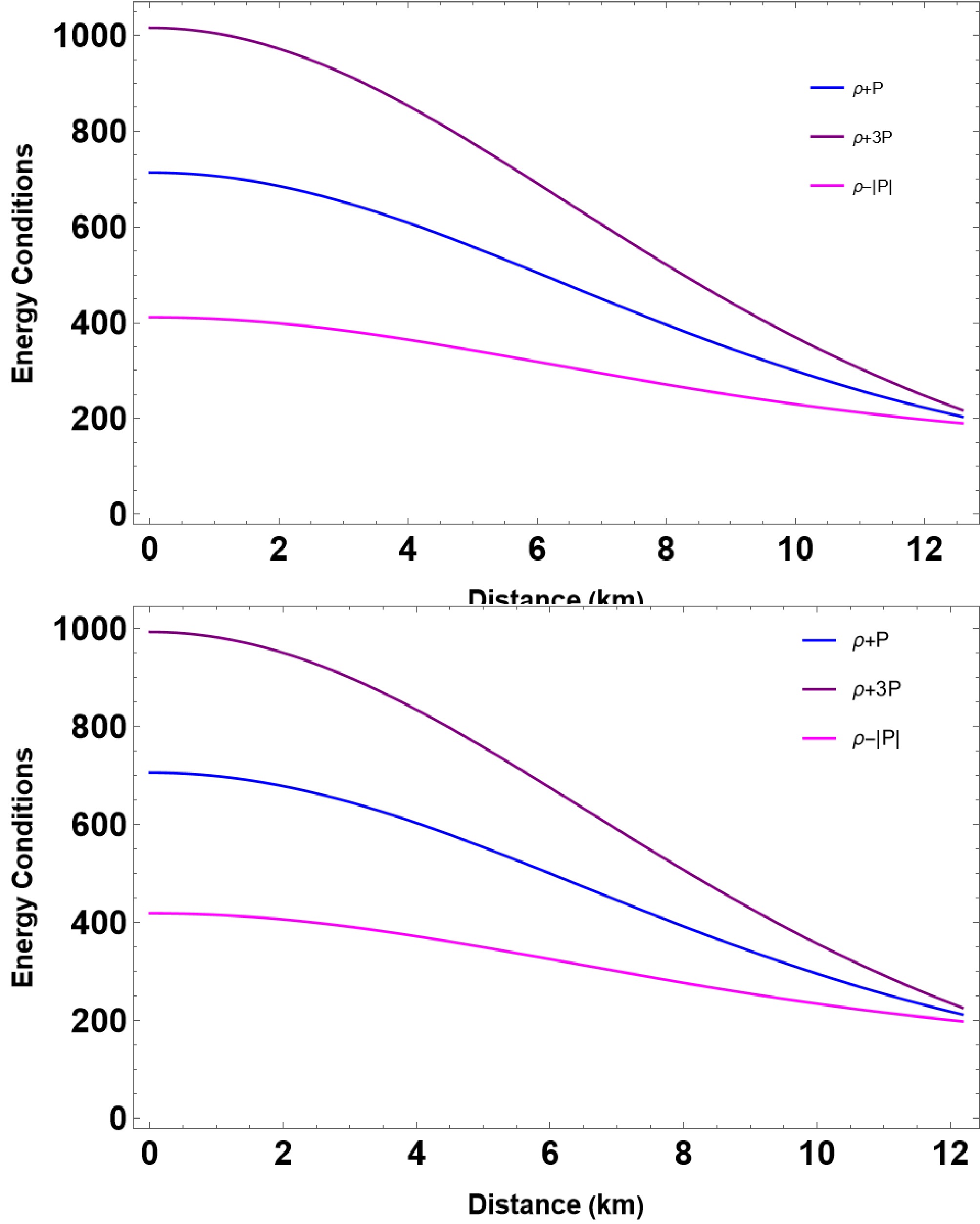
Next, we discuss classical energy conditions (ECs), which are important phenomenological methods for defining self-consistent and physically motivated theories of gravity. ECs also help to ensure physically consistent $ f(R, T) $ gravity. The ECs are a combination of the energy-momentum tensor components, and the four conditions are the null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC), and the dominant energy condition (DEC), given by

respectively. In Fig. 7, we plot the four ECS for several representative values of $ \bar{\lambda} $ and β. When plotting the ECs, we consider that $ B_{\rm{eff}} = 60 $ MeV/fm³, and other parameters are in combinations of $ \{\bar{\lambda}, \beta\} = \{0.3, 0.1\} $ and $\{\bar{\lambda}, \beta\} = \{0.2, 0.3\}$, respectively. The plots demonstrate that all ECs are met within the specified range of parameters for both cases, as depicted in Fig. 7.

Figure 7.  (color online) Energy condition profiles with respect to their values at $ \{\bar{\lambda}, \beta\} = \{0.3, 0.1\} $ and $ \{\bar{\lambda}, \beta\} = \{0.2, 0.3\} $, when $ B_{\rm{eff}} = 60 $ MeV/fm³ is fixed.

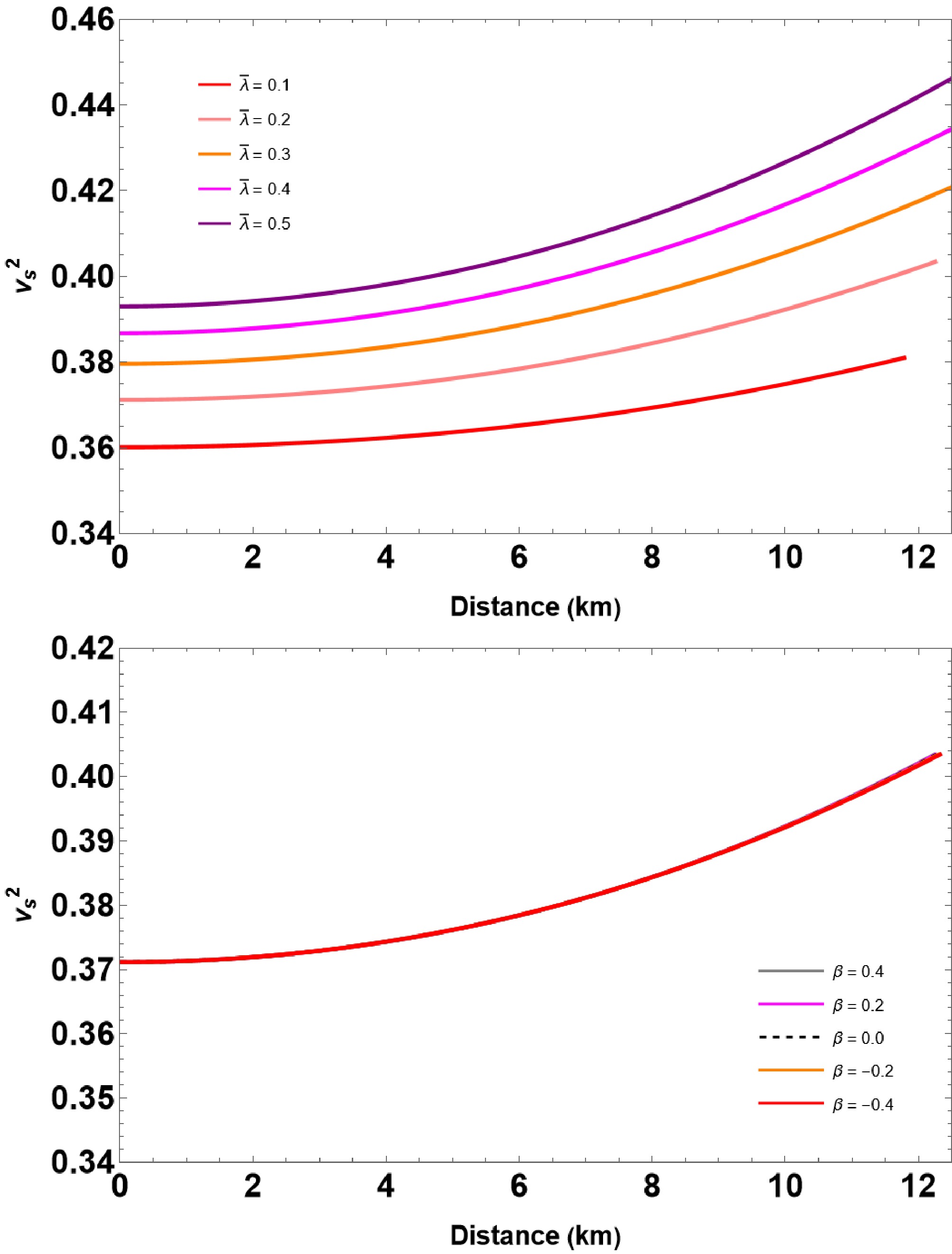
We extended our analysis by studying the squared speed of sound, defined as $ v_{s}^2 = {{\rm d}P}/{{\rm d}\rho} $, which is an important condition for stable configurations. Notably, the speed of sound should be less than the speed of light i.e., $ 0<v^2_s <1 $. In Fig. 8, we display the sound speed as a function of radial distance, and the obtained results again satisfy the condition $ 0 \leq v_{s}^2 \leq 1 $. Thus, we can say that QSs composed of IQM could exist in $ f(R,T) $ gravity.

Figure 8.  (color online) Plot of sound speed along the transverse direction within the stellar interior. The same parameter set used in Figs. 1 and 2 is considered.

The polytropic index $ \gamma = \dfrac{\partial \ln P}{\partial \ln E} $, where P is the pressure and E is the energy density, is a measure of the stiffness of the equation of state (EoS). According to the findings in [78], a polytropic index γ below 1.75 indicates the presence of quark matter cores in massive neutron stars. In our study, we calculate γ using the following expression:

For typical QS parameters $ B_{\text{eff}} = 60 \; \text{MeV/fm}^3 $ and $ \lambda = 0.2 \; \text{MeV} $, we evaluate γ across energy densities ranging from 200 to $ 1000\; \text{MeV/fm}^3 $. Our numerical results show that the polytropic index γ varies between 1.5 and 1.7, which is below the critical limit of 1.75. This behavior is consistent with the presence of quark matter cores, as suggested by Ref. [78, 79].

Thus, the polytropic index calculations confirm that the QS model in $ f(R,T) $ gravity adheres to the theoretical expectations for quark matter and satisfies the stability criteria.

In this study, we examined the implications of $ f(R,T) $ gravity for the structure and stability of QSs composed of IQM. By adopting a linear functional form for $ f(R,T) $, we derived the modified Einstein field equations and the corresponding TOV equations for a spherically symmetric, static spacetime. Our numerical analysis explored the mass-radius relation, stability criteria, adiabatic index, and energy conditions for QSs within this theoretical framework.

The results indicate that $ f(R,T) $ gravity significantly alters the properties of QSs compared to GR. Specifically, the modified gravity framework leads to the non-conservation of the energy-momentum tensor, introducing an extra force that affects the equilibrium configuration of QSs. Our findings show that the maximum mass and radius of QSs increase with the parameter $ \bar{\lambda} $, and the deviations from GR become more pronounced for higher values of the coupling constant β. The analysis also confirms that the $ f(R,T) $ gravity models can satisfy the stability criteria and energy conditions, making them viable candidates for describing compact stars.

We derived the modified Einstein field equations and conservation equations for $ f(R,T) $ gravity, focusing on a linear form $ f(R,T) = R + 2\beta T $. In this framework, the action integral depends on both the curvature scalar R and the trace of the energy-momentum tensor T, leading to modifications in the standard Einstein equations. These modifications introduce additional terms that account for the matter-geometry coupling, which significantly influence the structure of compact objects like QSs.

Using the modified TOV equations, we investigated the structural properties of QSs. We considered an IQM equation of state (EoS) that incorporates perturbative QCD corrections and color superconductivity. By solving these equations numerically, we obtained mass-radius relations for various values of the parameter $ \bar{\lambda} $ and the coupling constant β. Our results show that as $ \bar{\lambda} $ increases, the maximum mass and radius of QSs also increase, suggesting that the $ f(R,T) $ gravity allows for the existence of more massive and larger compact stars compared to GR.

The stability analysis involved examining the static stability criterion, adiabatic index, and sound speed. We found that the QSs in $ f(R,T) $ gravity satisfy the stability criterion ${\rm d}M/{\rm d}\rho_c > 0$ and possess adiabatic indices well above the critical value of $ 4/3 $, indicating stable configurations. Additionally, the sound speed remained below the speed of light within the stellar interior, satisfying the causality condition. We also explored the energy conditions (NEC, WEC, SEC, and DEC) to ensure that the solutions are physically viable. Our analysis confirmed that all energy conditions within the considered parameter ranges were met, further supporting the consistency of $ f(R,T) $ gravity in describing QSs.

Future work will focus on extending this study to rotating QSs and exploring the gravitational wave signatures of such objects in $ f(R,T) $ gravity. Additionally, further investigations into the parameter space of the IQM EoS and its implications for observational constraints will be pursued. These efforts aim to provide a deeper understanding of the role of modified gravity theories in astrophysics and their potential to explain the properties of dense, compact objects. We also plan to study the potential observational signatures of $ f(R,T) $ gravity in the context of upcoming astrophysical surveys and gravitational wave detections, which could offer new insights into the nature of gravity and matter under extreme conditions.

We would like to express our sincere gratitude to the Editor and anonymous referees for their insightful comments and suggestions, which have greatly improved the quality and clarity of this manuscript. Their valuable input was instrumental in refining our results and strengthening the scientific discussion. A. Pradhan thanks IUCCA, Pune, India, for providing facilities under the associateship programs. B. D. acknowledges support from the administration of the University of Nizwa. İ. Sakallı would like to acknowledge the networking support of COST Actions CA21106 and CA22113. He also appreciates TÜBİTAK, SCOAP3, and ANKOS for their support.