Strong coupling from inclusive semileptonic decay of charmed mesons

I. INTRODUCTION

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

In the Standard Model of elementary particle physics, Quantum Chromo-Dynamics (QCD) is the gauge field theory for the strong interaction. In QCD, gluons are force mediators, and $\alpha_S$ (the effective strong coupling constant) dictates many features of the strong interaction. Asymptotic freedom, in which the strength of $\alpha_S$ increases as the energy scale decreases, is one of the primary features of QCD. The value of $\alpha_S$ has been measured over the energy scale ranging from the τ lepton mass $m_\tau$ to several $\text{TeV}$, and it has been found to be consistent with the theoretical prediction. However, $\alpha_S$ has not been measured at energies below $m_\tau$ . In this regime, the QCD physics may enter the non-perturbative scheme and exhibit unknown behaviors. Therefore, measuring $\alpha_S$ at lower energies to further understand QCD and probe possible new physics is very desirable.

In the past five decades, significant progress has been achieved in the theoretical description of inclusive semileptonic decays of charmed and B mesons using the framework of the heavy quark expansion (HQE) model [1−7]. In the HQE framework, the features of the inclusive semileptonic decays of heavy quarks are expressed in terms of $\alpha_S$, quark masses, Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, and non-perturbative parameters. HQE calculations accurately describe experimental features of inclusive semileptonic decays of charmed and B mesons [5−10]. In addition, the HQE model has been employed as a reliable method for experimentally extracting the b quark mass and $|V_{cb}|$ with inclusive semileptonic decays of B mesons [8, 10−14]. In these studies, the b quark mass and $|V_{cb}|$ were determined from the fits to the observables of inclusive semileptonic decays of B mesons, where $\alpha_S$ was fixed to the value running from $\alpha_S(m_Z^2)$.

This procedure can also be applied to inclusive semileptonic decays of charmed mesons. Experimental measurements of $m_c$ and $|V_{cs}|$ have become more precise [15−17], which will enable $\alpha_S(m_c^2)$ to be determined as a parameter from charmed mesons, either by fixing the values of $m_c$ and $|V_{cs}|$ to those measured in processes other than semileptonic D decays, or through a fit that simultaneously extracts $m_c$, $|V_{cs}|$, and $\alpha_S(m_c^2)$ from inclusive semileptonic decays of charmed mesons. In this article, we present a determination of $\alpha_S(m_c^2)$ from inclusive semileptonic decays of charmed mesons.

II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

In this study, the theoretical calculation [5] of the inclusive semileptonic decay width ($\Gamma_{SL}$) for charmed mesons was employed to derive $\alpha_S(m_c^2)$. In [5], the authors considered ${\cal{O}}(\alpha_S)$ and ${\cal{O}}(\beta_0\alpha_S^2)$ corrections [18, 19], as well as ${\cal{O}}(1/m_c^3)$ contributions [20], when calculating $\Gamma_{SL}$. As shown in Eq. (1) [5], $\Gamma_{SL}$ is expressed in terms of $\alpha_S(m_c^2)$, quark masses, the CKM matrix element $|V_{cs}|$, and non-perturbative corrections. In Eq. (1), $G_F$ is the Fermi coupling constant, r is the square of the ratio of the strange quark mass to the charm quark mass ($m_s^2 / m_c^2$), $\alpha_S\equiv\alpha_S(m_c^2)$, $\mu^2_{\pi}$ and $\mu^2_{G}$ are the kinetic and chromomagnetic dimension five operators [21−23], respectively, and $\rho_{D}^3$ and $\rho_{LS}^3$ are the Darwin and the spin-orbital (LS) dimension six operators [23], respectively, in the HQE model. The weak annihilation (WA) contribution, $B_{WA}$, depends on the type of spectator quark within each charmed meson.

The coefficients of the perturbative and non-perturbative items, $f_{0,1,2}(r)$ and $f_{\pi, G, LS, D}(r)$, respectively, were calculated using Eq. (2) [5], where $n_f$ is the number of active flavors and $\beta_0$ is the QCD beta function, $\beta_0 = 11 - 2n_f/3$.

The infrared cutoff scale μ in the kinetic scheme was set to $0.5\ \text{GeV}$. In the theoretical expression for $f_D(r)$, $0.8\ \text{GeV}$ was treated as the $\overline{\text{MS}}$ renormalization scale ($\mu_{WA}$) associated with the mix of Darwin and WA operators [5, 24, 25]. In Eq. (1), only the process of $c\rightarrow s l\bar{\nu}$ (which was slightly different from experimental measurements [26, 27] because of missing Cabibbo-suppressed processes) was taken into account. A corresponding systematic uncertainty was assigned to cover the missing processes in the determination of $\alpha_S(m_c^2)$.

III. FITTING METHOD

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

The $\chi^2$ minimization method was employed to determine $\alpha_S(m_c^2)$ from fits of $\hat{\Gamma}_{SL}$, which is the $\Gamma_{SL}$ expression of Eq. (1) for different charmed mesons. The $\chi^2$ function is expressed as

where $D_i$ denotes $D^{+}$, $D^{0}$, or $D^{+}_s$; $\Gamma_{SL, D_i}$ and $\sigma_{\Gamma_{SL, D_i}}$ are the measured inclusive semileptonic decay width and the corresponding uncertainty of $D_i$, respectively; and $\theta_j =$ $\{m_c$, $m_s$, $|V_{cs}|$, $\mu_{G}^2$, $\mu_{\pi}^2$, $\rho_{D}^3$, $\rho_{LS}^3\}$ represents the constrained parameters (the values and uncertainties of which are $\theta^{\prime}_j$ and $\sigma_{\theta^{\prime}_j}$, respectively).

The variable $G_{F}$ was fixed at $1.1663788\times 10^{-5}$ [15]. According to [5], the values of $B_{WA}$ for $D^{+}$, $D^0$, and $D^{+}_s$ are fixed at $-0.001$, $-0.001$, and $-0.002\ \text{GeV}^3$, respectively. Except for $G_F$ and $B_{WA}$, the parameters were allowed to float when determining $\alpha_S(m_c^2)$. The value of $|V_{cs}|$ has been measured to be $0.975\pm0.006$ [15]. In the kinetic scheme, the expected values of $\mu_{G}^2$ and $\rho_{LS}^3$ do not run with respect to the energy scale, and they have been determined to be $0.288\pm0.049\ \text{GeV}^2$ and $-0.113\pm 0.090\ \text{GeV}^3$, respectively, from inclusive semileptonic B decays [10]. In [5, 8, 28], the values of $\mu_{\pi}^2(0.5\ \text{GeV})$ and $\rho_{D}^3(0.5\ \text{GeV})$ were determined to be $0.26\pm0.06\ \text{GeV}^2$ and $0.05 \pm 0.04\ \text{GeV}^3$, respectively, which were evolved to $\mu=0.5\ \text{GeV}$ using ${\cal{O}}(\alpha_S^2)$ expressions from values of $\mu=1\ \text{GeV}$. The mass of the strange quark was set to $93.4\pm8.6\ \text{MeV}$ [15].

The convergence of the perturbative series in the $\Gamma_{SL}$ expression is strongly affected by the mass definition of the charm quark [29−32]. In [16], the pole mass and the $\overline{\text{MS}}$ scheme exhibited bad convergence behaviors in the QCD corrections to $\Gamma_{SL}$. To avoid the divergence, the kinetic scheme [29, 31, 33] was introduced to calculate $\Gamma_{SL}$. The relationship between $\overline{\text{MS}}$ and the kinetic mass of the charm quark has been investigated to three-loop order ($\text{N}^3$LO) [16, 17]. For different choices of $\mu_s$ ($\overline{\text{MS}}$ scale), the value of $m_c$ at a scale of $0.5\ \text{GeV}$ in the kinetic scheme $m_c^{\rm kin}(0.5\ \text{GeV})$ has been obtained separately using the relationship in [16, 17]:

The average value of $m_c^{\rm kin}(0.5\ \text{GeV})$ from different $\mu_s$values was treated as the input value of $m_c(0.5\ \text{GeV})$ in the $\chi^2$ fit, which was determined to be $1370\ \text{MeV}$. For a conservative estimate, the largest difference between $m_c(0.5\ \text{GeV})$ and $m_c^{\rm kin}(0.5\ \text{GeV})$ was taken as the uncertainty in $m_c(0.5\ \text{GeV})$. To evaluate the bias caused by the choice of $m_c$ and $|V_{cs}|$, the first fit was performed with $m_c$ as a free parameter and with $|V_{cs}|$ allowed to vary within one standard error; the second fit was performed with $m_c$ and $|V_{cs}|$ both fixed at the world average. The results for $\alpha_S(m_c^2)$ from these fits were compared to check the consistency of the experiment.

IV. EXPERIMENTAL INPUTS

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

The experimental measurement of $\Gamma_{SL}$ was derived from the inclusive semileptonic decay branch fraction, ${\cal{B}}_{SL}$ [26, 27], and the lifetime, τ [15], via Eq. (5), where $D_i$ denotes $D^{+}$, $D^{0}$, or $D^{+}_s$:

In Eq. (5), $\tau_{D_i}$ is the mean life of $D_i$, and ${\cal{B}}_{SL}(D_i \rightarrow X e \nu_e)$ is the branch fraction of the inclusive semileptonic decay for $D_i$. The inclusive semileptonic branch fractions of $D^{+}$, $D^{0}$, and $D^{+}_{s}$ have been measured by the CLEO-c [26] detector using $818\ \text{pb}^{-1}$ and $602\ \text{pb}^{-1}$ open-charm data at $E_{CM} = 3.774\ \text{GeV}$ and $4.170\ \text{GeV}$. Because of limited statistics, the uncertainty in ${\cal{B}}_{SL, D^{+}_{s}}$ was much higher than that in ${\cal{B}}_{SL, D^{+}/D^{0}}$ in the CLEO-c measurements. Recently, ${\cal{B}}_{SL, D^{+}_{s}}$ has also been measured by the BESIII instrument using $3.19\ \text{fb}^{-1}$, $2.08\ \text{fb}^{-1}$, and $1.05\ \text{fb}^{-1}$ $e^+e^-$ collision data at $E_{CM} = 4.178\ \text{GeV}$, $4.189 - 4.219\ \text{GeV}$, and $4.225 - 4.230\ \text{GeV}$ [27]. The uncertainty in ${\cal{B}}_{SL, D^{+}_{s}}$ has been reduced by the additional data provided by the BESIII measurements. The ${\cal{B}}_{SL, D^{+}/D^{0}}$ value from CLEO-c and the ${\cal{B}}_{SL, D^{+}_{s}}$ value from BESIII were adopted to calculate the $\Gamma_{SL}$ values of $D^{+}$, $D^{0}$, and $D^{+}_{s}$. In Table 1, the input values of ${\cal{B}}_{SL}(D_i \rightarrow X e \nu_e)$, $\tau_{D_i}$, and $\Gamma_{SL, D_i}$ are displayed. The consistent $\Gamma_{SL}$ values of $D^0$ and $D^+$ indicate the reliability of the HQE model for inclusive semileptonic decays of $D^0$ and $D^+$.

Table 1

Table 1.  Input values of ${\cal{B}}_{SL}(D_i \rightarrow X e \nu_e)$, $\tau_{D_i}$, and $\Gamma_{SL, D_i}$.

$D_i$	${\cal{B}}_{SL}$ (%)	τ ($10^{-13}$s)	$\Gamma_{SL}$ ($10^{-15} \text{GeV}$)
$D^0$	$6.46\pm0.09\pm0.11$	$4.10\pm0.01$	$104\pm2$
$D^+$	$16.13\pm0.10\pm0.29$	$10.33\pm0.05$	$103\pm2$
$D^+_s$	$6.30\pm0.13\pm0.10$	$5.04\pm0.04$	$82\pm2$

DownLoad: CSV

Show Table

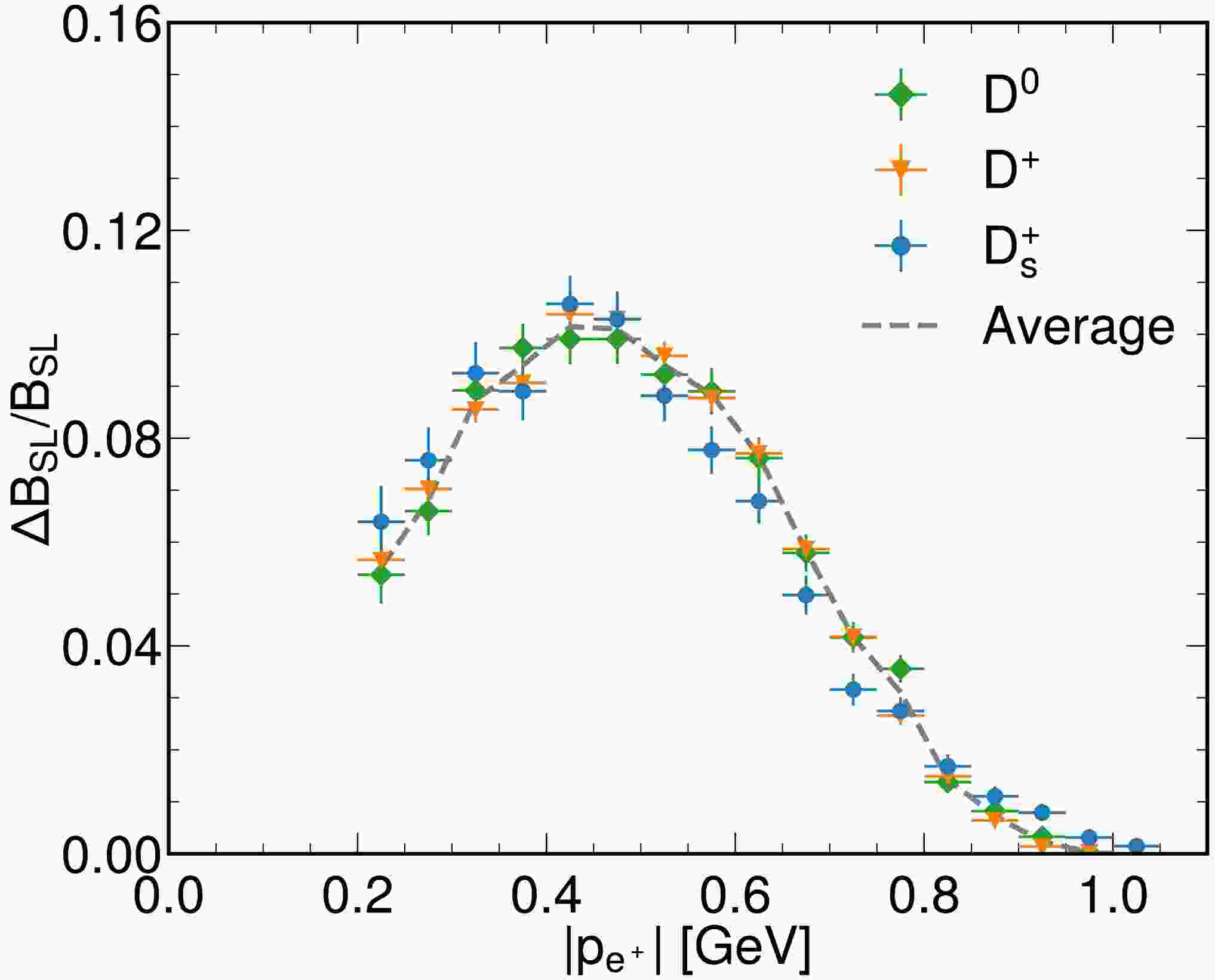
Except for ${\cal{B}}_{SL}$, the distributions of electron momentum ($|p_{e^{+}}|$) in the laboratory frame have been measured for inclusive semileptonic decays of $D^{+}$, $D^{0}$, and $D_s^+$ by CLEO-c and BESIII [26, 27], as shown in Fig. 1. The average $|p_{e^{+}}|$ values of $D^0$, $D^+$, and $D_s^+$ are also plotted in Fig. 1. Kolmogorov-Smirnov (KS) tests [34] between the distributions of $|p_{e^{+}}|$ and $\overline{|p_{e^{+}}|}$ were performed to further validate the reliability of the HQE model for inclusive semileptonic decays of charmed mesons. The results of the KS tests are shown in Table 2.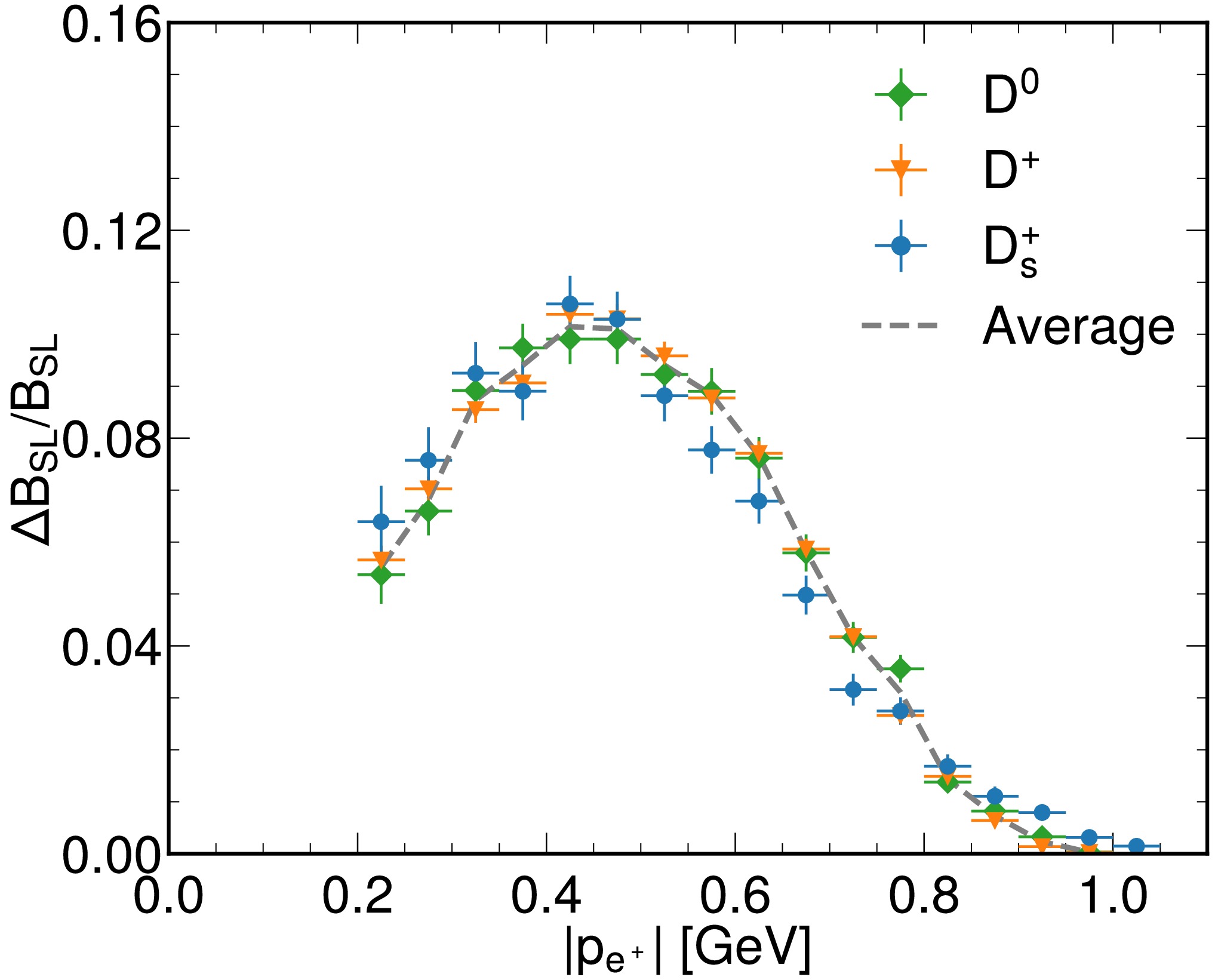

Figure 1

Figure 1.  (color online) Distributions of $|p_{e^{+}}|$ with $|p_{e^{+}}| > 200\ \text{MeV}$ from inclusive semileptonic decays of $D^{+}$, $D^{0}$, and $D_s^+$ in the laboratory frame. The green diamonds and orange triangles are the results of $D^0$ and $D^+$, respectively, measured by CLEO-c [26]. The blue dots are the results of $D_s^+$ measured by BESIII [27]. The dashed gray line is the average of $D^0$ and $D^+$.

DownLoad: Full-Size Img PowerPoint

Table 2

Table 2.  Results of the KS tests, in which the null hypothesis was that the two tested distributions are identical.

Test Distributions	Test Statistic	P Value
$|p_{e^{+}, D^0}|$ and $\overline{|p_{e^{+}}|}$	$0.125$	$1.000$
$|p_{e^{+}, D^+}|$ and $\overline{|p_{e^{+}}|}$	$0.125$	$1.000$
$|p_{e^{+}, D^+_s}|$ and $\overline{|p_{e^{+}}|}$	$0.132$	$0.992$

DownLoad: CSV

Show Table

The $|p_{e^{+}}|$ distributions for $D^{+}$, $D^{0}$, and $D_s^+$ were consistent. This was a strong indication that the HQE model was reliable for inclusive semileptonic decays of charmed mesons. Because experimental measurements of $|p_{e^{+}}|$ were not available in the center-of-mass frame of the charmed mesons, only $\Gamma_{SL}$ was used to extract $\alpha_S(m_c^2)$ in this study.

V. RESULTS

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

The value of $\alpha _S (m^2_c )$ was extracted from $D^+$, $D^0$, and $D^+_s$, including

● $D^+$, $D^0$, and $D^+_s$, respectively.

● $D^+$ and $D^0$ combined.

In the $\chi^2$ fit, high-order perturbative corrections needed to be taken into account for the inclusive semileptonic decays of the charmed mesons. The $\alpha_S^3$ order correction to $b\rightarrow c l \bar{\nu}$ has been determined to be less than 1% in the kinetic scheme [7]. For a conservative estimate, 5% of $\Gamma_{SL}$ was taken as the high-order perturbative corrections for the inclusive semileptonic decays of the charmed mesons. Furthermore, the theoretical calculation of $\Gamma_{SL}$ in Eq. (1) was the contribution of $c\rightarrow s l \bar{\nu}$, in which Cabibbo-suppressed processes were missed. To cover missed Cabibbo-suppressed processes, $|V_{cd}|^2 / (|V_{cd}|^2+|V_{cs}|^2) \approx 5$% was treated as the uncertainty in the $\Gamma_{SL}$ expression. In total, 10% is taken as the theoretical uncertainty in the calculation of $\Gamma_{SL}$ for a more conservative estimate. The input values of the dimension six HQE matrix elements were evolved from the results obtained in the inclusive semileptonic B decays at μ = 1 GeV. The treatment of the inputs of the dimension six HQE matrix elements may have impacted the systematic uncertainties, which can be improved by obtaining more precise measurements of the inclusive semileptonic decays in the charm sector. Despite the fact that the kinetic scheme was adopted to improve the convergence of the perturbative series, the contribution of higher-order corrections was larger owing to the slow convergence behavior in the charm sector, which may have caused the systematic uncertainties to be underestimated. To reduce the corresponding systematic uncertainty, more measurements in the charm sector, such as spectral moments, can benefit the determination of higher-order corrections. High-order perturbative corrections played an important role in this study, and advanced theoretical calculations of high-order perturbative corrections are highly desirable.

In Fig. 2 and Table 3, the fitted $\alpha_S(m^2_c)$ value of each sample is shown and compared to $\alpha_S(m^2_c)$ running from $\alpha_S(m_Z^2)$ using ${\bf{RunDec}}$ [35] with a renormalization group evolution equation. Because of relatively heavy spectator quarks in $D_s^+$, the combined result of $D^+$ and $D^0$ was chosen to measure $\alpha_S(m_c^2)$ in this study. Using the combined sample of $D^0$ and $D^+$, $\alpha_S(m_c^2)$ was determined to be $0.445\pm 0.009_{\text{exp.}}\pm 0.081_{m_c}\pm0.056_{\text{trun.}}\pm0.057_{\text{others}}$ at $m_c = 1.3701\ \text{GeV}$, where the first uncertainty is experimental, the second is the uncertainty in $m_c$, the third is associated with high-order perturbative corrections in the $\Gamma_{SL}$ expression, and the fourth is related to other sources. As shown in Fig. 3, the measured value of $\alpha_S(m_c^2)$ was consistent within 1σ of the value running from $\alpha_S(m^2_Z)$. The consistent values of $\alpha_S(m_c^2)$ among different charmed mesons indicated the robustness of this method. In the fit for the combined $D^{0}$ and $D^+$ sample, the value of $\chi^2 / dof$ of the fit was $0.1/6$, indicating good agreement between the data and the model. In Fig. 4, the profile contours of different samples confirmed the consistency among these charmed mesons and the robustness of this method.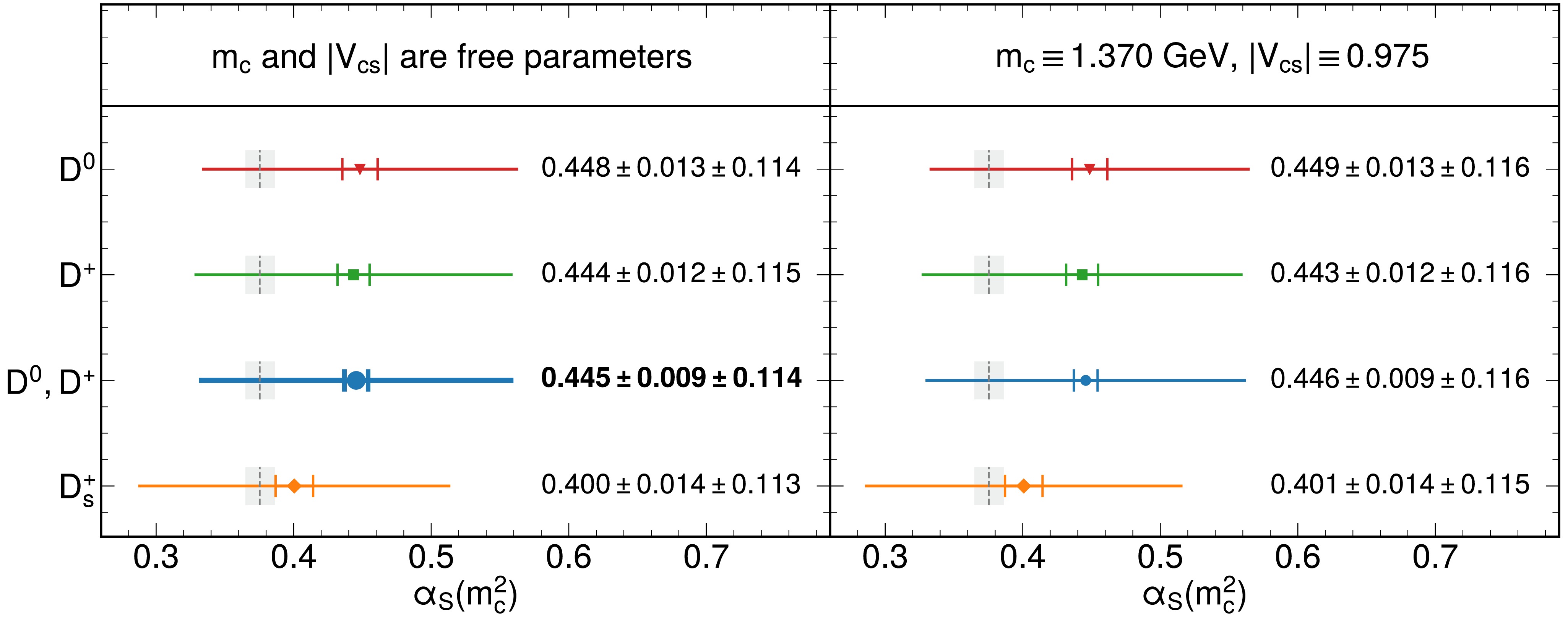

Figure 2

Figure 2.  (color online) In the left panel, $m_c$ and $|V_{cs}|$ were allowed to float in the fit; in the right panel, $m_c$ and $|V_{cs}|$ were fixed in the fit. Points with error bars are the determined central values of $\alpha_S(m_c^2)$, and the inner and the outer error bars are the experimental and total uncertainties, respectively. The dashed gray line and shaded box indicate the value of and uncertainty in $\alpha_S(m_c^2)$ running to $m_c$ from $\alpha_S(m_Z^2)$, respectively.

DownLoad: Full-Size Img PowerPoint

Table 3

Table 3.  Values of $\alpha_S(m_c^2)$ obtained for each sample, where the values of $m_c$ and $|V_{cs}|$ were allowed to change in the fit. The first and second uncertainties of $\alpha_S(m_c^2)$ are the experimental and theoretical uncertainties, respectively. The result, which was jointly obtained from $D^0$ and $D^+$ (bold), was similar to $0.375\pm0.011$, the value of $\alpha_S$ running from $m_Z$ down to $m_c$.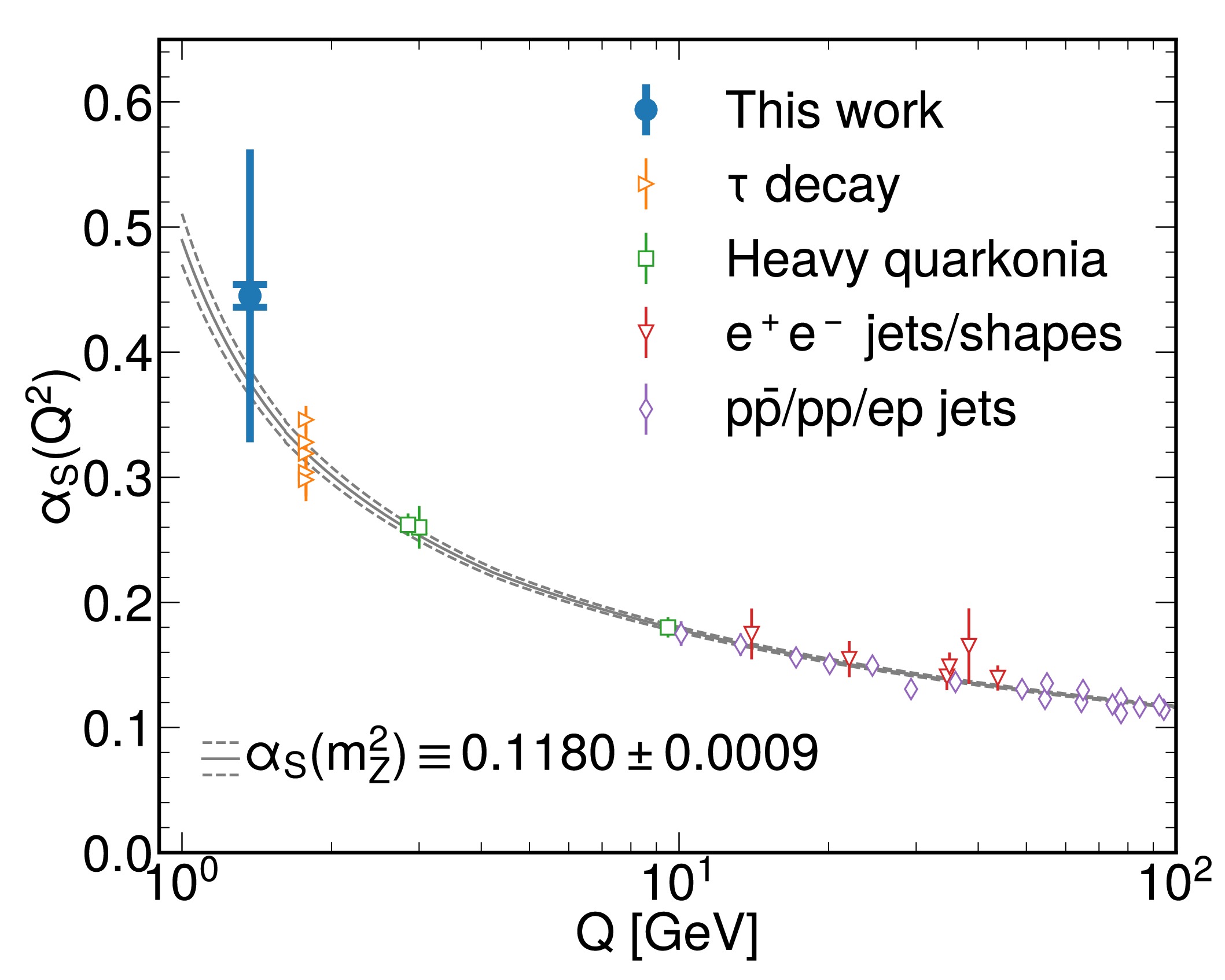

Sample	$D^0$	$D^+$	${\boldsymbol{D}}^+_s,\ {\boldsymbol{D}}^0$	$D^+_s$
$m_c [\text{GeV}]$	$1.3701\pm0.0339$	$1.3699\pm0.0340$	$\bf{1.3701\pm0.0338}$	$1.3699\pm0.0340$
$\alpha_S(m_c^2) [10^{-3}]$	$448\pm13\pm114$	$444\pm12\pm115$	$\bf{445\pm9\pm114}$	$400\pm14\pm113$

DownLoad: CSV

Show Table

Figure 3

Figure 3.  (color online) Values of $\alpha_S$ at different energy scales. The blue dot is the measured $\alpha_S(m_c^2)$ value obtained in this study, where the inner and the outer error bars are the experimental and total uncertainties, respectively. The other points are measurements of $\alpha_S$ at different energy scales [36−46]. The solid and dashed gray lines are the values and uncertainties of $\alpha_S$ running from $\alpha_S(m_Z^2)$, respectively.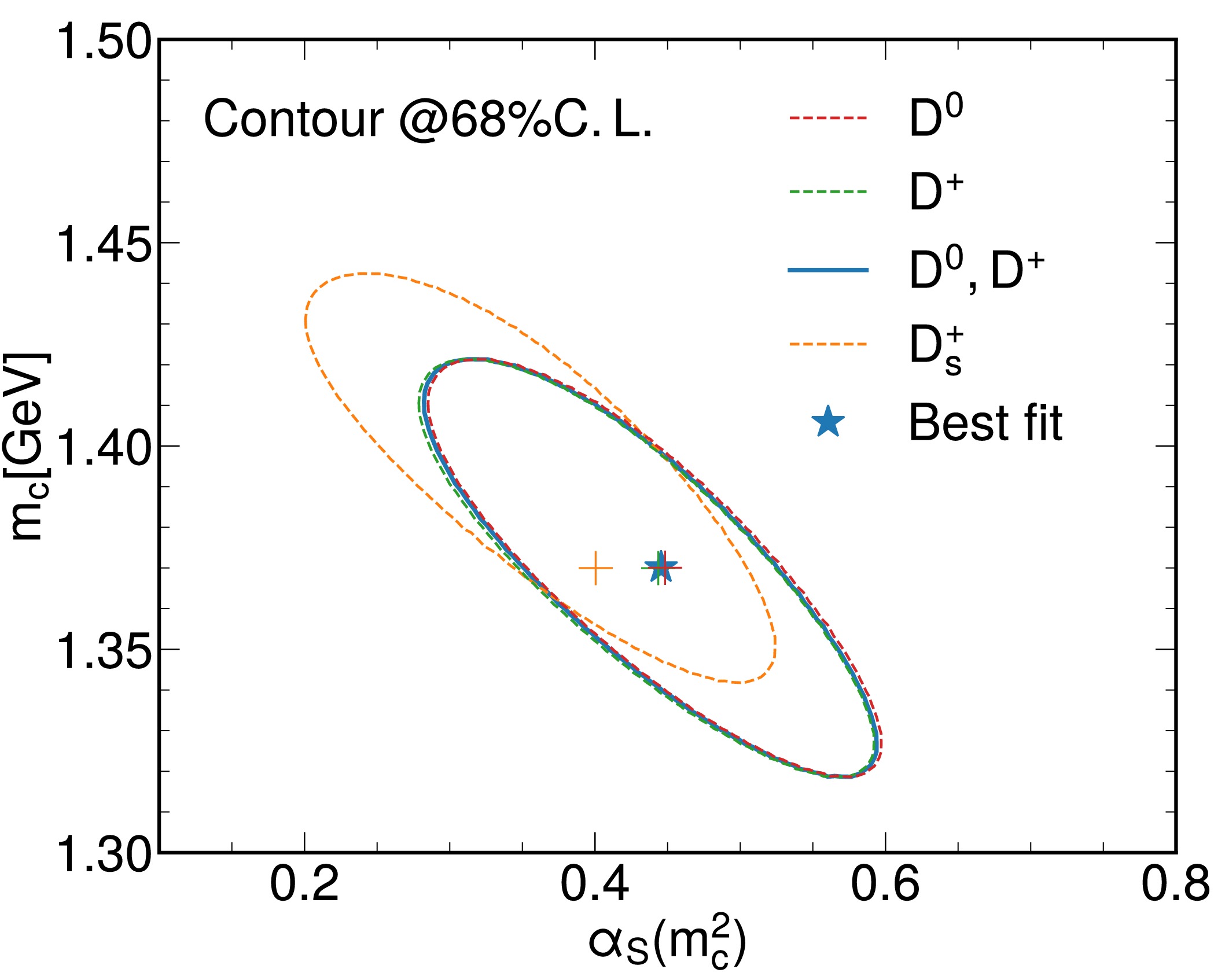

DownLoad: Full-Size Img PowerPoint

Figure 4

Figure 4.  (color online) Profile contours of the different samples at the 68% confidence level. The solid blue curve and star are the contour and best-fit value for $D^{0}$ and $D^{+}$ combined, respectively. The dashed orange curve and cross are the contour and best-fit value for $D_{s}^{+}$, respectively. The dashed red and the green curves and crosses are the contours and best-fit values for $D^{0}$ and $D^{+}$, respectively.

DownLoad: Full-Size Img PowerPoint

To check the stability of the results of this study, the value of $m_c$ was fixed at $1.370\pm0.034\ \text{GeV}$, and the corresponding uncertainty was estimated by varying the value of $m_c$ within $\pm1\sigma$. Usually, the value of $|V_{cs}|$ is obtained from exclusive semileptonic or leptonic charmed meson decays; however, this technique could have introduced bias in this study. Hence, obtaining a value for $|V_{cs}|$ without involving semileptonic charmed meson decays was necessary to validate the results of this study. Using $|V_{cd}| = 0.2181\pm 0.0049\pm0.0007$ from the leptonic decays of $D^+$ [47] and $|V_{cb}| = (41.1\pm1.2)\times10^{-3}$ [15], the value of $|V_{cs}|$ without involving semileptonic charmed meson decays was calculated to be $0.975\pm0.001$ via Eq. (6), which has a negligible bias in the determination of $\alpha_S(m_c^2)$.

Figure 2 presents the fitted $\alpha_S(m_c^2)$ values for different D meson samples for a fixed $m_c$. The robustness of this study was confirmed by the consistent values of $\alpha_S(m_c^2)$ obtained via fits with fixed and floating values of $m_c$.

VI. SUMMARY

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

In summary, the value of $\alpha_S(m_c^2)$ at $m_c = 1.37\ \text{GeV}$ was determined to be $0.445\pm0.009\pm0.114$ using the semileptonic decay widths of the $D^0$ and $D^+$ measured by CLEO-c, and it was cross-checked using the $\Gamma_{SL}$ of the $D^+_s$ meson reported by BESIII. This result for $\alpha_S(m_c^2)$ was in good agreement with the value obtained by running $\alpha_S(m^2_Z)$ to $m_c$. The values of $\alpha_S(m_c^2)$ were derived for each of the $D^0$, $D^+$, and $D^+_s$ mesons, and were found to be within $\pm 1\sigma$ of each other, illustrating the robustness of the analysis method. The leading uncertainty in $\alpha_S(m_c^2)$ was from the theoretical calculation of $\Gamma_{SL}$, which can be reduced by detailed experimental studies on the semileptonic decays of the D mesons as well as superior HQE calculations. This study represents the first measurement of $\alpha_S(m_c^2)$ obtained using a new approach. With additional statistical data and enhanced modeling of the HQE, the systematic uncertainty in the value of $\alpha_S(m_c^2)$ may be significantly reduced in the future.

VII. ACKNOWLEDGMENTS

• I. INTRODUCTION
• II. HEAVY QUARK EXPANSION MODEL IN THE KINETIC SCHEME
• III. FITTING METHOD
• IV. EXPERIMENTAL INPUTS
• V. RESULTS
• VI. SUMMARY
• VII. ACKNOWLEDGMENTS

The authors thank H. B. Li, X. T. Huang, X. Chen, G. Y. Zhang, J. L. Pei, H. Q. Zhang, Y. Q. Fang, and L. G. Shao for fruitful discussions.

References