Description of the critical point symmetry in ¹²⁴Te by IBM-2

The characterization of the underlying structure of ¹²⁴Te is difficult, and it has attracted a significant amount of attention in various theoretical and experimental studies [1-6]. The ¹²⁴Te lies outside the major shell $Z=50$ with two protons, and its ratio $E(4^+_1/2^+_1)=2.07$ is very close to the spherical vibrator value of 2.00. This indicates that the ¹²⁴Te is a vibrational or U(5) symmetric nucleus. However, the energy levels spread of the two-phonon multiplets do not suggest a vibrational character in ¹²⁴Te. Meanwhile, the energy level of the lowest excited 0⁺ state suggests that the ¹²⁴Te exhibits more $\gamma$ -unstable or O(6) behavior; however, the $E2$ decays of the 0 $^+_2$ state do not support the $\gamma$ -soft rotational nature.

On the contrary, shape coexistence in the Te isotopes is still elusive [4]. The appearance of strong $\rho(E0, 0^+_2\rightarrow0^+_1)$ transition is an important spectroscopic fingerprint that mostly supports the shape coexistence in nucleus [7]. For ¹²⁴Te, the experimental value of the electric monopole transition strength $\rho^2(E0, 0^+_2\rightarrow0^+_1)\times10^3$ is $12\pm3$ [8]. This value is very similar to the corresponding transition in the Cd isotopes; the latter demonstrates firm evidence for the nature of shape coexistence, providing strong support for the deformed intruder structure of the first-excited 0⁺ state in ¹²⁴Te isotopes. However, it does not provide conclusive proof for the shape coexistence in ¹²⁴Te yet [4]. Meanwhile, systematic research on the known experimental information suggests that ¹²⁴Te may be an example of the nucleus at the $E(5)$ critical point [9]. Recent investigations indicate that ¹²⁴Te exhibits $E(5)$ -like structure [5, 10]. However, the low-lying structure of ¹²⁴Te has still not been understood (see, e.g., Refs. [3, 10, 11] and references therein).

The $E(5)$ and $X(5)$ symmetries originally developed by Iachello [12, 13] correspond to an exact solution of the Bohr Hamiltonian for $\gamma$ -independent potentials and an approximate solution of the Bohr-Hamiltonian for $\gamma\approx 0^\circ$ , respectively. From the Bohr-Hamiltonian with $\gamma$ frozen at $\gamma=30^\circ$ , a four dimensional critical point symmetry model called $Z(4)$ was introduced [14]. Most recently, another four-dimensional critical point symmetry called $T(4)$ was obtained from the Bohr-Hamiltonian with the $\beta$ -soft potential and for a fixed value of $\gamma$ with $0^\circ \leqslant \gamma \leqslant 30^\circ$ [15].

In the nuclear system, the $E(5)$ symmetry can be used to describe a nucleus at the critical point of the second-order phase transition from a spherical vibrator to a $\gamma$ -soft rotor. In the interacting boson model (IBM-1) [16], which does not distinguish between the proton boson and neutron boson, the $E(5)$ represents a nucleus that is located at the critical point of the shape phase transition between the U $(5)$ and O $(6)$ symmetries. Because the neutron and proton degrees of freedom are explicitly taken into consideration, the proton-neutron interacting boson model (IBM-2)[16] has a complex phase diagram [17, 18]. The critical point of the second-order phase transition can occur at the phase transition from ${\rm U}_{\pi \nu}(5)$ to ${\rm O}_{\pi \nu}(6)$ symmetry and can be subsumed to the critical point of the second-order phase transition in IBM-1 [17-19]. Compared to their neighboring isotopes, nuclei at or close to the critical point of shape phase transition demonstrate drastic changes in the properties of the low-lying states, such as the energy levels, the $E2$ transition strengths, and $E2$ branching ratios [20]. However, so far, there has been no discussion on the critical point symmetry in the real nuclei for the phase transition between $\rm{U}_{\pi \nu}(5)$ and $\rm{O}_{\pi \nu}(6)$ in the IBM-2 phase diagram.

The low-lying levels of ¹²⁴Te have recently been examined with the ( ${n, n', \gamma}$ ) reaction. The spins, level energies, $B(E2)$ transition probabilities, and multipole-mixing ratios were obtained [3]. The experiment provides the basis for an in-depth study of the low-lying structure of ¹²⁴Te. In this work, we study the low-lying structure of the ¹²⁴Te within the framework of the IBM-2, with a focus on the key observables of the critical point of the second-order transition between $\rm{U}_{\pi \nu}(5)$ and $\rm{O}_{\pi \nu}(6)$ . We also calculate the low-lying energy levels and the $E2$ , $M1$ , and $E0$ transition strengths, and we compare the predictions of the critical point symmetry of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition with the experimental data. We attempt to describe the critical point symmetry in the ¹²⁴Te, and reveal the low-lying structure of ¹²⁴Te in IBM-2 space.

The outline of the paper is as follows. In Section 2, we introduce the Hamiltonians of IBM-2, E2, M1, and E0 operators, used in this work. The criteria adopted for the determination of the model parameters and the comparison of the numerical results with experimental data and the predictions of the critical point symmetry are presented in Section 3. Finally, the conclusions and summary are provided in Section 4.

The IBM-2 is an algebraic model, in which valence nucleons are coupled to form $s_{\rho}$ bosons (angular momentum $L$ =0) and $d_{\rho}$ bosons (angular momentum $L=2$ ), where $\rho= \pi$ denotes proton bosons and $\rho= \nu$ denotes neutron bosons, respectively. The microscopic structure of the model suggests that there are only two significant terms: the pairing interaction between identical nucleons and the quadrupole-quadrupole interaction between nonidentical nucleons. The simple standard IBM-2 Hamiltonian [16, 21] is written as

where $\hat{n}_{d\rho} = d^{\text{†}}_\rho \cdot\tilde{d_\rho}$ and ${\hat Q_\rho } = {\left( {s_\rho ^{\text{†}}{{\tilde d}_\rho } + d_\rho ^{\text{†}}{s_\rho }} \right)^{\left( 2 \right)}} + {\chi _\rho }{\left( {d_\rho ^{\text{†}}{{\tilde d}_\rho }} \right)^{\left( 2 \right)}}$ represent $d$ -boson number operator and quadrupole operator, respectively. The parameter ${\chi_\rho}$ determines the type of the deformation of the quadrupole operator. $\varepsilon_{d\rho}$ is the energy of the d bosons relative to the $s$ bosons, and $\kappa_{\pi\nu}$ is the strength of the quadrupole-quadrupole interaction between the neutron boson and the proton boson.

The Hamiltonian of Eq. (1) has a much richer shape phase structure, which contains $\rm{U}_{\pi \nu }(5)$ , $\rm{O}_{\pi \nu }(6)$ , $\rm{SU}_{\pi \nu }(3)$ , $\overline{\rm{SU}_{\pi \nu }(3)}$ , and ${\rm{SU}}_{\pi \nu }^ * \left( {\rm{3}} \right)$ dynamical symmetries, corresponding to the spherical vibrator, $\gamma$ -unstable rotor, axially symmetric prolate rotor, axially symmetric oblate rotor, and triaxial rotor, respectively. The shape phase transitions in nuclei can be characterized as the quantum phase transitions between the different dynamical symmetries in the IBM [17, 18, 22]. Although the standard IBM-2 Hamiltonian can provide a clearer space of dynamical symmetry, other physical dominant interactions must be included to describe the real nuclei more accurately. We use the following IBM-2 Hamiltonian in this study [16, 23, 24],

where $\hat{L_\rho}=\sqrt{10}[d^{\text{†}}_\rho \cdot\tilde{d_\rho}]^{(1)}$ is the angular momentum operator with a dipole proton-neutron interaction parameter $\omega_{\pi\nu}$ , and ${\hat M_{\pi \nu }} = {\lambda _2}{\left( {s_\pi ^{\text{†}}d_\nu ^{\text{†}} - s_\nu ^{\text{†}}d_\pi ^{\text{†}}} \right)^{\left( 2 \right)}} \cdot {\left( {{s_\pi }{{\tilde d}_\nu } - {s_\nu }{{\tilde d}_\pi }} \right)^{\left( 2 \right)}}+ \displaystyle\sum\limits_{k = 1, 3}$ ${{\lambda _k}} {\left( {d_\pi ^{\text{†}}d_\nu ^{\text{†}}} \right)^{\left( k \right)}} \cdot$ ${\left( {{{\tilde d}_\pi }{{\tilde d}_\nu }} \right)^{\left( k \right)}}$ is the Majorana interaction; the Majorana parameters $\lambda_{k}$ (k= 1, 2, 3) represent the strength of the Majorana interaction. If the Majorana term is not included in Eq. (2), the adopted parameters in the remaining four terms of Eq. (2) indicate that the nucleus described by the IBM-2 may be located on the the plane of $\rm{U}_{\pi \nu }(5)$ - $\rm{O}_{\pi \nu }(6)$ - $\rm{SU}^{\ast}_{\pi \nu }(3)$ , because the $\hat{L}_{\pi}\cdot\hat{L}_{\nu}$ only generates the physical rotational group $\rm{SO}_{\pi \nu }(3)$ of the IBM-2 [16-18]. On the contrary, in Ref. [25] the authors proposed a new algebraic model $F(5)$ based on the Euclidean dynamical symmetry in five dimensions ( $\rm{Eu(5)}$ ), which can build a symmetry intermediate between the $E(5)$ and $X(5)$ symmetries [22]. However, the $F(5)$ cannot directly be defined in the IBM-1 or IBM-2 because of the noncompactness of the $\rm{Eu(5)}$ group [25].

The decay properties of the low-lying states, such as the $B(E2)$ transition probabilities, the magnetic dipole $B(M1)$ transition strengths and the $\rho^2(E0)$ values between the lowest 0⁺ states are the characteristics of the phase structure. In the IBM-2, the E2 transition strength is given by the following expression

where $J'$ and $J$ are the angular momenta for the initial and final states, respectively. The $\hat{T}{(E2)}=e_{\pi} \hat{Q}_{\pi} + e_{\nu}\hat{Q}_{\nu}$ is the E2 operator, where the operator $Q_\rho$ is the same as in Eq. (1). The parameters $e_\pi$ and $e_\nu$ are the effective charges of proton bosons and neutron bosons, respectively. The values of $e_\nu$ and $e_\pi$ could be taken differently.

In the proton-neutron interacting boson model, the magnetic dipole $M1$ transition operator is defined as

where the $\hat{L}_\rho$ is the same as in Eq. (2). The $g_\pi$ and $g_\nu$ are the effective proton and neutron boson $g$ -factors, respectively. Typically, one can take the values of $g_\pi=1$ , $g_\nu=0$ in the calculations [21].

The $E0$ transition matrix element $\rho$ in the IBM-2 is written as [26, 27]

where $R=1.2A^{1/3}$ fm, $\beta_{0\pi}$ , and $\beta_{0\nu}$ are the effective monopole charges of proton and neutron boson in units of $e$ fm², respectively. The E0 operator is expressed as $\hat T\left( {E0} \right) = {\beta _{0\pi }}{\hat T_\pi }\left( {E0} \right) + {\beta _{0\nu }}{\hat T_\nu }\left( {E0} \right) = {\beta _{0\pi }}{\hat n_{d\pi }} + {\beta _{0\nu }}{\hat n_{d\nu }}$ , where the $\hat{n}_{d\rho}$ is the same as in Eq. (1).

The ¹²⁴Te is located between the vibrational nucleus and the deformed nucleus [28]. The IBM provides a powerful tool to describe the nuclear shapes and the shape phase transitions. Several studies have used this approach to describe the properties of the low-lying states of ¹²⁴Te isotope. In IBM-1, early studies regarded the ¹²⁴Te as an example of O $(6)$ symmetry; however, the energy levels of yrast states of ¹²⁴Te differ from the O(6) limit [29]. Further systematic investigations found that ¹²⁴Te was close to the U $(5)$ symmetry [30, 31]. Moreover, recent results of experiments and calculations indicate that ¹²⁴Te may possess the $E(5)$ features [3, 9, 5, 10]. In IBM-2, the calculations with and without the mixed configuration suggest that ¹²⁴Te is an O $(6)$ -like nucleus, but the $B(E2)$ decay pattern is not consistent with this symmetry [32]. A subsequent study showed that neither O $(6)$ nor U $(5)$ symmetries can describe the ¹²⁴Te well [33], although the potential energy surface of ¹²⁴Te exhibits an obvious manifestation of O $(6)$ limit [34]. Another recent experiment and IBM calculation support that ¹²⁴Te demonstrates soft triaxial behavior [6]. Although the low-lying structure of the ¹²⁴Te is still not understood, it is indubitable that these results indicate that ¹²⁴Te is a transitional nucleus between vibration U $(5)$ symmetry and $\gamma$ -unstable O $(6)$ symmetry in IBM, and might accompany with a slight soft triaxial rotation.

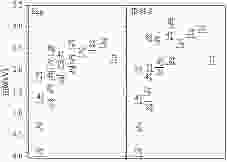
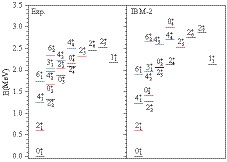
To describe the low-lying structure of ¹²⁴Te, we selected the doubly closed shell $^{132}_{50}$ Sn $_{82}$ as the inert core. There are $N_\pi=1$ particle-like bosons beyond the $Z=50$ major shell, and $N_\nu=5$ hole-like neutron bosons from the $N=82$ shell closure; the total number of bosons is $N_B=6$ . Considering that the proton bosons are particle-like and the neutron bosons are hole-like based on different single particle orbitals in ¹²⁴Te, we choose different relative energies for $d$ neutron and proton boson in this case, i.e., $\varepsilon_{d\pi}\neq\varepsilon_{d\nu}$ , similar to Refs. [35-37]. To describe the different type of valence neutrons and protons exhibiting opposite intrinsic quadrupole deformation, and to obtain the $\gamma$ -unstable O $(6)$ symmetry, we adopt $\chi_\pi+\chi_\nu=0$ . To introduce some characteristics of the soft triaxial rotation in ¹²⁴Te, the value of $\chi_\pi$ and $\chi_\nu$ should not be zero. In principle, the parameter $\varepsilon_{d\rho}$ mainly leads to vibrational solutions, while $\kappa_{\pi\nu}$ drives the system into a deformed shape, and the description of the electromagnetic properties is very sensitive to the parameters $\chi_\rho$ . The dipole interaction $\hat{L}_{\pi}\cdot\hat{L}_{\nu}$ can improve the rotational spectrum and can adjust the position of the 4 $^+_1$ relative to 2 $^+_2$ state; however, it does not affect the wave vectors [38]. The Majoranan operator mainly contributes to the mixed symmetry states including the scissors mode. All the free parameters in our calculations were fixed to reproduce the experimental energies and electromagnetic transition strengths of ¹²⁴Te. By fitting to the energy levels of the experimental data, especially for the 2 $^+_1$ state, we obtain the parameters of IBM-2 in this study as follows: $\varepsilon_{d\pi}=1.220$ MeV, $\varepsilon_{d\nu}=0.710$ MeV, $\kappa_{\pi\nu}=-0.140$ MeV, $\chi_\pi=-\chi_\nu=-1.00$ , $\omega_{\pi\nu}=-0.055$ MeV, $\lambda_1=-0.700$ MeV, $\lambda_2=0.220$ MeV, and $\lambda_3=-0.100$ MeV. The IBM-2 Hamiltonian will be numerically diagonalized by using the NPBOS code [39]. In Fig. 1, we compare the calculated level energies with the experimental results [3, 40]. The experimental level energies in Fig. 1 are separated into different bands based only on their order of appearance; only the low-spin positive parity states with uniquely assigned spin and parity are displayed in the figure.

Figure 1.  (color online) Comparison of the calculated and experimental [3, 40] low-lying positive-parity levels of ¹²⁴Te.

Figure 1 shows that the theoretical levels are in good agreement with the corresponding experimental levels. In particular, the 6 $^+_1$ state is dominated by two valence protons and is relatively unaffected by the increase of neutrons. The 6 $^+_1$ states remain at a nearly constant excitation energy for even-even ^122-130Te isotopes [3]. By introducing the dipole interaction term into the Hamiltonian [41-43], the structure of the yrast bands including the 6 $^+_1$ level are reproduced by the theoretical predictions. Similar to the 6 $^+_1$ state, the observed energy of 4 $^+_2$ level is only changed by approximately 135 keV from ¹²²Te to ¹³⁰Te isotopes. The present calculation reproduces the experimental energy of the 4 $^+_2$ level well. Meanwhile, the present calculated energies of the 2 $^+_{3, 4, 5}$ , and 6 $^+_2$ levels agree with the experimental observations. Even though the 0 $^+_2$ level is clearly higher than that is expected for a two-phonon multiple state, the description of the first two excitation 0 $^+$ states in energy sequence is satisfactory. Furthermore, the calculated energy level of the first scissor mode 1 $^+_1$ perfectly reproduces the experimental data. However, there are some discrepancies between the experimental observations and the theoretical predictions for higher energy states, such as 2 $^+_6$ , and 2 $^+_7$ states, which is a general feature of this model [44]. For the 0 $^+_4$ state, the calculated level is significantly higher than the experimental level. The IBM-2 with the mixed configuration shows that 0 $^+_4$ is an intruder state in ¹²⁴Te and is located outside the IBM-2 space [32].

In order to investigate the properties of the $E2$ transitions in ¹²⁴Te, the effective charges of the proton and neutron bosons were determined to reproduce the experimental $B(E2)$ values. Using the same method as in Refs. [45, 46] and exactly fitting to the experimental data of $B(E2, 2^+_1\rightarrow0^+_1)=31(5)$ W.u., we obtain $e_\pi=3.780$ $\sqrt{\rm {W.u.}}$ and $e_\nu=1.670$ $\sqrt{\rm {W.u.}}$ . The theoretical calculation of $B(E2)$ values for ¹²⁴Te in comparison with the available experimental data [1, 3, 10, 47-49] is given in Table 1.

${ J^\pi_i\rightarrow }$ ${ J^\pi_f }$	Expt.	IBM-2
${ { 2^+_1 }\rightarrow { 0^+_1 }}$	${31^5_5 }$	31.02
${ { 4^+_1 }\rightarrow { 2^+_1 }}$	54.51	48.06
${{ 2^+_2 }\rightarrow { 2^+_1 }}$	${ 55.5^{109}_{99} }$	49.53
${{ 2^+_2 }\rightarrow { 0^+_1 }}$	${0.83 ^{23}_{16} }$	0.24
${{ 0^+_2 }\rightarrow { 2^+_1 }}$	${ 20^{4}_{4} }$	27.92
${{ 0^+_3 }\rightarrow { 2^+_2 }}$	50.00	48.51
${{ 4^+_2 }\rightarrow { 2^+_2 }}$	${14.1 ^{30}_{28} }$	29.94
${ { 4^+_2 }\rightarrow { 4^+_1 }}$	${12.7 ^{74}_{59} }$	27.06
${ { 4^+_2 }\rightarrow { 2^+_1 }}$	${4.3 ^{9}_{9} }$	0.31
${{ 3^+_1 }\rightarrow { 2^+_2 }}$	${ 59^{10}_{10} }$	42.65
${ { 2^+_3 }\rightarrow { 0^+_1 }}$	${ 0.26^{4}_{4} }$	2.08
${{ 2^+_3 }\rightarrow { 2^+_1 }}$	${0.025 ^{4}_{3} }$	0.50
${{ 2^+_3 }\rightarrow{ 2^+_2 }}$	${\leqslant 2.7^{19}_{15} }$	4.03
${ { 2^+_3 }\rightarrow { 4^+_1 }}$	${0.81 ^{104}_{81} }$	5.38
${ { 2^+_3 } \rightarrow { 3^+_1 }}$	${0.26 ^{5}_{4} }$	0.37
${ { 2^+_4 }\rightarrow{ 2^+_2 }}$	${0.29 ^{39}_{33} }$	1.85
${ { 2^+_4 }\rightarrow{ 2^+_1 }}$	${1.6 ^{3}_{3} }$	1.39
${ { 2^+_4 }\rightarrow{ 0^+_1 }}$	${ 0.053^{17}_{14} }$	2.16
${{ 0^+_4 }\rightarrow{ 2^+_1 }}$	${ <0.5 }$	0.04
${ { 0^+_4 }\rightarrow{ 2^+_2 }}$	${ <50 }$	0.03
${ { 1^+_1 }\rightarrow{ 2^+_1 }}$	${1.2 ^{4}_{3} }$	4.99
${ { 1^+_1 }\rightarrow{ 2^+_2 }}$	${ 0.74^{38}_{38} }$	1.13
${{ 4^+_3 }\rightarrow { 2^+_2 }}$	${13.4 ^{49}_{39} }$	1.16
${{ 4^+_3 }\rightarrow{ 4^+_1 }}$	${ 6.7^{23}_{20} }$	2.89
${{ 4^+_3 }\rightarrow{ 2^+_1 }}$	${ 1.9^{6}_{5} }$	0.95
${{ 2^+_5 }\rightarrow{ 2^+_2 }}$	${0.61 ^{40}_{30} }$	1.02
${{ 2^+_5 }\rightarrow { 2^+_1 }}$	${0.06 ^{7}_{6} }$	0.15
${ { 2^+_5 }\rightarrow{ 0^+_1 }}$	${ 0.078^{50}_{42} }$	0.09
${{ 2^+_6 }\rightarrow{ 2^+_2 }}$	${ 1.6^{5}_{5} }$	1.67
${ { 2^+_6 }\rightarrow{ 4^+_1 }}$	${ 1.7^{5}_{4} }$	0.00
${{ 2^+_6 }\rightarrow{ 2^+_1 }}$	${0.046 ^{8}_{6} }$	0.23
${{ 2^+_6 }\rightarrow{ 0^+_1 }}$	${0.12 ^{3}_{2} }$	0.01
${{ 4^+_4 } \rightarrow{ 4^+_1 }}$	${ 2.6^{9}_{7} }$	0.10
${ { 4^+_4 }\rightarrow{ 2^+_1 }}$	${ 0.051^{28}_{22} }$	0.72
${{ 2^+_7 }\rightarrow{ 2^+_1 }}$	${4.0 ^{4}_{4} }$	0.56
${{ 2^+_7 }\rightarrow{ 2^+_2 }}$	${0.20 ^{10}_{11} }$	0.00
${ { 2^+_7 }\rightarrow{ 4^+_1 }}$	${ <1.6 }$	1.10

Table 1.  Experimental ${E2}$ transition strengths in ¹²⁴Te in units of W.u. are compared with the calculated results. The experimental data are taken from Refs. [1, 3, 10, 47-49]

Table 1 shows that the computed ${B}(E2)$ transition strengths are in overall agreement with the experimental data, although most cases of the experimental value have a large uncertainty. In particular, the typical strongly collective $E2$ transitions with tens of Weisskopf units are described by the theoretical predictions very well, some of them consist with each other within the experimental uncertainty. It is noteworthy that the experimental ${B}(E2, 4^+_1\rightarrow2^+_1)$ transition strength is $35.9(\pm 17)$ W.u. in Ref. [3], which is taken from Ref. [6]. In Ref. [48], the experimental values show that the lower and upper limits of this transition probability are 27.3 and 163.5 W.u., respectively. Similar to Ref. [47], we adopt the experimental averaged value 54.51 W.u. for this transition; the details are provided in Ref. [50]. The experimental value agrees with the present calculated value. At the same time, the experimental relatively strong $B(E2)$ transitions, which are comparable with the experimental transition probability of the first-excited state 2 $^+_1$ decay to the ground state with dozens of W.u., are reproduced by the calculated results perfectly except the ${B}(E2, 4^+_3\rightarrow2^+_2)$ transition strength. Furthermore, the calculated results are in good description of the properties of the experimental weakly collective $E2$ transitions with about one or even less than one W.u.. The theoretical $E2$ transition strengths from the scissor mode 1 $^+_1$ to the 2 $^+_1$ and 2 $^+_2$ states are in agreement with the corresponding experimental data, although the theoretical values are slightly higher than the experimental data test

To identify where the ¹²⁴Te can be placed in the $\rm{U}_{\pi \nu}(5)$ to $\rm{O}_{\pi \nu}(6)$ transition, we focus on a set of key observables [51], such as the energy ratios $R_{4_1/2_1}=E(4^+_1)/E(2^+_1)$ , $R_{2_2/2_1}=E(2^+_2)/E(2^+_1)$ , $R_{0_2/2_1}=E(0^+_2)/E(2^+_1)$ , $R_{0_3/0_2}=E(0^+_3)/$ $E(0^+_2)$ , and the $B(E2)$ ratios $R_{B, 42}=B(E2, 4^+_1\rightarrow2^+_1)/$ $B(E2, 2^+_1\rightarrow0^+_1)$ , $R_{B, 22}=B(E2, 2^+_2\rightarrow2^+_1)/B(E2, 2^+_1\rightarrow0^+_1)$ and $R_{B, 02}=B(E2, 0^+_2\rightarrow2^+_1)/B(E2, 2^+_1\rightarrow0^+_1)$ , which reflect the characteristics of the nucleus behavior at critical point of the phase transition from $\rm{U}_{\pi \nu}(5)$ to $\rm{O}_{\pi \nu}(6)$ in IBM-2 space [17]. These observables are the most crucial nuclear structure indicators [52]. Some indicators can even distinguish the first-order quantum phase transition from the second-order quantum phase transition [53-55]. The values of these key observables at the critical point of the phase transition from $\rm{U}_{\pi \nu}(5)$ to $\rm{O}_{\pi \nu}(6)$ for infinite numbers of bosons [12], as well as the experimental data and the calculated results in ¹²⁴Te, are listed in Table 2 for comparison.

	CPST	124Te	IBM-2
${R_{4_1/2_1} }$	2.20	2.07	2.06
${R_{2_2/2_1} }$	2.20	2.20	2.13
${R_{0_2/2_1} }$	3.03	2.75	2.35
${R_{0_3/0_2} }$	1.18	1.14	1.46
${R_{B, 42} }$	1.68	1.74	1.55
${R_{B, 22} }$	1.68	1.79	1.60
${R_{B, 02} }$	0.86	0.65	0.90

Table 2.  Comparison of the key observables of the states at the critical point of the ${\rm{U}_{\pi\nu}(5)}$ - ${\rm{O}_{\pi \nu}(6)}$ transition (taken from Ref. [12] and denoted as CPST), the experimental data of ¹²⁴Te (taken from Refs. [1, 3, 47-49] and labeled as ¹²⁴Te) and the calculated results (labeled as IBM-2).

Table 2 shows that the overall agreement is well. On the energy ratios, the experimental ratio $R_{2_2/2_1}$ is almost exactly reproduced to the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. The experimental ratio $R_{0_3/0_2}$ is very close to the value of CPST. Meanwhile, the experimental energy of the $0^+_2$ state, relative to $E(2^+_1)$ , satisfactorily matches the predicted value of CPST. The experimental $R_{4_1/2_1}$ lies between U $_{\pi\nu}(5)$ ( $R_{2_2/2_1}=2.00$ ) and $\rm{O}_{\pi \nu}(6)$ ( $R_{2_2/2_1}=2.50$ ) limits, although it deviates slightly from the predicted one. On the $B(E2)$ ratios, the experimental $R_{B, 42}$ is well reproduced by the theoretical prediction and clearly points to a structure intermediate between U $_{\pi\nu}(5)$ ( $R_{B, 42}=2.00$ ) and $\rm{O}_{\pi \nu}(6)$ ( $R_{B, 42}=10/7$ ). Meanwhile, the experimental value of $R_{B, 22}$ also approaches the predicted value of the critical point theory. In particular, the information of $R_{B, 02}$ is a signature for identifying the $\rm{U}_{\pi \nu}(5)$ from the $\rm{O}_{\pi \nu}(6)$ symmetry. In $\rm{U}_{\pi \nu}(5)$ limit, the $B(E2, 0^+_2\rightarrow2^+_1)$ transition strength is two times larger than $(B(E2, 2^+_1\rightarrow0^+_1)$ . In $\rm{O}_{\pi \nu}(6)$ limit, the $B(E2, 0^+_2\rightarrow2^+_1)$ transition is forbidden [56]. Here, both the experimental and theoretical values of the $R_{B, 02}$ can correctly reflect the nature of the $B(E2, 0^+_2\rightarrow2^+_1)$ transition, although the calculated value overestimates the experimental value by approximately 1.5 times. Therefore, all the available experimental information on the key observables for ¹²⁴Te is in good agreement with the predictions of critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. Meanwhile, Table 2 also shows that the present calculation of the characteristic feature of ¹²⁴Te is remarkable. However, the $R_{0_2/2_1}$ of CPST seems larger than the IBM's in Table 2; this is because the calculation of the CPST is given for the infinite $-N_B$ limit [12, 51]. For a finite number of bosons, Ref. [17] showed that the $R_{0_2/2_1}$ of a nucleus at the critical point of the phase transition from $\rm{U}_{\pi \nu}(5)$ to $\rm{O}_{\pi \nu}(6)$ with $N_{\pi} = N_{\nu} =5$ is 2.48, which agrees the result of the present calculations. From the above discussion, we conclude that the ¹²⁴Te may be a nucleus at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. Consequently, the $0^+_2$ state is the lowest possible state of the first-excited family of intrinsic levels predicted by the critical point symmetry.

An advantage of IBM-2 over IBM-1 is that the former can study the influence of the critical point symmetry on magnetic dipole transitions between the low-lying states [23]. In IBM-2, the pure $\rm{O}_{\pi\nu}(6)$ symmetry can be obtained only with $\chi_\pi=\chi_\nu=0$ . In this case, there does not exist any asymmetry between $\chi_\pi$ and $\chi_\nu$ . This implies that the mixed symmetry components could not mix into the low-lying states. Therefore, the $M1$ transitions between these states are forbidden in $\rm{O}_{\pi\nu}(6)$ limit [21]. The theoretical predictions show that the $B(M1)$ transition strengths among the low-lying states almost vanish when a nucleus is at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition [17]. For the scissors mode state 1 $^+_1$ , the $B(M1, 1^+_1\rightarrow 0^+_1)$ transition strength is $3N_\pi N_\nu(g_\nu-g_\pi)^2/{4\pi(2N_B+1)}$ for $\rm{O}_{\pi \nu}(6)$ limit; however, it is forbidden for $\rm{U}_{\pi\nu}(5)$ limit. The $B(M1, 1^+_1\rightarrow 0^+_2)$ value is $3N_\pi N_\nu(g_\nu-g_\pi)^2/{\pi N_B(N_B-1)}$ for $\rm{U}_{\pi\nu}(5)$ limit, whereas it vanishes for $\rm{O}_{\pi\nu}(6)$ limit [23, 57, 58]. At the critical point of $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition, the 1 $^+_1$ state allows $M1$ decays to first and second $0^+$ states. In the case of ¹²⁴Te, the $B(M1, 1^+_1\rightarrow 0^+_1)$ is 0.10 $\mu^2_N$ for $\rm{O}_{\pi \nu}(6)$ limit, and $B(M1, 1^+_1\rightarrow 0^+_2)$ is 0.50 $\mu^2_N$ for $\rm{U}_{\pi\nu}(5)$ limit, with the typical values $g_\pi=1$ and $g_\nu=0$ . Indeed, only a few $M1$ transitions, with very small absolute values of $B(M1)$ , among the low-lying states in ¹²⁴Te have been measured [49, 59]. By using Eq. (4) and also taking $g_\pi=1$ and $g_\nu=0$ , the calculated $M1$ transition probabilities, as well as the corresponding available experimental data for the scissors mode and the low-lying states in ¹²⁴Te, are provided in Table 3.

From Table 3, it can be seen that all the experimental $B(M1)$ transition strengths between the lowest 2 $^+$ states are of the order of approximately 0.01 $\mu^2_N$ or even less, which is far from the typical $B(M1)$ value of the mixed symmetry state. This demonstrates that the observed $M1$ transitions are in qualitative agreement with the predictions of the critical point symmetry of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. At the same time, Table 3 shows that the calculated results reasonably reproduce the characteristics of the $M1$ transitions among low-lying states. In particular, the calculated $B(M1, 1^+_1\rightarrow 0^+_1)$ strength is close to the experimental one, which is comparable to the predicted value of the critical point between the $\rm{U}_{\pi \nu}(5)$ and $\rm{O}_{\pi \nu}(6)$ limits. This indicates that both the experimental and the calculated results of the $B(M1, 1^+_1\rightarrow 0^+_1)$ transition reflect the property of the nucleus at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. Unfortunately, the $B(M1, 1^+_1\rightarrow 0^+_2)$ strength in ¹²⁴Te has not been measured, the calculated value for this transition is 0.035 $\mu^2_N$ , locating between the $\rm{U}_{\pi \nu}(5)$ and $\rm{O}_{\pi \nu}(6)$ transition similar to the case of $B(M1, 1^+_1\rightarrow 0^+_1)$ transition. All these results indicate that both the calculated and experimental $M1$ transitions are consistent with the characteristic behavior of the ¹²⁴Te nucleus at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition.

However, some deviations between the theoretical and experimental $M1$ transition strengths are also are displayed in Table 3; all the calculated $M1$ values are slightly larger than the corresponding experimental values. In IBM-2, $\chi_\pi=-\chi_\nu\neq0$ leads to a spectrum with many O(6) features. In addition, some mixed symmetry components from the asymmetry of $\chi_\pi$ and $\chi_\nu$ mix into the low-lying states beside the pure mixed symmetry states at higher energies [21, 61]. On the contrary, $\chi_\pi=-\chi_\nu\neq0$ makes the nucleus have some features of the $\rm{SU}^\ast_{\pi \nu}(3)$ symmetry, because the proton and neutron have opposite types of deformation [18]. The calculated $B(M1)$ values among the lowest states are systematically slightly larger than the experimental data, which implies that the description of ¹²⁴Te with the characteristics of the $\rm{SU}^\ast_{\pi \nu}(3)$ is slightly rather than the actual nucleus. Furthermore, the small $B(M1)$ values among the low-lying states in ¹²⁴Te also indicate that ¹²⁴Te may contain some components of $\rm{SU}^\ast_{\pi \nu}(3)$ symmetry. Therefore, the ¹²⁴Te may be the nucleus at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition and with a slight $\rm{SU}^\ast_{\pi \nu}(3)$ symmetry.

Transition	Expt.	IBM-2
${2^+_2 }$ ${\rightarrow }$ ${2^+_1 }$	0.0003	0.006
${2^+_3 }$ ${\rightarrow }$ ${2^+_2 }$	0.004	0.025
${2^+_3 }$ ${\rightarrow }$ ${2^+_1 }$	0.013	0.072
${2^+_4 }$ ${\rightarrow }$ ${2^+_2 }$	0.001	0.031
${2^+_4 }$ ${\rightarrow }$ ${2^+_1 }$	0.004	0.075
${1^+_1 }$ ${\rightarrow }$ ${0^+_1 }$	0.04	0.029
${1^+_1 }$ ${\rightarrow }$ ${0^+_2 }$		0.034

Table 3.  Comparison of the calculated ${M1}$ transition strengths (in units of ${\mu^2_N}$ ) and the experimental data for ¹²⁴Te. The experimental data are taken from Refs. [11, 48, 49, 60].

The electric monopole transition strengths between 0⁺ states can be considered as a characteristic of shape coexistence [7] and quantum phase transitions [62], and it can reflect the properties of $E(5)$ dynamical symmetry [9]. In fact, the $\rho^2(E0, 0^+_2\rightarrow0^+_1)$ value of ¹²⁴Te has been measured [8]. However, the $\rho^2(E0)$ value on the first-excited 0⁺ state in ¹²⁴Te has not been understood yet, as mentioned in the introduction [4]. In IBM, the $E0$ transitions do not occur in the U(5) dynamical limit, because $E0$ operator is proportional to $\hat{n}_d$ [63].While in O(6) limit, the selection rules require the $E0$ transition from the 0 $^+_2$ to ground state to be forbidden [64]. For the predicted $E(5)$ symmetry, the 0 $^+_2$ level, which is the lowest member (zero phonon) of the first-excited family, should have an allowed $E0$ branch to the 0 $^+_1$ state. However, so far, the studies of the behavior of $E(5)$ symmetry in ¹²⁴Te have not provided a detailed analysis of the properties of $E0$ transitions. In IBM-2 space, all the symmetrical states have correspondence with the IBM-1 states; therefore, IBM-2 subsumes the critical point of second-order transition of IBM-1[17, 23]. The critical point symmetry of $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ has considerably similarity to the predictions of the ${E}(5)$ symmetry [17]. Subsequently, the $0^+_2$ level should also have an allowed $E0$ decay to the ground state in this prediction of the critical point symmetry. We take the values of parameters $\beta_{0\nu}$ and $\beta_{0\pi}$ as in Ref. [65], namely, $\beta_{0\nu}=0.25$ and $\beta_{0\pi}=0.10$ $e$ fm². The calculated $\rho^2(E0, 0^+_2\rightarrow0^+_1)\times10^3$ value is $11.00$ , which is consistent with the experimental data within the experimental uncertainty. The theoretical and experimental $E0$ transitions prove that the 0 $^+_2$ state may be interpreted as the lowest state of the first-excited family of intrinsic levels in the critical point symmetry of second order $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition.

It is well known that the low-lying yrast states in other Te isotopes such as ^{112, 114}Te show similar behavior, i.e., typical vibrational like spectra, but other properties deviate from the vibrator's [6, 66-68]. These Te isotopes are located around the midshell ¹¹⁸Te. The large-scale shell-model calculations indicate that the behavior of the $B(E2)$ values of these nuclei is related to the competition between the seniority coupling and the neutron-proton correlations. From the viewpoint of the IBM model, ¹¹²Te is below the midshell ¹¹⁸Te; it has $N_\nu=5$ bosons beyond $N=50$ major shell. Both ¹¹²Te and ¹²⁴Te have the same numbers of bosons with $N_\pi=1$ and $N_\nu=5$ ; therefore, they show similar properties of spectrum. As for ¹¹⁴Te, the measured ratio of $B(E2, 4^+_1\rightarrow 2^+_1)$ to $B(E2, 2^+_1\rightarrow 0^+_1)$ is less than one, which is a very unusual deformation; no theoretical models can provide a satisfactory description [68].

In summary, the low-lying structure of the ¹²⁴Te was investigated within the framework of IBM-2. The calculated low-lying energy levels are in good agreement with the corresponding experimental data. In particular, the 6 $^+_1$ , 4 $^+_2$ levels, which are maintain a nearly constant excitation energy from ¹²²Te to ¹³⁰Te isotopes, have been satisfactorily reproduced by using the calculated results. In addition, the first two excited 0⁺ states were described well in the energy sequence, although the 0 $^+_2$ level is clearly higher than that is expected for a two-phonon multiple state. Furthermore, the calculated energy level of the first scissor mode 1 $^+_1$ perfectly reproduces the experimental data.

The calculations show that the computed ${B}(E2)$ transition strengths are in the overall agreement with the experimental data. The observed typical strongly collective $E2$ transitions with tens of Weisskopf units, and most of the experimental relatively strong $B(E2)$ transitions comparable to the experimental ${B}(E2, 2^+_1\rightarrow0^+_1)$ transition probability with dozens of W.u., are reproduced by the theoretical predictions nicely. Furthermore, the calculated results provide accurate description of the properties of the experimentally weakly collective $E2$ transition with approximately one or even less than one W.u.. Particularly, the theoretical $E2$ transitions from the scissor mode 1 $^+_1$ to the 2 $^+_1$ and 2 $^+_2$ states are in good agreement with the corresponding experimental data, although the theoretical values are slightly higher than the experimental data.

By comparing the key observables of the states at the critical point of the U $_{\pi\nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition with the experimental data and the IBM-2 calculations, we show that both the experimental data and the theoretical results of the ¹²⁴Te agree with the predicted properties of the states at the critical point of the phase transition from $\rm{U}_{\pi \nu}(5)$ to $\rm{O}_{\pi \nu}(6)$ very well. This indicates that the ¹²⁴Te may be a nucleus at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. Consequently, the $0^+_2$ state is the lowest possible state of the first-excited family of the intrinsic levels predicted by the critical point symmetry.

At the same time, the characteristics of the $B(M1)$ transition strengths among the low-lying states are consistent with the predictions of the critical point of the transition from $\rm{U}_{\pi \nu}(5)$ to $\rm{O}_{\pi \nu}(6)$ , and there is good agreement between the experiment and the theory for characteristics of the $B(M1)$ transition strengths. Especially, both the experimental and theoretical $B(M1, 1^+_1\rightarrow 0^+_1)$ values are located between the $\rm{U}_{\pi \nu}(5)$ and $\rm{O}_{\pi \nu}(6)$ limits. By analyzing the calculated results and the structure parameters of the quadrupole operators in this work, all quantities support that the ¹²⁴Te may be the nucleus at the critical point of the $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition and with feature of $\rm{SU}^\ast_{\pi \nu}(3)$ symmetry.

The calculated $\rho^2(E0, 0^+_2\rightarrow0^+_1)\times10^3$ value also exactly reproduced the observed data. Both the theoretical and experimental properties of $E0$ transition indicate that the 0 $^+_2$ state in ¹²⁴Te may be interpreted as the lowest state of the first-excited family of intrinsic levels at the critical point of second-order $\rm{U}_{\pi \nu}(5)$ - $\rm{O}_{\pi \nu}(6)$ transition. Therefore, we conclude that the ¹²⁴Te is a possible nucleus at the critical point of the second-order phase transition from vibration to unstable rotation, and such a critical point exhibits a slight triaxial rotation. The 0 $^+_2$ state in ¹²⁴Te can be interpreted as the lowest state of the first-excited family of intrinsic levels in the critical point symmetry. However, it should be mentioned that some of the measured $B(E2)$ and $B(M1)$ values have a large uncertainty and the experimental data of $B(M1, 1^+_1\rightarrow 0^+_2)$ is still missing. More theoretical and experimental investigations should focus on these aspects.

We are grateful to Prof. CaiWan Shen, and Dr. XiaoBao Wang of Huzhou University, Prof. YuXin Liu of Peking University, and Prof. GuiLu Long of Tsinghua University for their helpful discussions and good suggestions.