-
The study on dibaryons, such as
$ H $ particle, can be traced back more than half a century (refer to the review article by Clement [1]). In particular, the$ d^* $ dibaryon state has been intensively discussed in different approaches from hadronic degrees of freedom (HDF) to quark degrees of freedom (QDF). No convincing experimental evidence was released until 2009. It was the CELSIUS/WASA and WASA@COSY collaborations [2-5] who confirmed the existence of$ d^* $ dibaryon in their series of experiments. They found that their observed peak cannot be simply understood as a contribution from the intermediate Roper excitation or the t-channel intermediate$ \Delta\Delta $ state, but requires an introduction of an intermediate new resonance with the mass, width, and quantum numbers of$ 2370\sim 2380~ \rm{MeV} $ ,$ 70\sim 80 ~\rm{MeV} $ , and$ I(J^P) = 0(3^+) $ , respectively. Since the baryon number of this structure is 2, one believes that this is the$ d^*(2380) $ dibaryon that has been hunted for since several decades.In general, this experimentally observed structure could be "an exotic compact hexaquark state" in QDF, or "a hadronic molecule state" in HDF. Because the threshold (or cusp) effect may be much smaller in this state than in the exotic XYZ states [6-9], if one can identify this narrow structure as a hexaquark state, or at least a hexaquark dominated state, it would have considerable significance. Therefore, many theoretical models for the internal structure of
$ d^* $ have been proposed. Up to now, two of them have attracted great attention. The first one discusses$ d^* $ in QDF, and assumes that$ d^* $ has a compact structure and is an exotic hexaquark dominated state [10-16]. A similar assumption is that$ d^* $ is a deeply bound state of two$ \Delta s$ Ref. [17], however the width calculated with such an assumption is larger than the experimental measurement. The other model considers d* in HDF, and assigns a molecular-like hadronic state, which originates from an assumption of a three-body$ \Delta N \pi $ resonance or a$ D_{12}\pi $ molecular-like state [18-21]. Although the mass and partial widths of the double pionic decays for such a hypothetic state can be reasonably reproduced by both models, the described structures are entirely different. Therefore, it is necessary to seek other physical observables in some sophisticated kinematics region which might explicitly provide significantly different results for the two scenarios, so that the future experiments could distinguish its structure.It is well accepted that the quantum chromodynamics (QCD) is the fundamental theory of the strong interaction, in which the perturbative asymptotic freedom at high energies and non-perturbative confinement at low energies are the two essential characteristics. The well-known constituent counting rule (CCR), proposed just after the establishment of the QCD theory [22-24], gives the scaling behavior of the scattering amplitudes in the asymptotic region of QCD at high energies. The cross section data of the baryon-baryon and meson-baryon scatterings support the counting rule [25,26]. Therefore, one can directly estimate the fall-off scaling behavior for the cross section of the exclusive process. The constituent counting rule has been extensively studied and found to be applicable in a wide variety of field theories [27-34]. One believes that it is a powerful tool for justifying the internal constituents of a hadronic system.
Recently, the constituent counting rule has been applied to the study of exotic baryons, for example for estimating the scaling behavior of
$ \Lambda(1405) $ production, and for checking the effective valence degrees of freedom of this baryon (normal baryon with 3 quarks or$ KN $ molecule with 5 quarks) [26,35,36]. In particular, the counting rule has been applied to the study of exotic XYZ states, such as$ X(3872) $ and$ Z_{c}^{\pm}(4430) $ in Refs. [37-39]. It is found that two scenarios, the meson-meson molecule bound by the pion (Goldstone boson) exchange or the color van der Waals force [40], and the interpretation of the tetraquark with a colored diquark$ \delta $ and antidiquark$ \bar{\delta} $ [41-43], give quite different scaling behavior for the hard exclusive processes, like$ e^+e^-\to Z^+_{c}(4430)Z^-_c(4430) $ .In this work, we use constituent counting rule to discuss the scaling behavior of the hard exclusive process for the production of
$ d^* $ at high energies, and explicitly compare the results obtained for the above mentioned two types of structure of$ d^* $ . The paper is organized as follows. In Section 2, the structural model of the$ d^* $ state as a compact hexaquark dominated system in QDF is briefly shown. Section 3 is devoted to the discussion of the scaling behavior of the selected hard exclusive processes for$ d^* $ production in two different scenarios. In the last section, a short summary is given. -
In our early study of possible dibaryons, a
$ \Delta\Delta+C_8C_8 $ coupled channel structure with$ \big( {I(J^P)}) = $ $ (0(3^+)\big) $ (where$ I $ ,$ J $ ,$ P $ are the isospin, spin, and parity quantum numbers), was first proposed [10], and the binding energy and root mean square radius (RMS) of the system were predicted. After the observation of WASA@COSY, we further studied the decays of the observed structure, called$ d^* $ , within the structural model that we originally proposed, and found that in addition to the mass, all partial decay widths and the total width obtained with such a structure for$ d^* $ are consistent with the experimental data. It should be specifically mentioned that the calculations were done by employing an extended chiral SU(3) constituent quark model. This interaction model includes the basic effective quark-quark interactions caused by the exchange of chiral fields, including pseudo-scalar, scalar and vector mesons, to accommodate the non-perturbative effect of QCD in the medium- and long-range, as well as by the exchange of a gluon to provide the perturbative effect of QCD in the short-range. The model also includes a phenomenological quark-quark confining potential to furnish the long-range nonperturbative effect of QCD. The model parameters are chosen in such a way that some physical constraints, e.g. the stability conditions and the masses of the ground state baryons, are satisfied. The static properties of baryons, the binding energy of deuteron, the phase shifts of the$ N $ -$ N $ scattering and the cross sections of the N-hyperon (N-Y) interactions can be well reproduced, showing the predictive power of this model [44,45]. Therefore, we believe that the picture of a compact structure for$ d^* $ , namely an exotic hexaquark dominated state, is reasonable [10,12-16].More specifically, the trial wave function of this six-quark system with two-configuration,
$ \Delta\Delta $ and$ C_8C_8 $ ($ C_8 $ denotes the color-octet 3-quark cluster), can be written as$ \begin{split} \Psi_{6q}= &{\cal A} \Big [ \hat{\phi}^A_\Delta\!\left( {\vec{\xi}}_1, {\vec{\xi}}_2, \mu_{\Delta}^{A} \right) \hat{\phi}^B_\Delta\!\left( {\vec{\xi}}_4, {\vec{\xi}}_5, \mu_{\Delta}^{B}\right) \eta_{\Delta\Delta}\! \left({\vec{r}}\right)\\& +\hat{\phi}^A_{\rm C_8}\!\left( {\vec{\xi}}_1, {\vec{\xi}}_2, \mu_{\rm C_8}^{A}\right) \hat{\phi}^B_{\rm {C_8}}\!\left( {\vec{\xi}}_4, {\vec{\xi}}_5, \mu_{\rm C_8}^{B}\right) \eta_{\rm C_8C_8}\! \left({\vec{r}}\right) \Big ], \end{split} $

(1) where
$ {\cal A} $ is the anti-symmetrization operator due to the Pauli principle, which brings in the quark exchange effect;$ \hat{\phi}^{A(B)}_{\Delta {\rm(or \, C_8)}} $ is the anti-symmetrized internal wave function of the three-quark cluster A(B) for either$ \Delta $ or$ C_8 $ , with$ {\vec{\xi}}_i $ ($ i = 1,2 (4,5) $ ) the internal Jacobi coordinates;$ \mu_{\Delta {{\rm (or} \, C_8)}}^{A(B)} $ is an aggregate of the spin, isospin and color quantum numbers of the cluster A(B) for either$ \Delta $ or$ C_8 $ , with$[{\it S,I,C}]_{\Delta(C_8)} = [ 3/2,3/2,(00) (\,(3/2,1/$ $ 2,(11)\,)\,)\,] $ for the$ \Delta(C_8) $ cluster; and$ \eta_{\Delta\Delta { (C_8C_8)}} $ is the relative wave function between the$ \Delta(C_8) $ and$ \Delta(C_8) $ clusters, which should be determined by dynamical solving the RGM equation [12,13]. After an orthogonalization procedure for$ \eta_{\Delta\Delta} $ and$ \eta_{{C_8C_8}} $ , the wave function for$ d^* $ can be written as$ \begin{split} &\!\!\!|d^*(S_{d^*} = 3,M_{d^*})> = \sum_{ch = \Delta\Delta}^{C_8C_8} \sum_{pw = S}^{D} \Big [|ch>_{M_S}\chi_{ch}^{pw,m_l}(\vec{r})\Big ]_{S_{d^*} = 3,M_{d^*}}\\ &\quad\sim \Bigg [ \alpha\Big |C_8C_8>\otimes\chi_{C_8}^{S}(\vec{r}) +\beta\Big |\Delta\Delta>\otimes\chi_{\Delta}^{S}(\vec{r})\Bigg ]_{S_{d^*} = 3,M_{d^*}}, \!\!\!\!\!\!\!\!\end{split} $

(2) where
$ ch = \Delta\Delta $ and$ C_8C_8 $ denote the constituents of the configuration,$ M_{d^*} $ represents the magnetic quantum number of spin$ S_{d^*} $ ,$ pw = l = 0 $ and$ 2 $ are the$ S $ and$ D $ partial waves between the two clusters, respectively, and$ m_l $ is the magnetic quantum number. In the last step in Eq. (3), the$ D $ -wave components are neglected due to their small contribution. The obtained probabilities of$ C_8C_8 $ and$ \Delta\Delta $ components are$ \alpha^2\sim $ 0.68% and$ \beta^2\sim $ 0.31%, respectively, and the obtained relative wave function$ \chi_{C_8}^S $ is very similar to a typical single Gaussian with a width parameter$ 0.45 \rm{fm} $ . Therefore, in our structural model, the wave function of$ d^* $ is dominated by the hidden-color component$ C_8C_8 $ , and the size of$ d^* $ is narrow. In addition, our further calculations for the space-like electromagnetic form factors of$ d^* $ show that the charge distribution of$ d^* $ , in the picture of the compact hexaquark structure in QDF, is much more narrower than that in the$ N\Delta\pi $ picture [46,47]. -
We know that the constituent quark counting rule, proposed decades ago, represents the conformality and scale invariance of QCD at high energies. In an exclusive scattering process at a fixed
$ \theta_{CM} $ (with$ \cos\theta\sim 1+2s/t $ ) and at high energy$ \sqrt{s} $ , the constituent quark masses can be neglected and the three Mandelstam variables of the process,$ s $ ,$ -t $ , and$ u = -(s+t) $ , are all large. According to the constituent counting rule for an exclusive process, where all constituents participate in the hard scattering process on equal footing at high energy$ \sqrt{s} $ , the invariant matrix element or transition amplitude$ {\cal M} $ , the differential cross section$ {\rm d}\sigma/{\rm d}t $ , and the total cross section$ \sigma $ of a selected hard exclusive scattering process, like$ a+b\to c+d $ , have the scaling behavior$ \begin{aligned} {\cal M}\propto s^{-\frac{n}{2}+2},\quad \frac{{\rm d}\sigma}{{\rm d}t}\propto\frac{1}{s^{n-2}},\quad \sigma\propto \frac{1}{s^{n-3}}, \end{aligned} $

(3) in the asymptotic region of QCD, where
$ n = n_a+ $ $n_b+n_c+n_d $ is the total number of the constituents in the whole process. The constituent counting rule was first employed to study the exotic multiquark hadrons, like$ \Lambda(1405) $ , in the hard processes$\gamma+p\to K^++ $ $ \Lambda(1405) $ and$ \pi^-+p\to K^0+\Lambda(1405) $ in Refs. [26,35,36]. It was shown that the constituent counting rule is a valuable tool for probing the internal structure of hadrons at high energies, where the quark degrees of freedom may explicitly appear. It is a completely different method from other studies at low energies, and provides a new analysis of the exotic hadron properties by considering high energy processes. This analysis was further applied to the exotic XYZ states in Ref. [38]. So far, the constituent counting rule is expected to be rigorous and applicable up to the logarithmic-$ s $ ($ \ln s $ ) corrections [38,39].Apparently, the counting rule is sensitive to the fundamental constituents of the system in the kinematics region considered. As addressed in Refs. [37,38] , the physics of the tetraquark picture is embodied in the effective constituents of the color-
$ \bar{3} $ diquark$ \delta $ and color-$ 3 $ antidiquark$ \bar{\delta} $ . Since the interaction between the colored$ \delta $ and$ \bar{\delta} $ is color dependent, it might be different from the Van der Walls attraction considered in the case of a molecular structure. A sufficiently large energy is expected to separate the diquark and antidiquark clusters, yet the relative kinetic energy is gradually converted into potential energy between the colored$ \delta $ and$ \bar{\delta} $ clusters, which holds them together but splits them into meson pairs [37]. As a consequence, the substantial prompt production of exotic X(3872) in$ e^+e^- $ collisions, observed by the experiments, may be understood. It has also been pointed out that the constituent counting rule for some sophisticated processes with hidden flavor seems problematic [48], since the quark-antiquark pairs may be produced in vacuum, and not all constituents participate in the hard processes simultaneously. In a recent work [49], it is also argued that in the case where the vector meson dominant (VMD) is preserved, the real neutral vector meson could be produced by a photon with virtuality$ s_1 = m_V^2 $ , so that the number of constituents is$ N_{V^0} = 1 $ . On the other hand, when VMD breaks down at high energies, the number of the constituents becomes$ N_{V^0} = 2 $ . In addition, the analysis in Ref. [36] indicates that the number of constituents in$ \Lambda(1405) $ seems to be 5 at medium high energies$\sqrt{s} < $ $ 2.5~ \rm{GeV} $ within the$ KN $ picture, and becomes 3 at higher energies$ \sqrt{s} > 2.6~ \rm{GeV} $ .In analogy to Refs. [26,35,36,38], here we expect that the
$ d^*(2380) $ resonance can also be produced in the hard exclusive process, such as$ e^+e^-\to d^*(2380)\bar{d}^*(2380) $ at high energies, if it exists. The process may also give information about the time-like electromagnetic form factors of$ d^* $ , or the transition amplitudes. According to our discussion in Sec. 2 on quark degrees of freedom, the wave function of$ d^* $ in our compact structural model is dominated by the hidden-color component$ C_8C_8 $ . This feature is quite similar to the tetraquark picture of the XYZ particles with a colored$ \delta $ -$ \bar{\delta} $ structure [37-39].Based on the clustering phenomena in nuclear experiments at relatively low energies, the clusters in a two-baryon system play the role of effective degrees of freedom. When the relative energy increases, the constituent clusters can get closer. We believe that in some kinematics region with a sufficiently high energy, the two color-octet clusters may manifest themselves as fundamental constituents of
$ d^*(2380) $ . Actually, this argument is supported by our model calculations for the strong decays of$ d^* $ , where the component$ C_8C_8 $ does not directly contribute in the leading order approximation. However, when the energy of the system becomes sufficiently high, the collective mode of clustering may disappear, the colored clusters may be fused together, and the$ d^* $ system looks like a single cluster with six quarks as constituents. We can then analyze$ d^* $ in a similar way to analyzing$ \Lambda(1405) $ . In the process$e^+e^-\to d^*(2380) $ $ \bar{d}^*(2380) $ at medium high energies, one can consider that, according to Ref. [38], the$ d^* $ state in the compact hexaquark model consists of two$ C_8 $ constituents, and the final states of the process have in total four effective constituents, as shown in Fig. 1(a).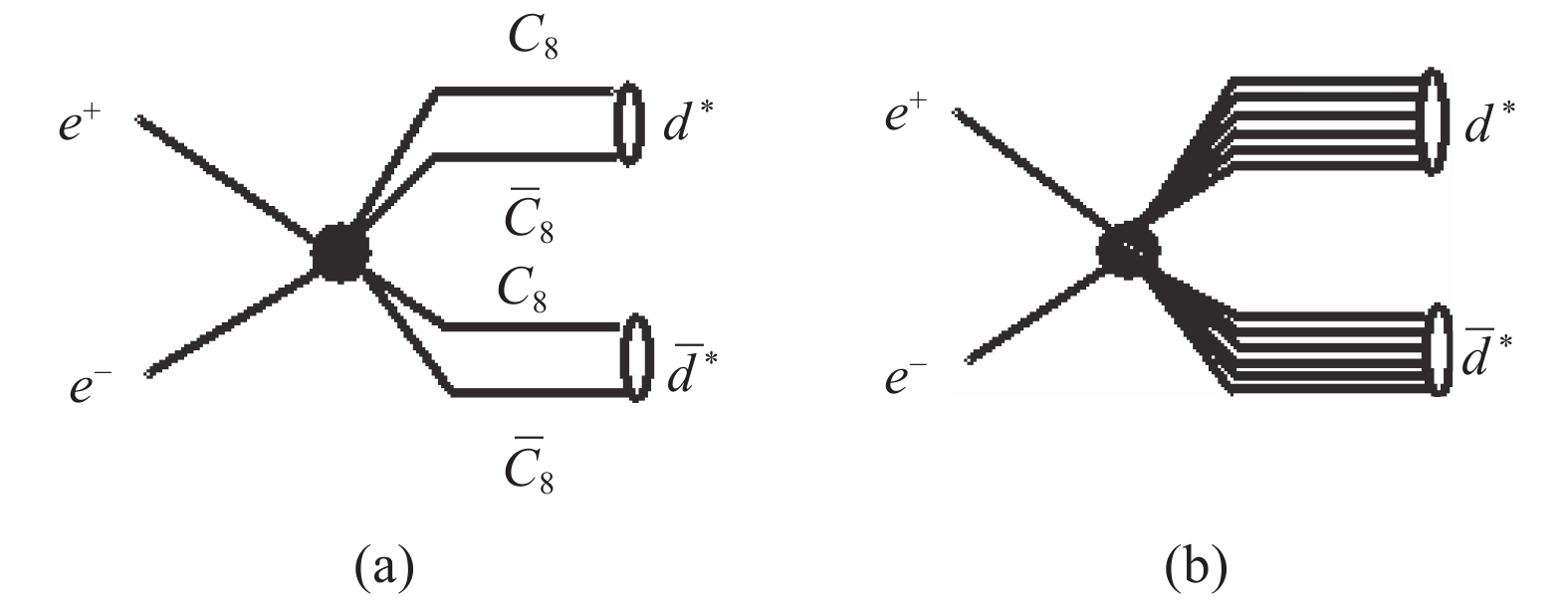
Figure 1. Hard exclusive process
$ e^+e^-\to d^*\bar{d}^* $ . (a) The effective constituents in the final states are$ C_8 $ ,$ \overline{C}_8 $ ,$ C_8 $ , and$ \overline{C}_8 $ . (b) The constituents in the final state are six quarks and six antiquarksThe scaling behavior is then
$ \begin{aligned} \frac{{\rm d}\sigma}{{\rm d}t}\Big (e^+e^-\to d^*(2380)+\bar{d}^*(2380)\Big )_{C_8C_8}\propto \frac{1}{s^4}. \end{aligned} $

(4) At high energies, the constituents of
$ d^* $ can be considered as six quarks. The final states then have 12 constituents and we have$ \begin{aligned} \frac{{\rm d}\sigma}{{\rm d}t}\Big (e^+e^-\to d^*(2380)+\bar{d}^*(2380)\Big )_{q^6}\propto \frac{1}{s^{12}}. \end{aligned} $

(5) Although our realistic wave function in quark degrees of freedom is a mixture of
$ C_8C_8 $ and$ \Delta\Delta $ components, the$ C_8C_8 $ component is dominant. We can then expect that the scaling behavior for$ d^* $ is$ 1/s^4 $ for the$ C_8C_8 $ component in the medium high energy region, and becomes$ 1/s^{12} $ for high energies. This difference might have a remarkable effect on the large hidden-color component or the constituent phenomena of$ d^* $ in the hard exclusive process.Let us now consider the scenario with the explicit
$ N\Delta\pi $ structure. Again, referring to Ref. [38], the final states of the hard exclusive process$e^++e^-\rightarrow d^*(2380) + $ $ \bar{d^*}(2380) $ , where$ d^*(2380) $ has an$ N\Delta \pi $ structure, have in total 16 constituents at high energies. The scaling behavior of the differential cross section is then$ \begin{aligned} \frac{{\rm d}\sigma}{{\rm d}t}\Big (e^+e^-\to d^*(2380)+\bar{d}^*(2380)\Big )_{N\Delta\pi} \propto 1/s^{16}. \end{aligned} $

(6) Comparing Eqs. (5, 6, 7), we clearly see that the scaling behavior for the different structures of
$ d^* $ is significantly different. The fall-off scaling behavior of the$ e^+e^-\to $ $ d^*(2380)+\bar{d}^*(2380) $ process, in the case of the compact hexaquark structure for$ d^* $ , is in general slower than in the case of the$ N\Delta\pi $ structure for$ d^* $ . We hope that this discrepancy could be observed in future experiments at BELLE2.Moreover, one may also calculate the ratio of the scaling behavior
$ R^{d^*} = \displaystyle\frac{\sigma(e^+e^-\to d^*+\bar{d}^*)}{\sigma(e^+e^-\to \mu^++\mu^-)} $ by using the constituent counting rule. In the case of our compact hexaquark dominated picture,$ \begin{split} R^{d^*}_{C_8C_8} &= \frac{\sigma\Big (e^+e^-\to d^*(2380)+\bar{d}^*(2380)\Big )_{C_8C_8}}{\sigma(e^+e^-\to\mu^++\mu^-)} \\&= \mid F^{d^*}_{C_8C_8}(s)\mid ^2\propto \frac{1}{s^2} \end{split} $

(7) at medium high energies where the effective degree of freedom is mainly
$ C_8C_8 $ , but it becomes$ R^{d^*}_{q^6}\propto 1/s^{10} $ at high energies where the structure of$ d^* $ is$ q^6 $ . In the case where the structure of$ d^* $ is$ N\Delta\pi $ , the ratio is$ R^{d^*}_{N\Delta\pi}\propto 1/s^{14} $ at high energies. In the above equation,$ F^{d^*}(s) $ stands for the time-like electromagnetic form factor of$ d^* $ . In our compact hexaquark structure model in QDF, we have$ F^{d^*}_{C_8C_8}\propto 1/s $ at medium high energies and$ F^{d^*}_{q^6}\propto 1/s^5 $ at high energies. Yet, in the explicit$ N\Delta\pi $ picture in HDF,$ F^{d^*}_{N\Delta\pi}\propto 1/s^{7} $ at high energies. Clearly, the relative reduction of$ R^{d^*} $ for the two structural models with the increase of energy is similar to that of the differential cross sections.Another energy saving exclusive process in
$ e^+e^- $ annihilation is$ e^+e^-\to \rm{deuteron}+\bar{d}^* $ (or$ e^+e^-\to pn +\bar{d}^* $ ). In this hard process, the effective constituents of the deuteron ($ d $ ) are six quarks because$ d $ is a weakly bound state of proton and neutron with a large size. Therefore, the ratio$ R^{d} = \frac{\sigma(e^+e^-\to d+\bar{d}^*)}{\sigma(e^+e^-\to \mu^+\mu^-)} $ in the compact hexaquark scenario is$ \begin{split} R^d_{C_8C_8} =& \frac{\sigma\Big (e^+e^-\to d+\bar{d}^*(2380)\Big )_{C_8C_8}}{\sigma(e^+e^-\to\mu^++\mu^-)} \\=& \mid F^{dd^*}_{C_8C_8}(s) \mid ^2\propto \frac{1}{s^6}, \end{split} $

(8) at medium high energies and
$ R^{d}_{q^6}\propto 1/s^{10} $ at high energies, while in the$ N\Delta\pi $ scenario, it becomes$ R^{d}_{N\Delta\pi}\propto 1/s^{12} $ at high energies. In Eq. (8),$ F^{dd^*}(s) $ is the time-like transition amplitude. It behaves as$ 1/s^3 $ and$ 1/s^5 $ at medium high and high energies, respectively, in the compact hexaquark picture, and as$ 1/s^6 $ at high energies, respectively, in the$ N\Delta\pi $ picture. Again, the relative reduction of$ R^{d} $ for the two structural models with the increase of energy is similar to$ R^{d^*} $ and to the differential cross sections.With the same argument,
$ d^*(2380) $ , if it exists, can also be produced in the$ p\bar{p} $ annihilation process at D0 or future$ \bar{\rm{P}}\rm{anda} $ facilities. The scaling behavior of the hard exclusive processes, like$p+\bar{p}\to d^*(2380) + $ $ \bar{d}^*(2380),\, p+$ $\bar{p}\to d (or\; pn)+\bar{d}^*(2380) $ at high energies, can also provide valuable information about the internal structure of$ d^*(2380) $ at different energy scales. According to the above analyses, one can expect that the fall-off scaling behavior of the exclusive processes at medium high or high energies should be much slower in the compact hexaquark scenario in the quark degrees of freedom than in the$ N\Delta\pi $ scenario in the hadronic degrees of freedom. Moreover, the scaling behavior of the other hard exclusive processes at high energies, like$ \pi+d \to d^*(2380)+\pi $ at JPARC,$\gamma(e)+d\to d^*(2380)+ $ $ \pi $ at MAINZ, COMPASS and the Research Center for Electron Photon Sciences (ELPH), and$ p+p\to d^*(2380)+ $ $\pi $ at the LHC, could also provide structure information about the dibaryon resonance$ d^*(2380) $ . -
In order to understand the internal structure of the
$ d^* $ resonance discovered by the CELSIUS/WASA and WASA@COSY collaborations, two major structural schemes were proposed recently. One of them, based on the quark degrees of freedom, deems that$ d^* $ is an exotic compact hexaquark dominated state due to the quark exchange effect and the short-range attraction in such a specific$ I(J)^P $ state; the other, based on the hadronic degrees of freedom, believes that it is a molecular-like hadronic state. Up to now, both structural models can explain the mass, total width, and partial widths for all observed double pionic decays of$ d^* $ . However, for the single pionic decay process, although the observed upper limit of the branching ratio [50] (less than 9%) can be explained by both the compact hexaquark dominated structure and the modified molecular-like hadronic structure, the explanations are different. The former results in a branching ratio of about 1% [51], which is not in contradiction with the experimental data. However, the result from a pure$ N\Delta\pi $ structure gives a branching ratio as large as 18%. Only after combining the$ D_{12}\pi $ (namely$ N\Delta\pi $ ) structure with a 'compact'$ \Delta\Delta $ structure, for example$ \displaystyle\frac{5}{7} [\Delta\Delta]+\displaystyle\frac{2}{7} [D_{12}\pi] $ in the hadronic degrees of freedom, can the upper limit be reproduced [52]. Of course, the realistic structure of$ d^* $ might be much more complicated. For instance, it might be an essential compact hexaquark dominated core surrounded by a$ D_{12}\pi $ cloud, just like the commonly believed nucleon where a three-quark core is surrounded by the meson cloud.We propose that the scaling behavior of the exclusive processes at high energies for the
$ d^* $ production could be used to test the structures of$ d^* $ , in addition to its electromagnetic properties. Theoretically, the fall-off scaling behavior for a hard exclusive process can be simply estimated by using the constituent counting rule from the asymptotic behavior of QCD at high energies. It is shown that the number of effective constituents in the above mentioned two structural models is different, especially at high energies. It should be particularly stressed that in the compact hexaquark dominated model, the effective constituents of two colored$ C_8 $ clusters at medium high energies, just like the colored diquark in the tetraquark for the exotic XYZ particles [37], would get much closer and then fuse into a single six-quark cluster (hexaquark) at high energies. Thus, the number of constituents in$ d^* $ will change from 2 to 6. On the other hand, for the explicit$ N\Delta\pi $ model, in the high energy limit, the number of constituents is 8. As a consequence, a remarkable difference of the fall-off scaling behavior between these two structural models in the hard exclusive process$ e^+ + e^- \rightarrow d^* + \bar{d^*} $ is shown. Our estimated ratios are$ R_{d^*}(R_d)\propto 1/s^{10} (1/s^{10}) $ at high energies in the compact hexaquark dominated model, and$ \propto 1/s^{14}(1/s^{12}) $ in the$ N\Delta\pi $ model. At medium high energies, when the$ C_8C_8 $ component manifests itself, the two ratios behave like ($ 1/ s^2 $ ) and ($ 1/s^6 $ ) in the compact hexaquark dominant model according to the constituent counting rule. If our approach and the assumption for the effective constituents are both correct, we expect that a rather large difference of the fall-off scaling behavior between the two models can be seen in the mentioned hard exclusive processes, and can be used to distinguish the structure of$ d^* $ at high energies.Authors thank the fruitful discussions with Zongye Zhang and Feng-Kun Guo.
Constituent counting rule and the production of ${{d^*(2380)}}$ at high energies
- Received Date: 2019-02-13
- Available Online: 2019-05-01
Abstract: The constituent counting rule, determining the scaling behavior of the transition amplitudes in an exclusive process at high energies, is applied to probe the internal structure of the newly observed






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: