Study of the ${{a_1}}$(1260) resonance in the ${{\gamma p \to \pi^+\pi^+\pi^- n}}$ reaction

1. Introduction

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

The $a_1(1260)$ resonance with quantum numbers $J^{PC} = 1^{++}$ is a candidate for the chiral partner of $\rho$ meson [1-3]. It is also described as a $q \overline{q}$ state in the Numbu-Jona-Lasino model [4, 5]. Apart from the quark model, it is considered as a gauge boson of the local hidden symmetry [6, 7]. By using the chiral unitary approach, $a_1(1260)$ is a state arising from the interactions of pairs of hadrons in coupled channels [8, 9]. In addition, the nature of $a_1(1260)$ has also been investigated using the $\tau$ decay spectrum into three pions [10-12], and multi-pion decays of light vector mesons [13, 14]. Recently, the $a_1(1260)$ resonance was studied in Ref. [15] in the decay of $\tau \to \nu_{\tau} \pi^- a_1(1260)$ through a triangle mechanism.

The dynamically generated nature of $a_1(1260)$ has been tested in the radiative decay process. The decay of $a_1(1260)$ into $\pi \gamma$ in Ref. [16] was also studied in Refs. [17, 18] and found to be in agreement with the experimental data if $a_1(1260)$ is associated with the dynamically generated picture. In Ref. [19], the lattice result for the coupling constant of $a_1(1260)$ into the $\rho\pi$ channel is similar to the one obtained in Ref. [8]. Recently, the production of $a_1(1260)$ in the $\pi^-p \to a_1(1260)^-p$ reaction within the effective Lagrangian approach was studied in Ref. [20] based on the results of [8]. Besides, it was found that the elementary $q\bar{q}$ component of $a_1(1260)$ is comparable to the hadronic composite [21-23]. Using the chiral unitary approach, the large $N_{\rm c}$ behavior of the $a_1(1260)$ state was investigated in Ref. [22], and it was found that $q\bar{q}$ is not the main component of $a_1(1260)$.

Based on the values obtained by two different experimental groups [24, 25], it is estimated that the mass and Breit-Wigner width of $a_1(1260)$ is $M_{a_1(1260)}$ = 1230 $\pm$ 40 MeV and $\Gamma_{a_1(1260)} = (250-600)$ MeV, respectively [26]^①. The large uncertainties of the mass and width of $a_1(1260)$ in the Particle Data Group (PDG) [26] show that the knowledge of $a_1(1260)$ is very limited. Therefore, a study of $a_1(1260)$ photoproduction could be helpful to determine the mass and width of this resonance.

Meson photoproduction off a proton provides one of the most direct platforms to extract information about the hadronic structure [27, 28]. We should point out that in the experiments, no signal representing $a_1(1260)^+ n$ photoproduction [29-33] could be isolated even though the $\pi \gamma$ radiative width of $a_1(1260)$ very likely exceeds that of $a_2(1320)$ [16, 34-36]. The absence of the $J^{PC} = 1^{++}$ state in charge exchange photoproduction is puzzling. In this paper, by investigating the $\gamma p \to a_1(1260)^+ n$ process within the $\pi$-exchange mechanism, we calculate its total cross-section. The $\pi^+\pi^+\pi^-$ mass distribution and the total cross-section of $\gamma p \to \pi^+\pi^+\pi^- n$ are studied. In addition, we consider the non-resonance contributions to the $\gamma p \to \pi^+\pi^+\pi^- n$ resonance, which involve nucleon pole terms. Other contributions, which involve $\Delta(1232)$ and nucleon excited states, can be removed based on the $\pi^+n$ invariant mass spectrum from the experiments [33].

The article is organized as follows. After the introduction, we present the reaction mechanism of $a_1(1260)$ photoproduction. The possible background relevant to the production of $a_1(1260)$ is discussed and the $\pi^+\pi^+\pi^-$ mass distribution is presented in Sec. 3. This work ends with a discussion and conclusion.

2. ${ \gamma p \to a_1(1260)^+ n}$ reaction

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

In this section, we discuss the $a_1(1260)$ production mechanism. Fig. 1 shows the basic tree-level Feynman diagram for the $a_1(1260)$ production in the $\gamma p \to$$a_1(1260)^+ n$ reaction via the $\pi$-exchange process.

Figure 1

Figure 1.  Feynman diagram for the $\gamma p \to {a_1}{\left( {1260} \right)^ + }n$ reaction via $\pi$-exchange.

DownLoad: Full-Size Img PowerPoint

For the $\pi NN$ vertex, we adopt the commonly used effective Lagrangian

where the standard value, $g_{\pi NN}^2/{4\pi} = 14.4$, is adopted as in Refs. [37, 38]. In addition, the form factor is introduced for suppressing the vertex coupling when one or two interacting particles go off-shell. For the $\pi NN$ vertex, the form factor satisfies the relation

where $\Lambda_{\pi}$ is a cut-off parameter [39, 40], which will be discussed in the following. $q_{\pi}$ is the momentum of the exchanged $\pi$ meson.

The vertex depicting the interaction of $a_1(1260)$ and $\pi \gamma$ is [17, 18]

where $\varepsilon_{\mu}(p_{a_1})$ and $\varepsilon_{\nu}(p_{\gamma})$ are the polarization vectors corresponding to $a_1(1260)$ and photon, respectively.

With the vertex above, we can easily get the partial decay width of $a_1\to \pi \gamma$,

where $M_{a_1} = 1230$ MeV is the nominal mass of $a_1(1260)$. Using the partial decay width $\Gamma_{a_1\to \pi \gamma} = 640\pm246$ keV of $a_1(1260)$ as listed in PDG [26], we get $g_{a_1\pi\gamma} = 244 \pm 94$ MeV, where the error is from the uncertainties of $\Gamma_{a_1\to \pi \gamma}$ and the mass of $a_1(1260)$. In the following calculations, we take the average value $g_{a_1\pi\gamma} = 244$ MeV.

With the above integrants, one can get the scattering amplitude of the $\gamma(p_1) p(p_2) \to a_1(1260)^+(p_4)+ n(p_3)$ process as

By defining $s = (p_1+p_2)^2$, the corresponding unpolarized differential cross-section reads

where $\theta$ is the scattering angle of $a_1^+$ meson relative to the beam direction in the c.m. frame, while $\vec{p}_1^{\ {\rm c.m.}}$ and $\vec{p}_4^{\ {\rm c.m.}}$ are the three-momenta of the initial photon and the final $a_1^+$, respectively.

In Fig. 2, the solid, dashed and dotted lines are obtained with $\Lambda_{\pi} = 1.0$, 1.3 and 1.6 GeV, respectively. From Fig. 2 one can see that the total cross-section via $\pi$ exchange increases very rapidly close to the threshold, and the peak position of the total cross-section is $E_{\gamma} \sim 2.6$ GeV. The total cross-section is proportional to $g_{a_1\pi\gamma}^2$, which indicates that the cross-section is proportional to the partial decay width $\Gamma_{a_1\to \pi \gamma}$. Since the exact value of $\Gamma_{a_1\to \pi \gamma}$ is not determined by theory or experiment, in this work we take $\Gamma_{a_1\to \pi \gamma} = 640$ keV. The result is comparable with the cross-section of $a_2(1320)$ photoproduction [41].

Figure 2

Figure 2.  Dependence of the total cross-section of $\gamma p \to {a_1}{\left( {1260} \right)^ + }n$ as a function of E_γ.

DownLoad: Full-Size Img PowerPoint

3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

Next, we consider the $\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to$$\pi^+\pi^+\pi^-n$ and $\gamma p\to \rho^0p\to\pi^+\pi^+\pi^-n$ processes. Here $\gamma p\to \rho^0p\to\pi^+\pi^+\pi^-n$ can occur via the nucleon pole term [42].

3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

The $\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n$ reaction with $\pi$ exchange is shown in Fig. 3, where the relevant kinematic variables are shown. As discussed in the introduction, we take the coupling of $a_1(1260)$ to the $\rho \pi$ channel as obtained in Ref. [8].

Figure 3

Figure 3.  Feynman diagram for the $\gamma p \to {a_1}{\left( {1260} \right)^ + }n \to {\rho ^0}{\pi ^ + }n \to$${\pi ^ + }{\pi ^ + }{\pi ^ - }n$ reaction via $\pi$ exchange.

DownLoad: Full-Size Img PowerPoint

The $a_1^+\rho^0\pi^+$ vertex can be written as

where $\varepsilon_{a_1}$ and $\varepsilon$ are the polarization vectors of $a_1(1260)$ and $\rho$, respectively. $g_{a_1\rho\pi}$ is the coupling of $a_1(1260)$ to $\rho\pi$. We take $g_{a_1\rho\pi} = (-3795+{\rm i}2330)$ MeV as obtained in Ref. [8], where only the $S$-wave interaction was considered. Note that there is also a $D$-wave contribution to the $a_1\rho\pi$ vertex as investigated in Ref. [43], where the $D$-wave contribution was found to be small.

For the vertex of $a_1(1260)^+$ interacting with $\rho^0\pi^+$, we also introduce a form factor $F_{a_1\rho\pi}$, which is

with a typical value of $\Lambda_{a_1} = 1.5$ GeV as in Refs. [20, 44].

The $a_1(1260)$ propagator is

where the width $\Gamma_{a_1}$ is dependent on its four-momentum squared, and we can take the form as in Refs. [45, 46],

where $\Gamma_{3\pi}$ is the decay width for the process $a_1(1260)\to$$\rho\pi \to 3\pi$ [44], and $\Gamma_0$ is the decay width for the other processes. Following the experimental result in Ref. [24] for the total decay width of $a_1(1260)$, we take $\Gamma_{0} = 201$ MeV for $\Gamma_{a_1} = 367$ MeV at $\sqrt{q_{a_1}^2} = 1230$ MeV.

For the structure of the $\rho \pi \pi$ vertex, we use the general interaction as,

where $<>$ stands for the trace in $SU(3)$ , and $g = \displaystyle\frac{m_{V}}{2f}$, with $m_{V} = m_{\rho}$ , and $f = 93$ MeV is the pion decay constant. The $\rho \pi \pi$ vertex can then be written as

For the vertex of $\rho$ interacting with $\pi\pi$, we also introduce a form factor $F_{\rho\pi\pi}$, which satisfies the relation

with a typical value of $\Lambda_{\rho} = 1.5$ GeV as used in Ref. [44].

The $\rho$ propagator is

where $\Gamma_\rho$ is energy dependent. Because the dominant decay channel of $\rho$ is $\pi \pi$, we take

with $\Gamma_{\rm on} = 149.1$ MeV, and

where $M^2_{\rm inv} = q_{\rho}^2 = (p_6+p_7)^2$ or $(p_5+p_7)^2$ is the invariant mass squared of the $\pi^+ \pi^-$ system. We take $m_\rho = 775.26$ MeV in this work.

It is worth to mention that the parametrization of the width of $\rho$ meson shown in Eq. (15) is meant to take into account the phase space of each decay mode as a function of the energy [40, 47, 48]. In the present work we take explicitly the phase space for the P-wave decay of the $\rho$ into two pions.

We finally obtain the scattering amplitude for the diagram shown in Fig. 3,

3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

Besides the resonance contribution of the $a_1(1260)$ resonance, we study another kind of reaction mechanism for the $\gamma p \to\pi^+\pi^+\pi^-n$ reaction, which is depicted in Fig. 4, where we have considered the contribution from $\gamma p \to\rho^0 p \to\pi^+\pi^-\pi^+n$. In Fig. 4, the relevant kinematic variables are also shown.

Figure 4

Figure 4.  Feynman diagram for the $\gamma p \to {\rho ^0}{\pi ^ + }n \to {\pi ^ + }{\pi ^ + }{\pi ^ - }n$ reaction via $\pi$ exchange.

DownLoad: Full-Size Img PowerPoint

To compute the contribution of Fig. 4, we take the interaction density for $\rho \gamma \pi$ as [49, 50],

where $A_{\beta},\pi$ and $\rho_{\nu}$ denote the fields of the photon, $\pi$ and $\rho$, respectively. The coupling constant $g_{\rho\gamma\pi}$ can be obtained from the experimental decay width $\Gamma_{\rho^0 \to \pi^0\gamma}$ [26] , which leads to $g_{\rho\gamma\pi} = 0.76$.

Other vertexes are the same as given above. With the above preparation, we get the transition amplitude for the diagram shown in Fig. 4,

with

where $\Lambda_{\pi} = 0.6$ GeV and $\Lambda_{N} = 0.5$ GeV are taken from Refs. [49, 50, 51]. This choice of the cut-off leads to a satisfactory explanation of the $\rho^0$ photoproduction at low energies. Note that the value of $\Lambda_{\pi}$ is different from the one we used for the $\gamma p \to na_1(1260)^+$ production. Other cut-off parameters are the same as given above.

3.3 Numerical results

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

The total cross-section of the $\gamma p\to\pi^+\pi^+\pi^-n$ reaction can be obtained by integrating the invariant amplitude in the four-body phase space:

with

where 2! is a statistical factor for the final two $\pi^+$ mesons, and the four-body phase space is defined as [26]

where $\vert\vec{p}_6^{\ *a}\vert$ and $\Omega_6^{*a}$ are the three-momentum and solid angle of the out-going $\pi^+$ in the c.m. frame of the final $\pi^+\pi^-$ system, $\vert \vec{p}_5^{\ *b} \vert$ and $\Omega_5^{*b}$ are the three-momentum and solid angle of the out-going $\pi^+$ in the c.m. frame of the final $\pi^+\pi^+\pi^-$ system, and $\vert \vec{p}_3 \vert$ and $\Omega_3$ are the three-momentum and solid angle of the out-going $n$ in the c.m. frame of the initial $\gamma p$ system. In the above equation, $M_{\pi^+\pi^-}$ is the invariant mass of the $\pi^+\pi^-$ two body system, and $M_{\pi^+\pi^+\pi^-}$ is the invariant mass of the $\pi^+\pi^+\pi^-$ three body system, and $s = (p_1+p_2)^2$ is the invariant mass squared of the initial $\gamma p$ system.

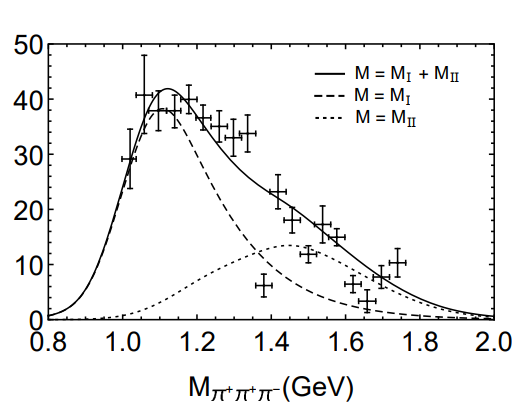
In Ref. [33], the $\gamma p\to\pi^+\pi^+\pi^-n$ reaction was studied in the photon energy range $4.8-5.4$ GeV. The 3$\pi$ mass distributions are measured from the $1^{++}(\rho\pi)_S$ partial wave. In Fig. 5, we show the theoretical results, $c_1{\rm d}\sigma/{\rm d}M_{\pi^+\pi^+\pi^-}$, for the $\pi^+\pi^+\pi^-$ invariant mass distributions for the $\gamma p\to\pi^+\pi^+\pi^-n$ reaction at $E_{\gamma} = 5.1$ GeV, compared with the experimental measurements of Ref. [33]. The theoretical results are obtained with $c_1 = 21.5$ and $c_1 = 18$ for $M_{a_1} = 1080$ and $1230$ MeV, respectively, which have been adjusted to the experimental data reported by the CLAS collaboration [33]. From Fig. 5, it is seen that the bump structure around $1.4-1.6$ GeV may account for the nuclear pole contribution. If we use $M_{a_1} = 1080$ MeV, the $\pi^+\pi^+\pi^-$ invariant mass distributions agree well with the experimental data. On the other hand, the theoretical results with $M_{a_1} = 1230$ MeV can not describe the bump structure around 1.1 GeV.

Figure 5

Figure 5.  The 3 $\pi$ invariant mass spectrum for the $\gamma p\to \pi^+\pi^+\pi^-n$ process compared with the data obtained by the CLAS collaboration from the $1^{++}(\rho\pi)_S$ partial wave [33]. Left and right plots correspond to $M_{a_1} = 1080$ and 1230 MeV , respectively.

DownLoad: Full-Size Img PowerPoint

In addition to the differential cross-section, we also calculated the total cross-section for the $\gamma p\to \pi^+\pi^+\pi^-n$ process as a function of the photon beam energy $E_{\gamma}$. The results are shown in Fig. 6, where one can see that the total cross-section increases rapidly near the threshold, and the peak of the total cross-section is at $E_{\gamma} = 2.5$ and 2.9 GeV corresponding to $M_{a_1} = 1080$ and $1230$ MeV, respectively. The differential and total cross-sections could be checked in future experiments, such as those at CLAS.

Figure 6

Figure 6.  Total cross-section for the $\gamma p\to \pi^+\pi^+\pi^-n$ process. Left and right plots correspond to $M_{a_1} = 1080$ and 1230 MeV , respectively.

DownLoad: Full-Size Img PowerPoint

4. Conclusion and discussion

• 1. Introduction
• 2. ${ \gamma p \to a_1(1260)^+ n}$ reaction
• 3. ${\gamma p \to \pi^+\pi^+\pi^- n}$ reaction
•      3.1 ${\gamma p\to a_1(1260)^+n\to\rho^0\pi^+n\to\pi^+\pi^+\pi^-n}$ reaction
•      3.2 ${\gamma p\to \rho^0p\to\pi^-\pi^+p\to\pi^+\pi^+\pi^-n}$ reaction
•      3.3 Numerical results
• 4. Conclusion and discussion

In recent years, it has been found that the $a_1(1260)$ resonance, although long accepted as an ordinary $q\overline{q}$ state, can be dynamically generated from the pseudoscalar-meson-vector-meson interaction, and therefore qualify as a pseudoscalar-vector molecule. In this work, we have proposed to study the $a_1(1260)$ resonance in the photoproduction process. Since $a_1(1260)$ was observed in the radiative decay of $a_1(1260)^+\to \pi^+\gamma$, the $\gamma p \to a_1(1260)^+ n$ reaction by $\pi$ meson exchange is the main process for producing $a_1(1260)$. Our numerical results show that the total cross-section of $\gamma p \to a_1(1260)^+ n$ is of the order of 10 μb, which is comparable with the cross-section for photoproduction of $a_2(1320)$.

In addition, taking the coupling constant obtained from the picture where the $a_1(1260)$ resonance is a dynamically generated state from pseudoscalar-meson-vector-meson interaction, the $\pi^+\pi^+\pi^-$ invariant mass distributions from the $\gamma p \to \pi^+\pi^+\pi^- n$ reaction were studied. With $M_{a_1} = 1080$ MeV, we can describe the experimental data for the $\pi^+\pi^+\pi^-$ invariant mass distributions fairly well. The total cross-section of the $\gamma p \to \pi^+\pi^+\pi^- n$ reaction was also studied using the model parameters determined from a comparison with the experimental data for the $\pi^+\pi^+\pi^-$ invariant mass distributions. It is expected that our model calculations could be tested by future experiments with the $\gamma p\to \pi^+\pi^+\pi^-n$ reaction at the photon beam energy $E_{\gamma}$ around 2.5~2.9 GeV.

One of us (Xu Zhang) would like to thank Yin Huang for helpful discussions.

References