Astrophysical ²²Mg(p, γ)²³Al reaction rates from asymptotic normalization coefficient of ²³Ne→²²Ne+n

1. Introduction

• 1. Introduction
• 2. Neutron ANCs of 23Ne
• 3. Proton ANC and width of 23Al
• 4. Astrophysical S-factors and reaction rates of 22Mg (p, γ)23Al
• 5. Summary and conclusion

Classical novae are believed to be closed binary systems comprising a white dwarf and a main sequence or red giant star. When the distance between the stars is below the Roche limit, the white dwarf in the system accretes the H-rich matter from its companion. A classical nova outburst takes place upon occurrence of a thermonuclear runaway (TNR), driven by compression of the H-rich matter [1]. Approximately 25–30% of the novae are of the ONe type containing massive ONe dwarfs [2]. Observations of Ne lines [3] demonstrate the enrichment of Ne in Neon novae. The NeNa and the MgAl cycles start to produce heavier nuclei after the breakout of the hot CNO cycles, as preexisting ²⁰Ne nuclei are present [4–7]. Novae observations provide evidence of productions of elements, such as Si and P [8]. Furthermore, the Ne-E meteoritic neon component enriched in ²²Ne may also originate from the novae [2, 9].

²²Na and ²⁶Al are long-lived isotopes that may be observed as $\gamma$-ray sources by detectors if they do not participate in any reactions before ejection [5, 10]. ²²Na, whose half-life is 2.602 y, $\beta^+$-decays to the first excited state in ²²Ne, and subsequently de-excites with the emission of an accompanying 1.275 MeV $\gamma$-ray [11]. Detections of the 1.275 MeV $\gamma$-ray from a classical nova outburst found little evidence of the 1.275 MeV line and only provided upper limits of the ejected ²²Na, either by the SMM [12] or the COMPTEL and OSSE instruments onboard the CGRO [13-16]. Several nuclear reaction network studies have predicted the ejected abundances of ²²Na in novae [17-20]; however, a large uncertainty still remains [7, 21]. Moreover, some theoretical estimations yielded abundances significantly higher than the upper limits obtained by observation [15, 22].

${}^{22} {\rm{Na}}$ is mainly produced via a reaction chain, ${}^{20} {{\rm{Ne}}} (p, \gamma){}^{21} {\rm{Na}}(p, \gamma){}^{22} {{\rm{Mg}}}(\beta^{+}\nu){}^{22} {\rm{Na}}$ [4–7]. While the proton capture reaction ${}^{22} {\rm{Na}}(p, \gamma){}^{23} {{\rm{Mg}}}$ is considered as the main approach of the destruction of ²²Na [23, 24], ${}^{22} {{\rm{Mg}}}(p, \gamma){}^{23} {{\rm{Al}}}$ may also deplete ${}^{22} {{\rm{Mg}}}$ on the reaction chain according to the temperature and density conditions [25]. Thus far, there has been no direct measurement of the reaction, mainly because of the unstable isotope ${}^{22} {{\rm{Mg}}}$ with the half-life of 3.88 s [11] involved in the entrance channel. To date, the ${}^{22} {{\rm{Mg}}}(p, \gamma){}^{23} {{\rm{Al}}}$ reaction was studied using a few indirect methods. The excitation energy of the first excited state in ²³Al was observed by the ²⁴Mg($^{7} {\rm{Li}}, {}^8 {\rm{He}}$) ²³Al reaction to be ($460\pm60$) keV for the first time [25] and ($550\pm20$) keV in a more accurate measurement [26]. Resonant and direct capture rates were deduced from the excitation energy values together with spectroscopic factors from shell-model calculations [25, 26]. Simplified network calculations revealed that proton capture rates of ²²Mg at those magnitudes only lead to limited ²³Al and ²⁴Si production [26]. The gamma width of the first excited state in ²³Al was determined to be $7.2\times10^{-7}$ eV using the coulomb-dissociation method in RIKEN [27, 28]. The spin and parity of the ²³Al ground state was found to be $J^{\Pi} = 5/2^+$ by independent measurements [29, 30]. New states in ²³Al were observed, and the reaction rates were reevaluated [31], adopting the experimental value of the gamma width in Ref. [28]. As for the direct capture contribution, the proton asymptotic normalization coefficient (ANC) for the ²³Al ground state was experimentally found to be $C_{d5/2}^{2}({}^{23} {{\rm{Al}}}) = (4.63 \pm0.77)\times$$10^{3}\;{\rm{fm}}^{-1}$ from the $^{13} {\rm{C}}(^{22} {{\rm{Ne}}} , {}^{23} {{\rm{Ne}}} )^{12} {\rm{C}}$ transfer reaction in the mirror nuclear system [32] and $C_{d5/2}^{2}({}^{23} {{\rm{Al}}}) =$$(3.90 \pm 0.44)\times10^{3}\;{\rm{fm}}^{-1}$ from the one-proton breakup reaction of ²³Al [33]. The measurement with a new transfer reaction will be helpful to independently verify the former ANCs.

In this study, we aim to determine the astrophysical S-factors and stellar rates of the ${}^{22} {{\rm{Mg}}}(p, \gamma){}^{23} {{\rm{Al}}}$ reaction from the previous experimental angular distributions of ${}^{22} {{\rm{Ne}}} (d, p){}^{23} {{\rm{Ne}}}$ [34, 35] based on the mirror symmetry of a strong interaction. The relationships between the neutron and proton ANCs or width in mirror nuclear systems were previously established by Timofeyuk et al. [36], and have been successfully applied in several studies [37-39]. The neutron ANCs of ${}^{23} {{\rm{Ne}}} \to{}^{22} {{\rm{Ne}}} +n$ for the ground state and the first excited state are derived from the angular distributions of ${}^{22} {{\rm{Ne}}} (d, p){}^{23} {{\rm{Ne}}}$ within the frame of the adiabatic distorted wave approximation (ADWA) [40] and continuum discretized coupled channel (CDCC) analysis [41]. The adiabatic approximation for the $(d, p)$ reactions was systematically investigated by Chazono et al. [42]. In comparison with other incident particles, the deuteron exhibits a simpler structure that is better understood.

We discuss the neutron ANCs for ${}^{23} {{\rm{Ne}}} \to{}^{22} {{\rm{Ne}}} +n$ in Section 2 and the proton ANC and width of the ²³Al ground state and the first excited state, respectively, in Section 3. The astrophysical S-factors and reaction rates are presented in Section 4. The conclusion is provided in Section 5.

2. Neutron ANCs of ²³Ne

• 1. Introduction
• 2. Neutron ANCs of 23Ne
• 3. Proton ANC and width of 23Al
• 4. Astrophysical S-factors and reaction rates of 22Mg (p, γ)23Al
• 5. Summary and conclusion

In the case of peripheral transfer reactions, the neutron ANCs for the virtual decay of ${}^{23} {{\rm{Ne}}} \to{}^{22} {{\rm{Ne}}} +n$ can be obtained by

where ${\left(\dfrac{{\rm d}\sigma}{{\rm d}\Omega}\right)}_ {{\rm{exp}}}$ and $\sigma^ {{\rm{th}}}_{l_ij_il_fj_f}$ are the experimental and theoretical differential cross-sections, respectively, $C_{l_ij_i}^{2}(d)$ and $C_{l_fj_f}^{2}({}^{23} {{\rm{Ne}}} )$ are the ANCs for $d \to p+n$ and ${}^{23} {{\rm{Ne}}} \to{}^{22} {{\rm{Ne}}} +n$, respectively, and $b_{l_ij_i}^{2}(d)$ and $b_{l_fj_f}^{2}({}^{23} {{\rm{Ne}}} )$ are the single-particle ANCs of the deuteron and ${}^{23} {{\rm{Ne}}}$, respectively. The experimental angular distributions are assumed from Refs. [34, 35].

The FRESCO code [43] was used to calculate theoretical angular distributions. The optical potential parameters of the entrance channel were obtained from the neutron-target and proton-target optical potentials within the adiabatic approximation [40], considering the breakup effects of the deuteron. Additionally, the CDCC calculations [41] were also performed to understand the uncertainty from the reaction models by comparison with the ADWA results. The continuum states were discretized up to $k_ {\rm{max}}=1\;{\rm{fm}}^{-1}$, with a step size of $\Delta{k}=0.05\;{\rm{fm}}^{-1}$. The exit channel parameters are the proton-target optical potential parameters at the corresponding outgoing energy. $C_{s1/2}^{2}(d)$ assumes the value of 0.76 fm^-1 from Ref. [44]. The nucleon-target potential parameters were provided by Varner et al. [45] and Koning et al. [46], as listed in Table 1.

Table 1

Table 1.  Entrance and exit optical potential parameters, where $V_{i}$ are in MeV, $r_{i0}$ and $a_{i}$ are in units of fm. If i represents null, the parameters will be real volume-central potentials. $SI$ depicts imaginary surface-central potentials, I depicts imaginary volume-central potentials, $SO$ depicts real spin-orbit potentials, and C depicts the Coulomb potential.

Method	Channel	Potential	V	$r_{0}$	a	$V_{\rm SI}$	$r_{\rm SI0}$	$a_{\rm SI}$	$V_{\rm I}$	$r_{\rm I0}$	$a_{\rm I}$	$V_{\rm SO}$	$r_{\rm SO0}$	$a_{\rm SO}$	$r_{\rm C0}$
ADWA	$d+^{22}$Ne	Varner	96.64	1.17	0.72	14.03	1.18	0.69	1.82	1.55	0.46	5.90	0.91	0.63	1.28
		Koning	99.42	1.16	0.71	14.46	1.30	0.57	0.97	1.55	0.46	5.66	0.95	0.57	1.36
	$p+^{23}$Ne	Varner	51.64	1.17	0.69	8.26	1.18	0.69	1.35	1.18	0.69	5.90	0.92	0.63	1.28
		Koning	53.77	1.16	0.67	8.77	1.30	0.53	1.25	1.16	0.67	5.47	0.96	0.59	1.35
CDCC	$p+^{22}$Ne	Varner	53.72	1.17	0.69	8.37	1.18	0.69	0.84	1.18	0.69	5.90	0.91	0.63	1.28
		Koning	56.58	1.16	0.68	7.72	1.30	0.53	0.51	1.16	0.68	5.66	0.95	0.59	1.36
	$n+^{22}$Ne	Varner	49.90	1.17	0.69	5.79	1.18	0.69	1.10	1.18	0.69	5.90	0.91	0.63	1.28
		Koning	50.32	1.16	0.68	6.86	1.30	0.54	0.59	1.16	0.68	5.60	0.95	0.59	1.36
	$p+^{23}$Ne	Varner	51.64	1.17	0.69	8.26	1.18	0.69	1.35	1.18	0.69	5.90	0.92	0.63	1.28
		Koning	53.77	1.16	0.67	8.77	1.30	0.53	1.25	1.16	0.67	5.47	0.96	0.59	1.35

DownLoad: CSV

Show Table

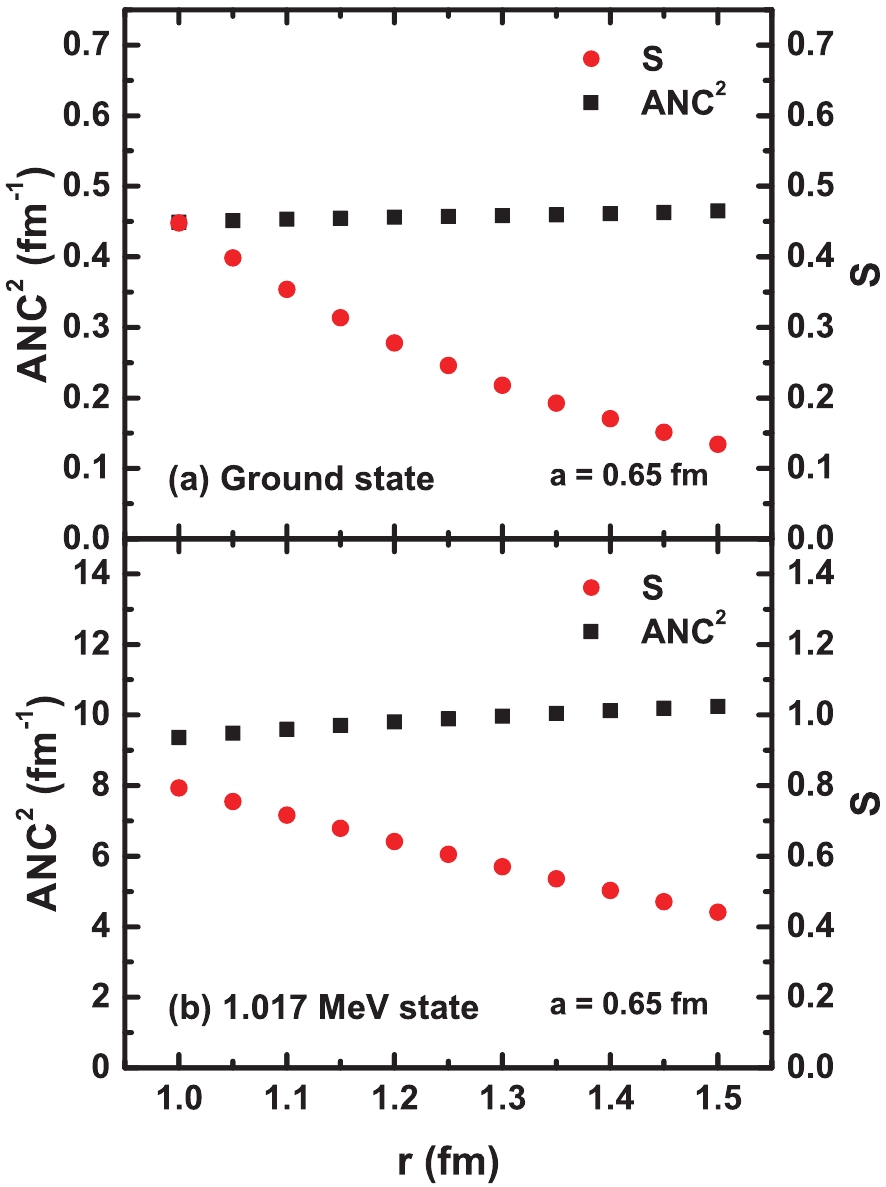
The neutron ANCs were extracted by normalization of the present ADWA and CDCC calculations to the experimental angular distributions via Eq. (1). The discrepancies between the ADWA and CDCC results were found to be 9% and 13% for the ANCs of the ground state and the first excited state, which is in agreement with the conclusion of the previous systematic study by Chazono et al. [42]. Figure 1 shows the normalized angular distributions of the ${}^{22} {{\rm{Ne}}} (d, p){}^{23} {{\rm{Ne}}}$ reaction, leading to the ground and first excited states of ²³Ne with the ADWA and CDCC approaches, together with the experimental data [34, 35]. Furthermore, the peripherality of the reaction should be ensured when the ANC method is adopted. The dependence of both the spectroscopic factors and the square of the ANCs on the radius of the binding potential is calculated, as shown in Fig. 2. The spectroscopic factors vary considerably, whereas the neutron ANCs are more stable, which indicates the peripherality of this reaction at the present energy. The uncertainties of 2% and 5% were derived for the ANCs of the ground state and the first excited state, respectively.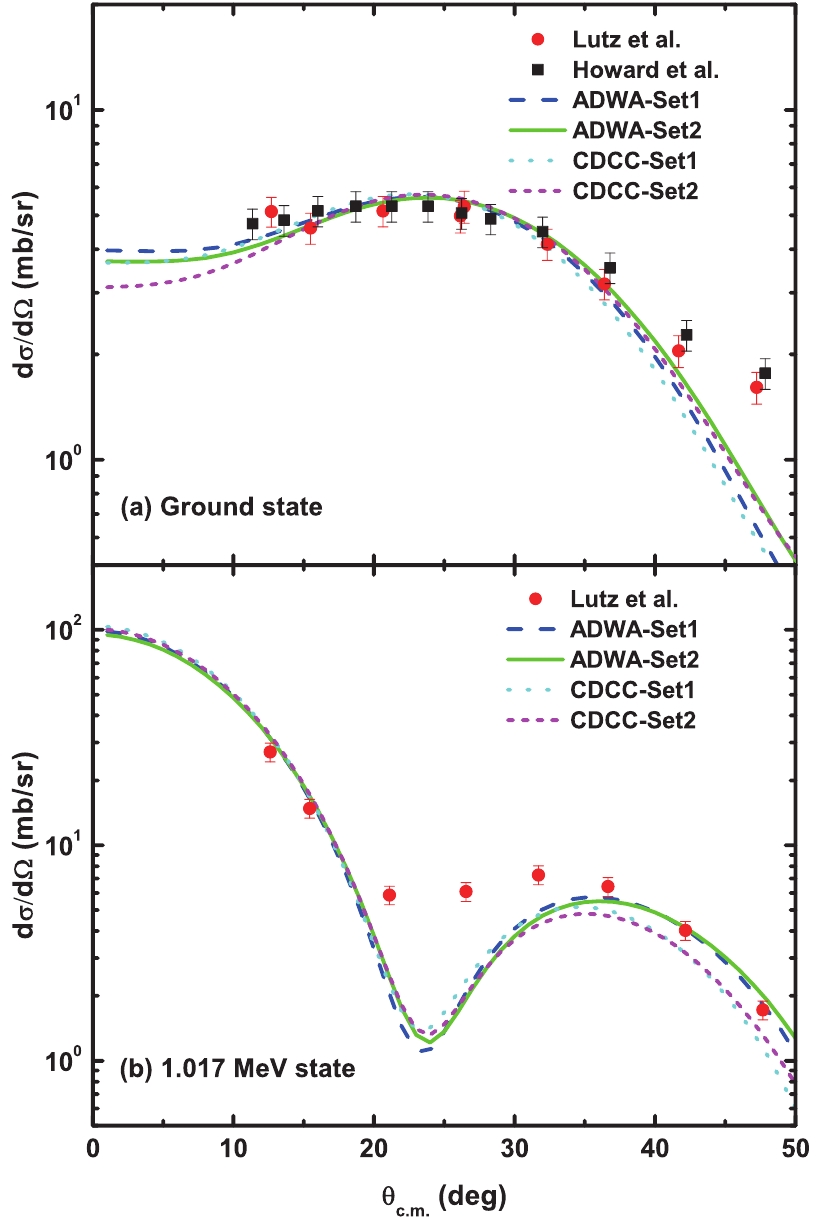

Figure 1

Figure 1.  (color online) Experimental and theoretical ${}^{22} {\rm{Ne}}(d, p){}^{23} {\rm{Ne}}$ differential cross-sections for the ground state and first excited state of ${}^{23} {\rm{Ne}}$ with an incident energy of 12.1 MeV. The red dots and black squares refer to the experimental angular distributions from Lutz et al. [34] and Howard et al. [35], respectively. The curves denote the present ADWA and CDCC calculations with the OMP parameters listed in Table 1.

DownLoad: Full-Size Img PowerPoint

Figure 2

Figure 2.  (color online) Dependence of spectroscopic factors and ANCs of the ground state and first excited state of ²³Ne on the radius of the binding potential. Results were given by the ADWA analysis of the data from Lutz et al. [34] using potentials from Varner et al. [45].

DownLoad: Full-Size Img PowerPoint

The square of the ANCs $C_{d5/2}^{2}({}^{23} {{\rm{Ne}}} )=(0.483\pm0.060)$ fm^-1 and $C_{s1/2}^{2}({}^{23} {{\rm{Ne}}} )=(9.7\pm2.3)\;{\rm{fm}}^{-1}$. The uncertainty arises from the statistics (4% for the ground state and 18% for the first excited state), different sets of the experimental data (1% for the ground state), two sets of optical model potentials (7% for both states), discrepancy between the ADWA and CDCC methods (9% for the ground state and 13% for the first excited state), and breakdown of peripherality (2% for the ground state and 5% for the first excited state).

In Table 2, we list the present ANCs of ²³Ne along with the previous results. The new neutron ANCs for the ground and first excited states are smaller than those from the (¹³C, ¹²C) reaction by a factor of ~2 [32].

Table 2

Table 2.  Present ANCs of ²³Ne in comparison with previous experimental results.

$E_{\rm x}$/MeV	$J_\pi$	ANC2/fm−1
		(13C, 12C)[32]	Present
0	$5/2^+$	$0.86\pm0.14$	$0.483\pm0.060$
1.017	$1/2^+$	$18.2\pm4.2$	$9.7\pm2.3$

DownLoad: CSV

Show Table

3. Proton ANC and width of ²³Al

• 1. Introduction
• 2. Neutron ANCs of 23Ne
• 3. Proton ANC and width of 23Al
• 4. Astrophysical S-factors and reaction rates of 22Mg (p, γ)23Al
• 5. Summary and conclusion

The ground states of ${}^{23} {{\rm{Al}}}$ and ${}^{23} {{\rm{Ne}}}$ are mirror pairs. The proton ANC of ${}^{23} {{\rm{Al}}}_{ {\rm{g.s.}}}$ can be extracted from the neutron ANC of ${}^{23} {{\rm{Ne}}} _{ {\rm{g.s.}}}$ as a result of charge symmetry. The spin and parity of ${}^{23} {{\rm{Al}}}_{ {\rm{g.s.}}}$ were measured to be $5/2^{+}$ [30, 33], which is the same as its mirror nucleus. The relationship is described as

where R is the ratio.

The relationship of the ANCs for mirror pairs was established as [36, 47]

where $F_{l}$ is the regular Coulomb wave function, $j_{l}$ is the Bessel function, $R_{N}$ is the radius of the nuclear interior, and $k_{p}$ and $k_{n}$ are the wave numbers of the proton and neutron related to the separation energies, respectively. The ratio R was derived to be 5,440 when $R_N=1.3 \times A^{1/3}$ fm. Furthermore, we investigated the dependence of R on $R_N$ by changing the $R_N$ values from $1.1 \times A^{1/3}$ to $1.5 \times A^{1/3}$ fm, and found that the deviation was less than 1%.

In contrast, based on the assumption that the difference in the spectroscopic factors for the mirror pairs can be ignored, R can also be obtained by

where $b_{d5/2}^{2}({}^{23} {{\rm{Al}}})$ and $b_{d5/2}^{2}({}^{23} {{\rm{Ne}}} )$ refer to the respective single-particle ANCs. The single-particle ANCs were calculated with the same geometry parameters $r_{0}$ and a, and the same spin-orbit interaction. The depth of the central potential was adjusted to reproduce the latest experimental proton binding energy 0.143 MeV in $^{23} {{\rm{Al}}}$ [30].

The ratios inferred from Eq. (3) and Eq. (4) were $5.44\times10^{3}$ and $5.47\times10^{3}$, respectively. The average was used for the following calculation, and their difference was included in the total uncertainty. The proton ANC of ${}^{23} {{\rm{Al}}}_{ {\rm{g.s.}}}$ was found to be $C_{d5/2}^{2}({}^{23} {{\rm{Al}}})=(2.65\pm0.33)\times10^{3}\;$ fm⁻¹. In Table 3, we list the present proton ANCs of ²³Al along with the previous results. The present proton ANC is significantly smaller than the previous experimental value of $(4.63\pm0.77)\times10^{3}\;{\rm{fm}}^{-1}$ from the (¹³C,¹²C) reaction [32]. This is because the present neutron ANC of ²³Ne from the ($d,\,p$) reaction is approximately half that from the (¹³C, ¹²C) reaction.

Table 3

Table 3.  Present ANC or width of ²³Al in comparison with previous experimental results.

$E_{\rm x}$/MeV	$J_\pi$	ANC2/fm-1 for the ground state, $\Gamma_p$/eV for the 0.550 MeV state
		p(22Mg, p)[31]	(13C, 12C)[32]	Breakup[33]	Present
0	$5/2^+$		$(4.63\pm0.77)\times10^3$	$(3.90\pm0.44)\times10^3$	$(2.65\pm0.33)\times10^{3}$
0.550	$1/2^+$	$32\pm5$			$57\pm14$

DownLoad: CSV

Show Table

Regarding the first excited state of ${}^{23} {{\rm{Al}}}$, the proton width $\Gamma_p$ of the resonance can also be deduced from the neutron ANC of its mirror state in ${}^{23} {{\rm{Ne}}}$ by

where $R^ {{\rm{res}}}$ is given by both [36, 48]

and

where $\Gamma_p^ {\rm{sp}}$ represents the single particle width. The average of the ratios from Eq. (6) and Eq. (7) was used to calculate the proton width of the ${}^{23} {{\rm{Al}}}$ first excited state, which was determined to be $\Gamma_p=(57\pm14)$ eV. The new width is in approximate agreement with the value of ($32 \pm 5$) eV from the measurement of the resonant proton scattering of ²²Mg+p by He et al. [31].

4. Astrophysical S-factors and reaction rates of ²²Mg (p, γ)²³Al

• 1. Introduction
• 2. Neutron ANCs of 23Ne
• 3. Proton ANC and width of 23Al
• 4. Astrophysical S-factors and reaction rates of 22Mg (p, γ)23Al
• 5. Summary and conclusion

The ANC can describe the tail of the overlap function of the bound state wave functions of the projectile, target, and residual nucleus. Then, the cross-section of the peripheral direct capture can be determined along with the scattering wave function in the entrance channel [49].

The RADCAP code [50] was utilized to calculate the cross-section and the astrophysical S-factor of the direct capture reaction. The depth of the proton binding potential was adjusted to reproduce the binding energy $0.143$ MeV [30], with the same geometry parameters $r_{0}$ and a as the ones used when calculating the neutron ANC of ${}^{23} {{\rm{Ne}}} _{ {\rm{g.s.}}}$. This direct capture reaction is mainly dominated by the E1 transition from the incoming p wave at low energies of astrophysical interest. The S-factors for direct capture are shown in Fig. 3. The direct S-factor at zero energy was found to be $S_{\rm{dir}}(0)=(0.53\pm0.07)$ keV b, whereas the values in previous studies were $(0.96\pm0.11)$ keV b [32] and $(0.73\pm0.10)$ keV b [33]. The difference was mainly caused by different ANCs.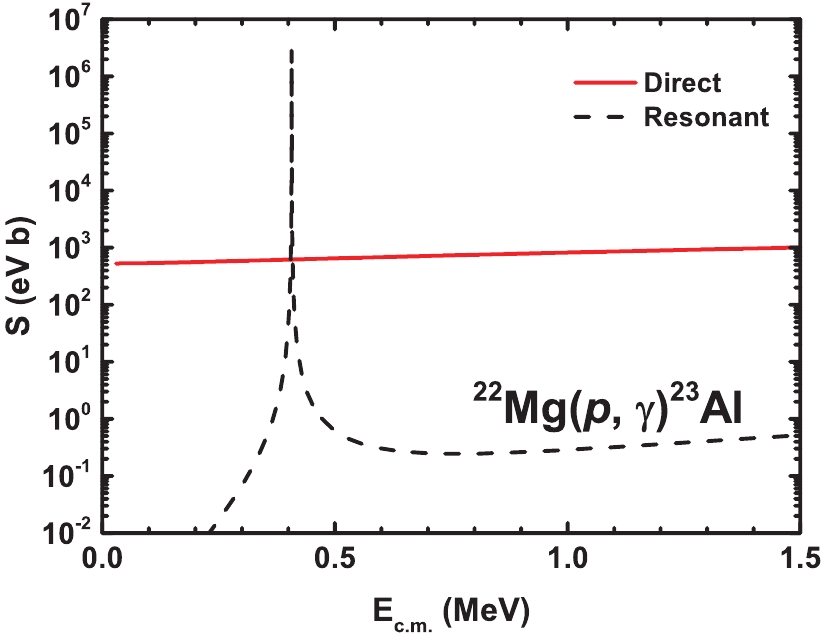

Figure 3

Figure 3.  (color online) Astrophysical S-factors of ${}^{22} {\rm{Mg}}(p, \gamma){}^{23} {\rm{Al}}$ direct capture (red solid curve) and resonant capture through the first excited state of $^{23} {\rm{Al}}$ (black dashed curve) at different center-of-mass energies.

DownLoad: Full-Size Img PowerPoint

The S-factor of the resonance through the $1/2^+$ state of ${}^{23} {{\rm{Al}}}$ can be deduced by the Breit–Wigner formula [51, 52]

where J, $J_1$, and $J_2$ depict the spins of ${}^{23} {{\rm{Al}}}$, the proton, and ${}^{22} {{\rm{Mg}}}$, respectively; $\Gamma_p$, $\Gamma_\gamma$ and $\Gamma_ {{\rm{tot}}}$ represent the proton, gamma, and total widths, respectively; $E_{\rm R}$ and $E_{\rm G}$ depict the resonance and Gamow energies, respectively. The energy dependence of the widths is given by [53, 54]

and

where Q represents the reaction Q value, and l represents the multipolarity of the gamma transition. The $S_{{\rm{res}}}$ factors are also shown in Fig. 3. This resonance was dominated by the $E2$ transition, and thus does not interfere with the direct capture dominated by the $E1$ transition.

The reaction rate of the capture reactions can be integrated by

where $N_{\rm A}$ and k refer to Avogadro's and Boltzmann's constant, $\mu$ is the reduced mass, and T is the temperature.

The reaction rates of the direct and resonant captures at different temperatures are shown in Fig. 4. The result shows that the direct capture dominates the ${}^{22} {{\rm{Mg}}}(p, \gamma){}^{23} {{\rm{Al}}}$ reaction at most temperatures of astrophysical relevance within the range $0.33<T_9<0.64$. The present numerical rates are listed in Table 4, along with the previous results. The differences with respect to other studies are mainly due to different values of the proton ANC of ${}^{23} {{\rm{Al}}}_{ {\rm{g.s.}}}$ adopted, as discussed in Sections 2 and 3.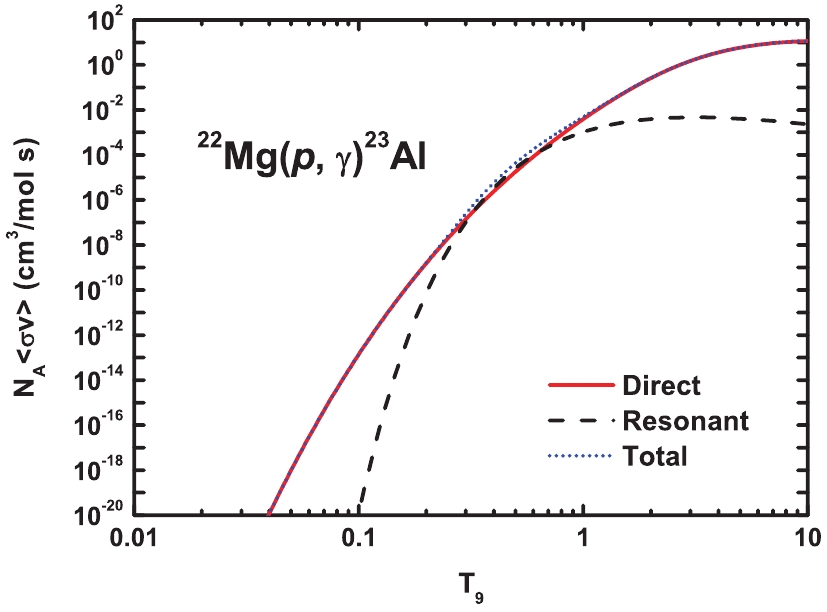

Figure 4

Figure 4.  (color online) Direct capture (red solid curve), resonant capture through first excited state of $^{23} {\rm{Al}}$ (black dashed curve), and total (blue dotted curve) astrophysical reaction rates of ${}^{22} {\rm{Mg}}(p, \gamma){}^{23} {\rm{Al}}$ as a function of temperature.

DownLoad: Full-Size Img PowerPoint

Table 4

Table 4.  Total astrophysical reaction rates of ${}^{22}{{\rm{Mg}}}(p, \gamma){}^{23}{{\rm{Al}}}$ capture reaction in comparison with previous results.

	Present	Wiescher et al. [25]		Caggiano et al. [26]		He et al. [31]		Al-Abdullah et al. [32]
$T_9$	$N_{\rm A}<\sigma v>$/(cm3/mol s)	$N_{\rm A}<\sigma v>$/(cm3/mol s)	ratio	$N_{\rm A}<\sigma v>$/(cm3/mol s)	ratio	$N_{\rm A}<\sigma v >$/(cm3/mol s)	ratio	$N_{\rm A}<\sigma v>$/(cm3/mol s)	ratio
$0.10$	$1.38\times10^{-13}$	$5.03\times10^{-14}$	0.36	$1.70\times10^{-13}$	1.23	$1.67\times10^{-13}$	1.21	$2.62\times10^{-13}$	1.90
$0.20$	$1.63\times10^{-9}$	$5.70\times10^{-10}$	0.35	$1.89\times10^{-9}$	1.16	$1.96\times10^{-9}$	1.20	$3.19\times10^{-9}$	1.96
$0.30$	$2.45\times10^{-7}$	$8.42\times10^{-8}$	0.34	$2.08\times10^{-7}$	0.85	$2.83\times10^{-7}$	1.15	$5.14\times10^{-7}$	2.10
$0.40$	$5.87\times10^{-6}$	$2.00\times10^{-6}$	0.34	$4.42\times10^{-6}$	0.75	$6.58\times10^{-6}$	1.12	$1.12\times10^{-5}$	1.91
$0.50$	$4.43\times10^{-5}$	$1.50\times10^{-5}$	0.34	$3.43\times10^{-5}$	0.77	$4.49\times10^{-5}$	1.01	$7.94\times10^{-5}$	1.79
$0.60$	$1.80\times10^{-4}$	$5.98\times10^{-5}$	0.33	$1.49\times10^{-4}$	0.83	$2.03\times10^{-4}$	1.12	$3.15\times10^{-4}$	1.75
$0.70$	$5.23\times10^{-4}$	$1.69\times10^{-4}$	0.32	$4.58\times10^{-4}$	0.88	$5.94\times10^{-4}$	1.14	$9.17\times10^{-4}$	1.75
$0.80$	$1.24\times10^{-3}$	$3.88\times10^{-4}$	0.31	$1.14\times10^{-3}$	0.92	$1.43\times10^{-3}$	1.15	$2.23\times10^{-3}$	1.80
$0.90$	$2.59\times10^{-3}$	$7.85\times10^{-4}$	0.30	$2.48\times10^{-3}$	0.96	$3.03\times10^{-3}$	1.17	$4.83\times10^{-3}$	1.86
$1.00$	$4.95\times10^{-3}$	$1.45\times10^{-3}$	0.29	$4.86\times10^{-3}$	0.98	$5.86\times10^{-3}$	1.18	$9.58\times10^{-3}$	1.94
$1.50$	$5.54\times10^{-2}$	$1.42\times10^{-2}$	0.26	$5.41\times10^{-2}$	0.98	$6.85\times10^{-2}$	1.24	$1.27\times10^{-1}$	2.29
$2.00$	$2.62\times10^{-1}$	$6.45\times10^{-2}$	0.25	$2.54\times10^{-1}$	0.97	$3.50\times10^{-1}$	1.34	$7.24\times10^{-1}$	2.77

DownLoad: CSV

Show Table

With REACLIB's standard formula [55, 56], the total reaction rate is fitted as

with fitting errors being less than 5% at the temperatures from 0.02 GK to 10 GK. The present rate with this formula can be conveniently used in stellar modeling.

In the nova models adopted in Ref. [21], the peak temperatures range from 0.145 GK to 0.418 GK. If the proton capture dominates over the $\beta$-decay of ²²Mg, the required hydrogen density values at those typical peak temperatures are larger than the corresponding peak densityvalues in the models by at least one order of magnitude.

5. Summary and conclusion

• 1. Introduction
• 2. Neutron ANCs of 23Ne
• 3. Proton ANC and width of 23Al
• 4. Astrophysical S-factors and reaction rates of 22Mg (p, γ)23Al
• 5. Summary and conclusion

We extracted the neutron ANCs for the ground state and the first excited state of ²³Ne from the experimental differential cross-sections of the ${}^{22} {{\rm{Ne}}} (d,p){}^{23} {{\rm{Ne}}}$ reaction through the ADWA and CDCC analysis. Then, the proton ANC for the ground state and the proton width of the first excited state of ${}^{23} {{\rm{Al}}}$ were deduced according to the charge symmetry of the mirror nuclei. The astrophysical S-factors and reaction rates of the direct capture to the ground state and the resonant capture to the first excited state in the ${}^{22} {{\rm{Mg}}}(p, \gamma){}^{23} {{\rm{Al}}}$ reaction were extracted from the present ANC and proton width. The present total reaction rates are approximately half that of the most recent values obtained from the measurement of the (¹³C, ¹²C) reaction [32]. This is because the present neutron ANC of ²³Ne from the ($d,\,p$) reaction is approximately half that from the (¹³C, ¹²C) reaction. It is highly desirable to understand such a large difference between the results from the ($d,\,p$) reaction and the (¹³C, ¹²C) reaction in the future. Our result supports the claim that the direct capture dominates the ${}^{22} {{\rm{Mg}}}(p,\,\gamma)^{23} {{\rm{Al}}}$ reaction at most astrophysical temperatures.

References