-
Since the milestone discovery of the Higgs boson at the CERN Large Hadron Collider (LHC) [1, 2], much attention has been drawn to the searches for new physics beyond the Standard Model (SM). Most of the theoretical model constructions beyond the SM contain the extended Higgs sector, most notably in the minimal Supersymmetric Standard Model (MSSM) [3] and the composite Higgs model such as the little Higgs theory [4]. Thus, there is strong motivation to search for the new heavy Higgs bosons beyond the SM. Such efforts have been actively carried out, particularly in the LHC experiments.
While the LHC and its luminosity upgrade (HL-LHC) will continue the journey of searching for new physics in the next two decades, future higher energy hadron colliders, such as the energy upgrade for the LHC to 27 TeV C.M. energy (HE-LHC) [5-8] and the future circular collider of about 100 TeV C.M. energy (FCC-hh) [9], are proposed to perform the direct searches at the energy frontier. In this paper, we set out an initial study for the discovery potential for the new heavy Higgs bosons at the HE-LHC. We take the Type-II Two Higgs Doublet Model (2HDM) for illustration.
The leading search channel for the non-SM neutral Higgses comes from their single production, followed by their conventional decays into pairs of SM particles. We thus study the clean gluon fusion processes
$ gg\rightarrow\phi\rightarrow W^+W^-, ZZ $ and investigate the implication on the parameter space of the Type-II 2HDM model. The$ \phi\rightarrow \tau^+\tau^- $ channel suffers from major SM backgrounds, such as multijet,$ Z/\gamma^\ast \rightarrow \tau\tau $ , and$ W\rightarrow \tau\nu $ [8]. For the charged Higgs heavier than the top quark, the typical search channel is the associated production of a charged Higgs boson and top quark. The decay mode$ H^\pm \rightarrow tb $ is dominant over other decays$ H^\pm\rightarrow \tau^\pm\nu, cs $ once kinematically accessible, but also suffers from large SM backgrounds ($ t\bar{t} $ + light-flavor jets,$ W/Z $ + jet(s),$ t\bar{t} $ + vector boson,$ t\bar{t} $ + Higgs, single top + W, etc.) [10]. For the sub-dominant decay$ H^\pm\rightarrow \tau^\pm \nu $ , the relevant SM backgrounds involve processes with$ W^\pm\rightarrow \tau^\pm\nu $ . The difference between the Yukawa coupling for$ H^\pm $ and the gauge interaction for$ W^\pm $ , in terms of the spin correlation in tau decay, can be used to distinguish the signal from the SM backgrounds.Although the above conventional signals for searching Higgs bosons benefit from large QCD production cross sections and simple kinematics, they all have a substantial dependence on additional 2HDM parameters, such as
$ \tan\beta $ and$ \cos(\beta-\alpha) $ . It is worth emphasizing the potential importance of the electroweak production of Higgs boson pairs, e.g.$ pp\rightarrow W^\ast \rightarrow H^\pm A^0 $ and$ pp\rightarrow Z^\ast/\gamma^\ast \rightarrow H^+ H^- $ . Their production cross sections are only governed by pure electroweak gauge couplings and quite complementary to the conventional signals in the determination of the nature of the Higgs.The rest of the paper is organized as follows. In Sec. 2, we give a brief overview of the 2HDM and discuss the constraints on the parameters relevant for our study. In Sec. 3, we analyze the single production of neutral Higgs bosons via gluon-gluon fusion and give the implication on the parameters of the Type-II 2HDM model. The prospect of probing single charged Higgs production is presented in Sec. 4. In Sec. 5, we study the signatures of non-SM Higgses pair production through pure electroweak interactions. Finally, in Sec. 6, we summarize our main results.
-
The Two Higgs Doublet Model [11] is a good representative prototype to study the Higgs boson properties beyond the SM. In the 2HDM, the Higgs sector is composed of two SU
$ (2)_L $ scalar doublets$ \begin{array}{*{35}{l}} {{H}_{i}}=\left( \begin{matrix} h_{i}^{+} \\ ({{v}_{i}}+{{h}_{i}}+{\rm i}{{P}_{i}})/\sqrt{2} \\ \end{matrix} \right),\ \ i=1,2. \\ \end{array}$

(1) After the electroweak symmetry breaking (EWSB), there are four more Higgs bosons (
$ H^0, A^0, H^\pm $ ) besides the SM-like Higgs boson ($ h^0 $ ) in the particle spectrum$\begin{array}{l} \left( \begin{array}{c} H^0 \\ h^0 \\ \end{array} \right) = \left( \begin{array}{cc} \cos\alpha & \sin\alpha \\ -\sin\alpha & \cos\alpha \\ \end{array} \right) \left( \begin{array}{c} h_1 \\ h_2 \\ \end{array} \right), \\ A^0 = -\sin\beta P_1 + \cos\beta P_2, \ \ H^\pm = -\sin\beta h_1^\pm + \cos\beta h_2^\pm . \end{array} $

(2) Here, the important parameter is defined as
$ \tan\beta = v_2/v_1 $ with$ \sqrt{v_1^2+v_2^2} = v = 246 $ GeV. Because of the absence of new physics signals from the searches at the LHC, we require that the non-SM Higgses are all heavier than$ h^0 $ and take their masses as free parameters. Certain discrete symmetries between the two doublets are often imposed to avoid unwanted flavor-changing-neutral currents (FCNC).Motivated by the construction of the minimal Supersymmetric Standard Model (MSSM), we assume the Type-II 2HDM in which
$ H_1 $ only couples to the down-type quarks and leptons and$ H_2 $ only couples to the up-type quarks. Their couplings to the SM fermions behave as$ \begin{split} g_{H^0u\bar{u}} =& {\sin\alpha\over \sin\beta} = \cos(\beta-\alpha)-\cot\beta\sin(\beta-\alpha), \\ g_{H^0d\bar{d}} =& g_{H^0l\bar{l}} = {\cos\alpha\over \cos\beta} = \cos(\beta-\alpha)+\tan\beta\sin(\beta-\alpha); \end{split}$

$ \begin{split} g_{A^0u\bar{u}} =& -{\rm i}\cot\beta\gamma_5, \ \ \ g_{A^0d\bar{d}} = g_{A^0l\bar{l}} = -{\rm i}\tan\beta\gamma_5; \\ g_{H^+\bar{u}d} =& -{{\rm i}\over \sqrt{2}v}V_{ud}^\ast\left[m_d\tan\beta(1+\gamma_5)+m_u\cot\beta(1-\gamma_5)\right], \\ g_{H^-u\bar{d}} =& -{{\rm i}\over \sqrt{2}v}V_{ud}\left[m_d\tan\beta(1-\gamma_5)+m_u\cot\beta(1+\gamma_5)\right], \\ g_{H^+\bar{\nu}l} =& -{{\rm i}\over \sqrt{2}v}m_l\tan\beta(1+\gamma_5), \\ g_{H^-\nu\bar{l}} =& -{{\rm i}\over \sqrt{2}v}m_l\tan\beta(1-\gamma_5), \end{split}$

(3) with a normalization factor of
${\rm i}m_{u,d,l}/v$ for neutral Higgses. The couplings between neutral Higgses and two gauge bosons are$ g_{H^0VV} = \cos(\beta-\alpha) $ and$ g_{A^0VV} = 0 $ . As such, the parameters involved in our analyses include$ \tan\beta $ ,$ \cos(\beta-\alpha) $ , and the relevant Higgs masses under consideration.As previously intimated, we identify the lighter CP-even scalar
$ h^0 $ as the SM-like Higgs observed at the LHC. This, together with the absence of exotic decays of the 125 GeV Higgs boson, implies the alignment limit [12, 13]. We will take the alignment limit$ \cos(\beta-\alpha) = 0 $ or assume the value of$ \cos(\beta-\alpha) $ near the alignment in the following analysis. The theoretical consideration of vacuum stability [14] and unitarity [15], along with the measurement of the electroweak precision observables, [16] suggest small mass splittings among the four non-SM Higgses. Thus, we assume degenerate heavy Higgs mass spectra (unless otherwise stated) and forbid exotic Higgs decay modes [17-21].In addition, there are strong constraints on the non-SM Higgs sector from the flavor constraints. In particular, the latest analyses on Br
$ (B\rightarrow X_s \gamma) $ have constrained the charged Higgs to be heavier than 600 GeV at 95% C.L. [22, 23]. Precision observables, particularly S and T oblique parameters, also impose correlations between the charged Higgs mass and the neutral ones:$ M_{H^\pm}\sim M_A $ or$ M_{H^\pm} \sim M_{H^0} $ . These limits, however, are typically model dependent and could be relaxed in Type-I 2HDM as shown in Ref. [23], or with additional contributions to the flavor or precision observables from other sectors in the new physics models [24, 25]. In this paper, since we focus on the collider aspect of beyond the SM Higgs bosons, we choose the mass spectrum of the non-SM Higgses to be characteristic of the absent exotic decay channels that we analyze and consider the heavy Higgs bosons as they satisfy the current direct collider search limits. The decays that we study in this paper could be applied to those extended models, with possible rescaling of the branching fractions. One should, however, keep those potentially dangerous indirect constraints in mind when considering a specific new physics model with an extended Higgs sector. -
Just like the Higgs boson discovery, the leading production channel for a heavy neutral Higgs boson is through the gluon fusion
$ gg\rightarrow H^0, \ A^0. $

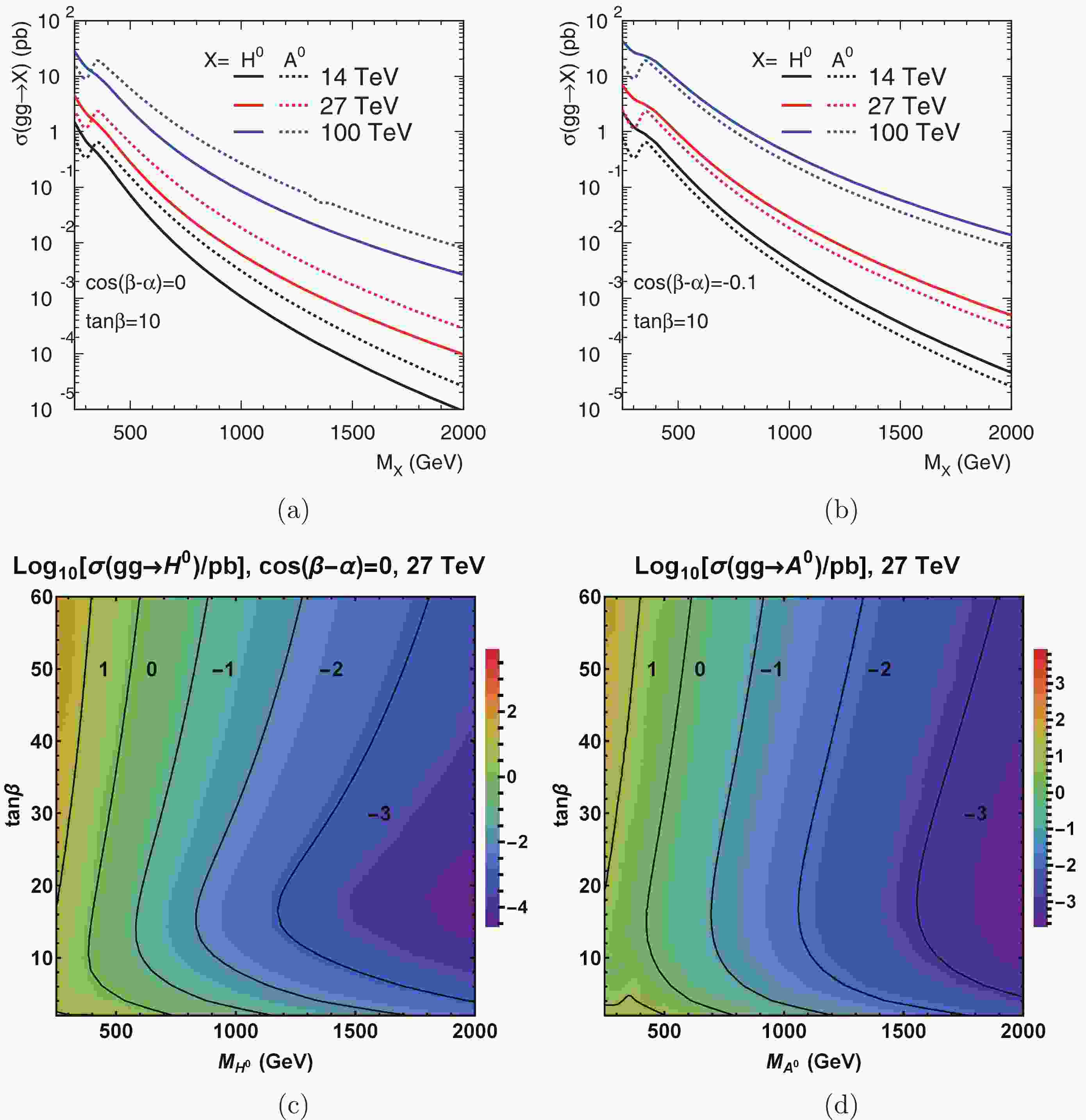
(4) These channels benefit from the large gluon luminosity at higher energies and the favorable phase space for a single particle production. We show the production cross sections versus the Higgs mass (from 250 GeV to 2 TeV) at the 14 TeV LHC, 27 TeV LHC, as well as the 100 TeV collider, in Fig. 1. The cross sections are obtained at NNLO in QCD using default SusHi [26] and LHAPDF [27] with the alignment limit
$ \cos(\beta-\alpha) = 0 $ or$ \cos(\beta-\alpha) = -0.1 $ (note that the$ gg\rightarrow A^0 $ production does not depend on$ \cos(\beta-\alpha) $ ). Note that the mixing angle$ \cos(\beta-\alpha) $ is also constrained through Higgs rate measurements, and$ \cos(\beta-\alpha) = -0.1 $ is at the edge of the 95% CL exclusion limit by fits to the measured rates of Higgs boson production and decays [28]. For illustration, we take a negative value of$ \cos(\beta-\alpha) $ here for$ H^0\rightarrow VV $ decays. One should note that a positive value of$ \cos(\beta-\alpha) $ near the alignment limit is also allowed. We see that the total production cross section at 27 TeV LHC ranges from 4 (2.8) pb at$ M_{H^0(A^0)} = 250 $ GeV to$ 1 \ (3) \times 10^{-4} $ pb at$ M_{H^0(A^0)} = 2 $ TeV for$ \tan\beta = 10 $ in the alignment limit. In addtiion, it increases by four times at$ M_{H^0/A^0} = 500 $ GeV and by eight times at$ M_{H^0/A^0} = 1.5 $ TeV from 14 TeV to 27 TeV C.M. energy. The$ gg\rightarrow A^0 $ production does not depend on$ \cos(\beta-\alpha) $ and its production cross section is larger than that of$ gg\rightarrow H^0 $ for$ \cos(\beta-\alpha) = 0 $ and$ \tan\beta = 10 $ . From$ \cos(\beta-\alpha) = 0 $ to$ \cos(\beta-\alpha) = -0.1 $ , the production cross section of$ gg\rightarrow H^0 $ increases and becomes larger than that of$ gg\rightarrow A^0 $ .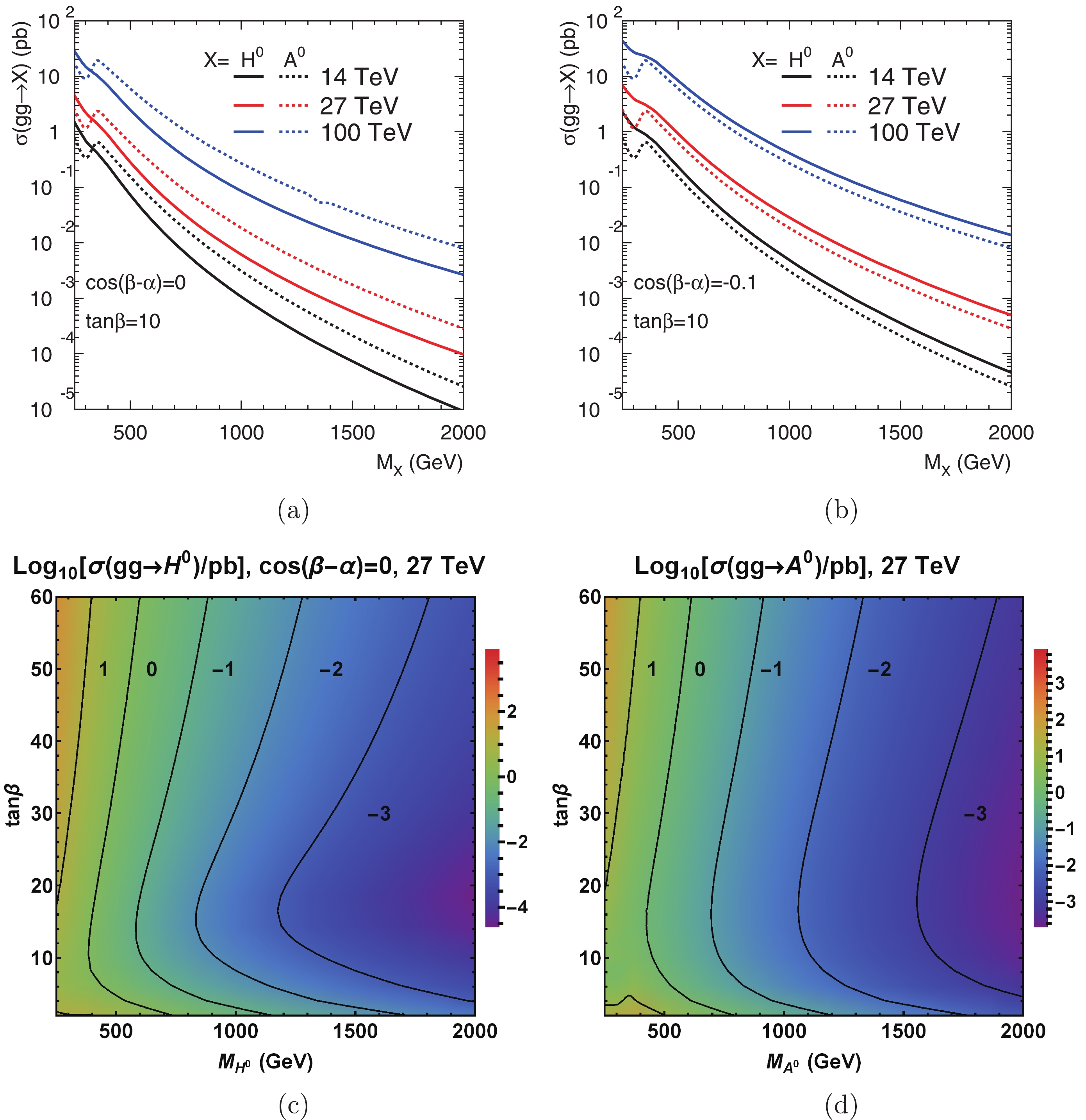
Figure 1. (color online) Top: Total production cross section versus the Higgs boson mass for
$gg \to H^0, A^0$ with$\cos(\beta-\alpha)=0$ (a) or$\cos(\beta-\alpha)=-0.1$ (b) and$\tan\beta=10$ at$pp$ collider with 14 TeV, 27 TeV and 100 TeV. Bottom: The cross section indicated by contour lines in the plane of$\tan\beta$ versus the Higgs boson mass for$gg\to H^0$ with$\cos(\beta-\alpha)=0$ (c) and$gg\to A^0$ (d) at the 27 TeV LHC.We explore the observability of the heavy neutral Higgs bosons by examining the specific decay channels. For the channels we consider, we use MadGraph5_aMC@NLO [29] to generate the signal and backgrounds events, and TAUOLA [30] interfaced with Pythia [31] to simulate the tau lepton decay. To simulate the detector effects in the following analysis, we smear the hadronic/leptonic energy using a Gaussian distribution whose width is parameterized as [32]
$\begin{split} {\Delta E\over E} =& {a\over \sqrt{E/{\rm{GeV}}}}\oplus b, \\ a_{\rm had} =& 100\%, b_{\rm had} = 5\%, a_\ell = 5\%, b_\ell = 0.55\%. \end{split}$

(5) The above energy resolution is the expected performance of the ATLAS detector for the LHC. Recently, Delphes-3.4.2 [33] was released for detector simulation and event reconstruction and included the beta card for HL-LHC and HE-LHC studies. Compared with the LHC case,
$b_{\rm had}, b_{\ell}$ remained almost the same, and$a_{\rm had}$ and$ a_{\ell} $ were reduced by 30% and enhanced by three times, respectively. As a values only affect the linear terms in the energy resolution, we expect that the change will not impact our results much.By far, the cleanest signals for heavy new physics would be the leptonic final states from the
$ W/Z $ decays. We now utilize those channels to search for the CP-even Higgs$ H^0 $ . The basic requirements for the leptons are$ p_T(\ell)\geqslant 30 \ {\rm{GeV}}, \ \ \ |\eta(\ell)|<2.5, \ \ \ \Delta R_{\ell\ell}\geqslant 0.4, $

(6) and we select the events satisfying
$ {\not\!\!{E}}_T>40 \ {\rm{GeV}}, \ \ \ p_T^{\rm{min}}(\ell)>65 \ {\rm{GeV}}, \ \ \ M_{\ell\ell}>M_{H^0}/3, $

(7) for
$ H^0\rightarrow W^+W^- $ channel. The mass of the$ H^0 $ resonance in the$ WW $ channel can be reconstructed by the$ WW $ transverse mass$\begin{split} M_T(W^+W^-) =& \sqrt{(E_T^{\ell\ell}+{\not\!\!{E}}_T)^2-(\vec{p}_T(\ell_1)+\vec{p}_T(\ell_2)+\vec{{\not\!\!{p}}}_T)^2}, \\ E_T^{\ell\ell} =& \sqrt{|\vec{p}_T^{\ell\ell}|^2+m_{\ell\ell}^2}, \end{split} $

(8) as shown in Fig. 2. The SM backgrounds are the same as those for
$ \tau^+\tau^- $ channel, but with gauge bosons' leptonic decay to electron/muon. The$ ZZ $ background has the opposite-sign lepton pairs$ \ell^+\ell^- $ from Z boson decay and can be further reduced by vetoing the invariant mass of opposite sign leptons if$ |M_{\ell\ell}-M_Z|<10 $ GeV. For the$ H^0\rightarrow ZZ $ channel, we simply require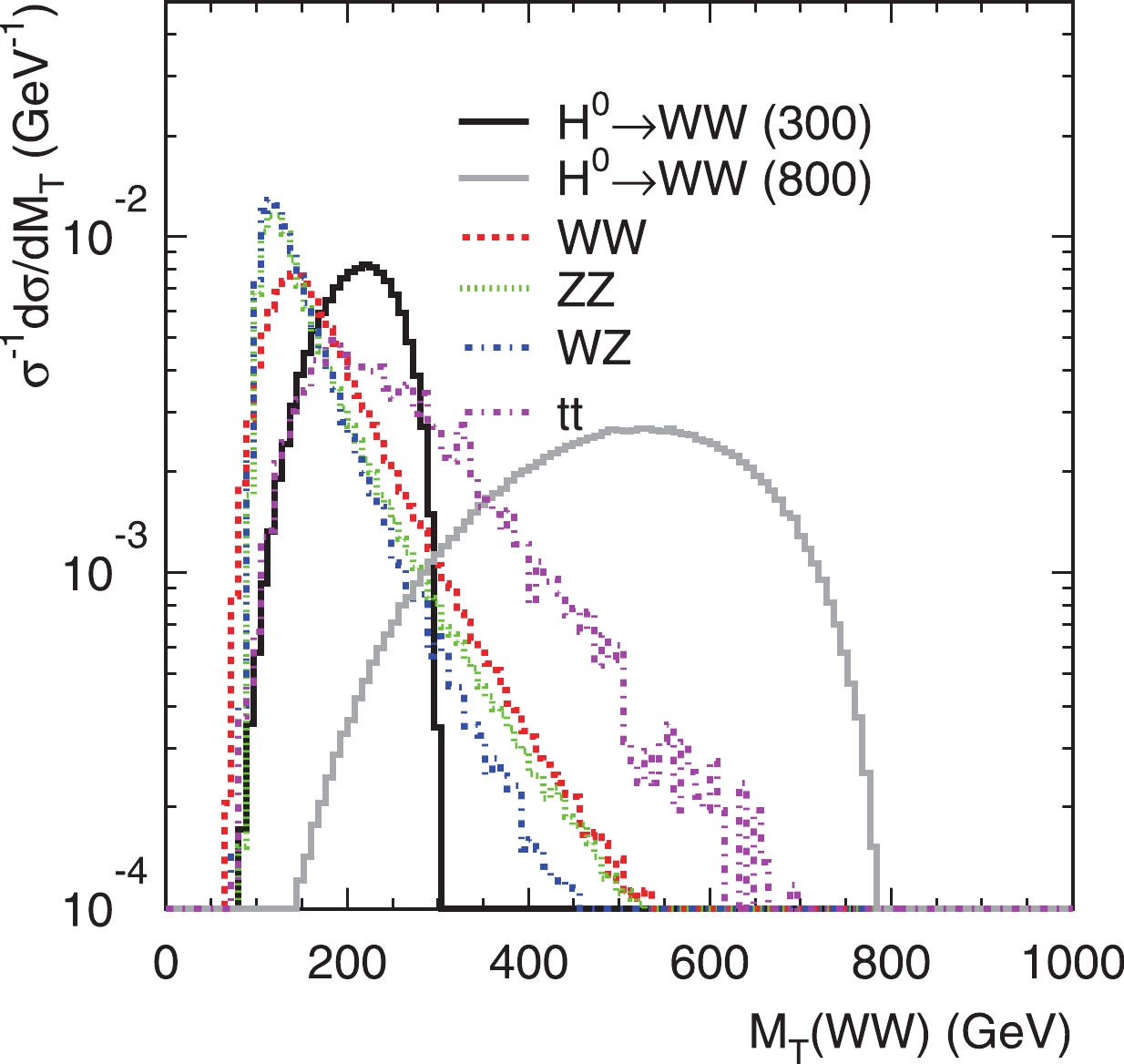
Figure 2. (color online) The differential cross section distributions of the
$WW$ transverse mass$M_T(WW)$ for the signal$gg\to H^0\to W^+W^-$ , together with SM backgrounds at the 27 TeV LHC.$ p_T^{\rm{min}}(\ell)>50 \ {\rm{GeV}}, \ \ \ |M_{4\ell}-M_{H^0}|<M_{H^0}/10, $

(9) for the minimal lepton
$ p_T $ and the invariant mass of the four leptons. The$ t\bar{t} $ production with pure leptonic decays can also be a reducible background after the two b-jets are vetoed if$ p_T(b)>30 \ {\rm{GeV}}, |\eta(b)|<4.9 $ [34]. The cut efficiencies are given in Tables 1 and 2 for$ WW $ and$ ZZ $ channels, respectively. One can see that the Z boson veto and the mass window requirement for$ H^0 $ resonance significantly suppress the$ ZZ $ background for$ H^0\rightarrow W^+W^- $ and$ H^0\rightarrow ZZ $ , respectively.cut efficiencies basic cuts ${\not\!\!{E} }_T$ 

$p_T^\ell$ 

$M_Z$ veto

$M_{\ell\ell}$ 

$H^0\to W^+W^- (300)$ 

0.52 0.35 0.082 0.082 0.082 $H^0\to W^+W^- (800)$ 

0.79 0.66 0.54 0.54 0.50 $WW$ (300)

0.23 0.1 0.016 0.016 0.016 $WW$ (800)

0.23 0.1 0.016 0.016 0.0071 $ZZ$ (300)

0.33 0.18 0.015 0.00099 0.00072 $ZZ$ (800)

0.33 0.18 0.015 0.00099 negligible $WZ$ (300)

0.046 0.02 0.0012 0.00048 0.00047 $WZ$ (800)

0.046 0.02 0.0012 0.00048 0.00021 $t\bar{t}$ (300)

0.0064 0.0047 0.0017 0.0017 0.0017 $t\bar{t}$ (800)

0.0064 0.0047 0.0017 0.0017 0.00082 Table 1. The cut efficiencies for
$gg\to H^0\to W^+W^-$ and the SM backgrounds after consecutive cuts at the 27 TeV LHC. We take$M_{H^0}=300$ or 800 GeV.cut efficiencies basic cuts $p_T^\ell$ 

$M_{4\ell}$ 

$H^0\to ZZ (300)$ 

0.3 0.053 0.053 $H^0\to ZZ (800)$ 

0.69 0.58 0.58 $ZZ (300)$ 

0.12 0.0097 0.0014 $ZZ (800)$ 

0.12 0.0097 0.00081 Table 2. The cut efficiencies for
$gg\to H^0\to ZZ$ and the SM backgrounds after consecutive cuts at the 27 TeV LHC. We take$M_{H^0}=300$ or 800 GeV.The decays of
$ H^0\rightarrow W^+W^-, ZZ $ are present away from the alignment limit, and can dominate with larger values of$ |\cos(\beta-\alpha)| $ . Assuming$ \cos(\beta-\alpha) = -0.1 $ and$ \tan\beta = 5, 10 $ in the top panels of Figs. 3 and 4, we show the reach of BR$ (H^0\rightarrow W^+W^-, ZZ) $ as a function of$ M_{H^0} $ at the 27 TeV LHC. The solid and dashed curves correspond to 3$ \sigma $ significance and 5$ \sigma $ discovery, respectively. The minimal branching fraction that can be reached with 15 ab$ ^{-1} $ luminosity is around$ (1-2)\times 10^{-2} $ and$ H^0 $ with the mass of about$ 1.2/1.3 $ TeV can be probed for 5$ \sigma $ discovery if BR$ (H^0\rightarrow WW/ZZ) = 1 $ and$ \tan\beta = 10 $ . For$ \tan\beta = 5 $ with a larger production cross section, a lower branching fraction and larger Higgs mass can be reached. The decays into massive gauge bosons are decreased for large$ \tan\beta $ as the decay into$ b\bar{b} $ dominates; thus, the realistic branching fraction of$ H^0\rightarrow WW/ZZ $ cannot reach the order of unity. We use package 2HDMC [35] to calculate all 2HDM branching fractions below.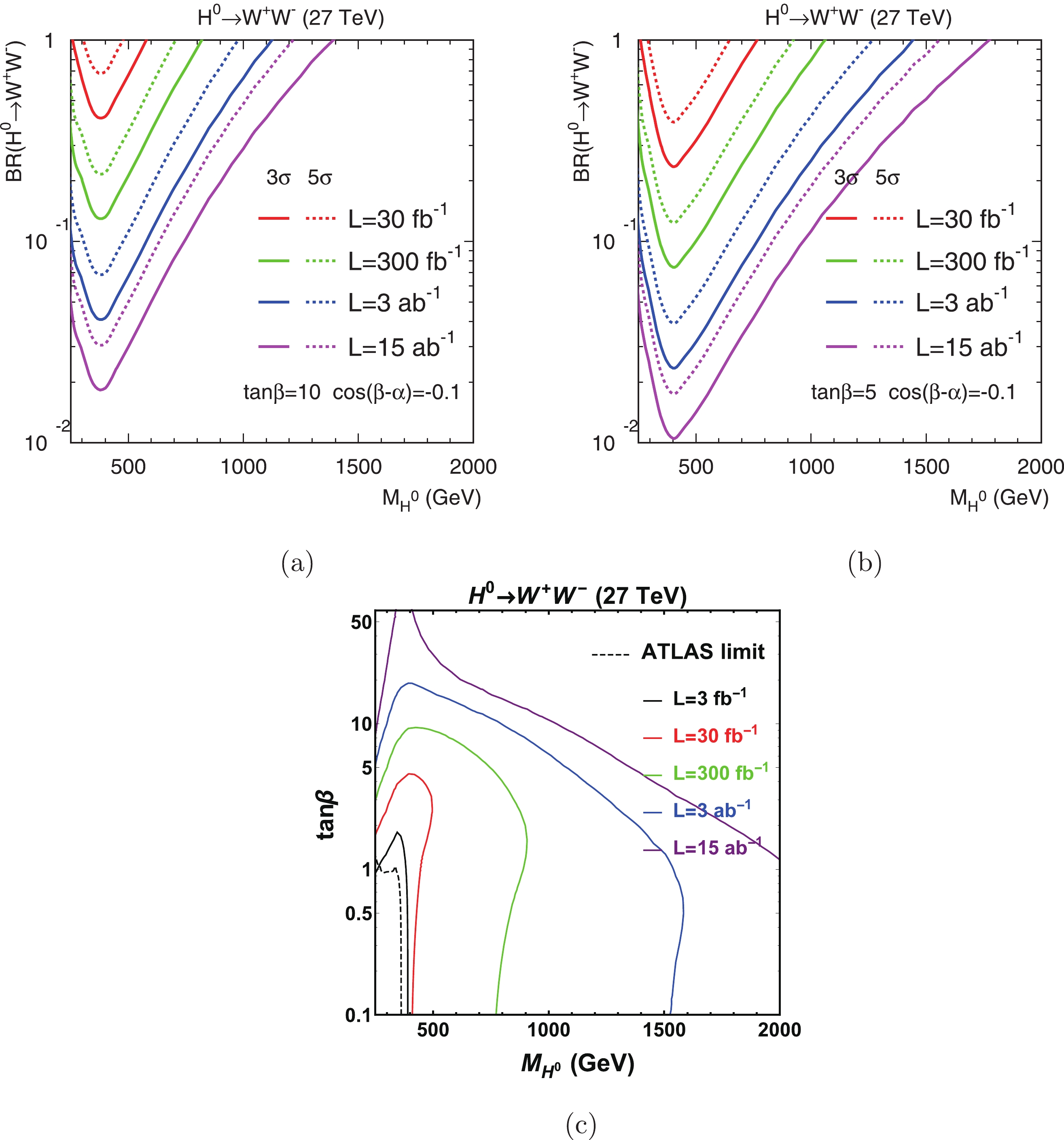
Figure 3. (color online) Top panels: Reach of BR
$(H^0\to W^+W^-)$ as a function of$M_{H^0}$ at the 27 TeV LHC. We assume$\tan\beta=10$ (a),$\tan\beta=5$ (b) and$\cos(\beta-\alpha)=-0.1$ . Bottom panel: Discovery contour in$\tan\beta$ versus$M_{H^0}$ plane for$gg\to H^0\to W^+W^-$ , with realistic BR$(H^0\to W^+W^-/ZZ)$ under the assumption of$\cos(\beta-\alpha)=-0.1$ . The excluded regions in the Type-II 2HDM are indicated by the dashed curves, based on$gg\to H^0\to WW$ search at the 13 TeV LHC [34].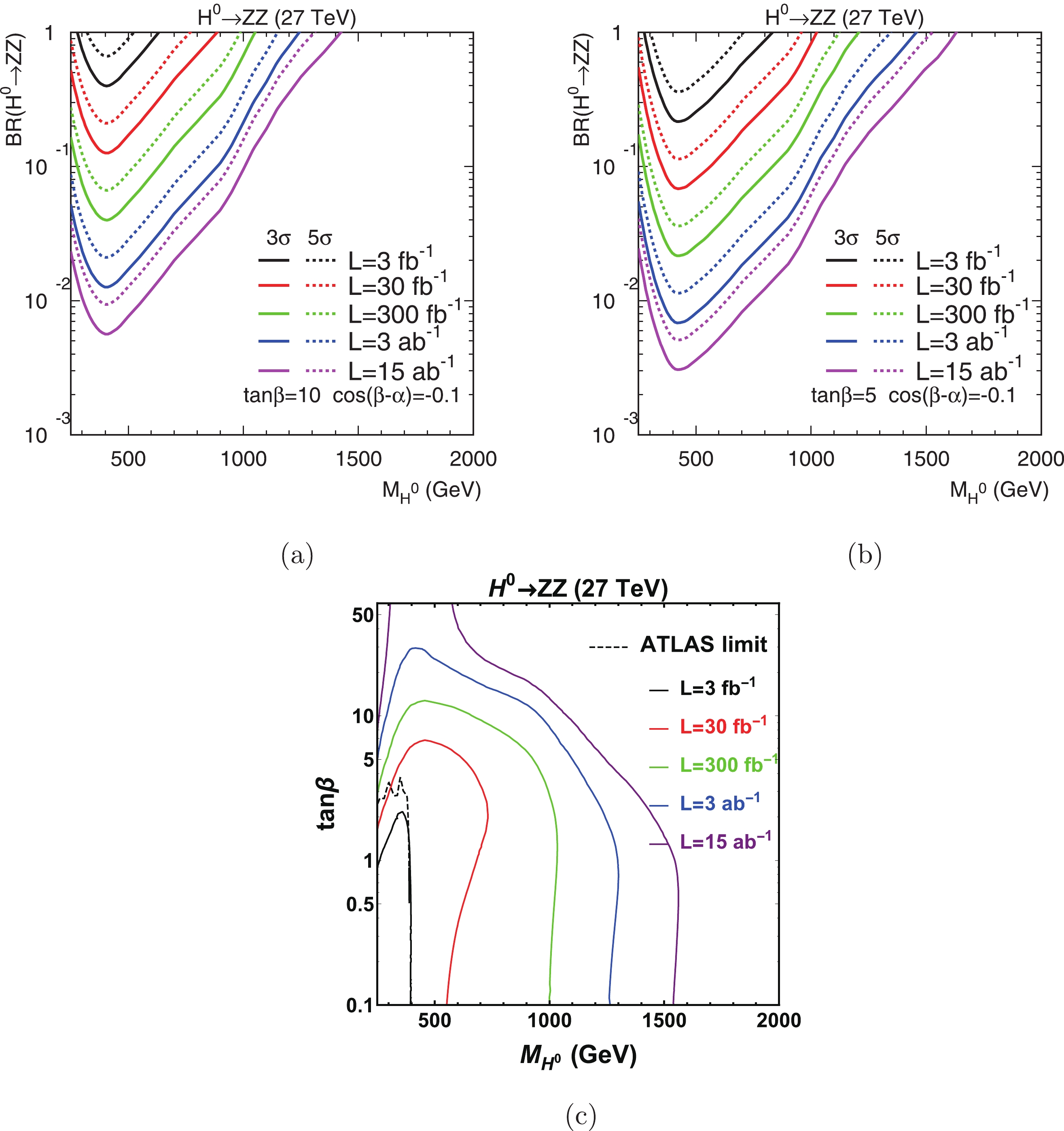
Figure 4. (color online) Top panels: Reach of BR
$(H^0\to ZZ)$ as a function of$M_{H^0}$ at the 27 TeV LHC. We assume$\tan\beta=10$ (a),$\tan\beta=5$ (b) and$\cos(\beta-\alpha)=-0.1$ . Bottom panel: Discovery contour in$\tan\beta$ versus$M_{H^0}$ plane for$gg\to H^0\to ZZ$ , with realistic BR$(H^0\to ZZ)$ under the assumption of$\cos(\beta-\alpha)=-0.1$ . The excluded regions in the Type-II 2HDM are indicated by the dashed curves, based on$gg\to H^0\to ZZ$ search at the 13 TeV LHC [36].The exclusion contours for the
$ H^0 $ decay to the SM gauge bosons by the 13 TeV LHC [34, 36] are added in the bottom panel of Figs. 3 and 4, assuming$ \cos(\beta-\alpha) = -0.1 $ . For the$ WW \ (ZZ) $ decay channel, the LHC has excluded the CP-even Higgs with masses up to 360 (390) GeV and$ \tan\beta $ below 1 (3). With realistic branching fractions at$ \tan\beta = 10 \ (1) $ , the 27 TeV LHC may discover the CP-even Higgs as heavy as 1 TeV ($ 1.5-2 $ TeV) through$ gg\rightarrow H^0\rightarrow W^+W^-, ZZ $ channels as shown in Figs. 3(c) and 4(c). The loss of sensitivity at the large$ \tan\beta $ is mainly due to the reduction of BR$ (H^0\rightarrow W^+W^-, ZZ) $ . It is known that the Higgs production in association with a$ b\bar{b} $ pair can enhance the sensitivity for$ \tan\beta \gtrsim 10 $ in the Type-II 2HDM [37, 38], which is beyond the scope of this article. -
If the charged Higgs boson is heavier than the top quark mass, the conventional production of heavy charged Higgs occurs through
$ gg\rightarrow t b H^\pm $ . However, in high energy colliders, an ordinary$ p_T $ cut (several tens of GeV) on the b-jet in final states is not sufficient as$ {\rm{log}}(\sqrt{\hat{s}}/p_T) $ is still very large. Thus, this exclusive contribution is only meaningful when detecting final state b-jet with a sufficiently large$ p_T $ cut as a regulator. A more dominant mode would be taking b as a parton and considering “inclusive” production. Thus, the leading production mechanism would be the associated production of$ H^\pm $ with a top quark [39, 40]$ g b \rightarrow t H^\pm . $

(10) Its total cross section is more accurately estimated in [41-43].
The production cross sections versus charged the Higgs mass are shown in Fig. 5 at the 14 TeV LHC, 27 TeV LHC, and the 100 TeV colliders. They are the leading order results with a running bottom quark Yukawa coupling at the scale of the pole mass
$ m_b = 4.6 $ GeV. The total production cross section at 27 TeV LHC ranges from 0.5 pb at$ M_{H^\pm} = 250 $ GeV to$ 4 \times 10^{-4} $ pb at$ M_{H^\pm} = 2 $ TeV for$ \tan\beta = 10 $ . We quantify the signal observability according to the leading decay channels.
Figure 5. (color online) Left: Total production cross section versus the Higgs boson mass for
$g b\to t H^\pm$ with$\tan\beta=10$ at$pp$ collider with 14 TeV, 27 TeV and 100 TeV. Right: The cross section indicated by contour lines in the plane of$\tan\beta$ versus the Higgs boson mass for$g b\to t H^\pm$ at the 27 TeV LHC.We consider the clean channel of the charged Higgs boson's leptonic decay, i.e.
$ H^\pm \rightarrow \tau^\pm \nu $ with$ \tau^\pm\rightarrow \pi^\pm \nu $ , with the branching fraction being$ {\rm{BR}}(\tau^\pm\rightarrow \pi^\pm \nu_\tau) = 0.11 $ , and the hadronic decay of the W boson from the top quark. This channel with the$ \tau $ lepton has been studied before and was argued to be a good production mode for the LHC energy upgrade to search [44, 45]. Another signal channel is through the$ \tau $ leptonic decay to an electron or a muon and two neutrinos [46]. The components of the SM backgrounds for this channel are more complicated as the$ e/\mu $ lepton in final states can be either from tau decay or from gauge boson decay. Also, as there are more missing neutrinos in the events, it is more difficult to reconstruct the tau leptons and extract the Higgs resonance mass. Thus, for simplicity we neglect this channel and make a conservative analysis based on pure hadronic decay of the tau lepton. We adopt the basic acceptance cuts$ p_T(b, \pi, j)\geqslant 25 \ {\rm{GeV}}; \ \ \ |\eta(b, \pi, j)|<2.5; \ \ \ \Delta R\geqslant 0.4. $

(11) The leading SM backgrounds are given by
$ gb\rightarrow W^\pm t $ with$ W^\pm\rightarrow \tau^\pm \nu_\tau $ . There are more reducible QCD backgrounds, such as the$ t\bar{t} $ production with one b-jet vetoed if$ p_T(b)>30 \ {\rm{GeV}}, |\eta(b)|<4.9 $ and multijet production with the$ \tau $ -fake rate being approximately$ 10^{-3}-10^{-2} $ [46].Note that, as the charged Higgs
$ H^{-} $ only coupled with the right-handed charged lepton, the right-handed$ \tau^-_R $ decays to a left-handed$ \nu_\tau $ and$ \pi^- $ . This causes the$ \pi^- $ to move preferentially along the$ \tau^- $ momentum direction. In contrast, the$ \tau^- $ coming from the$ W^{-} $ decay is left-handed, which has the opposite effect on the$ \pi^- $ . A similar feature holds for the$ \tau^+ $ from the$ H^{+} $ and$ W^+ $ decays. This is a well-known result of spin correlation in the$ \tau $ decay [47, 48]. Thus, the transverse momentum of$ \pi^\pm $ from the charged Higgs decay to the tau lepton yields a harder spectrum than that from the W decay in the SM backgrounds [49-51], as seen in Fig. 6(a). We thus tighten the missing energy and the$ p_T $ of pion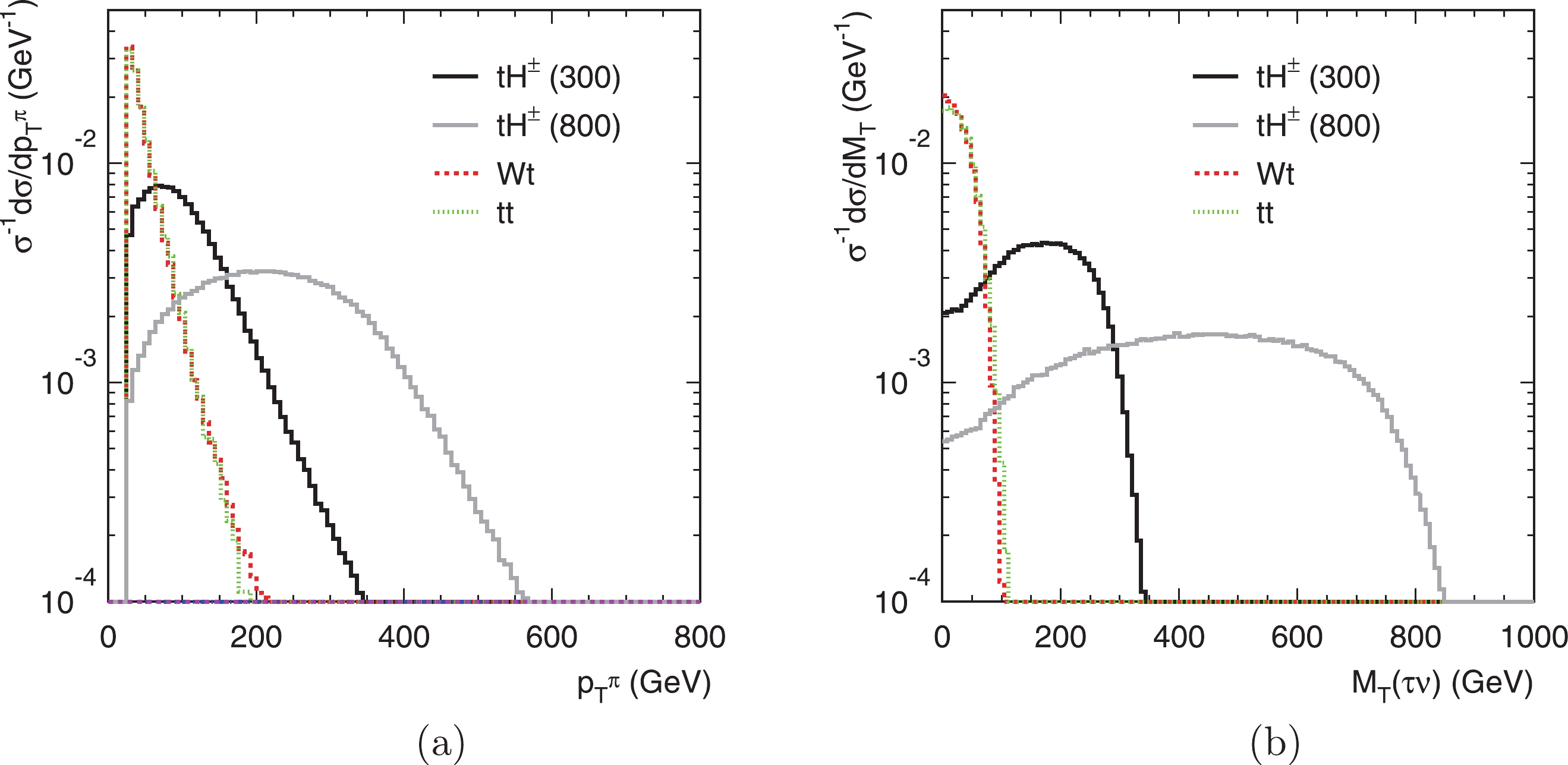
Figure 6. (color online) The differential cross section distributions of
$p_T(\pi)$ (a) and$M_T(\tau\nu)$ (b) for the signal$gb\to t H^\pm\to \tau^\pm \nu b W^\mp\to \tau^\pm \nu bjj$ and backgrounds at the 27 TeV LHC.$ {\not\!\!{E}}_T>100 \ {\rm{GeV}}, \ \ \ p_T(\pi)>65 \ {\rm{GeV}}. $

(12) Furthermore, Fig. 6(b) indicates that the transverse mass of the pion and missing neutrinos from the charged Higgs
$ M_{T}(\tau\nu) = \sqrt{(p_T(\pi)+{\not\!\!{E}}_T)^2-(\vec{p}_T(\pi)+\vec{{\not\!\!{p}}}_T)^2} $

(13) should be greater than 100 GeV in order to reduce the backgrounds. One can see that these cuts help reduce the backgrounds significantly from the cut efficiencies shown in Table 3.
cut efficiencies basic cuts ${\not\!\!{E} }_T$ 

$p_T^\pi$ 

$M_T$ 

$t H^\pm (300)$ 

0.36 0.22 0.16 0.14 $t H^\pm (800)$ 

0.40 0.36 0.34 0.33 $Wt$ 

0.1 0.034 0.0087 negligible $t\bar{t}$ 

0.026 0.012 0.0026 $5\times 10^{-6}$ 

Table 3. The cut efficiencies for
$gb\to t H^\pm\to \tau^\pm \nu b W^\mp\to \tau^\pm \nu bjj$ and the SM backgrounds after consecutive cuts at the 27 TeV LHC. We take$M_{H^{\pm}}=300$ or 800 GeV.If the exotic decay modes (one neutral Higgs with W boson) are absent, the charged Higgs decay is actually dominated by the
$ tb $ mode once it is kinematically open. The$ H^\pm\rightarrow \tau^\pm\nu $ decay is the secondary significant mode in the decays to the SM particles and becomes more important as$ \tan\beta $ increases. Figure 7(a) and (b) display the reachable limit of BR$ (H^\pm\rightarrow \tau^\pm\nu) $ at the 27 TeV LHC. The HE-LHC with 15 ab$ ^{-1} $ luminosity extends the reach of BR$ (H^\pm\rightarrow \tau^\pm\nu) $ to the$ 10^{-3}-10^{-2} $ level for$ \tan\beta = 10 $ and 4.
Figure 7. (color online) Top: Reach of BR
$(H^\pm\to \tau^\pm\nu)$ as a function of$M_{H^\pm}$ for$gb\to t H^\pm\to \tau^\pm \nu bjj$ channel at the 27 TeV LHC. We assume$\tan\beta=10$ (a) and$\tan\beta=4$ (b). Bottom: Discovery contour in$\tan\beta$ versus$M_{H^\pm}$ plane for$gb\to t H^\pm\to \tau^\pm \nu bjj$ with realistic BR$(H^\pm\to \tau^\pm\nu)$ . As a comparison, the 13 TeV LHC exclusion limit on$\tan\beta$ as a function of$M_{H^\pm}$ is also presented [52].The 13 TeV LHC performed the search for charged Higgs bosons through the production of a heavy charged Higgs boson in association with the t and b quarks [52, 53]. The results are interpreted in the framework of the hMSSM scenario, which is a Type-II 2HDM [54]. As a comparison, the 95% CL exclusion limit on
$ \tan\beta $ as a function of$ M_{H^\pm} $ is also presented in Fig. 7(c). The charged Higgs boson mass is excluded up to 1.1 TeV for$ \tan\beta = 60 $ , with the integrated luminosity of 36 fb$ ^{-1} $ [52]. With realistic BR$ (H^\pm\rightarrow \tau^\pm\nu) $ , the discovery region in the$ \tan\beta $ versus$ M_{H^\pm} $ planes is shown in Fig. 7(c) for the$ gb\rightarrow t H^\pm\rightarrow \tau^\pm \nu bjj $ channel at the 27 TeV LHC. The region below$ \tan\beta\sim 1 $ can not be covered by$ 5\sigma $ discovery due to the suppression of the decay branching fraction. The 27 TeV pp collider with 3 ab$ ^{-1} $ luminosity can discover the charged Higgs mass up to 1 TeV (2 TeV) for$ \tan\beta = 10 \ (60) $ . -
Besides the above leading production channels of the single Higgs boson, the electroweak production of Higgs boson pairs are potentially important. Their total production cross sections are independent of any model parameters except for the Higgs masses as they exist via pure electroweak gauge interactions. The pair productions of the Higgs bosons through pure gauge interactions are [49, 50, 55-57]
$ q\bar{q}'\rightarrow W^{\pm\ast}\rightarrow H^\pm A^0, \ \ \ q\bar{q}\rightarrow Z^\ast/\gamma^\ast\rightarrow H^+H^- . $

(14) The relevant Higgs couplings to gauge bosons scale is
$\begin{split}& ~~ WH^\pm A^0\propto g/2, \ ZH^+H^-\propto -g \cos 2\theta_W/(2c_W),\\&\gamma H^+H^-\propto -{\rm i}e , \end{split}$

(15) where g is the weak coupling and
$ \theta_W $ is the weak-mixing angle with$ c_W = \cos\theta_W $ . Figure 8 shows their total cross sections at 14 TeV LHC, 27 TeV LHC and 100 TeV$ pp $ collider. The total cross section of the$ H^\pm A^0 $ production at 27 TeV LHC ranges from$ 2.3\times 10^{-2} $ pb at$ M_{A^0} = M_{H^\pm} = 250 $ GeV to$ 1.5 \times 10^{-4} $ pb with 1 TeV Higgs mass. It is approximately twice as large as that of the$ H^+H^- $ production. We explore their observability based on the leading decay modes.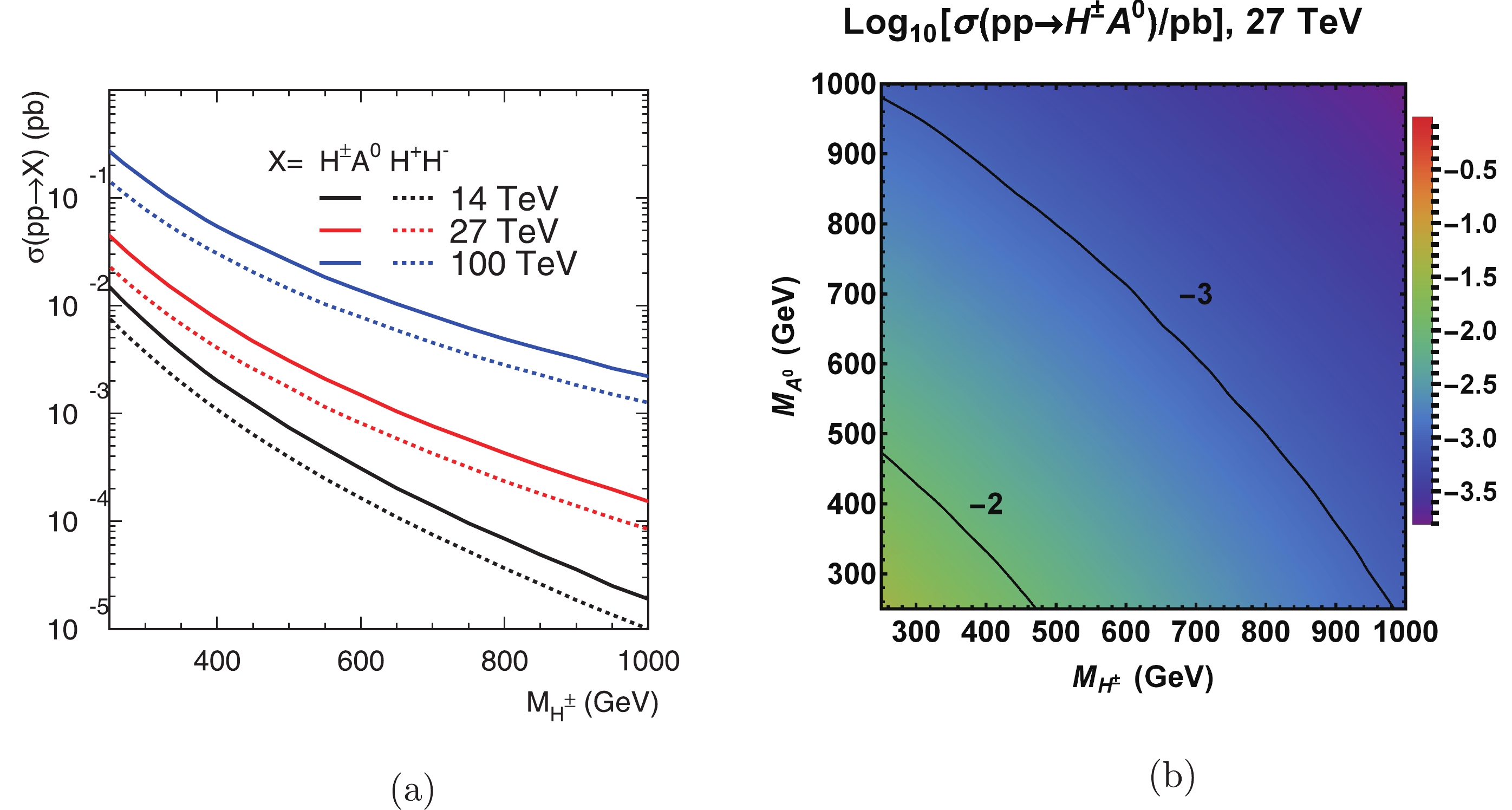
Figure 8. (color online) Left: Total production cross section versus the Higgs boson mass for
$q\bar q \to H^\pm A^0,\ H^+ H^-$ with$M_{A^0}=M_{H^\pm}$ at$pp$ collider with 14 TeV, 27 TeV and 100 TeV. Right: The cross section indicated by contour lines in the plane of$M_{A^0}$ versus$M_{H^\pm}$ for$q\bar q \to H^\pm A^0$ at the 27 TeV LHC. -
The first signal channel we consider is the associated production of the CP-odd Higgs
$ A^0 $ and the charged Higgs$ H^\pm $ , followed by$ A^0 $ and$ H^\pm $ decay to$ b\bar{b} $ and$ \tau^\pm \nu_\tau $ respectively; i.e.,$ pp\rightarrow H^{\pm}A^{0}\rightarrow \tau^\pm \nu_\tau b\bar{b} $ . We again adopt the$ \tau $ leading 2-body decay channel, i.e.$ \tau^\pm\rightarrow \pi^\pm \nu_\tau $ , with the branching fraction being$ {\rm{BR}}(\tau^\pm\rightarrow \pi^\pm \nu_\tau) = 0.11 $ . The b-jets and the charged pions$ \pi^\pm $ in final states satisfy the following basic cuts$ p_T(b,\pi)\geqslant 25 \ {\rm{GeV}}; \ \ \ |\eta(b,\pi)|<2.5; \ \ \ \Delta R_{bb}, \Delta R_{b\pi}\geqslant 0.4, $

(16) and any b-jets in the events are assumed to be tagged with an efficiency of 70%. The major SM backgrounds are thus from the following irreducible contributions:
● the gluon splitting process:
$ q\bar{q}'\rightarrow gW^\pm\rightarrow b\bar{b}W^\pm\rightarrow b\bar{b}\tau^\pm\nu $ ,● the single top production:
$ q\bar{q}'\rightarrow W^{\pm\ast}\rightarrow b\bar{t}(\bar{b}t)\rightarrow b\bar{b}W^\pm\rightarrow b\bar{b}\tau^\pm\nu $ ,and the reducible ones
● the
$ W^\pm $ -gluon fusion process with a forward jet:$ gq\rightarrow gq'W^{\pm\ast}\rightarrow q'b\bar{t}(\bar{b}t)\rightarrow q'b\bar{b}W^\pm\rightarrow q'b\bar{b}\tau^\pm\nu $ ,● the QCD
$ t\bar{t} $ production:$ t\bar{t}\rightarrow b\bar{b}W^+W^-\rightarrow b\bar{b}\tau^\pm \ell^\mp \nu's \ (\ell = e,\mu) $ .The last two processes having additional jets or leptons can be vetoed by requiring the extra objects with
$ p_T(j)>30 \ {\rm{GeV}}, |\eta(j)|<4.9; \ \ \ p_T(\ell)>7 \ {\rm{GeV}}, |\eta(\ell)|<3.5. $

(17) We display the distributions of signal and backgrounds after the basic cuts at the 27 TeV LHC in Fig. 9 (a) missing transverse energy
${\not\!\!{E}}_T$ and (b) transverse pion momentum$ p_T(\pi) $ . The signal exhibits a harder${\not\!\!{E}}_T$ spectrum than the SM backgrounds from the Jacobian peak around$ p_{T\nu}\sim M_{H^\pm}/2 $ . The mass peak of the resonance$ A^0 $ also leads to an enhanced distribution near$ p_{Tb}\sim M_{A^0}/2 $ . Furthermore, as discussed for the single$ H^\pm $ production with$ H^\pm \rightarrow \tau^\pm \nu $ in Sec. 4, the signal has a harder$ p_T $ distribution of$ \pi^\pm $ compared to the SM backgrounds. The charged Higgs mass$ M_{H^\pm} $ and the CP-odd Higgs mass$ M_{A^0} $ can be read from the edge of the transverse mass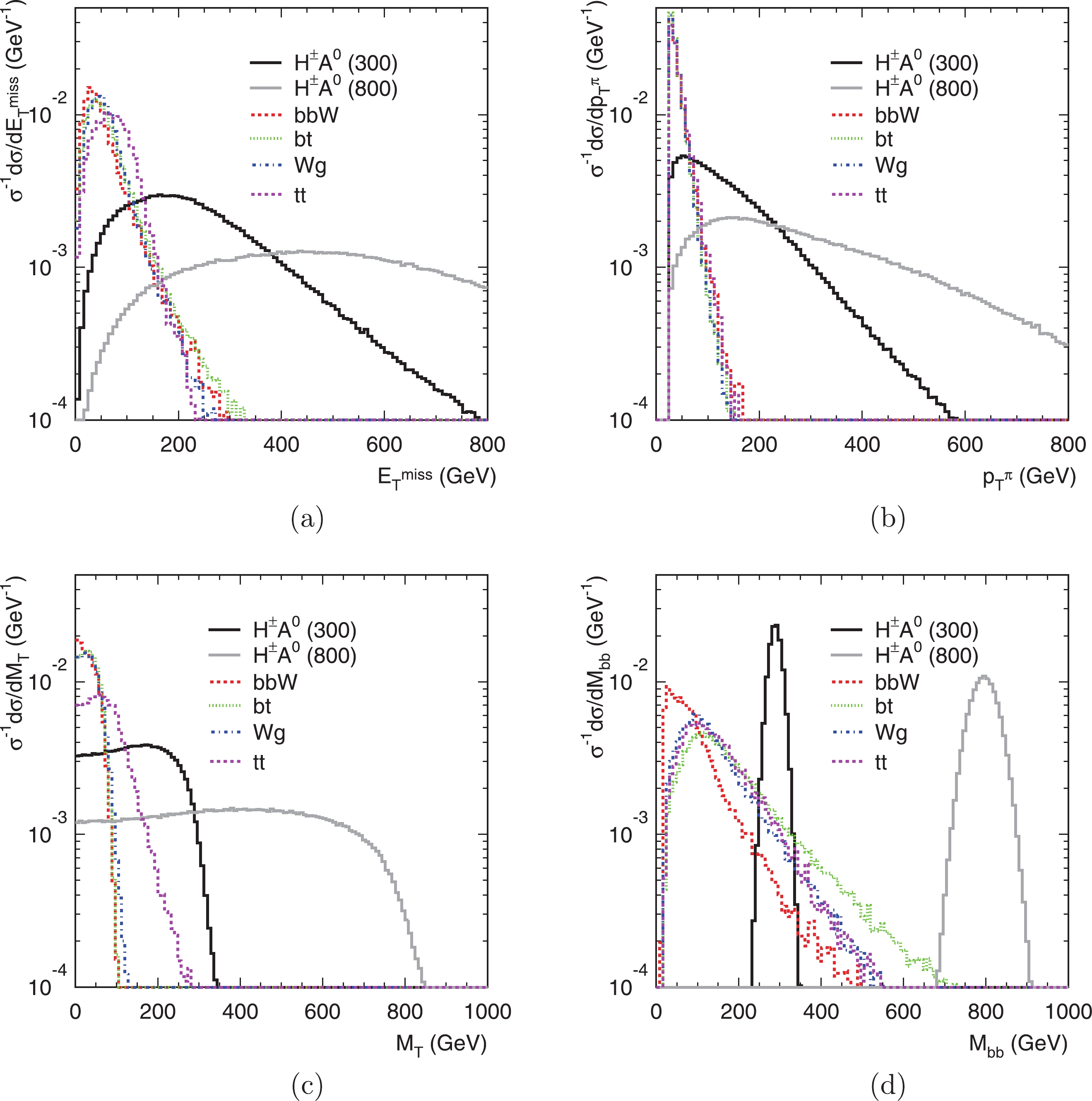
Figure 9. (color online) The differential cross section distributions of
${\not\!\!{E}}_T$ (a),$p_T(\pi)$ (b),$M_T(H^\pm)$ (c) and$M_{bb}$ (d) for the signal$pp\to H^{\pm}A^{0}\to \tau^\pm \nu_\tau b\bar{b}$ and SM backgrounds versus at the 27 TeV LHC.$ M_T(H^\pm) = \sqrt{(E_T(\pi)+{\not\!\!{E}}_T)^2-(\vec{p}_T(\pi)+\vec{{\not\!\!{p}}}_T)^2}, $

(18) and the invariant mass of two b-jets
$ M_{bb} $ , as shown in Figs. 9(c) and (d). We thus apply the following kinematic cuts$ \begin{split}& {\not\!\!{E}}_T>M_{H^\pm}/3, \ p_T^{\rm{max}}(b)>M_{A^0}/2, \\ &p_T(\pi)>M_{H^\pm}/10+40 \ {\rm{GeV}}, \ |M_{bb}-M_{A^0}|<M_{A^0}/10. \end{split}$

(19) The cut efficiencies of the signal and backgrounds after imposing the above cuts are summarized in Table 4. One can see that all the SM backgrounds could be sufficiently suppressed and we expect to achieve good signal significance although our signal is induced by a pure electroweak process.
cut efficiencies basic cuts $p_T^b$ 

${\not\!\!{E} }_T$ 

$p_T^\pi$ 

$M_{bb}$ 

$H^\pm A^0 (300)$ 

0.67 0.64 0.55 0.41 0.38 $H^\pm A^0 (800)$ 

0.86 0.81 0.68 0.57 0.55 $bbW$ (300)

0.0064 0.00093 0.00057 $0.00017$ 

$1.5\times 10^{-5}$ 

$bbW$ (800)

0.0064 $4.0\times 10^{-5}$ 

$2.5\times 10^{-5}$ 

$5.2\times 10^{-6}$ 

negligible $bt$ (300)

0.072 0.021 0.011 0.0017 $1.8\times 10^{-4}$ 

$bt$ (800)

0.072 0.0024 0.001 0.0001 $2.4\times 10^{-5}$ 

$Wg$ (300)

0.011 0.0021 0.0012 0.00022 $3.2\times 10^{-5}$ 

$Wg$ (800)

0.011 0.00012 $5.6\times 10^{-5}$ 

$8.5\times 10^{-6}$ 

$7.5\times 10^{-7}$ 

$t\bar{t}$ (300)

0.004 0.0006 0.00029 $4.3\times 10^{-5}$ 

$9.5\times 10^{-6}$ 

$t\bar{t}$ (800)

0.004 $5.5\times 10^{-6}$ 

$1.8\times 10^{-6}$ 

$2.5\times 10^{-7}$ 

negligible Table 4. The cut efficiencies for
$pp\to H^{\pm}A^{0}\to \tau^\pm \nu_\tau b\bar{b}$ and the SM backgrounds after consecutive cuts with$\tau^\pm\to \pi^\pm \nu_\tau$ channel at the 27 TeV LHC. We take$M_{H^{\pm}}=M_{A^0}=300$ or 800 GeV.As the
$ H^\pm A^0 $ production is independent of any model parameters except for the Higgs masses, the only unknown in our signal process can be extracted as the decay branching fractions of$ H^\pm $ and$ A^0 $ . In Fig. 10(a) we show the reach of the product of branching fractions, i.e.$ {\rm{BR}}(H^\pm\rightarrow \tau^\pm \nu_\tau)\times {\rm{BR}}(A^0\rightarrow b\bar{b}) $ , with the degenerate spectrum$ M_{A^0} = M_{H^\pm} $ and different luminosity assumptions. For$ M_{A^0} = M_{H^\pm}\simeq 300 $ GeV with 15 ab$ ^{-1} $ luminosity, the discovery limit of the branching fraction product can be as small as$ 3\times 10^{-2} $ . With$ {\rm{BR}}(H^\pm\rightarrow \tau^\pm \nu_\tau)\times {\rm{BR}}(A^0\rightarrow b\bar{b}) $ = 20%, the maximal discovery masses of the degenerate heavy Higgs bosons are approximately 450 GeV and 800 GeV with an integrated luminosity of 3 ab$ ^{-1} $ and 15 ab$ ^{-1} $ , respectively. We also vary the masses of the charged Higgs and the CP-odd Higgs, and display the discovery region with respect to the two masses in Fig. 10(b) by fixing the branching fraction product to be 20%. The regions to the left of the curves can be covered by 5$ \sigma $ discovery.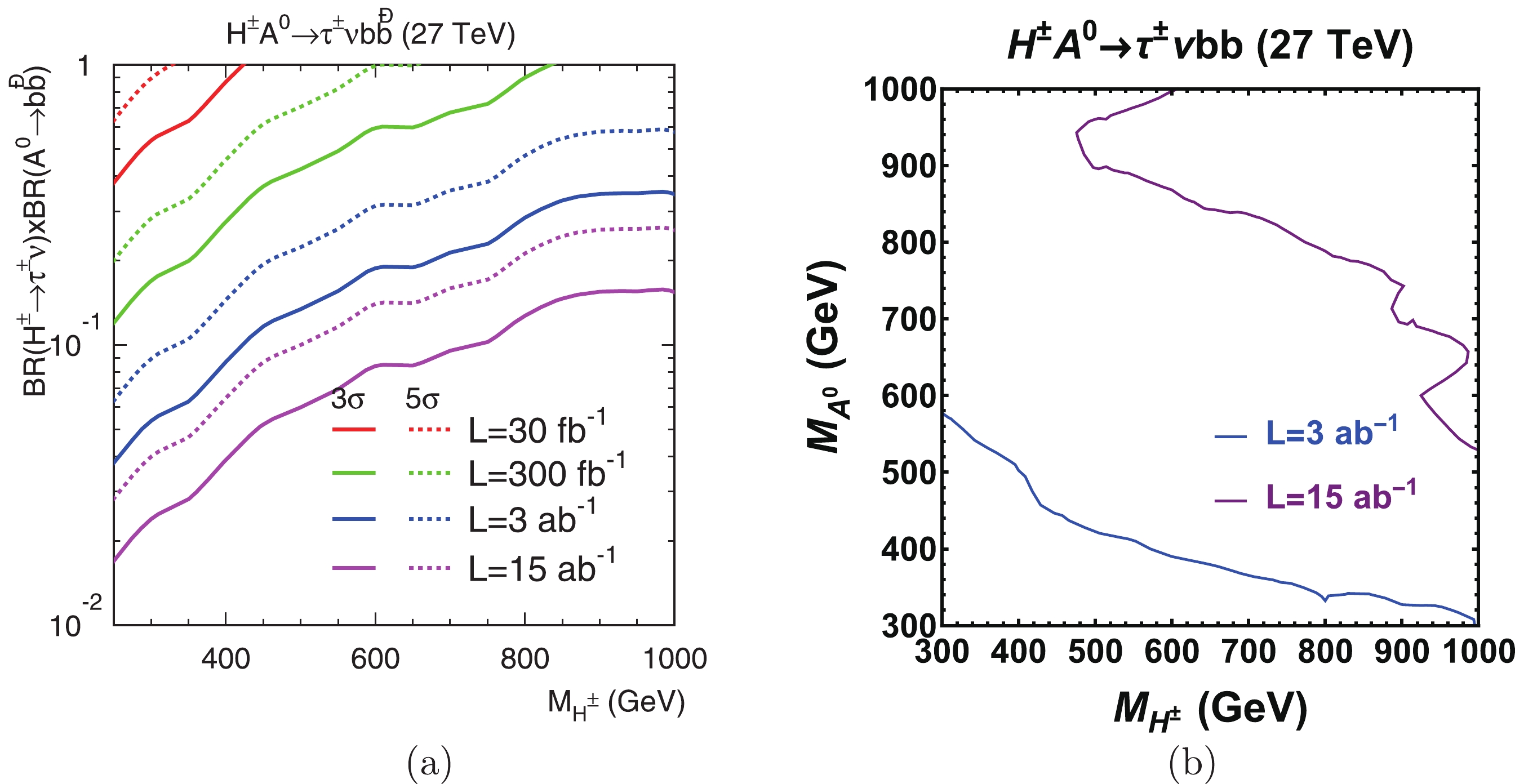
Figure 10. (color online) Left: Reach of
${\rm BR}(H^\pm\to \tau^\pm \nu_\tau)\times {\rm BR}(A^0\to b\bar{b})$ versus$M_{H^\pm}$ for$pp\to H^{\pm}A^{0}\to \tau^\pm \nu_\tau b\bar{b}$ . We assume$M_{A^0}=M_{H^\pm}$ . Right: Discovery contour in the plane of$M_{A^0}$ versus$M_{H^\pm}$ . We assume${\rm BR}(H^\pm\to \tau^\pm \nu_\tau)\times {\rm BR}(A^0\to b\bar{b})$ =20%. -
Next, we study the signal induced by
$ H^\pm \rightarrow tb $ with the top quark's leptonic decay, i.e.$ H^\pm A^0\rightarrow t\bar{b}(\bar{t}b) b\bar{b}\rightarrow bbbb\ell^\pm \nu $ , and the leading SM backgrounds including● the virtual W process:
$ q\bar{q}'\rightarrow gW^{\pm\ast}\rightarrow t\bar{b}(\bar{t}b) b\bar{b} $ ,●
$ tb $ production:$ q\bar{q}'\rightarrow W^{\pm\ast}\rightarrow gt\bar{b}(\bar{t}b)\rightarrow t\bar{b}(\bar{t}b) b\bar{b} $ .As we require the CP-odd Higgs to decay into
$ b\bar{b} $ , this case still has the Jacobian peak at approximately$ p_{Tb}\sim M_{A^0}/2 $ . The missing transverse energy here is softer than that in$ H^\pm A^0\rightarrow \tau^\pm\nu b\bar{b} $ mode as the neutrino is from the subsequent decay of the top quark. Thus, we apply the following kinematic cuts in addition to the basic acceptance cuts described in Sec. 3 and 4.$ {\not\!\!{E}}_T>40 \ {\rm{GeV}}, \ p_T^{\rm{max}}(b)>M_{A^0}/2. $

(20) As the missing neutrino is only from W’s leptonic decay, using W’s mass and the missing transverse momentum
$ {\not\!\!{\vec{p}}}_T $ , one can arrive at a solution of the longitudinal momentum of the neutrino and this W boson can thus be reconstructed [49]. Because of the complexity from the four b-jets in our signal, when requiring the correct combination to reconstruct$ M_{H^\pm} $ and$ M_{A^0} $ , we assume and make use of the nearly-equal mass spectra of$ H^\pm $ and$ A^0 $ . The obtained invariant masses of$ tb $ and$ b\bar{b} $ are shown in Figs. 11(a) and (b), respectively. Next, we can take two mass windows near the resonances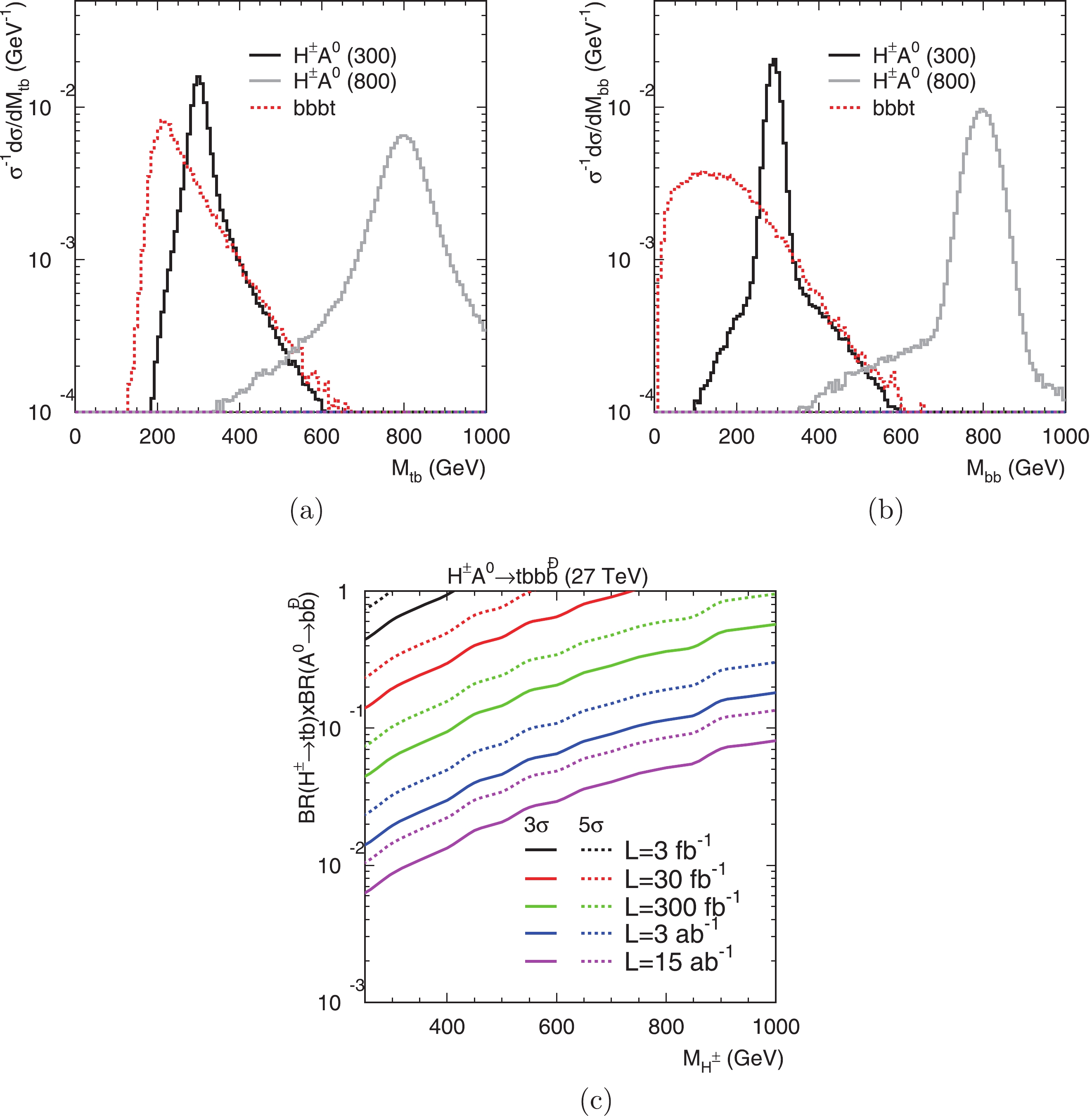
Figure 11. (color online) Top: The differential cross section distributions of
$M_{tb}$ (a) and$M_{bb}$ (b) for the signal$pp\to H^{\pm}A^{0}\to t\bar{b}(\bar{t}b) b\bar{b}\to bbbb\ell^\pm \nu$ and backgrounds at the 27 TeV LHC. Bottom: Reach of${\rm BR}(H^\pm\to tb)\times {\rm BR}(A^0\to b\bar{b})$ versus$M_{H^\pm}$ for$pp\to H^{\pm}A^{0}\to t\bar{b}(\bar{t}b) b\bar{b}\to bbbb\ell^\pm \nu$ , assuming$M_{A^0}=M_{H^\pm}$ .$ |M_{tb}-M_{H^\pm}|<M_{H^\pm}/10, \ \ |M_{bb}-M_{A^0}|<M_{A^0}/10. $

(21) The cut efficiencies are illustrated in Table 5.
cut efficiencies basic cuts $p_T^b$ 

${\not\!\!{E} }_T$ 

$M_{tb}$ 

$M_{bb}$ 

$H^\pm A^0 (300)$ 

0.34 0.33 0.25 0.16 0.14 $H^\pm A^0 (800)$ 

0.45 0.43 0.39 0.27 0.26 $bbbt$ (300)

0.032 0.016 0.012 0.0025 0.00048 $bbbt$ (800)

0.032 0.0024 0.0021 0.00011 $1.9\times 10^{-5}$ 

Table 5. The cut efficiencies for
$pp\to H^{\pm}A^{0}\to t\bar{b}(\bar{t}b) b\bar{b}\to bbbb\ell^\pm \nu$ and the SM backgrounds after consecutive cuts at the 27 TeV LHC. We take$M_{H^{\pm}}=M_{A^0}=300$ or 800 GeV.In our signal process, the only dependence is again the product of the decay branching fractions, which is
$ {\rm{BR}}(H^\pm\rightarrow tb)\times {\rm{BR}}(A^0\rightarrow b\bar{b}) $ here. As shown in Fig. 11(c), with the degenerate spectrum$ M_{A^0} = M_{H^\pm}\simeq 300 $ GeV and 15 ab$ ^{-1} $ luminosity, the reach of the branching fraction product extends low to the level of$ 10^{-2} $ . With$ {\rm{BR}}(H^\pm\rightarrow tb)\times {\rm{BR}}(A^0\rightarrow b\bar{b})$ = 10%, the heavy Higgs bosons with masses of 600 GeV and 900 GeV can be discovered with integrated luminosities of 3 ab$ ^{-1} $ and 15 ab$ ^{-1} $ , respectively. -
The first signal of
$ H^+H^- $ pair production consists of two tau leptons plus the missing energy$ H^+H^-\rightarrow \tau^+\tau^- \nu_\tau \bar{\nu}_\tau $ , followed by$ \tau^\pm\rightarrow \pi^\pm \nu $ . The irreducible SM backgrounds are from diboson productions$ W^+W^-\rightarrow \tau^+\nu_\tau\tau^-\bar{\nu}_\tau, \ ZZ\rightarrow \tau^+\tau^-\nu\bar{\nu}, $

(22) and the reducible contribution is
$ W^\pm Z\rightarrow \tau^+\tau^-\ell^\pm \nu_\ell, $

(23) which can also be vetoed by the requirement in Eq. (17).
The distributions of the signal and backgrounds at the 27 TeV LHC after the basic cuts are shown in Fig. 12 (a) missing transverse energy
${\not\!\!{E}}_T$ and (b) transverse pion momentum$ p_T(\pi) $ . One can see that the tau polarization effect mentioned above tends to be more dramatic in this channel (in comparison with the$ WW $ background). Thus, we strengthen the missing energy and$ p_T(\pi) $ as follows:
Figure 12. (color online) Top: The differential cross section distributions of
${\not\!\!{E}}_T$ (a) and$p_T(\pi)$ (b) for the signal$pp\to H^+H^-\to \tau^+\tau^- \nu_\tau \bar{\nu}_\tau$ and backgrounds at the 27 TeV LHC. Bottom: Reach of${\rm BR}(H^\pm\to \tau^\pm \nu)$ versus$M_{H^\pm}$ for$pp\to H^+H^-\to \tau^+\tau^- \nu_\tau \bar{\nu}_\tau$ .$ {\not\!\!{E}}_T> 100 \ {\rm{GeV}}, \ \ \ p_T^{\rm{max}}(\pi)> 100 \ {\rm{GeV}} . $

(24) The cut efficiencies are presented in Table 6. Due to the missing neutrinos from both the charged Higgs and the tau lepton in this channel, one is unable to reconstruct the charged Higgs boson or build a transverse mass to estimate the signal observability. The signal-to-background ratio is not expected to be improved as much as the associated production analyzed in Sec. 5.1. Figure 12(c) shows the reach of
$ {\rm{BR}}(H^\pm\rightarrow \tau^\pm \nu) $ versus$ M_{H^\pm} $ for$ pp\rightarrow H^+H^-\rightarrow \tau^+\tau^- \nu_\tau \bar{\nu}_\tau $ . One can see that this channel can access the decay branching fraction at 20% for the charged Higgs just above the top quark threshold with 15 ab$ ^{-1} $ luminosity.cut efficiencies basic cuts ${\not\!\!{E} }_T$ 

$p_T^\pi$ 

$H^+ H^- (300)$ 

0.7 0.49 0.46 $H^+ H^- (800)$ 

0.89 0.84 0.84 $WW$ 

0.024 0.00056 0.00056 $ZZ$ 

0.084 0.011 0.0052 $WZ$ 

0.0094 0.00062 0.00026 Table 6. The cut efficiencies for
$pp\to H^+H^-\to \tau^+\tau^- \nu_\tau \bar{\nu}_\tau$ and the SM backgrounds after consecutive cuts with$\tau^\pm\to \pi^\pm \overset{(-)}{\nu_\tau}$ channel at the 27 TeV LHC. We take$M_{H^{\pm}}=300$ or 800 GeV.Finally, we consider semi-leptonic channel
$ H^+H^-\rightarrow t\bar{b}\bar{t}b\rightarrow bbbbjj\ell^\pm\nu $ induced by$ H^\pm\rightarrow tb $ and the leading SM background$ b\bar{b}t\bar{t} $ . Using the methods mentioned in Sec. 5.2, the two charged Higgses can be fully reconstructed. The sensitivity of this search is limited by the efficiency of the top quark tagging due to smaller typical transverse momenta. Assuming BR$ (H^\pm \rightarrow tb) = 1 $ , we can accumulate 250 (9) signal events for$ M_{H^\pm} = 300 \ (800) $ GeV with 15 ab$ ^{-1} $ luminosity. To discover the charged Higgs with the mass of 300 GeV, one needs 50 ab$ ^{-1} $ luminosity. This mode is thus not promising for probing the charged Higgs.The existing searches for neutral Higgs pair productions
$ h^0 h^0, H^0 h^0, H^0 H^0 $ at the LHC are performed using gluon fusion with a top quark circulating in the loops and governed by Higgs trilinear couplings [58-65]. As there is no search for electroweak Higgs pair production at the LHC, we do not expect our study can be compared at this stage. We look forward to seeing dedicated searches in the near future. -
New Higgs bosons are present in many new physics models and their direct searches have yielded no signal observation in the LHC experiments so far. Thus, LHC upgrades with higher energy, such as the HE-LHC and FCC-hh, are motivated to carry out the search for heavy non-SM Higgs bosons.
In this paper, we investigate the discovery potential of the HE-LHC with 27 TeV C.M. energy for the heavy Higgses in Type-II 2HDM. To accommodate the theoretical bounds and experimental limits, we assume the degenerate Higgs spectrum
$ M_{H^0}\approx M_{A^0}\approx M_{H^\pm} $ and the parameter$ \cos(\beta-\alpha) $ near the alignment limit. We analyze the typical production and decay modes of non-SM Higgses and present the implications on the parameter space of Type-II 2HDM.We explore the observability of the heavy neutral Higgs bosons by examining the clean signals from
$ H^0\rightarrow W^+W^-, ZZ $ via gluon-gluon fusion production. With realistic decay branching fractions of$ H^0\rightarrow WW, ZZ $ channels for$ \tan\beta\sim 1 $ , the 27 TeV LHC can probe the neutral Higgs up to 1.5-2 TeV with the luminosity of 15 ab$ ^{-1} $ . For the charged Higgs bosons, we consider the inclusive process with the charged Higgs produced in association with a top quark that is$ gb\rightarrow t H^\pm $ . The final states with$ t H^\pm\rightarrow t\tau^\pm \nu $ prove to be a very sensitive channel for regions with large$ \tan\beta $ . For$ \tan\beta\sim 50 $ , the$ t\tau^\pm \nu $ channel can extend to reach$ M_{H^\pm}> 2 $ TeV with 15 ab$ ^{-1} $ luminosity. The region below$ \tan\beta\sim 1 $ can not be covered by$ 5\sigma $ discovery of$ H^\pm\rightarrow \tau^\pm \nu $ decay mode due to the suppression of the decay branching fraction.The electroweak productions of non-SM Higgs boson pairs provide complementary signals in the determination of the nature of the Higgs sector. They benefit from pure electroweak gauge interactions and are independent of additional model parameters except for Higgs masses. We explore the pair productions
$ H^\pm A^0 $ and$ H^+ H^- $ , followed by$ H^\pm \rightarrow \tau^\pm \nu, tb $ and$ A^0\rightarrow b\bar{b} $ decays. With$ {\rm{BR}}(H^\pm\rightarrow \tau^\pm \nu_\tau, tb)\times {\rm{BR}}(A^0\rightarrow b\bar{b}) = (10-20) $ %, the maximal discovery mass of degenerate heavy Higgs bosons is approximately$ 800-900 $ GeV with an integrated luminosity of 15 ab$ ^{-1} $ . The$ pp\rightarrow H^+ H^- $ production is not promising for probing the charged Higgs. The$ pp\rightarrow H^+H^-\rightarrow \tau^+\tau^-\nu\bar{\nu} $ channel can access the decay branching fraction$ {\rm{BR}}(H^\pm\rightarrow \tau^\pm \nu_\tau) $ to be 20% for the light charged Higgs with 15 ab$ ^{-1} $ luminosity.The discovery of heavy non-SM Higgs bosons would certainly be unambiguous evidence for new physics beyond the SM. Once those non-SM Higgses are discovered, kinematic reconstruction would provide important information about their mass spectrum. A cross check with the indirect flavor and precision constraints would be complementary and lead to new clues regarding new physics beyond the SM.
We would like to thank Tao Han for collaboration at the early stage of this project and valuable discussions.
Heavy Higgs bosons at the LHC upgrade
- Received Date: 2020-01-16
- Accepted Date: 2020-05-15
- Available Online: 2020-09-01
Abstract: We evaluate the discovery potential for the heavy Higgs bosons at the LHC energy upgrade with






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: