-
The accurate description of the elastic scattering is sensitive to the structure of the nuclei involved as well as to the nuclear potential [1-4]. In this way, the elastic scattering process comprises an essential part of the overall understanding of heavy-ion reaction dynamics that depend on the structure of the colliding nuclei. Therefore, the elastic scattering of the heavy-ion system is of pronounced importance as it provides information about the interaction potential, and measures the reflection of the flux as it reaches the region of the interaction. It is often described by optical model calculations with an optical model potential (OMP) having some adjustable parameters. Most reaction theories require the knowledge of the OMP derived from the elastic scattering angular distribution of the colliding nuclei involved or from more fundamental criteria, like double folding potentials.
The OMP can be used to estimate the cross sections of nuclear reactions; not only elastic scattering but also the other nuclear reactions such as breakup, transfer, and fusion, etc [5-7]. The interaction potential consists of nuclear and Coulomb potentials. The imaginary part of the nuclear potential represents the absorption from the elastic channel to other reaction channels, such as inelastic scattering, re-arrangement reactions, breakup channels (when weakly bound nuclei are involved), etc. The Coulomb potential between projectile and target nuclei is well known. The nuclear potential is often parameterized based on the optical potential. The potential parameters, which are related to the nuclear structure, can be extracted by fitting the elastic scattering angular distributions. Many kinds of studies have focused on the optical potential in heavy-ion physics for many years [8-17]. However, large ambiguities always existed for the optical potential parameters. Many studies devoted to deriving optical potentials have been performed in recent years, and several achievements were realized. Chamon et al. derived a global description of the nucleus-nucleus interactions within the double-folding model named the São Paulo potential (SPP), which can be successfully used for stable and unstable nuclei [18]. Xu et al. proposed a global single folding potential based on the elastic scattering angular distributions of
$ ^{6,7} $ Li on target nuclei with masses larger than 40 for energies ranging from 5 to 40 MeV/u [19]. Wang et al. obtained an energy independent Woods-Saxon potential at energies much higher than the Coulomb barrier [20]. Gan et al. selected several elastic scattering angular distributions of$ ^{12} $ C from target nuclei of A$ \geqslant $ 39 to extract the Woods-Saxon potential parameters [21]. The derived potential was able to reproduce many elastic scattering angular distributions induced not only by$ ^{12} $ C but also by other projectiles. In our work, we considered the double folding São Paulo potential [18], which has an energy dependence, as the nuclear potential.In collisions of typical strongly bound nuclei besides the elastic scattering, other relevant reaction channels, such as the inelastic scattering of projectile and target nuclei, are also accompanied. Therefore, the analysis of the elastic scattering, together with other relevant reaction channels, can be treated in the coupled channel (CC) method. The CC method is the most powerful tool to study multichannel scattering [22]. In this paper, the CC method is used to analyze the elastic scattering of
$ ^{12,13} $ C on zirconium isotopes.For stable Zr isotopes, the neutron numbers are at or close to the magic number of 50. Their neutron capture cross sections are relatively low [23, 24] and very scarce. In nuclear astrophysics, Zr isotopes occupy the intersection of the weak and main s-process, and the neutron capture reactions by Zr isotopes are particularly significant [25]. For this reason, researches focused on them have attracted great attention. The valuable information about the astrophysical medium, including the neutron flux density and temperature, can be extracted from the abundances of the Zr isotopes. Therefore, the neutron capture reaction rates of Zr isotopes should be determined with high accuracy. For example, in
$ ^{89} $ Zr(n,$ \gamma $ )$ ^{90} $ Zr, the direct neutron capture reaction rate contributes about 13% of the total reaction rate, which is much larger than the required accuracy of 5%. For the$ ^{93} $ Zr(n,$ \gamma $ )$ ^{94} $ Zr reaction rates, an accuracy of 3%-5% is required [25]. From the evaluated data of the National Nuclear Data Center, the direct neutron capture reaction rate contributes about 10% to the total reaction rates. For this reason, it is meaningful to accurately study the direct components of neutron capture reaction with various experiments. The spectroscopic factor can be used to estimate the direct component of the (n,$ \gamma $ ) cross section. The values of the spectroscopic factor can be obtained by comparing the experimental cross sections with the predicted ones from reaction models. Experimental measurements of the neutron spectroscopic factors about Zr isotopes have been done for several decades [26-28]. However, the published spectroscopic factors have large differences with one another, especially for$ ^{90} $ Zr. The published neutron spectroscopic factors vary from 3.4-10.0 for$ ^{90} $ Zr. Such a large difference may cause more than 20% uncertainty to the total reaction rate of$ ^{89} $ Zr(n,$ \gamma $ )$ ^{90} $ Zr. The main shortcoming of the previous studies is the large experimental errors [29, 30] and the neglect of the influence of optical potentials, which gives large uncertainties to the spectroscopic factors. To improve these defects, a more accurate experiment should be carried out. In this study,$ ^{12,13} $ C +$ ^A {\rm{Zr}}$ reaction systems were selected since$ ^{12} $ C is a typical stable nucleus, and the$ ^{12} $ C heavy-ion beam can be easily obtained and tuned with the accelerator. For the$ ^{13} $ C beam, it is used to extract the optical potentials of exit channels for the one-neutron transfer reaction of$ ^{12} $ C + Zr isotopes. For Zr isotopes, some unstable isotopes such as$ ^{89} $ Zr (t$ _{1/2} $ = 3.3 d),$ ^{93} $ Zr (t$ _{1/2} $ = 1.5$ \times 10^6 $ y), and$ ^{95} $ Zr (t$ _{1/2} $ = 64.0 d) exist. These Zr isotopes are not available as reaction targets. Thus, in the experiment using$ ^{13} $ C +$ ^{90,92,94,96} $ Zr reactions can be complemented with$ ^{13} $ C +$ ^{89,93,95} $ Zr to extract the OMP of the exit channels.This paper is organized as follows. In Sec. 2, we describe the experimental apparatus. In Sec. 3, we compare the experimental angular distributions with OMP and CC calculations. In Sec. 4, we study the influence of one-neutron stripping on the
$ ^{13} $ C+$ ^{90,91,92,94,96} $ Zr systems on the elastic scattering. The conclusions are presented in Sec. 5. -
The experiment was performed at the HI-13 Tandem accelerator at the China Institute of Atomic Energy (CIAE), Beijing, with the Q3D magnetic spectrometer. The Q3D magnetic spectrometer has a high-energy resolution of approximately 0.02%, and the angular distributions of elastic scattering can be measured with high precision. The beams of
$ ^{12} $ C at 66.0 MeV and$ ^{13} $ C at 64.0 MeV from the accelerator impinged on the carbon-supported zirconium enriched isotope targets of$ ^{90,91,92,94,96} $ ZrO$ _2 $ . The abundance of Zr isotopes in$ ^{90,91,92,94,96} $ ZrO$ _2 $ is shown in Table 1. The thicknesses of the$ ^{90,91,92,94,96} $ ZrO$ _2 $ targets were (32.9$ \pm $ 2.5), (27.3$ \pm $ 1.6), (30.0$ \pm $ 2.2), (41.0$ \pm $ 2.9), (34.4$ \pm $ 2.3) μg/cm$ ^2 $ , respectively, which were calibrated by normalizing the elastic scattering cross sections at forward angles to Rutherford's scattering cross sections.target names $^{90}$ Zr

$^{91}$ Zr

$^{92}$ Zr

$^{94}$ Zr

$^{96}$ Zr

$^{90}$ ZrO

$_2$ 

99.4 3.24 0.97 0.7 7.19 $^{91}$ ZrO

$_2$ 

0.3 94.59 0.51 0.2 1.46 $^{92}$ ZrO

$_2$ 

0.2 1.63 98.06 0.4 2.31 $^{94}$ ZrO

$_2$ 

0.1 0.46 0.41 98.6 0.89 $^{96}$ ZrO

$_2$ 

0.04 0.08 0.05 0.1 85.15 Table 1. Isotopic compositions of targets (%).
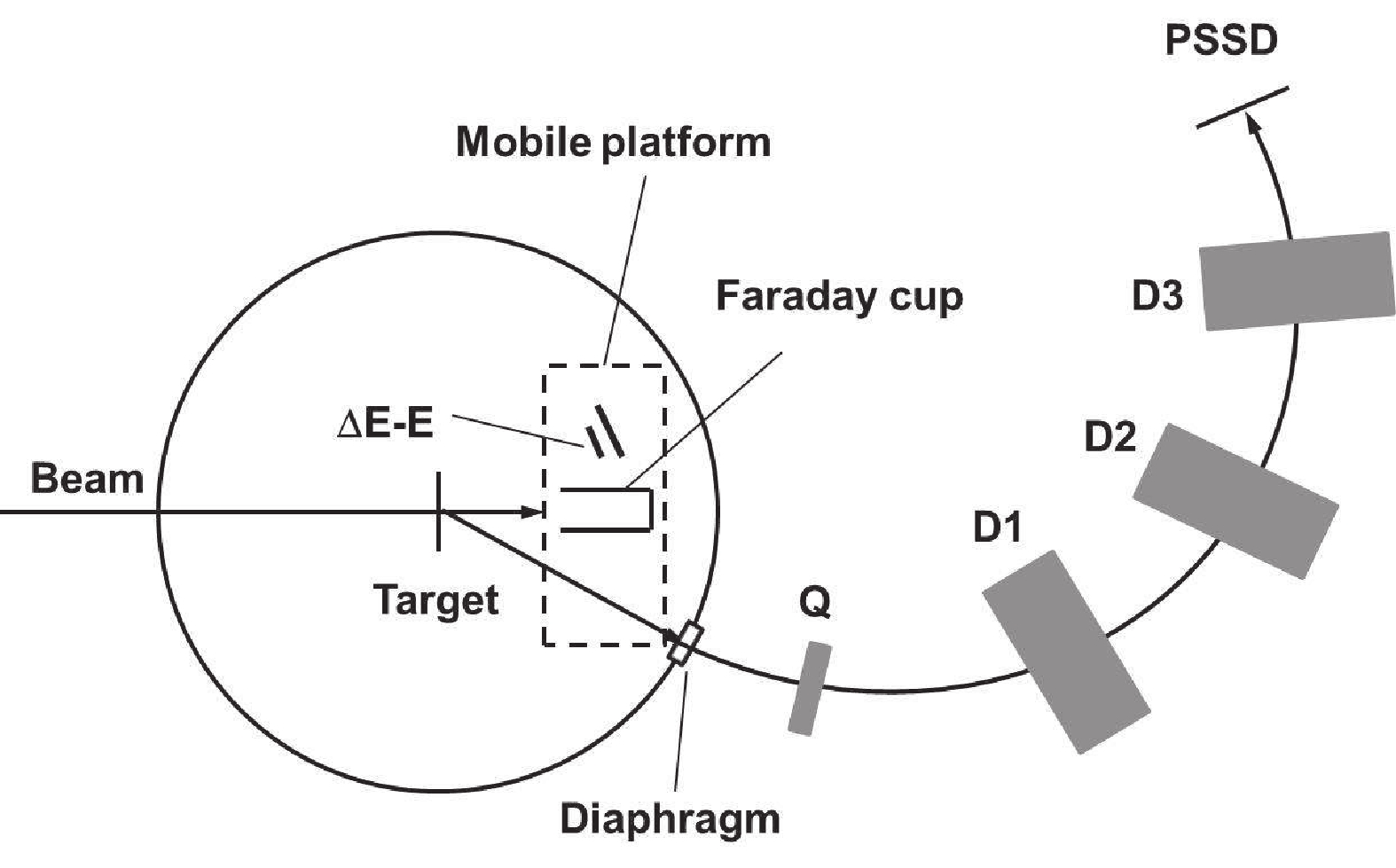
The experimental setup is shown in Fig. 1. The diameter of the target chamber was 479 mm. To provide a better angular resolution, a collimator with a diameter of 5 mm was put at the entrance (located at the diaphragm position of Fig. 1) of the Q3D magnetic spectrometer to certify the angular resolution of differential cross section better than 0.4
$ ^\circ $ . Accordingly, the solid angle acceptance of the Q3D magnetic spectrometer was set to be 0.34$ \pm $ 0.01 msr for excellent angular resolution. The targets were placed at the the center of the target chamber upstream of the Q3D magnetic spectrometer. A movable Faraday cup was placed behind the target to monitor the beam intensity, which was used for the absolute normalization of the reaction cross sections. A$ \Delta $ E-E detector telescopic system was set at approximately 23$ ^\circ $ downstream of the reaction targets for the cross-check of the beam intensity. The reaction products were separated by Q3D and then measured by a 50 mm$ \times $ 50 mm two-dimensional position-sensitive silicon detector (PSSD) at the focal plane. The PSSD consists of 16 strips at the horizontal and perpendicular directions, respectively. The width of each strip is 3 mm. In this experiment, we only focus on the horizontal position and do not consider the vertical position. The high momentum resolution of Q3D (the momentum dispersion is 0.025 mm/% at the final focal plane) and the position-energy information from PSSD enables us to identify the specific ions from other reaction channels since the horizontal position of PSSD reflects the radius/momentum of deflected ions in the magnetic spectrometer. i.e. the magnetic rigidity.The typical two-dimensional spectrum of kinetic energy versus the horizontal position for the
$ ^{96} $ Zr($ ^{12} $ C,$ ^{12} $ C)$ ^{96} $ Zr reaction at 26$ ^\circ $ is shown in Fig. 2(a). It can be seen that the object ions (the$ ^{12} $ C in this case) from the reactions can be clearly identified via the energy and position information. Thus, the number of object ions can be counted accurately through the position spectrum of object ions, as shown in Fig. 2(b). In Fig. 2(b), the width of the spectrum is determined by the set momentum range of Q3D. The position width is mainly related to three parameters: the energy spread of scattered ions, the characteristics of the magnetic spectrometer, and the position resolution of the PSSD. In the whole experiment, these three parameters were almost kept unchanged. Therefore, the position width was practically not changed. Through rotating the Q3D magnetic spectrometer, the angular distributions of elastic scattering of$ ^{12,13} $ C+Zr were measured in the range of 0$ ^\circ $ - 60$ ^\circ $ . The ratios of the experimentally obtained differential elastic scattering cross sections to Rutherford's differential cross sections with the change of angles are shown in Figs. 3 and 4 by circles for the reactions induced by$ ^{12} $ C and$ ^{13} $ C, respectively. The experimental errors mainly stem from the statistical error (3%) and the uncertainty of the target thickness (5%).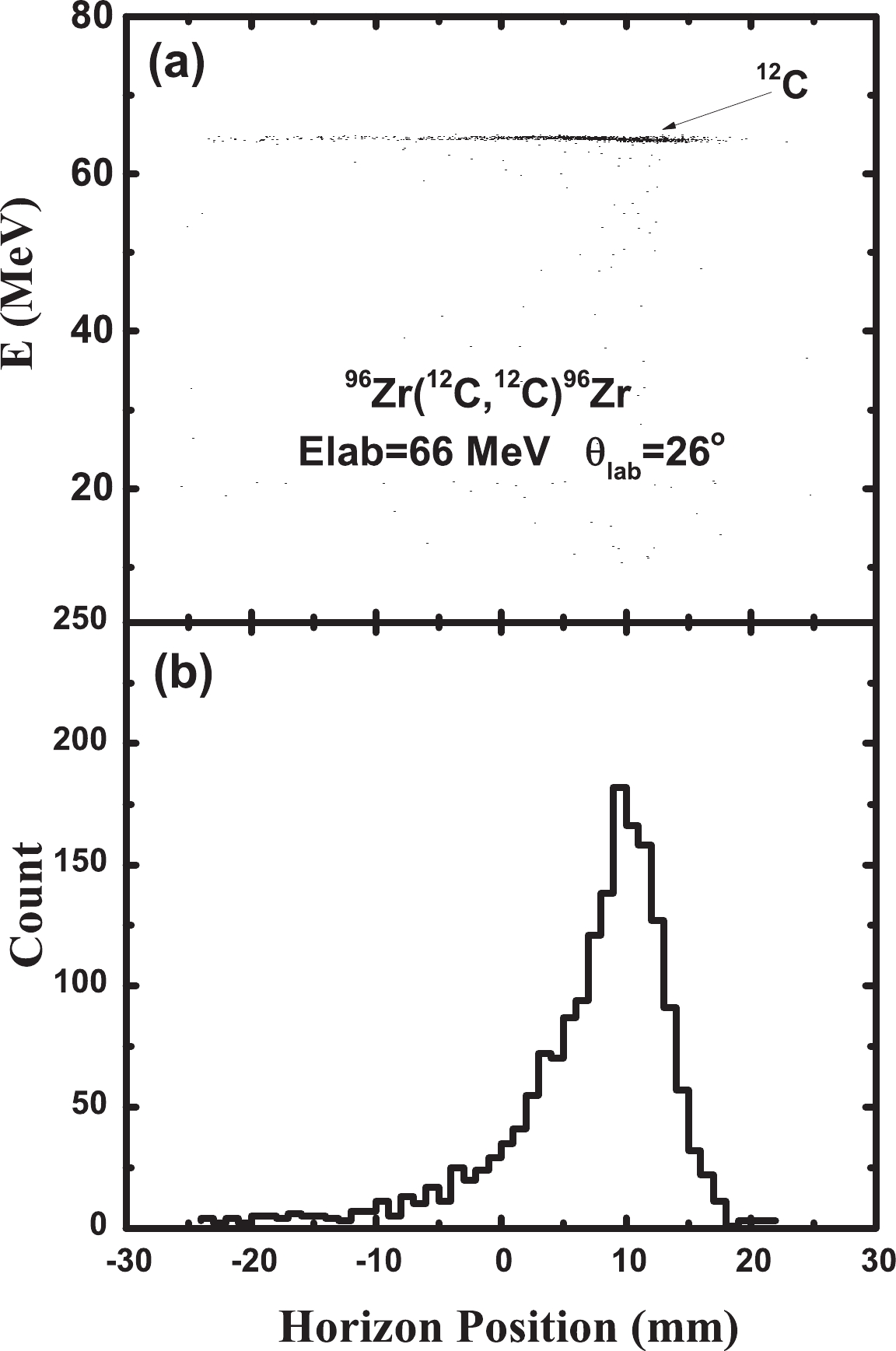
Figure 2. (a) The two-dimensional spectrum of kinetic energy versus the horizontal position and (b) the horizontal position spectrum of object ions for
$^{96}$ Zr($^{12}$ C,$^{12}$ C)$^{96}$ Zr at 26$^\circ$ . -
Different kinds of calculations can be performed to derive the elastic scattering angular distributions, depending on the goal of these calculations and the nuclei involved in the collision. Among these calculations, we employed the OMP calculation, usually devoted to determine the energy dependence of the optical potential and to derive the reaction cross sections, and the coupled channel calculations. The previous method is commonly applied to study the effect of channel couplings on elastic scattering, fusion, etc. Both methods solve a Shrödinger equation or the system of equations with specific boundary conditions that allow determining different observables. To describe the system of colliding nuclei, one must postulate a Hamiltonian that includes an optical potential (or potentials in the case of nuclei with cluster or halo structures that have low break up thresholds). The São Paulo potential (SPP) [18], which is a double folding potential with systematics for the matter density of the interacting nuclei, has been commonly used for the optical potential. As we are using the SPP in this work, some brief details about this potential will be given below.
The nuclear interaction part of the double folding potential is given by the following expression:
$ V_{\rm F}(R) = V_0 \int{\rho_1 (r_1)\rho_2 (r_2) \delta ({{R}} -{{{r}}_{{1}}}+ {{{r}}_{{2}}}){\rm d} {{{r}}_{{1}}}{\rm d} {{{r}}_{{2}}}}, $

(1) where
$ V_0 $ = − 456 MeV fm$ ^3 $ and$ \rho_i(r_i) $ ($ i = 1 $ − projectile and 2-target, respectively) is the matter densities. In the zero-range approach, where the range of the effective nucleon-nucleon interaction is negligible in comparison with the diffuseness of the nuclear densities, the usual M3Y [31] nucleon-nucleon interaction becomes$ V_0 \delta ({{R}} - {{{r}}_{\bf{1}}}+ {{{r}}_{\bf{2}}}) $ , where$ {{{r}}_{{i}}} $ is the coordinates of the nucleons inside the nuclei, and$ {{R}} $ is the vector joining the center of mass of the two interacting nuclei. The SPP accounts for the Pauli non-locality, which arises from quantum exchange effects; its local equivalent form is given by the following expression:$ V_{\rm LE}^{\rm SPP}(E,R) = V_{\rm F} (R) {\rm e}^{(-4v^2/c^2)}, $

(2) where
$ V_{\rm F}(R) $ is the double-folding potential of Eq. (1), c stands for the speed of light, and v is the local projectile-target relative velocity obtained from$ v^2(R,E) = \frac{2}{\mu}[E-V_{\rm C}(R)-V_{\rm LE}(R,E)], $

(3) where,
$ V_{\rm C} $ is the Coulomb potential. Many studies using the SPP as the optical potential to derive the elastic scattering to study its energy dependence and to calculate direct reaction cross sections have been reported (see for examples Refs. [4, 22, 32-37]).To describe the scattering cross sections for the
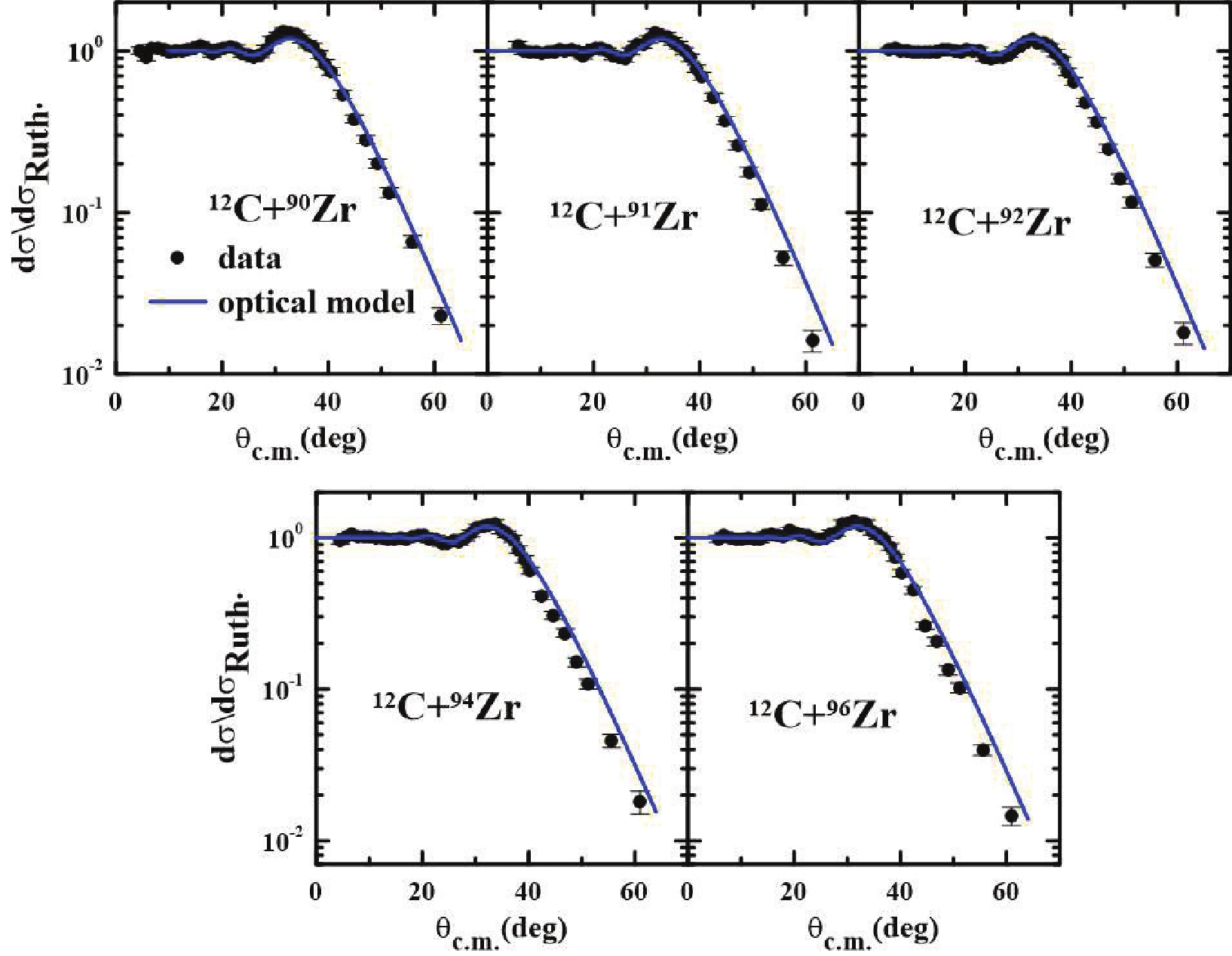
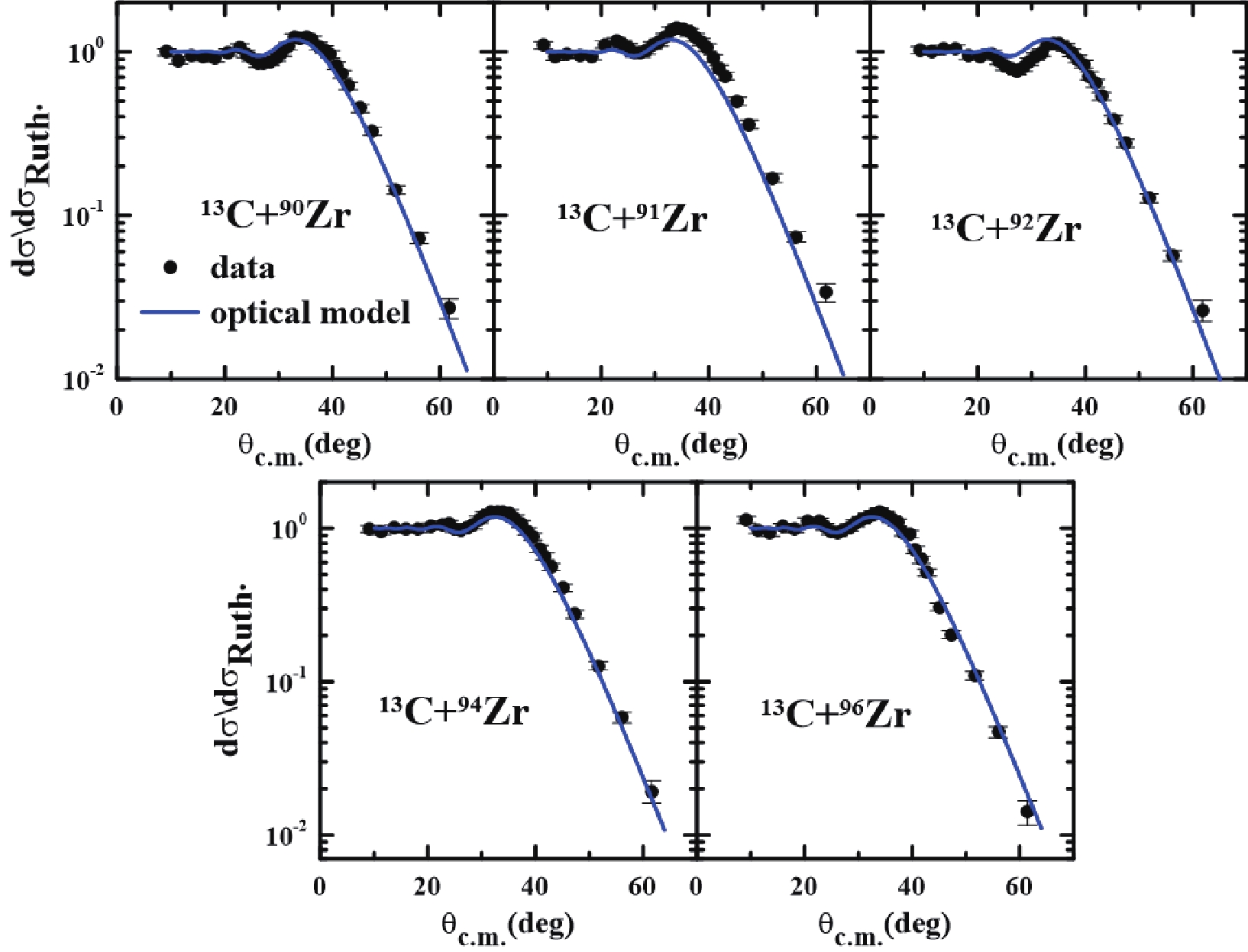
$ ^{12} $ C+$ ^{A} $ Zr at 66 MeV and$ ^{13} $ C+$ ^{A} $ Zr at 64 MeV with$ A = 90, 91, 92, 94 $ and$ 96 $ , we first performed optical model calculations considering only the ground state of each nucleus. The double-folding SPP was used in the optical potential in both the real and imaginary parts$ [U = (N_{\rm R} + {\rm i} N_{\rm I})V_{\rm SPP}] $ with$ N_{\rm R} = 1.0 $ and$ N_{\rm I} = 0.78 $ . These strength factors for the real and imaginary parts were adopted because we are not considering any coupling to the ground states. Many systems have had the elastic cross section well described by this value of the strength coefficients in a wide energy interval by means of optical model calculations [38]. The conclusion achieved in the mentioned paper was that these systematics are valid when there is no strong coupling of any relevant channel to the elastic scattering.Optical model calculations are important for understanding whenever there are strong couplings to the elastic scattering. Thus, to highlight dynamic effects such as strong couplings or static effects like cluster structures, we used the SPP at energies close to the barrier since this potential (in principle) does not take these effects into account in its systematics. Therefore, if the results do not describe the elastic experimental data, this means there are some relevant dynamic or static effects not included in the one-channel or optical model calculation. On the contrary, if the one-channel calculation describes the elastic scattering angular distributions, there are no important couplings to the elastic channel left out in the calculation, or there are polarizations of different signs that cancel each other. In Figs. 3 and 4, the comparison between the optical model calculations and the experimental data for
$ ^{12,13} $ C+$ ^{90,91,92,94,96} $ Zr elastic scattering is shown. One can see that the theoretical results have good agreement with the experimental data. However, when the projectile is$ ^{12} $ C (see Fig. 3), the theoretical results are slightly above the experimental data, which means there are some couplings with the elastic channels not included in the calculations. For the projectile$ ^{13} $ C (see Fig. 4), the results are slightly below the data when the target is$ ^{91} $ Zr.To explain this small difference between the experimental data and the theoretical elastic scattering, we performed CC calculations, including the inelastic states of the projectile and target, using the FRESCO code [39]. In Table 2, the states included in the coupling scheme are shown. To describe the transitions between the target and projectile states, a model-independent procedure to account for the Coulomb and nuclear deformations was used, and the electromagnetic transition B(E2) for
$ ^{91} $ Zr and B(E1) for$ ^{13} $ C were taken from Ref. [40]. The quadrupole ($ \beta_2 $ ) and octupole ($ \beta_3 $ ) deformation parameters to couple$ ^{13} $ C states were assumed to be equal to the ones reported for$ ^{12} $ C in Refs. [41] and [42], respectively. For the$ ^{90,92,94,96} $ Zr isotopes, a vibrational model was used, and the deformation parameters$ \beta_2 $ and$ \beta_3 $ were also taken from Refs. [41] and [42]. The values of deformation parameters are shown in Table 3. The Coulomb and nuclear deformations were considered to have the same values, as long as no statistic effect in matter distributions was expected for these nuclei. The transition form-factors were taken as derivatives of the monopole term, following the usual convention.nucleus $J^{\pi}$ 

energy/MeV $^{12}$ C

0 $^{+}$ 

0.0 2 $^{+}$ 

4.440 $^{13}$ C

1/2 $^{-}$ 

0.0 1/2 $^{+}$ 

3.089 3/2 $^{-}$ 

3.684 5/2 $^{+}$ 

3.854 $^{90}$ Zr

0 $^{+}$ 

0.0 2 $^{+}$ 

2.186 $^{91}$ Zr

5/2 $^{+}$ 

0.0 1/2 $^{+}$ 

1.205 5/2 $^{+}$ 

1.466 7/2 $^{+}$ 

1.882 3/2 $^{+}$ 

2.042 9/2 $^{+}$ 

2.131 $^{92}$ Zr

0 $^{+}$ 

0.0 2 $^{+}$ 

0.934 0 $^{+}$ 

1.383 4 $^{+}$ 

1.495 2 $^{+}$ 

1.847 $^{94}$ Zr

0 $^{+}$ 

0.0 2 $^{+}$ 

0.919 0 $^{+}$ 

1.300 4 $^{+}$ 

1.450 2 $^{+}$ 

1.671 $^{96}$ Zr

0 $^{+}$ 

0.0 2 $^{+}$ 

1.750 Table 2. Projectile and target states considered in the coupling scheme.
nucleus $\beta_2$ 

$\beta_3$ 

$^{12}$ C

0.582 — $^{13}$ C

0.582 0.44 $^{90}$ Zr

0.0894 — $^{92}$ Zr

0.1027 0.18 $^{94}$ Zr

0.090 — $^{96}$ Zr

0.080 0.27 nucleus $I'\rightarrow I$ 

B(E1) /w.u $^{13}$ C

$1/2+ \rightarrow 1/2-$ 

0.039 (4) B(E2) /w.u. $^{91}$ Zr

$1/2+ \rightarrow 5/2+$ 

15 (4) $5/2+ \rightarrow 5/2+$ 

10.7 (10) $7/2+ \rightarrow 5/2+$ 

7.7 (13) $3/2+ \rightarrow 5/2+$ 

59 (6) $9/2+ \rightarrow 5/2+$ 

4.2(6) The deformation parameters are related to the reduced electromagnetic transition probabilities by
$ \beta_{\lambda} = \dfrac{4\pi}{3ZR^{\lambda}}\dfrac{\sqrt{B(E\lambda,I\rightarrow I')}}{(-1)^{(I-I'+|I-I'|)/2}<IK\lambda0|I'K>}, $

(4) where Z is the nuclear charge,
$ R = r_0 A^{1/3} $ , A is the mass number, and$ r_0 = $ 1.06 fm is the reduced radius.$ \lambda $ stands for the multipolarity of the transition. I and$ I' $ are the spins of initial and final states, respectively, and K is their projection in the quantization axis. For the real part of the optical potential, the SPP was used along with a short-range potential in the imaginary part, which had the Woods-Saxon [43] form with$ W = 50 $ MeV,$ r_i = 1.06 $ fm, and$ a_i = 0.2 $ fm for the depth, reduced radius, and diffuseness, respectively. This short-range potential is important for accounting for the absorption of flux due to fusion because this process cannot be explicitly included in the calculations.The comparisons between the CC calculations and the experimental data for the
$ ^{12} $ C+$ ^{A} $ Zr systems are shown in Fig. 5. In this figure, the solid blue line stands for no coupling calculation, in which only the ground state of each nucleus is considered. The dashed green line represents the results when only couplings to the inelastic states of the projectile were considered. In the calculations, represented by the dashed dot red curve, we included only the inelastic states of the target in the coupling scheme. The dotted line is the full CC calculation, in which all couplings with inelastic states of the projectile and target were considered.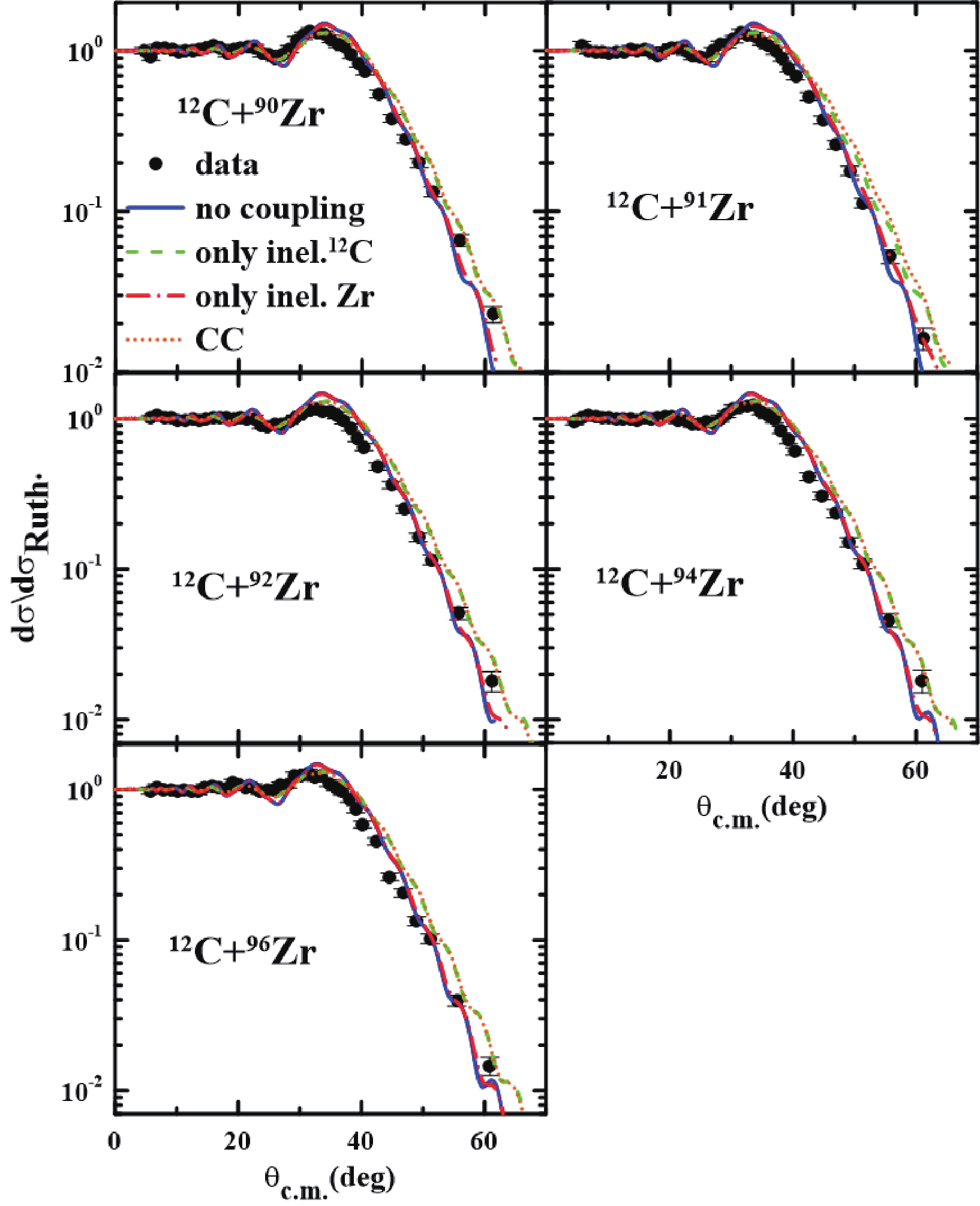
Figure 5. (color online) Comparison between CC calculations and elastic scattering data for
$^{12}$ C+$^{A} {\rm{Zr}}$ reactions at 66 MeV.One can note that the couplings with the inelastic states of the target (
$ ^{A} $ Zr - dashed red dot curve) do not have a significant influence on the elastic cross section. The coupling with the first excited state of$ ^{12} $ C or the full CC calculation has led to the results that slightly overestimate the angular distributions at backward angles.Similar CC calculations were performed for the reactions induced by
$ ^{13} $ C (see Fig. 6). Similar to the$ ^{12} $ C case, a good agreement of angular distributions is observed when the couplings to inelastic states of the projectile were included in the calculations (dashed green line).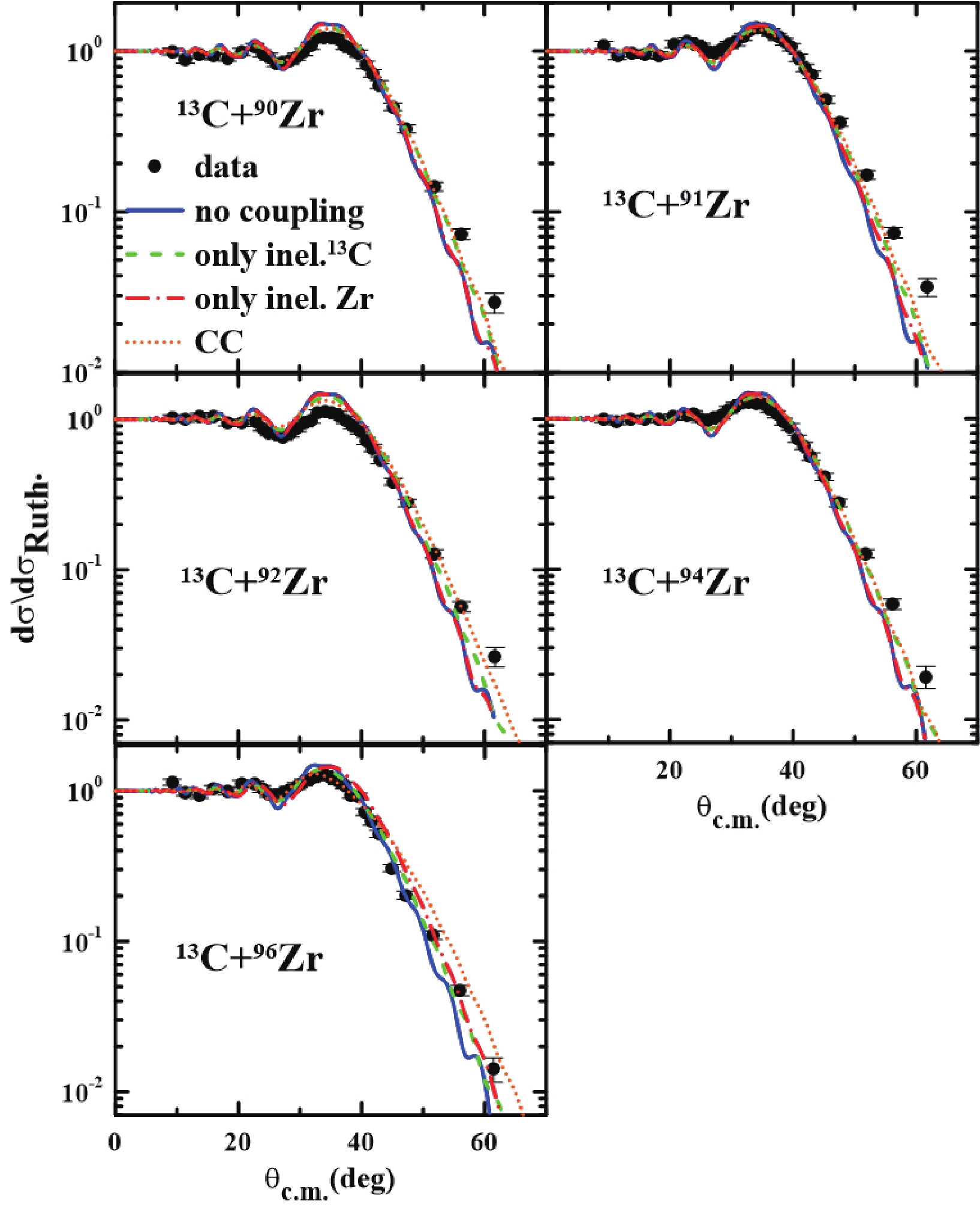
Figure 6. (color online) Comparison between CC calculations and elastic scattering data for
$^{13}$ C+$^{A} {\rm{Zr}}$ reactions at 64 MeV.Nevertheless, the full CC calculation underestimates the angular distribution from approximately 55
$ ^{\circ} $ for most of the systems. This might be an indication that there could be missing couplings, like the one-neutron transfer. -
To determine whether there were some missing couplings left out in the CC calculations, we performed finite-range Coupled Reaction Channel (CRC) calculations for the one-neutron transfer for some reactions involving the
$ ^{13} $ C+$ ^{A} $ Zr systems that have positive Q$ _{\rm value} $ (see Table 4). For the optical potential in the entrance partitions, the same potentials used in the CC calculations were used in the real and imaginary parts. In the final partitions, the SPP was used in both real and imaginary parts. Again, the imaginary part was multiplied for a coefficient$ N_{\rm I} = 0.78 $ because no couplings were considered. The single-particle wave functions were obtained using Woods-Saxon potentials with diffuseness and a reduced radius equal to 0.65 and 1.25 fm, respectively, for the target and projectile. The depths of the Woods-Saxon potentials were varied to fit the experimental one-neutron binding energy.reaction Q $_{\rm value} /{\rm MeV}$ 

$^{90}$ Zr(

$^{13}$ C,

$^{12}$ C)

$^{91}$ Zr

2.248 $^{91}$ Zr(

$^{13}$ C,

$^{12}$ C)

$^{92}$ Zr

3.688 $^{92}$ Zr(

$^{13}$ C,

$^{12}$ C)

$^{93}$ Zr

1.788 $^{94}$ Zr(

$^{13}$ C,

$^{12}$ C)

$^{95}$ Zr

1.516 $^{96}$ Zr(

$^{13}$ C,

$^{12}$ C)

$^{97}$ Zr

0.629 Table 4. Q
$_{value}$ for the one-neutron stripping transfer reaction for the$^{13}$ C+$^{A} {\rm{Zr}}$ systems.Shell-model calculations were performed to derive the spectroscopic amplitudes for the projectile and target overlaps, using the NuShellX code [44]. For the projectile overlaps, the psdpn model space and the psdmod effective phenomenological interaction [45] were used. This model space assumes the
$ ^4 $ He as a closed core with 1p$ _{3/2} $ , 1p$ _{1/2} $ , 1d$ _{3/2} $ , 1d$ _{5/2} $ , and 2s$ _{1/2} $ orbitals as valence orbitals for protons and neutrons. For most of the target overlaps, the glekpn model space and effective phenomenological interaction of the same name [46] were used. This model space uses 1f$ _{7/2} $ , 1f$ _{5/2} $ , 2p$ _{3/2} $ , 2p$ _{1/2} $ , and 1g$ _{9/2} $ as valence orbitals for protons and 1g$ _{9/2} $ , 1g$ _{7/2} $ , 2d$ _{5/2} $ , 2d$ _{3/2} $ ,and 3s$ _{1/2} $ for neutrons. Owing to our computational limitations to perform shell-model calculations using that large valence space, it was necessary to introduce some constraints to generate the spectroscopic amplitude. For this, the$ ^{86} $ Sr nucleus was considered to be a closed core, and the number of protons in the higher 2p$ _{1/2} $ and 1g$ _{9/2} $ orbitals was reduced. For neutrons, the 2d$ _{3/2} $ and 3s$ _{1/2} $ orbitals were also restricted. For the$ ^{96,97} $ Zr nuclei, this model space and interaction was not able to describe their structure characteristics (eigenvalues, spins, and parities). Thus, it was necessary to use the glepn [46] model space and interaction. This model space uses 2p$ _{3/2} $ , 1f$ _{5/2} $ , 2p$ _{1/2} $ , 1g$ _{9/2} $ , 3s$ _{1/2} $ , 2d$ _{5/2} $ and 2d$ _{3/2} $ as valence orbitals for protons and 2p$ _{3/2} $ , 1f$ _{5/2} $ ,2p$ _{1/2} $ , 1g$ _{9/2} $ , 3s$ _{1/2} $ , 2d$ _{5/2} $ , and 2d$ _{3/2} $ for neutrons. The same closed core ($ ^{86} $ Sr) considered in the previous calculations was used here, and the number of protons in the higher 1g$ _{9/2} $ orbitals was reduced and 2d$ _{5/2} $ and 2d$ _{3/2} $ were closed for protons. The overlap schemes for the projectile and target are shown in Figs. 7 and 8, respectively. The spectroscopic amplitudes for the projectile and target overlaps are given in Tables 5, 6, 7, 8, 9, and 10.initial state final state nlj spect. ampl. $^{13}$ C

$_{g.s}(1/2^-)$ 

$^{12}$ C

$_{g.s}(0^+)$ 

$1p_{1/2}$ 

−0.8009 $^{12}$ C

$_{4.439}(2^+)$ 

$1p_{3/2}$ 

0.9946 $^{13}$ C

$_{3.098}(1/2^+)$ 

$^{12}$ C

$_{g.s}(0^+)$ 

$2s_{1/2}$ 

0.8983 $^{12}$ C

$_{4.439}(2^+)$ 

$1d_{3/2}$ 

−0.0385 $1d_{5/2}$ 

0.3118 $^{13}$ C

$_{3.684}(3/2^-)$ 

$^{12}$ C

$_{g.s}(0^+)$ 

$1p_{3/2}$ 

−0.3617 $^{12}$ C

$_{4.439}(2^+)$ 

$1p_{1/2}$ 

−0.8194 $1d_{3/2}$ 

0.5415 $^{13}$ C

$_{3.854}(5/2^+)$ 

$^{12}$ C

$_{g.s}(0^+)$ 

$1d_{5/2}$ 

0.9108 $^{12}$ C

$_{4.439}(2^+)$ 

$2s_{1/2}$ 

0.1130 $1d_{3/2}$ 

−0.0586 $1d_{5/2}$ 

0.1965 Table 5. Spectroscopic amplitudes used in the CRC calculations for the one-neutron transfer using the psdpn model space with the psdmod effective phenomenological interaction for projectile overlaps. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.
initial state final state nlj spect. ampl. $^{90}$ Zr

$_{g.s}(0^+)$ 

$^{91}$ Zr

$_{g.s}(5/2^+)$ 

$2d_{5/2}$ 

−0.9872 $^{91}$ Zr

$_{1.205}(1/2^+)$ 

$3s_{1/2}$ 

−0.9158 $^{91}$ Zr

$_{1.466}(5/2^+)$ 

$2d_{5/2}$ 

0.0407 $^{91}$ Zr

$_{1.882}(7/2^+)$ 

$1g_{7/2}$ 

0.1135 $^{91}$ Zr

$_{2.042}(3/2^+)$ 

$2d_{3/2}$ 

0.9650 $^{91}$ Zr

$_{2.131}(9/2^+)$ 

$1g_{9/2}$ 

0.0007 $^{90}$ Zr

$_{2.186}(2^+)$ 

$^{91}$ Zr

$_{g.s.}(5/2^+)$ 

$3s_{1/2}$ 

−0.0095 $2d_{3/2}$ 

0.0141 $2d_{5/2}$ 

−0.0761 $1g_{7/2}$ 

0.0107 $1g_{9/2}$ 

0.0101 $^{91}$ Zr

$_{1.205}(1/2^+)$ 

$2d_{3/2}$ 

0.0850 $2d_{5/2}$ 

0.7814 $^{91}$ Zr

$_{1.466}(5/2^+)$ 

$3s_{1/2}$ 

0.0021 $2d_{3/2}$ 

0.0545 $2d_{5/2}$ 

−0.5699 $1g_{7/2}$ 

0.0564 $1g_{9/2}$ 

0.0017 $^{91}$ Zr

$_{1.882}(7/2^+)$ 

$2d_{3/2}$ 

−0.0583 $2d_{5/2}$ 

0.9029 $1g_{7/2}$ 

0.0618 $1g_{9/2}$ 

0.0012 $^{91}$ Zr

$_{2.042}(3/2^+)$ 

$3s_{1/2}$ 

0.1176 $2d_{3/2}$ 

0.0549 $2d_{5/2}$ 

0.1420 $1g_{7/2}$ 

0.0521 $^{91}$ Zr

$_{2.131}(9/2^+)$ 

$2d_{5/2}$ 

−0.7541 $1g_{7/2}$ 

−0.0536 $1g_{9/2}$ 

−0.0007 Table 6. Spectroscopic amplitudes used in the CRC calculations for the one-neutron transfer using the glekpn model space and effective phenomenological interaction for
$\left \langle ^{90}{\rm{Zr}}|^{91}{\rm{Zr}} \right \rangle$ ovelaps. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.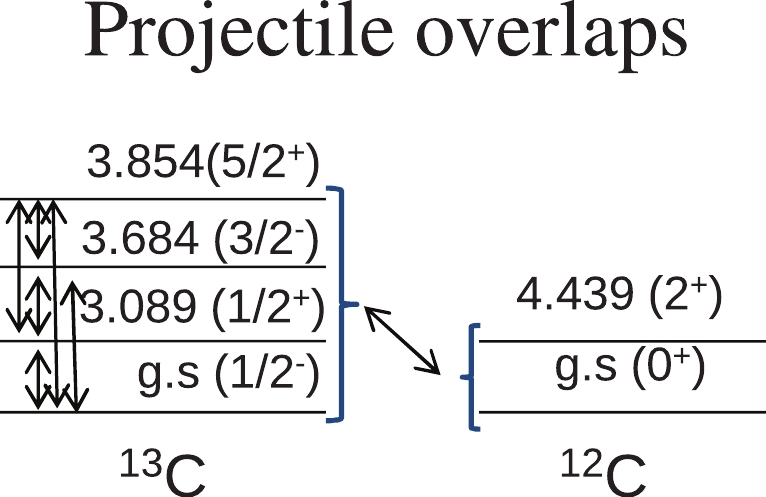
Figure 7. (color online) Coupling scheme for projectile overlaps used in the calculations. The double side arrows mean all the possible couplings between states.
initial state final state nlj spect. ampl. $^{92}$ Zr

$_{0.934}(2^+)$ 

$^{92}$ Zr

$_{g.s}(0^+)$ 

$2d_{5/2}$ 

1.3174 $^{91}$ Zr

$_{g.s}(5/2^+)$ 

$3s_{1/2}$ 

0.1597 $2d_{3/2}$ 

0.0580 $2d_{5/2}$ 

1.3631 $1g_{7/2}$ 

0.0227 $1g_{9/2}$ 

−0.0564 $^{92}$ Zr

$_{1.383}(0^+)$ 

$2d_{5/2}$ 

0.1529 $^{92}$ Zr

$_{1.495}(4^+)$ 

$2d_{3/2}$ 

−0.1639 $2d_{5/2}$ 

−0.1639 $1g_{7/2}$ 

−0.0210 $1g_{9/2}$ 

0.0171 $^{92}$ Zr

$_{1.847}(2^+)$ 

$3s_{1/2}$ 

−0.0381 $2d_{3/2}$ 

−0.0030 $2d_{5/2}$ 

0.1627 $1g_{7/2}$ 

−0.0269 $1g_{9/2}$ 

−0.0016 $^{91}$ Zr

$_{1.205}(1/2^+)$ 

$^{92}$ Zr

$_{g.s.}(0^+)$ 

$3s_{1/2}$ 

−0.3706 $^{92}$ Zr

$_{0.934}(2^+)$ 

$2d_{3/2}$ 

−0.0728 $2d_{5/2}$ 

−0.1586 $^{92}$ Zr

$_{1.383}(0^+)$ 

$3s_{1/2}$ 

0.2814 $^{92}$ Zr

$_{1.495}(4^+)$ 

$1g_{7/2}$ 

0.0248 $1g_{9/2}$ 

−0.0245 $^{92}$ Zr

$_{1.847}(2^+)$ 

$2d_{3/2}$ 

0.0383 $2d_{5/2}$ 

−0.0083 $^{91}$ Zr

$_{g.s}(5/2^+)$ 

$^{92}$ Zr

$_{g.s.}(0^+)$ 

$2d_{5/2}$ 

0.0893 $^{92}$ Zr

$_{0.934}(2^+)$ 

$3s_{1/2}$ 

0.022 $2d_{3/2}$ 

−0.0038 $2d_{5/2}$ 

0.0204 $1g_{7/2}$ 

0.0122 $1g_{9/2}$ 

0.00004 $^{92}$ Zr

$_{1.383}(0^+)$ 

$2d_{5/2}$ 

−1.2431 $^{92}$ Zr

$_{1.495}(4^+)$ 

$2d_{3/2}$ 

−0.0101 $2d_{5/2}$ 

0.0625 $1g_{7/2}$ 

−0.0050 $1g_{9/2}$ 

0.0009 $^{92}$ Zr

$_{1.847}(2^+)$ 

$3s_{1/2}$ 

−0.0651 $2d_{3/2}$ 

−0.0236 $2d_{5/2}$ 

−0.8603 $1g_{7/2}$ 

−0.0649 $1g_{9/2}$ 

0.0290 Continued on next page Table 7. Spectroscopic amplitudes used in the CRC calculations for the one-neutron transfer using the glekpn model space and effective phenomenological interaction for
$\left \langle ^{91}{\rm{Zr}}|^{92}{\rm{Zr}} \right \rangle$ overlaps. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.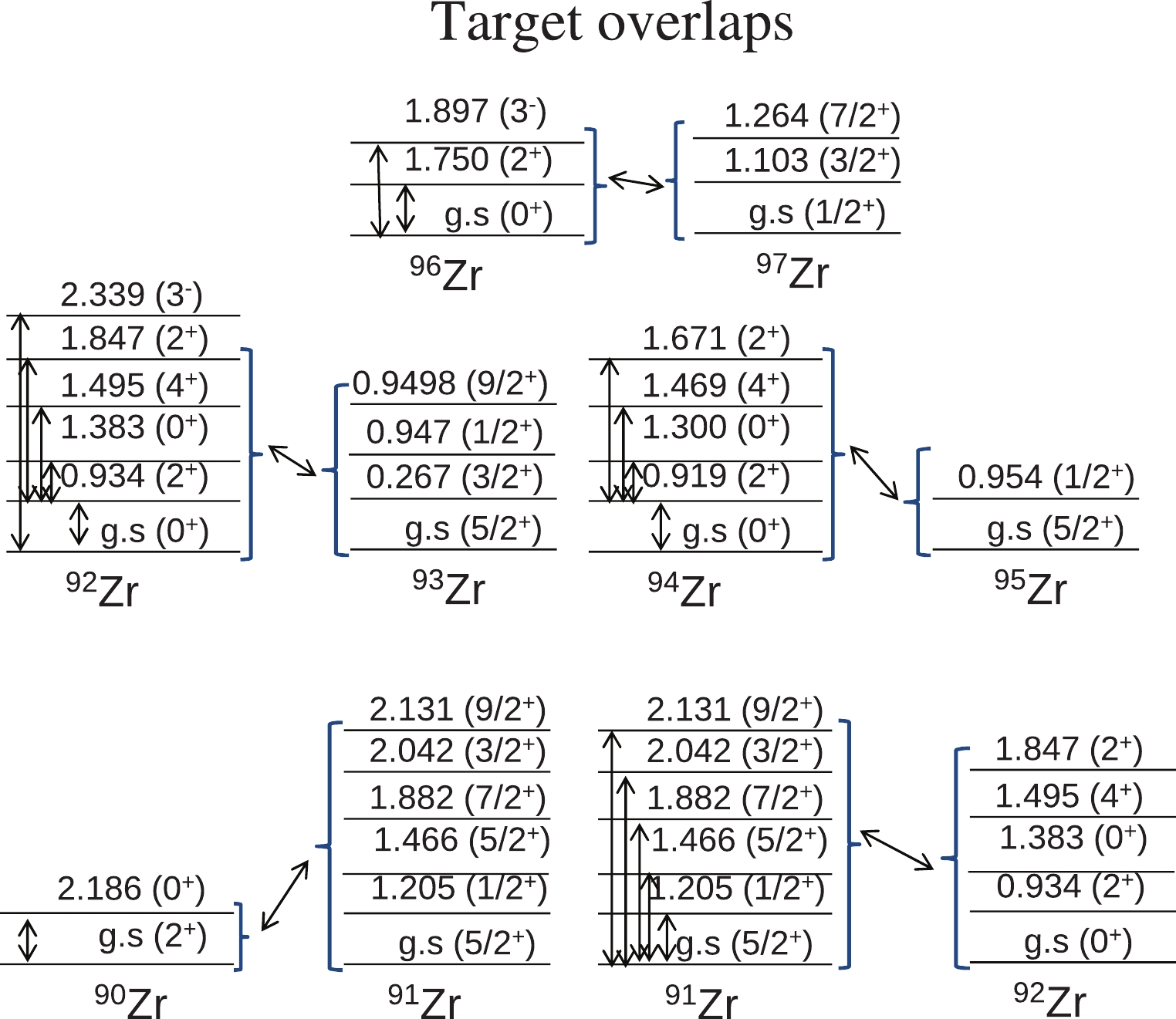
Figure 8. (color online) Coupling scheme for target overlaps used in the calculations. The double sided arrows indicate all the possible couplings between states.
Table 7-continued from previous page initial state final state nlj spect. ampl. $^{91}$ Zr

$_{1.992}(7/2^+)$ 

$^{92}$ Zr

$_{g.s.}(0^+)$ 

$1g_{7/2}$ 

0.0354 $^{92}$ Zr

$_{0.934}(2^+)$ 

$2d_{3/2}$ 

0.0185 $2d_{5/2}$ 

−0.1247 $1g_{7/2}$ 

0.0060 $1g_{9/2}$ 

−0.0029 $^{92}$ Zr

$_{1.383}(0^+)$ 

$1g_{7/2}$ 

−0.0762 $^{92}$ Zr

$_{1.495}(4^+)$ 

$3s_{1/2}$ 

0.0175 $2d_{3/2}$ 

−0.0165 $2d_{5/2}$ 

0.0170 $1g_{7/2}$ 

−0.0005 $1g_{9/2}$ 

0.0036 $^{92}$ Zr

$_{1.847}(2^+)$ 

$2d_{3/2}$ 

0.0013 $2d_{5/2}$ 

0.7293 $1g_{7/2}$ 

−0.0082 $1g_{9/2}$ 

0.0171 $^{91}$ Zr

$_{2.042}(3/2^+)$ 

$^{92}$ Zr

$_{g.s.}(0^+)$ 

$2d_{3/2}$ 

−0.2628 $^{92}$ Zr

$_{0.934}(2^+)$ 

$3s_{1/2}$ 

0.0755 $2d_{3/2}$ 

−0.0748 $2d_{5/2}$ 

0.0543 $1g_{7/2}$ 

−0.0327 $^{92}$ Zr

$_{1.383}(0^+)$ 

$2d_{3/2}$ 

0.0025 $^{92}$ Zr

$_{1.495}(4^+)$ 

$2d_{5/2}$ 

−0.1652 $1g_{7/2}$ 

0.0117 $1g_{9/2}$ 

0.0186 $^{92}$ Zr

$_{1.847}(2^+)$ 

$3s_{1/2}$ 

−0.0625 $2d_{3/2}$ 

0.0106 $2d_{5/2}$ 

−0.0201 $1g_{7/2}$ 

0.0162 $^{91}$ Zr

$_{2.131}(9/2^+)$ 

$^{92}$ Zr

$_{g.s.}(0^+)$ 

$1g_{9/2}$ 

−0.0360 $^{92}$ Zr

$_{0.934}(2^+)$ 

$2d_{5/2}$ 

0.0720 $1g_{7/2}$ 

−0.0046 $1g_{9/2}$ 

−0.0006 $^{92}$ Zr

$_{1.383}(0^+)$ 

$1g_{9/2}$ 

0.0547 $^{92}$ Zr

$_{1.495}(4^+)$ 

$3s_{1/2}$ 

−0.0210 $2d_{3/2}$ 

−0.0037 $2d_{5/2}$ 

−0.0681 $1g_{7/2}$ 

−0.0014 $1g_{9/2}$ 

0.0038 $^{92}$ Zr

$_{1.847}(2^+)$ 

$2d_{5/2}$ 

−0.4477 $1g_{7/2}$ 

0.0251 $1g_{9/2}$ 

−0.0097 initial state final state nlj spect. ampl. $^{92}$ Zr

$_{g.s.}(0^+)$ 

$^{93}$ Zr

$_{g.s.}(5/2^+)$ 

$2d_{5/2}$ 

0.8177 $^{93}$ Zr

$_{0.266}(3/2^+)$ 

$2d_{3/2}$ 

0.0522 $^{93}$ Zr

$_{0.947}(1/2^+)$ 

$3s_{1/2}$ 

0.7849 $^{93}$ Zr

$_{0.949}(9/2^+)$ 

$1g_{9/2}$ 

−0.0014 $^{92}$ Zr

$_{0.934}(2^+)$ 

$^{93}$ Zr

$_{g.s.}(5/2^+)$ 

$3s_{1/2}$ 

0.0234 $2d_{3/2}$ 

−0.0806 $2d_{5/2}$ 

−0.8425 $1g_{7/2}$ 

−0.0138 $1g_{9/2}$ 

−0.0291 $^{93}$ Zr

$_{0.266}(3/2^+)$ 

$3s_{1/2}$ 

−0.2468 $2d_{3/2}$ 

0.0387 $2d_{5/2}$ 

1.4099 $1g_{7/2}$ 

0.0025 $^{93}$ Zr

$_{0.947}(1/2^+)$ 

$2d_{3/2}$ 

−0.0795 $2d_{5/2}$ 

−0.1150 $^{93}$ Zr

$_{0.949}(9/2^+)$ 

$2d_{5/2}$ 

−0.7792 $1g_{7/2}$ 

0.0012 $1g_{9/2}$ 

−0.0297 $^{92}$ Zr

$_{1.384}(0^+)$ 

$^{93}$ Zr

$_{g.s.}(5/2^+)$ 

$2d_{5/2}$ 

0.0554 $^{93}$ Zr

$_{0.266}(3/2^+)$ 

$2d_{3/2}$ 

−0.0080 $^{93}$ Zr

$_{0.947}(1/2^+)$ 

$3s_{1/2}$ 

−0.4118 $^{93}$ Zr

$_{0.949}(9/2^+)$ 

$1g_{9/2}$ 

−0.0013 $^{92}$ Zr

$_{1.495}(4^+)$ 

$^{93}$ Zr

$_{g.s.}(5/2^+)$ 

$2d_{3/2}$ 

−0.0127 $2d_{5/2}$ 

−1.1493 $1g_{7/2}$ 

−0.0118 $1g_{9/2}$ 

−0.0244 $^{93}$ Zr

$_{0.266}(3/2^+)$ 

$2d_{5/2}$ 

−0.8747 $1g_{7/2}$ 

−0.0251 $1g_{9/2}$ 

−0.0730 $^{93}$ Zr

$_{0.947}(1/2^+)$ 

$1g_{7/2}$ 

−0.0369 $1g_{9/2}$ 

−0.0150 $^{93}$ Zr

$_{0.949}(9/2^+)$ 

$3s_{1/2}$ 

0.0866 $2d_{3/2}$ 

0.1659 $2d_{5/2}$ 

1.4825 $1g_{7/2}$ 

0.0301 $1g_{9/2}$ 

−0.0232 $^{92}$ Zr

$_{1.847}(2^+)$ 

$^{93}$ Zr

$_{g.s.}(5/2^+)$ 

$3s_{1/2}$ 

0.0039 $2d_{3/2}$ 

0.0135 $2d_{5/2}$ 

−0.1143 $1g_{7/2}$ 

0.0003 $1g_{9/2}$ 

−0.0031 $^{93}$ Zr

$_{0.266}(3/2^+)$ 

$3s_{1/2}$ 

−0.0059 $2d_{3/2}$ 

−0.0140 $2d_{5/2}$ 

0.1175 $1g_{7/2}$ 

−0.0018 $^{93}$ Zr

$_{0.947}(1/2^+)$ 

$2d_{3/2}$ 

0.0740 $2d_{5/2}$ 

−0.0573 $^{93}$ Zr

$_{0.949}(9/2^+)$ 

$2d_{5/2}$ 

−0.0568 $1g_{7/2}$ 

−0.0053 $1g_{9/2}$ 

−0.0065 Table 8. Spectroscopic amplitudes used in the CRC calculations for the one-neutron transfer using the glekpn model space and effective phenomenological interaction for
$\left \langle ^{92}{\rm{Zr}}|^{93}{\rm{Zr}} \right \rangle$ overlaps. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.initial state final state nlj spect. ampl. $^{94}$ Zr

$_{g.s.}(0^+)$ 

$^{95}$ Zr

$_{g.s.}(5/2^+)$ 

$2d_{5/2}$ 

−0.4773 $^{95}$ Zr

$_{0.954}(1/2^+)$ 

$3s_{1/2}$ 

0.8236 $^{94}$ Zr

$_{0.919}(2^+)$ 

$^{95}$ Zr

$_{g.s.}(5/2^+)$ 

$3s_{1/2}$ 

−0.1345 $2d_{3/2}$ 

0.0302 $2d_{5/2}$ 

1.1630 $1g_{7/2}$ 

0.0213 $1g_{9/2}$ 

0.0322 $^{95}$ Zr

$_{0.954}(1/2^+)$ 

$2d_{3/2}$ 

−0.0708 $2d_{5/2}$ 

−0.1705 $^{94}$ Zr

$_{1.300}(0^+)$ 

$^{95}$ Zr

$_{g.s.}(5/2^+)$ 

$2d_{5/2}$ 

0.2090 $^{95}$ Zr

$_{0.954}(1/2^+)$ 

$3s_{1/2}$ 

−0.3599 $^{94}$ Zr

$_{1.469}(4^+)$ 

$^{95}$ Zr

$_{g.s.}(5/2^+)$ 

$2d_{3/2}$ 

−0.0806 $2d_{5/2}$ 

−1.5742 $1g_{7/2}$ 

−0.0095 $1g_{9/2}$ 

−0.0181 $^{95}$ Zr

$_{0.954}(1/2^+)$ 

$1g_{7/2}$ 

0.0329 $1g_{9/2}$ 

0.0183 $^{94}$ Zr

$_{1.671}(2^+)$ 

$^{95}$ Zr

$_{g.s.}(5/2^+)$ 

$3s_{1/2}$ 

0.0242 $2d_{3/2}$ 

0.0050 $2d_{5/2}$ 

−0.2516 $1g_{7/2}$ 

−0.0034 $1g_{9/2}$ 

−0.0041 $^{95}$ Zr

$_{0.954}(1/2^+)$ 

$2d_{3/2}$ 

−0.0228 $2d_{5/2}$ 

−0.2061 Table 9. Spectroscopic amplitudes used in the CRC calculations for the one-neutron transfer using the glekpn model space and effective phenomenological interaction for
$\left \langle ^{94}{\rm{Zr}}|^{95}{\rm{Zr}} \right \rangle$ overlaps. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.initial state final state nlj spect. ampl. $^{96}$ Zr

$_{g.s.}(0^+)$ 

$^{97}$ Zr

$_{g.s.}(1/2^+)$ 

$3s_{1/2}$ 

0.8918 $^{97}$ Zr

$_{1.103}(3/2^+)$ 

$2d_{3/2}$ 

0.9583 $^{96}$ Zr

$_{1.750}(2^+)$ 

$^{97}$ Zr

$_{g.s.}(1/2^+)$ 

$2d_{3/2}$ 

0.1571 $2d_{5/2}$ 

1.0769 $^{97}$ Zr

$_{1.103}(3/2^+)$ 

$3s_{1/2}$ 

−0.0826 $2d_{3/2}$ 

−0.0726 $2d_{5/2}$ 

0.0338 $^{97}$ Zr

$_{1.264}(7/2^+)$ 

$2d_{3/2}$ 

0.0.0155 $2d_{5/2}$ 

−0.0356 Table 10. Spectroscopic amplitudes used in the CRC calculations for the one-neutron transfer using the glepn model space and effective phenomenological interaction for
$\left \langle ^{96}{\rm{Zr}}|^{97}{\rm{Zr}} \right \rangle$ overlaps. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.From Fig. 9, one notes that the one-neutron transfer (solid purple curve) has a small influence when compared to CC results for the elastic scattering angular distributions for
$ ^{A} $ Zr($ ^{13} $ C,$ ^{12} $ C)$ ^{A+1} $ Zr systems (with A = 90, 91, 92, 94, 96). The two curves, which correspond to CC and CRC calculations, cannot be clearly distinguished.
Figure 9. (color online) Comparison of CC and CRC calculations with the experimental elastic scattering angular distributions for the
$^{13}$ C+$^{A} {\rm{Zr}}$ system, for A = 90, 91, 92, 94, 96.From the present CC and CRC calculations analysis, one can conclude that, indeed, the couplings to direct reaction channels are weak. This is the reason why the
$ [U = (1.0 + 0.78{\rm i})V_{\rm SPP}] $ works well in potential scattering. In addition, it is evident that the optical potential used in these calculations is appropriate for describing the elastic cross section.Spectroscopic factors for the
$ \left \langle ^{90}{\rm{Zr}}|^{91}{\rm{Zr}} \right \rangle $ ,$ \left \langle ^{91}{\rm{Zr}}|^{92}{\rm{Zr}} \right \rangle $ and$ \left \langle ^{92}{\rm{Zr}}|^{93}{\rm{Zr}} \right \rangle $ overlaps were obtained in previous works [27, 47-50] by means of distorted wave Born approximation (DWBA) calculations. In Tables 11, 12, and 13 the SFs of these works and from shell-model calculations (present work) are compared. It is clear that the SFs for the ground to ground (elastic transfer) transitions agree quite well with each other. For the$ \langle $ $ ^{92} $ Zr$ |^{93} $ Zr$ \rangle $ overlaps, the SFs are very close for all the overlaps considered in Ref. [50] (see Table 12). In general, the SFs obtained in this study are in agreement with those previously published.transitions nlj SF present work Ref. [27] Ref. [47] Ref. [48] $\langle ^{90}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{g.s.} \rangle$ 

$2d_{5/2}$ 

0.97 0.75 1.04 0.95 $\langle ^{90}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{1.205} \rangle$ 

$3s_{1/2}$ 

0.84 0.66 0.93 0.66 $\langle ^{90}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{1.466} \rangle$ 

$2d_{5/2}$ 

0.001 0.028 0.03 0.024 $\langle ^{90}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{1.882} \rangle$ 

$1g_{7/2}$ 

0.013 0.082 0.08 0.13 $\langle ^{90}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{2.042} \rangle$ 

$2d_{3/2}$ 

0.93 0.56 0.63 0.55 Table 11. Comparison between one-neutron spectroscopic factors for
$\left \langle ^{90}{\rm{Zr}}|^{91}{\rm{Zr}} \right \rangle$ overlaps obtained by shell-model calculations and from (d,p) transfer reaction [27, 47, 48]. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.transitions nlj SF present work Ref. [27] Ref. [49] $\langle ^{92}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{g.s.} \rangle$ 

$2d_{5/2}$ 

1.73 1.18 1.86 $\langle ^{92}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{1.205} \rangle$ 

$3s_{1/2}$ 

0.14 0.045 0.06 $\langle ^{92}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{1.466} \rangle$ 

$2d_{5/2}$ 

0.008 0.011 — $\langle ^{92}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{1.882} \rangle$ 

$1g_{7/2}$ 

0.001 — — $\langle ^{92}{\rm{Zr}}_{g.s.}|^{91}{\rm{Zr}}_{2.042} \rangle$ 

$2d_{3/2}$ 

0.069 0.047 0.07 Table 12. Comparison between one-neutron spectroscopic factors for
$\left \langle ^{92}{\rm{Zr}}|^{91}{\rm{Zr}} \right \rangle$ overlaps obtained by shell-model calculations and from (p,d) transfer reaction [27, 49]. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.transitions nlj SF present work Ref. [50] $\langle ^{92}{\rm{Zr}}_{g.s.}|^{93}{\rm{Zr}}_{g.s.} \rangle$ 

$2d_{5/2}$ 

0.67 0.54 $\langle ^{92}{\rm{Zr}}_{g.s.}|^{93}{\rm{Zr}}_{0.266} \rangle$ 

$2d_{3/2}$ 

0.003 0.007 $^{*}$ 

$\langle ^{92}{\rm{Zr}}_{g.s.}|^{93}{\rm{Zr}}_{0.947} \rangle$ 

$3s_{1/2}$ 

0.62 0.53 *The authors consider the first excited state $^{93}$ Zr

$_{0.266}$ with spin equal to

$5/2^{+}$ .

Table 13. Comparison between one-neutron spectroscopic factors for
$\left \langle ^{92}{\rm{Zr}}|^{93}{\rm{Zr}} \right \rangle$ overlaps obtained by shell-model calculations and from (d,p) transfer reaction [50]. nlj are the principal quantum number, orbital, and total angular momentum of the neutron state, respectively.The main difference is that the spectroscopic amplitudes obtained in this study are derived from shell-model calculations and applied to heavy-ion interactions, where the high orders of the interactions and the transitions from excited states of the projectile or the target might be relevant [34, 51]. These kinds of effects can be masked by the overestimation of the spectroscopic amplitudes from the DWBA fits to the transfer cross sections (this seems not be the case for the present reactions. See discussion below).
In Fig. 10, the results for
$ ^{13} $ C +$ ^{90,91,92} $ Zr elastic scattering angular distributions from CRC results using different SFs obtained by shell-model calculations and derived from DWBA fits are compared. One can see that the theoretical results are very similar. The advantage of using SFs obtained from microscopic calculations is that these SFs are not fitted, which increases confidence in the results.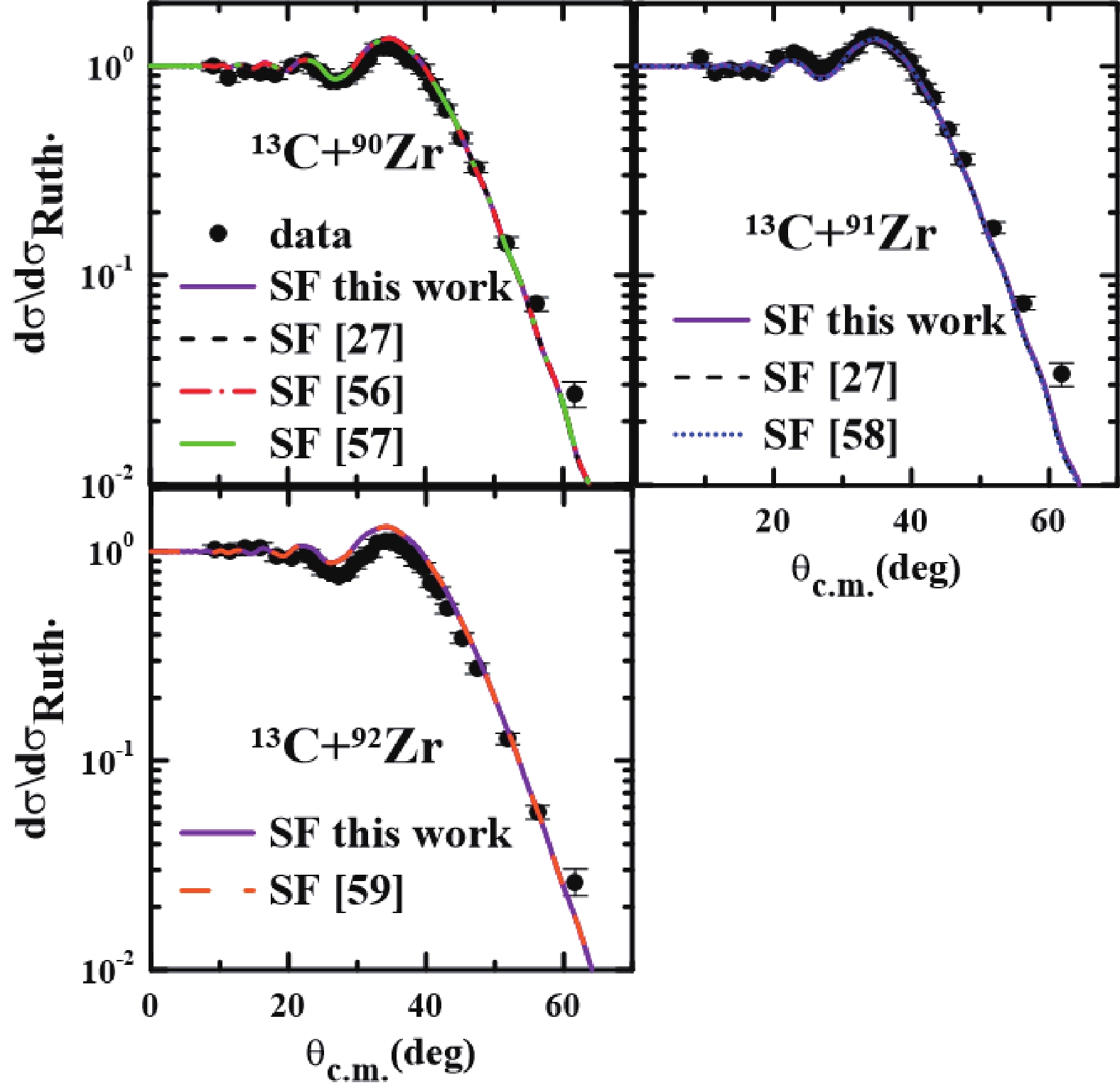
Figure 10. (color online) Effect of one-neutron transfer channel on the
$^{13}$ C +$^{90,91,92}$ Zr elastic angular distributions using different SFs (see text for details).Finally, we compared the theoretical CRC and DWBA results for
$ ^{90} $ Zr(d, p)$ ^{91} $ Zr and$ ^{92} $ Zr(p, d)$ ^{91} $ Zr one-neutron transfer reactions using the spectroscopic amplitudes derived in this study and those reported in Ref. [27] (see Tables 11 and 12). This comparison is shown in Figs. 11 and 12. It is evident that the transfer angular distributions are reasonably well described using the spectroscopic amplitudes derived microscopically and adjusted by the DWBA calculations. However, for the state at 1.466 MeV of$ ^{91} $ Zr the theoretical result using shell-model spectroscopic amplitude underpredict the experimental data. This occurs because the SF for this channel is very small compared to the SF from Ref. [27]. In addition, we should emphasize that our description for the transfer angular distributions is not as good as that reported in Ref. [27]. This is caused by the optical potential used to describe this reaction. We are not using the original optical potential used in Ref. [27], but the São Paulo potential, which might not be suitable for this (p,d) reaction.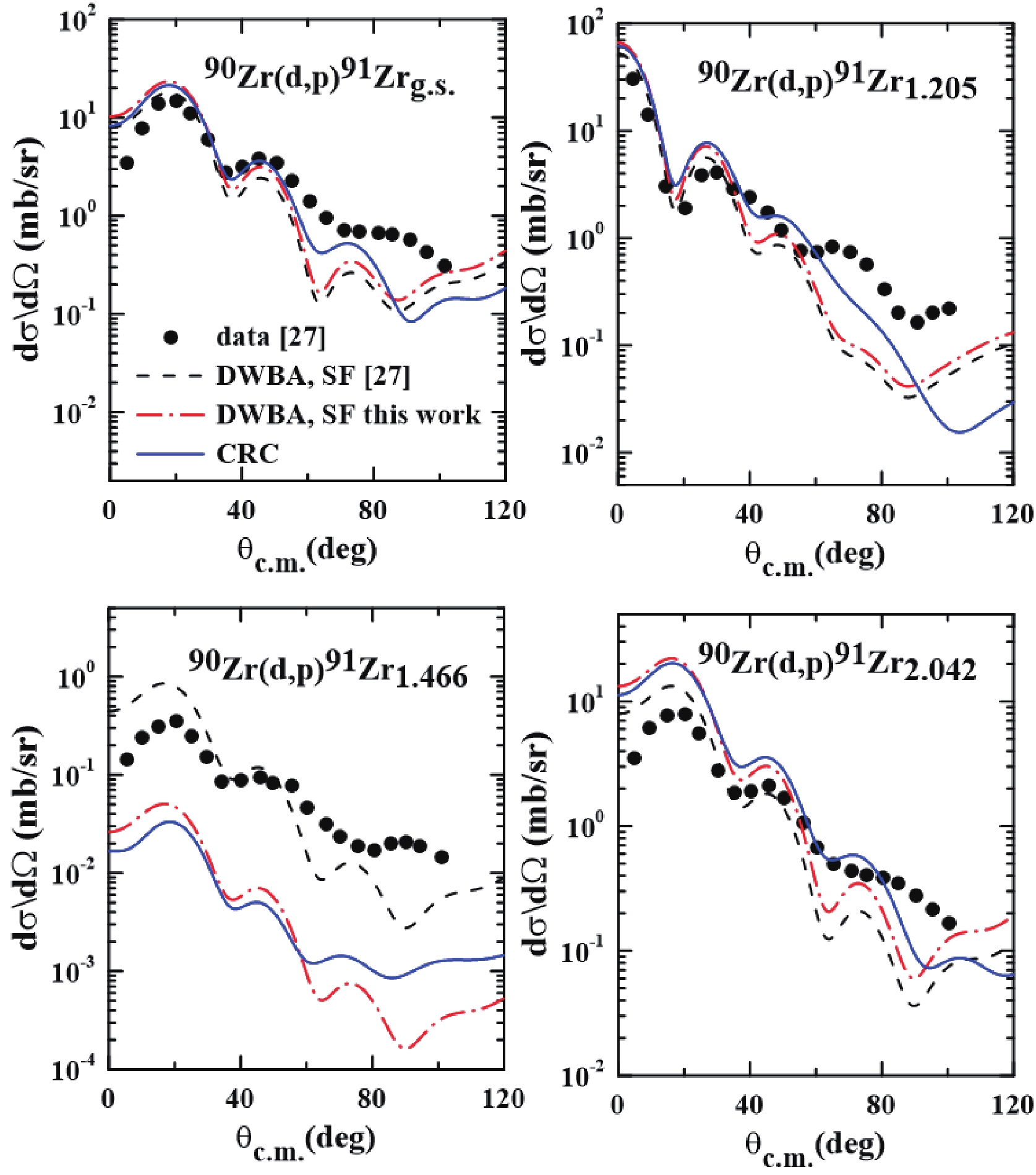
Figure 11. (color online) Transfer angular distribution for
$^{90}$ Zr(d, p)$^{91}$ Zr reaction at 15.89 MeV [27], using different reaction models and spectroscopic factors. For details, see the text.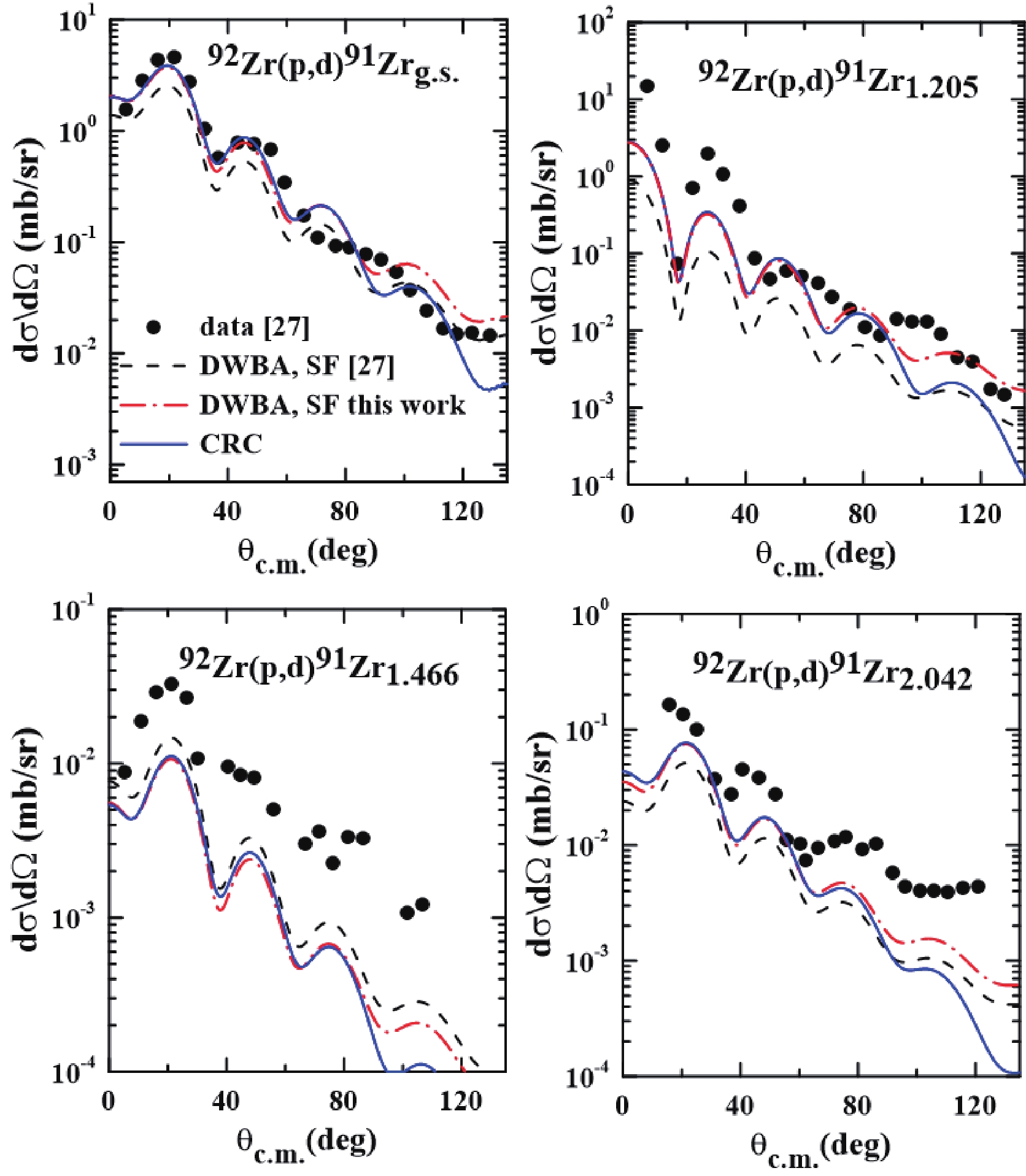
Figure 12. (color online) Transfer angular distribution from
$^{92}$ Zr(p, d)$^{91}$ Zr reaction at 22.11 MeV [27], using different reaction models and spectroscopic factors. For details, see the text.From Figs. 11 and 12, one also realizes that the high-order coupling terms are irrelevant for the very forward angles (compare full blue lines with the dash-dot red lines), but they are relevant for the other angular ranges. It is worth mentioning that the calculations performed in the present work do not have any fitted parameter or scaling factor.
From the present analysis we expected to find some effects of the one-neutron channel in systems involving
$ ^{13} $ C when compared to the reactions induced by$ ^{12} $ C. The ground state Q-value is positive for the reactions with the four zirconium isotopes included in our study (ranging between 0.63 MeV ($ ^{96} $ Zr) and 3.67 MeV ($ ^{91} $ Zr)). So, one might think of some effects on the elastic scattering angular distribution that could help to improve the accuracy of the determination of the spectroscopic factors for target overlaps.In the case of the fusion cross section, the effect on the neutron transfer channels is clear [52-55]. After the neutrons are transferred, the deformation of the nuclei is the relevant information that decides the dynamic of the reactions. If the deformation increases, the effective Coulomb barrier decreases, and the fusion cross section is enhanced. Concerning the effect on the elastic angular distribution, it is well known that breakup of neutron halo nuclei is usually governed by the dipole polarizability of these nuclei that produces a hindrance of the Fresnel peak and decreases the elastic scattering angular distribution [1, 2]. How does the neutron transfer affect the elastic cross section, and is Q value one of the ingredients that affect it? This is one of the questions that remain open. In this study, we attempted to contribute to this issue and also to improve our knowledge on the spectroscopy of the zirconium isotopes, although we found that the elastic angular distributions were not sensible to the spectroscopic details.
-
In this study, elastic scattering angular distributions for the
$ ^{12,13} $ C+$ ^{A} $ Zr (A = 90, 91, 92, 94, 96) reactions were measured at the HI-13 Tandem accelerator in China Institute of Atomic Energy (CIAE), Beijing. Optical model, coupled channel and coupled reaction channel calculations for$ ^{12,13} $ C+$ ^{A} $ Zr were performed and the results were compared with the experimental data.The theoretical calculations provided results very close to those obtained experimentally. The optical model calculations using the São Paulo potential described quite well the elastic angular distributions for
$ ^{12,13} $ C+$ ^{A} $ Zr systems. It was also observed that the couplings to the inelastic states of the$ ^{A} $ Zr did not affect the elastic cross section significantly. Still, the agreement with the experimental data was improved when the coupling to the lower excited states of$ ^{12,13} $ C was considered. The one-neutron stripping for$ ^{13} $ C+$ ^{A} $ Zr reactions also appeared as a weak channel. The effects of the one-neutron stripping channel ($ ^{13} $ C,$ ^{12} $ C) on the elastic scattering angular distributions were found to be negligible in the case of all the zirconium isotopes used as targets in this study, showing that the optical potential used in the calculations is reliable for describing the elastic cross section.Spectroscopic information for various overlaps of zirconium isotopes was obtained from shell-model calculations. The spectroscopic amplitudes presented in this study are close to previous ones and described reasonably well the transfer angular distribution for (d,p) and (p,d) reactions without any scaling factors.
Our results also show that, in the reactions with the considered zirconium isotopes, the presence of the extra neutron in
$ ^{13} $ C does not strongly affect the reaction mechanism that is governed by the collective excitation of the$ ^{12} $ C core. Similar results have been reported recently for the two-neutron transfer reactions$ ^{18} $ O +$ ^{12,13} $ C at 84 MeV, where the effect of the pairing correlations between the two transferred neutrons in the two-neutron stripping reaction was not affected by the presence of an extra neutron in$ ^{13} $ C [56-58].We are grateful to the staff of the China Institute of Atomic Energy for providing stable
$ ^{12,13} $ C beam throughout the experiment.
The angular distributions of elastic scattering of 12,13C+Zr
- Received Date: 2020-05-28
- Available Online: 2020-10-01
Abstract: To obtain the neutron spectroscopic amplitudes for





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: