-
Over the past several years, immense progress toward the observations of singly heavy baryons has been achieved at the LHC. In 2017, five extremely narrow
$ \Omega_c(X) $ states,$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ ,$ \Omega_c(3066) $ ,$ \Omega_c(3090) $ , and$ \Omega_c(3119) $ , were observed in the$ \Xi_c^{+}K^- $ channel by the LHCb Collaboration [1]. In 2018, the LHCb Collaboration observed a new bottom baryon,$ \Xi_b(6227)^- $ , in both$ \Lambda_b^0K^- $ and$ \Xi_b^0\pi^- $ decay modes [2] and two new resonances,$ \Sigma_b(6097)^{\pm} $ , in the$ \Lambda_b^0 \pi^{\pm} $ channels [3]. In 2020, the LHCb Collaboration also observed four new$ \Omega_b(X) $ states,$ \Omega_b(6316)^- $ ,$ \Omega_b(6330)^- $ ,$ \Omega_b(6340)^- $ , and$ \Omega_b(6350)^- $ , in the$ \Xi^0_bK^- $ mass spectrum [4]; three new$ \Xi_c(X) $ states,$ \Xi_c(2923)^0 $ ,$ \Xi_c(2939)^0 $ , and$ \Xi_c(2965)^0 $ , in the$ \Lambda_c^+K^- $ mass spectrum [5]; and a new$ \Xi_b(6227)^0 $ state in the$ \Xi_b^-\pi^+ $ channel [6]. Also in 2020, the CMS Collaboration observed a broad enhancement around 6070 MeV in the$ \Lambda^0_b\pi^+\pi^- $ invariant mass spectrum [7], which was confirmed by subsequent LHCb experiments with high statistical significance [8]. More recently, the CMS Collaboration observed a new excited beauty strange baryon,$ \Xi_b(6100)^- $ , decaying to$ \Xi^-_\mathrm{b} \pi^+ \pi^- $ [9].These newly observed resonances provide opportunities for establishing an abundant singly heavy baryon spectrum. For a singly heavy baryon, there are two kinds of excitations, "
$ \rho $ -mode" and "$ \lambda $ -mode". The$ \rho $ -mode excitation appears within the light diquark, while the$ \lambda $ -mode excitation occurs between the light diquark and the heavy quark. In the heavy quark limit,$ m_{Q} \to \infty $ , no mixing occurs between the$ \lambda $ - and$ \rho $ -mode excitations due to a strong suppression of the spin-dependent interactions by the heavy quark mass$ m_{Q} $ [10-12]. The$ \rho $ -mode excitation energy should be notably larger than that of the$ \lambda $ -mode [12-17], which can be understood using the simple harmonic oscillator model, as the frequency$ \omega_{\rho} $ of the$ \rho $ -mode is larger than the frequency$ \omega_{\lambda} $ of the$ \lambda $ -mode. The lower$ \lambda $ -mode excitation energy indicates that the$ \lambda $ -mode excitations should be more easily formed than$ \rho $ -mode excitations.In the literature, the masses for the
$ 1P $ -wave$ \lambda $ -mode$ \Omega_{c} $ ,$ \Omega_{b} $ ,$ \Xi_{c}' $ ,$ \Xi_{b}' $ , and$ \Sigma_{b} $ baryon states are predicted to be$ \sim 2.95-3.10 $ GeV [10, 12, 18-32],$ \sim 6.30-6.38 $ GeV [10, 12, 28-37],$ \sim 2.85-3.03 $ GeV [10, 13, 24-31],$\sim 6.15- $ $ 6.25$ GeV [10, 13, 28-31, 34], and$ \sim 6.07-6.20 $ GeV [10-12, 28-31, 34], respectively. The$ 1P $ -wave$ \rho $ -mode states lie$ 70-150 $ MeV above the$ \lambda $ -mode states according to the quark model predictions in Refs. [11-15]. It should be mentioned that the$ \rho $ -mode excitation energy calculated within QCD sum rules is slightly lower than that of the$ \lambda $ -mode in some other cases [25, 34, 38-43]. The newly observed singly heavy baryons,$ \Omega_c(X) $ ,$ \Omega_b(X) $ ,$ \Xi_c(X) $ ,$ \Xi_b(6227)^0 $ and$ \Sigma_b(6097)^{\pm} $ , are just within the predicted mass ranges of the$ 1P $ -wave excitations. Furthermore, prompted by the newly observed singly heavy baryon states and combined with mass spectrum, the strong decay properties have been studied using the QCD sum rules [38-45],$ ^3P_0 $ model [13, 19, 46-52], chiral quark model [16, 17, 53-55, 56], and heavy quark effective theory [18, 57].Based on the mass spectrum and strong decay analyses, the
$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ ,$ \Omega_c(3066) $ ,$ \Omega_c(3090) $ , and$ \Omega_c(3119) $ structures may be explained with the$ 1P $ -wave$ \lambda $ -mode$ \Omega_{c} $ states [18-22], although, there are different explanations about some resonances, such as$ \Omega_c(3090) $ and$ \Omega_c(3119) $ , which may be explained with radially excited ($ 2S $ -wave)$ \Omega_c $ states [45, 56-58]. It should be mentioned that the recent LHCb measurements show that the spin assignment of the four observed states$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ ,$ \Omega_c(3066) $ , and$ \Omega_c(3090) $ is consistent with λ-mode excitations with quantum numbers J = 1/2, 3/2, 3/2 and 5/2 [59]. It is interesting to notice that among various models, only the predicted JP quantum numbers in our previous work [56] are consistent with the above-mentioned scenario as pointed in the recent review of charmed baryon physics [60]. Similarly, the new$ \Omega_b(X) $ states,$ \Omega_b(6316)^- $ ,$ \Omega_b(6330)^- $ ,$ \Omega_b(6340)^- $ , and$ \Omega_b(6350)^- $ , can be assigned to the$ 1P $ -wave$ \lambda $ -mode$ \Omega_{b} $ states [35-37, 46], although the$ \Omega_b(6316)^- $ may be a$ \rho $ -mode excitation, as suggested in [43]. The new$ \Xi_c(X) $ states,$ \Xi_c(2923)^0 $ ,$ \Xi_c(2939)^0 $ , and$ \Xi_c(2965)^0 $ , are also good candidates for the$ 1P $ -wave$ \lambda $ -mode$ \Xi_{c}' $ states belonging to$ \mathbf{6}_F $ , as suggested in the literature [13, 38, 54], although different explanations exist for some resonances, such as$ \Xi_c(2939)^0 $ and$ \Xi_c(2965)^0 $ , which may be candidates of the$ 1P $ -wave$ \rho $ -mode excitations [13], and$ \Xi_c(2965)^0 $ , which may be the$ J^P = 1/2^+ $ $ \Xi_{c}'(2S) $ state [52, 61]. Additionally, the$ \Sigma_b(6097)^{\pm} $ and$ \Xi_b(6227)^0 $ resonances are good candidates for the$ 1P $ -wave$ \lambda $ -mode singly bottom baryons [16, 41-44, 48-51, 53, 62]. Finally, some unconventional interpretations, such as molecular or pentaquark, were also proposed in the literature for the newly observed resonances,$ \Omega_c(X) $ [63-74],$ \Omega_b(X) $ [75],$ \Xi_c(X) $ [76, 77], and$ \Xi_b(6227)^- $ [78-81]. As a whole, a fairly complete$ \lambda $ -mode$ P $ -wave spectrum in the$ \Omega_c $ ,$ \Xi_c' $ ,$ \Xi'_b $ ,$ \Omega_b $ , and$ \Sigma_b $ families may be established with discovery of the series of heavy baryons at the LHC. Based on our previous work [16, 17, 53-56], we provide a quark model classification of these newly observed resonances, summarized in Table 1.$ L $ -

$ S $ scheme

$ j $ -

$ j $ scheme

Observed states/structures belonging to the $ \mathbf{6}_F $ multiplet

$ |n^{2S+1}L_{\lambda}J^P\rangle $ 

$ |J^P,j\rangle\; (nl) $ 

$ \Omega_c $ states

$ \Xi_c' $ states

$ \Sigma_c $ states

$ \Omega_b $ states

$ \Xi_b' $ states

$ \Sigma_b $ states

$ |1^{2}S \dfrac{1}{2}^+\rangle $ 

$ |J^P = {1}/{2}^+,1\rangle(1S) $ 

$ \Omega_c(2695) $ 

$ \Xi_c'(2578) $ 

$ \Sigma_c(2455) $ 

$ \Omega_b(6046) $ 

$ \Xi_b'(5935) $ 

$ \Sigma_b(5810) $ 

$ |1^{4}S \dfrac{3}{2}^+\rangle $ 

$ |J^P = {3}/{2}^+,1\rangle(1S) $ 

$ \Omega_c^*(2770) $ 

$ \Xi_c^*(2645) $ 

$ \Sigma_c^*(2520) $ 

$ \cdots $ 

$ \Xi_b^*(5955) $ 

$ \Sigma_b^*(5830) $ 

$ |1P_\lambda \dfrac{1}{2}^-\rangle_1 $ 

$ |J^P = {1}/{2}^-,1\rangle(1P) $ 

$ \Omega_c(3000) $ 

$ \cdots $ 

$ \cdots $ 

$ \Omega_b(6316) $ 

$ \cdots $ 

$ \Sigma_b(6072) $ 

$ |1P_\lambda \dfrac{1}{2}^-\rangle_2 $ 

$ |J^P = {1}/{2}^-,0\rangle(1P) $ 

$ \cdots $ 

$ \Xi_c(2880) $ 

$ \cdots $ 

$ \cdots $ 

$ \cdots $ 

$ \cdots $ 

$ |1^{4}P_\lambda \dfrac{3}{2}^-\rangle $ 

$ |J^P = {3}/{2}^-,1\rangle(1P) $ 

$ \Omega_c(3050) $ 

$ \Xi_c(2923) $ 

$ \cdots $ 

$ \Omega_b(6330) $ 

$ \cdots $ 

$ \Sigma_b(6072) $ 

$ |1^{2}P_\lambda \dfrac{3}{2}^-\rangle $ 

$ |J^P = {3}/{2}^-,2\rangle(1P) $ 

$ \Omega_c(3065) $ 

$ \Xi_c(2939) $ 

$ \Sigma_c(2800) $ 

$ \Omega_b(6340) $ 

$ \Xi_b'(6227) $ 

$ \Sigma_b(6097) $ 

$ |1^{4}P_\lambda \dfrac{5}{2}^-\rangle $ 

$ |J^P = {5}/{2}^-,2\rangle(1P) $ 

$ \Omega_c(3090) $ 

$ \Xi_c(2965) $ 

$ \Sigma_c(2800) $ 

$ \Omega_b(6350) $ 

$ \Xi_b'(6227) $ 

$ \Sigma_b(6097) $ 

LHC experiments have demonstrated the capability for the discovery of heavy baryons. Therefore, the missing
$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ baryon states are likely to be discovered by forthcoming LHC experiments. The$ \Sigma_c $ mass spectrum has been studied theoretically using various approaches, such as the relativized quark model [11], relativistic quark model [28, 29, 82], non-relativistic quark model [10, 12, 24, 62, 83, 84], lattice QCD [26, 27], QCD sum rules [25, 32, 85], and more. Some quark model predictions of the masses for the$ \lambda $ -mode$ P $ -wave and$ S $ -wave$ \Sigma_c $ states are collected in Table 2 [11, 28-30, 83, 84]. Using the heavy-quark-light-diquark approximation, the masses of the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states in the relativistic quark model are predicted to be approximately$ 2.71-2.81 $ GeV [28, 29], which is consistent with that of the non-relativistic quark model [83]. With the hypercentral approximation, the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states in the non-relativistic quark model are predicted to be approximately$ 2.79-2.84 $ GeV [84]. By strictly solving the three body problem without the diquark and hypercentral approximations, the masses of the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states are predicted to be approximately$ 2.76-2.82 $ GeV and$ 2.80-2.84 $ GeV in the relativized quark model [11] and non-relativistic quark model [12], respectively. The masses for the two$ \rho $ -mode$ P $ -wave$ \Sigma_c $ states with$ J^P = 1/2^- $ and$ 3/2^- $ are predicted to be$ \sim 2.85-2.91 $ GeV [11, 12], which is approximately$ 70 $ MeV larger than the highest$ \lambda $ -mode excitation. Considering the mass, the$ \Sigma_c(2800) $ resonance [86] observed in the$ \Lambda_c \pi $ final states by the Belle and$ BABAR $ Collaborations [87, 88] may be experimental signals of the$ P $ -wave$ \Sigma_c $ states. The case of$ \Sigma_c(2800) $ as the$ \rho $ -mode$ P $ -wave excitations should be excluded as the$ \Lambda_c \pi $ decay channel is forbidden [89]. There are some discussions on the nature of$ \Sigma_c(2800) $ in the literature [17, 25, 28, 31, 40, 60, 89-93], however, these involve strong model dependencies. For example, the spin-parity ($ J^P $ ) numbers were suggested to be$ J^P = 3/2^- $ using the heavy hadron chiral perturbation theory approach [60, 91],$ J^P = 3/2^- $ or$ J^P = 5/2^- $ in the$ ^3P_0 $ model [90], and$ J^P = 1/2^- $ or$ 3/2^- $ using the QCD sum rule approach [25, 40]. In our previous work, it was found that$ \Sigma_c(2800) $ might favor the$ J^P = 3/2^- $ state$|\Sigma_c\; ^2P_{\lambda} {3}/{2}^- \rangle$ or the$ J^P = 5/2^- $ state$|\Sigma_c\; ^4P_{\lambda} {5}/{2}^- \rangle$ in the$ L $ -$ S $ coupling scheme [17].$|J^P,j\rangle$ 

Ref. [28] Ref. [29] Ref. [12] Ref. [11] Ref. [83] Ref. [84] Observed state $|J^P = {1}/{2}^+,1\rangle$ 

2439 2443 2460 2440 2456 2452 $\Sigma_c(2455)$ 

$|J^P = {3}/{2}^+,1\rangle$ 

2518 2519 2523 2495 2515 2501 $\Sigma^*_c(2520)$ 

$|J^P = {1}/{2}^-,0\rangle$ 

2795 2713 2802 2765 2702 2832 $\Sigma_c(2755)$ ?

$|J^P = {1}/{2}^-,1\rangle$ 

2805 2799 2826 2770 2765 2841 $\Sigma_c(2746)$ ?

$|J^P = {3}/{2}^-,1\rangle$ 

2761 2773 2807 2770 2785 2812 $\Sigma_c(2796)$ ?

$|J^P = {3}/{2}^-,2\rangle$ 

2799 2798 2837 2805 2798 2822 $\Sigma_c(2813)$ ?

$|J^P = {5}/{2}^-,2\rangle$ 

2790 2789 2839 2815 2790 2796 $\Sigma_c(2840)$ ?

Table 2. Predicted mass spectrum of
$1S$ -wave and$\lambda$ -mode$1P$ -wave$\Sigma_c$ states belonging to the$\mathbf{6}_F$ multiplet in various quark models. The$\Sigma_c$ states are denoted by$|J^P,j\rangle$ in the$j$ -$j$ coupling scheme, where$j$ stands for the total angular momentum quantum number of the two light quarks. The unit of mass is MeV.In this study, we revisit the
$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ baryon states. The main aims are as follows: (i) the spectrum was classified in the$ L $ -$ S $ coupling scheme in our previous work [17], where configuration mixing between two different states with the same$ J^P $ numbers, which may be caused by antisymmetric spin-orbit forces, is not considered. This configuration mixing may affect some of our predictions, thus, we include this effect here by adopting the$ j $ -$ j $ coupling scheme. (ii) We hope to provide more reliable predictions for the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ baryon states by combining the information from the most recent observations of the$ \Xi_c(X) $ and$ \Omega_c(X) $ states.This paper is organized as follows. In Sec. II, we provide a quark model classification of the singly heavy baryon states and the mass analysis of the
$ \lambda $ -mode$ 1P $ -wave$ \Sigma_c $ states by incorporating the recent observations of the singly-heavy baryons. Then, according to our chiral quark model calculations, their strong decay properties are discussed in Sec. III. To determine the contributions of the$ P $ -wave$ \Sigma_c $ states to the experimentally observed$ \Sigma_c(2800) $ resonance [86], we further analyze the$ \Lambda_c\pi $ invariant mass spectrum measured by$ BABAR $ [88] in Sec. IV. Finally, we summarize our results in Sec. V. -
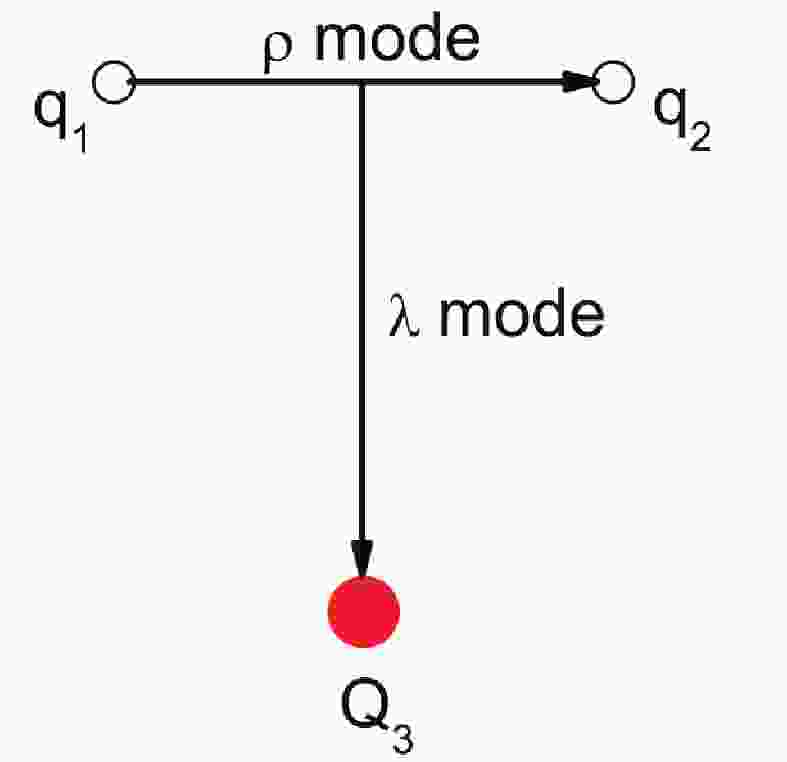
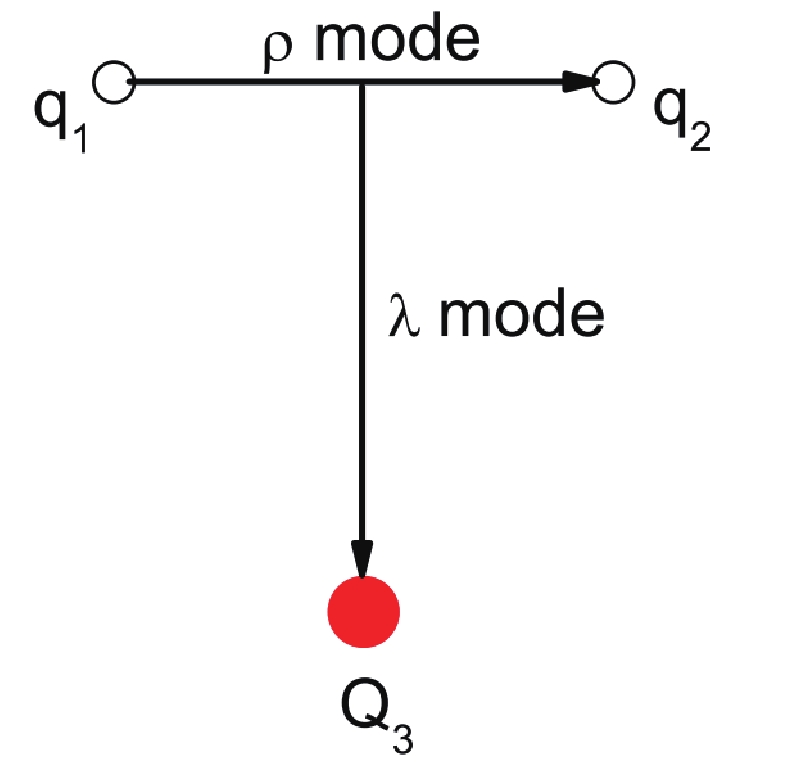
For a singly heavy baryon system
$ q_1q_2Q_3 $ , shown in Fig. 1, it is convenient to introduce two Jacobi coordinates,$ {\boldsymbol{\rho}} = \dfrac{1}{\sqrt{2}}(\mathbf{r}_1-\mathbf{r}_2), $

(1) $ {\boldsymbol{\lambda}} = \dfrac{1}{\sqrt{6}}(\mathbf{r}_1+\mathbf{r}_2-2\mathbf{r}_3), $

(2) where
$ \mathbf{r}_{1} $ and$ \mathbf{r}_{2} $ are coordinates for the light quarks$ q_1 $ and$ q_2 $ , respectively, while$ \mathbf{r}_3 $ is the coordinate for the heavy quark$ Q_3 $ . The orbital/radial excitation appearing between the light quarks$ q_1 $ and$ q_2 $ with a Jacobi coordinate$ \boldsymbol{\rho}$ is denoted by "$ \rho $ -mode", while the excitation appearing between the light diquark$ q_1q_2 $ and heavy quark$ Q_3 $ with a Jacobi coordinate$ \boldsymbol{\lambda} $ is denoted by "$ \lambda $ -mode".The heavy baryon containing a heavy quark violates the SU(4) symmetry. However, the SU(3) symmetry between the other two light quarks (
$ u $ ,$ d $ , or$ s $ ) is approximately kept. According to this symmetry, heavy baryons containing a single heavy quark belong to two different SU(3) flavor representations: the symmetric sextet$ \mathbf{6}_F $ and antisymmetric antitriplet$ \bar{\mathbf{3}}_F $ [17]. For charmed baryons$ \Lambda_c $ and$ \Xi_c $ belonging to$ \bar{\mathbf{3}}_F $ , the antisymmetric flavor wave functions can be written as$ \begin{array}{l} \phi^c_{\bar{\mathbf{3}}} = \begin{cases} \dfrac{1}{\sqrt{2}}(ud-du)c &{\rm{for}}\; \Lambda_c^+,\\ \dfrac{1}{\sqrt{2}}(us-su)c &{\rm{for}}\; \Xi_c^+,\\ \dfrac{1}{\sqrt{2}}(ds-sd)c &{\rm{for}}\; \Xi_c^0. \end{cases} \end{array} $

(3) For the charmed baryons belonging to
$ \mathbf{6}_F $ , the symmetric flavor wave functions can be written as$ \begin{array}{l}\phi^c_{\mathbf{6}} = \begin{cases} uuc &{\rm{for}}\; \Sigma^{++}_c,\\ \dfrac{1}{\sqrt{2}}(ud+du)c &{\rm{for}}\; \Sigma_c^+,\\ ddc &{\rm{for}}\; \Sigma^{0}_c,\\ \dfrac{1}{\sqrt{2}}(us+su)c &{\rm{for}}\; \Xi_c^{'+},\\ \dfrac{1}{\sqrt{2}}(ds+sd)c &{\rm{for}}\; \Xi_c^{'0},\\ ssc &{\rm{for}}\; \Omega_c^0. \end{cases} \end{array} $

(4) Furthermore, the heavy-quark symmetry as an approximation is commonly adopted for the study of the singly heavy baryons. In the heavy-quark symmetry limit, the quark model states may favor the
$ j $ -$ j $ coupling scheme [10]:$ \left|J^P,j\right\rangle = \left|\left\{\left[\left(\ell_\rho \ell_\lambda\right)_L s_{\rho}\right]_js_Q\right\}_{J^P}\right\rangle, $

(5) where
$ \ell_\rho $ and$ \ell_\lambda $ correspond to the quantum numbers of the orbital angular momentum$ {\boldsymbol{\ell}}_\rho $ within the light diquark and the orbital angular momentum$ {\boldsymbol{\ell}}_\lambda $ between the light diquark and the heavy quark, respectively;$ s_{\rho} $ and$ s_{Q} $ correspond to quantum numbers of the spins$ \mathbf{s}_{\rho} $ and$ \mathbf{s}_Q $ of the light diquark and heavy quark, respectively;$ L $ stands for the quantum number of the total orbital angular momentum$ \mathbf{L} = {\boldsymbol{\ell}}_\rho+ {\boldsymbol{\ell}}_\lambda $ ;$ j $ is the quantum number of the total angular momentum$ \mathbf{j} = {\boldsymbol{\ell}}_\rho+ {\boldsymbol{\ell}}_\lambda+\mathbf{s}_{\rho} $ of the light diquark, which is conserved in the heavy quark symmetry limit; and$ J $ is the quantum number of the total angular momentum$ \mathbf{J} = \mathbf{j}+\mathbf{s}_Q $ of the heavy baryon system. The parity of the state is determined by$ P = (-1)^{\ell_\rho+\ell_\lambda} $ . In the$ j $ -$ j $ coupling scheme, there are five$ \lambda $ -mode$ P $ -wave states belonging to$ \mathbf{6}_F $ :$|J^P = {1}/{2}^-,0\rangle$ ,$|J^P = {1}/{2}^-,1\rangle$ ,$|J^P = {3}/{2}^-,1\rangle$ ,$|J^P = {3}/{2}^-,2\rangle$ , and$|J^P = {5}/{2}^-,2\rangle$ . Their corresponding quantum numbers are displayed in Table 3.$|J^P,j \rangle$ 

$J^P$ 

$j$ 

$\ell_{\rho}$ 

$\ell_{\lambda}$ 

$L$ 

$s_{\rho}$ 

$s_{Q}$ 

$S$ 

$|J^P= {1}/{2}^-,0\rangle$ 

$\dfrac{1}{2}^-$ 

0 0 1 1 1 $\dfrac{1}{2}$ 

$\dfrac{1}{2},\,\dfrac{3}{2}$ 

$|J^P= {1}/{2}^-,1\rangle$ 

$\dfrac{1}{2}^-$ 

1 0 1 1 1 $\dfrac{1}{2}$ 

$\dfrac{1}{2},\,\dfrac{3}{2}$ 

$|J^P= {3}/{2}^-,1\rangle$ 

$\dfrac{3}{2}^-$ 

1 0 1 1 1 $\dfrac{1}{2}$ 

$\dfrac{1}{2},\,\dfrac{3}{2}$ 

$|J^P= {3}/{2}^-,2\rangle$ 

$\dfrac{3}{2}^-$ 

2 0 1 1 1 $\dfrac{1}{2}$ 

$\dfrac{1}{2},\,\dfrac{3}{2}$ 

$|J^P= {5}/{2}^-,2\rangle$ 

$\dfrac{5}{2}^-$ 

2 0 1 1 1 $\dfrac{1}{2}$ 

$\dfrac{3}{2}$ 

Table 3. Classification of the
$\lambda$ -mode$1P$ -wave singly heavy baryon states belonging to$\mathbf{6}_F$ in the$j$ -$j$ coupling scheme. The states in the$j$ -$j$ coupling scheme are denoted by$|J^P,j \rangle$ .The states within the
$ j $ -$ j $ coupling scheme are linear combinations of the configurations within the$ L $ -$ S $ coupling scheme, in which the quark model configurations are constructed by$ \left|^{2S+1}L_{J}\right\rangle = \left|\left[\left(\ell_\rho \ell_\lambda\right)_L\left(s_{\rho}s_Q\right)_S\right]_{J^P}\right\rangle, $

(6) where
$ S $ stands for the quantum number of the total spin angular momentum$ \mathbf{S} = \mathbf{s}_{\rho}+\mathbf{s}_Q $ . In the$ L $ -$ S $ coupling scheme, there are also five$ \lambda $ -mode$ P $ -wave states:$|1^{2}P_\lambda {1}/{2}^-\rangle$ ,$|1^{2}P_\lambda {3}/{2}^-\rangle$ ,$|1^{4}P_\lambda {1}/{2}^-\rangle$ ,$|1^{4}P_\lambda {3}/{2}^-\rangle$ , and$|1^{4}P_\lambda {5}/{2}^-\rangle$ . The relationship between the$ j $ -$ j $ and$ L $ -$ S $ coupling schemes is given by [10]$ \begin{aligned}[b] \left|\left\{\left[\left(\ell_\rho \ell_\lambda\right)_Ls_{\rho}\right]_js_Q\right\}_{J^P}\right\rangle =& (-1)^{L+s_\rho+J+\dfrac{1}{2}}\sqrt{2j+1} \sum_{S}\sqrt{2S+1} \; \; \\& \times\begin{Bmatrix}L &s_\rho &j\\s_Q &J &S \end{Bmatrix} \left|\left[\left(\ell_\rho \ell_\lambda\right)_L\left(s_{\rho}s_Q\right)_S\right]_{J^P}\right\rangle.\;\end{aligned}$

(7) The heavy quark symmetry may suggest that there is configuration mixing between singly heavy baryon states with the same
$ J^P $ numbers in the$ L $ -$ S $ coupling scheme. In the heavy quark limit, the mixing angles are determined by Eq. (7). The two$ J^P = 1/2^- $ states,$|J^P = {1}/{2}^-,0\rangle$ and$|J^P = {1}/{2}^-,1\rangle$ in the$ j $ -$ j $ scheme, are mixed states between$|^{2}P_\lambda {1}/{2}^-\rangle$ and$|^{4}P_\lambda {1}/{2}^-\rangle$ of the$ L $ -$ S $ coupling scheme with a mixing angle of$ \phi\simeq35^\circ $ . The two$ J^P = 3/2^- $ states,$|J^P = {3}/{2}^-,1\rangle$ and$|J^P = {3}/{2}^-,2\rangle$ , are mixed states via$|^{2}P_\lambda {3}/{2}^-\rangle$ -$|^{4}P_\lambda {3}/{2}^-\rangle$ mixing with a relatively small angle of$ \phi\simeq24^\circ $ . -
For
$ \Lambda_Q $ ,$ \Sigma_Q $ , and$ \Omega_Q $ ($ Q = c/b $ ) systems containing two light quarks with an equal mass$ m_q $ and one heavy quark with a mass$ m_Q $ , considering the simplified case of the harmonic oscillator potentials, the oscillator frequencies$ \omega_\rho $ and$ \omega_\lambda $ for the$ \lambda $ - and$ \rho $ -mode excitations satisfy the relation [12, 16, 17, 89]$ \dfrac{\omega_\lambda}{\omega_\rho} = \sqrt{\dfrac{1}{3}+\dfrac{2m_q}{3m_Q}}. $

(8) This relation approximately holds for
$ \Xi_Q $ ($ Q = b,c $ ) baryon systems as well, as the masses of$ m_{u/d} $ and$ m_s $ may be considered to be approximately equal in the SU(3) limit. From Eq. (8), when$ m_Q\gg m_q $ , the$ \lambda $ -mode excited energy is smaller than that of the$ \rho $ mode,$ \omega_\lambda<\omega_\rho $ . In the heavy quark limit,$ m_{Q} \to \infty $ , there is no mixing between the$ \lambda $ - and$ \rho $ -mode excitations [10-12]. This is due to the spin-dependent interaction, which causes the mixing, being suppressed by a factor of$ 1/m_Q $ . For the singly charm and bottom baryons, the$ \lambda $ - and$ \rho $ -modes are well separated [10,12]. For example, Yoshida et al. showed the probability of the$ \lambda $ - and$ \rho $ -modes of$ J^P = 1/2^- $ for the lowest$ \Sigma_Q $ and$ \Lambda_Q $ as a function of the heavy quark mass$ m_Q $ in Fig. 10 of their article [12]. One sees that the lowest state is almost purely in the$ \lambda $ -mode at$ m_Q\geqslant 1.5 $ GeV. It should be mentioned that in the SU(3) limit, i.e.,$ m_{Q} = m_q $ , the excited energies of the$ \lambda $ - and$ \rho $ -modes degenerate,$ \omega_\lambda = \omega_\rho $ ; while the$ \lambda $ - and$ \rho $ -modes in the light baryon systems are largely mixed. The relatively small excitation energy of the$ \lambda $ -mode indicates that a$ \lambda $ -mode excitation should be more easily formed than a$ \rho $ -mode excitation. This may explain why most of the newly observed singly heavy baryons,$ \Omega_c(X) $ ,$ \Omega_b(X) $ ,$ \Xi_c(X) $ ,$ \Sigma_b(6097)^{\pm} $ , and$ \Xi_b(6227)^0 $ , may favor the$ \lambda $ -mode excitations, as predicted in the literature [16, 17, 19, 38-40, 42-46, 48-56].In the
$ P $ -wave$ \Sigma_c $ states, there are two$ \rho $ -mode excitations:$ J^P = 1/2^- $ and$ J^P = 3/2^- $ , and five$ \lambda $ -mode excitations:$\Sigma_c|J^P = {1}/{2}^-,0\rangle$ ,$\Sigma_c|J^P = {1}/{2}^-,1\rangle$ ,$\Sigma_c|J^P = {3}/{2}^-, $ $ 1\rangle$ ,$\Sigma_c|J^P = {3}/{2}^-,2\rangle$ , and$\Sigma_c|J^P = {5}/{2}^-,2\rangle$ . In this study, we focus on the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ baryon states. There is a high likelihood that they will be discovered in future experiments, as many$ \lambda $ -mode-like states have been observed in the$ \Omega_c $ ,$ \Xi_c' $ ,$ \Xi'_b $ ,$ \Omega_b $ , and$ \Sigma_b $ families in recent years. Many theoretical approaches, such as the relativized quark model [11], relativistic quark model [28, 29, 82], non-relativistic quark model [10, 12, 24, 62, 83, 84], lattice QCD [26, 27], QCD sum rules [25, 32, 85], and others have been adopted in the literature to calculate the mass spectrum. In Table 2, we display some masses for the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states predicted within the heavy-quark-light-diquark approximation in both the relativistic quark model [28, 29] and non-relativistic quark model [83], using predicted using the hypercentral approximation in the non-relativistic quark model [84] and by strictly solving the three body problem in the relativized quark model [11] and non-relativistic quark model [12]. The masses predicted using various approaches with different approximations are comparable to each other, at$ \sim 2.71-2.84 $ GeV. Although, there is an obvious gap between the$ \rho $ - and$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states. The masses for the two$ \rho $ -mode$ P $ -wave$ \Sigma_c $ states with$ J^P = 1/2^- $ and$ 3/2^- $ are predicted to be$ \sim 2.85-2.91 $ GeV [11, 12], which is$ \sim70 $ MeV larger than the highest$ \lambda $ -mode excitation.The
$ \Sigma_c(2800) $ structure observed in experiments [87, 88] is just within the predicted mass range of$ \lambda $ -mode$ 1P $ -wave excitations. However, the predicted mass order and mass splitting between the$ P $ -wave spin multiplets is different for various models. Fortunately, one can determine the mass order and mass splitting for the$ 1P $ -wave$ \Sigma_c $ states from the newly observed$ \Xi_c(X) $ and$ \Omega_c(X) $ states. In our previous work [56], the$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ ,$ \Omega_c(3065) $ , and$ \Omega_c(3090) $ resonances were predicted to be the$ \lambda $ -mode$ 1P $ -wave states with$ J^P = 1/2^- $ ,$ J^P = 3/2^- $ ,$ J^P = 3/2^- $ , and$ J^P = 5/2^- $ , respectively. The newly observed states,$ \Xi_c(2923) $ ,$ \Xi_c(2939) $ , and$ \Xi_c(2965) $ , could be the flavor partners of$ \Omega_c(3050) $ ,$ \Omega_c(3065) $ , and$ \Omega_c(3090) $ , respectively [16, 54, 56].The equal spacing rule [94, 95] perfectly holds for the newly observed
$ \Xi_c(X) $ and$ \Omega_c(X) $ states, i.e.,$ \begin{array}{l} \quad m[\Omega_c(3050)]-m[\Xi_c(2923)^0]\\ \simeq m[\Omega_c (3066)] -m[\Xi_c(2939)^0]\\ \simeq m[\Omega_c(3090)]-m[\Xi_c(2965)^0]\simeq 125\;{\rm{MeV}}. \end{array} $

The equal spacing rule also perfectly holds for the
$ J^P = 3/2^+ $ charmed ground states:$ \begin{array}{l} \quad m[\Omega_c(2770)^0]- m[\Xi_c(2645)^0]\\ \simeq m[\Xi_c(2645)^0]-m[\Sigma_c(2520)^0]\simeq 125\;{\rm{MeV}}. \end{array} $

For the
$ J^P = 1/2^+ $ charmed ground states, the equal spacing rule also holds:$ m[\Omega_c]- m[\Xi'_c] $ $ \simeq m[\Xi'_c]-m[\Sigma_c]\simeq $ $ 120 $ MeV. Thus, the equal spacing rule is potentially universal for the charmed baryon states. Based on this, we predict that for the charmed baryon sector, the flavor partners of the four$ \Omega_c(X) $ states,$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ ,$ \Omega_c(3065) $ and$ \Omega_c(3090) $ , are likely to be$ \begin{array}{l}\Omega_c(3000): \Xi_{c}(2873)?, \Sigma_{c}(2746)?, \\ \Omega_c(3050): \Xi_{c}(2923),\ \Sigma_{c}(2796)?,\\ \Omega_c(3065): \Xi_{c}(2939),\ \Sigma_{c}(2813)?,\\ \Omega_c(3090): \Xi_{c}(2965),\ \Sigma_{c}(2840)?,\end{array} $

respectively. The states labeled with "
$ ? $ " are yet to be discovered by current experiments. Finally, the equal spacing rule can be further confirmed using other experimentally observed baryon and meson states. For example, the equal spacing rule holds:(i) for the
$ J^P = 3/2^+ $ light ground baryon states,$ \begin{array}{l} \quad m[\Omega(1672)]- m[\Xi(1530)]\\ \simeq m[\Xi(1530)]-m[\Sigma(1385)] \\ \simeq m[\Sigma(1385)]- m[\Delta(1232)]\simeq 145 \;{\rm{MeV}}; \end{array} $

(ii) for the well-established light unflavored
$ n\bar{n} $ ($ n = u,d $ ) and$ s\bar{s} $ meson states,$ \begin{array}{l} \quad m[\phi(1020)]-m[\omega(782)] \\ \simeq m[h_1(1380)]-m[h_1(1170)] \\ \simeq m[f_2(1270)]-m[f_2'(1520)]\simeq 240\;{\rm{MeV}}; \end{array} $

(iii) and for the
$ D $ and$ D_s $ meson states,$ \begin{array}{l} \quad m[D_s(1968)]-m[D(1865)^0]\\ \simeq m[D_s^*(2112)]-m[D^*(2007)^0] \\ \simeq m[D_{s1}(2536)]-m[D_1(2420)^0]\\ \simeq m[D_{s2}(2573)]-m[D_2(2460)^0]\simeq 105\;{\rm{ MeV}}. \end{array} $

Less is known about the
$ P $ -wave state$|J^P = {1}/{2}^-,0\rangle$ , with the only hint coming from the recent LHCb experiments, with a broad structure$ \Xi_c(2880) $ found in the$ \Lambda_c^+K^- $ mass spectrum with a small significance [5]. This$ \Xi_c(2880) $ may be a candidate for$|J^P = {1}/{2}^-,0\rangle$ in the$ \Xi_c' $ family. Thus, according to the equal spacing rule [94,95], the masses of the$\Sigma_c|J^P = {1}/{2}^-,0\rangle$ and$\Omega_c|J^P = {1}/{2}^-,0\rangle$ state are predicted to be 2755 and 3005 MeV, respectively. The two$ P $ -wave$ J^P = 1/2^- $ states,$|J^P = {1}/{2}^-,1\rangle$ and$ |J^P =|J^P = {1}/{2}^-,0\rangle$ , may be largely overlapping. It is worth mentioning that for the$ \lambda $ -mode$ P $ -wave states there is no place for$ \Omega_c(3119) $ , which was observed by LHCb [1]. The$ \Omega_c(3119) $ may be a candidate for the$ \lambda $ -mode$ 2S $ states with$ J^P = 1/2^+ $ or$ J^P = 3/2^+ $ [56]. Combining this assumption with the equal spacing rule, the masses of the$ \lambda $ -mode$ 2S $ state of$ \Sigma_c $ and$ \Xi_c $ are predicted to be approximately 2869 and 2994 MeV, respectively.By combining the precise experimental data of
$ \Omega_c(X) $ and$ \Xi_{c}(X) $ with the equal spacing rule [94, 95], we can determine the masses for the$ \Sigma_c(X) $ states model-independently as corresponding flavor partners of$ \Omega_c(X) $ and$ \Xi_{c}(X) $ . Then, according to our previous analysis of the strong decays and masses, the newly observed resonances$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ /$ \Xi_c(2923) $ ,$ \Omega_c(3065) $ /$ \Xi_c(2939) $ , and$ \Omega_c(3090) $ /$ \Xi_c(2965) $ can be naturally explained as the$ \lambda $ -mode$ 1P $ -wave states with$ J^P = 1/2^- $ ,$ J^P = 3/2^- $ ,$ J^P = 3/2^- $ , and$ J^P = 5/2^- $ , respectively [16, 17, 54, 56]. Finally, combining the masses determined from the equal spacing rule with possible configurations based on our previous analysis, we predict a mass spectrum for the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states, which are summarized in Table 2. For clarity and comparison, we also plot the mass spectra of the$ \lambda $ -mode$ P $ -wave$ \Omega_c $ ,$ \Xi_c $ and$ \Sigma_c $ baryon states in Fig. 2.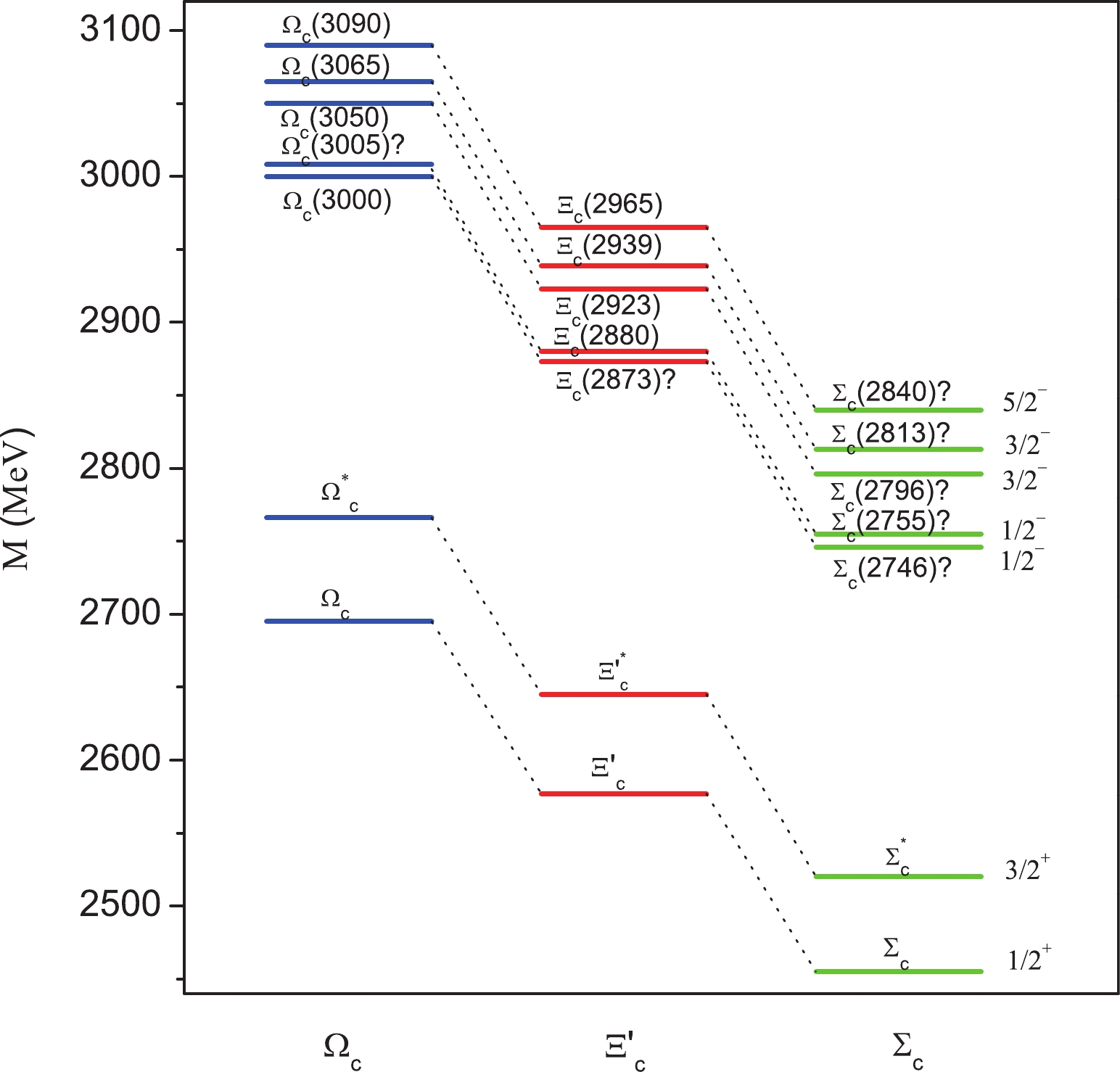
Figure 2. (color online) Mass spectra of the
$1S$ and$1P$ -wave$\Omega_c$ ,$\Xi_c'$ and$\Sigma_c$ baryon states belonging to$\mathbf{6}_F$ , predicted by combining the equal spacing rule with the recent observations of$\Omega_c(X)$ and$\Xi_c(X)$ baryons.Finally, it should be emphasized that the equal spacing rule perfectly holds for the
$ 1S $ -wave ground charmed baryon states$ \Sigma_c^{(*)} $ ,$ \Xi_c'^{(*)} $ and$ \Omega_c^{(*)} $ , which is illustrated in Fig. 2. Considering the newly observed$ \Omega_c(X) $ and$ \Xi_{c}(X) $ resonances as the$ \lambda $ -mode$ 1P $ -wave states, from Fig. 2 we observe that the equal spacing rule also holds for these higher excitations. This indicates that the equal spacing rule should hold for all$ 1P $ -wave charmed states. Thus, combining the equal spacing rule with the observations, a fairly reliable and precise prediction of the$ P $ -wave$ \Sigma_c $ states in a certain mass region can be obtained, as displayed in Fig. 2. The masses obtained with the equal spacing rule are comparable to the quark model predictions [11, 12, 28, 29, 83], although a precise prediction cannot be obtained by these models due to typical uncertainties of approximately 10s to 100 MeV. -
Combining the decay properties with the masses of the
$ P $ -wave$ \Sigma_c $ states can provide crucial references in searching for them in future experiments. In this study, we reinvestigate the strong decay properties of$ 1P $ -wave$ \Sigma_c $ baryons with the chiral quark model [96], which has been successfully applied to the strong decays of heavy-light mesons, and charmed and strange baryons [14,16,17,53-56,89,97-106]. In this model, the nonrelativistic transition operator for a strong decay process by emitting a pseudoscalar meson is adopted as [107-109]$ \begin{aligned}[b] H^{nr}_{m} =& \sum_j\Big\{\dfrac{\omega_m}{E_f+M_f} {\boldsymbol{\sigma}}_j\cdot {\bf{P}}_f+ \dfrac{\omega_m}{E_i+M_i} {\boldsymbol{\sigma}}_j \cdot {\bf{P}}_i \\& - {\boldsymbol{\sigma}}_j \cdot {\bf{q}} +\dfrac{\omega_m}{2\mu_q} {\boldsymbol{\sigma}}_j\cdot {\bf{p}}'_j\Big\}I_j {\rm e}^{-{\rm i}\mathbf{q}\cdot \mathbf{r}_j}, \end{aligned}$

(9) where
$ (E_i,\; M_i,\; \mathbf{P}_i) $ and$ (E_f,\; M_f,\; \mathbf{P}_f) $ denote the energy, mass, and three-vector momentum of the initial and final baryons, respectively;$ \omega_m $ and$ \mathbf{q} $ represent the energy and three-vector momentum of the final light pseudoscalar meson;$ \mathbf{\sigma}_j $ is the Pauli spin vector on the$ j $ th quark;$ \mathbf{p}'_j ( = \mathbf{p}_j-(m_j/M)\mathbf{P}_{\text{c.m.}}) $ denotes the internal momentum of the$ j $ th quark in the baryon rest frame; and$ \mu_q $ is a reduced mass, expressed as$ 1/\mu_q = 1/m_j+1/m'_j $ . The isospin operator$ I_j $ associated with$ \pi $ mesons has been defined in Refs. [107-109]. Using the wave functions for the initial and final baryon states, the transition amplitude$ \mathcal{M} $ of a decay process can be determined. For simplicity, harmonic oscillator wave functions are adopted for the initial and final baryon states in our calculations.The partial decay width for a decay process can be calculated using [89, 98]
$ \Gamma = \left(\dfrac{\delta}{f_m}\right)^2\dfrac{(E_f +M_f)|\mathbf{q}|}{4\pi M_i}\dfrac{1}{2J_i+1}\sum_{J_{iz}J_{fz}}|\mathcal{M}_{J_{iz},J_{fz}}|^2, $

(10) where
$ J_{iz} $ and$ J_{fz} $ are the third components of the total angular momenta of the initial and final baryons, respectively, and$ \delta $ is a global parameter accounting for the strength of the quark-meson couplings. Here, its value is fixed to that in Refs. [89, 98],$ \delta = 0.557 $ .For the calculations, the masses of well-established hadrons were taken from the Particle Data Group [86] and the standard quark model parameters have been determined previously [17]. For the harmonic oscillator space-wave functions,
$ \Psi^n_{lm} = R_{nl}Y_{lm} $ , the harmonic oscillator parameter$ \alpha_{\rho} $ in the wave functions for a$ uu/ud/dd $ system is taken as$ \alpha_{\rho} = 400 $ MeV. Another harmonic oscillator parameter$ \alpha_{\lambda} $ is related to$ \alpha_{\rho} $ by$ \alpha_{\lambda} = [3m_c/(2m_q+m_c)]^{1/4}\alpha_{\rho} $ , where$ m_q $ and$ m_c $ denote the light$ u/d $ quark mass and heavy charmed$ c $ quark mass, respectively. Here, we take$ m_q = 330 $ MeV and$ m_c = 1480 $ MeV. -
Using the predicted masses of the
$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states from the mass spectrum analysis in the above section, their strong decay properties are calculated using the chiral quark model. The predicted results are displayed in Table 4.State $|J^P,j\rangle$ 

Channel $\Gamma_{i}$ 

$\mathcal{B}_i$ 

$\Sigma_c(2746)$ 

$|J^P= {1}/{2}^-,1\rangle$ 

$\Lambda_c\pi$ 

$\cdot\cdot\cdot$ 

$\cdot\cdot\cdot$ 

$\Sigma_c\pi$ 

$28.06$ 

98.00% $\Sigma_c^*\pi$ 

$0.47$ 

2.00% total $28.53$ 

$\Sigma_c(2755)$ 

$|J^P= {1}/{2}^-,0\rangle$ 

$\Lambda_c\pi$ 

$15.23$ 

100.00% $\Sigma_c\pi$ 

$\cdot\cdot\cdot$ 

$\cdot\cdot\cdot$ 

$\Sigma_c^*\pi$ 

$\cdot\cdot\cdot$ 

$\cdot\cdot\cdot$ 

total $15.23$ 

$\Sigma_c(2796)$ 

$|J^P= {3}/{2}^-,1\rangle$ 

$\Lambda_c\pi$ 

$\cdot\cdot\cdot$ 

$\cdot\cdot\cdot$ 

$\Sigma_c\pi$ 

$3.21$ 

10.43% $\Sigma_c^*\pi$ 

$27.57$ 

89.57% total $30.78$ 

$\Sigma_c(2813)$ 

$|J^P= {3}/{2}^-, 2\rangle$ 

$\Lambda_c\pi$ 

$30.59$ 

75.42% $\Sigma_c\pi$ 

$7.53$ 

18.57% $\Sigma_c^*\pi$ 

$2.44$ 

6.01% total $40.56$ 

$\Sigma_c(2840)$ 

$|J^P= {5}/{2}^-,2\rangle$ 

$\Lambda_c\pi$ 

$37.63$ 

73.96% $\Sigma_c\pi$ 

$4.90$ 

9.63% $\Sigma_c^*\pi$ 

$8.35$ 

16.41% total $50.88$ 

Table 4. Strong decay properties of the
$\lambda$ -mode$P$ -wave$\Sigma_c$ states. The$\Sigma_c$ states are denoted by$|J^P,j\rangle$ in the$j$ -$j$ coupling scheme. The units of the partial widths$\Gamma_{i}$ and masses of the resonances are both MeV.The two
$ j = 1 $ states,$\Sigma_c(2746)|J^P = $ $ {1}/{2}^-,1\rangle$ and$\Sigma_c(2796)|J^P = {3}/{2}^-,1\rangle$ , should have very small decay rates into the$ \Lambda_c \pi $ final state, as this decay mode is forbidden in the heavy quark symmetry limit. The$\Sigma_c(2746)|J^P = $ $ {1}/{2}^-,1\rangle$ and$\Sigma_c(2796)|J^P = {3}/{2}^-,1\rangle$ states have similar widths of$ \Gamma\simeq 30 $ MeV, and predominantly decay into$ \Sigma_c\pi $ and$ \Sigma_c^*\pi $ , respectively. To established these two states, the$ \Lambda_c\pi\pi $ ($ \Sigma_c^{(*)}\pi\to \Lambda_c\pi\pi $ ) invariant mass spectrum should be observed in future experiments.The two
$ j = 2 $ states,$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840) |J^P = {5}/{2}^-,2\rangle$ , predominantly decay into the$ \Lambda_c\pi $ channel with a comparable branching fraction of$ \sim 75 $ %. Additionally, they have relatively large decay rates into$ \Sigma_c\pi $ and$ \Sigma_c^*\pi $ final states, with branching fractions of$ \sim 10 $ %. The decay widths for the$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ states are predicted to be$ \Gamma\simeq 41 $ and$ 51 $ MeV, respectively. These two states might contribute to the$ \Sigma_c(2800) $ structure observed in the$ \Lambda_c\pi $ invariant mass spectrum. It may be difficult to distinguish the$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ states from the$ \Lambda_c\pi $ invariant mass spectrum due to their highly overlapping masses, which is discussed later. Fortunately, as these two highly overlapping states have different$ J^P $ numbers, they may be separated by measuring the angular distributions.The
$ j = 0 $ state,$\Sigma_c(2755)|J^P = {1}/{2}^-,0\rangle$ , may be very narrow state with a width of$ \Gamma\simeq 15 $ MeV. Its decays are likely saturated by the$ \Lambda_c\pi $ channel, and the$ \Sigma_c\pi $ and$ \Sigma_c^*\pi $ decay modes are forbidden in the heavy quark symmetry limit. It might be interesting to search for this narrow state in the$ \Lambda_c\pi $ channel.Considering the case that the masses of the
$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states may be out of our predictions, in Fig. 3 we plot the strong decay properties as functions of the mass within a possible region, allowing the observation of the sensitivities of the decay properties to the mass. The uncertainties of the mass for the$ \lambda $ -mode$ P $ -wave$ \Sigma_c $ states do not affect our main conclusion.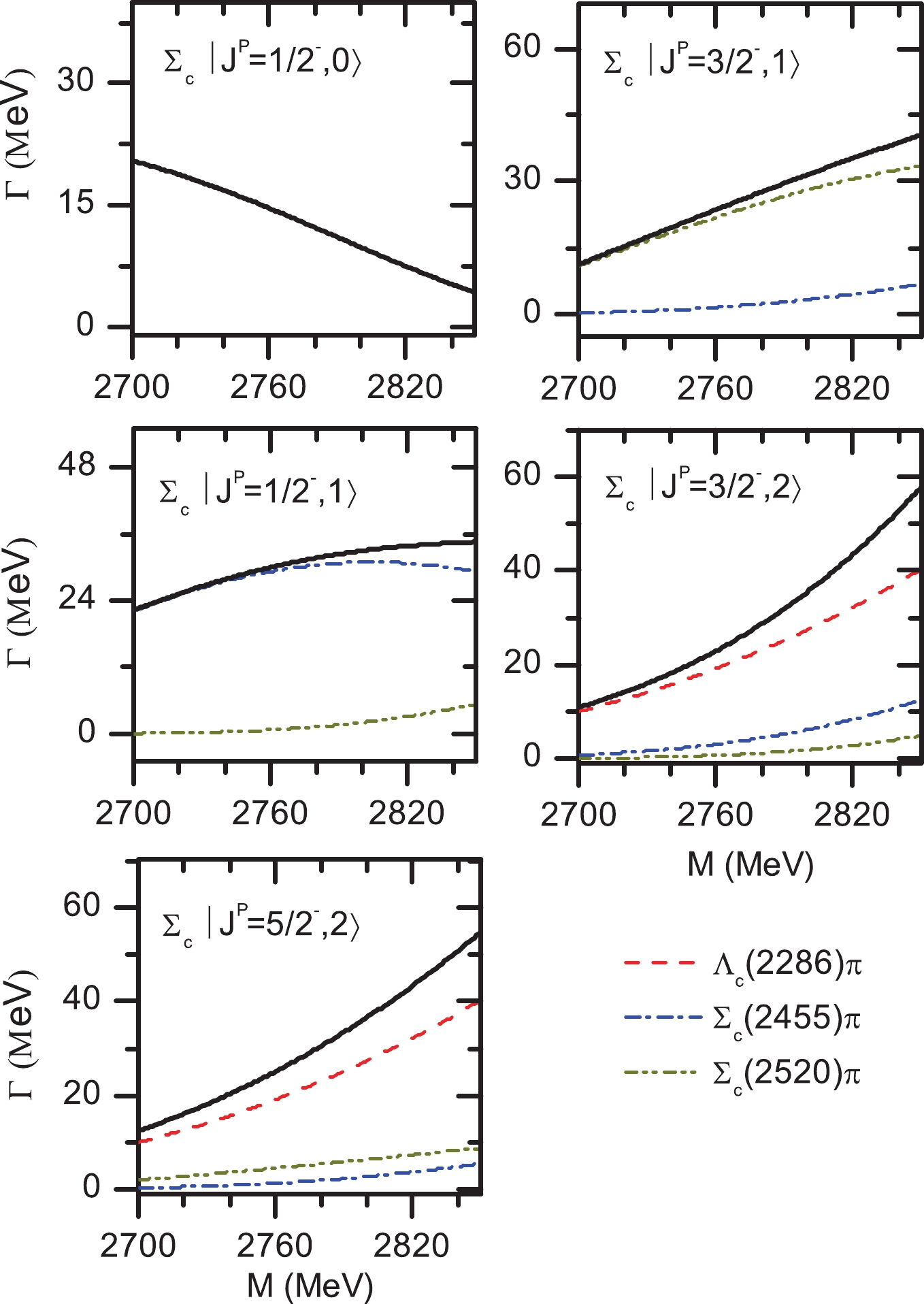
Figure 3. (color online) Strong decay properties of the
$\lambda$ -mode$1P$ -wave$\Sigma_c$ states as functions of the mass.Finally, the strong decay properties of the two
$ \rho $ -mode$ 1P $ -wave$ \Sigma_c $ states with$J^P = {1}/{2}^-$ and$J^P = {3}/{2}^-$ are also determined in this study. The$ \rho $ -mode$ 1P $ -wave states do not overlap with the$ \lambda $ -mode$ 1P $ -wave states according to the quark model predictions [11, 12]. Their masses were predicted to be$ M = 2909 $ and 2910 MeV in a recent study [12], which is approximately 70 MeV larger than that of the highest$ \lambda $ -mode$ P $ -wave state,$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ . Additionally, the$ \Lambda_c\pi $ decay mode is forbidden for the two$ \rho $ -mode$ 1P $ -wave$ \Sigma_c $ states. Taking the mass predicted in Ref. [12], we find the$J^P = {1}/{2}^-$ $ \rho $ -mode state has a width of$ \Gamma\simeq 78 $ MeV, and predominantly decays into$ \Sigma_c\pi $ and$ \Sigma_c^*\pi $ with branching fractions of$ \sim 65 $ % and$ \sim 35 $ %, respectively, while the$J^P = {3}/{2}^-$ state is relatively broad, with a width of$ \Gamma\simeq 90 $ MeV, and predominantly decays into$ \Sigma_c\pi $ and$ \Sigma_c^*\pi $ with branching fractions of$ \sim 25 $ % and$ \sim 75 $ %, respectively. -
To determine the contributions of the
$ P $ -wave$ \Sigma_c $ states to the experimentally observed$ \Sigma_c(2800) $ structure, we further analyze the$ \Lambda_c\pi $ invariant mass spectrum measured by$ BABAR $ [88]. In our analysis, we adopt a relativistic Breit-Wigner function to describe the event distribution:$ \dfrac{{\rm d}N}{{\rm d}m}\propto \left|f+\sum_R\dfrac{ C_R\mathcal{A}_R(m)\sqrt{\Phi (m)}}{m^2-m_R^2+i m_R\Gamma_R(m)}\right|^2, $

(11) where
$ m $ and$ m_{R} $ are the invariant mass and the resonance mass, respectively,$ \mathcal{A}_R(m) $ is the resonance strong decay amplitude for the$ \Lambda_c \pi $ channel, and$ \Gamma_R(m) $ denotes the energy-dependent total decay width of a resonance. The decay width of resonance is considered to be saturated by the two-body OZI-allowed strong decay modes. Thus, as an approximation,$ \Gamma^R(m) $ is a sum of the energy-dependent partial widths of all two-body OZI-allowed strong decay modes, calculated using the strong decay amplitudes extracted from our chiral quark model. Additionally,$ \Phi (m) $ is strong decay phase space and$ f $ represents the background contributions. In this study, a linear background,$ f = \sqrt{a +b m} $ , is adopted, where$ a\simeq248.0 $ MeV and$ b\simeq-67.0 $ , which were determined by fitting the backgrounds taken in Ref. [88]. Finally,$ \{C_R\} $ is a free parameter set related to the resonance production rates.According to our strong decay analysis, three
$ P $ -wave$ \Sigma_c $ states,$\Sigma_c(2755)|J^P = {1}/{2}^-,0\rangle$ ,$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ , predominantly decay into the$ \Lambda_c\pi $ channel. Due to the unknown production rates of these resonances, seven cases with different relative ratios,$ C_{\Sigma_c(2755)1/2^-}: C_{\Sigma_c(2813)3/2^-}:C_{\Sigma_c(2840)5/2^-} = 1:1: 1/0: $ $ 1:0/0: 0:1/1:2:1/1:1:1.5//1:2:2/0:1:1 $ , are considered to reproduce the$ \Lambda_c\pi $ invariant mass spectrum measured by$ BABAR $ with our predicted strong decay properties for the three resonances [88]. Our results are displayed in Figs. 4(a)-(g), respectively. Assuming the three resonances with$ J^P = 1/2^-,3/2^-,5/2^- $ have comparable production rates as illustrated in Figs. 4(a), (d), (e), and (f), the measured$ \Lambda_c\pi $ invariant mass spectrum can be described. In these cases,$\Sigma_c(2755)|J^P = {1}/{2}^-,0\rangle$ should contribute a very narrow peak to the invariant mass spectrum, while the interferences between$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ contribute to the main broad peak at approximately 2.8 GeV. The invariant mass spectrum may also be explained using the two state interferences between$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ [see Fig. 4(g)]. However, due to the large uncertainties, this analysis cannot exclude the possibility that the$ \Sigma_c(2800) $ structure is caused by a single resonance$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ or$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ [see Figs. 4(b) and (c)]. The measurements of the angular distributions are required to separate these two overlapping states.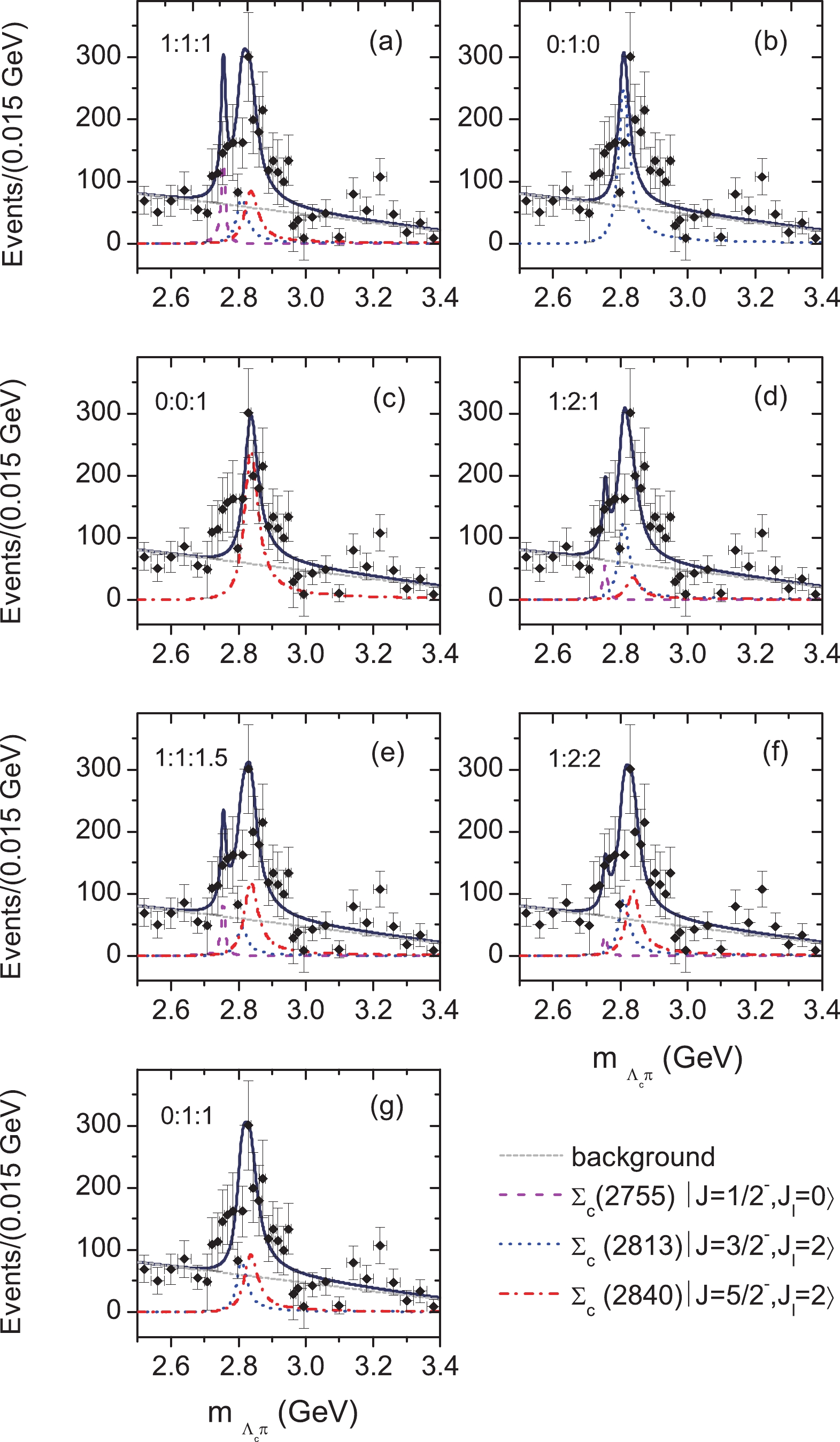
Figure 4. (color online) The
$\Lambda_c \pi$ invariant mass spectrum measured at$BABAR$ [88] (solid squares) compared to the theoretical description with three possible$\lambda$ -mode$1P$ -wave states,$\Sigma_c(2746)$ ,$\Sigma_c(2813)$ , and$\Sigma_c(2840)$ . The figures (a)-(e) show seven cases with different resonance production rate ratios,$C_{\Sigma_c(2755)1/2^-}:C_{\Sigma_c(2813)3/2^-}:C_{\Sigma_c(2840)5/2^-}= 1:1:1/0:1:0/ $ $ 0:0:1/1:2:1/1:1:1.5/1:2:2/0:1:1$ , respectively.According to our analysis of the
$ \Lambda_c\pi $ invariant mass spectrum, the$ \Sigma_c(2800) $ structure may be caused by two largely overlapping resonances,$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ , although an alternative explanation involving only one single resonance cannot be excluded. Evidence of the$\Sigma_c(2755)|J^P = {1}/{2}^-,0\rangle$ resonance, as a very narrow peak, may be seen in the$ \Lambda_c\pi $ invariant mass spectrum. More accurate measurements of the$ \Lambda_c\pi $ invariant mass spectrum along with the partial-wave analysis of the measured angular distributions are crucial for establishing$\Sigma_c(2755)|J^P = {1}/{2}^-,0\rangle$ ,$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ , and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ . -
In this study, by employing the equal spacing rule, the newly observed
$ \Xi_c(2923)^0 $ ,$ \Xi_c(2939)^0 $ , and$ \Xi_c(2965)^0 $ states appear to be flavor partners of$ \Omega_c(3050) $ ,$ \Omega_c(3066) $ , and$ \Omega_c(3090) $ , respectively. As the flavor partners of four$ P $ -wave candidates,$ \Omega_c(3000) $ ,$ \Omega_c(3050) $ ,$ \Omega_c(3066) $ , and$ \Omega_c(3090) $ , as suggested in the literature, four$ P $ -wave$ \Sigma_c $ baryon states,$ \Sigma_c(2746) $ ,$ \Sigma_c(2796) $ ,$ \Sigma_c(2813) $ , and$ \Sigma_c(2840) $ , are predicted using the equal spacing rule. According to our assignments for the$ \Omega_c(X) $ states,$ \Sigma_c(2746) $ ,$ \Sigma_c(2796) $ ,$ \Sigma_c(2813) $ , and$ \Sigma_c(2840) $ may correspond to the$ \lambda $ -mode$ P $ -wave states$ \Sigma_c|J^P = 1/2^-,1\rangle $ ,$ \Sigma_c|J^P = 3/2^-,1\rangle $ ,$\Sigma_c|J^P = 3/2^-,2\rangle$ , and$ \Sigma_c|J^P = 5/2^-,2\rangle $ , respectively, in the heavy quark symmetry limit.Furthermore, their strong decay properties are predicted using the chiral quark model. It is found that these
$ 1P $ -wave$ \Sigma_c $ states have relatively narrow widths, within the range of$ \sim 15-50 $ MeV. The$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ states have comparable decay widths of$ \Gamma\sim 40 $ MeV and predominantly decay into the$ \Lambda_c \pi $ channel. The$ \Sigma_c|J^P = 1/2^-,0\rangle $ state may be a very narrow state with a width of$ \Gamma\sim 15 $ MeV, with its decays nearly saturated by the$ \Lambda_c \pi $ channel. The$\Sigma_c(2755)|J^P = {1}/{2}^-,0\rangle$ ,$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ , and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ states may be established in the$ \Lambda_c\pi $ invariant mass spectrum with more accurate measurements and anglular distribution analysis in future experiments. The other two$ P $ -wave states,$\Sigma_c(2746)|J^P = {1}/{2}^-,1\rangle$ and$\Sigma_c(2796)|J^P = {3}/{2}^-,1\rangle$ , are relatively narrow states with widths of$ \Gamma\sim 30 $ MeV. Additionally, they mainly decay into$ \Sigma_c\pi $ and$ \Sigma^{*}_c\pi $ , respectively. To establish the existence of these two states, the$ \Lambda_c\pi\pi $ ($ \Sigma_c^{(*)}\pi\to \Lambda_c\pi\pi $ ) invariant mass spectrum is worth observing in future experiments.Then, using our predicted decay amplitudes, the
$ \Lambda_c\pi $ invariant mass spectrum measured by$ BABAR $ is further analyzed, which improves our understanding of the nature of$ \Sigma_c(2800) $ . It is found that the$ \Sigma_c(2800) $ structure can be explained with two largely overlapping resonances,$\Sigma_c(2813)|J^P = {3}/{2}^-,2\rangle$ and$\Sigma_c(2840)|J^P = {5}/{2}^-,2\rangle$ , although an alternate explanation with only one single resonance cannot be excluded. If the production rate of$\Sigma_c|J^P = 1/2^-,0\rangle$ is comparable with that of$\Sigma_c(2813)|J^P = 3/2^-,2\rangle$ and$ \Sigma_c(2840)|J^P = 5/2^-,2\rangle $ , a narrow peak will be observed in the$ \Lambda_c \pi $ mass spectrum at approximately$ 2.8 $ GeV.Finally, the equal spacing rule appears to perfectly hold for the charmed baryon states. The mass spectrum of the four
$ P $ -wave states,$ \Sigma_c(2746) $ ,$ \Sigma_c(2796) $ ,$ \Sigma_c(2813) $ , and$ \Sigma_c(2840) $ , is approximately extracted model-independently by combining the recent observations of the charmed baryon,$ \Omega_c(X) $ and$ \Xi_c(X) $ , with the equal spacing rule. The extracted masses are in the range of the quark model predictions, and should more precise than the quark model predictions due to the highly precise measurements from the LHCb Collaboration. A reliable determination of the mass spectrum alongside our detailed analysis of the decay properties for these$ P $ -wave$ \Sigma_c $ states should provide useful references for observations in future experiments.
Toward discovering low-lying P-wave excited Σc baryon states
- Received Date: 2021-04-06
- Available Online: 2022-02-15
Abstract: In this study, by combining the equal spacing rule with recent observations of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

































 DownLoad:
DownLoad: