-
Since the first discovery of a hypernucleus in cosmic rays [1], the study of hypernuclei has become one of the most interesting topics in nuclear physics on both the experimental and theoretical sides [2–8]. In particular,
$ {\Lambda} $ hypernuclei have been studied by many experiments and related theoretical analyses. Due to the limitation of current experimental conditions, the experimental data of hypernuclei are mainly for single-$ {\Lambda} $ hypernuclei [2, 3, 6, 7, 9–14], with only a few data available for double-$ {\Lambda} $ hypernuclei [4, 6, 8, 15–21]. Of particular interest is the fact that the addition of$ {\Lambda} $ hyperons can lead to the appearance of the so-called impurity effect [2, 7], since the hyperon(s) can enter deeply into the center of a hypernucleus regardless of the restriction of the Pauli exclusion principle, and thus can be used as a good probe to study the nuclear environment. The impurity effects of single-$ {\Lambda} $ hypernuclei have been investigated extensively in the past decades, such as the shrinkage effect [22–24], the modification of the drip lines [25, 26], and the modification of the deformation [27–33].Since the experimental discovery of double-
$ {\Lambda} $ hypernuclei [15–21], several kinds of nuclear models have been extended to study the$ {\Lambda}{\Lambda} $ hypernuclei sector. For example, the microscopic cluster model was used to study the$ {\Lambda} $ binding energies of light hypernuclei and reproduced well the observation of the ground state of$ ^{11}_{{\Lambda}{\Lambda}} $ Be [34, 35]. The Faddeev calculations with the Nijmegen soft-core potential NSC97 described well the binding energies of light$ {\Lambda}{\Lambda} $ hypernuclei [36]. The shell-model calculation showed how the$ {\Lambda} N $ spin-dependent interaction terms influence the$ {\Lambda}{\Lambda} $ hypernuclei across the nuclear$ p $ shell [37]. The beyond-mean-field approach was applied to study the evolution of nuclear deformation in$ {\Lambda}{\Lambda} $ hypernuclei and the hyperon impurity effect in hypernuclei with shape coexistence [38, 39]. Extensive research of binding energies and deformation effects has been carried out by the self-consistent mean-field model on the shape of hypernuclei [26, 27, 29, 40–44].Very recently, the impurity effects of multiple
$ {\Lambda} $ hyperons on the deformations in the hyperisotope chains$ ^{8+n}_{\ \ n{\Lambda}} $ Be ($ n = 2 $ , 4),$ ^{20+n}_{\ \ \ \ n{\Lambda}} $ Ne ($ n = 2 $ , 8), and$ ^{28+n}_{\ \ \ \ n{\Lambda}} $ Si ($ n = 2 $ , 8) have been studied using relativistic mean field (RMF) theory in Ref. [24]. It was pointed out that in the Ne hyperisotopes, the deformation is slightly reduced by the additional$ {\Lambda} $ hyperons, whereas it is significantly reduced or even disappears in the Si hyperisotopes. Studies on multi-$ {\Lambda} $ hyperisotopes have theoretical significance, although the corresponding experiments are currently unfeasible. First of all, the impurity effects in multi-$ {\Lambda} $ hyperisotopes are evidently stronger than those of single-$ {\Lambda} $ ones. Moreover, a multi-$ {\Lambda} $ system can provide important information on the$ {\Lambda}{\Lambda} $ interaction, and the effects of the core nucleus on the$ {\Lambda} $ hyperons can be studied.The aforementioned work in Ref. [24] studied only a few nuclei and did not address the impurity effects caused by six
$ {\Lambda} $ hyperons. Therefore, further studies on the impurity effect of$ n = $ 2, 4, 6, 8$ \;{\Lambda} $ hyperons on the properties of even–even nuclei ranging from$ ^8 $ Be to$ ^{40} $ Ca will be carried out in this work. In contrast to the RMF model adopted in Ref. [24], we will employ the deformed Skyrme–Hartree–Fock (SHF) approach [45–47], which is one of the widely used models for hypernuclei [26, 43, 48]. -
In the framework of the SHF approach, the energy of a hypernucleus is given by an energy-density functional,
$ \begin{array}{l} E = \int {\rm d}^3{\boldsymbol{r}}\;{\varepsilon}({\boldsymbol{r}}) \ , \quad {\varepsilon} = {\varepsilon}_{NN} + {\varepsilon}_{{\Lambda} N} + {\varepsilon}_{{\Lambda} {\Lambda}} \;, \end{array} $

(1) where
$ {\varepsilon}_{NN} $ ,$ {\varepsilon}_{{\Lambda} N} $ , and$ {\varepsilon}_{{\Lambda}{\Lambda}} $ account for the nucleon–nucleon ($ NN $ ) interaction, the hyperon–nucleon ($ YN $ ) interaction, and the hyperon–hyperon ($ YY $ ) interaction, respectively. The energy-density functional depends on the one-body densities$ \rho_q $ , kinetic densities$ \tau_q $ , and spin–orbit currents$ {\boldsymbol{J}}_q $ ,$ \begin{array}{l} \Big[ \rho_q, \; \tau_q, \; {\boldsymbol{J}}_q \Big] = \displaystyle\sum\limits_{i = 1}^{N_q} {n_q^i} \Big[ |\phi_q^i|^2 , \; |\nabla\phi_q^i|^2 , \; {\phi_q^i}^* (\nabla \phi_q^i \times \mathit{\boldsymbol{\sigma}})/i \Big] \:, \end{array} $

(2) where
$ \phi_q^i $ ($ i = 1, \; \ldots, \; N_q $ ) are the self-consistently calculated single-particle (s.p.) wave functions of the$ N_q $ occupied states for the species$ q = n, \; p, \; {\Lambda} $ in a hypernucleus. They satisfy the Schrödinger equation, obtained by the minimization of the total energy functional (1) according to the variational principle,$ \begin{array}{l} \bigg[ \nabla \cdot \dfrac{1}{2m_q^*({\boldsymbol{r}})}\nabla - V_q({\boldsymbol{r}}) + {i} {\boldsymbol{W}}_q({\boldsymbol{r}}) \cdot \left(\nabla\times\mathit{\boldsymbol{\sigma}}\right) \bigg] \phi_q^i({\boldsymbol{r}}) = e_q^i \, \phi_q^i({\boldsymbol{r}}) \:, \end{array} $

(3) in which
$ {\boldsymbol{W}}_q({\boldsymbol{r}}) $ is the spin–orbit interaction part for the nucleons as given in Refs. [45, 49]. The central mean fields$ V_q({\boldsymbol{r}}) $ , corrected by the effective-mass terms following the procedure described in Refs. [40, 42, 50] are$\begin{aligned}[b] V_N =& V_N^{\text{SHF}} + \frac{\partial{\varepsilon}_{N{\Lambda}}}{\partial{\rho_N}} \\ &+ \frac{\partial}{\partial{\rho_N}} \left(\frac{m_{\Lambda}}{m_{\Lambda}^*({\rho_N})}\right) \left( \frac{\tau_{\Lambda}}{2m_{\Lambda}} - \frac{3}{5}\frac{{\rho_\Lambda}(3\pi^2{\rho_\Lambda})^{2/3}}{2m_{\Lambda}} \right) \:, \end{aligned} $

(4) $\begin{aligned}[b] V_{\Lambda} = \frac{\partial ({\varepsilon}_{N{\Lambda}}+{\varepsilon}_{{\Lambda}{\Lambda}})}{\partial{\rho_\Lambda}} - \left( \frac{m_{\Lambda}}{m_{\Lambda}^*({\rho_N})} - 1 \right) \frac{(3\pi^2{\rho_\Lambda})^{2/3}}{2m_{\Lambda}} . \end{aligned}$

(5) For the nucleonic part
$ {\varepsilon}_{NN} $ , we use the Skyrme force SLy5 [47, 51], which has been fitted in a wide nuclear region. The energy-density contributions$ {\varepsilon}_{N{\Lambda}} $ [41, 42] and$ {\varepsilon}_{{\Lambda}{\Lambda}} $ [50] are parameterized as (densities$ \rho $ given in units of fm$ ^{-3} $ , energy density$ {\varepsilon} $ in MeVfm$ ^{-3} $ ):$\begin{aligned}[b] {\varepsilon}_{N{\Lambda}}({\rho_N}, {\rho_\Lambda}) =& -( {\varepsilon}_1 - {\varepsilon}_2{\rho_N} + {\varepsilon}_3{\rho_N}^2) {\rho_N}{\rho_\Lambda} \\& +( {\varepsilon}_4 - {\varepsilon}_5{\rho_N} + {\varepsilon}_6{\rho_N}^2) {\rho_N}{\rho_\Lambda}^{5/3} \:, \end{aligned}$

(6) $ {\varepsilon}_{{\Lambda}{\Lambda}}({\rho_\Lambda}) = -{\varepsilon}_7 {\rho_\Lambda}^2 \Theta(N_{\Lambda}>1)\:, $

(7) together with
$ \begin{array}{l} \dfrac{m_{\Lambda}^*}{m_{\Lambda}}({\rho_N}) = \mu_1 - \mu_2{\rho_N} + \mu_3{\rho_N}^2 \:. \end{array} $

(8) The parameters
$ {\varepsilon}_1, $ $ \ldots, $ $ {\varepsilon}_6 $ in Eq. (6) and the$ {\Lambda} $ effective-mass parameters$ \mu_i $ were determined in Brueckner–Hartree–Fock calculations of hypernuclear bulk matter with the Nijmegen potential NSC97f [41, 42], while the empirical expression involving the parameter$ {\varepsilon}_7 $ in Eq. (7) has been proposed by fitting the bond energy of$ ^{\ \ 6}_{{\Lambda}{\Lambda}} $ He in Ref. [50]. All parameters are listed in Table 1. This procedure gives a good description of the binding energies of single- and double-$ {\Lambda} $ hypernuclei [40, 42, 50].$ {\varepsilon}_1 $ 

$ {\varepsilon}_2 $ 

$ {\varepsilon}_3 $ 

$ {\varepsilon}_4 $ 

$ {\varepsilon}_5 $ 

$ {\varepsilon}_6 $ 

$ {\varepsilon}_7 $ 

$ \mu_1 $ 

$ \mu_2 $ 

$ \mu_3 $ 

384 1473 1933 635 1829 4100 33.25 0.93 2.19 3.89 The occupation probabilities
$ n^i_q $ (for nucleons only) in Eq. (2) are calculated by taking into account pairing within a BCS approximation. In this work, the pairing interaction is taken as a density-dependent$ \delta $ interaction [52],$ \begin{array}{l} V_{q}({\boldsymbol{r}}_1, {\boldsymbol{r}}_2) = V_0 \left[ 1 - \dfrac{{\rho_N}(({\boldsymbol{r}}_1+{\boldsymbol{r}}_2)/2)}{0.16\;\rm{fm}^{-3}} \right] \delta({\boldsymbol{r}}_1-{\boldsymbol{r}}_2) \:. \end{array} $

(9) For the
$ p $ -shell nuclei and their corresponding hypernuclei, the strength of the pairing force is set to$V_0 = $ $ -410\;$ MeVfm$ ^3 $ for both neutrons and protons, which gives reasonable binding energies for$ ^{12} $ C and$ ^{13}_{\ {\Lambda}} $ C [29, 53]. For the heavier (hyper)nuclei,$ V_0 $ is taken as$ -1000\; $ MeVfm$ ^3 $ for both neutrons and protons as in Ref. [29].Regarding
$ {\Lambda}{\Lambda} $ pairing, currently the$ {\Lambda}{\Lambda} $ pairing interaction is basically unknown, see e.g. Ref. [54], and there are no experimental data on hyperon pairing phenomena to date. Nevertheless some theoretical studies have been performed [55–57] with results depending on the theoretical assumptions made. It is thus premature to include this aspect in this work. Nevertheless, if$ {\Lambda}{\Lambda} $ pairing is strong, it might affect the deformation properties, especially the shape-coexistence features observed in C, O, S, and Ar hyperisotopes discussed later.In this work, we focus mainly on the impurity effects of multi-
$ {\Lambda} $ hyperons on the deformation of nuclei. The deformed SHF Schrödinger equation is solved in cylindrical coordinates$ (r, z) $ under the assumption of axial symmetry of the mean field [46, 47]. The optimal quadrupole deformation parameter$ \beta_2 = \sqrt{\frac{\pi}{5}} \frac{\langle 2z^2-r^2 \rangle}{\langle z^2+r^2 \rangle} $

(10) is determined by minimizing the energy-density functional.
-
Due to the lack of experimental data for multi-
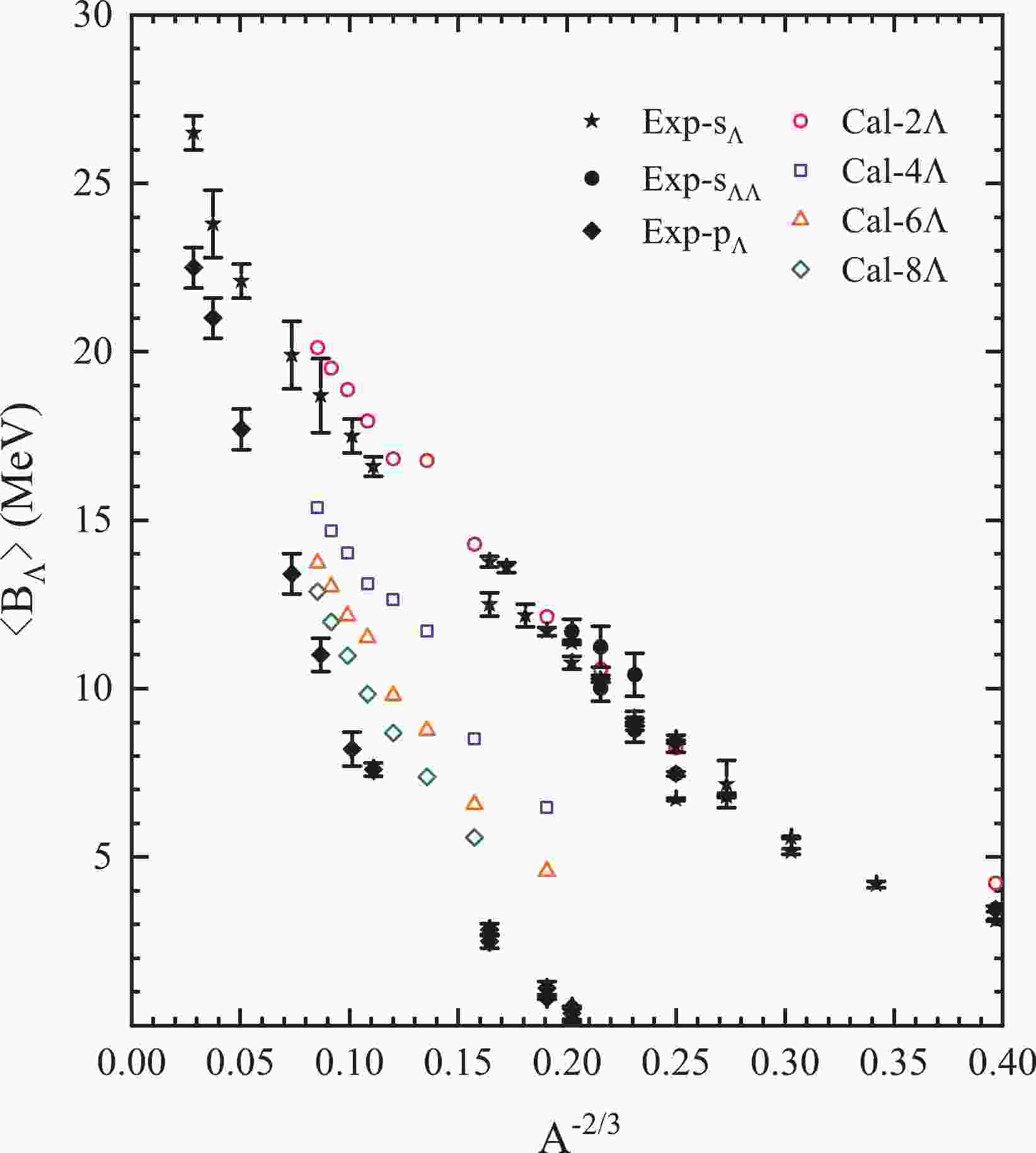
$ {\Lambda} $ hypernuclei, we compare in Fig. 1 the average$ {\Lambda} $ binding energy of multi-$ {\Lambda} $ hypernuclei,$ {\langle B_{\Lambda} \rangle} \equiv B_{n{\Lambda}}/n $ , with that of experimental single-$ s_{\Lambda} $ hypernuclei, double-$ s_{{\Lambda}{\Lambda}} $ hypernuclei, and single-$ p_{\Lambda} $ hypernuclei. Both theoretical and experimental results show that$ {\langle B_{\Lambda} \rangle} $ decreases with$ A^{-2/3} $ . Due to the weak$ {\Lambda}{\Lambda} $ interaction, the$ {\langle B_{\Lambda} \rangle} $ values of double-$ s_{{\Lambda}{\Lambda}} $ hypernuclei are very close to those of single-$ s_{\Lambda} $ hypernuclei. For a given isotope,$ {\langle B_{\Lambda} \rangle} $ decreases with increasing hyperon number, since the higher$ {\Lambda} $ s.p. orbits are being filled. As a consequence, the$ {\langle B_{\Lambda} \rangle} $ of 8$ {\Lambda} $ hypernuclei are close to those of the single-$ p_{\Lambda} $ hypernuclei. These comparisons are rather qualitative, and experimental binding energies of multi-$ {\Lambda} $ hypernuclei are necessary to perform a strict evaluation of the current theoretical calculations. Nevertheless, as the energies of single- and double-$ {\Lambda} $ hypernuclei are reasonably well reproduced, we continue the analysis for other quantities based on the current model.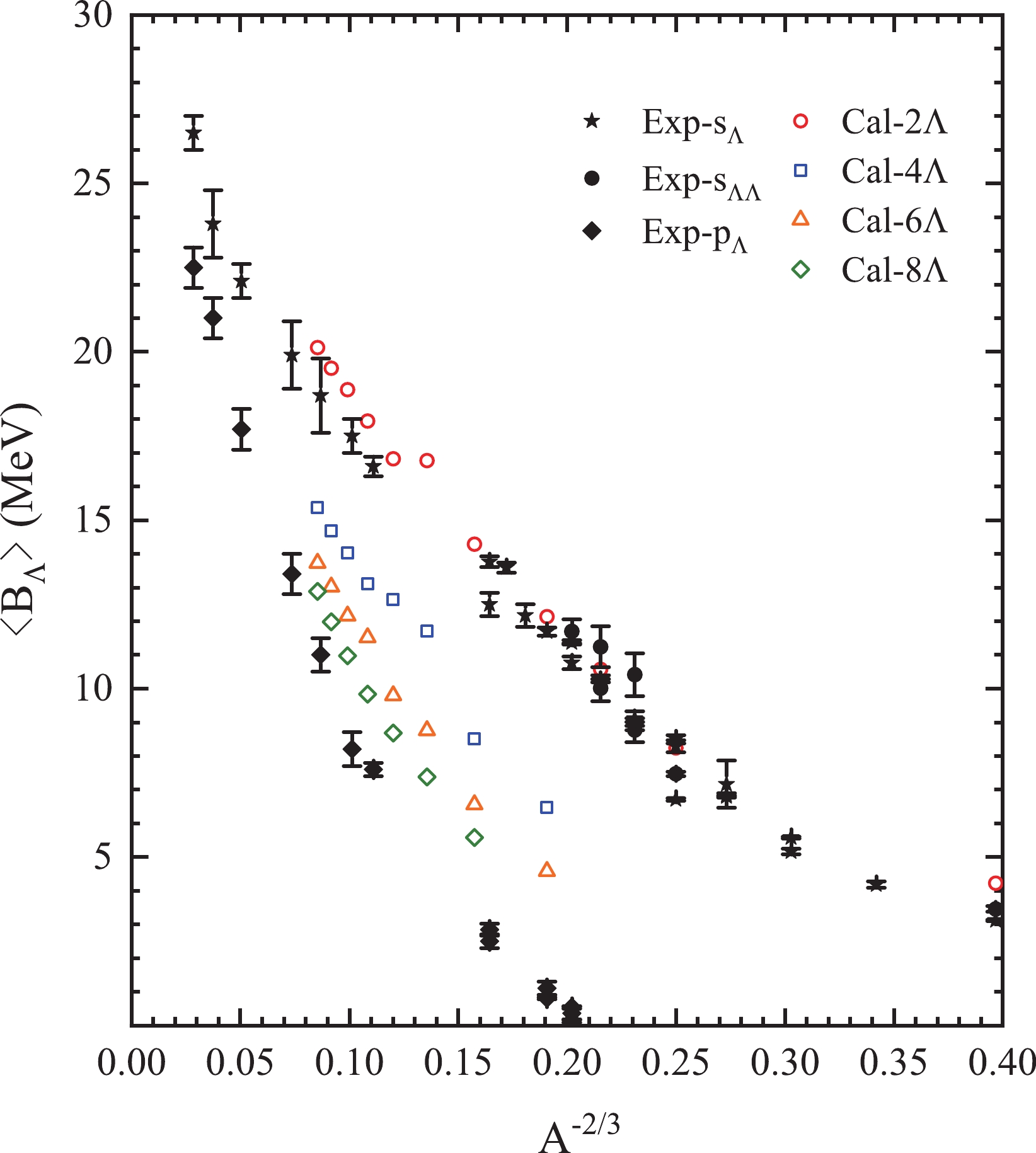
Figure 1. (color online) Average
$ {\Lambda} $ binding energies in multi-$ {\Lambda} $ hypernuclei$ {\langle B_{\Lambda} \rangle} \equiv B_{n{\Lambda}}/n $ as function of$ A^{-2/3} $ calculated by SHF in comparison with the experimental data of single-$ s_{\Lambda} $ hypernuclei, double-$ s_{{\Lambda}{\Lambda}} $ hypernuclei, and single-$ p_{\Lambda} $ hypernuclei. The experimental data are taken from Ref. [7] and references therein.The impurity effect of additional hyperons in single-
$ {\Lambda} $ or double-$ {\Lambda} $ hypernuclei is usually reflected by the shape shrinkage or deformation reduction of the nuclear core. To study the impurity effect of multi-$ {\Lambda} $ systems, we show in Fig. 2 the calculated potential energy surfaces as functions of the quadrupole deformation$ \beta_2 $ for even–even nuclei ranging from$ ^8 $ Be to$ ^{40} $ Ca and their corresponding multi-$ {\Lambda} $ ($ n_{\Lambda} = 2, \; 4, \; 6, \; 8 $ ) hypernuclei. All energies are normalized with respect to the binding energy of the absolute minimum for a given isotope. Apart from$ ^{12} $ C,$ ^{32} $ S,$ ^{36} $ Ar, and the doubly-magic nuclei$ ^{16+n}_{\ \ \ n{\Lambda}} $ O and$ ^{40+n}_{\ \ \ n{\Lambda}} $ Ca ($ n = 0, \; 2, \; 4, \; 6, \; 8 $ ), all other (hyper)nuclei are well deformed.$ ^{18}_{6{\Lambda}} $ C,$ ^{30}_{6{\Lambda}} $ Mg,$ ^{28+n}_{\ \ \ n{\Lambda}} $ Si ($ n = 0, \; 2, \; 4, \; 6, \; 8 $ ),$ ^{38}_{6{\Lambda}} $ S, and$ ^{42}_{6{\Lambda}} $ Ar are oblately deformed, while the others are prolately deformed.$ ^{8+n}_{\ \ n{\Lambda}} $ Be ($ n = 4, \; 6, \; 8 $ ) and$ ^{20}_{8{\Lambda}} $ C are unbound systems, i.e., the$ {\Lambda} $ dripline is reached before [40].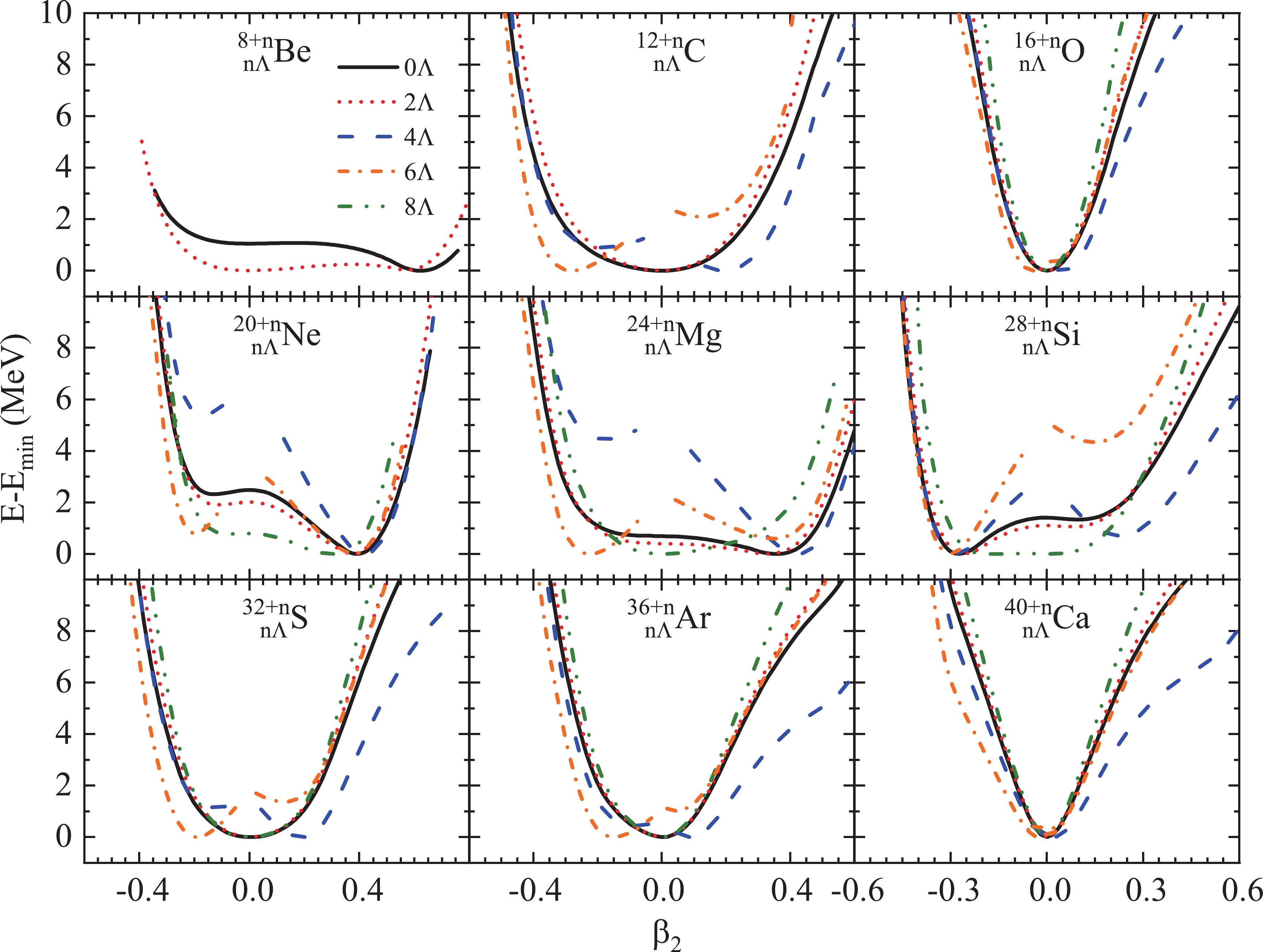
Figure 2. (color online) Potential energy surfaces as functions of quadrupole deformation
$ \beta_2 $ calculated by the self-consistent deformed SHF method for even–even nuclei ranging from$ ^8 $ Be to$ ^{40} $ Ca and their corresponding multi-$ {\Lambda} $ ($ n = 2 $ , 4, 6, 8) hypernuclei. Energies are normalized with respect to the binding energy of the absolute minimum for a given isotope. Positive (negative) values of$ \beta_2 $ correspond to prolate (oblate) deformation.We note that in this work we use the unmodified SLy5 Skyrme force, which predicts spherical core nuclei
$ ^{12} $ C,$ ^{32} $ S, and$ ^{36} $ Ar. In some other works [28, 48, 53, 58] the spin–orbit component of the Skyrme force is reduced in order to enforce a deformation for these nuclei at the cost of not reproducing the binding energy correctly.One observes that the impurity effects become stronger with more hyperons involved, but the dependence is not regular: For
$ 2{\Lambda} $ and$ 8{\Lambda} $ hypernuclei, the impurity effect gives similar results of deformation reduction as in the case of single-$ {\Lambda} $ hypernuclei. This observation is the same as that obtained by the RMF model in Ref. [24]. However, for$ 4{\Lambda} $ and$ 6{\Lambda} $ hypernuclei, the opposite impurity effect can be seen, namely the deformations of the hypernuclei become larger than those of the core nuclei. The energy differences between the prolate and oblate local minima in Ne, Mg, and Si isotopes are smaller than 2 MeV, which characterize them as typical nuclei with shape-coexistence phenomenon [59]. With the addition of hyperons, not only these nuclei retain their shape coexistence, but also other hypernuclei, such as C, O, S, and Ar, can develop the shape-coexistence phenomenon.Before analyzing the results in detail, we first test the robustness of the above findings with respect to other choices of the
$ NN $ and$ NY $ forces. In Fig. 3, taking$ ^{24} $ Mg and its corresponding multi-$ {\Lambda} $ hypernuclei as examples, the potential energy surfaces calculated with SLy5 [47, 51], SGII [60], or SIII [61] parameters for the$ NN $ interaction and NSC97f+EmpC or SLL4 [62] parameters for the$ YN $ interaction are shown. It is seen that the deformations of the core nuclei are always reduced by 2 or 8$ {\Lambda} $ hyperons while enhanced by adding 4 or 6$ {\Lambda} $ hyperons regardless of the parametrizations. Therefore, this feature is robust with respect to the choice of (realistic) interactions.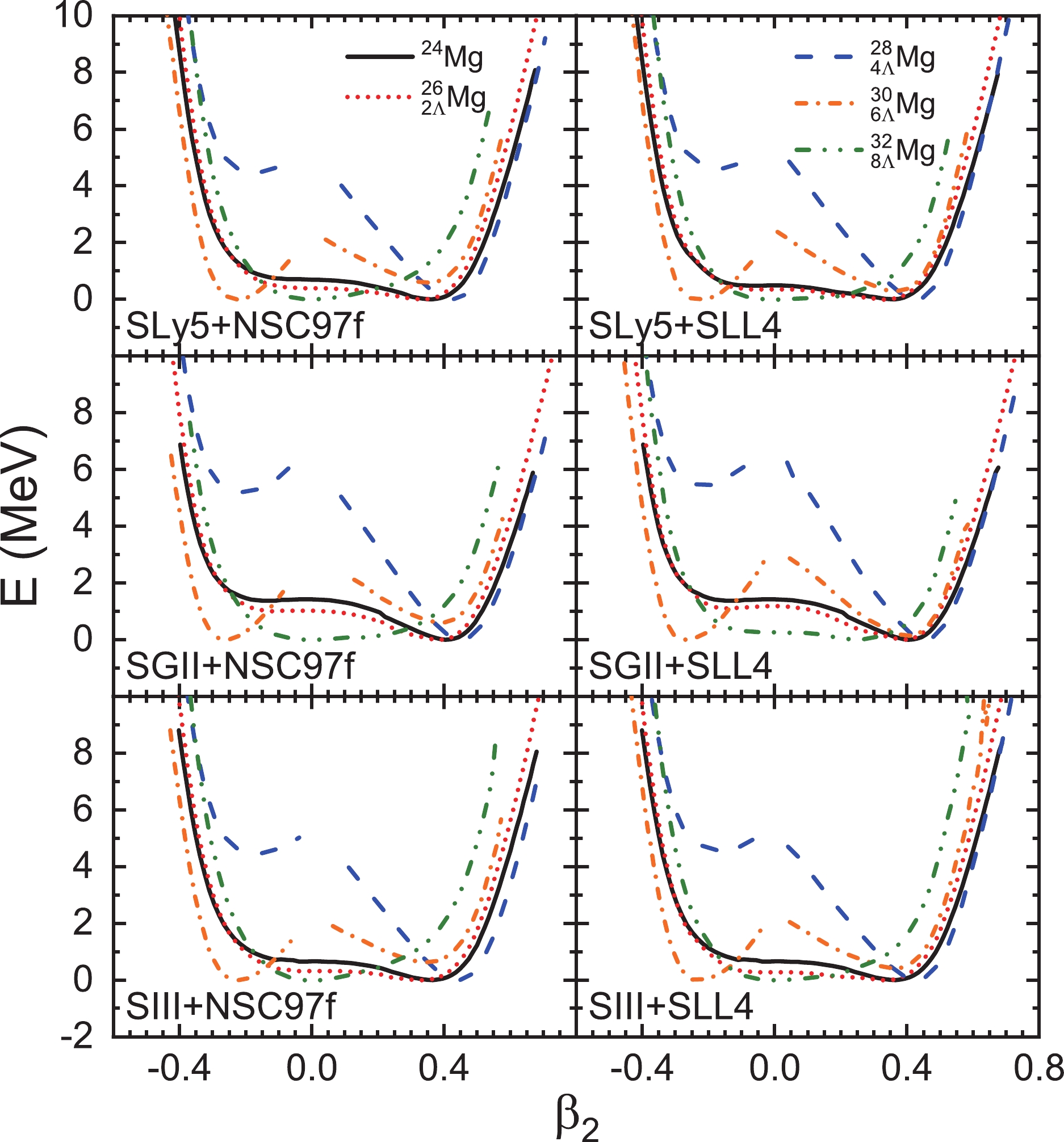
Figure 3. (color online) Potential energy surfaces of
$ ^{24} $ Mg and its multi-$ {\Lambda} $ hypernuclei calculated with SLy5, SGII, or SIII parameters for the$ NN $ interaction and NSC97f+EmpC or SLL4 parameters for the$ YN $ interaction.As pointed out before, for the light Be and C cores not all
$ {\Lambda} $ $ p $ -states can be filled, because the$ {\Lambda} $ dripline is reached first [40]. For heavier cores this is not an issue, but another mechanism that could limit the maximum number of stably bound$ {\Lambda} $ 's is the fact that$ {\Lambda} $ -rich hypernuclei might be unstable due to the$ {\Lambda}{\Lambda} \rightarrow \Xi^-p $ strong reaction [50, 63], which occurs when$S_{2{\Lambda}}+28.6{\;\rm{MeV}} < $ $ S_{\Xi^-}+S_p$ , where$ S_{2{\Lambda}} $ ,$ S_{\Xi^-} $ , and$ S_p $ are the relevant separation energies. We examine this possibility using a recent determination of the$ \Xi^- $ -nucleus interaction, SLX3 [64]. Taking the most$ {\Lambda} $ -rich hypernucleus$ ^{18}_{6{\Lambda}} $ C as an example, and neglecting the unknown$ {\Lambda}\Xi $ interaction, one estimates the separation energies as$ S_{2{\Lambda}} = E(^{16}_{4{\Lambda}}\text{C}) - E(^{18}_{6{\Lambda}}\text{C}) = 1.6{\;\text{MeV}} \:, $

(11) $ S_p = E(^{16}_{4{\Lambda}}\text{C}) - E(^{17}_{4{\Lambda}}\text{N}) = 7.7{\;\text{MeV}} \:, $

(12) $ S_{\Xi^-} = E(^{17}_{4{\Lambda}}\text{N}) - E(^{18}_{4{\Lambda}\Xi^-}\text{C}) $

(13) $ \quad\;\; \approx E(^{13}\text{N}) - E(^{14}_{\Xi^-}\text{C}) = 7.6{\;\text{MeV}} \:. $

(14) This leaves the above reaction blocked by an energy gap of about 15 MeV. Hence,
$ ^{18}_{6{\Lambda}} $ C as well as all other$ p $ -state hypernuclei in the current study are stable with respect to the$ {\Lambda}{\Lambda}\rightarrow \Xi^-p $ reaction.In order to achieve a microscopic understanding of the behavior of
$ {\langle B_{\Lambda} \rangle} $ in Fig. 1 and the impurity effects of multi$ {\Lambda} $ 's on the deformation in Figs. 2 and 3, we take$ ^{48}_{8{\Lambda}} $ Ca as example, and show in Fig. 4 the s.p. energies of$ {\Lambda} $ hyperons as a function of$ \beta_2 $ , and in Fig. 5 the density distributions at$ \beta_2 = 0 $ as functions of$ r $ ($ z = 0 $ ) and$ z $ ($ r = 0 $ ) for the occupied$ s $ and$ p $ $ {\Lambda} $ s.p. orbits. Note that the$ z $ axis is the symmetry axis.
Figure 4. (color online) Calculated
$ {\Lambda} $ hyperon$ s, p, d $ s.p. energy levels as function of quadrupole deformation$ \beta_2 $ in$ ^{48}_{8{\Lambda}} $ Ca.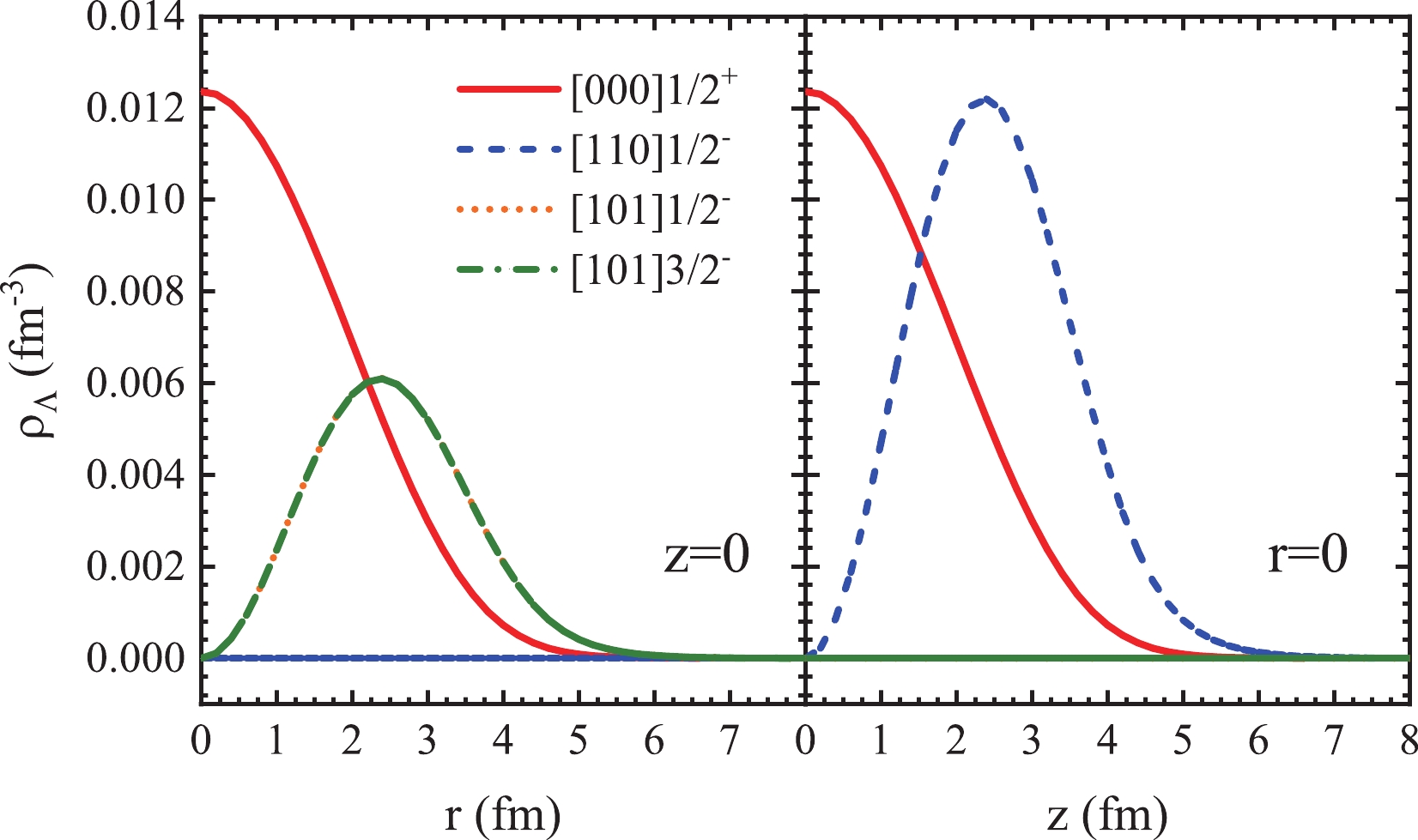
Figure 5. (color online) Density distributions for the occupied
$ s $ and$ p $ s.p. orbits of$ {\Lambda} $ hyperons in$ ^{48}_{8{\Lambda}} $ Ca at$ \beta_2 = 0 $ as functions of$ r $ ($ z = 0 $ ) and$ z $ ($ r = 0 $ ). The$ z $ axis is the symmetry axis.The figures show that the [000]1/2
$ ^+ $ $ s $ orbit is the lowest$ {\Lambda} $ s.p. energy level with a spherical density distribution concentrated at the center. As two hyperons can occupy this level, and their mutual interaction is small, the$ {\langle B_{\Lambda} \rangle} $ values of double-$ {\Lambda} $ hypernuclei are very close to those of single-$ {\Lambda} $ hypernuclei.Regarding the three negative-parity
$ p $ states, Fig. 4 shows that the [101]1/2$ ^- $ and [101]3/2$ ^- $ orbits are degenerate as the spin–orbit interaction is neglected in the$ {\Lambda}{\Lambda} $ channel. Their s.p. energies are lower than those of the [110]1/2$ ^- $ orbit on the oblate side, but higher on the prolate side. Therefore a partial filling of the$ p $ states (4$ {\Lambda} $ and 6$ {\Lambda} $ hypernuclei) allows a reduction of the total energy by increasing the magnitude of the deformation, whereas a complete filling (8$ {\Lambda} $ hypernuclei) does not exhibit this feature. As shown in Fig. 5, the [110]1/2$ ^- $ orbit is prolate with zero density at$ z = 0 $ , while the degenerate [101]1/2$ ^- $ and [101]3/2$ ^- $ orbits are both oblate with zero densities at$ r = 0 $ . When the 8 hyperons occupy fully the three$ p $ orbits, their density distribution becomes spherical.A more detailed visualization of the effects of hyperons on the deformation of hyperisotopes is given in Fig. 6, which shows the
$ {\Lambda} $ density distribution in the$ (r, z) $ plane. We choose the prolate Ne, the oblate Si, and the spherical Ca hyperisotopes as examples. It can be seen that the density distribution of double-$ {\Lambda} $ hypernuclei changes in accordance with the deformation of the core nuclei, since the additional two$ {\Lambda} $ s occupy the spherical [000]1/2$ ^+ $ orbital.
Figure 6. (color online) Density distribution of hyperons in the
$ (r, z) $ plane in Ne, Si, and Ca hyperisotopes. The$ z $ axis is the symmetry axis.When 4
$ {\Lambda} $ hyperons are filled in, the shape of the first$ p $ orbit occupied by the hyperons is the same as that of the core nuclei. For example, the hyperons of$ ^{24}_{4{\Lambda}} $ Ne with prolate deformation first fill into the [110]1/2$ ^- $ orbit, which is also prolate, and then gradually fill into the [101]1/2$ ^- $ and [101]3/2$ ^- $ orbits, which are oblate. Thus the deformation of$ ^{24}_{4{\Lambda}} $ Ne reaches the largest value due to the maximal distribution of 4$ {\Lambda} $ hyperons in the prolate orbit. When the hyperons begin to fill into the oblate orbits, a reduction of the deformation occurs in$ ^{26}_{6{\Lambda}} $ Ne. Finally, the spherical distribution of 8$ {\Lambda} $ 's renders also the core nucleus more spherical.The hyperons in
$ ^{28} $ Si hyperisotopes with oblate core nucleus first fill into the degenerate oblate orbits [101]1/2$ ^- $ and [101]3/2$ ^- $ . Therefore, the deformation increase can last up to 6$ {\Lambda} $ hypernuclei, when the deformation reaches the maximum. Then hyperons will fill into the prolate [110]1/2$ ^- $ orbit, and cause a reduction of the deformation. This also explains the different trends of deformation of prolate and oblate hyperisotopes with the increasing hyperon number as shown in Fig. 2.However, for spherical-core nuclei, such as
$ ^{16} $ O and$ ^{40} $ Ca, the 4$ {\Lambda} $ hypernuclei have no preference for oblate or prolate orbits; therefore their deformation trends have the characteristics of both oblate and prolate hypernuclei. As a consequence, they show a more or less soft potential energy surface around the spherical shape, in particular in the$ ^{16} $ O hypernuclei as shown in Fig. 2. -
We study within the deformed SHF formalism the impurity effects of
$ {\Lambda} $ hyperons on the deformation of even–even nuclei ranging from$ ^8 $ Be to$ ^{40} $ Ca, employing an effective$ {\Lambda} N $ interaction that reproduces well the experimental binding energies of single-$ {\Lambda} $ hypernuclei.The deformations of the nuclear core are generally reduced by adding 2 or 8
$ {\Lambda} $ hyperons, but enhanced by adding 4 or 6. These behaviors are interpreted in a microscopic manner by analyzing the$ {\Lambda} $ s.p. orbits and the density distributions for the occupied ones. It is demonstrated that the order of filling the hyperons into the$ p $ orbits is determined by the shape of the core nucleus. When the core nucleus is oblate, the hyperons are filled first into the degenerate oblate [101]1/2$ ^- $ and [101]3/2$ ^- $ orbits, so that the core deformation increases to the oblate side, and can reach a maximum when 6 hyperons are added. When the core nucleus is prolate, the hyperons are filled first into the prolate [110]1/2$ ^- $ orbit, which leads to an increase of the prolate core deformation, reaching a maximum when 4 hyperons are added. When the core nucleus is spherical, hyperons have no preferences for the shape of the$ p $ orbits and result in a soft potential energy surface.Future experimental data of multi-
$ {\Lambda} $ hypernuclei are necessary to examine these effects and refine the assumptions and ingredients of the model calculations presented here. While we think the qualitative phenomena reported here are robust, a more realistic quantitative evaluation will require in particular knowledge of the$ {\Lambda}{\Lambda} $ interaction including the residual pairing force and a beyond-mean-field formalism appropriate for reliably modelling shape-coexistence and weakly-bound hyperon states.
Effects of Λ hyperons on the deformations of even–even nuclei
- Received Date: 2022-01-25
- Available Online: 2022-06-15
Abstract: The deformations of multi-





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: