New γ-soft rotation in the interacting boson model with SU(3) higher-order interactions

In the simplest interacting boson model (IBM-1) [1], valence nucleon-pair coupling to angular momentum $ L=0 $ and $ L=2 $ are mapped to s and d bosons. Many features of even-even nuclei can be elegantly described with up to two-body interactions. With a consistent-Q formalism often used in this model [2–4],

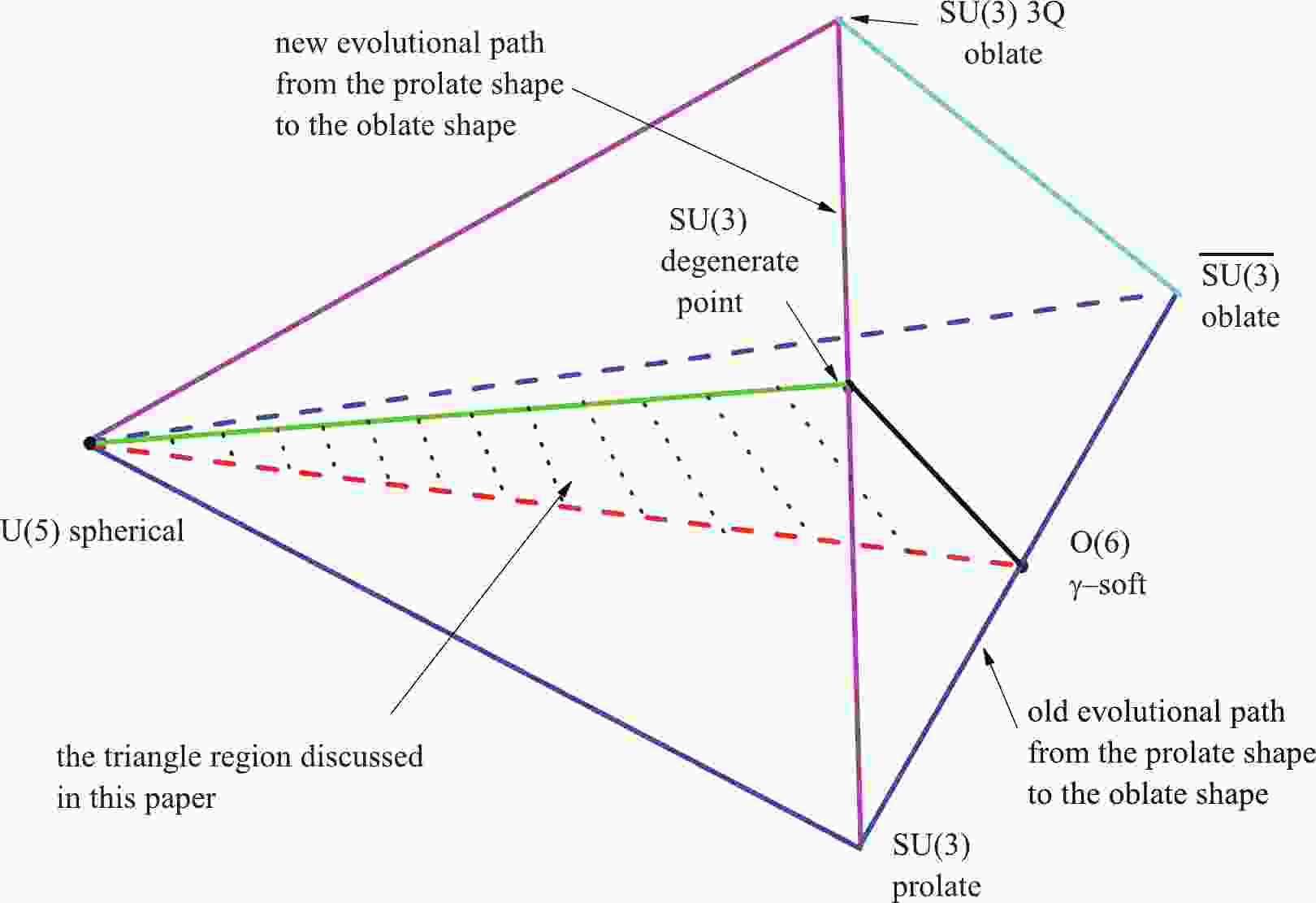
it can produce the spectra of spherical ($ \eta=0 $, $ U(5) $ limit), prolate ($ \eta=1 $, $ \chi=-{\sqrt{7}}/{2} $, $S U(3)$ limit), oblate ($ \eta=1 $, $ \chi={\sqrt{7}}/{2} $, $\overline{S U(3)}$ limit), and γ-soft ($ \eta=1 $, $ \chi=0 $, $ O(6) $ limit) nuclei. Here, $ \hat{n}_{d} $ is the d-boson number operator, $ \hat{Q}_{ \chi}=[d^{\dagger}\times\tilde{s}+s^{\dagger}\times \tilde{d}]^{(2)}+\chi[d^{\dagger}\times \tilde{d}]^{(2)} $ is the generalized quadrupole operator, N is the total boson number, c is a fitting parameter, and $ 0\leq \eta \leq 1, -{\sqrt{7}}/{2}\leq \chi \leq {\sqrt{7}}/{2} $. This Hamiltonian can be also exploited to describe the shape transitional behaviors between these typical collective excitation modes. An interesting result is that, when $ \eta=1 $ and χ changes from $ -{\sqrt{7}}/{2} $ to ${\sqrt{7}}/{2} $, γ-soft rotation can be observed as a critical property between the prolate and oblate shapes [5] (Fig. 1). This means that triaxiality may result from the competition between the prolate and oblate shapes.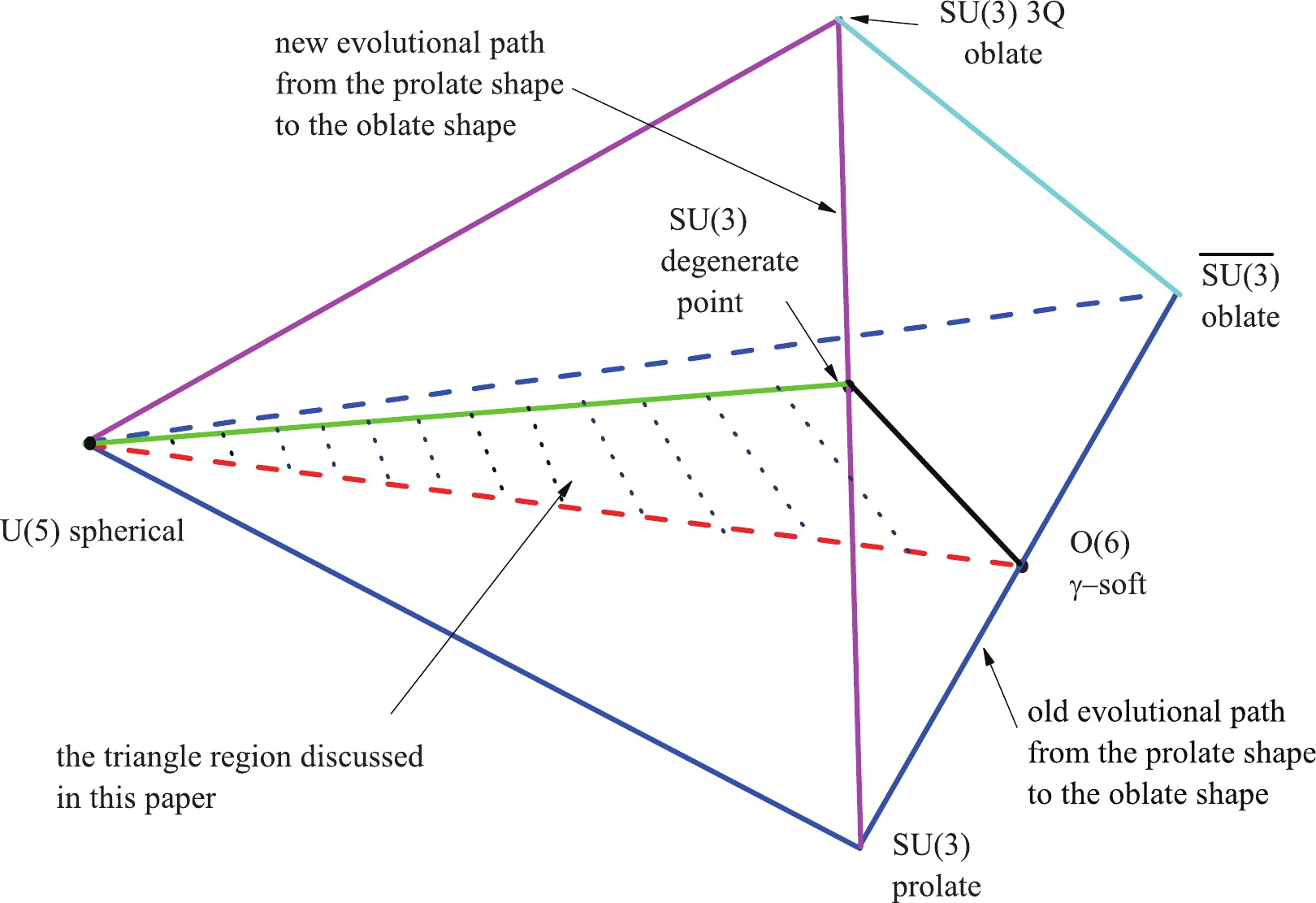

Figure 1.  (color online) Partial phase diagram in the cubic-Q interacting boson model Hamiltonian $ \hat{H}_{2} $.

However, this simple Hamiltonian cannot describe γ-rigid triaxial deformation. This deficiency can be overcome by considering higher-order interactions [6, 7]. $ [d^{\dagger}d^{\dagger}d^{\dagger}]^{(L)}\cdot[\tilde{d}\tilde{d}\tilde{d}]^{(L)} $ interactions have been investigated and can result in a stable γ-rigid triaxial deformation for the ground state of a nucleus. Subsequently, $S U(3)$ symmetry-conserving higher-order interactions have also been systematically investigated [8], and a realization of the rigid quantum asymmetric rotor within the $S U(3)$ limit was established [9, 10]. These studies discussed the functions of the $S U(3)$ third-order interactions ($ [\hat{Q}\times \hat{Q}\times \hat{Q}]^{(0)} $, $ [\hat{L}\times \hat{Q}\times \hat{L}]^{(0)} $) and fourth-order interactions ($ (\hat{Q}\cdot \hat{Q})^{2} $, $ [(\hat{L}\times \hat{Q})^{(1)}\times (\hat{L}\times \hat{Q})^{(1)}]^{(0)} $), where $ \hat{Q}=\hat{Q}_{-{\sqrt{7}}/{2}} $ is the $S U(3)$ quadrupole operator. $S U(3)$ third-order and fourth-order interactions are also discussed in Refs. [11–15]. These interactions can remove the degeneracy in the γ-band and β-band of the spectra within the $S U(3)$ limit and are also intimately connected with the rigid triaxial rotational spectra. Higher-order terms are also important in partial dynamical symmetry [16]. Isacker demonstrated that higher-order interactions $ (\hat{Q}_{0}\times\hat{Q}_{0}\times\hat{Q}_{0})^{(0)} $ can be individually used to present a rotational spectrum [17], where $ \hat{Q}_{0} $ is the quadrupole operator in the $ O(6) $ limit. This interesting result was further studied by [18, 19].

Inspired by the relationship between γ-rigid triaxial deformation and higher-order interactions, Fortunato et al. investigated triaxiality with a cubic-Q interacting boson model Hamiltonian [20]

where k is the coefficient of the cubic term. They state in their paper, "this looks like the simplest one and it is easy to justify on physical grounds as the first higher-order interaction term in an expansion based on the quadrupole operator". This Hamiltonian is only discussed in the large N limit within the intrinsic state formalism and the phase diagram is explored. One key result is that, when $ \chi=-{\sqrt{7}}/{2} $ in the $S U(3)$ limit, the cubic term corresponds to an oblate shape. Thus, a new evolutional path exists from the prolate shape to the oblate shape (Fig. 1). Based on the results, an analytically solvable prolate-oblate shape phase transitional description within the $S U(3)$ limit was investigated in [21], which offers a finite-N first-order shape transition. Most importantly, the phase transitional point is also a degenerate point [21] (Fig. 2), which may imply a hidden symmetry [22].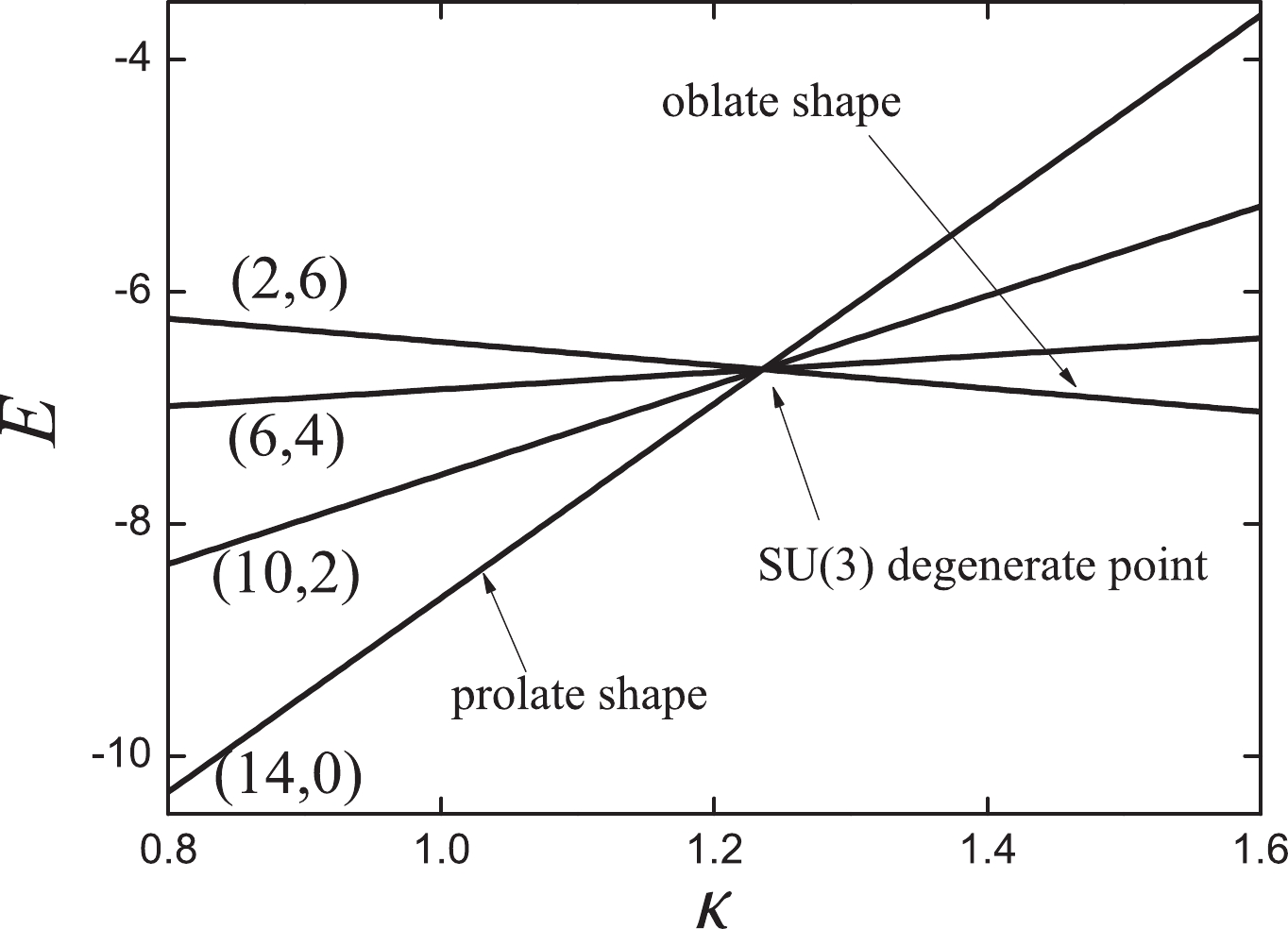

Figure 2.  Evolutional behaviors of the $S U(3)$ irreps (14,0), (10,4), (6,6), (2,8) for $ N=7 $ in $ \hat{H}^{(3)} $. The key observation is that the critical point is also a degenerate point.

Another key result is that this extended Hamiltonian $ \hat{H}_{2} $has only a very small region of rigid triaxiality in the large-N limit at $ \chi\approx -{\sqrt{7}}/{2} $ when the parameter changes from the $ U(5) $ limit to the $S U(3)$ degenerate point (green line in Fig. 1). Thus the shape transitional behaviors from the $ U(5) $ limit to the $S U(3)$ degenerate point will differ significantly from the ones from the $ U(5) $ limit to the $ O(6) $ γ-soft rotation (red line in Fig. 1). Based on these important new findings in Refs. [20, 21], it is very interesting to investigate the spectra of this transitional region for finite-N, which is related to rigid or soft γ-triaxiality.

Some experimental requirements remain to deepen our understanding on γ-soft triaxiality and its relationship with the higher-order interactions. In recent experimental investigations, a cluster of extremely neutron-deficient nuclei ¹⁶⁸Os [23], ¹⁶⁶W [24], ¹⁷²Pt [25], and ¹⁷⁰Os [26] were observed to have an unpredictably small ratio of reduced transition probabilities $ B_{4/2}=B(E2;4^{+}_{1}\rightarrow 2^{+}_{1})/ B(E2;2^{+}_{1}\rightarrow 0^{+}_{1}) $ along the yrast band. The $ B(E2) $ anomaly is considered a puzzle in the field of nuclear structures and cannot be explained by many existing theories. Recently, the author successfully described the $ B(E2) $ anomaly of the yrast band in ¹⁷⁰Os [27] for the first time via adding two third-order $S U(3)$ conserving interactions into the common Hamiltonian used in IBM-1. In this paper, the spectra of the nucleus is γ-soft. This unexpected discovery makes the $S U(3)$ higher-order interactions more important in the interacting boson models.

Wilets and Jean first provided a γ-soft solution based on the Bohr geometrical model [28]. When the IBM is determined, its $ O(6) $ limit can be used to fully describe γ-soft features [29, 30], which is considered a landmark for success of the IBM. However, realistic γ-soft nuclei still cannot be completely described using these models. For example, ¹⁹⁶Pt is the first candidate for the $ O(6) $ limit (see the spectra of ¹⁹⁶Pt in Fig. 3), but its quadrupole moment is not zero [31].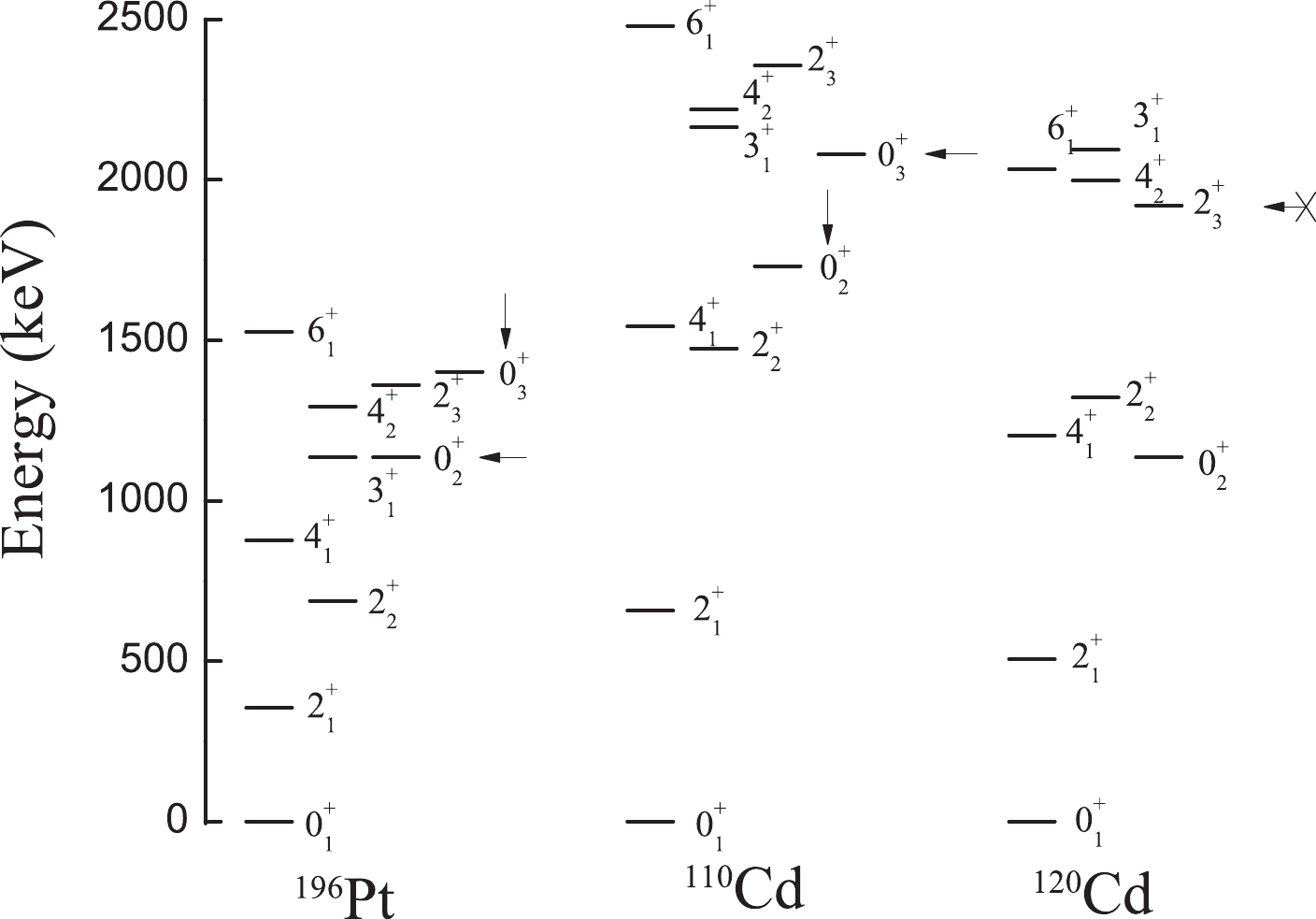

Figure 3.  Partial low-lying energy spectra of ¹⁹⁶Pt, ¹¹⁰Cd normal states and ¹²⁰Cd normal states. ¹⁹⁶Pt is a typical example of a γ-soft nucleus described by the $ O(6) $ limit, and there is no a $ 0^{+} $ state near energy levels $ 4^{+}_{1} $ and $ 2^{+}_{2} $. ¹¹⁰Cd has a typical spherical vibrational spectra, but ¹²⁰Cd has no the $ 0^{+}_{3} $ state in the three-phonon level.

Furthermore, the phonon modes as a major paradigm for description of nuclei near the closed shell have been questioned [32–35] and should be replaced by γ-soft rotation [36]. Figure 3 shows the spectra of the ¹¹⁰Cd normal states, which resembles the spherical spectra in the $ U(5) $ limit and is different from the $ O(6) $ γ-soft rotation (see the level positions of the $ 0^{+}_{2} $ and $ 0^{+}_{3} $ in ¹⁹⁶Pt and ¹¹⁰Cd normal states). In ¹²⁰Cd (Fig. 3), it is shown that, the $ U(5) $-like spectra is actually an illusion, and there is no $ 0^{+}_{3} $ state in the three-phonon level [37]. In recent studies [38, 39] the $ 0^{+}_{3} $ state is explained as intruder excitation for the $ 0^{+}_{3} $ state as a band-head of a rotational band has been established in ¹¹²Cd. Thus, in the normal states of the Cd isotopes, a $ 0^{+} $ state near the energy level of $ 6^{+}_{1} $ state does not exist. The problem is that the special γ-soft spectra of the normal states cannot be reproduced in the previous IBM Hamiltonian.

Recent detailed experimental investigations have revealed that the γ-soft behaviors in ^126-132Xe [40–42] and ^98-102Zr [43, 44] cannot also be explained using traditional γ-soft descriptions.

These results imply that our understanding of the γ-softness in nuclear structure theories is still incomplete. Searching for a new γ-soft rotational description is vital for our understanding of γ-softness and many theoretical deviations from experimental data. The aspects discussed above make a numerical study of the interacting bosom model with higher-order interactions meaningful: (1) The addition of higher-order interactions may induce new unpredicted phenomena, such as the $ B(E2) $ anomaly. (2) Rigid triaxiality may be described by this model or its extensions, which is different from the traditional approach discussed in [6, 7] and is important for us to understand γ-rigid triaxial nuclei ^76,78Ge [45–47]. (3) Some new insights on γ-soft rotation are required to explain various γ-softness anomalies.

In this paper, new γ-soft rotational behaviors are sought. A similar Hamiltonian with the formalism $ \hat{H}_{2} $ is investigated numerically. $ U(5) $-like and $ O(6) $-like γ-soft spectra are discovered, which can have large quadrupole moments. An unexpected partial $ O(5) $ dynamical symmetry is observed. The $ U(5) $-like spectra is applied in ¹¹⁰Cd normal states, which can reproduce the type of the normal states.

Our aim is to search for new γ-soft rotation, which is compared with the traditional γ-soft behaviors in the transitional regions from the $ U(5) $ limit to the $ O(6) $ limit; therefore, the parameters are selected as in the triangle in Fig. 1. A direct numerical calculation of the cubic-$ \hat{Q}_{\chi} $ interacting boson model Hamiltonian $ \hat{H}_{2} $ [20] is possible, but their spectra appear to lack regularity. To determine the hidden structure associated with the $S U(3)$ degenerate point, a new formalism should be developed. This new Hamiltonian consists of three parts. The first part is the common d boson number operator $ H^{(1)}=\hat{n}_{d}=d^{\dagger}\cdot \tilde{d} $ in the $ U(5) $ limit, which produces the simple harmonic vibration. The second part is the quadrupole-quadrupole interaction $ H^{(2)}=-\hat{Q}_{0}\cdot \hat{Q}_{0}/N $ in the $ O(6) $ limit, which produces the typical solvable γ-soft spectra. The combination of the two parts can describe the shape transitions from spherical to traditional γ-soft nuclei. The critical point of this transitional region can be described using $ E(5) $ dynamical symmetry [48]. A typical feature of γ-softness is the level degeneracy between the ground-band and quasi-γ rotational band due to the common $ O(5) $ symmetry, such as $ 4^{+}_{1},\;2^{+}_{2} $ or $ 6^{+}_{1},\;4^{+}_{2},\;3^{+}_{1} $ (Fig. 3).

When the third part is included, such as the quadrupole-quadrupole interaction $ -\hat{Q}\cdot \hat{Q}/N $ in the $S U(3)$ limit, γ-softness is destroyed, and the level degeneracy between the ground-band and quasi-γ band is removed [1]. It appears the framework of the IBM-1 offers no opportunity for a new γ-soft description. Since the emergence of the interacting boson model nearly fifty years ago, the γ-softness is always related to the $ O(6) $ dynamical symmetry.

The numerical results in this paper reveal that it is not the case. Here, the third part is a combination of the $S U(3)$ second-order and third-order Casimir operators,

which is investigated in detail in Ref. [21]. The two Casimir operators have relationships with the quadrupole second or third-order interactions in the $S U(3)$ limit as follows:

For a given $S U(3)$ irrep $ (\lambda,\mu) $, the eigenvalues of the two Casimir operators under the group chain $U(6)\supset S U(3) \supset O(3)$ are expressed as

Thus, in the $S U(3)$ limit, $ \hat{H}^{(3)} $ is solvable, which has a critical point at $ \kappa_{0}={(3N)}/{(2N+3)} $, (Fig. 2, when N=7, $ \kappa_{0}\approx 1.24 $). Note that each irrep $ (\lambda,\mu) $ corresponds to a special quadrupole deformation [9, 10]. When $ \kappa < \kappa_{0} $, it presents a prolate shape, and when $ \kappa >\kappa_{0} $, it is (nearly) an oblate shape. This shape phase transition is abrupt at the critical point. Importantly, the critical point is also a multiple-phase coexistence or degenerate point (Fig. 2). At this degenerate point, the $S U(3)$ irreps satisfying the condition $ \lambda+2\mu=2N $ are all degenerate, and the degeneracy degree is ${(N+2)}/{2} $ for an even N or $ {(N+1)}/{2} $ for an odd N. This degeneracy observed here is not accidental; thus, it may imply a hidden symmetry [22]. This degenerate point may be related to the important studies of Sebe and Akiyma, which are briefly discussed in Section VI. The Hamiltonian with $ \kappa_{0}={(3N)}/{(2N+3)} $ is adopted to the third part and is denoted as $ \hat{H}^{(3)} $.

Now, we discuss the full Hamiltonian for the new γ-soft deformation, which is expressed as

where $ 0\leq \eta \leq 1 $, and $ 0\leq \xi \leq 1 $. When $ \eta=0 $, it is the $ U(5) $ limit. When $ \eta=1, \xi=1 $, it represents the degenerate point in the $S U(3)$ limit, and when $ \eta=1, \xi=0 $, it is the $ O(6) $ limit (Fig. 1). The Hamiltonian is numerically investigated using the diagonalization method based on the $S U(3)$ interaction [3, 27].

For a new understanding on the spectra in Fig. 3 and their deviations from experimental data, the nine low-lying levels of '$ 2^{+}_{1} $', '$ 4^{+}_{1},2^{+}_{2},0^{+}_{2} $', and '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1},2^{+}_{3},0^{+}_{3} $' are emphasized. In the $ U(5) $ limit, they correspond to the one, two, and three phonon excited states, respectively. When moving to the $ O(6) $ limit (Fig. 4(a) ξ=0.0), the transitional behavior is very familiar to us. For the common $ O(5) $ symmetry, both '$ 4^{+}_{1},2^{+}_{2} $' and '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1},0^{+}_{2 or 3} $' are always degenerate. The energy levels of $ 0^{+}_{2} $ and $ 2^{+}_{3} $ (corresponding to the $ U(5) $ limit) shift upwards.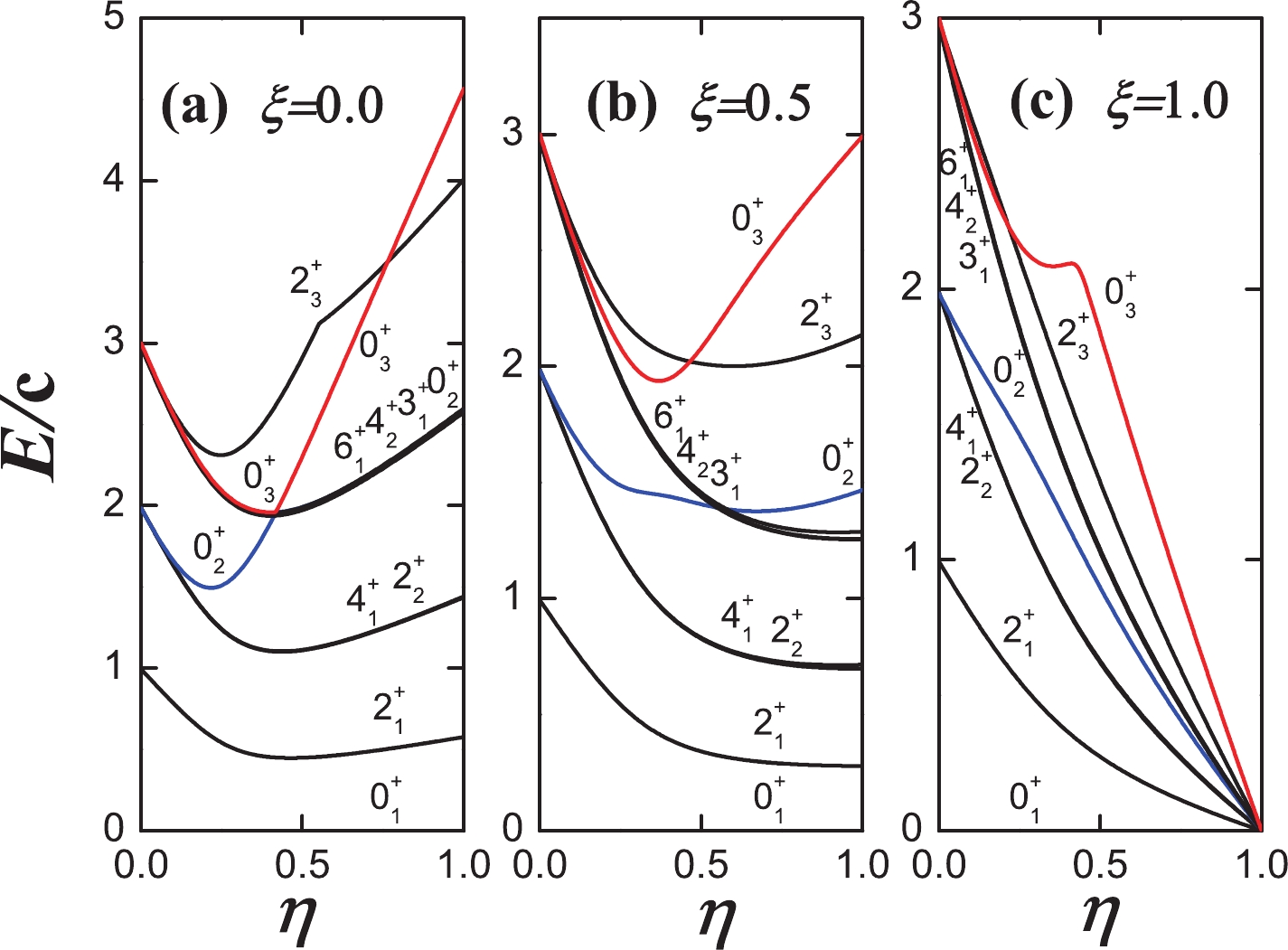

Figure 4.  (color online) Evolutional behaviors of partial low-lying levels when η changes from 0.0 to 1.0 and (a)$ \xi=0.0 $, (b) $ \xi=0.5 $, and (c) $ \xi=1.0 $ for $ N=7 $. It is clearly shown that, in the total parameter triangle, both '$ 4^{+}_{1},2^{+}_{2} $' and '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1} $' are always degenerate.

However, when $ \xi\neq 0.0 $, the mixing of the $S U(3)$ degenerate point cannot break the exact degeneracy between the ground and quasi-γ rotational bands. In the total parameter triangle, the degeneracy of '$ 4^{+}_{1},2^{+}_{2} $' is not broken and '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1} $' are also degenerate (Fig. 4(b), (c) and Fig. 5(a), (b)). The results shown here are for $ N=7 $; however, this degenerate behavior can hold for any $ \eta,\xi $ and any N. This result is astonishingly unexpected and resembles a partial $ O(5) $ dynamical symmetry [16]. Figure 4(c) shows the transitional behaviors from the spherical vibrational modes to the $S U(3)$ degenerate point, which is the main aim of this paper. The key finding is that the energy level of $ 0^{+}_{2} $ state (blue line) is always between the degenerate '$ 4^{+}_{1},2^{+}_{2} $' double states and degenerate '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1} $' triple states. The energy level of $ 2^{+}_{3} $ is slightly above those of the '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1} $' triple states, while the $ 0^{+}_{3} $ state is moved higher up (red line), and an abrupt change occurs. These $ U(5) $-like spectra were not expected before this study, and this new γ-softness is not connected with the $ O(6) $ dynamical symmetry. Figure 5(a) shows the transitional behaviors from the traditional $ O(6) $ γ-soft rotation to the $ SU(3) $ degenerate point, which shows that the spectra are all similar to the $ O(6) $ γ-soft ones. The transitional behaviors of the energy ratios $ E_{4/2} $ between $ E(4^{+}_{1}) $ and $ E(2^{+}_{1}) $ change from 2 to 2.5 in a similar style when moving from the $ U(5) $ limit to the $ O(6) $ limit and other various $ O(6) $-like locations (Fig. 6). When $ \xi=1.0 $ and $ \eta=0.5 $, the energy ratio $ E_{4/2} $ is approximately 2.3, slightly smaller than 2.5. This result is nearly the same as the ratio of the ¹¹⁰Cd nucleus (2.34).

Figure 5.  (color online) Evolutional behaviors of partial low-lying levels when ξ changes from 0.0 to 1.0 and (a)$ \eta=1.0 $ and (b) $ \eta=0.5 $ for $ N=7 $. The spectra in (a) resemble the one in the $ O(6) $ limit.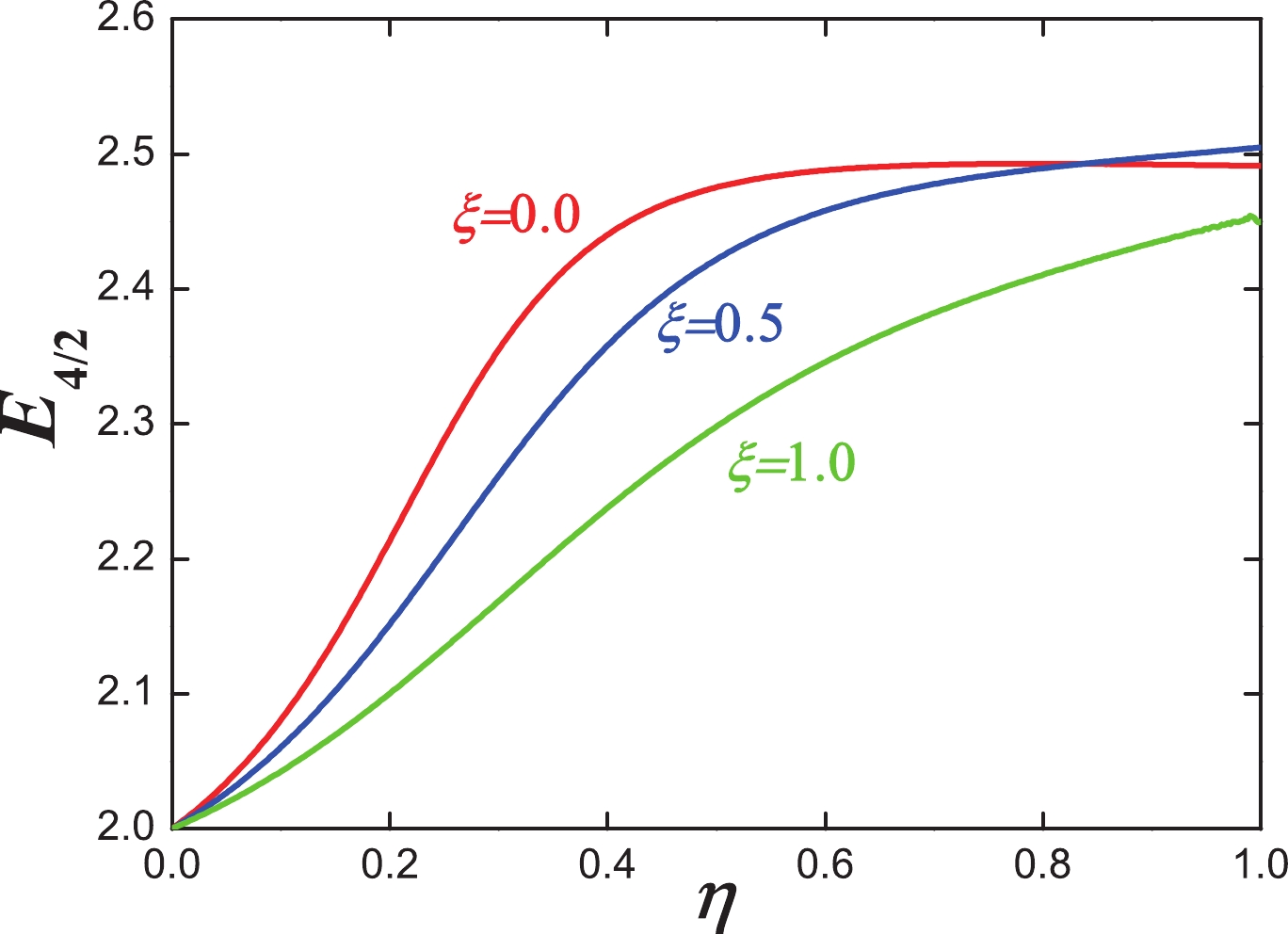

Figure 6.  (color online) Evolutional behaviors of $ E_{4/2} $ when η changes from 0.0 to 1.0 and $ \xi=0.0 $ (red line), $ \xi=0.5 $ (blue line), $ \xi=1.0 $ (green line) for $ N=7 $.

These results offer a new understanding for γ-soft rotations. Since the classical research on γ-soft spectra in [28], it has been a major paradigm of collective nuclear structure for more than sixty years. In this paper, we show that the simplest IBM-1 still has significantly more space for γ-soft rotational behaviors, except for the classical $ O(6) $ description via introducing higher-order interactions. The key aspect is the exact degeneracy in '$ 4^{+}_{1},2^{+}_{2} $' and '$ 6^{+}_{1},4^{+}_{2},3^{+}_{1} $', which is the typical feature of γ-softness. This type of degeneracy can hold for higher energy levels, such as '$ 8^{+}_{1},6_{2}^{+},5_{1}^{+},4_{3}^{+} $', which are not shown here.

The $ B(E2) $ values are necessary for us to understand the γ-softness. The operator is defined as

where e is the boson effective charge and $ \chi=-{\sqrt{7}}/{2}\xi $. The evolutional behaviors of the $ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $, $B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+})$, $ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $, $ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $, and $ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ values are plotted in Fig. 7 when η changes from 0.0 to 1.0 and $ \xi=0.0 $ (a), $ \xi=0.5 $ (b), and $ \xi=1.0 $ (c). The transitional behavior of the $ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ value is similar to the one from the $ U(5) $ limit to $ O(6) $ limit. The values of the $ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ are reduced whereas the ones of the $ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ are promoted. The values of the $ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ are also reduced. These are all the typical trends for the γ-soft rotation (Fig. 8).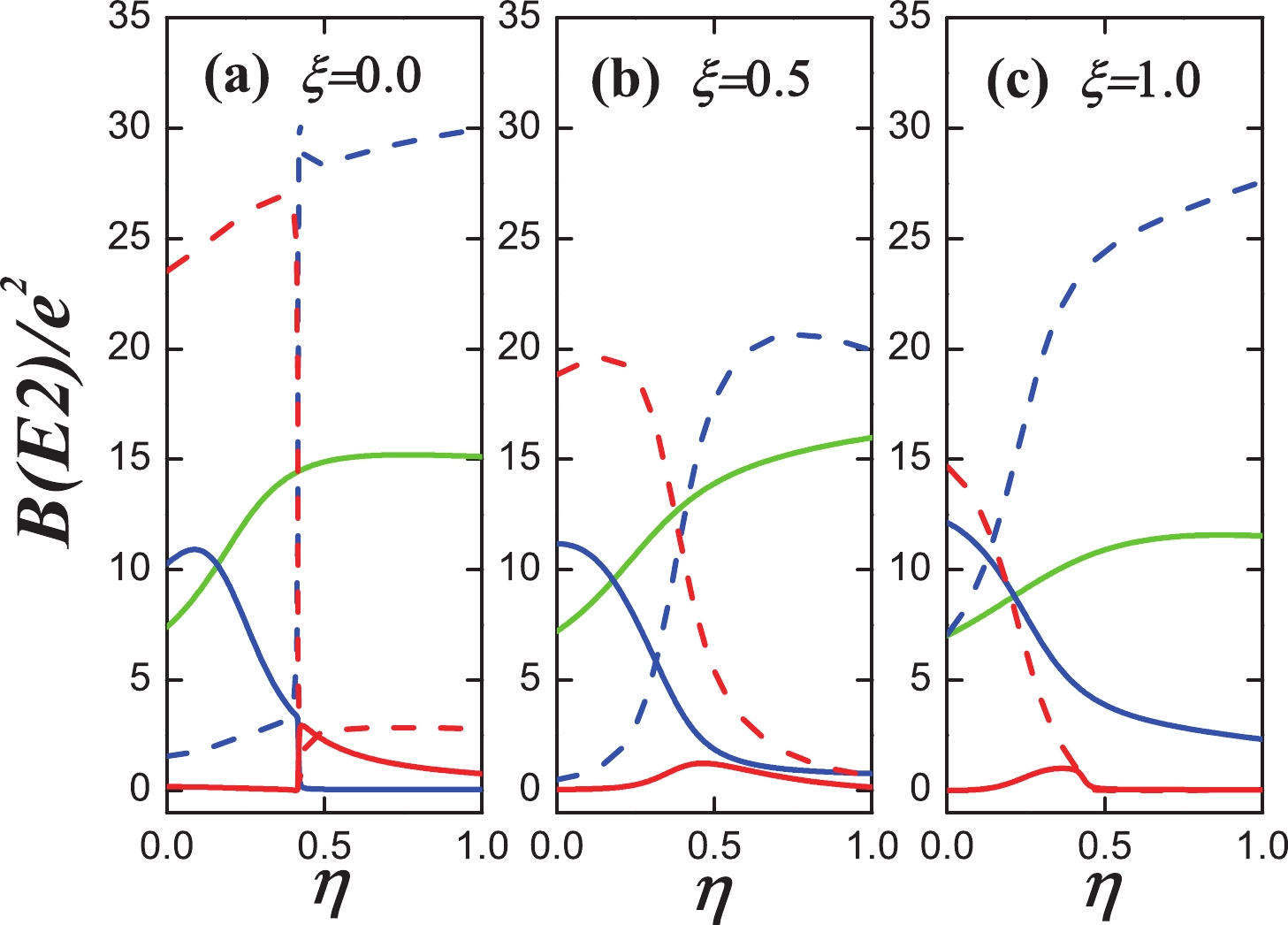

Figure 7.  (color online) Evolutional behaviors of $ B(E2; 2_{1}^{+}\rightarrow 0_{1}^{+}) $ (green solid line), $ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line), $ B(E2; 0_{2}^{+}\rightarrow 2_{2}^{+}) $ (blue dashed line), $ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and $ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when η changes from 0.0 to 1.0 and (a) $ \xi=0.0 $, (b) $ \xi=0.5 $, and (c) $ \xi=1.0 $ for $ N=7 $.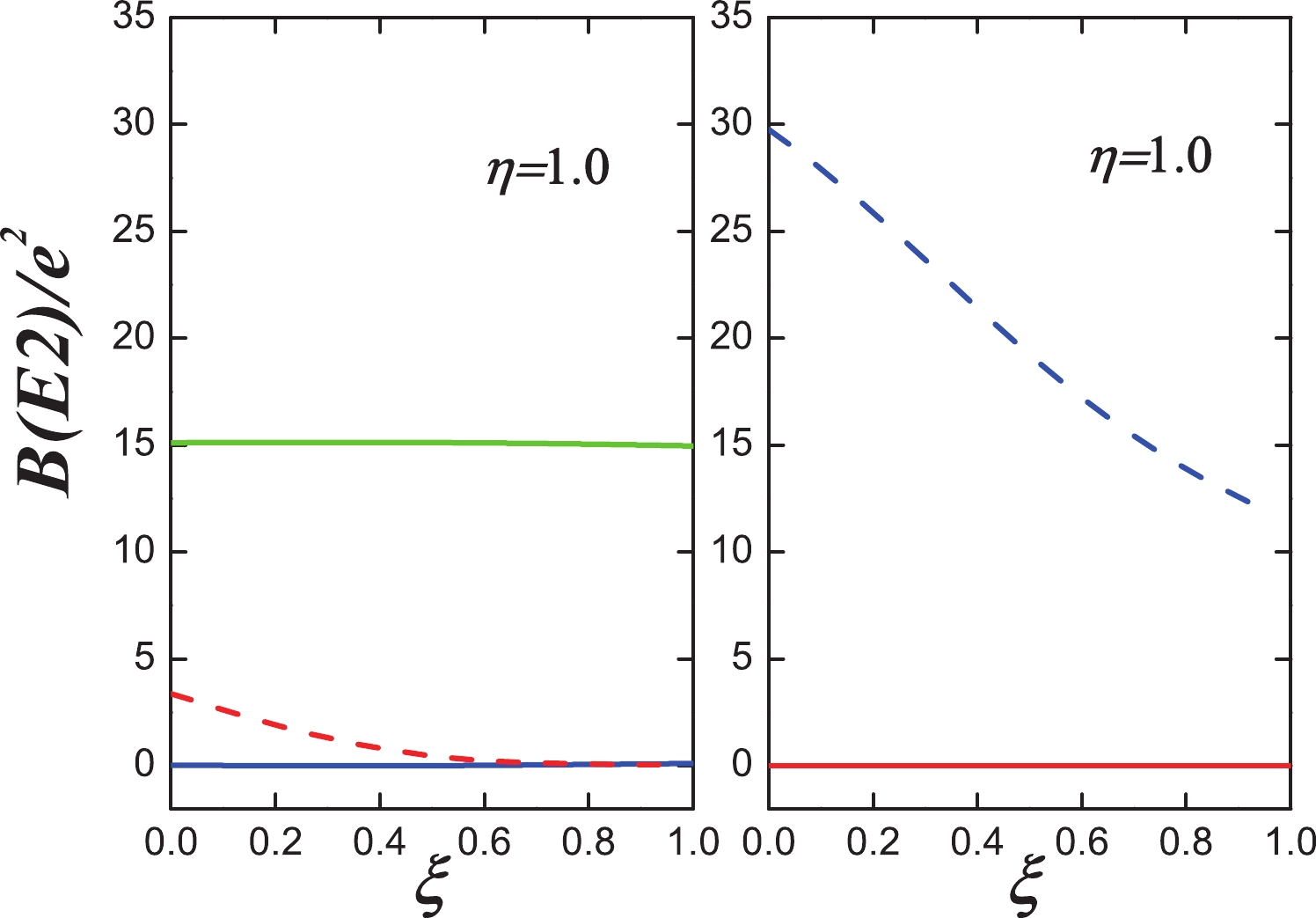

Figure 8.  (color online) Evolutional behaviors of $ B(E2; 2_{1}^{+}\rightarrow $$ 0_{1}^{+}) $ (green solid line), $ B(E2; 0_{2}^{+}\rightarrow 2_{1}^{+}) $ (blue solid line), $B(E2; 0_{2}^{+}\rightarrow $$ 2_{2}^{+})$ (blue dashed line), $ B(E2; 0_{3}^{+}\rightarrow 2_{1}^{+}) $ (red solid line), and $ B(E2; 0_{3}^{+}\rightarrow 2_{2}^{+}) $ (red dashed line) when ξ changes from 0.0 to 1.0 and $ \eta=1.0 $ for $ N=7 $.

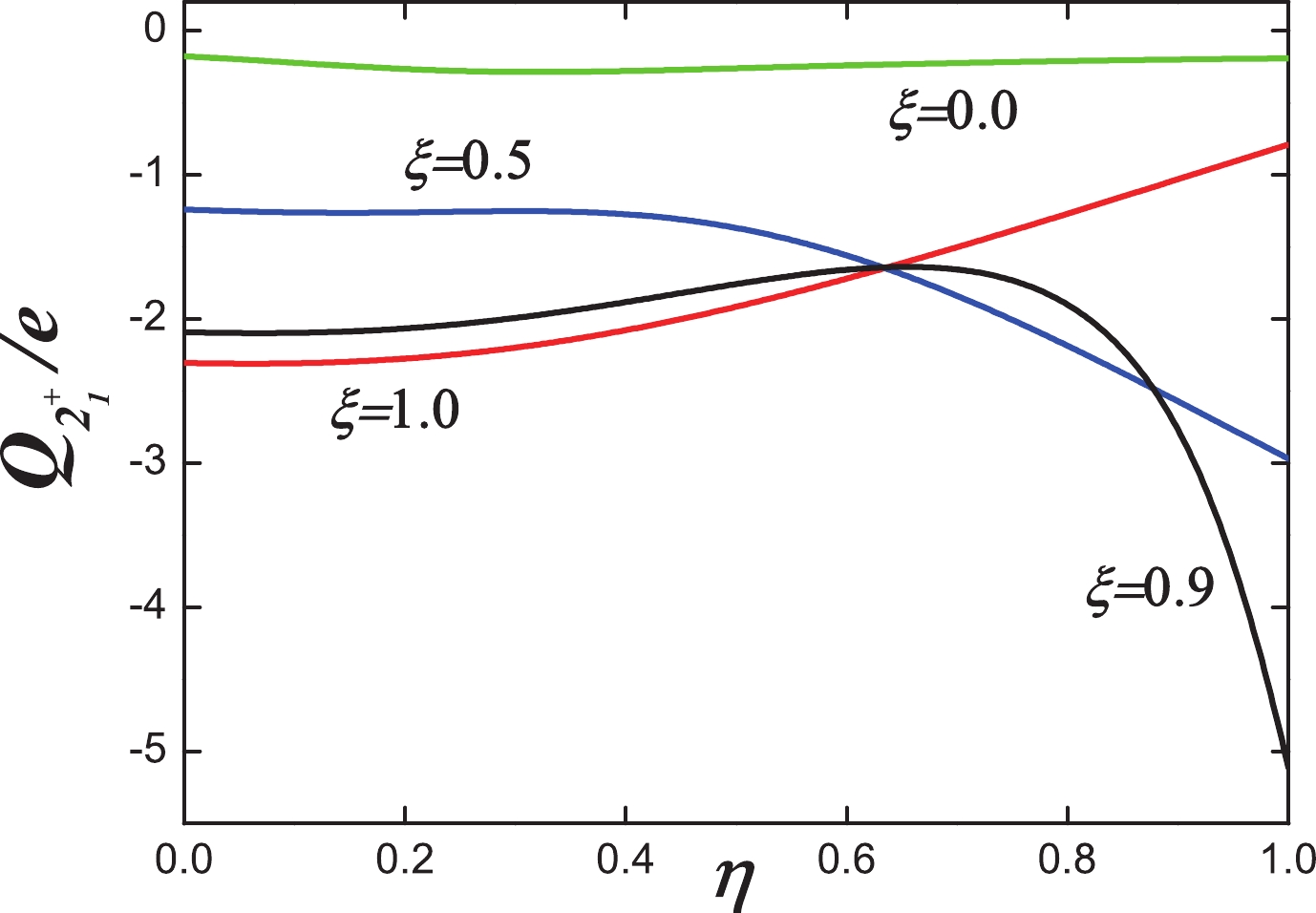
Now, we discuss the transitional pattern for the quadrupole moment of the $ 2^{+}_{1} $ state, which is shown in Fig. 9. This quantity in the $ O(6) $ limit is absolutely zero. If a $S U(3)$ two-body interaction is mixed, a large value can be obtained, but the γ-soft degeneracy will be significantly destroyed. This confusion has existed for many years. Specifically, this quantity is related to the first excited state, which is vital for a successful model [31]. Fig. 9 shows that the values increase when ξ changes from 0 to 1 for $ \eta=1.0 $, which may resolve the debates between γ-softness and large quadrupole moment.

Figure 9.  (color online) Evolutional behaviors of the quadrupole moment of the $ 2^{+}_{1} $ state when η changes from 0.0 to 1.0 and $ \xi=0.0 $ (green), $ \xi=0.5 $ (blue), $ \xi=0.9 $ (black), and $ \xi=1.0 $ (red) for $ N=7 $.

The $ U(5) $-like softness can be used to fit the spectra of ¹¹⁰Cd normal states, and the $ \hat{L}^{2} $ term is also incorporated. The Hamiltonian is

here $ \xi=1.0 $,$ \alpha=c(1-\eta) $,$ \beta=c\eta $, and γ is the coefficient of the $ \hat{L}^{2} $ term. Fig. 10 shows the partial low-lying levels for ¹¹⁰Cd normal states. The fitting results reproduce the style of experimental data; however, for higher-levels, the theoretical values are larger than the experimental ones. To reduce the energies of the higher-levels, Pan et al. presented a new method and observed an excellent fitting result for ¹⁹⁴Pt [49], which may be considered in future research to improve the fitting precision. The theoretical energy of the $ 0^{+}_{3} $ state is 3411.21 keV, which is significantly larger than the energy of the $ 6^{+}_{1} $ state, smaller than the $ 6^{+}_{2} $ state, and nearly twice the energy of the $ 0^{+}_{2} $ state. Experimentally, a $ 0^{+} $ state exists with an energy of 2662 keV, which is between the energies of the $ 6^{+}_{1} $ state (2480 keV) and $ 6^{+}_{2} $ state (2877 keV).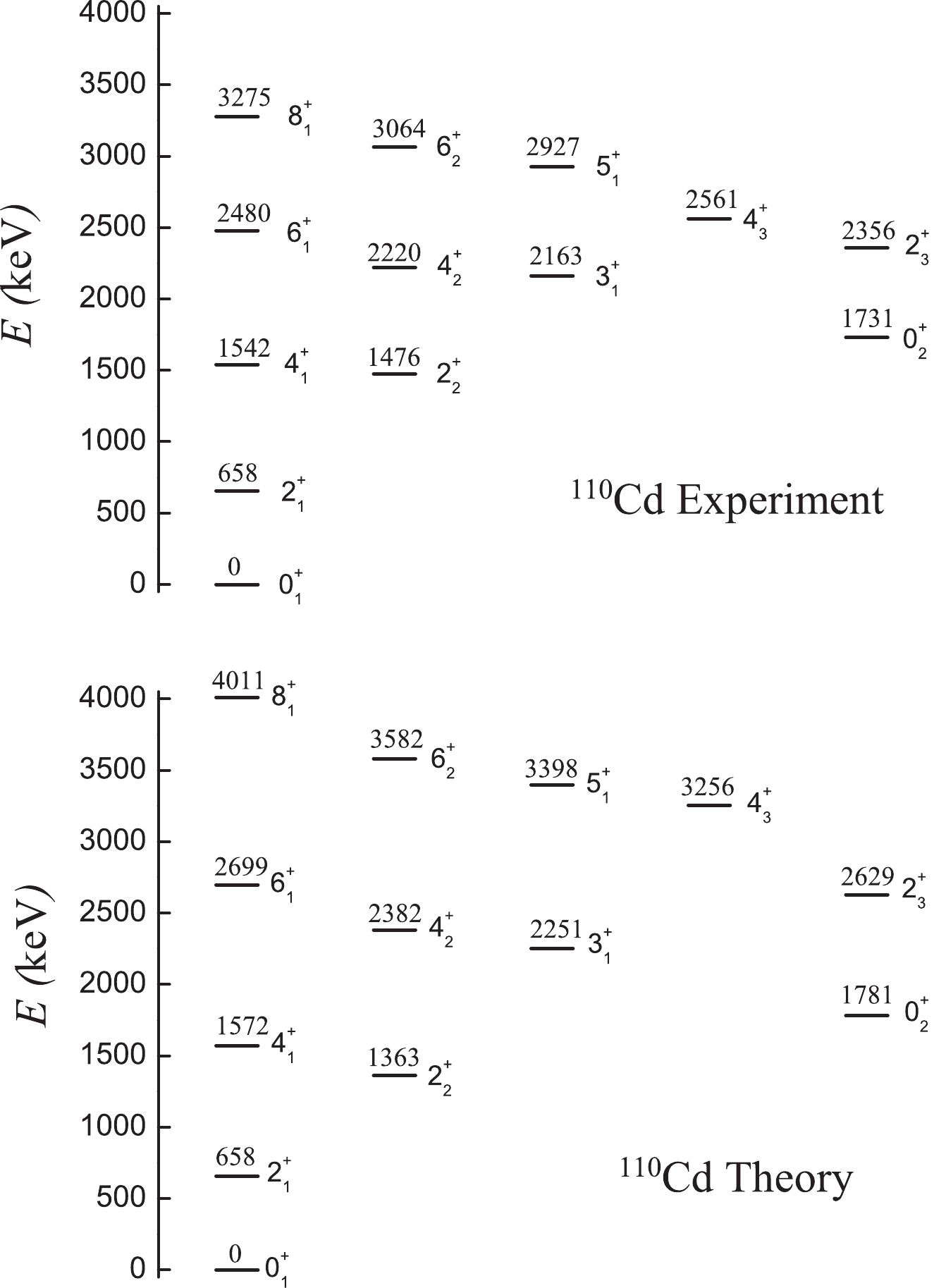

Figure 10.  Partial low-lying levels for ¹¹⁰Cd normal states. The values above are the experimental data and the ones below are the results of theoretical fitting.

The $ B(E2) $ values of the lowest levels are compared with the experimental results of the normal states in ¹¹⁰Cd, which are listed in Table 1. This γ-soft description can produce a good consistency with the empirical data qualitatively, which is different from the phonon descriptions. The quadrupole moment of the $ 2^{+}_{1} $ state is $ - $0.36 eb, which is also close to the experimental value of $ -0.39 $ eb. When weak mixing with the intruder states is considered, more reasonable results may be obtained [36]. Thus, our Hamiltonian may be also vital for understanding the Cd puzzle [51].

$ L_{i} $	$L_{f} $	Expt.	Results
$ 2_1^+ $	$0_1^+ $	27.0(8)	27.0
$ 4_1^+ $	$2_1^+ $	42(9)	39.0
$ 2_2^+ $	$2_1^+ $	$30(5);\;19(4) ^{\rm a}$	39.8
	$0_1^+ $	$1.35(20);\;0.68(14) ^{\rm a}$	0.17
$ 0_2^+$	$2_1^+ $	$<7.9 ^{\rm a} $	12.2
	$2_2^+ $	< 1680a	59.5
$ 6_1^+$	$4_1^+ $	$40(30);\;62(18) ^{\rm a}$	44.3
	$4_2^+ $	$<5 ^{\rm a} $	3.08
$ 4_2^+$	$4_1^+ $	$12 ^{+4}_{-6};\;{10.7^{+4.9}_{-4.8}}^{\rm a}$	21.1
	$2_1^+ $	$0.20 ^{+0.06}_{-0.09} ;\;0.14(6) ^{\rm a}$	0.04
	$2_2^+ $	$32 ^{+10}_{-14} ;\;22(10) ^{\rm a}$	23.2
$ 3_1^+$	$4_1^+ $	$5.9^{+1.8}_{-4.6} ;\; {2.4^{+0.9}_{-0.8}}^{\rm a}$	12.9
	$2_1^+ $	$1.1^{+0.3}_{-0.8} ;\;0.85(25) ^{\rm a}$	0.11
	$2_2^+ $	$32^{+8}_{-24} ;\;22.7(69) ^{\rm a}$	31.5
$ 2_3^+$	$4_1^+ $	$ <5 ^{\rm a} $	5.95
	$2_1^+ $	$ 2.8^{+0.6}_{-1.0} $	0.08
	$2_2^+ $	${{0.7} ^{+0.5}_{-0.6}}^{\rm a}$	3.62
	$0_2^+ $	24.2(22)a	24.2
a From Ref. [36].

Table 1.  Absolute $ B(E2) $ values in W.u. for $ E2 $ transitions from the low-lying normal states in ¹¹⁰Cd [36, 50] and present results when $ \alpha=956.54 $ keV, $ \beta=672.28 $ keV, and $ \gamma=14.41 $ keV with an effective charge of $ e=1.609 $ (W.u.)^1/2.

If "vibrational behavior at low energy is refuted'' [51], deformation has a dominant role when describing the collective nature of nuclei, and the description of triaxiality has a more important role than before. In IBM-1, protons and neutrons are not distinguished. If the rigid triaxial deformation for the ground state of a nucleus is included, the higher-order interactions must be considered [6]. However, in IBM-2 [1], protons and neutrons can be considered separately, and the triaxial shape can be described even with up to two-body interactions [52–55]. Three-body interactions $ [d^{\dagger}d^{\dagger}d^{\dagger}]^{(L)}\cdot[\tilde{d}\tilde{d}\tilde{d}]^{(L)} $ are also used in IBM-2 to investigate the γ triaxiality [56]. In the sdg-IBM, $ L=4 $ g bosons can be introduced and hexadecapole deformation can be discussed [57]. Except for the interacting boson models, triaxial shapes have also been investigated using many existing nuclear models [4, 51, 58–64].

In our paper, a new γ-soft rotational mode is observed, which is different from previous triaxial descriptions. In IBM-1 in particular, this finding can complement the existing O(6) γ-soft description. This γ-softness is related to the SU(3) degenerate point. Degeneracy implies symmetry [22]. Numerical results show that this symmetry is a O(5) partial dynamical symmetry. This finding is somewhat beyond expectation. We can observe that the degenerate point is generated by the states with the $S U(3)$ irreps satisfying the condition $ \lambda+2\mu=2N $. This degenerate condition may provide some clues. In IBM-1, nuclear states can be classified by U(6) symmetry [1]. In the SU(3) limit, symmetry reduction chain $U(6)\supset S U(3) \supset S O(3)$ is used. In 1968, Sebe indicated that for the special type of states with irreps $ \lambda+2\mu=2N $, the $U(6)\supset S U(3)$ reduction coefficient is identical to that for$U(3)\supset S O(3)$ [65]. This can be used to explain the emergence of the degenerate point^①. In 1985, when studying the sdg IBM in the SU(3) scheme, Akiyama observed that the SU(3) representations $ (\lambda,\mu) $ satisfying $ \lambda+2\mu= 4N $ belong to a special class. The reduction coefficient for the $U(15)\supset S U(3)$ chain is the same as that for $U(5)\supset S O(5)\supset S O(3)$ [66]. If the sd IBM-1 can be considered a reduction of the sdg IBM, the $U(6)\supset S U(3)$ reduction may correspond to parts of the $U(5)\supset S O(5)\supset S O(3)$ reduction, and O(5) partial dynamical symmetry may occur. A detailed discussion on this is required in the future. A numerical study on the transitional behaviors for our similar Hamiltonians from the U(5) limit to the SU(3) degenerate point in the sdg IBM would be extraordinarily interesting [67].

Triaxiality can be soft [28] or rigid [68]. The relationship between the two scenarios is an interesting topic under nuclear structures [56, 64]. In the large-N limit, Ref. [20] demonstrated that a rigid triaxial shape can exist from the U(5) limit to the SU(3) degenerate point. Our discussion directly corresponds to this interval. Numerical results have revealed that the triaxial deformation is γ-soft for small boson numbers. Thus, our model can connect the γ-soft and γ-rigid scenarios. Otsuka et al. demonstrated that, in finite systems, the soft and rigid triaxial descriptions can be identical [69], and they also provided a transitional description from γ-soft to γ-rigid shapes when the boson number N is increased [70]. With our model, it would also be interesting to study the transitional behaviors when N increases.

Since the Cd puzzle was proposed [32, 33, 51], some new attempts have been made to explain the experimental data. Garrett et al. indicated that no evidence exists for the strong mixing of the normal and intruder states, and the decay pattern is a signature of a γ-soft nucleus [36]. Nomura et al. conducted constrained self-consistent mean-field calculations to obtain the deformation energy surface, and a prolate global minimum was observed for ^108-116Cd [71]. An attractive explanation was provided by Leviatan et al. with U(5) partial dynamical symmetry [72]. The U(5) dynamical symmetry was partly broken, and large anharmonicity for some nonyrast states was introduced. The two-phonon $ 0^{+} $ state still exists, but at a higher excitation energy. This theory can excellently reproduce the data except for the $ 0^{+}_{4} $ state (two-phonon state). Our concept is similar to this; however, the U(5) dynamical symmetry is not kept and only O(5) dynamical is partly broken. The γ-soft mode can still exist. In the theory of Leviatan et al., the $ 0^{+} $ two-phonon state can have enhanced B(E2) values for decay to the $ 2^{+}_{1} $ state, which is not supported by existing experimental results [39]. This deficiency may be overcome in our theory.

Recently, Garrett et al. promoted the developments on the spherical nucleus puzzle [38, 39]. In their experiments, very weak decay branches from nonyrast states were observed, and the $ 0^{+}_{4} $ band was identified for ¹¹²Cd. Within this band, $ (E_{4^{+}_{1}}-E_{0^{+}_{1}})/(E_{2^{+}_{1}}-E_{0^{+}_{1}})=2.95 $, which is a signature of large deformation. These experimental data were interpreted using beyond-mean-field calculations, and they suggested the Cd isotopes exhibit a multiple shape coexistence. The ground state had a prolate shape. However, their explanation was insufficient for the intruder states quantitatively.

Finally, some subtle connections in some Zn-Ge isotopes has been observed to date. In ⁷⁰Zn and ^72,74Ge, the shape coexistence has been observed [73, 74]. ^76,78Ge are observed to have a rigid triaxial deformation for their ground states [45–47]. Interestingly, ^72,74Zn have an $ B(E2) $ anomaly [75]. Thus, a self-consistent nuclear model is required to explain these nuclei. A microscopic calculation based on the nuclear density functional theory predicted that most of the observed γ-soft Ge nuclei exhibit some features between the γ-rigid and γ-unstable rotor limits [76]. In our opinion, including the $S U(3)$ higher-order interactions into the common IBM-1 may be a simple and effective method.

New γ-soft triaxial rotation is observed in the interacting boson model with $S U(3)$ conserving higher-order interactions. This attempt appears meaningful. With the aid of introducing $S U(3)$ higher-order terms, the yrast $ B(E2) $ anomaly has been described successfully. In this paper, following the studies in Refs. [20, 21], the transitional behaviors from the $ U(5) $ limit to the $S U(3)$ degenerate point is numerically explored and compared with the transitional behaviors from the $ U(5) $ limit to the $ O(6) $ limit. In particular, spherical-like γ-soft triaxial rotational spectra actually exists, which may be what is required to solve the spherical nucleus puzzle [36]. $ O(6) $-like γ-soft spectra with large quadrupole moment are also shown. Importantly, in the parameter triangle, the degeneracy of the corresponding energy levels between the ground and quasi-γ bands are not broken, which is a partial $ O(5) $ dynamical symmetry [16]. This symmetry is related to the studies of Sebe and Akiyama [65, 66], and they will be discussed in the future.

The new γ-soft triaxial spectra may be intimately connected with the realistic spectra in Cd isotopes, and it may be an effective description of the spherical-like nuclei [34, 35, 51]. A further discussion for multiple shape coexistence in ¹¹⁰Cd and ¹¹²Cd [38, 39] will be conducted. Additionally, many new experimental γ-soft anomalies in ^126-132Xe [40–42] and ^98-102Zr [43, 44] will be investigated. The relationship between γ-rigid triaxial deformation in ^76,78Ge [45–47] and higher-order quadrupole interactions also require further discussion in the future.

In this paper, we show that $S U(3)$ higher-order interaction may be more important than expected before. Here, only the $S U(3)$ cubic interaction $ [\hat{Q}\times \hat{Q}\times \hat{Q}]^{(0)} $ is considered. In Ref. [27], two $S U(3)$ third-order interactions $ [\hat{Q}\times \hat{Q}\times \hat{Q}]^{(0)} $, $ [\hat{L}\times \hat{Q}\times \hat{L}]^{(0)} $ were included to explain the $ B(E2) $ anomaly successfully. In future discussions on fourth-order interactions, $ (\hat{Q}\cdot \hat{Q})^{2} $ should be also considered for it is related to the rigid triaxial rotation [9, 10], and any type of quadrupole deformation can be described in a consistent manner.

The partial $ O(5) $ dynamical symmetry revealed in this paper can be further used to discuss quantum chaos in nuclear physics [77–79], which may provide a new regular region in the interacting boson model [80, 81]. This will be discussed in the future. In addition, the numerical results for large N are also required to study the quantum phase transition of this transitional region from the $ U(5) $ limit to the $S U(3)$ degenerate point and the rigid triaxial rotation in the large-N limit described in Ref. [20].

One of the anonymous reviewers of this paper is acknowledged for reminding the author to notice Sebe's and Akiyama's important research, which is related to the O(5) partial dynamical symmetry.