-
Dark matter is a type of mysterious invisible substance that experiences only gravitational interactions, which may theoretically exist in the Universe based on cosmic observation data, including cosmic microwave background radiation and baryon acoustic oscillations [1, 2]. It is believed that dark matter constitutes approximately
$ 85 $ % of all matter in the Universe. However, the nature of dark matter is still unclear. Thus, understanding the properties of dark matter is an outstanding challenge.The first image of a black hole, released by the Event Horizon Telescope (EHT) Collaboration, confirmed the existence of a supermassive black hole at the center of the elliptical galaxy M87 [3, 4], which launched a new era of gravity testing in strong field regimes. Recent astronomical observations [5, 6], such as the spiral galaxy rotation curve and the mass-luminosity ratio of elliptical galaxies, indicate that dark matter may cluster at the center of galaxies and close to black holes. Thus, it is important and interesting to study the interaction between dark matter and black holes. If there is dark matter in the vicinity of a black hole, the dark matter and its distribution may modify the geometry of the black hole, which could lead to new observable effects arising from the dark matter. Kiselev [7] obtained a static black hole solution surrounded by specific matter. Because the equation of state is equal to zero, this solution describes the modification of black hole metrics caused by dark matter. Kiselev's black hole solution has also been generalized for the high dimension black hole case [8] and rotating black hole case [9]. By making use of a mass function related to distribution matter, several black hole metrics deformed by dark matter have been obtained [10–17]. Recently, Cardoso et al. [18] obtained an interesting static black hole solution by solving Einstein's equations with the energy momentum tensor originating from galactic matter, which describes a galactic black hole immersed in a dark matter halo with a Hernquist distribution. With this solution, the effects of a dark mater halo on quasinormal modes, scattering, and optical phenomena have been studied in [19–24]. The galactic black hole solution for a black hole surrounded by a dark matter halo with different distributions has been discussed in [25].
Tidal disruption is one of the most magnificent phenomena in galaxies, which occurs when a star passes sufficiently close to a supermassive black hole so that the tidal forces destroy the star. The electromagnetic emission caused in tidal disruption events can help probe the features of the corresponding supermassive black hole. Thus, significant effort has been dedicated to study tidal effects, including the shape deformation of a body in black hole spacetime. In Schwarzschild black hole spacetime, it is known that the tidal force stretches a body falling toward a black hole in the radial direction and compresses it in the angular direction [26]. In the Reissner-Nordström case [27], the charge of the black hole strongly affects the tidal force so that its radial and angular components change their signs as the body falls toward the center of the black hole. Tidal effects have been investigated in other static spacetimes, including regular black holes [28, 29], Kiselev black holes [30], and naked singularities [31]. Moreover, the effect of the Gauss-Bonnet coupling constant on tidal forces and the geodesic deviation vector has been studied in four-dimensional Gauss-Bonnet black hole spacetime [32]. This investigation also revealed [33] that in the ergosphere of a rotating black hole, a star broken by tidal interactions can emit a jet composed of debris, which may provide a potential mechanism for explaining the formation of jets near black holes. Subsequently, the study of tidal effects has also been performed in various black holes [34–40]. The main purpose of this paper is to study tidal effects in a galactic black hole with a dark matter halo [18] and to probe how dark matter mass and galaxy lengthscale affect tidal forces and the motion of the geodesic deviation vector.
This paper is organized as follows: In Sec. II, we briefly review the galactic black hole solution with a dark matter halo [18] and the geodesic equation. In Sec. III, we investigate the tidal forces on a body free falling in the radial direction in the galactic black hole solution with a dark matter halo. In Sec. IV, we present the dynamical evolution of a deviation vector in the spacetime of a black hole with a dark matter halo and analyze the effects of the dark matter halo and galaxy lengthscale. Finally, we conclude with a summary.
-
Let us now briefly review the galactic black hole solution with a dark matter halo obtained in [18]. It is well known that the Hernquist-type density distribution [41] can be used to describe the Sérsic profiles observed in bulges and elliptical galaxies.
$ \begin{equation} \rho=\frac{a_0 M}{2 \pi r \left(a_0+r\right)^3}, \end{equation} $

(1) where M is the total mass of the dark matter halo, and
$ a_0 $ is a typical lengthscale of the galaxy. With this matter density distribution, an interesting exact solution [18] was introduced to describe a black hole immersed in the center of a galaxy. The metric of the black hole solution has the form$ \begin{equation} {\rm{ds}}^2= -f(r){\rm{dt}}^2 +\frac{1}{1-\dfrac{2 m(r)}{r}}{\rm{dr}}^2 +r^2 \left({\rm{d \theta }}^2+ \sin^2\theta{\rm{d \phi }}^2\right), \end{equation} $

(2) where the mass distribution of matter around the black hole is [18]
$ \begin{equation} m(r)=M_{{\rm{BH}}}+\frac{M r^2}{\left(a_0+r\right){}^2} \left(1-\frac{2 M_{{\rm{BH}}}}{r}\right){}^2. \end{equation} $

(3) Here,
$ M_{{\rm{BH}}} $ is the mass of the black hole at the center. The function$ f(r) $ can be expressed as [18]$ \begin{equation} f(r)=\left(1-\frac{2 M_{{\rm{BH}}}}{r}\right) {\rm e}^{\Upsilon (r)}, \end{equation} $

(4) with
$ \Upsilon (r)=-\pi \sqrt{\dfrac{M}{\xi }} +2 \sqrt{\dfrac{M}{\xi }} \arctan \left(\frac{a_0-M+r}{\sqrt{M \xi }}\right), $

(5) $ \begin{array}{*{20}{l}} &&\xi=2 a_0+4 M_{{\rm{BH}}}-M. \end{array} $

(6) It must be noted that in solution (2), the dark matter surrounding the black hole is assumed to exhibit only non-zero tangential pressures and vanishing radial pressure. The spacetime in (2) is asymptotically flat, and the corresponding ADM mass is
$ M+M_{{\rm{BH}}} $ . It has a horizon at$ r_{H}=2M_{{\rm{BH}}} $ and a curvature singularity at$ r=0 $ . Eqs. (5) and (6) indicate that$ 2 a_0+4 M_{{\rm{BH}}}-M>0 $ , which is consistent with the best fit of galaxy observations where$ a_0> 10^4M $ [42]. In the spacetime of a black hole immersed in dark matter (2), the corresponding density function of dark matter becomes$ \begin{equation} \rho = \frac{2 M ( a_0 +2 M_{{\rm{BH}}}) \left(1-\dfrac{2 M_{{\rm{BH}}}}{r}\right)}{r ( a_0 +r)^3}, \end{equation} $

(7) which differs from the original Hernquist-type density distribution (1) owing to the interaction between dark matter and the black hole at the center of the galaxy. As the mass of the black hole
$ M_{{\rm{BH}}} $ tends to zero, the density function (7) reduces to the original function (1). At the horizon$ r_{H}=2M_{{\rm{BH}}} $ , the matter density vanishes. In fact, the parameters M,$ a_0 $ , and$ M_{{\rm{BH}}} $ determine the geometry of spacetime (2). The observation of galaxies corresponds to the regime$ a_0>10^4M $ [42]. Moreover, as$ a_0\gg M_{{\rm{BH}}} $ , the density function of dark matter (7) at large distances becomes the Hernquist-type density distribution (1). Thus, as in [18, 19], we focus on the regime in which$ M_{{\rm{BH}}}\ll M\ll a_0 $ . In particular, in this parameter region, the spacetime (2) only has a curvature singularity at$ r=0 $ , and the another singularity$ r=M-a_0\pm \sqrt{M(M-2a_0-4M_{{\rm{BH}}})} $ does not exist because$ M-2a_0- 4M_{{\rm{BH}}}<0 $ ; therefore, spacetime (2) is regular in the physical region$ r>r_H $ . Moreover, the choice of such a parameter region means that the Ricci scalar near the horizon$ R\sim M/(a^2_0M_{{\rm{BH}}}) $ can be decreased in a controlled manner and decays as$ R \sim4Ma_0/r^4 $ at large distances [18]. In Fig. 1, we also present the change in dark matter density distribution with the halo mass M and lengthscale parameter$ a_0 $ . It is shown that the density increases with the mass M at fixed$a_0= 10 M_{{\rm{BH}}}$ but decreases with$ a_0 $ for fixed$ M=10 M_{{\rm{BH}}} $ .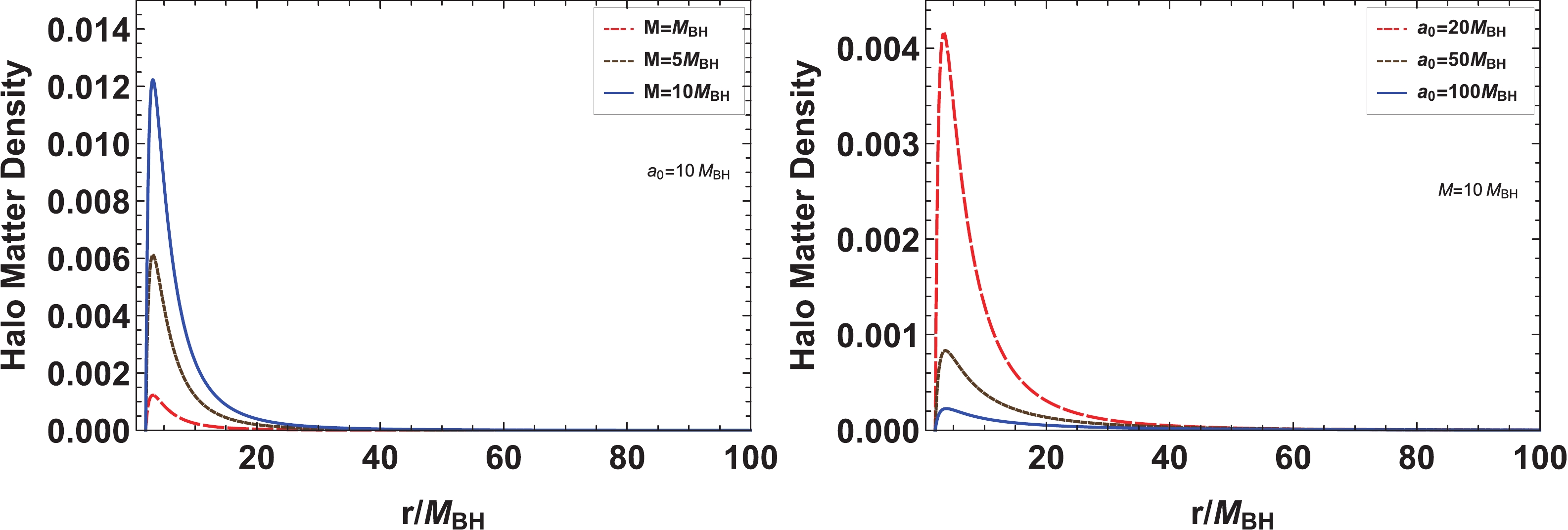
Figure 1. (color online) Change in density distribution with the halo mass M and lengthscale parameter
$ a_0 $ in black hole spacetime (2).In black hole spacetime (2), the geodesic motion equation for a massive test particle along the radial direction is [43]
$ \begin{equation} f(r) \dot{t}^2-\frac{\dot{r}^2}{1-\dfrac{2 m(r)}{r}}=1, \end{equation} $

(8) where the dot represents differentiation with respect to the proper time τ. It is clear that a massive particle moving along the geodesic in spacetime (2) has two conserved quantities: the energy E and angular momentum L. As in [44], with the equation
$ E=f(r) \dot{t} $ , Eq. (8) can be expressed as$ \begin{equation} \dot{r}^2=\left(\frac{E^2}{f(r)}-1\right) \left(1-\frac{2 m(r)}{r}\right). \end{equation} $

(9) The Newtonian radial acceleration [45] of the particle in the black hole surrounded by a dark matter halo (2) can be expressed as
$ \begin{aligned}[b] A^R=&\ddot{r}=\frac{rm'(r)-m(r)}{2r^2}-\frac{E^2}{2f(r)}\bigg[\frac{rm'(r)-m(r)}{r^2} +\frac{f'(r)}{2f(r)}\bigg(1-\frac{2 m(r)}{r}\bigg)\bigg] =-\frac{M_{{\rm{BH}}}}{r^2}-\frac{1}{(r+a_0)^3} \\& \times \bigg\{\frac{(r-2M_{{\rm{BH}}})M}{r^2}\bigg[r^2-(6M_{{\rm{BH}}}+a_0)r -2M_{{\rm{BH}}}a_0\bigg]+2E^2 M(2M_{{\rm{BH}}} +a_0){\rm e}^{\textstyle\sqrt{\frac{M}{2a_0+4M_{{\rm{BH}}}-M}}[(\pi-2\arctan{\frac{r-M+ a_0}{ \sqrt{M (2a_0+4M_{{\rm{BH}}}-M)}}}]}\bigg\}. \end{aligned} $ 
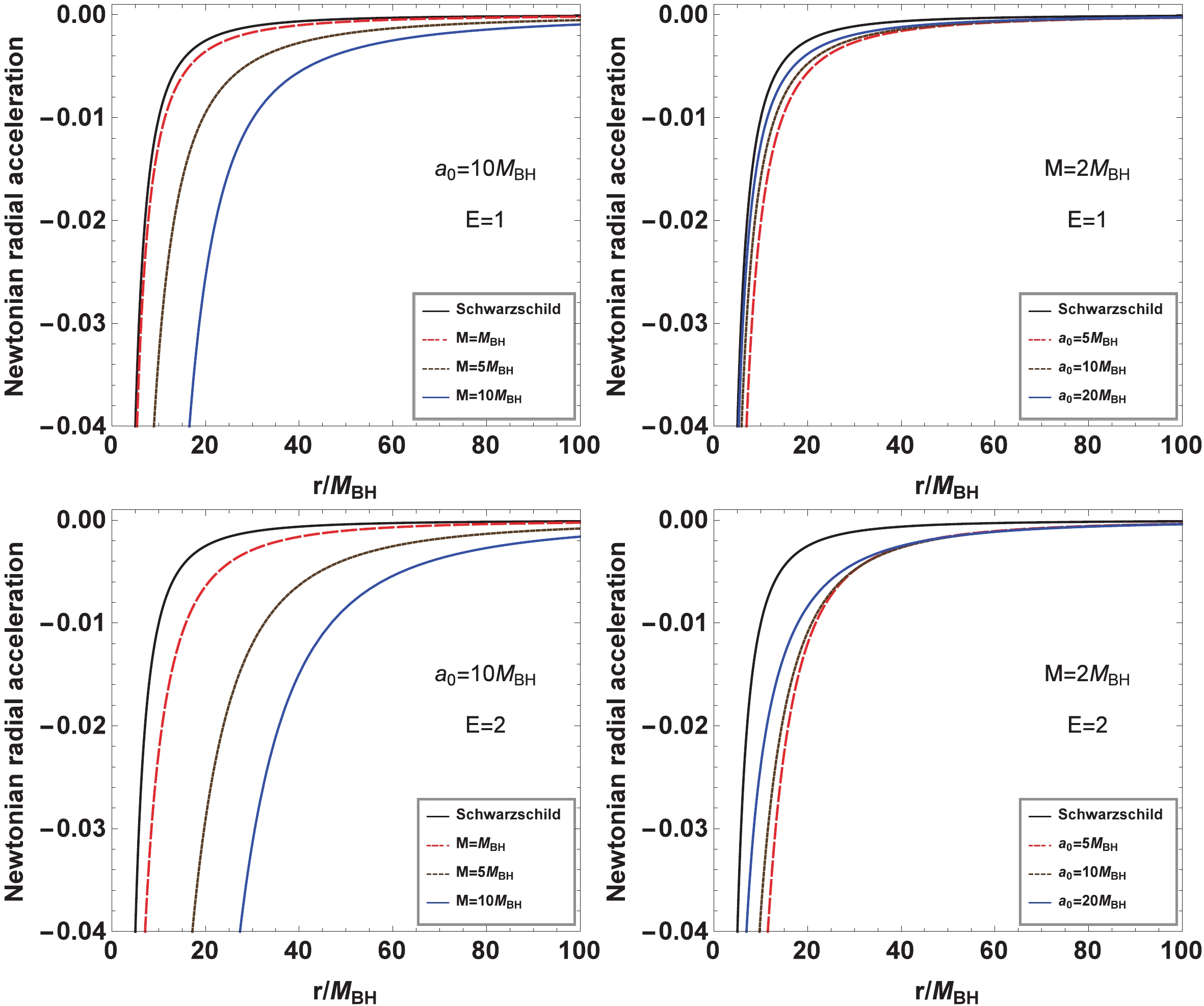
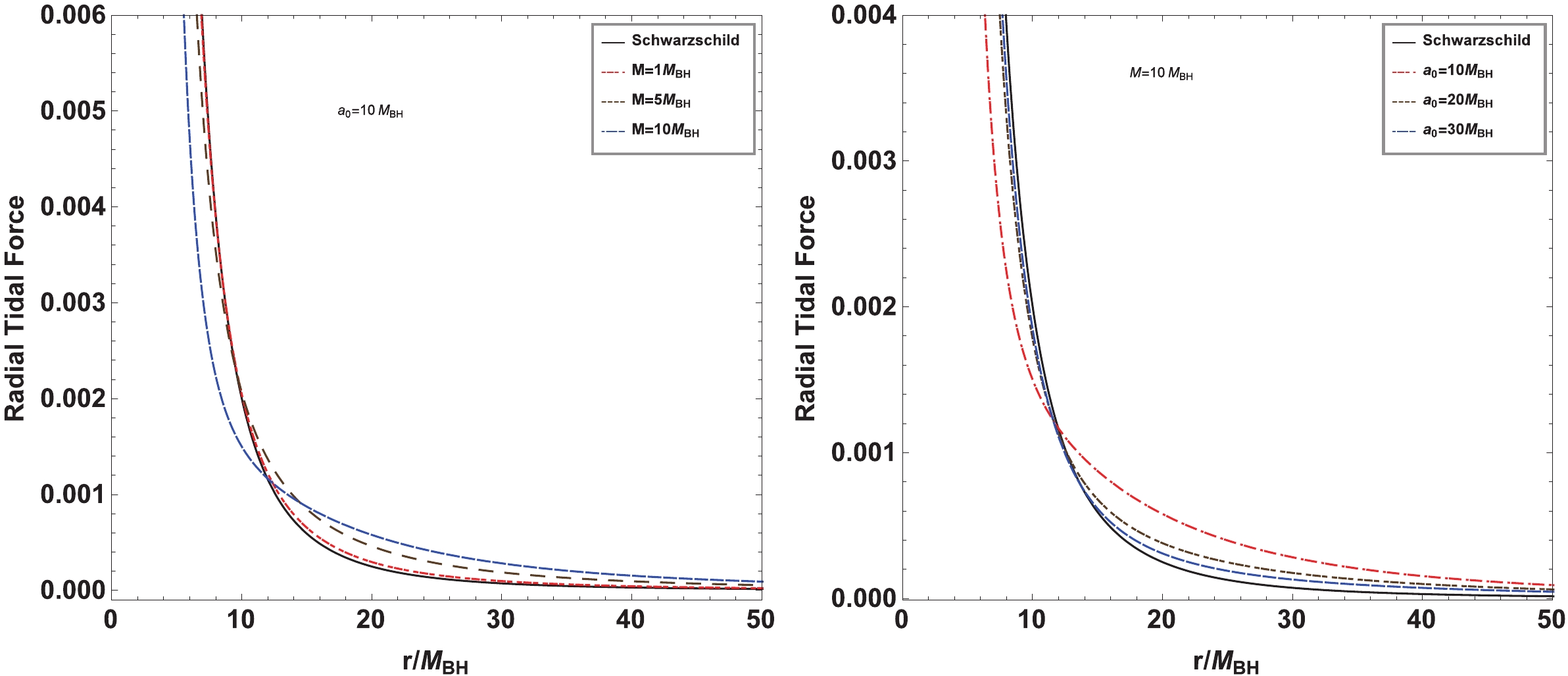
(10) Clearly, the absolute value of the Newtonian radial acceleration increases with the energy E of the test particle, which differs from that in Schwarzschild and Reissner-Nordström black hole spacetimes, where the Newtonian radial acceleration is independent of the test particle energy E. In Fig. 2, we present the change in Newtonian radial acceleration with parameters M and
$ a_0 $ for a test particle moving along the radial direction in a black hole with a dark matter halo (2). It is shown that the absolute value of the Newtonian radial acceleration increases with the dark matter mass M but decreases with the lengthscale parameter$ a_0 $ of the galaxy. Moreover, we find that the effects of parameters M and$ a_0 $ on the Newtonian radial acceleration become more remarkable in the case where the test particle has a higher energy E. From Eq. (9), we find that the test particle free falling from rest at$ r=b>r_H $ does not bounce back in its radial motion because Eq. (9) does not have another root satisfying$ \dot{r}=0 $ under the previous condition$ M<2 a_0+4 M_{{\rm{BH}}} $ , which is similar to that in the Schwarzschild case. -
Here, we study the tidal forces acting on a massive particle in the background of a galactic black hole with a dark matter halo (2). It is well known that tidal forces are governed by the geodesic deviation equation of a spacelike vector
$ \eta^{\mu} $ , which describes the distance between two infinitesimally close particles following geodesics [46, 47]. The geodesic deviation equation is$ \begin{equation} \frac{D^2 \eta ^{\mu }}{{\rm{ D \tau }}^2}-R_{\sigma \nu \rho}^{\mu } v^{\sigma} v^{\nu }\eta ^{\rho } =0, \end{equation} $

(11) where
$ v^{\nu } $ is the unit vector tangent to the geodesic. In the spacetime of a black hole with a dark matter halo (2), the tetrad basis related to a freely falling frame can be expressed as$ \begin{aligned}[b] \hat{e}_{\hat{0}}^{\mu }=\Bigg(\frac{E}{f(r)}, -\sqrt{\left(\frac{E^2}{f(r)}-1\right) \left(1-\frac{2 m(r)}{r}\right)}, 0, 0\Bigg), \end{aligned} $

$ \begin{aligned}[b] \hat{e}_{\hat{1}}^{\mu }&=\Bigg(-\frac{1}{f(r)}\sqrt{\frac{E^2}{f(r)}-1}, \frac{E}{f(r)} \sqrt{f(r) \left(1-\frac{2 m(r)}{r}\right)}, 0, 0\Bigg),\\ \hat{e}_{\hat{2}}^{\mu }&=\left(0, 0, \frac{1}{r}, 0\right),\\ \hat{e}_{\hat{3}}^{\mu }&=\left(0, 0, 0, \frac{1}{r \sin \theta }\right), \end{aligned} $

(12) which obeys the condition
$ \begin{equation} \hat{e}_{\alpha \hat{\nu }} \hat{e}_{\hat{\mu }}^{\alpha }=\eta _{\hat{\nu } \hat{\mu }}, \end{equation} $

(13) Here,
$ \eta _{\hat{\nu } \hat{\mu }} $ is the Minkowski metric. The indices with and without a hat correspond to the tetrad and coordinate basis indices, respectively. Moreover, we have$ \hat{e}_{\hat{0}}^{\mu }=v^{\mu } $ . With the tetrad basis (12), the geodesic deviation vector$ \eta^{\mu } $ can be expanded to$ \eta^{\mu }=\hat{e}_{\hat{\nu}}^{\mu } \eta ^{\hat{\mu }} $ with the fixed component$ \eta ^{\hat{0}}=0 $ . In the background of a black hole with a dark matter halo (2), the non-vanishing independent components of the Riemann tensor are [43]$\begin{aligned}[b] R^1{}_0{}_1{}_0=&\frac{1}{2}f''(r)\left(1-\frac{2 m(r)}{r}\right)\\&+\frac{1}{4}\bigg[f'(r)\left(1-\frac{2 m(r)}{r}\right)'-\left(1-\frac{2 m(r)}{r}\right)\frac{f'(r)^2}{f(r)}\bigg], \end{aligned} $

$ \begin{aligned}[b] R^1{}_2{}_1{}_2=&\frac{m(r)-rm'(r)}{r},\\ R^1{}_3{}_1{}_3=&\frac{m(r)-rm'(r)}{r} \sin ^2\theta , \\ R^2{}_3{}_2{}_3=&\frac{2 m(r) \sin ^2\theta}{r},\\ R^2{}_0{}_2{}_0=&R^3{}_0{}_3{}_0=\frac{f'(r)}{2 r}\left(1-\frac{2 m(r)}{r}\right). \end{aligned} $

(14) Making use of the relationship
$ R_{\hat{\beta} \hat{\gamma} \hat{\delta}}^{\hat{\alpha}}=e_{\mu}^{\hat{\alpha}} e_{\hat{\beta}}^{\nu} e_{\hat{\gamma}}^{\rho} e_{\hat{\delta}}^{\sigma} R_{\nu \rho \sigma}^{\mu} $ , we can obtain the Riemann curvature tensor in the tetrad basis$ \begin{aligned}[b] R_{\;\hat{1} \hat{0} \hat{1}}^{\hat{0}}=&-\frac{1}{4 f'(r)}\bigg[\frac{f'(r)^2}{f(r)} \left(1-\frac{2 m(r)}{r}\right) \bigg]',\\ R_{\;\hat{2} \hat{0} \hat{2}}^{\hat{0}}=& R_{\;\hat{3} \hat{0}\hat{3}}^{\hat{0}}=\frac{1}{2r}\bigg[E^2\bigg(\frac{r-2 m(r)}{rf(r)}\bigg)'-\bigg(1-\frac{2 m(r)}{r}\bigg)'\bigg]. \end{aligned} $

(15) Here, we also note that the components
$ R_{\;\hat{2} \hat{0} \hat{2}}^{\hat{0}} $ and$ R_{\;\hat{3} \hat{0}\hat{3}}^{\hat{0}} $ depend on the energy of the particle, which could lead to several new features of tidal force in the spacetime of a black hole with a dark matter halo (2). Substituting the above formula into the geodesic deviation equation (11), we can find that the equations for tidal forces in radial free-fall reference frames satisfy [48]$ \begin{aligned}[b] \ddot{\eta }^{\hat{1}}=&\frac{1}{r^3}\bigg\{2M_{{\rm{BH}}}+\frac{(r-2M_{{\rm{BH}}})M}{(r+a_0)^3}\\&\times\bigg[2r^2+(a_0-6M_{{\rm{BH}}})r- 4M_{{\rm{BH}}}a_0\bigg] \\& -\frac{Mr^2(2M_{{\rm{BH}}}+a_0)}{(r+a_0)[r^2+2(a_0-M)r+4MM_{{\rm{BH}}}+a^2_0]}\bigg\} \eta ^{\hat{1}}, \end{aligned} $

(16) and
$ \begin{aligned}[b] \ddot{\eta}^{\hat{i}}=&- \bigg\{\frac{M_{{\rm{BH}}}}{r^3}+\frac{(r-2M_{{\rm{BH}}})M}{r^3(r+a_0)^3}\bigg[r^2-(6M_{{\rm{BH}}}+a_0)r-2M_{{\rm{BH}}}a_0\bigg]\\ &+\frac{2E^2 M(2M_{{\rm{BH}}} +a_0)}{r(r+a_0)^3}{\rm e}^{\sqrt{\frac{M}{2a_0+4M_{{\rm{BH}}}-M}}[(\pi-2\arctan{\frac{r-M+ a_0}{\sqrt{M (2a_0+4M_{{\rm{BH}}}-M)}}}}]\bigg\}\eta^{\hat{i}}, \end{aligned} $

(17) where
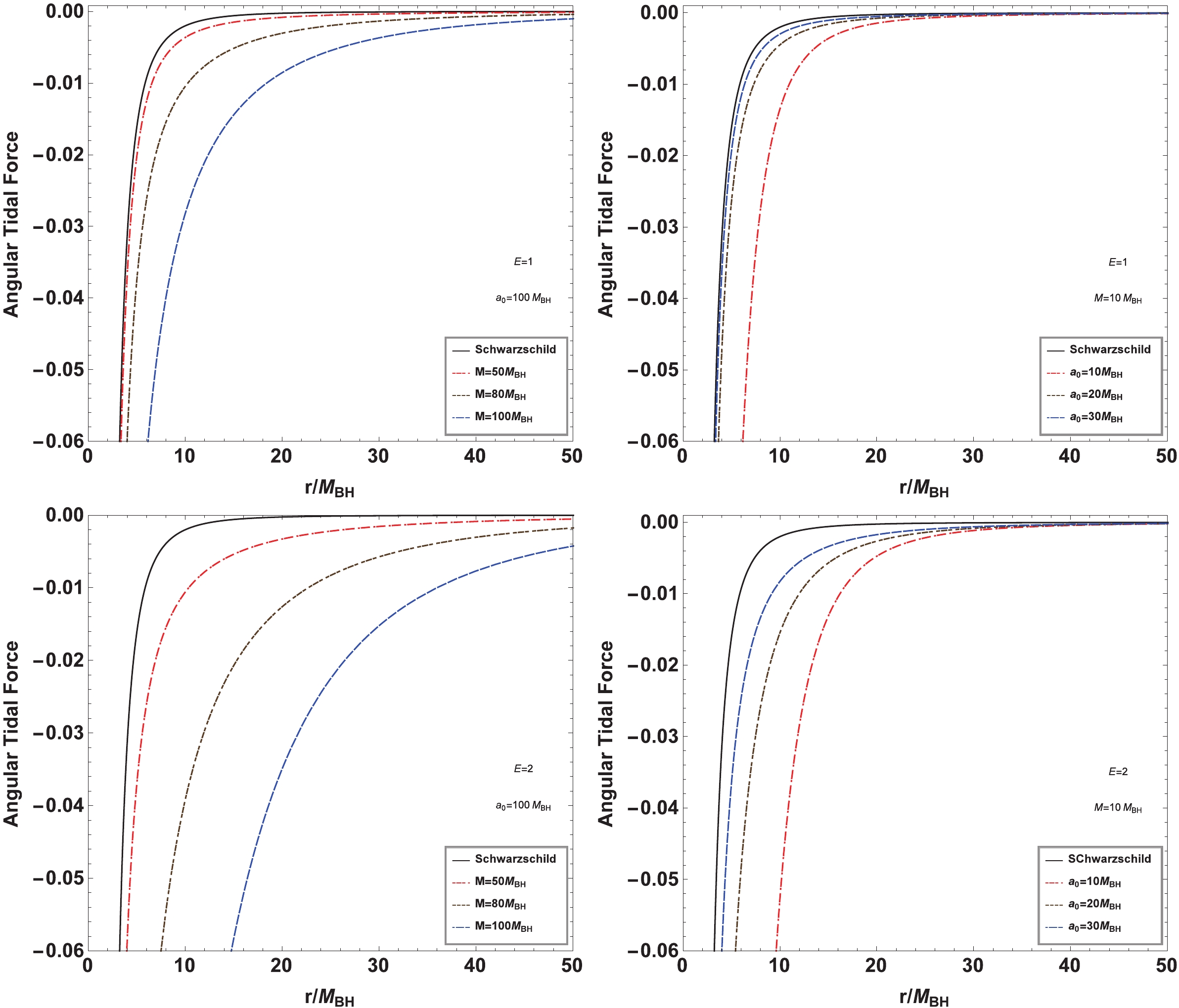
$ i= 2,3 $ correspond to the angular coordinates θ and ϕ, respectively. The radial and angular tidal forces depend on the black hole mass$ M_{{\rm{BH}}} $ , the mass of the dark matter halo M, and the typical lengthscale$ a_0 $ . Furthermore, the angular tidal force is related to the energy E of the test particle in spacetime. As the parameter M vanishes or$ a_0 $ tends to infinity, Eq. (16) and (17) reduce to those in Schwarzschild black hole spacetime, which can be explained by the fact that the dark matter density (7) vanishes in these two limit cases.The changes in tidal forces with the dark matter mass parameter M and typical lengthscale
$ a_0 $ of the galaxy are also shown in Figs. 3 and 4. For a fixed$ a_0 $ , we find that with increasing M, the radial tidal force increases in the region far from the black hole but decreases in the region near the black hole. This is understandable because the test particle in the far region of the gravity originating from the dark matter around the black hole has the same direction as that of the black hole at the center of the galaxy, which makes the gravitational field stronger than in the case without dark matter. However, for the particle in the near region, they are in opposite directions, which makes the gravitational field weaker than in the pure Schwarzschild case. Moreover, we find that the effect of$ a_0 $ on the radial tidal force is opposite to that of M in the background of a black hole with a dark matter halo. The main reason is that the dark matter density (7) increases with the mass parameter M but decreases with the scale parameter$ a_0 $ . Figure 4 shows that the angular tidal force is negative for all M and$ a_0 $ , which is consistent with the results in the Schwarzschild black hole case. The absolute value of the angular tidal force monotonously increases with dark matter halo mass but decreases with$ a_0 $ . We find that the angular tidal force also depends on the particle energy E, and the effects of M and$ a_0 $ become more distinct for the test particle with higher energy E, which differs from their behavior in typical static black hole spacetimes, where the angular tidal force is independent of the test particle energy E. -
In this section, we solve the geodesic deviation equations (16) and (17) and analyze the dynamical evolution of the deviation vector
$ \eta ^{\hat{\mu}} $ for a particle radially free-falling in the spacetime of a black hole with a dark matter halo (2). Making use of the equation$ \begin{equation} {\rm d}r/{{\rm{d \tau }}}=-\sqrt{\left(1-\frac{2 m(r)}{r}\right)\left(\frac{E^2}{f(r)}-1\right)}, \end{equation} $

(18) it is easy to find that the geodesic deviation equations (16) and (17) can be rewritten as
$ \begin{aligned}[b] &\left(\frac{E^2}{f(r)}-1\right)\left(1-\frac{2 m(r)}{r}\right) \frac{{\rm d}^2\eta^{\hat{1}}}{{\rm d}r^2} \\ + & \frac{1}{2}\bigg[ E^2 \bigg(\frac{r-2 m(r)}{rf(r)}\bigg)' - \left(1-\frac{2 m(r)}{r}\right)'\bigg]\frac{{\rm d}\eta^{\hat{1}}}{{\rm d}r}\\ + & \frac{1}{4 f'(r)}\bigg[\frac{f'(r)^2}{f(r)} \left(1-\frac{2 m(r)}{r}\right)\bigg]' \eta ^{\hat{1}}=0, \end{aligned} $

(19) $ \begin{aligned}[b] &\left(\frac{E^2}{f(r)}-1\right)\left(1-\frac{2 m(r)}{r}\right) \frac{{\rm d}^2\eta^{\hat{i}}}{{\rm d}r^2} \\+ & \frac{1}{2}\bigg[ E^2 \bigg(\frac{r-2 m(r)}{rf(r)}\bigg)'-\left(1-\frac{2 m(r)}{r}\right)'\bigg]\frac{{\rm d}\eta^{\hat{i}}}{{\rm d}r}\\ - & \frac{1}{2r}\bigg[ E^2 \bigg(\frac{r-2 m(r)}{rf(r)}\bigg)'-\left(1-\frac{2 m(r)}{r}\right)'\bigg]\eta^{\hat{i}}=0. \end{aligned} $

(20) The general solution for the angular component
$ \eta^{\hat{i}} $ can be expressed as$ \eta^{\hat{i}}=r\bigg[C_1+C_2\int \frac{{\rm d}r}{r^2\sqrt{\bigg(\dfrac{E^2}{f(r)}-1\bigg)\bigg(1-\dfrac{2 m(r)}{r}}\bigg)}\bigg], $

(21) where the coefficients
$ C_1 $ and$ C_2 $ are the constants of integration. However, for the radial component$ \eta^{\hat{1}} $ , we cannot find such analytical solutions. Thus, we must numerically solve the differential equation (19). As in [27], we consider two types of initial conditions describing the dust of particles starting at the region outside the event horizon$ r=b>r_{H} $ . The first type of initial condition, ICI, is$ \begin{equation} \eta ^{\hat{\alpha}}(b)=1,\quad \quad\dot{\eta}^{\hat{\alpha}}(b)=0, \end{equation} $

(22) which corresponds to particle-like dust released from rest at
$ r=b $ . This means that the four-velocity component of the particle$ \dot{r}=0 $ , and the energy of the dust is fixed at$ E=f(b) $ . The second type of initial condition, ICII, is$ \begin{equation} \eta ^{\hat{\alpha}}(b)=0, \quad\quad \dot{\eta}^{\hat{\alpha}}(b)=1, \end{equation} $

(23) which represents dust "exploding" at the starting point
$ r=b $ . Under the initial condition ICII, we find that$ \eta^{\hat{\mu}'}|_{r=b}=\frac{1}{\dot{r}}|_{r=b}=-\frac{1}{\sqrt{\left(1-\dfrac{2 m(b)}{b}\right)\left(\dfrac{E^2}{f(b)}-1\right)}}, $

(24) where the energy of the particle-like dust E is not a fixed parameter. The absolute value of
$ \eta^{\hat{\mu}'}|_{r=b} $ decreases with E, which means that the dust energy E will affect the dynamical evolution of the deviation vector in the case of the second type of initial condition, ICII.In Fig. 5, we present the change in the radial component of the geodesic deviation vector
$ \eta ^{\hat{1}} $ with the dark matter mass parameter M and typical lengthscale$ a_0 $ in the background of a black hole with a dark matter halo (2) with the initial conditions ICI and ICII. As the particle falls from rest at$ r=b $ , the radial component$ \eta ^{\hat{1}} $ increases for different M and$ a_0 $ under both initial conditions ICI and ICII. The length of$ \eta ^{\hat{1}} $ and its rate of increase are less than those in Schwarzschild black hole spacetime. Moreover, the deviation vector component$ \eta ^{\hat{1}} $ monotonously increases with the dark matter parameter M. With increasing$ a_0 $ , for the initial condition ICI, we find that$ \eta ^{\hat{1}} $ increases when the dust lies in the region far from black hole, whereas it first decreases and then increases when the dust lies in the region near the black hole. However, with the initial condition ICII,$ \eta ^{\hat{1}} $ always increases with$ a_0 $ , which indicates that the evolution of the deviation vector component$ \eta ^{\hat{1}} $ depends on the initial condition. With increasing b, we find that the component$ \eta ^{\hat{1}} $ increases, which is similar to the behavior observed in typical static black hole spacetimes. We find that the particle energy E also affects the component$ \eta ^{\hat{1}} $ ; the effects of M,$ a_0 $ , and b on$ \eta ^{\hat{1}} $ are suppressed by E.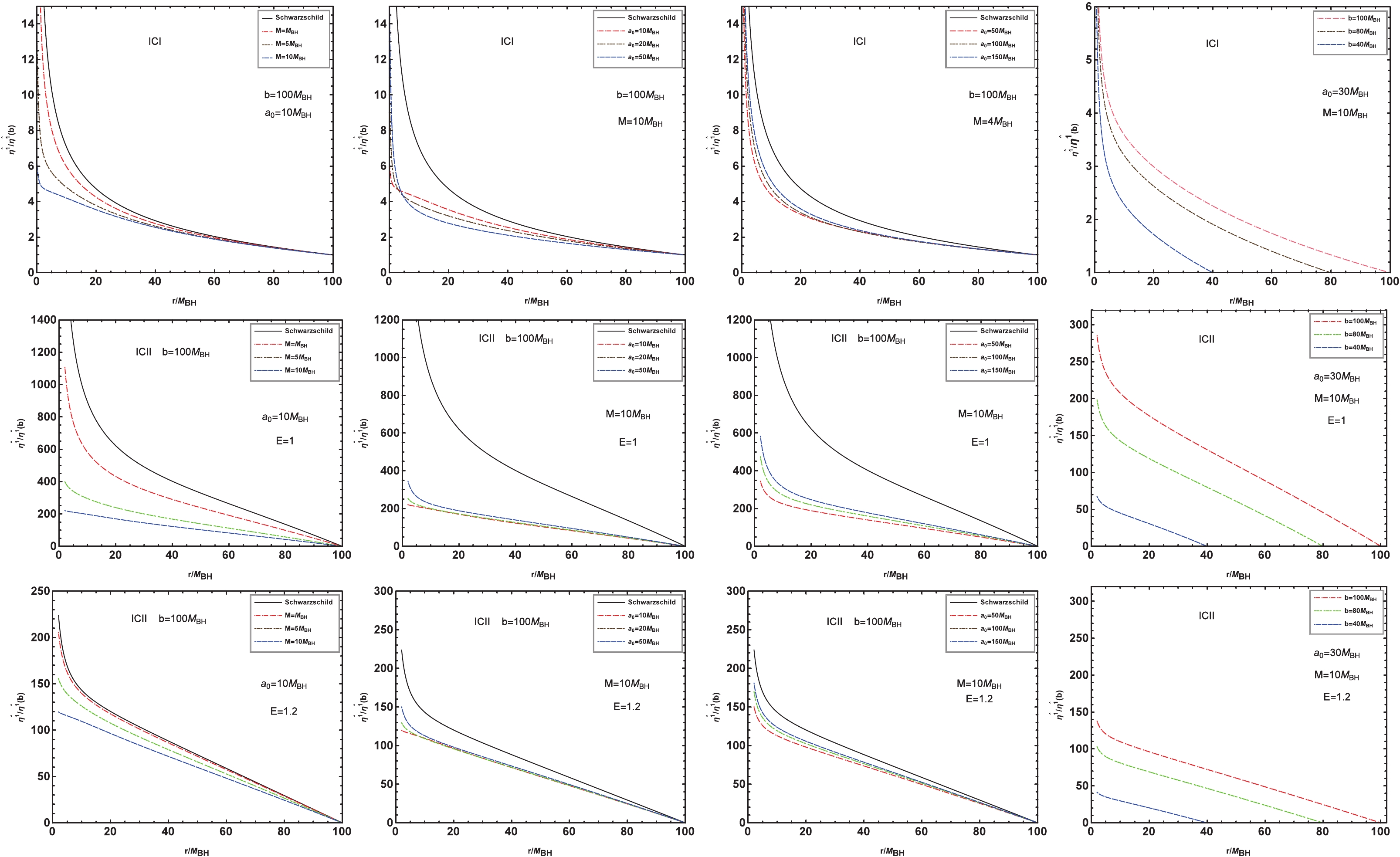
Figure 5. (color online) Dependence of the radial components
$ \eta ^{\hat{1}} $ of the geodesic deviation vector on the dark matter halo mass M and typical lengthscale$ a_0 $ in cases with the initial conditions ICI and ICII.Figure 6 shows the dependence of the angular components
$ \eta ^{\hat{i}} $ of the geodesic deviation vector on the dark matter halo mass M and typical lengthscale$ a_0 $ . With the initial condition ICI,$ \eta ^{\hat{i}} $ increases with M, but first increases and then decreases with$ a_0 $ . However, the effects of M and$ a_0 $ on$ \eta ^{\hat{i}} $ are small in this case. Moreover, for fixed M and$ a_0 $ ,$ \eta ^{\hat{i}} $ decreases with b. For the initial condition ICII, as the body falls from$ r=b $ , we find that there is a peak in the change curve of$ \eta ^{\hat{i}} $ with r, and the peak value of$ \eta ^{\hat{i}} $ and its corresponding position depend on the parameters M,$ a_0 $ , and b. Furthermore,$ \eta ^{\hat{i}} $ is a decreasing function of M but an increasing function of$ a_0 $ and b in this case, which means that the dynamical behaviors of the particle-like dust differ from those in the case with the initial condition ICI. Similar to the radial component$ \eta ^{\hat{1}} $ , the effects of M,$ a_0 $ , and b on$ \eta ^{\hat{i}} $ are suppressed by the particle energy E under the initial condition ICII. Thus, the tidal effects of a dark matter halo depend on the dark matter mass M and typical lengthscale of the galaxy$ a_0 $ as well as the initial condition of the particle-like dust. -
We investigate tidal forces and geodesic deviation motion in the spacetime of a black hole in a galaxy with a dark matter halo (2). Our results show that the tidal force and geodesic deviation motion depend on the dark matter halo mass M and typical lengthscale
$ a_0 $ of the galaxy. The effect of$ a_0 $ on tidal force is opposite to that of M in the background of a black hole with a dark matter halo. The main reason is that the dark matter density around a black hole increases with the mass parameter M but decreases with the scale parameter$ a_0 $ . With increasing mass M of dark matter, the radial tidal force increases in the region far from the black hole but decreases in the region near the black hole. The main reason is that for a test particle in the far region, gravity originating from the dark matter around the black hole has the same direction as that from the black hole at the center of the galaxy, whereas they are in opposite directions for a particle in the near region. The angular tidal force is negative for all M and$ a_0 $ ; the absolute value of angular tidal force monotonously increases with dark matter halo mass. We find that the angular tidal force also depends on the particle energy E, and the effects of M and$ a_0 $ become more distinct for the test particle with higher energy E, which is different from their behavior in typical static black hole spacetimes, where the angular tidal force is independent of the test particle energy E.We also present the change in the geodesic deviation vector in the spacetime of a black hole in a galaxy with a dark matter halo under two conditions, ICI and ICII. The dependence of the geodesic deviation vector on the initial position parameter b is similar to that in other black hole spacetimes. The radial deviation vector component
$ \eta ^{\hat{1}} $ monotonously increases with the dark matter parameter M. With increasing$ a_0 $ , for the first type of initial condition, ICI,$ \eta ^{\hat{1}} $ increases when dust lies in the region far from black hole, whereas it first decreases and then increases when dust lies in the region near the black hole. However, with the second type of initial condition, ICII,$ \eta ^{\hat{1}} $ always increases with$ a_0 $ . With the initial condition ICI, the angular components$ \eta ^{\hat{i}} $ increase with the dark matter mass parameter M but first increase and then decrease with$ a_0 $ . However, the effects of M and$ a_0 $ on$ \eta ^{\hat{i}} $ are small in this case. With the initial condition ICII,$ \eta ^{\hat{i}} $ is a decreasing function of M but an increasing function of$ a_0 $ and b, which means that the dynamical behaviors of the particle-like dust differs from those in the case with the initial condition ICI. We find that the particle energy E also affects the dynamical evolution of the geodesic deviation vector in black hole spacetime, and the effects of M,$ a_0 $ , and b on the deviation vector are suppressed by E. These behaviors of tidal forces and the geodesic deviation vector could help us understand tidal effects and dark matter halos around galactic black holes.
Tidal effects of a dark matter halo around a galactic black hole
- Received Date: 2022-05-04
- Available Online: 2022-10-15
Abstract: We investigate tidal forces and geodesic deviation motion in the spacetime of a black hole in a galaxy with a dark matter halo. Our results show that tidal forces and geodesic deviation motion depend on the mass of the dark matter halo and the typical lengthscale of the galaxy. The effect of the typical lengthscale of the galaxy on the tidal force is opposite to that of dark matter mass. With increasing dark matter mass, the radial tidal force increases in the region far from the black hole but decreases in the region near the black hole. Furthermore, the absolute value of angular tidal force monotonously increases with the dark matter halo mass. The angular tidal force also depends on the particle energy, and the effects of dark matter become more distinct for the test particle at higher energies, which differs from the behavior observed in typical static black hole spacetimes. We also present the change in the geodesic deviation vector with dark matter halo mass and the typical lengthscale of a galaxy under two types of initial conditions.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: