-
Proton radioactivity is a typical decay mode for odd-Z emitters beyond the proton drip line and is the only decay mode for some intermediate-mass nuclei [1]. Since its discovery in 1970 [2], proton radioactivity has become a powerful tool for studying the nature and structure of proton-rich nuclei because it can provide information on shell structure, bound and unbound nuclear states, etc. [3]. In addition, the proton radioactivity energy and orbital angular momentum carried by the emitted proton have a significant effect on the half-life of proton radioactivity [4]. Therefore, proton radioactivity studies help to determine the orbital angular momentum carried by the emitted proton and characterize its wave function within the nucleus [5−9].
To date, there have been many methods and models used to study the proton radioactivity half-life, which can be classified into two categories [10]. The first involves quantum mechanical tunneling through the nuclear mean-field of single-particle resonances [11–14]. Typical methods and models include the non-relativistic Hartree-Fock (HF) calculation using effective phenomenological interactions and covariant density functional theory (CDFT) in the relativistic mean-field (RMF) form [14, 15]. The second involves the calculation of the probability of proton penetration into the potential barrier via the Wentzel-Kramers-Brillouin (WKB) approximation [16, 17], such as the two-potential approach (TPA) [18], single-folding model (SFM) [19, 20], and Coulomb potential and proximity potential model (CPPM) [21, 22]. In the study of proton radioactivity, the nuclear potential between the emitted proton and daughter nucleus usually determines the accuracy of the model and calculations. In our previous study on the proton radioactivity half-life, we successfully described the nuclear potential of the emitted proton-daughter nucleus using the Skyrme-Hartree-Fock (SHF) microscopic model [23, 24]. Furthermore, we compared 115 sets of Skyrme interaction parameters constructed for different purposes and found that the most suitable Skyrme parameter for describing the proton radioactivity half-life is SLY7. The construction of Skyrme interaction parameters is undertaken mainly to reasonably describe the ground state properties of nuclei on the periodic table of elements and the saturation properties of symmetric nuclear matter (SNM) rather than to describe the proton radioactivity process of the nucleus. Therefore, all works using SHF to study proton radioactivity may require a set of Skyrme parameters specifically for proton radioactivity calculations instead of the existing Skyrme parameters. In this study, based on the relationship between the Skyrme parameter and the amount of macroscopic nuclear matter, we use the two-potential approach with SHF (TPA-SHF) to study the sensitivity of the proton radioactivity half-life to the amount of macroscopic nuclear matter [25]. Moreover, we present a set of Skyrme parameters for the study of proton radioactivity based on the constraints on the macroscopic quantities of nuclear matter.
This paper is organized as follows: In Sec. II, the theoretical framework for the proton radioactivity half-life is described in detail. In Sec. III, detailed calculations, discussion, and predictions are provided. Finally, a brief summary is given in Sec. IV.
-
The proton radioactivity half-life
$ T_\frac{1}{2} $ can be express-ed using the decay width Γ as follows:$ T_\frac{1}{2}=\frac{\ln 2\hbar}{\Gamma}. $

(1) In the framework of the TPA [18], Γ depends on the formation probability of the proton radioactivity
$ S_p $ , the normalized factor F, and the penetration probability of the emitted proton crossing the barrier P. It is given by$ \Gamma=\frac{\hbar^2 S_p F P}{4\mu}, $

(2) where
$ \hbar $ is the reduced Planck constant, and$\mu= \dfrac{M_d M_p}{(M_d+M_p)}$ is the reduced mass, with$ M_p $ and$ M_d $ as the masses of the emitted proton and daughter nuclei, respectively.In the classical WKB approximation, the penetration probability P and normalized factor F are given by
$ P=\exp \left[-2 \int_{r_2}^{r_3} k(r)\, {\rm d} r\right], $

(3) $ F \int_{r_1}^{r_2}\frac{1}{2k(r)}\, {\rm d} r=1. $

(4) Here,
$ r_1 $ ,$ r_2 $ , and$ r_3 $ represent the classical turning points, which satisfy the conditions$ V(r_1)=V(r_2)=V(r_3)= Q_p $ .$ k(r) $ is the wave number, which can be written as$ k(r)=\sqrt{\frac{2\mu}{\hbar^2}\left|Q_p-V(r)\right|}, $

(5) where
$ Q_p $ is the proton radioactivity energy. The total potential$ V(r) $ is given by$ V(r)=V_N(r)+V_{\rm C}(r)+V_l(r), $

(6) where
$ V_N(r) $ ,$V_{\rm C}(r)$ , and$ V_l(r) $ represent the nuclear, Coulomb, and centrifugal potentials, respectively. For the centrifugal potential$ V_{l}(r) $ ,$ l(l + 1) \rightarrow (l + 1/2)^2 $ is an essential correction [26]. In this study, the centrifugal potential$ V_{l}(r) $ is chosen to be in the Langer-modified form, which can be written as$ V_{l}(r)=\frac{\hbar^2(l+\frac{1}{2})^2}{2{\mu}r^2}, $

(7) where l is the orbital angular momentum taken by the emitted proton [27]. This can be obtained by the parity and angular momentum conservation laws. The Coulomb potential
$V_{\rm C}(r)$ is taken as the potential of a uniformly charged sphere connected to the sharp radius$ R=1.28A^{1/3}-0.76+0.8A^{-1/3} $ , where A is the mass number of the parent nucleus [28]. It can be expressed as$ \begin{array}{*{20}{l}} \ V_C(r)=\left\{\begin{array}{llll} \dfrac{Z_{p}Z_de^2}{2R}\left[3-\left(\dfrac{r}{R}\right)^2\right], &r<R, \\ \dfrac{Z_{p}Z_de^2}{r}, &r>R, \end{array}\right. \end{array} $

(8) where
$ Z_p $ and$ Z_d $ are the proton numbers of the emitted proton and daughter nuclei, respectively. -
The emitted proton–daughter nucleus nuclear potential
$ V_N(r)=U_q(\rho, \rho_p, {\boldsymbol{p}}) $ is calculated using SHF. The nuclear effective interactions with zero-range, momentum, and density dependent forms is given by [15]$ \begin{aligned}[b] V^{\rm Skyrme}_{12}({\boldsymbol{r}}_1, {\boldsymbol{r}}_2)=&t_0(1+x_0P_\sigma)\delta({\boldsymbol{r}})\\ &+ \frac{1}{2}t_1(1+x_1P_\sigma)[{\boldsymbol{P}}'^2\delta({\boldsymbol{r}})+\delta({\boldsymbol{r}}){\boldsymbol{P}}^2] \\ &+ t_2(1+x_2P_\sigma){\boldsymbol{P}}'\cdot\delta({\boldsymbol{r}}){\boldsymbol{P}}\\ &+ \frac{1}{6}t_3(1+x_3P_\sigma)[\rho({\boldsymbol{R}})]^{\alpha}\delta({\boldsymbol{r}}) \end{aligned} $

$ \begin{aligned}[b]\quad\quad\quad + {\rm i} {W_0} \mathit{\boldsymbol{\sigma}}\cdot[{\boldsymbol{P}}'\times\delta({\boldsymbol{r}}){\boldsymbol{P}}], \end{aligned} $

(9) where
$ {\boldsymbol{r}}={\boldsymbol{r}}_1-{\boldsymbol{r}}_2 $ ,$ {\boldsymbol{R}}=({\boldsymbol{r}}_1+{\boldsymbol{r}}_2)/2 $ ,$ {\boldsymbol{r}}_i $ (i = 1, 2) is the coordinate vector of the i-$ th $ nucleon,$ P_\sigma $ is the spin exchange operator,$ {\boldsymbol{P}}' $ and$ {\boldsymbol{P}} $ are the relative momentum operators acting on the left and right, respectively,$ t_0 $ ,$ t_1 $ ,$ t_2 $ ,$ t_3 $ ,$ x_0 $ ,$ x_1 $ ,$ x_2 $ ,$ x_3 $ ,$ W_0 $ , and α are the Skyrme parameters.In local density approximation, the single-nucleon potential from the SHF model can be expressed as [29]
$ \begin{array}{*{20}{l}} U_q(\rho, \rho_q, {\boldsymbol{p}})=a{\boldsymbol{p}}^2+b, \end{array} $

(10) where
$ {\boldsymbol{p}} $ is the momentum of the nucleon. The coefficient a and b are given by$ \begin{aligned}[b] a=&\frac{1}{8}[t_1(x_1+2)+t_2(x_2+2)]\rho\\ &+ \frac{1}{8}[-t_1(2x_1+1)+t_2(2x_2+1)]\rho_q, \end{aligned} $

(11) $ \begin{aligned}[b] b=&\frac{1}{8}[t_1(x_1+2)+t_2(x_2+2)]\frac{k^5_{f, n}+k^5_{f, p}}{5\pi^2}\\ &+\frac{1}{8}[t_2(2x_2+1)-t_1(2x_1+1)]\frac{k^5_{f, q}}{5\pi^2} \\ &+ \frac{1}{2}t_0(x_0+2)\rho-\frac{1}{2}t_0(2x_0+1)\rho_q \\ &+ \frac{1}{24}t_3(x_3+2)(\alpha+2)\rho^{(\alpha+1)} \\ &-\frac{1}{24}t_3(2x_3+1)\alpha\rho^{(\alpha-1)}(\rho^2_n+\rho^2_p) \\ &-\frac{1}{12}t_3(2x_3+1)\rho^\alpha\rho_q, \end{aligned} $

(12) where
$ k_{f, q}=(3\pi\rho_q)^{1/3} $ is the Fermi momentum of the nucleon,$ \rho_q $ is the proton (neutron) density with$ q=p (n) $ , and$ \rho=\rho_p+\rho_n $ represents the total nucleon density.The total energy E of a nucleon in a nuclear medium can be written as
$ E=U_q(\rho, \rho_q, {\boldsymbol{p}})+\frac{{\boldsymbol{p}}^2}{2m}=\frac{{\boldsymbol{p}}^2}{2m^{*}}+b, $

(13) where
$ m^{*} $ denotes the effective mass defined by$ \frac{1}{2m^{*}}=\frac{1}{2m}+a. $

(14) We assume that the total energy of the emitted protons remains constant during proton radioactivity.
$ \left|{\boldsymbol{p}}\right| $ can be derived from the total energy, nucleon density, and isospin asymmetry and is given by$ |\boldsymbol p|=\sqrt{2m^*(E-b)}. $

(15) The potential energy
$ U_q(\rho, \rho_p, {\boldsymbol{p}})=E-\dfrac{{\boldsymbol{p}}^2}{2m} $ .By comparing the expressions in the SHF with the corresponding expressions in the modified Skyrme-like (MSL) model [30], the nine parameters σ, β, γ, C, D, y,
$E^{\rm loc}_{\rm sym}(\rho_0)$ , the gradient$ G_s $ , and the symmetry-gradient coefficient$ G_v $ in the MSL model can be related to the nine Skyrme interaction parameters via the following analytic relations [25]:$ t_0=4 \sigma / 3 \rho_0, $

(16) $ t_1=20C /(9 \rho_0 (k^0_F)^2) +8 G_s/3, $

(17) $ t_2=\frac{4 (25 C -18 D)}{9 \rho_0 (k^0_F)^2}-\frac{8 (G_s+2 G_v)}{3}, $

(18) $ t_3=16 \beta / (\rho^{\gamma}_0(\gamma+1)), $

(19) $ x_0=3(y-1)E^{\rm loc}_{\rm sym}(\rho_0)/\sigma -1/2, $

(20) $ x_1=\frac{12G_v-4G_s-6D/(\rho_0 (k^0_F)^2)}{3 t_1}, $

(21) $ x_2=\frac{20G_v+4G_s-5(16C-18D)/( 3 \rho_0 (k^0_F)^2)}{3 t_2}, $

(22) $ x_3=-3y(\gamma+1)E^{\rm loc}_{\rm sym}(\rho_0)/(2\beta)-1/2, $

(23) $ \alpha=\gamma-1, $

(24) with
$ k^0_F=(1.5\pi^2\rho_0)^{1/3} $ . The seven parameters σ, β, γ, C, D, y, and$E^{\rm loc}_{\rm sym}(\rho_0)$ in the MSL model can be expressed analytically in terms of the seven macroscopic quantities, that is, the normal density$ \rho_0 $ , the equation of state at$\rho_0 $ $ E_0 $ $(\rho_0) $ , the incompressibility$ K_0 $ , the isoscalar effective mass$ m^*_{s,0} $ , the isovector effective mass$ m^*_{v,0} $ , the nuclear symmetry energy at$\rho_0 ~E_{\rm sym}~(\rho_0)$ , and the extracted density slope L [30]. The nine Skyrme interaction parameters$ t_0 $ ,$ t_1 $ ,$ t_2 $ ,$ t_3 $ ,$ x_0 $ ,$ x_1 $ ,$ x_2 $ ,$ x_3 $ , and α can also be expressed analytically in terms of the nine macroscopic quantities$ \rho_0 $ ,$ E_0(\rho_0) $ ,$ K_0 $ ,$ m^*_{s,0} $ ,$ m^*_{v,0} $ ,$E_{\rm sym}(\rho_0)$ , L,$ G_S $ , and$ G_V $ via the above relations. -
The aim of this study is to investigate the proton radioactivity half-life based on the relationship between macroscopic quantities and Skyrme parameters [25]. To study the sensitivity of proton radioactivity to macroscopic quantities [25], we adopt the set of Skyrme parameters MSL0 obtained using the empirical values of the macroscopic quantities to ensure that the adjustment of the macroscopic quantities is not out of line with the actual values. The macroscopic quantities and corresponding Skyrme parameters are listed in Table 1.
$ G'_0(\rho_0) $ is the Landau parameter, whose value can vary from approximately 0 to 1.6, depending on the method and model [31–33]. In this study, experimental data on spin, parity, the proton radioactivity energy$ Q_p $ , and the proton radioactivity half-lives are taken from the latest evaluated nuclear property table NUBASE2020 [34] and the latest evaluated atomic mass table AME2020 [35, 36], except for those of 140Ho, 144Tm, 151Lu, 159Re, and 164Ir, which are taken from Ref. [37]. The standard deviation Δ indicates the divergence between experimental data and the the proton radioactivity half-lives calculated using TPA-SHF, which can be expressed as$ \Delta=\sqrt{\sum ({{\rm{lg}}{T^{{\rm{exp}}}_{1/2}}(s)}-{{\rm{lg}}{T^{{\rm{cal}}}_{1/2}}(s)})^2/n} $ .Quantity MSL0 $ {\rm{Quantity}} $ 

MSL0 $ \rho_0 $ 

0.16 $\rm fm^{-3}$ 

$ t_0 $ 

−2118.06 MeV $\rm fm^{5}$ 

$ E_0(\rho_0) $ 

−16 MeV $ t_1 $ 

395.196 MeV $\rm fm^{5}$ 

$ K_0 $ 

230 MeV $ t_2 $ 

−63.953 MeV $\rm fm^{5}$ 

$ m^*_{s,0}/m $ 

0.8 $ t_3 $ 

12857.7 MeV $\rm fm^{3+3\alpha}$ 

$ m^*_{v,0}/m $ 

0.7 $ x_0 $ 

−0.0709496 $E_{\rm sym}(\rho_0)$ 

30 MeV $ x_1 $ 

−0.332282 L 60 MeV $ x_2 $ 

1.35830 $ G_S $ 

132 MeV $\rm fm^{5}$ 

$ x_3 $ 

−0.0228181 $ G_V $ 

$5\ \rm MeV\ fm^{5}$ 

α 0.235879 $ G'_0(\rho_0) $ 

0.42 $ W_0 $ 

133.3 MeV $\rm fm^{5}$ 

Table 1. Macroscopic quantities and corresponding Skyrme parameters in MSL0.
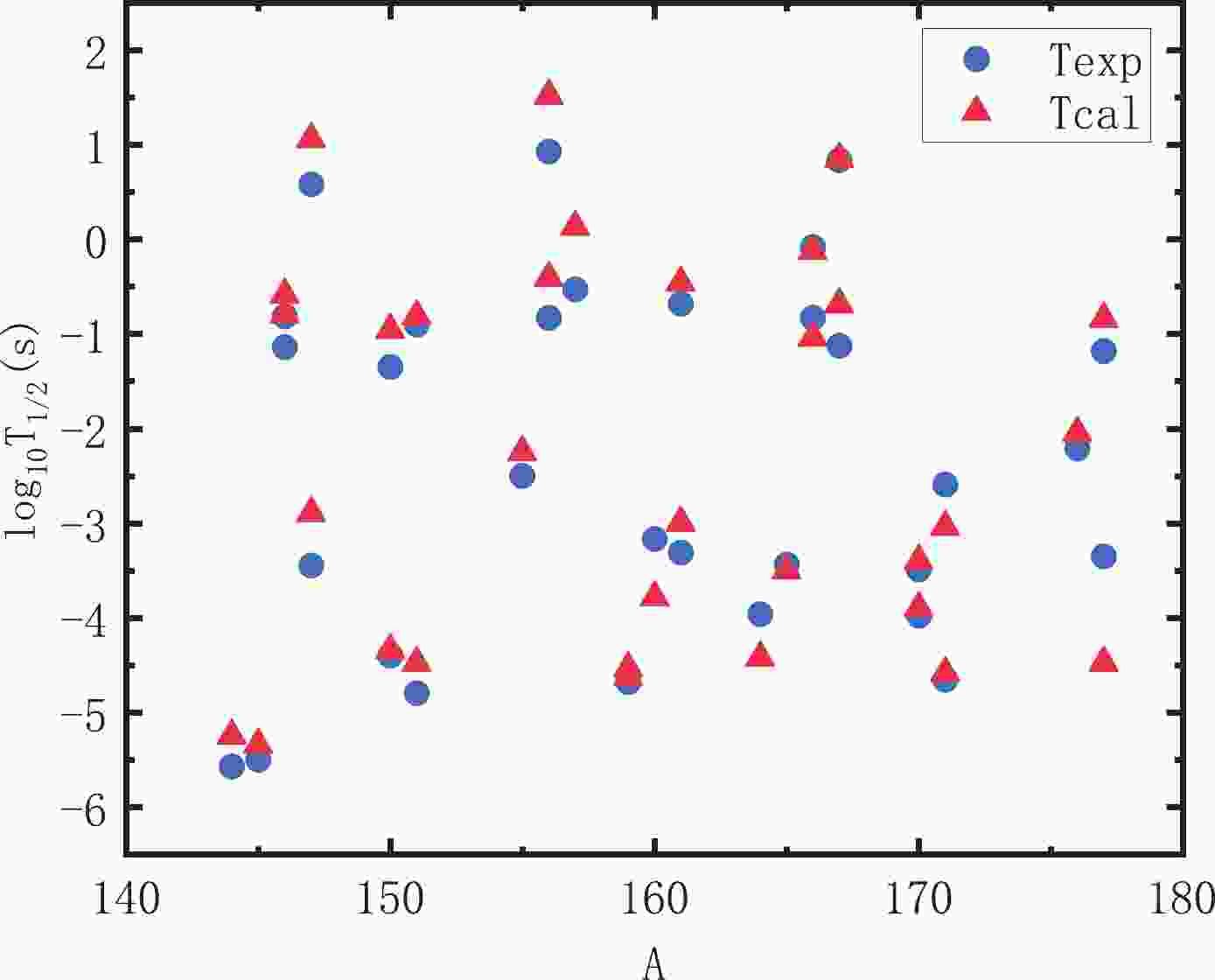
Using the MSL0 parameter set, we systematically calculate the proton radioactivity half-lives of
$ 69\leq Z \leq81 $ nuclei with$ S_p=1 $ [24]. The detailed results are plotted in Fig. 1. The blue circles and red triangles represent the logarithmic forms of the experimental data and the logarithmic forms of the calculated proton radioactivity half-life, respectively. As shown in Fig. 1, the proton radioactivity half-lives vary over a wide range from$ 10^{-6} $ s to$ 10^2 $ s. Although the proton radioactivity half-life variation is up to eight orders of magnitude, the theoretical points follow the experimental points well, almost coinciding with each other. Furthermore, we obtain the standard deviation Δ between the experimental data and the calculated proton radioactivity half-life as equal to 0.405, which means that the theoretical proton radioactivity half-lives calculated using TAP-SHF with MSL0 (TPA-SHF-MSL0) can reproduce the experimental data well.
Figure 1. (color online) Comparison of experimental proton radioactivity half-lives and theoretical proton radioactivity half-lives calculated using TPA-SHF-MSL0 (
$69\leq Z \leq81$ ).To clearly reveal the dependence of the theoretical proton radioactivity half-lives on each macroscopic quantity, we vary one aspect at a time while keeping all other macroscopic quantities at their default values in MSL0. In this study, the variation in each macroscopic quantity is controlled within the experimentally obtained values to ensure that the dependencies we obtain are meaningful. To intuitively reflect the relationship between the theoretical proton radioactivity half-life change and the evolution of each macroscopic quantity, we plot the standard deviations between experimental data and the calculated proton radioactivity half-lives corresponding to the change in each macroscopic quantity in Fig. 2. From this figure, we can clearly see that the variety of different macroscopic quantities causes different effects on the standard deviations between experimental data and the calculated proton radioactivity half-lives. The standard deviation exhibits a robust correlation with
$ \rho_0 $ and a relatively weak correlation with$ G_S $ . For the other seven macroscopic quantities, their changes have little effect on the standard deviations between experimental data and the calculated proton radioactivity half-lives. The discovery of this relationship means that we can constrain the Skyrme parameters using two macroscopic quantities that significantly affect the standard deviation, which have a higher weight in the standard deviation calculation. Thus, a new set of Skyrme parameters suitable for calculating the proton radioactivity half-life is obtained with as few adjustable parameters as possible. Similarly, such a relationship, in turn, limits the range of these two macroscopic parameters. This means that the actual value of$ \rho_0 $ is approximately 0.156$\rm fm^{-3}$ , and the real value of$ G_S $ is approximately 187 MeV$\rm fm^{5}$ .
Figure 2. (color online) Standard deviations Δ between experimental data and theoretical proton radioactivity half-lives calculated by individually varying
$\rho_0$ ,$E_0(\rho_0)$ ,$K_0$ ,$m^*_{s,0}$ ,$m^*_{v,0}$ ,$E_{\rm sym}(\rho_0)$ , L,$G_S$ , and$G_V$ .In this study, a new Skyrme parameter MQSP is given by fitting the two highest weight macroscopic quantities,
$ \rho_0 $ and$ G_S $ . The detailed results are listed in Table 2. The new theoretical value of the proton radioactivity half-life can be calculated using TAP-SHF with MQSP (TPA-SHF-MQSP). To verify the accuracy of our new Skyrme parameters in calculating the proton radioactivity half-life, the universal decay law for proton radioactivity (UDLP) is chosen as a comparison. The UDLP is given by Qi et al. [38], which is an extension of the universal decay law (UDL) [39, 40]. In the UDLP, the logarithm of proton radioactivity half-life can be expressed asQuantity MQSP $ {\rm{Quantity}} $ 

MQSP $ \rho_0 $ 

0.155 $\rm fm^{-3}$ 

$ t_0 $ 

−2134.31 MeV $\rm fm^{5}$ 

$ E_0(\rho_0) $ 

−16 MeV $ t_1 $ 

529.92 MeV $\rm fm^{5}$ 

$ K_0 $ 

230 MeV $ t_2 $ 

−187.13 MeV $\rm fm^{5}$ 

$ m^*_{s,0}/m $ 

0.8 $ t_3 $ 

13130.28 MeV $\rm fm^{3+3\alpha}$ 

$ m^*_{v,0}/m $ 

0.7 $ x_0 $ 

−0.0561957 $E_{\rm sym}(\rho_0)$ 

30 MeV $ x_1 $ 

−0.3721052 L 60 MeV $ x_2 $ 

0.159008 $ G_S $ 

182 MeV $\rm fm^{5}$ 

$ x_3 $ 

−0.21680 $ G_V $ 

$5\ \rm MeV\ fm^{5}$ 

α 0.24205 $ G'_0(\rho_0) $ 

0.42 $ W_0 $ 

133.3 MeV $\rm fm^{5}$ 

Table 2. Macroscopic quantities and corresponding Skyrme parameters obtained using MQSP.
$ \begin{array}{*{20}{l}} \log_{10}T_\frac{1}{2}=a\chi'+b\rho'+c+dl(l+1), \end{array} $

(25) where
$ \chi'={Z_p}Z_d\sqrt{\frac{\mu}{Q_p}} $ , and$ \rho'=\sqrt{\mu{Z_p}Z_d({A_d}^\frac{1}{3}+{A_p}^\frac{1}{3})} $ . Here, the parameters$ a=0.386, b=-0.502 $ ,$ c=-17.8 $ , and$ d= $ 2.386 are determined by fitting to the experimental data of proton radioactivity taken from Ref. [38]. As a comparison, we use TPA-SHF-MSL0, TPA-SHF-MQSP, and the UDLP to calculate the proton radioactivity half-life, and the results are listed in Table 3. In this table, columns one to four represent the parent nuclei, the orbital angular momentum l taken by the emitted proton, the proton radioactivity energy$ Q_p $ , and the logarithmic form of the experimental proton radioactivity half-lives, respectively. The following three columns represent the logarithmic forms of the theoretical proton radioactivity half-lives calculated using TPA-SHF with the Skyrme effective interaction of MSL0 (TPA-SHF-MSL0), TPA-SHF with the Skyrme effective interaction of MQSP (TPA-SHF-MQSP), and the UDLP, denoted as MSL0, MQSP, and UDLP, respectively. From this table, we can clearly see that the theoretical proton radioactivity half-lives calculated using TPA-SHF-MQSP can reproduce the experimental data well.Nucleus l $Q_{p}/{\rm{MeV} }$ 

Measured $\lg T^{ {\rm{MSL0} } }_{1/2}/{\rm{s} }$ 

$\lg T^{ {\rm{MQSP} } }_{1/2} /{\rm{s} }$ 

$\lg T^{ {\rm{UDLP} } }_{1/2} /{\rm{s} }$ 

144Tm 5 1.725 −5.569 −5.243 −5.42 −4.691 145Tm 5 1.736 −5.499 −5.339 −5.496 −4.767 146Tm $ ^m $ 

5 1.206 −1.137 −0.788 −0.958 −0.814 146Tm 0 0.896 −0.81 −0.583 −0.746 −0.482 147Tm 5 1.059 0.587 1.063 0.849 0.772 147Tm $ ^m $ 

2 1.12 −3.444 −2.89 −3.207 −2.713 150Lu $ ^m $ 

2 1.29 −4.398 −4.341 −4.52 −3.91 150Lu 5 1.27 −1.347 −0.954 −1.116 −0.988 151Lu $ ^m $ 

2 1.301 −4.796 −4.473 −4.647 −4.025 151Lu 5 1.255 −0.896 −0.81 −0.98 −0.863 155Ta 5 1.453 −2.495 −2.248 −2.39 −2.17 156Ta 2 1.02 −0.826 −0.401 −0.498 −0.417 156Ta $ ^m $ 

5 1.11 0.933 1.522 1.361 1.129 157Ta 0 0.935 −0.527 0.137 −0.005 0.123 159Re $ ^m $ 

5 1.801 −4.665 −4.531 −4.706 −4.181 159Re 5 1.816 −4.678 −4.62 −4.806 −4.268 160Re 0 1.267 −3.163 −3.778 −3.942 −3.408 161Re $ ^m $ 

5 1.317 −0.678 −0.455 −0.633 −0.611 161Re 0 1.197 −3.306 −2.992 −3.126 −2.689 164Ir 5 1.844 −3.959 −4.418 −4.594 −4.114 165Ir $ ^m $ 

5 1.711 −3.433 −3.496 −3.68 −3.306 166Ir 2 1.152 −0.824 −1.034 −1.169 −1.014 166Ir $ ^m $ 

5 1.332 −0.076 −0.118 −0.283 −0.335 167Ir 0 1.07 −1.12 −0.682 −0.804 −0.645 167Ir $ ^m $ 

5 1.245 0.842 0.855 0.688 0.523 170Au 2 1.472 −3.487 −3.891 −4.186 −3.716 170Au $ ^m $ 

5 1.752 −3.975 −3.394 −3.569 −3.234 171Au $ ^m $ 

5 1.702 −2.587 −3.037 −3.205 −2.915 171Au 0 1.448 −4.652 −4.578 −4.728 −4.157 176Tl 0 1.265 −2.208 −2.041 −2.162 −1.919 177Tl $ ^m $ 

5 1.963 −3.346 −4.473 −4.27 −4.206 177Tl 0 1.172 −1.178 −0.836 −0.982 −0.863 Table 3. Calculation of the spherical proton radioactivity half-lives. Measured,
$\lg T^{{\rm{MSL0}}}_{1/2}$ ,$\lg T^{{\rm{MQSP}}}_{1/2}$ , and$\lg T^{{\rm{UDLP}}}_{1/2}$ are the logarithmic forms of the experimental proton radioactivity half-life and the calculations using STPA-SHF-MSL0, TPA-SHF-MQSP, and the UDLP.To intuitively compare TPA-SHF-MSL0, TPA-SHF-MQSP, and UDLP with experimental data, the logarithmic deviations between the experimental data of the proton radioactivity half-lives and the calculated values are shown in Fig. 3. In this figure, the X-axis represents the mass number of the proton radioactivity parent nucleus, and the Y-axis represents the logarithmic deviations. The three different colors and symbols refer to the calculations obtained using three different models. From Fig. 3, we can clearly see that the values of
$\lg(T^{\rm cal}_{1/2}-T^{\rm exp}_{1/2})$ obtained using TPA-SHF-MQSP are mainly near zero, indicating that the theoretical half-life of proton radioactivity calculated using our model is in good agreement with the experimental data. Furthermore, this figure shows that the calculations using TPA-SHF-MQSP can better reproduce the experimental data than TPA-SHF-MSL0 and UDLP for most nuclei. To intuitively compare the deviations between the half-lives of proton radioactivity obtained using different models and experimental data, we calculate the standard deviation.$\Delta_{\rm MSL0}=$ 0.405,$\Delta_{\rm MQSP}=$ 0.362, and$\Delta_{\rm UDLP}=$ 0.459 represent the standard deviations between$\lg T^{\rm MSL0}_{1/2}$ ,$\lg T^{\rm MQSP}_{1/2}$ ,$\lg T^{\rm UDLP}_{1/2}$ , and the values of$\lg T^{\rm exp}_{1/2}$ , respectively. These results show that the TPA-SHF-MQSP method is better than the other models in calculating the spherical proton radioactivity half-lives. Therefore, it is credible to use TPA-SHF-MQSP to study the proton radioactivity half-lives. -
In summary, we systematically study the proton radioactivity half-life of 33 spherical nuclei by investigating the relationship between Skyrme parameters and the macroscopic quantities of nuclear matter. The calculated results indicate that the proton radioactivity half-lives and
$ \rho_0 $ show a robust correlation, whereas the correlation with$ G_S $ is relatively weak. For the other seven macroscopic quantities, their variations have little effect on the evolution of the standard deviations between experimental data and the calculated proton radioactivity half-lives. This effectively constrains the ranges of$ \rho_0 $ and$ G_S $ . Moreover, we obtain new Skyrme parameters, MQSP, by fitting$ \rho_0 $ and$ G_S $ , the two most weighted macroscopic quantities. Compared with the Skyrme parameters MSL0 and UDLP, the theoretical proton radioactivity half-life calculated using the Skyrme parameters MQSP can better reproduce the experimental data. This study can be used as a reference for future research on proton radioactivity.
Systematic study of proton radioactivity half-lives based on the relationship between Skyrme-Hartree-Fock and the macroscopic quantities of nuclear matter
- Received Date: 2022-05-17
- Available Online: 2022-10-15
Abstract: In this study, we systematically investigate the proton radioactivity half-lives of 33 spherical nuclei based on the relationship between Skyrme parameters and the macroscopic quantities of nuclear matter. Using the two-potential approach with the spherical Skyrme-Hartree-Fock model, the correlation between proton radioactivity half-life and the macroscopic quantities is analyzed. Moreover, we obtain a new Skyrme parameter set by fitting the two most weighted macroscopic quantities. Compared with the Skyrme parameters MSL0 and the theoretical model of proton radioactivity UDLP, the theoretical proton radioactivity half-life calculated using the new Skyrme parameter set can better reproduce the experimental data.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: