-
In nature, radioactive nuclei translate their unstable states to stable states, based on the minimum energy principle, by α, β, and/or γ emissions, or emitting particles heavier than α particles [1–3] but lighter than the lightest fission fragments, generally known as cluster radioactivity [4–10]. This subtle process, intermediate between α decay and spontaneous fission, undoubtedly involves vital nuclear structure information such as ground state half-life time, nuclear spin and parity, deformations of nuclear structure, and shell effects [11–13]. In 1980, S
$ \check{a} $ ndulescu, Poenaru, and Greiner first predicted this type of decay mode [14–17]. Experiments conducted by Rose and Jones in 1984 [15, 17], for observing 14C emitted particles from 223Ra, verified the realistic existence of this novel radioactivity. Soon afterwards, multiple extra elementary clusters such as 20O, 24Ne, 23F, 28Mg and 34Si were discovered experimentally in the trans-lead region [18, 19], leading to the doubly magic daughter nucleus 208Pb or its neighboring nuclei.Up to now, abundant theoretical models have been proposed to deal with this radioactivity process. In general, these models can be divided into two kinds of categories, α-like models and fission-like models [20–23], by virtue of the intermediate characteristics. The former, just like the tunnelling theory of α decay [24–27], considering this process as non-adiabatic process, supposes the cluster is preformed in the parent nucleus with a certain cluster formation probability, determined by the overlapping region of both the parent nucleus and the daughter nucleus before they could penetrate the barrier with an available decay energy of cluster radioactivity
$ Q_{c} $ [28]. For instance, in 2001, considering nuclear proximity energy and quasimolecular shape, Royer generalized the conventional liquid drop model (GLDM) [23] to systematically calculate the cluster radioactivity half-lives. Soon afterwards, considering the cluster preformation factor$ P_{c} $ as the charge-number dependence form, Ren$ et $ $ al. $ employed the microscopic density-dependent cluster model (DDCM) where the realistic M3Y nucleon-nucleon interaction is used to investigate this exotic decay mode [14]. In 2009, extending the quasi-bound wave function, first used in α decay, to cluster radioactivity, based on the DDCM, Ni$ et $ $ al. $ systematically studied the half-lives of cluster radioactivity [4]. In the latter, the cluster is assumed to be formed along with the emitted process, which is described as adiabatic with constant variations in geometric shape from the parent nucleus during its penetration through the nuclear barrier. Based on this assumption, in 2013, Santhosh$ et $ $ al. $ used the Coulomb and proximity potential model (CPPM) to calculate the half-lives of α decay and cluster radioactivity of$ ^{248-254} $ Cf isotopes for the purpose of exploring the stability of these nuclei against these decay modes [21]. Recently, Ajeet Singh$ et $ $ al. $ used the effective liquid drop model (ELDM) as well as the mass excess data calculated by the relativistic mean-field (RMF) to study cluster radioactivity half-lives [29]. In addition, many phenomenological semi-empirical formulas have been proposed to deal with this phenomenon. For instance, Ni$ et $ $ al. $ proposed a unified formula of half-lives for both α decay and cluster radioactivity in 2008 [30]. All of them can explicitly elaborate this exotic decay mode and provide a reliable theoretical foundation for future research.No matter in which theory,
$ P_{c} $ plays an indispensable role in calculating cluster radioactivity half-lives. Different models have different methods to deal with$ P_{c} $ . In the preformed cluster model (PCM) [31, 32] proposed by Gupta and Malik,$ P_{c} $ is calculated through solving the stationary Schr$ \ddot{o} $ dinger equation for the dynamical flow of mass and charge. In terms of fission-like models,$ P_{c} $ is regarded as the penetrability of the inner part of the barrier for the overlapping region. As for the unified fission model (UFM) [33],$ P_{c} $ is usually considered as unity. Based on the fact that the α particle is an N$ = $ Z system with a larger binding energy, it is reasonable to deem the preformation probability just as 1 within Gamow's theory for α decay. Nevertheless, as in the case of cluster radioactivity, the emitted particles in the whole cluster family are completely N$ \neq $ Z systems. The more nucleons aggregate as a cluster, the less the possibility exists in the parent nucleus [34]. Therefore, when the UFM is applied to calculate cluster radioactivity half-lives, the preformation probability, assumed to be 1, may be reevaluated. To this end, based on the Wentzel-Kramers-Brillouin (WKB) theory, considering cluster radioactivity preformation probability$ P_{c} $ , we systematically investigate the cluster radioactivity half-lives of 22 trans-lead nuclei ranging from 221Fr to 242Cm, while the interaction potential between the emitted cluster and daughter nucleus in the overlapping region is a sum of the repulsive Coulomb potential$ V_{C}(r) $ , a modified Woods-Saxon type nuclear potential$ V_{N}(r) $ , and the centrifugal potential$ V_{l}(r) $ . As for$ P_{c} $ , when$ A_{c} $ $ < $ 28 we calculate it within the cluster-formation model (CFM) [35–37] combined with the famous exponential relationship of$ P_{c} $ to$ P_{\alpha } $ proposed by R. Blendowske and H. Walliser [38]. However, with$ A_{c} $ going beyond the limit this relationship may not work [39]. As is clearly indicated in Fig. 2 from Ref. [39],$ P_{c} $ in logarithmical form maintains a good linear relationship with the mass number of the emitted cluster when$ A_{c} $ $ < $ 28. The curve is bent obviously when 28$ < $ $ A_{c}\le $ 40 and the slope of the curve begins to decrease with increasing emitted cluster mass number. Therefore, in this work, when$ A_{c}\geq{28} $ ,$ P_{c} $ is obtained by its charge-number dependence on the decay products in the DDCM proposed by Ren$ et $ $ al. $ [14].This article is organized as follows. A brief introduction to the theoretical framework for cluster radioactivity half-life, CFM, and semi-empirical formulas is presented in Sec. II. Detailed numerical results and discussion are given in Sec. III. Sec. IV is a simple summary.
-
The half-life for the cluster radioactivity is defined as [40]
$ \begin{equation} T_{1/2}=\frac{\ln 2}{\lambda}, \end{equation} $

(1) where λ is denoted as the decay constant determined as the product of the penetration probability P, the assault frequency ν, and the cluster-preformation probability
$ P_{c} $ . It can be expressed as [41]$ \begin{equation} \lambda=\nu PP_{c}. \end{equation} $

(2) Here, P is the penetrability of the cluster crossing the barrier, which is calculated by the Wentzel-Kramers-Brillouin (WKB) approximation. It can be expressed as
$ \begin{equation} P=\rm{exp}{\lbrace -\frac{2}{\hbar}\int_{R_{in}}^{R_{out}}\sqrt {2\mu (V(r)-Q_{c}) }\mathrm{d}r\rbrace}, \end{equation} $

(3) where
$ \hbar $ is the reduced Planck constant. μ =$\dfrac{M_{c} M_{d}}{M_{c}+M_{d}}$ is the reduced mass of the emitted cluster-daughter nucleus system with$M_{{c}}$ and$M_{{d}}$ being the masses of the emitted cluster and daughter nuclei, respectively [42].$R_{{\rm in}}$ =$ C_{1} $ +$ C_{2} $ [34] is the saddle point for the touching configuration with$ C_{i} $ =$ R_{i} $ $\left(1- \dfrac{b^2}{R_{i}^2}\right) $ (i=1,2) being the S$ \ddot{u} $ ssmann central radii [43] of the daughter and cluster nucleus on account of the surface correction to the sharp radius$ R_{i} $ . b=1$ {\rm fm} $ is the diffuseness parameter of the nuclear surface taken from Ref. [44]. The sharp radius$ R_{i} $ , is given by [45]$ \begin{equation} R_{i}=1.28A_{i}^{1/3}-0.76+0.8A_{i}^{-1/3}, \end{equation} $

(4) where
$ A_{i} $ ($ i=c,d $ ) are the mass number of the emitted cluster and daughter nucleus, respectively.$ R_{{\rm out}} $ is the outer turning point of the barrier and satisfies the condition$V(R_{{\rm out}})=Q_{c}$ [5]. In this work,$ Q_{c} $ can be obtained by$ \begin{equation} Q_{c}=B(A_{c},Z_{c})+B(A_{d},Z_{d})-B(A,Z), \end{equation} $

(5) where
$ B(A_{c},Z_{c}) $ ,$ B(A_{d},Z_{d}) $ and$ B(A,Z) $ are, respectively, the binding energies of the emitted cluster, daughter, and parent nuclei taken from AME2020 [46] and NUBASE2020 [47] with$ Z_{c} $ ,$ Z_{d} $ and Z being the proton numbers of the emitted cluster, daughter, and parent nuclei and A being the mass number of the parent nucleus.The
$ V(r) $ in Eq. (3) is the total interacting potential between the emitted cluster and the daughter nucleus including nuclear, Coulomb, and centrifugal potential barriers. It can be written as$ \begin{equation} V(r)=V_{N}(r)+V_{\rm C}(r)+V_{l}(r), \end{equation} $

(6) where
$ V_{N} $ (r) is the nuclear potential. In this work, we choose it as a Woods-Saxon form [22], which can be expressed as$ \begin{equation} V_{N}(r)=\frac{V_{0}}{1+{\rm exp}\left[\dfrac{r-R_{0}}{a}\right]} \end{equation} $

(7) with
$ \begin{equation} R_{0}=r_{c}+r_{d}-1.37. \end{equation} $

(8) Here,
$ r_{i} (i=c,d) $ are the nuclear charge radii. They can be expressed as$ \begin{equation} r_{i}=1.27A_{i}^{1/3},~ i=c,d. \end{equation} $

(9) The potential depth
$ V_{0} $ and diffuseness a are parameterized as [22]$ \begin{equation} V_{0}=-44.16[1-0.4(I_{d}+I_{c})]\frac{A_{d}^{1/3}A_{c}^{1/3}}{A_{d}^{1/3}+A_{c}^{1/3}}, \end{equation} $

(10) $ \begin{equation} a=0.5+0.33I_{d}. \end{equation} $

(11) Here,
$ I_{i} $ =$ \dfrac{N_{i}-Z_{i}}{A_{i}} $ ($ i=c,d $ ) are the relative neutron excess of the emitted cluster and daughter nucleus with$ N_{i} $ and Z$ _{i} $ ($ i=c,d $ ) being the neutron numbers of the emitted cluster and daughter nuclei, respectively.$V_{\rm C}$ is the Coulomb potential of a uniformly charged sphere, which can be given by$ \begin{equation} V_{{\rm C}}(r)=\frac{{\rm e}^{2}Z_{c}Z_{d}}{r}, \end{equation} $

(12) where
$e^2=1.4399652~ {\rm MeV}\cdot {\rm fm}$ is the square of the electronic elementary charge [17].$ V_{l} $ in Eq. (3) is the centrifugal potential. In this work, we choose it as the Langer modified form since$ l(l+1) $ $ \to $ $ (l+\dfrac{1}{2})^2 $ is a necessary correction for one-dimensional problems [41]. It can be written as$ \begin{equation} V_{l}(r)=\frac{\hbar^{2}\left(l+\dfrac{1}{2}\right)^{2}}{2\mu r^{2}}, \end{equation} $

(13) where l is the angular momentum carried by the emitted cluster. It can be obtained by
$ \begin{eqnarray} l=\left\{\begin{array}{llll} \Delta_{j}, &{\rm for \ even} \ \Delta_{j} \ {\rm and} \ \pi_{p}=\pi_{d} , \\ \Delta_{j}+1, &{\rm for \ even} \ \Delta_{j} \ {\rm and} \ \pi_{p}\neq\pi_{d},\\ \Delta_{j}, &{\rm for \ odd} \ \Delta_{j} \ {\rm and} \ \pi_{p}\neq\pi_{d}, \\ \Delta_{j}+1, & {\rm for \ odd} \ \Delta_{j} \ {\rm and} \ \pi_{p}=\pi_{d} , \end{array}\right. \end{eqnarray} $

(14) where
$ \Delta_{j}=\lvert j_{p}-j_{d}-j_{c} \rvert $ ,$ j_{c},\pi_{c},j_{p},\pi_{p},j_{d},\pi_{d} $ represent the isospin and parity values of the emitted cluster, parent, and daughter nuclei, respectively.The cluster moves back and forth inside the parent nucleus with a certain speed before penetrating the barrier. For the purpose of evaluating assaults per unit time for the ground state, ν is presented as [48, 49]
$ \begin{equation} \nu=\frac{\pi \hbar}{2\mu R_{{\rm in}}^2}. \end{equation} $

(15) For the preformation probability
$ P_{c} $ , when the mass number of the cluster$ A_{c} $ $ < $ 28, it can be expressed as [38]$ \begin{equation} P_{c}=[P_{\alpha}]^{\textstyle\frac{(A_{c}-1)}{3}}, \end{equation} $

(16) where
$ P_{\alpha} $ is the α decay preformation probability. In this work, it is obtained by the CFM [50]. For completeness, detailed information on the CFM is presented in the next subsection. When the mass number of the cluster$ A_{c} $ $ \geq $ 28, the exponential relationship of$ P_{c} $ to$ P_{\alpha} $ may not work [39]. Therefore, in this work,$ P_{c} $ is calculated through an empirical formula proposed by Ren$et\:\: al.$ [14] for$ A_{c} $ $ \geq $ 28. It can be expressed as$ \begin{eqnarray} {\rm log}_{10} P_{c}=\left\{\begin{array}{llll} -(0.01674Z_{c}Z_{d}-2.035466),\\ \rm{for \ even-even \ nuclei}\\ -(0.01674Z_{c}Z_{d}-2.035466)-1.175,\\ {\rm for \ odd}-A \ {\rm nuclei}. \end{array}\right. \end{eqnarray} $

(17) -
In CFM, the total initial clusterization state ψ of the considered emitted cluster-daughter nucleus system is a linear combination of all its n possible clusterization
$ \psi_{i} $ states [50]$ \begin{equation} \psi=\sum\limits_{i}^{N}a_{i}\psi_{i}, \end{equation} $

(18) $ \begin{equation} a_{i}=\int{\psi_{i}}^{*}\psi\mathrm{d}\tau, \end{equation} $

(19) where
$ a_{i} $ is the superposition coefficient of$ \psi_{i} $ , on account of the orthogonality condition [51]$ \begin{equation} \sum\limits_{i}^{N}\lvert a_{i} \rvert^{2}=1. \end{equation} $

(20) The total Hamiltonian H consists of the accordingly different clusterization configuration [52]. It can be expressed as
$ \begin{equation} H=\sum\limits_{i}^{N}H_{i}, \end{equation} $

(21) where
$ H_{i} $ is the i-th Hamiltonian of clusterization state$ \psi_{i} $ . On account of all the clusterizations describing the same nucleus, they are assumed to share the same total energy E of the total wave function [51]. Furthermore, considering the orthonormality of the clusterization wave functions, E can be written as$ \begin{equation} E=\sum\limits_{i}^{N}\lvert a_{i} \rvert^{2}E=\sum\limits_{i}^{N}E_{f_{i}}, \end{equation} $

(22) where
$ E_{f_{i}} $ is the formation energy for the cluster in clusterization state$ \psi_{i} $ . Therefore, the α decay preformation probability$ P_{\alpha} $ can be obtained by [50, 52, 53]:$ \begin{equation} P_{\alpha}=\lvert a_{\alpha} \rvert^{2}=\frac{E_{f_{\alpha}}}{E}. \end{equation} $

(23) Here,
$ a_{\alpha} $ and$ E_{f_{\alpha}} $ are, respectively, the coefficient of the α clusterization state and the formation energy of the α particle. The α formation energy$ E_{f_{\alpha}} $ and total system energy E can be classified as four different cases in the following expressions [35, 51]:Case I for even-even nuclei:
$ \begin{aligned}[b] E_{f_{\alpha}}=&3B(A,Z)+B(A-4,Z-2)\\& -2B(A-1,Z-1)-2B(A-1,Z), \end{aligned} $

(24) $ \begin{equation} E=B(A,Z)-B(A-4,Z-2). \end{equation} $

(25) Case
$\rm II$ for even-odd nuclei:$\begin{aligned}[b] E_{f_{\alpha}}=&3B(A-1,Z)+B(A-5,Z-2)\\& -2B(A-2,Z-1)-2B(A-2,Z), \end{aligned} $

(26) $ \begin{equation} E=B(A,Z)-B(A-5,Z-2). \end{equation} $

(27) Case
$\rm III$ for odd-even nuclei:$ \begin{aligned}[b] E_{f_{\alpha}}=&3B(A-1,Z-1)+B(A-5,Z-3)\\& -2B(A-2,Z-2)-2B(A-2,Z-1), \end{aligned} $

(28) $ \begin{equation} E=B(A,Z)-B(A-5,Z-3). \end{equation} $

(29) Case
$\rm IV$ for odd-odd nuclei:$ \begin{aligned}[b] E_{f_{\alpha}}=&3B(A-2,Z-1)+B(A-6,Z-3)\\& -2B(A-3,Z-2)-2B(A-3,Z-1), \end{aligned} $

(30) $ \begin{equation} E=B(A,Z)-B(A-6,Z-3). \end{equation} $

(31) -
In 2009, using the microscopic mechanism of the charged-particle emission within α-like R-matrix theory, Qi et al. [54, 55] proposed the universal decay law (UDL). It can be expressed as
$ \begin{equation} \log_{10} (T_{1/2})(s)=aZ_{c}Z_{d}\sqrt{\frac{\mathcal{A}}{Q_{c}}}+b\sqrt{\mathcal{A}Z_{c}Z_{d}(A_{c}^{1/3}+A_{d}^{1/3})}+c, \end{equation} $

(32) where
$ \mathcal{A} $ =$ \dfrac{A_{c}A_{d}}{A_{c}+A_{d}} $ is the reduced mass of the emitted cluster-daughter nucleus system measured in units of the nucleon mass. a = 0.4314, b = −0.3921, and c = −32.7044 are the adjustable parameters. -
Based on the Geiger-Nuttall (G-N) law, considering the mass asymmetry, Santhosh
$ et $ $ al. $ proposed a formula for estimating the half-lives of α decay and cluster radioactivity in 2008 [56]. It can be given by$ \begin{equation} \log_{10} (T_{1/2})(s)=aZ_{d}Z_{c}Q_{c}^{-1/2}+b\eta_{A}+c , \end{equation} $

(33) where
$ \eta_{A} $ =$ \dfrac{A_{d}-A_{c}}{A} $ is the mass asymmetry. The values of the three adjustable parameters are a = 0.727356, b = 40.3887 and c = −85.1625, respectively. -
Deduced from the WKB barrier penetration probability with some approximation, Ni
$ et $ $ al. $ have proposed a unified formula of half-lives for both α decay and cluster radioactivity [30]. It can be expressed as$ \begin{equation} \log_{10} (T_{1/2})(s)=a\sqrt{\mathcal{A}}Z_{d}Z_{c}Q_{c}^{-1/2}+b\sqrt{\mathcal{A}}(Z_{d}Z_{c})^{1/2}+c, \end{equation} $

(34) where a = 0.38617, b = −1.08676,
$ c_{e-e} $ = −21.37195, and$ c_{{\rm odd}-A} $ = −20.11223 are the adjustable parameters, respectively. -
Based on the Wentzel-Kramers-Brillouin (WKB) theory, considering the cluster preformation probability
$ P_{c} $ , we systematically calculate the cluster radioactivity half-lives of 22 nuclei in the emission of clusters 14C, 15N, 20O, 23F,$ ^{24,25,26} $ Ne,$ ^{28,30} $ Mg, and$ ^{32,34} $ Si from various parent nuclei 221Fr,$ ^{221-226} $ Ra,$ ^{223,228,230} $ Th, 231Pa,$ ^{232-234} $ U,$ ^{236,238} $ Pu, and 242Cm resulting in doubly magic 208Pb and its neighboring nuclei in this work. The experimental cluster radioactivity half-lives$ T^{\rm exp}_{1/2} $ are extracted from Ref. [4] and Ref. [22]. The detailed calculated results are given in Table 1. This table is divided into Part I and Part$ \rm II $ , which are characterized by$ A_{c}<28 $ and$ A_{c}\ge28 $ , respectively. In Table 1, the first to fourth columns represent the decay process, the cluster radioactivity decay energy$ Q_{c} $ , angular momentum l carried by the emitted cluster, and the experimental cluster radioactivity half-lives in logarithmical form, respectively denoted as Decay,$ Q_{c} $ , l and Exp. The fifth to seventh columns are the calculated results of UDL, Santhosh's semi-empirical model, and Ni's formula in logarithmical form, denoted as UDL, Santhosh and Ni, respectively. In our work,$ P_{c} $ is calculated through the exponential relationship of$ P_{c} $ to$ P_{\alpha} $ for$ A_{c} $ $ < $ 28 with$ P_{\alpha} $ obtained by CFM. Nevertheless, since the exponential relationship of$ P_{c} $ to$ P_{\alpha} $ may break down when$ A_{c}\ge $ 28,$ P_{c} $ is calculated through the charge-number dependence of$ P_{c} $ on the decay products in DDCM proposed by Ren$ et $ $ al. $ [14]. The calculated half-life results in logarithmical form are given in the eighth column denoted as Cal1. For comparison, the theoretical half-life calculations based on WKB theory with$ P_{c} $ being calculated through the same charge-number dependence of$ P_{c} $ when$ A_{c} $ $ < $ 28 are also presented in the ninth column denoted as Cal2. From this table, it is clear that the calculated half-life results using Ni's formula, Cal1, Cal2 , and UDL are basically in agreement with the experimental data. The results in Cal1 are better than those in Cal2 when$ A_{c} $ $ < $ 28.Decay $Q_{c}$ /MeV

l $\log_{10}T_{1/2}$ (s)

Exp UDL Santhosh Ni Cal $^{1}$ 

Cal $^{2}$ 

Part I: $A_{c}<28$ 

$^{221}$ Fr

$\to$ 

$^{207}$ Tl+

$^{14}$ C

$31.2911$ 

$3$ 

$14.56$ 

$ 12.70 $ 

$13.30 $ 

$14.63$ 

$ 14.76 $ 

$16.37 $ 

$^{221}$ Ra

$\to$ 

$^{207}$ Pb+

$^{14}$ C

$32.3961$ 

$3$ 

$13.39$ 

$ 11.46 $ 

$ 12.98 $ 

$13.48$ 

$ 13.55 $ 

$15.31 $ 

$^{222}$ Ra

$\to$ 

$^{208}$ Pb+

$^{14}$ C

$33.0486$ 

$0$ 

$11.22$ 

$ 10.07 $ 

$ 12.38 $ 

$11.02$ 

$ 12.10 $ 

$12.77$ 

$^{223}$ Ra

$\to$ 

$^{209}$ Pb+

$^{14}$ C

$31.8279$ 

$4$ 

$15.05 $ 

$ 12.57 $ 

$13.59 $ 

$14.56$ 

$ 14.75 $ 

$16.20$ 

$^{224}$ Ra

$\to$ 

$^{210}$ Pb+

$^{14}$ C

$30.5343$ 

$0$ 

$15.87$ 

$ 15.38 $ 

$14.94 $ 

$15.86$ 

$ 16.91 $ 

$17.43$ 

$^{226}$ Ra

$\to$ 

$^{212}$ Pb+

$^{14}$ C

$28.1966$ 

$0$ 

$21.20$ 

$ 20.95 $ 

$17.62 $ 

$20.94$ 

$ 21.89 $ 

$22.39$ 

$^{223}$ Ac

$\to$ 

$^{209}$ Bi+

$^{14}$ C

$33.0636$ 

$2$ 

$12.60$ 

$ 11.07 $ 

$13.15 $ 

$13.19$ 

$ 13.31 $ 

$14.93$ 

$^{228}$ Th

$\to$ 

$^{208}$ Pb+

$^{20}$ O

$44.7233$ 

$0$ 

$20.73$ 

$ 21.97 $ 

$19.49 $ 

$21.54$ 

$ 21.44 $ 

$22.39$ 

$^{231}$ Pa

$\to$ 

$^{208}$ Pb+

$^{23}$ F

$51.8828$ 

$1$ 

$26.02$ 

$24.90 $ 

$21.71 $ 

$25.59$ 

$ 24.06 $ 

$22.39$ 

$^{230}$ Th

$\to$ 

$^{206}$ Hg+

$^{24}$ Ne

$57.7599$ 

$0$ 

$24.63$ 

$ 25.39 $ 

$23.36 $ 

$24.58$ 

$ 23.57 $ 

$25.82$ 

$^{231}$ Pa

$\to$ 

$^{207}$ Tl+

$^{24}$ Ne

$60.4099$ 

$1$ 

$22.89$ 

$ 22.27 $ 

$22.64 $ 

$23.09$ 

$ 21.54 $ 

$25.21$ 

$^{232}$ U

$\to$ 

$^{208}$ Pb+

$^{24}$ Ne

$62.3095$ 

$0$ 

$20.39$ 

$ 20.59 $ 

$22.43 $ 

$20.36$ 

$ 19.73 $ 

$23.86$ 

$^{233}$ U

$\to$ 

$^{209}$ Pb+

$^{24}$ Ne

$60.4853$ 

$2$ 

$24.84$ 

$ 23.63 $ 

$23.60 $ 

$24.41$ 

$ 23.02 $ 

$21.35$ 

$^{234}$ U

$\to$ 

$^{210}$ Pb+

$^{24}$ Ne

$58.8250$ 

$0$ 

$25.93$ 

$26.52 $ 

$24.71 $ 

$25.81$ 

$25.01 $ 

$25.06$ 

$^{233}$ U

$\to$ 

$^{208}$ Pb+

$^{25}$ Ne

$60.7036$ 

$2$ 

$24.84$ 

$ 24.00 $ 

$23.11 $ 

$24.88$ 

$ 23.40 $ 

$25.15$ 

$^{234}$ U

$\to$ 

$^{208}$ Pb+

$^{26}$ Ne

$59.4125$ 

$ 0$ 

$25.93$ 

$27.01$ 

$23.63$ 

$26.52$ 

$ 25.53$ 

$26.21$ 

Part I: $A_{c}\ge28$ 

$^{234}$ U

$\to$ 

$^{206}$ Hg+

$^{28}$ Mg

$74.1108$ 

$0$ 

$25.53$ 

$ 25.77 $ 

$26.67 $ 

$25.25$ 

$25.76$ 

$-$ 

$^{236}$ Pu

$\to$ 

$^{208}$ Pb+

$^{28}$ Mg

$79.6700$ 

$0$ 

$21.52$ 

$20.64$ 

$25.83$ 

$20.76$ 

$21.81$ 

$ - $ 

$^{238}$ Pu

$\to$ 

$^{210}$ Pb+

$^{28}$ Mg

$75.9114$ 

$0$ 

$25.70$ 

$26.26$ 

$27.87$ 

$25.96$ 

26.28 $ - $ 

$^{238}$ Pu

$\to$ 

$^{208}$ Pb+

$^{30}$ Mg

$76.7930$ 

$0$ 

$25.70$ 

$26.06$ 

$26.72$ 

$26.10 $ 

$25.75$ 

$-$ 

$^{238}$ Pu

$\to$ 

$^{206}$ Hg+

$^{32}$ Si

$96.1867$ 

$0$ 

$25.28$ 

$25.48$ 

$29.68$ 

$25.59$ 

$26.00$ 

$-$ 

$^{242}$ Cm

$\to$ 

$^{208}$ Pb+

$^{34}$ Si

$96.5440$ 

$0$ 

$23.15$ 

$22.35$ 

$28.86$ 

$23.48$ 

$23.43$ 

$-$ 

Table 1. Comparisons between the experimental cluster radioactivity half-lives (in seconds) and the calculated ones using the UDL, Santhosh's model, Ni's formula, and our model in logarithmic form.
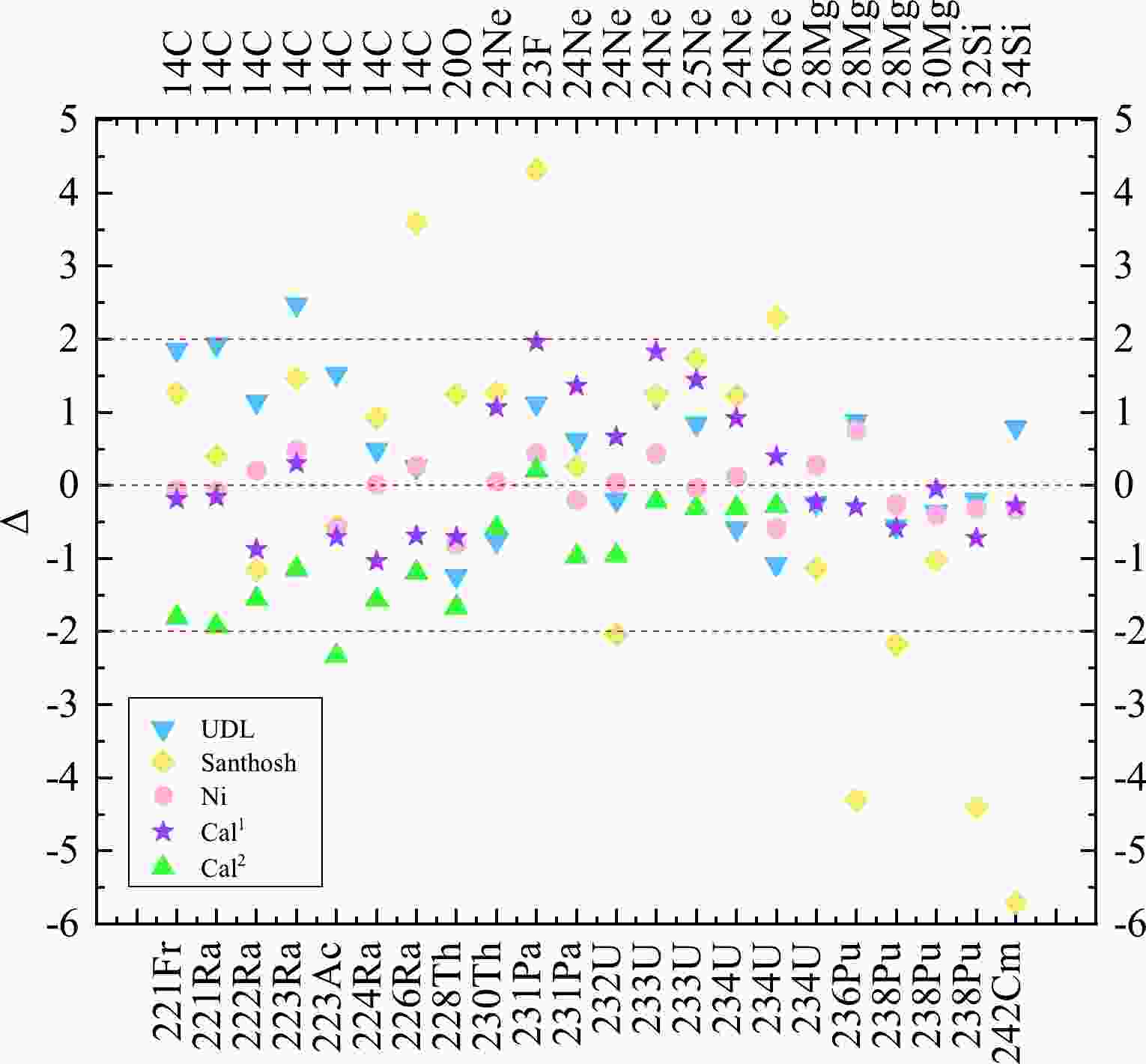
For the sake of intuitively comparing these results, we plot the differences between the experimental cluster radioactivity half-lives and the calculated ones by using the UDL, Santhosh's model, Ni's formula, Cal1, and Cal2 in logarithmical form in Fig. 1. From this figure, it is clear that the differences between the experimental data and the calculated results in Cal1 and Ni's formula are within
$ \pm2 $ on the whole, showing that the calculated cluster radioactivity half-lives in Cal1 as well as Ni's formula can reproduce the experimental data well. By contrast, in the case of 223Ra$ \to $ 209Pb+14C, there is a discrepancy of 2.482 the UDL. For 223Ac$ \to $ 209Bi+14C, there is a discrepancy of 2.325 in Cal2. The values of the discrepancies of 7 of the 22 nuclei are out of the scale of$ \pm $ 2 within Santhosh's model. Notably, for 231Pa$ \to $ 208Pb+23F and 242Cm$ \to $ 208Pb+34Si, the discrepancies reach 4.31 and 5.71, respectively. Furthermore, from the overall trend, the results in Cal1 converge more on the neighboring zero line area, relatively similar to the distribution of the UDL and Ni's formula. Nevertheless, the distribution of the results of Santhosh's model is slightly scattered. For further investigating the consistencies between the cluster radioactivity half-lives experimental data and the calculated ones obtained by UDL, Santhosh's model, Ni's formula, Cal1, and Cal2, the standard deviation σ is used, which is defined by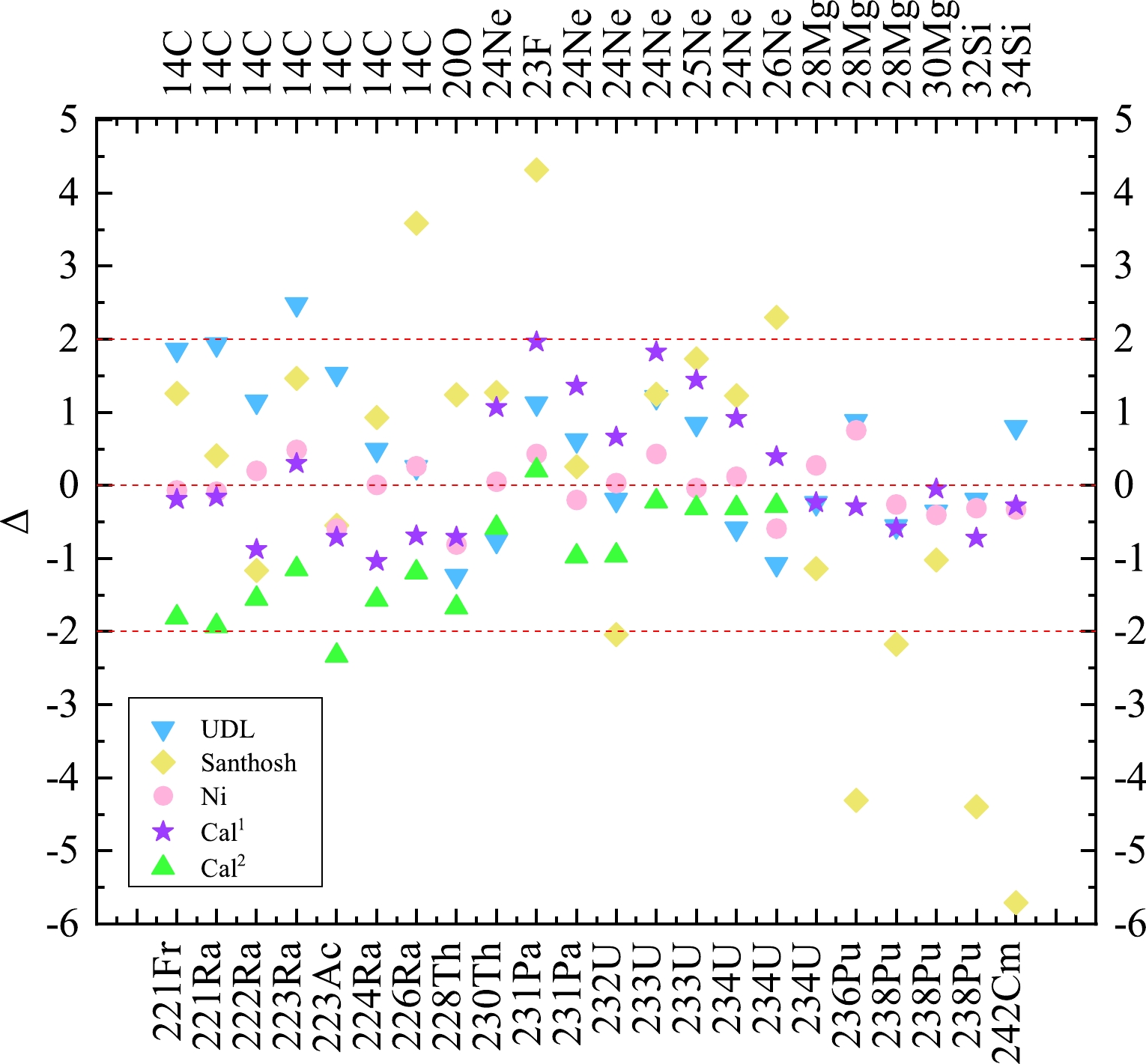
Figure 1. (color online) Comparison of the discrepancy in logarithmical form between the experimental cluster radioactivity half-lives and calculated ones obtained in the UDL, Santhosh's model, Ni's formula, and our model.
$ \begin{equation} \sigma=\Bigg[\sum\limits_{i}^{n}(\log_{10}T^{\rm exp}_{1/2_{i}}-\log_{10}T^{\rm cal}_{1/2_{i}})^2/n\Bigg]^{1/2}, \end{equation} $

(35) where
$ \log_{10}T^{\rm exp}_{1/2_{i}} $ and$ \log_{10}T^{\rm cal}_{1/2_{i}} $ denote the logarithmic form of the experimental cluster radioactivity half-lives and calculated ones for the i-th nucleus, respectively. The calculated results of σ using the UDL, Santhosh's model, Ni's formula, Cal1, and Cal2 are presented in Table 2. From this table, as$ A_{c} $ $ < $ 28, the σ value between the experimental data and the results obtained in CFM is 1.035, smaller compared to the results from Cal2, UDL, and Santhosh's model, which are 1.256, 1.244, and 1.880, respectively, larger than the results from Ni with 0.365. As$ A_{c} $ $ \ge $ 28, the σ values of Cal1 and Ni's formula are 0.423 and 0.425, smaller than those from the UDL and Santhosh's model, which are 0.569 and 3.594, respectively. For the total nuclei, it is clear that σ between the experimental data and the results calculated in Cal1 is 0.910, a better result than those resulting from the UDL and Santhosh's model, which are 1.102 and 2.469, respectively, closer to Ni's formula with 0.382, which is the least. Moreover, the calculated results in Cal1 are better than the ones based on different types of proximity potentials from Ref. [57], where the standard deviation σ between experimental and calculated half-lives ranges from 1.373 up to 7.951. This indicates that the our calculated cluster radioactivity half-lives results can reproduce the experimental data well. However, as for 231Pa$ \to $ 208Pb+23F with a discrepancy of 1.962 and 233U$ \to $ 209Pb+24Ne with a discrepancy of 1.825, the experimental data can not be properly reproduced. This may account for the imperfection of early detection technologies and radioactive beam equipment.Model UDL Santhosh Ni Cal $^{1}$ 

Cal $^{2}$ 

$\sigma(A_{c}<28)$ 

1.244 1.880 0.365 1.035 1.256 $\sigma(A_{c}\ge28)$ 

0.569 3.594 0.425 0.423 $-$ 

σ $1.102$ 

$2.469$ 

$0.382$ 

$0.910$ 

$-$ 

Table 2. Standard deviation σ between the experimental data and the calculated ones using different theoretical models and/or formulas for cluster radioactivity.
Encouraged by the good agreement between the experimental cluster radioactivity half-lives and the calculated ones within our model, in the following, we extend this model to predict the half-lives for the possible cluster radioactive candidates. The detailed calculated results are given in Table 3. In this table, the indications for the first to seventh columns are similar to Table 1. From Table 3, it is obvious that the predicted results in Cal1 are closer to those predicted using the UDL and Ni's formula except for the ones predicted using Santhosh's model. Note that most of the predicted results are of the same order of magnitude. For instance, in the case of 227Th
$ \to $ 209Pb+18O, the predicted cluster radioactivity half-lives using the UDL, Santhosh's model, Ni's formula, and Cal1 are 21.00, 20.59, 21.69, and 21.38, respectively. This implies that our predictions are reliable. This work may provide theoretical direction for future experiment.Decay $Q_{c}$ /MeV

l $\log_{10}T_{1/2}$ (s)

Exp UDL Santhosh Ni Cal $^{1}$ 

$^{219}$ Rn

$\to$ 

$^{205}$ Hg+

$^{14}$ C

$28.0974 $ 

$3$ 

− $ 19.09 $ 

$ 15.93 $ 

$20.29$ 

$20.41 $ 

$^{220}$ Rn

$\to$ 

$^{206}$ Hg+

$^{14}$ C

$28.5380 $ 

$0 $ 

− $17.95 $ 

$15.44 $ 

$18.05$ 

$18.98 $ 

$^{221}$ Fr

$\to$ 

$^{206}$ Hg+

$^{15}$ N

$34.1215 $ 

$3 $ 

− $21.55 $ 

$19.47 $ 

$22.16$ 

$22.06 $ 

$^{223}$ Ra

$\to$ 

$^{205}$ Hg+

$^{18}$ O

$40.3040 $ 

$1$ 

− $ 26.44 $ 

$ 22.03 $ 

$26.41$ 

$25.88 $ 

$^{225}$ Ra

$\to$ 

$^{211}$ Pb+

$^{14}$ C

$29.4661 $ 

$4$ 

− $ 17.84 $ 

$ 16.13 $ 

$19.37$ 

$19.68 $ 

$^{225}$ Ra

$\to$ 

$^{205}$ Hg+

$^{20}$ O

$40.4847 $ 

$1$ 

− $ 28.27 $ 

$ 21.21 $ 

$28.34$ 

$27.59 $ 

$^{226}$ Ra

$\to$ 

$^{206}$ Hg+

$^{20}$ O

$40.8173 $ 

$0$ 

− $ 27.46 $ 

$ 20.94 $ 

$26.41$ 

$26.34 $ 

$^{223}$ Ac

$\to$ 

$^{208}$ Pb+

$^{15}$ N

$39.4720 $ 

$3$ 

$>14.76$ 

$ 12.93 $ 

$ 16.25 $ 

$14.47$ 

$14.53 $ 

$^{227}$ Ac

$\to$ 

$^{207}$ Tl+

$^{20}$ O

$43.0872 $ 

$1$ 

− $ 23.95 $ 

$ 19.91 $ 

$24.55$ 

$23.78 $ 

$^{229}$ Ac

$\to$ 

$^{206}$ Hg+

$^{23}$ F

$48.3458 $ 

$2$ 

− $ 28.93 $ 

$ 22.43 $ 

$29.14$ 

$27.69 $ 

$^{226}$ Th

$\to$ 

$^{208}$ Pb+

$^{18}$ O

$45.7293 $ 

$0$ 

− $ 18.14 $ 

$ 19.35 $ 

$17.81$ 

$18.22 $ 

$^{226}$ Th

$\to$ 

$^{212}$ Po+

$^{14}$ C

$30.5475 $ 

$0$ 

$>16.76$ 

$17.55 $ 

$ 16.55 $ 

$17.83$ 

$18.78 $ 

$^{227}$ Th

$\to$ 

$^{209}$ Pb+

$^{18}$ O

$44.2021 $ 

$4$ 

$>15.30 $ 

$ 21.00 $ 

$ 20.59 $ 

$21.69$ 

$21.38 $ 

$^{228}$ Th

$\to$ 

$^{206}$ Hg+

$^{22}$ Ne

$55.7416 $ 

$0$ 

− $ 27.48 $ 

$ 25.37 $ 

$26.07$ 

$25.34 $ 

$^{229}$ Th

$\to$ 

$^{209}$ Pb+

$^{20}$ O

$43.4038 $ 

$2$ 

− $ 24.64 $ 

$ 20.60 $ 

$25.25$ 

$24.34 $ 

$^{229}$ Th

$\to$ 

$^{205}$ Hg+

$^{24}$ Ne

$57.8251 $ 

$3$ 

− $25.34 $ 

$ 23.28 $ 

$25.72$ 

$24.30 $ 

$^{231}$ Th

$\to$ 

$^{207}$ Hg+

$^{24}$ Ne

$56.2544 $ 

$2$ 

− $ 28.12 $ 

$ 24.42 $ 

$28.36$ 

$26.54 $ 

$^{231}$ Th

$\to$ 

$^{206}$ Hg+

$^{25}$ Ne

$56.7977 $ 

$2$ 

− $ 27.92 $ 

$ 23.69 $ 

$28.30$ 

$26.42 $ 

$^{232}$ Th

$\to$ 

$^{208}$ Hg+

$^{24}$ Ne

$54.6683 $ 

$0$ 

$>29.20$ 

$ 31.12 $ 

$ 25.57 $ 

$29.86$ 

$28.81 $ 

$^{232}$ Th

$\to$ 

$^{206}$ Hg+

$^{26}$ Ne

$55.9116 $ 

$0$ 

$>29.20 $ 

$ 30.37 $ 

$ 23.99 $ 

$29.45$ 

$28.25 $ 

$^{227}$ Pa

$\to$ 

$^{209}$ Bi+

$^{18}$ O

$45.8713 $ 

$2$ 

− $19.16 $ 

$ 20.13 $ 

$20.01$ 

$19.48 $ 

$^{229}$ Pa

$\to$ 

$^{207}$ Tl+

$^{22}$ Ne

$58.9558 $ 

$2$ 

− $23.31 $ 

$ 24.20 $ 

$23.63$ 

$22.31 $ 

$^{230}$ U

$\to$ 

$^{208}$ Pb+

$^{22}$ Ne

$61.3883 $ 

$0$ 

$>18.20$ 

$ 20.73 $ 

$ 23.62 $ 

$20.09$ 

$19.49 $ 

$^{230}$ U

$\to$ 

$^{206}$ Pb+

$^{24}$ Ne

$61.3521 $ 

$0$ 

$>18.20$ 

$22.34 $ 

$ 22.94 $ 

$21.78$ 

$20.88 $ 

$^{232}$ U

$\to$ 

$^{204}$ Hg+

$^{28}$ Mg

$74.3195 $ 

$0$ 

$>22.26$ 

$ 25.59 $ 

$ 26.47 $ 

$24.93$ 

$23.45 $ 

$^{233}$ U

$\to$ 

$^{205}$ Hg+

$^{28}$ Mg

$74.2271 $ 

$3$ 

$>27.59$ 

$ 25.66 $ 

$ 26.57 $ 

$26.33$ 

$24.42 $ 

$^{235}$ U

$\to$ 

$^{211}$ Pb+

$^{24}$ Ne

$57.3635 $ 

$1$ 

$>27.65$ 

$ 29.16 $ 

$ 25.73 $ 

$29.51$ 

$27.91 $ 

$^{235}$ U

$\to$ 

$^{210}$ Pb+

$^{25}$ Ne

$57.6832 $ 

$3$ 

$>27.65$ 

$ 29.41 $ 

$ 25.16 $ 

$29.86$ 

$28.25 $ 

$^{235}$ U

$\to$ 

$^{207}$ Hg+

$^{28}$ Mg

$72.4257 $ 

$1$ 

$>28.45$ 

$ 28.45 $ 

$ 27.65 $ 

$29.00$ 

$26.98 $ 

$^{235}$ U

$\to$ 

$^{206}$ Hg+

$^{29}$ Mg

$72.4772 $ 

$3$ 

$>28.45$ 

$ 29.03 $ 

$27.28 $ 

$29.67$ 

$29.44 $ 

$^{236}$ U

$\to$ 

$^{212}$ Pb+

$^{24}$ Ne

$55.9451 $ 

$0$ 

$>26.27$ 

$ 31.83 $ 

$ 26.75 $ 

$30.71$ 

$29.38 $ 

$^{236}$ U

$\to$ 

$^{210}$ Pb+

$^{26}$ Ne

$56.6920 $ 

$0$ 

$>26.27$ 

$32.10 $ 

$ 25.54 $ 

$31.23$ 

$29.70 $ 

$^{236}$ U

$\to$ 

$^{208}$ Hg+

$^{28}$ Mg

$70.7345 $ 

$0$ 

$>26.27$ 

$ 31.25 $ 

$ 28.67 $ 

$30.33$ 

$28.36 $ 

$^{236}$ U

$\to$ 

$^{206}$ Hg+

$^{30}$ Mg

$72.2719 $ 

$0$ 

$>26.27$ 

$29.94 $ 

$ 27.09 $ 

$29.47$ 

$28.74 $ 

$^{238}$ U

$\to$ 

$^{208}$ Hg+

$^{30}$ Mg

$69.4591 $ 

$0$ 

− $ 34.79 $ 

$ 28.83 $ 

$33.98$ 

$32.67 $ 

$^{231}$ Np

$\to$ 

$^{209}$ Bi+

$^{22}$ Ne

$61.9033 $ 

$3$ 

− $ 21.37 $ 

$ 24.26 $ 

$21.95$ 

$20.47 $ 

$^{233}$ Np

$\to$ 

$^{209}$ Bi+

$^{24}$ Ne

$62.1600 $ 

$3$ 

− $ 22.37 $ 

$ 23.48 $ 

$23.24$ 

$21.75 $ 

$^{235}$ Np

$\to$ 

$^{207}$ Tl+

$^{28}$ Mg

$77.0969 $ 

$2$ 

− $ 22.82 $ 

$ 26.12 $ 

$23.92$ 

$22.27 $ 

$^{237}$ Np

$\to$ 

$^{207}$ Tl+

$^{30}$ Mg

$74.7869 $ 

$2$ 

$>27.57$ 

$ 27.54 $ 

$ 26.75 $ 

$28.63$ 

$28.06 $ 

$^{237}$ Pu

$\to$ 

$^{209}$ Pb+

$^{28}$ Mg

$77.7263 $ 

$1$ 

− $23.49 $ 

$ 26.86 $ 

$24.66$ 

$23.23 $ 

Continued on next page Table 3. Predicted half-lives for possible cluster radioactive nuclei.
Table 3-continued from previous page Decay $Q_{c}$ (MeV)

l $\log_{10}T_{1/2}$ (s)

Exp UDL Santhosh Ni Cal $^{1}$ 

$^{237}$ Pu

$\to$ 

$^{208}$ Pb+

$^{29}$ Mg

$77.4527 $ 

$3$ 

− $ 24.51 $ 

$ 26.67 $ 

$25.73$ 

$25.94 $ 

$^{237}$ Pu

$\to$ 

$^{205}$ Hg+

$^{32}$ Si

$91.4574 $ 

$4$ 

− $ 25.17 $ 

$ 29.50 $ 

$26.48$ 

$27.04 $ 

$^{239}$ Pu

$\to$ 

$^{209}$ Pb+

$^{30}$ Mg

$75.0841 $ 

$4$ 

− $ 28.78 $ 

$ 27.68 $ 

$29.89$ 

$29.20 $ 

$^{239}$ Pu

$\to$ 

$^{205}$ Hg+

$^{34}$ Si

$90.8678 $ 

$1$ 

− $ 26.83 $ 

$29.19 $ 

$28.50$ 

$27.90 $ 

$^{237}$ Am

$\to$ 

$^{209}$ Bi+

$^{28}$ Mg

$79.8484 $ 

$2$ 

− $ 22.06 $ 

$26.76 $ 

$23.35$ 

$21.75 $ 

$^{239}$ Am

$\to$ 

$^{207}$ Tl+

$^{32}$ Si

$94.5021 $ 

$3$ 

− $ 22.65 $ 

$ 29.26 $ 

$24.38$ 

$25.11 $ 

$^{241}$ Am

$\to$ 

$^{207}$ Tl+

$^{34}$ Si

$93.9599 $ 

$3$ 

$>24.41$ 

$ 24.13 $ 

$ 28.92 $ 

$26.26$ 

$25.91 $ 

$^{240}$ Cm

$\to$ 

$^{208}$ Pb+

$^{32}$ Si

$97.5504 $ 

$0$ 

− $ 20.31 $ 

$ 29.00 $ 

$21.09$ 

$22.19 $ 

$^{241}$ Cm

$\to$ 

$^{209}$ Pb+

$^{32}$ Si

$95.3940 $ 

$4$ 

− $ 23.19 $ 

$ 29.99 $ 

$25.02$ 

$25.65 $ 

$^{243}$ Cm

$\to$ 

$^{209}$ Pb+

$^{34}$ Si

$94.7881 $ 

$2$ 

− $ 24.77 $ 

$ 29.69 $ 

$27.00$ 

$26.47 $ 

$^{244}$ Cm

$\to$ 

$^{210}$ Pb+

$^{34}$ Si

$93.1718 $ 

$0$ 

− $ 27.06 $ 

$ 30.48 $ 

$27.89$ 

$27.03 $ 

In addition, the correlations between the cluster radioactivity half-lives in logarithmical form log
$ _{10} $ $ T_{1/2} $ , penetration probability in logarithmical form log$ (P) $ , and daughter neutron number are plotted in Figs. 2 to 5. Figures 2 and 4 represent the cluster radioactivity half-lives in logarithmic form versus the daughter neutron numbers for the 14C emission from Ra isotopes and 24Ne emission from U isotopes, respectively. Figures. 3 and 5 denote the cluster radioactivity penetration probability in logarithmical form versus the daughter neutron numbers for the 14C emission from Ra isotopes and 24Ne emission from U isotopes, respectively. From Figs. 2 and 4, it is clear that with increasing daughter neutron number, log$ _{10} $ $ T_{1/2} $ begins to decrease almost linearly. When it arrives at the magic neutron number 126, the value of log$ _{10} $ $ T_{1/2} $ reaches a minimum, then increases linearly again. This is exactly opposite to the tendency for log$ (P) $ depicted in Figs. 3 and 5. Nevertheless, when the daughter neutron number is at the doubly magic daughter nucleus 208Pb, log$ _{10} $ $ T_{1/2} $ and log$ (P) $ both take minimum and maximum values. Consequently, this confirms that neutron shell closure plays a more crucial role than proton shell closure in cluster radioactivity, revealing that the neutron pairing effect is more influential than that of protons in this decay mode process [5].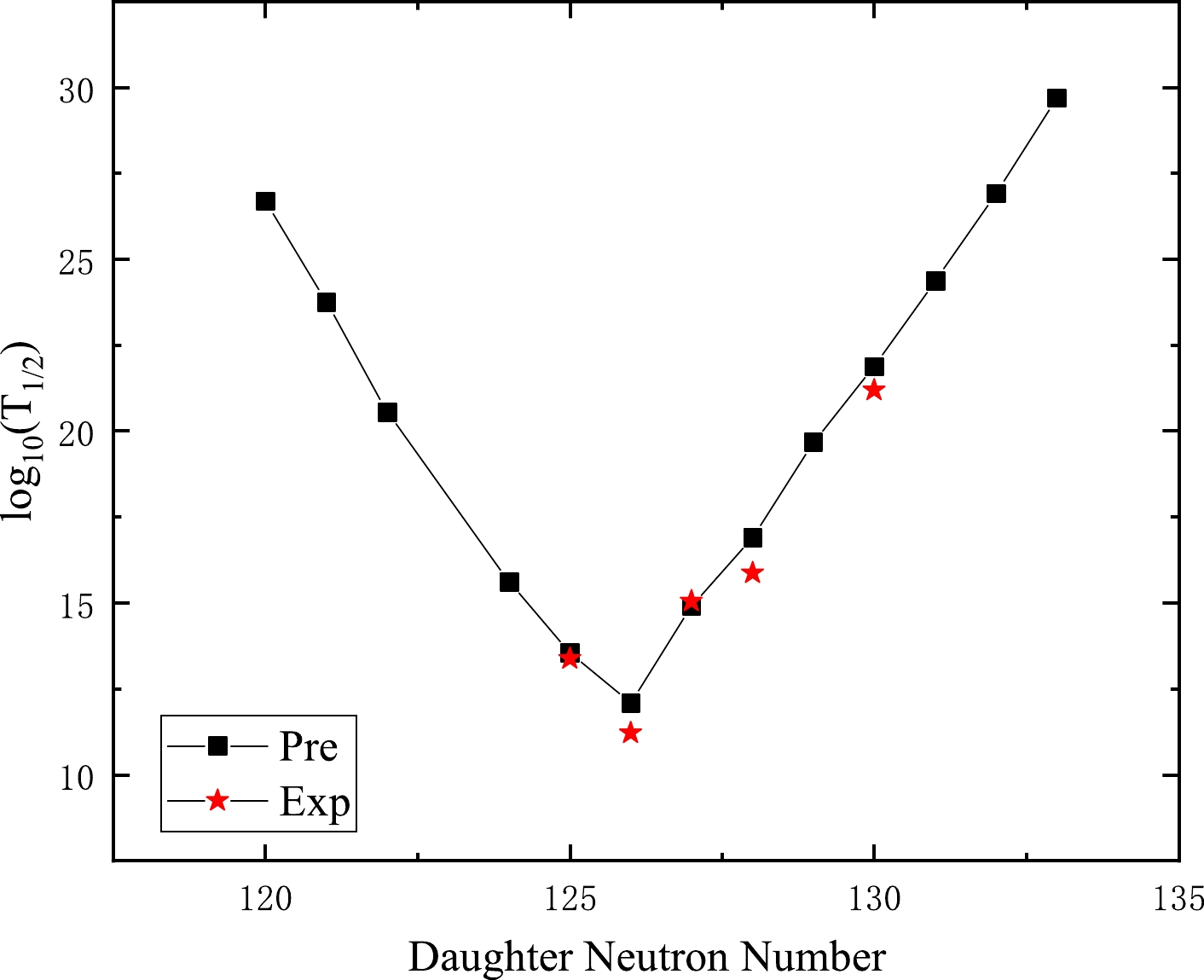
Figure 2. (color online) Plot of the computed log
$_{10}$ ($T_{1/2}$ ) values versus neutron numbers of daughter nuclei for the emission of cluster$^{14}$ C from Ra isotopes. The black squares and red stars represent the predicted and experimental half-lives, respectively.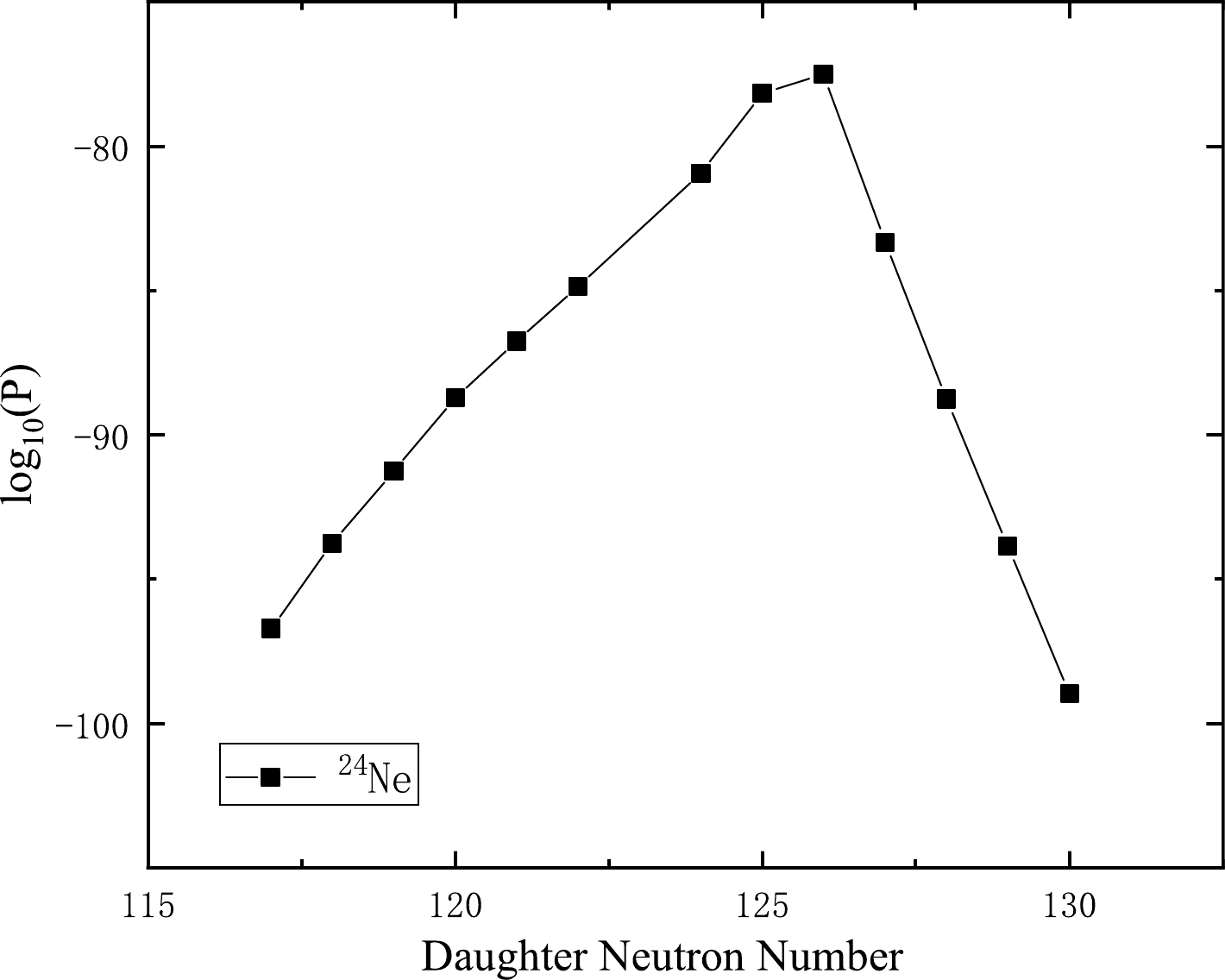
Figure 5. Plot of the computed log
$_{10}$ $(P)$ values versus neutron numbers of daughter nuclei for the emission of cluster$^{24}$ Ne from U isotopes.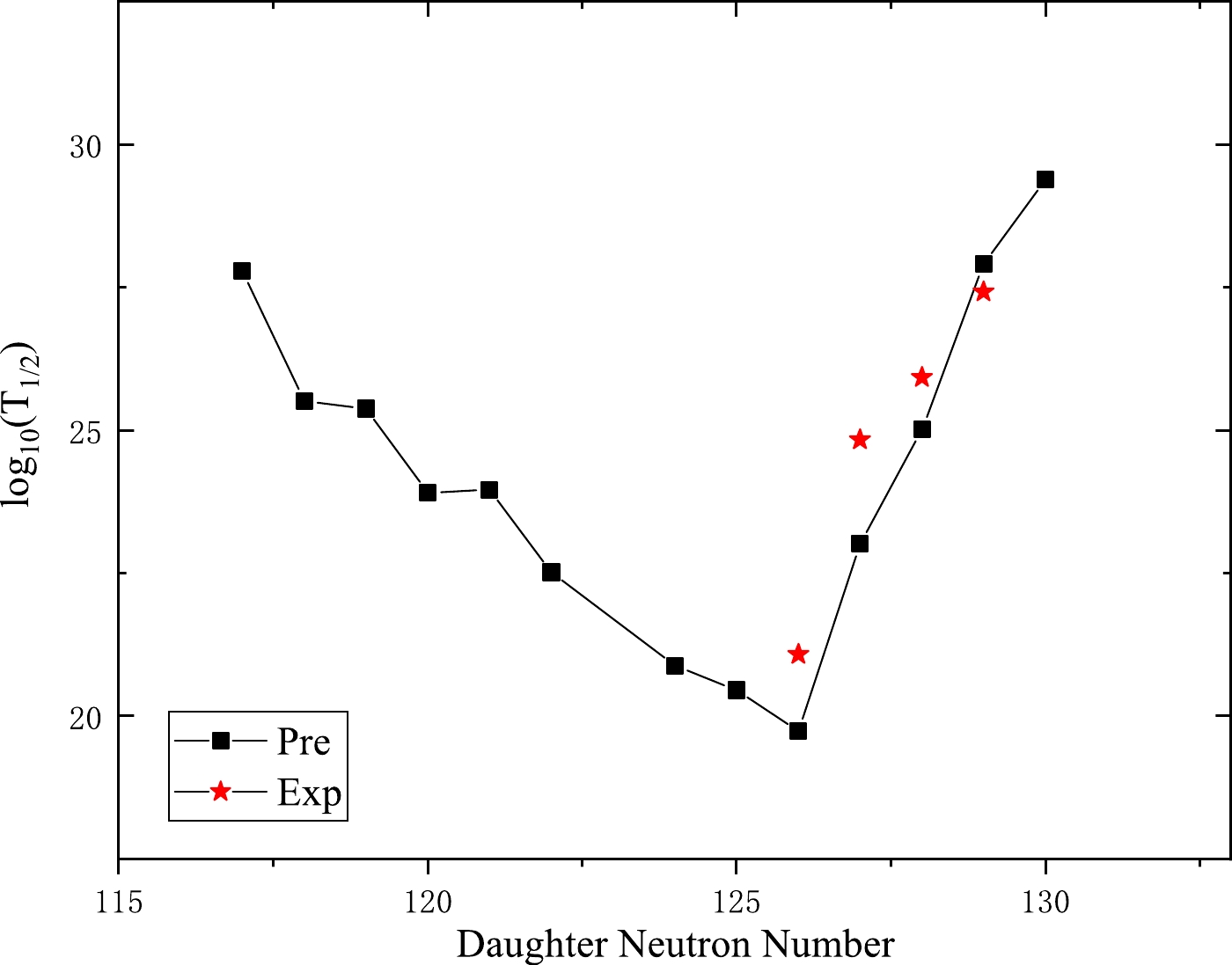
Figure 4. (color online) Plot of the computed log
$_{10}$ ($T_{1/2}$ ) values versus neutron numbers of daughter nuclei for the emission of cluster$^{24}$ Ne from U isotopes. The black squares and red stars represent the predicted and experimental half-lives, respectively.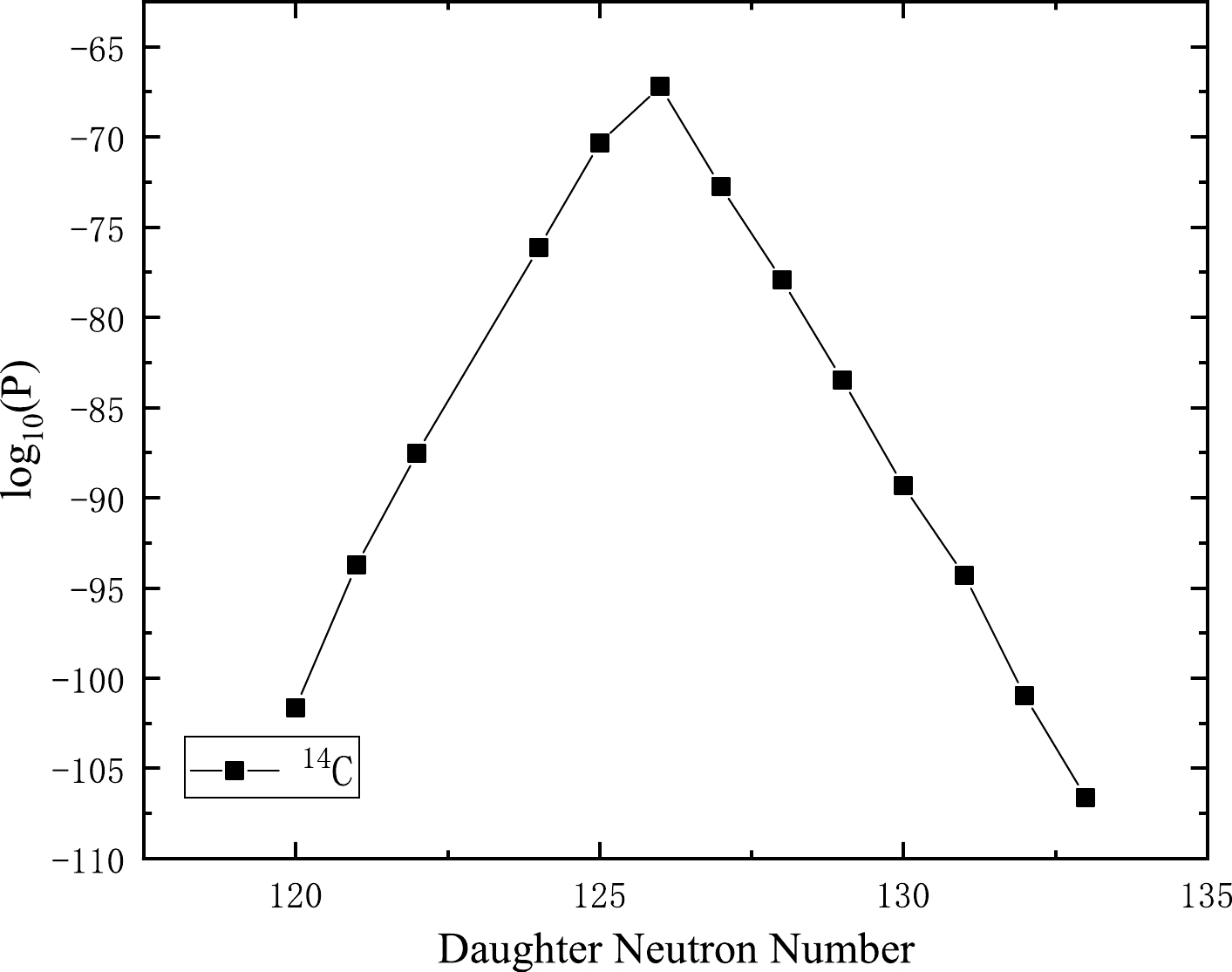
Figure 3. Plot of the computed log
$_{10}$ $(P)$ values versus neutron numbers of daughter nuclei for the emission of cluster$^{14}$ C from Ra isotopes.Furthermore, recent works have shown that the dynamical deformations of the shapes of both the cluster and daughter nuclei are also important in cluster radioactivity [58–63]. The barrier penetration can be changed due to the shape deformations of both the cluster and the residual nuclei in the cluster emission process [58]. The deformations can be reflected in the orientation angle dependent nuclear radius resulting in changes in barrier height [59, 60], which can influence the penetrability and alter the cluster radioactivity half-lives [61–63]. Therefore, it is meaningful to consider dynamical shape deformations of both the cluster and daughter nuclei to study this decay mode. We will also investigate the significance of the dynamical deformations of the shapes of both the cluster and daughter nuclei in cluster radioactivity in more detail in future work.
-
In summary, based on the WKB theory, considering the cluster radioactivity preformation probability
$ P_{c} $ and using a Woods-Saxon type nuclear potential, we systematically study the half-lives of 22 experimentally observed nuclei. The preformation factor$ P_{c} $ is obtained within CFM applied with the exponential relationship of$ P_{\alpha} $ when$ A_{c} $ $ < $ 28 and an effective empirical formula when$ A_{c} $ $ \ge $ 28. The calculated cluster radioactivity half-lives are compared with those obtained by using the UDL, Santhosh's semi-empirical model for both α decay and cluster radioactivity, and Ni's unified formula for both α decay and cluster radioactivity. The results are consistent with the experimental data. Moreover, we extend this model to predict the cluster radioactivity half-lives of the possible candidates. Finally, we confirm the neutron magicity at daughter neutron number 126 and that the neutron pairing effect is more influential than protons in cluster radioactivity.
Systematic calculations of cluster radioactivity half-lives in trans-lead nuclei
- Received Date: 2022-07-12
- Available Online: 2023-01-15
Abstract: In the present work, based on the Wentzel-Kramers-Brillouin (WKB) theory, considering the cluster preformation probability (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: