-
Quantum chromodynamics (QCD) is the fundamental theory of the strong interaction. Hadrons are
$ q\bar q $ mesons and$ qqq $ baryons in the conventional quark model [1, 2]. However, QCD itself allows for the existence of multiquarks. In 2015, the LHCb Collaboration reported two hidden-charm pentaquark states,$ P_c(4380) $ and$ P_c(4450) $ , in the$ J/\psi p $ invariant mass spectrum of$ \Lambda_b^0\to J/\psi pK $ decays [3].$ P_c(4450) $ was then further found to be separated into two structures,$ P_c(4440) $ and$ P_c(4457) $ , in the same process, in which a new narrow resonance$ P_c(4312) $ was also discovered [4]. Recently, the LHCb Collaboration announced the first evidence of a hidden-charm pentaquark state with strangeness,$ P_{cs}^0(4459) $ , in the$ J/\psi\Lambda $ invariant mass distribution of$ \Xi_b^0\to J/\psi\Lambda K $ decays [5]. Observations of these hidden-charm pentaquarks have immediately garnered extensively theoretical interest, considering them$ \bar D^{(\ast)}\Sigma_c^{(\ast)} $ ($ \bar D^{(\ast)}\Xi_c $ ) hadron molecules or compact pentaquarks with a quark content of$ \bar ccuud $ ($ \bar ccuds $ ) [6–10].If the above interpretations of
$ P_c $ are correct, analogous effects could also be expected at the hidden-strange$ P_s=\bar ssuud $ pentaquark. The study of the existence of hidden-strange pentaquarks was conducted considerably earlier than the observations of$ P_c $ states. Experiments and analysis of pentaquarks composed of light quarks date back to 1960, when the$ N\bar{K} $ molecular state was explained with$ \Lambda(1405) $ [11–17]. However, there are almost no results for light pentaquarks. From 1994–1999, experiments using the SPHINX spectrometer reported a resonance structure$ X(2000) $ as a candidate for the$ \bar ssuud $ state in the proton diffractive reactions$ p+N(C)\to X(\Sigma^0K^+)+ N(C) $ [18–21]. Although the extracted resonance had fairly poor statistics, it inspired several theoretical studies on the existence of hidden-strange pentaquarks. In Ref. [22], Williams and Gueye studied the color octet-octet$ [q\bar s][uds] $ configuration in a non-relativistic quark molecular model and predicted four candidates for$ P_s $ states. Using the quark delocalization color screening model (QDCSM), Huang et al. calculated the effective potential, masses, and decay widths of$ \Sigma^{(\ast)}K^{(\ast)} $ molecular states and found that the interactions between$ \Sigma^{(\ast)} $ and$ K^{(\ast)} $ were sufficiently strong to form bound states [23].Furthermore, a
$ \phi-N $ bound state was proposed by Gao et al., in which the QCD van der Waals attractive potential is sufficiently strong to bind a ϕ meson to a nucleon inside a nucleus to form a bound state [24]. The calculations in the chiral SU(3) quark model [25, 26], lattice QCD [27], chiral soliton model [28], and QDCSM [29] also support the existence of$ \phi N $ bound states. In Ref. [30], the authors proposed a possible$ \phi p $ resonance in the$\Lambda^+_c\to \pi^0\phi p$ decay by considering a triangle singularity mechanism. In Ref. [31], Lebed used a$ [su]_{\bf \bar 3}[\bar sud]_{\bf 3} $ diquark-triquark model to investigate the possible existence of$ P_s $ pentaquarks and further proposed to create such states through the$ \Lambda_c^+\to P_s\pi^0\to\phi p\pi^0 $ decay [32]. Unfortunately, the Belle Collaboration searched for$ \Lambda_c^+\to\phi p\pi^0 $ decays in 2017 and found no evidence of the intermediate hidden-strange pentaquark decay$ P_s\to\phi p $ [33].Comparing the hidden-charm
$ P_c $ states observed in the$ J/\psi p $ final state, one possible reason for the absence of$ P_s $ pentaquarks may be the limited phase space of the$ P_s\to\phi p $ decay. Nevertheless, it is still interesting to investigate the properties of$ P_s $ states in theory. In this study, we investigate$ \bar ssuud $ systems in both the$ [udu][\bar ss] $ and$ [uds][\bar su] $ configurations with quantum numbers$J^P= {1}/{2}^-$ using QCD sum rules [34–36].This paper is organized as follows. In Sec. II, we construct interpolating currents for hidden-strange pentaquarks in both the
$ [udu][\bar ss] $ and$ [uds][\bar su] $ configurations with$J^P= {1}/{2}^-$ and then evaluate the correlation functions and spectral densities for these interpolating currents. In Sec. III, we perform QCD sum rule analyses to extract the mass spectra of$ P_s $ pentaquarks. The final section contains a brief summary and discussion. -
In this section, we introduce QCD sum rules for hidden-strange pentaquarks with a quark content of
$ qqqs\bar s $ . The start of QCD sum rules is the two-point correlator$ \begin{aligned}[b] \Pi(q) &={\rm i} \int \mathrm{d}^4 x {\rm e}^{{\rm i} q \cdot x}\langle 0|T\{\eta(x) \bar{\eta}(0)\}| 0\rangle, \\ \Pi_{\mu \nu}(q) &={\rm i} \int \mathrm{d}^4 x {\rm e}^{{\rm i} q \cdot x}\left\langle 0\left|T\left\{\eta_\mu(x) \bar{\eta}_\nu(0)\right\}\right| 0\right\rangle, \end{aligned}$

(1) where
$ \eta(x) $ is a hidden-strange pentaquark interpolating current. There are two possible color configurations for such pentaquark operators:$ [\epsilon^{abc}q_aq_bq_c][\bar s_ds_d] $ and$ [\epsilon^{abc}q_aq_bs_c][\bar s_dq_d] $ , where$ a, b, c, d $ are color indices, q denotes a light quark, and s is a strange quark. We use both types of interpolating currents to investigate hidden-strange pentaquark systems. To construct the pentaquark currents, we use the following operators for$ L=0 $ baryons [36–38]:$ \begin{aligned}[b] \eta^p &=\epsilon^{abc}\left[(u^T_a C d_b)\gamma_5 u_c-(u^T_a C \gamma_5 d_b) u_c\right]\, , \\ \eta_\mu^p &=\epsilon^{abc}\left[(u^T_a C d_b)\gamma_{\mu} u_c-(u^T_a C \gamma_5 d_b)\gamma_{\mu} \gamma_5 u_c\right]\, , \\ \eta^\Lambda &=\epsilon^{abc}\left[(u^T_a C d_b)\gamma_5 s_c-(u^T_a C \gamma_5 d_b) s_c\right]\, , \\ \eta^\Sigma &=\epsilon^{abc}\left[(u^T_a C \gamma_{\mu} d_b)\gamma_{5}\gamma^{\mu}s_c\right]\, , \\ \eta_\mu^{\Sigma^\ast} &=\epsilon^{abc}\left[2(u^T_a C \gamma_{\mu} s_b)u_c + (u^T_a C \gamma_{\mu} u_b)s_c \right]\, , \end{aligned} $

(2) in which T denotes the transposition, and C is the charge conjugation matrix. Together with the operators
$ \bar q_a\gamma_5 q_a (0^-) $ and$ \bar q_a\gamma_\mu q_a (1^-) $ for$ L=0 $ mesons, we compose the following hidden-strange pentaquark currents with$J^P = {1}/{2}^{-}$ $ \begin{aligned}[b] \eta_1 &= \epsilon^{abc}\left[(u^T_a C d_b)\gamma_5 u_c-(u^T_a C \gamma_5 d_b) u_c\right]\left[\bar{s}_d\gamma_5 s_d\right]\, ,\\ \eta_2 &= \epsilon^{abc}\left[(u^T_a C d_b)\gamma_{\mu} u_c-(u^T_a C \gamma_5 d_b)\gamma_{\mu} \gamma_5 u_c\right]\left[\bar{s}_d\gamma^{\mu} s_d\right]\, ,\\ \eta_3 &= \epsilon^{abc}\left[(u^T_a C d_b)\gamma_5 s_c-(u^T_a C \gamma_5 d_b) s_c\right]\left[\bar{s}_d\gamma_5 u_d\right]\, ,\\ \eta_4 &= \epsilon^{abc}\left[(u^T_a C \gamma_{\mu} d_b)\gamma_{5}\gamma^{\mu}s_c\right]\left[\bar{s}_d\gamma_5 u_d\right]\,,\\ \eta_5 &=\epsilon^{abc}\left[2(u^T_a C \gamma_{\mu} s_b)u_c + (u^T_a C \gamma_{\mu} u_b)s_c \right] \left[\bar{s}_d\gamma^{\mu}d_d\right]\, , \end{aligned} $

(3) which can couple to
$ p\eta^\prime $ ,$ p\phi $ ,$ \Lambda K $ ,$ \Sigma K $ , and$ \Sigma^\ast K^\ast $ , respectively. We also compose the following hidden-strange pentaquark currents with$J^P = {3}/{2}^-$ $ \begin{aligned}[b] \eta_{6\mu} &=\epsilon^{abc}\left[(u^T_a C \gamma_{\nu} d_b)\gamma_{5}\gamma^{\nu}s_c\right]\left[\bar{s}_d\gamma_\mu u_d\right]\, ,\\ \eta_{7\mu} &=\epsilon^{abc}\left[2(u^T_a C \gamma_{\mu} s_b)u_c + (u^T_a C \gamma_{\mu} u_b)s_c \right] \left[\bar{s}_d\gamma_5 d_d\right]\, , \end{aligned} $

(4) which can couple to
$ \Sigma K^\ast $ and$ \Sigma^\ast K $ , respectively. In principle, these interpolating currents can couple to pentaquark states with both negative and positive parities.$ \langle 0| \eta(x)| X^- \rangle = f_{X^-} u(q)\, , $

(5) $ \langle 0| \eta(x)| X^+ \rangle = {\rm i} f_{X^+} \gamma_5u(q)\, , $

(6) where
$ u(q) $ is the Dirac spinor, and$ f_{X^-} $ and$ f_{X^+} $ are coupling constants. Accordingly, the two-point correlators induced by these pentaquark currents can be written as$ \begin{aligned}[b] \Pi^-(q) &={\rm i} \int \mathrm{d}^4 x {\rm e}^{{\rm i} q \cdot x}\langle 0|T\{\eta(x) \bar{\eta}(0)\}| 0\rangle \\ &={\not q}\Pi_q\left(q^2\right)+\Pi_m\left(q^2\right), \end{aligned}$

(7) $\begin{aligned}[b] \Pi^+(q) &={\rm i} \int \mathrm{d}^4 x {\rm e}^{{\rm i} q \cdot x}\left\langle 0\left|T\left\{\eta^{\prime}(x) \bar{\eta}^{\prime}(0)\right\}\right| 0\right\rangle \\ &={\not q} \Pi_q\left(q^2\right)-\Pi_m\left(q^2\right), \end{aligned}$

(8) where
$ \Pi_q(q^2) $ and$ \Pi_m(q^2) $ are the invariant functions proportional to$\not q$ and$ 1 $ , respectively. Note that these two invariant functions appear in$ \Pi^-(q) $ and$ \Pi^+(q) $ simultaneously, implying that they contain hadron information for both negative and positive parity pentaquark states. However, the signs of$ \Pi_m(q^2) $ in$ \Pi^-(q) $ and$ \Pi^+(q) $ are different owing to the coupling definitions in Eqs. (5)–(6). See Refs. [39–42] for detailed discussions.Moreover,
$ \eta_{6\mu}(x) $ and$ \eta_{7\mu}(x) $ can couple to both$J = {3}/{2}$ and${1}/{2}$ channels$ \Pi_{\mu\nu}(q) = \left(\frac{q_\mu q_\nu}{q^2}-g_{\mu\nu}\right)(\not {q}+M_X)\Pi^{3/2}(q)+\cdots\, , $

(9) where
$ \cdots $ contains the spin$ 1/2 $ components of$ \eta_{6\mu} $ or$ \eta_{7\mu} $ .At the hadronic level, the invariant functions can be described by the dispersion relation
$ \begin{equation} \Pi\left(q^{2}\right)=\frac{\left(q^{2}\right)^{N}}{\pi} \int_{4m_{s}^{2}}^{\infty} \frac{\operatorname{Im} \Pi(s)}{s^{N}\left(s-q^{2}-{\rm i} \epsilon\right)} {\rm d} s+\sum\limits_{n=0}^{N-1} b_{n}\left(q^{2}\right)^{n}\, , \end{equation} $

(10) where
$ b_n $ are N unknown subtraction constants and will be removed after performing a Borel transform. The imaginary part of the correlation function is usually defined as the spectral function$ \begin{aligned}[b] \rho (s)\equiv\frac{1}{\pi} \rm{Im}\Pi(s)&=\sum_n\delta\left(s-m_n^2\right)\langle 0|\eta|n\rangle\langle n|\bar\eta|0\rangle \\ &=f_{X}^{2}\delta(s-m_{X}^{2})+\cdots\, , \end{aligned} $

(11) in which the “pole plus continuum” parameterization assumption is adopted, and "
$ \cdots $ " contains contributions from the QCD continuum and higher excited states. The intermediate state$ |n\rangle $ can be either a positive or negative parity pentaquark. The parameters$ f_{X} $ and$ m_{X} $ are the coupling constant and hadron mass of the lowest-lying state, respectively.The two-point correlation function and spectral function can be evaluated as the functions of various QCD condensates via operator product expansion (OPE) at the quark-gluonic level. We use coordinate space expressions for the light quark and strange quark propagators [43]
$ \begin{aligned}[b] {\rm i} S^{ab}(x) = & \langle T\{q^a(x)\bar{q}^b(0)\}\rangle= \frac{{\rm i}\delta^{ab}}{2\pi^2x^4} +\frac{\rm i}{32\pi^2}t^n_{ab} g_s G^n_{\mu\nu}\frac{1}{x^2}(\sigma^{\mu\nu}\not {x} +\not {x}\sigma^{\mu\nu}) -\frac{\delta^{ab}}{12}\langle\bar{q}q\rangle +\frac{\delta^{ab}x^2}{192}\langle g_s \bar{q}\sigma Gq\rangle \\ & -\frac{{\rm i} g_s^2 \langle \bar {q}q\rangle^2x^2}{2^5\times 3^5}\delta^{ab}\not {x} - \frac{g_s^2\langle\bar{q}q\rangle\langle G^2\rangle x^4}{2^9\times3^3}\delta^{ab} -\frac{m_q\delta^{ab}}{4\pi^2x^2} +\frac{m_q}{16\pi^2}t^n_{ab}g_s G^n_{\mu\nu}\sigma^{\mu\nu}\log(-x^2) -\frac{\delta^{ab}\langle g_s^2G^2\rangle}{2^9\times3\pi^2}m_q x^2\log(-x^2) \\&+\frac{{\rm i}\delta^{ab}m_q\langle\bar{q}q\rangle}{48}\not {x} -\frac{{\rm i} m_q\langle g_s\bar{q}\sigma G q\rangle\delta^{ab}x^2}{2^7\times3^2}\not {x} - \frac{g_s^2 m_q\langle \bar{q}q\rangle^2}{2^7\times3^5}x^4\delta^{ab} +\cdots \end{aligned} $ 
(12) where
$ q=u, d, s $ quarks,$\not {x}=x^{\mu}\gamma_{\mu}$ , and$ t^n_{ab}=\lambda^n_{ab}/2 $ . In this study, we evaluate correlation functions and spectral functions up to dimension-11 condensates. As an example, we show the spectral function for the interpolating current$ \eta_1(x) $ as$ \begin{aligned}[b] \rho_1^q(s)= & \frac{s^5}{45875200 \pi ^7} -\frac{s^3 m_s \langle \bar{{s}} {s} \rangle }{40960 \pi ^5} +\frac{s^3 \langle g_s^2 G^2 \rangle }{1310720 \pi ^7} +\frac{g_s^2 s^2 \langle \bar{{u}} {u} \rangle ^2}{110592 \pi ^5} +\frac{g_s^2 s^2 \langle \bar{{s}} {s} \rangle ^2}{110592 \pi ^5} +\frac{g_s^2 s^2 \langle \bar{{d}} {d} \rangle ^2}{221184 \pi ^5} +\frac{s^2 \langle \bar{{s}} {s} \rangle ^2}{2048 \pi ^3} \\ & -\frac{415 s^2 m_s \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1572864 \pi ^5} +\frac{127 g_s^3 \langle \bar{{d}} {d} \rangle ^2 \langle g_s^2 G^2 \rangle }{31850496 \pi ^5} -\frac{g_s^2 m_s \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle }{6912 \pi ^3} -\frac{65 m_s \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{2359296 \pi ^5} \\ & -\frac{161 s m_s \langle \bar{{s}} {s} \rangle \langle g_s^2 G^2 \rangle }{2359296 \pi ^5} +\frac{161 \langle \bar{{s}} {s} \rangle ^2 \langle g_s^2 G^2 \rangle }{589824 \pi ^3} +\frac{65 g_s^3 \langle \bar{{s}} {s} \rangle ^2 \langle g_s^2 G^2 \rangle }{31850496 \pi ^5} +\frac{5 g_s^3 \langle \bar{{u}} {u} \rangle ^2 \langle g_s^2 G^2 \rangle }{663552 \pi ^5} +\frac{s \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{512 \pi ^3} \\ & +\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle ^2}{4096 \pi ^3} -\frac{g_s^2 m_s \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{3456 \pi ^3} +\frac{g_s^2 m_s \langle \bar{{s}} {s} \rangle ^3}{3456 \pi ^3}\, , \end{aligned} $ 
(13) $ \begin{aligned}[b] \rho_1^m(s) = & \frac{s^4 \langle \bar{{d}} {d} \rangle }{491520 \pi ^5} +\frac{s^2 \langle \bar{{d}} {d} \rangle \langle g_s^2 G^2 \rangle }{73728 \pi ^5} -\frac{s^2 m_s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{1536 \pi ^3} +\frac{s \langle g_s^2 G^2 \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{65536 \pi ^5} +\frac{g_s^2 s \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2}{10368 \pi ^3} +\frac{g_s^2 s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{10368 \pi ^3} \\ & -\frac{s m_s \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{768 \pi ^3} -\frac{m_s \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1024 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{192 \pi } +\frac{\langle \bar{{u}} {u} \rangle ^2 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{192 \pi } \\& +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{96 \pi } +\frac{\langle \bar{{d}} {d} \rangle \langle g_s^2 G^2 \rangle ^2}{1179648 \pi ^5} +\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^2 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{41472 \pi ^3} +\frac{s \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2}{96 \pi } +\frac{s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{192 \pi }\, , \end{aligned} $

(14) where
$ \rho^q(s)=\rm{Im}\Pi_q(s)/\pi $ and$ \rho^m(s)=\rm{Im}\Pi_m(s)/\pi $ are the spectral functions of the invariant structures$ \Pi_q(q^2) $ and$ \Pi_m(q^2) $ in Eqs. (7)–(8), respectively. Their dimensions are different because$ \Pi_q(q^2) $ is proportional to$\not {q}$ , whereas$ \Pi_m(q^2) $ is proportional to 1. As shown in Eqs. (13)–(14), there are more terms in$ \rho^q(s) $ than in$ \rho^m(s) $ , including the perturbative term. We use$ \rho^q(s) $ to perform our numerical analyses in the following section. The expressions for the spectral functions of other interpolating currents are given in Appendix A. Note that all the correlation functions in this study are evaluated at the leading order of$ \alpha_s $ . It is known that the$ \alpha_s $ corrections of the perturbative terms give important contributions for heavy quarkonium systems [35]; however, we do not consider the$ \alpha_s $ corrections here because of the complexity and difficulty of calculations. Nevertheless, the NLO effects in multiquark systems deserve to be studied, and we will attempt to conduct such research in the future.QCD sum rules can be established by assuming that the two-point correlation functions obtained from the hadronic and quark-gluonic levels are equal to each other. After applying the Borel transform, the correlation function can be written as
$ \begin{equation} \Pi(M_{\rm B}^2)\equiv\mathcal{B}_{M_{\rm B}^2}\Pi(q^2)=\int^{\infty}_{4m_s^2} {\rm d}s\,{\rm e}^{-s/M_{\rm B}^2}\rho(s)\, , \end{equation} $

(15) in which
$M_{\rm B}$ is the Borel parameter introduced by the Borel transform. It is clear that the Borel transform suppresses the contributions from the continuum and higher excited states in Eq. (11). The lowest-lying resonance is then chosen as$ \begin{equation} f^2_X {\rm e}^{-m^2_X/M_{\rm B}^2}=\int^{s_0}_{4m_s^2}{\rm d}s\,{\rm e}^{-s/M_{\rm B}^2}\rho(s)\, , \end{equation} $

(16) where
$ s_0 $ is the continuum threshold. The mass of the lowest-lying hadron can thus be extracted as$ m^2_X(s_0,M_{\rm B}^2)=\frac{\displaystyle\int^{s_0}_{4m_s^2}{\rm d}s\,{\rm e}^{-s/M_{\rm B}^2}s\rho(s)}{\displaystyle\int^{s_0}_{4m_s^2}{\rm d}s\,{\rm e}^{-s/M_{\rm B}^2}\rho(s)}, $

(17) which is a function of the two parameters
$M_{\rm B}^2$ and$ s_0 $ . We discuss the details in the next section to obtain suitable parameter working regions in the QCD sum rule analysis. -
To perform numerical analyses, we adopt parameter values for various QCD condensates and quark masses as follows [43–46]:
$ \langle \bar{u} u\rangle=\langle \bar{d} d\rangle=\langle \bar{q} q\rangle = - (0.24\pm0.01)^3 $ GeV$ ^3 $ ,$ \langle \bar{q} g_s\sigma G q\rangle = m_0^2\langle \bar{q} q\rangle $ ,$ m_0^2=-0.8 $ GeV$ ^2 $ ,$ \langle \bar{s} s\rangle = (0.8\pm0.1)\langle \bar{q} q\rangle $ ,$ \langle \bar{s} g_s\sigma G s\rangle = m_0^2\langle \bar{s} s\rangle $ ,$ \langle g_s^2GG\rangle = (0.44\pm0.02) $ GeV$ ^4 $ , and the$\rm\overline{MS}$ strange quark mass$ m_s = (0.095\pm0.005) $ GeV. We let$ m_u=m_d=m_q=0 $ ,$ \langle \bar{u} u\rangle=\langle \bar{d} d\rangle=\langle \bar{q} q\rangle $ , and$ \langle \bar{u} g_s\sigma\cdot G u\rangle=\langle \bar{d} g_s\sigma\cdot G d\rangle= \langle \bar{q} g_s\sigma\cdot G q\rangle $ for the up and down quarks in the chiral limit. The definition of the coupling constant$ g_s $ has a minus sign difference compared to that in Ref. [35].As shown in Eq. (17), the extracted hadron mass is a function of the Borel mass
$M_{\rm B}$ and continuum threshold$ s_0 $ . To choose suitable working windows for these two parameters, we must study the OPE convergence and pole contribution for the correlation function. On the one hand, the perturbative term should be two times larger than the nonperturbative contribution to ensure good OPE convergence, which will limit the lower bound on the Borel parameter$M_{\rm B}^2$ . On the other hand, we require the following pole contribution be larger than$ 10\% $ to give the upper bound on$M_{\rm B}^2$ $ \begin{equation} PC(s_0,M_{\rm B}^2)=\frac{\displaystyle\int^{s_0}_{4m_s^2}{\rm d}s\,{\rm e}^{-s/M_{\rm B}^2}\rho(s)}{\displaystyle\int^{\infty}_{4m_s^2}{\rm d}s\,{\rm e}^{-s/M_{\rm B}^2}\rho(s)}\, , \end{equation} $

(18) which is also the function of
$M_{\rm B}^2$ and$ s_0 $ . A proper value of$ s_0 $ is required before determining the Borel window.We take the interpolating current
$ \eta_4(x) $ as an example to present our numerical analysis of the hidden-strange$ \Sigma K $ pentaquark state. In Fig. 1, we plot the OPE behavior term by term with respect to$M_{\rm B}^2$ . It is shown that the most important nonperturbative contribution is from the$ \langle \bar{q}q\rangle^2 $ term. By requiring the perturbative term to be two times larger than the$ \langle \bar qq\rangle^2 $ term, we find the lower bound on the Borel parameter$M_{\min}^2 = 2.32$ GeV$ ^2 $ . To choose an optimum value of$ s_0 $ , we show the variation in the hadron mass with respect to$ s_0 $ at different values of the Borel mass in Fig. 2. The best choice of the threshold parameter is then fixed as$ s_0 = 8.35 $ GeV$ ^2 $ , around which the hadron mass is very stable against$M_{\rm B}^2$ .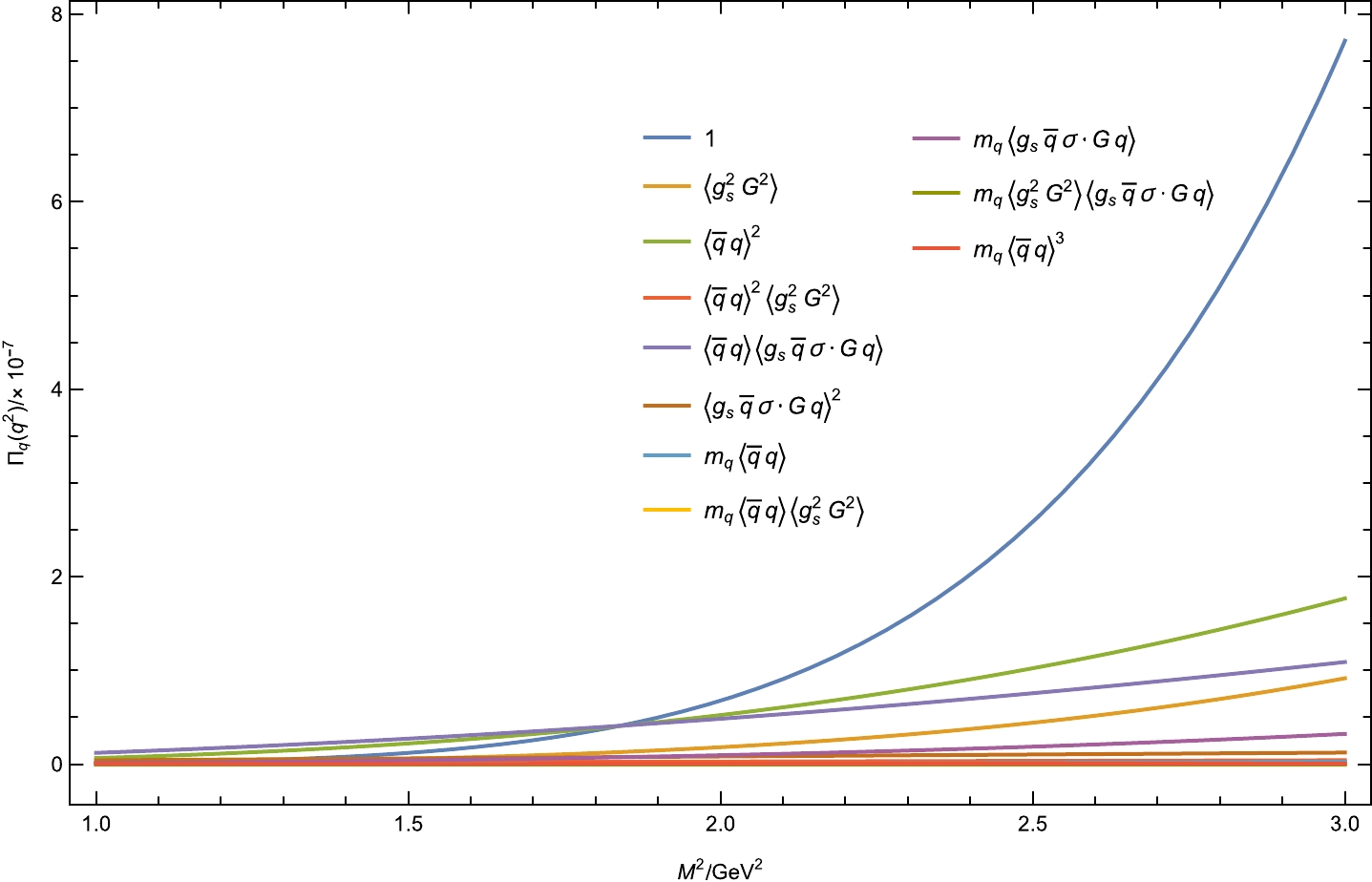
Figure 1. (color online) Contributions of each term in the OPE series for the interpolating current
$ \eta_4(x) $ with$J^P= {1}/{2}^-$ .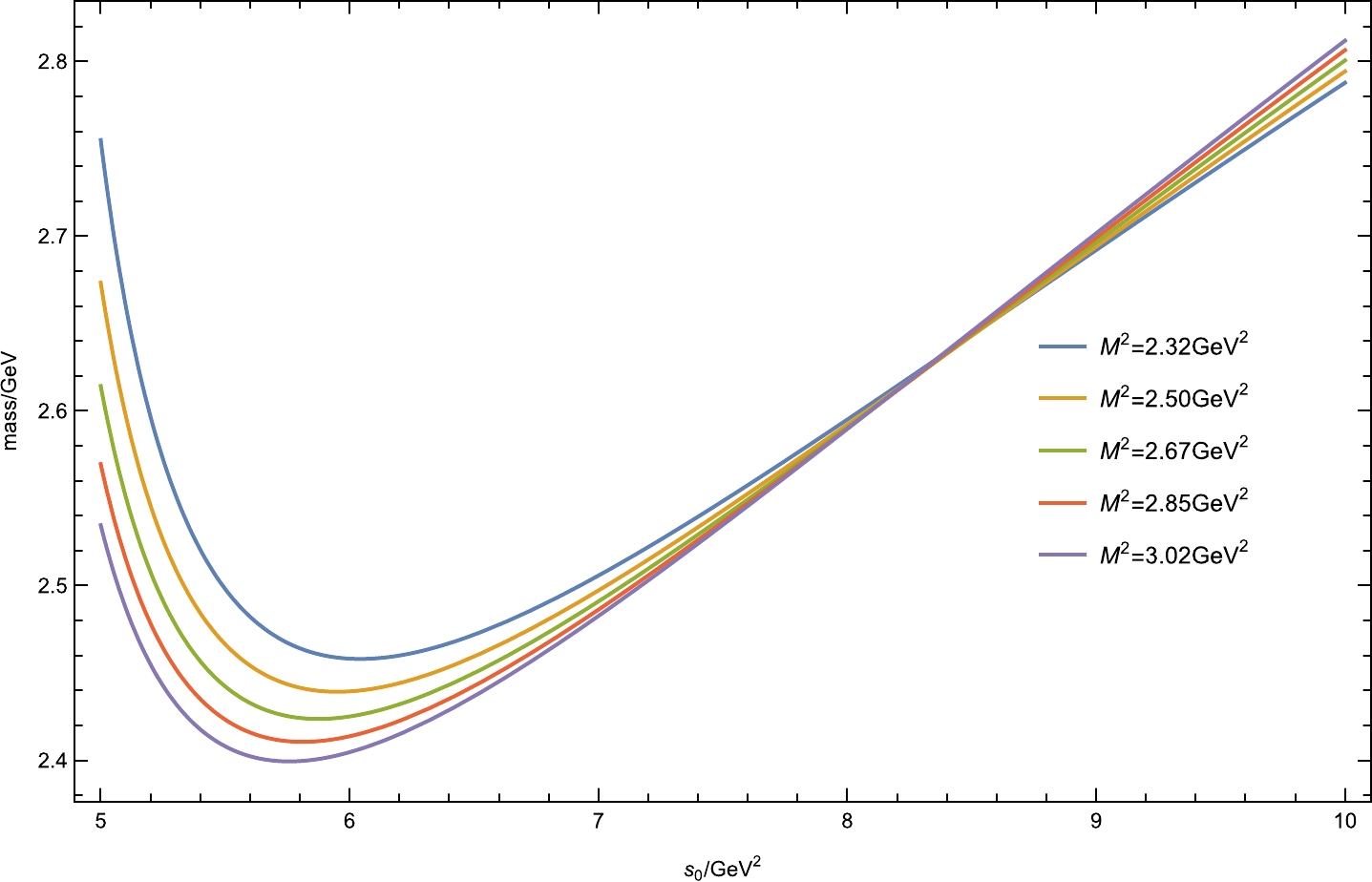
Figure 2. (color online) Hadron mass with respect to the threshold parameter
$ s_0 $ with different values of the Borel mass for$ \eta_4(x) $ .To determine the upper limit of
$M_{\rm B}^2$ , we study the pole contribution for$ s_0 = 8.35 $ GeV$ ^2 $ in Fig. 3. We find that the pole contribution is larger than$ 10\% $ for$M_{\rm B}^2\leq2.95$ GeV$ ^2 $ , which is the upper bound on the Borel window. Finally, we can study the behavior of the Borel curves in Fig. 4 using the parameter$ s_0 = 8.35 $ GeV$ ^2 $ and the Borel window$ 2.32 $ GeV$ ^2 $ $\leq M_{\rm B}^2\leq2.95$ GeV$ ^2 $ . We find that the mass curves are very stable with respect to$M_{\rm B}^2$ in the these parameter regions. The hadron mass for such a hidden-strange$ \Sigma K $ pentaquark with$J^P= {1}/{2}^-$ is extracted as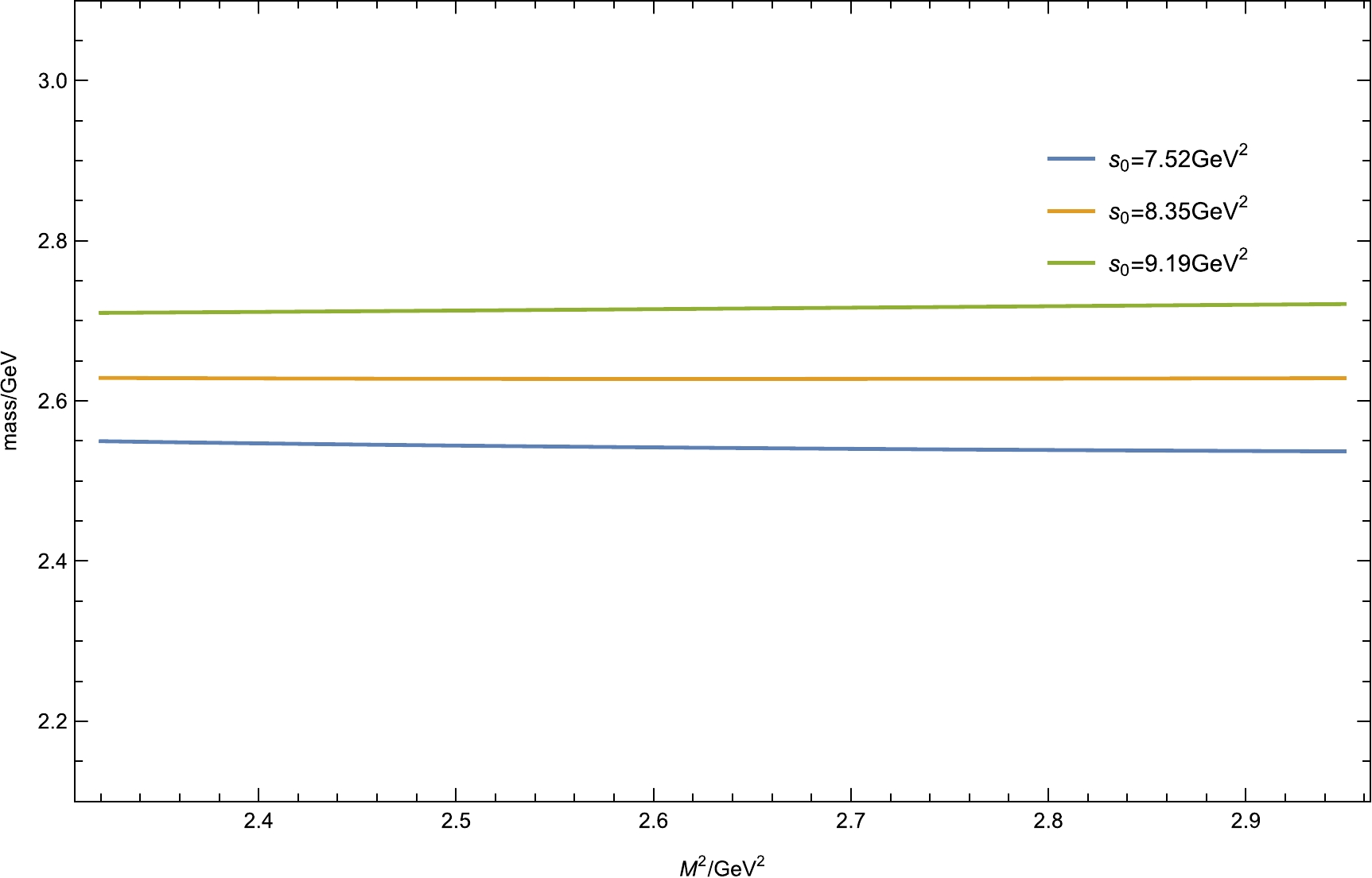
Figure 4. (color online) Variations in the hadron mass
$ m_X $ with respect to$M_{\rm B}^2$ for$ \eta_4(x) $ .$ \begin{equation} m_X=(2.63\pm 0.14\pm 0.13)\; \rm{GeV}\, , \end{equation} $

(19) in which the first error originates from the uncertainties in various input QCD parameters (mainly from the quark condensate), whereas the second error arises from the uncertainty in the threshold value
$ s_0 $ . For all other interpolating currents in Eq. (3), we perform analyses similar to the above procedure and obtain the hadron masses in Table 1. We find that the mass of the$ p\phi $ pentaquark is several MeV below the$ M_{p\phi} $ threshold. However, it is still considerably higher than the mass threshold of$ M_{\Sigma K} $ , which prevents the existence of such a$ p\phi $ pentaquark state with$J^P= {1}/{2}^-$ . Moreover, our results do not support the existence of bound states for the$ p\eta^\prime $ ,$ \Lambda K $ ,$ \Sigma K $ , and$ \Sigma^{\ast}K^{\ast} $ channels with$J^P={1}/{2}^-$ and$ \Sigma K^{\ast} $ and$ \Sigma^{\ast}K $ channels with$J^P= {3}/{2}^-$ because the obtained hadron masses are significantly higher than the corresponding two-hadron thresholds.Current Structure $ J^P $ 

$ m_X $ /GeV

Threshold $ s_0 $ /GeV

$ ^2 $ 

Borel window/GeV $ ^2 $ 

$ \eta_1(x) $ 

$ [p\eta^\prime] $ 

${1}/{2}^- $ 

$ 1.91\pm 0.06 \pm 0.19 $ 

4.77 2.35–2.48 $ \eta_2(x) $ 

$ [p\phi] $ 

$ {1}/{2}^- $ 

$ 1.95\pm 0.10 \pm 0.11 $ 

4.62 2.15–2.35 $ \eta_3(x) $ 

$ [\Lambda K] $ 

$ {1}/{2}^- $ 

$ 2.93\pm 0.16 \pm 0.20 $ 

10.57 2.10–3.51 $ \eta_4(x) $ 

$ [\Sigma K] $ 

$ {1}/{2}^- $ 

$ 2.63\pm 0.14 \pm 0.13 $ 

8.35 2.32–2.95 $ \eta_5(x) $ 

$ [\Sigma^\ast K^\ast] $ 

$ {1}/{2}^- $ 

$ 2.78\pm 0.08 \pm 0.12 $ 

9.60 2.47–3.32 $ \eta_{6\mu}(x) $ 

$ [\Sigma K^*] $ 

$ {3}/{2}^- $ 

$ 2.39\pm 0.08 \pm 0.11 $ 

6.95 2.47–3.32 $ \eta_{7\mu}(x) $ 

$ [\Sigma^* K] $ 

$ {3}/{2}^- $ 

$ 2.27\pm 0.10 \pm 0.10 $ 

5.82 3.06–3.62 Table 1. Extracted hadron masses of hidden-strange molecular pentaquark states with
$J^P= {1}/{2}^-$ and$J^P = {3}/{2}^-$ . -
Inspired by the observations of hidden-charm
$ P_c $ states, we investigate hidden-strange pentaquark states in both the$ [udu][\bar ss] $ and$ [uds][\bar su] $ configurations with quantum numbers$J^P= {1}/{2}^-$ and$J^P = {3}/{2}^-$ via the QCD sum rule method. We construct the corresponding interpolating currents using$ L=0 $ baryonic and mesonic operators. After calculating two-point correlation functions up to dimension-11, we perform mass sum rule analyses using the invariant structures proportional to$\not q$ and extract mass spectra for the$ p\eta^\prime $ ,$ p\phi $ ,$ \Lambda K $ ,$ \Sigma K $ , and$ \Sigma^\ast K^\ast $ pentaquarks with$J^P= {1}/{2}^-$ and$ \Sigma K^\ast $ and$ \Sigma^\ast K $ with$J^P= {3}/{2}^-$ .There is only a recombination of quarks before and after strong decay, in which all pentaquarks with
$J^P = {1}/{2}^-$ can decay into Σ and K. Our calculations show that the masses for all the$ p\eta^\prime $ ,$ p\phi $ ,$ \Lambda K $ ,$ \Sigma K $ , and$ \Sigma^\ast K^\ast $ pentaquarks are considerably higher than their two-hadron decay thresholds; hence, there is no bound hidden-strange pentaquark state in these channels.The states
$ \Sigma^\ast K $ and$ \Sigma K^\ast $ with$J^P = {3}/{2}^-$ can decay into the corresponding components$ \Sigma^{(\ast)} $ $ K^{(\ast)} $ . Our calculations show that these states also have masses higher than the mass thresholds of the corresponding components. Therefore, there is a no bound hidden-strange pentaquark state as well in such channels. This result is consistent with the experimental status of hidden-strange$ P_s $ states [33]. -
In this appendix, we show the spectral densities for the interpolating currents
$ \eta_2(x) $ ,$ \eta_3(x) $ ,$ \eta_4(x) $ , and$ \eta_5(x) $ , including both$ \rho_i^{q}(s) $ and$ \rho_i^{m}(s) $ structures proportional to$\not {q}$ and 1, respectively.$ \begin{aligned}[b]\\[-5pt] \rho_2^q= & \frac{s^5}{17203200 \pi ^7} +\frac{s^3 \langle g_s^2 G^2 \rangle }{983040 \pi ^7} +\frac{s^2 \langle \bar{{u}} {u} \rangle ^2}{1536 \pi ^3} +\frac{s^2 \langle \bar{{s}} {s} \rangle ^2}{1536 \pi ^3} -\frac{s^2 m_s \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{12288 \pi ^5} +\frac{g_s^2 s^2 \langle \bar{{u}} {u} \rangle ^2}{41472 \pi ^5} +\frac{g_s^2 s^2 \langle \bar{{s}} {s} \rangle ^2}{41472 \pi ^5} +\frac{g_s^2 s^2 \langle \bar{{d}} {d} \rangle ^2}{82944 \pi ^5} \\ & -\frac{s m_s \langle \bar{{s}} {s} \rangle \langle g_s^2 G^2 \rangle }{18432 \pi ^5} +\frac{s \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{384 \pi ^3} +\frac{s \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{768 \pi ^3} -\frac{m_s \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{24576 \pi ^5} +\frac{5 \langle \bar{{s}} {s} \rangle ^2 \langle g_s^2 G^2 \rangle }{9216 \pi ^3} \\& +\frac{\langle \bar{{u}} {u} \rangle ^2 \langle g_s^2 G^2 \rangle }{4608 \pi ^3} +\frac{g_s^3 \langle \bar{{s}} {s} \rangle ^2 \langle g_s^2 G^2 \rangle }{82944 \pi ^5} +\frac{g_s^3 \langle \bar{{u}} {u} \rangle ^2 \langle g_s^2 G^2 \rangle }{165888 \pi ^5} +\frac{g_s^2 m_s \langle \bar{{s}} {s} \rangle ^3}{1728 \pi ^3} +\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle ^2}{1024 \pi ^3}\, , \end{aligned}\tag{A1} $ 
$ \begin{aligned}[b] \rho_3^q= & \frac{11 s^5}{825753600 \pi ^7} +\frac{3 s^3 \langle g_s^2 G^2 \rangle }{5242880 \pi ^7} -\frac{s^3 m_s \langle \bar{{u}} {u} \rangle }{73728 \pi ^5} +\frac{11 s^3 m_s \langle \bar{{s}} {s} \rangle }{737280 \pi ^5} -\frac{s^2 \langle \bar{{u}} {u} \rangle ^2}{36864 \pi ^3} +\frac{5 s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{18432 \pi ^3} -\frac{13 s^2 m_s \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1179648 \pi ^5} \\ & -\frac{13 s^2 m_s \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{196608 \pi ^5} +\frac{11 g_s^2 s^2 \langle \bar{{u}} {u} \rangle ^2}{1990656 \pi ^5} +\frac{11 g_s^2 s^2 \langle \bar{{s}} {s} \rangle ^2}{1990656 \pi ^5} +\frac{11 g_s^2 s^2 \langle \bar{{d}} {d} \rangle ^2}{3981312 \pi ^5} -\frac{5 s m_s \langle \bar{{u}} {u} \rangle \langle g_s^2 G^2 \rangle }{110592 \pi ^5} \\ & +\frac{35 s m_s \langle \bar{{s}} {s} \rangle \langle g_s^2 G^2 \rangle }{589824 \pi ^5} +\frac{13 s \langle \bar{{u}} {u} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{18432 \pi ^3} +\frac{13 s \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{18432 \pi ^3} +\frac{s \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{18432 \pi ^3} +\frac{g_s^3 \langle \bar{{d}} {d} \rangle ^2 \langle g_s^2 G^2 \rangle }{442368 \pi ^5} \\ & -\frac{5 g_s^2 m_s \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle }{62208 \pi ^3} +\frac{11 g_s^2 m_s \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle }{124416 \pi ^3} +\frac{35 m_s \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1179648 \pi ^5} -\frac{5 m_s \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{196608 \pi ^5} \\ & +\frac{25 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle \langle g_s^2 G^2 \rangle }{110592 \pi ^3} -\frac{5 \langle \bar{{u}} {u} \rangle ^2 \langle g_s^2 G^2 \rangle }{221184 \pi ^3} +\frac{35 g_s^3 \langle \bar{{s}} {s} \rangle ^2 \langle g_s^2 G^2 \rangle }{7962624 \pi ^5} +\frac{7 g_s^3 \langle \bar{{u}} {u} \rangle ^2 \langle g_s^2 G^2 \rangle }{1990656 \pi ^5} +\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{1536 \pi ^3} \\ & +\frac{\langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2}{12288 \pi ^3} -\frac{5 g_s^2 m_s \langle \bar{{u}} {u} \rangle ^3}{62208 \pi ^3} +\frac{11 g_s^2 m_s \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{62208 \pi ^3} -\frac{5 g_s^2 m_s \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle }{124416 \pi ^3} +\frac{11 g_s^2 m_s \langle \bar{{s}} {s} \rangle ^3}{124416 \pi ^3} -\frac{m_s \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{1152 \pi } \\ & +\frac{5 m_s \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle }{1152 \pi }\, , \end{aligned}\tag{A2} $

$ \begin{aligned}[b] \rho_4^q= & \frac{11 s^5}{412876800 \pi ^7} +\frac{7 \langle g_s^2 G^2 \rangle s^3}{5898240 \pi ^7} +\frac{\langle \bar{{d}} {d} \rangle m_s s^3}{737280 \pi ^5} +\frac{11 \langle \bar{{s}} {s} \rangle m_s s^3}{368640 \pi ^5} -\frac{\langle \bar{{u}} {u} \rangle m_s s^3}{36864 \pi ^5} +\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 s^2}{1990656 \pi ^5} +\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^2 s^2}{995328 \pi ^5} \\ & -\frac{\langle \bar{{u}} {u} \rangle ^2 s^2}{18432 \pi ^3} +\frac{11 g_s^2 \langle \bar{{u}} {u} \rangle ^2 s^2}{995328 \pi ^5} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle s^2}{36864 \pi ^3} +\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle s^2}{18432 \pi ^3} +\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s^2}{9216 \pi ^3} +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s s^2}{131072 \pi ^5} \\ & -\frac{89 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s^2}{1179648 \pi ^5} -\frac{25 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s^2}{196608 \pi ^5} -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle s}{12288 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{12288 \pi ^3} +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{u}} {u} \rangle s}{6144 \pi ^3} \\ & +\frac{25 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle s}{18432 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{2048 \pi ^3} +\frac{25 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{18432 \pi ^3} +\frac{\langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{18432 \pi ^3} +\frac{13 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle m_s s}{884736 \pi ^5} \\ & +\frac{53 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle m_s s}{589824 \pi ^5} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle m_s s}{55296 \pi ^5} +\frac{5 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2}{884736 \pi ^5} +\frac{53 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2}{7962624 \pi ^5} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{110592 \pi ^3} \end{aligned} $

$ \begin{aligned}[b] \quad\quad & +\frac{35 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{3981312 \pi ^5} +\frac{\langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2}{8192 \pi ^3} -\frac{7 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{110592 \pi ^3} +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{24576 \pi ^3} +\frac{17 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle }{55296 \pi ^3} \\ & +\frac{25 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{55296 \pi ^3} +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{12288 \pi ^3} +\frac{5 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{4096 \pi ^3} +\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^3 m_s}{62208 \pi ^3} -\frac{5 g_s^2 \langle \bar{{u}} {u} \rangle ^3 m_s}{31104 \pi ^3} \\ & -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{2304 \pi } +\frac{g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{248832 \pi ^3} -\frac{11 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{1152 \pi } +\frac{g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{62208 \pi ^3} -\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{576 \pi } \\ & +\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{31104 \pi ^3} +\frac{ \langle g_s^2 G^2 \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s}{98304 \pi ^5} +\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle m_s}{62208 \pi ^3} +\frac{53 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{1179648 \pi ^5} \\ & -\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{31104 \pi ^3 }+\frac{5 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{576 \pi } -\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{62208 \pi ^3} +\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{576 \pi } -\frac{5 \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{98304 \pi ^5}\, , \end{aligned}\tag{A3} $

$ \begin{aligned}[b] \rho_5^q = & \frac{3 s^5}{11468800 \pi ^7} -\frac{ \langle g_s^2 G^2 \rangle s^3}{655360 \pi ^7} -\frac{3 \langle \bar{{d}} {d} \rangle m_s s^3}{20480 \pi ^5} +\frac{3 \langle \bar{{s}} {s} \rangle m_s s^3}{10240 \pi ^5} -\frac{\langle \bar{{u}} {u} \rangle m_s s^3}{5120 \pi ^5} +\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 s^2}{18432 \pi ^5} +\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 s^2}{9216 \pi ^5} \\ & +\frac{\langle \bar{{u}} {u} \rangle ^2 s^2}{512 \pi ^3} +\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^2 s^2}{9216 \pi ^5} +\frac{3 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle s^2}{1024 \pi ^3} +\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s^2}{256 \pi ^3} -\frac{9 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s s^2}{16384 \pi ^5} +\frac{7 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s^2}{8192 \pi ^5} -\frac{7 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s^2}{8192 \pi ^5} \\ & +\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle s}{512 \pi ^3} +\frac{3 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{512 \pi ^3} +\frac{7 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle s}{768 \pi ^3} +\frac{7 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{768 \pi ^3} +\frac{7 \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{768 \pi ^3} \\ & +\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle m_s s}{2048 \pi ^5} -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle m_s s}{6144 \pi ^5} +\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle m_s s}{2048 \pi ^5} -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2}{110592 \pi ^5} -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2}{82944 \pi ^5} \\ & -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{1536 \pi ^3} -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{165888 \pi ^5} +\frac{\langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2}{256 \pi ^3} -\frac{3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{2048 \pi ^3} +\frac{9 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{2048 \pi ^3} \\ & -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{768 \pi ^3} +\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{128 \pi ^3} +\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^3 m_s}{576 \pi ^3} -\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^3 m_s}{864 \pi ^3} +\frac{3 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{64 \pi } \\& -\frac{g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{2304 \pi ^3} -\frac{3 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{32 \pi } -\frac{g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{576 \pi ^3} +\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{16 \pi } +\frac{g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{288 \pi ^3} \\ & +\frac{15 \langle g_s^2 G^2 \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s}{32768 \pi ^5} +\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle m_s}{576 \pi ^3} -\frac{ \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{12288 \pi ^5} -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{864 \pi ^3} +\frac{\langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{16 \pi } \\ & -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{1728 \pi ^3} -\frac{3 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{8 \pi } +\frac{ \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{2048 \pi ^5}\, , \end{aligned} \tag{A4}$

$ \begin{aligned}[b] \rho_{6}^{q}= & \frac{31 s^5}{440401920 \pi ^7} -\frac{11 \langle g_s^2 G^2 \rangle s^3}{283115520 \pi ^7} +\frac{\langle \bar{{d}} {d} \rangle m_s s^3}{245760 \pi ^5} +\frac{37 \langle \bar{{s}} {s} \rangle m_s s^3}{491520 \pi ^5} -\frac{\langle \bar{{u}} {u} \rangle m_s s^3}{12288 \pi ^5} +\frac{89 g_s^2 \langle \bar{{d}} {d} \rangle ^2 s^2}{6635520 \pi ^5} +\frac{89 g_s^2 \langle \bar{{s}} {s} \rangle ^2 s^2}{3317760 \pi ^5} \\ & -\frac{3 \langle \bar{{u}} {u} \rangle ^2 s^2}{20480 \pi ^3} +\frac{89 g_s^2 \langle \bar{{u}} {u} \rangle ^2 s^2}{3317760 \pi ^5} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle s^2}{12288 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle s^2}{1536 \pi ^3} +\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s^2}{3072 \pi ^3} +\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s s^2}{131072 \pi ^5} \\ & +\frac{65 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s^2}{393216 \pi ^5} -\frac{25 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s^2}{65536 \pi ^5} -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle s}{4096 \pi ^3} -\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{4608 \pi ^3} +\frac{13 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{u}} {u} \rangle s}{24576 \pi ^3} \\& +\frac{113 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle s}{36864 \pi ^3} +\frac{17 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{24576 \pi ^3} +\frac{25 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{6144 \pi ^3} -\frac{25 \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{36864 \pi ^3} \\ & +\frac{13 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle m_s s}{294912 \pi ^5} -\frac{19 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle m_s s}{589824 \pi ^5} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle m_s s}{18432 \pi ^5} -\frac{59 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2}{11943936 \pi ^5} -\frac{25 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2}{7962624 \pi ^5} \\ & -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{73728 \pi ^3} +\frac{13 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{5971968 \pi ^5} -\frac{11 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2}{36864 \pi ^3} -\frac{7 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{36864 \pi ^3} -\frac{5 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{24576 \pi ^3} \end{aligned}$

$ \begin{aligned}[b] \quad\quad & -\frac{\langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle }{4608 \pi ^3} +\frac{25 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{18432 \pi ^3} -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{36864 \pi ^3} +\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{1024 \pi ^3} \\ & +\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^3 m_s}{13824 \pi ^3} -\frac{5 g_s^2 \langle \bar{{u}} {u} \rangle ^3 m_s}{10368 \pi ^3} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{768 \pi } +\frac{g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{82944 \pi ^3} -\frac{11 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{384 \pi } +\frac{g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{20736 \pi ^3} \\ & -\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{1152 \pi } +\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{6912 \pi ^3} +\frac{\langle g_s^2 G^2 \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s}{32768 \pi ^5} +\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle m_s}{13824 \pi ^3} \\& -\frac{25 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{1179648 \pi ^5} -\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{10368 \pi ^3} +\frac{5 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{192 \pi } -\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{20736 \pi ^3} +\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{288 \pi } \\ & -\frac{5 \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{32768 \pi ^5} \, , \end{aligned}\tag{A5} $

$ \begin{aligned}[b] \rho^q_{7} =& \frac{3 s^5}{18350080 \pi ^7} +\frac{19 \langle g_s^2 G^2 \rangle s^3}{7864320 \pi ^7} -\frac{7 \langle \bar{{d}} {d} \rangle m_s s^3}{40960 \pi ^5} +\frac{7 \langle \bar{{s}} {s} \rangle m_s s^3}{40960 \pi ^5} -\frac{\langle \bar{{u}} {u} \rangle m_s s^3}{4096 \pi ^5} +\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 s^2}{368640 \pi ^5} +\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^2 s^2}{184320 \pi ^5} \\ & +\frac{5 \langle \bar{{u}} {u} \rangle ^2 s^2}{2048 \pi ^3} +\frac{11 g_s^2 \langle \bar{{u}} {u} \rangle ^2 s^2}{184320 \pi ^5} +\frac{33 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle s^2}{10240 \pi ^3}+\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s^2}{1024 \pi ^3} -\frac{99 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s s^2}{163840 \pi ^5} +\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s^2}{81920 \pi ^5} \\ & -\frac{35 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s^2}{32768 \pi ^5} +\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle s}{512 \pi ^3} +\frac{3 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{512 \pi ^3} +\frac{35 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle s}{3072 \pi ^3} \\ & +\frac{35 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{3072 \pi ^3} +\frac{35 \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{3072 \pi ^3} +\frac{3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle m_s s}{8192 \pi ^5} +\frac{\langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle m_s s}{24576 \pi ^5} -\frac{35 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle m_s s}{24576 \pi ^5} \\ & -\frac{25 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2}{1327104 \pi ^5} -\frac{5 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2}{1990656 \pi ^5} +\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{1536 \pi ^3} +\frac{65 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2}{1990656 \pi ^5} +\frac{5 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2}{1024 \pi ^3} \\ & -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{4096 \pi ^3} +\frac{15 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{4096 \pi ^3} +\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{768 \pi ^3} +\frac{5 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{512 \pi ^3} \\ & +\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^3 m_s}{6912 \pi ^3} -\frac{5 g_s^2 \langle \bar{{u}} {u} \rangle ^3 m_s}{3456 \pi ^3} +\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{128 \pi } -\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{13824 \pi ^3} \\ & -\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{64 \pi } -\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{3456 \pi ^3} +\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{64 \pi } +\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{3456 \pi ^3} +\frac{25 \langle g_s^2 G^2 \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle m_s}{65536 \pi ^5} \\ & +\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle m_s}{6912 \pi ^3} -\frac{5 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{294912 \pi ^5} -\frac{5 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{3456 \pi ^3} +\frac{5 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{64 \pi } -\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle m_s}{6912 \pi ^3} \\& -\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{16 \pi } -\frac{15 \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{16384 \pi ^5} \, . \end{aligned}\tag{A6} $

The spectral densities
$ \rho_i^{m} $ are$ \begin{aligned}[b] \rho_2^m = & \frac{s^4 \langle \bar{{d}} {d} \rangle }{245760 \pi ^5} -\frac{s^2 m_s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{256 \pi ^3} -\frac{s^2 \langle \bar{{d}} {d} \rangle \langle g_s^2 G^2 \rangle }{18432 \pi ^5} +\frac{s \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2}{48 \pi } +\frac{s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{48 \pi } -\frac{3 s \langle g_s^2 G^2 \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{32768 \pi ^5} \\ & -\frac{5 s m_s \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{768 \pi ^3} +\frac{g_s^2 s \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle ^2}{5184 \pi ^3} +\frac{g_s^2 s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{5184 \pi ^3} +\frac{m_s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s^2 G^2 \rangle }{4608 \pi ^3} -\frac{\langle \bar{{d}} {d} \rangle \langle g_s^2 G^2 \rangle ^2}{196608 \pi ^5} \\ & +\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^2 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{20736 \pi ^3} +\frac{m_s \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{512 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{48 \pi } +\frac{\langle \bar{{u}} {u} \rangle ^2 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{96 \pi } \\ & +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{48 \pi }\, , \end{aligned}\tag{A7} $

$ \begin{aligned}[b] \rho_3^m= & \frac{5 s^2 m_s \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle }{4608 \pi ^3} -\frac{s^2 m_s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle }{4608 \pi ^3} -\frac{5 s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{576 \pi } +\frac{s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{1152 \pi } \frac{5 m_s \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle \langle g_s^2 G^2 \rangle }{6912 \pi ^3} \\ & -\frac{m_s \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s^2 G^2 \rangle }{6912 \pi ^3} +\frac{m_s \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{6144 \pi ^3} +\frac{s m_s \langle \bar{{u}} {u} \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{512 \pi ^3} +\frac{7 s m_s \langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{3072 \pi ^3} \\ & +\frac{m_s \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{768 \pi ^3} -\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle }{192 \pi } -\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1152 \pi } -\frac{7 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{1152 \pi }\, , \end{aligned} \tag{A8}$

$ \begin{aligned}[b] \rho_4^m= & \frac{11 m_s s^5}{117964800 \pi ^7} -\frac{11 \langle \bar{{s}} {s} \rangle s^4}{2949120 \pi ^5} -\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s^3}{589824 \pi ^5} +\frac{ \langle g_s^2 G^2 \rangle m_s s^3}{1048576 \pi ^7} -\frac{19 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle s^2}{884736 \pi ^5} \\& +\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 m_s s^2}{995328 \pi ^5}-\frac{11 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{18432 \pi ^3} +\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{1990656 \pi ^5}-\frac{\langle \bar{{u}} {u} \rangle ^2 m_s s^2}{9216 \pi ^3} +\frac{11 g_s^2 \langle \bar{{u}} {u} \rangle ^2 m_s s^2}{497664 \pi ^5} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s s^2}{2304 \pi ^3} \\ & +\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{2304 \pi ^3} +\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{2304 \pi ^3} -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^3 s}{124416 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 s}{576 \pi } +\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{1152 \pi } -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{62208 \pi ^3} \\ & -\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle s}{124416 \pi ^3} -\frac{3 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{131072 \pi ^5} -\frac{5 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle s}{576 \pi } -\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s}{288 \pi } -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle m_s s}{1536 \pi ^3} \\ & +\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{6144 \pi ^3} -\frac{47 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{73728 \pi ^3} +\frac{5 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{u}} {u} \rangle m_s s}{1536 \pi ^3} +\frac{11 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle m_s s}{6144 \pi ^3} \\ & +\frac{7 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{1536 \pi ^3} +\frac{11 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{3072 \pi ^3} -\frac{\langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{6144 \pi ^3} +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{1152 \pi } \\ & -\frac{7 g_s^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{248832 \pi ^3} -\frac{ \langle g_s^2 G^2 \rangle ^2 \langle \bar{{s}} {s} \rangle }{786432 \pi ^5} -\frac{13 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{497664 \pi ^3} -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{497664 \pi ^3} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{2304 \pi } \\ & -\frac{5 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{576 \pi } -\frac{11 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle }{1152 \pi } -\frac{11 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle }{2304 \pi } -\frac{11 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{2304 \pi } \\& -\frac{7 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{576 \pi } +\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{2304 \pi } +\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2 m_s}{221184 \pi ^5} +\frac{25 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{221184 \pi ^3} \\& -\frac{11 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{2654208 \pi ^5} +\frac{31 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle ^2 m_s}{36864 \pi ^3} +\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{110592 \pi ^3} +\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{331776 \pi ^5} -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s}{3456 \pi ^3} \\ & +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{12288 \pi ^3} +\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s}{3456 \pi ^3} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{27648 \pi ^3} +\frac{7 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{3072 \pi ^3} \\ & +\frac{13 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{12288 \pi ^3}\, , \end{aligned}\tag{A9} $

$ \begin{aligned}[b] \rho_5^m= & \frac{3 m_s s^5}{3276800 \pi ^7} -\frac{3 \langle \bar{{s}} {s} \rangle s^4}{81920 \pi ^5} -\frac{3 \langle \bar{{u}} {u} \rangle s^4}{40960 \pi ^5} -\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s^3}{4096 \pi ^5} -\frac{\langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s^3}{2048 \pi ^5} -\frac{ \langle g_s^2 G^2 \rangle m_s s^3}{262144 \pi ^7} +\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 m_s s^2}{9216 \pi ^5} \\ & -\frac{3 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{512 \pi ^3} +\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{18432 \pi ^5} +\frac{3 \langle \bar{{u}} {u} \rangle ^2 m_s s^2}{256 \pi ^3} +\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^2 m_s s^2}{4608 \pi ^5} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s s^2}{64 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{64 \pi ^3} \\& -\frac{3 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{128 \pi ^3} -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^3 s}{1152 \pi ^3} -\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^3 s}{576 \pi ^3} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 s}{16 \pi } -\frac{3 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{32 \pi } -\frac{g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{576 \pi ^3} -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle s}{1152 \pi ^3} \\ & +\frac{3 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{32768 \pi ^5} -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle s}{576 \pi ^3} -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle s}{288 \pi ^3} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s}{8 \pi } +\frac{3 \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{16384 \pi ^5} \\ & +\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle m_s s}{128 \pi ^3} +\frac{7 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{256 \pi ^3} -\frac{9 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{512 \pi ^3} +\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{u}} {u} \rangle m_s s}{128 \pi ^3} \end{aligned}$

$ \begin{aligned}[b] \quad\quad & -\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle m_s s}{128 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{32 \pi ^3} -\frac{45 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{1024 \pi ^3} +\frac{9 \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{256 \pi ^3} \\ & -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{32 \pi } -\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{64 \pi } -\frac{7 g_s^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{6912 \pi ^3} +\frac{ \langle g_s^2 G^2 \rangle ^2 \langle \bar{{s}} {s} \rangle }{196608 \pi ^5} -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1728 \pi ^3} \\ & -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{1728 \pi ^3} -\frac{7 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{96 \pi } +\frac{ \langle g_s^2 G^2 \rangle ^2 \langle \bar{{u}} {u} \rangle }{98304 \pi ^5} -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{16 \pi } \\ & -\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle }{16 \pi } -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{864 \pi ^3} -\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{2304 \pi ^3} -\frac{7 g_s^2 \langle \bar{{u}} {u} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{6912 \pi ^3} \\ & -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{12 \pi } -\frac{3 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{32 \pi } -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2 m_s}{331776 \pi ^5} -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{3072 \pi ^3} \\ & +\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{663552 \pi ^5} -\frac{5 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle ^2 m_s}{1024 \pi ^3} -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{256 \pi ^3} -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{82944 \pi ^5} +\frac{9 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2 m_s}{1024 \pi ^3} \\ & -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s}{768 \pi ^3} +\frac{7 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{512 \pi ^3} -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s}{768 \pi ^3} -\frac{ \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{1024 \pi ^3} \\ &+\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{64 \pi ^3} -\frac{9 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{512 \pi ^3}\, . \end{aligned} \tag{A10}$

$ \begin{aligned}[b] \rho_{6}^m = & \frac{11 m_s s^5}{45875200 \pi ^7} -\frac{11 \langle \bar{{s}} {s} \rangle s^4}{1179648 \pi ^5} -\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s^3}{983040 \pi ^5} -\frac{3 \langle g_s^2 G^2 \rangle m_s s^3}{524288 \pi ^7} +\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle s^2}{65536 \pi ^5} +\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 m_s s^2}{442368 \pi ^5} \\& -\frac{11 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{8192 \pi ^3} +\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{884736 \pi ^5} -\frac{\langle \bar{{u}} {u} \rangle ^2 m_s s^2}{4096 \pi ^3} +\frac{11 g_s^2 \langle \bar{{u}} {u} \rangle ^2 m_s s^2}{221184 \pi ^5} -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s s^2}{768 \pi ^3} +\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{1024 \pi ^3} \\ & +\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{768 \pi ^3} -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^3 s}{62208 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 s}{192 \pi } +\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{576 \pi } -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{31104 \pi ^3} -\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle s}{62208 \pi ^3} \\ & +\frac{13 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{98304 \pi ^5} -\frac{5 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle s}{192 \pi } -\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s}{144 \pi } -\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle m_s s}{512 \pi ^3} \\ & -\frac{31 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{18432 \pi ^3} -\frac{47 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{36864 \pi ^3} +\frac{5 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{u}} {u} \rangle m_s s}{768 \pi ^3} +\frac{89 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle m_s s}{18432 \pi ^3} \\ & +\frac{\langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{144 \pi ^3} +\frac{11 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{1024 \pi ^3} -\frac{13 \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{9216 \pi ^3} +\frac{\langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{384 \pi } \\ & +\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{1536 \pi } -\frac{5 g_s^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{165888 \pi ^3} +\frac{11 \langle g_s^2 G^2 \rangle ^2 \langle \bar{{s}} {s} \rangle }{1572864 \pi ^5} -\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{331776 \pi ^3} -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{331776 \pi ^3} \\ & +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{256 \pi } -\frac{5 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{384 \pi } -\frac{5 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle }{384 \pi } -\frac{5 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle }{384 \pi } \\ & -\frac{11 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{768 \pi } -\frac{5 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{384 \pi } +\frac{5 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{1536 \pi } -\frac{11 g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2 m_s}{1327104 \pi ^5} \\ & +\frac{25 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{147456 \pi ^3} +\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{589824 \pi ^5} -\frac{\langle g_s \bar{{s}} \sigma \cdot G {s} \rangle ^2 m_s}{768 \pi ^3} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{73728 \pi ^3} -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{82944 \pi ^5} \\& -\frac{\langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2 m_s}{2048 \pi ^3} -\frac{\langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s}{1152 \pi ^3} -\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{4096 \pi ^3} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s}{4608 \pi ^3} \\& -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{9216 \pi ^3} +\frac{5 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{2048 \pi ^3} +\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{1024 \pi ^3} \, , \end{aligned} \tag{A11}$

$ \begin{aligned}[b] \rho_7^m = & \frac{31 m_s s^5}{45875200 \pi ^7} -\frac{13 \langle \bar{{s}} {s} \rangle s^4}{491520 \pi ^5} -\frac{13 \langle \bar{{u}} {u} \rangle s^4}{245760 \pi ^5} -\frac{7 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s^3}{40960 \pi ^5} -\frac{7 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s^3}{20480 \pi ^5} +\frac{29 \langle g_s^2 G^2 \rangle m_s s^3}{2621440 \pi ^7} \\ & -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle s^2}{24576 \pi ^5} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle s^2}{12288 \pi ^5} +\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 m_s s^2}{13824 \pi ^5} -\frac{\langle \bar{{s}} {s} \rangle ^2 m_s s^2}{256 \pi ^3} +\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 m_s s^2}{27648 \pi ^5} +\frac{9 \langle \bar{{u}} {u} \rangle ^2 m_s s^2}{512 \pi ^3} \\& +\frac{g_s^2 \langle \bar{{u}} {u} \rangle ^2 m_s s^2}{6912 \pi ^5} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s s^2}{64 \pi ^3} +\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{64 \pi ^3} -\frac{\langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s s^2}{64 \pi ^3} -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^3 s}{20736 \pi ^3} -\frac{11 g_s^2 \langle \bar{{u}} {u} \rangle ^3 s}{10368 \pi ^3} \\ & -\frac{11 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle ^2 s}{192 \pi } -\frac{9 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{64 \pi } -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle ^2 s}{10368 \pi ^3} -\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{s}} {s} \rangle s}{20736 \pi ^3} -\frac{41 \langle g_s^2 G^2 \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle s}{196608 \pi ^5} \\ & -\frac{11 g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle \bar{{u}} {u} \rangle s}{10368 \pi ^3} -\frac{11 g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle \bar{{u}} {u} \rangle s}{5184 \pi ^3} -\frac{11 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle s}{96 \pi } -\frac{41 \langle g_s^2 G^2 \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle s}{98304 \pi ^5} \\ & +\frac{11 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle m_s s}{512 \pi ^3} +\frac{77 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{3072 \pi ^3} -\frac{11 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s s}{1024 \pi ^3} +\frac{11 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{u}} {u} \rangle m_s s}{512 \pi ^3} \\ & -\frac{11 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle m_s s}{768 \pi ^3} +\frac{11 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{384 \pi ^3} -\frac{55 \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{2048 \pi ^3} +\frac{27 \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s s}{512 \pi ^3} \\ & -\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle ^2}{128 \pi } -\frac{9 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{128 \pi } -\frac{7 g_s^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle ^2}{13824 \pi ^3} -\frac{\langle g_s^2 G^2 \rangle ^2 \langle \bar{{s}} {s} \rangle }{131072 \pi ^5} -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{3456 \pi ^3} \\ & -\frac{g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{3456 \pi ^3} -\frac{7 \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle }{128 \pi } -\frac{\langle g_s^2 G^2 \rangle ^2 \langle \bar{{u}} {u} \rangle }{65536 \pi ^5} -\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle }{64 \pi } \\ & -\frac{3 \langle \bar{{d}} {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle \bar{{u}} {u} \rangle }{64 \pi } -\frac{g_s^2 \langle \bar{{d}} {d} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{1728 \pi ^3} -\frac{5 g_s^2 \langle \bar{{s}} {s} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{4608 \pi ^3} -\frac{7 g_s^2 \langle \bar{{u}} {u} \rangle ^2 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{13824 \pi ^3} \\& -\frac{\langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{16 \pi } -\frac{9 \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle }{64 \pi } -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle ^2 m_s}{73728 \pi ^5} +\frac{\langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{2048 \pi ^3} \\ & -\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle ^2 m_s}{49152 \pi ^5} +\frac{5 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle ^2 m_s}{2048 \pi ^3} +\frac{3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{256 \pi ^3} +\frac{g_s^3 \langle g_s^2 G^2 \rangle \langle \bar{{u}} {u} \rangle ^2 m_s}{18432 \pi ^5} +\frac{27 \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle ^2 m_s}{2048 \pi ^3} \\& -\frac{\langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{s}} {s} \rangle m_s}{1024 \pi ^3} +\frac{21 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle m_s}{2048 \pi ^3} -\frac{\langle g_s^2 G^2 \rangle \langle \bar{{d}} {d} \rangle \langle \bar{{u}} {u} \rangle m_s}{1024 \pi ^3} -\frac{5 \langle g_s^2 G^2 \rangle \langle \bar{{s}} {s} \rangle \langle \bar{{u}} {u} \rangle m_s}{2048 \pi ^3} \\ & +\frac{3 \langle g_s \bar{{d}} \sigma \cdot G {d} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{256 \pi ^3} -\frac{3 \langle g_s \bar{{s}} \sigma \cdot G {s} \rangle \langle g_s \bar{{u}} \sigma \cdot G {u} \rangle m_s}{1024 \pi ^3} \, . \end{aligned}\tag{A12} $

QCD sum rule study for hidden-strange pentaquarks
- Received Date: 2022-08-03
- Available Online: 2023-01-15
Abstract: Inspired by the LHCb observations of hidden-charm






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: