-
The study of heavy baryons containing two heavy charm or bottom quarks has attracted attention during the last few years. In 2002, the lightest flavored charm-charm baryon was observed by the SELEX Collaboration in the analysis of decay modes
$ \Xi ^{+}_{cc} \rightarrow \Lambda _{c}^{+} K^{-}\pi ^{+} $ and$ \Xi ^{+}_{cc} \rightarrow \rho D^+ K^{-} $ [1, 2]. They reported$ M_{\Xi ^{++}_{cc}}=3518\pm1.7 $ MeV. It was the first observation of double heavy baryons. Later, the LHCb collaboration reported the new mass values of the$ \Xi ^{++}_{cc} $ state as$ 3621.40\pm0.72\pm0.14\pm0.27 $ MeV and$3620.6\pm1.5\pm0.4\pm 0.3$ MeV on different decay modes [3, 4]. Such important observations undoubtedly promote the investigation on the hadron spectroscopy and also on the weak decays of double heavy baryons. The beauty-charmed and double-beauty baryons are different types of doubly heavy baryons. Considering that the doubly heavy baryon states can be generated at the LHC or future high luminosity$ e^+e^- $ colliders, proposing theoretical studies on this subject is important.A detailed understanding of semileptonic transitions necessitates an understanding of the interesting interplay between the weak and the strong interactions. The transition form factors and exclusive decay rates provide information about the heavy baryon structures and also provide another opportunity to measure the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements. There are different theoretical [5–11] and experimental [12–16] achievements on semileptonic decays of single heavy baryons. However, for doubly heavy baryons, no experimental data are reported and only a limited number of theoretical calculations are available.
Some theoretical explanations are proposed to analyze the semileptonic weak decays of double heavy baryons based on the QCD sum rules (QCDSR) [17, 18], covariant confined quark model [19], Bethe-Salpeter equation [20], heavy quark spin symmetry (HQSS) [21], relativistic quark model (RQM) [22], non-relativistic quark model (NRQM) [23, 24], light-front quark model (LFQM) [25], and heavy diquark effective theory (HDET) [26]. However, the studies on semileptonic decays presented by the different approaches lead to essentially different values for the decay rates.
We aim to give a description of doubly heavy baryon properties within the non-relativistic hypercentral quark model. First, we calculate the mass spectra and magnetic moments of the ground-state Ω and Ξ baryons containing two heavy quarks (bottom or charm). Then, we study the semileptonic decays of doubly heavy baryons for specific decay modes and focus on the studies of exclusive
$ b\rightarrow c $ semileptonic decays of doubly heavy$ \Omega(J=1/2) $ and$ \Xi(J=1/2) $ baryons. We proceed with our model close to the zero recoil point in which all the weak transition form factors between double heavy baryons can be expressed through a single universal function$ \eta(\omega) $ [27]. Introducing a phenomenological potential model, we calculate the mass spectra and magnetic moments of double heavy baryons, and then, using the obtained results, we report our numerical results for the semileptonic decay widths of doubly heavy Ω and Ξ baryons.Many studies have presented various methods to solve the Schrödinger equation of the three-body baryonic system, which are mostly long and complicated. The purpose of the present study is to simplify the solution of the three-body problem using the hypercentral approach and calculate the semileptonic decay widths in the limit
$ m_b, m_c\gg\Lambda_{QCD} $ to reduce the independent number of form factors and evaluate the decay widths in a simple way.Our paper is structured as follows. We introduce our phenomenological potential model in Sec. II and simplify the three-body problem of the baryonic system using the hypercentral approach. In Secs. III and IV, we present our predictions for the ground-state masses and magnetic moments of doubly heavy baryons, respectively. In Sec. V, we simplify the transition form factors in the heavy quark limit and introduce an Isgur-Wise (IW) function to evaluate the semileptonic decay rates and branching ratios of doubly heavy baryons for
$ b\rightarrow c $ transitions. We also calculate the averaged values of asymmetry parameters. Section 6 presents our conclusions. -
To obtain the heavy baryon masses, we need to calculate the energy eigenvalues and also the eigenfunctions of the baryon states. We study the doubly heavy baryons and therefore, the non-relativistic formalism is an appropriate method. We consider the baryon system as a bound state of three constituent quarks. Using the hypercentral constituent quark model [28, 29], we can simplify the three-body problem of the baryon states. After removal of the center of mass coordinates, R, the configurations of the three quarks can be described by the Jacoobi coordinates, ρ and λ,
$ \vec{\rho} = \frac{1}{\sqrt{2}}(\vec{r_1} - \vec{r_2}), \qquad \vec{\lambda} = \frac{1}{\sqrt{6}}(\vec{r_1} + \vec{r_2} - 2 \vec{r_3})$

(1) such that
$ m_{\rho} = \frac{2 m_1 m_2}{m_1 + m_2}, \qquad m_{\lambda} = \frac{3 m_3 (m_1 + m_2)}{2 (m_1 + m_2 + m_3)} $

(2) Here,
$ m_1 $ ,$ m_2 $ , and$ m_3 $ are the constituent quark masses. Instead of ρ and λ, one can introduce the hyperspherical coordinates, which are given by the angles$ \Omega_{\rho}=(\theta_{\rho},\phi_{\rho}) $ and$ \Omega_{\lambda}=(\theta_{\lambda},\phi_{\lambda}) $ together with the hyperradius x and the hyperangle ζ defined in terms of the absolute values of ρ and λ by$ x = \sqrt{\rho^2 + \lambda^2}, \qquad \xi = \arctan \left(\sqrt{\frac{\rho}{\lambda}}\right). $

(3) Therefore, the Hamiltonian of three-body system is given by
$ H=\frac{p^{2}_{\rho}}{2m_{\rho}}+\frac{p^{2}_{\lambda}}{2m_{\lambda}}+V(x). $

(4) and the kinetic energy operator takes the form (
$ \hbar=c=1 $ )$ -\left(\dfrac{\Delta_{\rho}}{2m_{\rho}}+\dfrac{\Delta_{\lambda}}{2m_{\lambda}}\right)=-\dfrac{1}{2\mu}\left(\frac{{\rm d}^{2}}{{\rm d}x^{2}}+\frac{5}{x}\frac{\rm d}{{\rm d}x}-\frac{L^{2}(\Omega_{\rho},\Omega_{\lambda},\xi)}{x^{2}}\right), $

(5) where μ is the reduced mass
$ \begin{array}{*{20}{l}} \mu=\dfrac{2m_{\rho}m_{\lambda}}{m_{\rho}+m_{\lambda}}, \end{array} $

(6) and
$ \Omega_{\rho} $ and$ \Omega_{\lambda} $ are the angles of the hyperspherical coordinates. In the hypercentral approach, the three-quark interaction is assumed to be hypercentral, that is, the energy of the system depends only on the distance of quarks x.The eigenfuctions of
$ L^{2} $ are hyperspherical harmonics$ \begin{array}{*{20}{l}} L^{2}(\Omega_{\rho},\Omega_{\lambda},\xi)Y_{[\gamma],l_{\rho},l_{\lambda}}(\Omega_{\rho},\Omega_{\lambda},\xi)=\gamma(\gamma+1)Y_{[\gamma],l_{\rho},l_{\lambda}}(\Omega_{\rho},\Omega_{\lambda},\xi), \end{array} $

(7) where γ is the grand angular quantum number given by
$ \gamma=2n+l_\rho+l_\lambda $ ;$ l_\rho $ and$ l_\lambda $ are the angular momenta associated with the ρ and λ variables, and n is a non-negative integer number. The wave function of any system containing three particles can be expanded in the hyperspherical harmonic basis:$ \Psi(\rho,\lambda)=\Sigma_{\gamma,l_{\rho},l_{\lambda}} N_{\gamma}\psi_{\nu,\gamma}(x)Y_{[\gamma],l_{\rho},l_{\lambda}}(\Omega_{\rho},\Omega_{\lambda},\xi), $

(8) where ν determines the number of nodes of the wave function. The hyperradial wave funtion
$ \psi_{\nu,\gamma}(x) $ is obtained as a solution of the hyperradial equation [29–32]$ \left[\frac{{\rm d}^2}{{\rm d}x^2}+\frac{5}{x}\frac{\rm d}{{\rm d}x}-\frac{\gamma(\gamma+4)}{x^2}\right]\psi_{\nu,\gamma}(x)=-2\mu[E_{\nu,\gamma} -V(x)]\psi_{\nu,\gamma}(x). $

(9) For the ground-state doubly heavy baryons, we have
$ \gamma=\nu=0 $ . Here, μ is a free parameter with dimension of mass [30–32]. We consider the Coulomb-plus-linear potential known as the Cornell potential and given by$ V(x)=-\frac{\tau}{x}+\beta x. $

(10) Here, x is the hyper radius and τ and β are constant. In the present study, we solve the Schrödinger Eq. (9) numerically.
In our model, the spin dependent interaction is treated as perturbation. We make the following model for the spin-spin hyperfine interaction:
$ V_{\rm spin}=\frac{A_{s}}{m_\rho m_\lambda}\frac{e^{\frac{-x}{x_{0}}}}{x x_{0}^2}\Sigma_{i<j}(\overrightarrow{s_{i}}.\overrightarrow{s_j}), $

(11) where
$ \overrightarrow{s_i} $ is the spin operator of the$i^{\rm th}$ quark, and$ A_s $ and$ x_0 $ are constants. We have neglected the isospin dependent potential. The isospin mass splittings for doubly heavy baryons have been studied in Ref. [33] with the results$ \begin{aligned}[b] m_{\Xi^{++}_{cc}}-m_{\Xi^+_{cc}}=(1.5\pm 2.7)\;{\rm{MeV}}, \\ m_{\Xi^+_{bc}}-m_{\Xi^{0}_{bc}}=(-1.5\pm0.9)\;{\rm{MeV}},\\ m_{\Xi^-_{bb}}-m_{\Xi^{0}_{bb}}=(6.3\pm1.7)\;{\rm{MeV}}. \end{aligned}$

(12) Thus, the isospin splittings are at most a few MeV and can be neglected in our calculations.
-
From the experimental side, only the mass of the
$ \Xi_{cc} $ state has been measured. Other than the double-charm$ \Xi_{cc} $ baryons, the masses of other doubly heavy baryons are not known yet and may be measured in the future. Recently, several experimental efforts have been made on the exclusive channels$ \Xi^0_{bc}\rightarrow D^0 p K^- $ [34] and$ \Xi^0_{bc}\rightarrow \Xi_c^+ \pi^- $ [35] to search for the beauty-charm baryons, but no signals have been observed. Recently, an inclusive decay channel$ \Xi_{bc}\rightarrow \Xi_{cc}^{++}+X $ has been proposed [26] to search for the$ \Xi_{bc} $ baryons where, X stands for all the possible particles. The theoretical results on the mass spectrum of doubly heavy baryons would be also helpful and can be tested in the near future.In theory, the mass of the baryon is simply given by the energy of the baryonic system. One can calculate the baryon masses by the sum of the quark masses, energy eigenvalues, and perturbative hyperfine interaction
$\langle V_{\rm spin}\rangle$ as$ M_{\rm baryon}=m_{1}+m_{2}+m_{3}+E+\langle V_{\rm spin} \rangle, $

(13) All the model parameters (listed in Table 1) are taken from our previous work [32] in which we have studied the properties of charm and bottom heavy baryons in a quark model. Our results for the ground-state baryons are listed in Table 2 and compared to those reported within a relativistic quark model [36], non-relativistic quark model [37–39], and QCD sum rules [40]. Our evaluation for
$ M_{\Xi_{cc}} $ is 58 MeV higher than the experimental value reported by LHCb collaboration [3]. Our predicted masses are in good agreement with the ones reported by Ref. [38]. For the$ \Omega_{bb}^* $ , our mass prediction is the same as that reported by Ref. [38].Parameter Value Parameter Value $ m_{q} $ 

$330\;{\rm{MeV}} $ 

τ 4.59 $ m_{s} $ 

$469\;{\rm{MeV}} $ 

β $1.61 \; {\rm fm}^{-2}$ 

$ m_{c} $ 

$1600\;{\rm{MeV}} $ 

$ A_s $ 

67.4 $ m_{b} $ 

$4908\;{\rm{MeV }}$ 

$ x_0 $ 

$2.87\; {\rm fm}$ 

$\mu $ 

$0.884\;{\rm fm}^{-1}$ 

Table 1. Quark-model parameters. q refers to the light quarks u and d.
Baryon Content Our results [36] [37] [38] [39] [40] $ \Xi_{cc} $ 

$ qcc $ 

3.679 3.620 3.613 3.676 3.685 $ \Xi_{cc}^* $ 

$ qcc $ 

3.763 3.727 3.707 3.753 3.754 3.690 $ \Xi_{bc} $ 

$ qbc $ 

7.003 6.933 6.928 7.020 $ \Xi_{bc}^* $ 

$ qbc $ 

7.056 6.980 6.996 7.078 7.250 $ \Xi_{bb} $ 

$ qbb $ 

10.325 10.202 10.198 10.340 10.314 $ \Xi_{bb}^* $ 

$ qbb $ 

10.350 10.237 10.237 10.367 10.339 10.400 $ \Omega_{cc} $ 

$ scc $ 

3.830 3.778 3.712 3.815 3.832 $ \Omega_{cc}^* $ 

$ scc $ 

3.891 3.872 3.795 3.876 3.883 3.780 $ \Omega_{bc} $ 

$ sbc $ 

7.149 7.088 7.013 7.147 $ \Omega_{bc}^* $ 

$ sbc $ 

7.187 7.130 7.075 7.191 7.300 $ \Omega_{bb} $ 

$ sbb $ 

10.466 10.359 10.269 10.456 10.447 $ \Omega_{bb}^* $ 

$ sbb $ 

10.486 10.389 10.307 10.486 10.467 10.500 Table 2. Masses of the ground states of double heavy baryons (in GeV).
$ ^* $ refers to the$s=\dfrac{3}{2}$ baryons.For the mass splittings between
$ J=\dfrac{3}{2} $ and the corresponding$ J=\dfrac{1}{2} $ doubly heavy baryons, our calculations show that$ M_{\Xi_{cc}^*}-M_{\Xi_{cc}}=84 $ MeV,$ M_{\Xi_{bc}^*}-M_{\Xi_{bc}}=53 $ MeV,$M_{\Xi_{bb}^*}- M_{\Xi_{bb}}=25$ MeV,$ M_{\Omega_{cc}^*}-M_{\Omega_{cc}}=61 $ MeV,$ M_{\Omega_{bc}^*}-M_{\Omega_{bc}}=38 $ MeV, and$ M_{\Omega_{bb}^*}-M_{\Omega_{bb}}=20 $ MeV. The obtained results of Ref. [38] show that$ M_{\Xi_{cc}^*}-M_{\Xi_{cc}}77= $ MeV,$ M_{\Xi_{bc}^*}-M_{\Xi_{bc}}= $ 58 MeV,$ M_{\Xi_{bb}^*}-M_{\Xi_{bb}}=27 $ MeV,$ M_{\Omega_{cc}^*}-M_{\Omega_{cc}}=61 $ MeV,$ M_{\Omega_{bc}^*}-M_{\Omega_{bc}}=44 $ MeV, and$ M_{\Omega_{bb}^*}-M_{\Omega_{bb}}=30 $ MeV, which are very close to our calculations, respectively. For doubly bottom baryons, our evaluated mass splittings$ M_{\Xi_{bb}^*}-M_{\Xi_{bb}} $ and$ M_{\Omega_{bb}^*}-M_{\Omega_{bb}} $ are the same as those obtained by Ref. [39].For the mass splittings between the double heavy baryons containing two identical heavy quarks and corresponding bottom-charm baryons we find
$ \begin{aligned}[b] m_{\Xi_{bc}}-m_{\Xi_{cc}}=3324\; {\rm{MeV}}, \\ m_{\Xi_{bb}}-m_{\Xi_{bc}}=3322\; {\rm{MeV}},\\ m_{\Omega_{bc}}-m_{\Omega_{cc}}=3319\; {\rm{MeV}},\\ m_{\Omega_{bb}}-m_{\Omega_{bc}}=3317\; {\rm{MeV}}. \end{aligned} $

(14) All the splittings are close to the mass difference of the bottom and charm quarks
$ m_b-m_c=3309 \;{\rm{MeV}}. $

(15) In the case of
$ m_{\Xi_{bb}}-m_{\Xi_{bc}} $ , our results are the same as the mass splittings reported in Refs. [37] and [38].It is also interesting to point out the mass difference
$ \Delta_M=M_{\Omega_{QQ}}-M_{\Xi_{QQ}} $ between Ω and the corresponding Ξ doubly heavy baryons. In our calculations, it takes the value of$\Delta_M=142 \sim151\; {\rm{MeV}}$ , which is close to the$\Delta_M=155\sim158\; {\rm{MeV}}$ reported by Ref. [36]. -
The orbital part of the magnetic moment is defined in terms of the velocities
$ \overrightarrow{v} $ of the quarks. In the present study, we investigate the ground-state heavy baryons and also how the orbital magnetic moments vanish and the magnetic moment of the baryon is entirely given by the spin contribution. The magnetic moment operator is given as$ \overrightarrow{\mu}=\sum\limits_i \mu_i \overrightarrow{\sigma}_i, $

(16) where
$ \begin{array}{*{20}{l}} \mu_i=\dfrac{e_{i}}{2m_{i}}, \end{array} $

(17) and
$ e_i $ and$ \sigma_i $ represent the charge and spin of the$i^{\rm th}$ quark respectively$ \left(s_i=\dfrac{\sigma_i}{2}\right) $ . The magnetic moment of the baryon is obtained in terms of its constituent quark magnetic moments ($ \mu_i $ ). By sandwiching the magnetic moment operators between the appropriate baryon wave functions we get$ \begin{aligned}[b] \mu=& \langle B_{\rm sf}\mid \mu_i \overrightarrow{\sigma}_i \mid B_{\rm sf} \rangle \\ =& \left\langle B_{\rm sf}\left| \dfrac{e_{Q_1}}{m_{Q_1}}(\overrightarrow{s}_{Q_1})_z+\dfrac{e_{Q_2}}{m_{Q_2}}(\overrightarrow{s}_{Q_2})_z+\dfrac{e_{q}}{m_{q}}(\overrightarrow{s}_{q})_z \right| B_{\rm sf} \right\rangle, \end{aligned}$

(18) where Q and q refer to the heavy and light quarks, respectively, and
$\mid B_{\rm sf} >$ is the spin-flavor wave function of the baryon. The 17 matrix elements are evaluated as follows$ \begin{aligned}[b]& \mu_{B(J=1/2)}\longrightarrow \dfrac{2}{3}\left(\dfrac{e_{Q_1}}{2m_{Q_1}}+\dfrac{e_{Q_2}}{2m_{Q_2}}-\dfrac{1}{2}\dfrac{e_{q}}{2m_{q}}\right), \\& \mu_{B(J=3/2)}\longrightarrow \dfrac{e_{Q_1}}{2m_{Q_1}}+\dfrac{e_{Q_2}}{2m_{Q_2}}+\dfrac{e_{q}}{2m_{q}}. \end{aligned} $

(19) With
$ m_b\gg m_u,m_d,m_s $ , the contribution from the b quark is negligible compared to those of the light quarks. This is also true to a lesser extent for the c quark.The spin-flavor wave functions of doubly heavy Ξ baryons and their magnetic moments in terms of the constituent quark magnetic moments are presented in Table 3. In the same way, if the light (u and d) quarks are replaced by the s quark, we can obtain the results for the corresponding Ω doubly heavy baryons. In Table 4 we present our numerical results for the magnetic moments of doubly heavy baryons in terms of the nuclear magneton
$ \mu_{N} $ and compare them to those obtained by different approaches [24, 41–43].Baryon Spin-flavour wave function $ \mu_B $ 

$ \Xi_{cc}^{++} $ 

$ \dfrac{2}{\sqrt{6}}(2u_-c_+c_+-c_-u_+c_+-u_+c_-c_++2c_+u_-c_+-c_+c_-u_+ $ 

$ -c_-c_+u+-c_+u_+c_–u_+c_+c_-+2c_+c_+u_-) $ 

$ \dfrac{4}{3}\mu_c-\dfrac{1}{3}\mu_u $ 

$ \Xi_{cc}^{+} $ 

$ \dfrac{2}{\sqrt{6}}(2d_-c_+c_+-c_-d_+c_+-d_+c_-c_++2c_+d_-c_+-c_+c_-d_+ $ 

$ -c_-c_+d+-c_+d_+c_–d_+c_+c_-+2c_+c_+d_-) $ 

$ \dfrac{4}{3}\mu_c-\dfrac{1}{3}\mu_d $ 

$ \Xi_{bb}^{0} $ 

$ \dfrac{2}{\sqrt{6}}(2u_-b_+b_+-b_-u_+b_+-u_+b_-b_++2b_+u_-b_+-b_+b_-u_+ $ 

$ -b_-b_+u+-b_+u_+b_–u_+b_+b_-+2b_+b_+u_-) $ 

$ \dfrac{4}{3}\mu_b-\dfrac{1}{3}\mu_u $ 

$ \Xi_{bb}^{-} $ 

$ \dfrac{2}{\sqrt{6}}(2d_-b_+b_+-b_-d_+b_+-d_+b_-b_++2b_+d_-b_+-b_+b_-d_+ $ 

$ -b_-b_+d+-b_+d_+b_–d_+b_+b_-+2b_+b_+d_-) $ 

$ \dfrac{4}{3}\mu_b-\dfrac{1}{3}\mu_d $ 

$ \Xi_{bc}^{+} $ 

$ \dfrac{-1}{6}(b_+c_-u_++c_+b_-u_++u_+c_-b_++u_+b_-c_+-2b_+u_-c_+ $ 

$ -2c_+u_-b_++b_-c_+u_++c_-b_+u_+-2u_-c_+b_+-2u_-b_+c_+ $ 

$ \dfrac{2}{3}\mu_b+\dfrac{2}{3}\mu_c-\dfrac{1}{3}\mu_u $ 

$ +b_-u_+c_++c_-u_+b_+-2b_+c_+u_–2c_+b_+u_-+u_+c_+b_- $ 

$ +u_+b_+c_-+b_+u_+c_-+c_+u_+b_-) $ 

$ \Xi_{bc}^{0} $ 

$ \dfrac{-1}{6}(b_+c_-d_++c_+b_-d_++d_+c_-b_++d_+b_-c_+-2b_+d_-c_+ $ 

$ -2c_+d_-b_++b_-c_+d_++c_-b_+d_+-2d_-c_+b_+-2d_-b_+c_+ $ 

$ \dfrac{2}{3}\mu_b+\dfrac{2}{3}\mu_c-\dfrac{1}{3}\mu_d $ 

$ +b_-d_+c_++c_-d_+b_+-2b_+c_+d_–2c_+b_+d_-+d_+c_+b_- $ 

$ +d_+b_+c_-+b_+d_+c_-+c_+d_+b_-) $ 

$ \Xi_{cc}^{*++} $ 

$ \dfrac{1}{\sqrt{3}}(c_+c_+u_++c_+u_+c_++u_+c_+c_+) $ 

$ 2\mu_c+\mu_u $ 

$ \Xi_{cc}^{*+} $ 

$ \dfrac{1}{\sqrt{3}}(c_+c_+d_++c_+d_+c_++d_+c_+c_+) $ 

$ 2\mu_c+\mu_d $ 

$ \Xi_{bb}^{*0} $ 

$ \dfrac{1}{\sqrt{3}}(b_+b_+u_++b_+u_+b_++u_+b_+b_+) $ 

$ 2\mu_b+\mu_u $ 

$ \Xi_{bb}^{*-} $ 

$ \dfrac{1}{\sqrt{3}}(b_+b_+d_++b_+d_+b_++d_+b_+b_+) $ 

$ 2\mu_b+\mu_d $ 

$ \Xi_{bc}^{*+} $ 

$ \dfrac{1}{\sqrt{6}}(b_+c_+u_++c_+b_+u_++b_+u_+c_+ $ 

$ +u_+b_+c_++c_+u_+b_++u_+c_+b_+) $ 

$ \mu_b+\mu_c+\mu_u $ 

$ \Xi_{bc}^{*0} $ 

$ \dfrac{1}{\sqrt{6}}(b_+c_+d_++c_+b_+d_++b_+d_+c_+ $ 

$ +d_+b_+c_++c_+d_+b_++d_+c_+b_+) $ 

$ \mu_b+\mu_c+\mu_d $ 

Table 3. Spin-flavor wave functions of Ξ doubly heavy baryons and their magnetic moments in terms of the constituent quarks magnetic moments.
$ ^* $ refers to the$s=\dfrac{3}{2}$ baryons.Baryon Our results [24] [41] [42] [43] $ \Xi_{cc}^{++} $ 

−0.110 −0.208 −0.137 $ \Xi_{cc}^{+} $ 

0.836 0.785 0.859 $ \Xi_{cc}^{*++} $ 

2.676 2.670 2.749 2.590 $ \Xi_{cc}^{*+} $ 

−0.165 −0.311 −0.168 −0.200 $ \Xi_{bc}^+ $ 

−0.413 −0.475 −0.400 −0.387 $ \Xi_{bc}^0 $ 

0.533 0.518 0.476 0.499 $ \Xi_{bc}^{*+} $ 

2.222 2.270 2.052 2.011 $ \Xi_{bc}^{*0} $ 

−0.620 −0.712 −0.567 −0.551 $ \Xi_{bb}^0 $ 

−0.716 −0.742 −0.656 −0.665 $ \Xi_{bb}^- $ 

0.230 0.251 0.190 0.208 $ \Xi_{bb}^{*0} $ 

1.767 1.870 1.576 1.596 $ \Xi_{bb}^{*-} $ 

−1.074 −1.110 −0.951 −0.984 $ \Omega_{cc}^+ $ 

0.743 0.635 0.783 $ \Omega_{cc}^{*+} $ 

0.114 0.139 0.121 0.120 $ \Omega_{bc}^0 $ 

0.440 0.368 0.396 0.399 $ \Omega_{bc}^{*0} $ 

−0.339 −0.261 −0.316 −0.279 $ \Omega_{bb}^{-} $ 

0.137 0.101 0.109 0.111 $ \Omega_{bb}^{*-} $ 

−0.794 −0.662 −0.711 −0.703 Table 4. Magnetic moments of the Ξ and Ω doubly heavy baryons (in
$ \mu_{N} $ ). -
In a semileptonic decay, a hadron decays weakly into another hadron with the emission of a lepton and a neutrino. In this section, we study different doubly heavy
$ B(1/2^+)\rightarrow B^{\prime}(1/2^+) $ baryon semileptonic decays for$ b\rightarrow c $ transitions where a doubly heavy baryon B with$ J=1/2 $ decays into another doubly heavy baryon$ B^{\prime} $ with the same spin. The transition matrix element for the semileptonic decay is$ \begin{array}{*{20}{l}} T=\dfrac{G_F}{\sqrt{2}}V_{cb}J_{\mu}\mathcal{L}^{\mu} \end{array} $

(20) with
$ G_F $ and$V_{cb}$ representing the Fermi Coupling constant and CKM matrix element, respectively.$ J_{\mu} $ is the flavor changing (weak) hadronic current and$ \mathcal{L}^{\mu} $ is the leptonic current given as$ J_{\mu} = V_{\mu}-A_{\mu}= \bar{\psi}^c\gamma_{\mu}(I-\gamma_5)\psi^b, \quad\mathcal{L}^{\mu}=\bar{l}\gamma^{\mu}(1-\gamma_5)\nu_l , $

(21) where
$ \psi^{b(c)} $ refers to the bottom (charm) quark field.$ V_{\mu}\equiv\bar{\psi}^c\gamma_{\mu}\psi^b $ and$ A_{\mu}\equiv\bar{\psi}^c\gamma_{\mu}\gamma_5\psi^b $ are the vector and axial-vector weak currents, respectively. The leptonic current of the semileptonic decay can be calculated from first principles of Quantum mechanics but not the hadronic matrix element,$ H_{\mu} $ . The hadron matrix elements can be parametrized in terms of six form factors as$\begin{aligned}[b] H_{\mu}= & \langle B^{\prime}(p^{\prime},s^{\prime})\mid V_{\mu}-A_{\mu}\mid B(p,s)\rangle=\langle B^{\prime}(p^{\prime},s^{\prime})\mid \bar{\psi}^c\gamma_{\mu}(I-\gamma_5)\psi^b\mid B(p,s)\rangle \\ =&\bar{u}^ {\prime}(p^{\prime},s^{\prime})\left\lbrace \gamma_{\mu}(F_1(\omega)-\gamma_5G_1(\omega))+v_{\mu}(F_2(\omega)-\gamma_5G_2(\omega)) \right. \\ & \left. +v^{\prime}_{\mu}(F_3(\omega)-\gamma_5G_3(\omega))\right\rbrace u(p,s),\\[-12pt] \end{aligned} $

(22) where
$\mid B(p,~s) >$ and$\mid B^{\prime}(p^{\prime},~s^{\prime}) >$ represent the initial and final baryons.$u(p,~s)$ and$u^{\prime}(p^{\prime},~s^{\prime})$ are dimensionless Dirac spinors, normalized as$ \bar{u}u=1 $ , and$v_{\mu}=p_{\mu}/ m_B \cdot (v^{\prime}_{\mu}=p^{\prime}_{\mu}/m_B^{\prime})$ is the four velocity of the initial B (final$ B^{\prime} $ ) baryon.The differential decay rates from transversely
$ \Gamma_T $ and longitudinally$ \Gamma_L $ polarized W's, are given as$ \dfrac{{\rm d}\Gamma}{{\rm d}\omega}=\dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}+\dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}. $

(23) Neglecting the lepton masses, the differential decay rates
$ \Gamma_T $ and$ \Gamma_L $ for the case$ B^{1/2}\rightarrow B^{\prime 1/2} $ are given as [23, 24]$\begin{aligned}[b] \dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}=&\dfrac{G_F^2\vert V_{cb}\vert ^2M_{B^{\prime}}^3}{12\pi^3}\sqrt{\omega^2-1}q^2\lbrace(\omega-1)\vert F_1(\omega)\vert^2\\&+(\omega+1)\vert G_1(\omega)\vert^2\rbrace, \end{aligned} $

(24) and
$ \begin{aligned}[b] \dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}=&\frac{G_F^2\vert V_{cb}\vert ^2M_{B^{\prime}}^3}{24\pi^3}\sqrt{\omega^2-1}\lbrace(\omega-1)\vert \mathcal{F}^V(\omega)\vert^2\\&+(\omega+1)\vert \mathcal{F}^A(\omega)\vert^2\rbrace, \end{aligned} $

(25) where
$ \begin{aligned}[b] \mathcal{F}^{V,A}(\omega)=&\left[ (m_B\pm m_{B^{\prime}})F_1^{V,A}(\omega)+(1\pm\omega) \right.\\& \times \left.\left( m_{B^{\prime}}F_2^{V,A}(\omega)+m_BF_3^{V,A}(\omega)\right) \right] ,\\& F_j^V\equiv F_j(\omega), \quad F^A_j\equiv G_j(\omega), \quad j=1,2,3 \end{aligned} $

(26) $ \omega=v.v^{\prime} $ is the velocity transfer, and$q^2= (p- p^{\prime})^2= m_B^2+m^2_{B^{\prime}}-2m_B m_{B^{\prime}}\omega$ is the momentum transfer squared between the initial and final baryons. The form factors are functions of ω and$ q^2 $ . In the decay ω ranges from$ \omega=1 $ corresponding to zero recoil of the final baryon to a maximum$\omega_{\max}=(m_B^2+m^2_{B^{\prime}})/(2m_B m_{B^{\prime}})$ .Integrating over the parameter ω, we can obtain the total decay width
$ \Gamma=\int^{\omega_{\rm max}}_1 {\rm d}\omega\dfrac{{\rm d}\Gamma}{{\rm d}\omega}=\int^{\omega_{\rm max}}_1 {\rm d}\omega\left(\dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}+\dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}\right). $

(27) We can also calculate the polar angle distribution [23, 24]
$ \dfrac{{\rm d}^2\Gamma_L}{{\rm d}\omega \, {\rm d}{\rm cos}\theta}=\dfrac{3}{8}\left(\dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}+2\dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}\right) \left\lbrace 1+2\alpha^{\prime} {\rm cos}\theta+\alpha^{\prime\prime} {\rm cos}^2\theta\right\rbrace, $

(28) where θ is the angle between the four momenta of the final baryon and the final lepton measured in the off-shell W rest frame. α and
$ \alpha^{\prime \prime} $ are asymmetry parameters given by$ \alpha^{\prime}=-\frac{G_F^2\vert V_{cb}\vert ^2M_{B^{\prime}}^3}{6\pi^3}\dfrac{q^2(\omega^2-1)F_1(\omega)G_1(\omega)}{{\rm d}\Gamma_T/{\rm d}\omega+2{\rm d}\Gamma_L/{\rm d}\omega}, $

(29) and
$ \alpha^{\prime\prime}=\dfrac{{\rm d}\Gamma_T/{\rm d}\omega-2{\rm d}\Gamma_L/{\rm d}\omega}{{\rm d}\Gamma_T/{\rm d}\omega+2{\rm d}\Gamma_L/{\rm d}\omega} $

(30) Averaging over ω, we obtain
$ < \alpha^{\prime} >=-\frac{G_F^2\vert V_{cb}\vert ^2}{6\pi^3} \dfrac{M^3_{B^{\prime}}}{\Gamma_T} \dfrac{\int ^{\omega_{\rm max}}_1 q^2(\omega^2-1)F_1(\omega)G_1(\omega)d\omega}{1 + 2R_{L/T}}, $

(31) $ < \alpha^{\prime \prime} >=\dfrac{1-2R_{L/T}}{1+2R_{L/T}}, \quad \quad R_{L/T}=\dfrac{\Gamma_L}{\Gamma_T}. $

(32) To study the semileptonic transitions of baryons, we need the form factors, which can be parametrized in different ways. Some earlier works [27, 44–46] simplified the transition form factors using different methods. The authors of Ref. [27] have studied the form factors and semileptonic decays of doubly heavy baryons using a manifestly Lorentz covariant constituent three-quark model. In the heavy quark limit and close to zero recoil point, the expressions for the rates can be simplified considerably, and the weak transition form factors between doubly heavy baryons can be expressed by a single IW function
$ \eta(\omega) $ [27, 47, 48]$ \begin{aligned}[b]& F_1(\omega)=G_1(\omega)=\eta(\omega), \quad \quad \quad \quad \quad\quad\\& F_2(\omega)=F_3(\omega)=G_2(\omega)=G_3(\omega)=0 . \end{aligned}$

(33) The universal function
$ \eta(\omega) $ depends on the kinematical parameter ω [27]$ \eta(\omega)={\rm exp}\left( -3(\omega-1)\frac{m_{cc}^2}{\Lambda_B^2}\right) $

(34) with
$ m_{cc}=2m_c $ for the$ bc\rightarrow cc $ weak transitions. The cut-off parameter$ \Lambda_B $ is an adjustable parameter related to the size of a baryon and its value has been determined as$ 2.5\leqslant \Lambda_B\leqslant 3.5 $ GeV [27]. The values of the size parameter$ \Lambda_B $ are fixed using data on fundamental properties of mesons and baryons such as leptonic decay constants, magnetic moments, and radii. By replacing$ m_{cc}\rightarrow m_{bb} $ in the IW function, one can obtain the results for the$ bb\rightarrow bc $ transitions. Close to zero recoil, the IW functions for$ bb\rightarrow bc $ and$ bc\rightarrow cc $ transitions explicitly contain the flavor factors$ m_{cc} $ and$ m_{bb} $ , respectively, and there exists only spin symmetry. There is no dependence on the light quark masses. At zero recoil ($ \omega=1 $ ) there exists a spin-flavor symmetry, and$ \eta(1)=1 $ means that the$ bb\rightarrow bc $ and$ bc\rightarrow cc $ transitions are identical.Using Eq. (33), we obtain the following relations for the differential decay rates:
$ \dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}= \frac{G_F^2\vert V_{cb}\vert ^2M_{B^{\prime}}^3}{6\pi^3}q^2\omega\sqrt{\omega^2-1} \eta^2(\omega), $

(35) and
$ \begin{aligned}[b] \dfrac{d\Gamma_L}{d\omega}=& \frac{G_F^2\vert V_{cb}\vert ^2M_{B^{\prime}}^3}{24\pi^3}\sqrt{\omega^2-1} \\& \times\left[ (\omega-1)(m_B+m_{B^{\prime}})^2+(\omega+1)(m_B-m_{B^{\prime}})^2 \right] \eta^2(\omega). \end{aligned} $

(36) Using the obtained masses listed in Table 2 and Eqs. (27), (35), and (36), one can calculate the semileptonic decay rates of doubly heavy Ξ and Ω baryons. For that purpose, we need to fix a value for
$ \vert V_{cb}\vert $ . We take$ \vert V_{cb}\vert=0.0422 $ [49]. We neglect the mass difference between the u and d light quarks.The Q values of the semileptonic decays are not large enough to allow for the semileptonic τ modes. However, the Q values are sufficiently large to allow one to neglect the lepton masses in the semileptonic e and μ modes.
The behaviors of differential decay widths
$\dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}$ and$\dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}$ with dependence on ω are shown in Figs. 1 and 2 for the$ \Xi_{bb}\rightarrow \Xi_{bc} $ and$ \Xi_{bc}\rightarrow \Xi_{cc} $ transitions. We find that the results for doubly heavy Ξ and Ω decays (not shown) are very close to each other.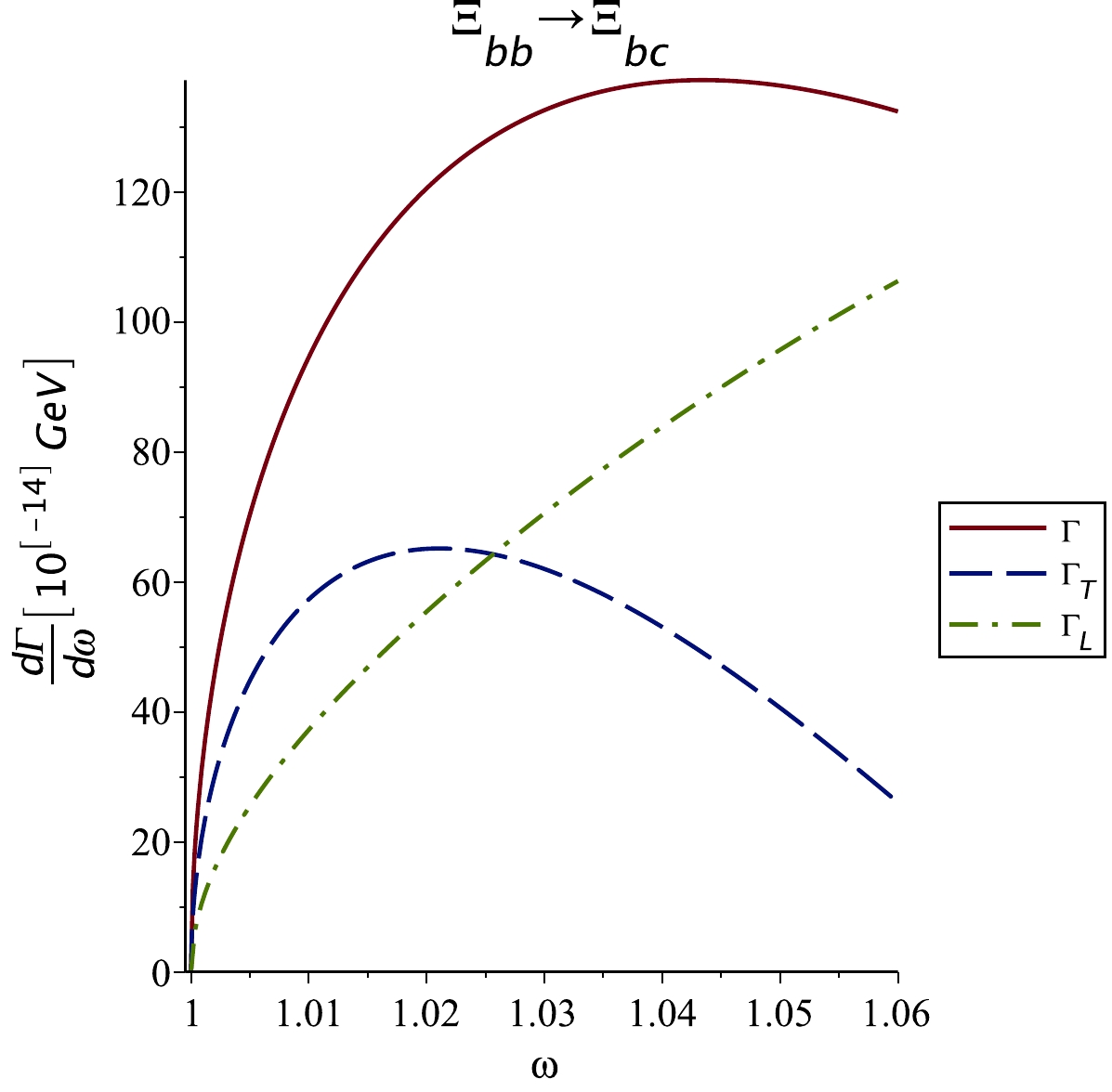
Figure 1. (color online)
$\dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}$ ,$\dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}$ , and$\dfrac{{\rm d}\Gamma}{{\rm d}\omega}$ semileptonic decay widths in units of$ 10^{-14} $ GeV for$ \Xi_{bb}\rightarrow \Xi_{bc}\ell \bar {\nu}_{\ell} $ transition with$ \Lambda_B=2.5 $ GeV and$ \ell=e $ or μ. The results for$ \Omega_{bb} $ decay (not shown) are very similar.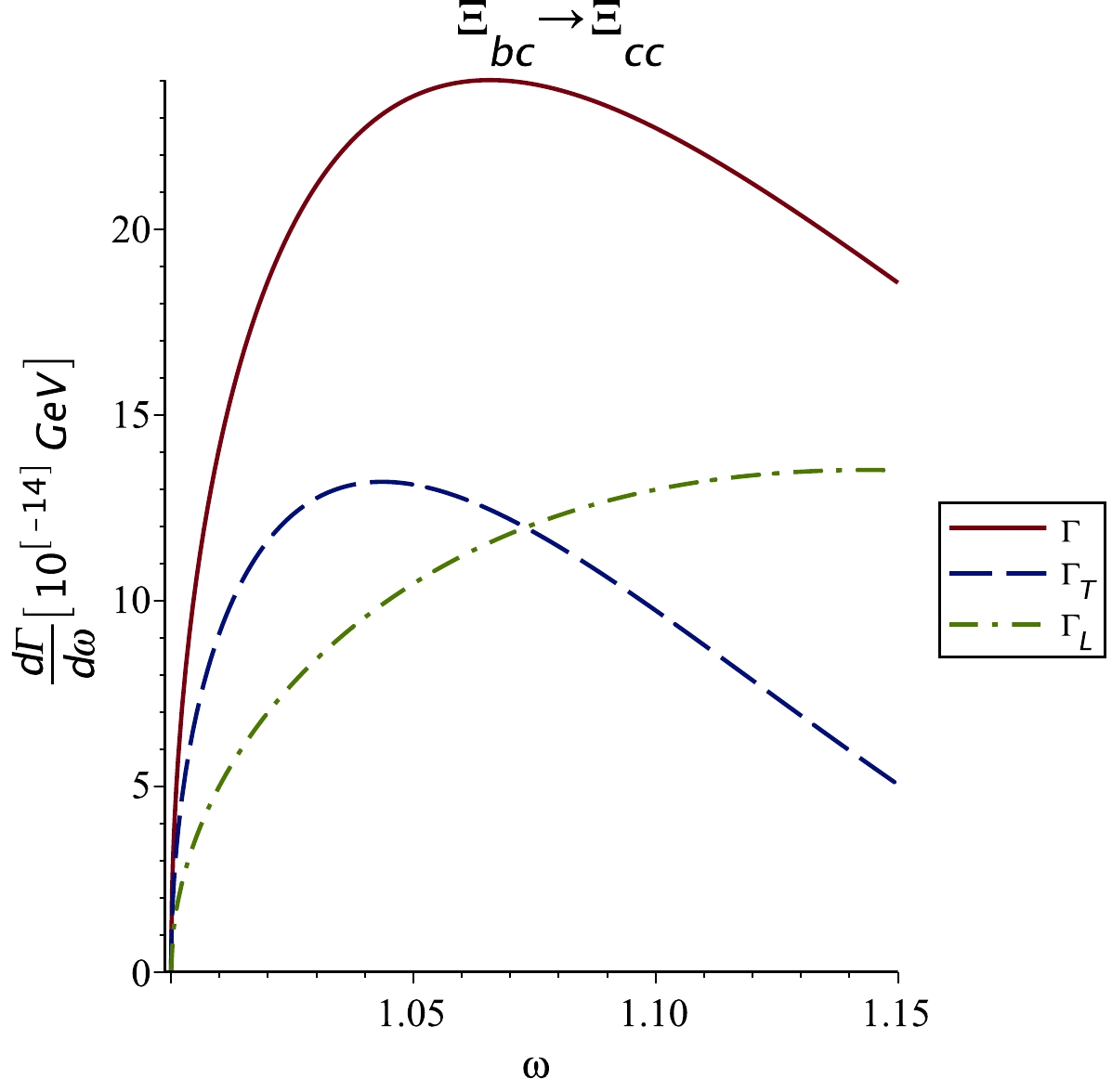
Figure 2. (color online)
$\dfrac{{\rm d}\Gamma_T}{{\rm d}\omega}$ ,$\dfrac{{\rm d}\Gamma_L}{{\rm d}\omega}$ , and$\dfrac{{\rm d}\Gamma}{{\rm d}\omega}$ semileptonic decay widths in units of$ 10^{-14} $ GeV for$ \Xi_{bc}\rightarrow \Xi_{cc}\ell \bar {\nu}_{\ell} $ transition with$ \Lambda_B=2.5 $ GeV and$ \ell=e $ or μ. The results for$ \Omega_{bc} $ decay (not shown) are very similar.In Table 5, our results for the semileptonic decay widths (transverse
$ \Gamma_T $ , longitudinal$ \Gamma_L $ , and total Γ) are presented. In Table 6, we compare our results to those calculated in different models [24, 27, 36, 50, 51].Decay $ \Gamma_T $ 

$ \Gamma_L $ 

Γ Decay $ \Gamma_T $ 

$ \Gamma_L $ 

Γ $ \Xi_{bb}\rightarrow \Xi_{bc}\ell \bar {\nu}_{\ell} $ 

0.55 0.42 0.98 $ \Omega_{bb}\rightarrow \Omega_{bc}\ell \bar {\nu}_{\ell} $ 

0.58 0.45 1.03 $ \Xi_{bc}\rightarrow \Xi_{cc}\ell \bar {\nu}_{\ell} $ 

1.32 1.75 3.08 $ \Omega_{bc}\rightarrow \Omega_{cc}\ell \bar {\nu}_{\ell} $ 

1.40 1.91 3.32 Table 5. Semileptonic decay widths of doubly heavy baryons in units of
$ 10^{-14} $ GeV.$ \Gamma_T $ and$ \Gamma_L $ stand for the transverse and longitudinal contributions to the width Γ. l stands for a light lepton,$l=e,~ \mu$ .Decay Our results NRQM [51] RCQM [27] NRQM [50] RQM [36] NRQM [24] $ \Xi_{bb}\rightarrow \Xi_{bc}\ell \bar {\nu}_{\ell} $ 

0.98 $ 1.75\pm 0.73 $ 

$ 0.80\pm 0.30 $ 

0.94 1.63 $ 1.92^{+0.25}_{-0.05} $ 

$ \Xi_{bc}\rightarrow \Xi_{cc}\ell \bar {\nu}_{\ell} $ 

3.08 $ 4.39\pm0.83 $ 

$ 2.10\pm 0.70 $ 

3.01 2.30 $ 2.57^{+0.26}_{-0.03} $ 

$ \Omega_{bb}\rightarrow \Omega_{bc}\ell \bar {\nu}_{\ell} $ 

1.03 $ 1.87\pm 0.76 $ 

$ 0.86\pm 0.32 $ 

0.99 1.70 $ 2.14^{+0.20}_{-0.02} $ 

$ \Omega_{bc}\rightarrow \Omega_{cc}\ell \bar {\nu}_{\ell} $ 

3.32 $ 4.70\pm0.83 $ 

$ 1.88\pm 0.62 $ 

3.28 2.48 $ 2.59^{+0.20} $ 

Table 6. Semileptonic decay widths of doubly heavy baryons in units of
$ 10^{-14} $ GeV. l stands for a light lepton,$l=e,~ \mu$ .For semileptonic decays of doubly heavy baryons, no experimental data are available at present. From the numerical results in Table 6, we can see that the decay widths are approximately on the order of
$10^{-13}\sim 10^{-14}\;{\rm s}^{-1}$ . Different forms for the Isgur-Wise function may result in different decay widths. However, the order is not changed. Further, the results are insensitive to the size parameter$ \Lambda_B $ . The authors of Refs. [51] and [27] have allowed the parameter$ \Lambda_B $ to vary in the range$2.5\leqslant \Lambda_B\leqslant 3.5$ GeV. However, there are some uncertainties in their works. The error bars in the third and fourth columns of Table 6 denote the variations of the size parameter$ \Lambda_B $ in their calculations, which are larger than the variations repored in Ref. [24]. Note that a smaller value of$ \Lambda_B $ gives smaller decay widths and vice versa. In our calculations, we take$ \Lambda_B=2.5 $ GeV [50, 52, 53]. Regarding$ \Lambda_B=3.5 $ GeV, our values of decay widths would be larger by a factor of$ \sim1.8 $ and$ \sim1.4 $ for$ bb\rightarrow bc $ and$ bc\rightarrow cc $ transitions, respectively.The authors of Refs. [23] and [24] have studied the semileptonic decays of doubly heavy baryons in a non-relativistic quark model and evaluated the hadronic matrix elements parametrized in terms of six form factors. In the present work, we follow their strategy. We develop their approach in the heavy quark limit and provide a way to simplify their evaluation of the hadronic matrix elements and form factors. From the last column of Table 6, one can see that our results agree with their predicted decay widths. Our results of predictions for
$ bb\rightarrow bc $ transitions are lower than the estimates in Ref. [24], while for$ bc \rightarrow cc $ transitions, our Γ values are higher than theirs. The same applies for the estimates presented in the relativistic quark model [36]. Meanwhile, the predictions of Ref. [27] in a relativistic covariant quark model are lower than ours. In comparison with those of Ref. [50], our results are in good agreement with the ones presented in.By using the relation
$ Br=\Gamma\times\tau $ , one can get the branching ratios of double heavy baryons, where τ is the lifetime of the initial baryon. We use$\tau_{\Xi_{bb}}=370\times 10^{-15}\;{\rm s}$ ,$\tau_{\Xi_{bc}}=244 \times 10^{-15}\;{\rm s}$ [54],$\tau_{\Omega_{bc}}=220 \times 10^{-15}\;{\rm s}$ , and$\tau_{\Omega_{bb}}= 800 \times 10^{-15}\;{\rm s}$ [55, 56].Our evaluated results are presented in Table 7 and compared to those of other works [25, 50, 51]. Our calculations for the branching ratios of
$ bc \rightarrow cc $ decays are in good agreement with the ones reported by Ref. [50]. The predictions presented in Refs. [25] and [51] are higher than ours for all the transitions. Especially for the$\Xi_{bb}\rightarrow \Xi_{bc}\ell \bar {\nu}_{\ell}$ and$ \Omega_{bb}\rightarrow \Omega_{bc}\ell \bar {\nu}_{\ell} $ decays, the predicted ratios given in Ref. [25] exceed our estimates by a factor of$ \sim3.5 $ .Process Our results [50] [25] [51] $ \Xi_{bc}\rightarrow \Xi_{cc}\ell \bar {\nu}_{\ell} $ 

1.14 $ \times10^{-2} $ 

$ 1.11\times10^{-2} $ 

$ 1.67\times10^{-2} $ 

$ 1.63\times10^{-2} $ 

$ \Xi_{bb}\rightarrow \Xi_{bc}\ell \bar {\nu}_{\ell} $ 

0.55 $ \times10^{-2} $ 

$ 0.28\times10^{-2} $ 

$ 1.86\times10^{-2} $ 

$ 0.98\times10^{-2} $ 

$ \Omega_{bc}\rightarrow \Omega_{cc}\ell \bar {\nu}_{\ell} $ 

1.10 $ \times10^{-2} $ 

$ 1.10\times10^{-2} $ 

$ 1.32\times10^{-2} $ 

$ 1.57\times10^{-2} $ 

$ \Omega_{bb}\rightarrow \Omega_{bc}\ell \bar {\nu}_{\ell} $ 

1.26 $ \times10^{-2} $ 

$ 4.49\times10^{-2} $ 

$ 2.27\times10^{-2} $ 

Table 7. Branching fractions of semileptonic decay widths for double heavy baryons.
One notes that the rates for the exclusive semileptonic decay modes
$ bb\rightarrow bc $ and$ bc\rightarrow cc $ are rather small when compared to the total semileptonic inclusive rate. The remaining part of the inclusive rate would be filled in by decays into excited or multi-baryonic states.In Table 8, we compile our calculations for the averaged angular asymmetries
$ \alpha^{\prime} $ and$ \alpha^{\prime\prime} $ , as well as the$ R_{L/T}=\Gamma_L/\Gamma_T $ ratio. From Table 8, one can see that the values of the averaged angular asymmetries for the$ \Xi_{bb} $ ($ \Xi_{bc} $ ) and$ \Omega_{bb} $ ($ \Omega_{bc} $ ) semileptonic transitions are almost the same. This means that the mean values of the asymmetry parameters are independent of the light quark flavors ($u,~ d$ and s) inside the considered baryons. Meanwhile, by increasing the size parameter$ \Lambda_B $ , the mean values of the asymmetry parameters increase. The increase of$ R_{L/T} $ for the$ bb \rightarrow bc $ and$ bc \rightarrow cc $ transitions would be approximately$ 20 \% $ and$ 40 \% $ , respectively, in the region$ \Lambda_B=2.5\sim 3.5 $ GeV.Decay $ \langle \alpha^{\prime}\rangle $ 

$ \langle \alpha^{\prime\prime}\rangle $ 

$ R_{L/T} $ 

Decay $ \langle \alpha^{\prime}\rangle $ 

$ \langle \alpha^{\prime \prime}\rangle $ 

$ R_{L/T} $ 

$ \Xi_{bb}\rightarrow \Xi_{bc}\ell \bar {\nu}_{\ell} $ 

−0.05 −0.21 0.76 $ \Omega_{bb}\rightarrow \Omega_{bc}\ell \bar {\nu}_{\ell} $ 

−0.05 −0.21 0.77 $ \Xi_{bc}\rightarrow \Xi_{cc}\ell \bar {\nu}_{\ell} $ 

−0.09 −0.45 1.32 $ \Omega_{bc}\rightarrow \Omega_{cc}\ell \bar {\nu}_{\ell} $ 

−0.08 −0.46 1.35 Table 8. Averaged values of the asymmetry parameters
$ \alpha^{\prime} $ and$ \alpha^{\prime\prime} $ and$ R_{L/T} $ ratio. -
In summary, we have evaluated the mass spectra, magnetic moments, and semileptonic decays of the ground-state doubly heavy Ξ and Ω baryons. The calculations have been performed in the framework of a non-relativistic quark model with the use of the hypercentral approach. By introducing a simple form of the universal function, we could simplify the weak transition form factors in the heavy quark limit. Finally, we have investigated the semileptonic decay rates and branching ratios driven by a
$ b\rightarrow c $ quark transition for the$J= {1}/{2}$ baryons. We have worked near the zero recoil point and in the heavy quark limit, with lepton mass neglected. The results for doubly heavy Ω decays are almost identical to the corresponding ones for doubly heavy Ξ decays. Because we have two heavy quarks, the light quark acts as a spectator and makes the results almost independent of the light quark mass. According to Ref. [27] the value of the size parameter$ \Lambda_B $ varies in the range$ 2.5\leqslant \Lambda_B\leqslant 3.5 $ GeV. We have selected$ \Lambda_B=2.5 $ GeV. The decay widths obtained in Ref. [51] are larger than ours for all the transitions. If we select$ \Lambda_B=3 $ GeV, the evaluated decay rates and branching ratios will be very close to the calculations of Ref. [51]. A comparison between our results and those of other theoretical studies shows that our results are acceptable. Note that the triplet$\left(J={3}/{2}\right)$ doubly heavy baryons are dominated by the strong or electromagnetic decays. If these excited states are the initial ones, owing to the smallness of the weak coupling, the weak decays cannot be observed in the experiments. Therefore, one can neglect the calculations for the semileptonic decays of$J= {3}/{2}$ doubly heavy baryons because of the difficulty in the experiments. We hope that our results can be used to extract the CKM parameters$ V_{cb} $ from future experiments on the semileptonic decays of doubly heavy baryons.
Static properties and semileptonic transitions of lowest-lying double heavy baryons
- Received Date: 2022-10-22
- Available Online: 2023-03-15
Abstract: The static properties and semileptonic decays of ground-state doubly heavy baryons are studied in the framework of a non-relativistic quark model. Using a phenomenological potential model, we calculate the ground-state masses and magnetic moments of doubly heavy Ω and Ξ baryons. In the heavy quark limit, we introduce a simple form of the universal Isgur-Wise function used as the transition form factor and then investigate the exclusive






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: