-
Until the recent remarkable progress made by the Event Horizon Telescope (EHT) collaboration, the identification of compact massive objects (CMOs) as black holes via astronomical observation has been a challenge. The successful detection of black holes at the center of M87 and Sgr A* announced the coming of a new age of the study of black holes as genuine astrophysical objects [1, 2]. In this direction of study, detecting the photon sphere closely surrounding a black hole silhouette plays a key role in measuring various parameters of black holes, such as the size, mass, and spin.
It is well known that the existence of black hole solutions in general relativity introduces several fundamental problems that are notoriously difficult to solve in theoretical physics. Among them, the most famous is the singularity problem, which tells us that the scalar curvature becomes divergent at the center of black holes [3−7]. This problem became severe after Hawking radiation was discovered, a phenomenon that leads to the evaporation of black holes and finally the information loss paradox [8−16]. Theoretically, it is believed that the infinity of the Kretschmann scalar curvature simply implies that classical general relativity would not be applicable to space time with an extreme environment, and the singularity at the center of a classical black hole might be removed or avoided by the quantum effects of gravity [17−26]. One widely accepted belief is that when the effects of quantum gravity are considered, any object should have a minimal observable length of the Planck length order. In theory, two prominent quantum effects of gravity may give rise to the minimal observable length: the generalized uncertainty principle (GUP) [27] and modified dispersion relations (MDR) [28]. Their impacts on the thermodynamics of black holes have been extensively investigated in literature, for instance, in [29, 30] and [31, 32]. Owing to the effects of the MDR or GUP, a black hole will stop radiating at the final stage and prevent the Hawking temperature from diverging. Nevertheless, all these effects are considered for radiation particles over the background of ordinary Schwarzschild black holes, which contain the singularity at the center of the black holes. Therefore, it is highly desirable to overcome this weak point by constructing the geometry of spacetime without a singularity directly based on the effects of quantum gravity. In contrast, regular black holes or non-singular black holes are candidates that do not suffer from the singularity problem because their Kretschmann scalar curvature is finite everywhere. Furthermore, when the mass of regular black holes decreases below some value at the late stage of evaporation, the horizon disappears such that the remnant becomes a CMO with vanishing Hawking temperature, which provides more a reasonable result for the fate of black hole evaporation. Previously, some well-known regular black holes, such as Bardeen/ Hayward/Frolov [33−35] black holes, were constructed by considering the violation of energy conditions and adding exotic matter. From our perspective, it is highly desirable to directly link these regular black holes to quantum gravity effects. Such an attempt was made in [12]. The GUP may lead to a modified Newton's constant such that an ordinary black hole may be modified into a regular black hole. Our theoretical consideration can be summarized as follows: Recalling that the GUP provides the minimal observable length of any object, if an object enters a curved space-time, for instance, outside the horizon of a black hole, it would be affected by the tidal force. Moreover, it turns out that the effects of the tidal force can be equivalently described by an effective gravitational field strength, which is introduced to calculate the interaction between gravity and the quantum object, leading to a modified metric with the characteristic of an effective Newtonian constant [12]. Explicitly, if the uncertainty relation is modified as
$ [p,x]=-{\rm i}z(p) $

(1) in the GUP, where
$ z(p) $ is a function of momentum p, it is expected that Newton's constant is modified as$ G=z^{-1}G_N, $

(2) where
$ G_N $ is the ordinary Newton's constant. This scenario is supported by many thought experiments, as described in [12]. In this route, one can successfully derive Bardeen/Hayward/Frolov black holes as the result of the modification of Newton potential owing to the effects of quantum gravity. It is found that the lowest bound for the black hole mass is naturally defined by the existence of the horizon, which may be caused because the minimal observable length of the black hole can no longer be ignored after it evaporates to a small size approaching the Planck length scale. The quantum effects of gravity alter the classical geometry of a black hole such that it stops evaporating at a certain scale and leaves behind a black hole remnant. Going further, a new type of regular black hole was proposed in [12] and [36]. In comparison with the well-known Bardeen/Hayward/Frolov black holes, which are characterized by the de-Sitter core at the center, this new type of black hole has an exponentially suppressed Newton potential and is characterized by a Minkowski core at the center. Recently, more features of this type of black hole were investigated in [37, 38].Currently, although we are still far from a complete understanding on these regular black holes, it is intriguing to link these regular black holes to astrophysical observation and explore if there is any evidence or signature implying that the detected black holes in the sky are of the regular type rather than traditional black holes with singularities. Obviously, at the current stage, it is impractical to distinguish between singular and regular black holes by diving into the horizon or detecting any signal emerging from the interior of the horizon. Nevertheless, the difference inside black holes may leave signatures on the featured phenomena outside the black holes, such as the photon sphere or the trajectories of massive particles [39−46]. Therefore, in this paper, we intend to provide a detailed analysis of the photon sphere and marginally stable circular orbit of massive particles over the recently proposed regular black holes with sub-Planckian curvature. We expect that our theoretical investigation will provide a basis and useful information for distinguishing between different types of black holes via astrophysical observation in the near future.
The paper is organized as follows: In the next section, we present a short review of regular black holes with sub-Planckian curvature, which are characterized by the two factors
$ (x,n) $ . We focus on the structure of the horizon, which usually contains two branches, namely, the inner and outer horizons. When the mass is below some value, the horizon will disappear and the black hole becomes a horizonless CMO. In Sections III and IV, we consider two regular black holes, with$ (x=2/3, n=2) $ and$ (x=1,n=3) $ , and determine the radius of circular photon orbits, with an analysis of the stability of these orbits. For massive particles, the curve of the marginally stable circular orbit becomes double-valued in the CMO phase. Via a comparison with those of Bardeen and Hayward black holes, we find that the locations of the photon sphere and marginally stable circular orbit over the horizonless CMO with a Minkowskian core are evidently different from those over the CMO with a dS core, which potentially provides a way to distinguish between these two types of black holes by astronomical observation. In Section V, based on the observed shadow diameter of M87*, we provide the observational constraint on the parameter$ \alpha_0 $ for such regular black holes by considering the modification of the impact parameter with the parameter$ \alpha_0 $ . It turns out that within a reasonable range of$ \alpha_0 $ , the shadow of these regular black holes may fit well with the observed shadow from the black hole M87*. Our study provides guiding significance for the observation of regular black holes. -
In Ref. [36], a new type of regular black hole with sub-Planckian Kretschmann scalar curvature was proposed with the following metric:
$ {\rm d} s^{2}=-(1+2 \psi(r)) {\rm d} t^{2}+\frac{1}{(1+2 \psi(r))} {\rm d} r^{2}+r^{2} {\rm d} \Omega^{2}, $

(3) where
$ \psi(r) $ is understood as the modified Newton potential, which is specified as$ \psi(r)=-\frac{M}{r} {\rm e}^{\frac{-\alpha_0M^x}{r^n}}. $

(4) The modified Newton potential is characterized by an exponentially suppressed form with a deviation parameter
$ \alpha_0 $ . Obviously, when$ \alpha_0=0 $ , it returns to the standard Schwarzschild black hole. The metric of this type of regular black hole was originally proposed in [36] based on the motivation that the GUP may introduce the effects of tidal force on any object with finite size bounded below by the minimal length [12, 47]. In this sense, the dimensionless parameter$ \alpha_0 $ arises from the quantum effects of gravity and characterizes the modification of the standard Heisenberg uncertainty principle due to quantum gravity1 . Furthermore, the exponentially suppressed form of the modified Newtonian potential seems reasonable because its corrections become significant only in the range of the center of the black hole, such that the classical singularity can be avoided, and simultaneously without significantly changing the geometry in the region with weak gravity. Alternatively, several motivations leading to the modified Newton potential can be found in literature from the viewpoint of classical gravity theory. For instance, in [48], some regular black hole solutions are generated by coupling nonlinear electrodynamics and gravity theory, in which the deviation parameter$ \alpha_0 $ plays the role of the magnetic charge of the nonlinear field. The behavior of Kretschmann scalar curvature at the core depends on both the factors x and n. In Ref. [36], it was noted that to guarantee the existence of the horizon and for the scalar curvature to be sub-Planckian, the two factors must satisfy the conditions$ n\geq x \geq n/3 $ and$ n\geq 2 $ . Furthermore, as$ r\rightarrow 0 $ , the space time is characterized by a Minkowskian core, unlike well-known regular black holes, such as Bardeen, Hayward, and Frolov black holes, which are characterized by a de-Sitter core. Nevertheless, a one-to-one correspondence between such regular black holes with a Minkowskian core and those with a de-Sitter core was constructed in [36]. Explicitly, given a regular black hole with a Minkowskian core, which is described by Eq. (4), there is a corresponding regular black hole with a de-Sitter core whose Newton potential$ \psi(r) $ is given by$ \psi(r)=-\frac{M r^{\frac{n}{x}-1}}{(r^n+x \alpha_0 M^{x})^{1/x}}. $

(5) Bardeen black holes are simply given by specifying
$x=2/3,\;n=2$ , whereas Hayward black holes are given by$x=1,\; n=3$ . These two types of regular black holes exhibit identical asymptotic behaviors at large scales but possess different cores at the center. Therefore, it is intriguing to explore practical ways to distinguish between them via possible astronomical observation in the future. Here, as the starting point, we investigate this issue from the theoretical perspective by comparing the distinct behavior of the photon spheres and marginally stable circular orbits of massive particles over the two types of backgrounds.Now, we present several basic properties of regular black holes with the metric given by Eqs. (3) and (4). In general, the location of the horizon is determined by
$ 1+2\psi(r_h)=0 $ , namely,$ 2M=r_h{\rm e}^{{\alpha_0M^x}/{r_h^n}}. $

(6) From this equation, we may obtain the radius of the horizon
$ r_h $ as the function of mass,$ r_H=\left[-\frac{M^xn\alpha_0}{W(-2^{-n}M^{x-n}n\alpha_0)}\right]^{\frac{1}{n}}, $

(7) where W is the Lambert-W function, which allows two possible branches of solutions with appropriate values of
$ \alpha_0 $ , corresponding to the outer and inner horizons.Next, we consider the geodesics of photons and massive particles over such a background. First, we express the geodesic equation over these regular black holes with metric (3), which gives the form
$ \begin{aligned}[b] g_{\mu \nu}\frac{{\rm d}x^{\mu}}{{\rm d}\lambda}\frac{{\rm d}x^{\nu}}{{\rm d}\lambda}=&-(1+2\psi)\left(\frac{{\rm d}t}{{\rm d}\lambda}\right)^2+\frac{1}{(1+2\psi)}\left(\frac{{\rm d}r}{{\rm d}\lambda}\right)^2\\&+r^2\left(\frac{{\rm d}{\theta}}{{\rm d}\lambda}\right)^2+r^2\sin^2\theta\left(\frac{{\rm d}\phi}{{\rm d}\lambda}\right)^2=\epsilon, \end{aligned} $

(8) where
$ \epsilon=0 $ for photons, and$ \epsilon=-1 $ for massive particles. Because there are two Killing vectors, namely,$ (\partial /\partial t)^a $ and$ (\partial /\partial \phi)^a $ , for the space time, there are two corresponding conservative quantities for freely moving particles, namely, the energy E and angular momentum L, which are separately by$ E=(1+2\psi)\left(\frac{{\rm d}t}{{\rm d}\lambda}\right);\quad \quad L=r^2\left(\frac{{\rm d}\phi}{{\rm d}\lambda}\right). $

(9) In spherically symmetric space-time, without loss of generality, we may consider orbits with
$ \theta= {\pi}/{2} $ . We then substitute E and L into Eq. (8) and obtain the following equation:$ E^2=\left(\frac{{\rm d}r}{{\rm d}\lambda}\right)^2+(1+2\psi)\left(\frac{L^2}{r^2}-\epsilon\right). $

(10) Now, from this equation, it is straightforward to express the effective potential for geodesic orbits as
$ V_\epsilon(r)=\left(1+2\psi\right)\left(\frac{L^2}{r^2}-\epsilon\right). $

(11) As a result, the location of the photon sphere
$ r_c $ is determined by the vanishing of the derivative of the effective potential with respect to the radial coordinate, giving rise to$ -3Mr_c^n+{\rm e}^{M^xr_c^{-n}\alpha_0}r_c^{1+n}+M^{1+x}n\alpha_0=0. $

(12) In parallel, for massive particles, the location of the marginally stable circular orbit is denoted as
$ r_{e} $ , which is determined by the equation$ \begin{aligned}[b]& r_{e}^{2n}\left(-6M+{\rm e}^{M^{x}r_{e}^{-n}\alpha_{0}}r_{e}\right)\\ - & M^{x}n r_{e}^{n}\left[2M(-4+n)-{\rm e}^{M^{x}r_{e}^{-n}\alpha_{0}}n r_{e}\right]\alpha_0 \\ - & M^{2x}n^{2}\left(2M+{\rm e}^{M^{x}r_{e}^{-n}\alpha_{0}}r_{e}\right)\alpha_0^2=0. \end{aligned} $

(13) The derivation of this equation can be found in the next sections for special x and n.
Following the strategy presented in [41], we may define two dimensionless quantities as
$ \omega=\frac{r}{\alpha_0^{1/(n-x)}};\quad\quad\quad z=\frac{M}{\alpha_0^{1/(n-x)}}, $

(14) and then Eqs. (7), (12), and (13) can be rewritten as
$ \omega_{H}=2z\left[\frac{\theta}{W(\theta)}\right]^{\frac{1}{n}}; \quad\quad \theta=-\frac{n}{2^n z^{n-x}}, $

(15) and
$ -3z\omega_c^n+{\rm e}^{z^{x}\omega_c^{-n}}\omega_c^{1+n}+z^{1+x}n=0, $

(16) and
$ \begin{array}{l} ~~~\omega_{e}^{2n}\left(-6z+{\rm e}^{z^{x}\omega_{e}^{-n}}\omega_{e}\right)-z^{x}n \omega_{e}^{n}\left[2z(-4+n)-{\rm e}^{z^{x}\omega_{e}^{-n}}n \omega_{e}\right] \\ -z^{2x}n^{2}\left(2z+{\rm e}^{z^{x}\omega_{e}^{-n}}\omega_{e}\right)=0. \end{array}$

(17) This means that under the condition
$ x\neq{n} $ , we may plot the locations of the horizon, photon sphere, and marginally stable circular orbit as functions of z, which exhibit a universal behavior independent of the deviation parameter$ \alpha_0 $ . Nevertheless, we can easily derive the effects of the deviation parameter using the parameters$ M=z\alpha_0^{\frac{1}{n-x}} $ and$ r=\omega\alpha_0^{\frac{1}{n-x}} $ . -
In this section, we investigate the photon sphere and marginally stable circular orbit over a regular black hole with
$ x=2/3 $ and$ n=2 $ , which correspond to a Bardeen black hole at large scales. The thermodynamic behavior of this black hole as well as the feature of Kretschmann scalar curvature was investigated in detail in [36].First, we present the basic properties of the regular black hole with
$ x=2/3 $ and$ n=2 $ . The location of the horizon is given by Eq. (7). Note that the Lambert-W function has two branches in the real region [49, 50, 51], which give rise to the inner and outer horizons separately for this regular black hole as$ \omega_{H^+}=2z\left[\frac{\theta}{W_{0}(\theta)}\right]^{1/2};\quad \omega_{H^-}=2z\left[\frac{\theta}{W_{-1}(\theta)}\right]^{1/2};\quad \theta=-\frac{1}{2z^{4/3}}. $

(18) We plot the inner and outer horizons as functions of mass in Fig. 1. As shown in this figure, with the decrease in the mass, the inner and outer horizons become closer and finally merge at some critical point. The location of this critical point can be evaluated using a feature of the Lambert-W function as follows:
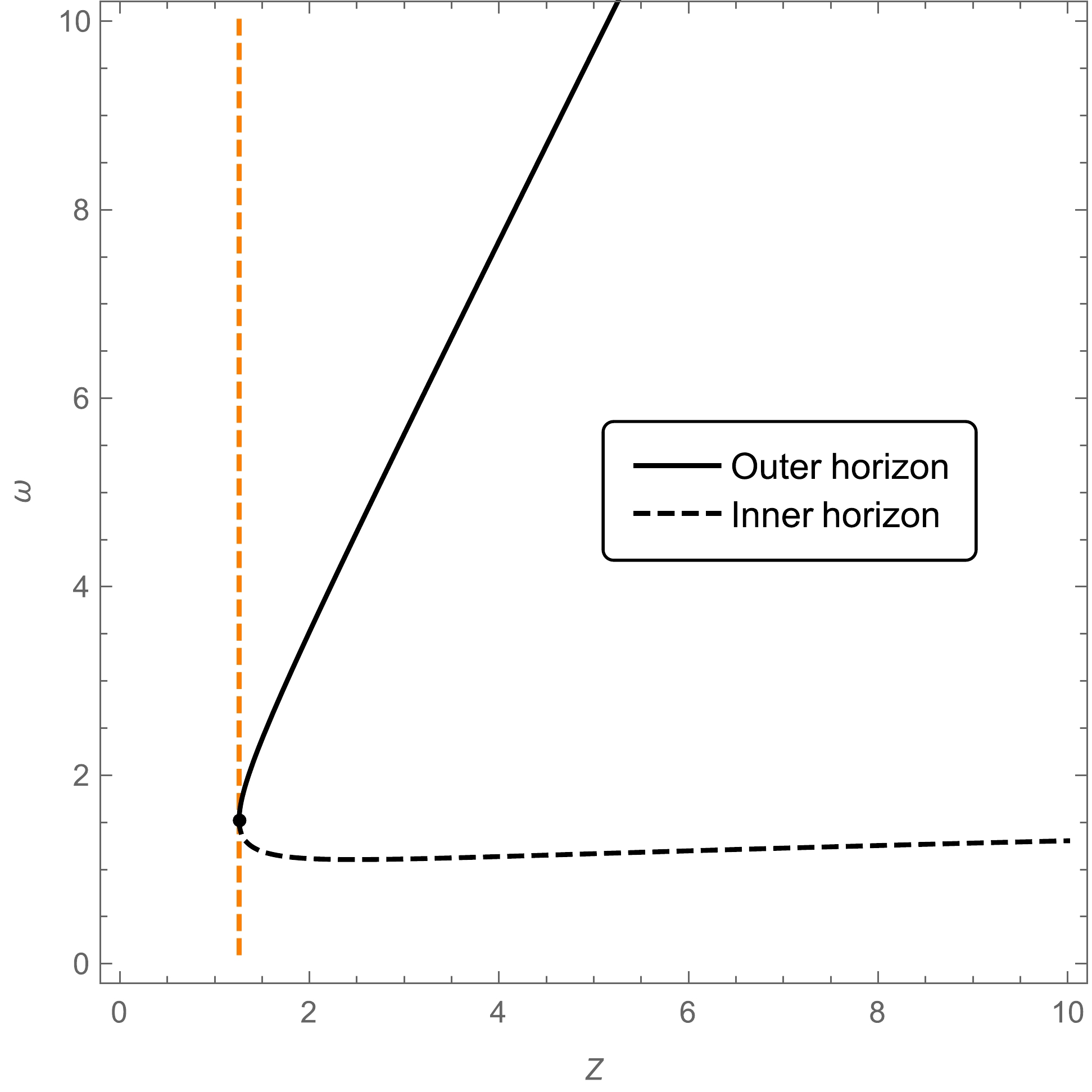
Figure 1. (color online) Outer horizon (black solid line) and inner horizon (black dashed line) of the black hole with
$ x=2/3 $ and$ n=2 $ . The vertical dashed line in orange is the borderline between the region in the black hole phase (right) and the region in the horizonless CMO phase (left).The two branches of the Lambert-W function merge at
$ W_{-1}(\theta)=W_{0}(\theta) $ , implying that$ W(\theta)=-1 $ . Using the identity of the Lambert-W function$ \theta=W(\theta){\rm e}^{W(\theta)}, $

(19) we find that the inner and outer horizons merge at
$ \theta= -1/e $ , namely,$ z=\frac{M}{\alpha_0^{3/4}}=\left(\frac{e}{2}\right)^{3/4}=1.258...;\quad \omega= \frac{r}{\alpha_0^{3/4}}=1.526.... $

(20) As a result, the condition for the existence of the horizon is
$ \theta\geq -1/e $ , namely,$ z\geq \left(\frac{e}{2}\right)^{3/4}, $

(21) below which the horizon disappears such that the black hole becomes a CMO. It is interesting to note that this situation is in contrast with that of the standard Schwarzschild black hole, where the horizon does not disappear as the mass decreases but deceases to zero with its mass.
-
Next, we consider the property of photon spheres over this background. The effective potential is given by
$ V_\epsilon(\omega)=\left(1-\frac{2z {\rm e}^{-\frac{z^{2/3}}{\omega^2}}}{\omega}\right)\left(\frac{L^2}{\omega^2}-\epsilon\right). $

(22) For null trajectories, the effective potential is
$ V_0(\omega)=\left(1-\frac{2z{\rm e}^{-\frac{z^{2/3}}{\omega^2}}}{\omega}\right)\left(\frac{L^2}{\omega^2}\right). $

(23) Thus, the location of the circular photon orbit can be determined by
$ V_{0}'(\omega_{c})=0 $ , leading to$ -3z\omega_{c}^2+{\rm e}^\frac{z^{2/3}}{\omega_{c}^2}\omega_{c}^3+2z^{5/3}=0. $

(24) We numerically plot the radius of the photon sphere as a function of mass in Fig. 2. First, we note without surprise that the radius of the photon sphere is always larger than the outer horizon. In particular, if we rewrite the equation for the photon sphere in terms of M and r, it becomes
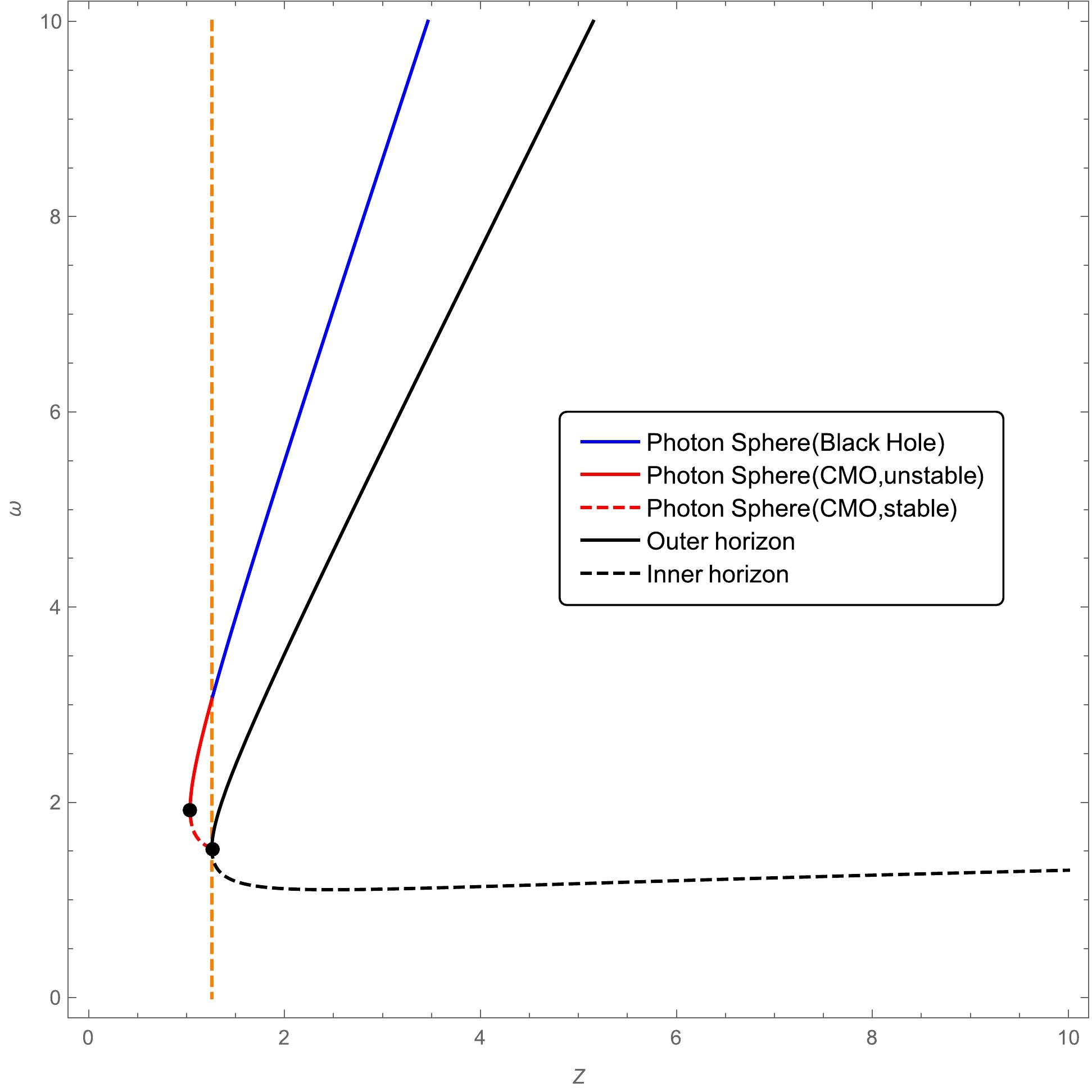
Figure 2. (color online) Location of photon spheres in the spacetime with
$ x=2/3 $ and$ n=2 $ . The blue line represents the location of photon spheres in the black hole phase, whereas the red solid line is the location of unstable photon spheres in the CMO phase, and the red dashed line is the location of stable photon spheres in the CMO phase. The turning point of each curve is marked by a black dot.$ -3Mr_{c}^{2}+{\rm e}^{\frac{M^{2/3}\alpha_0}{r_{c}^{2}}}r_{c}^3+2M^{5/3}\alpha_0=0. $

(25) Obviously, when
$ \alpha_0 $ is vanishing, the location of the photon sphere is$ r_c=3m $ , which is a well-known result for Schwarzschild black holes. Second, we find that in the horizonless CMO phase, the radius of the photon sphere becomes double-valued, as illustrated in Fig. 2. This phenomenon is consistent with the results presented in [52, 53], where it was found that photon spheres always appear in pairs outside a horizonless compact object. The location of the turning point is given by${\rm d}z/{\rm d}\omega_{c}=0$ , namely,$ \frac{{\rm d}z}{{\rm d}{\omega_{c}}}=\frac{2{\rm e}^\frac{z^{2/3}}{\omega_{c}^2}z^{2/3}+6z\omega_{c}-3{\rm e}^\frac{z^{2/3}}{\omega_{c}^2}\omega_{c}^{2}}{10z+2{\rm e}^\frac{z^{2/3}}{\omega_{c}^2} \omega_{c}-9z^{1/3}\omega_{c}^2}=0. $

(26) Numerically, we find that the coordinates of the turning point are
$ (z=1.037..., \omega=1.929...) $ .In summary, we argue that photon spheres exhibit an abundant structure in this background. In the region of the black hole phase
$ (z\geq 1.258) $ , the radius of the photon sphere is single-valued and approaches$ 3M $ as$ \alpha_0 $ tends to zero. In the region of the CMO phase with$ (1.258 \geq z\geq 1.037) $ , the radius of the photon sphere has two solutions with the same mass, whereas in the region with$ (z < 1.037) $ , we find no photon sphere. -
Next, we consider the stability of photon spheres, which is related to the second order of the derivative of the effective potential. The stable photon orbit is located at a place where
$ V''_{0}(\omega_{c})\geq 0 $ ,$ V''_{0}(\omega_{c})= \frac{2{\rm e}^{-\frac{z^{2/3}}{\omega_{c}^2}}L^2\left(-12z\omega_{c}^{4}+3{\rm e}^{\frac{z^{2/3}}{\omega_{c}^2}}+18z^{5/3}\omega_{c}^2-4z^{7/3}\right)}{\omega_{c}^{9}}\geq 0. $

(27) Therefore, we have
$ -12z\omega_{c}^4+3{\rm e}^\frac{z^{2/3}}{\omega_{c}^2}\omega_{c}^5+18z^{5/3}\omega_{c}^2-4z^{7/3}\geq 0. $

(28) We can identify the stable region of photon orbits by numerically solving this equation. Combining Eqs. (24) and (28), we can obtain the demarcation point of whether the photon sphere orbit is stable or unstable, as illustrated in Fig. 2. We find that the photon sphere is not stable in the region of the black hole phase, whereas in the region of the CMO phase, the upper branch is unstable, but the lower branch is stable.
-
For massive particles, we set
$ \epsilon=-1 $ in the effective potential$ V_{-1}(\omega)=\left(1-\frac{2z {\rm e}^{-\frac{z^{2/3}}{\omega^2}}}{\omega}\right)\left(\frac{L^2}{\omega^2}+1\right). $

(29) Hence, the radius of circular orbits can be determined by
$ V'_{-1}(\omega_{e})=0 $ , leading to$ z\omega_{e}^{4}-2\omega_{e}^{5/3}z^{2}-L^{2}\left(-3z\omega_{e}^{2}+{\rm e}^{\frac{z^{2/3}}{\omega_{e}^2}}\omega_{e}^3+2z^{5/3}\right)=0. $

(30) With the above equation, the angular momentum can be written as
$ L^2=\frac{z\omega_{e}^{4}-2\omega_{e}^{5/3}z^{2}}{-3z\omega_{e}^{2}+{\rm e}^\frac{z^{2/3}}{\omega^{2}}\omega_{e}^{3}+2z^{5/3}}. $

(31) The positivity of the angular momentum
$ (0 \leq L^2 < \infty) $ constrains the conditions for the existence of the circular orbit as$ z\omega_{e}^{4}-2\omega_{e}^{5/3}z^2 \geq 0 ;\quad -3z\omega_{e}^{2}+{\rm e}^{\frac{z^{2/3}}{\omega_{e}^2}}\omega_{e}^{3}+2z^{5/3} >0. $

(32) Furthermore, the stability of these circular orbits is determined by the second derivatives of the effective potential, namely,
$ V_{-1}''(\omega_{e})\geq 0 $ , which requires$ \begin{aligned}[b]& -\omega_{e}\left(\omega_{e}^{4}+4z^{2/3}\omega_{e}^{2}-4z^{4/3}\right)\\&+{\rm e}^\frac{-z^{2/3}}{\omega_{e}^{2}}\left(6z\omega_{e}^{4}-8z^{5/3}\omega_{e}^{2}+8z^{7/3}\right) \geq 0. \end{aligned} $

(33) The equals sign in the above equation gives rise to the location of the marginally stable circular orbit, which is plotted as a curve in the
$ (z, \omega) $ plane, as illustrated in Fig. 3. As shown in this figure, in the black hole phase, the marginally stable circular orbit is single-valued, whereas in the region of the CMO phase, there are two possible marginally stable circular orbit locations for a fixed value of z. Moreover, the curve of the marginally stable circular orbit does not terminate at the horizon but at the photon sphere. This result is similar to that of other regular black holes in [41].
Figure 3. (color online) Location of the marginally stable circular orbit for massive particles in the spacetime with
$ x=2/3 $ and$ n=2 $ . The purple solid line represents the location of the marginally stable circular orbit in the black hole phase, whereas the purple dashed line is the marginally stable circular orbit in the CMO phase. In the region shaded in orange, all the circular orbits are unstable, whereas in the region shaded in pink, all the circular orbit are stable. The region shaded in green denotes the place where the circular orbit does not exist. The turning point of each curve is marked by a black dot.The turning point of the curve of the marginally stable circular orbit can be obtained by solving
${\rm d} z/{\rm d}\omega_{e}=0$ , which gives rise to$ \begin{aligned}[b]& 16z^{3}-16z^{3/7}\omega_{e}^{2}+4{\rm e}^{\frac{z^{2/3}}{\omega_{e}^2}} z^{4/3}\omega_{e}^{3}-4z^{5/3}\omega_{e}^{4}\\ - & 12 {\rm e}^{\frac{z^{2/3}}{\omega_{e}^2}}z^{2/3}\omega_{e}^{5}+24z\omega_{e}^{6}-5{\rm e}^{\frac{z^{2/3}}{\omega_{e}^2}}\omega_{e}^{7}=0\end{aligned} $

(34) The numerical analysis indicates that the turning point is located at
$ z=\frac{M}{\alpha_{0}^{3/4}}=0.850...;\quad \omega=\frac{r}{\alpha_{0}^{3/4}}=2.807.... $

(35) In summary, we remark that the circular orbits of massive particles exist only in the region outside photon spheres. In particular, those between the curve of the marginally stable circular orbit and the curve of the photon sphere are unstable, whereas those outside the curve of the marginally stable circular orbit are stable, as illustrated in Fig. 3.
-
It is instructive to compare the photon sphere as well as marginally stable circular orbits over the spacetime with
$(x=2/3,\; n=2)$ and those over Bardeen spacetime because these two spacetimes have the same asymptotic behavior at large scales in the radial direction.Bardeen black holes have a dS core. A previous investigation on photon orbits over Bardeen black holes can be found in [54]. With the same value of the deviation parameter
$ \alpha_0 $ , the effective potential is given by$ V_\epsilon(\omega)=\left[1-\frac{2z\omega^2}{\left(\omega^2+\dfrac{2}{3}z^{2/3}\right)^{3/2}}\right]\left(\frac{L^2}{\omega^2}-\epsilon\right). $

(36) Thus, the radius of the photon circular orbits is determined by
$ V'_0(\omega_{c_{2}})=0 $ , namely,$ -\frac{2}{\omega_{c_2}^3}+\frac{54\sqrt3 z\omega_{c_2}}{\left(3\omega_{c_2}^2+2z^{2/3}\right)^{5/2}}=0. $

(37) For massive particles, the marginally stable circular orbit can be obtained in a parallel way to that of the black hole with
$ x=2/3 $ and$ n=2 $ , which is given by$ \begin{aligned} &64 z^2 \left({2z^{2/3}+3\omega_{e_2}^2}\right)^{1/2}-162z^{2/3}\omega_{e_2}^{4}\left(2z^{2/3}+3\omega_{e_2}^{2}\right)^{1/2}\\ - & 27\omega_{e_2}^{6}\left[\left(2z^{2/3}+3\omega_{e_2}^{2}\right)^{1/2}-6\left(3\right)^{1/2}z\right]=0. \end{aligned} $

(38) We compare the radius of photon spheres as well as marginally stable circular orbits in these two spacetimes with the same deviation parameter in Fig. 4. In the black hole phase, it is difficult to distinguish between the regular black hole with
$(x=2/3,\; n=2)$ and the Bardeen black hole by detecting either the photon sphere or the marginally stable circular orbit because these curves almost overlap. Nevertheless, we may theoretically analyze their differences by expanding the radius of the photon sphere in series of the deviation parameter$ \alpha_0 $ for these two black holes. For Bardeen black holes, we find
Figure 4. (color online) Comparison of photon spheres and marginally stable circular orbits in the spacetime with a Minkowskian core
$ (x=2/3, n=2) $ and those in Bardeen spacetime with a dS core.$ r_{c_2}=3M+\frac{5}{9M^{1/3}}\alpha_{0}+\mathcal{O}[\alpha_0]^2, $

(39) whereas for the black hole with
$ (x=2/3,n=2) $ , we have$ r_{c}=3M-\frac{5}{9M^{1/3}}\alpha_0+\mathcal{O}[\alpha_0]^2. $

(40) First, in comparison with the standard result of a Schwarzschild black hole, which is
$ 3M $ , we find that the radius of the photon sphere in the Bardeen black hole increases, whereas the radius of the photon sphere in the black hole with$ (x=2/3, n=2) $ decreases. In particular, with the decrease in mass, the discrepancy becomes larger. We remark that the above result coincides with the result in [38], where the shadow of these regular black holes were compared and it was found that the shadow of the black hole with$ (x=2/3, n=2) $ was more deformed and the size was smaller. We may also expand the radius of the marginally stable circular orbit in the two spacetimes near$ \alpha \rightarrow 0 $ . For Bardeen black holes, we find$ r_{e_2}=6M+\frac{19}{18M^{1/3}}\alpha_0+\mathcal{O}[\alpha_0]^{2}. $

(41) For the black hole with
$ (x=2/3, n=2) $ , we have$ r_{e}=6M+\frac{19}{3M^{1/3}}\alpha_0+\mathcal{O}[\alpha_0]^{2}. $

(42) We find that both radii are larger than
$ 6M $ , but the radius of the marginally stable circular orbit in the black hole with$ (x=2/3, n=2) $ is slightly larger than that in the Bardeen black hole. In the region of the CMO phase, which could be viewed as the remnants of the evaporation of these two black holes, the behavior of these curves are different and, in principle, can be distinguished by the observation, as demonstrated in Fig. 4. From Eqs. (37) and (38), we can obtain the turning points of the curves of the photon sphere and marginally stable circular orbit using${\rm d}z/{\rm d}\omega_{e}=0$ for Bardeen spacetime. We collate the locations of these turning points in the two different space times in Table 1.Horizon Photon sphere Marginally stable circular orbit $ n=2, x=1 $ 

( $ 1.359 $ ,

$ 1.649 $ )

( $ 1.050 $ ,

$ 1.953 $ )

( $ 0.806 $ ,

$ 2.660 $ )

$ n=2, x=2/3 $ 

( $ 1.259 $ ,

$ 1.527 $ )

( $ 1.037 $ ,

$ 1.929 $ )

( $ 0.850 $ ,

$ 2.807 $ )

$ Bardeen $ 

( $ 1.092, 1.189 $ )

( $ 0.927, 1.592 $ )

( $ 0.788, 2.424 $ )

$ n=3, x=1 $ 

( $ 1.010 $ ,

$ 1.465 $ )

( $ 0.794 $ ,

$ 1.731 $ )

( $ 0.595 $ ,

$ 2.403 $ )

$ Hayward $ 

( $ 0.918, 1.224 $ )

( $ 0.743, 1.549 $ )

( $ 0.576, 2.258 $ )

Table 1. Turning points of the curves representing the location of the horizon, photon sphere, and marginally stable circular orbit in the
$ (z,\omega) $ plane for various regular black holes. -
In this section, we investigate photon spheres and marginally stable circular orbits for massive particles in the spacetime with
$ x=1 $ and$ n=3 $ , which corresponds to Hayward black holes at large scales. Its thermodynamic behavior and the feature of Kretschmann scalar curvature can be found in [36].In this background, the outer and inner horizons are given by
$ \omega_{H^+}=2z\left[\frac{\theta}{W_{0}(\theta)}\right]^{1/3};\quad \omega_{H^-}=2z\left[\frac{\theta}{W_{-1}(\theta)}\right]^{1/3};\quad \theta=-\frac{3}{8z^2}. $

(43) We plot the locations of the outer and inner horizons in Fig. 5. The point where the inner and outer horizons meet is given by
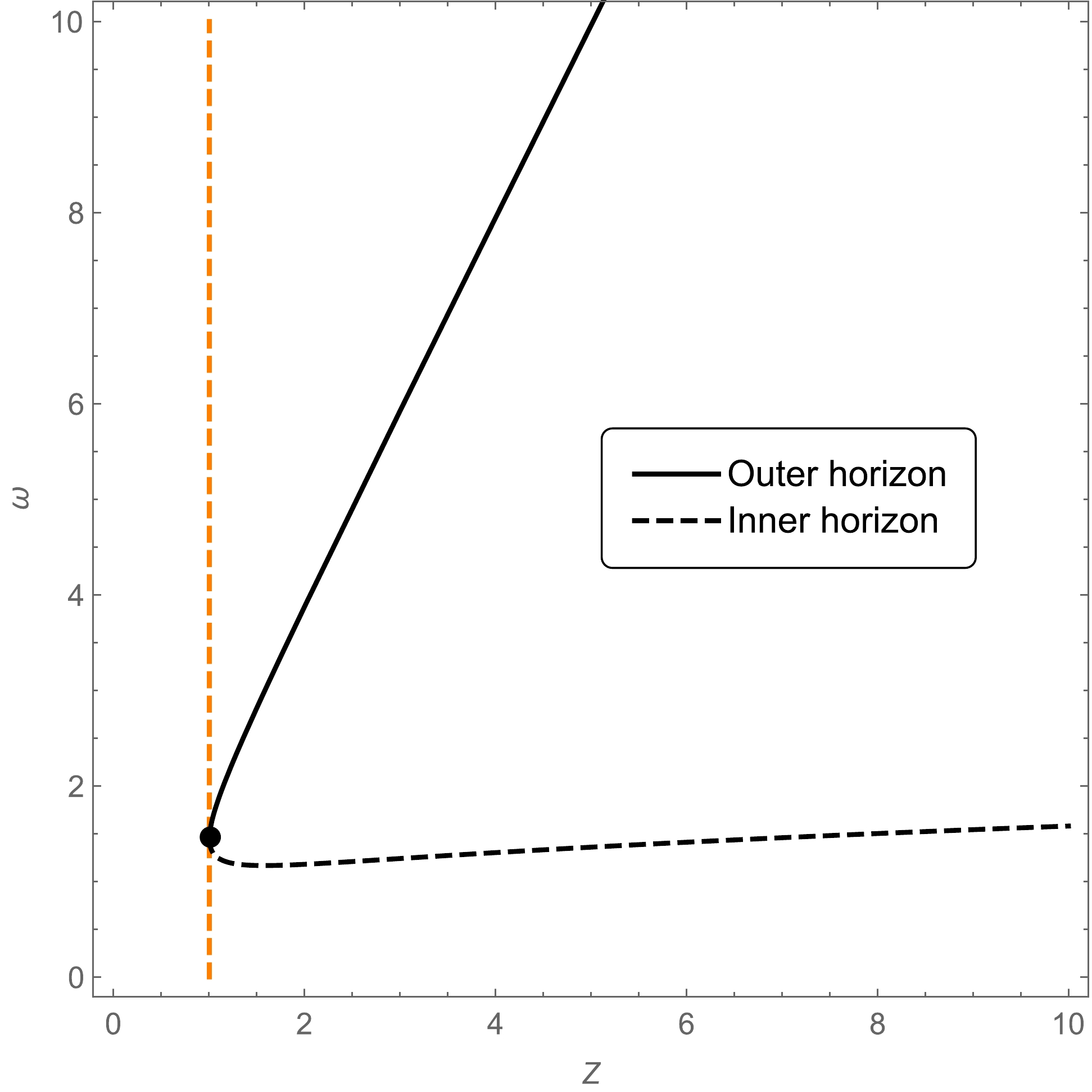
Figure 5. (color online) Outer horizon (black solid line) and inner horizon (black dashed line) of the black hole with
$ x=1 $ and$ n=3 $ . The vertical dashed line in orange is the borderline between the region in the black hole phase (right) and the region in the CMO phase (left).$ z=\frac{M}{\alpha_0^{1/2}}=1.010...;\quad \omega=\frac{r}{\alpha_0^{1/2}}=1.465.... $

(44) -
The effective potential used to determine the geodesic trajectory of photons is given by
$ V_0(\omega)=\left(1-\frac{2z {\rm e}^\frac{-z}{\omega^3}}{\omega}\right)\left(\frac{L^2}{\omega^2}\right). $

(45) Setting
$ V_{0}'(\omega_c)=0 $ , we find that the radius of circular photon orbits is determined by$ -3z\omega_{c}^3+{\rm e}^\frac{z}{\omega_{c}^3}\omega_{c}^4+3z^2=0. $

(46) Similarly, the stability of photon spheres requires
$ V_{0}''(\omega_c)\geq0 $ , leading to$ -4z\omega_{c}^6+{\rm e}^\frac{z}{\omega_{c}^3}\omega_{c}^7+10z^2 \omega_{c}^3-3z^3 \geq 0. $

(47) We obtain the turning point using
${\rm d}z/{\rm d}\omega_{c}=0$ , which gives rise to$ z=\frac{M}{\alpha_0^{1/2}}=0.794...;\quad \omega=\frac{r}{\alpha_0^{1/2}}=1.731.... $

(48) We plot the radius of photon spheres as a function of mass in Fig. 6.

Figure 6. (color online) Location of photon spheres in the spacetime with x = 1 and n = 3. The blue line represents the location of photon spheres in the black hole phase, whereas the red solid line is the location of unstable photon spheres in the CMO phase, and the red dashed line is the location of stable photon spheres in the CMO phase. The turning point of each curve is marked by a black dot.
-
For massive particles, the effective potential is given by
$ V_{-1}(\omega)=\left(1-\frac{2z {\rm e}^\frac{-z}{\omega^3}}{\omega}\right)\left(\frac{L^2}{\omega^2}+1\right). $

(49) Then, the radius of circular orbits
$ \omega_{e} $ is determined by$ V_{-1}'(\omega_{e})=0 $ , which gives$ z\omega_{e}^2\left(\omega_{e}^3-3z\right)-L^2\left(-3z\omega_{e}^3+{\rm e}^\frac{z}{\omega_{e}^3}\omega_{e}^4+3z^2\right)=0. $

(50) Furthermore, the angular momentum for all circular orbits must satisfy
$ L^2=\frac{z\omega_{e}^2\left(\omega_{e}^3-3z\right)}{-3z\omega_{e}^3+{\rm e}^\frac{z}{\omega_{e}^3}\omega_{e}^4+3z^2}\geq 0, $

(51) which gives the region where the circular orbit for massive objects is allowed. The location of the marginally stable circular orbit is given by
$ {\rm e}^\frac{z}{\omega_{e}^3}\omega_{e}^7-18z^3+3z^2\omega_{e}\left(2\omega_{e}^2-3{\rm e}^\frac{z}{\omega_{e}^3}\right)+z\left(-6\omega_{e}^6+9{\rm e}^\frac{z}{\omega_{e}^3}\omega_{e}^4\right)= 0, $

(52) which produces a curve in the
$ (z, \omega) $ plane. We plot the location of the marginally stable circular orbit as a function of mass in Fig. 7. Keep going further, the turning point of the curve of marginally stable circular orbit is calculated by${\rm d}z/{\rm d}\omega_{e}=0$ , which turns out to be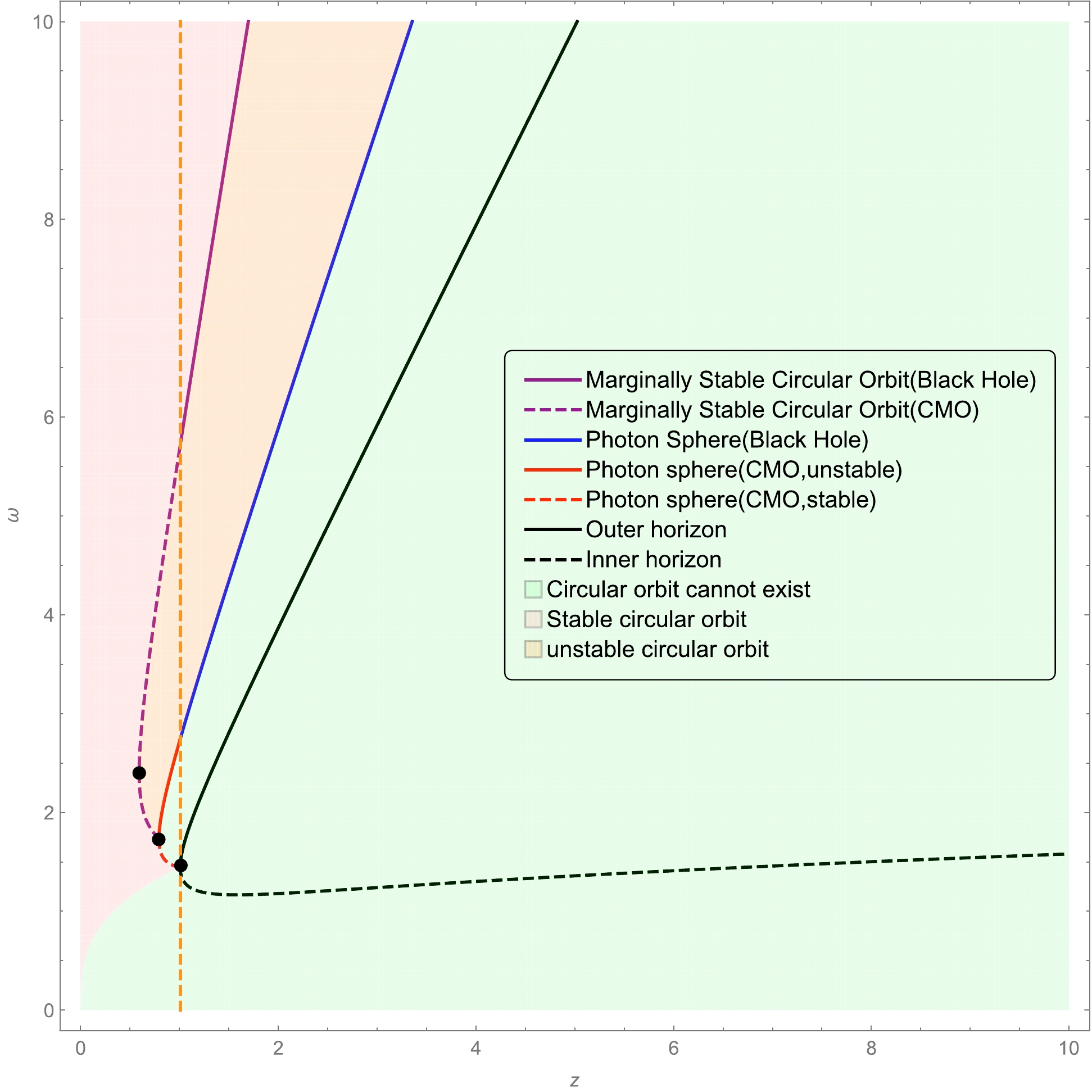
Figure 7. (color online) Location of the marginally stable circular orbit for massive particles in the spacetime with
$ x=1 $ and$ n=3 $ . The purple solid line represents the location of the marginally stable circular orbit in the black hole phase, whereas the purple dashed line is the marginally stable circular orbit in the CMO phase. In the region shaded in orange, all the circular orbits are unstable, whereas in the region shaded in pink, all the circular orbit are stable. The region shaded in green denotes the place where the circular orbit does not exist. The turning point of each curve is marked by a black dot.$ z=\frac{M}{\alpha_0^{1/2}}=0.595...;\quad \omega=\frac{r}{\alpha_0^{1/2}}=2.403.... $

(53) -
The effective potential of a Hayward black hole with a de-Sitter core is
$ V_\epsilon(\omega)=\left(1-\frac{2z\omega^2}{\omega^3+ z}\right)\left(\frac{L^2}{\omega^2}-\epsilon\right). $

(54) For null trajectories, the radius of photon spheres is given by
$ V_{0}'(\omega_{c_{2}})=0 $ , leading to$ \omega_{c_{2}}^5\left(-3z+\omega_{c_{2}}\right)+2z\omega_{c_{2}}^3+z^2=0. $

(55) For massive particles, the marginally stable circular orbit is given by
$ -8z^2+11z\omega_{e_2}^3+\omega_{e_2}^5\left(-6z+\omega_{e_2}\right)=0. $

(56) A similar discussion on circular orbits in Hayward spacetime can be found in [55]. Now, we compare photon spheres as well as the marginally stable circular orbits in these two different spacetimes in Fig. 8. In the black hole phase, the radius of the circular orbits of photons and massive particles can be expanded as a series of the deviation parameter
$ \alpha $ . (The left equation is for Hayward spacetime and the right equation is for the spacetime with$ (x=1,n=3) $ ).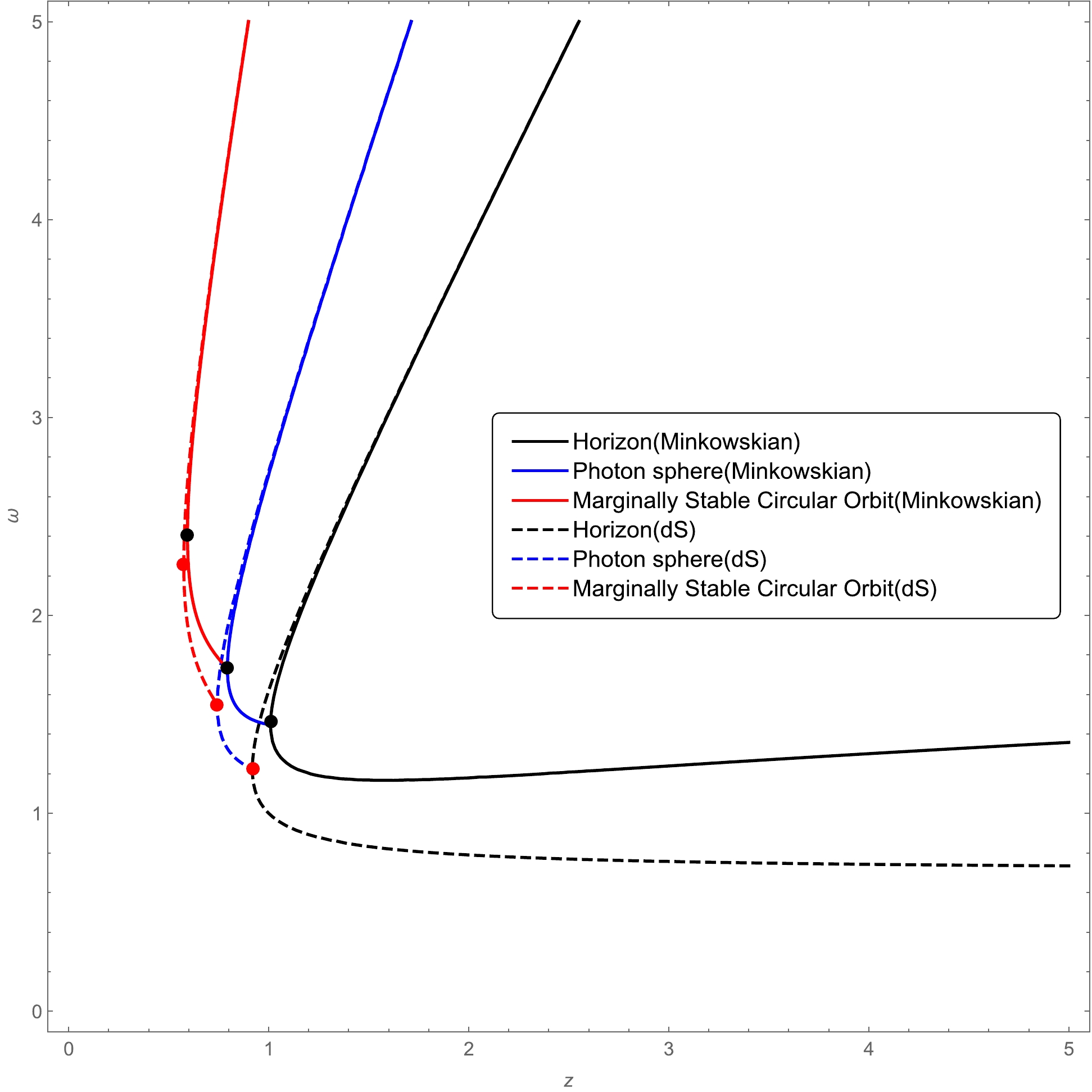
Figure 8. (color online) Comparison of photon spheres and marginally stable circular orbits in the spacetime with a Minkowskian core
$ (x=1, n=3) $ and those in Hayward spacetime with a dS core.Photon sphere:
$ r_{c_2}=3M+\frac{2}{9M}\alpha_0+\mathcal{O}[\alpha_0]^2;\quad r_{c}=3M-\frac{2}{9M}\alpha_0+\mathcal{O}[\alpha_0]^2. $

(57) Marginally stable circular orbit:
$ r_{e_{2}}=6M+\frac{11}{36M}\alpha_0+\mathcal{O}[\alpha_0]^2;\quad r_{e}=6M+\frac{19}{M}\alpha_0+\mathcal{O}[\alpha_0]^2. $

(58) Note that the radius of the photon sphere in the Hayward black hole is larger than the standard result
$ 3M $ in a Schwarzschild black hole, whereas that in the spacetime with$ x=1 $ and$ n=3 $ is smaller than$ 3M $ . The radius of the marginally stable circular orbit in both spacetimes is larger than the standard result$ 6M $ in a Schwarzschild black hole. In the CMO phase, both photon spheres and marginally stable circular orbits exhibit distinct behaviors in these two spacetimes. In particular, setting${\rm d}z/{\rm d}\omega_{e}=0$ and${\rm d}z/{\rm d}\omega_{c}=0$ , we can obtain the turning point of the curves of the photon sphere and marginally stable circular orbit in the two different spacetimes. These results are shown in Table 1. -
Strictly speaking, the photon sphere cannot be observed in celestial body observation. Instead, the critical impact parameter b is an observable measurement related to the radius of the photon sphere. In this section, we provide the constraint on the parameter
$ \alpha_0 $ by the observation data from the supermassive black hole at the center of the galaxy, M87*. We link the shadow diameter to the critical impact parameter, which receives corrections for regular black holes due to the presence of the modified Newton potential. Following the method proposed by Luminet in [56], we derive the critical impact parameter form for regular black holes with metric (3) as$ b=\sqrt{\frac{r^2_c}{1+2\psi(r_c)}}, $

(59) where
$ r_c $ is the radius of the photon sphere. For the black hole with$ n=2 $ and$ x=2/3 $ , the photon sphere is given by Eq. (25). In particular, for a small parameter$ \alpha_0 $ , we may expand the impact parameter as a series of$ \alpha_0 $ by combining Eqs. (40) and (59)$ b_1=3\sqrt{3}M-\frac{\alpha_0}{\sqrt{3}M^{1/3}}+\mathcal{O}[\alpha_0]^2. $

(60) In parallel, from Eqs. (57) and (59), we expand the impact parameter for the black hole with
$ n=3 $ and$ x=1 $ as$ b_2=3\sqrt{3}M-\frac{\alpha_0}{3\sqrt{3}M}+\mathcal{O}[\alpha_0]^2. $

(61) When
$ \alpha_0 \rightarrow 0 $ and$ b \rightarrow 3\sqrt{3}M $ , both$ b_1 $ and$ b_2 $ return to the standard result for Schwarzschild spacetime.According to the results of [57], M87* has rotation, but the degree of distortion caused by rotation is not significant. Thus, the M87* black hole can be approximately viewed as a rough circle, which can then be used to constrain the parameters of static spherically symmetric black holes. In [58], the diameter of the shadow of M87* is given by
$ d_{M87}=\frac{D \delta}{M} \approx 11.0\pm 1.5, $

(62) where D is the distance to M87*, and
$ \delta $ is the size of the shadow angle of the black hole at the center of the M87 galaxy. Within$ 1\sigma $ uncertainties, the shadow diameter ranges from 9.5 to 12.5 with the black hole mass M as the unit. Theoretically, because this quantity corresponds to$ 2b/M $ , we may constrain the parameter$ \alpha_0 $ by requiring that the theoretical value of the shadow diameter falls into this range for regular black holes. Specifically, for the black hole with$ n=2 $ and$ x=2/3 $ , we define the new coordinates$ \rho=r/M $ and$ \tau_1=\alpha_0/{M^{4/3}} $ . With these coordinates, we rewrite Eq. (25) and the horizon as$ -3{\rho}^2_{c_1}+{\rm e}^{\frac{\tau_1}{\rho_{c_1}^2}}\rho_{c_1}^3+2\tau_1=0;\quad \rho_{h_1}=2{\rm e}^{\frac{-\tau_1}{\rho_{h_1}^2}}. $

(63) Using Eq. (63), we can obtain the analytic form of
$ \tau_1 $ as$ \tau_1=\frac{1}{2}\left[ 3\rho^2_{c_1}-2\rho^2_{c_1} W\left(\frac{1}{2}{\rm e}^{3/2}\rho_{c_1}\right)\right]. $

(64) Then, the theoretical value of the shadow diameter can be written as a function of
$ \rho_c $ $ \chi_1=\frac{2b_1}{M}=2\sqrt{\frac{\rho^2_{c_1}}{1+2\psi(\rho_{c_1})}}. $

(65) Figure 9 illustrates the change in the location of the photon sphere and horizon with the deviation parameter
$ \tau $ after fixing M. For the black hole with$ n=2 $ and$ x=2/3 $ , Eq. (63) gives the range of the two parameters$ \tau_1 $ and$ \rho_1 $ under the condition that there is a horizon and photon spheres in the black hole phase,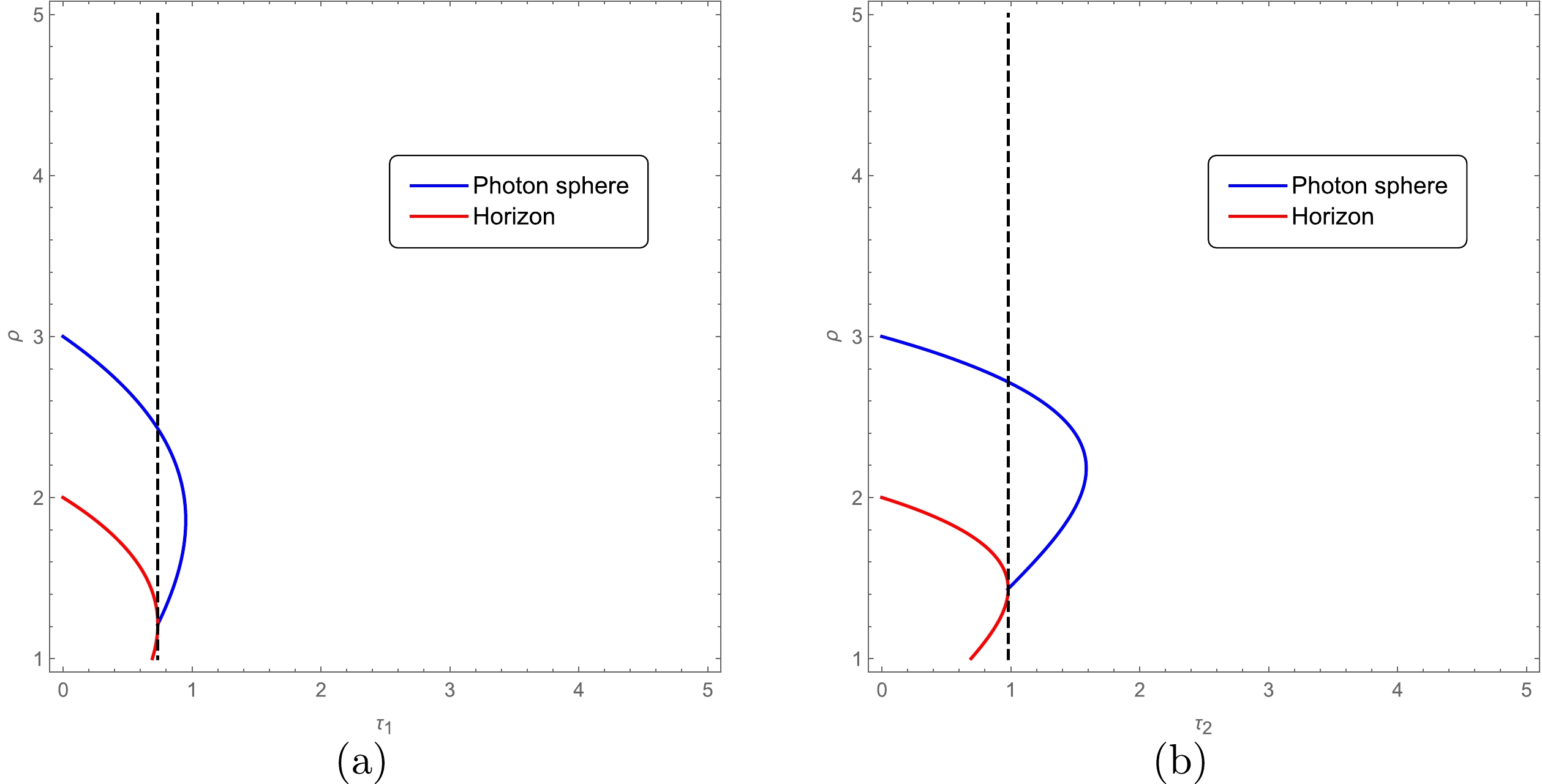
Figure 9. (color online) Relationship between the location of the photon sphere and the deviation parameter for the black hole with
$ n=2 $ and$ x=2/3 $ (a),$ n=3 $ and$ x=1 $ (b). The blue solid line is the location of the photon sphere, and the red solid line is the location of the horizon. The left region of the black dashed line is the phase of the black hole, and the right region is the phase of the CMO.$ 2.43 \leq \rho_1 \leq 3;\quad 0 \leq \tau_1 \leq 0.74, $

(66) which can also be observed from Fig. 9. Correspondingly, from Eq. (65), we obtain the range of
$ \chi_1 $ as$ 9.28 \lesssim \chi_1 \lesssim 10.39. $

(67) To be consistent with the astronomical observation, we know the shadow diameter
$ \chi_{1} $ is restricted to be no less than$ 9.5 $ . From Eqs. (65) and (64), we find that the ranges of$ \rho_{1} $ and$ \tau_{1} $ are further constrained as follows:$ 2.54 \leq \rho_1 \leq 3;\quad 0 \leq \tau_1 \leq 0.63. $

(68) That is, under the condition
$ 0 \lesssim \alpha_0 \lesssim 0.63 M^{4/3} $ , the range of the shadow diameter for this regular black hole is$ 9.50 \lesssim \chi_{1} \lesssim 10.39 $ , falling well into the observation range$ 9.50 \lesssim d \lesssim 12.5 $ .Similarly, for the black hole with
$ n=3 $ and$ x=1 $ , the new coordinates are$ \rho=r/M $ and$ \tau_2=\alpha_0/{M^2} $ . The relationship between the location of the photon sphere and the deviation parameter can be rewritten as$ -3\rho_{c_2}+{\rm e}^\frac{\tau_2}{\rho^3_{c_2}}\rho^4_{c_2}+3\tau_2=0 ;\quad \rho_{h_2}=2{\rm e}^{-\frac{\tau_2}{\rho^3_{h_2}}}. $

(69) Solving Eq. (69),
$ \tau_2 $ can be expressed as a function of$ \rho_{c_2} $ $ \tau_2=\rho^3_{c_2}-\rho^3_{c_2}W\left( \frac{e\rho_{c_2}}{3}\right). $

(70) Thus, the shadow diameter
$ \chi_2 $ is given by$ \chi_2=\frac{2b_2}{M}=2\sqrt{\frac{\rho^2_{c_2}}{1+2\psi(\rho_{c_2})}}. $

(71) In the black hole phase, the condition that there is a horizon and photon spheres requires that the range of the two parameters are
$ 0 \lesssim\tau_2 \lesssim 0.97;\quad 2.72 \lesssim \rho_{2} \lesssim 3.00. $

(72) This means that the range of the parameter
$ \alpha_0 $ is$ 0 \lesssim \alpha_0 \lesssim 0.97M^2 $ . The corresponding shadow diameter lies in the range$ 9.94 \lesssim \chi_2 \lesssim 10.39 $ , which is highly compatible with the current black hole diameter observed for M87*. It is worth noting that because the primary role of$ \alpha_0 $ is to prevent black holes from completely evaporating, its effect is more noticeable as$ r \rightarrow 0 $ , and a more precise range may be obtainable at this region. However,$ \alpha_0 $ has a relatively small influence on observables in the region outside the event horizon; therefore, the range of$ \alpha_0 $ obtained near$ r=r_c $ is relatively approximate. As astronomical observation accuracy improves or black holes in the late stages of evaporation are observed, it is expected that a more accurate range of$ \alpha_0 $ may be obtained. -
In this paper, we investigate the circular orbits of photons and massive particles in regular black holes with sub-Planckian curvature and a Minkowskian core, which exhibit an abundant structure and contrast with the results of standard Schwarzschild black holes. We find that in the black hole phase, the location of the photon sphere and marginally stable circular orbit is singe-valued, whereas in the CMO phase, it is double-valued. We also study the stability of these circular orbits. In the black hole phase, the photon sphere is unstable, whereas in the CMO phase, the upper branch is unstable and the lower branch is stable. The marginally stable circular orbit has two branches in the CMO phase. In the region between the curve of the photon sphere and the curve of the marginally stable circular orbit, all the circular orbits for massive particles are unstable, whereas outside the curve of the marginally stable circular orbit, all the circular orbits are stable. We also compare the locations of the photon sphere and marginally stable circular orbit in spacetime with a Minkowskian core and those in spacetime with a dS core. In the black hole phase, we find that the radius of the photon sphere in spacetime with a Minkowskian core is smaller than that in spacetime with a dS core. In the CMO phase, we calculate the turning points of the curves of the photon sphere and marginally stable circular orbit and find that these points are distinct in the two different types of spacetimes. This study provides a theoretical basis for the possible detection of regular black holes in astrophysical observation. Finally, we investigate the constraint on the parameter
$ \alpha_0 $ using the observation data from the black hole M87*. We find that within a reasonable range of$ \alpha_0 $ , the shadow of such regular black holes is highly compatible with the observed shadow from the black hole M87*. Our study provides guiding significance for the observation of regular black holes in the future.As the first step, we only study the astrophysical observables in spherically symmetric spacetime. One could definitely extend the analysis to rotating Kerr-like black holes with sub-Planckian curvature. In this case, the null geodesics with a circular orbit near the horizon of the black hole were derived and the shadow of black holes was plotted in [38]. However, detailed analyses on the circular orbits of massive particles and the CMO phase as the remnant of the evaporation of black holes are still absent. In addition, to conjecture that the remnant of the evaporation may be a candidate of dark matter, the stability of horizionless CMOs should be considered seriously. Thus, it is worth studying the quasinormal modes of this type of spacetime in the CMO phase.
-
We are grateful to Meng-He Wu, Zhong-Wen Feng, and Yun-Xian Chen for helpful discussions. In particular, we would like to thank the anonymous referee for valuable comments and suggestions, which helped improve the manuscript.
Astrophysical observables for regular black holes with sub-Planckian curvature
- Received Date: 2023-04-13
- Available Online: 2023-08-15
Abstract: We investigate the photon sphere and marginally stable circular orbit of massive particles over the recently proposed regular black holes with sub-Planckian curvature and a Minkowskian core. We derive the effective potential for geodesic orbits and determine the radius of circular photon orbits, with an analysis of the stability of these orbits. We extend our analysis to the background of a compact massive object (CMO) without a horizon, whose mass is below the lowest bound for the formation of a black hole. For massive particles, marginally stable circular orbits become double-valued in the CMO phase. Through a comparison with Bardeen and Hayward black holes, we also find that the locations of the photon sphere and marginally stable circular orbit in the CMO phase with a Minkowskian core are evidently different from those in the CMO phase with a dS core, which potentially provides a way to distinguish between these two types of black holes by astronomical observation. Finally, we present the observational constraint on the deviation parameter for such regular black holes using observed data from the black hole M87*.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: