-
Recently, the CDF collaboration announced their new measurement of the mass of the W boson,
$m_W = 80.4335\pm0.0094\; {\rm GeV}$ [1]. Such a value indicates a$ 7\sigma $ deviation from the standard model (SM) prediction$m_W^{\rm SM} = 80.357\pm0.006\; {\rm GeV}$ [1−3]. Meanwhile, it is also in tension with previous experimental measurements, including the most precise one from the ATLAS experiment$ m_W^{\rm ATLAS}=80.370\pm0.019\; {\rm GeV} $ [4] at$ \sim 3\sigma $ . Although the discrepancy might be caused by some unknown experimental or theoretical uncertainties, which requires comparative studies by other experiments and theorists, it could hint at new physics, and considerable effort has been made to provide an explanation in this direction [5−43].It is well-known that there is a residual global
$S U(2)$ symmetry of the Higgs potential in SM. Higgs doublet potential is invariant under$S O(4)\cong S U(2)_L\times S U(2)_R$ symmetry, while the Higgs vacuum expectation value (VEV) only breaks it down to the diagonal$S U(2)_V$ subgroup. Such a symmtery guarantees the tree-level value of the Veltman ρ parameter [44] to be unity,$ \begin{align} \rho\equiv\frac{m_W}{m_Z \cos\theta_W}=1\Big|_{\text{tree}}+\cdots, \end{align} $

(1) where
$ \cos\theta_W $ is the Weinberg mixing angle. Although the hypercharge$ U(1)_Y $ and Yukawa interactions explicitly break the custodial symmetry$S U(2)_V$ , their effects only emerge at the loop-level and result in small deviations from unity at the sub-percentage level. Given that previous measurements in the electroweak (EW) sector are consistent with SM predictions, beyond the SM (BSM) extensions with new scalars usually assume that the custodial symmetry$S U(2)_V$ is preserved in the scalar sector. For general k multiplet scalars, the tree-level formula of ρ is shown as [45, 46]$ \rho^{\rm tree} =\frac{\sum_k\eta_k\left[2j_k\left(j_k+1\right)-Y_k^2/2\right]\langle \phi_k \rangle^2} {\sum_k Y_k^2\langle \phi_k \rangle^2}, $

(2) where
$ \left\langle{\phi_k} \right\rangle $ is the VEV of the scalar field$ \phi_k $ ,$ j_k $ is the weak-isospin, and$ Y_k $ is its hypercharge, related to the electric charge by$ Q_k=j_{k,3}+Y_k/2 $ . Here, we assume that the real representations only have vanishing hypercharge, and therefore$ \eta_k $ is equal to$ 1 $ ($ 1/2 $ ) for a complex (real) representation. The tree-level relation$ \rho^{\rm tree}=1 $ can be automatically fulfilled for scalars with quantum numbers satisfying the condition$ (2j_k+1)^2-3Y_k^2=1 $ , regardless of whether the extra scalars develop VEVs or not.However, the newly released CDF II W mass indicates an obvious custodial symmetry violation (CSV) at a certain level. One can parameterize the effects of new physics phenomena in the EW sector using the oblique parameters S, T, and U [47−49], and the latest global fit of EW precision observables (EWPOs) including the
$ m_W $ anomaly shows that a large T value is favored for$\rm ST$ model and a large U parameter is favored for$\rm STU$ model [12]. Because both the T and U parameters violate custodial symmetry, it is time to re-examine the CSV models and the effects of custodial symmetry on the EWPOs and W boson mass. Because fermionic and vector bosonic extensions of the SM only generate CSV at the loop-level1 , we focus on the scalar extensions in this study to compare the CSV effect from the tree and loop levels, for example, whether the VEV parameterizing the CSV is zero or not.The paper is organized as follows. In Sec. II, we discuss the most general scalar extensions of the SM. Based on the symmetry property of the scalar potential, these can be categorized into two classes: the scalar sector with custodial symmetry and the scalar sector without custodial symmetry. In Sec. III, we introduce single scalar extensions of the SM and perform EW precision fit by directly calculating their S, T, and U parameters to check if they can help reduce the tension between the SM EW fit and the new CDF II
$ m_W $ measurement. The preferred new regions of parameter space are shown, and the effects of the extra scalar VEV are also discussed, in that without a VEV, the custodial symmetry can still be preserved in the Higgs doublet. We analyze the Georgi-Machacek (GM) model in Sec. IV as an example for custodial symmetric scalar extensions. The loop effects can alleviate the tension with several hundred GeV new scalars. Finally, we provide a conclusion in Sec. V. -
We consider models that extend the SM scalar sector with the addition of general
$S U(2)_L$ multiplets. Unitarity of scattering amplitudes involving pairs of scalars and pairs of$S U(2)_L$ gauge bosons constrains a complex scalar to have weak isospin$ j\leq 7/2 $ and a real scalar to have$ j\leq 4 $ , and scatterings involving a$ U(1)_Y $ gauge boson also place an upper limit on hypercharge Y depending on the size of multiplet [50]. These constraints become stronger if additional multiplets are added. Furthermore, to ensure no non-trivial electric charge ($ Q=j_3+Y/2 $ ), there is only a finite number of scalar multiplets that can be self-consistent.As mentioned in Sec. I, the relation
$ \rho^{\rm tree}=1 $ can be automatically satisfied under the condition$ \begin{align} (2j_k+1)^2-3Y_k^2=1. \end{align} $

(3) The only possibility beyond
$ j=1/2, Y=1 $ is a representation with weak isospin$ j=3 $ and$ Y=4 $ . Therefore, the scalar sector with arbitrary numbers of the doublet with$ Y=1/2 $ and septet with$ Y=4 $ automatically preserves the custodial symmetry in the scalar potential [51, 52]. The simplest model in this class is the two-Higgs-doublet model (2HDM), which has been discussed to explain the CDF-II W mass anomaly [1] and the newly oblique parameter fitting values [12] in Refs. [13−24, 26, 31, 36]. We do not discuss this case here and refer the readers to these references for further details2 . The septet model possesses highly charged scalars (Q up to 5), which may have unique (unusual) collider signatures [53]. It also predicts a negative S, which is favored by the W mass but might contradict the$ ST $ parameter fit assuming negligible U [51, 52]. Therefore, we leave the case of the scalar septet for future studies.In the SM, the custodial symmetry
$S U(2)_V$ can be identified as the residual diagonal subgroup of an accidental global$S U(2)_L\times S U(2)_R$ symmetry after EW symmetry breaking. It is, in principle, possible to have a scalar sector with multipleN-plets preserving custodial $S U(2)_V$ if imposing the global$S U(2)_L\times S U(2)_R$ symmetry on the entire scalar sector. These are the GM model [54, 55] and its generalizations [56−60], which lead to$ \rho=1 $ at tree-level.Apart from the above two classes, general scalar extensions of the SM do not possess symmetry in their scalar sector to preserve
$ \rho=1 $ at tree-level without parameter tuning. To simplify our discussion, we only consider single scalar extensions for the scenario where there is no custodial symmetry in the scalar sector. -
Though there is no custodial symmetry to preserve
$ \rho=1 $ at tree-level in single scalar extensions of the SM, the SM doublet itself still has a custodial symmetry as long as the additional scalar has a vanishing VEV, and the SM tree-level prediction of the ρ parameter is kept as$ \begin{aligned}[b] \rho^\text{tree}-1\simeq \left\{\eta\left[j\left(j+1\right)-Y^2\right]-2Y^2\right\}\times\left[4\frac{\left\langle{\phi}\right\rangle ^2}{v^2}+\mathcal{O}\left(\frac{\left\langle {\phi}\right\rangle ^4}{v^4}\right)\right]. \end{aligned} $

(4) A VEV of a scalar multiplet can contribute differently to the mass terms of the four components of the SM doublet in the Feynman–'t Hooft gauge, which can be understood as an explicit breaking of the custodial symmetry of the SM doublet potential.
Hence, to clarify our discussion, we consider two cases in this section: Case A, where no further VEV is developed except the SM Higgs doublet and only loop contributions can shift ρ, and Case B, where a VEV is developed for the additional scalar multiplet breaking the custodial symmetry of the SM doublet. We especially use real triplet and complex triplet extensions as our examples for the study of Case B.
-
A global
$ U(1) $ or$ \mathbb{Z}_2 $ symmetry arises accidentally in the renormalizable level scalar potential, which could protect the scalars from VEVs. Assuming that the parameters of the scalar potential are chosen to respect such symmetry without spontaneously breaking, there is no VEV being developed and the lightest particle is thus forced to be stable, which might be a possible dark matter candidate [61−65].The most general forms of the renormalizable scalar potential are discussed in detail in Refs. [53, 64, 65], and there are usually three free parameters for ϕ-H Higgs portal interactions depending on the quantum number of the multiplet in the
$ \mathbb{Z}_2 $ symmetric case. Two of these parameters, shown in Eq. (5), generate mass splittings among different isospin components, as discussed below [62, 63]. For the complex representation case, there is generally an additional term, whose exact form depends on the isospin and hypercharge of the scalar multiple. However, we note that this extra term only presents in high dimensional representation cases [64] and specific values of hypercharge ($ Y=0,\,\pm 1 $ ). Furthermore, it splits the complex neutral component into two real particles and also induces mixing between the charged states$ \phi^{+Q} $ and$ \phi^{-Q*} $ . For simplification, we do not consider such interaction here, and keeping this term will not significantly modify our conclusions.The most general gauge-invariant potential satisfying our requirements can be universally expressed as
$ \begin{aligned}[b] V=&m^2 H^\dagger H+\lambda\left(H^\dagger H\right)^2+m_\phi^2\phi^\dagger\phi+\lambda_1 H^\dagger H\phi^\dagger\phi\\&+\lambda_2 H^\dagger\tau^a H\phi^\dagger T^a\phi+\mathcal{O}\left(\phi^4\right), \end{aligned} $

(5) where
$ \tau^a $ and$ T^a $ are the generators of$S U(2)_L$ in the doublet and N-plet representations, respectively.$ \mathbb{Z}_2 $ symmetry (or global$ U(1) $ symmetry) forbids any terms with odd numbers of one of the fields. For$ j\geq 2 $ , the potential preserves an additional accidental global$ U(1) $ symmetry [63, 66]. The spontaneous breaking of the global$ U(1) $ symmetry would lead to an additional massless Goldstone, which would mediate a long-range interaction that has not yet been observed. The spontaneous breaking of$ \mathbb{Z}_2 $ through a VEV of the multiplet generally also breaks the EW symmetry, which can be used to explain the CDF-II anomaly, but is also tightly constrained by the ρ parameter. As emphasized at the beginning of this section, this part of our study is performed in a region of parameter space where multiplets do not develop any VEVs. It is known that the neutral component in the multiplet in such a case provides a good dark matter candidate. The VEV-developed case is studied in Sec. III.B for triplet models.The mass of particle
$ \phi^Q $ with charge$ Q=j_3+Y/2\geq 0 $ is given by$ \begin{align} m_{\phi^Q}^2=m_\phi^2+\frac{v^2}{2}\left(\lambda_1-\frac{1}{2}\lambda_2 j_3\right)\equiv m_{\phi^0}^2-\frac{1}{4}\lambda_2 v^2 Q ,\end{align} $

(6) where
$ v\simeq 246 $ GeV is the SM Higgs VEV, and we define the neutral particle mass as$ \begin{align} m_{\phi^0}^2\equiv m_\phi^2+\frac{v^2}{2}\left(\lambda_1+\frac{1}{4}\lambda_2 Y\right). \end{align} $

(7) To have a neutral particle, the value of
$ Y/2 $ cannot be arbitrary but must be one of$ \{-j_3, -j_3+1,\cdots, j_3\} $ , and we stick to such choices. Provided that the lightest stable particle$ \phi^0 $ is neutral,$ Y=2j_3 $ and$ \lambda_2<0 $ are required. However, we also consider the case where the lightest particle can be charged; therefore, we use the mass splitting$ \delta m\equiv(|\lambda_2|v^2/4)^{1/2} $ as a free parameter instead of$ \lambda_2 $ itself and do not worry about the sign of$ \lambda_2 $ 3 . Furthermore, note that in the case of a real multiplet (for example, a real triplet), the reality of the multiplet forbids the presence of a term proportional to$ \lambda_2 $ [53, 62, 65], which provides a degenerate spectrum at tree-level, and can hardly explain the observed W mass anomaly at this level. However, we find that loop effects can evade this issue and leave some valid parameter space, although it is not accessible in current or planned experiments (see the upper right panel in Fig. 2).
Figure 2. (color online) 90% (solid) and 99% (light) CL regions for the real (upper row + lower left panel) and complex (lower right) triplet models in light of the CDF II result [1]. See text for details.
The dominant constraints from EWPOs arise in the oblique parameters S, T, and U [47, 48] in a large set of BSM models known as "universal" models, in which deviations from the SM reside only in the self-energies of the vector bosons as long as the new states only couple to SM fermions via
$S U(2)_L\times U(1)_Y$ currents [49]4 . The W boson mass can then be expressed as a function of these oblique parameters [68, 69],$ \begin{align} m_W=m_{W}^{\rm SM}\left[1 - \frac{{\alpha}}{4\left({c_W}^{2}-{s_W}^{2}\right)}S + \frac{\alpha {c_W}^{2}}{2\left({c_W}^{2}-{s_W}^{2}\right)}T + \frac{{\alpha}}{8 {s_W}^{2}}U\right]. \end{align} $

(8) Although new physics can generally induce further effects, the scalar extensions we consider belong to "universal" theories, especially in that our scalars are inert without couplings to fermions.
The contribution of a general scalar multiplet of weak-isospin j and hypercharge Y to the oblique parameters has been previously calculated [70, 71], the expressions of which are
$ \begin{aligned}[b] S=&-\frac{Y}{6\pi}\sum_{l=-j}^j l\ln{m_l^2},\\ T=&\frac{1}{4\pi s_w^2 c_w^2 m_Z^2}\Bigg[\sum_{l=-j}^j(j^2+j-l^2)m_l^2\ln{m_l^2}\\&-\sum_{l=-j}^{j-1}(j-l)(j+l+1)f_2(m_l,m_{l+1})\Bigg],\\ U=&\frac{1}{4\pi s_w^2 c_w^2 m_Z^2}\Bigg[\sum_{l=-j}^{j-1}(j-l)(j+l+1)f_1(m_l,m_{l+1})\\&-\sum_{l=-j}^j\frac{l^2}{3}\ln{m_l^2}\Bigg]. \end{aligned} $

(9) Here, the functions
$ f_1(m_1, m_2) $ and$ f_2(m_1, m_2) $ are defined by$ f_1(m_1, m_2)=\int_0^1 {\rm d} x x(1-x)\ln{\left[x m_1^2+(1-x)m_2^2\right]}, $

(10) $ f_2(m_1, m_2)=\int_0^1 {\rm d} x \left[x m_1^2+(1-x)m_2^2\right]\ln{\left[x m_1^2+(1-x)m_2^2\right]}. $

(11) To obtain the favored parameter space by considering the W mass anomaly, we adopt a
$ \chi^2 $ analysis defined as$ \begin{align} {\chi^2=\chi^2(S,T,U) = \chi^2(S(g_i,m_i),T(g_i,m_i),U(g_i,m_i)),} \end{align} $

(12) where the first equality is obtained from a global fit on the oblique parameters, for which we use the results in the conservative scenario of Ref. [12] when the CDF II data are included in the fit, and the results in Ref. [72] when they are not. For the second equality,
$ g_i $ and$ m_i $ are some of the parameters of a generic UV model, within which the oblique parameters can be expressed as functions of them, as shown in Eq. (9). We plot$ \Delta\chi^2\equiv\chi^2-\chi^2_{\rm min} $ with$ \chi^2_{\rm min} $ as the minimum of$ \chi^2(g_i,m_i) $ to obtain the allowed parameter space at the 90% and 99% confidence levels.Before discussing the results, we wish to comment on the construction of
$ \chi^2 $ . To obtain the parameter space that is consistent with the CDF II measurement, one might choose to compute$ \chi^2 $ from two oblique parameters$ \chi^2(S(g_i,m_i), T(g_i,m_i)) $ , or even a single oblique parameter, for example,$ \chi^2(S(g_i,m_i)) $ , for simplicity, even when$ T/U $ is non-vanishing from the prediction of a certain model. However, owing to the strong correlations between the oblique parameters, this procedure may lead to results that are too optimistic such that one may then incorrectly exclude that model up to a certain scale. Furthermore, note that a full$ STU $ parameter fit including the CDF II data results in a sizable non-vanishing U parameter [12], which indicates a new large multiplet with sufficiently low masses of the components beyond the SM [70]. Although the operator analysis within the framework of SMEFT predicts that the U parameter is generated by$ dim $ -8 operators, which is suppressed with respect to the$ dim $ -6 operator generated S and T, explicit calculations of the UV models show that the values of S and T can be considerably smaller than that of U in some regions of parameter space owing to accidental cancellation between different terms. Therefore, we believe a full$ STU $ analysis considering the correlations should use as much information as possible to give the best constraints on the UV models.The favored parameter spaces for different quantum numbers of N-plets are shown in Fig. 1, where we define the mass splitting parameter
$ \delta m\equiv(|\lambda_2| v^2/4)^{1/2} $ . In each plot, we use blue (ligh-blue) for the EW precision fits without including the CDF II data at the 90% (99%) CL, and magenta (light-magenta) for those including the CDF II data. The$ m_W $ anomaly indicates a significant mass splitting in the spectrum while the original PDG data prefers degenerate multiplet states. Although a larger hypercharge and more states may reduce the values of mass splitting to fulfill the new$ STU $ parameter fit, it becomes difficult to obtain a sufficiently large correction to$ m_W $ , especially for a lighter$ m_{\phi^0} $ , as shown in the lower right panel. The unitarity or perturbability of the theory gives an upper bound on the mass splitting$ \delta m $ , shown by a black dashed line, which excludes heavier neutral states with masses above$ 1.7 $ TeV for$ j=1, Y=2 $ multiplet,$ 2.8 $ TeV for$ j=3/2, Y=1 $ , and$ 2.9 $ TeV for$ j=3/2, Y=3 $ .
Figure 1. (color online) 90% (solid) and 99% (light) CL regions for scalar multipets with quantum number
$ j=1, Y=2 $ (upper left),$ j=3/2, Y=1 $ (upper right),$ j=3/2, Y=3 $ (lower left), and$ j=2, Y=4 $ (lower right) in light of the CDF II result [1]. In each plot, "PDG" ("CDF II") corresponds to the constraints obtained from electroweak precision fits without (with) the inclusion of the CDF II data. The green region shows the 1σ region consistent with the CDF-II W mass value. -
In this section, we discuss the general real and complex triplet models. The real triplet model is phenomenologically interesting as it can provide a dark matter candidate and also predict the existence of a long-lived particle. See Ref. [73] for a recent study on this at colliders. Conversely, the complex triplet model contains a doubly-charged Higgs particle that can decay into a same-sign dilepton final state. This channel would be very clean at colliders and serves as the smoking-gun signature for a model discovery. See Ref. [74] for a detailed study at a future 100 TeV
$ pp $ collider and Ref. [75] for gravitational wave production within this model.In light of the recent W mass anomaly from the CDF II experiment[1], these two triplet models are particularly interesting because relatively light real triplet and complex triplet particles are still allowed. Specifically, from disappearing charged track searches, Ref. [73] found that a real triplet around 250 GeV is still allowed from current data. Similarly, with a relatively large VEV for the complex triplet model, a very light complex triplet in the
$ \mathcal{O}(100) $ GeV range is not yet ruled out. Such light states can generate non-negligible values of the U parameter. Moreover, as noted, non-zero VEVs of their neutral components can be developed resulting in tree-level custodial symmetry breaking, which exhibits very different properties. These points motivate our study on the two models to explain the the W mass anomaly and explore their effects on EWPOs.For the following discussion, we adopt the conventions established in Refs. [73,76] for the complex and real triplet models, respectively. For reference, the model definitions for these two models are as follows:
● The real triplet model: The scalar sector Lagrangian of the real triplet model can be expressed as
$ \begin{align} {\cal L}_{\rm real}\supset \left(D_{\mu}H \right)^{\dagger}\left(D^\mu H\right)+\rm{Tr}\left[\left(D_{\mu}\Sigma \right)^{\dagger}\left(D^{\mu}\Sigma\right)\right]-V\left(H,\Sigma \right), \end{align} $

(13) where the SM Higgs doublet H and real triplet scalar Σ are given by
$ \begin{align} H= \begin{pmatrix} G^+\\ \dfrac{1}{\sqrt{2}}\left(v_H+h+{\rm i} G^0\right) \end{pmatrix}, \quad \Sigma=\frac{1}{2} \begin{pmatrix} \Sigma^0 + v_\Sigma & \sqrt{2}\Sigma^+\\ \sqrt{2}\Sigma^- & -\Sigma^0 + v_\Sigma \end{pmatrix}, \end{align} $

(14) with the Higgs VEVs
$ v_H^2+4v_\Sigma^2\simeq 246\; \text{GeV}^2 $ determined from the muon lifetime.$ D_{\mu}\Sigma\equiv\partial_{\mu}\Sigma+ {\rm i} g_2\left[W_{\mu},\Sigma \right] $ , where$ W_{\mu}=W^a_{\mu}\tau^a/2 $ , with$ \tau^a $ as the Pauli matrices. The definition for$ D_\mu H $ is standard, and the scalar potential can be written in a compact form as [76]$ \begin{aligned}[b] V\left(H, \Sigma \right)=&-\mu^2H^{\dagger}H+\lambda_0\left(H^{\dagger}H \right)^2-\frac{1}{2}\mu^2_{\Sigma} F+\frac{b_4}{4}F^2\\&+\frac{a_2}{2}H^{\dagger}H F + a_3 H^\dagger\Sigma H, \end{aligned} $

(15) where
$ F\equiv\left(\Sigma^0 \right)^2+2\Sigma^+\Sigma^- $ . Note that the last term would imply the decay of Σ into SM particles. Thus, besides a vanishing triplet VEV, an extra discrete$ \mathbb{Z}_2 $ symmetry must be applied to render the neutral component of Σ stable as a possible dark matter candidate. However, with a vanishing triplet VEV, the charged component will receive radiative corrections at higher loops and hence will be approximately 166 MeV heavier than the neutral component [61, 77]. As a consequence, the charged component is long-lived, and a disappearing charge track signature can be observed at colliders. This feature has been utilized in Ref. [73] in detail, and it was found that a real triplet as light as$ \sim $ 250 GeV was still experimentally allowed. However, to saturate the dark matter relic density, it is well-known that the real triplet must be around 3 TeV in the minimal scenario with$ a_2 $ =0 [61, 78]. As shown below, for the vanishing real triplet VEV scenario, the real triplet model would be ruled out beyond the 90% CL from the CDF II data when the triplet is below$ \sim $ 40 TeV. Thus, for the following discussion, we mainly assume the triplet to have a non-vanishing VEV such that the masses of the charged and neutral components of Σ are independent. The Peskin-Takeuchi parameters in this model, to the leading order in$ v_\Sigma/v_H $ , are given as [79]$ \begin{aligned}[b] S \approx &0,\\ T=&\frac{4v_\Sigma^2}{\alpha v_H^2}+\frac{1}{8\pi s_{w}^{2} c_{w}^{2}m_{Z}^{2}}\left(m_{\Sigma^0}^{2}+m_{\Sigma^\pm}^{2}-\frac{2 m_{\Sigma^0}^{2} m_{\Sigma^\pm}^{2}}{m_{\Sigma^0}^{2}-m_{\Sigma^\pm}^{2}} \ln{\frac{m_{\Sigma^0}^{2}}{m_{\Sigma^\pm}^{2}}}\right),\\ U=&-\frac{1}{3\pi}\Bigg[\frac{3m_{\Sigma^\pm}^{2}m_{\Sigma^0}^{4}-m_{\Sigma^0}^{6}}{\left(m_{\Sigma^0}^{2}-m_{\Sigma^\pm}^{2}\right)^{3}}\ln{\frac{m_{\Sigma^0}^{2}}{m_{\Sigma^\pm}^{2}}}\\ &+\frac{5\left(m_{\Sigma^0}^{4}+m_{\Sigma^\pm}^{4}\right)-22 m_{\Sigma^0}^{2} m_{\Sigma^\pm}^{2}}{6\left(m_{\Sigma^0}^{2}-m_{\Sigma^\pm}^{2}\right)^{2}}\Bigg]\; , \end{aligned} $

(16) where the T parameter is composed of two parts: the tree-level CSV contribution (1st term) from the non-vanishing VEV of the triplet, and the one-loop CSV contribution (2nd term) from mass splitting between the charged and neutral components. The contributions of the order
$ \mathcal{O}(m_Z/m_\Sigma^\pm) $ and higher are neglected.● The complex triplet model: We parameterize the Lagrangian of this complex triplet model as
$ \begin{align} {\mathcal{L}\supset\mathcal{L}_{\rm kinetic}(\Delta) - V(H,\Delta),} \end{align} $

(17) with
$ \begin{align} \mathcal{L}_{\rm kinetic}(\Delta)&={\rm{Tr}}[(D_\mu \Delta)^\dagger (D^\mu \Delta)], \end{align} $

(18) $ \begin{aligned}[b] V(H,\Delta)=& - m^2 H^\dagger H + M^2{\rm{Tr}}(\Delta^\dagger\Delta)+\Big[\mu H^T {\rm i} \tau_2\Delta^\dagger H\\&+\rm{h.c.}\Big] +\lambda_1(H^\dagger H)^2 +\lambda_2\left[\rm{Tr}(\Delta^\dagger\Delta)\right]^2 \\ &+\lambda_3\rm{Tr}[\Delta^\dagger\Delta \Delta^\dagger\Delta] +\lambda_4(H^\dagger H)\rm{Tr}(\Delta^\dagger\Delta)\\ & +\lambda_5 H^\dagger\Delta\Delta^\dagger H. \end{aligned} $

(19) The covariant derivative of Δ is defined as
$D_\mu \Delta\equiv \partial_\mu \Delta + {{\rm i}g}[\tau^aW_\mu^a,\Delta]/{2}+{{\rm i}g'Y_{\Delta}}B_\mu\Delta/{2}$ , where$ Y_{\Delta}=2 $ . The components of the SM Higgs doublet H are the same as defined above, whereas those of the complex triplet are defined as$ \begin{align} { \Delta = \left( \begin{array}{cc} \dfrac{\Delta^+}{\sqrt{2}} & H^{++}\\ \dfrac{1}{\sqrt{2}}(\delta+v_\Delta+{\rm i}\eta) & -\dfrac{\Delta^+}{\sqrt{2}} \end{array}\right).} \end{align} $

(20) The complete mass spectrum of this model can be found, for example, in Ref. [74], which we cite in the following:
$ \begin{aligned}[b]& m_h^2\simeq2v^2\lambda_1,\\& m_H \simeq M_\Delta \simeq m_A,\\& m_{H^\pm}^2\simeq M_\Delta^2-\frac{\lambda_5}{4}v_H^2,\,\\& m_{H^{\pm\pm}}^2\simeq M_\Delta^2-\frac{\lambda_5}{2}v_H^2, \end{aligned} $

(21) considering the fact that
$ v_\Delta\ll v_H $ , as required by the ρ parameter. While the triplet VEV$ v_\Delta $ is relatively tiny compared to$ v_H $ , its magnitude has a non-trivial impact on the phenomenological side. In particular, when$ v_\Delta $ is below$ \sim10^{-4} $ GeV, the same-sign dilepton channel dominates the decay of the doubly charged triplet, acting as the smoking-gun signature for model discovery. In contrast, when$ v_\Delta $ is above$ \sim10^{-4} $ GeV but fulfills the requirement of the ρ parameter, the same-sign di-W boson final state dominate instead – see Ref. [74] for details. However, as shown below, the CDF II data are not sensitive to such small values of$ v_\Delta $ ($ v_\Delta\lesssim 1 $ GeV), and it is thus important to keep in mind the impact on the phenomenologies from$ v_\Delta $ . The$ STU $ parameters are calculated in Refs. [70, 80],$ \begin{aligned}[b] S=&-\frac{1}{3 \pi} \ln \frac{m_{+1}^{2}}{m_{-1}^{2}}-\frac{2}{\pi} \sum_{T_{3}=-1}^{+1}\left(T_{3}-Q s_{w}^{2}\right)^{2} \xi\left(\frac{m_{T_{3}}^{2}}{m_{Z}^{2}}, \frac{m_{T_{3}}^{2}}{m_{Z}^{2}}\right), \\ T=&-\frac{2v_\Delta^2}{\alpha\left(v_H^2+4v_\Delta^2\right)}+\frac{1}{16 \pi c_{w}^{2} s_{w}^{2}} \sum_{T_{3}=-1}^{+1}\left(2-T_{3}\left(T_{3}-1\right)\right)\\&\times \eta\left(\frac{m_{T_{3}}^{2}}{m_{Z}^{2}}, \frac{m_{T_{3}-1}^{2}}{m_{Z}^{2}}\right), \\ U=&\frac{1}{6 \pi} \ln \frac{m_{0}^{4}}{m_{+1}^{2} m_{-1}^{2}}+\frac{1}{\pi} \sum_{T_{3}=-1}^{+1}\left[2\left(T_{3}-Q s_{w}^{2}\right)^{2} \xi\left(\frac{m_{T_{3}}^{2}}{m_{Z}^{2}}, \frac{m_{T_{3}}^{2}}{m_{Z}^{2}}\right)\right.\\ &\left.-\left(2-T_{3}\left(T_{3}-1\right)\right) \xi\left(\frac{m_{T_{3}}^{2}}{m_{W}^{2}}, \frac{m_{T_{3}-1}^{2}}{m_{W}^{2}}\right)\right], \end{aligned} $

(22) with
$ \begin{align} m_{+1,0,-1}= m_{H^{\pm\pm},H^\pm,H}, \end{align} $

(23) $ \begin{aligned}[b] \xi(x, y)=& \frac{4}{9}-\frac{5}{12}(x+y)+\frac{1}{6}(x-y)^{2} \\& +\frac{1}{4}\left[x^{2}-y^{2}-\frac{1}{3}(x-y)^{3}-\frac{x^{2}+y^{2}}{x-y}\right] \ln \frac{x}{y}\\&-\frac{1}{12} d(x, y) f(x, y), \end{aligned} $

(24) $ \begin{align} d(x, y)=&-1+2(x+y)-(x-y)^{2}, \end{align} $

(25) $ \begin{align} f(x, y)=&\left\{\begin{array}{ll} -2 \sqrt{d(x, y)}\left[\arctan \dfrac{x-y+1}{\sqrt{d(x, y)}}-\arctan \dfrac{x-y-1}{\sqrt{d(x, y)}}\right], & \text { for } \quad d(x, y)>0 \\ \sqrt{-d(x, y)} \ln \left[\dfrac{x+y-1+\sqrt{-d(x, y)}}{x+y-1-\sqrt{-d(x, y)}}\right], & \text { for } \quad d(x, y) \leq 0 \end{array}\right. \end{align} $ 
(26) $ \begin{align} \eta(x, y)= x+y-\frac{2 x y}{x-y} \ln \frac{x}{y}. \end{align} $

(27) Using the full
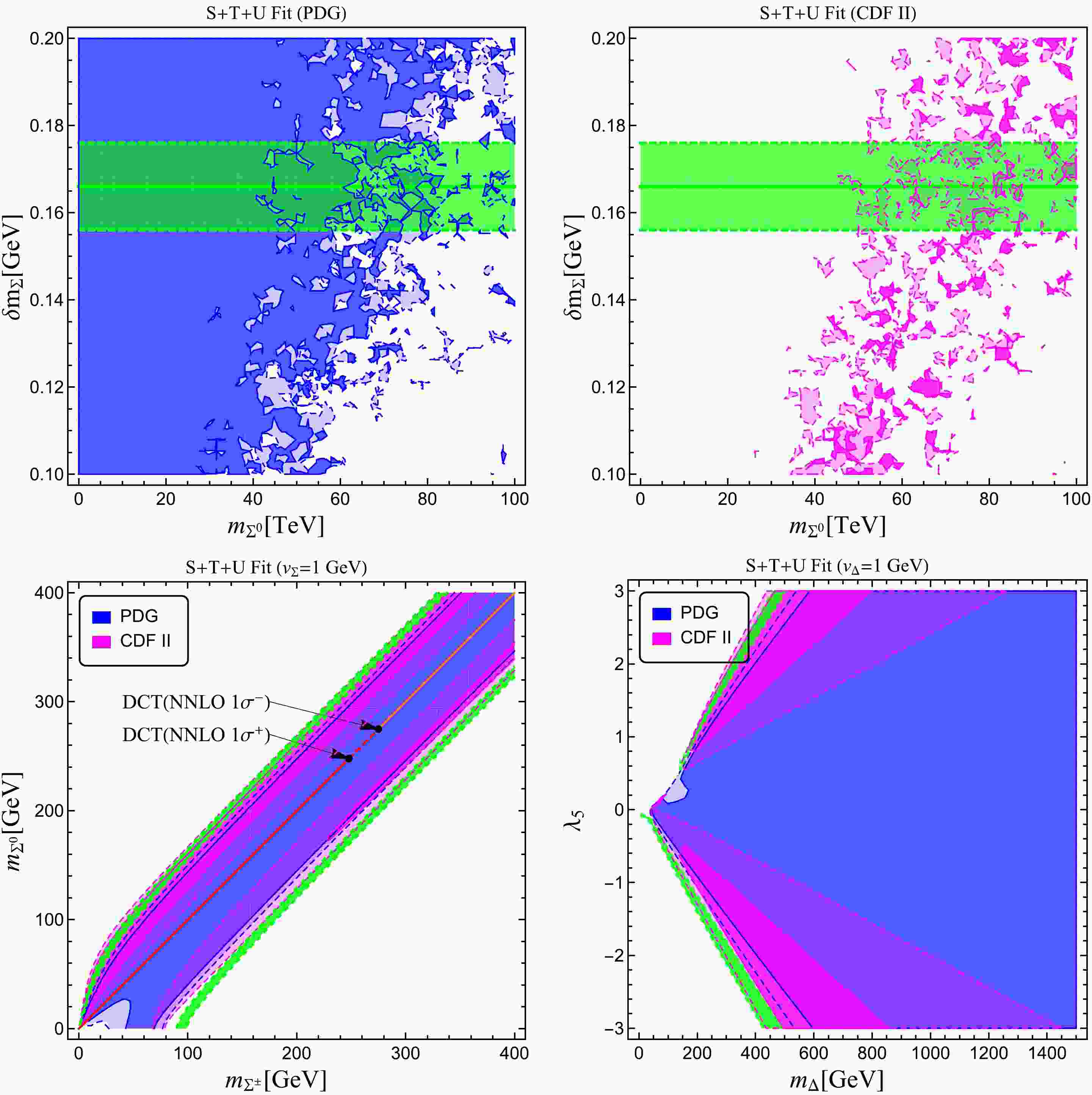
$ \chi^2 $ obtained by considering the correlations among the oblique parameters, we present the results for the real and complex triplet models in Fig. 2 using the same color notation as in Fig. 1. Several points should be addressed:● The upper row of Fig. 2 corresponds to the real triplet model in the vanishing VEV scenario, and the lower left plot of Fig. 2 is that in the non-vanishing VEV scenario. Note that in the former case, as discussed above, the mass splitting between the charged and neutral particles in the triplet is fixed at approximately 166 MeV at the one-loop order and will be further modified by a few MeV at the two-loop level. This is reflected by the green region in the first row. From these two plots, it is clear that the CDF II data will generically prefer a heavier triplet. On the other hand, in the non-vanishing VEV scenario, the masses of the two triplet particles can vary independently. Although the CDF-II data indicate manifested custodial symmetry breaking at some level, which prefers a non-vanishing VEV, because the low energy measurement of the ρ parameter (the ratio of neutral-to-charged current interaction strengths) is constrained to be close to one [2], the value of
$ v_\Sigma $ cannot exceed a few GeV, indicating that$ v_\Sigma\ll v $ is a good approximation. Therefore, we only show the result at a fixed value of$ v_\Sigma $ ($ v_\Sigma=1\; $ GeV) by performing a two-parameter fit instead of a full three-parameter fit. The allowed parameter space shrinks when we increase$ v_\Sigma $ unless$ v_\Sigma $ is below$ \mathcal{O}(\text{GeV}) $ , where the sensitivity of our$ \chi^2 $ to$ v_\Sigma $ is lost. We find that with or without the inclusion of the CDF II data, the preferred parameter space lies along the diagonal region on the$ M_{\Sigma^0}-M_{\Sigma^\pm} $ plane, with the difference being that the CDF II data generally prefer a larger mass splitting between the two triplet particles. For reference, we also show the constraints from the disappearing charged track search obtained in Ref. [73] when the two particles have the degenerated mass spectrum in red, where the upper (lower) point corresponds to a mass splitting of 172 (160) MeV. The orange color indicates the still allowed parameter space from the current disappearing charged track search.● We also comment on the appearance of separated islands in the first row of Fig. 2 at large
$ M_{\Sigma^0} $ . These islands are merely a reflection of partial cancellation between different types of corrections to the oblique parameters. For illustration, we can look at the$ \delta\chi^2 $ in this vanishing VEV scenario from the PDG, for which we find5 $ \begin{aligned}[b] (\delta\chi^2)^{\rm PDG}\simeq & \, 2.4774 + \frac{8.96 \delta M_\Sigma}{M_{\Sigma^0}} + \frac{3.18\times 10^{-2} \delta M_\Sigma^2}{M_{\Sigma^0}^2} \\ & + 1.82\times 10^{-6} \delta M_\Sigma^4 + \frac{5.96\times 10^{-3} \delta M_\Sigma^4}{M_{\Sigma^0}^2} + \frac{13.24 \delta M_\Sigma^4}{M_{\Sigma^0}^4}\\ & - 4.84\times10^{-3} \delta M_\Sigma^2 - \frac{6.34\times 10^{-3} \delta M_\Sigma^3}{M_{\Sigma^0}} - \frac{8.00 \delta M_\Sigma^3}{M_{\Sigma^0}^3}. \end{aligned} $

(28) Clearly, accidental partial cancellation between the third line and the first two lines is expected for different values of
$ \delta M_\Sigma $ and$ M_{\Sigma^0} $ . For this reason, increasing or decreasing the numerical precision to obtain these plots will lead to slightly different results; thus, our results in the first row of Fig. 2 are only for quantitative illustration instead of trying to be exact. However, we stress that the pattern of these plots, and thus our conclusion presented above and below, remains unchanged.● The results for the complex triplet model are shown in the lower right panel of Fig. 2. Similar to the real triplet case, we find that
$ v_\Delta $ cannot exceed a few GeV. Note that the non-vanishing$ v_\Delta $ gives an incorrect sign contribution to explain the CDF-II results. We expect that the one-loop correction dominates over or at least at the same level as the tree-level correction, which also indicates that the approximation$ v_\Delta\ll v $ is valid. For this reason, we also fix$ v_\Delta $ to 1 GeV for illustration, and increasing the value of the VEV of the complex triplet shrinks the allowed parameter region unless$ v_\Delta\lesssim 1 $ GeV, where our$ \chi^2 $ is insensitive to$ v_\Delta $ . Clearly, the CDF II data imply a considerably more constrained parameter space than the previous experiments. Especially, with$ \lambda_5 $ within the perturbativity bound, a light triplet below approximately 1 TeV would be able to explain the W mass anomaly. One could thus expect to exploit the same-sign di-lepton (di-W) channel for the model discovery at future colliders [74].● The contributions to the T parameter from the non-zero VEVs in the real and complex triplet models have opposite signs. The non-vanishing
$ v_\Delta $ of the complex triplet partially cancels the radiative corrections in the T parameter, which might result in rather small T values compared to U, whereas the effect of the VEV of a real triplet has the exact opposite characteristic. Therefore, a complete three-parameter fit including the VEV prefers a non-vanishing VEV for the real triplet, which is also favored by lifting the degeneracy between the charged and neutral components. -
In general, a custodial symmetric scalar sector needs at least two extra scalar multiplets besides the original SM doublet. The simplest model of this type is the GM model with a real triplet and complex triplet with
$ Y=2 $ , which are combined into a bitriplet under global$ S U(2)_L\times S U(2)_R $ symmetry. One simple way to understand why this model preserves custodial symmetry is via the perspective of EFT, in which the Wilson coefficients of the dim-6 custodial breaking operator$ \mathcal{O}_{\rm HD} $ after integrating the real and complex scalar triplet have opposite signs [81, 82], which can cancel each other by requiring the triplets to form a bi-triplet.To generalize this model, it is useful to consider large bi-multiplet representations of
$S U(2)_L\times S U(2)_R$ symmetry. After considering the unitarity constraint, there are only four models including the GM model [60, 83], which are listed in Table 1.Model name $S U(2)_L\times S U(2)_R$ reps.

j Y Real/complex GM $ (2\times 2)+(3\times 3) $ 

$ 1/2 $ 

$ 1 $ 

$ \mathbb{C} $ 

$ 1 $ 

$ 2 $ 

$ \mathbb{C} $ 

$ 1 $ 

$ 0 $ 

$ \mathbb{R} $ 

GGM4 $ (2\times 2)+(4\times 4) $ 

$ 1/2 $ 

$ 1 $ 

$ \mathbb{C} $ 

$ 3/2 $ 

$ 3 $ 

$ \mathbb{C} $ 

$ 3/2 $ 

$ 1 $ 

$ \mathbb{C} $ 

GGM5 $ (2\times 2)+(5\times 5) $ 

$ 1/2 $ 

$ 1 $ 

$ \mathbb{C} $ 

$ 2 $ 

$ 4 $ 

$ \mathbb{C} $ 

$ 2 $ 

$ 2 $ 

$ \mathbb{C} $ 

$ 2 $ 

$ 0 $ 

$ \mathbb{R} $ 

GGM6 $ (2\times 2)+(6\times 6) $ 

$ 1/2 $ 

$ 1 $ 

$ \mathbb{C} $ 

$ 5/2 $ 

$ 5 $ 

$ \mathbb{C} $ 

$ 5/2 $ 

$ 3 $ 

$ \mathbb{C} $ 

$ 5/2 $ 

$ 1 $ 

$ \mathbb{C} $ 

Table 1. Scalar field content in the generalized Georgi– Machacek models.
All of these models share unique features. Since the GM model is the simplest one and the least constrained, in this section, we use it as an example to discuss whether these types of models can solve the
$ m_W $ anomaly and how the VEVs and custodial symmetry affect the W mass and EWPOs. The custodial symmetry can be preserved at the tree-level even when the VEVs of the two triplets are set to be the same. Thus, the VEVs of the triplets can be as large as$ \mathcal{O}(\rm{GeV}) $ .Because the custodial symmetry originates from
$S U(2)_L\times S U(2)_R$ before EW symmetry breaking (EWSB), the Lagrangian in the GM model preserves$S U(2)_L\times S U(2)_R$ symmetry. This may be explicitly shown when the scalars are written in bidoublet and bitriplet forms, which are$ \begin{aligned}[b] \Phi =& \left( {\rm i}\tau^2 H^*\; \; H \right), \\ \Xi =& \left( \begin{array}{ccc} \left( \Delta^0 \right)^* & \Sigma^+ & \Delta^{++} \\ - \left( \Delta^+ \right)^* & \Sigma^0 & \Delta^+ \\ \left( \Delta^{++} \right)^* & -\left( \Sigma^+ \right)^* & \Delta^0 \end{array} \right)\; . \end{aligned} $

(29) Here, Φ is the bidoublet form of the SM Higgs, and Ξ combines a real scalar triplet Σ and complex scalar triplet Δ. The scalar potential is written as
$ \begin{aligned}[b] V(\Phi,\Xi) = & \frac12 m_{\Phi}^2 {\rm tr} \left[\Phi^\dagger \Phi \right] + \frac12 m_{\Xi}^2 {\rm tr} \left[\Xi^\dagger \Xi \right] \\&+ \lambda_1 \left( {\rm tr} \left[\Phi^\dagger \Phi \right] \right)^2 + \lambda_2 \left( {\rm tr} \left[\Xi^\dagger \Xi \right] \right)^2 \\ & + \lambda_3 {\rm tr} \left[\left( \Xi^\dagger \Xi \right)^2 \right] + \lambda_4 {\rm tr} \left[\Phi^\dagger \Phi \right] {\rm tr} \left[\Xi^\dagger \Xi \right] \\& + \lambda_5 {\rm tr} \left[\Phi^\dagger t^a \Phi t^b \right] {\rm tr} \left[\Xi^\dagger T^a \Xi T^b \right] \\ & - M_1 {\rm tr} \left[( \Phi^\dagger t^a \Phi t^b ) ( U \Xi U^\dagger )_{ab} \right] \\&- M_2 {\rm tr} \left[( \Xi^\dagger t^a \Xi t^b ) ( U \Phi U^\dagger )_{ab} \right] \; , \end{aligned} $

(30) where
$ t^a $ and$ T^a $ are$S U(2) $ generators in the$ 2\times 2 $ and$ 3\times 3 $ representations, and the matrix U is given by$ \begin{align} U=\begin{pmatrix} -\dfrac{1}{\sqrt{2}} & 0 & \dfrac{1}{\sqrt{2}} \\ -\dfrac{\rm i}{\sqrt{2}} & 0 & \dfrac{\rm i}{\sqrt{2}} \\ 0 & 1 & 0 \end{pmatrix}. \end{align} $

(31) The VEVs of the triplets Σ and Δ are the same as those required by the custodial symmetry; therefore, their difference
$ \nu=\langle \Sigma^0 \rangle-\langle \Delta^0 \rangle =0 $ . For simplicity, we define$ v_\chi\equiv\left\langle{\Sigma^0} \right\rangle =\left\langle{\Delta^0} \right\rangle $ , and$ v_H^2+8v_\chi^2\simeq 246\; \text{GeV}^2 $ .In the GM model, there are 5-plet (
$ H_5 $ ), 3-plet ($ H_3 $ ), and two singlet Higgs bosons under the classification of the custodial$S U(2)_V$ symmetry, where the latter two can mix with each other with mixing angles of β and α. The mixing angle β is defined by$ t_\beta=2\sqrt{2}v_\chi/v_H $ 6 , whereas α is determined by the quartic coupling constants in the Higgs potential, which is treated as a free input parameter in our analysis. The custodial symmetry requires mass degeneracy within each Higgs multiplet; therefore, we denote$ m_3 $ and$ m_5 $ as the masses of the 5-plet and 3-plet, respectively. Among the mass eigenstates of the two singlet fields, one (h) should be identified as the observed 125 GeV SM-like Higgs, and the other one (H) has mass$ m_H $ .The
$ STU $ parameters in GM model are calculated in Refs. [52, 84], and we adopt the results given in Ref. [52]. It is well-known that the predicted T parameter contains some UV divergence, which is a result of custodial symmetry breaking in the GM potential at the loop level [85−87]. Accordingly, to absorb the infinities of the T parameter at the one-loop level, a counterterm of ν must be added, which consequently introduces some renormalization scale dependence to the results. The previous experimental values for the T parameter are nearly zero [2], which means that custodial symmetry is almost preserved; hence, earlier studies on the GM model usually set T to be zero as an input parameter [52, 86−89]. Refs. [86, 87] estimated the amount of the CSV effect at higher energy scales when the ρ parameter at the weak scale was fixed to be almost one. Given the$ m_W $ measured from CDF II, a larger T value is predicted, indicating a large custodial symmetry breaking. A more self-consistent way to deal with renormalization is by explicitly adding custodial symmetry breaking terms to the Lagrangian, as performed in Ref. [88], which typically generates misaligned VEVs. Such misalignment can address the CDF II anomaly, as shown in Refs. [8, 9]. However, this procedure makes the model deviate from the original idea of the GM model. Hence, here we consider the custodial symmetric case with aligned VEVs, assuming that some fine-tuning exists at the UV to align two triplet VEVs, and focus on the pure one-loop effects ($ STU $ parameters) on EWPOs and W mass. To accommodate the lack of knowledge of the UV, we marginalize over the T parameter in our$ \chi^2 $ analysis.We show the results for the GM model in Figs. 3−4 using marginalization over T and assuming the two triplets have the same VEV to preserve the custodial symmetry
$S U(2)_V$ at the tree-level. Owing to the relatively large number of parameters, we produce plots by projecting onto the$ m_5-m_{3,H} $ plane in the plots of Fig. 3 and the$ m_3-m_H $ and$ v_\chi-s_\alpha $ planes in Fig. 4. All notations in our plots follow those in Ref. [52, 85, 91]. For projections onto the$ m_5-m_3 $ and$ m_5-m_H $ mass planes, we find that the CDF II data generally prefer a lighter$ m_5 $ , as indicated by the magenta regions in Fig. 3, and note that the conclusion remains qualitatively the same when varying the other model parameters. In contrast, as observed in the upper left panel of Fig. 4, with$ m_5 $ and the other model parameters fixed, the CDF II data would prefer a larger$ m_{3,\, H} $ . In particular, negative mass splittings between$ m_{3,\, H} $ and$ m_5 $ would be relatively disfavored by the CDF II data. Relatively large values of$ m_{3,\, H} $ can satisfy the CDF II data, which used to be ruled out by PDG data. Lastly, in the remaining plots of Fig. 4, we show the sensitivity to the triplet VEV$ v_\chi $ and mixing angle$ s_\alpha $ in the degenerated mass spectrum scenario. We find that (1) when the GM model is at the weak scale, the allowed parameter space is insensitive to$ s_\alpha $ for small$ v_\chi $ ($ v_\chi\lesssim 40 $ GeV), whereas the CDF II data will rule out slightly more parameter space where$ |s_\alpha| $ is close to one and$ v_\chi $ is close to$ 80 $ GeV. (2) When the GM model is above a few TeV, a new parameter space, as indicated by, for example, the magenta region with the blue boundary, opens up to account for the CDF II result in the negative$ s_\alpha $ region. (3) However, the current Higgs coupling measurements (especially the couplings between Higgs and massive gauge bosons) require a positive$ s_\alpha $ under our notations, indicating that the new negative$ s_\alpha $ region allowed by the CDF II result is not consistent with Higgs measurements.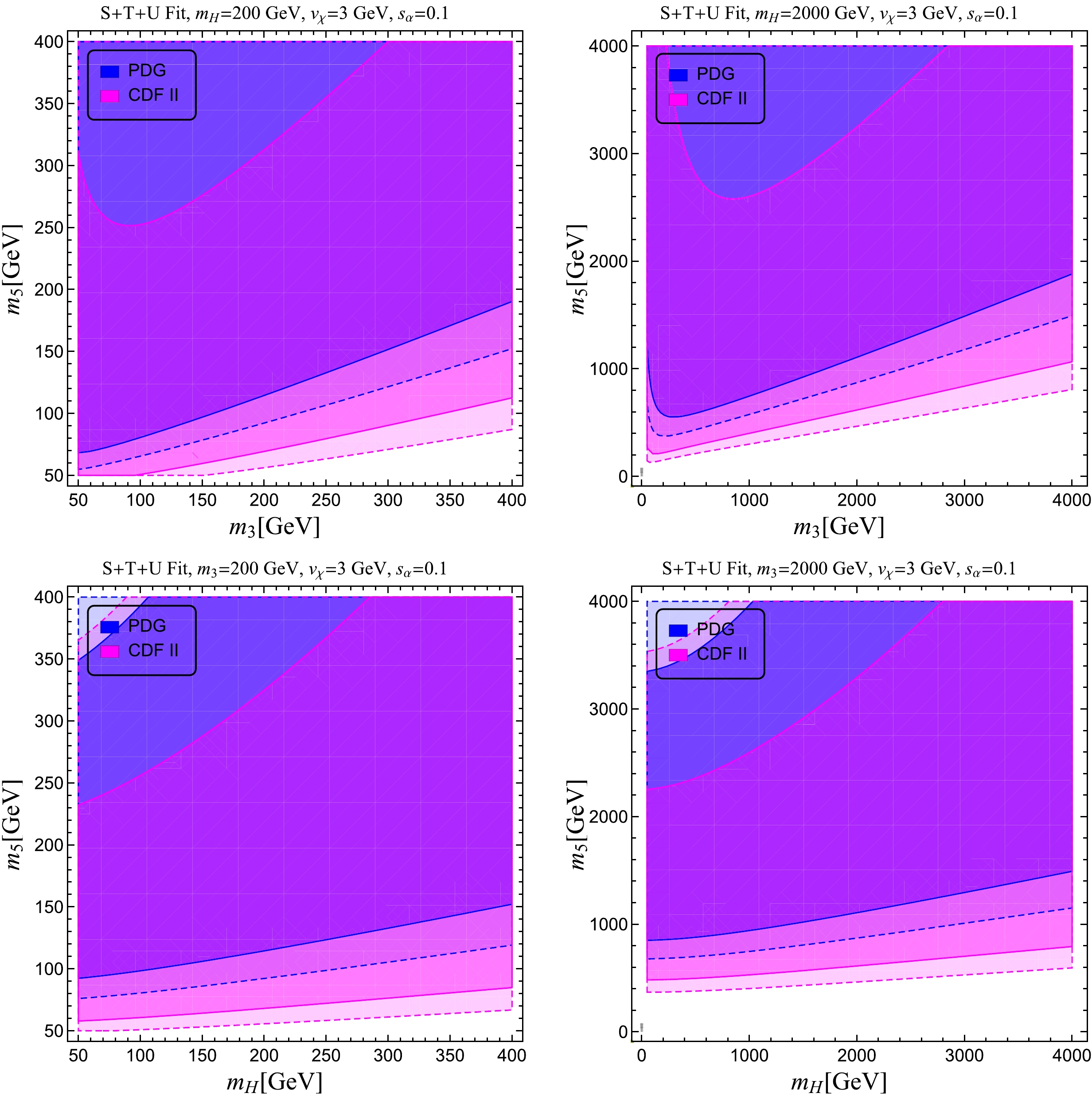
Figure 3. (color online) Same as Fig. 2 but for the Georgi-Machacek model. See text for details.
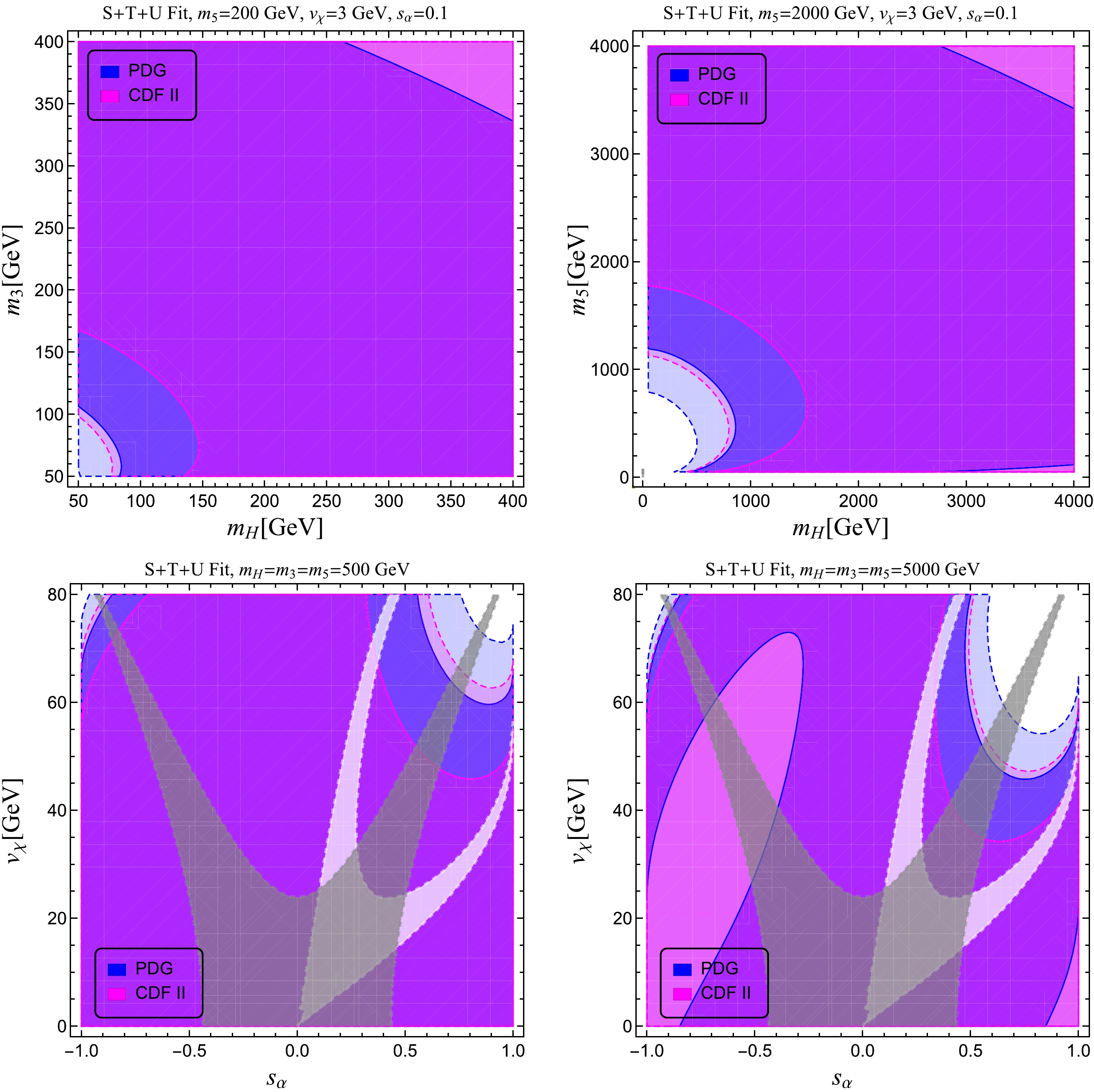
Figure 4. (color online) Same as Fig. 3. In the lower two panels of the
$ v_\chi-s_\alpha $ plots, we also show the allowed 1-σ regions of the ratios of the couplings of the SM-like h to the weak gauge bosons$ \kappa_V $ (white) and the fermions$ \kappa_f $ (gray) to the corresponding SM values from the ATLAS and CMS combined measurements [72]. Such Higgs coupling measurements favor positive values of$ s_\alpha $ because$ \kappa_V=c_\alpha c_\beta+2\sqrt{6}s_\alpha c_\beta/3 $ is an asymmetric function of$ s_\alpha $ [52, 90]; therefore, we choose$ s_\alpha=0.1 $ as our benchmark value in the other plots. -
While the SM has been very successful and precisely tested, it has been known for a while that we must go beyond it to address several profound problems in nature. These include the baryon asymmetry problem, dark matter, and non-vanishing neutrino masses. Scalar extensions of the SM have been actively investigated in literature in the past owing to their possible ability to the explain two or even all of these three problems simultaneously. More importantly, not all of these new scalars below the TeV scale have been fully ruled out at the LHC; thus, it will be possible to further test these scalar models at current and/or future colliders. In light of the recent anomaly on the W mass measurement from CDF II, we address this issue in the framework of scalar extensions of the SM and pin down the regions that have been previously ruled out ahead of the CDF II result. To that end, we consider two scenarios in this study: scalar extensions without custodial symmetry (Scenario I) and those with custodial symmetry, such as the GM model and its generalizations (Scenario II).
In Scenario I, we analyze two cases: Case A focuses on the scenario where only the SM doublet can develop a non-vanishing VEV after EW spontaneous symmetry breaking, whereas Case B focuses on the scenario where new scalars can also develop non-vanishing VEVs. We consider a generic SU(2) N-plet in Case A, realized by imposing an extra discrete
$ \mathbb{Z}_2 $ symmetry. For Case B, we specifically consider the real and complex triplet model because relatively light particles at the$ \mathcal{O}(100\,\rm GeV) $ scale are still permitted [73, 74], providing interesting targets for future collider searches.Our results for Cases A and B in Scenario I are shown in Figs. 1 and 2, respectively. In either case, we find new parameter spaces that were previously disfavored prior to the CDF II result. Specifically, in the N-plet case, we find that the CDF II data generally prefer larger mass splittings between the multiplet particles. For the real triplet in Case B, the conclusion depends significantly on whether the real triplet develops a non-vanishing VEV after EWSB. (1) If the real triplet has a vanishing VEV after symmetry breaking, CDF II would prefer heavier real triplet particles above 40 TeV than those of the PDG data. (2) In contrast, if the real triplet has a non-vanishing VEV after symmetry breaking, we find that while the PDG roughly favors a degenerate spectrum for the real triplet, the CDF II result would prefer a region where the neutral component of the real triplet is heavier than its charged one. On the other hand, for the complex triplet, we find that a relatively light complex triplet below the TeV scale is preferred by the CDF II data, making it an interesting target at colliders.
Inspired by the possibility of light triplet masses and also the custodial symmetric property of the scalar potential, we further consider the GM model, a mixture of the SM doublet and the real and complex triplet scalars, as a particular example of Scenario II. Requiring vacuum alignment between the complex and real triplets, pure loop effects in such a model can still alleviate the tension between the CDF II data and EWPOs with EW scale new particles. A particular hierarchy of the mass spectrum of the GM model is favored by the CDF II data,
$ m_{3,\, H}>m_5 $ , whereas they do not give more constraints on the extra scalar VEV or singlet mixing angle α considering the LHC Higgs data.With the observed CDF II W mass anomaly, it is time to reconsider the effects of custodial symmetry in the BSM. Our study takes the first step in this direction by analyzing the scalar extensions of the SM. However, there are still several unanswered questions. In particular, given the huge enthusiasm for SMEFT in the community, whether SMEFT is a suitable description for our nature if custodial symmetry is broken by a tree-level VEV is still questionable [92, 93]. We will leave these for future studies in a subsequent publication.
Note added. We note that Ref. [94] studied the compatibility of the spectrum preferred by the CDF II W mass with other EWPOs and Higgs precision data in an inert complex triplet extension (with hypercharge
$ Y=2 $ ) of the SM, and Ref. [95] studied both complex and real triplet extensions by directly performing a global fit to$ 19 $ EWPOs with CDF II$ m_W $ via Bayesian analysis. Both references also discuss some related collider phenomenology. Our$ STU $ fit results for complex and real triplet qualitatively agree with theirs, although we focus more on the general scalar extensions and the effects from custodial symmetry. -
We thank Yong Du for his work at the early stage of this project. H.S. also thanks Wei Su for useful discussions. H.S. is supported by the International Postdoctoral Exchange Fellowship Program.
Custodial symmetry violation in scalar extensions of the standard model
- Received Date: 2023-04-21
- Available Online: 2023-10-15
Abstract: The new measurement of the W boson mass from the CDF collaboration shows a significant tension with the standard model prediction, which evidences violation of custodial symmetry in the scalar sector. We study the scalar extensions of the standard model, which can be categorized into two classes, the scalar sector with custodial symmetry (Georgi-Machacek model and its generalizations) and the scalar sector without custodial symmetry, and explore how these extensions fit to electroweak precision data and the new CDF






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: