-
Relativistic heavy-ion collision experiments provide a platform for studying quantum chromodynamics (QCD) matter under extreme conditions. It has been expected that quark gluon plasma (QGP) can be created through heavy ion collisions (HICs) [1]. In a specific case, a non-central collision, QGP is created with a large orbital angular momentum (OAM) at a range of
$ 10^{4}-10^{5}\hbar $ [2−4]. Meanwhile, a strong magnetic field can reach the magnitude of$ 10 m_{\pi}^{2} $ at the initial time of the HICs and evolves with time [5−7]. The magnitude of the magnetic field decays severely while the averaged angular velocity still maintains its magnitude along the axis, which is perpendicular to the reaction plane [2]. Therefore, the effects of a rotating medium will play significant roles in the QCD phase diagram, dilepton production rate, and spin polarization.Spin alignment of vector meson ϕ and
$ K^{*0} $ has been one of the intriguing topics in HICs. Experimental evidence suggests that spin density matrix element$ \rho_{00} $ has a remarkable deviation from$ 1/3 $ [8, 9]. ALICE collaboration has measured$ \rho_{00} $ for$ K^{*0} $ and ϕ meson at$ \sqrt{s_{NN}}= $ 2.76 TeV in Pb-Pb collisions [9], and a negative deviation from$ 1/3 $ at lower transverse momentum has been reported. STAR collaboration has measured$ \rho_{00} $ between$ \sqrt{s_{NN}}=11.5 $ and$ 200 $ GeV in Au-Au collisions [8]. In this collision energy range, a positive deviation form$ 1/3 $ is reported for$ \rho_{00} $ of vector meson ϕ, which can be explained by a ϕ-meson field [10].In fact, spin alignment is a multifactorial phenomenon in heavy ion collisions. Theoretical researchers have developed a quark coalescence model for explaining the contribution of the vorticity and magnetic field [11, 12]. Furthermore, other physical mechanisms also contribute to the spin alignment, such as turbulent color fields[13], local vorticity [14], glasma fields [15], and gradient corrections in the vector-meson medium [16, 17].
Both the magnetic field and vorticities are expected to contribute to the spin alignment. In Ref. [18], the effect of magnetic field on spin alignment was studied. In this work, we introduce the effects of global rotation on quark matter. Generally, the rotation has an inhibition effect on quark and anti-quark pairing [19], which is different from Magnetic Catalysis (MC) [20−23]. As a consequence, chiral condensate will disappear as the angular velocity grows. Since the chiral condensate is an order parameter for chiral phase transition, its behaviors demonstrate that first order phase transition occurs at low temperature regions and crossover occurs in high temperature regions. The characteristics imply an analogy between the rotation and chemical potential [24, 25]. However, it is found that the rotation behaves beyond an effective chemical potential in dilepton production [26] and the rotation enhances the dilepton production rate and induces the ellipticity of lepton pairs.
It is also worth emphasizing that previous studies have assumed an infinite size without boundary conditions [2, 24, 27]. The boundary conditions on a finite size system should be taken into account for a rotating system [28−31], and inhomogeneous chiral condensation will be developed [32, 33]. For example, no-flux or MIT bag boundary conditions are applied in a spherical or cylindrical system [34−36]. The choice of boundary conditions will influence the behavior of chiral condensate near the surface. In particular, when no-flux boundary condition is applied in a cylindrical system, chiral condensate will almost keep a constant in the inner part of the cylinder but get enhanced like a Gibbs phenomenon near the surface [28].
In QCD phase diagram studies, it is also possible to consider inhomogeneous rotation with boundary conditions. Chiral condensate is enhanced near the area where the angular velocity changes severely, and this phenomenon is called the centrifugal effect [32]. Furthermore, chiral condensate reveals the dynamical mass of quarks. Besides the light quarks u and d, heavy flavor quarks, like s and c, are studied in electromagnetic and rotational fields [37]. Corresponding
$ \phi, D $ mesons are expected to be influenced by rotation as well. However, describing the freeze-out of heavy particles from the QGP is complicated [38]. Therefore, we only consider light-flavor vector meson modes excited and annihilated in a rotating medium.External fields, such as magnetic and vortical fields, will induce the mass splitting of spin-1 vector mesons. In recent years, considerable attention has been paid to the magnetic field effect of vector mesons, such as
$ \rho,~\phi $ . For example, for charged ρ mesons, mass splitting behaves like:$ \begin{equation} M_{\rho^{\pm}}(eB) = M_{\rho^{\pm}}(0)\mp \kappa eB, \end{equation} $

(1) where κ is a coefficient. For point-like particles,
$ \kappa=1 $ ; when quark-antiquark loop effect is considered,$ \kappa\neq 1 $ . Similarly, ρ meson under rotation also exhibits a mass splitting phenomenon [39]:$ \begin{equation} M_{\rho}(\Omega)=M_{\rho}(0)-s_{z}\Omega. \end{equation} $

(2) This relation indicates that vector mesons tend to occupy the
$ s_{z}=+1 $ state. In this study, a similar result can be obtained for vector meson ϕ.Recently, the mass splitting and spin alignment of vector meson ϕ was investigated under a magnetic field [18]. Further, another important contribution from the rotation on the spin alignment should also be considered. Therefore, in this work, we calculate the rotational contribution on matrix element
$ \rho_{00} $ .This paper is organized as follows. In Sec. II, quantum field theory in a rotating frame is introduced. Based on this, the quark propagator and the self-energy are modified by uniform rotation. Consequently, the masses of vector mesons are obtained by random phase approximation. In Sec. III, the numerical results of quark mass, meson mass, and spin alignment are presented. Finally, the conclusion and summary are provided in Sec. IV.
-
In quantum field theory, a Lorentz vector field
$ V^{a}(x) $ can be described by tetrad$ e_{a}(x)=e_{a}^{\mu}(x)\dfrac{\partial}{\partial x^{\mu}} $ in curved space-time. In this section, Latin letters,$ a,b=0,1,2,3 $ , stand for Lorentz indices. And Greek letters,$ \mu,\nu= $ 0, 1, 2, 3, stand for coordinate indices. Parallel transport of$ V^{a}(x) $ acts as follows:$ \begin{equation} V^{a}(x+{\rm d}x)=V^{a}(x)+\Gamma_{ab\mu}V^{b}{\rm d}x^{\mu}, \end{equation} $

(3) where
$ \Gamma_{ab\mu} $ is called the spin connection. Metric compatibility ensures$ \Gamma_{ab\mu}=-\Gamma_{ba\mu} $ , and non-torsion condition provides a relation between the tetrad and the spin connection:$ \begin{aligned}[b] \Gamma_\mu^{a b}=&\frac{1}{2}\left[e^{a \nu}\left(\partial_\mu e_\nu^b-\partial_\nu e_\mu^b\right)-e^{b \mu}\left(\partial_\mu e_\nu^a-\partial_\nu e_\mu^a\right)\right. \\& \left.-e^{a \rho} e^{b l}\left(\partial_\rho e_{c \sigma}-\partial_\sigma e_{c \rho}\right) e_\mu^c\right]. \end{aligned} $

(4) For spinor field, corresponding spinor connection is given by
$ \Gamma_{\mu}=\sigma^{ab}\Gamma_{ab\mu} $ , where$ \sigma^{ab} $ is spinor representation of Lorentz group. In the co-moving frame of the QGP, free fermions are described by the modified Dirac equation:$ \begin{equation} [i\bar{\gamma}^{\mu}(\partial_{\mu}+\Gamma_{\mu})-M_{f}]\psi=0, \end{equation} $

(5) where
$ M_{f} $ is the mass of a fermion and$ \bar{\gamma}^\mu=e_a^\mu \gamma^a $ satisfies$ \{\bar{\gamma}_{\mu},\bar{\gamma}_{\nu}\}=g^{\mu\nu} $ .Particularly, in a uniformly rotating frame, the tetrad can be described by
$ \begin{equation} e_\mu^a=\delta_\mu^a+\delta_i^a \delta_\mu^0 v_i, \quad e_a^\mu=\delta_a^\mu-\delta_a^0 \delta_i^\mu v_i, \end{equation} $

(6) where
$ \vec{v}=\vec{\Omega} \times \vec{x} $ gives the velocity in the lab frame. We use the capital Greek letter Ω to represent the magnitude of angular velocity. If we substitute Eq. (6) into Eq. (4), non-zero terms of spin connection will be expressed as follows:$ \begin{aligned}[b] \Gamma_{i j 0}=\frac{1}{2}\left(\partial_i v_j-\partial_j v_i\right), & \Gamma_{i 0 j}=\frac{1}{2}\left(\partial_i v_j+\partial_j v_i\right), \\ \Gamma_{0 i j}=-\frac{1}{2}\left(\partial_i v_j+\partial_j v_i\right), & \Gamma_{0 i 0}=-\frac{1}{2}\left(v_j \partial_i v_j+v_j \partial_j v_i\right) . \end{aligned} $

(7) Finally, in a uniformly rotating frame, Dirac equation can be rewritten by [40]
$ \begin{equation} [{\rm i}\gamma^{a}\partial_{a}+\gamma^{0}\Omega \hat{J_{z}}-M_{f}]\psi=0. \end{equation} $

(8) Here, the z-axis is chosen as the direction of the rotation, and it is perpendicular to the reaction plane. The total angular momentum
$ \hat{J_{z}} $ can be expressed as$ \hat{J}_{z}=\hat{L}_{z}+\hat{S}_{z} $ where$ \hat{L}_{z} $ is the orbital angular momentum and$ \hat{S}_{z}=\dfrac{1}{2}\left(\begin{array}{cc} \hat{\sigma}_{z} & 0 \\ 0 & \hat{\sigma}_{z} \\ \end{array} \right) $ contributes to the spin part.For solving modified Dirac equation Eq. (8), Ref. [19] has given the solutions in the cylindrical coordinates where a position in space-time is labeled by
$ \tilde{r}=(t, r, \theta, z) $ . We can write down a complete set of commuting operators: the Hamiltonian$ \hat{H} $ , the longitudinal momentum$ \hat{k}_z $ , the square of transverse momentum$ \hat{\vec{k}}_t^2 $ , the total angular momentum$ \hat{J}_z $ , and the helicity operator on transverse plan$ \hat{h}_t $ . The eigenstates for fermion and anti-fermion [19] are given by$ \begin{aligned} U=\sqrt{\frac{E_k+M_{f}}{4 E_k}} {\rm e}^{{\rm i} k_z z} {\rm e}^{{\rm i} n \theta}\left(\begin{array}{c} J_n\left(k_t r\right) \\ s {\rm e}^{{\rm i} \theta} J_{n+1}\left(k_t r\right) \\ \dfrac{k_z-{\rm i} s k_t}{E_k+M_{f}} J_n\left(k_t r\right) \\ \dfrac{-s k_z+{\rm i} k_t}{E_k+M_{f}} {\rm e}^{{\rm i}\theta} J_{n+1}\left(k_t r\right) \end{array}\right), \end{aligned} $

(9) $ \begin{equation} V=\sqrt{\frac{E_k+M_{f}}{4 E_k}} {\rm e}^{-{\rm i} k_z z} {\rm e}^{{\rm i} n \theta}\left(\begin{array}{c} \dfrac{k_z-{\rm i} s k_t}{E_k+M_{f}} J_n\left(k_t r\right) \\ \dfrac{s k_z-{\rm i} k_t}{E_k+M_{f}} {\rm e}^{{\rm i} \theta} J_{n+1}\left(k_t r\right) \\ J_n\left(k_t r\right) \\ -s {\rm e}^{{\rm i} \theta} J_{n+1}\left(k_t r\right) \end{array}\right), \end{equation} $

(10) where
$ J_n\left(k_t r\right) $ is the n-th order Bessel function and$ n\in \mathbb{Z} $ stands for the quantum number of angular momentum. In Eq. (9) and Eq. (10),$ k_{t} $ and$ k_{z} $ are the eigenvalues of transverse and longitudinal momentum, respectively, and$ s=\pm 1 $ is the eigenvalue of the helicity operator$ \hat{h}_t $ . Besides,$ E_{k} $ is defined by$ E_k \equiv \sqrt{k_z^2+k_t^2+M_{f}^2} $ and the energy is given by$ E=\pm E_k-(n+1/2) \Omega $ .Based on the solutions of the Dirac equation, the quark propagator can be defined as follows:
$ S\left(\tilde{r};\tilde{r}^{\prime}\right)= \langle 0\left|T\psi(\tilde{r})\bar{\psi}\left(\tilde{r}^{\prime}\right)\right| 0\rangle $ . As a standard procedure,$ \psi(\tilde{r}) $ and$ \bar{\psi}\left(\tilde{r}^{\prime}\right) $ are expanded by Eq. (9) and Eq. (10), and an explicit form can be obtained as follows:$ \begin{aligned}[b] S\left(\tilde{r} ; \tilde{r}^{\prime}\right)= & \frac{1}{(2 \pi)^2} \sum_n \int \frac{{\rm d} k_0}{2 \pi} \int k_t {\rm d} k_t \int {\rm d} k_z \frac{{\rm e}^{{\rm i} n\left(\theta-\theta^{\prime}\right)} {\rm e}^{-{\rm i} k_0\left(t-t^{\prime}\right)+{\rm i} k_z\left(z-z^{\prime}\right)}}{\left[k_0+\left(n+\dfrac{1}{2}\right) \Omega\right]^2-k_t^2-k_z^2-M_f^2+{\rm i} \epsilon} \\ & \times\left\{\left[\left[k_0+\left(n+\frac{1}{2}\right) \Omega\right] \gamma^0-k_z \gamma^3+M_f\right]\left[J_n\left(k_t r\right) J_n\left(k_t r^{\prime}\right) \mathcal{P}_++{\rm e}^{{\rm i}\left(\theta-\theta^{\prime}\right)} J_{n+1}\left(k_t r\right) J_{n+1}\left(k_t r^{\prime}\right) \mathcal{P}_-\right]\right. \\ & \left.-{\rm i} \gamma^1 k_t {\rm e}^{{\rm i} \theta} J_{n+1}\left(k_t r\right) J_n\left(k_t r^{\prime}\right) \mathcal{P}_+-\gamma^2 k_t {\rm e}^{-{\rm i} \theta^{\prime}}J_n\left(k_t r\right) J_{n+1}\left(k_t r^{\prime}\right) \mathcal{P}_-\right\}. \end{aligned} $ 
(11) Here, we have simplified the expression by projection operators
$\mathcal{P}_{\pm}=\dfrac{1}{2}\left(1 \pm {\rm i} \gamma^1 \gamma^2\right)$ . In Appendix A, we will present another procedure for obtaining the quark propagator in a rotating medium.Nevertheless, Eq. (11) is the result under the infinite size approximation. A finite size version with a boundary condition can be found in Ref. [28]. The transverse momentum
$ k_{t} $ is discrete, and its integral is replaced by the summation of the series. In this study, we have to first calculate the spectral functions of vector mesons in a rotating medium. Therefore, we apply the infinite size approximation to avoid the tedious summation of the series. This compromise will violate the causality in the case of a large angular velocity. In this work, we study the phenomena and quantities at a fixed radius$ r=0.1\; \text{GeV}^{-1} $ and in a range of angular velocity from$ \Omega=0 $ GeV to$ \Omega= 1.2 $ GeV so that the velocity of a fixed point is smaller than the speed of light, i.e.$ \Omega r < 1 $ . -
In order to study the microscopic properties of vector mesons, we use the Nambu-Jona-Lasinio(NJL) model to estimate the strong interaction[41]. The 3-flavor NJL model is required to investigate ϕ meson, which contains s quark [42]. The Lagrangian of the 3-flavor NJL model is given as follows:
$ \begin{aligned}[b] \mathcal{L}_{3 \mathrm{NJL}}=& \bar{\psi}[{\rm i}\bar{\gamma}^{\mu}(\partial_{\mu}+\Gamma_{\mu})-m_{f}]\psi\\ &+G_{S} \sum_{a=0}^8\left[\left(\bar{\psi} \lambda^a \psi\right)^2+\left(\bar{\psi} {\rm i} \gamma_5 \lambda^a \psi\right)^2\right] \\ &-G_{V} \sum_{a=0}^8\left[\left(\bar{\psi} \gamma_{\mu}\lambda^a \psi\right)^2+\left(\bar{\psi} {\rm i} \gamma_{\mu}\gamma_5 \lambda^a \psi\right)^2\right] \\ &-K\left[\operatorname{det} \bar{\psi}\left(1+\gamma_5\right) \psi+\operatorname{det} \bar{\psi}\left(1-\gamma_5\right) \psi\right], \end{aligned} $

(12) where K is the coupling constant of six-fermion interaction,
$ G_{s} $ and$ G_{V} $ are coupling constants of four-fermion interaction for scalar and vector channels, respectively. In the 3-flavor NJL model,$ \psi=(\psi_{u},\psi_{d},\psi_{s}) $ is a Dirac spinor which contains u, d and s quarks. Correspondingly,$ \lambda_{a} $ are the Gell-Man matrices and$ m_{f} $ is the current quark mass with different flavors.The NJL model is an effective model which only contains quarks. The rotation affects the quark dynamics through the non-zero term of spinor connection
$ \Gamma^{\mu} $ . Furthermore, by applying the mean field approximation, the Lagrangian can be rewritten as$ \begin{aligned}[b] \mathcal{L}_{\mathrm{MF}}=& \sum_{f=u, d, s} \bar{\psi}_f\left[{\rm i} \bar{\gamma}_\mu (\partial_{\mu}+\Gamma_{\mu})-M_f\right] \psi_f \\ &-2 G_S \sum_{f=u, d, s} \sigma_f^2+4 K \sigma_u \sigma_d \sigma_s \end{aligned} $

(13) where
$ \sigma_{f} $ is the chiral condensate$ \sigma_f \equiv\langle\bar{\psi}_f \psi_f\rangle $ for a specific flavor. And$ M_{f} $ is dynamical quark mass, which is given by$ \begin{equation} M_f \equiv m_f-4 G_S \sigma_f+2 K \prod\limits_{f^{\prime} \neq f} \sigma_{f^{\prime}}. \end{equation} $

(14) In a uniformly rotating medium, the spinor connection
$ \Gamma^{\mu} $ has been estimated in Sec. II.A. We assume the direction of rotation is parallel to the z-axis. By applying the standard procedure in finite-temperature field theory [43], the grand potential for quarks with specific flavors is shown as follows:$\begin{aligned}[b] \Omega_{f}(r)=&\frac{N_c}{8 \pi^2} T \sum_n \int {\rm d} k_t^2 \int {\rm d} k_z\left[J_n\left(k_t r\right)^2+J_{n+1}\left(k_t r\right)^2\right] \\ &\times\left[E_{k}/T+\ln \left(1+{\rm e}^{-\left(E_k-\left(n+\frac{1}{2}\right) \Omega\right) / T}\right)\right. \\ &\left.+\ln \left(1+{\rm e}^{-\left(E_k+\left(n+\frac{1}{2}\right) \Omega\right) / T}\right)\right]. \end{aligned} $

(15) Consequently, the total grand potential is
$ \begin{equation} \Omega_{\text{tot}}(r)=\sum\limits_{f=u, d, s}\left(2 G_S \sigma_f^2-\Omega_f\right)+4 K \sigma_u \sigma_d \sigma_s. \end{equation} $

(16) Here,
$ N_{c}=3 $ is the degeneracy of color, and T is the temperature of the medium. We can obtain the dynamical quark mass$ M_{f} $ and chiral condensate$ \sigma_{f} $ by solving the gap equations:$ \begin{equation} \frac{\partial \Omega_{\text{tot}} }{ \partial \sigma_f}=0, \quad \frac{\partial^{2} \Omega_{\text{tot}} }{ \partial \sigma_f^{2}}>0. \end{equation} $

(17) In principle, if other parameters are fixed, the dynamical quark mass
$ M_{f}(r) $ will be a function of radius r. Currently, most studies have assumed that$ M_{f}(r) $ is changed smoothly, i.e.$ \partial M_{f}(r)/\partial r\simeq 0 $ . Such an assumption is called local density approximation(LDA) [19, 24, 32]. In this paper, we use the LDA and choose a fixed radius$r=0.1~\text{GeV}^{-1}$ . Then,$ M_{f}(\Omega) $ will be evaluated numerically in Sec. II.A. -
In the NJL model, the vector meson ϕ is treated as a
$ s\bar{s} $ bound state or a resonance state, and it can be constructed by quark-antiquark scattering [41]. In the random phase approximation (RPA), the vector meson propagator can be obtained by summation of quark loops, and the one loop polarization function is given by$ \begin{equation} \Pi^{\mu\nu}(q)=-{\rm i} \int {\rm d}^{4}\tilde{r}\text{Tr}_{sfc}[{\rm i} \gamma^{\mu}S(0;\tilde{r})i \gamma^{\nu}S(\tilde{r};0)]{\rm e}^{{\rm i} q\cdot \tilde{r}}. \end{equation} $

(18) Here,
$ \text{Tr}_{sfc} $ stands for the trace in the spinor, flavor, and color spaces. Since ϕ meson is purely constituted by s quark,$ S(0;\tilde{r}) $ stands for the s quark propagator with the dynamical mass$ M_{s} $ given by mean field approximation. The polarization function of ϕ meson is supposed to be modified in a rotating medium.Currently, we focus on the mesons which remain at rest in the rotating frame, i.e.
$ \vec{q}=0 $ . In this case, polarization vectors are given by$ \begin{aligned}[b] \epsilon^{\mu}_{1}&=\frac{1}{\sqrt{2}}(0,1,i,0),\\ \epsilon^{\mu}_{2}&=\frac{1}{\sqrt{2}}(0,1,-i,0),\\ b^{\mu}&=(0,0,0,1) \end{aligned} $

(19) where
$ \epsilon^{\mu}_{1} $ and$ \epsilon^{\mu}_{2} $ are the right and left-hand polarization vectors, respectively. The longitudinal polarization vector is parallel to the direction of rotation. Correspondingly, the projection operators are given by$ \begin{aligned}[b] P^{\mu\nu}_{1}&=-\epsilon^{\mu}_{1}\epsilon^{\nu}_{1},(s_{z}=-1 \text{ for } \phi \text{ meson }),\\ P^{\mu\nu}_{2}&=-\epsilon^{\mu}_{2}\epsilon^{\nu}_{2},(s_{z}=+1\text{ for } \phi \text{ meson }),\\ L^{\mu\nu}&=-b^{\mu}b^{\nu},(s_{z}=0 \text{ for } \phi \text{ meson }). \end{aligned} $

(20) As we have assumed
$ \vec{q}=0 $ , nonzero elements of the polarization functions can be read in the following matrix:$ \begin{equation} \Pi^{\mu\nu}_{\phi}=\left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & \Pi^{11} & \Pi^{12} & 0 \\ 0 & \Pi^{21} & \Pi^{22} & 0 \\ 0 & 0 & 0 & \Pi^{33} \\ \end{array} \right). \end{equation} $

(21) The explicit expressions of matrix elements are shown in Ref. [26]. This tensor can be decomposed by projection operators in Eq. (20) as follows:
$ \begin{equation} \Pi^{\mu\nu}_{\phi}=A_{-1,-1}P^{\mu\nu}_{1}+A_{11}P^{\mu\nu}_{2}+A_{00}L^{\mu\nu}, \end{equation} $

(22) Similarly, the vector meson propagator can be decomposed as follows:
$ \begin{equation} D^{\mu\nu}_{\phi}(q)=D_{-1,-1}(q)P^{\mu\nu}_{1}+D_{11}(q)P^{\mu\nu}_{2}+D_{00}(q)L^{\mu\nu}. \end{equation} $

(23) Here, coefficients
$ D_{\lambda} $ are obtained by RPA summation and expressed by:$ \begin{equation} D_{\lambda\lambda}(q)=\frac{4G_{V}}{1+4G_{V}A_{\lambda\lambda}}, \end{equation} $

(24) where
$ \begin{aligned}[b] A_{-1,-1}&=-(\Pi_{11} - {\rm i} \Pi_{12}), &(s_{z}=-1 \text{ for } \phi \text{ meson }),\\ A_{11}&=-\Pi_{11} - {\rm i} \Pi_{12}, &(s_{z}=+1\text{ for } \phi \text{ meson }),\\ A_{00}&=-\Pi_{33}, &(s_{z}=0 \text{ for } \phi \text{ meson }). \end{aligned} $

(25) Then, we can obtain the corresponding spectrum functions for different spin components, taking the following form:
$ \begin{aligned}[b] \xi_{\lambda\lambda}(\omega) &\equiv \frac{1}{\pi} \operatorname{Im} D_{\lambda\lambda}(\omega)\\ &=\frac{\left(4 G_V\right)^2 \operatorname{Im} A_{\lambda\lambda}(\omega)}{\pi\left\{\left[1+4 G_V \operatorname{Re} A_{\lambda\lambda}(\omega)\right]^2+\left[4 G_V \operatorname{Im} A_{\lambda\lambda}(\omega)\right]^2\right\}}, \end{aligned} $

(26) where ω is the energy of the meson, and we set the momentum to
$ \vec{q}=0 $ . -
Heavy-ion collisions will create an ensemble of particles under extreme conditions. Particularly, we consider vector meson ϕ with spin-1. For a fixed direction, a normalized spin state of a ϕ meson is labeled by
$ |\lambda\rangle $ with$ \lambda=1,0,-1 $ . Spin density operator ρ is defined by$ \begin{equation} \rho=\sum\limits_{\lambda\lambda^{\prime}} \rho_{\lambda\lambda^{\prime}}\left|\lambda\rangle\langle\lambda^{\prime}\right|, \end{equation} $

(27) Here,
$ \rho_{\lambda\lambda^{\prime}} $ comprises a$ 3\times 3 $ spin density matrix as follows:$ \begin{equation} \rho_{\lambda\lambda^{\prime}}=\left(\begin{array}{ccc} \rho_{11} & \rho_{10} & \rho_{1,-1}\\ \rho_{01} & \rho_{00} & \rho_{1,-1}\\ \rho_{-1,1}& \rho_{-1,0} & \rho_{-1,-1} \end{array}\right)\,, \end{equation} $

(28) An ensemble of ϕ mesons, for which spin information is described by
$ \rho_{\lambda\lambda^{\prime}} $ , will decay to$ \begin{equation} \phi \rightarrow K^++K^-. \end{equation} $

(29) In this process, daughter particles will have an angular distribution [44, 45]:
$ \begin{aligned}[b] \frac{{\rm d} N}{{\rm d} \Omega^{*}}= & \frac{3}{4 \pi}\left\{\cos ^2 \theta \rho_{00}+\sin ^2 \theta\left(\rho_{11}+\rho_{-1-1}\right) / 2\right. \\ & -\sin 2 \theta\left(\cos \phi \operatorname{Re} \rho_{10}-\sin \phi \operatorname{Im} \rho_{10}\right) / \sqrt{2} \\ & +\sin 2 \theta\left(\cos \phi \operatorname{Re} \rho_{-10}+\sin \phi \operatorname{Im} \rho_{-10}\right) / \sqrt{2} \\ & \left.-\sin ^2 \theta\left[\cos (2 \phi) \operatorname{Re} \rho_{1-1}-\sin (2 \phi) \operatorname{Im} \rho_{1-1}\right]\right\} . \end{aligned} $

(30) From experimental data of θ-distribution,
$ \rho_{00} $ can be obtained as a coefficient of angular distribution. Since experiments can measure the value of$ \rho_{\lambda\lambda^{\prime}} $ , theoretical studies should explain the results of spin alignment and evaluate$ \rho_{\lambda\lambda^{\prime}} $ qualitatively. Magnetic field and vorticity are two factors considered in many models. The approaches are generalized as follows:$ \begin{equation} \operatorname{B, \Omega}\left(\text{quarks}\right) \stackrel{\text { influence }}{\longrightarrow} \rho_{\lambda\lambda^{\prime}}\left( \phi\right) \stackrel{\text { determine }}{\longrightarrow} \frac{{\rm d} N}{{\rm d} \Omega^{*}}\left( K^+,K^-\right). \end{equation} $

(31) Theoretical studies are interested in the first step of Eq. (31). In a real heavy-ion collision process, the evolution is complicated, and the history will influence
$ \rho_{\lambda\lambda^{\prime}} $ after the freeze out. One possible method is the quark coalescence model. However, it is unable to take the medium effects into account in the quark coalescence model. As we mentioned in previous sections, the quark and meson masses will be modified in a rotating medium.In this investigation, we aim at a uniformly rotating medium, and the created ϕ mesons are in global equilibrium. In this case, the particle number density
$ \overline{\rho}_{\lambda\lambda^{\prime}}({\bf q}) $ can be expressed by$ \begin{equation} \overline{\rho}_{\lambda\lambda^{\prime}}({\bf q})=\int {\rm d}\omega\,\frac{2\omega}{{\rm e}^{\omega/T}-1}\xi_{\lambda\lambda^{\prime}}(\omega, \bf q)\,, \end{equation} $

(32) where
$ \xi_{\lambda\lambda^{\prime}}(\omega, \bf k) $ is the spectral function given in Eq. (26). At the one loop level, the spectral function in a rotating medium is calculated in Ref. [26], and we present it in Appendix B for convenience. Generally, the spectral function is the imaginary part of the full propagator:$ \begin{equation} \xi_{\lambda\lambda^{\prime}}(q)\equiv\frac{1}{\pi}\text{Im}D_{\lambda\lambda^{\prime}}(q)\,. \end{equation} $

(33) For a general nonzero momentum
$ {\bf q} $ , the matrix$ \xi_{\lambda\lambda^{\prime}}(\omega, \bf q) $ and$ \overline{\rho}_{\lambda\lambda^{\prime}}({\bf q}) $ may have nonzero off-diagonal elements. Particularly, if the quantization direction coincides with the rotation axis and the momentum$ {\bf q} $ is parallel/antiparallel to the rotation axis, or$ {\bf q}=0 $ ,$ \xi_{\lambda\lambda^{\prime}}(\omega, \bf q) $ and$ \overline{\rho}_{\lambda\lambda^{\prime}}({\bf q}) $ will become diagonal:$ \begin{equation} \overline{\rho}_{\lambda\lambda^{\prime}}({\bf q})=\left(\begin{array}{ccc} \overline{\rho}_{11} & 0 & 0\\ 0 & \overline{\rho}_{00} & 0\\ 0 & 0 & \overline{\rho}_{-1,-1} \end{array}\right)\,. \end{equation} $

(34) Therefore, we divide the spectral function into two parts: a delta function part and a continuum part, i.e.
$ \begin{equation} \xi_{\lambda\lambda}(\omega, \mathbf{q})=\delta\left(\omega^2-M_{\phi, \lambda}^2\right)+\xi_{\lambda\lambda}^*(\omega,\bf q), \end{equation} $

(35) where
$ \xi_{\lambda\lambda}^*(\omega,\bf q) $ is the continuum part of spectral function and$ M_{\phi,\lambda} $ is the vector meson mass for different spin components. Correspondingly, the particle number density$ \bar{\rho}_{\lambda\lambda}({\bf q}) $ takes the form of:$ \begin{equation} \bar{\rho}_{\lambda\lambda}({\bf q})=\frac{1}{\exp \left(M_{\phi,\lambda} / T\right)-1}+\int {\rm d} \omega \frac{2 \omega \xi_{\lambda\lambda}^*(\omega, \bf q)}{\exp (\omega / T)-1} .\end{equation} $

(36) In experiment measurement, spin alignment is evaluated by matrix element
$ \rho_{00} $ which can be expressed by:$ \begin{equation} \rho_{00}({\bf q})\equiv\frac{\overline{\rho}_{00}({\bf q})}{\sum_{\lambda=0,\pm1}\overline{\rho}_{\lambda\lambda}({\bf q})}\,. \end{equation} $

(37) In the non-rotating case, ϕ mesons with different spin components have the same mass
$ M_{\phi}(s_{z}=0,\pm 1) $ , which leads to$ \rho_{00}=1/3 $ . In a finite angular velocity, the mass of ϕ meson with$ s_{z}=+1 $ component decreases linearly; thus, ϕ mesons tend to occupy the$ s_{z}=+1 $ state. Consequently, spin polarization and alignment can be obtained in our formalism.In this section, Eqs. (32)−(37) are momentum-dependent. However, in this investigation, we evaluate the spectral functions and spin alignment with
$ {\bf q}={\bf 0} $ , which means vector mesons are staying at rest in the rotating frame. In general, Ref. [18] has revealed the spin density matrix for arbitrary measuring direction, which is characterized by Euler angles$ (\alpha,\,\beta,\,\gamma) $ . The explicit form is:$ \overline{\rho}_{\lambda\lambda^{\prime}}({\bf 0};\alpha,\beta,\gamma) =\sum_{\lambda_{1},\lambda_{2}}R_{\lambda\lambda_{1}}(\alpha,\beta,\gamma)\overline{\rho}_{\lambda_{1}\lambda_{2}}({\bf 0})R_{\lambda_{2}\lambda^{\prime}}^{-1}(\alpha,\beta,\gamma)\,. $

(38) Here,
$ R_{\lambda\lambda^{\prime}}(\alpha,\beta,\gamma) $ is the spin-1 representation of the rotation. As a result, the spin alignment only depends on Euler angles β, and the explicit form is:$ \begin{equation} \rho_{00}({\bf 0};\alpha,\beta,\gamma)=\frac{\overline{\rho}_{00}({\bf 0})\cos^{2}\beta+\overline{\rho}_{11}({\bf 0})\sin^{2}\beta}{\bar{\rho}_{00}({\bf 0})+\bar{\rho}_{11}({\bf 0})+\bar{\rho}_{-1,-1}({\bf 0})}\,. \end{equation} $

(39) In Sec. III.C, numerical results will be presented for
$ \beta=0 $ , and the following formula is used:$ \begin{equation} \rho_{00}^{\Omega}({\bf 0})\equiv\frac{\bar{\rho}_{00}({\bf 0})}{\bar{\rho}_{00}({\bf 0})+\bar{\rho}_{11}({\bf 0})+\bar{\rho}_{-1,-1}({\bf 0})}\,. \end{equation} $

(40) -
Since a rotating system has broken the Lorentz symmetry, it is not necessary to use Pauli-Villas regularization. In fact, the Bessel function will not reflect the oscillation behavior in the cut-off energy scale Λ. Therefore, we choose a soft cut-off function:
$ \begin{equation} f_{\Lambda}=\frac{\Lambda^{2*10}}{\Lambda^{2*10}+p^{2*10}}, \end{equation} $

(41) where
$\Lambda=620.411~ \text{MeV}$ is the energy scale for cut-off, and the corresponding coupling constants are:$ \mathrm{G_{S}}=\dfrac{1.710}{\Lambda^2} $ ,$ G_{V}=0.67 * \dfrac{1.710}{\Lambda^2} $ and$ K=\dfrac{12035}{1000 \Lambda^5} $ . In this case,$ m_{\pi}=140 $ MeV and$ m_{\phi}=1020 $ MeV in vacuum. Current quark masses are:$ m_{u}=m_{d}=5.5 $ MeV,$ m_{s}=135.433 $ MeV. -
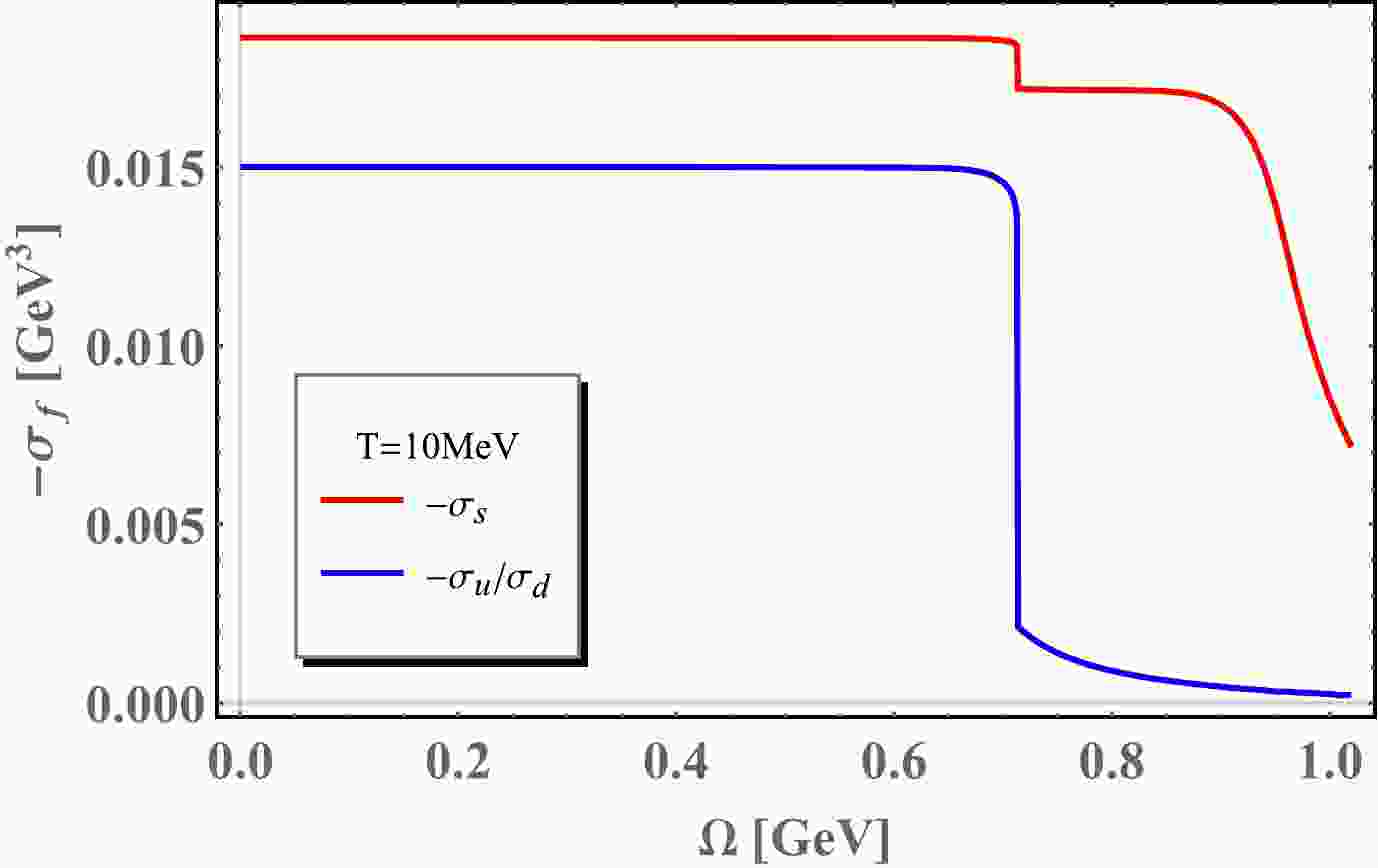
As mentioned in previous sections, chiral condensate will be suppressed under rotation. In Fig. 1 and Fig. 2, chiral condensates are demonstrated as a function of angular velocity Ω at temperature
$ T=10 \;\text{MeV} $ and$T=$ 150 MeV, respectively. Correspondingly, dynamical quark masses are also demonstrated as a function of angular velocity Ω in Fig. 3 and Fig. 4. Chiral symmetry will be restored as angular velocity grows. In Fig. 1 and Fig. 3, at an almost zero temperature,$T=10 ~\text{MeV}$ , rotation induces a first order transition at angular velocity$ \Omega_{c}= $ 0.713 GeV. Both$ M_{u} $ and$ M_{d} $ stay at a constant mass when the angular velocity is below$ \Omega_{c} $ . From Eq. (14), we know that dynamical quark masses are determined by the chiral condensates$ \sigma_{u} $ ,$ \sigma_{d} $ and$ \sigma_{s} $ . In fact,$ \sigma_{u}=\sigma_{d} $ and drops at$ \Omega_{c} $ while$ \sigma_{s} $ still varies smoothly. Consequently,$ M_{s} $ has a small jump at$ \Omega_{c} $ and then decrease smoothly. The behavior of$ M_{u,d,s} $ as a function of angular velocity, Ω is very similar to the case of finite quark chemical potential [46, 47], but the first order phase transition will occur at$ \mu_c\simeq 0.33 $ GeV at finite density.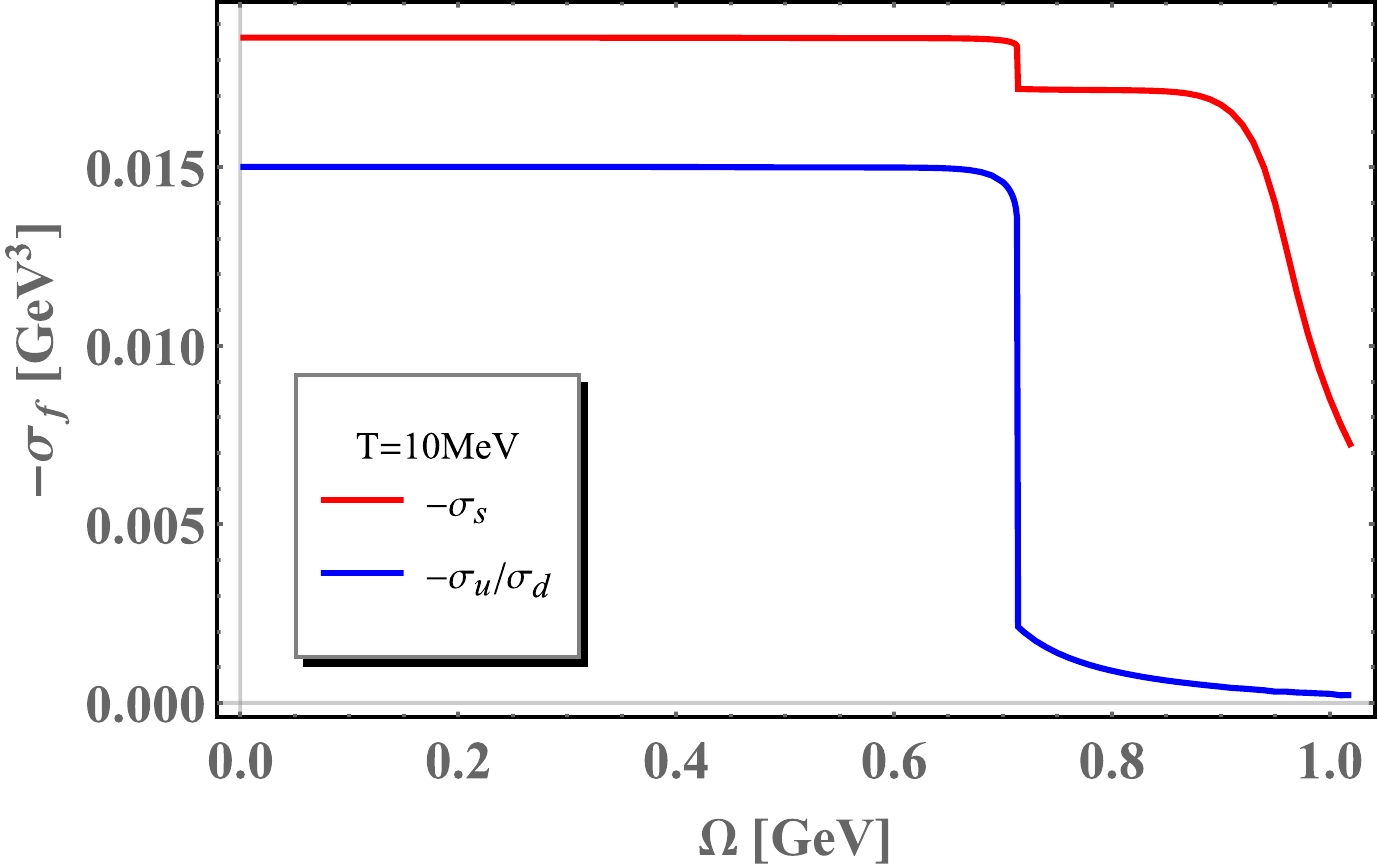
Figure 1. (color online) Chiral condensates as functions of angular velocity at temperature
$ T=10 $ MeV. Red lines stand for$ -\sigma_{s} $ and the blue lines stand for$ -\sigma_{u} $ and$ -\sigma_{d} $ .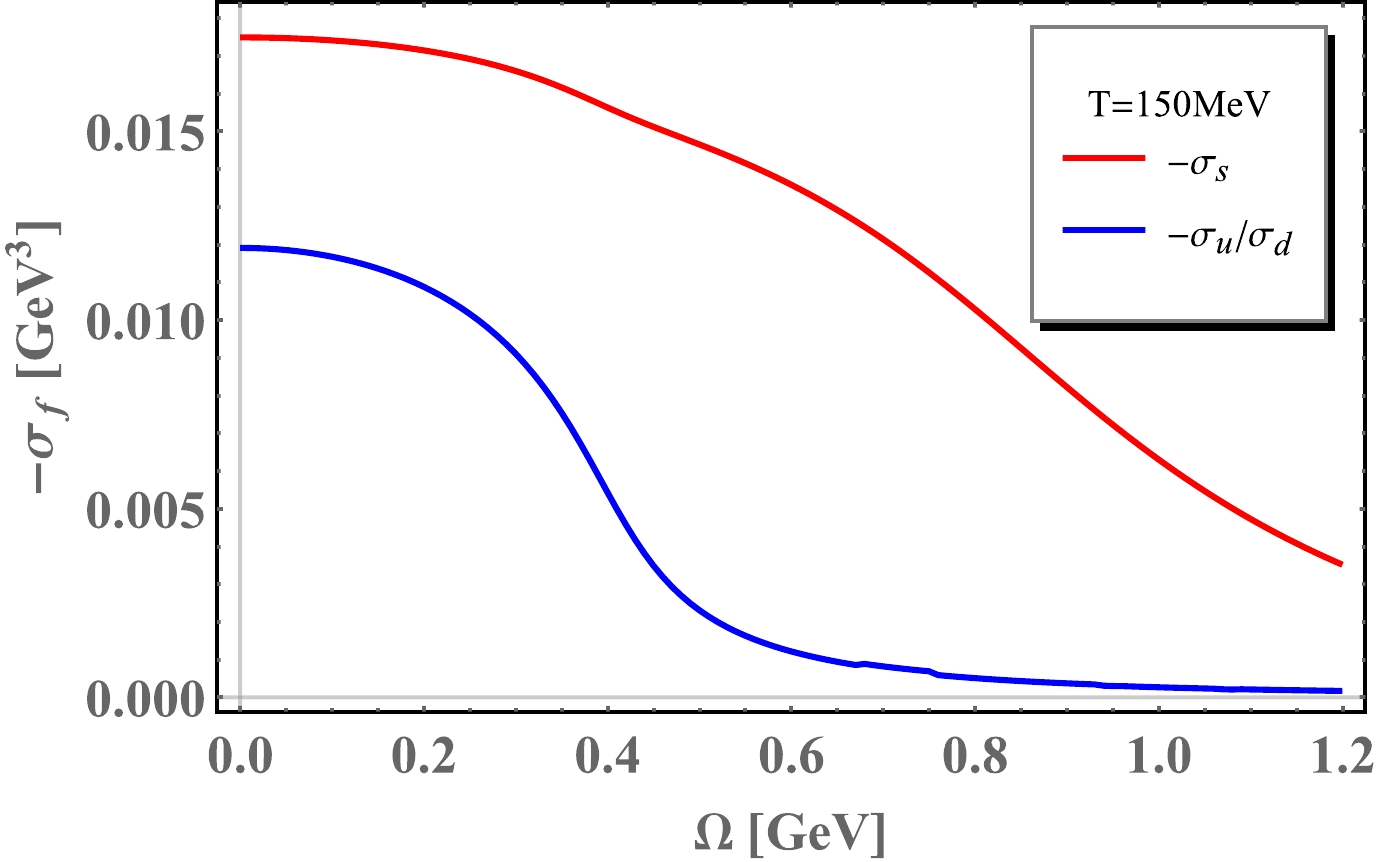
Figure 2. (color online) Chiral condensates as functions of angular velocity at temperature
$ T=150 $ MeV. Red lines stand for$ -\sigma_{s} $ and the blue lines stand for$ -\sigma_{u} $ and$ -\sigma_{d} $ .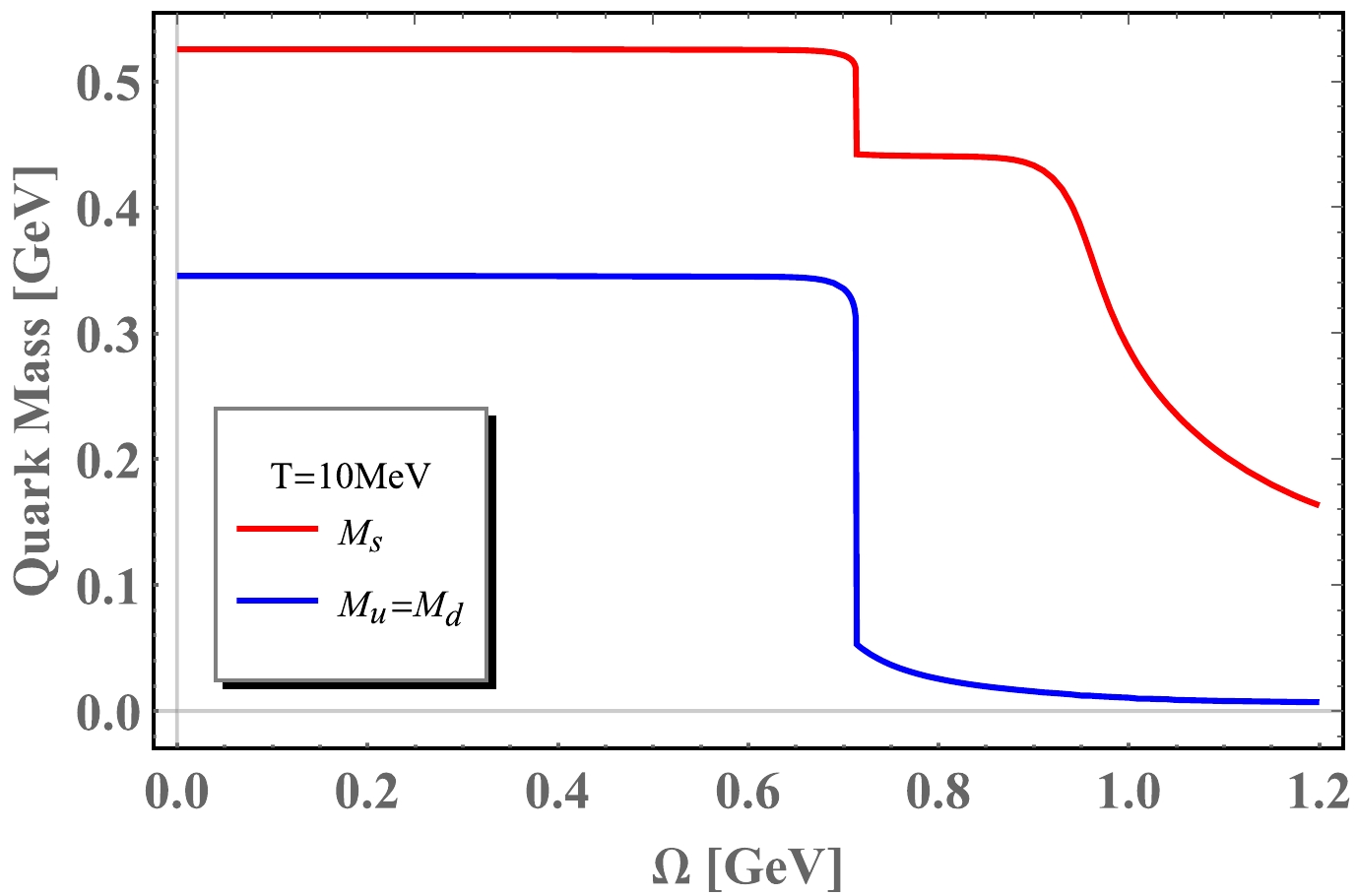
Figure 3. (color online) Dynamical quark masses as functions of angular velocity at temperature
$ T=10 $ MeV. Red lines stand for mass of s quark and the blue lines stand for light quark u and d.
Figure 4. (color online) Dynamical quark masses as functions of angular velocity at temperature
$ T=150 $ MeV. Red lines stand for mass of s quark and the blue lines stand for light quark u and d.At a higher temperature,
$ T=150 $ MeV, Fig. 4 reveals that the chiral phase transition will be a crossover, which occurs around$ \Omega_{c}\sim 0.4 $ GeV. The phase transition takes place in a smaller angular velocity. Furthermore, It is noticed that the mass decreases slowly before the phase transition. Above all, the rotational effect on the dynamical quark mass is similar to that of the chemical potential$ \mu_{q} $ . -
After we obtain the dynamical quark masses in different temperatures and angular velocities, we can apply this result in Eq. (18) and obtain corresponding meson masses.
At zero temperature and low temperatures, similar to ρ meson, ϕ meson mass with different spin components
$ s_z=0,\pm1 $ also show mass splitting effect with$M_{\phi}(\Omega)= M_{\phi}(0)- s_{z}\Omega$ .At
$ T=150 $ MeV and$ \mu=0 $ MeV, Fig. 5 shows ϕ meson mass with different spin components$ s_z=0,\pm1 $ as a function of angular velocity. The mass of$ s_{z}=0 $ component for ϕ meson almost remains unchanged with the angular velocity. The mass of$ s_{z}=-1 $ component of ϕ meson grows almost linearly with the angular velocity. It implies that ϕ meson will be less likely to stay at the$ s_{z}=-1 $ state. In contrast, the$ s_{z}=+1 $ component ϕ meson mass decreases almost linearly with the angular velocity.$ s_{z}=+1 $ component will be a preferred state under the rotation. Above all, the nearly linear mass splitting behavior of ϕ meson at$ T=150 $ MeV can be summarized in the following expression:
Figure 5. (color online) ϕ meson mass as a function of angular velocity at temperature
$ T=150 $ MeV and$ \mu=0 $ MeV.$ \begin{equation} M_\phi(\Omega)\sim M_\phi(0)-s_{z}\Omega. \end{equation} $

(42) In Fig. 6, we reveal the deviation of ϕ meson mass from Eq. (42) at
$ T=150 $ MeV. From Eq. (42), we will know that:$ M_{\phi}(\Omega)+s_{z}\Omega\sim M_{\phi}(0) $ , and the Fig. 6 has shown the difference between "$ \sim $ " and "=". The deviation is caused by the inhibition of chiral condensate. If we expand$ M_\phi(\Omega) $ to order$ \Omega^2 $ , the deviation can be revealed as follows: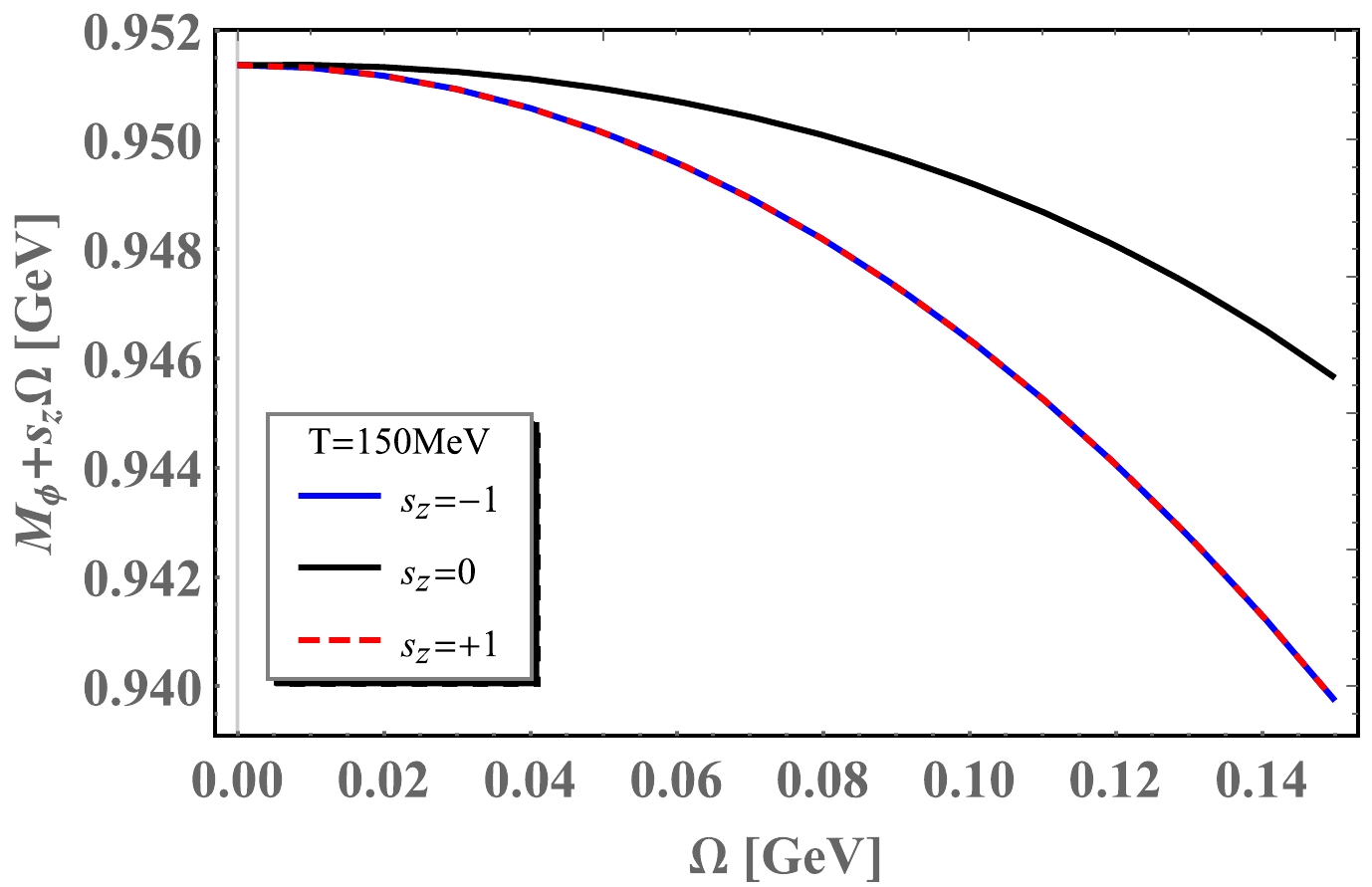
Figure 6. (color online) The deviation of ϕ meson mass as a function of angular velocity at temperature
$ T=150 $ MeV.$ \begin{aligned}[b] M_\phi(\Omega,s_{z}=+1)&=0.95-1.00 \Omega-0.54 \Omega^2,\\ M_\phi(\Omega,s_{z}=0)&=0.95+0.01 \Omega-0.31 \Omega^2,\\ M_\phi(\Omega,s_{z}=-1)&=0.95+1.00\Omega-0.54 \Omega^2. \end{aligned} $

(43) Eq. (43) shows the deviation of
$ s_{z}=0,\pm 1 $ components, caused by quark mass descending in finite temperature and angular velocity. ϕ meson is an almost pure$ s\bar{s} $ state [41], so its mass is obviously influenced by the quark mass. It is seen that the deviation of the$ s_{z}=\pm 1 $ component states are larger than that of the$ s_{z}=0 $ component state.Figure 7 and Fig. 8 reveal rotational effect on the spectra function
$ \xi(\omega) $ for ϕ meson and ρ meson with different spin components as a function of the frequency ω respectively. The blue lines stand for spectral functions at$ \Omega=0 $ without rotation, while the red, orange, and gray dashed lines stand for spectral functions under finite rotation for$ \Omega=0.1, 0.2 $ , and$ 0.3 $ GeV, respectively. In the zero rotation case, ϕ mesons with different spin states shared the same spectral function which is constituted by a delta function part and a continuum part. The location of the delta function indicates the pole mass.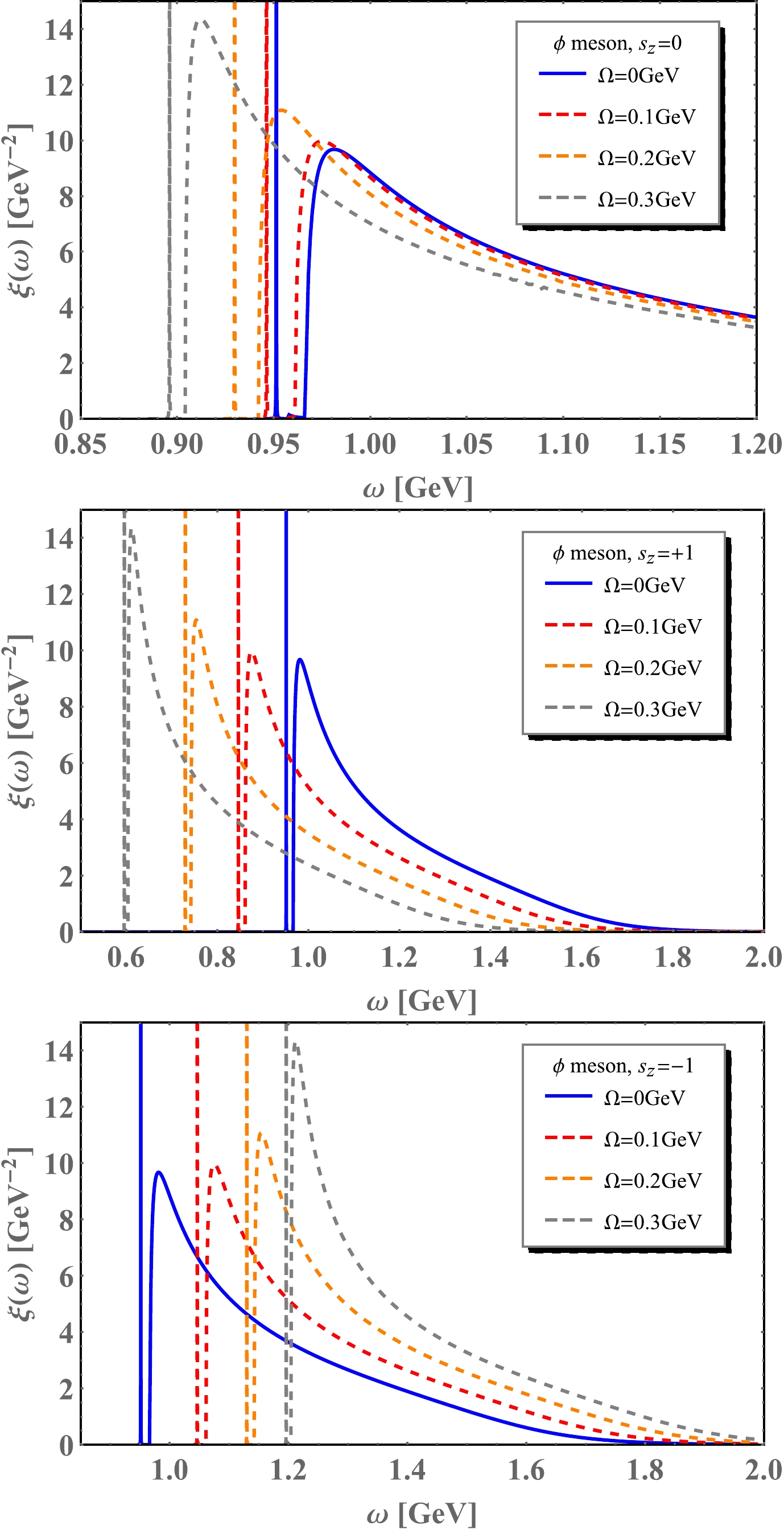
Figure 7. (color online) The spectral function
$ \xi(\omega) $ for ϕ meson with different spin component as a function of the frequency ω under different angular velocities$\Omega=0,~0.1,~0.2,~0.3$ GeV at$ T=150 $ MeV and$ \mu=0 $ .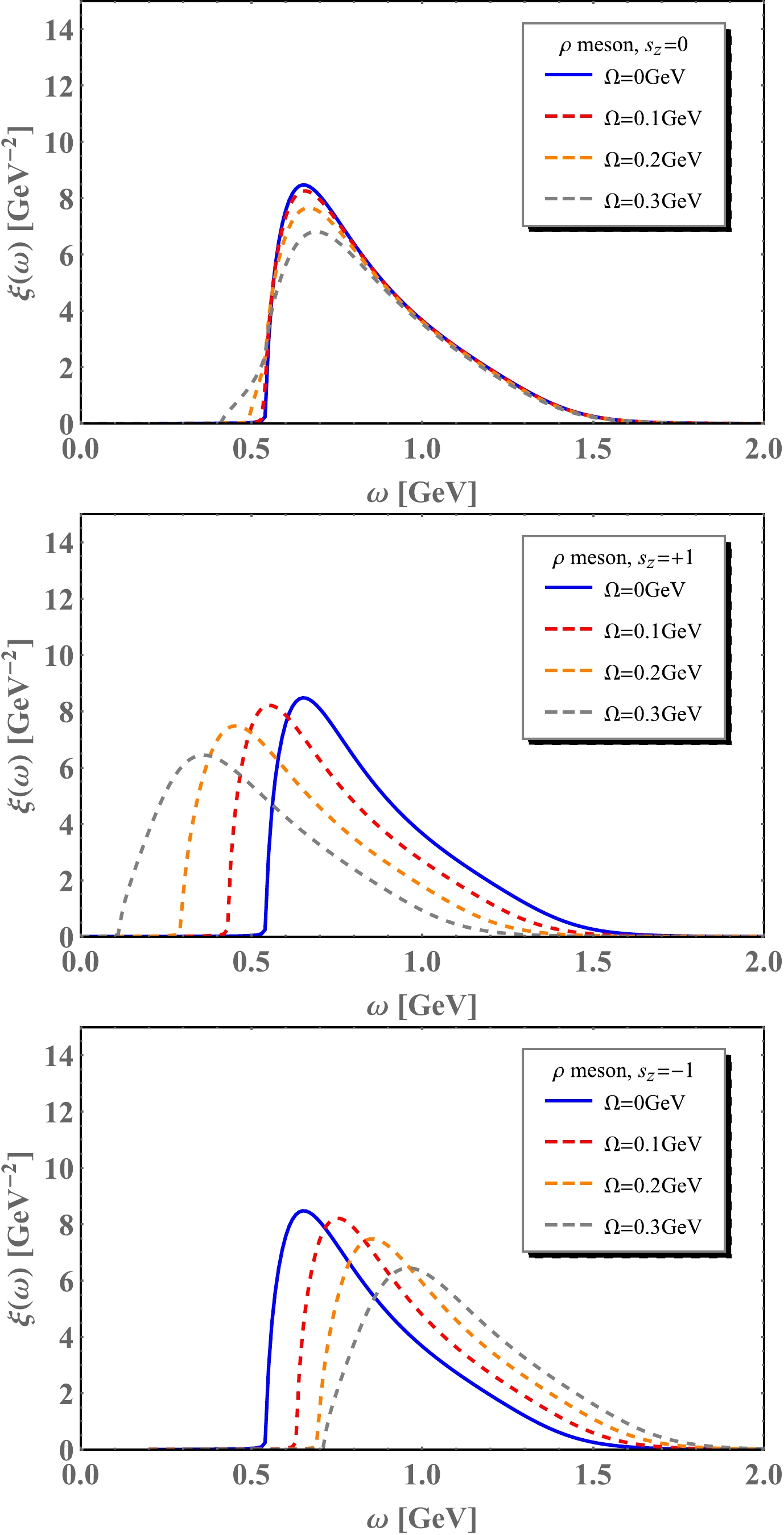
Figure 8. (color online) The spectral function
$ \xi(\omega) $ for ρ meson with different spin component as a function of the frequency ω under under different angular velocities$\Omega=0,~0.1,~0.2,~0.3$ GeV at$ T=150 $ MeV and$ \mu=0 $ .For the
$ s_{z}=0 $ component of ϕ meson, the rotational effect is less remarkable than in the other two cases. So, the scale has been amplified, and we only present the$ \xi(\omega) $ in the range of energy ω from 0.85 GeV to 1.20 GeV. It is found that spectral functions are shifted to the left slightly. And the peaks of the continuum parts are enhanced significantly.For
$ s_{z}=+1 $ component of ϕ meson, the rotational effect will shift the spectral function to the left side, and the rotation will change the height or the shape of the continuum part of the spectral function as well. For the$ s_{z}=-1 $ component, the spectral function is shifted to the right side correspondingly.A similar analysis can be applied for the vector meson ρ, since we have assumed
$ M_{u}=M_{d} $ . We can obtain the spectral function by substituting$ M_{s} $ for$ M_{u}/M_{d} $ . For ϕ mesons, a bound state is labeled by mass$ M_{\phi} $ , which is very close to the$ 2 M_{s} $ . However, ρ mesons are dissociated at temperature$ T=150 $ MeV. So, in Fig. 8, a spectral function only has a continuum part and appears as a single peak. The top panel in Fig. 8 shows the spectral functions of ρ mesons with spin components$ s_{z}=0 $ . Different colored lines stand for different strengths of angular velocities ranging from$ \Omega=0, ~0.1,~ 0.2 $ and$ 0.3 $ GeV. Rotational effects are reflected in two aspects: the heights of the peaks are suppressed, and the widths are broadened by the angular velocities. It can be understood that mesons tend to be less bounded in a rotating medium. The location of the peaks is almost unchanged in the case of$ s_{z}=0 $ . However, in the case of$ s_{z}=+1 $ , the locations of resonance peaks are shifted to the left side by rotation. Similarly, in the case of$ s_{z}=-1 $ , mass spectra are shifted to the right side by rotation. Above all, on the shape of spectral functions, the rotation effects are similar. -
In Fig. 9, we show the deviation of spin alignment
$ \rho_{00} $ from 1/3 for ϕ meson as a function of angular velocity at a finite temperature T = 150 MeV. In the case of rotation,$ \rho_{00} $ is always smaller than 1/3, and the deviation will become more significant as the angular velocity grows. Furthermore, resonance states will contribute less to spin alignment and the deviation between the bounded state and the total result is negligible. In Fig. 10, we compare the spin alignment$ \rho_{00} $ from 1/3 for ϕ meson with ρ meson, and it is found the difference is quite small.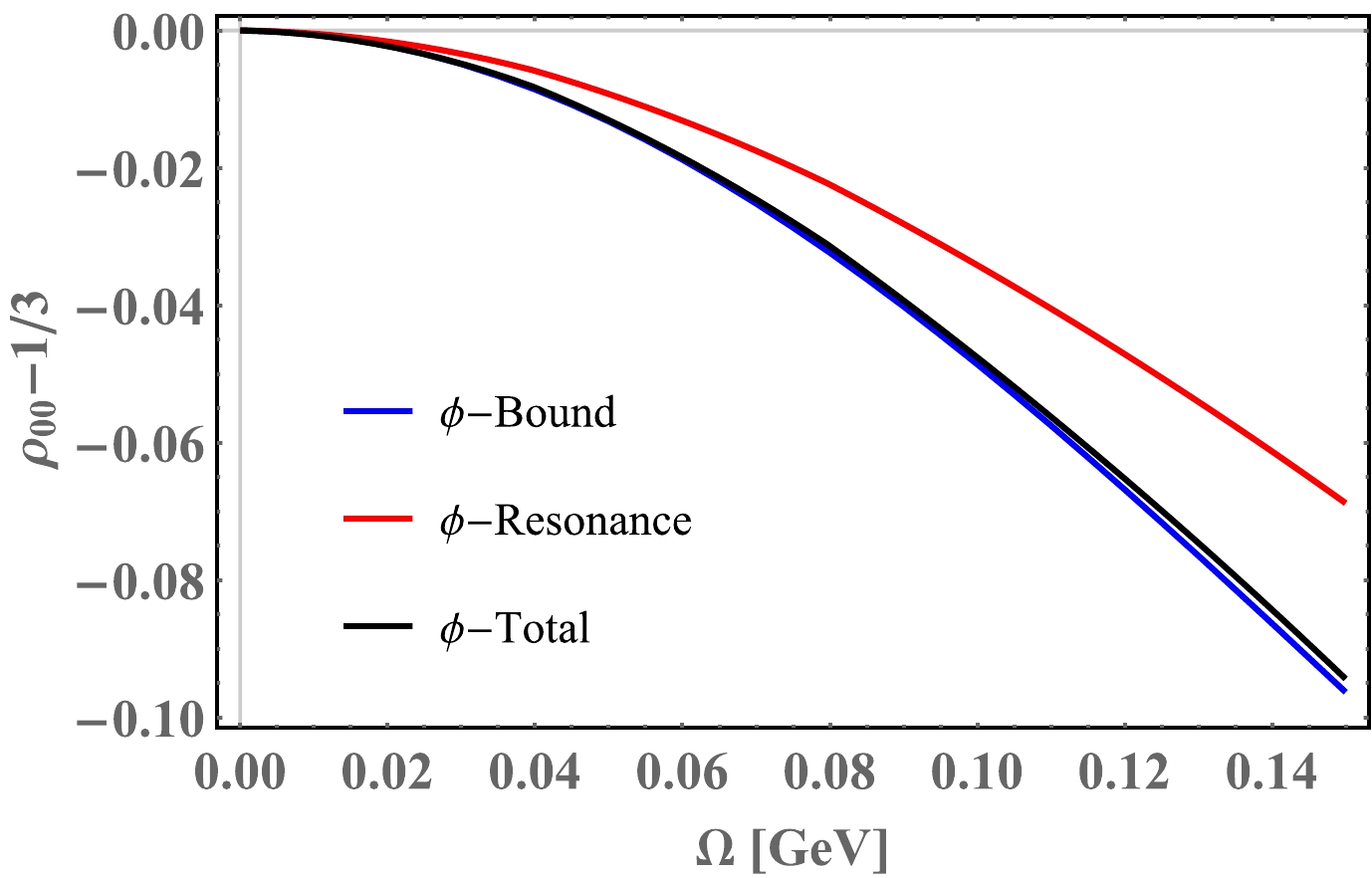
Figure 9. (color online) Spin alignment
$ \rho_{00} $ for vector meson ϕ as a function of angular velocity at temperature$ T=150 $ MeV.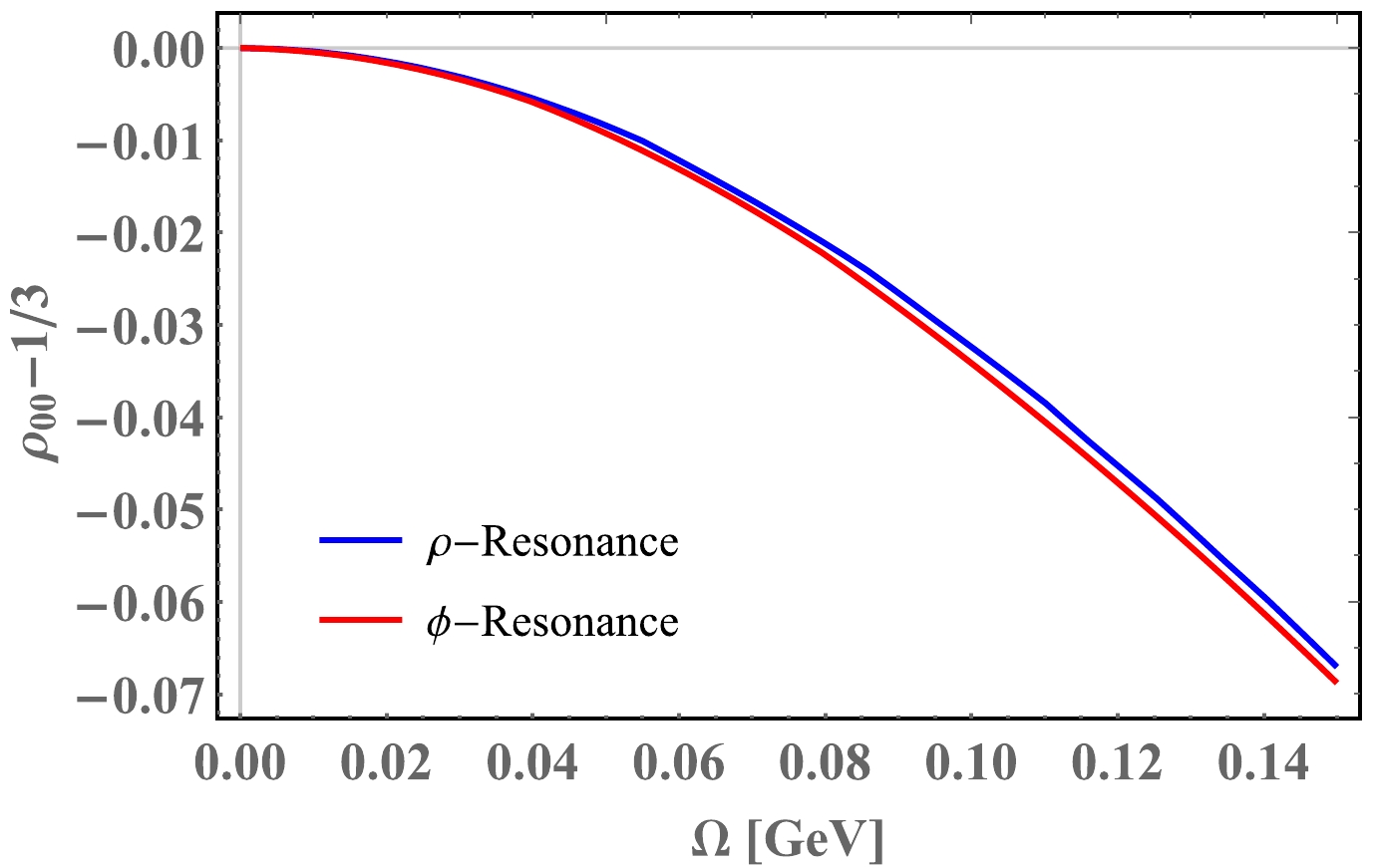
Figure 10. (color online) Spin alignment
$ \rho_{00} $ for resonance states of vector meson ρ and ϕ as a function of angular velocity at temperature$ T=150 $ MeV.Here, we mention the result from the quark coalescence model [11]:
$ \begin{equation} \rho_{00}^{\phi}(\Omega)=\frac{1}{3}-\frac{1}{9}(\beta \Omega)^2, \end{equation} $

(44) where
$ \beta=1/T $ is the inverse of temperature. Eq. (44) is only valid in the vicinity of$ \Omega=0 $ GeV, and the value of the coefficient is$ -\dfrac{1}{9}\beta^{2}=-4.94 ~\text{GeV}^{-2} $ for$ T=0.15 ~\text{GeV} $ . As a comparison, we fit our result with polynomial functions in a range of angular velocities from$ \Omega=0 $ GeV to$ \Omega=0.15 $ GeV. The numerical results give:$ \begin{equation} \rho^{\phi}_{00}(\Omega)=\frac{1}{3}-5.10 \Omega^2+39.62 \Omega^4. \end{equation} $

(45) Here, the dimensions of the angular velocity and the coefficients are omitted. In the vicinity of
$ \Omega=0 $ GeV, the absolute value of the coefficient of$ \Omega^{2} $ is larger than$-\dfrac{1}{9}\beta^{2}=-4.94~ \text{GeV}^{-2}$ .Compared with the spin alignment under an external magnetic field and rotation, the deviation
$ \rho_{00}-1/3 $ is positive under the magnetic field, while it is negative in the presence of rotation. It is natural to understand from quark dynamics that the spin of a particle tends to align along the direction of angular momentum due to the spin-orbital coupling. For$ s_{z}=+1 $ component, the vector$ \phi,\rho $ mesons masses are suppressed in the rotating medium. As a consequence, vector mesons are more likely to occupy the$ s_{z}=+1 $ state and less likely to occupy$ s_{z}=0 $ state. So,$ \rho_{00}-1/3 $ is negative in the rotating medium. On the contrary,$ \rho_{00}-1/3 $ of ϕ meson is positive under the magnetic field [18]. Actually, vector meson masses in the magnetic field are charge dependent. The ϕ meson is a neutral particle; its property under the magnetic field can be extended from the result of neutral$ \rho^0 $ meson mass spectra under the magnetic field [48]. Under the magnetic field, neutral ϕ meson with$ s_{z}=\pm 1 $ will have a larger mass than ϕ meson with$ s_{z}=0 $ . So, ϕ mesons are more likely to occupy the$ s_{z}=0 $ state in the presence of the magnetic field, which naturally explains why$ \rho_{00}-1/3 $ for ϕ meson is positive under the magnetic field.Similarly, our theoretical method can be applied to other species of vector mesons, such as ρ and
$ K^{*0} $ . The difference is the dynamical mass of constituent quarks u, d, and s in the rotating medium. In Eq. (18), only one species of quark propagator exists in the one loop polarization function. Since we have applied the assumption$ M_{u}=M_{d} $ , spin alignment of ρ meson is demonstrated in Fig. 10. In the rotating medium with a temperature of 150 MeV, ρ mesons are resonance states. So, we compare it with the resonance states of ϕ mesons in Fig. 10. The tendency of the deviation$ \rho_{00}-1/3 $ is still close to the quadratic polynomial.It is worth reminding that those results are calculated for vector mesons that stay at rest in a rotating medium, i.e., at
$ \vec{q}=0 $ . In the$ \vec{q}\neq 0 $ case, the calculation will be more complicated, and it is still a puzzle to switch the physical quantities in the rotating frame into the counterparts in the lab frame. Above all, the contribution from the rotating medium is significant, although the spin alignment of vector mesons is affected by a combination of many factors. -
In this study, we investigated the spin alignment of vector mesons ϕ and ρ induced by rotation. By applying a three flavor NJL model with a vector interaction channel, we obtain the dynamical quark mass under rotation. The curves of
$ M_{f}(\Omega) $ is similar to$ M_{f}(\mu) $ . For the s quark, the first order phase transition occurs at a critical angular velocity$ \Omega_{c} $ , and$ M_{s} $ decreases smoothly after the phase transition, which is similar to the quark mass behavior at a finite chemical potential.After substituting the dynamical quark mass, the mass spectra of vector mesons can be obtained through the quark-antiquark polarization function. The rotating angular velocity induces mass splitting of spin components for vector
$ \phi,\rho $ mesons$ M_{\phi,\rho}(\Omega)\simeq M_{\phi,\rho}(\Omega=0)-s_{z}\Omega $ . This behavior contributes to the spin alignment of vector mesons$ \phi,\rho $ in an equilibrium medium. In a rotating medium,$ \rho_{00} $ of vector mesons has a negative deviation from$ 1/3 $ , indicating a spin alignment phenomenon, which can be easily understood from quark dynamics that the spin of a particle tends to align along the direction of angular momentum due to spin-orbital coupling. For the$ s_{z}=+1 $ component, the vector mesons masses are suppressed in the rotating medium. As a consequence, vector mesons are more likely to occupy the$ s_{z}=+1 $ state and less likely to occupy the$ s_{z}=0 $ state. Therefore,$ \rho_{00}-1/3 $ is negative in the rotating medium.On the contrary, the deviation
$ \rho_{00}-1/3 $ is positive under the magnetic field, which can also be easily understood from quark dynamics. Under the magnetic field, the$ s_{z}=\pm 1 $ components of$ \phi,\rho $ meson will have a larger mass than that of the$ s_{z}=0 $ component of$ \phi,\rho $ mesons. Therefore,$ \phi,\rho $ mesons are more likely to occupy the$ s_{z}=0 $ state in the presence of the magnetic field, which naturally explains the positive$ \rho_{00}-1/3 $ for ϕ meson under the magnetic field.Based on a dynamical quark model, we calculated the spin alignment
$ \rho_{00} $ for the transverse momentum dependent case. Furthermore, we can apply it for vector meson$ K^{*0} $ in the future. In this series of studies, we have studied the vector meson ϕ and ρ. In this case, the quark loops only contain s and$ \bar{s} $ quarks, and light quarks are assumed to have the same value of mass, i.e.$ M_{u}=M_{d} $ . For vector meson$ K^{*0} $ , the mass difference of quarks is expected to explain the different measurements between vector meson ϕ and$ K^{*0} $ in the experiment. Our study is an attempt at this target in a rotating medium. -
We are grateful for the helpful discussions with Li Yan, Anping Huang, Xinli Sheng, and Kun Xu.
-
To obtain the quark propagator in a rotating and dense medium, we adopt the method from Vladimir A. Miransky and Igor A. Shovkovy [23]. This derivation has considered the chemical potential μ and the rotation term
$ \Omega \cdot \hat{J_z} $ . According to an alternative definition, the quark propagator is given by$ \begin{equation} S\left(\tilde{r}, \tilde{r}^{\prime}\right)={\rm i}\langle\tilde{r}\left|\left[\left({\rm i} \partial_t+\mu+\Omega \cdot \hat{J_z}\right) \gamma^0-\vec{\pi} \cdot \vec{\gamma}-M_{f}\right]^{-1}\right| \tilde{r}^{\prime}\rangle \,, \end{equation} \tag{A1}$

where
$ \vec{\pi} $ is the canonical momentum and$ \vec{\gamma} $ is the Dirac matrix. Their expressions depend on the coordinates of the position$ \tilde{r} $ . At this moment, we treat them as abstract operators, and the propagator can be rewritten as$ \begin{aligned}[b] S (\tilde{r}, \tilde{r}^{\prime} ) =& {\rm i}\langle\tilde{r} | [ ({\rm i} \partial_{t}+\mu+\Omega \cdot \hat{J}_z ) \gamma^{0}-\vec{\pi} \cdot \vec{\gamma}+M_{f} ] \\&\times [ ({\rm i} \partial_{t}+\mu+\Omega \cdot\hat{J}_z ) \gamma^{0}-\vec{\pi} \cdot \vec{\gamma}+M_{f} ]^{-1} \\ & { [ ({\rm i} \partial_{t}+\mu+\Omega \cdot \hat{J_z} ) \gamma^{0}-\vec{\pi} \cdot \vec{\gamma}-M_{f} ]^{-1} |\tilde{r}^{\prime}\rangle} \\ =& {\rm i}\langle\tilde{r} | [ (\partial_{t}+\mu+\omega \cdot \hat{J_z} ) \gamma^{0}-\vec{\pi} \cdot \vec{\gamma}+M_{f} ]\\&\times [ ({\rm i} \partial_{t}+\mu+\Omega\cdot \hat{J}_z )^2-\vec{\pi}^2-M_{f}^2 ]^{-1} | \tilde{r}^{\prime}\rangle \\ \end{aligned}\tag{A2} $

Owing to the translation invariance in the
$ t- $ and$ z- $ directions, we can perform the Fourier transformation on the quark propagator as follows:$ S\left(E, k_{z} ; \mathbf{r}_{\perp}, \mathbf{r}_{\perp}^{\prime}\right)=\int {\rm d} t {\rm d} z {\rm e}^{{\rm i} E\left(t-t^{\prime}\right)-{\rm i} k_{z}\left(z-z^{\prime}\right)} S\left(\tilde{r}, \tilde{r}^{\prime}\right). \tag{A3} $

Here,
$ \mathbf{r}_{\perp}=(r,\theta) $ is the position in cylindrical coordinates, and E is the energy. The propagator can be expressed as follows:$ \begin{aligned}[b] &S\left(E, k_{z} ; \mathbf{r}_{\perp}, \mathbf{r}_{\perp}^{\prime}\right)\\ = & {\rm i}\left[\left(E+\mu+\Omega \cdot \hat{J}_{z\left(\mathbf{r}_{\perp}\right)}\right) \gamma^0-\vec{\pi}_{\mathbf{r}_\perp} \cdot \vec{\gamma}_{\perp}-k_{z} \gamma^3+M_{f}\right] \\ & \cdot\langle \mathbf{r}_{\perp} \left| \left[\left(E+\mu+\Omega \cdot \hat{J}_z\right)^2-\left(k_{z}\right)^2-\vec{\pi}_{\perp}^2-M_{f}^2\right]^{-1}\right| \mathbf{r}_\perp^{\prime}\rangle \end{aligned} \tag{A4} $

where
$ \vec{\pi}_{\mathbf{r}_\perp} $ and$ \hat{J}_{z\left(r_{\perp}\right)} $ are the canonical momentum and the angular momentum operator in cylindrical coordinate space, respectively. According to Ref. [19], the operators$ \vec{\pi}_\perp^2 $ and$ \hat{L}_z $ commute with each other and have a common eigenstate$ |n k_{t}\rangle $ , in which the explicit form in coordinate space is given by Eqs. (9) and (10). Here, we present several useful equations:$ \begin{aligned}[b] \langle\mathbf{r}_{\perp} \mid n k_{t}\rangle&={\rm e}^{{\rm i} n \theta} J_n (k_t r )\\ \hat{L}_z \mid n k_{t}\rangle&=n \mid n k_{t}\rangle\\ \vec{\pi}_{\perp} \mid n k_{t}\rangle&=k_{t} \mid n k_{t}\rangle, \end{aligned} \tag{A5} $

where
$ \hat{L}_z $ is the operator of orbital angular momentum. As a result, the right hand side of Eq. (49) can be evaluated as follows:$ \begin{aligned}[b]\\[-15pt] & \langle \mathbf{r}_{\perp} \left|\left[\left(E+\mu+\Omega \cdot \hat{J}_z\right)^2-\left(k_{z}\right)^2-\vec{\pi}_{\perp}^2-M_{f}^2\right]^{-1} \right|\mathbf{r}_{\perp}^{\prime}\rangle \\ = & \sum_n \int k_t {\rm d} k_t\langle \mathbf{r}_{\perp}\left|\left[\left(E+\mu+\Omega \cdot \hat{J}_z\right)^2-\left(k_{z}\right)^2-\vec{\pi}_{\perp}^2-M_{f}^2\right]^{-1}\right| n k_t\rangle\langle n k_t \mid \mathbf{r}_{\perp}^{\prime}\rangle \\ = & \sum_n \int k_{t} {\rm d} k_t\langle \mathbf{r}_{\perp} \left|\left[\left(E+\mu+\Omega \cdot \hat{L}_z\right)^2+2(E+\mu) \Omega \cdot S_{z}+\Omega^2\left(S_{z}\right)^2-{k_z^2}-\vec{\pi}_{\perp}^2-{M_f^2}\right]^{-1} \right|n k_{t}\rangle\langle n k_t \mid \mathbf{r}_{\perp}^{\prime}\rangle\\ = & \sum_n \int_0^{+\infty} k_t {\rm d} k_t J_n\left(k_t r\right) J_n\left(k_t r^{\prime}\right) {\rm e}^{{\rm i} n\left( \theta-\theta^{\prime}\right)}\left[(E+\mu+\Omega n)^2+2(E+\mu)\Omega S_{z}+\Omega^2 \cdot \frac{1}{4}-{k_z^2}-{k_t^2}-{M_f^2}\right]^{-1} , \end{aligned} \tag{A6}$ 
(51) where
$S_{z}=\dfrac{\rm i}{2} \gamma^{1}\gamma^{2}$ is the spin angular momentum term. We have inserted the completeness condition in the second line of Eq. (51). Now, it is easy to obtain Eq. (11) using projection operator$\mathcal{P}_{\pm}=\dfrac{1}{2}\left(1 \pm {\rm i} \gamma^1 \gamma^2\right)$ . By inserting$ I_4=\mathcal{P}_{-}+\mathcal{P}_{+} $ , the summation in Eq. (51) can be replaced by:$ \sum_n \frac{J_n\left(k_t r\right) J_n\left(k_t r^{\prime}\right) {\rm e}^{{\rm i} n\left( \theta-\theta^{\prime}\right)}\mathcal{P}_++ J_{n+1}\left(k_t r\right) J_{n+1}\left(k_t r^{\prime}\right) {\rm e}^{{\rm i} (n+1)\left( \theta-\theta^{\prime}\right)}\mathcal{P}_-}{\left[E+\mu+\left(n+\dfrac{1}{2}\right) \Omega\right]^2-k_z^2-k_t^2-M_{f}^2}. \tag{A7} $

Finally, we can calculate Eq. (49) by acting the operators
$ \hat{J}_{z\left(\mathbf{r}_{\perp}\right)} \gamma^0 $ ,$ \vec{\pi}_{\mathbf{r}_\perp} \cdot \vec{r}_{\perp} $ and$ k_{z} \gamma^3 $ on Eq. (52). -
The explicit form and the derivation of spectral functions can be found in Refs. [26, 39]. In our previous work, we have utilized the properties of Bessel functions, i.e.
$ J_{n}(0)=0 $ for$ n \neq 0 $ and$ J_{0}(0)=1 $ . As a consequence, the infinite summation is reduced to finite terms. Then, Eq. (18) can be evaluated at zero and finite temperature. To save space in this manuscript, we merely present one component of polarization functions. For example, the imaginary part of the 00-component is [26]:$ \begin{aligned}[b] \operatorname{Im} \Pi^{00}(\omega, \vec{q})= & -\frac{\pi}{2} N_f N_c \sum_{\eta=\pm 1} \int \frac{{\rm d}^3 \vec{p}}{(2 \pi)^3} \frac{1}{E_p E_k}\left\{\left[E_p E_k+\vec{p} \cdot \vec{k}+M_f^2\right]\left[f\left(E_p-\mu-\frac{\eta \Omega}{2}\right)+f\left(E_p+\mu-\frac{\eta \Omega}{2}\right)\right]\right. \\ & \times\left[\delta\left(\omega+E_p-E_k\right)-\delta\left(\omega-E_p+E_k\right)\right]+\left[E_p E_k-\vec{p} \cdot \vec{k}-M_f^2\right] \delta\left(\omega-E_p-E_k\right) \\ & \left.\times\left[1-f\left(E_p-\mu-\frac{\eta \Omega}{2}\right)-f\left(E_p+\mu-\frac{\eta \Omega}{2}\right)\right]\right\}. \end{aligned} \tag{B1} $ 
where
$ k=p+q $ and$ E_{k}=\sqrt{\vec{k}^{2}+M_{f}^{2}} $ . Here,$ N_{f} $ and$ N_{c} $ are the flavor number and color number in the quark loop, and$ f(x) $ is Fermi-Dirac distribution functions with a finite temperature T. Other components can be obtained similarly.
Spin alignment of vector mesons from quark dynamics in a rotating medium
- Received Date: 2023-05-19
- Available Online: 2023-10-15
Abstract: Vorticities in heavy-ion collisions (HICs) are supposed to induce spin alignment and polarization phenomena of quarks and mesons. In this work, we analyze the spin alignment of vector mesons ϕ and ρ induced by rotation from quark dynamics in the framework of the Nambu-Jona-Lasinio (NJL) model. The rotating angular velocity induces mass splitting of spin components for vector






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: