-
In recent years, there has been a growing interest in expanding the periodic table and exploring the elusive island of stability, which has led to the development of various theoretical models aimed at understanding the synthesis mechanisms of superheavy nuclei (SHN). These models play a crucial role in accurately reproducing the evaporation residue cross-sections (ERCSs) in experiments and making reasonable predictions for the synthesis of unknown SHN [1−4]. However, a significant challenge faced by these models lies in the reliability of basic nuclear mass data. There is a lack of experimental data in the superheavy nuclear region, making it necessary to rely on mass models to provide the required data for these theoretical models [5]. Among the diverse range of mass models available, the finite-range droplet model (FRDM) stands out as a relatively effective macroscopic-microscopic approach for predicting critical nuclear masses [6]. The “Atomic Mass Evaluation 2020” (AME2020) recommended the masses of 3557 atomic nuclei, 2457 of which were derived from corresponding experimental data [7−13]. It is worth noting that the heaviest nuclide among these 2457 data points is
$ ^{270} $ Ds. By comparing the predicted values from the FRDM with the 2457 experimental values, a root mean square error (RMSE) of 0.606 MeV has been calculated.With the rapid and remarkable development of computer technology, the application of machine learning in the field of nuclear physics has gained significant momentum [14−21]. In this study, we propose an optimized method for estimating atomic nucleus masses by combining the FRDM with the support vector machine (SVM) algorithm. The SVM algorithm employs support vector-based decision boundaries to select optimal classification hyperplanes by maximizing the margin between the decision boundary and the support vectors. This approach effectively mitigates overfitting issues and enhances the model's generalization capability. Furthermore, by utilizing kernel functions, the SVM can map data from the original feature space to a higher-dimensional feature space, transforming linearly inseparable problems in the original feature space into linearly separable ones in the new feature space. This enables the SVM to effectively handle nonlinear classification problems [22]. Leveraging the advantages offered by the SVM, our research aims to enhance the accuracy of atomic nucleus mass estimation in the field of nuclear physics.
With the availability of accurate nuclear mass data, we aim to investigate the ERCSs of heavy ion fusion evaporation reactions. The process of heavy ion fusion evaporation involves three distinct stages: capture, fusion, and survival. Among the various theoretical models for SHN synthesis, capture cross sections exhibit minimal differences, and variations arise primarily in the fusion and survival processes. According to a review by Loveland [23], although all models give similar ERCS predictions, their fusion probabilities differ by orders of magnitude. In Ref. [24], the authors mention that uncertainties in the fission barriers can accommodate the discrepancies of the fusion probabilities. In general, the capture cross-sections are nearly the same. Thus, the difference between various models lies in the fusion and survival processes. The di-nuclear system (DNS) model, among numerous other models, has demonstrated its effectiveness in accurately describing heavy ion fusion evaporation reactions [25−34]. Notably, its fusion probability depends on the details of the driving potential, whereas its survival probability depends on the fission barrier and neutron separation energy of the compound nuclei. Therefore, leveraging the obtained precise nuclear mass data, this study employs the DNS model to calculate the ERCSs of heavy ion fusion evaporation reactions. Furthermore, we conduct an analysis of the impact of mass uncertainties on both the fusion and survival processes.
This paper is organized as follows. In Sec. II, we introduce the FRDM-SVM approach. Additionally, we present the general form of the DNS model to explicitly display each term and its relationship with the nuclear mass data. In Sec. III, we first obtain optimized nuclear mass data. Then, we calculate the ERCS for the reaction
$ ^{48} $ Ca+$ ^{238} $ U and present new predictions for the synthesis of SHN with$ Z=119 $ and$ Z=120 $ . In Sec. IV, we summarize our study. -
The method employed by this research institute is a regression algorithm in supervised learning. The selected feature values for our dataset are the proton number Z and neutron number N of atomic nuclei, and the target variable
$ {y_i} $ is the difference between the predicted values from the FRDM model and the experimental values. For this study, we choose a dataset of 2457 data points consisting of the differences between experimental data and FRDM predicted data from AME2020. To build the algorithmic model, the 2457 data points are randomly shuffled and divided in an 8: 2 ratio, with 80% of the data used as the training set and 20% as the test set. The training set is used to train the algorithmic model, whereas the test set is used for model parameter tuning and a preliminary assessment of the model's generalization ability. Finally, the optimized nucleus mass can be represented as follows:$ \begin{array}{*{20}{l}} M\left( {Z,N} \right) = {M_{{\rm{FRDM}}}}\left( {Z,N} \right) + {y_i}, \end{array} $

(1) where
$ M\left({Z,N} \right) $ is the optimized nucleus mass,$ {M_{{\rm{FRDM}}}}\left({Z,N} \right) $ is the nuclear mass predicted using the FRDM, and$ {y_i} $ is the target variable. Ultimately, we employ the RMSE between the optimized mass data and experimental values as the criterion for assessment, which can be expressed as follows:$ {\rm RMSE} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {M\left( {Z,N} \right) - {M_{\rm exp}}\left( {Z,N} \right)} \right)}^2}} } , $

(2) where N is the total number of data, and
${M_{\rm exp}}\left({Z,N} \right)$ is the experimental value of mass. -
Next, we introduce the general formalism of the DNS model to explicitly show each term and how it is related to the nuclear mass data. In the DNS concept, the ERCS is expressed as
$ \begin{aligned}[b] {\sigma _{\rm ER}}\left( {{E_{\rm c.m.}}} \right) =& \sum\limits_J {{\sigma _{\rm cap}}\left( {{E_{\rm c.m.}},J} \right)} \times {P_{CN}}\left( {{E_{\rm c.m.}},J} \right)\\ &\times {W_{\rm sur}}\left( {{E_{\rm c.m.}},J} \right). \end{aligned} $

(3) In this formula,
${{E_{\rm c.m.}}}$ is the center-of-mass incident energy,${\sigma _{\rm cap}}$ is the capture cross section [35],${P_{\rm CN}}\left({{E_{\rm c.m.}},J} \right)$ is the fusion probability, and${W_{\rm sur}}\left({{E_{\rm c.m.}},J} \right)$ is the survival probability of the formed compound nucleus, which can be estimated using a statistic model. To obtain the fusion probability in the DNS model, we describe the fusion process as a diffusion process by numerically solving a set of master equations on the potential energy surface. The time evolution of the distribution probability function,$ P\left({{Z_1},{N_1},{E_1},t} \right) $ , at time t to find$ {Z_1} $ protons and$ {N_1} $ neutrons in fragment$ 1 $ with excitation energy$ {E_1} $ can be described by the following master equation [36]:$ \begin{aligned}[b]& \frac{{{\rm d}P({Z_1},{N_1},{E_1},t)}}{{dt}} \\= &\sum\limits_{{{Z'}_1}} {{W_{{Z_1},{N_1};{{Z'}_1},{N_1}}}} (t) \times [{d_{{Z_1},{N_1}}}P({{Z'}_1},{N_1},{E_1},t)\\ &- {d_{{{Z'}_1},{N_1}}}P({Z_1},{N_1},{E_1},t)]\\ &+ \sum\limits_{{{N'}_1}} {{W_{{Z_1},{N_1};{Z_1},{{N'}_1}}}} (t) \times [{d_{{Z_1},{N_1}}}P({Z_1},{{N'}_1},{E_1},t)\\ &- {d_{{Z_1},{{N'}_1}}}P({Z_1},{N_1},{E_1},t)]\\ &- \left\{ {{\Lambda ^{qf}}\left[ {\Theta \left( t \right)} \right] + {\Lambda ^{fs}}\left[ {\Theta \left( t \right)} \right]} \right\}P\left( {{Z_1},{N_1},{E_1},t} \right). \end{aligned} $

(4) Here,
$ {{W_{{Z_1},{N_1};{{Z'}_1},{N_1}}}} $ is the mean transition probability from the channel$ \left({{Z_1},{N_1}} \right) $ to$ \left({{{Z'}_1},{N_1}} \right) $ , and$ {d_{{N_1},{Z_1}}} $ denotes the microscopic dimension corresponding to the macroscopic state$ \left({{Z_1},{N_1}} \right) $ . All the possible proton and neutron numbers of fragment 1 are taken into the sum, but only one nucleon transfer is considered in the model$ \left({{N'}_1 = {N_1} \pm 1, {Z'}_1 = {Z_1} \pm 1} \right) $ . The evolution of the DNS along the distance between nuclei R leads to quasifission. The quasifission rate$ {\Lambda ^{qf}} $ and$ {\Lambda ^{fs}} $ fission rate are estimated with the one-dimensional Kramers formula. The driving potential of the DNS in the fusion process is defined as$ \begin{aligned}[b] U\left( {{Z_1},{N_1},{Z_2},{N_2},R} \right) =& E({Z_1},{N_1}) + E({Z_2},{N_2}) \\ & - E({Z_{CN}},{N_{CN}}) + {V_C}\left( R \right) + {V_N}\left( R \right) , \end{aligned} $

where
$ {Z_{1,2}} $ and$ {N_{1,2}} $ are the proton and neutron numbers of two fragments, respectively,$ E({Z_i},{N_i}) $ and$ E({Z_{CN}},{N_{CN}}) $ are the nuclear mass of the fragment$ ({Z_i},{N_i}) $ and compound nucleus, respectively, and$ {V_C} $ and$ {V_N} $ are the Coulomb and nuclear potentials, respectively [37].The survival probability of the excited compound can be expressed as$ \begin{aligned}[b] {W_{\rm sur}}\left( {E_{CN}^*,x,J} \right) =& P\left( {E_{CN}^*,x,J} \right)\\ & \times {\prod\limits_{i = 1}^x {\left( {\frac{{{\Gamma _n}\left( {E_i^*,J} \right)}}{{{\Gamma _n}\left( {E_i^*,J} \right) + {\Gamma _f}\left( {E_i^*,J} \right)}}} \right)} _i}. \end{aligned} $

In the formula,
$ E_{CN}^* $ represents the excitation energy of the composite nuclei,$ P\left({E_{CN}^*,x,J} \right) $ is the realization probability of emitting x neutrons [38], and$ {\Gamma _n}\left({E_i^*,J} \right) $ and$ {\Gamma _f}\left({E_i^*,J} \right) $ represent the partial wave decay width of evaporating neutrons and fission, respectively. The survival probability${W_{\rm sur}}$ reflects the competition between the neutron evaporation and fission of the excited compound nucleus. Therefore, the neutron separation energy and fission barrier of the compound nucleus are particularly important in the survival process. The neutron separation energy$ {B_n} $ can be expressed as$ \begin{array}{*{20}{l}} {B_n} = B\left( {Z,N} \right) - B\left( {Z,N - 1} \right), \end{array} $

(5) $ B\left({Z,N} \right) $ and$ B\left({Z,N - 1} \right) $ are the binding energies of the nucleus, and the fission barrier$ {B_f} $ can be expressed as$ \begin{array}{*{20}{l}} {B_f} = B_f^{\rm LD} + B_f^{\rm SH}, \end{array} $

(6) where the macroscopic fission barrier height
$B_f^{\rm LD}$ is taken from Ref. [39]. The value of$B_f^{\rm SH}$ is taken from the microscopic correction value given in Ref. [6], which is given by the difference between the calculated ground-state atomic mass excess and the spherical macroscopic energy. Therefore, we use the FRDM to improve the microscopic correction values by optimizing the excess mass of the ground state atomic nucleus, thereby changing the fission barrier. -
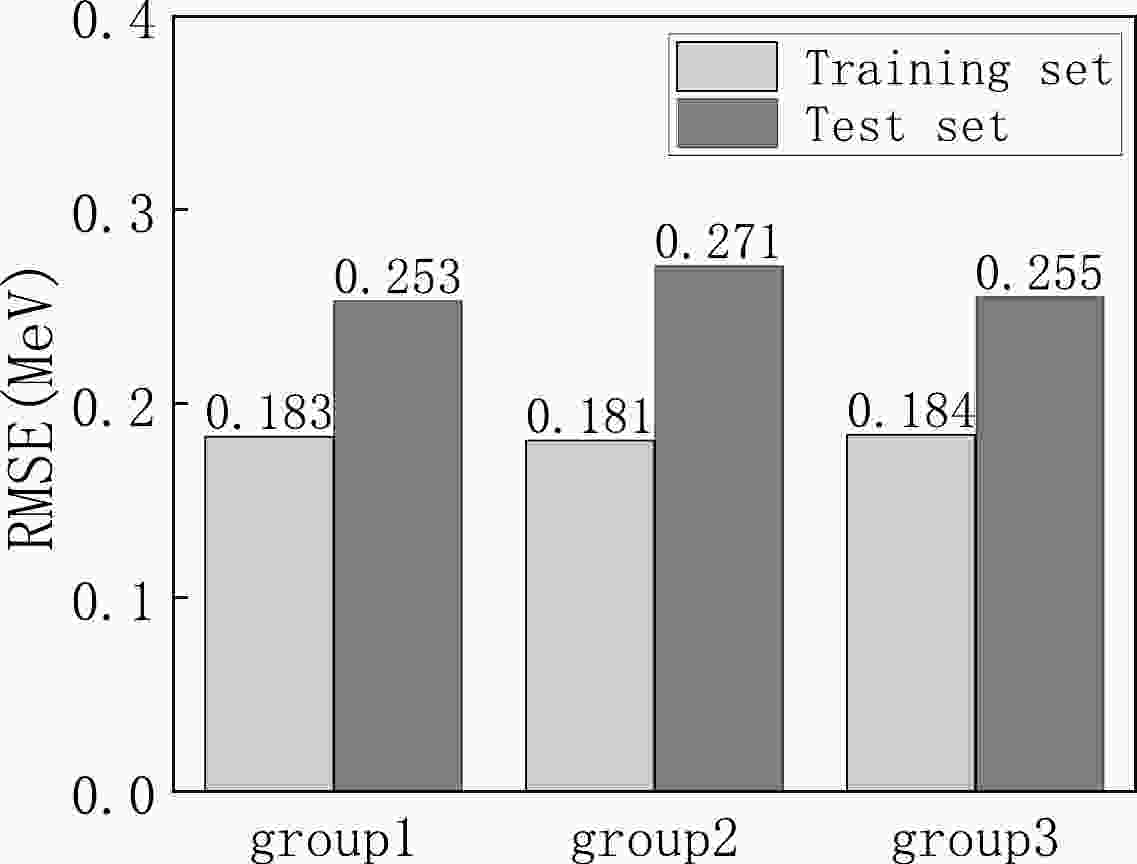
We select 2457 nuclear mass difference data points and randomly divide them into three groups, with a training set of 1966 data points and a test set of 491 data points for each group. Figure 1 displays the results obtained from these three different training and test set combinations. As shown, the first group achieves an RMSE of 0.183 MeV for the training set and 0.253 MeV for the test set. The second group exhibits an RMSE of 0.181 MeV for the training set and 0.271 MeV for the test set. Similarly, the third group shows an RMSE of 0.184 MeV for the training set and 0.255 MeV for the test set. These results indicate that all three groups perform well for the test set. They also demonstrate improved accuracy compared to those of the FRDM.
Figure 2 illustrates the deviation between the predicted and experimental values of nuclear mass. The black squares represent the results obtained using the FRDM, whereas the red spheres are the results obtained using the FRDM-SVM. The predictions generated with the FRDM exhibit relatively noticeable fluctuations. In contrast, the results obtained using the FRDM-SVM demonstrate a significant reduction in these fluctuations, indicating enhanced accuracy and reliability in the predictions.

Figure 2. (color online) Deviation between the predicted and experimental values [13] as a function of proton number Z. Black squares are the FRDM results, and the red spheres are the FRDM-SVM results.
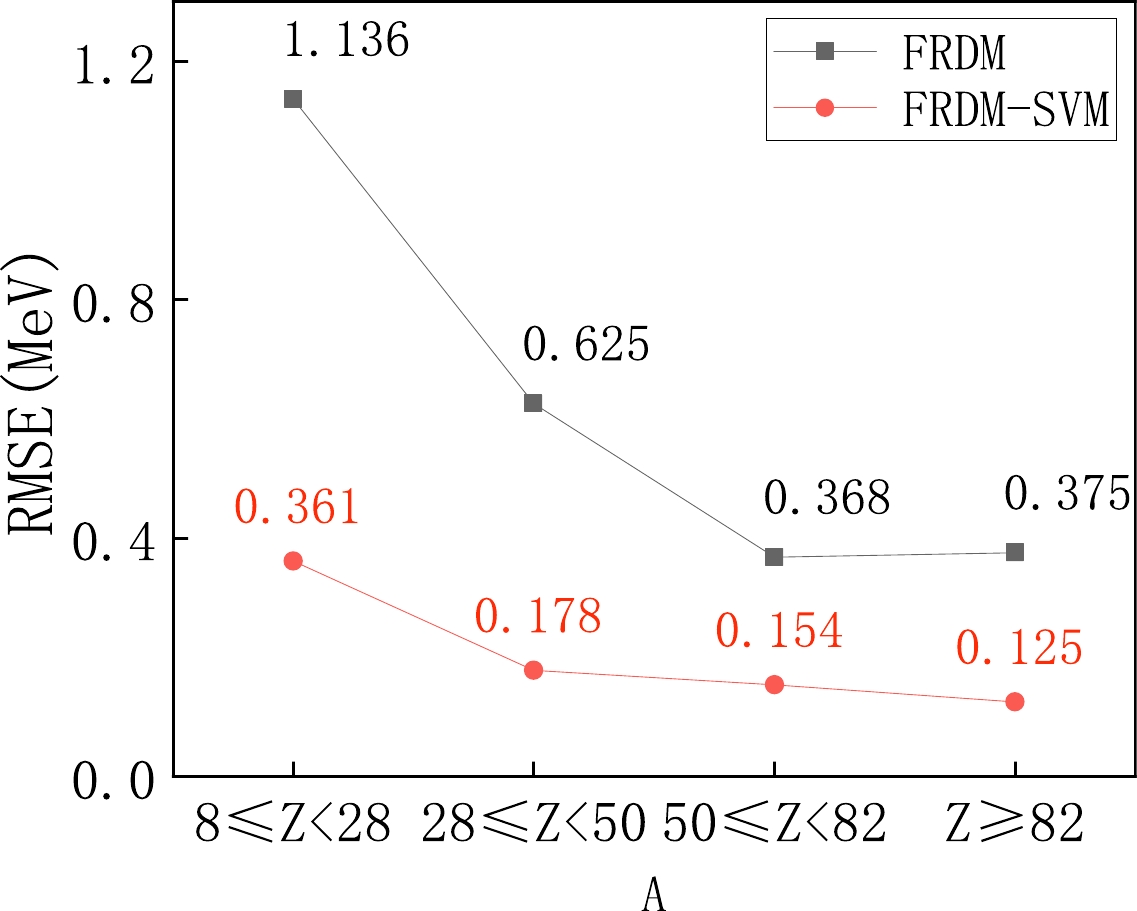
This significant improvement in accuracy demonstrates the effectiveness of the FRDM-SVM approach. However, it is not sufficient to provide the RMSE of the mass for the global region of nuclei. We should also consider the dependence of the model accuracy on the nuclear region. Therefore, we divide the global region of nuclei into four sub-regions:
$ 8\le Z < 28 $ ,$ 28\le Z < 50 $ ,$ 50\le Z < 82 $ , and$ Z \ge 82 $ . The RMSE of each region is shown in Fig. 3. Compared with the FRDM, the FRDM-SVM improves the accuracy of the nuclear mass systematically while passing from lighter to heavier nuclei. This trend suggests that optimized mass data will exhibit outstanding performance in the SHN region, where experimental data is lacking. -
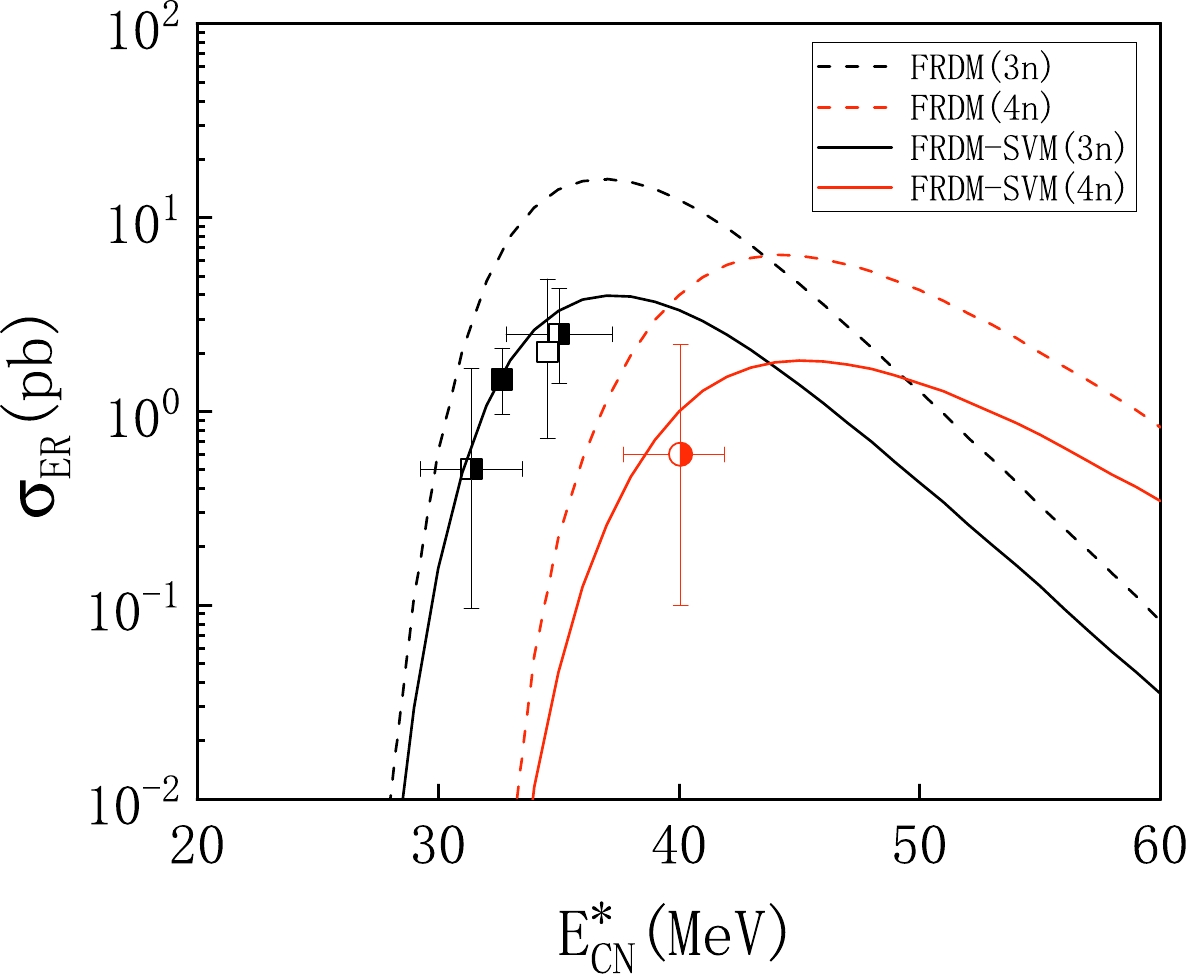
As previously mentioned, the synthesis of SHN relies primarily on the competition between the fusion and survival processes. The fusion probability is mainly determined by the details of the driving potential, whereas the survival process depends on factors such as neutron separation energy and the fission barrier. We use the optimized nuclear mass data and reconstruct the driving potential, neutron separation energy, and fission barrier within the framework of the DNS model. By leveraging these refined calculations, we obtain the ERCSs for the reaction
$ ^{48} $ Ca+$ ^{238} $ U, particularly focusing on the 3n and 4n channels. Subsequently, we carefully compare the calculated ERCSs with experimental data. The results are presented in Fig. 4, which shows that there is a noticeable discrepancy between the excitation functions calculated solely using the FRDM and those obtained through the FRDM-SVM approach. The results obtained from FRDM calculations exhibit a trend of overestimating the experimental values. However, the ERCSs calculated using the FRDM-SVM approach demonstrate good consistency within the range of experimental uncertainties, successfully reproducing the observed data. By refining the driving potential, neutron separation energy, and fission barrier based on the optimized nuclear mass data, our study provides a more accurate and reliable representation of the ERCSs in the synthesis of SHN.The ERCS is determined using the product of the capture cross-section, fusion probability, and survival probability. The use of FRDM and FRDM-SVM data does not affect the calculation of the capture cross section. Therefore, the improvement in the ERCS, when using FRDM-SVM data, stems from the fusion and survival probabilities. In Fig. 5, we present the functions depicting the variation in the fusion and survival probabilities with respect to excitation energy. The fusion probability calculated using FRDM-SVM data is slightly lower. As for the survival probability of compound nuclei in excited states, the usage of FRDM-SVM data leads to a slightly lower survival probability, although the extent of reduction is considerably less than that of the fusion probability.
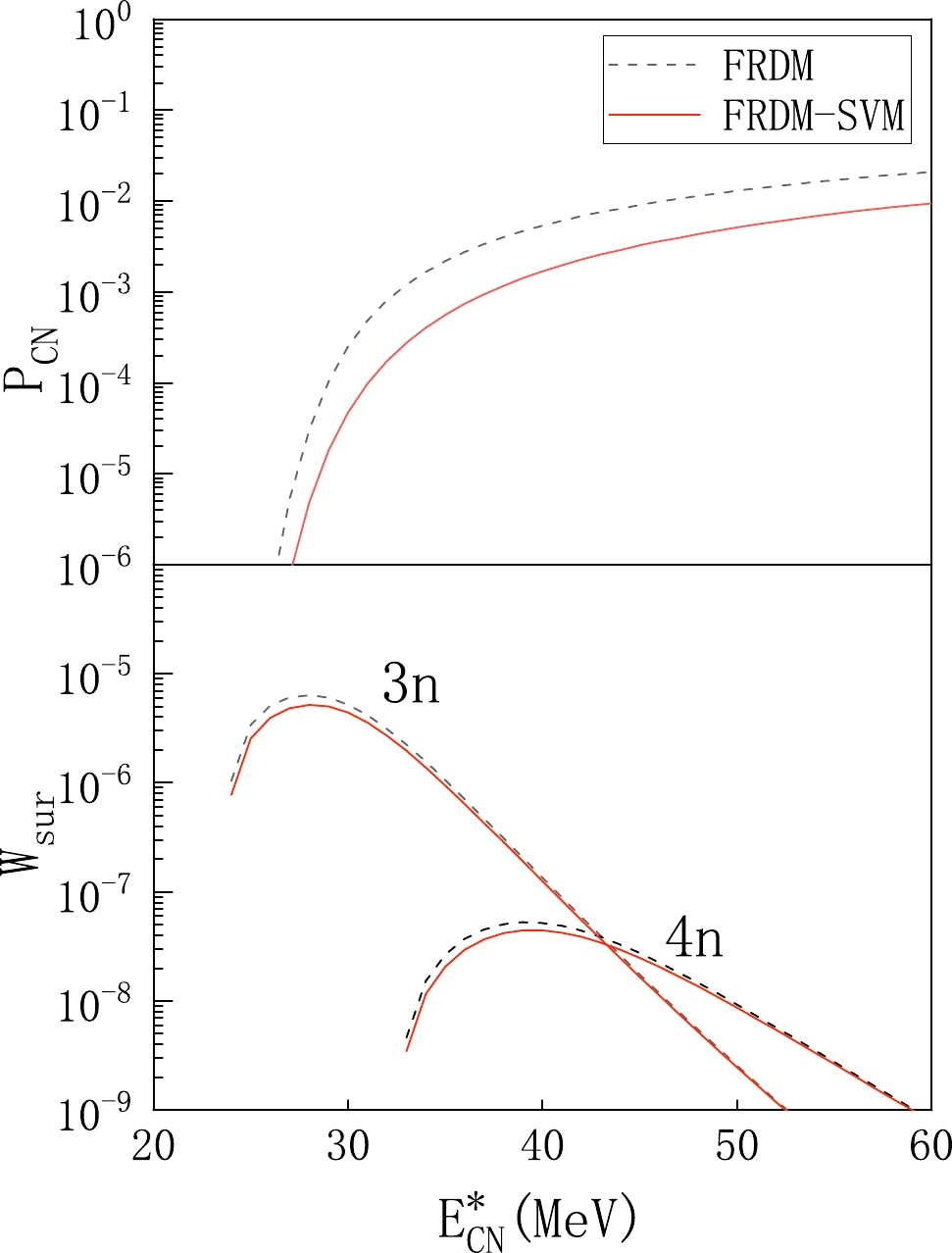
Figure 5. (color online) Fusion probability
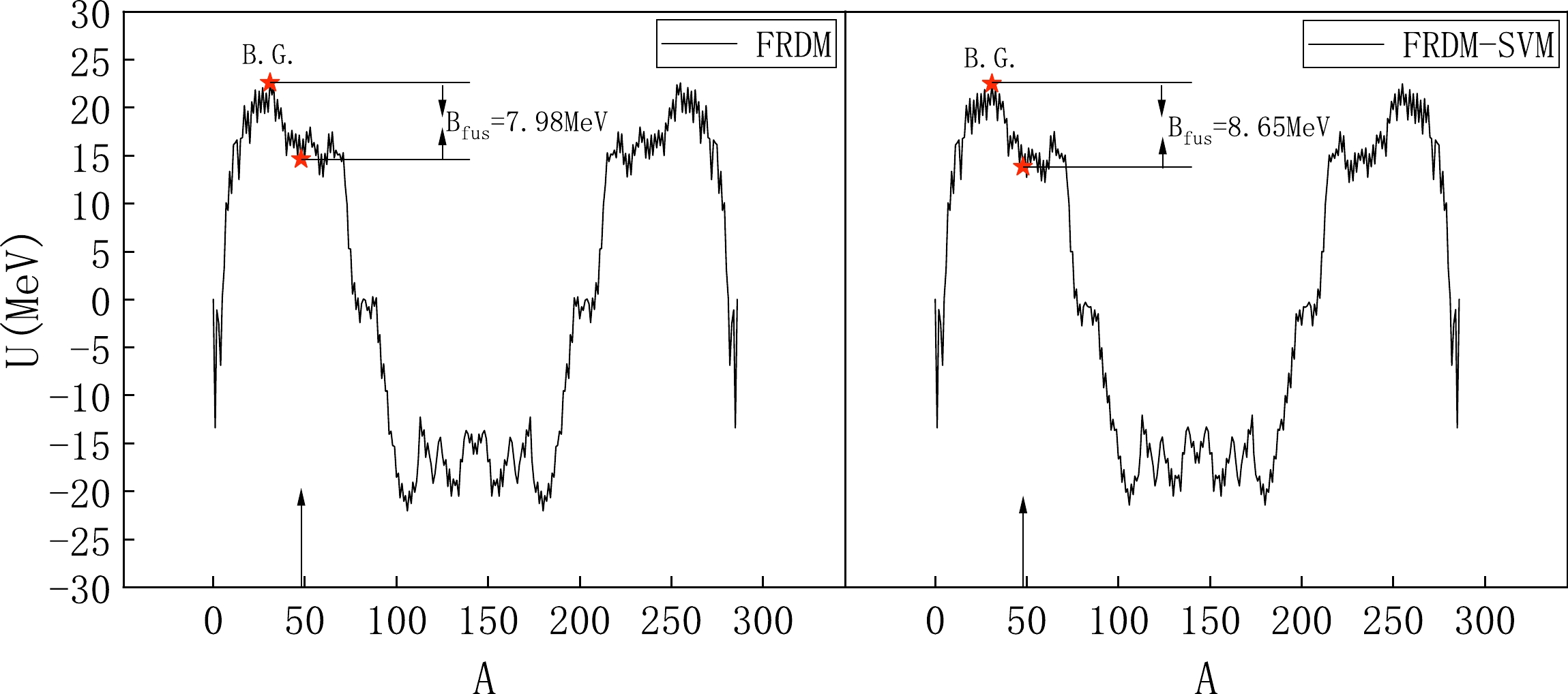
$ P_{CN} $ and survival probability$W_{\rm sur}$ as a function of excitation energy$ E_{CN}^* $ in the reaction 48Ca+238U.Next, we delve into the reasons for these changes in fusion and survival probability. The alterations in fusion probability primarily arise from the changes in the driving potential due to the use of FRDM-SVM data. In Fig. 6, we compare the driving potentials constructed using these two types of data. As shown, the inner fusion barrier
$B_{\rm fus}$ obtained from FRDM data is 7.98 MeV, whereas it is 8.65 MeV when using FRDM-SVM data. Within the framework of the DNS model, a higher inner fusion barrier implies a more challenging evolution of the two-nucleus system toward compound nucleus formation, thus resulting in a higher probability of quasi-fission. Consequently, the fusion probability obtained using FRDM-SVM data tends to be slightly lower.The changes in survival probability primarily stem from the neutron separation energy and fission barrier of the compound nucleus. Table 1 lists the single neutron separation energy and fission barrier of the compound nucleus produced by the reaction
$ ^{48} $ Ca+$ ^{238} $ U. There is little difference between the single neutron separation energies obtained from the FRDM and FRDM-SVM, with a variation of only a few keV. However, the fission barrier obtained from FRDM-SVM data is approximately 100 keV smaller than that obtained from FRDM data. A relatively lower fission barrier hampers the survival of the compound nucleus. Therefore, the survival probability calculated using FRDM-SVM data is slightly lower, although the difference is not very pronounced.Nucleus $ {B_{f}}/{\rm{MeV}} $ 

$ B_{f}^{\text {SVM}} /{\rm{MeV}}$ 

$ {B_{n}} /{\rm{MeV}}$ 

$ B_{n}^{\text {SVM}} /{\rm{MeV}}$ 

286112 6.620 6.536 7.021 7.019 285112 6.630 6.548 5.851 5.849 284112 6.190 6.109 7.281 7.279 283112 6.150 6.070 6.101 6.099 282112 5.680 5.602 7.611 7.610 Table 1. Fission barrier
$ B_{f} $ and one-neutron separation energy$ B_{n} $ from the FRDM and FRDM-SVM.Overall, the use of FRDM-SVM data leads to slight decreases in the fusion and survival probabilities for the ERCS calculation. These changes can be attributed to the modifications in the driving potential and the reduced fission barrier provided by the FRDM-SVM data, respectively.
-
In the previous subsection, we compare the fusion probability, survival probability, and ERCSs of the
$ ^{48} $ Ca+$ ^{238} $ U reaction. We observe a significant change in the fusion probability, which is a result of the precise driving potentials obtained from the optimized nuclear data. As expected, the change in survival probability is not significant, as the mass of the compound nuclei generated in this reaction is extrapolated using the FRDM-SVM approach and does not change significantly from the predicted valuse of the FRDM. Finally, we find that the ERCSs fit better with the experimental values when using the more accurate FRDM-SVM data.Although the optimized mass data obtained from the FRDM-SVM approach improve the accuracy, there may still be deviations from the experimental data. These deviations inevitably affect the driving potentials, neutron separation energy, and fission barriers, thus influencing the fusion probability, survival probability, and ultimately the ERCSs. We assume that there is a deviation of 250 keV across the entire region of the optimized data. Based on this assumption, we analyze the impact of 250 keV mass uncertainties on the fusion probability, survival probability, and final ERCSs of the
$ ^{48} $ Ca+$ ^{238} $ U reaction.In Fig. 7, we present the uncertainty ranges of the fusion and survival probabilities, calculated using the optimized nuclear mass data within a 250 keV error range. It is observed that under the 250 keV mass uncertainty, the survival and fusion probabilities exhibit significant variations. An increase in mass uncertainty to 1 MeV results in magnitude-level changes. Additionally, in Fig. 8, we provide the error band of the excitation curve for the reaction
$ ^{48} $ Ca+$ ^{238} $ U and find that the experimental data falls within the range we provide.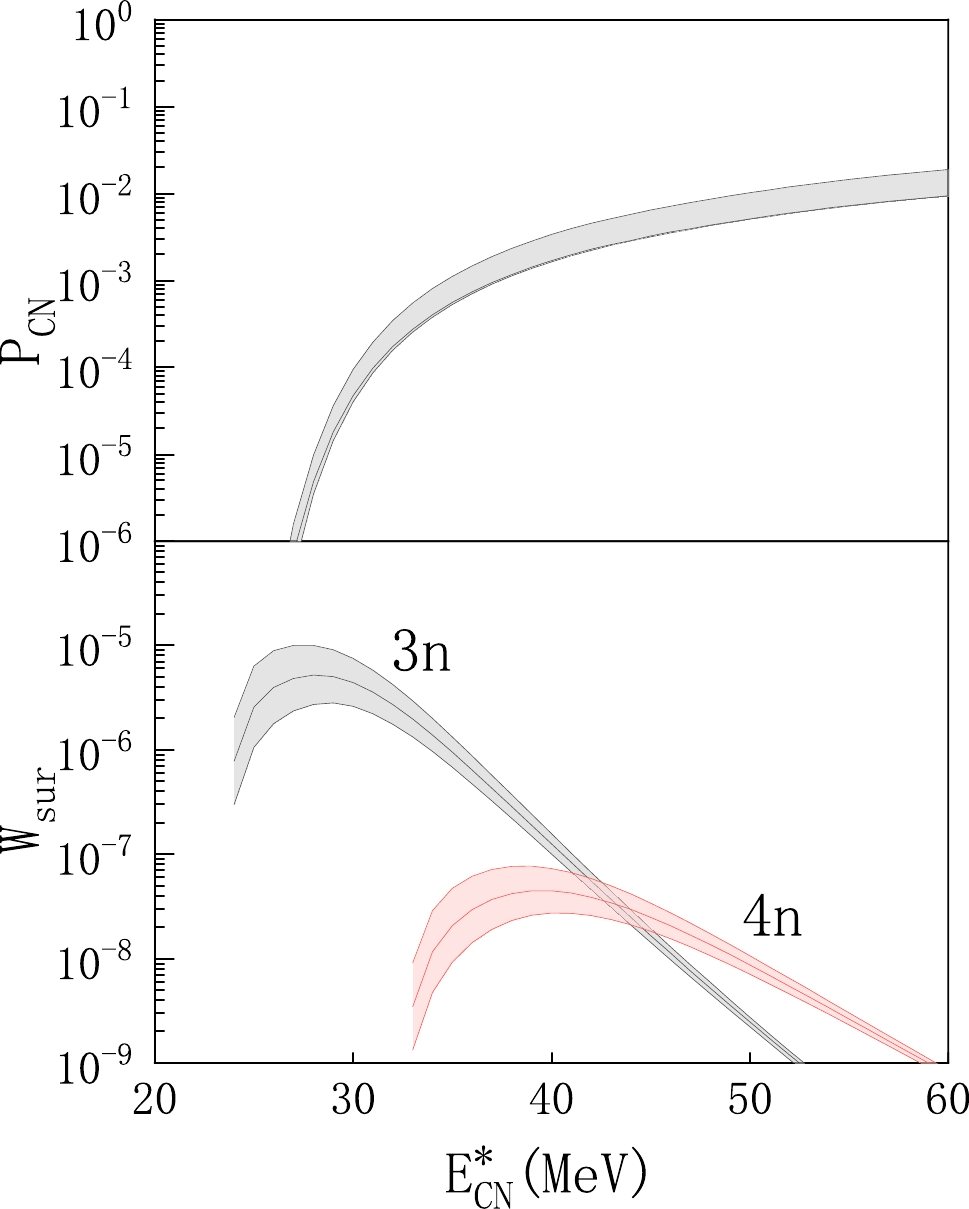
Figure 7. (color online) Fusion probability
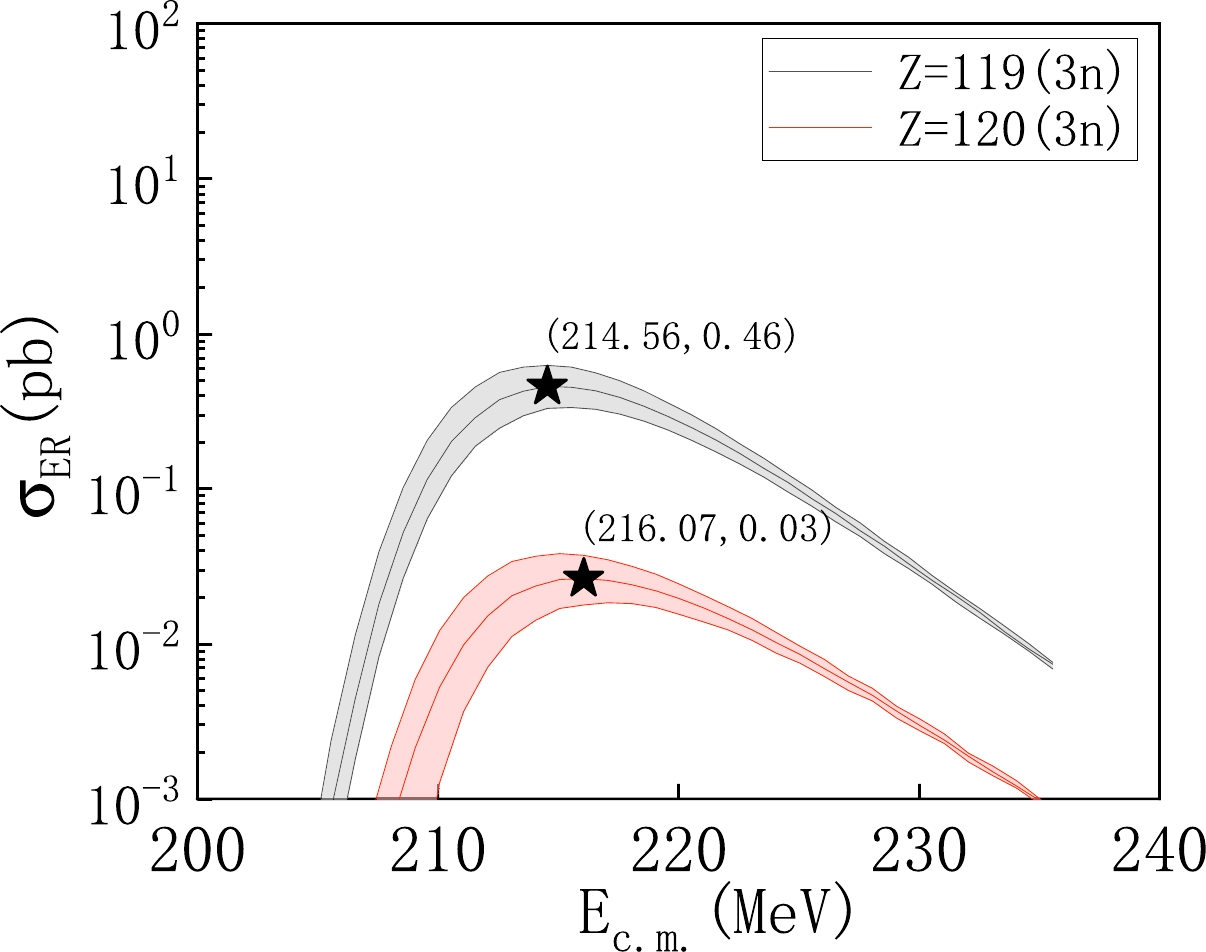
$ P_{CN} $ and survival probability$W_{\rm sur}$ with error range for the 48Ca+238U reaction.In our previous studies [42, 43], we predicted the maximum ERCSs for synthesizing new elements with
$ Z=119 $ and$ Z=120 $ to be 0.29 pb and 22.3 fb, respectively. These values were obtained through the$ ^{45} $ Sc+$ ^{248} $ Cf reaction for$ Z=119 $ and the$ ^{45} $ Sc+$ ^{252} $ Es reaction for$ Z=120 $ . Building upon this, we recalculate the ERCSs of these two reactions using the optimized nuclear mass data and provide their error ranges. Figure 9 displays the excitation functions for these reactions and indicate the optimal incident energy and maximum cross-section of the reactions. We hope that these new results can serve as valuable references for future experiments on the synthesis of new elements. -
In summary, this study proposes an optimized method for estimating atomic nuclear masses by combining the FRDM with the SVM algorithm. The optimization process improves the accuracy of FRDM predictions, reducing the RMSE from 0.606 to 0.253 MeV. Based on this, the driving potential, neutron separation energy, and fission barrier are reevaluated. The fusion probability, survival probability, and ERCSs for the reaction
$ ^{48} $ Ca+$ ^{238} $ U are compared using these two sets of mass data. The results indicate that the utilization of optimized data for the reaction leads to a decrease in both fusion and survival probabilities, with a more pronounced decrease observed in fusion probability. This can be primarily attributed to the varying degrees of alterations in the driving potential and fission barrier caused by the optimized data. The ERCSs calculated using the optimized mass data can effectively reproduce experimental data. Furthermore, the impact of the 250 keV uncertainty of nuclear mass on fusion probability, survival probability, and ERCSs is investigated. The results indicate that the 250 keV uncertainty has a significant impact on both fusion and survival probability. Finally, error ranges for the predicted ERCSs of the new elements 119 and 120 are provided, considering the uncertainty in nuclear mass.
Evaporation residue cross sections of superheavy nuclei based on optimized nuclear data
- Received Date: 2023-07-25
- Available Online: 2023-12-15
Abstract: This study proposes an optimized method for estimating atomic nucleus masses by combining the finite-range droplet model (FRDM) with the support vector machine algorithm. The optimization process significantly improves the accuracy of the FRDM by reducing the root mean square error from 0.606 to 0.253 MeV. The optimized mass data obtained from this method are then used to calculate the evaporation residue cross-sections (ERCSs) for fusion-evaporation reactions, employing the di-nuclear system model. The experimental results for the 48Ca+238U reaction are relatively well reproduced using these optimized mass data. Additionally, the study investigates the impact of mass uncertainties on fusion and survival probabilities. By considering the mass uncertainties, the ERCSs for new elements 119 and 120 are predicted based on the obtained optimized mass data.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: