-
The CP violating observables in
$ b\to s \ell^+ \ell^- $ with$ \ell= (e,\mu, \tau) $ play important roles in probing new physics (NP) as they are highly suppressed in the standard model (SM) [1−7]. In recent years, special attention has been given to$ B \to K^{(*)} \mu^+ \mu^- $ and$ B_{s}\to \phi \mu^+ \mu^- $ [8−10]. Precise measurements of angular observables are now accessible owing to experimental developments [11−19]. They are useful in disentangling helicities, providing reliable methods to probe the Lorentz structure of NP [20−27]. Besides, the ratios of$R_{K^{(*)}} \equiv \Gamma(B \to K^{(*)} \mu^+ \mu^-)/ \Gamma(B \to K^{(*)} e^+ e^-)$ were measured, where discrepancies against the SM were found. In particular, 3.1σ and 2.5σ deviations have been found in$ R_K(1.1 \text{GeV}^2\leq q^2 \leq6.0\text{GeV}^2) $ and$ R_{K^*}(0.045 \text{GeV}^2\leq q^2 \leq6.0\text{GeV}^2) $ [28, 29], showing that the lepton universality may be violated by NP. Very recently, a global fit of$ b\to s \ell^+ \ell^- $ with B meson experiments was performed [30], and the experimental data permitted the large complex Wilson coefficients beyond the SM.The baryonic decays of
$\Lambda_b \to \Lambda(\to p \pi^-) \ell^+ \ell^-$ are interesting for several reasons. For polarized$ \Lambda_b $ , the decays provide a couple dozen angular observables, which are three times more than those in$ B \to K \mu^+ \mu^- $ . The polarization fraction$ (P_b) $ of$ \Lambda_b $ is reported as$ (6\pm 7) $ % at the center of mass energy of 7 TeV of$ pp $ collisions [31]. The full angular distribution of$ \Lambda_b \to \Lambda(\to p \pi^-) \mu^+ \mu^- $ has been measured at the LHCb [19]. Notably, the experiment obtains that$ \begin{array}{*{20}{l}} K_{10} = -0.045\pm 0.037 \pm 0.006 \,, \end{array} $

(1) deviating from the SM prediction of
$ K_{10} \approx 0 $ by$ 1.2\sigma $ . It is reasonable to expect that the precision will be improved in the forthcoming update. In this study, we explicitly show that$ K_{10} $ is a T-odd quantity, which can be sizable in the presence of NP.Theoretically, the angular distributions of
$ \Lambda_b \to \Lambda \mu^+ \mu^- $ have been studied intensively [26, 27, 32]. In particular, an analysis of NP with real Wilson coefficients has been performed in Ref. [33], where they found$ P_b= (0\pm 5) $ % at$ 1\sigma $ confidence level. In this study, we focus on the time-reversal (T) violating observables induced by the complex NP Wilson coefficients. Unlike the direct CP asymmetries in decay widths, T violation does not require a CP-conserving phase. This feature is very useful in leptonic decays, as strong phases are often negligible. The roles of the (pseudo)scalar operators in$ \Lambda_b \to \Lambda \tau^+\tau^- $ are studied for the first time. Their effects are enhanced by$ m_\tau $ and play an important role in examining NP.This paper is organized as follows. In Sec. II, we decompose
$ \Lambda_b\to \Lambda \ell^+\ell^- $ into products of two-body decays. In Sec. III, we construct the T-odd observables. In Sec. IV, we briefly review the angular distributions of$\Lambda_b \to \Lambda (\to p \pi^-) \ell^+ \ell^-$ and identify the T-odd observables. In Sec. V, we estimate the effects of the (pseudo)scalar operators on the T-odd observables. We conclude the study in Sec. VI. -
The amplitudes of
$ \Lambda_b \to \Lambda \ell^+ \ell^- $ , induced by the$ b\to s\ell^+ \ell^- $ transitions at the quark level, are given as [34]:$ \begin{aligned}[b]& \frac{G_{\rm F}}{\sqrt 2} \frac{\alpha V^{*}_{ts} V_{tb}}{2\pi } ( \langle \Lambda|\bar{s} j_V^\mu b |\Lambda_b\rangle \bar{\ell}\gamma_{\mu} \ell + \langle \Lambda|\bar{s} j_A^\mu b |\Lambda_b\rangle \bar{\ell} \gamma_ {\mu} \gamma_5 \ell \\&+ \langle \Lambda |\overline{s} j_S b| \Lambda_b\rangle \overline{\ell}\ell + \langle \Lambda |\overline{s} j_P b| \Lambda_b\rangle \overline{\ell}\gamma_5\ell ) , \end{aligned} $

(2) where
$G_{\rm F}$ is the Fermi constant,$ V_{tq} (q=s,b) $ are the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements,$ \begin{aligned}[b] &j_V^\mu = ( C_9^{\rm eff}+C^{\text{NP}}_9) L^\mu -\frac{2 m_{b}}{q^2}C_{7\gamma}^{\rm eff} i\sigma^{\mu q}(1+\gamma_5) + (C_{L}+C_{R})R^{\mu} \,, \\ &j_A^\mu = (C_{10} + C^{\text{NP}}_{10}) L^ \mu + (C_{R}-C_{L})R^{\mu} \,, \\ &j_S = C_S (1-\gamma_5)\,, \; \; \; j_P = C_P (1-\gamma_5)\,, \end{aligned} $

(3) $C^{\rm(eff)}$ represents the (effective) Wilson coefficients,$\sigma^{\mu q} = {\rm i}(\gamma^{\mu}\gamma^{\nu}-\gamma^{\nu}\gamma^{\mu})q_{\nu}/2$ with$ q = (q^0, \vec{q}\;) $ being the four-momentum of$ \ell^+ \ell^- $ ,$ L^{\mu} = \gamma^{\mu}(1-\gamma_5) $ ,$ R^{\mu} = \gamma^{\mu}(1+\gamma_5) $ , and$ m_{q} $ is for the quark mass. We only consider the NP operators with the right-handed strange quark in$ j_{S,P} $ , as the heavy quark mass would suppress the effects of the left-handed ones.The first (second) term in Eq. (2) can be interpreted as
$\Lambda_b \to \Lambda j_{\rm eff}^{V(A)}$ followed by$j_{\rm eff}^{V(A)}\to \ell^+ \ell^-$ , where$j_{\rm eff}^{V(A)}$ is an effective off-shell (axial) vector boson, conserving the parity in its cascade decays, and$ j^\mu_{V,A} $ are the couplings of$b-s-j_{\rm eff}^{V,A}$ . Alternatively, the interpretation can be rephrased as$\Lambda_b \to \Lambda j_{\rm eff}^{R,L} \to \Lambda \ell^+ \ell^-$ by$ \begin{aligned}[b]& \langle \Lambda|\bar{s} j_V^\mu b |\Lambda_b\rangle \bar{\ell}\gamma_{\mu} \ell + \langle \Lambda|\bar{s} j_A^\mu b |\Lambda_b\rangle \bar{\ell} \gamma_ {\mu} \gamma_5 \ell \\=& \langle \Lambda|\bar{s} j_R^\mu b |\Lambda_b\rangle \bar{\ell}R_\mu\ell + \langle \Lambda|\bar{s} j_L^\mu b |\Lambda_b\rangle \bar{\ell} L_\mu \ell , \end{aligned} $

(4) where
$ j_{R(L)}^{\mu}= (j_V^{\mu} \pm j_A^{\mu})/2 $ and$ j_{\rm eff}^{R(L)} $ clearly couple only to the right-handed (left-handed) leptons. As parity is conserved in$ j_{\rm eff}^{V,A} \to \ell^+ \ell^- $ , it is easier to obtain the angular distributions with the$ j_{\rm eff}^{V,A} $ interpretation. In this study, the angular distributions are obtained using$j_{\rm eff}^{V,A}$ , while for NP,$ j_{\rm{eff}}^{R,L}$ is used. Similarly, the third (fourth) term describes$ \Lambda_b\to \Lambda j_{\rm eff}^{S(P)} $ , with$ j_{\rm eff}^{S(P)} $ , the (pseudo)scalar boson, decaying to$ \ell^+\ell^- $ subsequently.In the SM,
$ C^{\text{NP}}_{9,10} = C_{S,P,L,R}=0 $ and the others are [26, 35]$ \begin{aligned}[b] C_{7\gamma}^{\rm eff}=&-0.313, \\ C_{9}^{\rm eff} =& C_{9} + h\left(\frac{m_c}{m_b} ,\frac{q^2}{m_b ^2}\right) -\frac{1}{2} h\left(1,\frac{q^2}{m_b ^2}\right)(4C_{3} +4C_4 +3C_5 +C_6) \\&-\frac{1}{2} h\left(0,\frac{q^2}{m_b ^2}\right)(C_{3} +3C_4 ) +\frac{2}{9} (3C_3 +C_4 +3C_5 +C_6), \end{aligned} $

(5) where
$ \begin{aligned}[b] &h\left(\frac{m_c}{m_b}, \frac{q^2}{m_b}\right) =-\frac{8}{9} \ln \frac{m_c}{m_b}+\frac{8}{27}+\frac{4}{9} x-\frac{2}{9}(2+x) \\ &\quad \times|1-x|^{1 / 2}\left\{\begin{array}{r} \left(\ln \left|\dfrac{\sqrt{1-x}+1}{\sqrt{1-x}-1}\right|-i \pi\right), \text { for } x <1, \\ 2 \arctan \dfrac{1}{\sqrt{x-1}}, \text { for } x>1, \end{array}\right. \\ &h\left(0, \frac{q^2}{m_b}\right) =\frac{8}{27}-\frac{4}{9} \ln \frac{q^2}{m_b}+\frac{4}{9} {\rm i} \pi, \end{aligned} $

(6) and
$ x = 4m_c^2/q^2 $ . Their explicit values are found in Ref. [35].By decomposing the Minkowski metric as
$ g^{\mu \nu } = \epsilon_t^\mu \epsilon_t^{*\nu} - \sum\limits_{\lambda=0,\pm} \epsilon_\lambda^\mu \epsilon_\lambda^{*\nu}\,, $

(7) we arrive at
$ \frac{G_{\rm F}}{\sqrt 2} \frac{\alpha V^{*}_{ts} V_{tb}}{2\pi } \sum\limits_{m=V,A,S,P} \left( L_t^m B_t^m - \sum\limits_{\lambda=0,\pm} L_{\lambda}^m B_{\lambda} ^m \right)\,, $

(8) where
$ \begin{aligned}[b] &B_{\lambda_m} ^{V,A} = \epsilon_{\lambda_m} ^{\ast\mu} \langle \Lambda | \bar{s} j_{V,A}^\mu b | \Lambda_b \rangle\,,\; \; \; L_{\lambda_m}^V = \epsilon_{\lambda_m}^{\mu} \bar{u}_{\ell} \gamma_ {\mu} v_{\ell} \,,\\& L_{\lambda_m}^A = \epsilon_{\lambda_m}^{\mu} \bar{u}_{\ell} {\gamma_ {\mu}\gamma_5} v_{\ell} \,,\;\;\; B^{S,P} = \langle \Lambda | \bar{s} j_{S,P} b | \Lambda_b \rangle\,, \\&\; L^S_t = \bar{u}_{\ell} v_{\ell} \,,\; \; \; L^P_t = \bar{u}_{\ell} {\gamma_5} v_{\ell} \,, \end{aligned} $

(9) $ {\lambda_m} = (t, 0,\pm) $ is the helicity of$j_{\rm eff}^m$ , with t indicating spin-0 off-shell contributions, and$ \epsilon $ are the polarization vectors of$j_{\rm eff}^m$ , given as [36]$ \begin{aligned}[b] & {\epsilon} ^\mu _\pm = \frac{1}{\sqrt{2}}(0, \pm 1, {\rm i} , 0 )^T\,, \\& {\epsilon}_0^\mu = (0 ,0,0,-1 )^T \,, \\& {\epsilon}^\mu _t = ( -1 ,0,0,0 )^T\,, \end{aligned} $

(10) and
$ \begin{aligned}[b]& {\epsilon} ^\mu _\pm = \frac{1}{\sqrt{2}}(0, \mp 1, {\rm i} , 0 )^T\,, \\& {\epsilon}_0^\mu = \frac{1}{\sqrt{q^2}}(|\vec{q}\,| ,0,0,-q^0 )^T \,, \\& {\epsilon}^\mu _t =-\frac{1}{\sqrt{q^2}} q^\mu , \end{aligned} $

(11) in the center of mass (CM) frames of
$j_{\rm eff}^m$ and$ \Lambda_b $ , respectively. Note that$ L_{\lambda}^{S,P} = 0 $ , as they do not contain the spacelike component. In Eq. (8), the amplitudes are decomposed as the products of Lorentz scalars, where$ B_{\lambda_m} $ and$ L_{\lambda_m} $ describe$\Lambda _b \to \Lambda j_{\rm eff}^m$ and$j_{\rm eff}^m \to \ell^+ \ell^-$ , respectively, reducing the three-body problems to two-body ones.To deal with the spins, we adopt the helicity approach. The projection operators in the
$S O(3)$ rotational$(S O(3)_R)$ group are given by$ \begin{aligned}[b] |J, M\rangle \langle J, N| =&\frac{2J+1}{8 \pi^2 }\int {\rm d} \phi {\rm d}\cos{\theta} {\rm d} \psi R_z(\phi)\\&\times R_y(\theta) R_z(\psi) D^{J\dagger} (\phi,\theta,\psi)^N\,_M \,, \end{aligned} $

(12) where N and M are the angular momenta toward the
$ \hat{z} $ direction, the Wigner-D matrices are defined by$ \begin{array}{*{20}{l}} D^J(\phi,\theta,\psi) ^{M}\,_N \langle J,N|J,M \rangle = \langle J, N\left | R_z(\phi) R_y(\theta) R_z(\psi) \right| J,N \rangle \,, \end{array} $

(13) and
$ R_{y(z)} $ are the rotation operators pointing toward$ \hat{y}(\hat{z}) $ . Notably, it is important for Eq. (12) to be a linear superposition of$ R_{y,z} $ , which commutes with scalar operators. In the following, we take the shorthand of$ D^J(\phi,\theta)\equiv D^J(\phi,\theta,0) $ .The simplest two-particle state with a nonzero momentum is defined by
$ \begin{array}{*{20}{l}} |p\hat{z}, \lambda_1,\lambda_2 \rangle \equiv L_z|\vec{p}= 0 , J_z = \lambda_1 \rangle_1 \otimes L_z' |\vec{p}=0, J_z= - \lambda_2 \rangle_2\,, \end{array} $

(14) where
$ \lambda_{1,2} $ are the helicities, the subscript denotes the particles, and$ L^{(\prime)}_z $ is the Lorentz boost, which brings the first (second) particle to$ (-)p\hat{z} $ . As$ L_z^{(\prime)} $ commutes with$ R_z $ , the state defined by Eq. (14) is an eigenstate of$ J_z = \lambda_1- \lambda_2 $ . Plugging Eq. (12) into Eq. (14) with$ N= \lambda_1-\lambda_2 $ , we arrive at$ \begin{aligned}[b] &|\vec{p}\,^2, \lambda_1,\lambda_2 ;J,J_z\rangle \\=& \frac{2J+1 }{4\pi} \int {\rm d}\phi {\rm d}\cos\theta R_z(\phi) R_y(\theta) |p\hat{z}, \lambda_1,\lambda_2\rangle_{1,2} D^{J*}(\phi,\theta)^{J_z}\,_{N}\,, \end{aligned} $

(15) which expresses the angular momentum eigenstate as the linear superpositions of the three-momentum eigenstate. Conversely, we have
$ | p \hat{z}, \lambda_1 ,\lambda_2 \rangle = \sum\limits_{J} | \vec{p}\,^2, \lambda_1 ,\lambda_2; J,N \rangle\,. $

(16) Note that the identities of Eqs. (15) and (16) are purely obtained from the mathematical consideration. The simplification occurs when the angular momentum conservation is considered. At the CM frames of
$ \Lambda_b $ and$ j_{\rm eff}^{m} $ , it is clear that only$ J=1/2 $ and$ J=(0,1) $ need to be considered for the$\Lambda j_{\rm eff}^{m}$ and$ \ell^+\ell^- $ systems, respectively.Utilizing Eq. (16), we find that
$ \begin{array}{*{20}{l}} \langle \vec{p}\,^2 ,\lambda_1,\lambda_2 ; J, N | {\cal S} | J , J_z;i \rangle = \langle p\hat{z},\lambda_1,\lambda_2 |{\cal S}| J , J_z;i \rangle\,, \end{array} $

(17) where
$ {\cal S} $ is an arbitrary scalar operator, and$ |J, J_z;i\rangle $ stands for an arbitrary initial state. In Eq. (17), the final state on the left side possesses a definite angular momentum, which is irreducible in the$S O(3)_R$ group, i.e., it contains only the dynamical details. On the contrary, the one on the right side is a three-momentum eigenstate, containing fewer physical insights but providing a way to compute the helicity amplitude.Let us return to
$\Lambda_b \to \Lambda j_{\rm eff}^{m}$ and$ j_{\rm eff}^{m} \to \ell^+ \ell^- $ . We take the uppercase and lowercase of H and h for the helicity amplitudes of$ \Lambda_b \to \Lambda j_{\rm eff}^{m} $ and$ j_{\rm eff}^{m} \to \ell^+ \ell^- $ , respectively. To be explicit, we have$ \begin{aligned}[b] H_{\lambda_\Lambda \lambda_m}^m &= B_{\lambda_m}^m\left( \lambda_{\Lambda_b} = \lambda_{\Lambda} - \lambda_m, \lambda_{\Lambda} , \vec{p}_{\Lambda} = -\vec{q} = |\vec{p}_{\Lambda} | \hat{z} \right)\,,\\ h_{0,\lambda_+ \lambda_-}^{m } &= L_{t}^m(\lambda_+, \lambda_-, \vec{q}=0, \vec{p}_+ = -\vec{p}_- =| \vec{p}_+| \hat{z} )\,, \\ h_{1, \lambda_+ \lambda_-}^{m } &= L_{\lambda_+ - \lambda_- }^m( \lambda_+, \lambda_-, \vec{q}=0, \vec{p}_+ = -\vec{p}_- =| \vec{p}_+| \hat{z} )\,, \end{aligned} $

(18) where
$ \lambda_{\Lambda_b} (\lambda_{\Lambda},\lambda_\pm) $ corresponds to the angular momentum (helicities) of$ \Lambda_{b }\; (\Lambda, \ell^\pm) $ , and$ \vec{p}_{\Lambda} $ ($ \vec{p}_\pm $ ) is the three-momentum of Λ ($ \ell^\pm) $ in the CM frame of$\Lambda_ b (j_{\rm eff}^m)$ . Theoretically, the dynamical parts of the amplitudes are extracted by Eq. (17), whereas the kinematic dependencies are governed by$ D^J $ .For compactness, we take the abbreviations
$ \begin{aligned}[b] &|a^m_\pm \rangle = |\Lambda j_{\rm eff}^m, \pm 1/2,0 \rangle, \quad|b^m_\pm\rangle = |\Lambda j_{\rm eff}^m, \mp 1/2,\mp 1 \rangle, \\ & |c^m_\pm \rangle = |\Lambda j_{\rm eff}^m, \pm 1/2,t \rangle, \quad a^{m}_{\pm} = H^{m}_{\pm \frac{1}{2}0} = \langle a_\pm ^m | {\cal S}_{\rm eff}^m|\Lambda_b\rangle ,\\ & b^{m}_{\pm}= H^{m}_{\mp \frac{1}{2}\mp1} = \langle a^m_\pm | {\cal S}_{\rm eff}^m |\Lambda_b\rangle , \quad c^{m}_{\pm} = H^{m}_{\pm \frac{1}{2}t} = \langle c_\pm ^m | {\cal S}_{\rm eff}^m |\Lambda_b\rangle , \end{aligned} $

(19) where
$ {\cal S}_{\rm eff}^m $ is the transition operator responsible for$ \Lambda_b \to \Lambda j_{\rm eff}^m $ , and$ J_z $ is not written down explicitly. The artificial$ {\cal S}_{\rm eff}^m $ is needed to interpret$ \Lambda_b\to \Lambda \ell^+ \ell^- $ as products of two-body ones. For the$ \Lambda_b\to \Lambda j_{\rm eff}^{R,L} $ interpretation, the helicity amplitudes are$ \begin{aligned}[b]&a_\pm^R = \frac{1}{\sqrt{2}}(a_\pm^V + a_\pm ^A)\,,\; \; \; a_\pm^L = \frac{1}{\sqrt{2}} (a_\pm^V - a_\pm^ A)\,,\\ &b_\pm^R = \frac{1}{\sqrt{2}}(b_\pm^V + b_\pm ^A)\,,\; \; \; \; b_\pm^L = \frac{1}{\sqrt{2}} (b_\pm^V - b_\pm ^A)\,,\\ &c_\pm^R = \frac{1}{\sqrt{2}}(c_\pm^V + c_\pm ^A)\,,\; \; \; \; c_\pm^L = \frac{1}{\sqrt{2}} (c_\pm^V - c_\pm ^A)\,. \end{aligned} $

(20) -
From Eq. (3), we see that the NP contributions are absorbed into the couplings of
$ b-s-j_{\rm eff}^m $ , whereas the Lorentz structures of$ j_{\rm eff}^m \to \ell^+ \ell^- $ are plain. Thus, to discuss the NP effects, it is sufficient to study$ \Lambda_b \to \Lambda j_{\rm eff}^m $ .The most simple T-odd operator in
$ \Lambda_b \to \Lambda j_{eff}^m $ is defined as [37]$ \begin{array}{*{20}{l}} \hat{T} = (\vec{s}_{\Lambda} \times \vec{s}_{m} )\cdot \hat{p}_{\Lambda}, \end{array} $

(21) $ \vec{s}_{\Lambda} $ and$ \vec{s}_{m} $ are the spin operators of Λ and$j^{m}_{\rm eff}$ , respectively, and$ \hat{p}_{\Lambda} $ is the unit vector of$ \vec{p}_{\Lambda} $ . The spin operators can only be defined for the massive objects, given as$ M\vec{s} = P^0 \vec{J} - \vec{p} \times \vec{K } - \frac{1}{P^0 + M }\vec{p}(\vec{p}\cdot \vec{J})\,, $

(22) where M is the particle mass, and
$ P^0 $ ,$ \vec{p} $ ,$ \vec{J} $ , and$ \vec{K} $ are the time translation, space translation, rotation, and Lorentz boost generators, respectively. Note that$ (\vec{p}, \vec{J}) $ and$ \vec{s} $ are T-odd, whereas$ \vec{K} $ is T-odd. In addition,$ \vec{s} $ satisfies the relations$ \begin{array}{*{20}{l}} & \vec{s} \cdot \vec{p} = \vec{J} \cdot \vec{p} \,,\; \; \; [s_i,s_j] = {\rm i} \epsilon^{ijk} \epsilon_k\,,\; \; \; [s_i,p_j] =0 \,, \\ & \vec{s} \exp({\rm i}\vec{K}\cdot \vec{\omega})|\vec{p}=0, J_z = M \rangle = \exp({\rm i}\vec{K}\cdot \vec{\omega}) \vec{J} |\vec{p}=0,J_z =M\rangle\,, \end{array}$

(23) with arbitrary
$ \vec{\omega} $ . The key to solving the eigenstates of$ \hat{T} $ relies on$ \hat{T} $ being a scalar operator. Thus, we have$ \begin{aligned}[b] &\hat{T}|\vec{p}\,^2, \lambda_1,\lambda_2 ;J,J_z\rangle \\ = &\frac{2J+1 }{4\pi} \int {\rm d}\phi {\rm d}\cos\theta R_z(\phi) R_y(\theta) \hat{T} |p\hat{z}, \lambda_1,\lambda_2\rangle_{1,2} \\&\times D^{J*}(\phi,\theta)^{J_z}\,_{\lambda_1-\lambda_2}\,, \end{aligned} $

(24) and
$ \hat{T} |p \hat{z}, \lambda_1, \lambda_2 \rangle = \frac{\rm i}{2} (s_\Lambda^+ s_m^- - s_\Lambda^- s_m^+) |p \hat{z}, \lambda_1, \lambda_2 \rangle \,, $

(25) with
$s^\pm = s_x \pm {\rm i}s_y$ . It is then straightforward to show that$ \hat{T} |a^{m}_\pm \rangle =\pm \frac{\rm i}{\sqrt{2}}|b^{m}_\pm\rangle ,\; \; \; \hat{T} |b^{m}_\pm \rangle = \mp \frac{\rm i}{\sqrt{2}}|a^{m}_\pm \rangle , \; \; \; \hat{T} |c^{m}_\pm \rangle = |0 \rangle , $

(26) resulting in the eigenstates
$ \begin{aligned}[b] &|\lambda_{T}^m=\pm\frac{1}{\sqrt{2}},\lambda_{\text{tot}} = \frac{1}{2} \rangle = \frac{1}{\sqrt{2}}(|a^{m}_+ \rangle \mp {\rm i}|b^{m}_+ \rangle),\\ &|\lambda_{T}^m=\pm\frac{1}{\sqrt{2}},\lambda_{\text{tot}} = -\frac{1}{2} \rangle = \frac{1}{\sqrt{2}}(|a^{m}_- \rangle \pm {\rm i}|b^{m}_- \rangle)\,, \end{aligned} $

(27) where
$ \lambda_T^m $ and$ \lambda_{\text{tot}} $ are the eigenvalues of$ \hat{T} $ and$ \vec{J}\cdot \vec{p} $ , respectively. They are also the eigenstates of$ \vec{J}\cdot \vec{p} $ , as$ \hat{T} $ commutes with both$ \vec{J} $ and$ \vec{p} $ . Note that$ c_{\pm}^{m} $ are not involved since they are contributed by spinless$j_{\rm eff}^m$ .Because
$ \hat{T} $ and$ \vec{J}\cdot\vec{p} $ are T-odd and T-even, respectively, we have$ \begin{array}{*{20}{l}} {\cal I}_t |\lambda_T^m, \lambda_{\text{tot}}\rangle = {\rm e}^{{\rm i}\theta_T} |-\lambda_T^m, \lambda_{\text{tot}}\rangle\,,\; \; \; {\cal I}_s |\lambda_T^m, \lambda_{\text{tot}}\rangle = |-\lambda_T^m, -\lambda_{\text{tot}}\rangle\,, \end{array} $

(28) where
$ {\cal I}_{t(s)} $ is the time-reversal (space-inversion) operator, and$ \theta_{T} $ depends on the convention. On the other hand,$ {\cal I}_s $ would interchange$ j_{\rm eff}^R $ and$ j_{\rm eff}^L $ , given as$ \begin{array}{*{20}{l}} {\cal I}_s |\lambda_T^R, \lambda_{\text{tot}}\rangle = |-\lambda_T^L, -\lambda_{\text{tot}}\rangle\,,\; \; \; {\cal I}_s |\lambda_T^L, \lambda_{\text{tot}}\rangle = |-\lambda_T^R, -\lambda_{\text{tot}}\rangle\,, \end{array} $

(29) with
$ \begin{aligned}[b] |\lambda_T^R , \lambda_{\text{tot}} \rangle =& \frac{1}{\sqrt{2}}\left( |\lambda_T^V , \lambda_{\text{tot}} \rangle + |\lambda_T^A , \lambda_{\text{tot}} \rangle \right)\,,\\ |\lambda_T^L , \lambda_{\text{tot}} \rangle =& \frac{1}{\sqrt{2}}\left( |\lambda_T^V , \lambda_{\text{tot}} \rangle - |\lambda_T^A , \lambda_{\text{tot}} \rangle \right)\,, \end{aligned} $

(30) since
$ j_{\rm eff}^V $ and$ j_{\rm eff}^A $ have opposite parity.For each combination of
$ \lambda_{\text{tot}} $ and$j_{\rm eff}^m$ , we define a T-odd quantity$ \begin{aligned}[b] {\cal T}_{\lambda_{\text{tot}}}^{\,m} \equiv & |\langle \lambda_T^m =1/\sqrt{2},\lambda_{\text{tot}} | {\cal S}_{eff} | \Lambda_b \rangle|^2 \\& - |\langle \lambda_T^ m = -1/\sqrt{2},\lambda_{\text{tot}} | {\cal S}_{\rm eff} | \Lambda_b \rangle|^2\,, \end{aligned} $

(31) which vanishes if
${\cal S}_{\rm eff}$ is invariant under$ {\cal I}_t $ . Explicitly, we find that$ \begin{array}{*{20}{l}} & {\cal T}_+ ^{\,m} =- 2 \text{Im} \left (a_+^m \overline{b_+^m} \right ) \,,\; \; &{\cal T}_- ^{\,m} = 2 \text{Im} \left (a_-^m \overline{b_-^m} \right )\,, \end{array} $

(32) which are proportional to the relative complex phase. They are called T-odd quantities, as
$ {\cal I}_t $ interchanges the final states of the two terms in Eq. (31).The operator of
$ \hat{T} $ contains$ \vec{s}_\Lambda $ , which is difficult to measure directly. To probe the spin of Λ, it is plausible to study the cascade decays of$ \Lambda \to p \pi^- $ . Subsequently, the final states involve four particles$ p \pi^- \ell^+ \ell^- $ , containing three independent three-momenta. It is then possible to observe the triple product, given by$ \begin{array}{*{20}{l}} \alpha ( \vec{p}_+\times \vec{p}_p ) \cdot \vec{p}_\Lambda, \end{array} $

(33) where α is the polarization asymmetry in
$ \Lambda \to p \pi^- $ , and$ \vec{p}_p $ is the three momentum of the proton. Notice that α is a necessary component in Eq. (33), as$ \vec{s}_\Lambda $ does not affect$ \vec{p}_p $ if$ \alpha = 0 $ . As the product in Eq. (33) is P-even, we have to construct P-even observables from Eq. (32). From the transformation rules, it is easy to see that$ \begin{array}{*{20}{l}} {\cal T} ^{1} \equiv {\cal T}_- ^{R} - {\cal T}_+^{L}\,,\; \; \; {\cal T} ^{2} \equiv {\cal T}_-^{L} - {\cal T}_+ ^{R} \,, \end{array} $

(34) are both T-odd and P-even.
-
The lepton helicity amplitudes are calculated as
$ \begin{aligned}[b] h_{0,++}^V &= 0 \,,\; \; \; \quad h_{1,++}^V = 2M_\ell \,, \\ h_{0,++}^A &= 2M_\ell \,,\; \; \; \quad h_{1,++}^A = 0 \,,\\ h_{1,+-}^V &= -\sqrt{2q^2} \,, \; \; \; \quad h_{1,+-}^A = \sqrt{2q^2(1-\delta_\ell)}\,, \\ h_{0,++}^S & =\sqrt{2q^2(1-\delta_\ell)} \,,\; \; \; \quad h_{0,++}^P =\sqrt{2q^2} \,, \\ \end{aligned} $

(35) where
$ \delta_\ell = 4M_\ell^2 / q^2 $ with$ M_\ell $ being the lepton mass. In contrast, the baryon matrix elements are conventionally parameterized by the form factors, given by$ \begin{aligned}[b] \langle \Lambda|\bar{s} \gamma^\mu b|\Lambda_b\rangle&= \bar u_{\Lambda}\bigg[f_1^V(q^2)\gamma^\mu-f_2^V(q^2){\rm i} \sigma^{\mu\nu}\frac{q_\nu}{M_{\Lambda_b}}+f_3^V(q^2)\frac{q^\mu}{M_{\Lambda_b}}\bigg] u_{\Lambda_b},\\ \langle \Lambda|\bar{s} \gamma^\mu\gamma_5 b|\Lambda_b\rangle&= \overline u_{\Lambda}\bigg[f_1^A(q^2)\gamma^\mu-f_2^A(q^2) {\rm i} \sigma^{\mu\nu}\frac{q_\nu}{M_{\Lambda_b}}+f_3^A(q^2)\frac{q^\mu}{M_{\Lambda_b}}\bigg] \gamma_5 u_{\Lambda_b},\\ \langle \Lambda | \bar{s} {\rm i} \sigma^{\mu q} b | \Lambda_b \rangle &= \bar{u}_\Lambda \left[ \frac{f_1^{TV}(q^2)}{M_{\Lambda_b}} \left(\gamma^\mu q^2 - q^\mu \not {q} \right) - f_2^{TV}(q^2) {\rm i}\sigma^{\mu q} \right] u_{\Lambda_b}, \\ \langle \Lambda | \bar{s} {\rm i} \sigma^{\mu q}\gamma_5 b | \Lambda_b \rangle &=\bar{u}_\Lambda \left[ \frac{f_1^{TA}(q^2)}{M_{\Lambda_b}} \left(\gamma^\mu q^2 - q^\mu \not {q} \right) - f_2^{TA}(q^2) {\rm i} \sigma^{\mu q} \right]\gamma_5 u_{\Lambda_b}, \\ \langle \Lambda |\overline{s} (1-\gamma_5)b| \Lambda_b\rangle &= \overline{u}_{\Lambda} (f_s- g_a \gamma_5 )u_{\Lambda_b}\,, \end{aligned} $ 
(36) where
$ u_{\Lambda_{(b)}} $ and$ M_{\Lambda_{(b)}} $ are the Dirac spinor and mass of$ \Lambda _{(b)} $ , respectively. In turn, we find that$ H^{Vm}_{\frac{1}{2},\,0} = \sqrt{\frac{Q_-}{q^2}}\left[M_+ F^{Vm}_1(q^2) +\frac{q^2}{M_{\Lambda_b}} F^{Vm}_2(q^2)\right]\,, $

(37) $ H^{Vm}_{\frac{1}{2},\, 1} =\sqrt{2Q_-}\left[ F^{Vm}_1(q^2)+\frac{M_+}{M_{\Lambda_b}} F^{Vm}_2(q^2)\right]\,, $

(38) $ H^{Vm}_{\frac{1}{2},\,t}= \sqrt{\frac{Q_+}{q^2}} \left[M_- F^{Vm}_1(q^2) +\frac{q^2} {M_{\Lambda_b}} F^{Vm}_3(q^2)\right]\,, $

(39) $ H^{Am}_{\frac{1}{2},\,0} = \sqrt{\frac{Q_+}{q^2}}\left[M_- F^{Am}_1(q^2) -\frac{q^2}{M_{\Lambda_b}} F^{Am}_2(q^2)\right]\,, $

(40) $\begin{aligned}\\[-8pt] H^{Am}_{\frac{1}{2},\, 1} =\sqrt{2Q_+}\left[ F^{Am}_1(q^2)+\frac{M_-}{M_{\Lambda_b}} F^{Am}_2(q^2)\right]\,, \end{aligned}$

(41) $ H^{Am}_{\frac{1}{2},\,t}= \sqrt{\frac{Q_-}{q^2}} \left[M_+ F^{Am}_1(q^2) -\frac{q^2} {M_{\Lambda_b}} F^{Am}_3(q^2)\right]\,, $

(42) $ H^{S}_{\pm\frac{1}{2},\,t}= C_S \left[ f_s \frac{\sqrt{Q_+ q^2}}{M_{\Lambda_b}} \pm g_a \frac{\sqrt{Q_- q^2}}{M_{\Lambda_b}}\right] \,, $

(43) $ H^{P}_{\pm\frac{1}{2},\,t}= C_P \left[ f_s \frac{\sqrt{Q_+ q^2}}{M_{\Lambda_b}} \pm g_a \frac{\sqrt{Q_- q^2}}{M_{\Lambda_b}}\right]\,, $

(44) where
$ M_\pm = M_{\Lambda_b } \pm M_{\Lambda} $ ,$ Q_\pm = (M_\pm)^2 - q^2 $ , and$ \begin{aligned}[b] F^{VV}_1(q^2)=&[ C_9^{\rm eff}+C^{\text{NP}}_9 + (C_L + C_R)]f^{V}_1(q^2)\\& - \frac{2m_b}{M_{\Lambda_b}}C_{7\gamma}^{\rm eff}f^{TV}_1(q^2)\,, \end{aligned} $

(45) $ \begin{aligned}[b] F^{VV}_2(q^2)=&[ C_9^{\rm eff}+C^{\text{NP}}_9 + (C_L + C_R) )]f^{V}_2(q^2) \\& - \frac{2m_b M_{\Lambda_b}}{q^2}C_{7\gamma}^{\rm eff}f^{TV}_2(q^2)\,, \end{aligned} $

(46) $ \begin{aligned}[b] F^{VV}_3(q^2)=&[ C_9^{\rm eff}+C^{\text{NP}}_9 + (C_L + C_R)]f^{V}_3(q^2)\\& +\frac{2m_b M_-}{q^2}C_{7\gamma}^{\rm eff}f^{TV}_1(q^2)\,, \end{aligned} $

(47) $ \begin{aligned}[b] F^{AV}_1(q^2)=&[ C_9^{\rm eff}+C^{\text{NP}}_9 - (C_L + C_R)]f^{A}_1(q^2)\\& +\frac{2m_b}{M_{\Lambda_b}}C_{7\gamma}^{\rm eff}f^{TA}_1(q^2)\,, \end{aligned} $

(48) $ \begin{aligned}[b] F^{AV}_2(q^2)=&[ C_9^{\rm eff}+C^{\text{NP}}_9 - (C_L + C_R) )]f^{A}_2(q^2)\\& +\frac{2m_b M_{\Lambda_b}}{q^2}C_{7\gamma}^{\rm eff}f^{TA}_2(q^2)\,, \end{aligned} $

(49) $ \begin{aligned}[b] F^{AV}_3(q^2)=&[ C_9^{eff}+C^{\text{NP}}_9 - (C_L + C_R)]f^{A}_3(q^2)\\&+\frac{2m_b M_+}{q^2}C_{7\gamma}^{eff}f^{TA}_1(q^2)\,, \end{aligned} $

(50) $ F^{VA}_i(q^2)=[C_{10} +C^{\text{NP}}_{10} + (C_R - C_L)]f^{V}_i(q^2)\,, $

(51) $ F^{AA}_i(q^2)=[C_{10} +C^{\text{NP}}_{10} - (C_R - C_L)]f^{A}_i(q^2)\,, $

(52) with
$ i=(1,2,3). $ Combining the relations$\begin{aligned}[b]& H^{m}_{\lambda_\Lambda\lambda_m} = H^{Vm}_{\lambda_\Lambda\lambda_m}-H^{Am}_{\lambda_\Lambda\lambda_m}\,,\;\quad H^{Vm}_{-\lambda_\Lambda,\,-\lambda_m}= H^{Vm}_{\lambda_\Lambda,\, \lambda_m}\,, \;\\& H^{Am}_{-\lambda_\Lambda,\,-\lambda_m}= -H^{Am}_{\lambda_\Lambda,\, \lambda_m}, \end{aligned}$

the evaluations of H are completed once the form factors are given.
The angular distributions of
$ \Lambda_b \to \Lambda (\to p \pi^-) \ell ^+ \ell^- $ , related to the kinematic part, are given by piling$ D^J $ , read as$ \begin{aligned}[b] {\cal D}(q^2,\vec{\Omega})\equiv& \frac{\partial^6 \Gamma(\Lambda_b \to \Lambda ( \to p \pi^-) \ell ^+ \ell^-)}{\partial q ^2 \partial \cos \theta \partial \cos \theta_b \partial \cos \theta_\ell \partial \phi_b \partial\phi_\ell } = \mathcal{B}(\Lambda \to p \pi^-) \frac{\zeta(q^2)}{32\pi^2} \sum\limits_{ \lambda_p \,,\lambda_\pm\,,\lambda_b }\rho_{\lambda_b\lambda_b}\left| A_{\lambda_p } \right|^2 \\ & \times \left|\sum\limits_m \sum\limits_{\lambda_{m},\lambda_{\Lambda} } (-1) ^{J_m } H_{\lambda_{\Lambda}\lambda_m }^m D^{\frac{1}{2}*}(0,\theta)^{\lambda_b }\, _{\lambda_{\Lambda} - \lambda_m } D^{\frac{1}{2}*}(\phi_b,\theta_b)^{\lambda_{\Lambda}}\,_{\lambda_p } h^m_{J_m,\lambda_+ \lambda_-} D^{J_m *}(\phi_\ell,\theta_\ell )^{\lambda_m }\,_{\lambda_+ -\lambda_-} \right|^2, \\ \zeta(q^2) =& \frac{\alpha^2 G_F^2 |V_{ts}^\dagger V_{tb}|^2}{32 \pi^5 } \frac{q^2|\vec{p}_{\Lambda}|}{24M_{\Lambda_b}^2} \sqrt{1-\delta_\ell}, \end{aligned} $ 
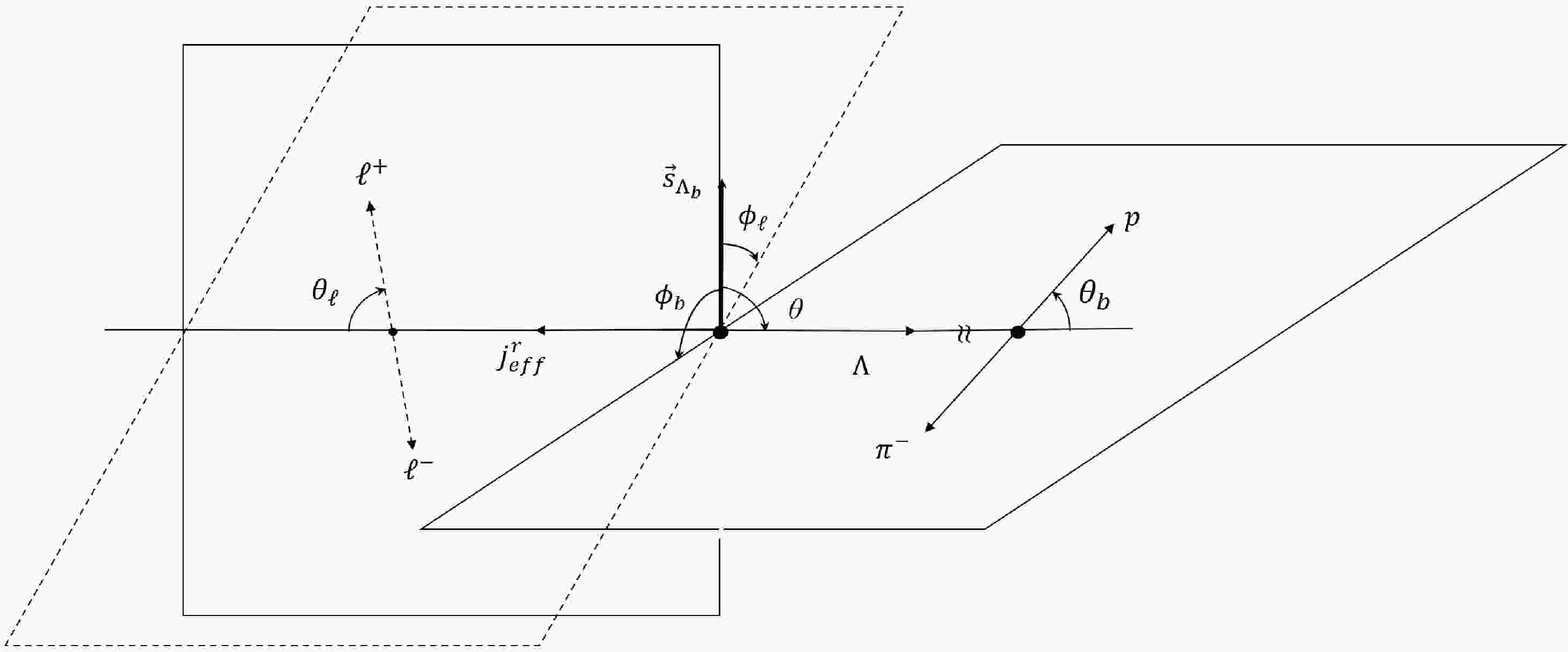
(53) where
$ \rho_{\pm,\pm }=(1\pm P_b)/2 $ ,$ |A_\pm|^2 = (1\pm \alpha) /2 $ ,$ \lambda_{p} = \pm 1/2 $ ,$ |\vec{p}_{\Lambda}| = \sqrt{Q_+Q_-}/2M_{\Lambda_b} $ , and$ J_m=0\; (1) $ for$ \lambda_m = t\; (\pm,0) $ . The angles are defined in Fig. 1, where$ \theta,\theta_b $ and$ \theta_\ell $ are defined in the CM frames of$ \Lambda _{b},\Lambda $ and$ \ell^+ \ell^- $ , respectively, and$ \phi_{b,\ell} $ are the azimuthal angles between the decay planes.The breakdown of the physical meaning of Eq. (53) is as follows:
●
$ H^m_{\lambda_\Lambda\lambda_m} D^{\frac{1}{2}*}(0,\theta)^{\lambda_b}\,_{\lambda_\Lambda- \lambda_m} $ is responsible for$ \Lambda_b \to \Lambda j_{eff}^m $ , where H and D describe the dynamical and kinematic parts of the amplitudes.● The kinematic part of
$ \Lambda \to p \pi^- $ is described by$ D^{\frac{1}{2}*}(\phi_b,\theta_b)^{\lambda_{\Lambda}}\,_{\lambda_p } $ and the dynamical part by$ |A_{\lambda_p}| $ .●
$ h^m_{J_m,\lambda_+ \lambda_-} $ and$ D^{J_m *}(\phi_\ell,\theta_\ell)^{\lambda_m }\,_{\lambda_+ -\lambda_-} $ describe the dynamical and kinematic parts of$ j^m_{\rm eff} \to \ell^+ \ell^- $ , respectively.The derivation is similar to those in the appendices in Ref. [36]. We cross-check our result of
$ \mathcal{D} (\vec{\Omega}) $ with Ref. [32] and find that they match. For practical purposes,$ \mathcal{D} (\vec{\Omega}) $ is expanded as follows [19]:$ \begin{aligned}[b] {\cal D}(q^2, \vec{\Omega} ) =& \frac{3}{32\pi^{2}} \Big( \left(K_1\sin^2\theta_l+K_2\cos^2\theta_l+K_3\cos\theta_l\right) + \left(K_4\sin^2\theta_l+K_5\cos^2\theta_l+K_6\cos\theta_l\right)\cos\theta_b \\& + \left(K_7\sin\theta_l\cos\theta_l+K_8\sin\theta_l\right)\sin\theta_b\cos\left(\phi_b+\phi_l\right) + \left(K_9\sin\theta_l\cos\theta_l+K_{10}\sin\theta_l\right)\sin\theta_b\sin\left(\phi_b+\phi_l\right) \\& + \left(K_{11}\sin^2\theta_l+K_{12}\cos^2\theta_l+K_{13}\cos\theta_l\right)\cos\theta + \left( K_{14}\sin^2\theta_l+K_{15}\cos^2\theta_l+K_{16}\cos\theta_l\right)\cos\theta_b \cos\theta \\& + \left(K_{17}\sin\theta_l\cos\theta_l+K_{18}\sin\theta_l\right)\sin\theta_b\cos\left(\phi_b+\phi_l\right)\cos\theta + \left(K_{19}\sin\theta_l\cos\theta_l+K_{20}\sin\theta_l\right)\sin\theta_b\sin\left(\phi_b+\phi_l\right) \cos\theta \\& +\left(K_{21}\cos\theta_l\sin\theta_l+K_{22}\sin\theta_l\right)\sin\phi_l \sin\theta + \left(K_{23}\cos\theta_l\sin\theta_l+K_{24}\sin\theta_l\right)\cos\phi_l \sin\theta \\&+ \left(K_{25}\cos\theta_l\sin\theta_l+K_{26}\sin\theta_l\right)\sin\phi_l\cos\theta_b \sin\theta + \left(K_{27}\cos\theta_l\sin\theta_l+K_{28}\sin\theta_l\right)\cos\phi_l\cos\theta_b \sin\theta \\& + \left(K_{29}\cos^2\theta_l+K_{30}\sin^2\theta_l\right)\sin\theta_b\sin\phi_b \sin\theta + \left(K_{31}\cos^2\theta_l+K_{32}\sin^2\theta_l\right)\sin\theta_b\cos\phi_b \sin\theta \\& + \left(K_{33}\sin^2\theta_l \right) \sin\theta_b\cos\left(2\phi_l+\phi_b\right) \sin\theta + \left(K_{34}\sin^2\theta_l \right) \sin\theta_b\sin\left(2\phi_l+\phi_b\right) \sin\theta \Big)\; \,, \end{aligned} $ 
(54) with
$ \begin{array}{*{20}{l}} K_i(i=1\sim34)\equiv K^{VA}_i + K^{SP}_i\,, \end{array} $

(55) where the definitions of
$ K^{VA}_i $ and$ K^{SP}_i $ can be found in Appendix A and Appendix B, respectively. We note that$ K_{11\sim 34} $ are proportional to$ P_b $ , imposing difficulties in extracting physical meanings since$ P_b $ depends on their production. Interestingly, in the SM,$ K_9 $ and$ K_{10} $ are found to be$ \begin{aligned}[b] K_9 &= -\frac{\sqrt{2}\alpha\left(1 - \delta_{\ell}\right)}{4} \left( {\cal T}^1 + {\cal T}^2 \right)\,, \\ K_{10} &= \frac{\sqrt{2}\alpha\sqrt{1 - \delta_{\ell}}}{4}\left( {\cal T}^1 - {\cal T}^2\right)\,, \\ \end{aligned} $

(56) which are T-odd according to Eq. (34). Notably,
$ K_{19,20} $ ,$ K_{21,22} $ ,$ K_{25,26} $ ,$ K_{29,30} $ , and$ K_{34} $ are also sensitive to the complex phases of NP, as they are proportional to the imaginary parts of the helicity amplitudes. -
After identifying the T-odd observables, we are ready to estimate the NP contributions. If (pseudo)scalar operators from NP are involved, their contributions are divided into two categories: one is from the interference between NP, which scales as
$ \mathcal{O}(C_{S,P}^2) $ , and the other arises from the interference of (pseudo)scalar operators with the SM, scaling as$ {\cal O}(C_{S,P}) $ . We focus on the latter, as it is expected to be larger. As the contributions are proportional to the lepton masses, our main concern lies in the decay channel of$ \Lambda_b \to \Lambda(\to p \pi^-) \tau^+ \tau^- $ . Furthermore, this channel is contaminated a little by the charmonia resonance, providing a clean background to probe NP. We take$C_{L,R}=C^{\rm NP}_{9,10}=0$ in$ \Lambda_b \to \Lambda(\to p \pi^-) \tau^+ \tau^- $ and notice that$ K_{9} $ would not be influenced by the (pseudo)scalar operators. However,$ K_{10} $ is sensitive to$ C_{S} $ and$ C_{P} $ .In this work, we evaluated the form factors of
$ \Lambda_b \to \Lambda $ from the homogeneous bag model, the details of which are given in Appendix C and good accordance to the experiments is found in$ {\cal B}(\Lambda_b \to \Lambda \mu ^+ \mu^-) $ . The results are plotted in Figs. 2 to 5 with error bands, where$ K_{10} = 0 $ when$ C_S=C_P=0 $ . In Figs. 2 and 3,$ C_{S,P} $ are set to be purely real, whereas in Figs. 4 and 5, they are purely imaginary.
Figure 2. (color online)
$ q^2 $ -dependencies of$ K_{10} $ with different values of$ C_S $ ($ \ell=\tau\,,\,C_P=0 $ ).
Figure 5. (color online)
$ q^2 $ -dependencies of$ K_{10} $ with different values of$ C_P $ ($ \ell=\tau\,,\,C_S=0 $ ).
Figure 3. (color online)
$ q^2 $ -dependencies of$ K_{10} $ with different values of$ C_P $ ($ \ell=\tau\,,\,C_S=0 $ ).
Figure 4. (color online)
$ q^2 $ -dependencies of$ K_{10} $ with different values of$ C_S $ ($ \ell=\tau\,,\,C_P=0 $ ).We find that
$ K_{10} $ is more sensitive to the imaginary part of$ C_S $ . In the region of$ 16\; \text{GeV}^2<q^2<18\; \text{GeV}^2 $ , the interference between (axial)vector and (pseudo)scalar operators can be significantly enhanced. To estimate the experimental results, we consider the integrated$ K_{10} $ related to Figs. 2 to 5 in Table 1. The integrated$ K_i $ is defined as$ \text{Re}(C_S) $ 

$ \text{Re}(C_P) $ 

$ \langle K_{10} \rangle $ 

$ \text{Im}(C_S) $ 

$\text{Im} (C_P) $ 

$ \langle K_{10} \rangle $ 

$ 1 $ 

$ 0 $ 

$ -0.0031(2) $ 

$ 1 $ 

$ 0 $ 

$ 0.0202(10) $ 

$ 2 $ 

$ 0 $ 

$ -0.0062(3) $ 

$ 2 $ 

$ 0 $ 

$ 0.0403(20) $ 

$ 0 $ 

$ 1 $ 

$ 0.0002 $ 

$ 0 $ 

$ 1 $ 

$ -0.0014(1) $ 

$ 0 $ 

$ 2 $ 

$ 0.0004 $ 

$ 0 $ 

$ 2 $ 

$ -0.0027(2) $ 

Table 1. The (psuedo)scalar Wilson coefficients and
$ \langle K_{10}\rangle $ with$ \ell=\tau $ .$ \langle K_i \rangle = \frac{1}{\Gamma} \int^{\kappa'}_{\kappa} \zeta K_i {\rm d} q^2 \,,\; \; \; \Gamma = \int^{\kappa'} _ {\kappa} \zeta ( K_1 + 2 K_2 ) {\rm d} q^2\,. $

(57) where
$ (\kappa,\kappa') = (4 M_\tau ^2, (M_{\Lambda_b} - M_{\Lambda})^2) $ . From the table, we find that the contributions from the imaginary part of$ C_S $ are primary and larger than others by one order of magnitude. If we take$ N_{\Lambda_b}=5\times 10^{12} $ at the LHCb Run3&Run4, a reconstruction efficiency$ \epsilon=10^{-4} $ , and$ \text{Im}(C_S)=1 $ , we have$ \epsilon N_{\Lambda_b}\langle K_{10}\rangle\mathcal{B}{\tau}\approx 20 $ , which can be measured at the LHCb Run3&Run4.To consider the NP contributions in
$ \Lambda_b \to \Lambda(\to p \pi^-) \mu^+ \mu^- $ , we may ignore the contributions from (pseudo)scalar operators, as they are suppressed by the muon mass. From the global fit in the B meson decays [30], the permitted imaginary parts of the NP Wilson coefficients are found in Table 2 with four different scenarios1 . To illustrate this, we calculate$ \langle K_j \rangle $ with$ K_j \in \{ K_9,K_{10},K_{19},K_{30} \} $ and$ (\kappa, \kappa')=(15\; \text{GeV}^2,20\; \text{GeV}^2) $ in different scenarios given in Table 2. We fit$ P_b $ from the experimental$ K_{1-34} $ and find that$ P_b $ is consistent with zero regardless of the presence of NP.Scenarios $\text{Im}(C_9^{\rm NP})$ 

$\text{Im}(C_{10}^{\rm NP})$ 

$ \text{Im}(C_L) $ 

$ \text{Im} (C_R) $ 

$ K_9 $ 

$ K_{10} $ 

$ K_{19} $ 

$ K_{30} $ 

$ P_b $ 

Scenario #1 $ \pm0.73 $ 

0 0 0 Scenario #2 0 $ \pm1.86 $ 

0 0 $ 0 $ 

$ \mp 4 $ 

$ 0 $ 

$ 0 $ 

$ -0.022(72) $ 

Scenario #3 $ \pm 1.66 $ 

$ \mp 1.66 $ 

0 0 $ 0 $ 

$ \pm 3 $ 

$ 0 $ 

$ 0 $ 

$ -0.021(65) $ 

Scenario #4 $ \pm0.77 $ 

0 $ \mp0.77 $ 

$ \mp0.77 $ 

$ \mp 1 $ 

$ \mp 42 $ 

$ \mp 1 $ 

$ 0 $ 

$ -0.019(64) $ 

Table 2. The Wilson coefficients and
$ \langle K_j \rangle $ in units of$ 10^{-3} $ in four NP scenarios.In the absence of relative complex phases in the SM,
$ \langle K_j \rangle $ are found to be less than$ 10^{-4} $ . Therefore, they provide excellent opportunities to test the SM. Although$ K_j $ are proportional to the imaginary parts of the NP Wilson coefficients, which have not yet been determined, their signs remain unknown. However, nonzero values in the experiments would be a smoking gun in NP, regardless of the signs. Scenario #1 affects little in$ \langle K_j \rangle $ , and the results are not listed. We find that$ \langle K_9 \rangle $ is very small in all scenarios, which is consistent with the experiments. Remarkably, the experimental data of$ \langle K_{10} \rangle $ can be explained by Scenario #4. On the other hand,$ K_{19} $ and$ K_{30} $ are highly suppressed by$ P_b $ .Since the CP-conserving phases are absent, the T-odd observables are proportional to the imaginary parts of the Wilson coefficients. Noting that
$ \overline{\alpha} = - \alpha$ , we deduce that$ (K_9,K_{10}, K_{19}, K_{30}) $ in$\overline{\Lambda}_b \to \overline{\Lambda} (\to \overline{p} \pi^+) \ell^+ \ell^- $ are equal to those in$\Lambda_b \to \Lambda(\to p \pi^-) \ell^+ \ell^- $ . Here,$ \overline{\alpha}$ represents the decay asymmetry of$\overline{\Lambda} \to \overline{p} \pi^+ $ . -
We derived the angular distributions of
$ \Lambda_b \to \Lambda(\to p \pi^-) \ell^+ \ell^- $ based on the effective schemes of$\Lambda_b \to \Lambda(\to p \pi^-) j_{\rm eff}^m(\to \ell^+ \ell^-)$ , and the results were found to be consistent with those in the literature. By studying the effective two-body decays of$\Lambda_b \to \Lambda j_{\rm eff}^m$ , we identified the T-odd correlations in the form of$ (\vec{s}_\Lambda \times \vec{s}_m) \cdot \hat{p} $ . We found that$ K_9 $ and$ K_{10} $ are related to$ (\vec{s}_\Lambda \times \vec{s}_m) \cdot \hat{p}_\Lambda $ , and$ K_{10} $ is sensitive to the complex phases generated by NP. For$ \Lambda_b \to \Lambda(\to p \pi^-) \mu^+ \mu^- $ , we found that$ C_R =-0.77 {\rm i} $ can explain the$ K_{10} $ puzzle. We recommend revisiting the experiment, considering$ K_{10} $ for a stringent constraint. In$ \Lambda_b \to \Lambda(\to p \pi^-) \tau^+ \tau^- $ , we focused on the effects of the interference of (pseudo)scalar operators with (axial)vector operators and found that the effects of the (pseudo)scalar operators can be largely enhanced in the high$ q^2 $ region. -
Here, all
$ K_{i} $ are real. They are given by$ \begin{aligned}[b]\\ K^{VA}_1 =& \frac{1}{4} \Big(- \delta_{\ell} a^{A}_+ \overline{a^{A}_+} - \delta_{\ell} a^{A}_- \overline{a^{A}_-} + \frac{\delta_{\ell} b^{V}_+ \overline{b^{V}_+}}{2} - \frac{\delta_{\ell} b^{A}_+ \overline{b^{A}_+}}{2} + \frac{\delta_{\ell} b^{V}_- \overline{b^{V}_-}}{2} - \frac{\delta_{\ell} b^{A}_- \overline{b^{A}_-}}{2} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} \\&+ \delta_{\ell} c^{A}_- \overline{c^{A}_-} + a^{V}_+ \overline{a^{V}_+} + a^{A}_+ \overline{a^{A}_+} + a^{V}_- \overline{a^{V}_-} + a^{A}_- \overline{a^{A}_-} + \frac{b^{V}_+ \overline{b^{V}_+}}{2} + \frac{b^{A}_+ \overline{b^{A}_+}}{2} + \frac{b^{V}_- \overline{b^{V}_-}}{2} + \frac{b^{A}_- \overline{b^{A}_-}}{2} \Big),\\ K^{VA}_2 = & \frac{1}{4} \Big(\delta_{\ell} a^{V}_+ \overline{a^{V}_+} + \delta_{\ell} a^{V}_- \overline{a^{V}_-} - \delta_{\ell} b^{A}_+ \overline{b^{A}_+} - \delta_{\ell} b^{A}_- \overline{b^{A}_-} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} + \delta_{\ell} c^{A}_- \overline{c^{A}_-} + b^{V}_+ \overline{b^{V}_+} + b^{A}_+ \overline{b^{A}_+} + b^{V}_- \overline{b^{V}_-} + b^{A}_- \overline{b^{A}_-} \Big),\\ K^{VA}_3 =& - \frac{K^{VA}_{16}}{P_b} =\frac{ \sqrt{1 - \delta_{\ell}}}{4} \Big(b^{V}_+ \overline{b^{A}_+} + b^{A}_+ \overline{b^{V}_+} - b^{V}_- \overline{b^{A}_-} - b^{A}_- \overline{b^{V}_-} \Big)\\ K^{VA}_4 =& \frac{1}{4}\alpha \Big(- \delta_{\ell} a^{A}_+ \overline{a^{A}_+} + \delta_{\ell} a^{A}_- \overline{a^{A}_-} - \frac{\delta_{\ell} b^{V}_+ \overline{b^{V}_+}}{2} + \frac{\delta_{\ell} b^{A}_+ \overline{b^{A}_+}}{2} + \frac{\delta_{\ell} b^{V}_- \overline{b^{V}_-}}{2} - \frac{\delta_{\ell} b^{A}_- \overline{b^{A}_-}}{2} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} \\&- \delta_{\ell} c^{A}_- \overline{c^{A}_-} + a^{V}_+ \overline{a^{V}_+} + a^{A}_+ \overline{a^{A}_+} - a^{V}_- \overline{a^{V}_-} - a^{A}_- \overline{a^{A}_-} - \frac{b^{V}_+ \overline{b^{V}_+}}{2} - \frac{b^{A}_+ \overline{b^{A}_+}}{2} + \frac{b^{V}_- \overline{b^{V}_-}}{2} + \frac{b^{A}_- \overline{b^{A}_-}}{2} \Big),\\ K^{VA}_5 =& \frac{1}{4}\alpha \Big(\delta_{\ell} a^{V}_+ \overline{a^{V}_+} - \delta_{\ell} a^{V}_- \overline{a^{V}_-} + \delta_{\ell} b^{A}_+ \overline{b^{A}_+} - \delta_{\ell} b^{A}_- \overline{b^{A}_-} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} - \delta_{\ell} c^{A}_- \overline{c^{A}_-} - b^{V}_+ \overline{b^{V}_+} - b^{A}_+ \overline{b^{A}_+} + b^{V}_- \overline{b^{V}_-} + b^{A}_- \overline{b^{A}_-}\Big),\\ K^{VA}_6 =& -\frac{K^{VA}_{13}}{P_b} =\frac{\alpha\sqrt{1 - \delta_{\ell}}}{4} \Big(- b^{V}_+ \overline{b^{A}_+} - b^{A}_+ \overline{b^{V}_+} - b^{V}_- \overline{b^{A}_-} - b^{A}_- \overline{b^{V}_-} \Big), \\ K^{VA}_7 - i K^{VA}_9 =& \frac{\sqrt{2}\alpha\left(1 - \delta_{\ell}\right)}{4} \Big( a^{V}_- \overline{b^{V}_-} + a^{A}_- \overline{b^{A}_-} - b^{V}_+ \overline{a^{V}_+} - b^{A}_+ \overline{a^{A}_+}\Big),\\ K^{VA}_8 - i K^{VA}_{10} = &- \frac{\sqrt{2}\alpha\sqrt{1 - \delta_{\ell}}}{4} \Big( a^{V}_- \overline{b^{A}_-} + a^{A}_- \overline{b^{V}_-} + b^{V}_+ \overline{a^{A}_+} + b^{A}_+ \overline{a^{V}_+} \Big),\\ K^{VA}_{11} = & \frac{P_b}{4} \Big(- \delta_{\ell} a^{A}_+ \overline{a^{A}_+} + \delta_{\ell} a^{A}_- \overline{a^{A}_-} + \frac{\delta_{\ell} b^{V}_+ \overline{b^{V}_+}}{2} - \frac{\delta_{\ell} b^{A}_+ \overline{b^{A}_+}}{2} - \frac{\delta_{\ell} b^{V}_- \overline{b^{V}_-}}{2} + \frac{\delta_{\ell} b^{A}_- \overline{b^{A}_-}}{2} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} \\&- \delta_{\ell} c^{A}_- \overline{c^{A}_-} + a^{V}_+ \overline{a^{V}_+} + a^{A}_+ \overline{a^{A}_+} - a^{V}_- \overline{a^{V}_-} - a^{A}_- \overline{a^{A}_-} + \frac{b^{V}_+ \overline{b^{V}_+}}{2} + \frac{b^{A}_+ \overline{b^{A}_+}}{2} - \frac{b^{V}_- \overline{b^{V}_-}}{2} - \frac{b^{A}_- \overline{b^{A}_-}}{2} \Big),\\ K^{VA}_{12} =&\frac{P_b}{4} \Big(\delta_{\ell} a^{V}_+ \overline{a^{V}_+} - \delta_{\ell} a^{V}_- \overline{a^{V}_-} - \delta_{\ell} b^{A}_+ \overline{b^{A}_+} + \delta_{\ell} b^{A}_- \overline{b^{A}_-} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} - \delta_{\ell} c^{A}_- \overline{c^{A}_-} + b^{V}_+ \overline{b^{V}_+} + b^{A}_+ \overline{b^{A}_+} - b^{V}_- \overline{b^{V}_-} - b^{A}_- \overline{b^{A}_-} \Big),\\ \end{aligned}\tag{A1} $ 
$ \begin{aligned}[b] K^{VA}_{14} = & \frac{P_b}{4}\alpha \Big(- \delta_{\ell} a^{A}_+ \overline{a^{A}_+} - \delta_{\ell} a^{A}_- \overline{a^{A}_-} - \frac{\delta_{\ell} b^{V}_+ \overline{b^{V}_+}}{2} + \frac{\delta_{\ell} b^{A}_+ \overline{b^{A}_+}}{2}- \frac{\delta_{\ell} b^{V}_- \overline{b^{V}_-}}{2} + \frac{\delta_{\ell} b^{A}_- \overline{b^{A}_-}}{2}+ \delta_{\ell} c^{A}_+ \overline{c^{A}_+} \\&+ \delta_{\ell} c^{A}_- \overline{c^{A}_-} + a^{V}_+ \overline{a^{V}_+} + a^{A}_+ \overline{a^{A}_+} + a^{V}_- \overline{a^{V}_-} + a^{A}_- \overline{a^{A}_-} - \frac{b^{V}_+ \overline{b^{V}_+}}{2} - \frac{b^{A}_+ \overline{b^{A}_+}}{2} - \frac{b^{V}_- \overline{b^{V}_-}}{2} - \frac{b^{A}_- \overline{b^{A}_-}}{2} \Big),\\ K^{VA}_{15} =& \frac{P_b}{4}\alpha \Big(\delta_{\ell} a^{V}_+ \ \overline{a^{V}_+} + \delta_{\ell} a^{V}_- \overline{a^{V}_-} + \delta_{\ell} b^{A}_+ \overline{b^{A}_+} + \delta_{\ell} b^{A}_- \overline{b^{A}_-} + \delta_{\ell} c^{A}_+ \overline{c^{A}_+} \\&+ \delta_{\ell} c^{A}_- \overline{c^{A}_-} - b^{V}_+ \overline{b^{V}_+} - b^{A}_+ \overline{b^{A}_+} - b^{V}_- \overline{b^{V}_-} - b^{A}_- \overline{b^{A}_-}\Big),\\ K^{VA}_{17} - {\rm i} K^{VA}_{19} =& -\frac{\sqrt{2}P_b\alpha\left(1 - \delta_{\ell}\right)}{4} \Big( a^{V}_- \overline{b^{V}_-} + a^{A}_- \overline{b^{A}_-} + b^{V}_+ \overline{a^{V}_+} + b^{A}_+ \overline{a^{A}_+}\Big),\\ K^{VA}_{18} - {\rm i} K^{VA}_{20} =& -\frac{\sqrt{2}P_b\alpha\sqrt{1 - \delta_{\ell}}}{4} \Big(- a^{V}_- \overline{b^{A}_-} - a^{A}_- \overline{b^{V}_-} + b^{V}_+ \overline{a^{A}_+} + b^{A}_+ \overline{a^{V}_+}\Big),\\ K^{VA}_{23} - {\rm i} K^{VA}_{21} =& \frac{P_b\sqrt{2}(1-\delta_{\ell})}{4} \Big( b^{V}_+ \overline{a^{V}_-} - a^{V}_+ \overline{b^{V}_-} - a^{A}_+ \overline{b^{A}_-} + b^{A}_+ \overline{a^{A}_-} \Big),\\ K^{VA}_{24} - {\rm i} K^{VA}_{22} = & -\frac{P_b\sqrt{2}\sqrt{(1-\delta_{\ell})}}{4} \Big( a^{V}_+ \overline{b^{A}_-} + a^{A}_+ \overline{b^{V}_-} + b^{V}_+\overline{a^{A}_-} + b^{A}_+ \overline{a^{V}_-}\Big),\\ K^{VA}_{27} - {\rm i} K^{VA}_{25} =& -\frac{P_b\alpha\sqrt{2}(1-\delta_{\ell})}{4} \Big( - a^{V}_+ \overline{b^{V}_-} - a^{A}_+ \overline{b^{A}_-} - b^{V}_+ \overline{a^{V}_-} - b^{A}_+ \overline{a^{A}_-}\Big),\\ K^{VA}_{28} - {\rm i} K^{VA}_{26} =& -\frac{P_b\alpha\sqrt{2}\sqrt{(1-\delta_{\ell})}}{4} \Big(a^{V}_+ \overline{b^{A}_-} + a^{A}_+ \overline{b^{V}_-} - b^{V}_+ \overline{a^{A}_-} - b^{A}_+\overline{a^{V}_-}\Big),\\ K^{VA}_{31} - {\rm i} K^{VA}_{29} = & - \frac{P_b\alpha\delta_{\ell}}{2} \Big( a^{V}_- \overline{a^{V}_+} +c^{A}_- \overline{c^{A}_+}\Big),\\ K^{VA}_{32} - {\rm i} K^{VA}_{30} =& -\frac{P_b\alpha}{2} \Big( - a^{V}_- \overline{a^{V}_+} - a^{A}_- \overline{a^{A}_+} \Big) +\delta_{\ell} \Big(a^{A}_- \overline{a^{A}_+} -c^{A}_- \overline{c^{A}_+}\Big),\\ K^{VA}_{33} - {\rm i} K^{VA}_{34} = & \frac{P_b\alpha}{4} b^{V}_+ \overline{b^{V}_-}.\\ \end{aligned}\tag{A2} $

-
For real
$ K_{i} $ , we have$ \begin{aligned}[b] K^{SP}_1 =& \sqrt{2q^2} M_{\ell}\big(\sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{A}_+ \overline{c^{P}_+}}{2} - \frac{ \alpha c^{A}_+ \overline{c^{P}_+}}{2} - \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{A}_- \overline{c^{S}_-}}{2} + \frac{ \alpha c^{A}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{P}_+ \overline{c^{A}_+}}{2} \\& - \frac{ \alpha c^{P}_+ \overline{c^{A}_+}}{2}- \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{S}_- \overline{c^{A}_-}}{2} + \frac{\alpha c^{S}_- \overline{c^{A}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{A}_+ \overline{c^{P}_+}}{2} + \frac{3 c^{A}_+ \overline{c^{P}_+}}{2} - \sqrt{1 - \delta_{\ell}}\frac{ c^{A}_- \overline{c^{S}_-}}{2} \\& + 2 c^{A}_- \overline{c^{P}_-} + \frac{ c^{A}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}} \frac{ c^{P}_+ \overline{c^{A}_+}}{2} + \frac{3 c^{P}_+ \overline{c^{A}_+}}{2} + 2 c^{P}_- \overline{c^{A}_-} - \sqrt{1 - \delta_{\ell}} \frac{ c^{S}_- \overline{c^{A}_-}}{2} + \frac{ c^{S}_- \overline{c^{A}_-}}{2} \big) + \mathcal{O}(C_{S,P}^2) \end{aligned}\tag{B1} $

$ \begin{aligned}[b] K^{SP}_2 =& \sqrt{2q^2} M_{\ell}\big(\sqrt{1 - \delta_{\ell}}\frac{ c^{A}_+ \overline{c^{P}_+}}{2} + \frac{3 c^{A}_+ \overline{c^{P}_+}}{2} - \sqrt{1 - \delta_{\ell}}\frac{ c^{A}_- \overline{c^{S}_-}}{2} + 2 c^{A}_- \overline{c^{P}_-} + \frac{ c^{A}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{P}_+ \overline{c^{A}_+}}{2} \\& + \frac{3 c^{P}_+ \overline{c^{A}_+}}{2} + 2 c^{P}_- \overline{c^{A}_-} - \sqrt{1 - \delta_{\ell}}\frac{ c^{S}_- \overline{c^{A}_-}}{2} + \frac{ c^{S}_- \overline{c^{A}_-}}{2} \big) + \mathcal{O}(C_{S,P}^2) \end{aligned}\tag{B2} $

$ \begin{aligned}[b] K^{SP}_3 =& \sqrt{2q^2} M_{\ell} \big(\sqrt{1 - \delta_{\ell}}\frac{ \alpha a^{V}_+ \overline{c^{P}_+}}{2} - \frac{ \alpha a^{V}_+ \overline{c^{P}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ a^{V}_+ \overline{c^{P}_+}}{2} + 2 \sqrt{1 - \delta_{\ell}} a^{V}_+ \overline{c^{S}_+} - \frac{ a^{V}_+ \overline{c^{P}_+}}{2} \\&- \sqrt{1 - \delta_{\ell}}\frac{ \alpha a^{V}_- \overline{c^{S}_-}}{2} + \frac{ \alpha a^{V}_- \overline{c^{S}_-}}{2} +\sqrt{1 - \delta_{\ell}} \frac{3 a^{V}_- \overline{c^{S}_-}}{2} + \frac{ a^{V}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{P}_+ \overline{a^{V}_+}}{2} - \frac{ \alpha c^{P}_+ \overline{a^{V}_+}}{2} \\& - \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{S}_- \overline{a^{V}_-}}{2} + \frac{ \alpha c^{S}_- \overline{a^{V}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{P}_+ \overline{a^{V}_+}}{2} - \frac{ c^{P}_+ \overline{a^{V}_+}}{2} + 2 \sqrt{1 - \delta_{\ell}} c^{S}_+ \overline{a^{V}_+} + \sqrt{1 - \delta_{\ell}}\frac{3 c^{S}_- \overline{a^{V}_-}}{2} + \frac{ c^{S}_- \overline{a^{V}_-}}{2} \big) \end{aligned}\tag{B3} $

$ \begin{aligned}[b] K^{SP}_4 = K^{SP}_5 =& \sqrt{2q^2} M_{\ell}\alpha \big( \sqrt{1 - \delta_{\ell}} c^{A}_+ \overline{c^{P}_+} + c^{A}_+ \overline{c^{P}_+} + \sqrt{1 - \delta_{\ell}} c^{A}_- \overline{c^{S}_-} - 2 c^{A}_- \overline{c^{P}_-} - c^{A}_- \overline{c^{S}_-}\\&+ \sqrt{1 - \delta_{\ell}} c^{P}_+ \overline{c^{A}_+} + c^{P}_+ \overline{c^{A}_+} - 2 c^{P}_- \overline{c^{A}_-} + \sqrt{1 - \delta_{\ell}} c^{S}_- \overline{c^{A}_-} - c^{S}_- \overline{c^{A}_-} \big) + \mathcal{O}(C_{S,P}^2) \end{aligned}\tag{B4} $

$ \begin{aligned}[b] K^{SP}_6 =& \sqrt{2q^2} M_{\ell} \alpha \big[ (\sqrt{1 - \delta_{\ell}}-1)a^{V}_+ \overline{c^{P}_+} + 2 \sqrt{1 - \delta_{\ell}} a^{V}_+ \overline{c^{S}_+} - (\sqrt{1 - \delta_{\ell}}+1) a^{V}_- \overline{c^{S}_-} \\ & + (\sqrt{1 - \delta_{\ell}}-1) c^{P}_+ \overline{a^{V}_+} + 2 \sqrt{1 - \delta_{\ell}} c^{S}_+ \overline{a^{V}_+} - (\sqrt{1 - \delta_{\ell}}+1) c^{S}_- \overline{a^{V}_-} \big] \end{aligned}\tag{B5} $

$ \begin{aligned}[b] K^{SP}_7 =& K^{SP}_9=0 \\ K^{SP}_8 - {\rm i} K^{SP}_{10} =& \alpha M_{\ell} \sqrt{q^2} \left[ (\sqrt{1 - \delta_{\ell}}-1) (b^{V}_+ \overline{c^{P}_+} )+ 2 \sqrt{1 - \delta_{\ell}} (b^{V}_+ \overline{c^{S}_+}) - (\sqrt{1 - \delta_{\ell}}+1) (c^{S}_- \overline{b^{V}_-} ) \right] \\ K^{SP}_{11} =&\sqrt{2q^2} M_{\ell} (\sqrt{1 - \delta_{\ell}} \frac{ \alpha c^{A}_+ \overline{c^{P}_+}}{2} - \frac{ \alpha c^{A}_+ \overline{c^{P}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{A}_- \overline{c^{S}_-}}{2} - \frac{ \alpha c^{A}_- \overline{c^{S}_-}}{2} +\sqrt{1 - \delta_{\ell}} \frac{ \alpha c^{P}_+ \overline{c^{A}_+}}{2} \\ &- \frac{ \alpha c^{P}_+ \overline{c^{A}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{S}_- \overline{c^{A}_-}}{2} - \frac{ \alpha c^{S}_- \overline{c^{A}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{A}_+ \overline{c^{P}_+}}{2} + \frac{3 c^{A}_+ \overline{c^{P}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{A}_- \overline{c^{S}_-}}{2} \\ &- 2 c^{A}_- \overline{c^{P}_-} - \frac{ c^{A}_- \overline{c^{S}_-}}{2} + \frac{ c^{P}_+ \sqrt{1 - \delta_{\ell}} \overline{c^{A}_+}}{2} + \frac{3 c^{P}_+ \overline{c^{A}_+}}{2} - 2 c^{P}_- \overline{c^{A}_-} + \sqrt{1 - \delta_{\ell}}\frac{ c^{S}_- \overline{c^{A}_-}}{2} - \frac{ c^{S}_- \overline{c^{A}_-}}{2}) + \mathcal{O}(C_{S,P}^2) \end{aligned}\tag{B6} $

$ \begin{aligned}[b] K^{SP}_{12} =& \sqrt{2q^2} M_{\ell} ( \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{A}_+ \overline{c^{P}_+}}{2} - \frac{ \alpha c^{A}_+ \overline{c^{P}_+}}{2} + \sqrt{1 - \delta_{\ell}} \frac{ \alpha c^{A}_- \overline{c^{S}_-}}{2} - \frac{ \alpha c^{A}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{P}_+ \overline{c^{A}_+}}{2} \\ & - \frac{ \alpha c^{P}_+ \overline{c^{A}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ \alpha c^{S}_- \overline{c^{A}_-}}{2} - \frac{ \alpha c^{S}_- \overline{c^{A}_-}}{2} + \sqrt{1 - \delta_{\ell}} \frac{ c^{A}_+ \overline{c^{P}_+}}{2} + \frac{3 c^{A}_+ \overline{c^{P}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{A}_- \overline{c^{S}_-}}{2} \\ &- 2 c^{A}_- \overline{c^{P}_-} - \frac{ c^{A}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{P}_+ \overline{c^{A}_+}}{2} + \frac{3 c^{P}_+ \overline{c^{A}_+}}{2} - 2 c^{P}_- \overline{c^{A}_-} + \sqrt{1 - \delta_{\ell}}\frac{ c^{S}_- \overline{c^{A}_-}}{2} - \frac{ c^{S}_- \overline{c^{A}_-}}{2}) + \mathcal{O}(C_{S,P}^2) \end{aligned}\tag{B7} $

$ \begin{aligned}[b] K^{SP}_{13} =& \sqrt{2q^2} M_{\ell}(\sqrt{1 - \delta_{\ell}}\frac{ a^{V}_+ \alpha \overline{c^{P}_+}}{2} - \frac{ a^{V}_+ \alpha \overline{c^{P}_+}}{2} + \sqrt{1 - \delta_{\ell}} \frac{ a^{V}_+ \overline{c^{P}_+}}{2} + 2\sqrt{1 - \delta_{\ell}} a^{V}_+ \overline{c^{S}_+} - \frac{ a^{V}_+ \overline{c^{P}_+}}{2} \\ &+ \sqrt{1 - \delta_{\ell}}\frac{ a^{V}_- \alpha \overline{c^{S}_-}}{2} - \frac{ a^{V}_- \alpha \overline{c^{S}_-}}{2} - \sqrt{1 - \delta_{\ell}} \frac{3 a^{V}_- \overline{c^{S}_-}}{2} - \frac{ a^{V}_- \overline{c^{S}_-}}{2} + \sqrt{1 - \delta_{\ell}} \frac{ \alpha c^{P}_+ \overline{a^{V}_+}}{2} - \frac{ \alpha c^{P}_+ \overline{a^{V}_+}}{2} \\ &+ \sqrt{1 - \delta_{\ell}} \frac{ \alpha c^{S}_- \overline{a^{V}_-}}{2} - \frac{ \alpha c^{S}_- \overline{a^{V}_-}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{P}_+ \overline{a^{V}_+}}{2} - \frac{ c^{P}_+ \overline{a^{V}_+}}{2} + 2 \sqrt{1 - \delta_{\ell}} c^{S}_+ \overline{a^{V}_+} - \sqrt{1 - \delta_{\ell}}\frac{3 c^{S}_- \overline{a^{V}_-}}{2}- \frac{ c^{S}_- \overline{a^{V}_-}}{2}) \end{aligned}\tag{B8} $

$ \begin{aligned}[b] K^{SP}_{14} =& K^{SP}_{15} = \sqrt{2q^2} M_{\ell}( \sqrt{1 - \delta_{\ell}}c^{A}_+ \overline{c^{P}_+} + c^{A}_+ \overline{c^{P}_+} - \sqrt{1 - \delta_{\ell}} c^{A}_- \overline{c^{S}_-} + 2 c^{A}_- \overline{c^{P}_-} + c^{A}_- \overline{c^{S}_-} \\ &+ \sqrt{1 - \delta_{\ell}} c^{P}_+ \overline{c^{A}_+} + c^{P}_+ \overline{c^{A}_+} + 2 c^{P}_- \overline{c^{A}_-} - \sqrt{1 - \delta_{\ell}} c^{S}_- \overline{c^{A}_-} + c^{S}_- \overline{c^{A}_-} )+ \mathcal{O}(C_{S,P}^2) \end{aligned} \tag{B9}$

$ \begin{aligned}[b] K^{SP}_{16} =& \sqrt{2q^2} M_{\ell}( \sqrt{1 - \delta_{\ell}}\frac{ a^{V}_+ \overline{c^{P}_+}}{4} + \sqrt{1 - \delta_{\ell}} \frac{ a^{V}_+ \overline{c^{S}_+}}{2} - \frac{ a^{V}_+ \overline{c^{P}_+}}{4} + \sqrt{1 - \delta_{\ell}} \frac{ a^{V}_- \overline{c^{S}_-}}{4} + \frac{ a^{V}_- \overline{c^{S}_-}}{4} \\ & + \sqrt{1 - \delta_{\ell}}\frac{ c^{P}_+ \overline{a^{V}_+}}{4} - \frac{ c^{P}_+ \overline{a^{V}_+}}{4} + \sqrt{1 - \delta_{\ell}}\frac{ c^{S}_+ \overline{a^{V}_+}}{2} + \sqrt{1 - \delta_{\ell}}\frac{ c^{S}_- \overline{a^{V}_-}}{4} + \frac{ c^{S}_- \overline{a^{V}_-}}{4})+ \mathcal{O}(C_{S,P}^2) \end{aligned}\tag{B10} $

$ K^{SP}_{17} = K^{SP}_{19} = 0 \tag{B11}$

$ K^{SP}_{18} - {\rm i} K^{SP}_{20} = M_{\ell} \sqrt{q^2}(2 \sqrt{1 - \delta_{\ell}} b^{V}_+ \overline{c^{P}_+} + 4 \sqrt{1 - \delta_{\ell}} b^{V}_+ \overline{c^{S}_+} - 2 b^{V}_+ \overline{c^{P}_+} + 2 \sqrt{1 - \delta_{\ell}} c^{S}_- \overline{b^{V}_-} + 2 c^{S}_- \overline{b^{V}_-})\tag{B12} $

$ K^{SP}_{23} = K^{SP}_{21} = 0 \tag{B13} $

$ \begin{aligned}[b] K^{SP}_{24} - {\rm i} K^{SP}_{22} =& - M_{\ell} \sqrt{q^2}( \sqrt{1 - \delta_{\ell}} \alpha b^{V}_+ \overline{c^{S}_-} - \alpha b^{V}_+ \overline{c^{S}_-} + \sqrt{1 - \delta_{\ell}} \alpha c^{P}_+ \overline{b^{V}_-} - \alpha c^{P}_+ \overline{b^{V}_-} \\ & - 3 \sqrt{1 - \delta_{\ell}} b^{V}_+ \overline{c^{S}_-} - b^{V}_+ \overline{c^{S}_-} + \sqrt{1 - \delta_{\ell}} c^{P}_+ \overline{b^{V}_-} - c^{P}_+ \overline{b^{V}_-} + 4 \sqrt{1 - \delta_{\ell}} c^{S}_+ \overline{b^{V}_-}) \end{aligned}\tag{B14} $

$ K^{SP}_{25} = K^{SP}_{27} = 0 \tag{B15} $

$ K^{SP}_{28} - {\rm i} K^{SP}_{26} = -2 M_{\ell} \sqrt{q^2} ( \sqrt{1 - \delta_{\ell}}b^{V}_+ \overline{c^{S}_-} + b^{V}_+ \overline{c^{S}_-} + \sqrt{1 - \delta_{\ell}} c^{P}_+ \overline{b^{V}_-} - c^{P}_+ \overline{b^{V}_-} + 2 \sqrt{1 - \delta_{\ell}} c^{S}_+ \overline{b^{V}_-}) \tag{B16} $

$ K^{SP}_{31} - {\rm i} K^{SP}_{29} = K^{SP}_{32} - {\rm i} K^{SP}_{30} = \sqrt{2q^2} M_{\ell} (- c^{A}_- \sqrt{1 - \delta_{\ell}} \overline{c^{P}_+} - c^{A}_- \overline{c^{P}_+} - 2 c^{P}_- \overline{c^{A}_+} + c^{S}_- \sqrt{1 - \delta_{\ell}} \overline{c^{A}_+} - c^{S}_- \overline{c^{A}_+}) + \mathcal{O}(C_{S,P}^2) \tag{B17} $

$ K^{SP}_{33} = K^{SP}_{34} = 0 \tag{B18}$

-
In this study, we estimate the form factors using the homogeneous bag model (HBM), where the calculation details are given in Ref. [38]. The bag parameters adopted in this work are given as
$ \begin{aligned}[b]& (m_s\,,m_b) = (0.28,4.8)\; \text{GeV} \,,\\& 0.313\; \text{GeV}< E_{u,d}< 0.368\; \text{GeV}\,, \end{aligned}\tag{C1} $

where
$ R=4.8\; \text{GeV}^{-1} $ is the bag radius, and$ E_{q} $ is the quark energy. Recently, α has been updated by BESIII [39, 40] with remarkable precision. We take$ \alpha =0.732\pm0.014 $ ,$ M_{\Lambda_b} = 5.6196 $ GeV, and the$ \Lambda_b $ lifetime of$ \tau_b=1.471\times 10^{-12} $ s from the particle data group [41]. The main uncertainties of the HBM model are attributed to$ E_q $ affecting the form factors largely at the low$ q^2 $ region.The total branching fractions obtained by integrating
$ \vec{\Omega} $ and$ q^2 $ in Eq. (53) are given as$ {\cal B}_\ell = {\cal B}(\Lambda_b \to \Lambda \ell^+\ell^-) = \tau_b \int^{M_-^2} _ {4 m_\ell^2} \zeta ( K_1 + 2 K_2 ) {\rm d}q^2\,. \tag{C2} $

Their computed values and the ones in the literature within the SM are listed in Table C1. In the literature, Refs. [26, 42] consider the covariant quark model (CQM), Refs. [43−45], the light-cone QCD sum rules (LCSR), Ref. [35], the relativistic quark model (RQM), and Ref. [46], the Bethe-Salpeter equation (BSE). Our results of
$ {\cal B}_\ell $ agree with the results of the CQM and RQM as well as current experimental data but are systematically smaller than the results obtained from LCSR. Notably, we find that$ {\cal B}_e>{\cal B}_\mu $ is consistent with Refs. [35] and [43]. Nevertheless, the tendency has not been found in the BSE and CQM. Explicitly, we obtain that$ {\cal B}_e/{\cal B}_\mu = $ 1.15 with a little uncertainty due to the correlations. Future experiments on$ {\cal B}_e/{\cal B}_\mu $ may distinguish between the approaches.HBM CQM[26] LCSR[43] LCSR [44] BSE[46] CQM[42] LCSR[45] RQM[35] Exp[41] $ {\cal B}_e $ 

0.91(25) 1.0 4.6(1.6) $ 0.660\sim1.208 $ 

$ 2.03(^{26}_{9}) $ 

1.07 1.08(28) $ {\cal B}_\mu $ 

0.79(18) 1.0 4.0(1.2) $ 6.1(^{5.8}_{1.7}) $ 

$ 0.812\sim1.445 $ 

0.70 1.05 $ {\cal B}_\tau $ 

0.21(2) 0.2 0.8(3) $ 2.1(^{2.3}_{0.6}) $ 

$ 0.252\sim0.392 $ 

0.22 0.26 Table C1.
$ {\cal B}_\ell $ in units of$ 10^{-6} $ .The integrated hadron (lepton) forward-backward asymmetry of
$ A_{FB}^h\; (A_{FB}^\ell) $ is related to$ \langle K_i \rangle $ via$ A_{FB}^h = \langle K_4 \rangle + \frac{1}{2} \langle K_5 \rangle \,,\; \; \; A_{FB}^\ell = \frac{3}{2} \langle K_3 \rangle \,, \tag{C3} $

while
$ A_{FB}^{\ell h} = \frac{3}{4} \langle K_6 \rangle \,,\; \; \; F_L = 2 \langle K_1 \rangle - \langle K_2 \rangle \,, \tag{C4}$

are the combined forward-backward asymmetry and longitudinal polarized fraction, respectively. The average decay branching fraction is defined as
$ \left \langle \frac{ \partial {\cal B}}{\partial q^2} \right \rangle \equiv \frac{\tau_b}{\kappa' - \kappa} \Gamma_\kappa\,. \tag{C5} $

Notice that the
$ q^2 $ region of$ [\kappa,\kappa'] =[8,11] $ and$ [12.5,15] $ in units of GeV$ ^2 $ are contaminated largely by the charmonium resonance and are not considered.The computed results within the HBM are given in Table C2, along with those from the literature and the experimental data [18, 19]. The computed values of
$ A_{FB}^{h,\ell,h\ell} $ and$ F_L $ have little uncertainties as$ K_i $ are correlated in the model calculations. In the literature, Ref. [47] employs the lattice QCD, and Ref. [35] includes the contributions from the charmonium resonances. We see that the angular observables in the literature and this study are basically consistent. Our results of$ \langle A^h_{FB}\rangle $ and$ \langle A^{\ell h}_{FB}\rangle $ are slightly larger than the others owing to the updated α2 . Notably, the experimental values of$ A_{FB}^{\ell h} $ are nearly twice larger than the theoretical predictions.$ [\kappa,\kappa'] $ 

HBM RQM [35] lattice [47] LHCb [18, 19] $ \left \langle\dfrac{\partial{\cal B}}{\partial q^2} \right \rangle $ 

$ [0.1,2] $ 

0.25(11) 0.34 0.25(23) $ 0.36(^{14}_{13}) $ 

$ [2, 4] $ 

0.16(7) 0.31 0.18(12) $ 0.11(^{12}_9) $ 

$ [4, 6] $ 

0.20(8) 0.40 0.23(11) $ 0.02(^9_1) $ 

$ [6, 8] $ 

0.26(9) 0.57 0.307(94) $ 0.25(^{13}_{12}) $ 

$ [11,12.5] $ 

0.44(11) 0.65 0.75(21) $ [15, 16] $ 

0.61(10) 0.72 0.796(75) 1.12(30) $ [16, 18] $ 

0.65(8) 0.68 0.827(76) 1.22(29) $ [1.1,6] $ 

0.18(7) 0.34 0.20(12) $ 0.09(^6_5) $ 

$ [15, 20] $ 

0.60(6) 0.61 0.756(70) $ 1.20(^{26}_{27}) $ 

$ A_{FB}^\ell $ 

$ [0.1,2] $ 

0.076(0) 0.067 0.095(15) $ 0.37(^{37}_{48}) $ 

$ [11,12.5] $ 

$ -0.357(6) $ 

$ -0.35 $ 

$ 0.01(^{20}_{19}) $ 

$ [15, 16] $ 

$ -0.403(8) $ 

$ -0.41 $ 

$ -0.374(14) $ 

$ -0.10(^{18}_{16}) $ 

$ [16, 18] $ 

$ -0.396(9) $ 

$ -0.36 $ 

$ -0.372(13) $ 

$ -0.07(^{14}_{13}) $ 

$ [18, 20] $ 

$ -0.320(9) $ 

$ -0.32 $ 

$ -0.309(15) $ 

$ 0.01(^{16}_{15}) $ 

$ [15, 20] $ 

$ -0.369(7) $ 

$ -0.33 $ 

$ -0.350(13) $ 

$ -0.39(4) $ 

$ A_{FB}^h $ 

$ [0.1,2] $ 

$ -0.294(2) $ 

$ -0.26 $ 

$ -0.310(18) $ 

$ -0.12(^{34}_{32}) $ 

$ [11,12.5] $ 

$ -0.408(2) $ 

$ -0.30 $ 

$ -0.50(^{11}_{4}) $ 

$ [15, 16] $ 

$ -0.384(4) $ 

$ -0.32 $ 

$ -0.3069(83) $ 

$ -0.19(^{14}_{16}) $ 

$ [16, 18] $ 

$ -0.358(6) $ 

$ -0.31 $ 

$ -0.2891(90) $ 

$ -0.44(^{10}_{6}) $ 

$ [18, 20] $ 

$ -0.275(6) $ 

$ -0.25 $ 

$ -0.227(10) $ 

$ -0.13(^{10}_{12}) $ 

$ [15, 20] $ 

$ -0.333(4) $ 

$ -0.29 $ 

$ -0.2710(92) $ 

$ -0.30(5) $ 

$ A_{FB}^{h\ell} $ 

$ [0.1,2] $ 

$ -0.028(0) $ 

$ -0.021 $ 

$ -0.0302(51) $ 

$ [2, 4] $ 

$ -0.001(1) $ 

0.010 $ -0.0169(99) $ 

$ [4, 6] $ 

0.047(2) 0.045 0.021(13) $ [6, 8] $ 

0.084(1) 0.072 0.053(13) $ [15, 20] $ 

0.179(1) 0.129 0.1398(43) 0.25(4) $ F_L $ 

$ [0.1,2] $ 

0.541(4) 0.66 0.465(84) $ 0.56(^{24}_{56}) $ 

$ [11,12.5] $ 

0.615(0) 0.51 $ 0.40(^{37}_{36}) $ 

$ [15, 16] $ 

0.507(1) 0.41 0.454(20) $ 0.49(30) $ 

$ [16, 18] $ 

0.469(0) 0.38 0.417(15) $ 0.68(^{15}_{21}) $ 

$ [18, 20] $ 

0.416(1) 0.35 0.3706(79) $ 0.62(^{24}_{27}) $ 

Table C2. Decay observables, where
$ \langle \partial {\cal B} / \partial q^2\rangle $ and$ \kappa^{(\prime)} $ are in units of$ 10^{-7} $ GeV$ ^{-2} $ and GeV$ ^2 $ , respectively.Integrating Eq. (54) over
$ \vec{\Omega} $ , we get the differential decay rate as$ \frac{{\rm d}\Gamma}{{\rm d} q^2} = 2K_1+K_2 , \tag{C6} $

we use the differential decay rate to normalize our angular observables. The first ten K observables are accessible even if
$ P_b $ is zero, i.e., the$ \Lambda_b $ baryon is unpolarized, which is the case that most$ \Lambda_b $ baryons produced at the LHC satisfied.The completeness relations read as
$ 1 = \sum\limits_{J,J_z,\lambda_1,\lambda_2} \frac{4\pi }{2 J+1 }| J , J_z, \lambda_1 , \lambda_2 \rangle \langle J , J_z, \lambda_1 , \lambda_2 |\,. \tag{C7} $

Time-reversal asymmetries in $ {\boldsymbol\Lambda_{\boldsymbol b} {\bf\to} {\boldsymbol\Lambda}{\bf (\to}{\boldsymbol p} \boldsymbol\pi^{\bf -}{\bf)}\boldsymbol\ell^{\bf +}\boldsymbol\ell^{\bf -} }$
- Received Date: 2023-10-31
- Available Online: 2024-03-15
Abstract: We study the decays of







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: