-
In the pursuit of the boundaries of the nuclidic chart, the exploration of the heaviest nuclei and their α-decay properties has been a frontier in nuclear physics and even chemistry. Many new elements and isotopes between Z = 114 and Z = 118 have been synthesized through cold-fusion reactions [1−3] with
$ ^{208} $ Pb or$ ^{209} $ Bi targets and hot-fusion reactions [4−6] induced by$ ^{48} $ Ca projectiles over the past decades and appended to the nuclidic chart [7−9]. Meanwhile, various attempts to detect the existence of the heaviest elements have been undertaken in natural objects [10−12]. According to the experimental cross-sections of several observed neutron-rich isotopes with Z ≤ 98, multi-nucleon-transfer reactions [13−15] are regarded as a special method to obtain new neutron-rich heaviest isotopes or elements. However, determining how many protons and neutrons can be held in a single nucleus remains an open question due to short lifetimes and extremely low production cross sections of SHN. Hence, the synthesis and detection of new elements and new isotopes for the nuclei above Z = 118 have been a challenging but attractive subject for researchers.These synthesized heavy and superheavy nuclei are primarily identified by a continuous α-decay chain from unknown nuclei to known nuclei, usually ending in an existing α-decaying or spontaneous-fissioning nucleus. In fact, α decay is one of the most significant tools for studying nuclear structural properties, such as half-lives, stability, spin parity, and nuclear interactions [16−19]. Soon after the observation of α radioactivity, Gamow [20] and Gurney-Condon [21] successfully explained the α-decay phenomenon as quantum tunneling, which is considered to be the first successful quantum description of nuclear phenomenon. Nowadays, the widely accepted consensus is that α decay consists of the preformation of an α particle and the subsequent penetration through the surrounding Coulomb barrier. The treatment of penetration processes can be mainly divided into two types, namely the Wentzel-Kramers-Brillouin (WKB) approximation [18, 22−29] and the direct solution of the Schrödinger equation [30]. The key point during these processes is the choice of the α-core potential. In the current market, numerous models have been used to describe the α-core potential, such as the effective liquid drop model (ELDM) [25], the preformed cluster model (PCM) [26], the modified generalized liquid drop model (MGLDM) [18, 27], the Coulomb and proximity potential model (CPPM) [28], and the double-folding potential model [30]. In previous studies, the
$ Q_{\alpha} $ value, as a crucial input, is adopted from the measurements in the calculation of α-decay half-lives owing to its high sensitivity to the decay width. Once the experimental$ Q_{\alpha} $ value is introduced, the α-core potential will be fixed through the quantization rule [31, 32], not to mention the determination of the classical turning points in the WKB approximation. When it comes to the unknown SHN or the nuclei to be synthesized, the Weizsäcker-Skyrme (WS*4) [33], Hartree-Fock-Bogoliubov (HFB) [34, 35], and other nuclear mass models (see Refs. [36, 37] and references cited therein) have been proposed to predict the$ Q_{\alpha} $ values for the experimental design. Nevertheless, different mass models are found to generate quite different$ Q_{\alpha} $ results for unknown superheavy nuclei. Instead, with the fixed α-core potential, one can obtain the α-decay energies and decay widths in turn through the direct solution of the Schrödinger equation. Following this, several studies [38, 39] have been conducted to locally predict the α-decay properties of the yet unknown nuclei with double-folding potentials, such as the nucleus$ ^{296}118 $ [39].In previous work, the properties of α-cluster structure have been systematically investigated with the nuclear potential of (1 + Gaussian)(W.S. + W.S.
$ ^{3} $ ) shape [40−42]. Then, a natural thought is that the α-core potential (plus the relevant parameters) in α-decay calculations should be identical with the case in the α-cluster structure for the same two-body system. Consequently, the same nuclear potential has been applied here, and a key parameter will be determined via the local systematics in the SHN region, aiming at the new way to predict the α decay quantities of unknown nuclei. More importantly, we propose a new scheme in this study to calculate the α decay width by focusing on the asymptotic region of the α-core relative motion wave function. Besides, the syntheses of new isotopes and new elements like$ Z = 119,120 $ are being implemented or planned in several important laboratories with international collaboration [43−45]. One objective of our present study is to accurately predict the$ Q_{\alpha} $ values and half-lives of SHN with 117 ≤ Z ≤ 120 using a novel method, serving the design of these ongoing and forthcoming experiments.This article is organized as follows: In Sec. II, the calculations of α-decay energies and half-lives are simultaneously given within the cluster model. We present the results and corresponding discussions of superheavy nuclei with 117 ≤ Z ≤ 120 in Sec. III. The conclusions of our work are drawn in the last section.
-
Assuming the α emitter and the residual daughter nucleus as a two-body system, the bound state of the system will transform into a quasi-bound state because the energy level of the nucleus exceeds the threshold value, causing the α-decay intuitively. The radial wave function can be achieved by solving the Schrödinger equation for the α -core relative motion (the relative angular momentum is zero in the ground state), which is given by
$ \left[\frac{-\hbar^{2}}{2\mu}\nabla^{2}+V(r)\right]{u_{nlm}}=Q_\alpha{u_{nlm}}. $

(1) The nuclear potential
$ V_N(r) $ is evidently crucial to the total interaction potential$ V(r) $ . In this study, we chose the slightly modified Woods-Saxon type nuclear potential plus its higher order term (i.e., W.S.+W.S$ ^{3} $ ) as mentioned in Refs. [40−42], which has been used to systematically evaluate the ground-state rotational bands. The specific nuclear potential form can be parameterized as follows:$ \begin{aligned}[b] V_{N}(r) = & -V_{0}\left[1+\lambda \exp \left(-\frac{r^{2}}{\sigma^{2}}\right)\right]\\& \times \left\{\frac{b}{1+\exp [(r-R)/a]} + \frac{1-b}{\big\{1+\exp [(r-R)/3a]\big\}^{3}}\right\}, \end{aligned} $

(2) where R is a free parameter, and a, b, λ, σ, and
$ V_0 $ are completely fixed parameters. Taken from the effective interaction between the emitted α particle and a homogeneously charged sphere of radius R, the repulsive Coulomb potential of the system is$ \begin{array}{*{20}{l}} V_{C}(r) = \left\{ \begin{array}{ll} \dfrac{Z_{d} Z_{\alpha} {\rm e}^{2}}{r}, & r > R_{C},\\ \dfrac{Z_d Z_\alpha {\rm e}^{2}}{2R_C}\left[3-\left(\dfrac{r}{R_C}\right)^{2}\right], & r \leq R_{C}. \\ \end{array} \right. \end{array} $

(3) The Coulomb radius
$ R_{C} $ is taken to be the separation radius R to reduce the number of free parameters. The total interaction potential obtained from the sum of the attractive nuclear potential, the repulsive Coulomb potential, and the additional centrifugal potential, depending on the angular momentum of the emitted nucleus, is written by$ \begin{array}{*{20}{l}} V(r)=V_{N}(r)+V_{C}(r)+\dfrac{\hbar^{2}\ell(\ell+1)}{2\mu r^{2}}, \end{array} $

(4) where μ denotes the reduced mass of the α-nucleus system and
$ \ell $ is the angular momentum carried by the emitted α cluster. Due to the limited data of SHN, the spin parities of parent and daughter nuclei are usually treated as the same value for odd-A and odd-odd isotopes, leading to a zero angular momentum for the α-core relative motion. Consequently, the centrifugal term does not contribute to the total potential in Eq. (4) here. Obviously, as long as the total potential$ V(r) $ is fixed, the wave function$ u_{nlm} $ will be obtained by solving Eq. (1). As for the nuclear potential$ V_N(r) $ in Eq. (2), the fixed parameters are consistent with Ref. [40]. Regardless of the α-cluster structure and α-decay calculations in previous studies, the free parameter R for each nucleus is precisely determined by the experimental$ Q_{\alpha} $ value and the internal nodes, which are restricted by the Wildermuth condition [46],$ G=2N+l=\sum\limits_{i=1}^4(2n_{i}+\ell_{i})=\sum\limits_{i=1}^4g_{i}. $

(5) Here, G is the global quantum number, N is the number of internal nodes in the radial wave function, and l is the relative angular momentum carried by the α particle emitter.
$ n_{i} $ and$ l_{i} $ are the corresponding oscillator quantum numbers of the nucleons composing the α cluster, which are restricted by the Pauli principle. In this way, we take G = 22 for nuclei with neutron number N$ > $ 126, which agrees with previous studies [47−49].Owing to the lack of experimental
$ Q_{\alpha} $ values, the above work cannot be carried out successfully for unknown SHN. On the other hand, owing to the large discrepancies among various mass models, there will be, as mentioned before, obvious uncertainties in their predictions of the$ Q_\alpha $ values. As an alternative, the nuclear potential$ V_{N}(r) $ is fixed here subsequently after the determination of the parameter R with systematic analyses in the local region of SHN. The$ Q_{\alpha} $ values and wave function are then obtained by the direct solution of Eq. (1). Let us note that all the parameters in Eq. (2) are the same as those in previous studies [40]. The only parameter that needs to be determined is radius R. As mentioned in the standard textbook, the nuclear radius is believed to be related to the mass number, namely$R \propto A_{\rm core}^{1/3}$ , which has been well checked in experiments and further extended with more structural ingredients [30, 39, 50−54]. Inspired by this, the radius parameter R is considered to behave similarly in this study. Predictions on α-decay energies and half-lives of SHN can then be made without input from mass models. Specifically, the radius R of SHN is determined using the two following methods:$ \mathbf{Case\; \; I:\; \; based\; \; on\; \; the\; \; decay\; \; chains} $ For example, in a decay chain,
$ ^{A+8}_{Z+4} {\rm{T}} \stackrel{\alpha}{\longrightarrow} ^{A+4}_{Z+2} {\rm{X}} \stackrel{\alpha}{\longrightarrow} ^{A}_{Z} {\rm{Y}} \stackrel{\alpha}{\longrightarrow} \cdots $ , the radius R of an existing nucleus, such as$ ^{A+4}_{Z+2} {\rm{X}} $ ,$ ^{A}_{Z} {\rm{Y}} $ , and so on, can be achieved through their experimental α-decay energies in the above procedure. On the other hand, the radius R of an α-decay chain is assumed to have a linear relationship with$ A_d^{1/3} $ , namely$ \begin{array}{*{20}{l}} R=pA_{d}^{1/3}+q. \end{array} $

(6) Here,
$ A_{d} $ is the mass number of the daughter nucleus in the α-decay process. Hence, after the parameters p and q are fixed, the crucial parameter R of the unknown nucleus$ ^{A+8}_{Z+4} {\rm{T}} $ can be then obtained using Eq. (6).$ \mathbf{Case\; \; II:\; \; based\; \; on\; \; the\; \; isotopic\; \; chains} $ As for the two adjacent α-decay chains,
$^{A+10}_{Z+4} {\rm{T}} \stackrel{\alpha}{\longrightarrow} ^{A+6}_{Z+2} {\rm{X}} \stackrel{\alpha}{\longrightarrow} ^{A+2}_{Z} {\rm{Y}} \stackrel{\alpha}{\longrightarrow} \cdots$ and$^{A+8}_{Z+4} {\rm{T}} \stackrel{\alpha}{\longrightarrow} ^{A+4}_{Z+2} {\rm{X}} \stackrel{\alpha}{\longrightarrow} ^{A}_{Z} {\rm{Y}} \stackrel{\alpha}{\longrightarrow} \cdots$ , a similar linear fit as Case I between the R and$ {A_d}^{1/3} $ of known isotopes$ ^{A+6}_{Z+2} {\rm{X}} $ and$ ^{A+4}_{Z+2} {\rm{X}} $ can be obtained, i.e.,$ R=p_1A_d^{1/3}+q_1 $ . The other linear fit of known isotopes$ ^{A+2}_{Z} {\rm{Y}} $ and$ ^{A}_{Z} {\rm{Y}} $ can also be expressed by,$ R=p_2A_d^{1/3}+q_2 $ . Both p and q are supposed to have a linear relationship with proton number Z, respectively. Consequently, the key radius parameter R of the above two adjacent α-decay chains can be determined by the linear relationship,$ \begin{array}{*{20}{l}} R=(d_1Z+d_2)A_d^{1/3}+d_3Z+d_4. \end{array} $

(7) After the radius R is determined, the above process will proceed smoothly. Let us mention the other new point of this study, which addresses the α-decay width calculation. The decay width formula, like the Thomas classical expression, seems to be dependent on the channel radius [55]. Of course, the final result of decay width Γ is technically independent of the radius choice. However, the Γ value is actually sensitive to the radius during the numerical calculation, which more or less brings the difficulty to the convergency. Here, we propose a new strategy to conquer (or, say, avoid) this problem. The general idea is that the α-decay width can be achieved by calculating the pure particle flow wave function in the (enough) infinite area. As for the condition of pure particle flow, there needs to be a match between the normalization wave function in the quasi-bound state and the Coulomb function in the asymptotic area, namely
$ \begin{array}{*{20}{l}} u_{n\ell m}(r)\backsimeq A[G_\ell(kr)+{\rm i}F_\ell(kr)]\xrightarrow{r\rightarrow \infty} A{\rm exp}({\rm i}kr+\delta). \end{array} $

(8) Notably, both the amplitude of the real and imaginary parts of the wave function tend to be stable to A when the wave function is located in the gradual area (about
$ r \geq $ 20 fm). With this in mind, the real part$ \mathrm{Re}(u_{n\ell m}) $ and imaginary part$ \mathrm{Im}(u_{n\ell m}) $ can be achieved by linear superposition of any two different quasi-bound state wave functions. We take$ r_1 $ and$ r_2 $ as any two adjacent points in the gradual area of the wave functions, and the corresponding wave functions are$ u_1=1 $ and$ u_2=1 $ (or$ u_1=1 $ and$ u_2=-1 $ ), which have similar waveforms inside the nucleus, respectively. Both the wave functions$ u_1 $ and$ u_2 $ appear as sinusoidal fluctuations at the far end, and the phase difference between$ u_1 $ and$ u_2 $ is$ \pi/2 $ . On account of the only two linearly independent solutions of the quasi-bound state wave functions,$ u_1 $ and$ u_2 $ can be achieved by linear superposition of real and imaginary parts of the wave function$ u_{n\ell m} $ ,$ \begin{array}{*{20}{l}} \left\{ \begin{array}{ll} u_1= \dfrac{\cos \theta}{\cos \theta+\sin \theta}\mathrm{Re}(u_{n\ell m})+\dfrac{\sin \theta}{\cos \theta+\sin \theta}\mathrm{Im}(u_{n\ell m}),\\ \\ u_2= \dfrac{\sin \theta}{\cos \theta-\sin \theta}\mathrm{Re}(u_{n\ell m})+\dfrac{\cos \theta}{\cos \theta-\sin \theta}\mathrm{Im}(u_{n\ell m}), \end{array} \right. \end{array} $

(9) where θ is the phase difference between
$ u_1 $ and$ \mathrm{Re}(u_{n\ell m}) $ . Then,$ A_1 $ and$ A_2 $ , which are the amplitudes of$ u_1 $ and$ u_2 $ , respectively, have a certain form with the amplitude A, i.e.,$ \begin{array}{*{20}{l}} \left\{ \begin{array}{ll} A_1= \dfrac{A}{| \cos \theta+\sin \theta |},\\ \\ A_2= \dfrac{A}{| \cos \theta-\sin \theta |}. \end{array} \right. \end{array} $

(10) After
$ A_1 $ and$ A_2 $ of the wave function in the gradual area are determined, the amplitude A of the wave function of the pure particle flow in the gradual area can be calculated from the equation,$ \lim\limits_{r \rightarrow \infty}| \Psi_{n \ell m}(r) |^{2} = |A|^{2} = \frac{2|A_1|^{2} |A_2|^{2}}{|A_1|^{2}+|A_2|^{2}}. $

(11) To avoid the absolute values of
$ \sin\theta $ and$ \cos\theta $ being too close to each other, we selected multiple initial value points in the gradual region during the calculation process. This pair of wave functions can be used to evaluate the α-decay width when the solved amplitudes are closed at the far end.After obtaining the asymptotic behavior of the quasi-bound state wave function in the outflow state, the α-decay width and half-life can be determined by
$ \Gamma=\dfrac{\hbar^{2}k}{\mu}|A| ^{2}, $

(12) $ T_{1/2}=\frac{\hbar\ln2}{P_\alpha\Gamma}, $

(13) where the wave number
$ k=\sqrt{2\mu Q_\alpha}/\hbar $ , and$ P_\alpha $ is the preformation factor. Based on the experimental analyses of the (n, α) and (p, α) reactions [56], it is shown that the$ P_\alpha $ varies smoothly in the open-shell region and is smaller than 1. Nevertheless, it is quite difficult to evaluate the$ P_\alpha $ values microscopically owing to the complexity of the nuclear potential and nuclear many-body system. The α preformation factor is chosen as a uniform constant respectively for even-even, even-odd, odd-even, and odd-odd nuclei, which is consistent with other models [22, 23, 39]. Admittedly, nuclear deformation occurs in the heavy and superheavy nuclei, which should be included in the whole calculation. As a preliminary step, the present study aims to check the reliability of obtaining the decay energy and the half-life simultaneously within a fixed cluster-core potential. Moreover, to minimize the model parameters, the deformation effect is not considered here, which deserves further investigation and is being in progress. -
As mentioned before, with the available experimental
$ Q_{\alpha} $ values of Z$ > $ 110, the key parameter R in the nuclear potential is determined by systematics from the decay and isotopic chains. The$ Q_\alpha $ values and α-decay half-lives of unknown elements and isotopes in the local region of$ 117 \leqslant $ Z$ \leqslant $ 120 have then been simultaneously predicted within the cluster-core model.The experimentally known
$ Q_\alpha $ values and half-lives are taken from Ref. [57] and Ref. [58], respectively. In order to better understand and conduct the above process, the separation radius R is plotted versus$ A_d^{1/3} $ for each decay chain of even-Z SHN in Fig. 1. The same color in the picture represents the same decay chain. The points on the dashed lines denote the R values of unknown nuclei, and other points denote the results of fitting from Case I. For example, the$ ^{297}118 $ and$ ^{301}120 $ of the decay chain are the unsynthesized nuclei to be predicted in this work. Based on the decay chains, the relationship of separation radius R and$ A_d^{1/3} $ of the known SHN in each decay chain is obtained based on their available α-decay energies and Eq. (6). Subsequently, the reliability of Case I can be tested by comparing the radius R of the known SHN and the R values can be locally extrapolated. As can be seen from Fig. 1, the uncertainty bars of chain$ ^{297}120 $ and chain$ ^{299}120 $ appears to increase as$ A_{d}^{1/3} $ increases, while chains$ ^{298}120 $ and$ ^{301}120 $ are the other way around. This is because the measured$ Q_{\alpha} $ values of chains with different ranges lead to this starkly contrasting situation. For convenience, the decay chains of odd-Z nuclei with a similar change pattern will not be presented here.
Figure 1. (color online) The separation radius R is plotted versus
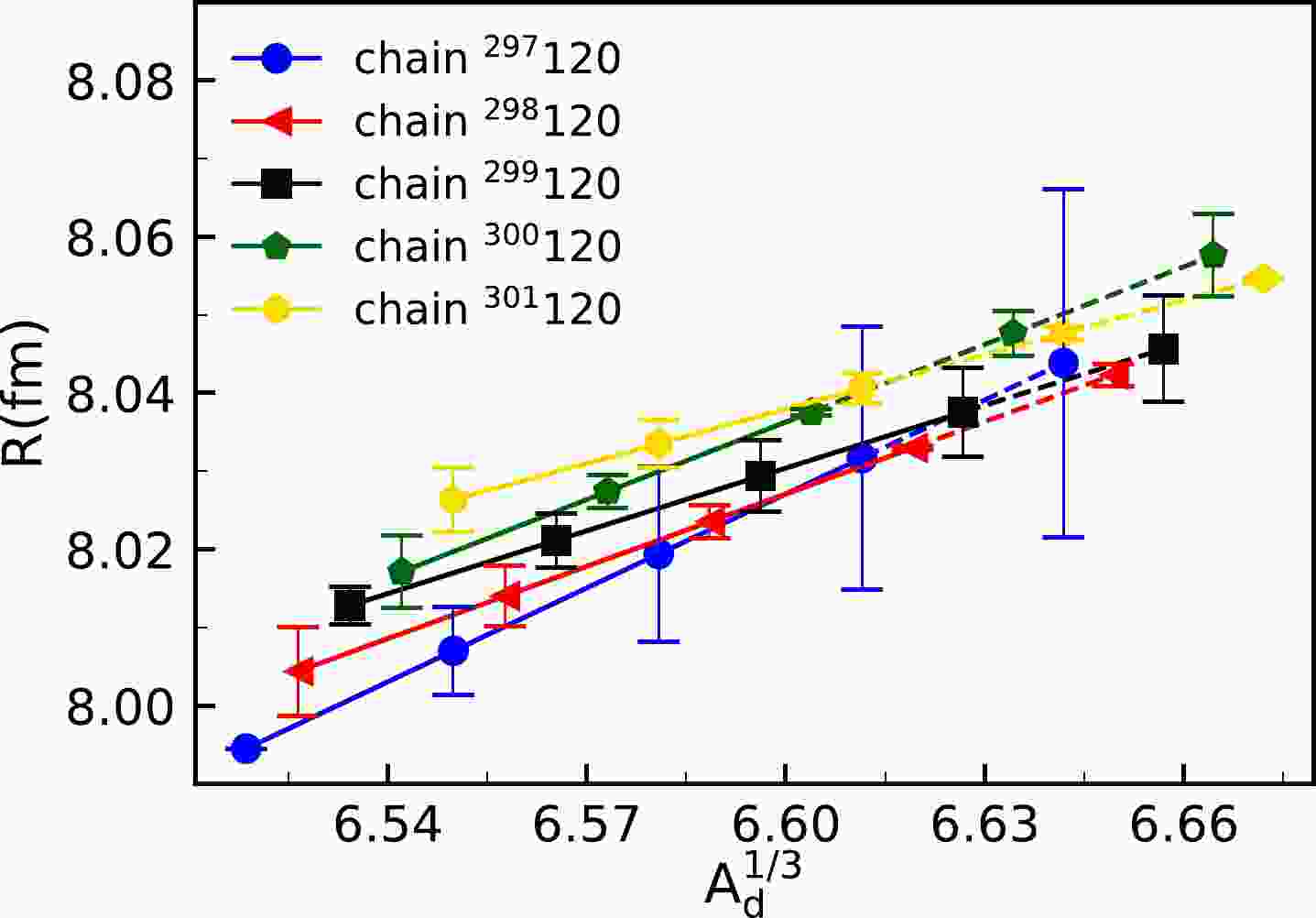
$ A_d^{1/3} $ for the even-Z isotopes, obtained in the present framework and Eq. (6). The points after the dashed line are the predicted values of the parameter R of unknown superheavy nuclei, and the points before the dashed line are the parameterized R with the available experimental values from known superheavy nuclei [57].Case II, based on isotopic chains, has been also investigated as a comparative study. Likewise, only the prediction of even-Z isotopic chains is presented in Fig. 2, where the line segments of the same color represent the same type of nuclei, namely the even-odd and even-even nuclei. The end points of the dashed line segments are plotted using the calculated data and Eq. (7). It is obvious from Fig. 2 that the slope of the line segment for the same isotopic chain decreases as the proton number Z increases. It is found that the R values of both isotopic chains
$ ^{301}120 $ and$ ^{300}120 $ grow initially and then reduce with the gradual enlargement of$ A_d^{1/3} $ , which is worthy of further investigation. By combining case I with case II, we hope to give a more comprehensive prediction for the unknown SHN. Obviously, after predicting the radius R, we would get the wave function by solving Eq. (1). The decay widths are then determined using Eq. (12). As mentioned before, the preformation factor$ P_{\alpha} $ is taken as a constant for the same type of nuclei to reduce the parameters. Based on the available experimental$ Q_{\alpha} $ values and half-lives, the$ P_\alpha $ values for superheavy nuclei with Z$ > $ 110 can be extracted by$P_\alpha={\hbar\ln2}/{T_{1/2}^{\rm expt.}\Gamma^{\rm calc.}}$ . The$ P_\alpha $ values are respectively averaged for different types of nuclei, namely$ P_\alpha $ = 0.4067 for even-even nuclei,$ P_\alpha $ = 0.1902 for even-odd nuclei,$ P_\alpha $ = 0.0910 for odd-even nuclei and$ P_\alpha $ = 0.0444 for odd-odd nuclei.
Figure 2. (color online) The separation radius R is plotted versus
$ A_d^{1/3} $ , obtained in the present framework and Eq. (7). The end points of the dashed segments correspond with the separation radius R of the predicted nuclei. Line segments of the same color represent the same isotopic chain. The experimentally known$ Q_\alpha $ values are taken from Ref. [57].The details on the comparison of theoretical α-decay energies and half-lives of superheavy nuclei from Z = 111 to Z = 118 with measured data are initially presented in Table 1. The first column denotes the parent nuclei and the experimental α-decay energies; the evaluated
$ Q_{\alpha} $ values in case I and case II evaluation methods are in the sequence listed in the three subsequent columns. The last three columns show the experimental half-lives and theoretical values of the two methods, respectively. All the {$ Q_{\alpha} $ } values and half-lives obtained using these two methods are shown to be in excellent agreement with the experimental values, except the$ Q_{\alpha} $ values for$ ^{279} $ 111,$ ^{283} $ 113, and$ ^{288} $ 115 in case I. The odd nucleon blocking effect in the above nuclei possibly makes it difficult for α particles to form on their surfaces. As for the unknown but attractive nucleus$ ^{296} $ 118, the predictions of$ Q_{\alpha}^II $ =$ 11.80_{-0.064}^{+0.101} $ MeV and$ T_{1/2}^II $ =$ 0.50_{-0.20}^{+0.19} $ ms are coherent with the results of$ Q_{\alpha} $ =$ 11.655 \pm 0.095 $ MeV and$ T_{1/2} $ = 0.825 ms with an uncertainty of a factor of 4 in Ref. [39], which uses the smooth and regular behavior of the α-nucleus double-folding potential parameters. Additionally, Ref. [59] also provides reliable prediction from the point of view of empirical formulas for$ ^{296}118 $ with$ Q_{\alpha} $ = 11.45 MeV, which is close to the result of$ Q_{\alpha}^I $ =$ 11.30\pm0.080 $ MeV in case I.Nucleus $Q_{\alpha}^{\rm expt.}$ /MeV [57]

$Q_{\alpha}^{\rm I}$ /MeV

$Q_{\alpha}^{\rm II}$ /MeV

$T_{1/2}^{\rm expt.}$ [58]

$T_{1/2}^{\rm I}$ 

$T_{1/2}^{\rm II}$ 

$ ^{279}111 $ 

$ 10.53 \pm 0.17 $ 

$ 10.32 \pm 0.091 $ 

$ 10.45_{-0.087}^{+0.353} $ 

$ 90_{-40}^{+170} $ ms

$ 51_{-21}^{+36} $ ms

$ 23_{-20}^{+16} $ ms

$ ^{280}111 $ 

$ 10.149 \pm 0.01 $ 

$ 9.98 \pm 0.052 $ 

$ 10.04_{-0.077}^{+0.213} $ 

$ 4.2_{-0.4}^{+0.6} $ s

$ 0.85_{-0.24}^{+0.33} $ s

$ 0.57_{-0.42}^{+0.35} $ s

$ ^{281}111 $ 

$ 9.9 \pm 0.4 $ 

$ 9.72 \pm 0.292 $ 

$ 9.94_{-0.118}^{+0.247} $ 

$ 2.14_{-1.81}^{+13.02} $ s

$ 0.54_{-0.42}^{+0.61} $ s

$ ^{282}111 $ 

$ 9.55\pm 0.1 $ 

$ 9.41 \pm 0.086 $ 

$ 9.47_{-0.062}^{+0.239} $ 

$ 100_{-30}^{+70} $ s

$ 36_{-16}^{+30} $ s

$ 23_{-19}^{+12} $ s

$ ^{283}111 $ 

$ 9.37 \pm 0.1 $ 

$ 9.31 \pm 0.117 $ 

$ 9.42_{-0.149}^{+0.140} $ 

$ 35_{-19}^{+45} $ s

$ 16_{-10}^{+30} $ s

$ ^{281}112 $ 

$ 10.43\pm 0.06 $ 

$ 10.25 \pm 0.001 $ 

$ 10.30_{-0.030}^{+0.063} $ 

$ 0.13_{-0.04}^{+0.12} $ s

$ 78_{-0.05}^{+0.06} $ ms

$ 59_{-18}^{+11} $ ms

$ ^{282}112 $ 

$ 10.15\pm 0.2 $ 

$ 9.98 \pm 0.156 $ 

$ 10.13_{-0.157}^{+0.157} $ 

$ 0.2_{-0.13}^{+0.35} $ s

$ 78_{-48}^{+130} $ ms

$ ^{283}112 $ 

$ 9.89\pm 0.11 $ 

$ 9.74 \pm 0.066 $ 

$ 9.83_{-0.086}^{+0.071} $ 

$ 4.52_{-0.76}^{+1.18} $ s

$ 1.97_{-0.69}^{+1.08} $ s

$ 1.08_{-0.39}^{+0.81} $ s

$ ^{284}112 $ 

$ 9.67\pm 0.15 $ 

$ 9.62 \pm 0.127 $ 

$ 9.67_{-0.114}^{+0.114} $ 

$ 2.08_{-1.19}^{+2.96} $ s

$ 1.51_{-0.80}^{+1.72} $ s

$ ^{285}112 $ 

$ 9.39\pm 0.12 $ 

$ 9.36 \pm 0.113 $ 

$ 9.37_{-0.142}^{+0.079} $ 

$ 28_{-6}^{+9} $ s

$ 26_{-14}^{+32} $ s

$ 24_{-10}^{+42} $ s

$ ^{283}113 $ 

$ 10.42\pm0.11 $ 

$ 10.64\pm0.156 $ 

$ 10.33_{-0.067}^{+0.169} $ 

$ 75_{-30}^{+136} $ ms

$ 35_{-21}^{+52} $ ms

$ 221_{-140}^{+110} $ ms

$ ^{284}113 $ 

$ 10.28\pm 0.04 $ 

$ 10.43 \pm 0.067 $ 

$ 10.19_{-0.173}^{+0.091} $ 

$ 0.97_{-0.10}^{+0.12} $ s

$ 0.25_{-0.08}^{+0.12} $ s

$ 1.07_{-0.45}^{+2.09} $ s

$ ^{285}113 $ 

$ 10.01\pm 0.04 $ 

$ 10.19 \pm 0.187 $ 

$ 9.94_{-0.101}^{+0.097} $ 

$ 4.2_{-0.8}^{+1.4} $ s

$ 0.5_{-0.34}^{+1.12} $ s

$ 2.52_{-1.17}^{+2.33} $ s

$ ^{286}113 $ 

$ 9.79\pm 0.05 $ 

$ 9.96 \pm 0.067 $ 

$ 9.72_{-0.102}^{+0.147} $ 

$ 9.5_{-2.7}^{+6.3} $ s

$ 4.56_{-1.59}^{+2.47} $ s

$ 22_{-13}^{+21} $ s

$ ^{287}113 $ 

$ 9.65\pm 0.2 $ 

$ 9.77 \pm 0.167 $ 

$ 9.55_{-0.135}^{+0.026} $ 

$ 7.39_{-4.90}^{+15.17} $ s

$ 33_{-5}^{+52} $ s

$ ^{285}114 $ 

$ 10.56\pm 0.07 $ 

$ 10.75 \pm 0.156 $ 

$ 10.50_{-0.230}^{+0.215} $ 

$ 0.15_{-0.05}^{+0.14} $ s

$ 18_{-11}^{+27} $ ms

$ 79_{-57}^{+240} $ ms

$ ^{286}114 $ 

$ 10.36\pm 0.04 $ 

$ 10.55 \pm 0.107 $ 

$ 10.32_{-0.099}^{+0.099} $ 

$ 0.2_{-0.06}^{+0.13} $ s

$ 27_{-12}^{+24} $ ms

$ 0.11_{-0.05}^{+0.09} $ s

$ ^{287}114 $ 

$ 10.17\pm 0.05 $ 

$ 10.35 \pm 0.097 $ 

$ 10.14_{-0.221}^{+0.221} $ 

$ 0.48_{-0.09}^{+0.14} $ s

$ 0.19_{-0.08}^{+0.15} $ s

$ 0.73_{-0.53}^{+2.29} $ s

$ ^{288}114 $ 

$ 10.076\pm 0.012 $ 

$ 10.18 \pm 0.058 $ 

$ 10.00_{-0.057}^{+0.057} $ 

$ 0.66_{-0.10}^{+0.14} $ s

$ 0.26_{-0.08}^{+0.12} $ s

$ 0.81_{-0.25}^{+0.36} $ s

$ ^{289}114 $ 

$ 9.95\pm 0.07 $ 

$ 10.01 \pm 0.083 $ 

$ 9.77_{-0.211}^{+0.191} $ 

$ 1.9_{-0.4}^{+0.7} $ s

$ 1.68_{-0.69}^{+1.20} $ s

$ 7.67_{-5.48}^{+24.58} $ s

$ ^{287}115 $ 

$ 10.76\pm 0.07 $ 

$ 10.95 \pm 0.220 $ 

$ 10.71_{-0.059}^{+0.123} $ 

$ 37_{-13}^{+44} $ ms

$ 25_{-17}^{+62} $ ms

$ 103_{-53}^{+42} $ ms

$ ^{288}115 $ 

$ 10.65\pm 0.05 $ 

$ 10.88 \pm 0.184 $ 

$ 10.73_{-0.231}^{+0.089} $ 

$ 174_{-18}^{+22} $ ms

$ 79_{-51}^{+149} $ ms

$ 187_{-75}^{+54} $ ms

$ ^{289}115 $ 

$ 10.49\pm 0.05 $ 

$ 10.67 \pm 0.082 $ 

$ 10.44_{-0.095}^{+0.087} $ 

$ 330_{-80}^{+120} $ ms

$ 130_{-49}^{+82} $ ms

$ 491_{-200}^{+388} $ ms

$ ^{290}115 $ 

$ 10.41\pm 0.04 $ 

$ 10.51 \pm 0.048 $ 

$ 10.36_{-0.143}^{+0.175} $ 

$ 650_{-200}^{+490} $ ms

$ 685_{-170}^{+228} $ ms

$ 1.70_{-1.11}^{+2.42} $ s

$ ^{291}115 $ 

$ 10.30\pm 0.2 $ 

$ 10.24 \pm 0.217 $ 

$ 10.18_{-0.132}^{+0.050} $ 

$ 1.73_{-1.27}^{+5.13} $ s

$ 2.48_{-0.67}^{+3.28} $ s

$ ^{289}116 $ 

$ 11.10\pm 0.3 $ 

$ 11.25 \pm 0.310 $ 

$ 11.09_{-0.170}^{+0.286} $ 

$ 4.7_{-3.81}^{+21.58} $ ms

$ 11_{-9}^{+17} $ ms

$ ^{290}116 $ 

$ 11.00\pm 0.06 $ 

$ 11.13 \pm 0.058 $ 

$ 11.06_{-0.045}^{+0.045} $ 

$ 8.3_{-1.9}^{+3.5} $ ms

$ 4.2_{-1.14}^{+1.57} $ ms

$ 6.40_{-1.39}^{+1.81} $ ms

$ ^{291}116 $ 

$ 10.89\pm 0.09 $ 

$ 10.97 \pm 0.128 $ 

$ 10.83_{-0.094}^{+0.253} $ 

$ 19_{-6}^{+17} $ ms

$ 23_{-12}^{+24} $ ms

$ 49_{-38}^{+36} $ ms

$ ^{292}116 $ 

$ 10.791\pm 0.012 $ 

$ 10.74 \pm 0.011 $ 

$ 10.87_{-0.004}^{+0.004} $ 

$ 13_{-4}^{+7} $ ms

$ 39_{-2.44}^{+2.61} $ ms

$ 19_{-0.35}^{+0.42} $ ms

$ ^{293}116 $ 

$ 10.68\pm 0.06 $ 

$ 10.65 \pm 0.053 $ 

$ 10.57_{-0.246}^{+0.221} $ 

$ 56_{-17}^{+43} $ ms

$ 142_{-38}^{+53} $ ms

$ 232_{-169}^{+813} $ ms

$ ^{291}117 $ 

$ 11.48\pm 0.4 $ 

$ 11.28 \pm 0.284 $ 

$ 11.58_{-0.062}^{+0.216} $ 

$ 17_{-14}^{+67} $ ms

$ 3.38_{-2.27}^{+1.28} $ ms

$ ^{292}117 $ 

$ 11.53\pm 0.4 $ 

$ 11.33 \pm 0.301 $ 

$ 11.65_{-0.221}^{+0.206} $ 

$ 27_{-21}^{+114} $ ms

$ 4.81_{-3.12}^{+10.49} $ ms

$ ^{293}117 $ 

$ 11.32\pm 0.05 $ 

$ 11.14 \pm 0.021 $ 

$ 11.45_{-0.101}^{+0.214} $ 

$ 22_{-4}^{+8} $ ms

$ 37_{-4}^{+5} $ ms

$ 6.97_{-4.69}^{+5.01} $ ms

$ ^{294}117 $ 

$ 11.18\pm 0.04 $ 

$ 11.06 \pm 0.029 $ 

$ 11.38_{-0.116}^{+0.321} $ 

$ 51_{-16}^{+38} $ ms

$ 119_{-18}^{+21} $ ms

$ 20_{-16}^{+18} $ ms

$ ^{295}117 $ 

$ 10.71 \pm 0.266 $ 

$ 11.31_{-0.141}^{+0.212} $ 

$ 0.45_{-0.35}^{+1.79} $ s

$ 15_{-10}^{+17} $ ms

$ ^{293}118 $ 

$ 11.92\pm 0.5 $ 

$ 11.75 \pm 0.464 $ 

$ 12.08_{-0.593}^{+0.275} $ 

$ 1.3_{-1.20}^{+14.28} $ ms

$ 0.26_{-0.19}^{+5.04} $ ms

$ ^{294}118 $ 

$ 11.87\pm 0.03 $ 

$ 11.71 \pm 0.009 $ 

$ 11.93_{-0.101}^{+0.169} $ 

$ 0.69_{-0.22}^{+0.64} $ ms

$ 0.76_{-0.03}^{+0.04} $ ms

$ 0.25_{-0.14}^{+0.17} $ ms

$ ^{295}118 $ 

$ 11.7\pm 0.2 $ 

$ 11.58 \pm 0.159 $ 

$ 11.92_{-0.380}^{+0.223} $ 

$ 3.2_{-1.80}^{+4.25} $ ms

$ 0.59_{-0.39}^{+3.57} $ ms

$ ^{296}118 $ 

$ 11.30\pm 0.080 $ 

$ 11.80_{-0.064}^{+0.101} $ 

$ 6.85_{-2.42}^{+3.75} $ ms

$ 0.50_{-0.20}^{+0.19} $ ms

$ ^{297}118 $ 

$ 11.30\pm 0.024 $ 

$ 11.75_{-0.169}^{+0.171} $ 

$ 15_{-2}^{+2} $ ms

$ 1.36_{-0.79}^{+1.92} $ ms

Encouraged by our predictions of α-decay energies and half-lives of heaviest nuclei with 111
$ \leq$ Z$ \leq$ 118, we have also explored the α-decay properties for more unknown heaviest elements. Table 2 displays the comparison of the calculated α-decay energies and half-lives with other related predictions for Z = 119 and 120 [30, 60]. Table 2 shows that the theoretical calculations for Z = 119 with case II are in very good agreement with$ Q_{\alpha}^{2} $ and$ T_{1/2}^{2} $ in Ref. [30] based on the FRDM masses [62], especially for the$ Q_{\alpha} $ value of nucleus$ ^{295}119 $ and half-life of nucleus$ ^{297}119 $ . Furthermore, the calculated$ T_{1/2} $ and$ Q_{\alpha} $ values for Z = 120 in case II are found to be generally consistent with other theoretical values with a small discrepancy. This work heavily relies on measured data. However, the kinetic energies of these nuclei in the experiments span a wide range, even reaching 1 MeV [57], which may lead to some discrepancies between our predictions and other theoretical outcomes. Besides, the experimental data of α decay, especially in these superheavy nuclei, are always reported with error bars, representing the uncertainties in the determination of R, not to mention that in the fitting process. The subsequent results for$ Q_{\alpha} $ and$ T_{1/2} $ are therefore given with an error range. By contrast, it is visible that case II calculations are overall higher than case I for α-decay energies and lower for half-lives with 117$ \leqslant $ Z$ \leqslant $ 120. Combining Table 1 with Table 2, these two methods, based on experimental data and the systematics of decay chains and isotopic chains, are feasible and effective in the local region within the cluster model, especially case II. We hope these studies can be useful in ongoing or forthcoming experiments to investigate unknown superheavy nuclei and isotopes.Nucleus $ Q_{\alpha}^{1} $ /MeV

$ Q_{\alpha}^{2} $ /MeV

$Q_{\alpha}^{\rm I}$ /MeV

$Q_{\alpha}^{\rm II}$ /MeV

$ T_{1/2}^{1} $ 

$ T_{1/2}^{2} $ 

$T_{1/2}^{\rm I}$ 

$T_{1/2}^{\rm II}$ 

$ ^{295}119 $ 

$ 11.77 $ 

$ 12.95 $ 

$ 11.60 \pm 0.35 $ 

$ 12.96_{-0.08}^{+0.45} $ 

$ 3.68 $ ms

$ 10.3\mu $ s

$ 12.2_{-10.2}^{+68.9} $ ms

$ 17.3_{-14.7}^{+7.03}\mu $ s

$ ^{296}119 $ 

$ 11.57 $ 

$ 13.14 $ 

$ 11.78 \pm 0.42 $ 

$ 12.97_{-0.14}^{+0.44} $ 

$ 16.7 $ ms

$ 6.72\mu $ s

$ 9.64_{-8.45}^{+78.9} $ ms

$ 34.1_{-28.9}^{+30.8}\mu $ s

$ ^{297}119 $ 

$ 11.35 $ 

$ 12.81 $ 

$ 11.62 \pm 0.12 $ 

$ 12.94_{-0.12}^{+0.48} $ 

$ 34.9 $ ms

$ 18.2\mu $ s

$ 11.2_{-5.37}^{+10.5} $ ms

$ 18.5_{-16.1}^{+12.8}\mu $ s

$ ^{298}119 $ 

$ 11.39 $ 

$ 12.57 $ 

$ 11.61 \pm 0.01 $ 

$ 12.79_{-0.02}^{+0.58} $ 

$ 43 $ ms

$ 87.1\mu $ s

$ 23.6_{-1.22}^{+1.27} $ ms

$ 74.7_{-68.8}^{+8.44}\mu $ s

$ ^{299}119 $ 

$ 11.54 $ 

$ 12.86 $ 

$ 11.18 \pm 0.32 $ 

$ 12.93_{-0.16}^{+0.51} $ 

$ 11.4 $ ms

$ 14\mu $ s

$ 125_{-103}^{+645} $ ms

$ 19.8_{-17.6}^{+20.7}\mu $ s

$ ^{297}120 $ 

$ 13.51\pm0.18 $ 

$ 13.65 $ 

$ 12.26 \pm 0.62 $ 

$ 13.45_{-0.55}^{+0.18} $ 

$ 0.46\pm0.31\mu $ s

$ 0.18\mu $ s

$ 0.41_{-0.38}^{+9.01} $ ms

$ 1.82_{-0.97}^{+17.7}\mu $ s

$ ^{298}120 $ 

$ 13.64\pm0.18 $ 

$ 13.24 $ 

$ 12.30 \pm 0.04 $ 

$ 13.16_{-0.14}^{+0.11} $ 

$ 0.27\pm0.18\mu $ s

$ 1.23\mu $ s

$ 158_{-27.8}^{+33.6}\mu $ s

$ 3.00_{-1.16}^{+2.54}\mu $ s

$ ^{299}120 $ 

$ 13.95\pm0.18 $ 

$ 13.73 $ 

$ 12.20 \pm 0.19 $ 

$ 13.39_{-0.28}^{+0.11} $ 

$ 0.09\pm0.06\mu $ s

$ 0.18\mu $ s

$ 0.54_{-0.32}^{+0.84} $ ms

$ 2.44_{-0.92}^{+5.56}\mu $ s

$ ^{300}120 $ 

$ 13.81\pm0.18 $ 

$ 13.70 $ 

$ 11.87 \pm 0.15 $ 

$ 13.10_{-0.10}^{+0.03} $ 

$ 0.45\pm0.29\mu $ s

$ 0.56\mu $ s

$ 1.36_{-0.72}^{+1.57} $ ms

$ 3.95_{-0.44}^{+2.18}\mu $ s

$ ^{301}120 $ 

$ 13.20\pm0.18 $ 

$ 13.62 $ 

$ 11.95 \pm 0.01 $ 

$ 13.32_{-0.01}^{+0.04} $ 

$ 4.30\pm2.95\mu $ s

$ 0.47\mu $ s

$ 1.94_{-0.05}^{+0.06} $ ms

$ 3.28_{-0.53}^{+0.08}\mu $ s

Table 2. Comparison of the calculated
$ \alpha $ decay energies and half-lives with other related calculations for$ ^{295-299} $ 119 and$ ^{297-301} $ 120. The comparative theoretical results of Z = 119 and 120 are respectively taken from Ref. [30] and Ref. [60], where the$ Q_{\alpha}^{1} $ and$ T_{1/2}^{1} $ of Z = 119 are based on the Koura-Tachibana-Uno-Yamada model in 2005 (KTUY05) [61], the$ Q_{\alpha}^{2} $ and$ T_{1/2}^{2} $ of both Z = 119 and 120 are from the finite-range droplet model (FRDM) [62], and the results of$ Q_{\alpha}^{1} $ and$ T_{1/2}^{1} $ for Z = 120 are based on the Macroscopic-microscopic approach [60]. -
In summary, the α-decay energies and half-lives of SHN in the
$ 117 \leq Z \leq 120 $ range were systematically calculated within a cluster model plus a modified W.S. type nuclear potential, which is consistent with previous α-cluster structure studies. As a new choice, the decay width was defined from the perspective of the wave function of pure particle flow, with concentration on its asymptotic behavior. During this procedure, the separation radius R, which is a crucial parameter, was determined from the systematic analysis of the decay and isotopic chains. In this way, one can get both the$ Q_\alpha $ values and the half-lives simultaneously, avoiding the large uncertainties caused by using different mass models to predict the decay energies. More importantly, we hope that these detailed local extrapolations on α-decay energies and half-lives of unknown SHN, e.g., for the attractive isotopes of Z = 119 and 120, can be useful in ongoing or forthcoming experimental detection and design.
α-decay properties of superheavy nuclei with 117 ≤ Z ≤ 120 from the systematics of decay chains and isotopic chains
- Received Date: 2023-09-20
- Available Online: 2024-03-15
Abstract: Recently, the synthesis of new elements above Z = 118 has been a hot topic in nuclear physics. Meanwhile, the α-decay chain is expected to be the unique tool to identify these heaviest nuclei. We have systematically calculated the α-decay energies and half-lives on the same footing for superheavy nuclei (SHN) within the cluster model along with a slightly modified Woods-Saxon (W.S.) potential as the nuclear potential. Based on the available experimental data, the key radius parameter (R) in the α-core potential is determined via the systematic trend from the α-decay and isotopic chains. The α-decay energy (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: