-
At present, there is great interest in exploring nuclear interactions for the reactions involving weakly bound stable nuclei. This is a natural step toward a deeper understanding of the exotic nuclei at the interface between the cases of tightly bound stable and exotic nuclei [1]. Therefore, investigation of heavy-ion reactions involving weakly bound nuclei represents one of the leading research subjects in low energy nuclear physics, and is important for exploring the properties of radioactive nuclei [2]. Establishing the optical potentials of these nuclei is fundamental to determine how they interact. Some possible information can be collected from the scattering of such nuclei from analysis of the relevant data. In particular, the global phenomenological optical potential (GPOP) provides a convenient average description of the overall trend of the interaction as a function of mass and energy, although it should not be expected to provide an adequate description of a nucleon-nucleus interaction because the nuclear structure differences among adjacent nuclei cannot be cast into a simple and smooth Z- and A-dependence of the Woods-Saxon parameters [3].
Lithium, as the lightest metal, has attracted extensive attention from both experimental and theoretical nuclear physicists. 6,7Li are subject of many studies aiming to build a bridge between the elastic scattering of light and heavy ions because they are the lightest heavy-ion projectile [4, 5]. Thus far, we have established the 6,7Li GPOPs for the reactions of 6,7Li on medium and heavy nuclei [6, 7] via fitting of the experimental data of elastic scattering angular distributions and reaction cross sections in the target mass range of 24–209 below 250 MeV. However, this does not provide a good description of these reactions for targets with mass numbers below 20 [6–9]. Nuclear reactions of 6,7Li on light targets are more complicated than those for heavy targets, such as the reactions of 6,7Li induced 1p-shell nuclei. Complicated reaction dynamics are involved, i.e., strong collective excitations, breakup, and transfer reactions [10–13]. Some phenomenological optical potentials (POPs) of 7Li induced 1p-shell nuclei have been realized. However, most of them are suitable to individual target and single incident energy. Thus, a reliable GPOP of 7Li projectile on 1p-shell nuclei should be established in wide energy and mass ranges. Accordingly, some nuclear reaction mechanisms are being further investigated and analyzed, such as the transfer or breakup reactions [14–16].
The goal of this work is to obtain a GPOP describing the elastic scattering of 7Li on 1p-shell nuclei. To achieve this, existing experimental data of elastic scattering angular distributions are simultaneously considered and fitted for 7Li projectile on 9Be, 10B, 11B, 12C, 13C, 15N, and 16O nuclei from 4.5 to 131.8 MeV. While for the reaction of 7Li + 7Li, the potential is searched separately from the other 1p-shell nuclei. As described in Sec. II, the corresponding GPOP parameters differ significantly from the other 1p-shell nuclei, which may be attributed to their weak binding energies and cluster structures. Therefore, the elastic scattering angular distributions are reanalyzed using a microscopic method within the framework of the new version of double folding São Paulo potential (SPP2) [17]. Based on the obtained GPOPs, the contributions of transfers to the elastic scattering are also estimated using the distorted wave Born approximation (DWBA) method to better describe the elastic scattering at backward angles. In addition, a coupled channels (CC) method is employed to assess the inelastic scattering angular distributions considering the obtained GPOPs.
The rest of this paper is organized as follows: In Sec. II, we first present brief descriptions of the formulas and methods adopted. The obtained GPOPs are also displayed in this section. Then, in Sec. III, the results are compared with the experimental data, in addition to a further detailed analysis. Finally, we provide a brief summary of the present work in Sec. IV.
-
The potential of Woods-Saxon (WS) shape is expressed as:
$ \begin{aligned}[b] U(r, E)=&V_{R}(E)f(r, R_{R}, a_{R})+ {\rm i} W_{V}(E)f(r, R_{V}, a_{V})\\ &+ {\rm i} W_{S}(E)(-4a_{S})\frac{{\rm d} f(r, R_{S}, a_{S})}{{\rm d} r}+V_{C}(r), \end{aligned} $

(1) where
$ V_{R}(E) $ ,$ W_{V}(E) $ , and$ W_{S}(E) $ are the depths of the real, volume-imaginary, and surface-imaginary parts, respectively. f is the WS form factor, given by:$ f(r, R_{i}, a_{i})=-\frac{1}{1+\exp[(r-R_{i})/a_{i}]}. $

(2) The energy dependences of potential depths [6, 7, 18, 19]
$ V_{R}(E) $ ,$ W_{S}(E) $ , and$ W_{V}(E) $ are defined as:$ V_{R}(E)=V_{0}+V_{1}E+V_{2}E^{2}, $

(3) $ W_{S}(E)=\max\{0, W_{0}+W_{1}E\}, $

(4) $ W_{V}(E)=\max\{0, U_{0}+U_{1}E+U_{2}E^{2}\}. $

(5) The Coulomb potential
$ V_{C}(r) $ is written as:$ V_{C}(r)=\left\{ \begin{array}{ll} \dfrac{zZe^{2}}{2R_{C}}\left(3-\dfrac{r^{2}}{R^{2}_{C}}\right) &\quad r<R_{C}, \\ \dfrac{zZe^{2}}{r} & \quad r\geq R_{C}, \end{array} \right. $

(6) where the index
$ i=R, V, S, C $ , which represents the real, imaginary, and Coulomb components,$ R_{i}=r_{i}(A_{T}^{\frac{1}{3}}+A_{P}^{\frac{1}{3}}) $ is the interaction radius, and$ a_{i} $ is the nuclear diffuseness. -
The elastic scattering angular distributions for the reactions of 7Li on 1p-shell nuclei were collected and investigated including targets from 7Li to 16O below 131.8 MeV. All the experimental data involved in the analyzsis are displayed in Table 1.
Target E/MeV Ref. 7Li 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0 [20] 20.0, 25.0 [21] 42.0 [22] 9Be 15.75, 19.0, 24.0, 30.0 [23] 17.7, 21.9 [24] 34.0 [25] 63.0, 130.0 [26] 10B 24.0 [27] 39.0 [28] 11B 9.85, 13.3, 18.3, 23.3, 28.3 [29] 34.0 [30] 12C 4.5, 5.8, 11.0, 13.0 [31] 7.5, 9.0, 12.0, 15.0 [32] 21.1 [27] 34.0 [33] 36.0 [34] 48.0 [35] 63.0, 78.7 [36] 89.0 [37] 131.8 [38] 13C 5.8, 9.0, 13.0, 20.0, 36.0 [31] 34.0 [34] 63.0, 130.0 [26] 15N 28.8 [39] 44.0 [40] 16O 9.0, 13.0 [41] 20.0 [31] 26.0 [42] 36.0 [34] 42.0 [43] 50.0 [44] Table 1. The elastic scattering angular distributions database of 7Li projectile on 1p-shell nuclei. E is the incident energy for different targets in the laboratory system.
The experimental elastic scattering angular distributions for all 1p-shell nuclei were adjusted using improved computer code APMN [45], which can automatically search POP parameters relying on the improved fastest falling method [46] below 300 MeV. In the adjustment process, the optimal POP parameters are determined via minimization of deviation
$ \chi^{2} $ of the results. χ2 is calculated using the optical potential from the experimental data and defined by:$ \chi^{2}=\frac{1}{N}\sum\limits_{i=1}^{N}\left[\frac{\sigma_{i}^{\rm th}-\sigma_{i}^{\rm ex}}{\Delta\sigma_{i}^{\rm ex}}\right]^{2}, $

(7) where N is the number points of experimental data,
$\sigma_{i}^{\rm th}$ and$\sigma_{i}^{\rm ex}$ are the theoretical and experimental values of the elastic scattering angular distributions, and$ \Delta\sigma $ is the experimental error. It should be noted that 10% of experimental uncertainties are uniformly assumed for all data for comparison of the degree of agreement between different data when calculating the$ \chi^{2} $ values in the work. Detailed descriptions for the procedure in the data analysis can be found in Refs. [6, 9].For the reaction of 7Li + 7Li, the corresponding systematics are presumed to be inconsistent with those established for the other 1p-shell nuclei because 7Li has very weakly bound properties with 3H cluster structure. Thus, the potential parameters of the 7Li + 7Li system are searched separately.
The GPOP parameters for the reactions of 7Li induced 1p-shell nuclei are obtained via fitting of the experimental data of elastic scattering angular distributions in the mass number range of 7–16, which are listed in Table 2. The parameters for 7Li target clearly exhibit remarkably different behavior in comparison to the other 1p-shell nuclei. This may relate to the weakly bound nature of these two nuclei and their cluster structures. Generally, the POP parameters for scattering from light target nuclei are more likely to show fluctuations owing to nuclear structure and channel-coupling effects [29, 33]. Thus, one of the parameters for some lighter and deformed targets, such as 9Be, 10B, 11B, and 15N, are slightly adjusted to better fit the present experimental data due to the different structures. For example, 12C and 16O have a pronounced cluster structure and are N-alpha nuclei [47]. However, the 9Be nucleus has an interesting structure known as the Borromean structure, in which the 9Be consists of two alpha particles and one weakly bound neutron. 10B is a weakly bound stable nucleus that may breakup into different partitions, the most energetically favorable being 10B → 6Li + 4He (Q = –4.461 MeV) [2]. The 11B nucleus is a strongly bound nucleus with the binding energy of 8.67 MeV in respect to the 7Li + α channel decay, and has a nonzero ground state deformation indicating a nonspherical symmetric charge distribution [48]. 15N is odd-A nuclei and has the ground state spin of 1/2. Accordingly, the diffuseness parameter of real part
$ a_{R} $ is 0.624 fm for the 9Be target, and the diffuseness parameter of imaginary part surface absorption$ a_{S} $ is 0.582 fm for the 15N target. While the radius parameters of real part$ r_{S} $ are 0.810 and 1.060 fm for 10, 11B targets, respectively.Parameter 7Li 1p Unit $V_{0}$ 

49.257 70.668 MeV $V_{1}$ 

−0.449 −0.0344 $V_{2}$ 

0.000580 $W_{0}$ 

19.363 18.676 MeV $W_{1}$ 

−0.187 −0.298 $U_{0}$ 

−1.201 −1.539 MeV $U_{1}$ 

0.0739 0.424 $U_{2}$ 

−0.00144 $r_{R}$ 

0.900 0.845 fm $r_{S}$ 

1.312 1.060 fm $r_{V}$ 

1.800 1.039 fm $r_{C}$ 

1.800 1.800 fm $a_{R}$ 

0.842 0.774 fm $a_{S}$ 

0.385 0.432 fm $a_{V}$ 

1.050 0.850 fm Table 2. The GPOP parameters of 7Li induced 1p-shell nuclei.
-
The double folding potential is computed as a Hartree-Fock (HF)-type potential according to the following relation:
$ V_{F}(R)=\iint{\rho_{1}(\vec{r_{1}})\rho_{2}(\vec{r_{2}})v_{NN}(\vec{R}-\vec{r_{1}}+\vec{r_{2}}){\rm d}\vec{r_{1}}{\rm d}\vec{r_{2}}}, $

(8) where
$ \rho_{1} $ and$ \rho_{2} $ are the ground state nuclear matter density distributions for the projectile and target, respectively, and$ v_{NN} $ represents effective$ NN $ interaction.The SPP2 effective interaction is proposed to successfully describe the low energy α + α experimental phase-shifts within the context of the double-folding approach [17], which is a new version of the original SPP [49] that includes a dependence on the relative velocity between two interacting nuclei. This effective interaction is parameterized as follows:
$ v_{NN}^{\rm SPP2}(r)=-U_{0}\exp(-\vec{r}/a)^{2}\exp(-4v^{2}/c^{2}), $

(9) where
$ U_{0} $ = 735.813 MeV and a = 0.5 fm.Accordingly, an extension of the SPP model for the real and imaginary components with different normalization values was successfully applied to the elastic scattering of stable nuclei [50]. The final folded potential is used as a complex optical potential (OP) by scaling it with a complex renormalization factor as:
$ V_{\rm OP}(R)=N_{R}V_{F}(R)+{\rm i} N_{I}V_{F}(R), $

(10) where
$ N_{R} $ and$ N_{I} $ represent the real and imaginary renormalization factors, respectively. -
The elastic scattering angular distributions determined using the present GPOPs were systematically analyzed via comparison with the experimental data for the reactions of 7Li on 1p-shell nuclei. Comparisons between the experimental data [20–22] and the calculations of the GPOP for 7Li target are plotted in Fig. 1. It is apparent that the calculations agree well with the corresponding experimental data in the range of 8.0–42.0 MeV.
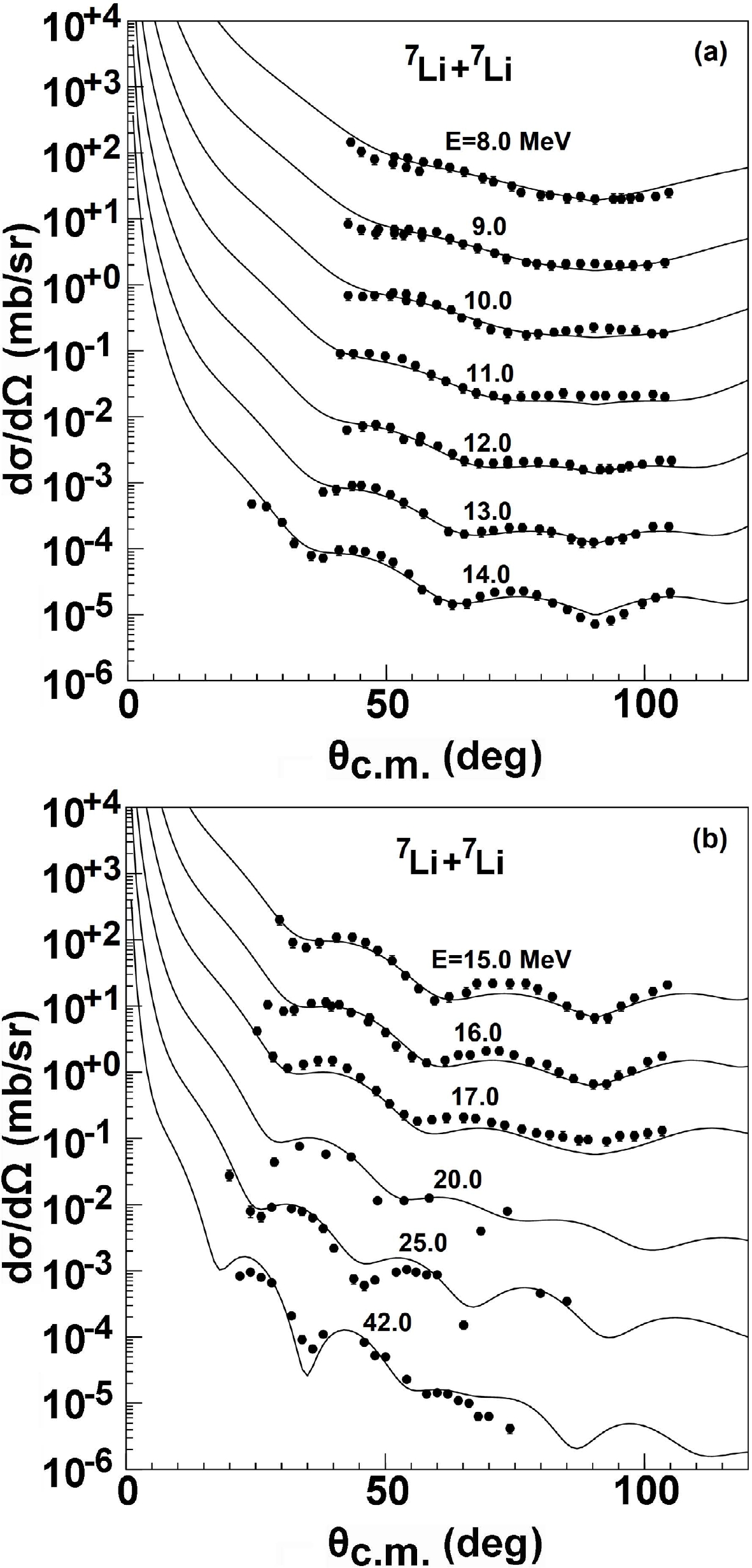
Figure 1. Comparisons of the elastic scattering angular distributions with the experimental data for 7Li target from 8.0 to 42.0 MeV.
The elastic scattering differential cross sections calculated using the GPOP for 9Be are also compared with the experimental data [23–26], as shown in Fig. 2. From the figure, the present calculations are in good agreement with the experimental data between 15.75 and 130.0 MeV. Figure 3 presents further comparisons of the angular distributions with the corresponding experimental data [29, 30] for 11B from 9.85 to 34.0 MeV. The results provide a reasonable description of the data except for 34.0 MeV at backward angles, where there may be some contribution from the other reaction mechanism. In addition, as both 7Li and 11B have quadrupole moments, there can be contributions to the elastic scattering of 7Li + 11B due to the quadrupole reorientation of the projectile, or the target, or both simultaneously [30]. In the next work, such contributions will be further considered in the calculation to improve the fits.
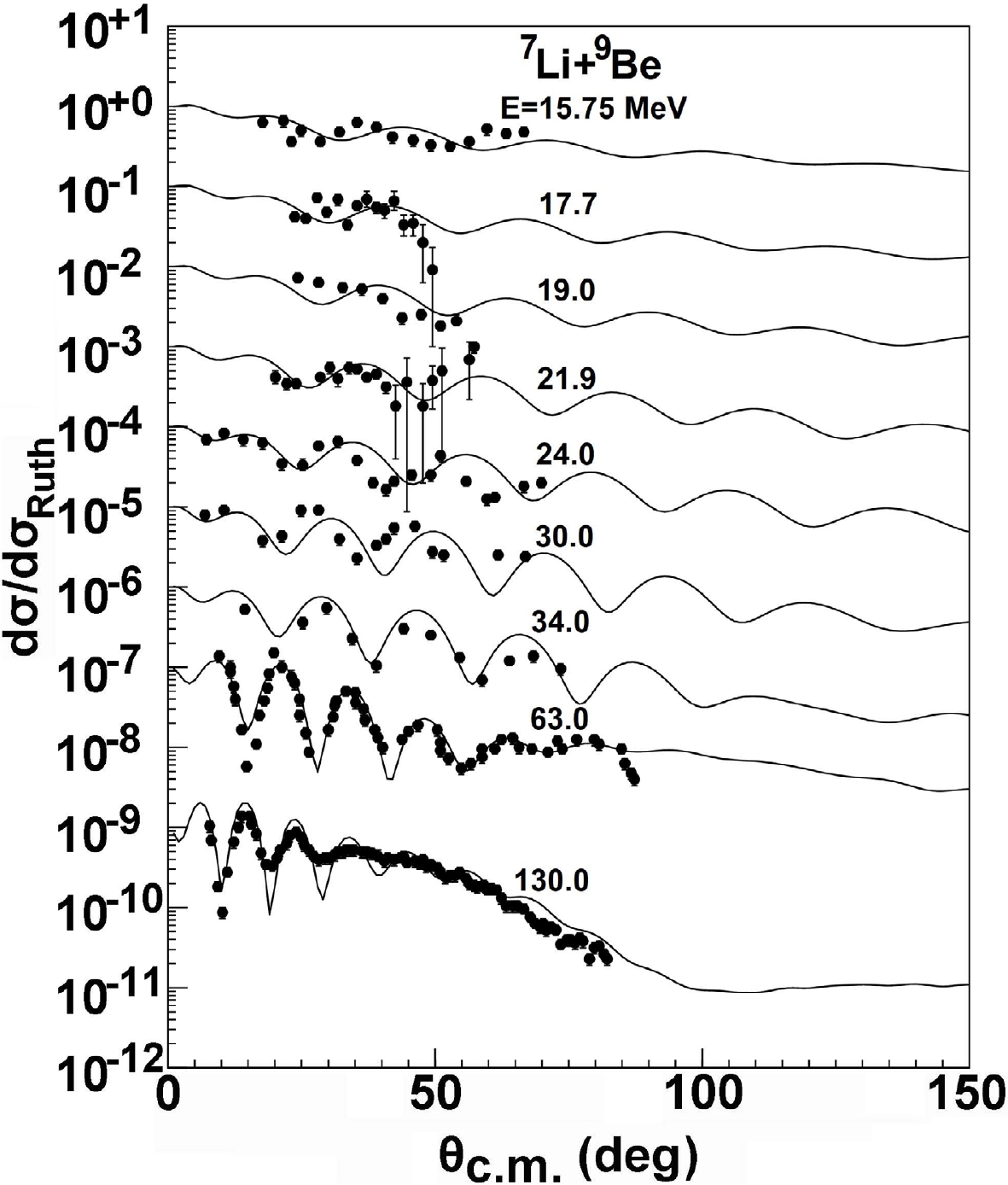
Figure 2. Same as Fig. 1, but for 9Be target from 15.75 to 130.0 MeV.
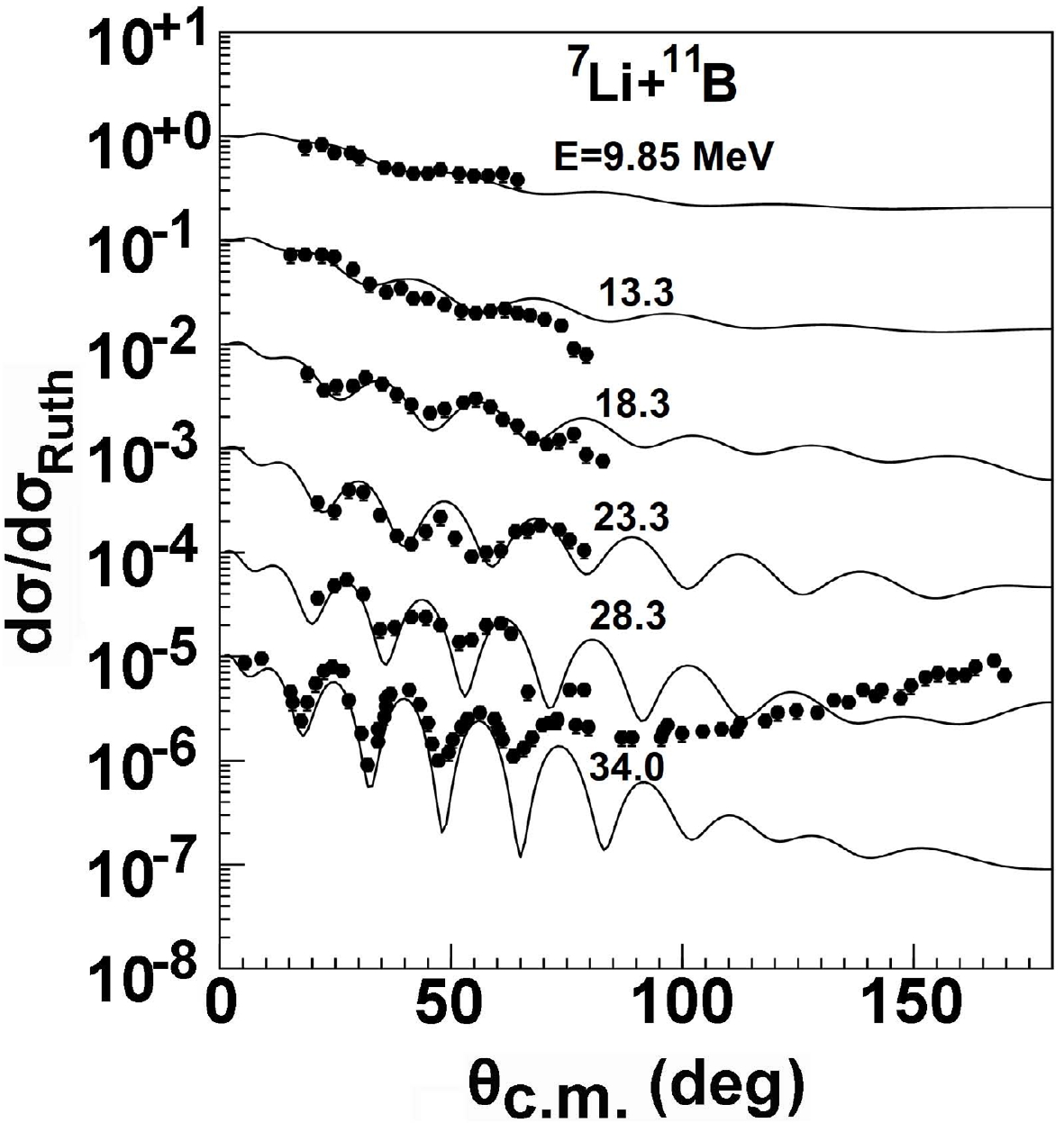
Figure 3. Same as Fig. 1, but for 11B targets from 9.85 to 34.0 MeV MeV.
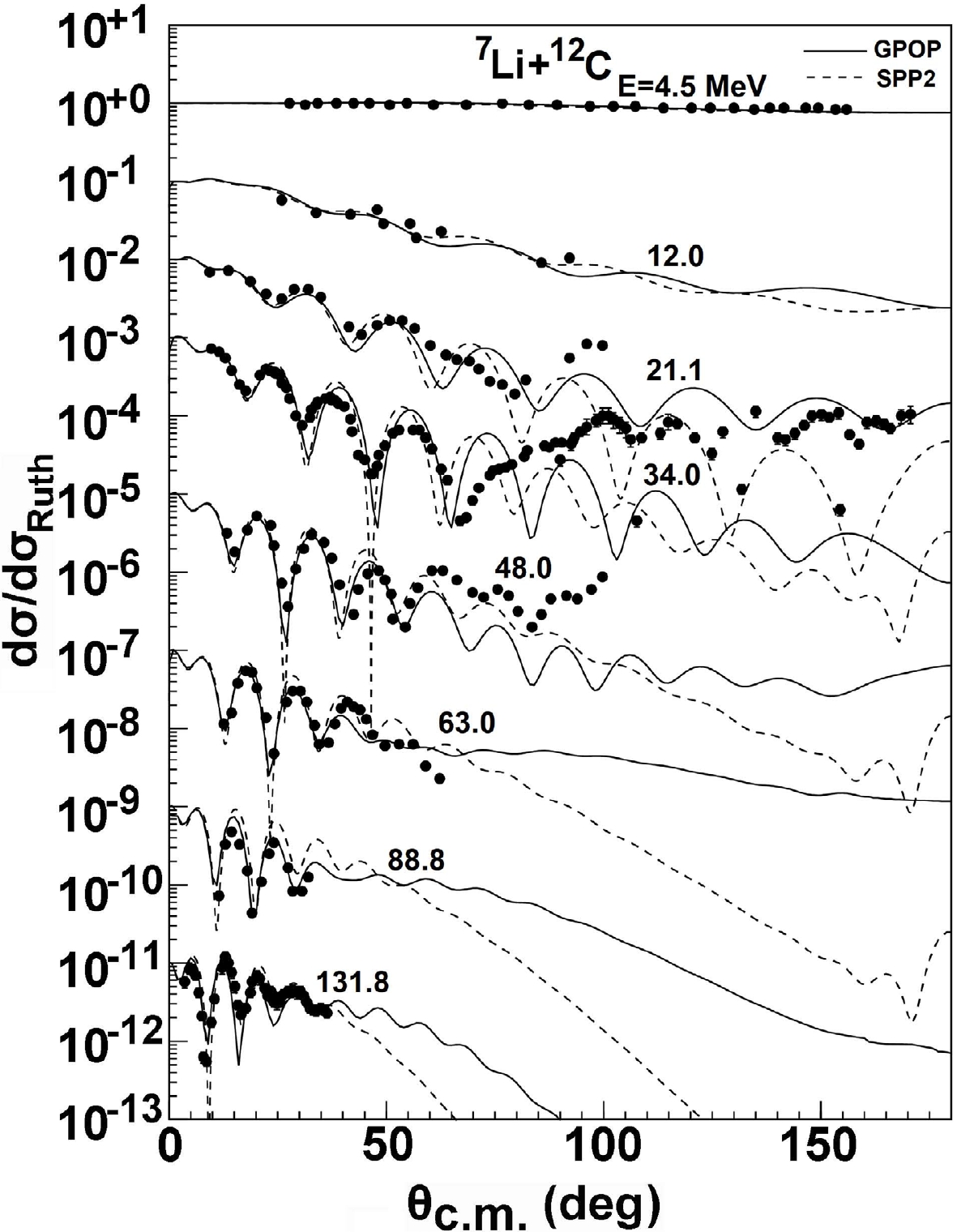
The elastic scattering angular distributions for 12C target are also compared with the various experimental data [27, 31–38], as displayed in Fig. 4. The range of energy is 4.5–131.8 MeV. A good fit is obtained between the calculations and the experimental data at most of the energies in this range. For incident energies 34.0 and 48.0 MeV, the results are also consistent with the data except for at larger angles (θ > 90°), where an upward trend is observed. Meanwhile, a widely expected physics scenario in this case is the strong contribution from the elastic transfer channels to the elastic 7Li + 12C scattering [51, 52].
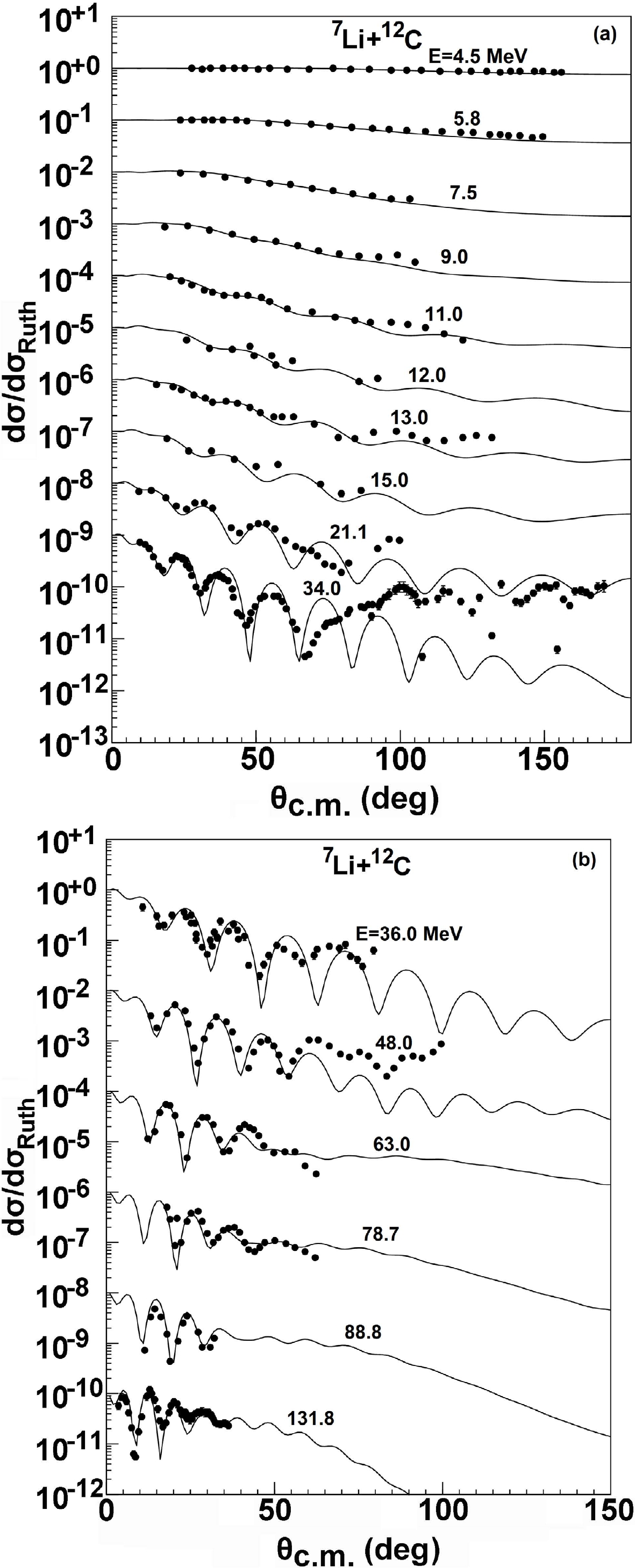
Figure 4. Same as Fig. 1, but for 12C target from 4.5 to 131.8 MeV.
Furthermore, some experimental data of the elastic scattering angular distributions for the 7Li + 13C system are available [26, 31, 34]. Comparisons between the calculations and these data are presented in Fig. 5. As can be observed, they exhibit good consistency from 5.8 to 130.0 MeV, except for 63.0 and 130.0 MeV at backward angles. These data show complex forms with characteristic rapid oscillations at forward angles followed by a marked change in shape at intermediate angles: a plateau develops at θ = 50°–70° which is followed by a deep minimum at θ
$ < $ 80°. This was interpreted as a diffractive effect arising from an angular-momentum-dependent absorption. We adopted an opposite point of view and interpret these structures as refractive effects arising from a fine balance between the real and imaginary components of the optical potential [26, 53].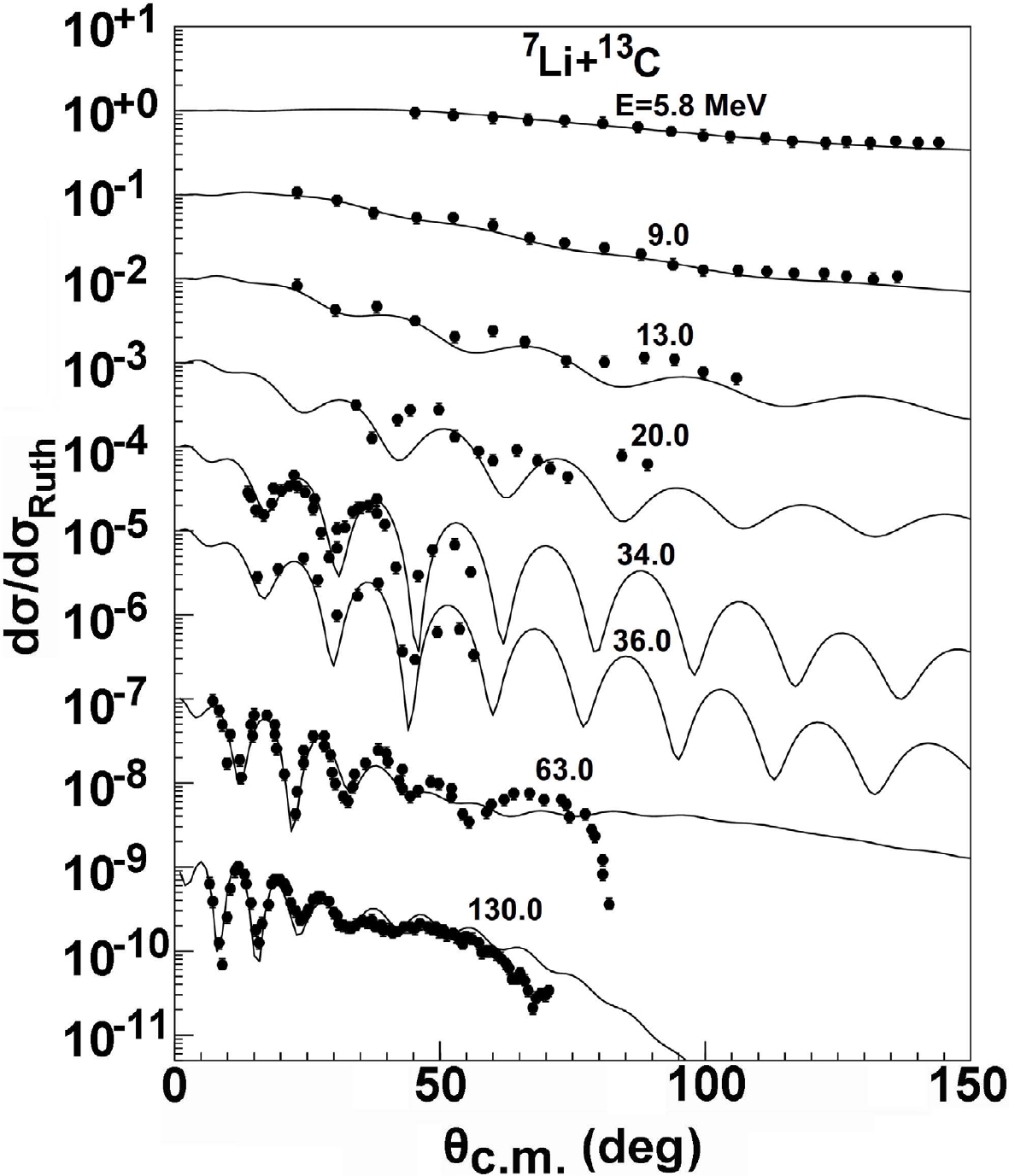
Figure 5. Same as Fig. 1, but for 13C target from 5.8 to 130.0 MeV.
The angular distributions of elastic scattering cross sections for 16O are calculated and compared with the experimental data [31, 34, 41–44], as is shown in Fig. 6. We can see that the results are consistent with the experimental data over the entire range of energies and angles. The elastic scattering angular distribution were measured using different experiments for 10B and 15N [27, 28, 39, 40]. The calculations of the present GPOP also provide a satisfactory description of the elastic scattering data. The results are depicted in Fig. 7.
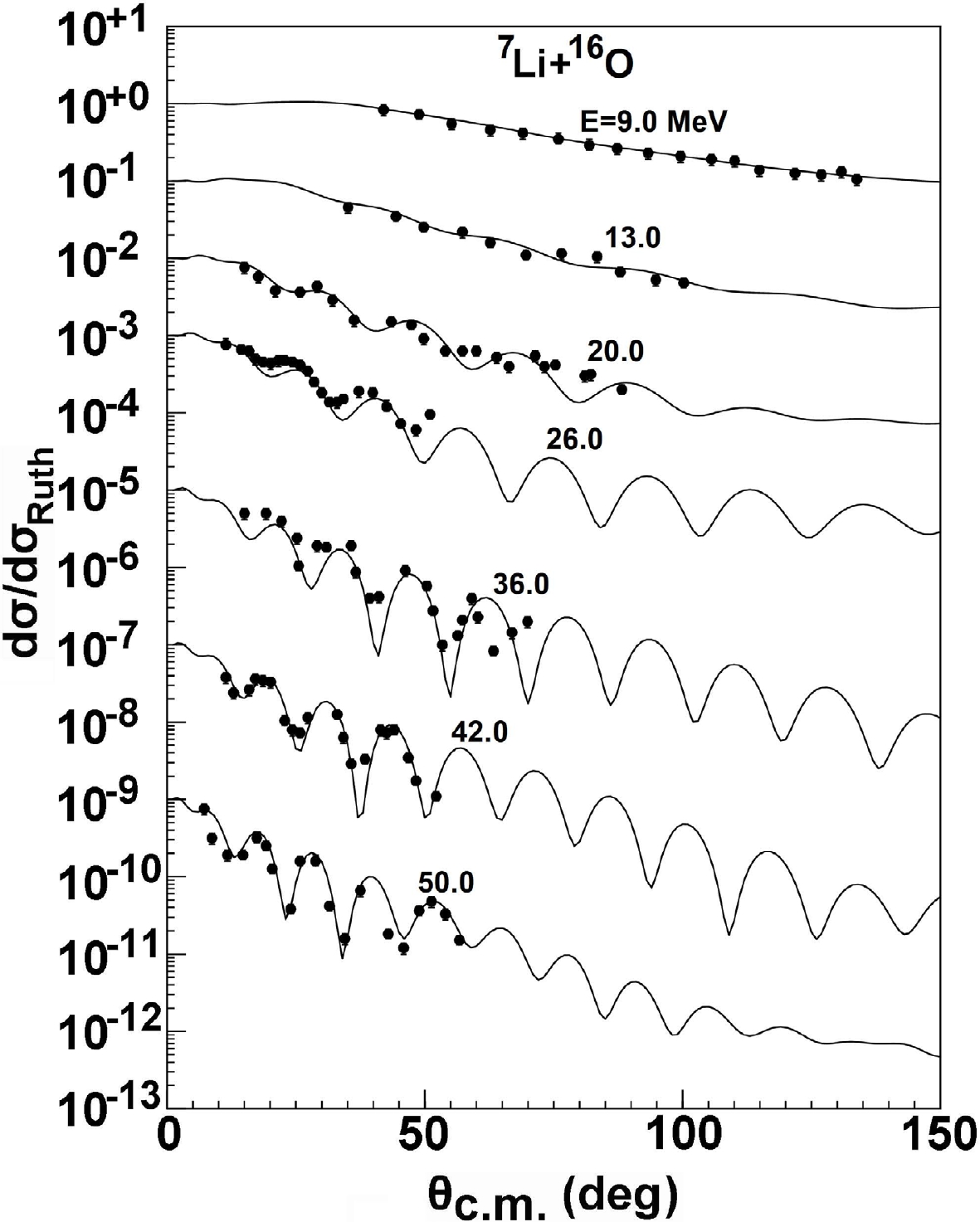
Figure 6. Same as Fig. 1, but for 16O target from 9.0 to 50.0 MeV.
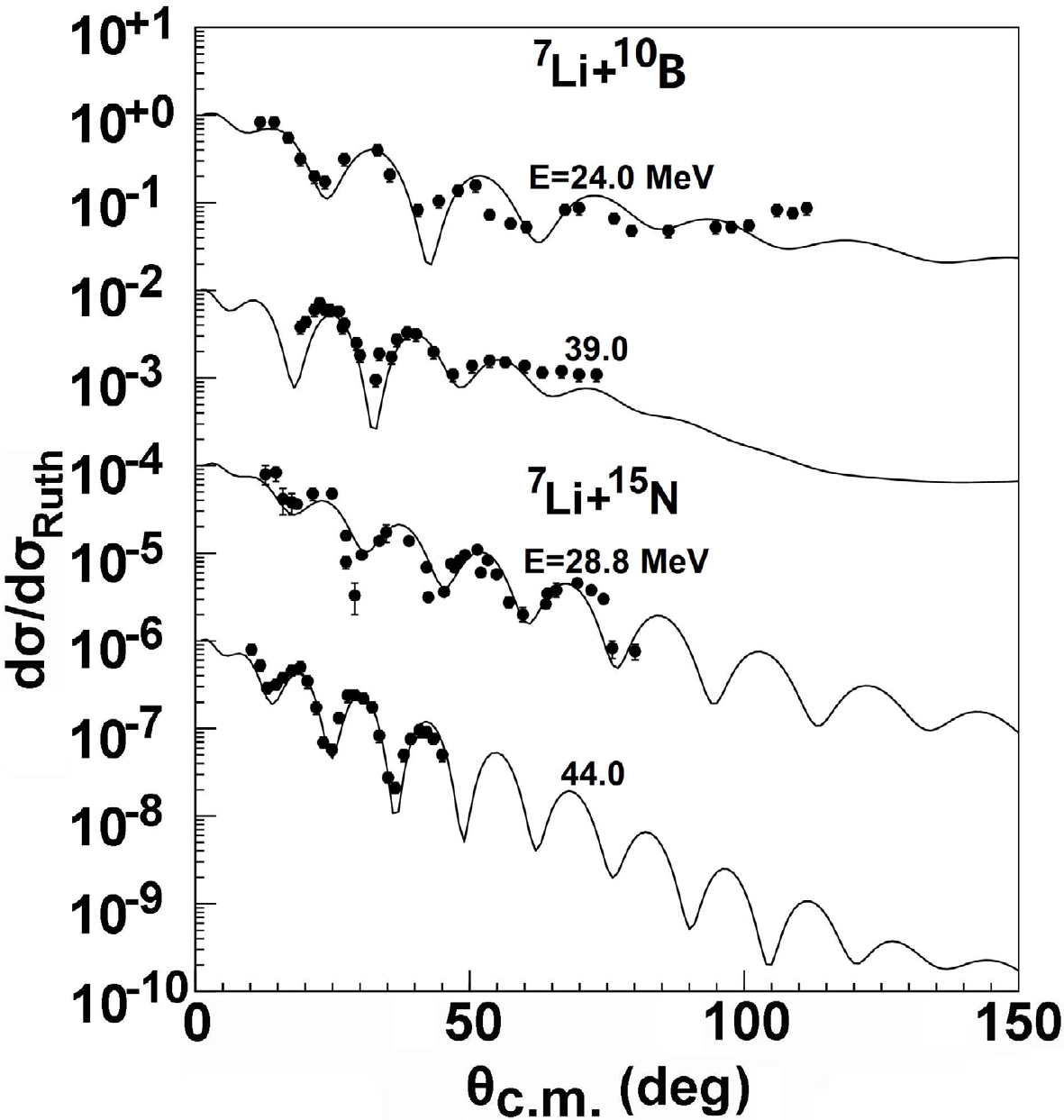
Figure 7. Same as Fig. 1, but for 10B, 15N targets from 24.0 to 44.0 MeV.
Through the above comparison of theoretical calculation results with experimental data, it can be seen that the new GPOPs account well for the overall behavior of the elastic scattering data for 7Li on 1p-shell nuclei over a wide range of energies. Moreover, only small departures from the average parameters are required to obtain fits at each energy as good as those that can be acquired by fitting each angular distribution separately for lighter nuclei. While for backward scattering angles (scattering angle θ > 90°), the calculation is out of phase with the data that exhibit the upward trend. Even these individual fits cannot precisely describe the data in the backward-angle area. This discrepancy shows the possible need for the additional contribution of the other reactions other than those arising from pure shape elastic scattering. The elastic scattering for 7Li on 1p-shell nuclei have been further examined using the microscopic double folding model, which was previously used to study the systematics of 6,7Li and 8B projectiles [49, 54, 55]. In the present calculations, we use the effective nucleon-nucleon (NN) interactions SPP to describe the elastic scattering, which has already been shown to be a reliable potential for the analysis of elastic scattering induced by stable weakly bound nuclei.
We considered the latest version of the SPP, SPP2 [17], which includes realistic information regarding nuclear density of stable isotopes or away from the stability valley. The original SPP has been used as a standard optical potential in many applications, where the standard normalization [50] values
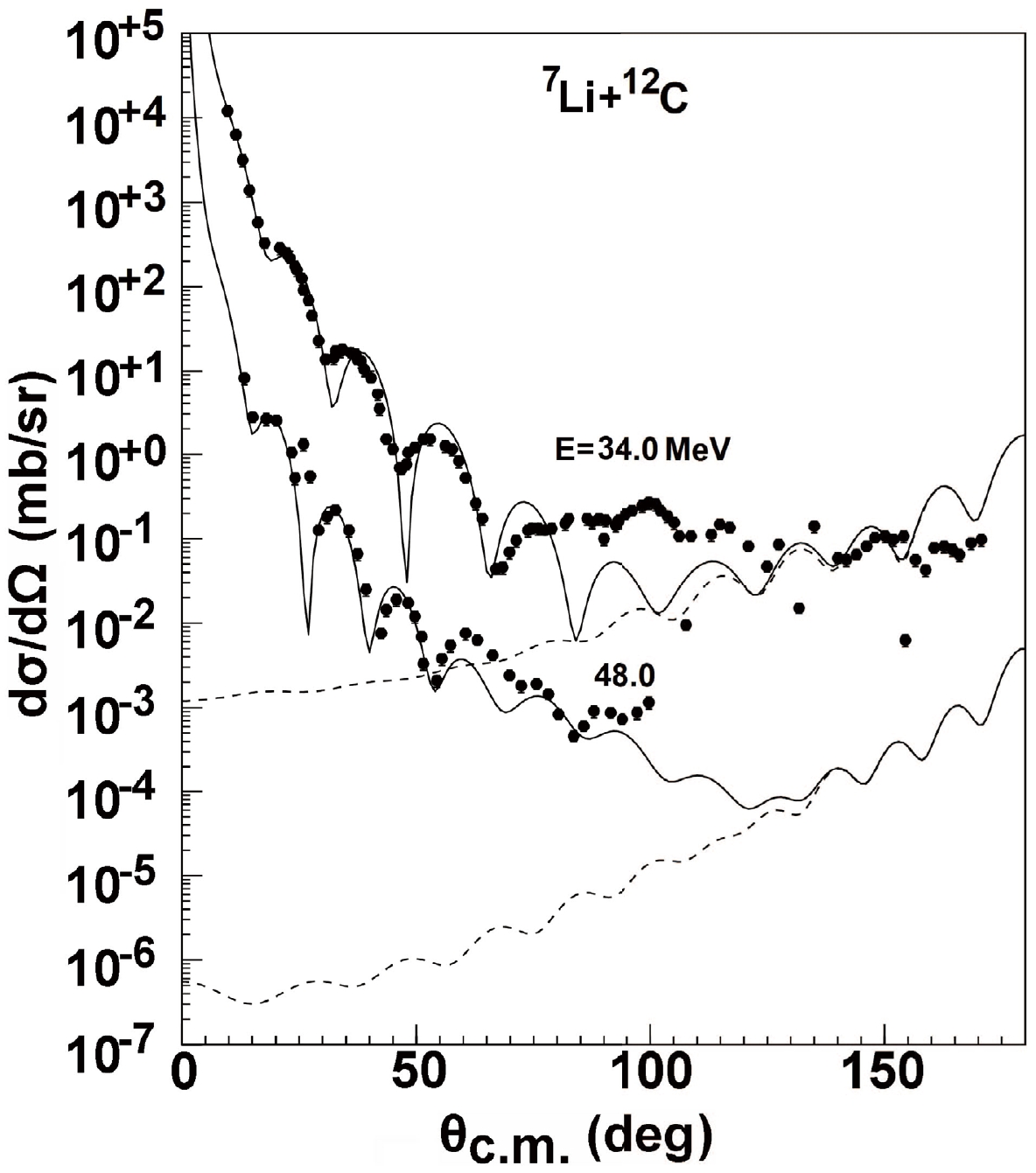
$ N_{R} $ = 1 and$ N_{I} $ = 0.78 for all systems. We consider that the SPP2 can also be used in standard calculations, as long as the parameter values generally assumed for the SPP are adopted, i.e.,$ N_{R} $ = 1,$ N_{I} $ $ \thickapprox $ 0.8. Only in this restricted sense can the SPP2 be considered a parameter-free model. Eventually, to better reproduce the data, the renormalization factors$ N_{R} $ and$ N_{I} $ of real and imaginary parts of the optical potential are allowed to freely vary to best fit the data. For different targets,$ N_{R} $ and$ N_{I} $ differ. The calculations are further compared with the results of Woods-Saxon GPOPs. Figure 8 presents the comparison results of the elastic scattering angular distributions calculated using the Woods-Saxon GPOPs and double folding SPP2 for 7Li on 12C at some energies. Good agreement is apparent with the values obtained when$ N_{R} $ and$ N_{I} $ are tuned to produce the optimum fit to the forward angle elastic scattering data. Here, the real and imaginary normalizations for the SPP2 are$ N_{R} $ = 0.65 and$ N_{I} $ = 0.75, respectively. In the case of scattering, the backward rise due to other processes than direct scattering is quite obvious. The mechanism of elastic transfer is discussed through the DWBA approach in the next section. -
From the above discussion, the global potential reproduces well the positions of the diffraction minima for forward scattering angles, but does not reproduce the scattering data at backward angles, where these experimental data show the upward trend. It is well established that the elastic scattering of nearly identical nuclei at low energies often involves the elastic transfer [56], which leads to a quickly oscillating elastic cross section at backward angles. In this section, the elastic transfer is calculated using a more consistent approach, particular for reproducing the elastic cross sections in the backward angles.
For the system of 7Li + 12C, the target 12C may have the configuration 12C → 7Li + 5Li. The elastic 5Li transfer from 12C to 7Li leads to the final state that is indistinguishable from that of the true elastic 7Li + 12C scattering. Therefore, the elastic 7Li + 12C data at backward angles might include the contribution from the 5Li transfer.
A straightforward method to estimate the strength of the direct (elastic) 5Li transfer in the elastic 7Li + 12C scattering is to add the elastic 5Li transfer amplitude in the DWBA to the elastic scattering amplitude [57, 58]. As the ground state spin-parity of 12C is
$ J^{\pi} = 0^{+} $ , an 5Li particle coupled to a 7Li core with$ J^{\pi} = 3/2^{-} $ can be found in two differential orbitals with angular momentum$ L = 0 $ or$ L = 2 $ . In the calculations, the cluster quantum numbers for a given configuration were obtained from the harmonic oscillator approximation$ {\sum_{i}} 2n_{i} + l_{i} = 2N + L + 1 = 5 $ , where$ n_{i} $ and$ l_{i} $ are the quantum numbers for the cluster constituent nucleons in 12C, and N and L are the principal and orbital quantum numbers for the cluster coupled to the 7Li core. Therefore, 2$ s_{3/2} $ and 1$ d_{3/2} $ configurations are considered in the calculation. Regarding such an approach, our DWBA calculation presents a reasonable description of the elastic 7Li + 12C data at different energies, and specifically at backward angles. The spectroscopic amplitudes (SAs) for the configuration 12C$ \rightarrow $ 7Li + 5Li were obtained as 1.41 and 0.9 for the 2$ s_{3/2} $ and 1$ d_{3/2} $ orbits, respectively. The results for 7Li + 12C at 34.0 and 48.0 MeV are displayed in Fig. 9. From the figure, it is clear that the results provide a significantly improved description of the backward angle angular distributions. While the calculations underestimate the data at the intermediate angles, where the contribution of 7Li breakup coupling effect may occur [59–61]. This will be the focus in the followup research. -
Furthermore, the inelastic scattering angular distributions of different excited states for the reactions of 7Li induced 1p-shell nuclei were calculated and compared with different experimental data [20, 30, 34, 62]. As is known, the reliable GPOP can produce a reasonable description of the inelastic scattering angular distributions. Therefore, we used the obtained GPOP of 7Li on 1p-shell nuclei to predict the inelastic scattering angular distributions. To investigate the effects of the target excitation on the elastic channel as well as to analyze the data of inelastic scattering to the excited states for different targets, we performed a CC calculation, neglecting an explicit inclusion of the coupling to the projectile breakup states. The calculations were performed using the code FRESCO [63].
Figure 10 presents the inelastic scattering angular distributions of the first discrete levels for 7Li, which were compared with the experimental data [20] between 8.0 and 17.0 MeV. From these figures, we can see that the predictions using the GPOP of 7Li on 7Li nuclei are in good agreement with the experimental data of inelastic scattering angular distributions. Figure 11 presents the inelastic scattering angular distributions of the first discrete levels for 12C, which are compared with the experimental data [34, 62] between 34.0 and 131.8 MeV. The overall agreements between the CC results and the data are satisfactory at different incident energies.
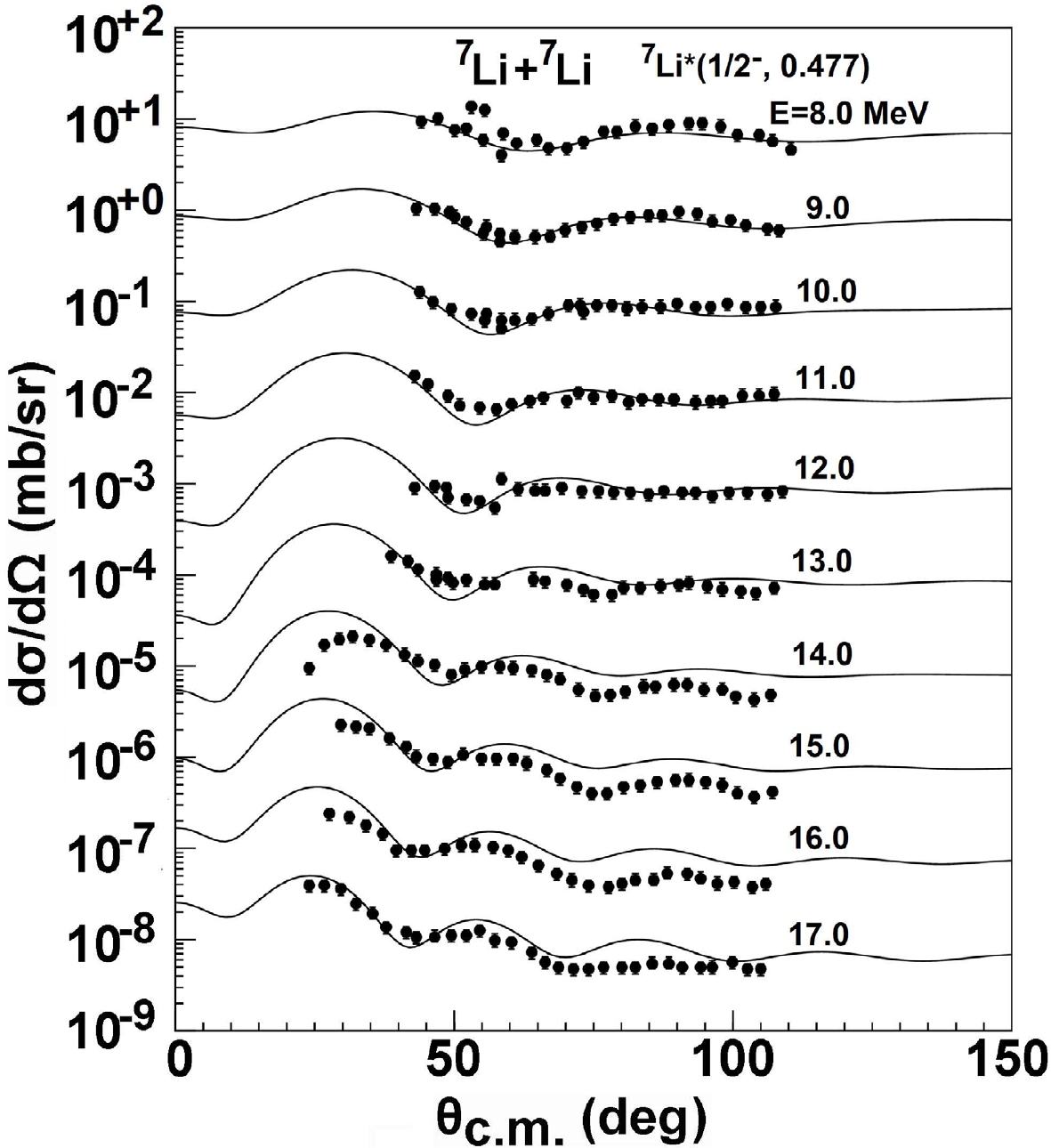
Figure 10. The inelastic scattering angular distributions of the first excited state are calculated and compared with the experimental data for the reaction of 7Li induced 7Li target at different incident energies.

Figure 11. Same as Fig. 10, but for 12C target.
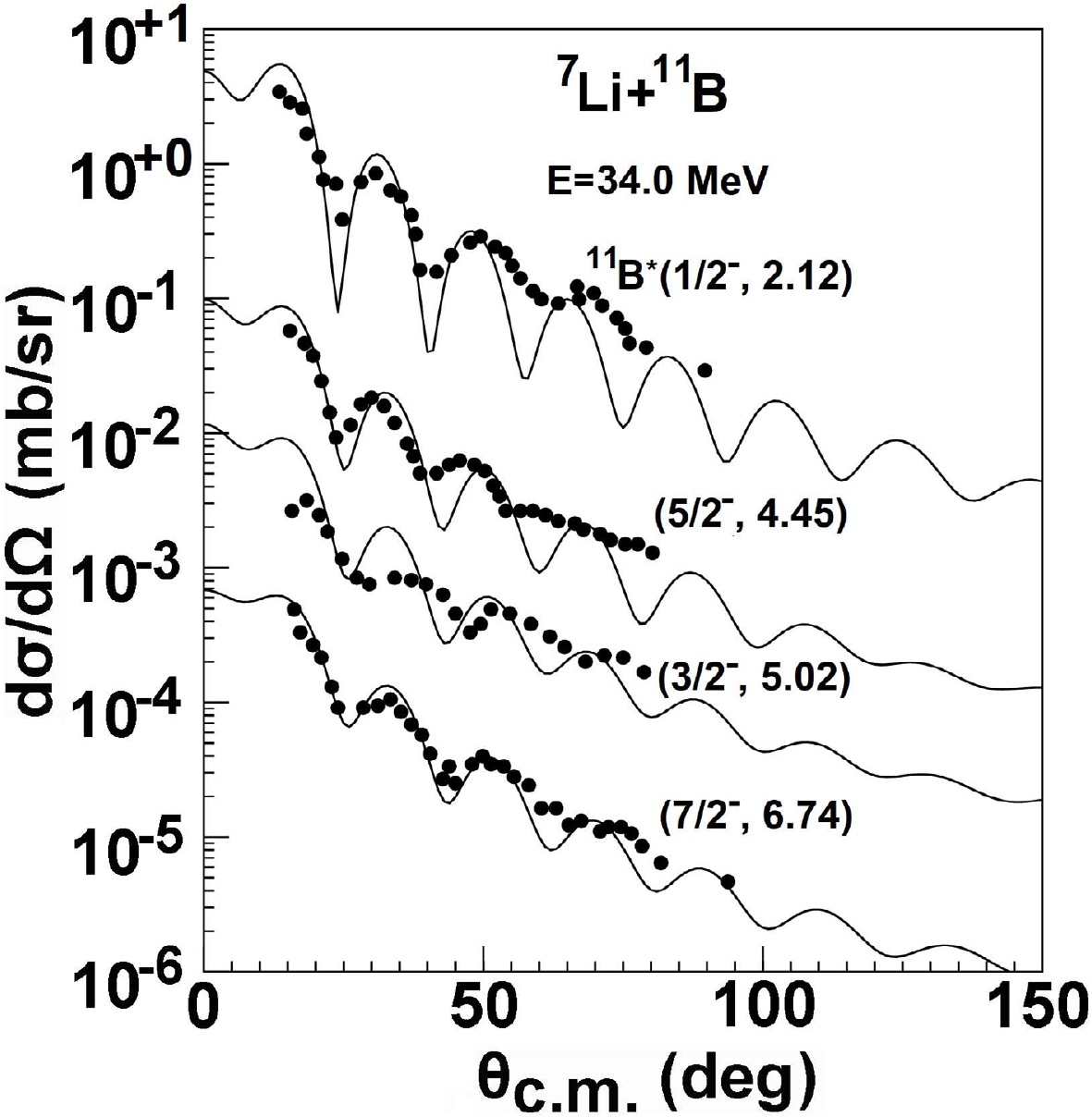
Figure 12 depicts the inelastic scattering angular distributions for the target 11B at 34.0 MeV for various excited states. The results provide a reasonable description for the inelastic scattering data. Although the strength of the experimental cross section is not perfectly reproduced by the CC calculations, the obtained shapes of both the theoretical and experimental angular distributions are quite similar.
-
The GPOPs of 7Li induced 1p-shell nuclei were constructed considering the experimental data of elastic scattering angular distributions from 9Be to 16O targets in the energy range of 4.5–131.8 MeV, as well as the elastic scattering data with the 7Li target from 8.0 to 42.0 MeV. The GPOPs provide a satisfactory description of elastic scattering data due to the simple energy dependence of the potential parameters. For backward angles at some energies, the elastic scattering data exhibit an upward trend, which may be caused by the contribution of other reaction mechanisms. Furthermore, the elastic scattering angular distributions were reanalyzed using a microscopic method within the framework of the new SPP2 for these reactions via adjustment of the real and imaginary normalizations. The results were compared with the experimental data and those of the GPOPs. Similar degrees of coincidence were determined between the calculations and the experimental data. Furthermore, the elastic 5Li transfer was investigated using the DWBA approach to improve the fit between the calculations and the experimental data at backward angles. Reasonable agreements were achieved between them. Considering the obtained GPOPs, the inelastic scattering angular distributions were predicted for different excited states using the CC method. A satisfactory agreement was also realized between them. Overall, the theoretical results using the obtained GPOPs of 7Li induced 1p-shell nuclei provide a good description of the experimental elastic and inelastic scattering angular distributions. However, more experimental data for lighter targets is still required to understand the importance of the contributions from different reaction mechanisms on the elastic scattering in detail.
Description of elastic scattering for 7Li-induced reactions on 1p-shell nuclei
- Received Date: 2023-11-27
- Available Online: 2024-02-15
Abstract: The experimental data of elastic scattering angular distributions for 9Be, 10B, 11B, 12C, 13C, 15N, and 16O targets from 4.5 to 131.8 MeV and 7Li target from 8.0 to 42.0 MeV are fitted to realize the global phenomenological optical potentials (GPOPs) for the 7Li-induced reactions on 1p-shell nuclei. Thus, the 7Li elastic scattering from the 1p-shell nuclei can be systematically described using the established GPOPs. The elastic scattering angular distributions are also reanalyzed using a microscopic method within the framework of the new version of double folding São Paulo potential (SPP2). To better describe the elastic scattering at backward angles, the contribution of elastic transfer is further estimated by the distorted wave Born approximation (DWBA) method. Based on the obtained GPOPs, the inelastic scattering angular distributions are also obtained through the coupled channels (CC) method for the different excited states.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: