-
Luminosity monitoring is the standard task for all collider experiments. One of the traditional processes for high-precision luminosity measurements at electron-positron colliders is Small-Angle Bhabha Scattering (SABS). This process has a clean detector signature and very large cross section that sharply increases at small scattering angles. From a theoretical point of view, it is almost a pure Quantum Electrodynamics (QED) process; therefore, it can be described very accurately within the perturbative quantum field theory. SABS occupies a special place in the physics programme of future
$ e^+e^- $ colliders such as FCCee [1] and CEPC [2]. Given the extremely large expected statistics, luminosity measurements with precision of$ 10^{-4} $ or better are required. The theoretical accuracy for SABS calculations must be significantly better than this target precision in order not to worsen the resulting uncertainty.The most advanced codes for theoretical estimation of luminosity with the help of
$\mathrm{SABS}$ are$\mathrm{BabaYaga}$ [3–7] and$\mathrm{BHLUMI}$ [8]. Monte Carlo (MC) generator$\mathrm{BHLUMI}$ is a pure QED tool; its theoretical uncertainty is estimated to be approximately 0.037% (see Table 2 in [9]). In that study, future prospects of a theoretical precision of$ 1 \times 10^{-4} $ were presented for luminosity measurements in future colliders at the Z peak.The new release of
$\mathrm{BabaYaga}$ [10] accounts for the various sources of radiative corrections, i.e., QED, and (electro)weak and higher-order effects. This generator is mainly intended for large angle Bhabha scattering, with theoretical errors of approximately 0.1%.In this paper, we present a study of SABS based on the
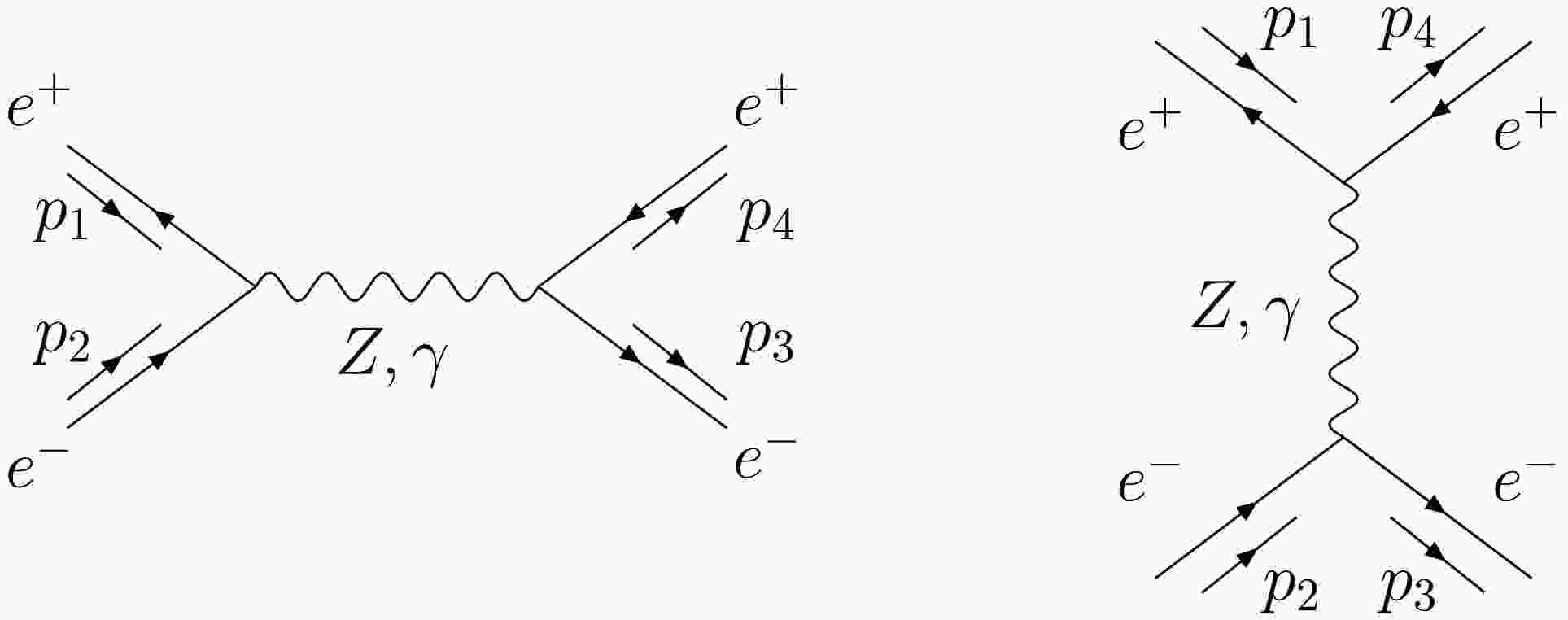
$\mathrm{MCSANC}$ integrator [11] and$\mathrm{ReneSANCe}$ generator [12]. The process of polarized Bhabha scattering (see Fig. 1)$ e^+(p_1) + e^-(p_2) \rightarrow e^-(p_3) + e^+(p_4) + (\gamma (p_5)) $

was calculated at the complete one-loop electroweak level [13]. In addition, we consider the higher-order corrections using the
$ \Delta\rho $ formalism, which are necessary to meet the high-precision requirements of future$ e^+e^- $ experiments. The ρ parameter [14] is defined as the relative strength between the neutral- and charged-current interactions and is used for description of universal propagator corrections. At the tree level, it is equal to unity. Deviation of ρ from unity due to higher-order electroweak corrections is called$ \Delta\rho $ . The details of Bhabha scattering implementation into MC$\mathrm{ReneSANCe}$ are described in [12].The aim of the present paper is to report on the study of the Bhabha scattering cross section at arbitrarily small or even vanishingly small scattering angles. The contribution from electron scattering at very small angles introduces additional, potentially sizeable, effects in the theoretical interpretation of the measured
$\mathrm{SABS}$ cross section value. We provide an advanced assessment of SABS events with scattering angles under 10 mrad. Previously, this kinematic region was described by$\mathrm{BHAGEN-1PH}$ [15]; however, the calculations were limited to the contribution of hard photon Bremsstrahlung.The outline of the paper is as follows. In Section II, we compare the results for alternative MC codes in the conditions and setup of the CERN Workshop [16]. In Section III, we report on numerical results for the integral cross sections and angular event distributions of experimental interest in
$\mathrm{SABS}$ . We also discuss different sources of radiative corrections and study the effect from the minimum cut-off on electron scattering angle. -
To verify the technical precision of our codes, we conducted a tuned comparison with results presented in the proceedings of the CERN Workshop [16], devoted to event generators for Bhabha scattering at LEP for the non-calorimetric event selection called BARE1 and the calorimetric one called CALO1. All numbers were produced within the setup of this workshop for the
$ {\cal{O}} (\alpha) $ matrix element without contribution of the Z exchange, s-channel, up-down interference and vacuum polarization, and for various values of the energy-cut$ z_{\rm{min}} = s'/s $ , where$ s' $ is the collision energy after initial state radiation (ISR). Table 1 shows a good agreement within numerical precision.$ z_{\rm{min}} $ 

$\mathrm{ReneSANCe}$ 

$\mathrm{BHLUMI}$ 

$\mathrm{ReneSANCe}$ 

$\mathrm{BHLUMI}$ 

BARE1: σ /nb CALO1: σ/nb .100 166.06(1) 166.05(2) 166.34(1) 166.33(2) .300 164.76(1) 164.74(2) 166.06(1) 166.05(2) .500 162.26(1) 162.24(2) 165.30(1) 165.29(2) .700 155.44(1) 155.43(2) 161.80(1) 161.79(2) .900 134.39(1) 134.39(2) 149.93(1) 149.93(2) Table 1. Comparison of BARE1 and CALO1 for the
$ {\cal{O}} (\alpha) $ matrix element. Z exchange, s-channel, up-down interference, and vacuum polarization are switched off. The center-of-mass energy is$ \sqrt{s} = 92.3 $ GeV. Results for various values of the energy-cut$z_{\rm{min}} = s'/s$ are shown. -
All results were obtained in the
$ \alpha(0) $ electroweak scheme using the set of input parameters listed in Table 2.$ \alpha^{-1}(0) $ = 137.035999084

$ M_W $ = 80.379 GeV

$ \Gamma_W $ = 2.0836 GeV

$ M_Z $ = 91.1876 GeV

$ \Gamma_Z $ = 2.4952 GeV

$ M_H $ = 125.0 GeV

$ m_e $ = 0.51099895 MeV

$ m_\mu $ = 0.1056583745 GeV

$ m_\tau $ = 1.77686 GeV

$ m_d $ = 0.083 GeV

$ m_s $ = 0.215 GeV

$ m_b $ = 4.7 GeV

$ m_u $ = 0.062 GeV

$ m_c $ = 1.5 GeV

$ m_t $ = 172.76 GeV.

Table 2. Input parameters.
In addition, the following conditions were assumed:
● electrons were allowed to scatter by any angle, down to zero,
● luminosity acceptance was assumed to be
$30 \; {\rm{mrad}} < \theta < 174.5\; {\rm{mrad}}.$ To demonstrate
$\mathrm{ReneSANCe}$ capabilities, we generated 100 million events for the Bhabha cross section for the two center-of-mass (c.m.s.) energies$ \sqrt{s}= 91.18$ GeV and 240 GeV; each arm of the luminometer registered an energy shower from an electron or photon. We did not apply any restrictions on the minimum scattering angle of an electron, i.e., the electron was allowed to scatter down to zero.We used two different setups for event selection (ES) called ES-BARE (non-calorimetric) and ES-CALO (calorimetric). In the ES-BARE case, we defined the SABS cross section by choosing events where each arm of the calorimeter was hit by an electron or positron. These electrons or positrons must have an energy of at least half the energy of the beam (
$ E_{\rm{beam}} $ ). Regarding the ES-CALO setup, we considered a calorimetric detector that cannot distinguish electrons from photons. In other words, the cross section was determined by events in which each arm of the calorimeter was hit by either a photon or an electron carring at least half of the beam energy. -
To present the main sources of theoretical uncertainties of the one-loop cross section
$ \sigma^{\rm{1-loop}} $ , we divided it into gauge-invariant subsets. When evaluating the contribution cross section at the Born level (leading order, LO)$ \sigma^{\rm{Born}} $ , both photon and Z-boson exchanges were taken into account. To quantify the impact of different contributions, we divided them into gauge-invariant subsets: QED one-loop corrections$ \sigma^{\rm{QED}} $ , vacuum polarization contribution$ \sigma^{\rm{VP}} $ , and pure weak contribution$ \sigma^{\rm{weak}} $ as the difference between the complete one-loop electroweak correction and its pure QED part$ \sigma^{\rm{QED}} $ . The leading higher-order (ho) corrections are denoted as$ \sigma^{\rm{ho}} $ .In Table 3, we show the results of the various radiative contributions to the total cross section for the Z-pole and
$ \sqrt{s}=240 $ GeV and evaluate the corresponding relative corrections as$ \delta = {\sigma^{\rm{contr.}}}/{\sigma^{\rm{Born}}} $ .$ \sqrt{s} $ /GeV

91.18 240 $ \sigma^{\rm{Born}} $ , pb

$ 135008.970(1) $ 

$ 19473.550(1) $ 

$ \delta^{\rm{one}-loop} $ , %

$ -1.562(1) $ 

$ -0.821(1) $ 

$ \delta^{\rm{total}} $ , %

$ -1.420(1) $ 

$ -0.574(1) $ 

$ \delta^{\rm{QED}} $ , %

$ -6.296(1) $ 

$ -7.002(1) $ 

$ \delta^{\rm{VP}} $ , %

$ 4.6527(1) $ 

$ 6.1866(1) $ 

$ \delta^{\rm{weak}} $ , %

$ 0.0088(1) $ 

$ -0.0064(1) $ 

$ \delta^{\rm{ho}} $ , %

$ 0.1418(1) $ 

$ 0.2475(1) $ 

Table 3. Results of the various radiative contributions to the total cross section for the Z-pole and
$ \sqrt{s} $ = 240 GeV for ES-BARE.The leading higher-order EW corrections
$ \delta^{\rm{ho}} $ to SABS are included in our calculations through the$ \Delta\alpha $ and$ \Delta\rho $ parameters. A detailed description of our implementation of this contribution was presented in [17]. At two-loop level, the above corrections consist of the EW at$ {\cal{O}}(G_{\mu}^2) $ and mixed EW$ \otimes $ QCD at$ {\cal{O}}(G_{\mu}\alpha_s) $ parts. For SABS, the bulk of the considered higher-order effects is due to running α. -
Another possible bias for luminosity measurements arises from events in which an electron is scattered at a very small angle and escapes detection. Such events can be accepted by a luminometer owing to energetic photons radiated at angles large enough to be detected in the detector. This effect would lead to a bias in luminosity measurements if the data are analyzed with an MC tool that uses a minimum scattering angle cut-off.
We used the
$\mathrm{MCSANC}$ integrator to compare results from the ES-BARE setup (ignoring photons) with the ES-CALO setup in which the calorimeter can be hit by either an electron or a photon. The presence of a high-energy photon provides a natural regularization of divergence at zero electron scattering angles. Although electrons are allowed to be scattered by zero angle, the number of such events is small because of the requirement to have an energetic photon within the acceptance of the calorimeter. We defined the luminosity acceptance in the range of 30 mrad to 10 degrees (174.5 mrad), which is typical for LEP detectors and for future$ e^+e^- $ colliders such as FCCee, CEPC, and ILC.This effect is reflected in Table 4. Note that the ES-CALO cross-section at
$ \sqrt{s}= 91.18 $ and 240 GeV is 3% larger than the ES-BARE Bhabha cross-section; both beam particles must hit the luminometer. The largest part of the difference is due to events with collinear photon or events in which an electron is scattered by an angle larger than the luminosity acceptance, while a hard ISR photon hits the luminometer. Such effect does not introduce any experimental bias because the electron can be detected by large-angle calorimeters and the process can be simulated by any Bhabha generator.$ \sqrt{s} $ /GeV

91.18 240 $ \sigma^{\rm{Born}} $ , pb

$ 135008.970(1) $ 

$ 19473.550(1) $ 

$ \delta_1^{\rm{QED}} $ , %

$ -6.296(1) $ 

$ -7.002(1) $ 

$ \delta_2^{\rm{QED}} $ , %

$ -3.618(1) $ 

$ -3.986(1) $ 

$ \delta_3^{\rm{QED}} $ , %

$ -3.488(1) $ 

$ -3.854(1) $ 

$ \Delta^{\rm{QED}}({\rm{\vartheta}< 0.030}) $ 

$ 1.30(1)\times 10^{-3} $ 

$ 1.32(1)\times 10^{-3} $ 

Table 4. Born cross sections and relative corrections for
$ \sqrt{s} $ = 91.18 GeV and 240 GeV. Here,$ \delta_1^{\rm{QED}} = \delta $ (ES-BARE) is the QED correction for the ES-BARE setup,$ \delta_2^{\rm{QED}} = \delta $ (ES-CALO,$ \vartheta > 0.030) $ is the QED correction for the ES-CALO setup with electron scattering angles larger than the minimum luminosity acceptance, and$ \delta_3^{\rm{QED}} = \delta $ (ES-CALO) is the QED correction for the ES-CALO setup with arbitrary electron scattering angles.Additionally, it was found that approximately 1.4 permille of the total cross section for both energies is represented by events with electron scattering angles below the given luminometer acceptance angle of 30 mrad. The size of this effect,
$ \Delta^{\rm{QED}}({\rm{\vartheta} < 0.030}) $ , can be derived from Table 4 as the difference between$ \delta_3^{\rm{QED}} $ and$ \delta_2^{\rm{QED}} $ . Note that the Table only includes the technical uncertainty of numerical integration; estimates of the corresponding theoretical uncertainties will be presented timely. -
Next, we show the numerical results for several angular distributions obtained with MC generator
$\mathrm{ReneSANCe}$ . We considered the distribution of electron scattering angles between the outgoing and incoming electrons as well as the distribution according to the angle at which the photon was emitted.We present angular distributions of two types:
a) distribution of events by scattering angle of the Bremsstrahlung photon
$ \vartheta_{15}=\vartheta_\gamma $ , i.e., the angle between particle$ p_1 $ (initial positron) and particle$ p_5 $ (photon),b) distribution of events by positron scattering angle
$ \vartheta_{14} $ , i.e., the angle between particle$ p_1 $ and particle$ p_4 $ .Z resonance
Figure 2 presents the angular distributions of type a) on the left side and type b) on the right side for c.m.s.
$ \sqrt{s} = 91.18 $ GeV. The vertical axes show the relative fraction of events in a given bin. The sum of all events is normalized to 1.0 and the numbers in the frames show the fractions of events within the range of a given plot. As can be seen from the plots, the event yield vanishes when the lepton scattering angle approaches zero. Sharp edges at 1.7 and 10 degrees correspond to the acceptance of the luminometer. Events with leptons scattered beyond the luminometer acceptance correspond to detection of energetic photons.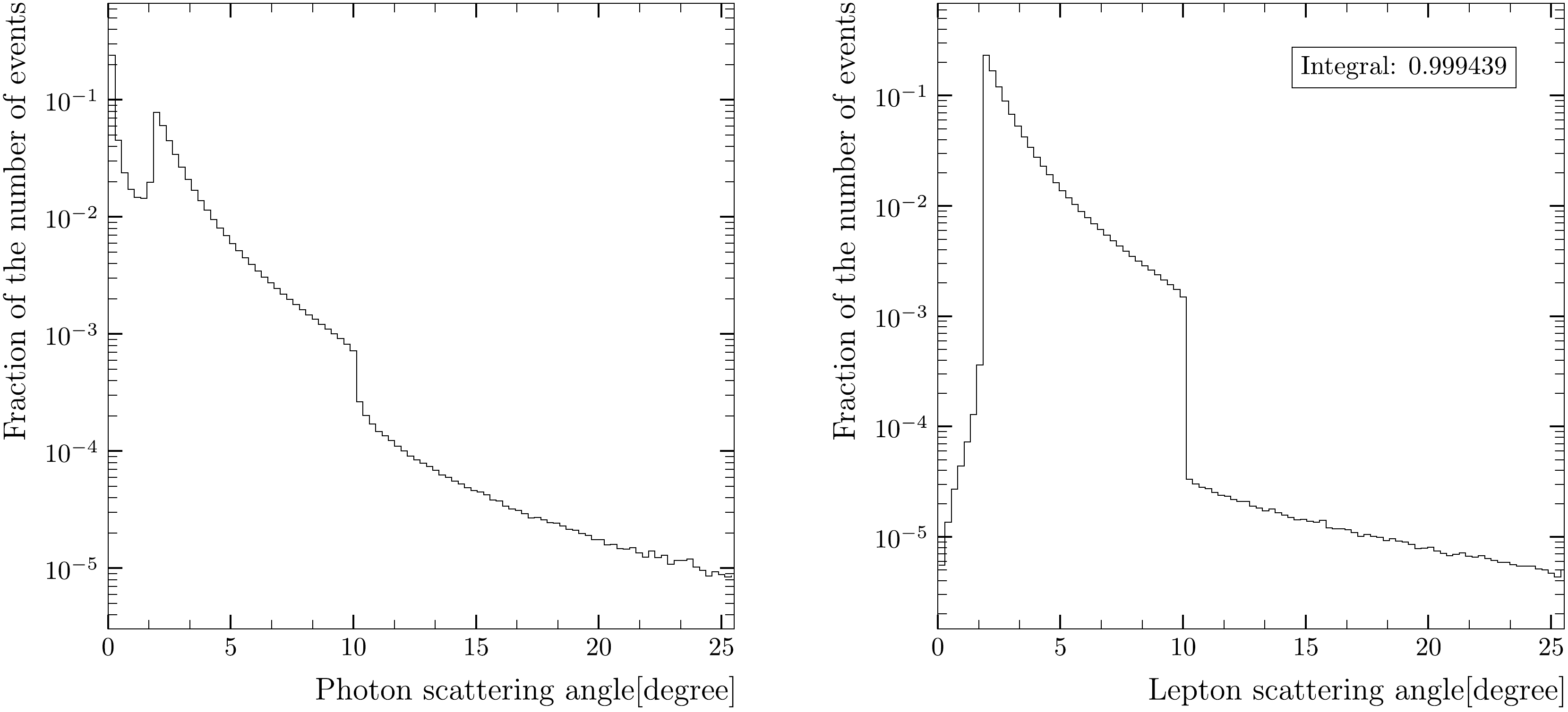
Figure 2. Angular distributions of type a) on the left side and type b) on the right side for
$ \sqrt{s} = 91.18 $ GeV.Figure 3 shows the distributions of electrons scattered at an angle less than the acceptance of the luminosity calorimeter. The peak at nearly zero electron scattering angles is due to the terms proportional to
$ m_e^2/t^2 $ (here t is the square of the electron momentum transferred), which are present in the differential cross section of the radiative Bhabha process (see for instance Ref. [18]). The total fraction of the events within the angular range of$ (0, 30) $ mrad is approximately 1.3 permille. For the angular range of 0−10 mrad, the relative event yield is$0.65\times 10^{-4}$ . Therefore, an MC generator cut-off on electron (and positron) scattering angles less than 10 mrad would be safe if the experimental systematic error on luminosity measurement is expected to be at a level of$ 10^{-4} $ .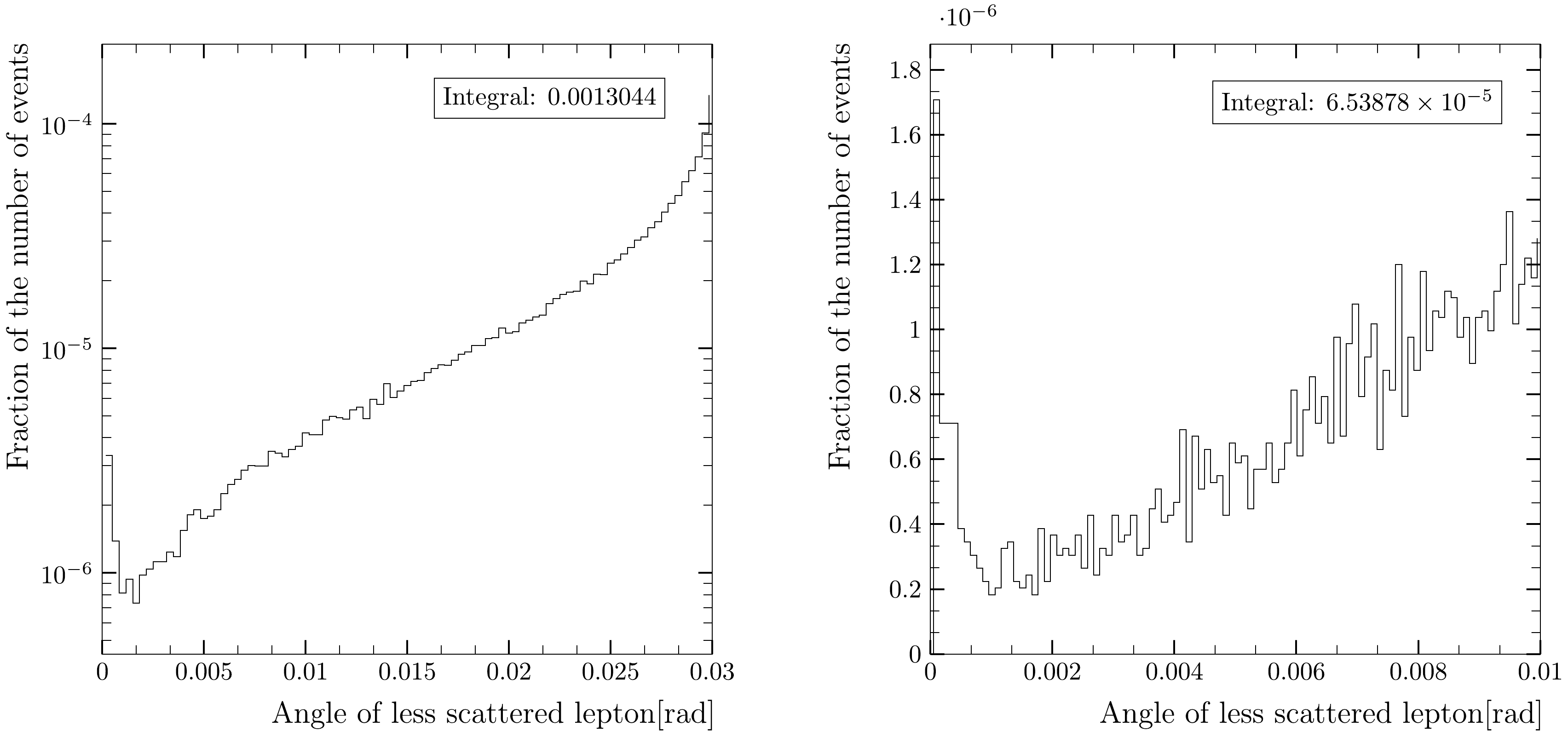
Figure 3. Angular distributions of type b) in a range of
$ (0, 30) $ mrad (left) and$ (0, 10) $ mrad (right) for$ \sqrt{s} = 91.18 $ GeV.Center-of-mass energy of 240 GeV
Figures 4, 5 show the same angular distributions for the 240 GeV collision energy. The relative event yields are similar to the case of Z resonance, i.e., 1.3 permille below 30 mrad and less than
$ 10^{-4} $ below 10 mrad.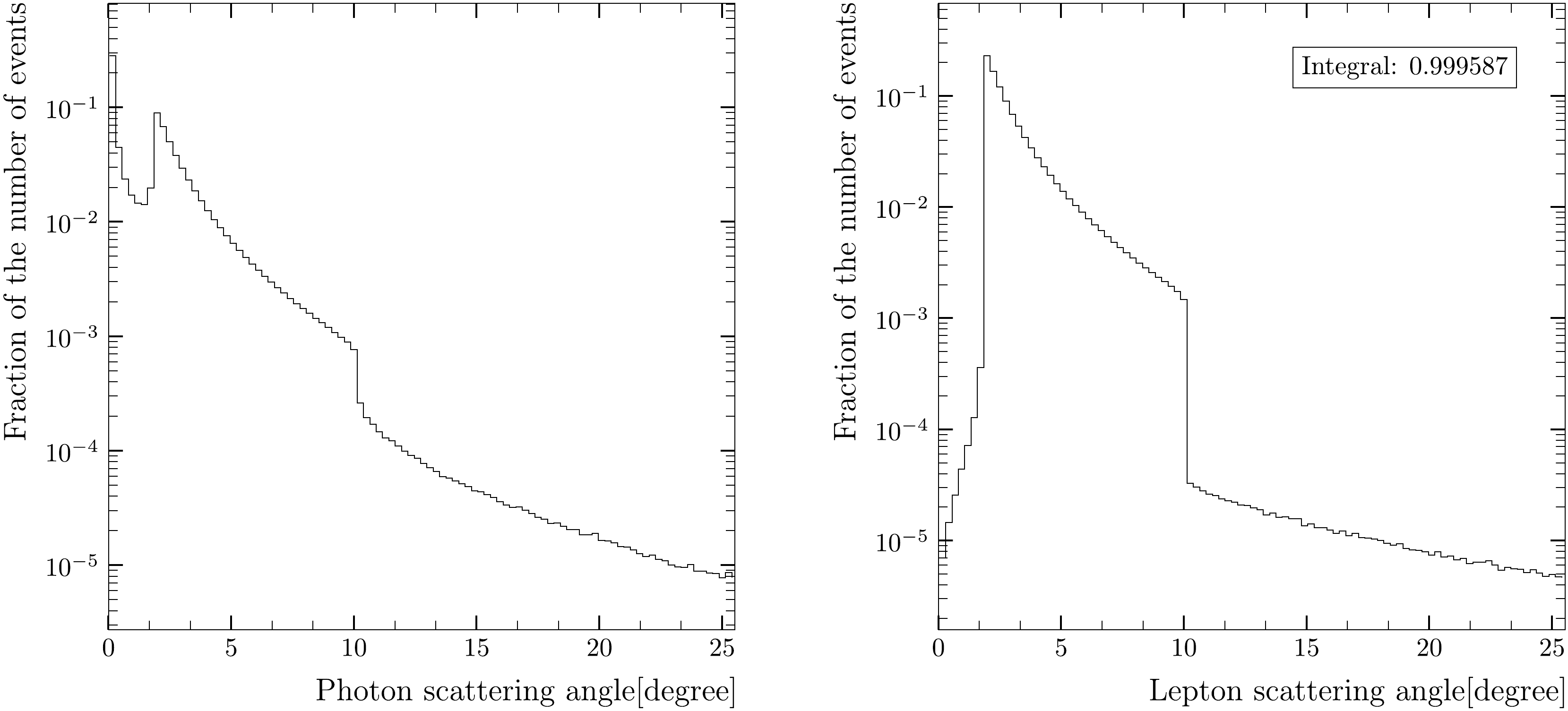
Figure 4. Angular distributions of type a) on the left side and type b) on the right side for
$ \sqrt{s} = 240 $ GeV.
Figure 5. Angular distributions of type a) on the left side and type b) on the right side for
$ \sqrt{s} = 240 $ GeV.Angular cut-off of 18.9 mrad
The OPAL experiment at LEP has partially taken into account the effect of very low angle scattering of electrons by generating events with a minimum angular cut-off of 18.9 mrad [19], which is considerably lower than the experimental acceptance domain. The contribution of scattering by smaller angles was estimated by extrapolation to be less than
$2\times 10^{-5}$ and was neglected. However, this simple extrapolation could underestimate the neglected contribution because of the peak at extremely small angles shown in Fig. 5. Our calculations show that this neglected contribution amounts to approximately$2.3 \times 10^{-4}$ at a collision energy of 91 GeV. This is still within the total theoretical uncertainty of$5.4\times 10^{-4}$ assumed in [19]1 . -
We applied the Monte Carlo
$\mathrm{MCSANC}$ integrator and$\mathrm{ReneSANCe}$ generator to describe small-angle Bhabha scattering. We verified that the results of the two programs are consistent with each other within statistical errors. At the level of one-loop QED radiative corrections, their results also agree with those of the BHLUMI event generator [8]. We considered the leading effects due to higher-order electroweak corrections and vacuum polarization. We examined SABS as a possible process to monitor the luminosity in future$ e^+e^- $ experiments aiming at a level of uncertainty of$ 10^{-4} $ . In this study, we limited ourselves to considering only perturbative effects, whereas in a realistic situation, other effects must be taken into account, for example, beamstrahlung and the final size of the beams [20, 21].The unique features of the
$\mathrm{SANC}$ tools allow generating radiative Bhabha events with electron scattering angles down to zero. This in turn allows considering events in which one arm of the luminosity calorimeter is fired by an energetic ISR photon, while an electron is scattered by a very small angle and escapes detection. Based on calculations from both the$\mathrm{MCSANC}$ integrator and$\mathrm{ReneSANCe}$ generator, we observed a contribution of 1.3−1.4 permille from events with scattering angles less than 30 mrad, both at Z pole and 240 GeV. This effect represents a significant bias given the high experimental precision expected in future colliders. In particular, the bias can influence the measurements of total luminosity, the effective number of neutrino flavors$ N_\nu $ , etc. To meet the expected precision of future colliders ($ \sim 10^{-4} $ ), we recommend to generate events with an angular cut-off less than 10 mrad or use generators capable of generating zero scattering angles.To match the required uncertainty, our codes must implement the complete two-loop QED radiative corrections to Bhabha scattering and the leading and sub-leading contributions enhanced by large logarithms.
${\mathrm{SANC}}$ Monte Carlo programs for small-angle Bhabha scattering
- Received Date: 2023-11-29
- Available Online: 2024-04-15
Abstract: Luminosity monitoring at







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: