-
Relativistic heavy-ion collisions provide a unique laboratory to create a deconfined, hot, and dense medium called the quark-gluon plasma (QGP) and study its properties [1–4]. In such collisions, incoming nuclei can be stopped at midrapidity with their kinetic energies deposited for the QGP formation. Since nuclei are composed of baryons, this phenomenon is usually referred to as baryon stopping [5–7]. Understanding the baryon stopping mechanism is of prime importance for studying the QGP as it provides the initial conditions for QGP creation.
Baryon stopping can be investigated via the rapidity distribution of the net-baryon number, i.e., the difference between the number of baryons and anti-baryons in heavy-ion collisions. This is because the baryon number is a strictly conserved quantity and has to originate from the colliding nuclei. Since only protons and neutrons are long-lived baryons and detecting neutrons is much more difficult than protons, baryon stopping is usually probed experimentally via the net-proton (proton minus anti-proton) distribution. Rapidity distributions of net-protons have been measured at colliders such as Alternating Gradient Synchrotron (AGS), Super Proton Synchrotron (SPS), Relativistic Heavy Ion Collider (RHIC), and Large Hadron Collider (LHC), covering a large range of center-of-mass energy per nucleon-nucleon pair (
${\sqrt{s_{NN}}}$ ) [6–12]. At the AGS with low collision energies of$3.63 \le {\sqrt{s_{NN}}}\le4.85$ GeV, a large amount of net-protons are observed at midrapidity, which rapidly decrease towards forward rapidities. This is close to the extreme scenario of full stopping. On the other hand, at the LHC energy of${\sqrt{s_{NN}}}$ = 2.76 TeV, nearly vanishing net-protons are measured at midrapidity, close to the the extreme scenario of full transparency. Heavy-ion collisions at RHIC sit between these two extreme cases, and a finite number of net-protons are observed at midrapidity, which increase slowly towards forward rapidity (up to$ y\approx 3 $ ), indicating high but still partial transparency.While general features of baryon stopping have been established in heavy-ion collisions, the underlying mechanism has not been fully understood. One key ingredient is identifying the baryon number carrier in a nucleus. Traditionally, valence quarks are assumed to carry the baryon number in the QCD. Event generators of heavy-ion collisions, such as the Heavy Ion Jet Interaction Generator (HIJING) [13], the Ultra relativistic Quantum Molecular Dynamics (UrQMD) [14, 15], and a multi-phase transport (AMPT) [16, 17], implement valence quark stopping by assuming that a nucleon comprises a tightly bounded diquark and a quark. However, none of the models can reproduce the measured net-proton yields at midrapidity out of the box owing to the difficulty in moving valence quarks from incoming nuclei over a large rapidity gap (more than 5 units at
${\sqrt{s_{NN}}}$ = 200 GeV) to midrapidity. Instead, the valence quark stopping in those models should be enhanced parametrically to match experimental data.Alternatively, a "baryon junction" mechanism was proposed as the carrier of the baryon number [18–20]. Some followup work can be found at [21–29]. Unlike the traditional picture of the baryon structure, a baryon in this mechanism is composed of three valence quarks and a string junction linked to them by gluons, as illustrated schematically in Fig. 1. The string junction is a non-perturbative Y-shaped configuration of gluon fields, which traces the baryon number instead of valence quarks. When the junction is pulled away from the baryon, the strings between the junction and valence quarks break up and
$ q\bar{q} $ pairs are produced. The resulting baryon comprises three sea quarks with possibly different quark flavor content than the original baryon, while the valence quarks emerge as mesons. The baryon junction is expected to contain an infinite number of gluons and, therefore, carries, on average, an infinitely small fraction of the baryon's momentum. Consequently, the baryon junction has a longer interaction time and is thus more likely to be stopped at midrapidity than valence quarks, leading to enhanced baryon stopping.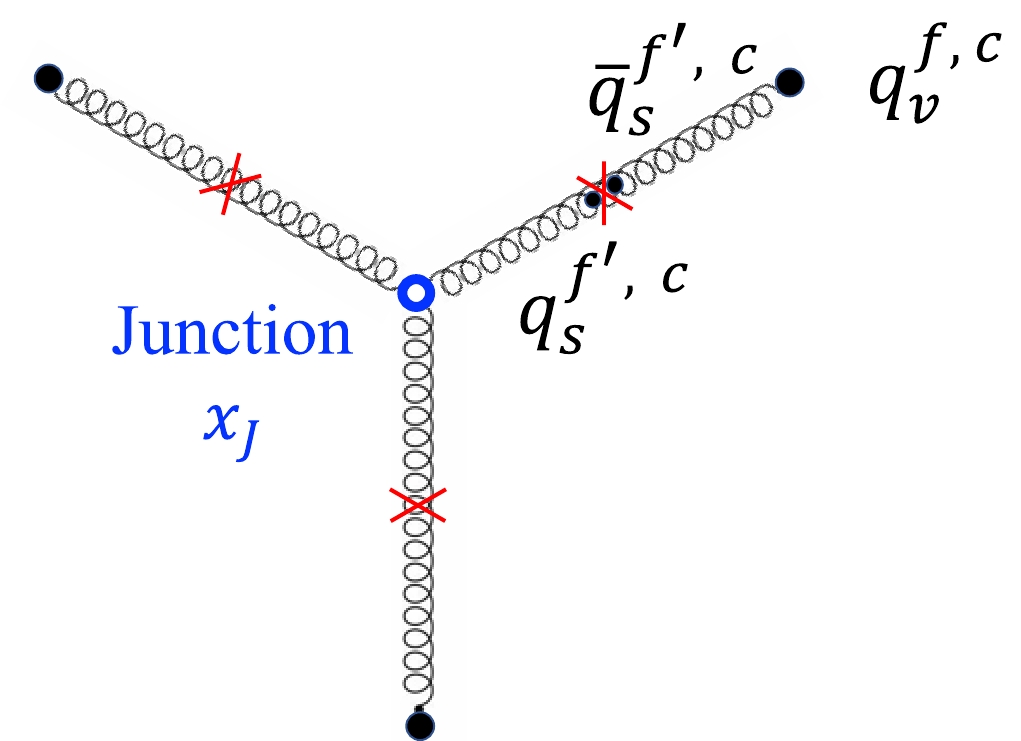
Figure 1. (color online) Illustration of a baryon junction linking to three valence quarks in a baryon. The Wilson lines can be excited and fragment into
$ q\bar{q} $ sea quark pairs. The anti-sea-quark connected to a valence quark has the same color as the valence quark but can have a different flavor.Whether the stopped baryons come from valence quarks or baryon junctions could potentially be discriminated via the correlation of stopped baryons and charges at midrapidity in heavy-ion collisions [30], since the valence quarks carry the electric charge. In valence quark stopping, the stopped charges and baryons are expected to be proportional to the atomic number (Z) and mass number (A) of the colliding nuclei, respectively. In the case of baryon junction stopping, stopped baryons are expected to scale with A, while the stopped charges do not correlate with Z. As illustrated in Fig. 1, the stopped baryon comprises three sea quarks from the fragmentation of the three Wilson lines linked to valence quarks. The three sea quarks can have different flavors from the valence quarks. Consequently, although the baryon number of the stopped baryon is similar to the wounded baryon, their charges are not correlated.
In this study, correlations of baryon and charge stopping are studied using the UrQMD event generator, which employs valence quarks as the baryon number carriers. Such studies will serve as a baseline for obtaining the baryon junction in heavy-ion experiments. The rest of the paper is organized as follows: Section II introduces the UrQMD model, datasets, and methods. Net-baryon and net-charge distributions and their correlations in collisions of various nucleus species are discussed in Sec. III.A and III.B, respectively. The differences between the net-charge and net-baryon yields at midrapidity in isobaric Ru+Ru and Zr+Zr collisions are shown in Sec. III.C, and finally, a conclusive summary is provided in Sec. IV.
-
UrQMD is a microscopic transport model based on the covariant propagation of hadrons on classical trajectories in combination with stochastic binary scattering and resonance decays [14, 15]. It deals with both hadronic and partonic interactions through string formation and fragmentation. Cross sections of inelastic hadron-hadron interactions are either tabulated, parameterized, or extracted from other cross sections via general principles such as detailed balance or the additive quark model. As mentioned earlier, baryon stopping in UrQMD is realized by the excitation and fragmentation of the strings between the diquark and quark. Incoherent multiple inelastic scatterings between the valence quark and diquark are the dominant mechanisms preventing the baryons from colliding with the target and projectile. The diquark breaking process is also included but is of minor importance. Notably, UrQMD uses Gaussian parameterization for longitudinal fragmentation, which was tuned to match net-proton and net-baryon rapidity distributions measured in heavy-ion collisions by enhancing valence quark stopping [14, 15, 31].
In this study, collisions of
$ _8^{16}{\rm{O}} $ +$ _8^{16}{\rm{O}} $ ,$ _{13}^{27}{\rm{Al}} $ +$ _{13}^{27}{\rm{Al}} $ ,$ _{29}^{64}{\rm{Cul}} $ +$ _{29}^{64}{\rm{Cu}} $ ,$ _{40}^{96}{\rm{Zr}} $ +$ _{40}^{96}{\rm{Zr}} $ ,$ _{44}^{96}{\rm{Ru}} $ +$ _{44}^{96}{\rm{Ru}} $ ,$ _{79}^{197}{\rm{Au}} $ +$ _{79}^{197}{\rm{Au}} $ , and$ _{92}^{238}{\rm{U}} $ +$ _{92}^{238}{\rm{U}} $ at${\sqrt{s_{\rm {NN}}}}$ = 200 GeV are simulated using UrQMD. The atomic number Z, the mass number A, and their ratios for the colliding nuclei are listed in Table 1. Z has almost an order of magnitude coverage, and Z/A varies by about 23% among different nuclei. To indicate the collision geometry, centrality, determined based on the impact parameter, is employed with a central (peripheral) collision corresponding to a small (large) impact parameter or large (small) nuclear overlap. The centrality can be quantified using the number of participating nucleons (${\langle N_{\rm{part}} \rangle}$ ) in each heavy-ion collision.Nucleus Z A $ Z/A $ 

O 8 16 0.500 Al 13 27 0.481 Cu 29 64 0.453 Zr 40 96 0.417 Ru 44 96 0.458 Au 79 197 0.401 U 92 238 0.386 Table 1. Atomic number (Z), mass number (A), and their ratios for various nuclei under study.
The charge and baryon stopping are quantified with the net-charge and net-baryon numbers at midrapidity, respectively. The net-charge number (Q) is defined as the sum of charges in the unit of electron charge (e) for all final-state particles within the desired acceptance. The net-baryon number (B) is defined as the sum of the signed baryon numbers of all baryons (p, n, Λ, Σ, Ξ, Ω and their antiparticles). For simplicity, Q and B denote the average net-charge and net-baryon numbers over all analyzed events for each collision system of a given centrality class. When integrated over the full phase space, Q and B are found to be exactly twice the Z and A of the colliding nuclei, respectively. This confirms the implementation of the conservation laws for charge and baryon quantum numbers in the UrQMD.
-
Rapidity distributions of net-charge and net-baryon numbers in 0−20% central Au+Au and Cu+Cu collisions at
${\sqrt{s_{NN}}}$ = 200 GeV are shown in the top panel of Fig. 2. Finite net-charges and net-baryons are stopped at midrapidity. The peak at$ y\approx y_{\rm{beam}}=5.36 $ corresponds to the nucleons not participating in the collisions (spectators). The rest of the net-charge and net-baryon distributions peak at$ y \approx 3.4 $ (3.8), about 2.0 (1.6) units smaller than the beam rapidity, in Au+Au (Cu+Cu) collisions. The rapidity peak position for Au+Au collisions is about 0.4 units smaller than that for Cu+Cu collisions, indicating the system size dependence of charge and baryon stopping. The larger the collision size, the larger the stopping power. The bottom panel shows the net-charge and net-baryon densities at midrapidity ($ |y|<1.0 $ ) as a function of${\langle N_{\rm{part}} \rangle}$ . They increase dramatically from peripheral to central collisions. The net-charge and net-baryon yields in Cu+Cu collisions are higher than those in Au+Au collisions at the same${\langle N_{\rm{part}} \rangle}$ , likely owing to the different geometrical shapes of the overlapping region. At the same${\langle N_{\rm{part}} \rangle}$ , the mean thickness of the overlapping region in Cu+Cu collisions is larger than that in Au+Au collisions. Consequently, the partons in Cu+Cu collisions experience more scatterings on average and, thus, are more likely to be stopped at midrapidity.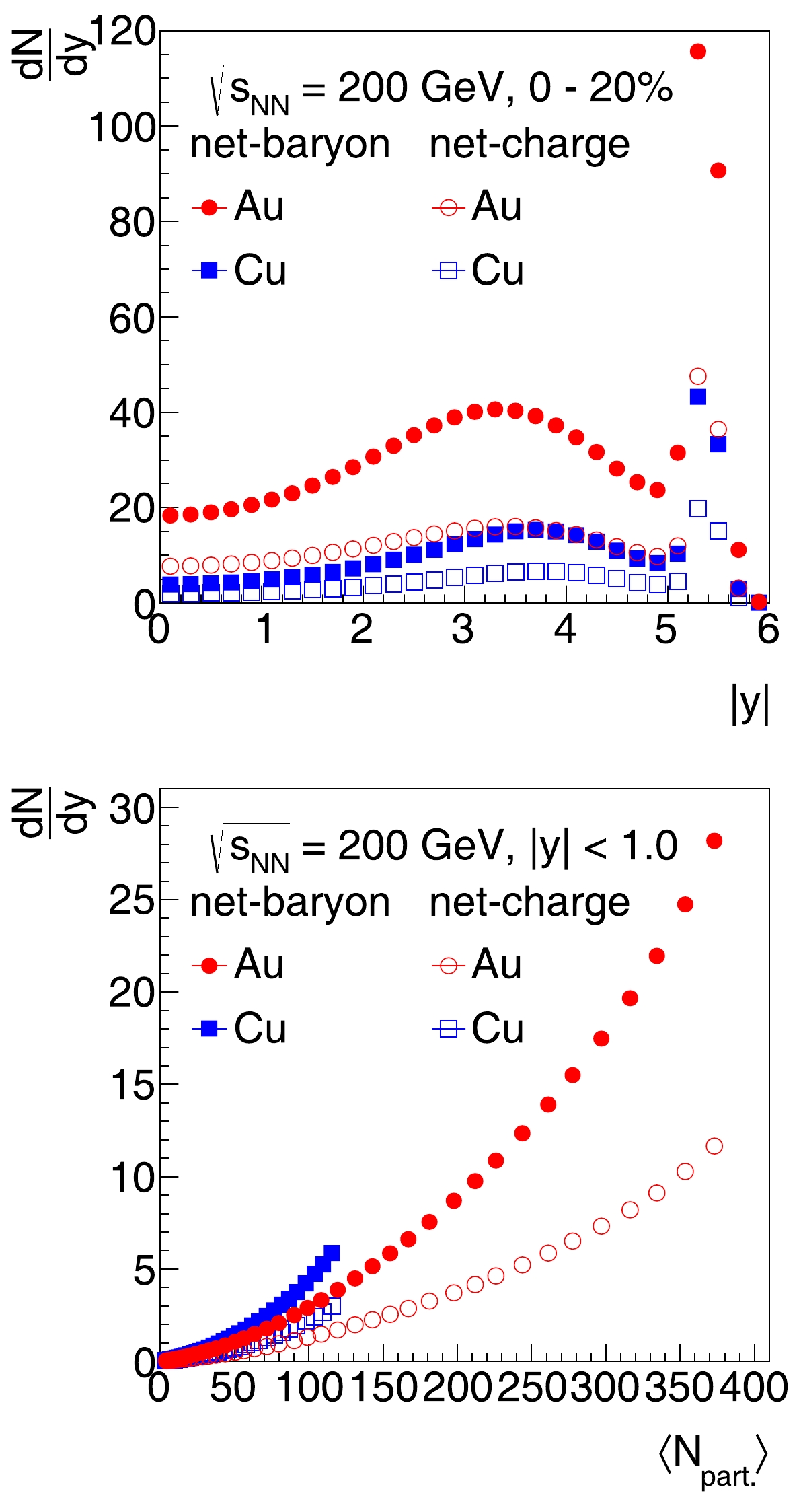
Figure 2. (color online) Top: Net-charge and net-baryon rapidity distributions in 0−20% central Au+Au and Cu+Cu collisions at
${\sqrt{s_{NN}}}$ = 200 GeV. Bottom: Net-charge and net-baryon rapidity density at midrapidity ($ |y|<1.0 $ ) as a function of${\langle N_{\rm{part}} \rangle}$ in Au+Au and Cu+Cu collisions. -
Figure 3 shows the correlations of net-charge (
${\rm d}Q/{\rm d}y$ ) and net-baryon (${\rm d}B/{\rm d}y$ ) densities at midrapidity ($ |y|<1.0 $ ) in collisions of heavy ions with various Z and A at${\sqrt{s_{NN}}}$ = 200 GeV. Centrality classes for each collision system are from 0 to 100% with steps of 10%. The leftmost data points correspond to the most peripheral collisions (90%−100%), while 0−10% central collisions correspond to the largest net-baryon densities. In all collision systems, the net-charge and net-baryon numbers are strongly correlated. To quantify the correlation, data points are fitted with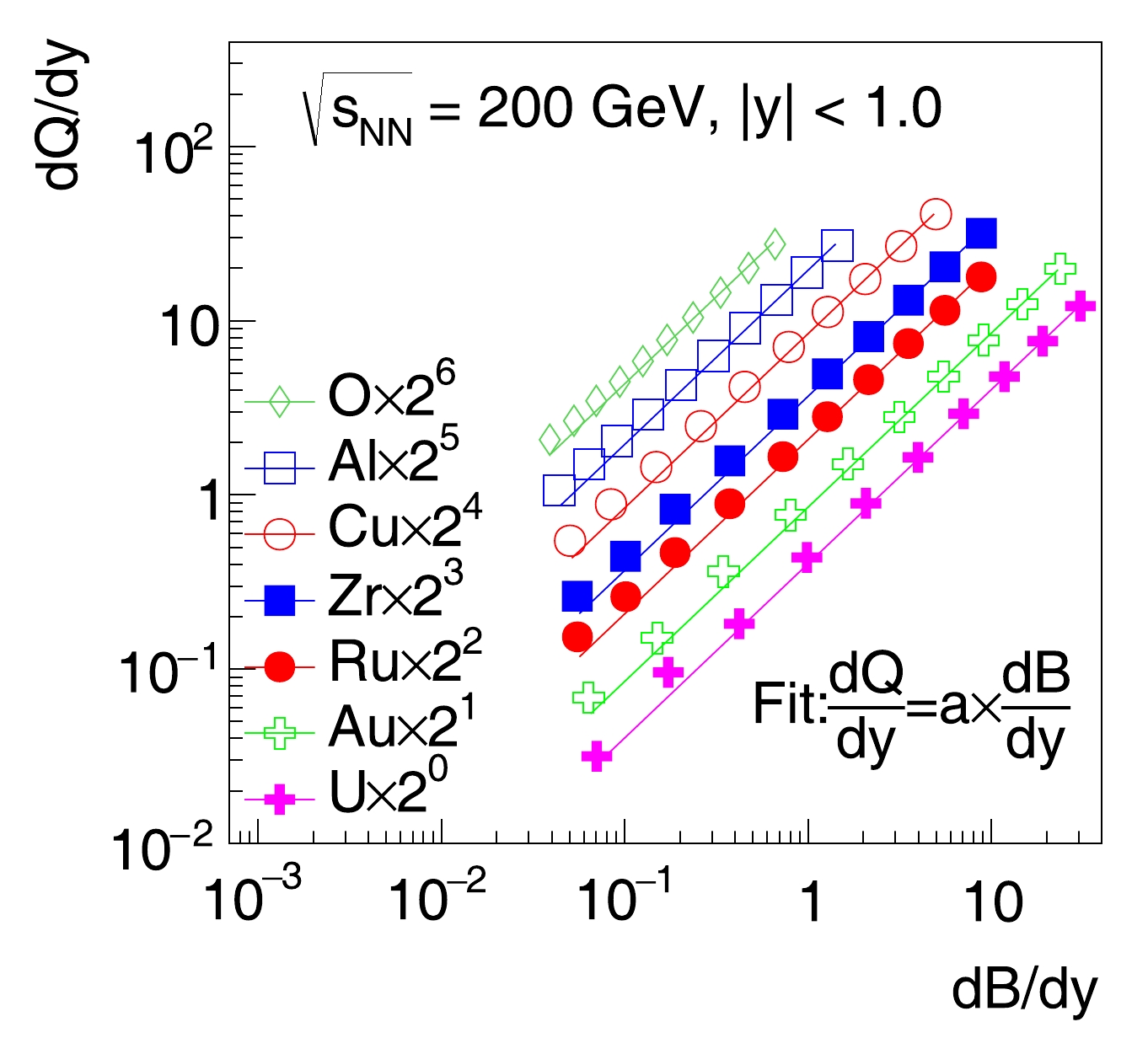
Figure 3. (color online) Net-charge density as a function of net-baryon density at midrapidity in heavy-ion collisions of O+O, Al+Al, Cu+Cu, Zr+Zr, Ru+Ru, Au+Au and U+U at
${\sqrt{s_{NN}}}$ = 200 GeV. Data points are scaled up by factors of$ 2^n $ ($ n = 1 - 6 $ ) from Au to O for clarity. Solid curves indicate fit results to different sets of data points.$ \frac{{\rm d}Q}{{\rm d}y} = a \times \frac{{\rm d}B}{{\rm d}y}, $

(1) where a is the slope. The fitted results are shown as solid lines in Fig. 3, which describe the data points in central collisions well but underestimate those in peripheral collisions. The different behaviors in central and peripheral collisions could be due to the effect of multiple scatterings, which grows stronger with a larger collision system size. The slope a increases from
$ 0.401 \pm 0.001 $ in U+U collisions to$ 0.677 \pm 0.001 $ in O+O collisions, approximately proportional to$ Z/A $ . This is different from the expectation of baryon junction stopping, which predicts the slope to be around 0.5 and independent of$ Z/A $ , as the produced quarks linked to the stopped baryon junctions are from sea quarks.To further study the scaling behavior in different collision systems, distributions of
${\rm d}Q/{\rm d}y$ , scaled by$ A/Z $ , are shown in Fig. 4 as a function of${\rm d}B/{\rm d}y$ . Results from O+O to U+U collisions collapse to a universal curve, which can be described by a power-law function: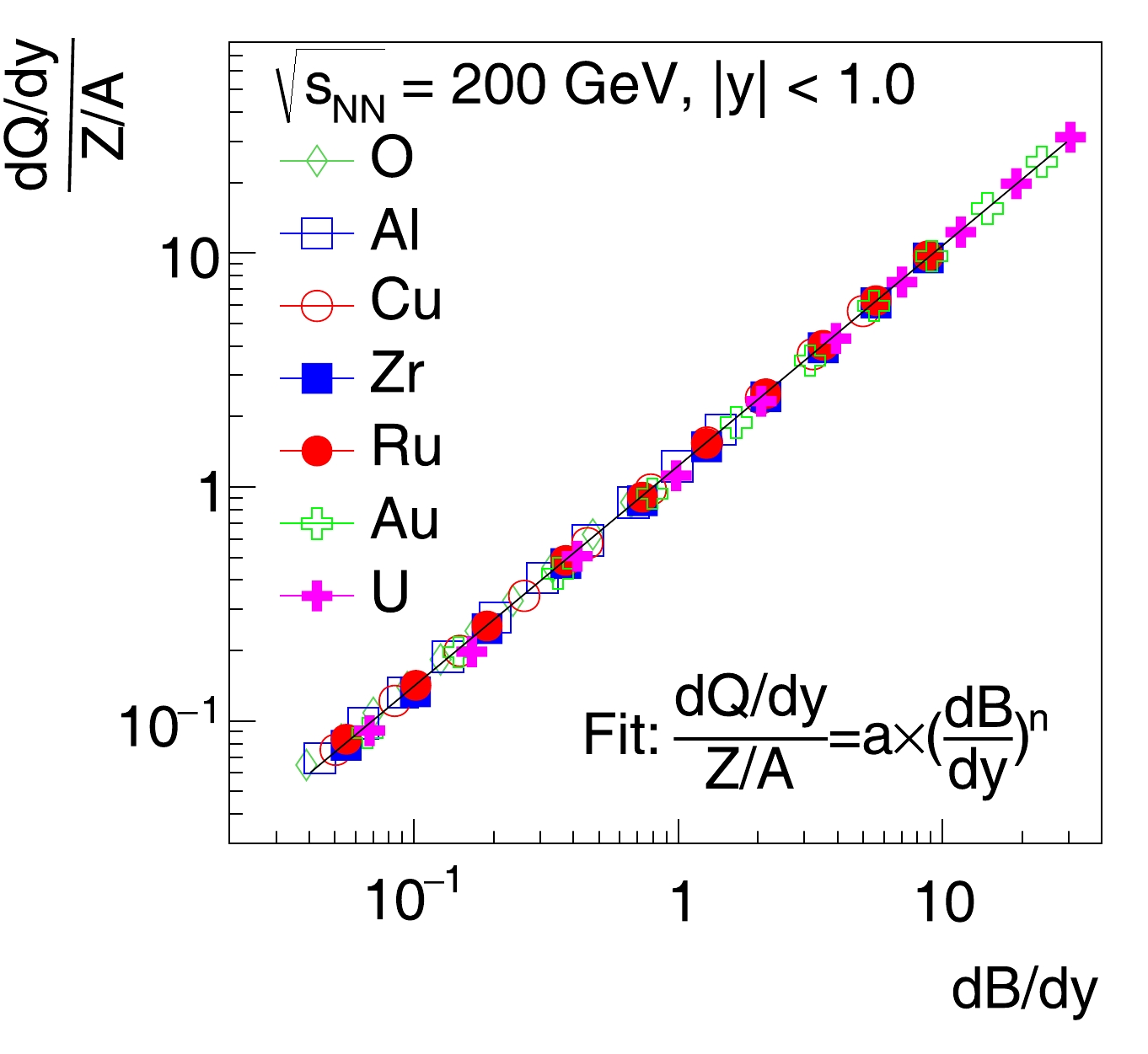
Figure 4. (color online)
${\rm d}Q/{\rm d}y$ , scaled by$ A/Z $ , versus${\rm d}B/{\rm d}y$ at midrapidity ($ |y|<1.0 $ ) from different colliding systems. The solid line represents a simultaneous fit to all data points.$ \frac{{\rm d}Q/{\rm d}y}{Z/A} = a \times ({\rm d}B/{\rm d}y)^n. $

(2) The fitted parameters are:
$ a=1.2302 \pm 0.0007 $ and$ n= 0.9413 \pm 0.0003 $ .The ratios of
$ A/Z $ -scaled${\rm d}Q/{\rm d}y$ and${\rm d}B/{\rm d}y$ as a function of${\rm d}B/{\rm d}y$ in collisions of O+O to U+U are shown in Fig. 5. They follow a similar trend, being significantly larger than unity in small-system collisions with low net-baryon yields and approaching unity in large-system collisions with high net-baryon yields. A possible reason for the larger-than-unity ratio in small systems is that it is easier for transported valence quarks to form baryons at rapidities closer to the beam rapidity compared to at midrapidity. Thus, mesons tend to have a flatter rapidity distribution than baryons, resulting in a larger net-charge to net-baryon yield ratio than$ Z/A $ at midrapidity. This is more obvious for strange hadrons. In large systems, the multiple scattering effect is more pronounced, and more quarks are present per unit of rapidity. These effects tend to wash out the difference in net-charge and net-baryon production against rapidity. The strong correlation of net-charge and net-baryon production from the valence quark transport provides a unique probe of baryon number carriers in nucleons with relativistic heavy ion collisions. The STAR Collaboration has collected large samples of Ru+Ru and Zr+Zr collisions in 2018, O+O collisions in 2021, and Au+Au collisions in 2019 and 2023. These data could be used to test whether the ratio of net-charge and net-baryon at mid-rapidity is correlated with$ Z/A $ or not.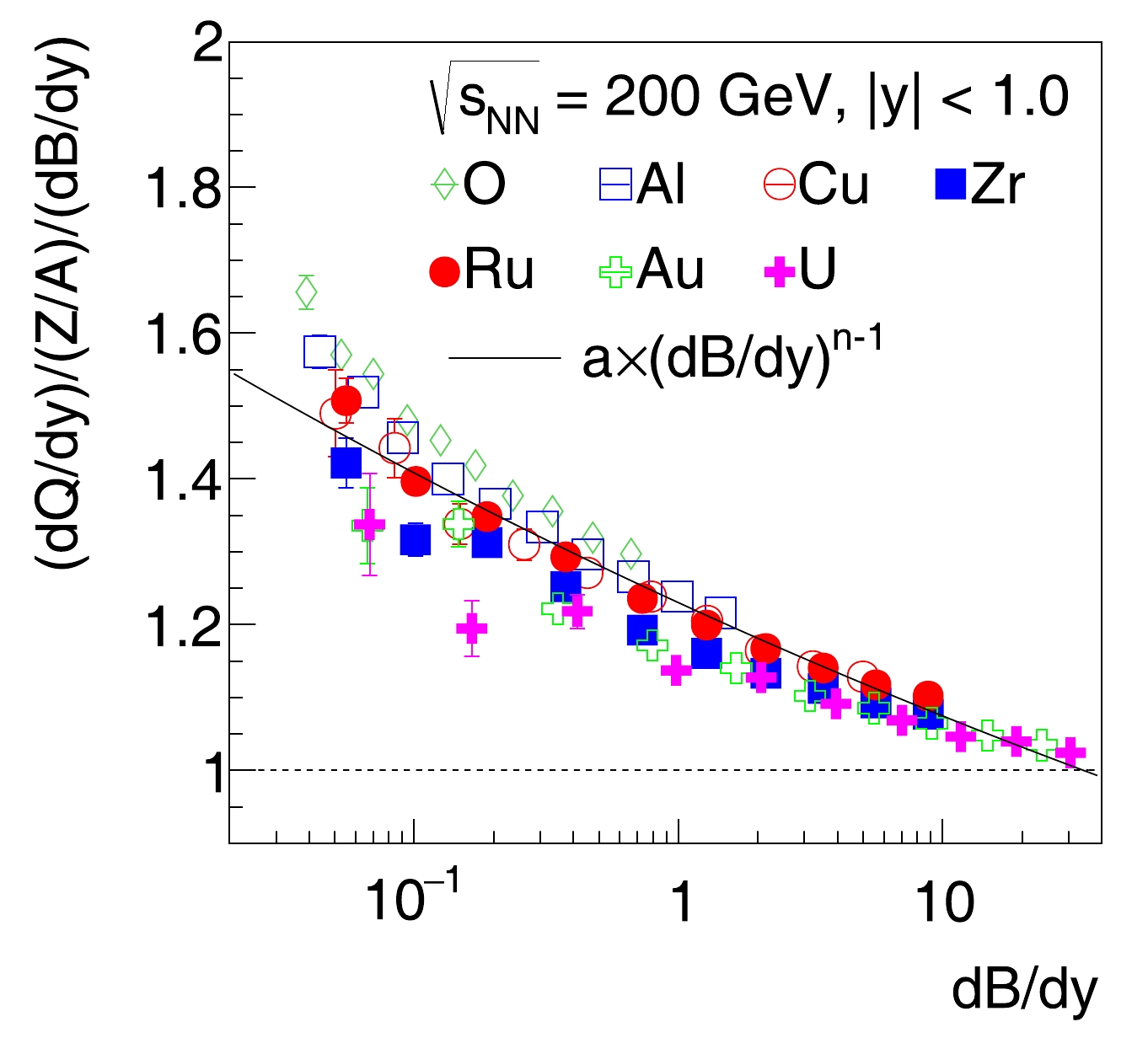
Figure 5. (color online) The ratio of net-charge to net-baryon yield, scaled by
$ Z/A $ , as a function of the net-baryon density within$ |y|<1.0 $ . The solid line corresponds to the fitted curve shown in Fig. 4. -
While examining the correlations between charge and baryon stopping at midrapidity provides a promising channel to discriminate between valence quarks and baryon junctions as the baryon number carriers, it is very difficult to measure the net-charge yield precisely in heavy-ion collisions. This is because realistic detectors have finite detection efficiencies and limited coverage in transverse momentum (
${p_{T}}$ ). For example, about 30% of pions are missing below$ {p_{T}} < 0.2 $ GeV/c in the measurement with the STAR experiment at RHIC [11]. Corrections for these effects usually depend on particle species and have non-negligible uncertainties. While such uncertainties on the particle yields are generally acceptable, they can render the net-charge measurement completely useless since the net-charge is calculated as the small difference between large yields of positive and negative particles. Measuring the net-charge difference between isobaric collisions of$ _{40}^{96}{\rm{Zr}} $ +$ _{40}^{96}{\rm{Zr}} $ and$ _{44}^{96}{\rm{Ru}} $ +$ _{44}^{96}{\rm{Ru}} $ was proposed to overcome this difficulty [30]. This is motivated by the STAR experiment at RHIC in 2018, which recorded large samples of Ru+Ru and Zr+Zr collisions with almost identical running conditions [32]. The net-charge difference ($ \Delta Q = Q_{\rm{Ru}}-Q_{\rm{Zr}} $ ) can be calculated based on double ratios between positive and negative particles and between Ru+Ru and Zr+Zr collisions [30]. Uncertainties in double ratios are negligible owing to the cancellation of the uncertainties for different components of the double ratios. Consequently, one can compare$ \Delta Q $ with$ B\times \Delta Z/A $ , where$ \Delta Z = Z_{\rm{Ru}}-Z_{\rm{Zr}} $ , and B is the net-baryon number expected to be the same for the two isobaric collisions since the incoming nuclei carry the same baryon number.$ \Delta Q $ should be close to$ B\times \Delta Z/A $ in case of valence quark stopping, while for baryon junction stopping,$ \Delta Q < B\times \Delta Z/A $ is expected.To provide the baseline for the baryon junction search using isobaric collisions, Fig. 6 shows the
${\rm d}Q/{\rm d}y$ and${\rm d}B/{\rm d}y$ differences as a function of rapidity between Ru+Ru and Zr+Zr collisions at${\sqrt{s_{NN}}}$ = 200 GeV for 0−20%, 20%−40%, 40%−60%, and 60%−80% centralities. As expected, the net-baryon difference is consistent with 0 in Ru+Ru and Zr+Zr collisions (open circles). However, there are significantly more net-charges in Ru+Ru collisions than those in Zr+Zr collisions (filled circles) since the Ru nucleus carries 10% more charges than the Zr nucleus.${\rm d}B/{\rm d}y \times \Delta Z/A$ is also shown for comparison. The net-charge difference is close to${\rm d}B/{\rm d}y \times \Delta Z/A$ , but they exhibit slightly different rapidity dependence. The net-charge is larger than${\rm d}B/{\rm d}y \times \Delta Z/A\Delta Z/A$ at midrapidity, and vice-versa at forward rapidity. The transition occurs at$ y=2-3 $ .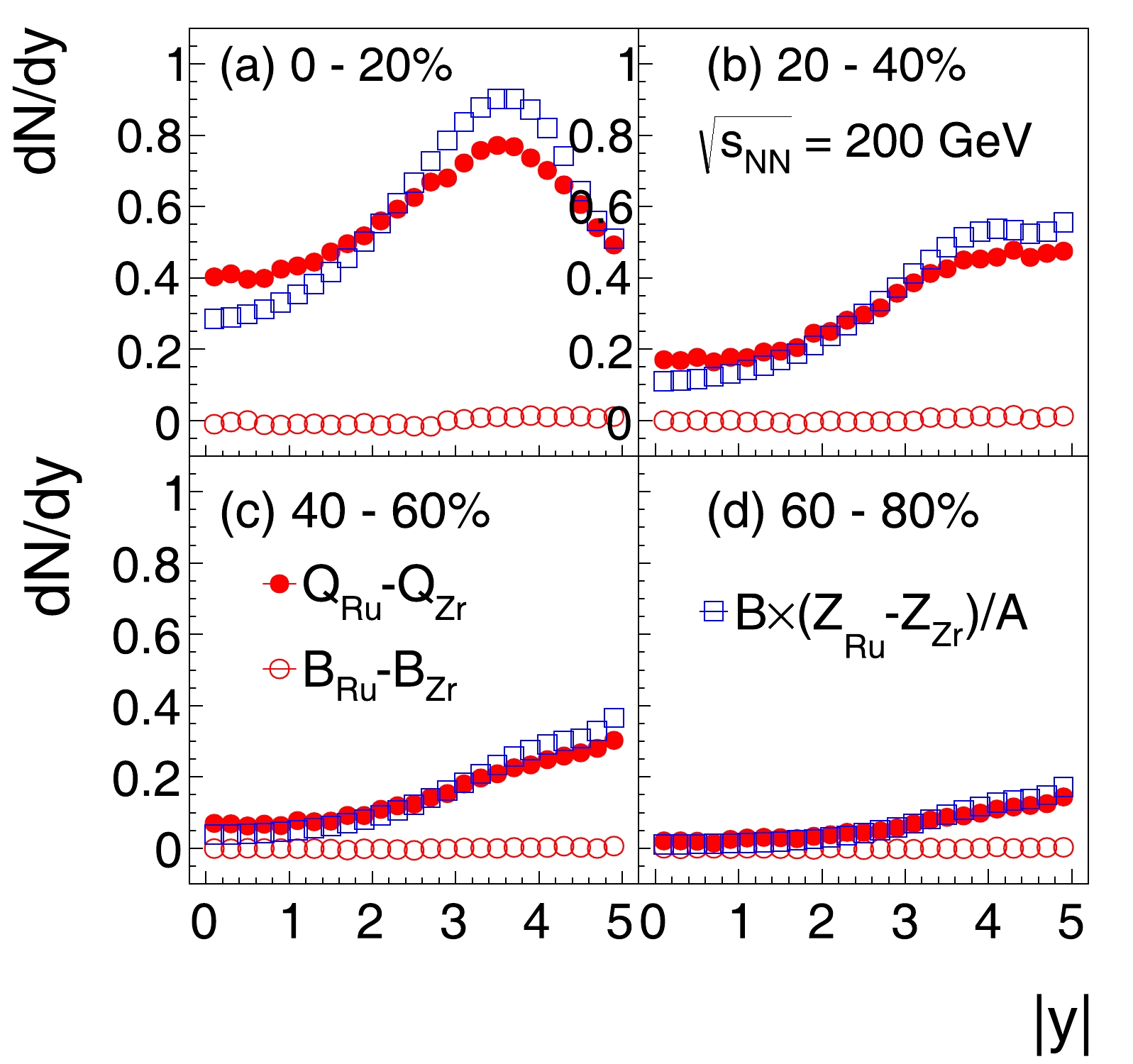
Figure 6. (color online) Differences of
${\rm d}Q/{\rm d}y$ and${\rm d}B/{\rm d}y$ between Ru+Ru and Zr+Zr collisions as a function of rapidity for 0−20%, 20%−40%, 40%−60%, and 60%−80% centralities.${\rm d}B/{\rm d}y \times \Delta Z/A$ is also shown for comparison.The ratios of
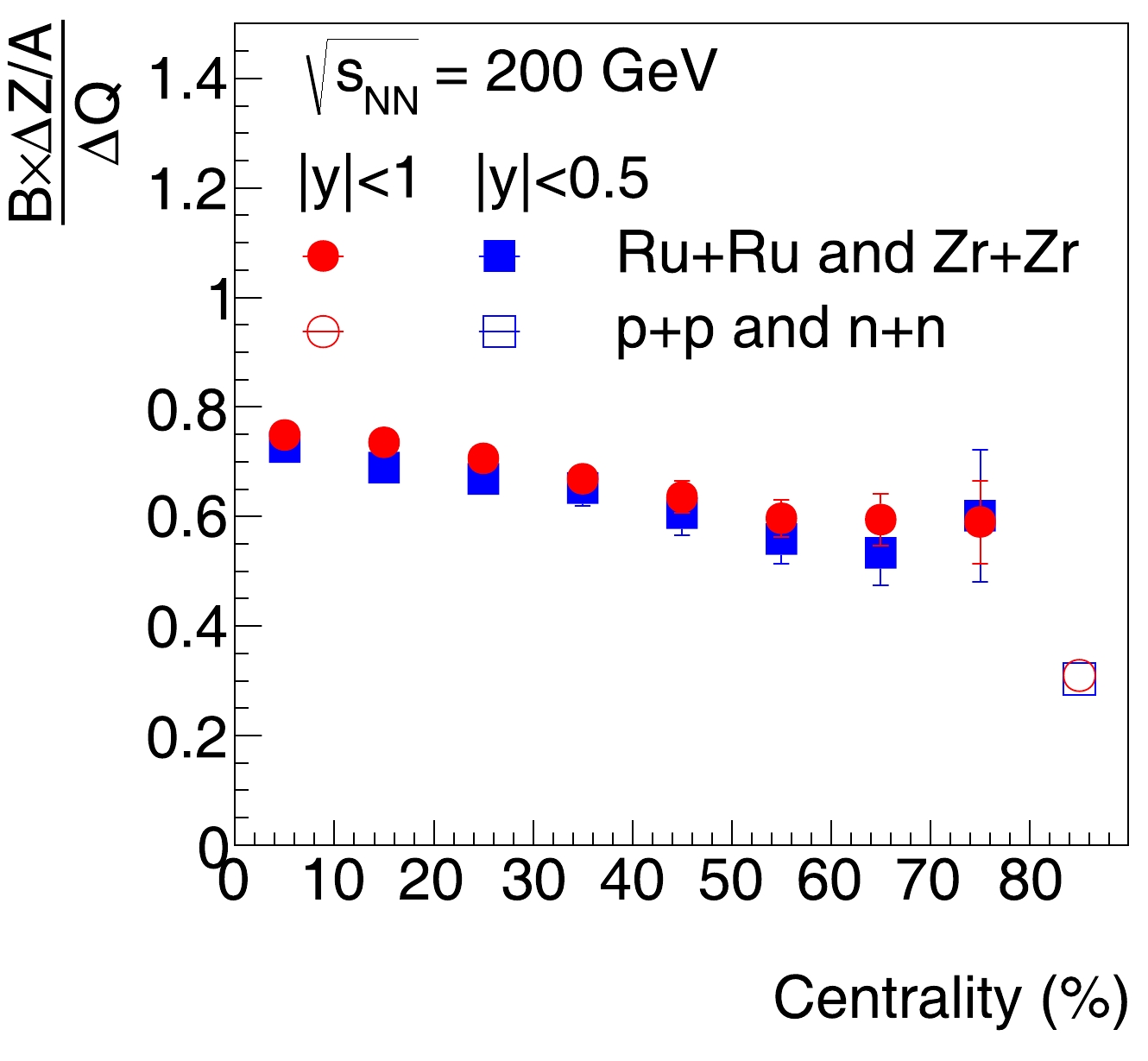
$ B \times \Delta Z/A $ over$ \Delta Q $ , integrated over midrapidity ($ |y|<1.0 $ ), are calculated in various centrality classes of 200 GeV Ru+Ru and Zr+Zr collisions and shown in Fig. 7. They are below unity, mainly owing to the different rapidity distributions of net-baryons and net-charges, as shown in Fig. 6. The effect is more obvious in peripheral collisions than in central collisions. Results for a narrower rapidity acceptance ($ |y|<0.5 $ ) are also shown. They are similar to those for$ |y|<1.0 $ , indicating weak rapidity dependence within$ |y|<1.0 $ for such measurements. These results can be directly compared to experimental measurements in search for the baryon junction. The results from$ p+p $ and$ n+n $ collisions simulated with UrQMD at the same energy are also shown as open symbols, and they roughly follow the centrality dependence trend observed in Ru+Ru and Zr+Zr collisions. Recent STAR preliminary results show that the ratio of$ B\times \Delta Z/A $ and$ \Delta Q $ is significantly larger than unity in the isobaric collisions [33–35]. -
In summary, the correlation between charge stopping and baryon stopping is studied in the collisions of various nuclei (from
$ _{8}^{16}{\rm{O}} $ to$ _{92}^{238}{\rm{U}} $ ) at${\sqrt{s_{NN}}}$ = 200 GeV with the UrQMD model, in which valence quarks carry the baryon number. The ratios of$ A/Z $ -scaled net-charge yield over net-baryon yield at midrapidity as a function of the net-baryon yield follow a universal trend in various collisions. In isobaric collisions ($ _{44}^{96}{\rm{Ru}} $ +$ _{44}^{96}{\rm{Ru}} $ and$ _{40}^{96}{\rm{Zr}} $ +$ _{40}^{96}{\rm{Zr}} $ ), the net-charges measured at midrapidity are correlated with the initial nuclear charge, and the ratios of$ \Delta Z/A $ -scaled net-baryon over the net-charge difference in the two isobaric collisions are finite and below unity. This provides an important baseline for the experimental search of the baryon junction in heavy-ion collisions. -
The authors would like to thank Drs. Declan Keane, Lijuan Ruan, James Daniel Brandenburg, and Nicole Lewis for valuable discussions.
Correlations of baryon and charge stopping in heavy ion collisions
- Received Date: 2023-11-21
- Available Online: 2024-04-15
Abstract: Baryon numbers are theorized to be carried by valence quarks in the standard QCD picture of the baryon structure. Another theory proposed an alternative baryon number carrier, a non-perturbative Y-shaped configuration of the gluon field, called the baryon junction in the 1970s. However, neither of these theories has been verified experimentally. Recently, searching for the baryon junction by investigating the correlation of net-charge and net-baryon yields at midrapidity in heavy-ion collisions has been suggested. This paper presents studies of such correlations in collisions of various heavy ions from oxygen to uranium with the UrQMD Monte Carlo model. The UrQMD model implements valence quark transport as the primary means of charge and baryon stopping at midrapidity. Detailed studies are also conducted for isobaric





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: