Critical behavior and Joule-Thomson expansion of charged AdS black holes surrounded by exotic fluid with modified Chaplygin equation of state

The thermodynamic characteristics of black holes have become a pivotal intersection in the domains of general relativity (GR), thermodynamics, and quantum gravity. The discovery made by Hawking regarding the thermodynamic emission of particles from black holes has significantly heightened interest in these celestial objects, leading to extensive investigations into their various thermodynamic properties [1−5]. The pioneering research by Hawking and Page explored the thermodynamics of anti-de Sitter (AdS) black holes, revealing a phase transition from a stable Schwarzschild black hole [6]. Furthermore, this phase transition can be extended to include charged AdS black holes, and findings indicate that this phenomenon is associated with the van der Waals fluid system [7, 8]. The interpretation of the cosmological constant is crucial in exploring thermodynamic black holes and is regarded as the pressure existing within the black hole that precisely aligns with the Smarr formula. The black hole mass is regarded as the enthalpy instead of its internal energy, and the thermodynamic volume of the conjugate pressure can be obtained using the laws of black hole thermodynamics [9].

The study of phase transitions in the extended phase space for black holes has attracted considerable attention, leading to the discovery of numerous thermodynamic phase transition phenomena and phase structures. For example, Kubiznak and Mann studied the critical behavior of an AdS black hole and made a precise comparison between the phase transition from small to large black holes with liquid-gas systems [10]. Reentrant phase transitions and triple points have been observed in various AdS black hole configurations [11, 12]. Subsequently, Wei et al. identified a remarkable triple point within a charged Gaussian-Bonnet black hole [13], investigated the reentrant phase transition of single-spin black holes, and analyzed the impact of different dimensions on the critical point [14]. The investigation of the second-order phase transition of black holes involves the introduction of number density for black hole molecules to enhance our understanding of the microstructure [15]. A novel methodology was introduced by Hendi et al. to determine the critical pressure and horizon radius of black holes, facilitating the identification of the specific phase transition occurring in black holes [16, 17]. Recently, there has been extensive research on the thermodynamic topological properties of various black holes based on Duan's ϕ-mapping theory [18−27], which contributes to a more profound understanding of the thermodynamic characteristics of black holes.

The cosmological constant is used to define the pressure exerted by a black hole, and considerable advancements have been achieved in the examination of the black hole phase transition. However, in the context of GR theory, the cosmological constant is regarded as a constant value associated with the AdS geometric background, and the interpretation of it as a variable pressure would be conceptually flawed. Conversely, when considering Q as a thermodynamic variable, there will be similarities to van der Waals phase transitions and critical phenomena [7, 8]. However, this approach poses mathematical challenges and deviates from conventional physical principles. Therefore, the authors Sheykhi et al. developed a novel Smarr formula by substituting $ Q^{2} $ with Q to rectify the principle of black hole thermodynamics within an alternative phase space [28]. The identification of the critical behavior and occurrence of a first-order phase transition in the Lifshitz expansion black hole has been successfully achieved [29]. Similarly, the thermodynamic phase transitions of other black holes in the alternative phase space have been extensively explored [30−33].

The classical thermodynamic concept of Joule Thomson (J-T) expansion is commonly recognized as the migration of gas from a region of higher pressure to one of lower pressure at an equivalent speed, and during the process, there is no alteration in enthalpy. Özgür Ökcü and Ekrem Aydiner initially applied the principles of J-T expansion to investigate the thermodynamics of black holes. They conducted a comprehensive analysis of the J-T effect exhibited by charged AdS black holes, resulting in the derivation of the inversion temperature and curve. The distinct areas associated with the cooling and warming processes were effectively identified using the $ T-P $ diagram [34, 35]. Consequently, J-T expansion rapidly gained widespread popularity among various categories of black holes, such as in the effects of quintessence dark energy (DE) [36], the space-time dimension [37], angular momentum [38], and Rainbow gravity [39] on J-T expansion. We previously investigated the effects of the space-time dimension on the minimum inversion temperature and cooling-heating effect for charged dilatonic black holes [40]. For further related discussions, see [41−45].

In the context of the standard cosmological model, astronomical observations have confirmed that DE constitutes approximately 73% of the universe, whereas dark matter (DM) constitutes around 23%, and baryonic matter accounts for a mere 4% [46]. Different models have been proposed for DE, offering both empirical and theoretical predictions for the Universe's accelerated expansion, such as quintessence and quintom models, to explain these observations [47, 48]. In an endeavor to more comprehensively explain the accelerated expansion of the Universe, researchers have proposed a novel mixing of DM and DE. Specifically, they have suggested employing a Chaplygin gas (CG) model [49], such as generalized Chaplygin gas (GCG) [50, 51]. The effect of Chaplygin-like fluids on black hole spacetime was first considered in reference [52]. Subsequently, such a model was extended to modified CG (MCG) [53, 54]. The thermodynamic phase transition behavior [55] and shadows [56] of black holes in Chaplygin-like dark fluid have also been discussed. It is worth noting that the relativistic framework has been employed to address charged AdS black holes with MCG. The author conducted an investigation on the criticality of P-V and observed a similarity between the phase transition of small/large black holes and the liquid/gas phase transition in van der Waals [57]. To advance our understanding of the thermodynamic properties of a charged AdS black hole enveloped by MCG, this study aims to analyze the fixed parameter associated with the cosmological constant and explore criticality from an alternative perspective using a novel equation-of-state pair featuring variable $ Q^{2} $ charge. Furthermore, we undertake an investigation into how black hole characteristics affect their influence on J-T expansion.

This paper is arranged as follows. In Section II, we provide a concise overview of the solution for the charged AdS black hole with MCG, and a comprehensive analysis is conducted to examine the impact of MCG parameters on the critical behavior and Gibbs free energy associated with black holes. In Section III, we initially analyze the impact of the black hole charge Q on both the J-T coefficient and Hawking temperature, subsequently deriving the inversion temperature and pressure for a black hole surrounded by MCG. Using visual figures, we thoroughly discuss the variation trends of MCG parameters in terms of the ratio T_min/T_c and isenthalpic curves. The final section summarizes our findings.

In this section, we direct our attention toward an AdS black hole with an MCG structure within the context of GR, as elucidated by the subsequent action [57]

where $ {\cal{R}} $ is the Ricci scalar, $ g_{\mu\nu} $ is the determinant of the metric tensor, denoted as $ g=\det (g_{\mu\nu}) $, $ \ell $ represents the AdS length, and the field strength of the electromagnetic field is given by $ F_{\mu\nu}=\partial_\mu A_\nu-\partial_\nu A_\mu $ , with $ A_\mu $ being the gauge potential; these are all involved in this context. $ {\cal{I}}_M $ is the matter contribution arising from the MCG background. MCG is an extension of the Chaplygin gas, which is widely regarded as a perfect exotic fluid. In this study, we consider the following form of MCG:

where the values of A and β must be non-negative, and A and B are considered constants in adiabatic processes [58]. If specific values are assigned to the parameters, MCG will transition into alternative models of DM and DE. The conditions $ \beta >1 $ and $ A = 0 $ can be transformed into the concept of GCG: $ p=-\dfrac{B }{ \rho^{\beta}} $. However, if the parameters satisfy the conditions $ \beta =1 $ and $ A = 0 $, MCG will degenerate into a simple pure CG: $ p=-\dfrac{B }{ \rho} $, which is an accurate characteristic of the aerodynamic process that generates lifting forces on the wing of an aircraft. Varying the action $ (1) $ leads to the following field equations:

the Einstein tensor $ G_{\mu\nu} $, along with $ T_{\mu\nu}^{\text{CMG}} $ refers to the energy-momentum tensor associated with MCG, whereas $ T_{\mu\nu}^{\text{EM}} $ represents the specific formulation of the energy-momentum tensor related to the electromagnetic field,

In this case, we consider a four-dimensional space-time that is static and exhibits spherical symmetry,

where the metric function $ f(r) $ is dependent on the variable r, and ${\rm d} \Omega^2= {\rm d} \theta^2+\sin ^2 \theta {\rm d} \phi^2$. To accurately determine the expression for energy density, we provide the metric function in equation $(6)$ and consider applying conservation conditions to the energy momentum tensor. This consideration yields an intriguing result, such as [53, 57]

where the utilization of an integration constant, denoted as $ \gamma>0 $, is crucial. Note that the energy density is confined to approximately $\left(\dfrac{B}{1+A}\right)^{{1}/{(1+\beta})}$. As a consequence, MCG exhibits characteristics akin to a cosmological constant in regions distant from the black hole but progressively manifests increased gravitational density as it nears the black hole.

Now, we can derive a concise expression for the analytical solution $ f(r) $

where the variables M and Q denote the physical attributes of black hole mass and charge, respectively, and the hypergeometric function $ {_2}F_1[\alpha, \nu; \lambda; \xi] $ can be expressed as a power series,

where $ \lvert \xi\rvert<1 $, the Pochhammer symbol is denoted by $ (n)_k $ [59], and the parameter sets $ (\alpha, \nu, \lambda, \xi) $ can be expressed as

Next, we focus on examining the phase transition and critical behavior. To this end, by utilizing the line element presented in Eq. (8), the mass at the horizon radius can be written as

The investigation of black hole thermodynamic phase transitions is commonly conducted within the extended phase space, where the cosmological constant and the corresponding conjugate quantities are defined as pressure and volume [60, 61],

where l represents the radius of AdS, and Λ denotes a cosmological constant with a negative value. To calculate the Hawking temperature, we must initially consider the surface gravity [62]. Specifically,

The thermodynamic quantities of the system can be determined by considering the first law of black hole thermodynamics [63],

where $ \mu_{i} $ denotes the chemical potentials linked to the conserved charges $ {\cal{N}}i $. The area of the event horizon can be written as

and we can calculate the entropy of the black hole as follows:

Next, we explore the phase transition of the system in a novel phase space. Specifically, the cosmological constant is fixed while considering $ Q^{2} $ as the thermodynamic variable. To this end, by incorporating Eq. (15) into the mass expression, we can obtain

Based on this, we can obtain the conjugate variables as follows:

where T denotes the temperature. The aforementioned thermodynamic quantities adhere to the principles of the first law of thermodynamics within the new phase space,

The consideration of charge Q as a thermodynamic variable poses mathematical challenges and deviates from conventional physical principles [7, 8]. In other words, the variables Q and ϕ ($ \phi=\partial M /\partial Q $) are not mathematically independent because $ \phi=Q/r_+ $, which can lead to physically irrelevant quantities such as $ \partial Q /\partial \phi $. This selection is conducive to the relation

Combining Eqs. (12) and (16), when considering a fixed Λ, the term $\psi {\rm d} Q^{2}$ (i.e., $ Q^{2} $ as a thermodynamic variable) is substituted for the term $\phi {\rm d} Q$ , as indicated by Eq. (19) as the best choice. We then substitute $ r_{+}=1 /(2 \psi) $ into the Hawking temperature, resulting in the equation of state for $ Q^2(T, \psi) $ as follows:

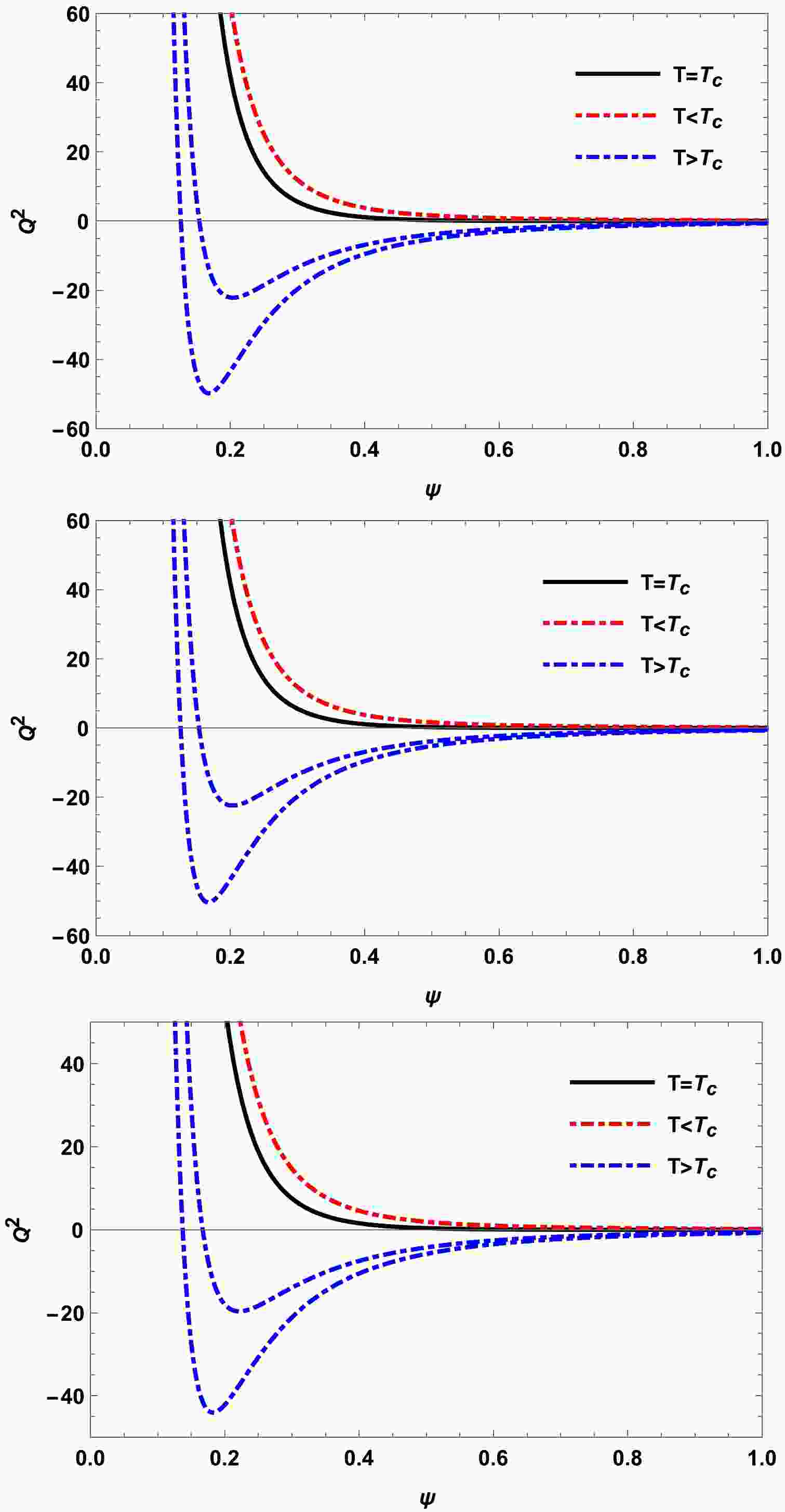
An isothermal diagram of a charged black hole in the $ Q^{2}-\psi $ plane is presented in Fig. 1, illustrating the physical makeup acceptance region. When the Hawking temperature falls below the critical temperature $(T_{c}=0.2169; T_{c}=0.2175;~ T_{c}=0.2458)$, an anomalous negative $ Q^{2} $ component can be observed within this region on the isothermal diagram. This phenomenon bears resemblance to that observed in a typical van der Waals fluid, where pressure may also exhibit negativity at certain values [28, 64]. The inherent instability of these features can be effectively mitigated through the conventional Maxwell equal area construction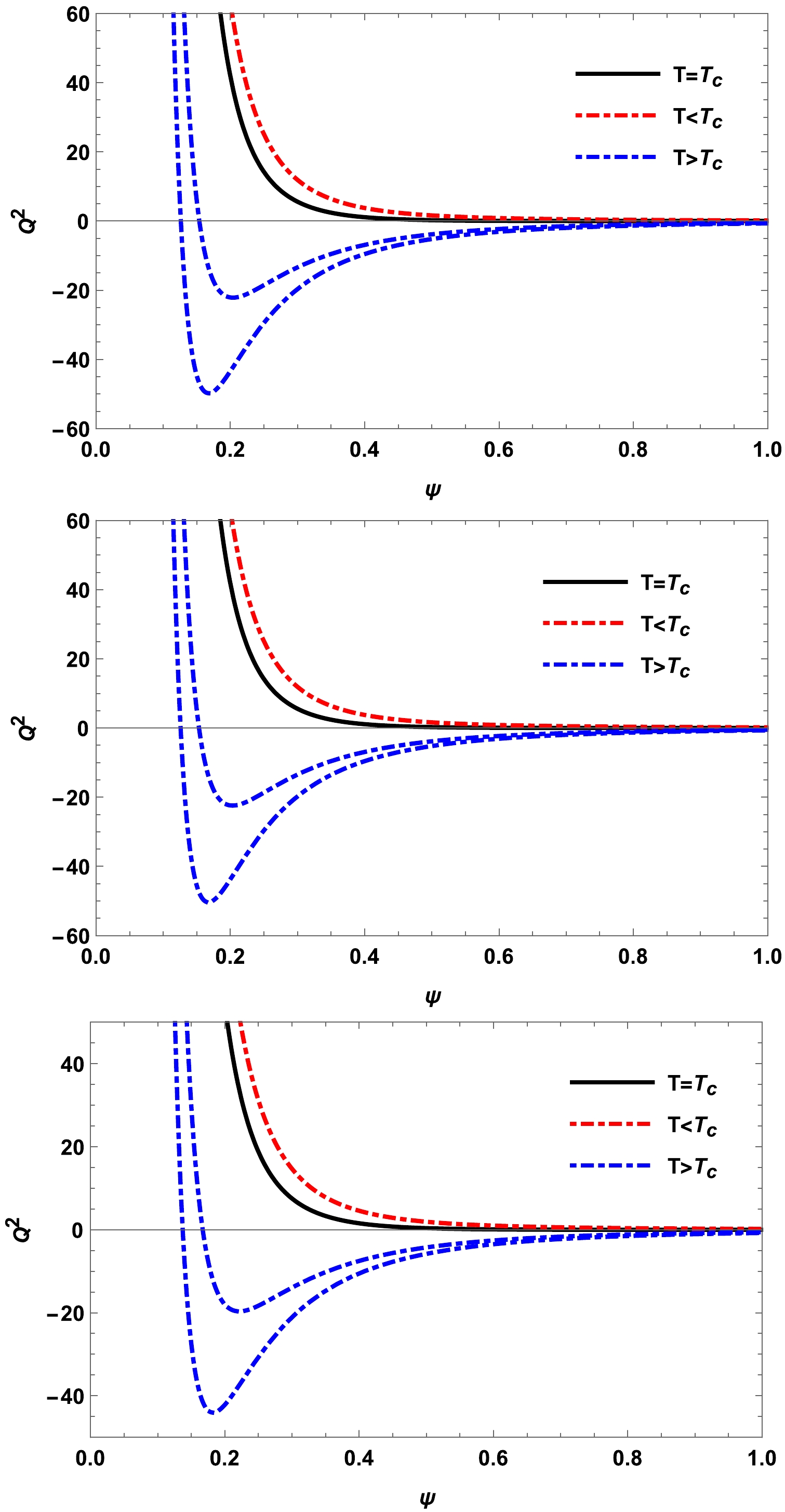

Figure 1.  (color online) $ Q^{2}-\psi $ diagram. Upper panel: ($\beta=B $$ =l=1, \; A=0, \; \gamma=0.1$). Middle panel: ($B=l=1,\;\beta=2,\; A=0, $$ \gamma=0.1$). Lower panel: ($A=B=l=1,\;\beta=\gamma=0.1$).

where the presence of an critical point signifies the occurrence of a phase transition. The critical point is determined by

and the black hole thermodynamic critical quantity ($ T_c, Q_c^2 $) can be expressed as

In this case, some numerical calculations are necessary to study the impact of the parameters on their phase transitions. As shown in Table 1, we observe the following:

A	β	B	γ	$\psi_{c}$	$T_{c}$	$Q^{2}_{c}$
0	1	0.1	0.01	1.14918	0.24629	0.02975
0	1	0.1	0.1	1.40746	0.23993	0.00292
0	1	1	0.01	0.99805	0.21229	0.04134
0	1	1	0.1	0.94249	0.21685	0.01686
0	0.1	1	0.01	1.00592	0.21167	0.03898
0	0.1	0.1	0.1	1.41903	0.23800	0.00304
0	0.1	1	0.1	1.11226	0.20416	0.01097
0	2	0.1	0.1	1.42095	0.24076	0.00271
0.1	0.1	0.1	0.01	1.20822	0.25448	0.02656
0.1	0.1	0.1	0.05	1.25885	0.25086	0.01497
0.1	1	0.1	0.05	1.18060	0.24977	0.01579
1	0.1	0.1	0.05	1.11785	0.26206	0.01665
1	0.1	1	0.05	1.04269	0.23892	0.02490

Table 1.  Critical values for $l=1$ with different parameters.

i. For $ (A=0,\beta=1) $, $ T_{c} $ and $ Q_{c}^{2} $ decrease with an increase in the parameter γ, whereas $ \psi_{c} $ exhibits the opposite trend. The increase in the parameter B leads to a decrease in both $ \psi_{c} $ and $ T_{c} $, whereas $ Q_{c}^{2} $ experiences an increase. The phase transition can be more readily achieved by increasing the parameter γ instead of B.

ii. For $ (A=0,\beta=2) $, the results indicate that the values of $ \psi_{c} $ and $ T_{c} $ exhibit an increasing trend with higher β, whereas $ Q_{c}^{2} $ demonstrates an inverse relationship.

iii. For $ (A\neq0) $, the values of $ T_{c} $ and $ Q_{c}^{2} $ increase as the parameter A increases, whereas the growth trend of $ \psi_{c} $ is inhibited by A. Note that changing the parameter B significantly alters the critical thermodynamic quantity of the black hole, resulting in a reversed $ CG $ contrast.

The characterization of the phase transition can be effectively achieved through the Gibbs free energy, which is expressed as follows:

In Fig. 2, we show a $ G-Q^{2} $ diagram with the critical values of thermodynamic quantities ((i) $\beta=l=1,\;A=0, B=0.1,\gamma=0.01$,$\psi_{c}=1.14918, \; T_{c}=0.24629,\; Q^{2}_{c}= 0.02975$; (ii) $\beta=2,\; l=1,\; A=0, \;B=0.1,\;\gamma=0.01$, $\psi_{c}= 1.12122, \; T_{c}= 0.23908,\;Q^{2}_{c}= 0.03263$; (iii) $A=B=\beta=0.1, \; l=1, \gamma=0.01$, $\psi_{c}=1.20822,\; T_{c}=0.25448,\; Q^{2}_{c}= 0.02659$). Note that, when the Hawking temperature is less than or equal to the critical temperature, the charged black hole is stable, which can also be verified from the $ Q^{2}-\psi $ diagram in Fig. 1. However, when the temperature of the system exceeds a certain critical point, it displays a characteristic swallowtail behavior, which suggests that there is a first-order phase transition taking place. Next, we compute the critical exponents within this novel phase space methodology. The characteristics of thermodynamic functions in close proximity to the critical point are determined by the critical exponents, defined by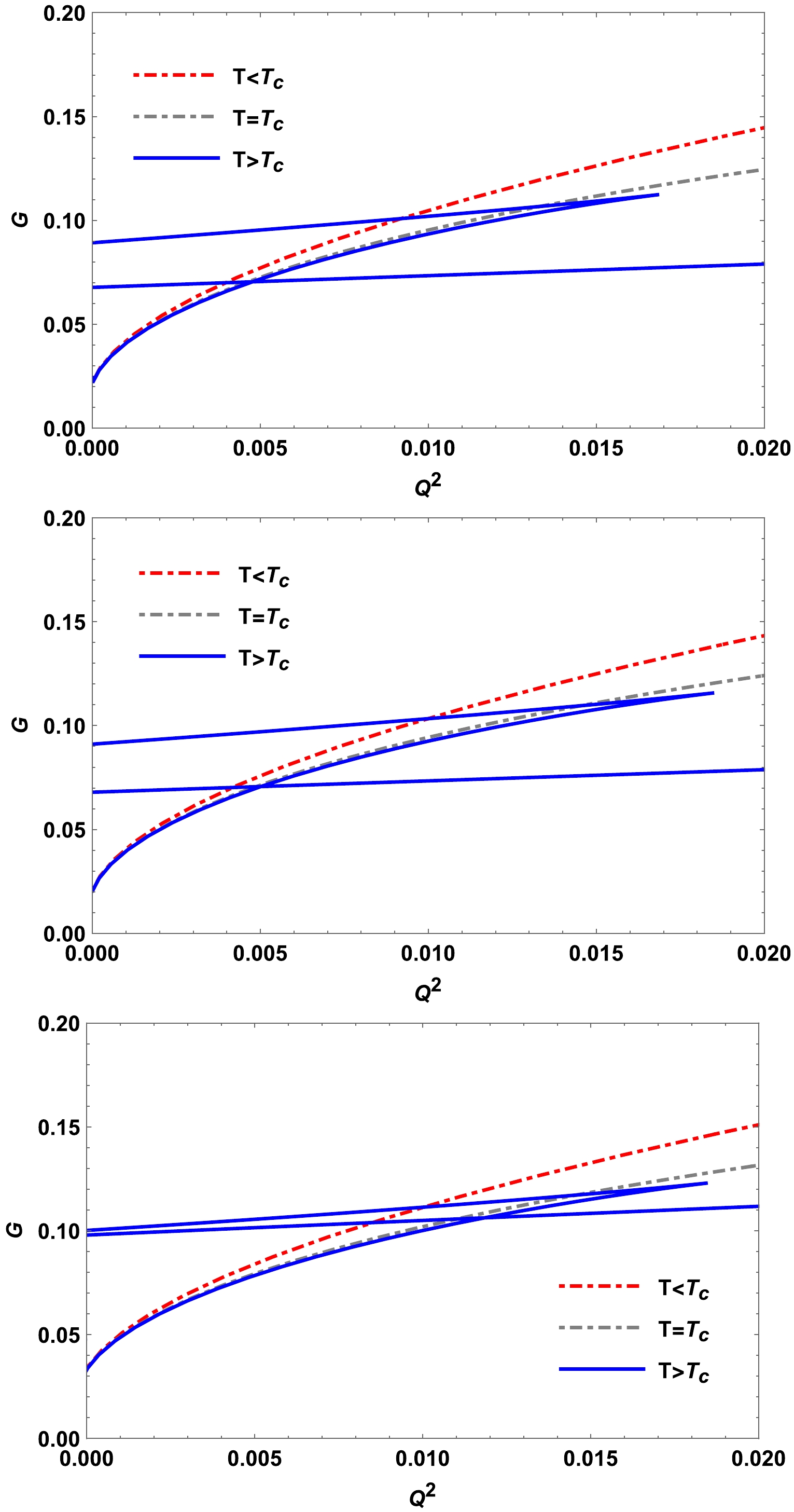

Figure 2.  (color online) $ G-Q^{2} $ diagram Upper panel: $(\beta=l=1, $$ A=0,\; B=0.1,\; \gamma=0.01)$. Middle panel: $(\beta=2,\;l=1,\;A=0, $$ B=0.1,\gamma=0.01)$. Lower panel: $(A=B=\beta=0.1,\;l=1,\;\gamma=0.01$).

where we use $ \tilde{\alpha} $, $ \tilde{\gamma} $ , and χ to describe the critical exponent, isothermal compression coefficient, and order parameter, respectively, because these symbols also describe the MCG parameters in this article. To determine the critical exponent, we establish the following dimensionless quantities:

Initially, we consider the temperature T as a determinant of entropy,

and we find that the temperature has no effect on entropy. If ψ is fixed, the specific heat can be expressed as

Based on this, $ \tilde{\alpha} $ characterizes the behavior of specific heat in close proximity to the critical point, and we can obtain

To determine other critical exponents, we define the reduced variables as follows:

By considering Eq. (28), Eq. (21) can be translated into a state equation in close proximity to critical points,

where

By assuming that $ Q^{2} $ remains constant and t is a positive value, based on Maxwell’s equal area theory, we can obtain

Furthermore, the value of the critical exponent χ can be determined as follows:

By substituting $ t=0 $, we can readily obtain the critical exponent δ,

Finally, the critical exponents related to the behavior of isothermal compression are calculated as follows:

Based on this, the findings indicate that the critical exponent of the system aligns with that obtained in the van der Waals fluid system [10].

In this section, we study the J-T expansion of a charged AdS black hole accompanied by MCG. It is widely recognized that in AdS space, the mass of a black hole is considered its enthalpy [60, 65]. During the expansion process, the temperature undergoes changes in response to pressure fluctuations while maintaining a constant enthalpy, and the J-T coefficient is given by

where positive and negative J-T coefficients characterize the cooling $ (\mu>0) $ and heating $ (\mu<0) $in gas adiabatic expansion, respectively [66]. The heat capacity $ C_{P} $ is defined by

with

$\varrho_1=\left(-3(1+A) \gamma\left(\dfrac{\gamma}{r_{+}^3}\right)^{A+\beta+A \beta}-B r_{+}^3(-1+\xi)\right)$,

$\varrho_2=B\left(3 Q^2-r_{+}^2+8 P \pi r_{+}^4\right)(1-\xi)^\alpha(-1+\xi)$.

We present the variation in μ and T with the horizon radius $ r_{+} $ in Figs. 3 and 4. By setting $ P=A=1, B=\beta= \gamma=0.1 $, we can observe the constraints of the charge Q on the J-T coefficient μ and temperature T and find that the divergence point (vertical curve) and zero point move to the right as the charge increases. The zero point of $ T-r_{+} $ is the same as the $ \mu-r_{+} $ divergence, and the divergence points $(0.42846,~0.61696,~0.76147,~0.88281)$ correspond to the charge values $ 1, 2, 3 $, and $ 4 $, respectively. In addition, we observe a decrease in the Hawking temperature as the charge Q increases, and the thermodynamic characteristics of the black hole are greatly influenced by the charge.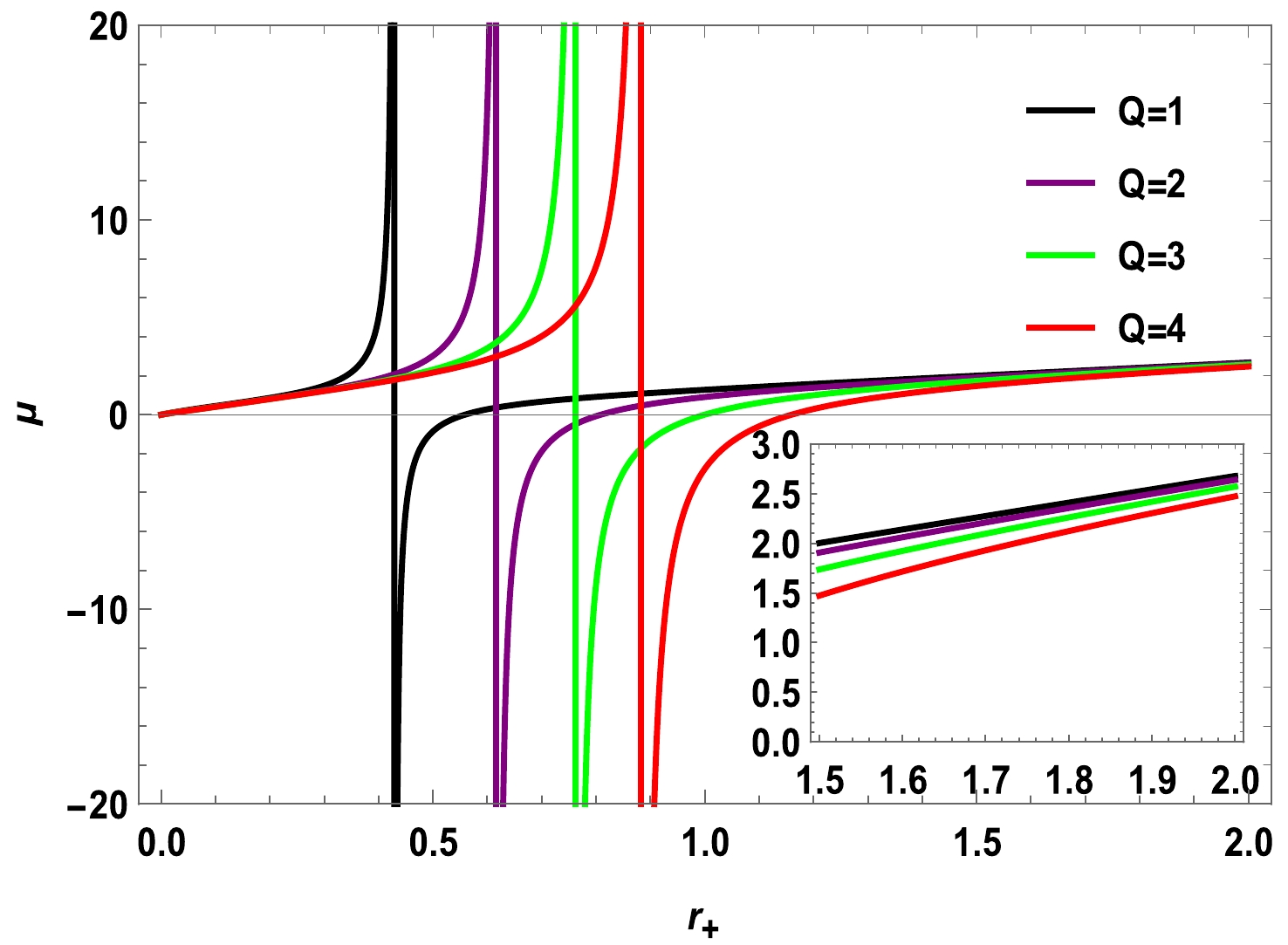

Figure 3.  (color online) J-T coefficient μ of charged black holes for $ P=A=1, B=\beta=\gamma=0.1 $.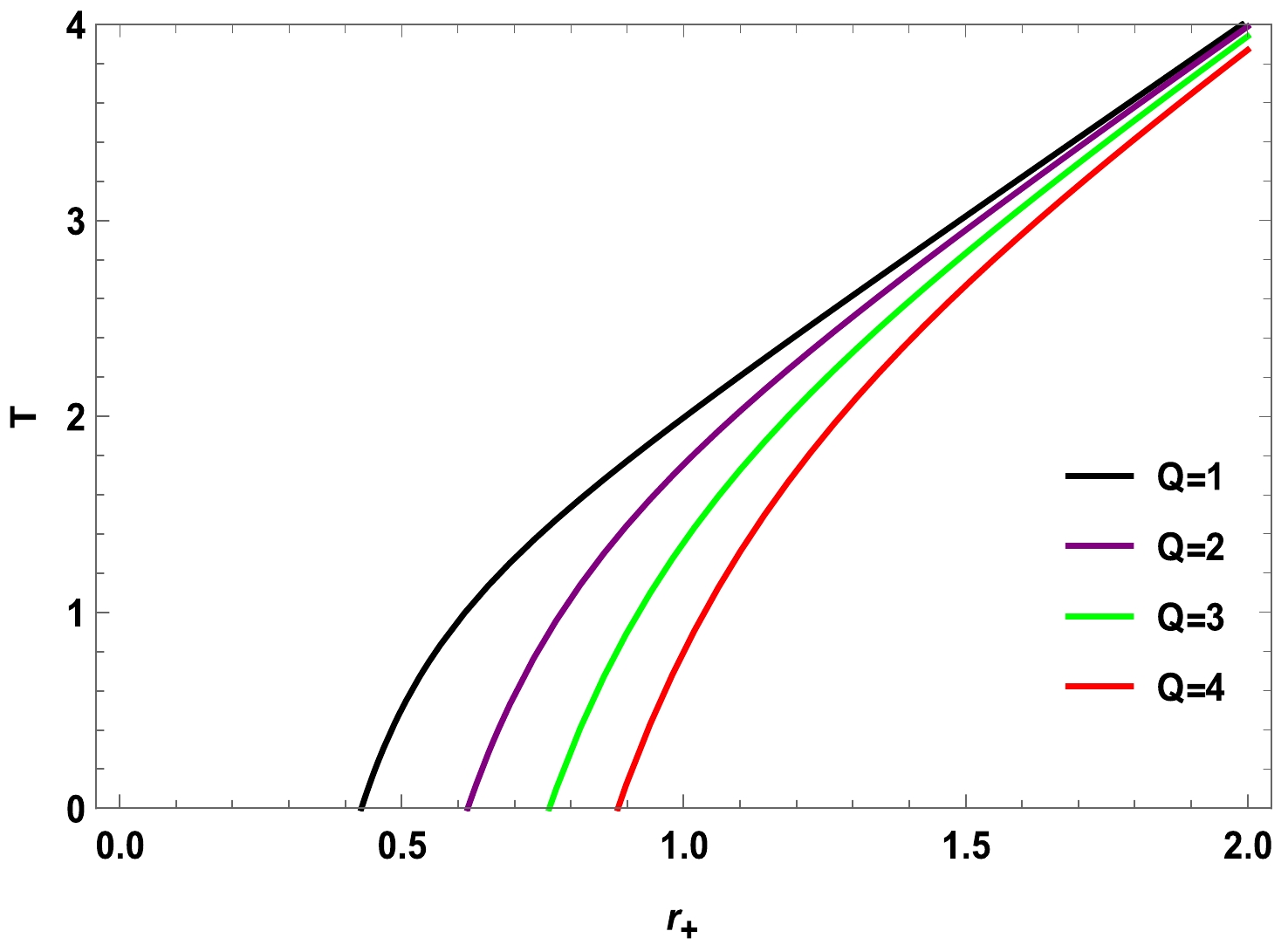

Figure 4.  (color online) Hawking temperature of charged black holes for $ P=A=1,B=\beta=\gamma=0.1 $.

Next, we investigate the potential impact of a negative heat capacity on J-T expansion. To this end, we present the changes in the J-T coefficient and heat capacity as a function of horizon radius, as depicted in Fig. 5. The results show that the heat capacity has only one root ($ Q=P=A=1,B=\beta=\gamma=0.1 $, $ r_{0}=0.42846) $. If the horizon radius $ r_{+} $ is smaller than $ r_{0}(C_{p}=0) $, the heat capacity exhibits negativity and the J-T coefficient demonstrates positivity, indicating the presence of a cooling process. In addition, if the heat capacity and $ \left[T\left(\dfrac{\partial V}{\partial T}\right)-V\right] $ are negative, μ will be positive, which can perfectly interpret Eq. (40). If the J-T coefficient is reduced to zero, we can determine the values of inversion temperature and pressure, which can be represented as follows: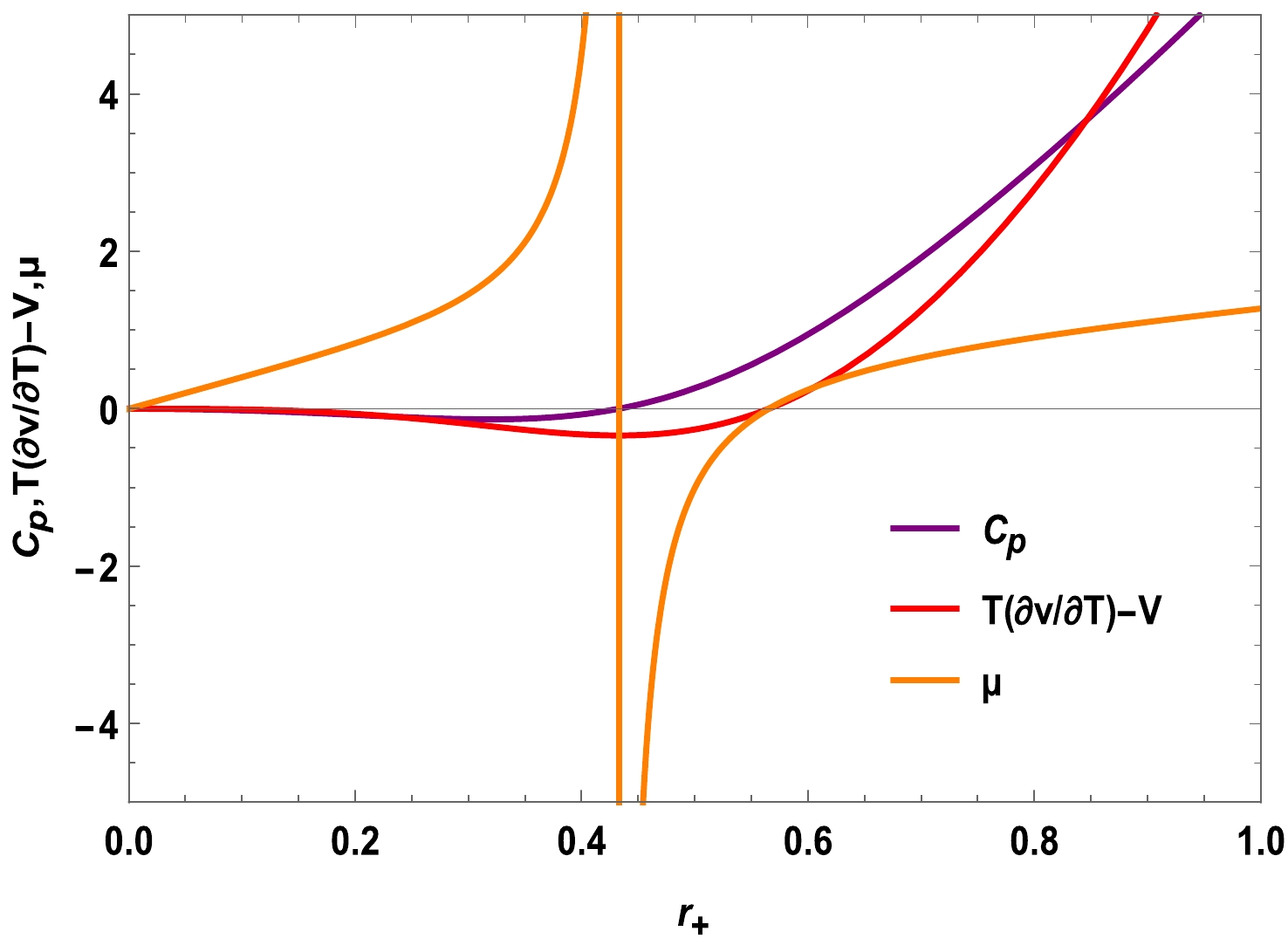

Figure 5.  (color online) Graphical behavior of the J-T coefficient, heat capacity, and $ \left[T\left(\dfrac{\partial V}{\partial T}\right)-V\right] $ of charged black holes for $ Q=P=A=1, B=\beta=\gamma=0.1 $.

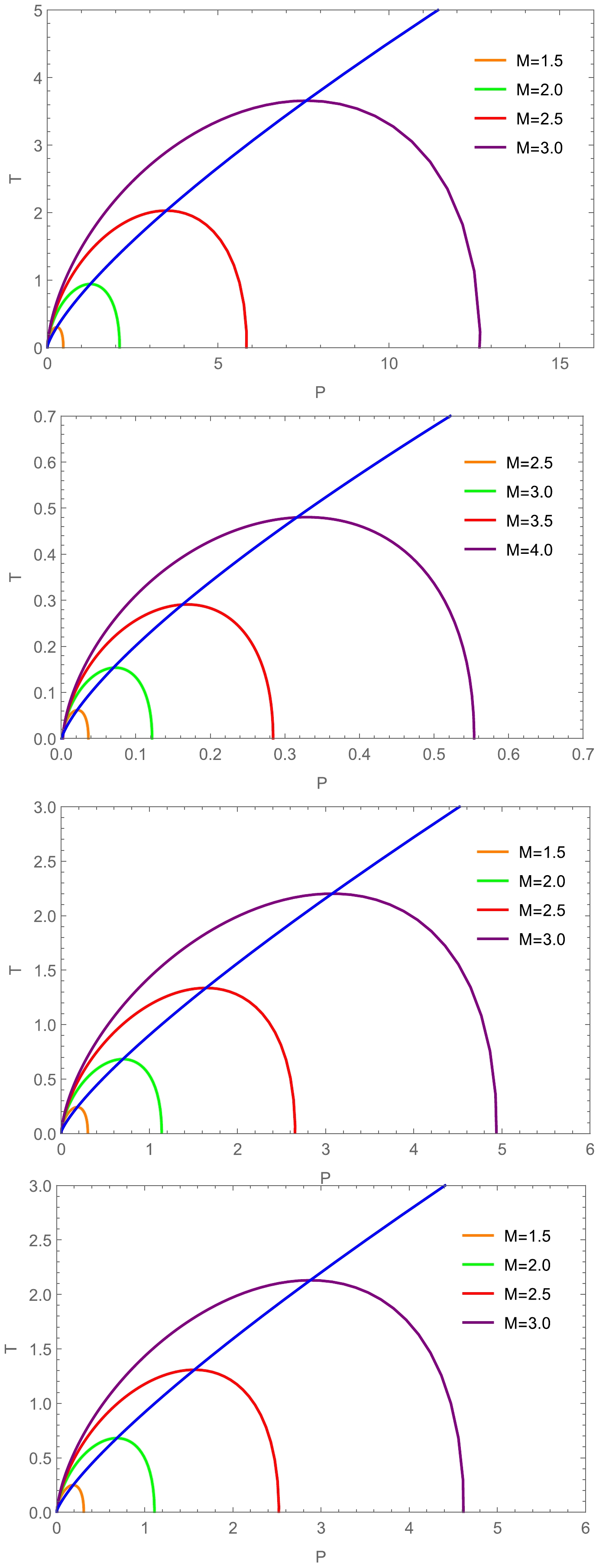
The effects of different values of the charge Q and parameters γ, A, and β on the inversion curves can be observed in Fig. 6. From top to bottom, we set ($ A=1, B= \beta=\gamma=0.1 $), ($ A=1,B=\beta=Q=0.1 $), ($ \beta=\gamma=B=Q=0.1 $), and ($ A=1, \gamma=B=Q=0.1 $), respectively. From the previous two images, we find that the charge Q and parameter γ have similar effects on the inversion curve, that is, an increase in charge Q and parameter γ leads to a decrease in the inversion curve at low pressure, whereas the opposite behavior exists under high pressure. As shown in the last two images, the parameters A and β have opposite effects on the inversion curve. Interestingly, the presence of mixed DM and DE yields a similar influence on charged black holes as on most multidimensional black hole systems [37]. The presence of a minimum inversion temperature, at which $ P_{i} $ becomes zero, is evident from Fig. 6.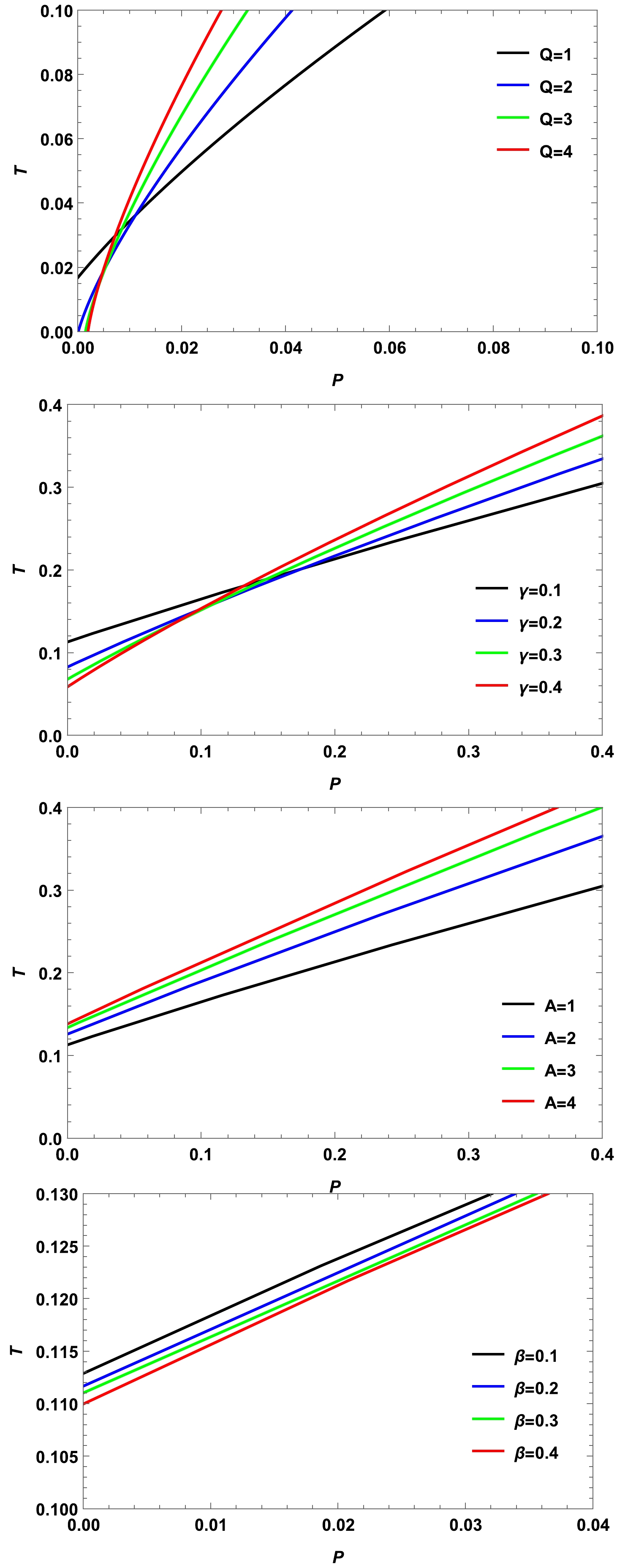

Figure 6.  (color online) Inversion curve for different parameter spaces. From top to bottom, we set ($ A=1,B= \beta=\gamma=0.1 $), ($ A=1,B=\beta=Q=0.1 $), ($ \beta=\gamma=B=Q=0.1 $), and ($A=1, \gamma= $$ B=Q=0.1$).

Next, we investigate the ratio problem associated with the minimum inversion temperature. By ensuring that $ P_{i} $ is zero, we can derive $r_{\min}$ and $T_{\min}$ as follows:

In addition, the expression for the critical temperature can be calculated by $ \left(\partial_{r_+} P\right)_{T}=0 $, $ \left(\partial_{r_+,r_+} P\right)_{T}=0 $

As shown in Fig. 7, an initial increase occurs followed by a subsequent decrease in the ratio $\dfrac{T_{\min}}{T_{c}}$ as the charge increases. For smaller Q, the ratio increases with an increase in the parameters β and γ. When Q is increased, the ratio decreases with an increase in the parameters β and γ. For larger Q, an increase in the β parameter decreases the zero point of the ratio. However, an increase in γ has no effect on the zero point of the ratio.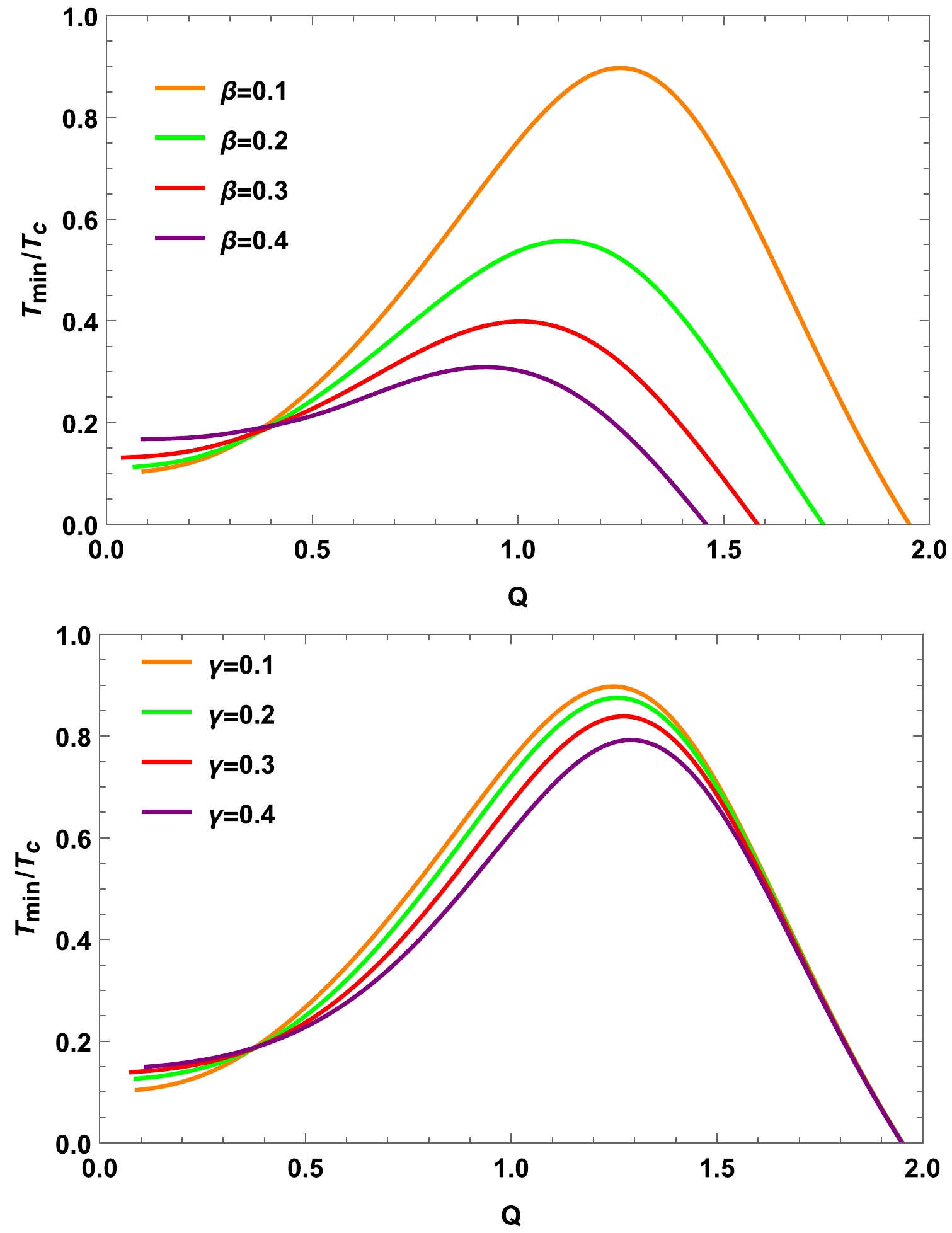

Figure 7.  (color online) Effect of the parameters β and γ on the ratio $\dfrac{T_{\min}}{T_{c}}$. Upper panel: ($ A=1,B=\gamma=0.1 $). Lower panel: ($ A=1,B=\beta=0.1 $).

Next, we conduct an analytical examination of the ratio in specific scenarios. For example, for $ \beta = 0 $, $ \gamma = 0 $, and $ B\rightarrow0 $, r_min has two roots:

and when we consider positive roots, the ratio is expressed as

If the parameter $ A = 0 $, the ratio $ \dfrac{T_{\rm min }}{T_c}=\dfrac{1}{2} $, which is completely consistent with the results of the charged AdS black hole [34].

Next, we further examine the isenthalpic curve. As shown in Fig. 8, the inversion curve (blue curve) coincides with the maximum value of the isenthalpy curve (Non-blue curve). We can observe a distinct region where the slope of the constant enthalpy curve exceeds that of the inverse temperature curve, suggesting a cooling phenomenon takes place in this particular area. The sign of the slope on the isenthalpic curve changes under inverse temperature curves, suggesting warming signs in certain regions. We determine the demarcation line between regions of heating and cooling for black holes using the inversion curve and observe an upward trend in the inversion point as the mass increases, whereas a significant decline is observed with increasing charge Q. The influence of MCG parameters on the inversion point is relatively small but cannot be ignored.

Figure 8.  (color online) Isenthalpic curves (Non-blue) and inversion curves (blue). From top to bottom, we set ($ \beta=\gamma= $$ B=0.1,A=Q=1 $), ($ \beta=\gamma=B=0.1,A=1, Q=2 $), ($ \beta=0.1, B=0.1, $$ \gamma=0.5, A=Q=1 $), and ($ \beta=0.5, B=0.1,\gamma=0.5, A=Q=1 $).

In summary, we focus on investigating a charged AdS black hole surrounded by an exotic fluid, with MCG as our primary subject. The phase transition and critical behavior of the system are thoroughly studied. Additionally, we investigate the influence of MCG parameters and charge on J-T expansion in the extended phase space. Our main findings are as follows.

$\rm (i)$ The presence of an anomalous negative $ Q^{2} $ component can be observed within this region on the $ Q^{2}-\psi $diagram when the Hawking temperature falls below the critical temperature. The black hole remains stable as long as the Hawking temperature does not exceed the critical temperature. However, when the Hawking temperature exceeds the critical temperature, a characteristic pattern of a swallowtail behavior is observed, which indicates the emergence of a first-order phase transition. Note that the critical exponent of the system is found to be in complete agreement with that observed in the van der Waals fluid system.

$\rm (ii)$ The displacement of the divergence point (vertical curve) and zero point shifts to the right with increasing charge. When the $ \mu-r_{+} $ divergence coincides with the $ T-r_{+} $ zero point, the heat capacity is negative, indicating that the occurrence of a cooling process. At low pressure, an increase in the charge Q and parameter γ leads to a decrease in the inversion temperature. Conversely, at the high pressure, an increase in the charge Q and the parameter γ results in an increase in the inversion temperature.

$\rm (iii)$ The parameters β and γ have a non-negligible effect on the ratio ${T_{\min}}/{T_{c}}$. For larger Q, increasing the β parameter results in a decrease in the zero point of the ratio. However, altering γ has no impact on the zero point of the ratio. We also observe that the parameters Q and M have opposite effects on the inversion point. Changes in the MCG parameters have a relatively small effect on the inversion point.

We would like to thank the anonymous referees for their valuable comments on improving our paper.