-
Nuclear deformation is a fundamental concept in nuclear physics that characterizes deviations of atomic nuclei from an ideal spherical shape [1]. The quadrupole deformation parameter plays a critical role in understanding the structural and dynamic properties of atomic nuclei [2–5]. In heavy-ion fusion reactions, several models are frequently utilized, including the dinuclear system model [6–10], two-step model [11–13], time-dependent Hartree-Fock theory [14–16], and diffusion-fusion model [17]. These models intricately incorporate quadrupole deformation parameters to capture the dynamic complexities inherent in heavy-ion fusion reactions. Given the limited experimental data available on quadrupole deformation, the reliance on theoretical models to derive these parameters becomes imperative. Notably, models such as the finite range droplet model (FRDM) [18], Koura-Tachibana-Uno-Yamada mass formula [19], Weizsäcker-Skyrme (WS) model [20], relativistic mean field model [21], Hartree-Fock-Bogoliubov model [22], and Duflo-Zuker mass formula [23] are commonly employed. Nonetheless, substantial inconsistencies prevail among the quadrupole deformation parameters derived from these theoretical models, underscoring the urgent need for precise parameter predictions.
Neural network methodologies have become instrumental in data analysis across scientific domains, including nuclear physics. Leveraging their nonlinear fitting capabilities and pattern recognition proficiency, neural networks have displayed potential in addressing various physics problems, particularly in predicting energy spectra [24] and nuclear mass [25–27]. Their success in these areas is largely attributable to the extensive experimental data available for training. However, the paucity of experimental data can impede the neural networks' ability to extract meaningful physical insights, consequently weakening their generalization capabilities. In the realm of neural networks, noteworthy progress has been achieved in studies related to nuclear deformation [28–30]. Inspired by these studies, we present an innovative neural network framework designed to predict nuclear quadrupole deformation parameters. Initially, a substantial dataset of quadrupole deformation parameters obtained from prevalent theoretical models is used to comprehensively pre-train the neural network model. This foundational step is aimed at providing the neural network model with a robust theoretical footing, enabling it to comprehend the general characteristics of nuclear quadrupole deformation. Subsequent fine-tuning of the model using experimental data through transfer learning techniques [31–34] helps rectify biases present in theoretical models, improving the model's precision in predicting specific nuclear data. The transfer learning method implemented in this study is realized by retraining the final layer of the network with experimental data. Additionally, other methods, such as modifying the loss function to facilitate transfer learning, as illustrated in Refs. [35, 36], merit equal attention.
The aim of this study is to achieve more precise predictions of quadrupole deformation parameters in nuclear physics, providing a more accurate description of the dynamics involved in heavy-ion fusion reactions. Additionally, we emphasize the potential of integrating transfer learning with theoretical and experimental data, offering new perspectives for research in fields with limited experimental data. This article is organized as follows. In Sec. II, we introduce our neural network approach, highlighting the pivotal role of quadrupole deformation parameters in computing capture cross-sections for heavy-ion fusion reactions. In Sec. III, the results are presented and discussed. Finally, in Sec. IV, we provide a concise summary of our study.
-
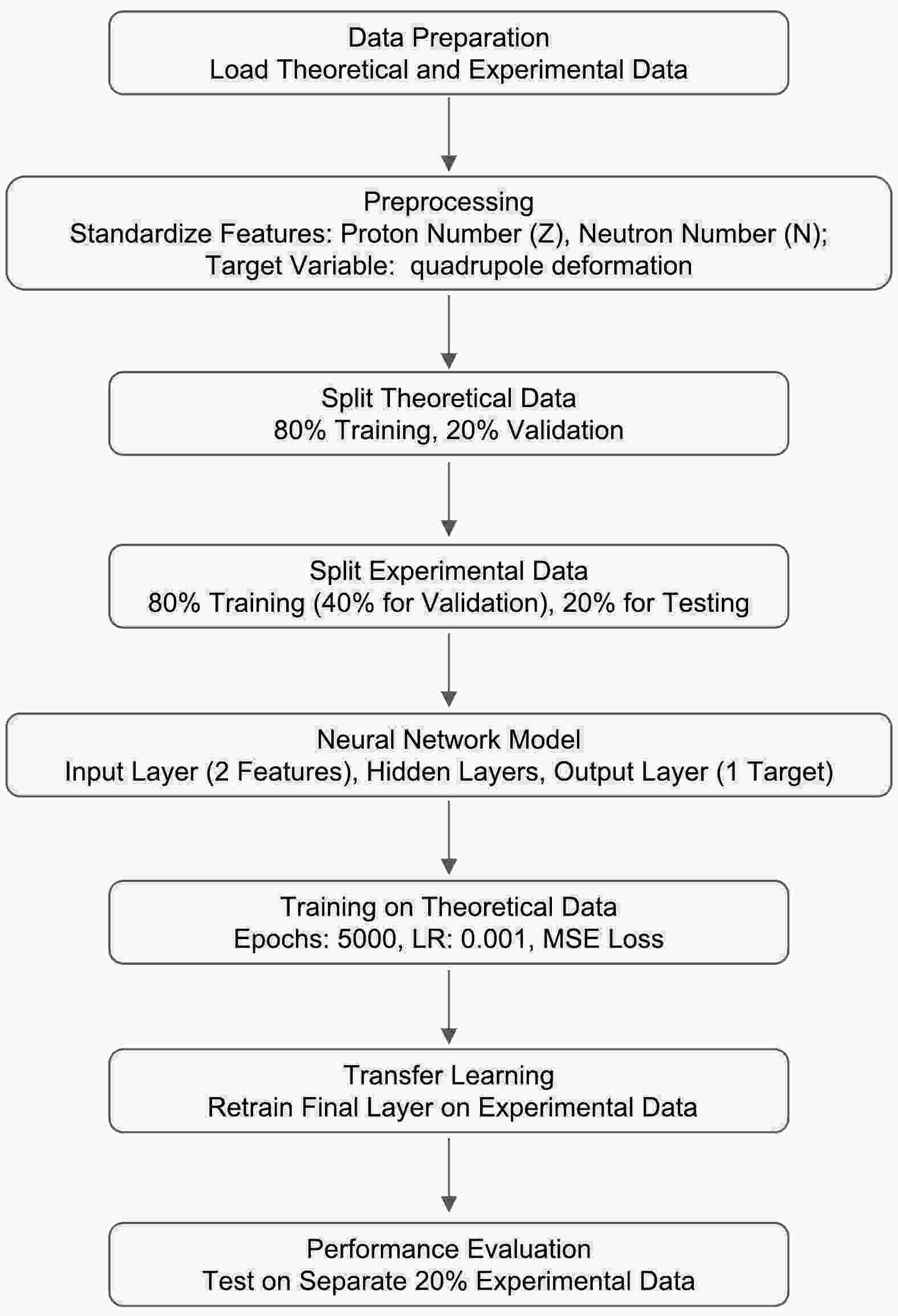
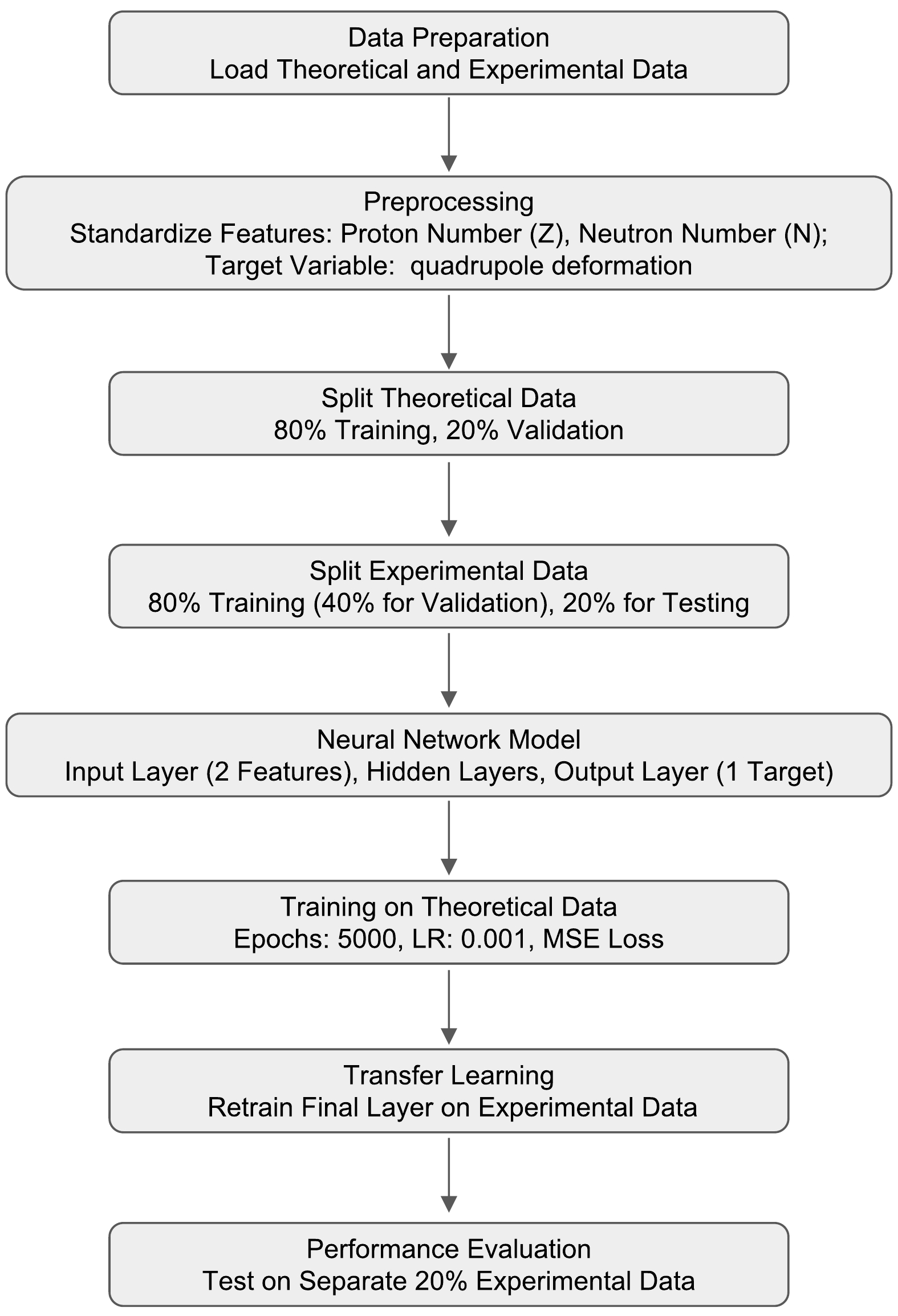
The process used to optimize and predict the quadrupole deformation parameters in our study is illustrated in Fig. 1. Theoretical and experimental datasets are utilized in this study, and key features include the proton number Z and neutron number N. These features are standardized to ensure uniform scaling, which is crucial for neural network training. The datasets are strategically partitioned into training, validation, and testing sets. Specifically, the theoretical data are allocated into two distinct sets: 60% for training and the remaining 40% for validation purposes. For the experimental dataset, a more nuanced division is employed. Initially, 80% of the dataset is designated for a retraining phase, of which 40% is subsequently earmarked for validation. The residual 20% of the overall dataset is exclusively reserved for final testing and evaluation, ensuring a robust assessment of the model's predictive capabilities.
The neural network architecture is specifically designed to address the characteristics of nuclear quadrupole deformation data, with its configuration and experimental details outlined in Table 1. It comprises an input layer, two hidden layers, and an output layer, each serving a distinct purpose in the data processing flow. The input layer is configured to receive the standardized proton number Z and neutron number N. Following this, there are two hidden layers, each consisting of 64 neurons. These layers play a pivotal role in feature extraction and executing non-linear transformations of the data. Both hidden layers utilize rectified linear units (ReLUs) as the activation function, enhancing the network's non-linear processing capabilities and mitigating gradient vanishing issues. The architecture concludes with an output layer housing a single neuron employing the Sigmoid activation function. In this study, the neuron number in the hidden layer is determined after several trials. The final value gives the best results.
Parameter/Setting Value/Description Input layer size 2 (Z, N) Hidden layers 2 Neurons per hidden layer 64 Output layer size 1 Activation function (hidden) ReLU Activation function (output) Sigmoid Loss function MSE Optimizer Adam Learning rate 0.001 Epochs (theoretical data) 5000 Epochs (experimental data) 5000 Train-validation split (theory) 60%−40% Train-validation-test split (exp) 48%−32%−20% Random seed 0 (fixed) Transfer learning layers frozen Two hidden layers Table 1. Neural network configuration and experiment details.
Our approach consists of two primary stages: Initially, we conduct pre-training of the neural network on the theoretical dataset, adjusting its weights by utilizing this data. The training epoch is set to 5000, with a learning rate (LR) of 0.001. The comparison between the expected output and the neural network's output is facilitated using a loss function, employing the mean squared error (MSE). Subsequently, we fine-tune the model on a limited experimental dataset. The weights of the input and hidden layers of the neural network model are frozen during this phase of transfer learning. This implies that these weights remain unchanged throughout the transfer learning process. This approach is chosen because these layers have already learned the fundamental features of quadrupole deformation from the pre-training phase. We exclusively retrain the output layer and update its weights based on the experimental dataset, thereby fine-tuning the pre-trained network. Finally, to test the model, performance metrics such as the MSE, mean absolute error (MAE) and root MSE (RMSE) can be employed to evaluate the results estimated by the neural network model and determine the performance level. The calculation methods for these performance metrics are as follows:
$ {\rm{MSE}} = \frac{1}{n} \sum\limits_{i=1}^{n} (E_i - P_i)^2, $

(1) $ {\rm{MAE}} = \frac{1}{n} \sum\limits_{i=1}^{n} |E_i - P_i|, $

(2) $ {\rm{RMSE}} = \sqrt{\frac{1}{n} \sum\limits_{i=1}^{n} (E_i - P_i)^2}, $

(3) where n is the total number of data, and
$ E_i $ and$ P_i $ denote the experimental and predicted values of the ith sample. -
Next, we elucidate the calculation of the capture cross-section in heavy-ion fusion reactions, highlighting the pivotal role of quadrupole deformation parameters in these computations. The empirical coupled channel model is utilized for the computation of this capture cross-section [37, 38]. The capture cross-section is expressed as [39]
$ \sigma_{\rm cap} = \frac{\pi \hbar^2}{2\mu E_{\rm c.m.}}\sum\limits_J (2J + 1) T(E_{\rm c.m.}, J), $

(4) where
$E_{\rm c.m.}$ is the center-of-mass incident energy, and the transmission probability$T(E_{\rm c.m.}, J)$ is calculated using the Hill-Wheeler formula [40]. Integrating the effect of coupling channels through the potential barrier distribution function, the transmission probability is$ \begin{aligned}[b] T(E_{\text{c.m.}}, J) =\; &\int f(B) \bigg[ 1 + \exp \Bigg( -\frac{2\pi}{\hbar \omega(J)} \\ &\times\left[ E_{\text{c.m.}} - B - \frac{\hbar^2}{2\mu R_B^2(J) } J(J + 1) \right] \Bigg) \bigg]^{-1} {\rm d}B, \end{aligned} $

(5) where
$ \hbar\omega(J) $ is the width of the parabolic form at the position of the barrier$ R_B(J) $ . The barrier distribution function$ f(B) $ takes an asymmetric Gaussian shape,$ f(B) = \left\{\begin{array}{*{20}{l}} {\dfrac{1}{N} \exp \left[ -\left( \dfrac{B - B_m}{\Delta_1} \right)^2 \right], }& {B < B_m} \\ {\dfrac{1}{N} \exp \left[ -\left( \dfrac{B - B_m}{\Delta_2} \right)^2 \right],} & {B > B_m} \end{array} \right. $

(6) where
$ B_m = \dfrac{B_s + B_0}{2} $ , with$ B_0 $ as the Coulomb barrier height at waist-to-waist orientation, and$ B_s $ as the minimal height influenced by the dynamical deformation parameters$ \beta_1 $ and$ \beta_2 $ . N is the normalization constant,$ \Delta_2 = (B_0 - B_s)/2 $ , and$ \Delta_1 $ is typically 2−4 MeV less than$ \Delta_2 $ [41]. Incorporating quadrupole deformation, the nucleus-nucleus interaction potential is formulated as$ \begin{aligned}[b] V\left( {r,{\beta _1},{\beta _2},{\theta _1},{\theta _2}} \right) =\;& {V_C}\left( {r,{\beta _1},{\beta _2},{\theta _1},{\theta _2}} \right)\\ &+ {V_N}\left( {r,{\beta _1},{\beta _2},{\theta _1},{\theta _2}} \right)\\ &+ \frac{1}{2}{C_1}{\left( {{\beta _1} - \beta _1^0} \right)^2} \\ &+ \frac{1}{2}{C_2}{\left( {{\beta _2} - \beta _2^0} \right)^2}, \end{aligned} $

(7) where
$ \beta_1 (\beta_2) $ is the dynamical quadrupole deformation parameter for the projectile (target), and$ \beta_1^0 (\beta_2^0) $ is the static deformation parameter.$ \theta_1 (\theta_2) $ represents the angle between the radius vector and the symmetry axes of the statically deformed projectile (target). The stiffness parameters$ C_{1,2} $ are derived using the liquid drop model [42]. The Coulomb and nuclear potentials,$ V_C $ and$ V_N $ , are as specified in Ref. [39]. Therefore, in the calculations of barrier heights and capture cross-section in heavy-ion fusion reactions, the quadrupole deformation parameter emerges as an indispensable parameter that cannot be overlooked. -
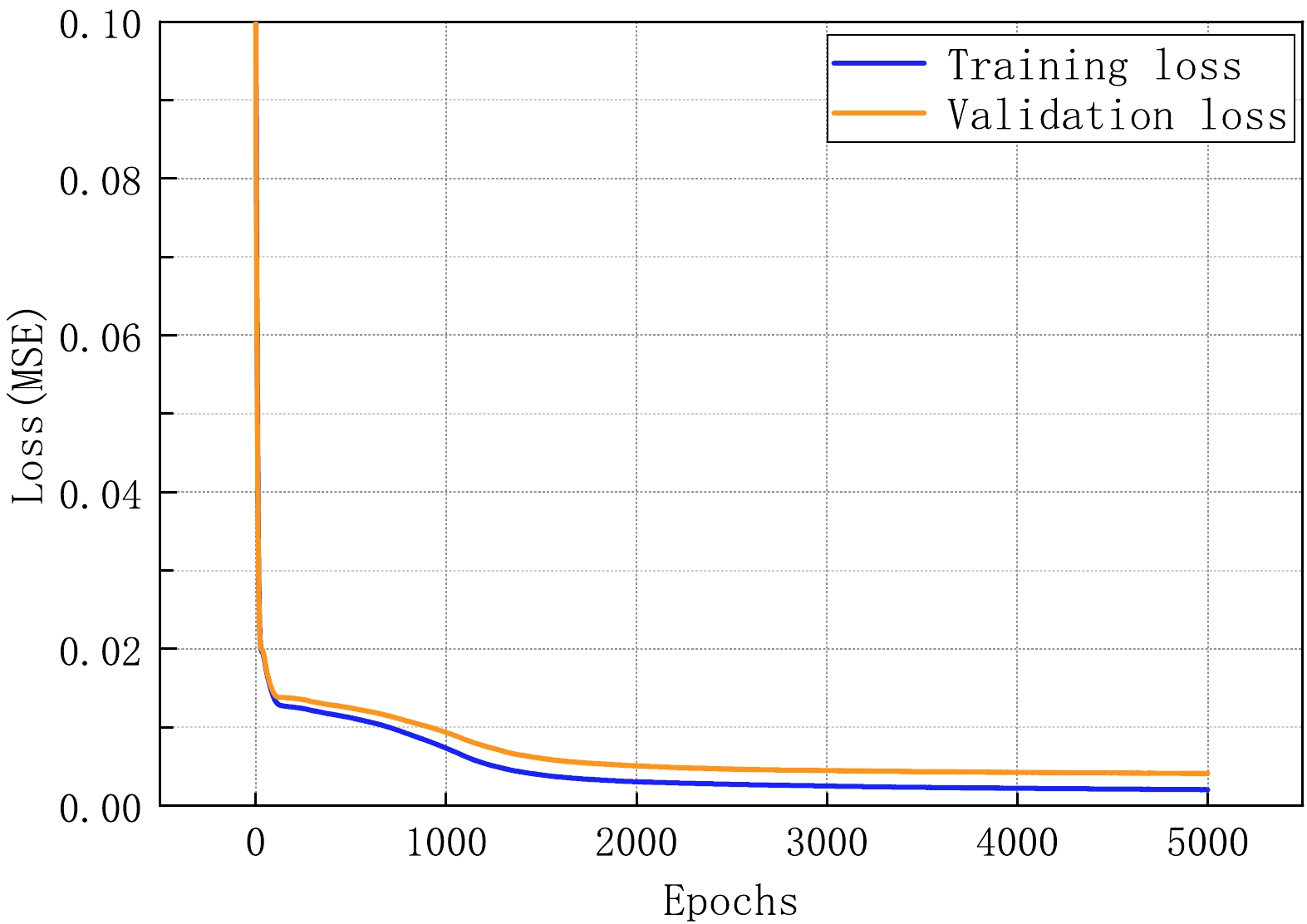
In the pre-training phase, the theoretical data for the quadrupole deformation parameters are sourced from the FRDM [18], focusing on the even-even nuclei ranges with proton number (
$8 \leq Z \leq 134$ ) and neutron number ($ N \geq 8 $ ), which encompass a total of 2331 datasets. Here, the values under consideration are the absolute values of quadrupole deformation. Figure 2 displays the loss curves for both the training and validation sets. The blue line represents the training set loss, reflecting the model's learning performance on the training data. Conversely, the orange line represents the validation set loss, showcasing the model's generalization to unseen data. The consistent downward trend in loss across epochs implies effective learning. Moreover, the close alignment between both curves indicates a balanced model fit, suggesting minimal signs of overfitting or underfitting.In the transfer learning phase, we only retrain the output layer, and the weights of this layer are updated and retrained based on the experimental dataset, thereby fine-tuning the pre-trained network. The experimental data are obtained from Ref. [43], focusing on the nuclear ranges of even-even nuclei with proton number (
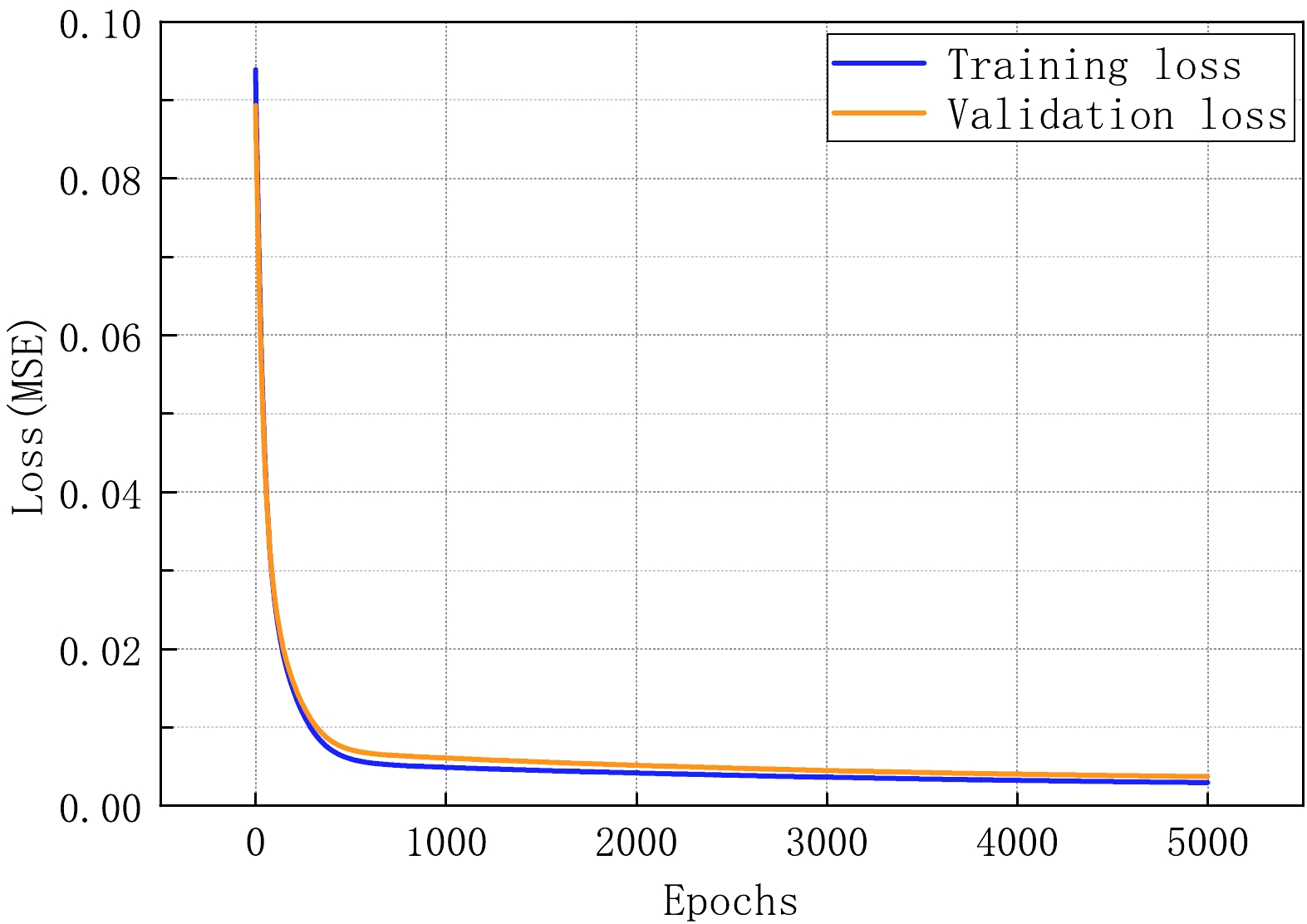
$8 \leq Z \leq 92$ ) and neutron number ($ N \geq 8 $ ), which comprise a total of 388 data points. This experimental dataset is initially divided such that 80% is used for both training and validation purposes (310 data points), whereas the remaining 20% is reserved as the test set (78 data points), which is crucial for evaluating the model's performance on unseen data. Furthermore, the 310 data points allocated for training and validation are subdivided, with 60% used as the training set and the remaining 40% serving as the validation set. In Fig. 3, we illustrate the training and validation loss curves during the transfer learning phase. We do not observe distinct signs of overfitting or underfitting.To assess the final neural network model, we analyze the test set. The deviations between the predicted quadrupole deformation parameters of 78 atomic nuclei in the test set and the corresponding experimental values, as depicted in Fig. 4, are indicative of the performance of two different models. The results from the FRDM are represented by red hollow circles. It is observed that, particularly for nuclei with proton number
$Z<50$ , the deviations from the experimental values are notably significant. In contrast, the predictions made by our neural network model, represented by green solid circles, exhibit a marked improvement in accuracy. Notably, the deviations are largely contained below 0.1 across the entire range. This substantial reduction in discrepancy demonstrates the efficacy of our neural network approach in predicting nuclear quadrupole deformation parameters. Such improved predictive performance highlights the potential of advanced machine learning techniques in enhancing our understanding of nuclear structure properties.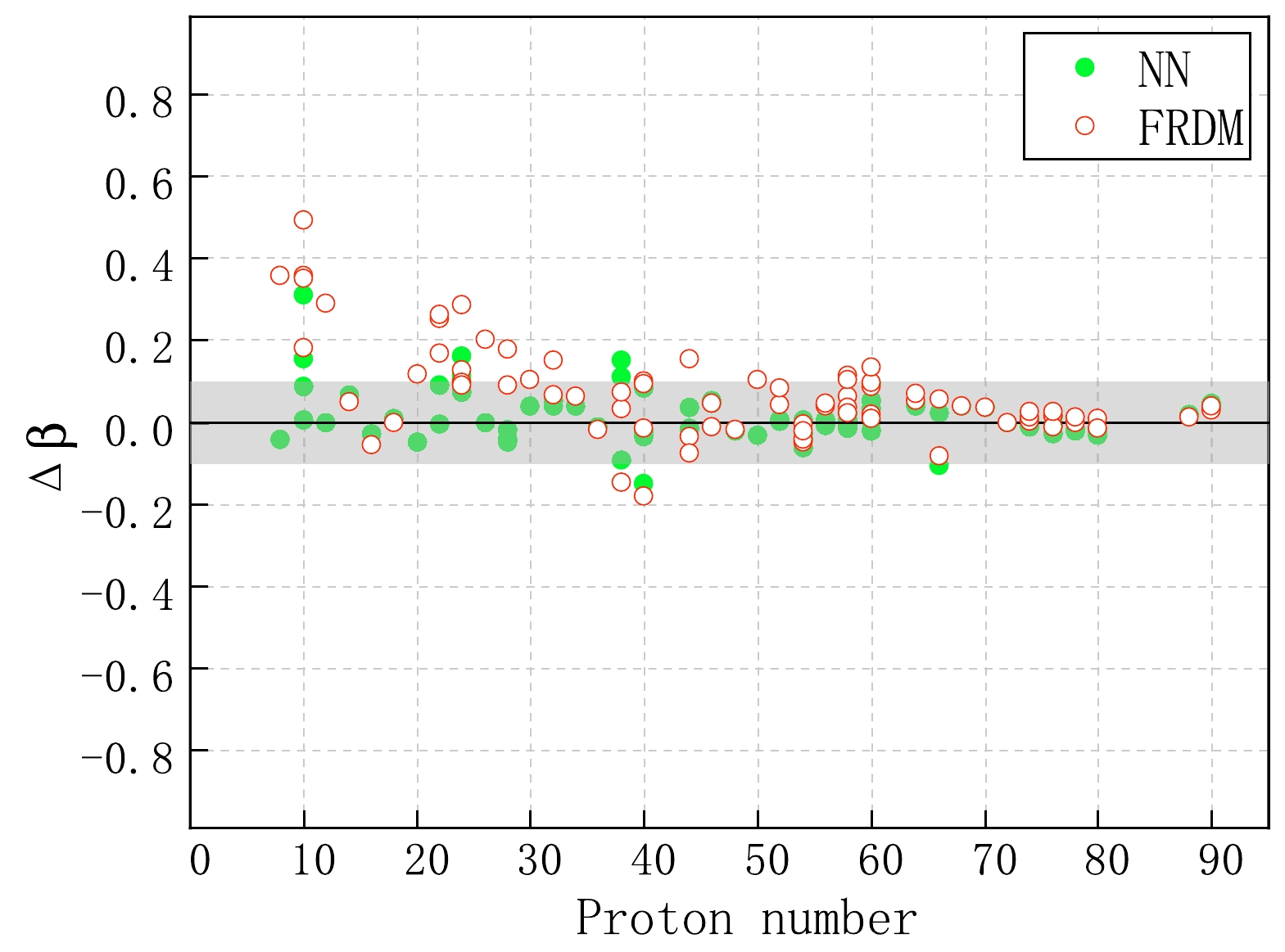
Figure 4. (color online) Difference
$ \Delta \beta $ (for quadrupole deformation parameters) between predicted and experimental values in the test set. The red hollow spheres represent the results from the FRDM, whereas the green solid spheres represent the results from our neural network (NN) model.To further validate our model within the test set, we showcase the calculated performance metrics, including the RMSE, MAE, and MSE, based on the predictions of the two models in Fig. 5. The results indicate that the FRDM yields an RMSE of 0.1247, an MAE of 0.0927, and an MSE of 0.0181. In contrast, our neural network model demonstrates markedly enhanced performance with an RMSE of 0.0666, an MAE of 0.045, and an MSE of 0.0044. Evidently, in comparison with the conventional FRDM, our neural network model exhibits superior accuracy in predicting the quadrupole deformations of atomic nuclei. This improvement not only confirms the effectiveness of the transfer learning technique employed in our neural network, which retains the general physical characteristics of theoretical models, but also showcases its adeptness in aligning with experimental data.
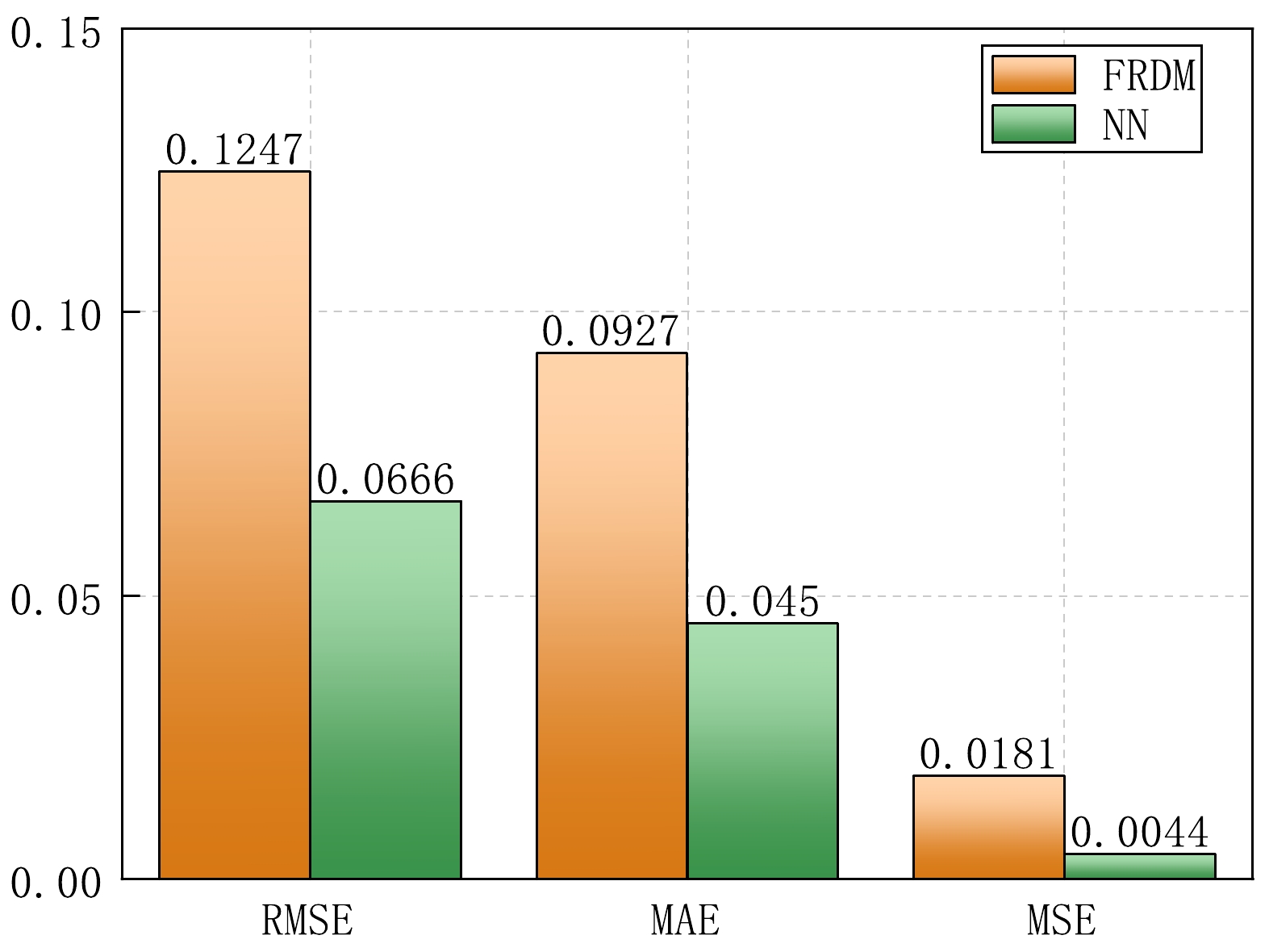
Figure 5. (color online) RMSE, MAE, and MSE for the predicted values from the test set from both the FRDM and our neural network (NN) model.
In the experimental data provided in Ref. [43], the highest proton number Z is 98. During the transfer learning phase, we select experimental data in the range
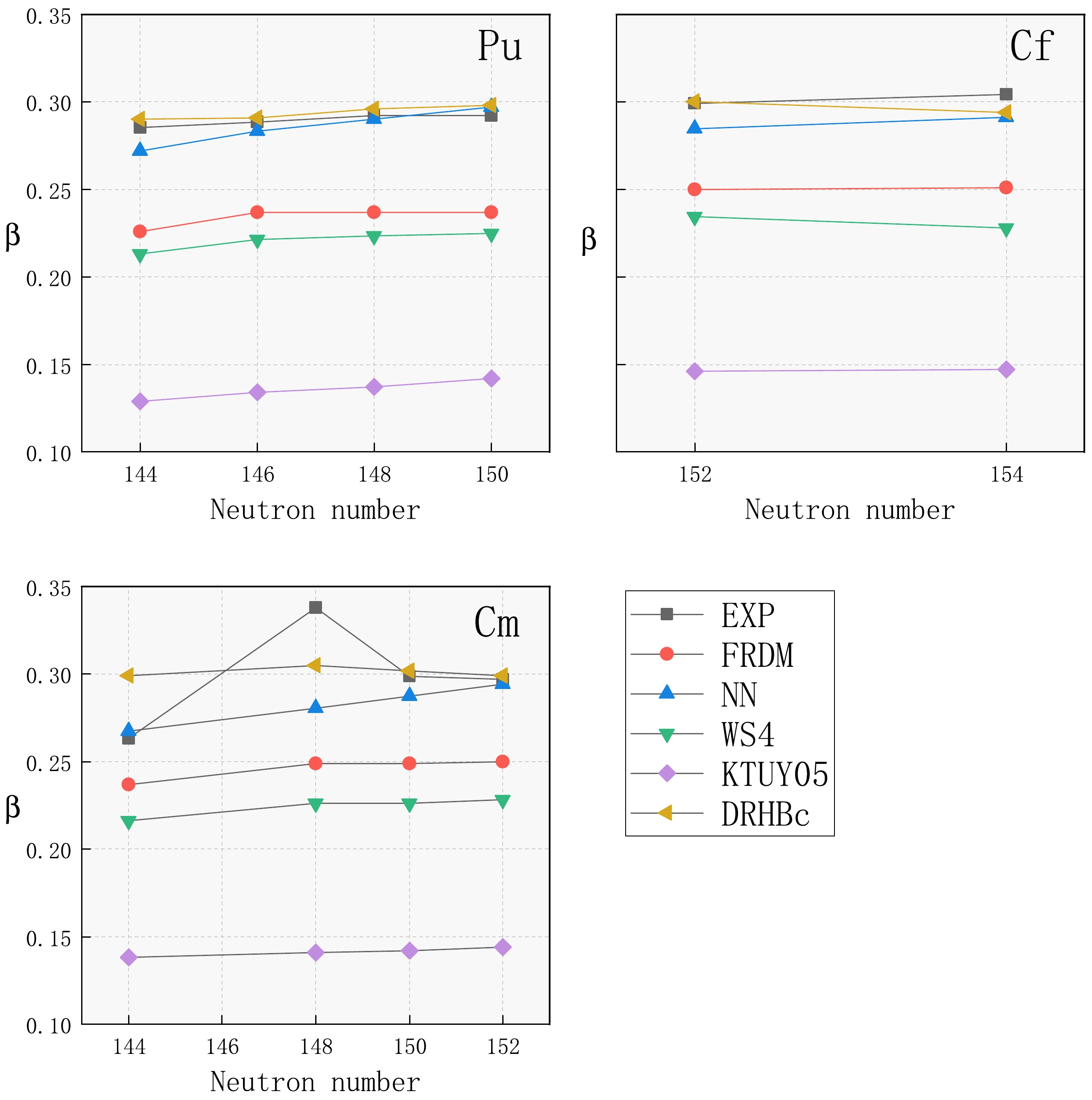
$8 \leq Z \leq 92$ . This approach aims to test the performance of our model in nuclear regions far from the experimental data used in transfer learning. In Fig. 6, our neural network model predicts the quadrupole deformation parameters for the isotopic chains of${\rm{Pu}}$ ($Z=94$ ),${\rm{Cm}}$ ($Z=96$ ), and${\rm{Cf}}$ ($Z=98$ ), and these predictions are compared with those of other theoretical models such as FRDM, WS4, KTUY05, and DRHBc. We find that the predicted quadrupole deformation parameters from different theoretical models exhibit significant variations, with the maximum error reaching approximately 0.15. Moreover, the majority of these theoretical models tend to predict values lower than the experimental data. For instance, the predictions from the FRDM generally fall approximately 0.1 below the experimental values. Our neural network model undergoes pretraining based on the FRDM predicted data and then incorporates transfer learning techniques to formulate the final neural network model. Through this methodology, we notably address the issue of the FRDM's tendency for lower predictions, resulting in better alignment with experimental data. Consequently, even in regions significantly far from those covered in the transfer learning phase, our neural network model demonstrates strong performance, effectively reproducing the quadrupole deformation parameters of the${\rm{Pu}}$ ,${\rm{Cm}}$ , and${\rm{Cf}}$ isotopic chains.As previously mentioned, quadrupole deformation parameters play an indispensable role in describing the heavy-ion capture process. Therefore, we investigate the impact of quadrupole deformation parameters during the capture stage. This stage is characterized by the projectile nucleus bombarding the target nucleus, overcoming the Coulomb barrier between them, and forming a compound nucleus system. During this interaction, the shapes of both the projectile and target nuclei influence barrier dynamics, thereby affecting the capture cross-section. In Fig. 7, we present the capture cross-sections for the heavy-ion fusion reactions
$^{48}{\rm{Ca}} + ^{244}{\rm{Pu}}$ and$^{48}{\rm{Ca}} + ^{248}{\rm{Cm}}$ , calculated using quadrupole deformations predicted using different models. The orange line represents the results obtained using quadrupole deformation parameters from the FRDM model, whereas the blue line represents those from our neural network model. We observe that the capture cross-section increases with increasing incident energy, which is attributed to the higher probability of overcoming the Coulomb barrier at elevated energies. Additionally, we note that quadrupole deformation parameters exert a slight influence on the capture cross-section. At incident energies below 200 MeV, the capture cross-sections calculated using quadrupole deformations predicted with the FRDM and our neural network model are nearly identical. Above 200 MeV, the capture cross-sections calculated using our neural network model's predictions are slightly lower than those calculated using the FRDM, although these differences are not pronounced. Notably, for the reaction$^{48}{\rm{Ca}} + ^{248}{\rm{Cm}}$ , the capture cross-section calculated using quadrupole deformation parameters predicted with our neural network model is more consistent with the experimental data.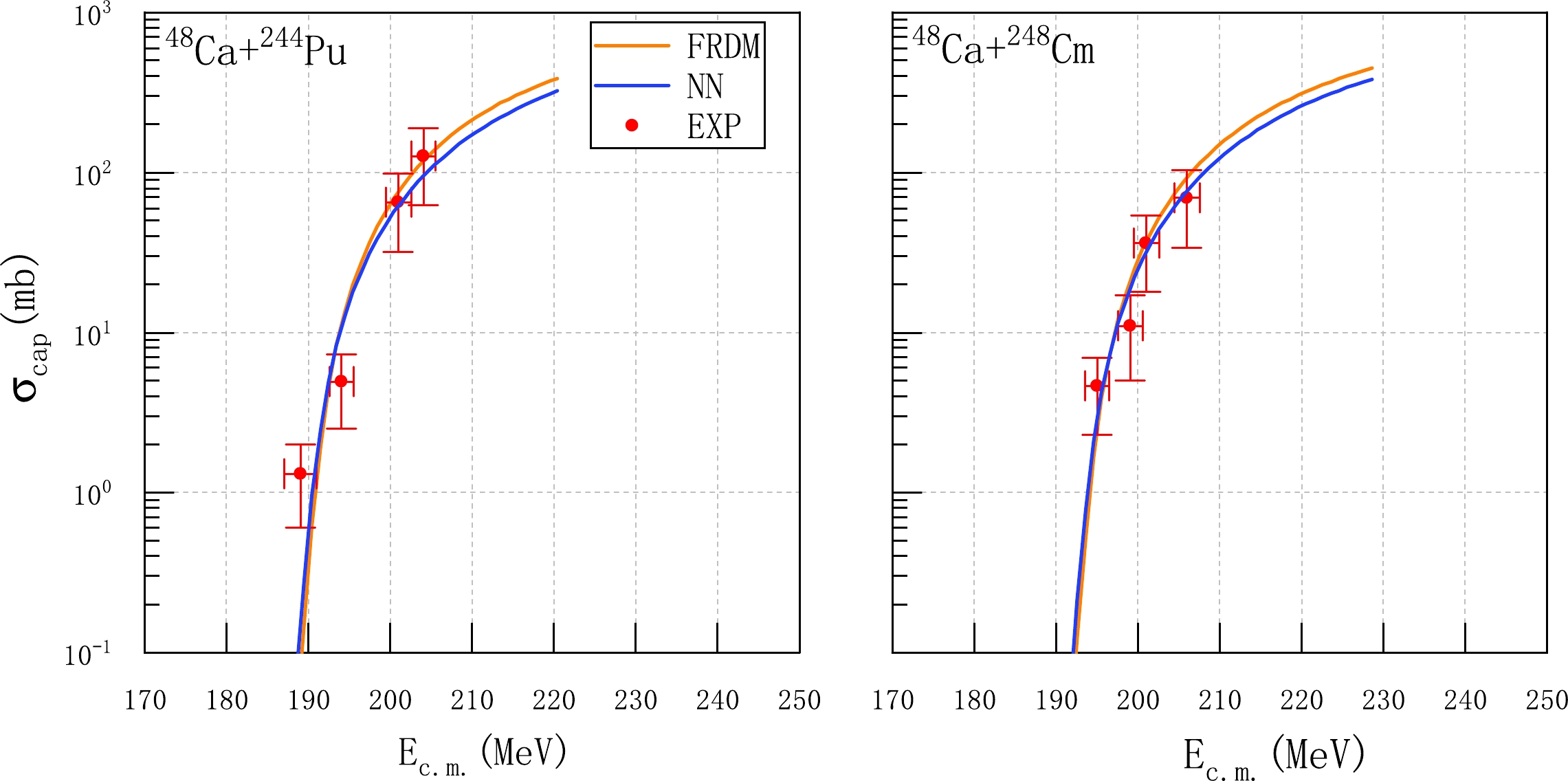
Figure 7. (color online) Capture cross-sections for the heavy-ion fusion reactions
$^{48}{\rm{Ca}} + ^{244}{\rm{Pu}}$ and$^{48}{\rm{Ca}} + ^{248}{\rm{Cm}}$ , calculated based on quadrupole deformations predicted using different models. The experimental values are taken from Ref. [45]. -
In summary, we integrate neural networks with transfer learning techniques to estimate the quadrupole deformation parameters of even-even nuclei. Comparing our results with those from existing theoretical models, we find that our neural network model presents results that are typically reasonable and reliable. Compared to the quadrupole deformation parameters from the FRDM used in our pre-training phase, our neural network model shows significant improvements in accuracy, with the RMSE on the test set reduced from 0.1247 to 0.0666, the MAE from 0.0927 to 0.045, and the MSE from 0.0181 to 0.0044. Moreover, our model also reasonably reproduces the quadrupole deformation parameters of the Pu, Cm, and Cf isotopic chains, even in nuclear regions far from those involved in the transfer learning. Finally, we observe that quadrupole deformation parameters have a modest impact on the capture cross-sections of heavy-ion fusion reactions, and using our derived parameters, we successfully reconstruct the capture cross-sections for the reactions
$ ^{48}{\rm{Ca}} + ^{244}{\rm{Pu}} $ and$ ^{48}{\rm{Ca}} + ^{248}{\rm{Cm}} $ within error margins. This study demonstrates the efficacy of combining advanced machine learning techniques with nuclear physics data, offering valuable insights and enhanced predictive capabilities in a field often constrained by limited experimental data. -
We are grateful to the Youth Innovation Team of Shaanxi Universities.
Transfer learning and neural networks in predicting quadrupole deformation
- Received Date: 2024-01-22
- Available Online: 2024-06-15
Abstract: Accurately determining the quadrupole deformation parameters of atomic nuclei is crucial for understanding their structural and dynamic properties. This study introduces an innovative approach that combines transfer learning techniques with neural networks to predict the quadrupole deformation parameters of even-even nuclei. With the application of this innovative technique, the quadrupole deformation parameters of 2331 even-even nuclei are successfully predicted within the nuclear region defined by proton numbers





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: