-
Since the first charmonium-like state
$ X(3872) $ was discovered by the Belle experiment via the process$ e^+e^-\to\gamma_{ISR}\pi^+\pi^- J/\psi $ , a new era of the study of charmonium-like states commenced [1]. A series of mesons composed of charmed and anticharmed quark pairs, such as Y(4260),$ X(3915) $ , and Zc(3900), were subsequently discovered, and most of them were confirmed by different experiments [2−11]. The understanding of the nature of these particles has turned out to be a notable challenge. Many of them have properties that are significantly different from those of conventional charmonium, e.g., a low open-charm decay rate or the absence of hadronic transitions to other charmonium states. To explain these anomalous features, many models have been proposed by theorists, including charmonium molecule mixed states [12, 13],$ c\bar{c}g $ hybrid states [14], and tetra-quarks [15]. In addition, the production rates for some of these charmonium-like states are significantly low in most experiments compared to that of conventional charmonium states. This limits the measurement precision of the resonant parameters and the determination of the corresponding quantum numbers, which makes the interpretation of these particles difficult. The Particle Data Group (PDG) [16] renamed$ X(3915) $ and$ X(3872) $ as$ \chi_{c0}(3915) $ and$ \chi_{c1}(3872) $ , respectively, according to their spin-parities. We follow the PDG naming convention in this paper.As a member of the charmonium-like family of states,
$ \chi_{c0}(3915) $ was first observed by the Belle experiment in the process$ B\to K J/\psi\omega $ in a data sample containing$ 275\times10^6 \;\; B\bar{B} $ pairs [9]. The mass and width were determined to be$ 3943\pm11\pm13 $ MeV/$ c^2 $ and$ 87\pm22\pm26 $ MeV, respectively, with the assumption that$ \chi_{c0}(3915) $ is an S-wave Breit-Wigner (BW) resonance. The particle was confirmed by the BaBar experiment in the same decay mode with a$ 383\times10^6 \;\; B\bar{B} $ event data sample [10]; in this case, the reported mass and width were$ 3914.6^{+3.8}_{-3.4}\pm2.0 $ MeV/$ c^2 $ and$ 34^{+12}_{-8}\pm5 $ MeV, respectively. The BaBar experiment subsequently updated their measurements with a larger data sample of$ 467\times10^{6} \;\; B\bar{B} $ events and looser$ M(\pi^+\pi^-\pi^0) $ requirement that additionally revealed a X(3872) signal [11]; the updated values of mass and width were$ 3919.1^{+3.8}_{-3.4}\pm2.0 $ MeV/$ c^2 $ and$ 31^{+10}_{-8}\pm5 $ MeV, respectively. In addition,$ \chi_{c0}(3915) $ was also observed in the two-photon collision process$ \gamma\gamma\to\omega J/\psi $ by both the BaBar and Belle experiments [7, 8]. Their measured masses and widths are listed in Table 1. BaBar performed a spin-parity measurement in their analysis, obtaining a quantum number$ J^P=0^+ $ and identifying$ \chi_{c0}(3915) $ as the$ \chi_{c0}(2P) $ charmonium state. However, this assignment was disputed because of the large rate for the$ \chi_{c0}(3915)\to\omega J/\psi $ decay and the absence of$\chi_{c0}(3915) \to D\bar{D}$ decays [17, 18]. Moreover, the mass difference between$ \chi_{c2}(2P) $ and$ \chi_{c0}(3915) $ was only approximately 10 MeV, which is too small for fine splitting of$ P $ -wave charmonia [17]. In 2020, the LHCb experiment made an amplitude analysis of the$ B^+\to D^+D^-K^+ $ decay [19] and reported that a spin-0 resonance is needed to properly describe the data. They determined its mass and width to be$ 2923.8\pm1.5\pm0.4 $ MeV/$ c^2 $ and$ 17.4\pm5.1\pm0.8 $ MeV, respectively.Experiment Production $ M $ /(MeV/

$ c^2 $ )

$ \Gamma $ /MeV

Belle [9] $ B\to\omega J/\psi K $ 

$ 3943\pm11\pm13 $ 

$ 87\pm22\pm26 $ 

BaBar [11] $ B\to\omega J/\psi K $ 

$ 3919.1^{+3.8}_{-3.4}\pm2.0 $ 

$ 31^{+10}_{-8}\pm5 $ 

Belle [7] $ \gamma\gamma\to\omega J/\psi $ 

$ 3915\pm3\pm2 $ 

$ 13\pm6\pm3 $ 

BaBar [8] $ \gamma\gamma\to\omega J/\psi $ 

$ 3919.4\pm2.2\pm1.6 $ 

$ 17\pm10\pm3 $ 

LHCb [19] $ B^+\to D^+D^-K^+ $ 

$ 3923.8\pm1.5\pm0.4 $ 

$ 17.4\pm5.1\pm0.8 $ 

PDG [16] $ 3921.7\pm1.8 $ 

$ 18.8\pm3.5 $ 

This study $ 3920.9\pm0.9 $ 

$ 18.2\pm2.4 $ 

Table 1. Mass (
$ M $ ) and width ($ \Gamma $ ) of$ \chi_{c0}(3915) $ measured by different experiments; the first uncertainty is statistical, whereas the second is systematic. The results from PDG and those obtained in this study are listed in the last two rows.In this study, we performed a simultaneous
$ \chi^2 $ fit to the distributions of invariant mass of$ \omega J/\psi $ in the processes$ \gamma\gamma\to \omega J/\psi $ measured by BaBar [denoted as (a)],$ \gamma\gamma\to \omega J/\psi $ by Belle [(b)],$ B^0\to \omega J/\psi K^0 $ by BaBar [(c)],$ B^+\to \omega J/\psi K^+ $ [(d)] by BaBar, and$ B\to \omega J/\psi K $ by Belle [(e)] to extract the mass and width of$ \chi_{c0}(3915) $ . The distributions of$ M(\omega J/\psi) $ for these processes are shown in Fig. 1. Furthermore, LHCb's results were taken into account as an additional constraint in the$ \chi^2 $ calculation. Compared to the values from PDG, which also provides the mass and width of$ \chi_{c0}(3915) $ by combining the measurements from these experiments, we used more detailed information of the$ \omega J/\psi $ invariant mass spectrum. This was expected to provide results with higher precision.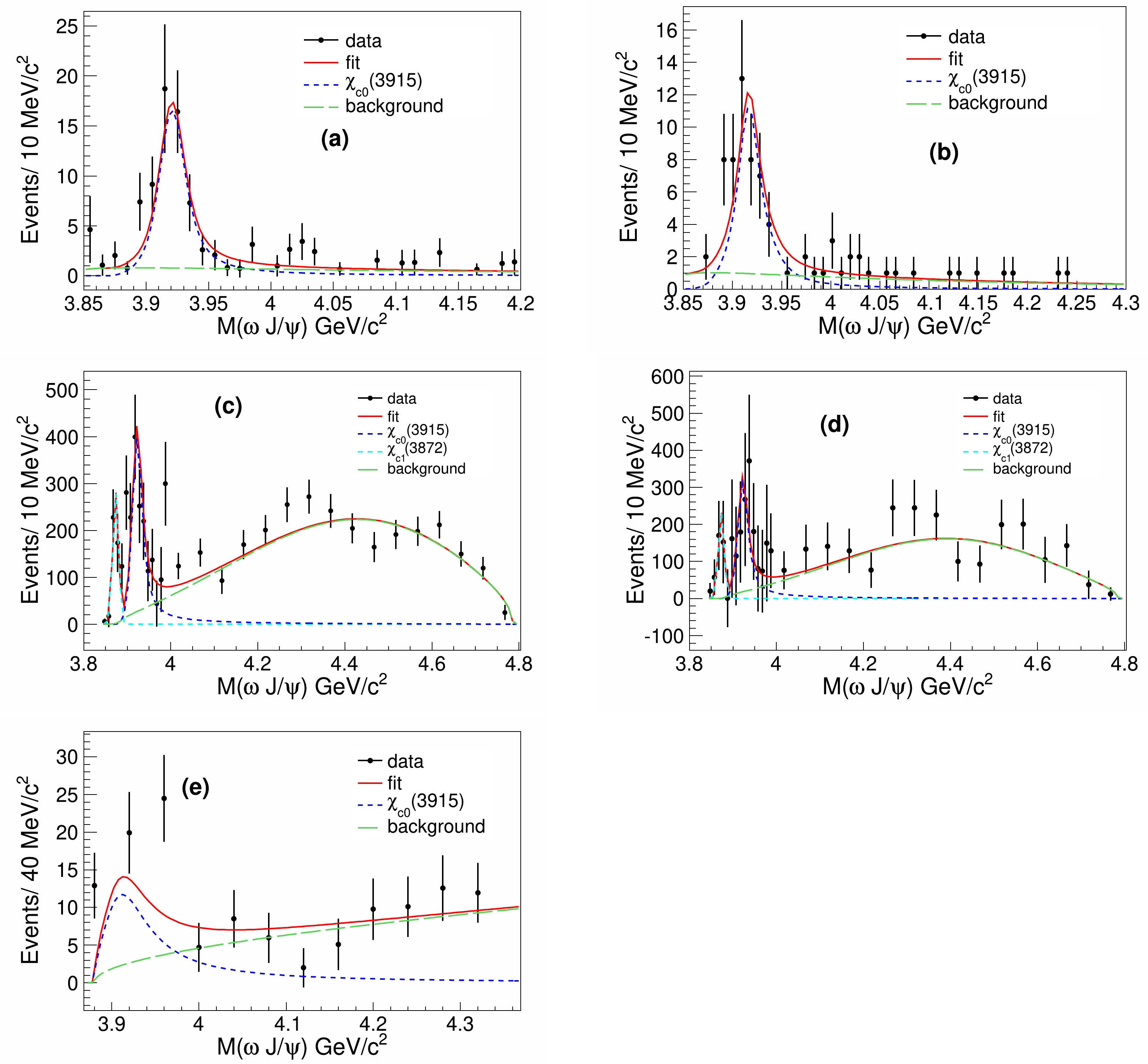
Figure 1. (color online) Fit to the distributions of the
$ \omega J/\psi $ invariant mass obtained in the processes (a)$ \gamma\gamma\to \omega J/\psi $ by BaBar, (b)$ \gamma\gamma\to \omega J/\psi $ by Belle, (c)$ B^0\to \omega J/\psi K^0 $ by BaBar, (d)$ B^+\to \omega J/\psi K^+ $ by BaBar, and (e)$ B\to \omega J/\psi K $ by Belle. The black dots with error bars represent the data mentioned in the main text. The red solid curves are the fit results, the cyan/blue dashed curves indicate the$ \chi_{c1}(3872) $ /$ \chi_{c0}(3915) $ signals, and the green dashed curves show the backgrounds. -
In the simultaneous
$ \chi^2 $ fit, the functions used to fit the$ M(\omega J/\psi) $ spectra in Fig. 1 were similar to those applied in their corresponding publications. The fit function comprises signal and background components. The$ \chi_{c0}(3915) $ signal shape is described by an S-wave BW function convoluted with the detector resolutions, which are also from the mentioned publications. The BW is${\Gamma(p^*/p_{0})} / [{(m^2-M^2)^2+(M\Gamma(p^*/p_{0}))^2}]$ , where$ M $ is the peak mass,$ p^* $ is the momentum of the$ J/\psi $ momentum in the rest frame of a$ \omega J/\psi $ system, and$ p_0=p^* $ when$ m=M $ [9].$ M $ and$ \Gamma $ are common parameters for the five measurements that are allowed to float in the fit. The contributions of$ \chi_{c1}(3872) $ are needed for distributions (c) and (d), as shown in Fig. 1. The signal shape of$ \chi_{c1}(3872) $ is described with a Gaussian function featuring a fixed deviation of 6.7 MeV/$ c^2 $ and a free mean value. The detector resolution of$ \gamma\gamma\to\omega J/\psi $ for Belle is described by a double Gaussian function; one Gaussian has mean and deviation values of 4.5 MeV and 0 MeV, respectively, with a coefficient of 0.59, whereas the other Gaussian has a mean and deviation of 16 MeV and –4.0 MeV, respectively, with a cofficient of 0.41 [7]. Conversely, the resolution for the same process conducted by BaBar is described by a single Gaussian with a deviation of$ 5.7 $ MeV and a mean value of zero. Similarly, the resolution for the measurement$ B\to K\omega J/\psi $ by BaBar (Belle) is described by a single Gaussian function with a deviation of 6.7 MeV (6 MeV) and a mean value of zero. All these resolution details were extracted from the corresponding publications. The non-resonance background shapes for measurements (a) and (b) are described as$ p^*(m){\rm exp}(-\delta p^*(m)) $ , where$ \delta $ is a parameter that is allowed to float in the fit, and$ m=m(J/\psi\omega) $ [8]. The background shapes of measurements (c) and (d) are described by a Gaussian function with parameters that float in the fit [11]. The shape of the background in measurement (e) is described by a threshold function of the form$ p^*(m) $ , which is the$ J/\psi $ momentum in the rest frame of a$ \omega J/\psi $ system.$ \chi^2 $ is defined as$\chi^2 = \sum\limits_{i=1}^{5}\sum\limits_{j=1}^{N_i} \left(\frac{x_{ij}-\mu_{ij}}{\sigma_{ij}}\right)^2+\left(\frac{M_{h}-M}{\sigma_{M_{h}}}\right)^2+\left(\frac{\Gamma_h-\Gamma}{\sigma_{\Gamma_{h}}}\right)^2, $

(1) where
$ i $ takes values from 1 to 5, corresponding to the measurements from (a) to (e),$ x_{ij} $ and$ \sigma_{ij} $ are the observed signals and corresponding errors in each bin, as shown in Fig. 1,$ \mu_{ij} $ is the expected value in each bin calculated with the fitting shape mentioned above, and$ N_i $ is the number of bins in each measurement. The numbers of events in many bins for measurements (a), (b), and (e) are very small, so we reset the bin width to ensure that there was at least nine events in each bin to make a meaningful calculation of their contribution to the$ \chi^2 $ value. The numbers of bins in measurements (a) and (b) are$ N_1 $ =6 and$ N_2 $ =8. For measurements (c) and (d), the bin width in the mass region from 3.8425 to 3.9925 GeV/$ c^2 $ is 10 MeV/$ c^2 $ , and it is 50 MeV/$ c^2 $ in the region beyond 3.9925 GeV/$ c^2 $ , as shown in Fig. 1. The numbers of bins$ N_3 $ and$ N_4 $ are both 31. For measurement (e),$ N_5 $ =9. The last two components of the$ \chi^2 $ formula,$({M_{h}-M})/{\sigma_{M_{h}}}$ and$({\Gamma_{h}-\Gamma}) /{\sigma_{\Gamma_{h}}}$ , are from the measurements of the LHCb experiment [19], where$ M_h $ and$ \Gamma_h $ are the measured mass and width, and$ \sigma_{M_h} $ and$ \sigma_{\Gamma_h} $ are the corresponding statistical uncertainties.By minimizing
$ \chi^2 $ with minuit [20], we obtained a fit result of$ M=3920.9\pm0.8 $ MeV/$ c^2 $ and$ \Gamma=18.2\pm2.2 $ MeV. The fit goodness is$ \chi^2/ndf= 89.1/66 $ , where$ ndf $ is the number of degrees of freedom in the fit. The fit results are also shown in Fig. 1.The total systematic uncertainty of the mass and width, denoted as
$ \sigma_{\rm sum} $ , was obtained with the formula$ \dfrac{1}{\sigma_{\rm sum}^2}=\sum _{i=1}^{5}\dfrac{1}{\sigma_{i}^2} $ , where$ i $ takes values from 1 to 5 corresponding to each measurement listed in Table 1, and$ \sigma_{i} $ is the systematic uncertainty of the$ i $ -th measurement. In combination with the statistical uncertainties from our fit, we finally obtained$ M=3920.9\pm0.9 $ MeV/$ c^2 $ and$ \Gamma=18.2\pm2.4 $ MeV. -
We determined the resonant parameters of
$ \chi_{c0}(3915) $ by simultaneously fitting the measurements provided by the Belle, BaBar, and LHCb experiments. The mass and width were determined to be$ M=3920.9\pm 0.9 $ MeV/$ c^2 $ and$ \Gamma=18.2\pm2.4 $ MeV, respectively. which are consistent with the average values in PDG listed in Table 1 within one standard deviation but with higher precision.
Determination of the resonant parameters of ${ \boldsymbol\chi_{\boldsymbol c \bf 0}\bf (3915)} $ with global fit
- Received Date: 2024-03-06
- Available Online: 2024-06-15
Abstract: Particle







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: