-
Describing baryon-baryon interactions within a unified model has always been a challenge in both particle and nuclear physics [1–4]. Strong constraints and well-established models exist for nucleon-nucleon interactions [1, 2]. However, there are still difficulties in precisely modeling hyperon-nucleon scattering, especially hyperon-hyperon interactions, owing to the lack of experimental measurements. To date, only a few measurements of hyperon-nucleon scattering [5–19] and one of hyperon-hyperon scattering [20] have been reported, leaving theoretical models largely unconstrained [21–36].
The properties of hyperons in dense matter have attracted considerable interest owing to their close connection with hypernucleus and the hyperon component in neutron stars [4]. Hyperons may exist within the inner layer of neutron stars whose structure strongly depends on the equation of state (EOS) of nuclear matter at supersaturation densities [37]. The appearance of hyperons in the core softens the EOS, resulting in neutron stars with masses lower than 2
$ M_\odot $ [38], where$ M_\odot $ is the mass of the sun. However, studies based on observations from the LIGO and Virgo experiments [39] indicate that the EOS can support neutron stars with masses above$ 1.97M_\odot $ . This is the so-called "hyperon puzzle in neutron stars," which warrants further experimental and theoretical studies on the hyperon-nucleon interaction.Most of the previous measurements (
$ \Lambda p \to \Lambda p $ ,$ \Sigma^- p\to \Sigma^- p, \Lambda n, \Sigma^0 n $ , and$ \Sigma^+ p\to \Sigma^+ p $ ) were accomplished in the bubble chamber era of the 1960s and 1970s [5–9] using hyperons with momenta less than 1 GeV/c2. After a gap of 20 years, an experimental group in KEK studied$ \Sigma^+ p $ and$ \Sigma^- p $ elastic scattering processes with a scintillating fiber block [10–12]; in this case, the momentum of the$ \Sigma^{\pm} $ hyperon was within [0.35, 0.75] GeV/c2, slightly higher than that used in Ref. [5]. Later, one group in KEK first measured the total cross section of the$ \Xi^- p\to \Lambda\Lambda $ reaction at$ p_{\Xi} \sim 0.5 $ GeV/c2 [13]. Subsequently, the E40 collaboration in the J-PARC Hadron Experimental Facility updated the measurements of the$ \Sigma^{\pm} p\to \Sigma^{\pm} p $ and$ \Sigma^- p \to \Lambda n $ scattering processes with 0.4 GeV/c2 <$p_{\Lambda}<0.85 $ GeV/c2 [14, 15, 17], and the CLAS collaboration performed improved measurements on the cross section of the$ \Lambda p $ elastic scattering process with 0.9 GeV/c2 <$p_{\Lambda}<2.0 $ GeV/c2 [16]. The uncertainties of all the above measurements are large. Recently, reactions${\Xi^0} + {^{9}{\rm{Be}}} \to {\Xi^-} + p + {^{8}{\rm{Be}}}$ and$ \Lambda + {^{9}{\rm{Be}}} \to \Sigma^+ + X $ have been measured by the BESIII collaboration with$p_{\Xi^0} \approx 0.818\; {\rm{GeV}}/c^{2}$ and$ p_{\Lambda} \approx 1.074\; {\rm{GeV}}/c^{2} $ [ 18, 19]; the method employed for these measurements is introduced in this paper.On the theoretical side, many models have been proposed to describe the hyperon-nucleon and hyperon-hyperon interactions, including the meson-exchange model (with Jülich [21] or Nijmegen [22] potentials), chiral effective field theory (χEFT) approaches [23–30], calculations on the lattice from HALQCD [31, 32] and NPLQCD [33, 34], low-momentum models [35], and quark model approaches [36]. The precision of the aforementioned models will definitely be further improved by additional experimental measurements.
Experimental studies of hyperon-nucleon interactions still suffer from difficulties in the realization of a stable hyperon beam. First, the lifetime of ground-state hyperons is usually on the order of
$ O(10^{-10})\; {\rm{s}} $ owing to their weak decay, which is too short to achieve a stable beam. Meanwhile, hyperons historically used for fixed-target experiments are commonly produced in$ K p $ and$ \gamma p $ collisions, such as those in J-PARC and CLAS experiments, with a high hadronic background level. Compared with fixed-target experiments, many more hyperons are accessible from the decay of charmonia produced at$ e^+ e^- $ colliders, which have recently been used at BESIII to measure hyperon-nucleus interactions [18, 19]. Furthermore, the abundant antihyperons produced in pair with hyperons create exciting prospects to probe antihyperon-nucleus/nucleon interactions that have rarely been measured and studied.In this paper, the prospects to study hyperon-nucleus/nucleon interactions at BESIII are discussed. The hyperon pairs from the decays of 10 billion
$ J/\psi $ and 2.7 billion$ \psi(3686) $ [40] provide an intense and high-quality hyperon beam, which makes it possible to study the hyperon-nucleus/nucleon interactions by scattering between hyperons and nucleus in the materials of the beam pipe and other supporting structures of the spectrometer.Using this method, the cross sections of two hyperon-nucleus interactions were measured at BESIII [18, 19]. Subsequently, the cross sections of the corresponding hyperon-nucleon reactions were extracted from further phenomenological calculations. In the near future, these measurements will definitely benefit from improved techniques and larger datasets at the proposed Super Tau-Charm Factory (STCF) [41].
Next, we briefly introduce the expected measurements at BESIII and analyze recently measured [19] reaction
$J/\psi \to \Lambda \bar{\Lambda},\; \bar{\Lambda} \to \bar{p} \pi^+,\; \Lambda + {}^{9}{\rm{Be}} \to \Sigma^+ + X$ as an example. -
The BESIII detector is a magnetic spectrometer [42] located at the Beijing Electron Positron Collider (BEPCII). The cylindrical core of the BESIII detector consists of a helium-based multilayer drift chamber (MDC), a plastic scintillator time-of-flight system (TOF), and a CsI(Tl) electromagnetic calorimeter (EMC), which are all enclosed in a superconducting solenoidal magnet providing a 1.0 T magnetic field.
The BESIII detector exhibits excellent performance on the reconstruction of long-lived particles, such as
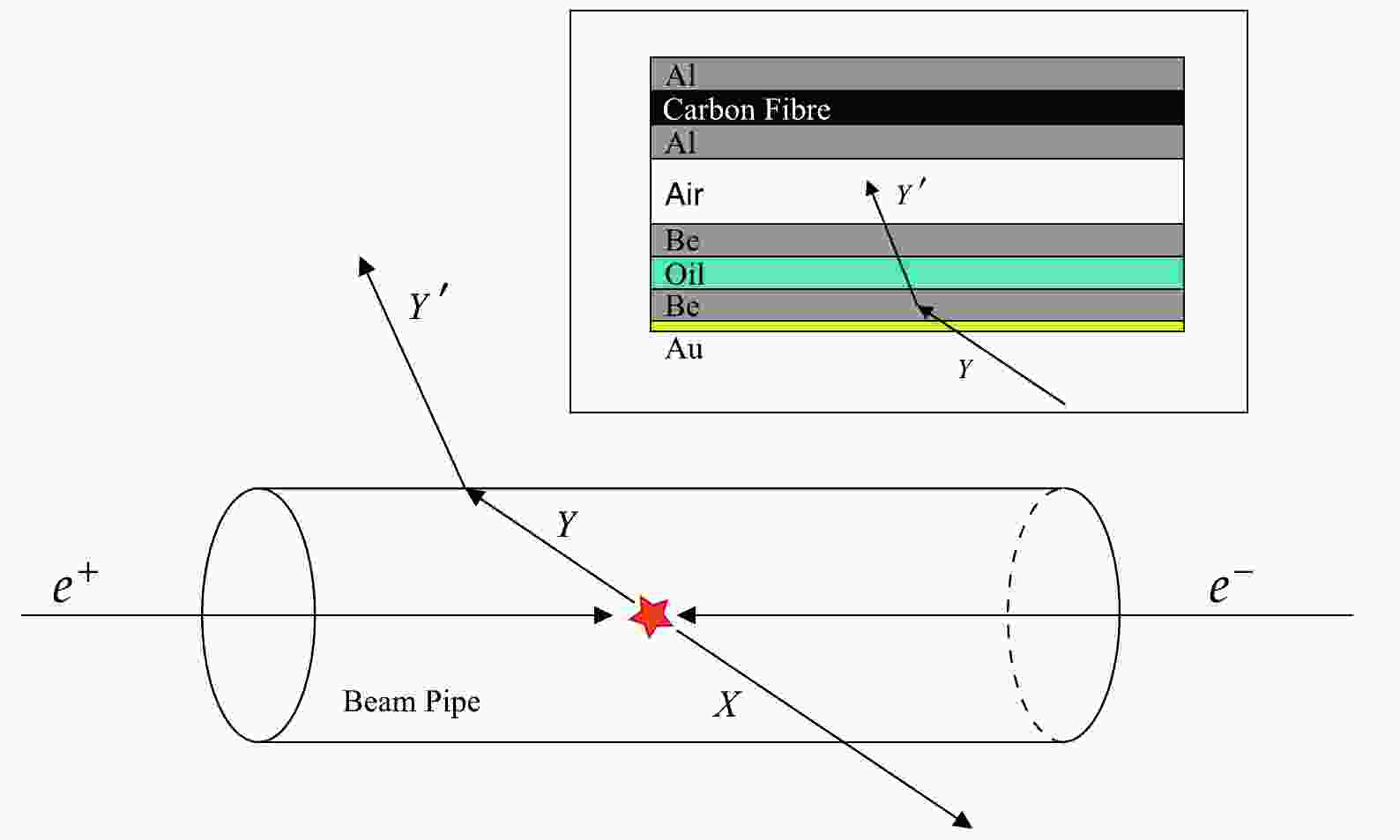
$ K_S $ and ground-state hyperons (Λ,$ \Sigma^{+,-} $ ,$ \Xi^{0,-} $ and$ \Omega^- $ ), and numerous studies on hyperon physics have been published [43–48]. To date, BESIII has collected the largest data samples worldwide within the designed energy region [40].As shown in Fig. 1, hyperon pairs or final states including hyperons are produced by the collision of
$ e^+ e^- $ inside the beam pipe. They fly in the direction of the momentum. Some of the hyperons reach the target (the beam pipe and inner wall of the MDC) before decaying and scattering elastically or inelastically with the nucleus inside the material. As an example at BESIII, Λ hyperons may interact with Be nucleus inside the beam pipe and subsequently transform to$ \Sigma^+ $ by exchanging a π or K meson with these nucleus. Simultaneously, Be nucleus transform to another nuclide. Fig. 2 shows an overview and Feynman diagrams of examples of such processes, without covering all possible meson exchanges.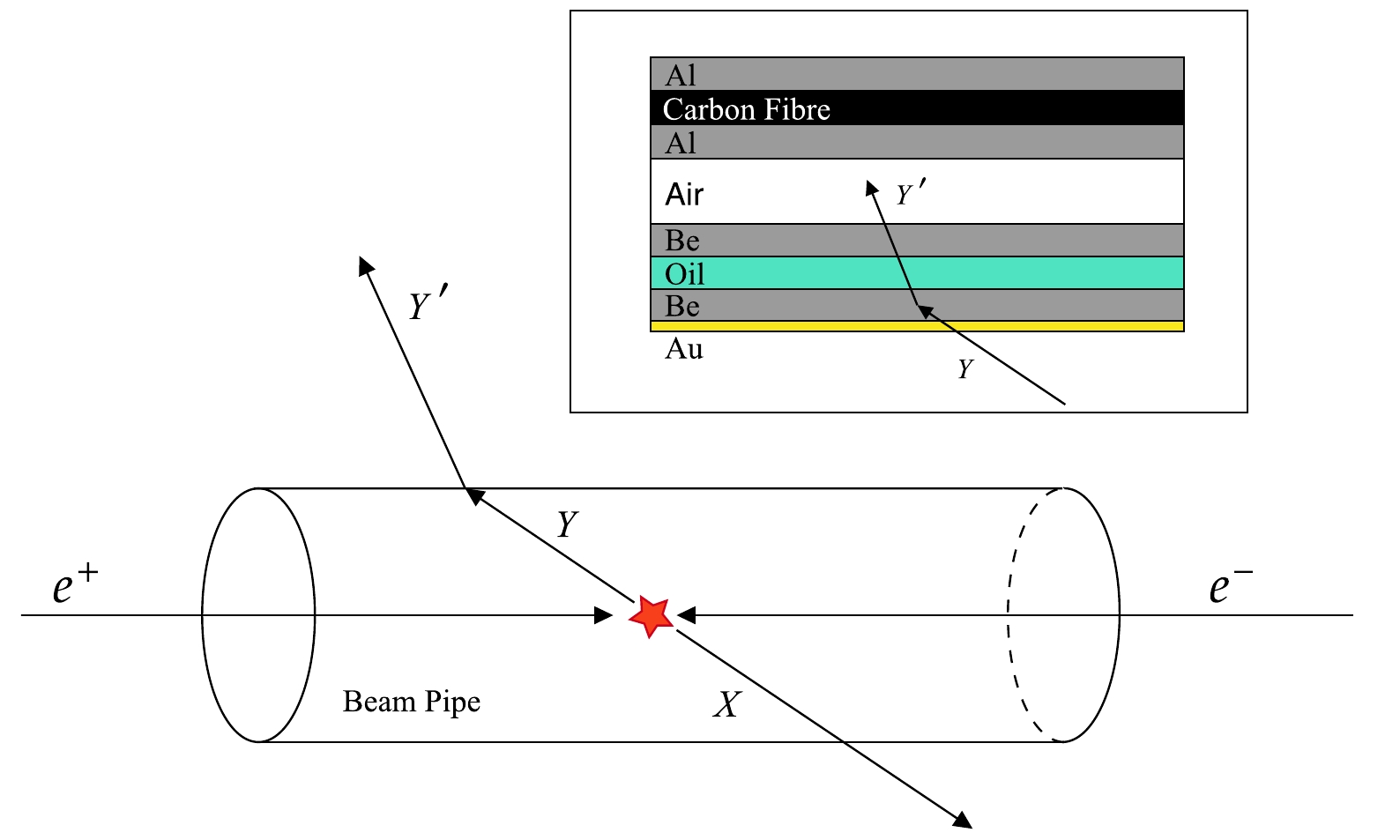
Figure 1. (color online) Schematic of the hyperon-nucleus interactions at the
$ e^+ e^- $ collider represented by BESIII. Symbol Y denotes the hyperon interacting with the nucleus and X represents the other particles produced in the$ e^+ e^- $ collision together with Y. Symbol$ Y^{\prime} $ denotes the particles produced in the hyperon-nucleus interaction. The structure of the target is shown at the top right corner. See Fig. 3 for a more detailed view of the target.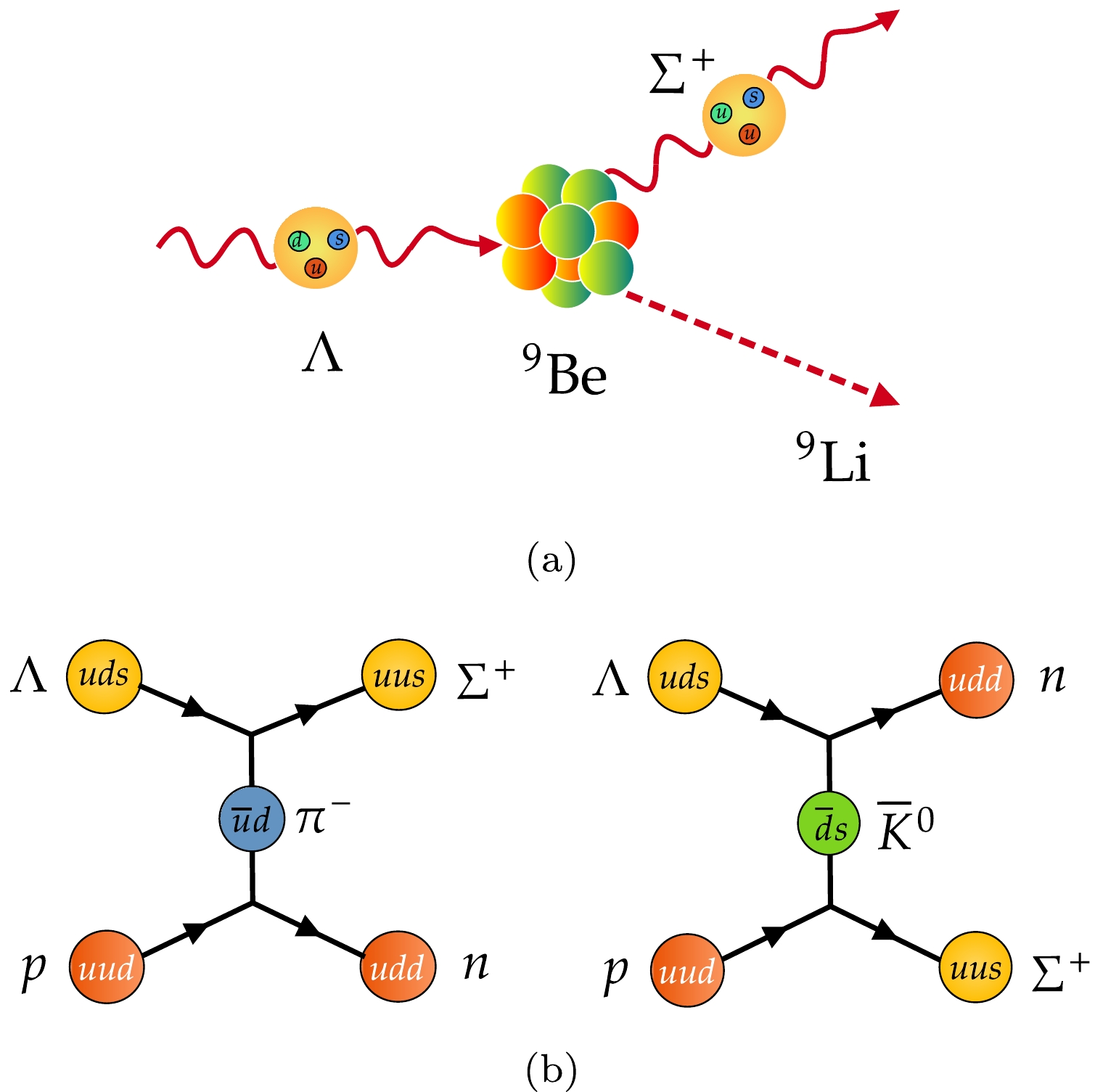
Figure 2. (color online) (a) Overview and (b) Feynman diagram of the interaction between Λ hyperons and Be nucleus.
$ \Sigma^+ $ hyperons are produced in this process.The structure of the target used in this study is presented in Fig. 3. This target comprises multiple layers made of gold (197Au), beryllium (9Be), oil (
$m_{^{12}{\rm{C}}}:m_{^{1}{\rm{H}}} = 84.923{\text{%}}:15.077{\text{%}}$ ), aluminum (27Al), and carbon fiber ($m_{^{12}{\rm{C}}}:m_{^{1}{\rm{H}}}:m_{^{16}{\rm{O}}} = 69.7{\text{%}}:0.61{\text{%}}: 29.69{\text{%}}$ ), where$ m_{\rm{A}} $ denotes the mass fraction of the corresponding nucleus. Symbol O represents the$ e^+ e^- $ collision. The horizontal axis represents the direction of the$e^-$ beam, whereas the vertical axis (r-axis) represents the distance away from the beam;$ r_{i} $ and$ t_{i} $ refer to the radius and thickness of each layer, respectively. Hyperon Y is emitted in the direction of polar angle θ and reacts with the nucleus in the target materials at scattering point H, resulting in the production of particle$ Y^{\prime} $ ; therefore,$ AB $ ,$ BC $ ,...,$ GH $ denote the track length of Y in each layer, and their sum is the total track length inside the target. The corresponding density and molar mass are expressed in Eqs. (1) and (2), where$ \rho_{T} $ and M refer to the density and molar mass, respectively. The molar mass of the oil and carbon fiber in the target is calculated by averaging the molar mass of C, H, and O nucleus weighted by the number of each type of nucleus inside the unit volume.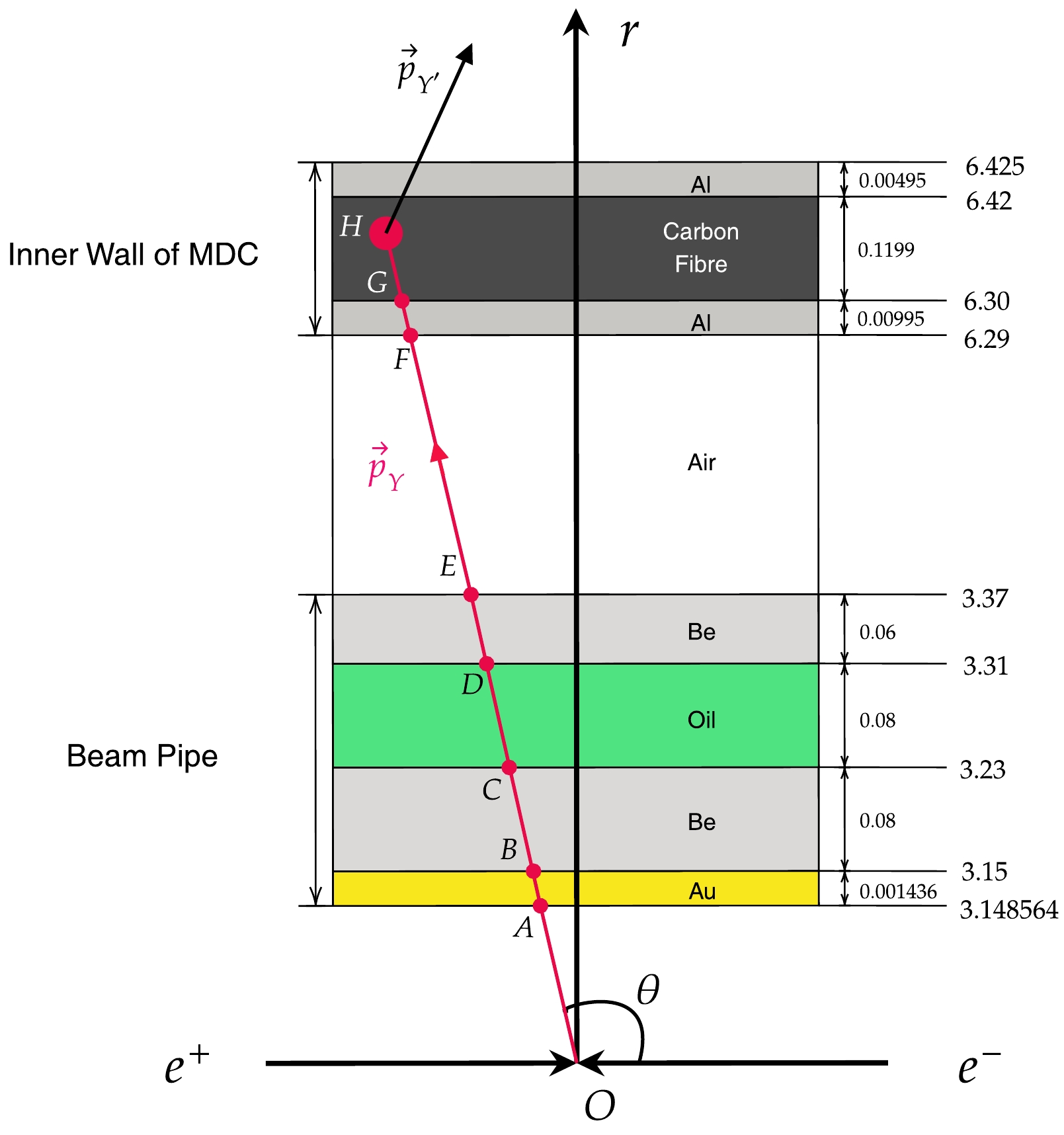
Figure 3. (color online) Target structure and path length of Y inside the target. The target comprises multiple layers made of gold, beryllium, oil, aluminum, and carbon fiber. O is the interaction point of the
$ e^+ e^- $ collision. The horizontal axis represents the$ e^+e^- $ beam line, whereas vertical axis (r-axis) represents the distance away from the beam line. The position and thickness of each layer are listed in the figure, and the unit is centimeter. θ is the angle between the incident Y and z-axis.$ r_{i}\left\{{ \begin{array}{l} r_1 = 3.148564\; {\rm{cm}} \\ r_2 = 3.15\; {\rm{cm}} \\ r_3 = 3.23\; {\rm{cm}} \\ r_4 = 3.31\; {\rm{cm}} \\ r_5 = 3.37\; {\rm{cm}} \\ r_6 = 6.29\; {\rm{cm}} \\ r_7 = 6.30\; {\rm{cm}} \\ r_8 = 6.42\; {\rm{cm}} \\ r_9 = 6.425\; {\rm{cm}} \end{array}} \right. t_{i}\left\{{ \begin{array}{l} t_1 = 0.001436\; {\rm{cm}} \\ t_2 = 0.08\; {\rm{cm}} \\ t_3 = 0.08\; {\rm{cm}} \\ t_4 = 0.06\; {\rm{cm}} \\ t_5 = 0.00995\; {\rm{cm}} \\ t_6 = 0.1199\; {\rm{cm}} \\ t_7 = 0.00495\; {\rm{cm}} \end{array}} \right. $

(1) $ \rho_T,\; M\left\{{ \begin{array}{*{20}{l}} {\rho({\rm{Au}}) = 19.32\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Au}}) = 197\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_1 \le r \le r_2 } \\ { \rho({\rm{Be}}) = 1.848\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Be}}) = 9\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_2 \le r \le r_3 } \\ { \rho({\rm{Oil}}) = 0.81\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Oil}}) = 4.51\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_3 \le r \le r_4 } \\ { \rho({\rm{Be}}) = 1.848\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Be}}) = 9\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_4 \le r \le r_5 } \\ { \rho({\rm{Al}}) = 2.7\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Al}}) = 27\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_6 \le r \le r_7 } \\ { \rho({\rm{Carb}}) = 1.57\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Carb}}) = 12.09\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_7 \le r \le r_8 } \\ { \rho({\rm{Al}}) = 2.7\; {{\rm{g}} \cdot {\rm{cm}}^{-3}}, } & { M({\rm{Al}}) = 27\; {{\rm{g}} \cdot {\rm{mol}}^{-1}}, } & { r_8 \le r \le r_9 } \end{array}} \right. $ 
(2) -
To thoroughly study the potential measurements at BESIII, MC samples of the decays of
$ J/\psi(\psi(3686)) $ to hyperon-antihyperon pairs$ Y\bar{Y} $ (Y and$ \bar{Y} $ represent the hyperon and antihyperon, respectively), including$ \Sigma^{+}\bar{\Sigma}^{-} $ ,$ \Sigma^{-}\bar{\Sigma}^{+} $ ,$ \Sigma^{0}\bar{\Sigma}^{0} $ ,$ \Xi^-\bar{\Xi}^{+} $ ,$ \Xi^{0}\bar{\Xi}^{0} $ , and$ \Omega^- \bar{\Omega}^{+} $ , were generated.The angular distribution can be described as [49, 50]
$ \frac{{\rm{d}}N(Y)}{{\rm{dcos}}\theta} \propto 1+\alpha_{\psi}{\rm{cos}}^{2}\theta, $

(3) where
$ \alpha_{\psi} $ is the parameter of the angular distribution experimentally measured [43–48], and θ denotes the angle between hyperon Y and the direction of the$ e^+ $ beam. Given that there are hyperons that decay along the track that may not reach the beam pipe or the inner wall of the MDC, the probability for hyperons from$ x_{0} $ to be alive at x is given by$ P(x) = {\rm{exp}}\left[-\frac{M}{p}\frac{x-x_0}{\tau}\right], $

(4) where M, p, and τ are the rest mass, momentum, and intrinsic lifetime of hyperon Y, respectively.
After considering the acceptance range of the BESIII detectors, we obtained the ratio of surviving hyperons over the total number of hyperons produced by charmonium decay, as shown in Fig. 4. Note that the starting points of the curves of different hyperons are not the same. This is because different hyperons have different angular distributions when they are produced, and we only registered hyperons with
$ |{\rm{cos}}\theta|<0.8 $ , according to the acceptance of the BESIII spectrometer.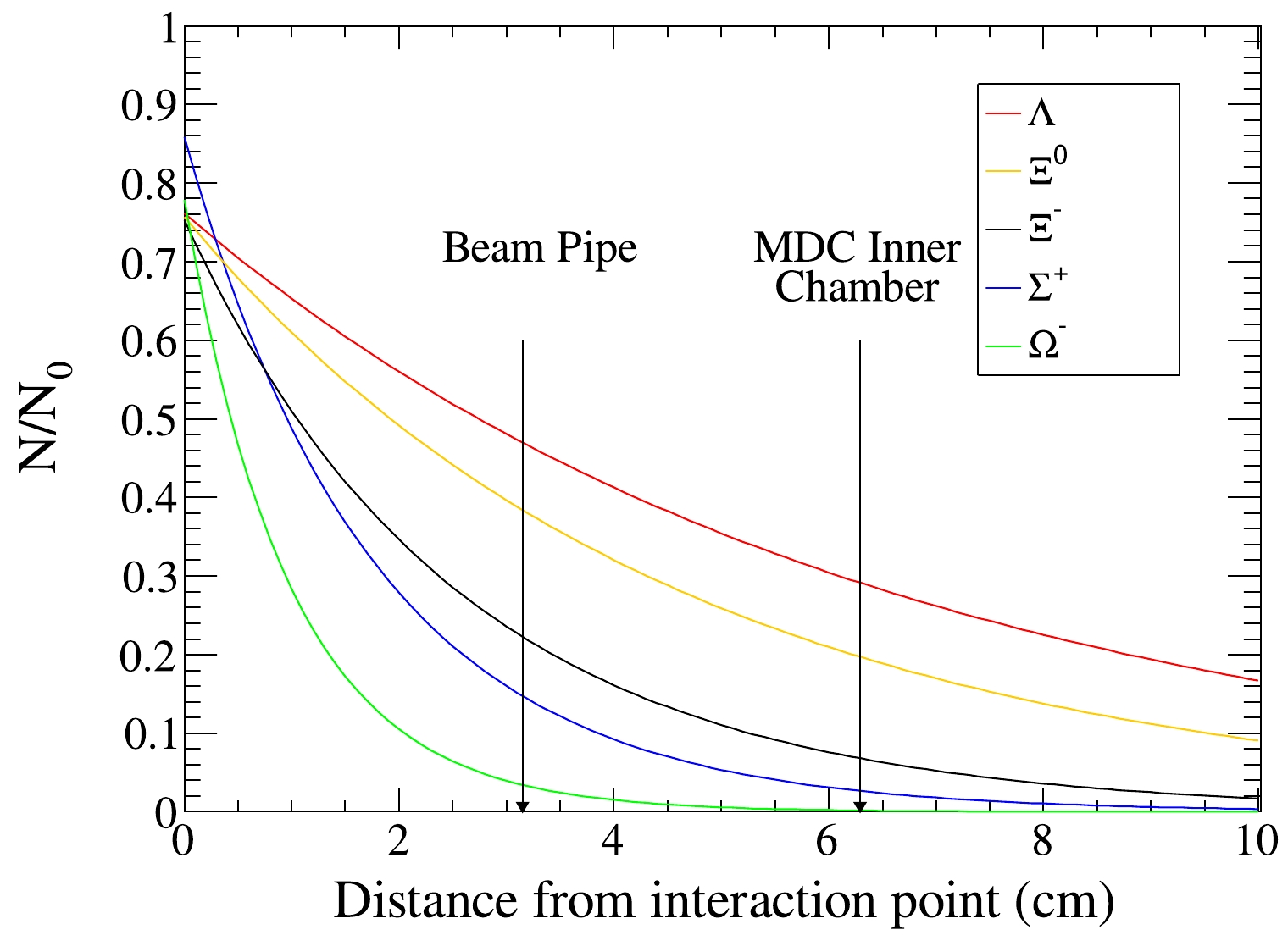
Figure 4. (color online) Ratio of surviving hyperons over the total number of hyperons produced by charmonium decay. Only hyperons with
$ |{\rm{cos}}\theta|<0.8 $ were registered, according to the acceptance range and detection efficiency of the BESIII spectrometer.The reactions between the hyperon or antihyperon and the material of the BESIII spectrometer were simulated by the official physics list
$ {\rm{QGSP\_BERT}} $ defined by Geant4 [51]; the hyperon was simulated by the Bertini intra-nuclear cascade model [52, 53]. The implementation of this model in Geant4 employs many of the standard intra-nuclear cascade features developed by Bertini and Guthrie [54]:* Classical scattering without matrix elements;
* Free hadron-nucleon cross sections and angular distributions taken from experiments;
* Step-like nuclear density distributions and potentials.
The second feature, in principle, allows the model to be extended to any particles for which there exist sufficient double-differential cross section measurements. However, it hinders the simulation of processes that are rarely measured through experiments, such as inelastic scattering of the hyperon and nucleon.
In the simulations, the decay of the incident hyperon has been considered using the measured lifetime. Thus, the hyperons may decay before entering the target or inside the target if they do not interact with the target. This is reflected in the calculations of
$ {\cal{L}}_{Y} $ , as described in Sec. II.C. -
As shown in Fig. 1, considering process
$\psi \to XY, YA \to Y^{\prime} A^{\prime}$ (Y is the hyperon that interacts with nucleons, X is the particle other than Y produced in the decay of charmonia,$ Y^{\prime} $ is the new hyperon created by the hyperon-nucleon interaction, and A and$ A^{\prime} $ are the nucleus inside the target before and after the interaction), an experimental method called "Double Tag" can be used for such measurements.Accurate information of hyperon Y that interacts with the material, including momentum and direction, can be obtained by reconstructing the other particles denoted as X at the final state; this is called "single-tag". The yield of the hyperons of interest
$ N_{\rm{ST}} $ is obtained by fitting the recoil mass distribution of X ($ RM_{X} $ ) defined as$ RM_{X} = \sqrt{|p_{e^+ e^-} - p_{X}|^{2}}, $

(5) where
$ p_{e^+ e^-} $ and$ p_{X} $ are the 4-momenta of$ e^+ e^- $ and X. The$ RM_{X} $ distribution reaches a peak around the intrinsic mass of Y.The hyperon denoted as
$ Y^{\prime} $ , produced by hyperon-nucleon scattering, is reconstructed using the final states of its decay, which is called "double-tag". The yield of$ Y^{\prime} $ , denoted as$ N_{\rm{DT}} $ , is obtained by fitting the distribution of the invariant mass of$ Y^{\prime} $ , which can be expressed as$ N_{\rm{DT}}={{\cal{L}}}_{Y} \cdot \sigma(YA \rightarrow Y^{\prime}A^{\prime}) \cdot {{\cal{B}}}(Y^{\prime}) \cdot \epsilon_{\rm{sig}}, $

(6) where
$ \sigma(YA \rightarrow Y^{\prime}A^{\prime}) $ is the cross section of the hyperon-nucleon process of interest,$ {{\cal{B}}}(Y^{\prime}) $ is the branching fraction of the decay channel used to reconstruct$ Y^{\prime} $ , and$ \epsilon_{\rm{sig}} $ is the selection efficiency of$ Y^{\prime} $ for the specific decay channel obtained from the signal MC sample. To finally determine the cross section of such processes, a specifically defined variable$ {\cal{L}}_{Y} $ , named "effective luminosity," is introduced to account for the properties of the target and the behavior of the incident hyperon beam; it is estimated using the signal MC samples described in Sec. II.B.The formula to calculate
$ {\cal{L}}_{Y} $ is$ {\cal{L}}_{Y} = N_{\rm{ST}} \cdot \frac{N_{A} \cdot \rho_{T} \cdot l}{M}, $

(7) where
$ N_{\rm{ST}} $ is the number of single-tagged events,$ N_{A} $ is the Avogadro constant,$ \rho_{T} $ is the density of the target, l is the average path length of the Y beam inside the target, and M is the molar mass of the target. In this study, the target comprises several layers made of different materials. The total value of$ {\cal{L}}_{Y} $ is the sum of the contributions of each layer; it is expressed as$ {\cal{L}}_{Y} = \sum\limits_{j}^{7} {\cal{L}}_{Y}^{j} = N_{\rm{ST}} \cdot N_{A} \cdot \sum\limits_{j}^{7} \frac{\rho_{T}^{j} \cdot l^{j}}{M^{j}} \cdot {\cal{R}}_{\sigma}^{j}, $

(8) where j is the index of the layers. Given that the contributions from each layer and cross section for different types of nucleus are not the same, a ratio of the scattering cross section (
$ {{\cal{R}}}_{\sigma} $ ) of incident Y for each type of material is necessary. According to previous studies, scattering occurs mostly with single nucleons on the nucleus surface in the case of low and intermediate energies [55–60]. If we jointly define the effective proton number ($ Z_{\rm{eff}} $ ) and effective neutron number ($ N_{\rm{eff}} $ ) as the number of nucleons inside a single nucleus that may interact with the incident hyperon,$ {\cal{R}}_{\sigma} $ becomes proportional to$ Z_{\rm{eff}} $ or$ N_{\rm{eff}} $ in the scenario described above; it is expressed as${\cal{R}}_{\sigma} \propto Z_{\rm{eff}} = A^{\frac{2}{3}} \times \dfrac{Z}{A} = \dfrac{Z}{A^{\frac{1}{3}}}$ for the interactions with protons and${\cal{R}}_{\sigma} \propto N_{\rm{eff}} = A^{\frac{2}{3}} \times \dfrac{N}{A} = \dfrac{N}{A^{\frac{1}{3}}}$ for the interactions with neutrons, where A, Z, and N are the number of nucleons, protons, and neutrons in a single nucleus. Taking$J/\psi \to \Lambda \bar{\Lambda}, \bar{\Lambda} \to \bar{p} \pi^+, ~ \Lambda A \to \Sigma^+ X$ as an example, the value of$ {\cal{R}}_{\sigma} $ for each layer is$ {{\cal{R}}}_{\sigma}^{j}\left\{{ \begin{array}{l} {{\cal{R}}}_{\sigma}^{1} = 7.06, \\ {{\cal{R}}}_{\sigma}^{2} = 1.0, \\ {{\cal{R}}}_{\sigma}^{3} = 0.789, \\ {{\cal{R}}}_{\sigma}^{4} = 1.0, \\ {{\cal{R}}}_{\sigma}^{5} = 2.253, \\ {{\cal{R}}}_{\sigma}^{6} = 1.365, \\ {{\cal{R}}}_{\sigma}^{7} = 2.253, \end{array}} \right. $

(9) after normalizing the cross sections for each layer to the largest component of target 9Be. The ratio of the oil and carbon fiber is the average of the ratios of C, H, and O weighted by the total number of the corresponding nucleus inside the unit volume; it is expressed as
$ {\cal{R}}_{\sigma}^{\rm{mixture}} = \frac{{\cal{R}}_{\sigma}^{C}N^{C} + {\cal{R}}_{\sigma}^{H}N^{H} + {\cal{R}}_{\sigma}^{O}N^{O}}{N^{C} + N^{H} + N^{O}}, $

(10) where
$N^{\rm C}$ ,$N^{\rm H}$ , and$N^{\rm O}$ are the numbers of C, H, and O nucleus inside the unit volume, respectively.Average path length
$ l^{j} $ inside each layer is calculated using the signal MC sample of$ YA \rightarrow Y^{\prime}A^{\prime} $ ; in this calculation, the decay of the Y beam is taken into consideration as described in detail in Sec. II.B. Thus,$ l^{j} $ is calculated event by event as$ l^{j} = \frac{\sum_{i}^{N_{\rm{ST}}^{\rm{MC}}} l^{ij}}{N_{\rm{ST}}^{\rm{MC}}}, $

(11) where
$ N_{\rm{ST}}^{\rm{MC}} $ is the total number of single-tagged events in the MC sample and$ l^{ij} $ refers to the path length of Y for the$ i_{\rm{th}} $ event inside the$ j_{\rm{th}} $ layer. As shown in Fig. 3, H represents the scattering points of Y and the nucleus such that$ AB $ ,$ BC $ ,...,$ GH $ jointly represent the track length of Y in each layer obtained from the true information of the signal MC sample; it will be 0 if hyperon Y does not enter the layer. The sum of all the segments is the total track length inside the target. For$ J/\psi \to \Lambda \bar{\Lambda}, \bar{\Lambda} \to \bar{p} \pi^+, \Lambda {^{9}{\rm{Be}}} \to \Sigma^+ {^{9}{\rm{Li}}} $ ,$ l^{j} $ becomes$ l^{j}\left\{{ \begin{array}{l} l^{1} = 0.10 \times 10^{-3} \; {\rm{cm}}, \\ l^{2} = 5.76 \times 10^{-3} \; {\rm{cm}}, \\ l^{3} = 5.68 \times 10^{-3} \; {\rm{cm}}, \\ l^{4} = 4.21 \times 10^{-3} \; {\rm{cm}}, \\ l^{5} = 0.43 \times 10^{-3} \; {\rm{cm}}, \\ l^{6} = 5.13 \times 10^{-3} \; {\rm{cm}}, \\ l^{7} = 0.21 \times 10^{-3} \; {\rm{cm}}. \\ \end{array}} \right. $

(12) The calculation of the average path length takes into account the decay of incident hyperons and the potential interactions with the target material. Given that the rate of hyperon-nucleus interactions is approximately 1% of the hyperon decay inside the target,
$ l_{j} $ is slightly influenced by the hyperon-nucleus interactions; however, in terms of the final statistical uncertainty, this influence is negligible.Combining Eqs. (8) and (11),
$ {\cal{L}}_{Y} $ becomes$ {\cal{L}}_{Y} = N_{\rm{ST}} \cdot \frac{N_{A}}{N_{\rm{ST}}^{\rm{MC}}} \cdot \sum\limits_{j}^{7} \sum\limits_{i}^{N_{\rm{ST}}^{\rm{MC}}} \frac{\rho_{T}^{j} \cdot l^{ij}}{M^{j}} \cdot {\cal{R}}_{\sigma}^{j}. $

(13) $ {\cal{L}}_{Y} $ contains information about the number of incident hyperons and the properties of the target. The beam intensity, or single-tagged events$ N_{\rm{ST}} $ , could not be accurately obtained in this study, but can be obtained by fitting data from BESIII. In this paper, we only report the values of$ {\cal{L}}_{Y}/N_{\rm{ST}} $ that can be calculated using MC samples and are independent of the data of the BESIII experiment.Using the signal MC sample, we calculated the value of
$ {\cal{L}}^{j}_{\Lambda}/N_{\rm{ST}} $ for the$ \Lambda {^{9}{\rm{Be}}} \to \Sigma^+ {^{9}{\rm{Li}}} $ reaction of each layer using Eq. (14). For the whole target, we obtained${\cal{L}}_{\Lambda}/N_{\rm{ST}} = 23.59 \times 10^{21} {{\rm{cm}}^{-2}}$ . The value of$ {\cal{L}}_{Y}/N_{\rm{ST}} $ for other hyperons can be found in Table 1.Hyperon $ c\tau $ /cm

decay mode ${\cal B}_{\rm decay}$ [62]

($ \times 10^{-3} $ )

$ p_{\rm{max}} $ 

(MeV/c)$ n^Y_{\rm{BP}} $ (

$ \times 10^5 $ for BESIII

or$ \times 10^8 $ for STCF)

${\cal{B} }_{\rm tag}$ (%)

$ {\cal{L}}_{Y}/N_{\rm{ST}} (10^{21}\cdot {{\rm{cm}}^{-2}}) $ 

Estimated signal
yield ($ \times 10^3 $ for STCF)

Λ 7.89 $ J/\psi\to \Lambda\bar{\Lambda} $ 

$ 1.89\pm0.09 $ 

1074 26 64 23.59 5290 $ \Sigma^+ $ 

2.40 $ J/\psi\to \Sigma^+ \bar{\Sigma}^- $ 

$ 1.07\pm0.04 $ 

992 4 52 4.83 537 $ \Xi^0 $ 

8.71 $ J/\psi\to \Xi^0 \bar{\Xi}^0 $ 

$ 1.17\pm0.04 $ 

818 7 64 15.81 2368 $ \Xi^- $ 

4.91 $ J/\psi\to \Xi^- \bar{\Xi}^+ $ 

$ 0.97\pm0.08 $ 

807 3 64 7.44 924 $ \Omega^- $ 

2.46 $ \psi(3686)\to \Omega^-\bar{\Omega}^+ $ 

$ 0.056\pm0.003 $ 

774 0.05 43 2.61 3 Table 1. Expected signal yields of hyperon-nucleus scattering at BESIII considering the acceptance range and selection efficiency of BESIII.
$ p_{\rm{max}} $ is the maximum momentum of the antihyperon,${\cal{B}}_{\rm decay}$ is the branching fraction of the given decay channel of charmonium,$ n^Y_{\rm{BP}} $ is the number of tagged antihyperons reaching the beam pipe,${\cal{B}}_{\rm tag}$ is the branching fraction of the decay channel used in the single-tag side, and$ {\cal{L}}_{Y} $ is the effective luminosity of the hyperon beam. The last column lists the expected signal yields for different hyperons before reconstruction. Predictions for the Super Tau-Charm Factory (STCF) are also listed in this table.$ {{\cal{L}}}_{\Lambda}^{j}/N_{\rm{ST}}\left\{{ \begin{array}{l} {\cal{L}}_{\Lambda}^{1}/N_{\rm{ST}} = 0.43 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ {\cal{L}}_{\Lambda}^{2}/N_{\rm{ST}} = 7.12 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ {\cal{L}}_{\Lambda}^{3}/N_{\rm{ST}} = 4.85 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ {\cal{L}}_{\Lambda}^{4}/N_{\rm{ST}} = 5.21 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ {\cal{L}}_{\Lambda}^{5}/N_{\rm{ST}} = 0.58 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ {\cal{L}}_{\Lambda}^{6}/N_{\rm{ST}} = 5.12 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ {\cal{L}}_{\Lambda}^{7}/N_{\rm{ST}} = 0.28 \times 10^{21} \; {{\rm{cm}}^{-2}}, \\ \end{array}} \right. $

(14) Using Eq. (6),
$ \sigma(YA \rightarrow Y^{\prime}A^{\prime}) $ is expressed as$ \sigma(YA \rightarrow Y^{\prime}A^{\prime}) = \frac{N_{\rm{DT}}}{\epsilon_{\rm{sig}} \cdot {{\cal{L}}_{Y}}} \cdot \frac{1}{{{\cal{B}}}(Y^{\prime})}. $

(15) -
To date, 10 billion
$ J/\psi $ and 2.7 billion$ \psi(3686) $ events have been collected at BESIII, in which tens of millions of ground-state hyperons were produced. In addition to precisely measuring rare decays of hyperons [61], interactions between hyperons and nucleons can also be studied.Using the MC samples described in Sec. II.B and the method described in Sec. II.C, we estimated potential measurements of hyperon-nucleus interactions at BESIII; the results are listed in Table 1 assuming a cross section of such interactions of
$ 20\; {\rm{mb}} $ . Only hyperon pairs from charmonium decay were calculated. Nevertheless, the proposed method can also be applied to other hyperon-involved multi-body final states. As many as several thousand scattering events will occur at BESIII before reconstruction. Assuming a reconstruction efficiency of different hyperon-antihyperon pairs of$ 5\% \sim 30\% $ , there will be a considerable quantity of signals for data analysis. -
The raw measurements at BESIII are hyperon-nucleus instead of hyperon-nucleon cross sections, which are more important for theoretical studies. The corresponding hyperon-nucleon cross sections can be extracted by calculating the effective nucleon number. In Sec. II.C, we describe a scenario to calculate the effective nucleon number by assuming that the cross section is proportional to the number of nucleons in the nucleus surface at low and intermediate energies [55–60]. Using the ratio of the effective nucleon number of multiple materials, denoted as
$ {\cal{R}}_{\sigma} $ in Sec. II.C, and that provided by$ {\cal{L}}_{Y}/N_{\rm{ST}} $ for each layer, the measured cross section can be normalized to any type of nucleus, thereby achieving a natural integration with a single nucleon.Next, we describe another scenario to calculate the effective nucleon number based on an assumption with a quasifree scattering process. We consider the Eikonal Approximation [56, 63, 64], through which the connection between hyperon-nucleus and hyperon-nucleon cross sections can be established via the effective nucleon number calculated by
$ \begin{aligned}[b] N_{{\rm{eff}}}\left(Z_{{\rm{eff}}}\right) =\;& \frac{N(Z)}{A}\int \rho({\bf{r}}) \exp \Bigg\{-\bar{\sigma}_{i} \int_{-\infty}^z \rho\left(x, y, z^{\prime}\right) {\rm d} z^{\prime}\\&- \bar{\sigma}_{f} \int_z^{\infty} \rho\left(x, y, z^{\prime}\right) d z^{\prime}\Bigg\} {\rm d}^3 {\bf{r}}, \end{aligned} $

(16) where N (
$ N_{\rm{eff}} $ ) and Z ($ Z_{\rm{eff}} $ ) are the (effective) neutron and proton numbers of the nucleus, respectively; A is the atom mass; ρ is the nuclear density distribution with$A = \int \rho({\bf{r}}) {\rm d}{\bf{r}}$ ; and$ \bar{\sigma}_i $ and$ \bar{\sigma}_f $ are the isospin-averaged cross sections of the elastic scattering between the two particles of the incoming and outgoing states, respectively. When the momentum of the incident hyperon is larger, the hyperon-nucleon scattering cross section has an approximate relationship with the hyperon-nucleus cross section of$ \sigma_{Y-A} = \sigma_{Y-n} \times N_{{\rm{eff}}}(Z_{{\rm{eff}}}) $ .As an example, let us consider that the calculation of the cross section of
$ \Lambda + p\to \Sigma^+ + n $ from the recently measured cross section of$ \Lambda + {^{9}{\rm{Be}}} \to \Sigma^+ + X $ by BESIII as$ \sigma = (37.3 \pm 4.7 \pm 3.5)\; {\rm{mb}} $ [19]. The cross section for corresponding hyperon-nucleon scattering$\Lambda + p \to \Sigma^+ + n$ is calculated using the scenario described in Sec. II.C as$ \sigma(\Lambda + p \to \Sigma^+ + n) = (19.3 \pm 2.4 \pm 1.8)\; {\rm{mb}} $ .The nuclear density of
$ {^9{\rm{Be}}} $ is expressed by the two-parameter parameterization of the Fermi distribution as follows [65]:$ \rho(r) = \rho_0\left[1+\alpha\left(\frac{r}{a}\right)^2\right] \operatorname{Exp}\left[-\left(\frac{r}{a}\right)^2\right], $

(17) where
$ \alpha = 0.63 $ fm and$ a = 1.77 $ fm;$ \rho_{0} $ is the normalization factor.To calculate the effective proton number in the
$ {^{9}{\rm{Be}}} $ nucleus, there are two possible scenarios: using the experimentally measured or the theoretically predicted elastic cross sections of$ \Lambda p $ and$ \Sigma^+ n $ .Based on the measurements reported in Refs. [12, 16], we can approximately obtain the mean elastic cross sections,
$ \bar{\sigma}(\Lambda p) \approx (17.8\pm2.4) $ $ {\rm{mb}} $ and$ \bar{\sigma}(\Sigma^+ n) \approx 51.3_{-25.5}^{+51.7}\; {\rm{mb}} $ , with a momentum of the$ \Lambda/\Sigma $ hyperon of approximately 1 GeV/c2. Hence, we can evaluate the effective proton number to be$ Z_{{\rm{eff}}} \in [1.1,2.1] $ for the$ \Lambda + {^{9}{\rm{Be}}} \to \Sigma^+ + {^{9}{\rm{Li}}} $ reaction, where a large uncertainty arises mostly from the measurements of the Σ-nucleon elastic cross section. Setting a central value of 1.6 as a reference, the cross section of$ \Lambda p \to \Sigma^+ n $ can be obtained,$ \sigma(\Lambda p \to \Sigma^+ n) = (23.3 \pm 3.7 ^{+11.0}_{-5.5})\; {\rm{mb}} $ , where the first term of the uncertainty is from the measured hyperon-nucleus cross section and the second term from the uncertainty of$ Z_{{\rm{eff}}} $ .These uncertainties are significantly reduced by considering the theoretically calculated values, in particular
$ \bar{\sigma}(\Lambda p) = (17.0 \pm 2.5)\; {\rm{mb}} $ and$ \bar{\sigma}(\Sigma^+ n) = (28.5\pm 2.5)\; {\rm{mb}} $ , from χEFT methods [28, 30]. Using the method described above, one can estimate the effective proton number to be$ Z_{{\rm{eff}}} \in [1.9, ~2.2] $ . Setting a central value of 2.1 as a reference, the cross section of$ \Lambda p \to \Sigma^+ n $ can be calculated to be$ \sigma(\Lambda p \to \Sigma^+ n) = (17.8 \pm 2.8 ^{+1.8}_{-0.8})\; {\rm{mb}} $ , where the first term of the uncertainty is from the measured hyperon-nucleus cross section and the second term from the uncertainty of$ Z_{{\rm{eff}}} $ .Regardless of whether the input elastic cross sections from experimental measurements or theoretical calculations are used, the cross section of the
$ \Lambda + p \to \Sigma^+ + n $ reaction calculated under the scenario described above is consistent with the cross section calculated under the scenario described in Section II.C. In the future, the uncertainty of the effective nucleon number will be reduced by the proposed measurements of elastic cross sections by BESIII. -
Differential cross sections of hyperon-nucleus interactions can also be extracted using the proposed method. For process
$ \psi \to XY,\; YA \to Y^{\prime} A^{\prime} $ , the momentum of Y can be obtained by studying the recoiling system of tagged hyperon X for which the angle between$ Y^{\prime} $ and Y is available. With the momentum of$ Y^{\prime} $ , the differential cross sections can be measured within the whole phase space if the statistics are sufficiently large.Furthermore, the polarization of hyperon pairs from the decay of charmonia produced at BESIII has been thoroughly studied both experimentally [43–48] and theoretically [49] in recent years. It has been found that the polarization is a function of the polar angle of the hyperons, which inspires us to hypothesize that the relationship between the cross sections and polarization of the incident hyperons can also be studied in detail by constraining the phase space. The polarization-dependent mechanism for such processes will be of great significance to determine the role of spin in hyperon-nucleon interactions and the potential of strong interaction. Meanwhile, large polarization effects have been observed in the hadrons produced during the study of elastic hadronic scattering. Similarly, the polarization of the produced hyperons in hyperon-nucleon interactions will also be a possible topic for research at BESIII by measuring the angular distribution of the particles from the hyperon decay. This is expected to provide clues for the spin-involved interaction between hyperons and nucleons.
Similar to hyperons, the interactions between antihyperons and nucleus/nucleons, including scattering and annihilation, can also be studied by tagging the hyperons produced in pair. This is expected to provide crucial information for theoretical research given that the measurements of such processes presently available are not sufficient at all.
In the near future, a new generation of
$ e^+ e^- $ collider with a super high intensity beam, called the STCF, will provide a peak luminosity of$1\times10^{35}\; {\rm cm^{-2}\,s^{-1}}$ [41], which is 100 times that of the present BEPCII. Notably, the uncertainty of the center-of-mass energy will improve from$ 1.2\; {\rm{MeV}} $ to$ 20 \sim 80\; {\rm{keV}} $ if monochromatic collisions can be realized at narrow resonances such as$ J/\psi $ [66]. Thus, the cross section of$ J/\psi $ production will further increase by a factor of 10. Given that there will be$ 10^{12} \sim 10^{13} $ $ J/\psi $ produced at the STCF per year,$ 10^6 \sim 10^7 $ scattering events will be available, according to the calculations reported in Table 1. This will significantly advance the research on hyperon-nucleus/nucleon interactions and assist in solving the puzzle of the internal structure of neutron stars. -
This paper describes a method to study hyperon-nucleus interactions by measuring the scattering between hyperons from charmonium decay at BESIII and the nuclei inside the dense matter in the beam pipe or other supporting structures and, subsequently, extracting the cross sections of the corresponding hyperon-nucleon interactions from further phenomenological calculations. This method, which was verified by recent measurements from BESIII [18, 19], significantly broadens the frontier of physics at
$ e^+ e^- $ colliders. Thanks to the double-tag method, differential cross sections of such interactions can also be measured, which will provide exciting hints for research on the potential of strong interaction and the origin of color confinement. Similarly, kaon-nucleus/nucleon or antihyperon-nucleus/nucleon interactions can also be studied using the same method and the abundant kaon and antihyperon beams resulting from the decay of certain quantities of charmonia. In particular, at the STCF, millions of events of hyperon-nucleus scattering and many more events of kaon-nucleus scattering will occur. This will definitely benefit the realization of precise probes of hyperon-nucleon interactions and establish essential constraints for the internal structure of neutron stars and a unified model for baryon-baryon interactions. -
The authors thank Prof. Ziyan Deng from IHEP, Prof. Li-Sheng Geng and Dr. Zhiwei Liu from Beihang University, Prof. Catalina Curceanu from INFN, and Prof. Emiko Hiyama from RIKEN for the fruitful discussions.
Prospects to study hyperon-nucleon interactions at BESIII
- Received Date: 2024-03-20
- Available Online: 2024-07-15
Abstract: The prospects to study hyperon-nucleus/nucleon interactions at BESIII and similar





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: