-
Heavy Majorana right-handed neutrinos are very attractive because they naturally induce tiny neutrino masses through the seesaw mechanism [1–4]; their decays in the early universe generate the Universe's baryon asymmetry through leptogenesis [5]. It is well known that all gauge anomalies involving the
$ U(1)_{B-L} $ symmetry [4] are canceled out if we introduce three right-handed neutrinos in the standard model (SM). Therefore, it is very interesting to consider the gauge$ U(1)_{B-L} $ extension of the SM as the next step beyond the SM.It has been pointed out that the
$ B-L $ gauge boson can be identified with dark matter (DM) if$ B-L $ gauge coupling constant$ g_{B-L} $ is sufficiently small [6–8]. We call it the "féeton" or "féeton DM" [8].Two of the present authors (W.L. and T.T.Y.) have recently shown [9] that 511-keV gamma-ray excess from the center of our galaxy [10–12] can be explained by the decay of the féeton to an electron and positron pair. It successfully explains the upper bound of the positron injection energy that is inferred from the non-detection of the 1−3 MeV diffused gamma ray [13]. However, several caveats exist in such a scenario. First, to avoid overproduction of electron-positron pairs, the féeton can only constitute a small fraction of DM. Second, a small fraction of DM means that it is much more difficult to search for the signal of neutrinos decayed from féeton DM. Third, it suffers from a mild tension that the resultant positron-annihilation flux is insufficiently sharp toward the Galactic center (GC), which is a common challenge for all proposals with DM decays [14]
1 .In this study, we consider a new scenario for forming the positronium that allows the féeton to be the dominant DM and significantly enhances the detectability. This new scenario predicts the neutrino flux of its energy peak at 511 keV with no higher-energy continuum. We discuss how to test this neutrino with low-energy neutrino experiments like Borexino and Juno.
-
In this section, we discuss a new parameter region of the original féeton DM model [8]. The low-energy physics is described by only two free parameters, mass
$ m_ \mathfrak{f} $ and gauge coupling constant$ g_{B-L} $ of the féeton. These two parameters are related by$ m_ \mathfrak{f} = 2g_{B-L} V_{B-L} $ , where$ V_{B-L} $ is the Vacuum Expectation Value (VEV)) of Higgs boson Φ with a$ B-L $ charge of$ +2 $ . Here, the right-handed neutrinos,$ N_i\; \; (i=1-3) $ , acquire Majorana masses of$ h_i V_{B-L} $ with constant parameters$ h_i $ defined by Yukawa interactions$ \frac{1}{2}h_i \Phi N_iN_i $ . We have assumed all leptons, including the right-handed neutrinos, to have a$ B-L $ charge of$ -1 $ 2 .Decay rate
$ \Gamma_{\mathfrak{f} } $ of the féeton is given by$ \begin{align} \Gamma_{\mathfrak{f} } = \frac{g_{B-L}^2 m_{\mathfrak{f}}}{24 \pi} \left[ 3 + 2 \sqrt{1-\frac{4 m_e^2}{m_{\mathfrak{f}}^2}} \left(1+\frac{2 m_e^2}{m_{\mathfrak{f}}^2}\right)\right], \end{align} $

(1) where we assume
$ m_{\mathfrak{f}}>2m_e $ to include both the decays to the neutrino-anti-neutrino and electron-positron pair;$ m_e $ is the electron mass, and the neutrino masses have been ignored. If the féeton is the dominant DM with$ m_\mathfrak{f} > 2m_e + 13.6\, $ eV, the positrons produced from féeton decay can form positroniums via the charge exchange of positrons with hydrogen atoms. Such positroniums eventually annihilate into gamma rays. However, the electron-positron pairs would be over-produced, and the resultant Galactic 511-keV gamma ray would largely exceed the observed value [9].Now, we are at the main point of this paper. If féeton mass
$ m_{\mathfrak{f}} $ is very close to the threshold of the decay to the electron-positron pair, that is,$ m_{\mathfrak{f}}\simeq 2 m_e $ , such a decay is strongly suppressed, and the branching ratio to the$ e+{\bar e} $ final state becomes very small such that the predicted excess of the 511-keV gamma ray can be consistent with the observation, while the féeton is the dominant DM. However, this does not appear successful. The intermediate state of positronium is often assumed to be formed by the produced positrons through charge exchanges with neutral hydrogen atoms [13]. This can occur only if the kinetic energy of the positron is larger than the corresponding threshold of 6.8 eV—the difference in the binding energy between neutral hydrogen and a positronium. This sets the lower bound of the féeton mass and hence the$ e+{\bar e} $ branching ratio.However, if the produced positrons have a kinetic energy smaller than 6.8 eV, instead of with neutral hydrogen atoms, they can predominantly form positronium with free electrons in warm or hot ionized gas; see, e.g., Fig. 27 in [16]. This possibility has been largely ignored in the literature. Thus, we consider the following scenario. The féeton constitutes the total DM and has a mass very close to the threshold of the decay to an electron-positron pair, more explicitly,
$ 2m_e<m_{\mathfrak{f}}<2m_e+13.6 $ eV. It decays to electrons and positrons with a small branching ratio compared with the decay to neutrinos and anti-neutrinos. The produced positrons mainly form positroniums with free electrons in ionized environments, which subsequently annihilate to produce 511-keV gamma rays.We assume that sufficient free electrons exist such that the positron produced from the féeton decay annihilates immediately and the gamma-ray emission rate traces the féeton decay rate. The angular differential gamma-ray flux is given in [9]. In the first order of
$ \Delta m/m_e $ , it is given by$ \begin{aligned}[b] \frac{{\rm d}\Phi_{511}}{{\rm d}\Omega} =\;&4\times10^3\left(\frac{g_{B-L}}{10^{-20}}\right)^2\left(\frac{\Delta m}{m_e}\right)^{1/2} \\ & \times \tilde{D}_{N}(\cos\theta)\,[{\rm cm}^{-2}{\rm s}^{-1}{\rm sr}^{-1}]\,, \end{aligned} $

(2) where
$ \Delta m\equiv m_{\mathfrak{f}}-2m_e $ , and$\tilde{D}_{N}(\cos\theta)$ is a function that represents the morphology of the flux and is normalized such that$\int \tilde{D}_{N}\,{\rm d}\Omega=4\pi$ . Angle between the direction of the flux and GC θ is defined by$ \cos\theta \equiv \cos b\cos\ell $ with galactic coordinates$ (b, \ell) $ . Morphology function$ \tilde{D}_{\rm N}(\cos\theta) $ depends on the Galactic DM distribution, for which we have adopted a Navarro-Frenk-White (NFW) profile [17].Ref. [18] measured a 511-keV gamma-ray intensity of
$ 0.96\pm0.07 $ cm$ ^{-2} $ s$ ^{-1} $ from the bulge region with a Full-Width-at-Half-Magnitude (FWHM) of$ 20.55 $ degrees. To proceed, we integrate (2) within$ \theta<10.28 $ degrees from the GC and set it as half of the measured bulge flux to be the observed bulge 511-keV gamma-ray intensity. This gives us the féeton DM parameter space that can explain the observed 511-keV gamma ray, which is shown as the red line in Fig. 1. We also show the parameter space excluded by the lifetime constraint (purple) and that with a super-Planckian VEV (gray). As expected, the féeton mass should be close to twice the electron mass. The closer$ m_ \mathfrak{f} $ is to$ 2m_e $ , the larger the gauge coupling constant should be to account for the 511-keV gamma ray intensity. For the maximally allowed gauge coupling constant, i.e.,$ g_{B-L}\simeq6\times10^{-20} $ , we require$ (\Delta m/m_e)^{1/2}\simeq10^{-8} $ . Mass difference$ \Delta m $ is identified to be the total kinetic energy of the electron-positron pair produced by the féeton decay; thus, the positrons are non-relativistic3 .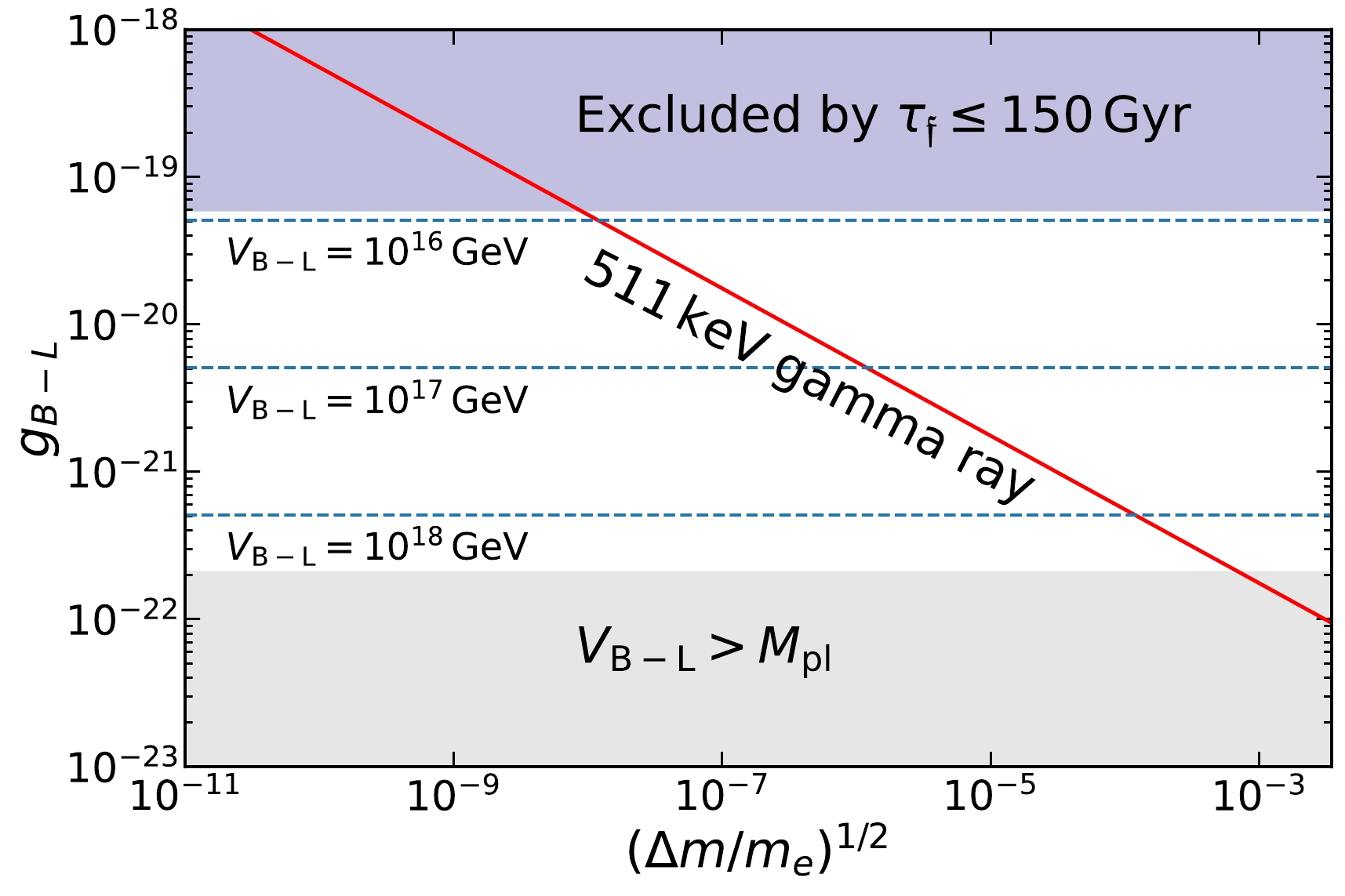
Figure 1. (color online) Red line shows the corresponding
$ g_{B-L} $ to explain the observed 511-keV gamma ray excess. The blue-shaded region is excluded by assuming that the lifetime of féeton should be larger than ten times the universe age,$ \tau_{\mathfrak{f}} > 150\, $ Gyr. The gray-shaded region represents$V_{B- L} > $ $ M_{\rm pl} = 2.4 \times 10^{18}$ GeV.The above analysis demonstrates that the féeton can constitute the total DM, while being able to explain the intensity of the 511-keV gamma ray considering that the non-relativistic positrons produced from féeton decays form positronium with free electrons in ionized environments. Because the féeton is not merely a tiny fraction of DM, it significantly enhances the neutrino and anti-neutrino fluxes produced from féeton decays compared with the scenario in the previous study [9]. In addition, the neutrino and anti-neutrino energies peak at 511 keV, which is above the threshold for directional determination by current detectors that use Cherenkov lights. Thus, the new scenario proposed in this paper has much better detectability than that in [8].
-
The main decay mode of the féeton is that to a neutrino-anti-neutrino pair. The energy of the resultant neutrinos peaks at
$ \simeq 511 $ keV because the féeton mass is immediately above the threshold of the decay, that is,$ m_{\mathfrak f} \simeq 2 m_e $ , as explained in the previous section. The neutrino flux from the GC and the extra-galactic féeton DM decay have been calculated in [8]. In this section, we discuss the detectability of the corresponding neutrino flux by setting the féeton mass to$ \simeq1 $ MeV and taking the optimal coupling constant allowed by the DM lifetime constraint, i.e.,$ g_{B-L}=5.85\times10^{-20} $ ; see Ref. [8]. This value of$ g_{B-L} $ is also the most motivated value, as we shall explain.We first discuss the detectability for solar neutrino experiments because the predicted energy falls into their target energy range. Adopting Eq. (5) in [8] with
$ g_{B-L}=5.85\times10^{-20} $ , we observe that the neutrino flux of the féeton decay is$ \simeq3.4\times10^6 $ cm$ ^{-2} $ s$ ^{-1} $ , which is three-orders-of-magnitude smaller than the$ ^7 $ Be neutrino flux [19] although the peak energy is different. We then evaluate the electron recoil spectrum per unit mass of the liquid scintillator as the neutrinos from the féeton decay scatter electrons in neutrino detectors. The energy differential event count is$ \begin{align} \frac{{\rm d} N}{{\rm d}E_e} = \int {\rm d} E_{\nu} \frac{{\rm d} \Phi_{\nu}} {{\rm d}E_{\nu}} \cdot \frac{{\rm d} \sigma}{{\rm d}E_{e}}(E_\nu) \cdot N_T \cdot t. \end{align} $

(3) Here,
$ E_e $ is the kinetic energy of the recoil electron,$ \dfrac{{\rm d} \Phi_{\nu}}{{\rm d}E_{\nu}} $ is the neutrino flux from the féeton decay [8, 9],$ N_T = (3.307 \pm 0.015) \times 10^{29} $ is the number of electrons per ton of the liquid scintillator [20], and t is the exposure time, which was set as one year for illustration. Moreover, the neutrino-electron scattering differential cross section is given by [21]$ \begin{aligned}[b] \frac{\mathrm{d} \sigma}{\mathrm{d} E_e} =\;& \frac{G_F^2 m_e}{2 \pi} \left[ \left(g_{\mathrm{V}}+g_{\mathrm{A}}\right)^2+\left(g_{\mathrm{V}}-g_{\mathrm{A}}\right)^2\left(1-\frac{E_e}{E_\nu}\right)^2 \right.\\& \left.-\left(g_{\mathrm{V}}^2-g_{\mathrm{A}}^2\right) \frac{m_e E_e}{E_\nu^2}\right]\,. \end{aligned} $

(4) For electric neutrino-electron scattering,
$ g_V = 1/2 + 2 e^2/g^2 $ and$ g_A = 1/2 $ . For$ \nu_\mu $ - and$ \nu_\tau $ -electron scattering,$ g_V = (-1/2+ 2 e^2/g^2) $ and$ g_A = -1/2 $ , where g is the weak gauge coupling. For anti-neutrino electron scattering, the corresponding cross sections can be obtained by replacing$ g_A $ with$ -g_A $ in Eq. (4).The resultant electron recoil spectrum caused by the neutrino flux from the féeton decay is shown by the red line in Fig. 2, along with those for the solar neutrinos of different channels. We observe that the spectrum for the féeton case is of the same order as that of
$ ^{8} $ B and almost three-orders-of-magnitude smaller than that of$ ^{7} $ Be.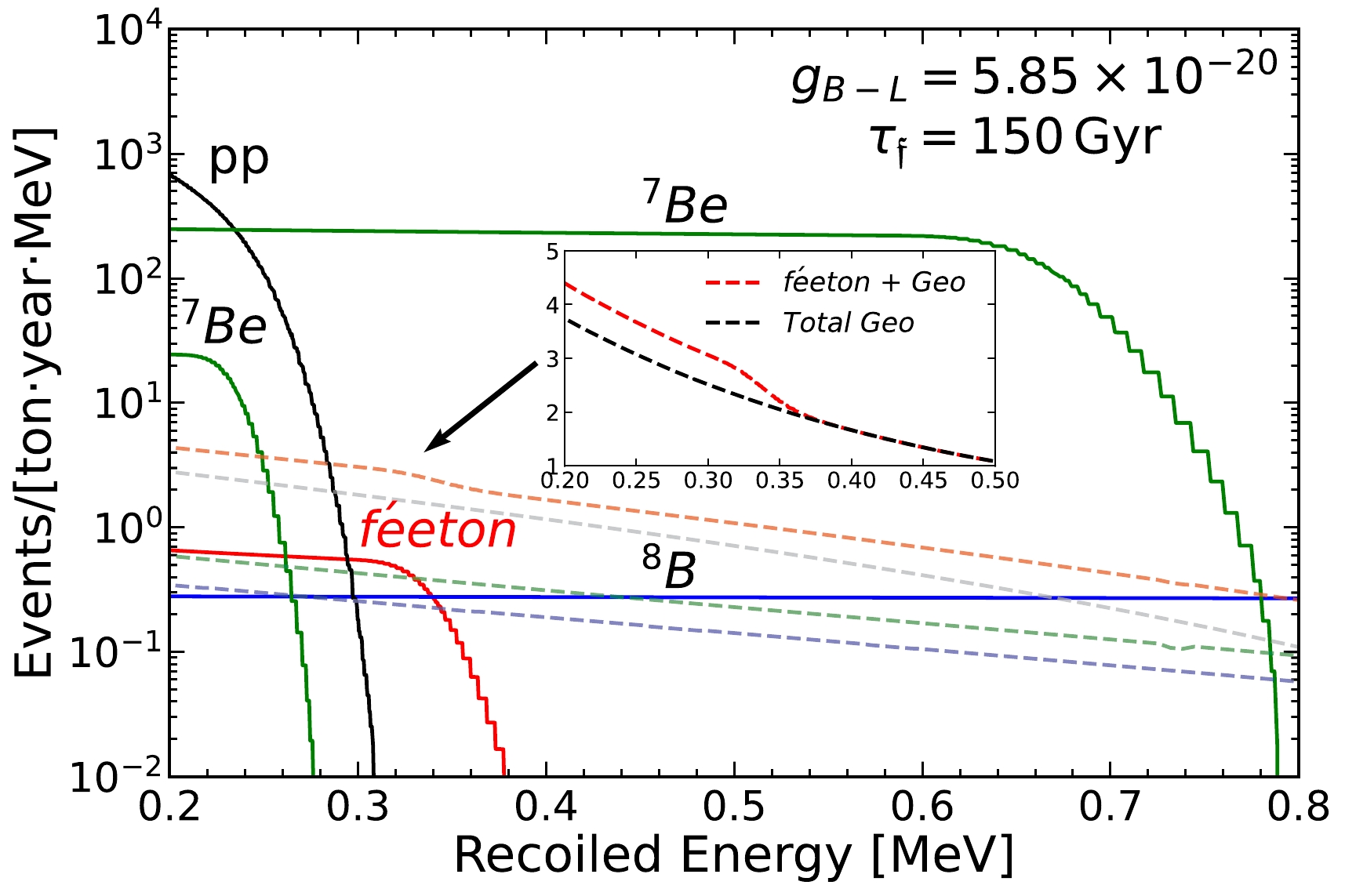
Figure 2. (color online) Electron recoil energy spectra caused by different neutrino sources. The red line shows the electron recoil spectrum for the maximum neutrino flux from féeton decay by assuming
$ \tau_{\mathfrak{f}} = 150 $ Gyr, which corresponds to$g_{B-L} = $ $ 5.85 \times 10^{-20}$ . The electron recoil spectrum from solar$ pp $ ($ ^7 $ Be,$ ^8 $ B) is shown as a black (green, blue) line. The geo-neutrino contribution from K (U, Th) decay is shown as a gray (green, blue) dashed line. The red-dashed curve shows the spectrum for the total geo-neutrinos plus féeton neutrinos. For comparison, the total geo-neutrino background is shown in the subfigure as a black dashed line.The most significant problem is the presence of several isotope decays inside the scintillators in low-energy solar neutrino experiments such as Borexino. For example, the beta decay of
$ ^{210} $ Po produces neutrinos whose energy range covers 511 keV and flux is$7 - 8$ orders of magnitude larger than the féeton neutrino flux [22, 23]. Removing such contamination is crucial for searching for the féeton neutrino flux. In this paper, we will not discuss the purification mechanism [24] of such isotopes and only assume that we can remove such background neutrinos at a sufficient level for the detection of the féeton neutrinos and discuss the possible discrimination of féeton signals from the solar neutrinos, primarily$ ^{7} $ Be neutrinos.Another problem is geo-neutrino contamination. Geo-neutrinos consist of electron-type anti-neutrinos produced by the beta decay of radionuclides, mostly
$ {}^{40} $ K,$ {}^{232} $ Th, and$ {}^{235} $ U, in the Earth [25]. Their energies range from$ 0.1 $ to$ 3 $ MeV. As the dashed lines in Fig. 2 show, the geo-neutrino contributions for the electron recoils are larger than that for the féeton neutrino. However, a Borexino-type experiment can still distinguish it through direction information.To mitigate the problems from the solar neutrinos and geo-neutrinos, one may utilize the direction dependence and time modulation of neutrino fluxes. The solar neutrino flux results from the sun, and our féeton neutrino flux is more concentrated toward the GC. Figure 3 shows the angular dependence of the féeton neutrino flux assuming the féeton DM distribution follows an NFW profile [17] in our galaxy, where θ is the angle between the line of sight and GC. The féeton neutrino flux from GC is the most intense and thus allows the highest directionality. In Fig. 3, we also include the uniform neutrino flux decayed from the extragalatic féeton DM.
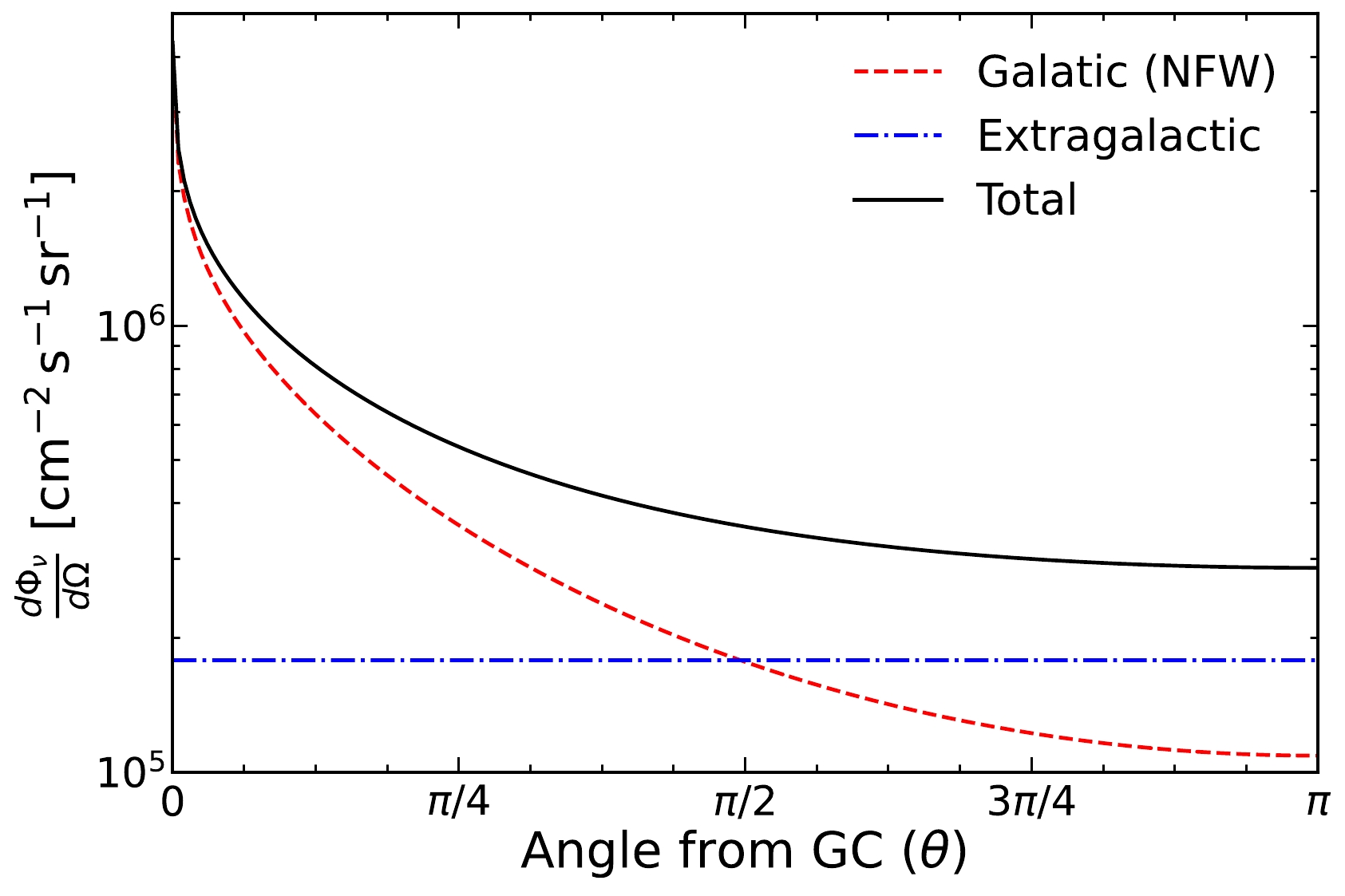
Figure 3. (color online) Angle distribution for the neutrino flux from féeton DM decay with mass
$ m_ \mathfrak{f} \simeq 2 m_e $ and coupling$ g_{\rm B-L} = 5.85 \times 10^{-20} $ . The red dashed line shows the Galactic contribution with NFW profile, and the blue dash-dotted line shows the extra-galactic contribution. Their combination is the black solid curve.Some recent solar neutrino detectors are already equiped with direction determination capability. For instance, the Borexino experiment combines both the water Cherenkov and liquid scintillator detectors, and it gathers the first directional measurement of sub-MeV solar neutrinos [26]. Light signals are produced via neutrinos scattering off electrons. For water Cherenkov detectors, if the recoil electron moves faster than the speed of light in water, the directional Cherenkov light is produced. Because the speed of light in water is approximately
$ v_c \simeq 0.75c $ , the kinetic energy of the recoil electron should be larger than$ E_e \simeq 0.5 m_e $ to produce Cherenkov lights. The corresponding minimum energy of the neutrino is$ 420\, $ keV. Thus, the energy of the féeton neutrinos is above the threshold, which enables us to determine direction via water Cherenkov detectors. In contrast, an electron with a kinetic energy of$ 0.5 m_e $ is relativistic. Such a large recoil energy can only be produced by an almost-forward scattering by a 511-keV neutrino. Therefore, for the féeton neutrino case, the direction of the recoil electron almost tracks the direction of the incoming neutrino.Because the Earth is orbiting the sun, the direction of the sun is changing while that of the GC is not. The sun and galaxy center have nearly opposite directions related to the Earth around June, which makes féeton neutrino flux the most distinguishable from the solar neutrinos in terms of direction. Similarly, geo-neutrinos emanate only from the inside of the Earth. Based on the GC location around June, a detector should be placed in the south hemisphere for the geo-neutrinos and féeton neutrinos from the GC region to be in opposite directions.
The above discusses the difference in the direction of each signal. However, the geo-neutrinos are much more diffuse than the solar neutrinos and are more difficult to eliminate using direction determination. Fortunately, the total geo-neutrino intensity is only several times larger than that of the féeton neutrinos. If the solar neutrino signal can be sufficiently identified and subtracted using direction determination, we can obtain the electron recoil spectrum for the total geo-neutrinos and féeton neutrinos, which we show by the red dashed curve in Fig. 3. We observe a characteristic kink at
$ \sim0.35 $ MeV. This feature at that specific energy is so far unique for all known neutrino sources. While some uncertainty exists in the geo-neutrino intensity, this feature persists in the otherwise smooth geo-neutrino electron-recoil spectrum as long as the 511-keV féeton neutrinos exist. Detecting such a kink would be a smoking gun to the 511-keV neutrinos and the féeton DM. -
Taking
$ m_ \mathfrak{f}\simeq 2m_e $ , the DM lifetime constraint sets an upper bound of$ g_{B-L}\lesssim6\times10^{-20} $ , as explained in Ref. [8]. In contrast, we still have a large parameter space on the lower bound of gauge coupling constant$ g_{B-L} $ , which is determined by the upper bound of the$ B-L $ breaking scale. Considering conservative upper bound$V_{B-L} < M_{Pl}$ , where$ M_{Pl}\simeq2.4\times10^{18} $ GeV is the reduced Planck mass, we obtain$ g_{B-L} \gtrsim2\times 10^{-22} $ using$ m_ \mathfrak{f}=2g_{B-L}V_{B-L} $ and$ m_ \mathfrak{f}\simeq2m_e $ .However, not all of the parameter space between
$ 6\times10^{-22}\lesssim g_{B-L}\lesssim2\times10^{-20} $ is equally motivated. Remarkably, observed neutrino mass$ m_{\nu} \simeq 0.05\, $ eV naturally predicts$ B-L $ breaking scale$ V_{B-L} $ to be$ O(10^{16}) $ GeV [27], provided that all the Yukawa coupling constants for third family right-handed neutrino$ N_3 $ such as$ h_3 $ are$ O(1) $ . Setting$ V_{B-L}\simeq10^{16} $ GeV and$ m_ \mathfrak{f}\simeq2m_e $ as required to explain the Galactic 511-keV gamma-ray excess, we obtain$ g_{B-L}\simeq 5 \times10^{-20} $ . Thus, the value of$ g_{B-L} $ we use in Sec. III.A is not merely an optimal coupling constant but also a very motivated one. More importantly, with these values of$ g_{B-L} $ and$ m_ \mathfrak{f} $ , we predict that the féeton DM lifetime to be$ \sim150 $ Gyr. This is very encouraging because it is already close to the cosmological constraint on the DM lifetime obtained with the cosmic background and large-scale-structure (LSS) probes [28–31]. Therefore, the féeton DM scenario proposed in this paper implies that the cosmological effects due to the féeton DM decay can soon be detected via cosmological probes with the near-future galaxy surveys such as LSST4 , DESI5 , Euclid6 , and WFIRST7 and the on-going mission JWST8 . -
In this paper, we showed a scenario in which the féeton is the dominant DM and consistently explains the observed magnitude of the Galactic 511-keV gamma-ray excess through the féeton DM decay into electrons and positrons. The scenario indicates the mass of the féeton as very close to
$ 2m_e $ ; thus, the electron and positron produced by féeton decay are highly non-relativistic. The injection kinetic energy of the positrons is less than$ 13.6 $ eV; therefore, they do not form positroniums via charge exchanges with neutral hydrogen atoms, which is often assumed in the literature. In contrast, we consider that they form positroniums with free electrons in ionized environments. Different from the previous cases [8, 9], the scenario in this study produces larger neutrino and anti-neutrino fluxes with an energy that is sufficiently high for direction determination with current solar neutrino experiments. Future solar neutrino experiments with improved angular resolution are promising for the detection of the neutrinos decaying from the féeton DM. The parameter space that is consistent with the high-scale seesaw mechanism also predicts that the féeton lifetime is close to the current cosmological constraint. Thus, this implies that the effects on the cosmic background evolution and LSS should be soon detected via near-future galaxy surveys.Because the produced positrons are highly non-relativistic, no higher-energy continuum in the gamma-ray excess may be produced as high-energy positrons fly through the Galactic medium. This provides another crucial test of the scenario. Future experiments, such as the Compton Spectrometer and Image (COSI) mission that aims at detecting the soft gamma-ray of
$0.2- 5\;$ MeV [32] will provide us strong constraints on the present féeton DM model.In this study, we assume that the féeton is the dominant component of the DM in the present Universe. Generally, producing the féeton in the early Universe appears to be challenging becasue its gauge coupling constant
$ g_{B-L} $ is extremely small. However, light gauge bosons$ \cal{V} $ can be produced abundantly during the inflation independent of the magnitude of their gauge coupling constant. Abundance$ \Omega_{\cal V} $ is given by [33]$ \begin{align} \Omega_{\cal V} \simeq 0.3 \left(\frac{m_{\cal V}}{6\times10^{-6}\,{\rm eV}} \right)^{1/2} \left(\frac{H_{\rm inf}}{10^{14}\,{\rm GeV}} \right)^2, \end{align} $

(5) where
$ m_{\cal V} $ and$ H_{\rm inf} $ are the mass of the gauge boson and the Hubble constant during inflation, respectively. With a féeton mass of$ m_{\mathfrak f} \simeq 1 $ MeV and setting$ \Omega_{\cal V}=\Omega_ \mathfrak{f}\simeq0.25 $ , we predict$ H_{\rm inf} \simeq 1.6\times 10^{11} $ GeV, which is a rather low-energy inflation. Recall that$ H_{\rm inf}\simeq2.6\,r^{1/2}\times10^{14} $ GeV assuming a slow-roll inflation [34], where r is the primordial tensor-to-scalar ratio. The ratio r is then predicted to be very low, i.e.,$ r\simeq4\times10^{-7} $ . Thus, if the next-generation Cosmic Microwave Background (CMB) experiments detect the primordial B-mode polarization, the above féeton DM production scenario would be falsified, and either the féeton is not the dominant DM or it is produced by other mechanisms [35].Finally, we give a general comment on the féeton DM hypothesis. Figure 4 shows different neutrino fluxes from the known sources in increasing order of energy [25]. It spans from the cosmic neutrino background (CNB) of
$ 10^{-6} $ eV to the atmospheric neutrino of$ 10^{12}\, $ eV. However, a blank exists between 0.1 eV and 1 keV. Although different from the scenario proposed in this paper, an interesting scenario would be for the féeton neutrino to be a candidate to fill the blank if the féeton mass is$ m_ \mathfrak{f} = 0.1 $ eV$- 1$ keV, which can be achieved with a low-energy seesaw mechanism. Taking$ m_{\mathfrak f} = 1\, $ eV for example, the neutrino contribution from the féeton decay is shown as the red solid curve in Fig. 4, whereas the anti-neutrino contribution with the same flux is shown as the dashed curve. An interesting search for the féeton neutrino is performed by the measurement of anti-neutrinos. An example has been proposed for the measurement of the cosmic anti-neutrino [36, 37]. It uses the capture of the electron-type anti-neutrino on the$ ^{163} $ Ho atom,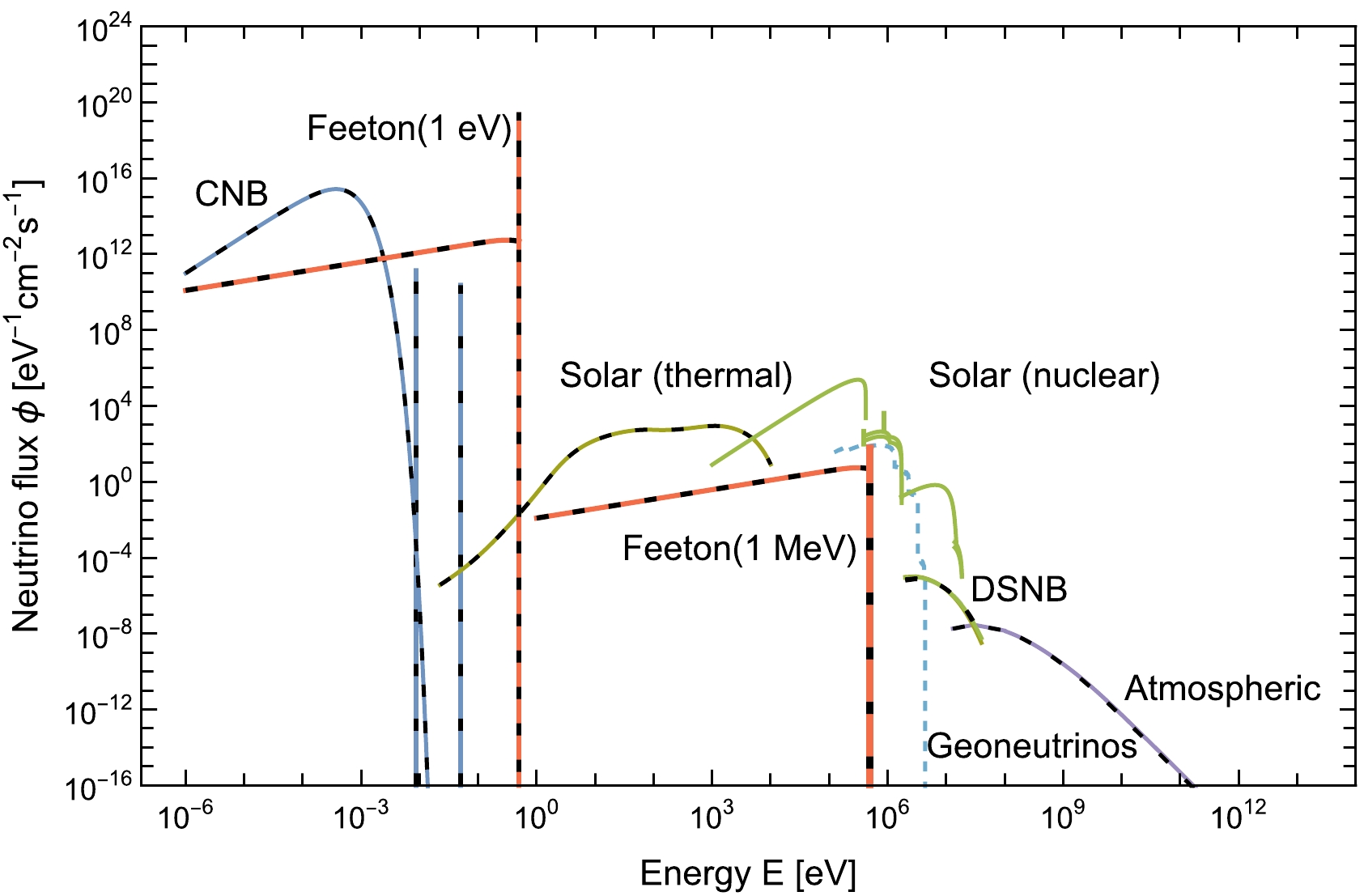
Figure 4. (color online) Energy spectra of neutrino flux from different sources with different colors [25]. Solid lines represent the neutrino flux, whereas dashed lines represent the anti-neutrino flux. Among them, the red lines show the neutrino flux from féeton decay with a féeton mass of
$ m_ \mathfrak{f} = 1\, $ eV and$ 1\, $ MeV. The galactic signal is a delta-line spectrum with a total flux of$ 3.5 \times 10^{12}\, $ cm$ ^{-2} $ s$ ^{-1} $ for$ m_ \mathfrak{f} = 1\, $ eV and$ 3.5 \times 10^{6}\, $ cm$ ^{-2} $ s$ ^{-1} $ for$ m_ \mathfrak{f} = 1\, $ MeV. We convolute the delta function spectrum from the 1 MeV féeton decay with the energy resolution of the Borexino experiment in the MeV region,$ \Delta E / E = 5 $ %. The continuous spectrum corresponds to the extra-galactic signal. Note that the two blue vertical lines correspond to the two heavy generations of neutrinos in the CNB.$ \begin{align} {\bar \nu_e} \; +\; ^{163}{\rm Ho} \rightarrow \; ^{163}{\rm Dy} \; +\; E_i, \end{align} $

(6) where
$ E_i $ is a binding energy from the de-excitation of the Dy atom. Based on the red dashed curve in Fig. 4, the integrated anti-neutrino flux from féeton decay with$ m_{\mathfrak f} \sim 1 $ eV is larger than that of the CNB. This means that the capture rate of the féeton anti-neutrino on$ ^{163} $ Ho is larger than that of the cosmic anti-neutrino. Therefore, the low-mass féeton can be tested in such experiments. Furthermore, it would be interesting to investigate if the féeton DM scenario can fit the recent observation of the$ 511\, $ -keV emission from dwarf spheroidal galaxies [38]; however, we will address this is a topic in future research. -
T. T. Y. thanks Shigeki Matsumoto for the discussion on the possible suppression of the electron-positron coupling of the feeton.
Féeton (B-L gauge boson) dark matter for the 511-keV gamma-ray excess and the prediction of low-energy neutrino flux
- Received Date: 2024-02-22
- Available Online: 2024-08-15
Abstract: The féeton is the gauge boson of the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: