-
The Event Horizon Telescope (EHT) Collaboration has published the images of supermassive black holes located at the center of the giant elliptical galaxy M87 [1–6] and the Milky Way Galaxy [7–12]. The brightness depression inside the bright asymmetric ring in the black hole image resolved by the EHT is highly likely to be a black hole shadow, which is caused by the absorption of light into the event horizon [13–16]. The black hole shadow contains valuable information about the compact object, making it a vital tool in the study of black holes for constraining black hole parameters [17–23], exploring fundamental physics issues such as dark matter [24–28], and testing various gravity theories [29–42]. Black hole shadows have also been investigated in previous studies [43–80].
Gravitational collapse can result in the emergence of a spacetime singularity. But the cosmic censorship conjecture demands that singularities should be hidden by event horizons. However, the cosmic censorship conjecture requires further verification. Thus, the observations of naked singularities play a crucial role in testing the cosmic censorship conjecture and are also significant for general relativity. In a black hole, the shadow appears because the light rays enter the event horizon, but its boundary is determined by the unstable photon sphere (PS). The PS is a region in space where photons can orbit the black hole in spherical orbits. It consists of both prograde and retrograde photon spherical orbits (PSOs). The prograde and retrograde light rings (LRs), representing the circular photon orbits in the equatorial plane, are the leftmost and rightmost orbits within the PS. If the PS is composed of a continuum of PSOs that connect the prograde and retrograde LRs, then this PS is complete. In general, a naked singularity cannot cast a shadow. However, numerous studies indicate that a naked singularity can indeed cast a shadow [43–45]. For some spherically symmetric naked singularities, the shadows are casted by the naked singularities themselves [44, 45]. For a rotating naked singularity, the unstable prograde LR is typically absent, resulting in an incomplete unstable PS, which gives rise to the appearance of an arc-shaped shadow [17, 46]. Due to the Kerr naked ring singularity, the light rays can pass through the inside of the singular ring (the other world
$ r<0 $ ), leading to a dark spot emerging in the image of the Kerr naked singularity [17]. When observed on the equatorial plane, a black straight line will emerge in the image of the Kerr naked singularity because the light rays hit on the ring singularity [17].In this study, we mainly research the LRs, PSs, and images of Konoplya-Zhidenko naked singularities. The Konoplya-Zhidenko metric describes an asymptotically flat, stationary, and axisymmetric spacetime beyond General Relativity by adding a static deformation from the Kerr spacetime, which sharply modifies the structures of spacetime in the strong-field region [81]. The effects of the deformation parameter on the quasinormal modes and superradiance of the Konoplya-Zhidenko black hole were investigated in Refs. [82, 83]. The PS and LR are closely related to the ringdown stage and the shadow of the black hole. In the Konoplya-Zhidenko naked singularity spacetime, both prograde and retrograde unstable LRs could exist, leading to the presence of a complete unstable PS. Furthermore, both prograde and retrograde stable LRs could also exist in this spacetime, and so does the complete stable PS. This will lead to novel results for the shadow of the Konoplya-Zhidenko naked singularity.
The paper is organized as follows. In Section II, we briefly introduce the spacetime of the Konoplya-Zhidenko naked singularity and describe in detail the unstable and stable as well as retrograde and prograde LRs. In Section III, we present the ring-shaped and arc-shaped shadows cast by the Konoplya-Zhidenko naked singularity and discuss the influence of the naked singularity parameters and observer's inclination angle on its shadow. Finally, we present a conclusion. In this paper, we employ the geometric units
$ G=c=M=1 $ . -
The Konoplya-Zhidenko spacetime describes an asymptotically flat, stationary, and axisymmetric spacetime that deviates from the Kerr one by adding an extra deformation [81]. The metric of the Konoplya-Zhidenko spacetime is described as follows:
$ \begin{aligned}[b] {\rm d}s^{2} =\;& -\left(1-\frac{2Mr+\frac{\eta}{r}}{\rho^{2}}\right){\rm d}t^{2}+\frac{\rho^{2}}{\Delta}{\rm d}r^{2}+\rho^{2} {\rm d}\theta^{2}\\&+\sin^{2}\theta\bigg[r^{2}+a^{2}+\frac{2(M+\frac{\eta}{2r^{2}})ra^{2}\sin^{2}\theta}{\rho^{2}}\bigg]{\rm d}\phi^{2}\\ &-\frac{4(M+\frac{\eta}{2r^{2}})ra\sin^{2}\theta}{\rho^{2}}{\rm d}t{\rm d}\phi, \end{aligned} $

(1) where
$ \Delta=a^{2}+r^{2}-2Mr-\frac{\eta}{r},\;\;\;\;\;\;\;\;\;\; \rho^{2}=r^{2}+a^{2}\cos^{2}\theta. $

(2) Here, M is the mass of a Konoplya-Zhidenko compact object, a is the rotation parameter, and η is the deformation parameter describing the deformation from the Kerr spacetime. When
$ \eta=0 $ , the metric will reduce to the usual Kerr metric. The position of the event horizon can be defined by$ \Delta=0 $ [47, 48, 82, 83]. The condition for the existence of the event horizon is$ \eta >-\frac{2}{27}(\sqrt{4M^{2}-3a^{2}}+2M)^{2}(\sqrt{4M^{2}-3a^{2}}-M),\; {\rm for} \;|a|< M, $

(3) $ \eta >0,\qquad {\rm for} \;\;\;|a|\geq M. $

(4) On the
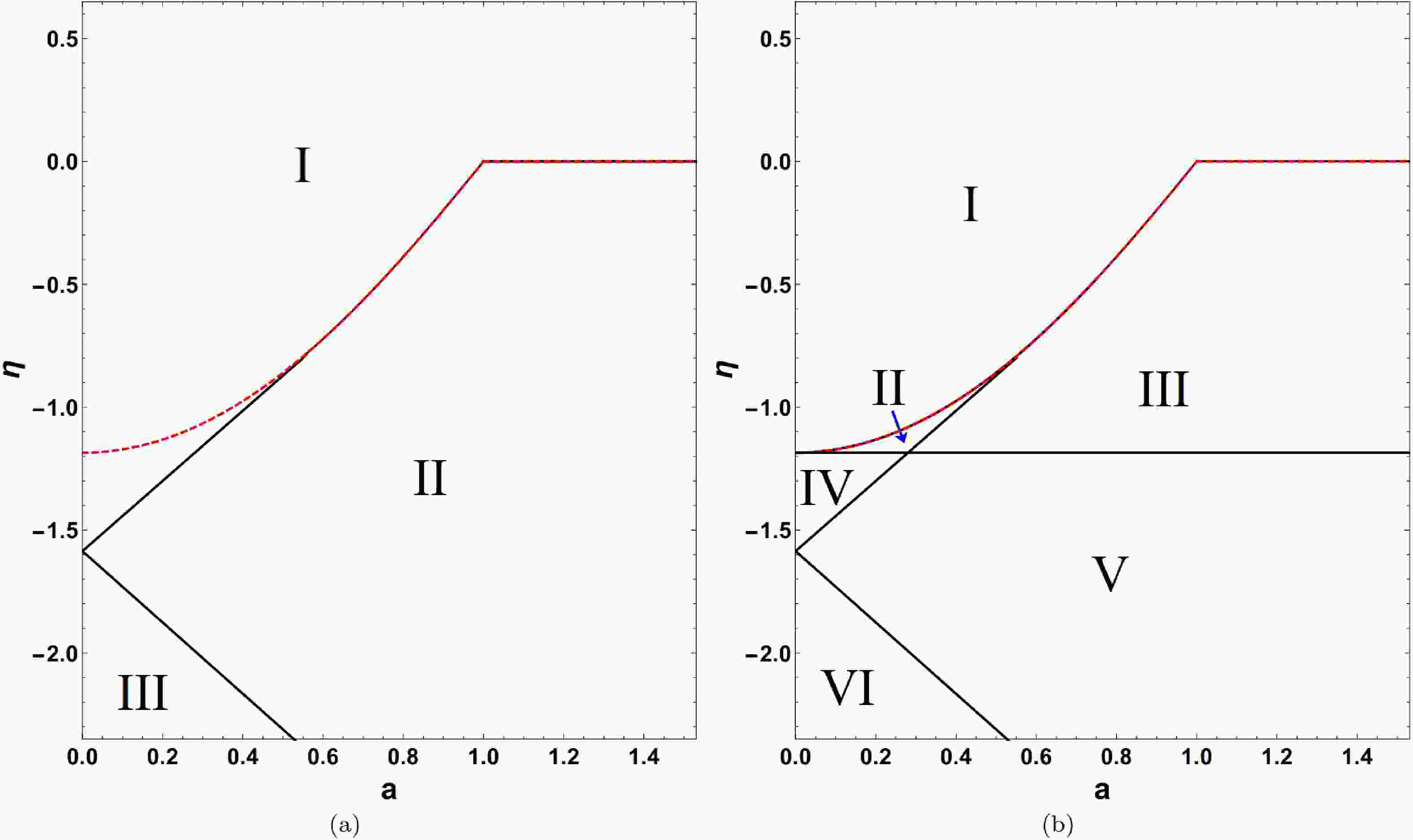
$ (a, \eta) $ plane, the region of existence of the event horizon is the area above the red dashed curve in Fig. 1. Compared with that of the Kerr black hole, the deformation parameter η extends the allowed range of the rotation parameter a. It allows$ |a|\geq M $ for$ \eta>0 $ .
Figure 1. (color online) The region of existence of the event horizon is the area above the red dashed curve. (a) Dependence of the existence of unstable light rings (LRs) on the rotation parameter a and deformation parameter η. In Region I, both the prograde and retrograde unstable LRs exist. In Region II, only the unstable retrograde LR appears. In Region III, neither the prograde nor retrograde unstable LR exists. (b) Dependence of the existence of stable LRs on a and η. In Region I and VI, neither the prograde nor the retrograde stable LR appears. In Region II, two stable prograde LRs exist. In Region III, one stable prograde LR exists. In Region IV, both the prograde and retrograde stable LRs appear. In Region V, only one stable retrograde LR exists.
The Hamiltonian of a photon propagation in the Konoplya-Zhidenko spacetime can be characterized by
$ H(x,p)=\frac{1}{2}g^{\mu\nu}(x)p_{\mu}p_{\nu}=\frac{1}{2\rho^{2}}(p_{\theta}^{2}+\Delta p_{r}^{2}+V_{\rm eff})=0, $

(5) where the effective potential
$V_{\rm eff}$ is defined as$ V_{\rm eff}=-\frac{1}{\Delta}[a L_{z}-(r^{2}+a^{2})E]^{2}+\left(\frac{L_{z}}{\sin\theta}-aE\sin\theta\right)^{2}. $

(6) The energy E and z-component of the angular momentum
$ L_{z} $ of a photon are two conserved quantities with the following forms:$ E=-p_{t}=-g_{tt}\dot{t}-g_{t\phi}\dot{\phi},\quad L_{z}=p_{\phi}=g_{\phi\phi}\dot{\phi}+g_{\phi t}\dot{t}.$

(7) The variables r and θ in the Hamiltonian (5) can be separated, and thus, the null geodesic equations can be written as
$ R(r)=\Delta^{2} p_{r}^{2}=[aL_{z}-(r^{2}+a^{2})E]^{2}-\Delta K, $

(8) $\Theta= p_{\theta}^{2}=K-\frac{1}{\sin^{2}\theta}(L_{z}-aE\sin^{2}\theta)^{2}, $

(9) where the quantity K is the constant of separation associated with the hidden symmetries of the spacetime.
The PS is closely associated with the shadows of compact objects. It satisfies
$ \dot{r}=0 $ and$ \ddot{r}=0 $ , which is equivalent to$ \begin{aligned}[b] R(r)=\;&[aL_{z}-(r^{2}+a^{2})E]^{2}-\Delta K=0,\\ R'(r)=\;&4Er[(r^{2}+a^{2})E-aL_{z}]-2K\left(r-M+\frac{\eta}{2r^{2}}\right)=0. \end{aligned} $

(10) Two conserved parameters are introduced, the impact parameter ξ and σ, as follows:
$ \xi=\frac{L_{z}}{E},\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sigma=\frac{K}{E^{2}}. $

(11) Solving Eq. (10), the constants ξ and σ of the spherical photon motion have the form
$ \xi=\frac{a^2 \left(\eta-2M r^{2}-2r^{3}\right)+6 M r^4+5 \eta r^2-2 r^5}{a \left(2 r^3 -2M r^2+\eta\right)}, $

(12) $ \sigma=\frac{16 r^5 \left(r^{3}+a^{2}r-2Mr^{2}-\eta\right)}{\left(2 r^3 -2M r^2+\eta\right)^2}. $

(13) $ R''(r)>0 $ represents the unstable photon spherical orbit (UPSO).$ R''(r)<0 $ represents the stable photon spherical orbit (SPSO). Θ must be non-negative, which is deduced from Eq. (9). By substituting the constants ξ (12) and σ (13) of the spherical photon motion into Eq. (9), one can obtain$ \begin{aligned}[b] \Theta_{s} =\;&\sigma-\frac{1}{\sin^{2}\theta}(\xi-a\sin^{2}\theta)^{2}\\ =\;&\frac{16 r^5 \left(r^{3}+a^{2}r-2Mr^{2}-\eta\right)}{\left(2 r^3 -2M r^2+\eta\right)^2}-\frac{1}{\sin^{2}\theta}\\&\times\bigg[\frac{a^2 \left(\eta-2M r^{2}-2r^{3}\right)+6 M r^4+5 \eta r^2-2 r^5}{a \left(2 r^3 -2M r^2+\eta\right)}-a\sin^{2}\theta\bigg]^{2}. \end{aligned} $

(14) The condition
$ \Theta_{s}\geq 0 $ gives the region of the PS.$ \Theta_{s}=0 $ denotes the boundary of the PS, which consequently defines the silhouette of the black hole shadow. The LR is given by$\begin{aligned}[b] \Theta_{s}\big|_{\theta=\frac{\pi}{2}}=\;&\frac{16 r^5 \left(r^{3}+a^{2}r-2Mr^{2}-\eta\right)}{\left(2 r^3 -2M r^2+\eta\right)^2}\\&-\bigg[\frac{a^2 \left(\eta-2M r^{2}-2r^{3}\right)+6 M r^4+5 \eta r^2-2 r^5}{a \left(2 r^3 -2M r^2+\eta\right)}-a\bigg]^{2}\\=\;&0. \\[-20pt]\end{aligned}$

(15) The radius
$ r_{c} $ of LRs can be determined by Eq. (15), and its value depends on the rotation parameter a and deformation parameter η. For rotating black holes, two LRs with different radii typically exist: one rotating in the same direction as the compact object's rotation and the other rotating in the opposite direction. The radius$ r_{c} $ of the unstable prograde LR is smaller, with a positive impact parameter ξ, corresponding to the leftmost point of the PS and black hole shadow. In contrast, the unstable retrograde LR has a larger$ r_{c} $ and a negative ξ, corresponding to the rightmost point of the PS and black hole shadow. Therefore, the unstable prograde and retrograde LRs are crucial for the existence of a complete unstable PS and black hole shadow.Figure 1(a) exhibits the dependence of the existence of the unstable LR on the rotation parameter a and deformation parameter η. In Fig. 1(a), the
$ (a, \eta) $ plane is divided into three regions by black curves: Regions I, II, and III. In Region I, both the prograde and retrograde unstable LRs exist; in Region II, only the unstable retrograde LR appears, whereas in Region III, neither the prograde nor the retrograde unstable LR exists. Due to the fact that the prograde and retrograde LRs are the leftmost and rightmost orbits within the PS, they are essential for a complete PS. Through our research, we found that the complete unstable PS exists only in Region I, whereas the unstable PSs in other regions are incomplete. When the event horizon exists in the Konoplya-Zhidenko spacetime (above the red dashed curve in Region I), both the prograde and retrograde unstable LRs exist, and so does the complete unstable PS. However, in Region I, there is an area (below the red dashed curve in Region I) where the event horizon does not exist, yet the complete unstable PS can still exist. Figure 1(b) exhibits the dependence of the existence of stable LRs on a and η. In Fig. 1(b), six regions (I−VI) divided by black curves can be observed. In Regions I and VI, neither the prograde nor retrograde stable LR exists, which indicates that the stable LR cannot exist for the Konoplya-Zhidenko black hole. Only two stable prograde LRs exist in Region II, and one stable prograde LR appears in Region III. In Region IV, both the prograde and retrograde stable LRs exist. In Region V, only one stable retrograde LR exists. For the stable PS, we found that the complete stable PS exists only in Region IV, whereas the stable PSs in other regions are incomplete. -
To calculate the shadow of a compact object, the celestial coordinates must be established in the observer's sky. In Refs. [32, 48–56], we calculate the celestial coordinates in an axially symmetric spacetime as
$ \begin{aligned}[b] & x=-r\frac{p^{\hat{\phi}}}{p^{\hat{r}}}\Big|_{(r_{o},\theta_{o})}, \\ & y=r\frac{p^{\hat{\theta}}}{p^{\hat{r}}}\Big|_{(r_{o},\theta_{o})}, \end{aligned} $

(16) where
$ p^{\hat{\mu}} $ denotes the four-momentum of photons measured locally by the observer at ($ r_{o}, \theta_{o} $ ). The locally measured four-momentum$ p^{\hat{\mu}} $ can be expanded using the four-momentum$ p^{\mu} $ of a photon as follows [14, 32, 48–62] :$ \begin{aligned}[b] p^{\hat{t}} =&\sqrt{\frac{g_{\phi \phi}}{g_{t\phi}^{2}-g_{tt}g_{\phi \phi}}} E-\frac{g_{t\phi}}{g_{\phi\phi}}\sqrt{\frac{g_{\phi \phi}}{g_{t\phi}^{2}-g_{tt}g_{\phi \phi}}}L_{z}, \\ p^{\hat{r}} =&\frac{1}{\sqrt{g_{rr}}}p_{r},\;\;\;\;\; p^{\hat{\theta}}=\frac{1}{\sqrt{g_{\theta\theta}}}p_{\theta},\;\;\;\;\; p^{\hat{\phi}}=\frac{1}{\sqrt{g_{\phi\phi}}}L_{z}, \end{aligned} $

(17) The image points in the boundary of the black hole shadow correspond to the light rays that spiral asymptotically toward the unstable PS. By substituting the constants ξ and σ of the PS (12, 13) into the celestial coordinates (16) and taking the limit as
$ r_{o} $ approaches$ \infty $ , one can derive the analytic expressions for the silhouette of the Konoplya-Zhidenko compact object shadow [14, 32, 48–62],$ \begin{aligned}[b] x =&-\frac{\xi}{\sin \theta_{o}}, \\ y =&\pm\sqrt{\sigma+2a\xi-\xi^{2}\csc^{2}\theta_{o}-a^{2}\sin^{2}\theta_{o}}. \end{aligned} $

(18) Figure 2 displays the shadows of the Konoplya-Zhidenko compact object under various scenarios depicted in Fig. 1. The red lines represent the unstable PSs composed of UPSOs, and the purple dashed lines represent the stable PSs composed of SPSOs, which are plotted using analytical methods based on Eq. (18). In Fig. 2(a) and (b),
$ a=1.1 $ ,$ \eta=0.2 $ and$ a=1.15 $ ,$ \eta=0.15 $ , respectively. In these cases, both an event horizon and unstable PS exist, meaning that the light rays entering the unstable PS will eventually reach the event horizon. Therefore, the shadow of the Konoplya-Zhidenko black hole corresponds to the area enclosed by the unstable PS (the red circle). Figure 2(b) displays three branches of UPSOs and two branches of SPSOs. However, this is only a subset of the UPSOs that define the shadow's boundary, leading to the distinctive cusp-shaped shadow of the Konoplya-Zhidenko black hole, as we have researched in Ref. [48]. This phenomenon is further illustrated in Figs. 3, 4, and 5, with a detailed discussion. Figure 2(c), (d), (e), and (f) exhibit the shadows of the Konoplya-Zhidenko naked singularity. In Fig. 2(c) and (d),$ a=0.1 $ ,$ \eta=-1.3 $ and$ a=0.27 $ ,$ \eta=-1.13 $ , respectively. Differing from the Kerr naked singularity, in these scenarios, not only an unstable retrograde LR but also an unstable prograde LR exists, enabling the formation of a complete unstable PS. However, due to the absence of the event horizon, the area enclosed by the unstable PS is not the dark shadow. The shadow of the Konoplya-Zhidenko naked singularity is only the image of the unstable PS, shown as a ring-shaped shadow (the red circle). Furthermore, we show this ring-shaped shadow of the Konoplya-Zhidenko naked singularity in Fig. 6 using the backward ray-tracing method [14, 32, 48–62]. In the cases of$ a=1.1 $ ,$ \eta=-0.2 $ (shown in Fig. 2(e)) and$ a=0.2 $ ,$ \eta=-1.5 $ (shown in Fig. 2(f)), the absence of the unstable prograde LR results in an incomplete unstable PS, leading to the formation of an arc-shaped shadow (the red curve). In the Konoplya-Zhidenko black hole spacetime, the stable LR is absent. However, SPSOs may appear, as can be observed in the case of$ a=1.15 $ and$ \eta=0.15 $ (Fig. 2(b)). In contrast, in the Konoplya-Zhidenko naked singularity spacetime, the stable LR could exist. For the case of$ a=0.1 $ and$ \eta=-1.3 $ (shown in Fig. 2(c)), both prograde and retrograde stable LRs exist, resulting in the presence of a complete stable PS. The purple dashed ellipse in Fig. 2(c) represents the image of the complete stable PS. As a increases, we find that the ellipse becomes more elongated and shifts to the right owing to the drag effect. Nevertheless, due to the stability of the photon orbits in the stable PS, the observers cannot perceive the image of the stable PS. Therefore, we did not further investigate the stable PS. When$ a=0.27 $ and$ \eta=-1.13 $ (shown in Fig. 2(d)), there are two stable prograde LRs and two branches of SPSOs. For the case of$ a=1.1 $ and$ \eta=-0.2 $ (shown in Fig. 2(e)), one stable prograde LR and three branches of SPSOs emerge. When$ a=0.2 $ and$ \eta=-1.5 $ (shown in Fig. 2(f)), only one stable retrograde LR and one branch of SPSO exist.
Figure 2. (color online) Figures (a) and (b) represent the shadows (area enclosed by the red lines) of the Konoplya-Zhidenko black hole, whereas Figures (c), (d), (e), and (f) depict the shadows (the red lines) of the Konoplya-Zhidenko naked singularity. The red lines represent the unstable photon spheres (PSs) composed of unstable photon spherical orbits (UPSOs), and the purple dashed lines represent the stable PSs composed of stable photon spherical orbits (SPSOs).

Figure 3. (color online) Cusp shadow for the Konoplya-Zhidenko black hole with
$ a=1.15 $ and$ \eta=0.15 $ . The red and magenta dashed curves represent UPCOs; the purple dashed curve represents SPCOs.
Figure 4. (color online) Continua of UPCOs and SPCOs for
$ a=1.15 $ and$ \eta=0.15 $ on the ($ r, \theta $ ), ($ \xi, \theta $ ), and ($ r, \xi $ ) planes.
Figure 5. (color online) Photon trajectories corresponding to the pixels
$ A, B, F, G, H, I, J, K, L, M, N, O, P, Q, R, S $ in Fig. 3. The blue line represents the event horizon of the Konoplya-Zhidenko black hole, and the dark area represents the forbidden region for photons ($V_{\rm eff} > 0$ ).
Figure 6. (color online) Image of the Konoplya-Zhidenko naked singularity with
$ a=0.1 $ and$ \eta=-1.3 $ . The red dashed circle represents the shadow (the complete unstable PS composed of UPSOs); the purple dashed circle represents the image of the complete stable PS composed of SPSOs.Figure 3 shows the cusp shadow for the Konoplya-Zhidenko black hole with
$ a=1.15 $ and$ \eta=0.15 $ using the backward ray-tracing method [14, 32, 48–62]. In the backward ray-tracing method, the light rays are assumed to evolve backward in time from the observer by solving the null geodesic equations numerically. Here, we set the observer at$ r_{o}=50, \theta_{o}=\pi/2 $ . The spherical background light source is the same as that we set in Refs. [49–54], with a radius of$ r_{s}=50 $ . In Fig. 3, the black area is the Konoplya-Zhidenko black hole shadow, and the bright area is the image of the background light source. The red and magenta dashed curves represent UPCOs; the purple dashed curve represents SPCOs, which are plotted using Eq. (18). The UPCOs can form a complete unstable PS to determine the boundary of the black hole shadow. It can be observed that the shadows obtained through numerical and analytical methods are consistent. Figure 4(a), (b), and (c) show these UPCOs and SPCOs on the ($ r, \theta $ ), ($ \xi, \theta $ ), and ($ r, \xi $ ) planes, respectively. D represents the unstable prograde LR, giving rise to a continuum of UPCOs marked as$ D-I-L-N $ . R represents the unstable retrograde LR, giving rise to a continuum of UPCOs$ R-P-S-G-E $ . Moreover, there is another continuum of UPCOs$ C-B $ and two continua of SPCOs$ C-A $ and$ E-F $ . These UPCOs and SPCOs, labeled with capital letters, are also marked in the black hole image (Fig. 3). It is shown that only the continua of UPCOs$ D-I-L $ and$ R-P-S $ determine the boundary of the black hole shadow. These UPCOs can form a complete unstable PS$ D-I-L(S)-P-R $ . One can find that each UPSO or SPSO has an invariant radial coordinate r and oscillating angular coordinate θ with respect to$ \pi/2 $ . These photon trajectories are shown in Fig. 5. Figure 5(a) shows the SPCO A and UPCO B. SPCO A is stable, so it does not enter the black hole nor escape to infinity. Although UPCO B can enter the black hole, it is isolated from the distant observers, so it is unrelated to the black hole shadow observed by observers. In Fig. 5(b), one can find the UPCOs$ G, I $ and SPCO F. However, only UPCO I determines the boundary of the shadow, as it has a smaller passing angle$ \Delta\theta $ , as illustrated in Fig. 5(b). The light rays that can pass through UPCO G but not through UPCO I are still unable to become part of the shadow, such as the light ray H in Fig. 5(b). The light ray J passes through UPCO I, and enters the black hole, becoming part of the shadow. The lights H and J also are marked in Fig. 3. In Fig. 5(c), one can find the UPCOs$ L, S $ , and SPCO K. UPCOs L and S have the same passing angle$ \Delta\theta $ , but UPCO L is on the outer layer (has a larger radial coordinate r). Light rays$ L' $ and$ L'' $ both reach UPCO L, but light ray$ L' $ passes through UPCO L, becoming part of the shadow, whereas light ray$ L'' $ does not pass through UPCO L, escaping to infinity. In Fig. 5(d), one can find the UPCOs$ P, N $ , and SPCO M. Only UPCO P determines the boundary of the shadow because it determines a smaller passing angle$ \Delta\theta $ . Light ray Q passes through UPCO P and becomes part of the shadow. Light ray O does not pass through UPCO P and escapes to infinity. Lights Q and O also are marked in Fig. 3.Using analytical methods, we have computed the images of a complete PS for the Konoplya-Zhidenko naked singularity, as shown in Fig. 2(c) and (d). Similar to the PS for a black hole, it is also a circle. Thus, it is easy to mistakenly perceive the interior region of the PS as the shadow. Therefore, we plot the shadow of the Konoplya-Zhidenko naked singularity with
$ a=0.1 $ ,$ \eta=-1.3 $ using the backward ray-tracing method [14, 32, 48–62] in Fig. 6. It can be observed that in Fig. 6, no dark disk shadow is present; instead, an infinite number of relativistic Einstein rings appear [84], as indicated by the red dashed circle. It is, in fact, the image of the unstable PS, resulting from light rays spiraling toward the unstable PS from various directions and eventually reaching the observer. The purple dashed circle in Fig. 6 indicates the presence of a complete stable PS, which cannot be observed in the image of the Konoplya-Zhidenko naked singularity. Figure 7(a), (b), and (c) show the complete unstable and stable PSs on the ($ r, \theta $ ), ($ \xi, \theta $ ), and ($ r, \xi $ ) planes, respectively. The complete unstable PS is composed of a continuum of UPSOs, marked as$ C-E-H-K $ , where C and K represent the unstable prograde and retrograde LRs. The complete stable PS is composed of a continuum of SPSOs marked as$ A-B-D-G-J-L $ , where A and L represent the stable prograde and retrograde LRs. These UPSOs and SPSOs, labeled with capital letters, are also marked in the image of the Konoplya-Zhidenko naked singularity (Fig. 6). One can find that SPSOs have smaller radii than UPSOs. Figure 8 exhibits the photon trajectories corresponding to the pixels$A,\; B,\; C,\; D,\; E,\; F,\; G, H,\; I,\; J,\; K$ , and L in Fig. 6, where the dark area represents the forbidden region for photons ($ V_{\rm eff}>0 $ ). In Fig. 8(a) and (f), A and L are the stable prograde and retrograde LRs with impact parameter$ \xi=5.04 $ and$ -9.1 $ , respectively. In Fig. 8(b) and (e), C and K are the unstable prograde and retrograde LRs with impact parameter$ \xi=4.42 $ and$ -4.95 $ , respectively. In Fig. 8(b)−(e),$ B, D, G $ , and J represent SPSOs, and E and H represent UPSOs. In Fig. 8(c) and (d), the light rays F and I pass through UPSOs E and H, respectively, meaning that they enter the PS, but then they turn back, escaping to infinity.
Figure 7. (color online) The unstable PS composed of UPSOs and stable PS composed of SPSOs for
$ a=0.1 $ and$ \eta=-1.3 $ on the ($ r, \theta $ ), ($ \xi, \theta $ ), and ($ r, \xi $ ) planes.
Figure 8. (color online) Photon trajectories corresponding to the pixels
$ A, B, C, D, E, F, G, H, I, J, K, L $ in Fig. 6. The dark area represents the forbidden region for photons ($V_{\rm eff} > 0$ ).Figure 9 illustrates the variations of the shadows of the Konoplya-Zhidenko naked singularity with respect to the spin parameter a under various scenarios. The solid lines represent the shadows (the unstable PSs), and the dashed lines represent the images of the stable PSs composed of SPSOs. Regardless of whether it is a ring- or arc-shaped shadow, they both shift gradually to the right as a increases, similar to the shadow of the Kerr black hole. In Fig. 9(a) and (d), the image of the stable PS also shifts to the right as a increases. In Fig. 9(b) and (c), one branch of the SPSOs shifts to the right, whereas the other shifts to the left as a increases. Figure 10 illustrates the variation in the shadows of the Konoplya-Zhidenko naked singularity with respect to the deformation parameter η under various scenarios. In Fig. 10(a) and (b), the ring-shaped shadow exhibits almost no change with η. In Fig. 10(c) and (d), the arc-shaped shadow gradually becomes smaller as
$ |\eta| $ increases. The image of the stable PS becomes smaller as$ |\eta| $ increases in Fig. 10(a) and (d). One branch of the SPSOs shifts to the right, while the other shifts to the left as$ |\eta| $ increases in Fig. 10(b) and (c).
Figure 9. (color online) Variations of the shadows of the Konoplya-Zhidenko naked singularity with respect to spin parameter a under various scenarios. The solid lines represent the shadows (the unstable PSs), and the dashed lines represent the images of the stable PSs composed of SPSOs.

Figure 10. (color online) Variations of the shadows of the Konoplya-Zhidenko naked singularity with respect to the deformation parameter η under various scenarios. The solid lines represent the shadows (the unstable PSs), and the dashed lines represent the images of the stable PSs composed of SPSOs.
Figure 11 illustrates the variation of the shadows of the Konoplya-Zhidenko naked singularity with respect to the observer's inclination angle
$ \theta_{o} $ under various scenarios. The solid lines represent the shadows (the unstable PSs), and the dashed lines represent the images of the stable PSs composed of SPSOs. In Fig. 11(a), both the ring-shaped shadow and the image of the complete stable PS shift to the right as$ \theta_{o} $ increases, and the latter becomes larger. In Fig. 11(b), the ring-shaped shadow also shifts to the right as$ \theta_{o} $ increases, and the image of the complete stable PS transforms to represent two branches of SPSOs as$ \theta_{o} $ increases. In Fig. 11(c) and (d), the arc-shaped shadow shifts to the right and enlarges as$ \theta_{o} $ increases. However, no shadow emerges when$ \theta_{o}=0 $ . The image of the incomplete stable PS transforms into three branches of SPSOs as$ \theta_{o} $ increases in Fig. 11(c) and enlarges as$ \theta_{o} $ increases in Fig. 11(d).
Figure 11. (color online) Variations in the shadows of the Konoplya-Zhidenko naked singularity with respect to the observer's inclination angle
$ \theta_{o} $ under various scenarios. The solid lines represent the shadows (the unstable PSs), and the dashed lines represent the images of the stable PSs composed of SPSOs. -
We study the shadows of the Konoplya-Zhidenko naked singularity. In the spacetime of the Konoplya-Zhidenko naked singularity, not only the unstable retrograde LR but also the unstable prograde LR exists, leading to the formation of a complete PS. Due to the absence of an event horizon, a dark disc-shaped shadow does not appear; instead, a ring-shaped shadow is observed. This occurs because the light rays passing through the unstable PS eventually escape to infinity. Furthermore, we calculate the image of the Konoplya-Zhidenko naked singularity using the backward ray-tracing method and find that the ring-shaped shadow appears as an infinite number of relativistic Einstein rings. For some parameter values (such as
$a=1.1,\; \eta=-0.2$ or$a=0.2, \eta=-1.5$ ), only the unstable retrograde LR exists, resulting in an incomplete unstable PS and thus giving rise to the arc-shaped shadow for the Konoplya-Zhidenko naked singularity. The shadow of the Konoplya-Zhidenko naked singularity gradually shifts to the right as the rotation parameter a increases and gradually becomes smaller as the deformation parameter$ |\eta| $ increases. Moreover, stable LRs and SPSOs can exist in the Konoplya-Zhidenko naked singularity spacetime, but they have no effect on the image of the naked singularity. This study demonstrates that a rotating naked singularity can exhibit not only an arc-shaped shadow but also a ring-shaped shadow.
The ring-shaped shadow of a rotating naked singularity with a complete photon sphere
- Received Date: 2024-03-07
- Available Online: 2024-10-15
Abstract: We investigate the shadows of the Konoplya-Zhidenko naked singularity. In the spacetime of the Konoplya-Zhidenko naked singularity, not only an unstable retrograde light ring (LR) but also an unstable prograde LR exists, leading to the formation of a complete photon sphere (PS). Due to the absence of an event horizon, a dark disc-shaped shadow does not appear; instead, a ring-shaped shadow is observed. The ring-shaped shadow appears as an infinite number of relativistic Einstein rings in the image of the naked singularity. For some parameter values, only the unstable retrograde LR exists, resulting in an incomplete unstable PS and thus giving rise to an arc-shaped shadow for the Konoplya-Zhidenko naked singularity. The shadow of the Konoplya-Zhidenko naked singularity gradually shifts to the right as the rotation parameter a increases and gradually becomes smaller as the deformation parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: